Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами. Практика
Подготовка к ЕГЭ по математике
Эксперимент
Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами.
Практика
Конспект урока
Пример №1. Упростить выражение: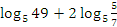 
.
Для решения воспользуемся свойством: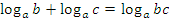 
.
Рассмотрим несколько способов решения:
1 способ:
.
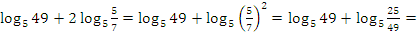
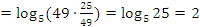2 способ:
.
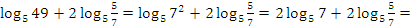
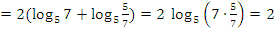3 способ:
.
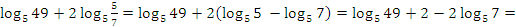
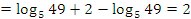Пример №2.(Типовое задание B7) Упростить выражение: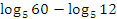 
.
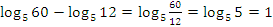Пример №3. Упростить выражение: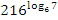 
.
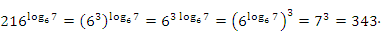
Пример №4. Упростить выражение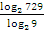 
.
Рассмотрим несколько способов решения:
1 способ:
.
2 способ:
.
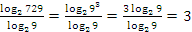Пример №5. Упростить выражение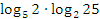 
.
Пример №6. Найти значение выражения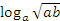 
, если 
.
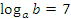Рассмотрим несколько способов решения:
1 способ:
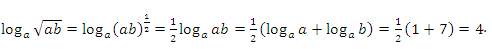
2 способ:
.
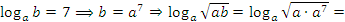
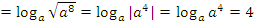Пример №1. Упростить выражение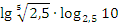 
.
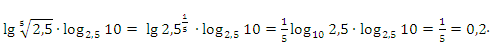
Пример №2. Найти значение выражения: 
, если 
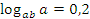
Рассмотрим несколько способов решения:
1 способ:
.
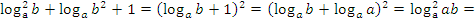
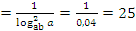2 способ:
.
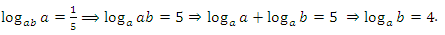
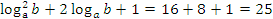Пример №3. Упростить выражение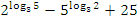 
.
.
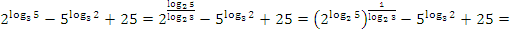
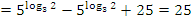Пример №4. Упростить выражение 
.
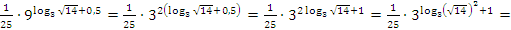
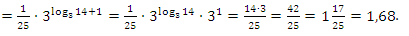
Пример №5. Упростить выражение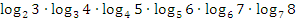 
.
.
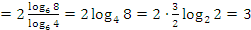Пример №1. Вычислить значение выражения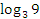 
.
Рассмотрим два способа решения:
1 способ:
Воспользуемся свойством логарифма: 
.
.
2 способ:
).
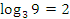
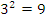Пример №2. Вычислить значение выражения: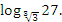 
.
Пример №3. Вычислить значение выражения: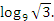 
.
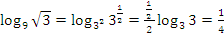Логарифмы в решении практических задач
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Эпиграф:
“Изобретение логарифмов, сократив работу астронома, продлило ему жизнь”.
П.С.Лаплас
Цели урока:
Образовательные:
- Обобщить знания учащихся по теме “Применение логарифмов при решении практических задач”; расширить кругозор, знания о возможном применении логарифма к решению практических задач; показать межпредметные связи; прививать познавательный интерес к математике; повысить мотивацию студентов к обучению.
Развивающие:
- Развивать математическое мышление, умение применять обобщенные знания, умения и навыки в новых условиях.
Воспитательные:
- Воспитывать у студентов устойчивый интерес к изучению математики, познавательную активность, математическую культуру речи.
Тип урока: комбинированный урок.
Оборудование: ноутбук, мультимедиа, экран, доска, раздаточный материал, тетрадь, презентация на электронном носителе.
Ход урока
1. Организационный момент.
Организация готовности студентов к работе.
2. Формулирование темы, постановка цели и мотивации к учебной деятельности.
Введение темы урока используя эпиграф; формирование цели урока.
(Презентация, Слайд № 1)
3. Актуализация знаний.
Устная работа: вспомнить определение и свойства логарифма.
(Презентация, Слайд № 2)
4. Всесторонняя проверка знаний.
Выполните задания, записанные на доске.
(Трое студентов работают в качестве консультантов с учениками своего варианта, остальные в тетрадях. Затем, консультанты записывают образцы решения на доске, комментируя их, и, обращая внимание студентов на недочеты в работе).
1 вариант:
Вычислить
+
2 вариант:
Решить уравнение
3 вариант:
Решить неравенство
5. Изучение нового материала.
Преподаватель:
Мы с вами уже знаем, что более 300 лет логарифмы использовались для облегчения вычислений. Но вычисления не исчерпывают роль логарифмов. Использование логарифмов необходимо для описания самых разнообразных процессов роста, происходящих в природе и обществе.
Рассмотрим и решим две задачи, которые связывают понятия разных дисциплин.
К доске вызывается сильный ученик, получивший опережающее домашнее задание — подготовить тему “Измерение количества информации”.
Задача дисциплины “Информатика”
Ученик:
— Информация является важнейшим понятием и основным объектом изучения в информатике. Неудивительно поэтому, что проблема измерения информации имеет фундаментальное значение.
Пусть алфавит, с помощью которого записываются все сообщения, состоит из M символов. Для простоты предположим, что все они появляются в тексте с одинаковой вероятностью.
Тогда в рассматриваемой постановке применима формула Хартли для вычисления количества информации:
Решить задачу:
Определить информацию, которую несет в себе один символ в кодировках ASCII и Unicode.
Решение.
1) В алфавите ASCII предусмотрено 256 различных символов, т.е.
M = 256, а I = log2 256 = 8 бит = 1 байт
Ответ: 1 байт.
2) В современной кодировке Unicode заложено гораздо большее количество символов. В ней определено 256 алфавитных страниц по 256 символов в каждой.
Таким образом:
I = log2 (256 * 256) = 8 + 8 = 16 бит = 2 байта
Ответ:2 байта.
(Презентация, Слайды № 3-5)
Задача из дисциплины “Биология”. Решает весь класс под руководством учителя.
В начальный момент времени было 8 бактерий. Через 2 часа после помещения бактерий в питательную среду, их число возросло до 100. Через сколько времени с момента размещения в питательную среду следует ожидать появления 500 бактерий?
Решение.
Для решения данной задачи, необходимо вспомнить понятия скорости и ускорения.
| Было -8 Стало- 100 |
||
| 1 изменение: | ||
=> конечное значение скорости распространения бактерий при первом изменении —
| Было -8 Стало- 500 |
||
| 2 изменение: | ||
=> конечное значение скорости распространения бактерий при втором изменении — .
Составим формулу для ускорения, учитывая, что начальная скорость (т.е. было -8, стало -8):
= =Т.к. ускорение постоянно => =>
Перейдем к натуральному основанию логарифмов, для того, чтобы можно было воспользоваться табличными значениями:
Ответ: приблизительно 3часа 15 минут.
(Презентация, Слайды № 6-9)
6. Рефлексия.
Учащиеся получают карточки для проведения опроса.
Отметьте букву выбранного Вами ответа:
1. Знаете ли вы определение логарифма?
А) да Б) нет В) Приблизительно
2. Знаете ли вы свойства логарифмов?
А) да Б) нет В) Больше половины
3. Умеете ли ВЫ применять определение и свойства логарифмов при вычислениях?
А) да Б) нет В) Не всегда
4. Научились ли вы применять определение и свойства логарифмов при решении практических задач?
А) да Б) нет В) Не всегда
| № вопроса | 1 | 2 | 3 | 4 |
| Буква ответа |
7. Домашнее задание.
Задача из дисциплины “Физика”.
Для обогрева помещения, температура в котором равна Тп = 200С, через радиатор отопления, пропускают горячую воду температурой Тв = 1000С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т0С, при чём
где с = 4200Дж/кг*С — теплоемкость воды
= 42 Вт/м * 0С— коэффициент теплообмена
a = 1,4 — постоянная.
До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?
(Ответ: 60?.)
8. Итог урока:
Мы с вами завершили тему “Логарифмы”, научились вычислять логарифмы и применять полученные знания в новых условиях, рассмотрели применение логарифмов на практике при решении задач различных дисциплин, узнали какое широкое применение имеют логарифмы в различных областях человеческой деятельности.
А теперь пусть каждый из вас задаст себе вопрос: (Презентация, Слайды № 11). и попробует ответить на него.
Учитель озвучивает оценки за урок.
Конспект урока по теме «Решение задач на вычисление логарифмов»
Самостоятельная работа по теме: « Логарифмы и их свойства» I вариант
1. Найдите х:
log3 x = -2; log36 x = 
; log3 x = 3;
log64 4 = x; log3 
= x; log2 16 = x;
logx 16 = 2; logx 
= -3; logx 5 = 
.
2. Вычислите:
log49 + 2 log48 – 2 log43; log6
— log6
; log3cos
— log3sin ; 21 + log25
3. Известно, что 
и 
. Выразите через а и b: 
4. Сравните: log310 и log103.
Самостоятельная работа по теме: « Логарифмы и их свойства» II вариант
1. Найдите х:
log2 x = -3; log49 x = ; log2 x = 3;
log625 5 = x; log2 
= x; log3 27 = x;
logx 25 = 2; logx = -3; logx 4 = .
2. Вычислите:
log83 + 3 log84 – log89; log7
— log7
; log5ctg
+ log5tg ; 5 log510 — 1
3. Известно, что и . Выразите через а и b: 
.
4. Сравните: log27 и log72.
Самостоятельная работа по теме: « Логарифмы и их свойства» III вариант
1. Найдите х:
log4 x = -2; log64 x = ; log4 x = 3;
log16 2 = x; log3 
= x; log4 64 = x;
logx 49 = 2; logx 
= -3; logx 3 = .
2. Вычислите:
log69 + 2 log62 – lg1; lg
— lg
; lgsin — lgcos ; 4 log48 — 1
3. Известно, что и . Выразите через а и b: 
.
4. Сравните: log38 и log83.
Самостоятельная работа по теме: « Логарифмы и их свойства» IV вариант
1. Найдите х:
log2 x = -4; log81 x = ; log5 x = 3;
log27 3 = x; log2 = x; log6 216 = x;
logx 64 = 2; logx 
= -3; logx 2 = .
2. Вычислите:
lg 4 + 2 lg5 – lg1; log5 — log5 ; log2tg
+ log2ctg ; 31 + log34
3. Известно, что и . Выразите через а и b: 
.
4. Сравните: log45 и log54.
Практическая работа по математике на тему «ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ»
Математика 1 курс 234 часа
Шаповалова Н.В.
ПРАКТИЧЕСКАЯ РАБОТА
Тема работы: ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ.
Тип занятия: практическое занятие.
Цели работы:
Образовательная – закрепить понятие логарифма, научить применять свойства логарифмов при решении логарифмических выражений;
Развивающая — содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;
Воспитательная — вырабатывать самостоятельность при работе на уроке; способствовать формированию максимальной работоспособности.
Организационный момент: дежурные, отсутствующие.
Ход работы:
Основная часть урока
Повторение лекционного материала
Задачи этапа: повторить пройденный материал, необходимый для выполнения практической работы.
Рассмотрим действие обратное действию возведения в степень – нахождение логарифма
Вопрос: в какую степень надо возвести число 3, чтобы получить 243?
Ответ на этот вопрос дает действие нахождения логарифма
Говорится так: «логарифм по основанию 3 от числа 243». Тройка (маленькая и пишется чуть ниже) называется «основанием логарифма», а число 243 так и называют «числом».
Найти логарифм – это значит найти показатель степени, в которую надо возвести основание логарифма, чтобы получить стоящее под логарифмом число.
Логарифмом числа b по основанию a называется такое число, обозначаемое , что . Т.е. .
a – основание логорифма,
Десятичный логарифм: .
Натуральный логарифм: , где e=2,71828…
Функция, заданная формулой , где , называется логарифмической
Основные логарифмические тождества.
Примеры
Закрепление нового материала:
Задачи этапа: научить применять практические приемы решения показательных уравнений
Практические задания:
Задание на дом: невыполненные задания завершить и сдать на следующее занятие.
Вопросы:
Определение логарифма.
Виды логарифмов.
Что такое основание логарифма, что оно показывает?
Как задается логарифмическая функция?
Перечислите основные логарифмические свойства.