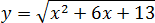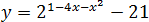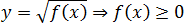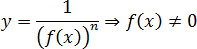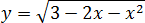Как решать задачи B15 без производных
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность.
Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x1 и x2 этого отрезка выполняется следующее:
x1 < x2 ⇒ f (x1) < f (x2).
Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x1 и x2 этого отрезка выполняется следующее:
x1 < x2 ⇒ f (x1) > f (x2).
Другими словами, для возрастающей функции чем больше x,тем больше f (x). Для убывающей функции все наоборот: чем больше x,тем
Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.
f (x) = logax (a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
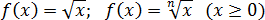
Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:
f (x) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
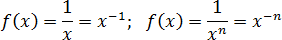
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax2 + bx + c. Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.
Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:
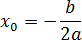
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x0 для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы x0, координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы y = ax2 + bx + c и найти ее вершину по формуле: x0 = −b/2a;
- Найти значение исходной функции в этой точке: f (x0). Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Задача. Найдите наименьшее значение функции:
Под корнем стоит квадратичная функция y = x2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.
Вершина параболы:
x0 = −b/(2a) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке x0 = −3 функция y = x2 + 6x + 13 принимает наименьшее значение.
Корень монотонно возрастает, значит x0 — точка минимума всей функции. Имеем:
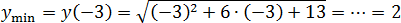
Задача. Найдите наименьшее значение функции:
y = log 2 (x2 + 2x + 9)
Под логарифмом снова квадратичная функция: y = x2 + 2x + 9. График — парабола ветвями вверх, т.к. a = 1 > 0.
Вершина параболы:
x0 = −b/(2a) = −2/(2 · 1) = −2/2 = −1
Итак, в точке x 0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2x — монотонная, поэтому:
ymin = y(−1) = log 2 ((−1)2 + 2 · (−1) + 9) = … = log 2 8 = 3
Задача. Найдите наибольшее значение функции:
В показателе стоит квадратичная функция y = 1 − 4x − x2. Перепишем ее в нормальном виде: y = −x2 − 4x + 1.
Очевидно, что график этой функции — парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:
x0 = −b/(2a) = −(−4)/(2 · (−1)) = 4/(−2) = −2
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x0 = −2:
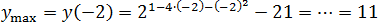
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Аргумент логарифма должен быть положительным:
y = logaf (x) ⇒ f (x) > 0
Арифметический квадратный корень существует только из неотрицательных чисел:

Знаменатель дроби не должен равняться нулю:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: y = 3 − 2x − x2. Ее график — парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.
Выписываем область допустимых значений (ОДЗ):
3 − 2x − x2 ≥ 0 ⇒ x2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒x ∈ [−3; 1]
Теперь найдем вершину параболы:
x0 = −b/(2a) = −(−2)/(2 · (−1)) = 2/(−2) = −1
Точка x0 = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x
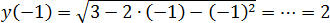
y(−3) = y(1) = 0
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
y = log 0,5 (6x − x2 − 5)
Внутри логарифма стоит квадратичная функция y = 6x − x2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6x − x2 − 5 > 0 ⇒ x2 − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒x ∈ (1; 5)
Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.
Ищем вершину параболы:
x0 = −b/(2a) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: x0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x0:
ymin = y(3) = log 0,5 (6 · 3 − 32 − 5) = log 0,5 (18 − 9 − 5) =log 0,5 4 = −2
Смотрите также:
- Показательные функции в задаче B15: хитрости решения

- Задача B15: работаем с показательной функцией без производной

- Тест к уроку «Что такое числовая дробь» (средний)

- Правила комбинаторики в задаче B6

- Пример решения задачи 15

- Задача B2 про комиссию в терминале

www.berdov.com
Решение задач без нахождения производной

Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции с произведениями. Смысл заданий тот же – требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции.
В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?
В условии дана иррациональная, логарифмическая или показательная функция:

при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:

Рассмотрим подход без нахождения производной. Вы увидите, что такие задачи можно решать устно.
Что необходимо знать? Свойство параболы, напомним его:
Если а > 0, то её ветви направлены вверх.
Если а < 0, то её ветви направлены вниз.
Далее вспомним координату (абсциссу) вершины параболы:

То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.
Следующий важный факт (ключевой для этих задач):
Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.
Почему? Давайте рассмотрим отдельно функции подробнее.
Квадратичная функция в показателе степени (при чём n>1):

Смотрите! Представим, что ax2+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом.
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a до бесконечности z увеличивается.
Это означает, что и сама функция у=nf(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция у=nf(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.
Квадратичная функция под знаком логарифма (при чём n>1):

Представим, что ax2+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом:
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a до бесконечности z увеличивается.
Это означает, что и сама функция lognz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция lognz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).
Квадратичная функция под знаком корня:

Представим, что ax2+bx+c=z. Можем записать:

Получается что:
При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.
При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.
Таким образом, сформулируем ключевое правило:

ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется, важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.
И конечно, не теряйте из виду область допустимых значений заданной функции:
— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).
— выражение стоящее под знаком логарифма, есть положительное число.
— выражение стоящее в знаменателе дроби не равно нулю.
В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).
Рассмотрим примеры:
*Контент (более шести решенных заданий) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.
В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
matematikalegko.ru
Графики функций. Прямая. Парабола. Функция корня. Тригонометрические функции
Факт 1.
\(\bullet\) Линейная функция – функция вида \(f(x)=kx+b\), где \(k,b\) – некоторые числа.
\(\bullet\) Графиком линейной функции является прямая.
\(\bullet\) Если \(b=0\), то прямая проходит через начало координат.
\(\bullet\) Графиком \(x=a\) является прямая, параллельная оси \(Oy\).
\(\bullet\) Графиком \(y=с\) является прямая, параллельная оси \(Ox\).
\(\bullet\) Для \(f(x)=kx+b\) коэффициент \(k\) равен тангенсу угла наклона прямой к положительному направлению оси \(Ox\).

\(k_1=\mathrm{tg}\alpha\), \(k_2=\mathrm{tg}\beta\).
\(\bullet\) Если две прямые \(y=k_1x+b_1\) и \(y=k_2x+b_2\) параллельны, то \(k_1=k_2\).
\(\bullet\) Если эти прямые взаимно перпендикулярны, то \(k_1\cdot
k_2=-1\).
Факт 2.
\(\bullet\) Квадратичная функция – функция вида \(f(x)=ax^2+bx+c\), где \(a, b, c\) – некоторые числа, причем \(a\ne 0\).
\(\bullet\) Графиком квадратичной функции является парабола.
\(\bullet\) Если \(a>0\), то ветви параболы направлены вверх, если \(a<0\) – ветви направлены вниз.
\(\bullet\) Абсцисса вершины параболы \[x_0=-\dfrac b{2a}\] \(\bullet\) Всякая парабола симметрична относительно прямой \(x=x_0\).
\(\bullet\) Корни уравнения \(ax^2+bx+c=0\) – точки пересечения параболы с осью \(Ox\).

Факт 3.
\(\bullet\) Кубическая функция – функция вида \(f(x)=ax^3+bx^2+cx+d\), где \(a, b, c, d\) – некоторые числа, причем \(a\ne 0\).
\(\bullet\) Графиком кубической функции является кубическая парабола.
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 1 корень, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((1)\).
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 2 корня, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((2)\).
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 3 корня, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((3)\).

Факт 4.
\(\bullet\) Функция корня – функция \(f(x)=\sqrt x\).
\(\bullet\) График функции \(y=\sqrt x\):
\(\bullet\) Заметим, что \(y=\sqrt x\) определена при \(x\geqslant 0\) и принимает значения \(y\geqslant 0\).
Факт 5.
\(\bullet\) Графиком функции \(y=\sin x\) является синусоида
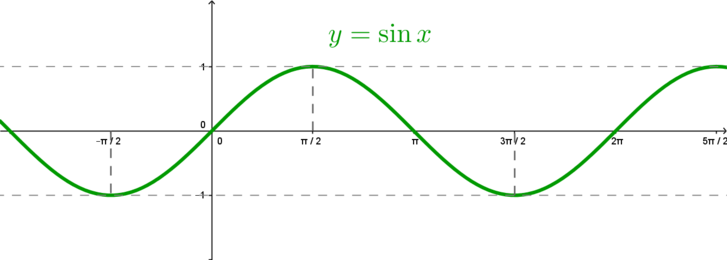
\(\bullet\) Графиком функции \(y=\cos x\) также является синусоида, но сдвинутая на \(\frac{\pi}2\) единиц влево по оси \(Ox\)

\(\bullet\) Обе функции \(y=\sin x\) и \(y=\cos x\) периодичны с периодом \(2\pi\). Обе функции могут принимать значения \(y\in [-1;1]\).
\(\bullet\) Функция \(y=\sin x\) – нечетная, функция \(y=\cos x\) – четная.
Факт 6.
\(\bullet\) График функции \(y=\mathrm{tg} \,x\)

Прямые \(x=k\cdot \frac{\pi}2\), где \(k\) – нечетное число, являются асимптотами графика (то есть график их не пересекает).
\(\bullet\) График функции \(y=\mathrm{ctg} \,x\)

Прямые \(x=n\cdot \pi\), где \(n\) – целое число, являются асимптотами графика (то есть график их не пересекает).
\(\bullet\) Обе функции \(y=\mathrm{tg} \,x\) и \(y=\mathrm{ctg} \,x\) периодичны с периодом \(\pi\) и нечетны.
Факт 7.
\(\bullet\) Показательная функция \(f(x)=a^x\) при \(a>1\) является возрастающей при всех \(x\), область значений \(a^x\in (0;+\infty)\):

Ее график всегда проходит через точку \((0;1)\).
\(\bullet\) Показательная функция \(f(x)=a^x\) при \(0<a<1\) является убывающей при всех \(x\), область значений также \(a^x\in (0;+\infty)\):

Ее график всегда проходит через точку \((0;1)\).
Факт 8.
\(\bullet\) Логарифмическая функция \(y=\log_ax\) при \(a>1\) является возрастающей, ее область определения \(x>0\), ее область значений \((-\infty;+\infty)\):

Ее график всегда проходит через точку \((1;0)\).
\(\bullet\) Логарифмическая функция \(y=\log_ax\) при \(0<a<1\) является убывающей, ее область определения \(x>0\), ее область значений \((-\infty;+\infty)\):
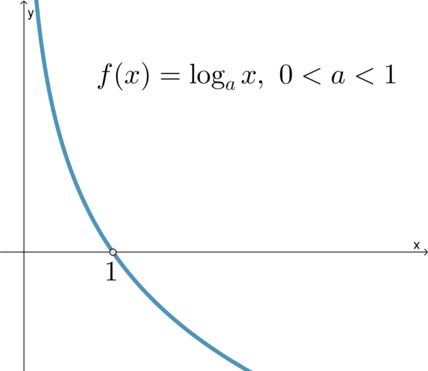
Ее график всегда проходит через точку \((1;0)\).
shkolkovo.net
Функция y = √x. Её свойства и график. Решение задач. Видеоурок. Алгебра 8 Класс
Данный урок мы посвятим решению типовых задач на построение графика функции 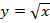 . Вспомним определение квадратного корня.
. Вспомним определение квадратного корня.
Определение. Квадратным корнем из неотрицательного числа 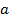 называется такое неотрицательное число
называется такое неотрицательное число 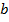 , квадрат которого равен
, квадрат которого равен 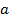 .
.
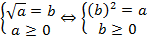 .
.
Изобразим график 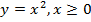 – это правая ветвь параболы (рис. 1).
– это правая ветвь параболы (рис. 1).
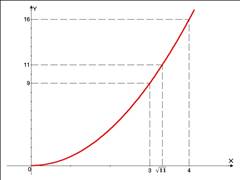
Рис. 1.
На графике наглядно виден смысл вычисления квадратного корня. Например, если рассмотреть ординату 16, то ей будет соответствовать абсцисса 4, т. к.  . Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку
. Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку 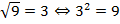 , ординате 11 соответствует абсцисса
, ординате 11 соответствует абсцисса 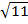 , т. к.
, т. к.  (квадратный корень из 11 не извлекается в целых числах).
(квадратный корень из 11 не извлекается в целых числах).
Теперь вспомним график функции 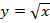 (рис. 2).
(рис. 2).

Рис. 2.
На графике для наглядности изображены несколько точек, ординаты которых вычисляются с помощью извлечения квадратного корня: 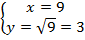 ,
, 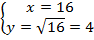 ,
, 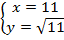 .
.
Пример 1. Постройте и прочтите график функции: а) 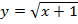 , б)
, б) 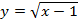 .
.
Решение. а) Построение начинается с простейшего вида функции, т. е. в данном случае с графика 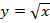 (пунктиром). Затем для построения искомого графика график функции
(пунктиром). Затем для построения искомого графика график функции 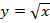 необходимо сдвинуть влево на 1 (рис. 3). При этом все точки графика сдвинутся на 1 влево, например, точка с координатами (1;1) перейдет в точку с координатами (0;1). В результате получаем искомый график (красная кривая). Проверить такой способ легко при подстановке нескольких значений аргумента.
необходимо сдвинуть влево на 1 (рис. 3). При этом все точки графика сдвинутся на 1 влево, например, точка с координатами (1;1) перейдет в точку с координатами (0;1). В результате получаем искомый график (красная кривая). Проверить такой способ легко при подстановке нескольких значений аргумента.

Рис. 3.
Прочтем график: если аргумент меняется от 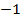 до
до 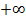 , функция возрастает от 0 до
, функция возрастает от 0 до 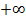 . Область определения (ОДЗ) при этом требует, чтобы подкоренное выражение было неотрицательным, т. е.
. Область определения (ОДЗ) при этом требует, чтобы подкоренное выражение было неотрицательным, т. е. 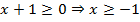 .
.
б) Для построения графика функции 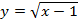 поступим аналогичным образом. Сначала строим график
поступим аналогичным образом. Сначала строим график 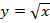 (пунктиром). Затем для построения искомого графика график функции
(пунктиром). Затем для построения искомого графика график функции 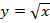 необходимо сдвинуть вправо на 1 (рис. 4). При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами (1;1) прейдет в точку с координатами (2;1). В результате получаем искомый график (красная кривая).
необходимо сдвинуть вправо на 1 (рис. 4). При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами (1;1) прейдет в точку с координатами (2;1). В результате получаем искомый график (красная кривая).
Рис. 4.
Прочтем график: если аргумент меняется от 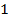 до
до 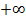 , функция возрастает от 0 до
, функция возрастает от 0 до 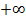 . Область определения (ОДЗ) аналогична предыдущему случаю:
. Область определения (ОДЗ) аналогична предыдущему случаю: 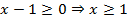 .
.
Замечание. На указанных примерах несложно сформулировать правило построения функций вида:
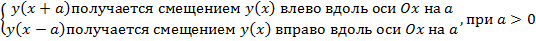 .
.
Пример 2. Постройте и прочтите график функции: а) 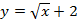 , б)
, б) 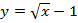 .
.
Решение. а) Этот пример также демонстрирует преобразование графиков функций, но только уже другого типа. Начинаем построение с простейшей функции 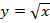 (пунктиром). Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;3).
(пунктиром). Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;3).

Рис. 5.
Прочтем график: если аргумент меняется от 0 до 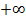 , функция возрастает от 2 до
, функция возрастает от 2 до  . Область определения (ОДЗ):
. Область определения (ОДЗ):  .
.
б) Также начинаем построение с простейшей функции  (пунктиром). Затем график построенной функции (рис. 6) смещаем на 1 вниз и получаем искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;0).
(пунктиром). Затем график построенной функции (рис. 6) смещаем на 1 вниз и получаем искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;0).
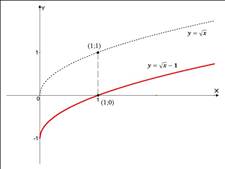
Рис. 6.
Прочтем график: если аргумент меняется от 0 до 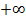 , функция возрастает от
, функция возрастает от 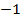 до
до 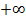 . Область определения (ОДЗ):
. Область определения (ОДЗ): 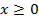 .
.
Замечание. С помощью указанных примеров сформулируем правило построения функций вида:
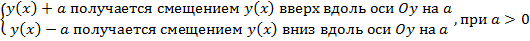 .
.
Пример 3. Постройте и прочтите график функции  .
.
Решение. Метод построения указанной функции представляет собой комбинацию двух методов, которые мы видели в предыдущих примерах. Сначала строим основную функцию 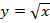 (пунктиром), затем смещаем ее на 1 вправо и на 2 вверх (рис. 7). При этом, например, точка с координатами (1;1) сначала перейдет в точку (2;1), а затем в точку (2;3). Искомая кривая изображена красным цветом.
(пунктиром), затем смещаем ее на 1 вправо и на 2 вверх (рис. 7). При этом, например, точка с координатами (1;1) сначала перейдет в точку (2;1), а затем в точку (2;3). Искомая кривая изображена красным цветом.

Рис. 7.
Прочтем график: если аргумент меняется от 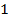 до
до 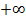 , функция возрастает от 2 до
, функция возрастает от 2 до 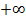 . Область определения (ОДЗ) – подкоренное выражение неотрицательно:
. Область определения (ОДЗ) – подкоренное выражение неотрицательно: 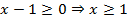 .
.
Замечание. Как видно на указанном примере, преобразования графиков функций, которые мы рассмотрели, можно применять последовательно в комплексе.
Пример 4. Постройте и прочтите график функции  .
.
Решение. Для построения данной составной функции изображаем ее части в приведенных диапазонах построения (рис. 8). Для этого сначала изображаем пунктиром всю функцию 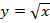 , затем всю функцию
, затем всю функцию 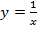 , а затем наводим (красная кривая) только те их области, которые заданы условием задачи. Сливаются два участка кривой в точке с координатами (1;1).
, а затем наводим (красная кривая) только те их области, которые заданы условием задачи. Сливаются два участка кривой в точке с координатами (1;1).
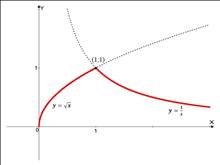
Рис. 8.
Прочтем график: если аргумент меняется от 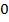 до 1, функция возрастает от 0 до
до 1, функция возрастает от 0 до 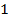 , если аргумент меняется от 1 до
, если аргумент меняется от 1 до 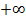 , функция убывает от 1 до 0. Область определения (ОДЗ) – подкоренное выражение неотрицательно:
, функция убывает от 1 до 0. Область определения (ОДЗ) – подкоренное выражение неотрицательно: 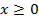 .
.
Пример 5. Графически решить систему уравнений 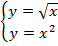 .
.
Решение. Для решения системы графическим способом необходимо построить графики функций (рис. 9), представляющих собой уравнения системы, и определить координаты их точек пересечения.
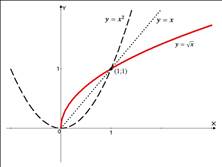
Рис. 9.
На графике изображен полезный факт, демонстрирующий, что графики квадратичной функции и квадратного корня симметричны относительно графика функции 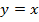 . По графику видно, что имеем две точки пересечения, т. е. система имеет два решения. Для определения точных значений этих решений подставим стандартные значения аргумента в обе исследуемые функции: 0 и 1. При этом получим:
. По графику видно, что имеем две точки пересечения, т. е. система имеет два решения. Для определения точных значений этих решений подставим стандартные значения аргумента в обе исследуемые функции: 0 и 1. При этом получим: 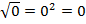 и
и 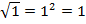 , т. е. координаты точек пересечения графиков и решения системы:
, т. е. координаты точек пересечения графиков и решения системы: 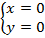 и
и 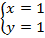 .
.
Ответ. (0;0), (1;1).
Пример 6. (С параметром). При каких значениях параметра 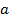 имеет решение уравнение
имеет решение уравнение 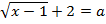 ?
?
Решение. Для исследования значений параметра 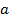 воспользуемся графическим методом и построим график функции
воспользуемся графическим методом и построим график функции  . Мы его уже строили на сегодняшнем уроке, поэтому воспользуемся готовым рисунком 10.
. Мы его уже строили на сегодняшнем уроке, поэтому воспользуемся готовым рисунком 10.
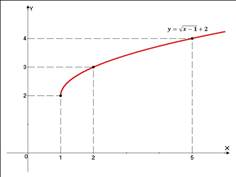
Рис. 10.
Прочтем график: если аргумент меняется от 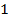 до
до 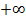 , функция возрастает от 2 до
, функция возрастает от 2 до 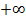 . Из этого следует, что функция принимает значения только
. Из этого следует, что функция принимает значения только  , причем при аргументе
, причем при аргументе 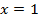 она принимает свое минимальное значение
она принимает свое минимальное значение 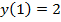 . Из полученного диапазона изменения
. Из полученного диапазона изменения  можно сделать однозначный вывод, что параметр
можно сделать однозначный вывод, что параметр 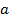 , который в уравнении приравнивается к рассмотренной функции, может принимать такие же значения
, который в уравнении приравнивается к рассмотренной функции, может принимать такие же значения  . Например, при
. Например, при 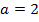 имеем, что
имеем, что 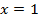 , т. е. у уравнения есть корень и т. д.
, т. е. у уравнения есть корень и т. д.
Ответ. .
.
На следующем уроке мы рассмотрим свойства квадратных корней.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Математика = это легко! 😉 (Источник).
2. Фестиваль педагогических идей «Открытый урок» (Источник).
3. Квадратный корень из х (Источник).
Домашнее задание
1. №313, 316, 317. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Решите графически уравнение 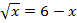 .
.
3. Постройте график функции 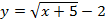 .
.
4. Решите графически уравнение: 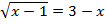
interneturok.ru
Как строятся графики функций y=Корень из (-x^2+6х-5) Объясните пожалуйста Вот линейные по двум точкам Просто квадратичн
Просто исследуешь функцию: находишь область определения, точки экстремума, промежутки знакопостоянства производной функции, которые определяют промежутки монотонности исходной функии
Насколько правомерен Ваш вопрос? Неужели Вы можете объяснить как построить параболу по 5 точкам? Кажется, что график кривой строится по бесконечному количеству точек. . Ваша функция y=V(-x^2+6х-5) вполне конкретно описана. Другое дело, когда параболу y=ax^2+bx+c предлагают провести через несколько заданных точек, то есть требуется найти а, b,c. Если точек много, то может оказаться, что параболу провести нельзя, если мало точек задано, то можно провести много различных парабол. По линейке прямую построить просто. Но имея параболические лекала и ровно столько точек, сколько нужно, произвольную параболу построить точно невозможно, если число b/a неизвестно. Не угадаешь с выбором лекал. Но если две точки даны на одной вертикали, а третья в стороне от вертикали, то можно точно сказать, что из функций второго порядка на роль кривой пригодна только окружность, и найти её точную формулу очень легко. Надеюсь, теперь понятно, что каждую функцию надо анализировать, и не всякие точки на плоскости пригодны для той или иной кривой. Если дана общая формула кривой типа y=ax^2+bx+c и точки на плоскости, расположенные по вертикали, и параболу или гиперболу построить нельзя, то может быть поставлена задача, повернуть или кривую, или плоскость с точками на ней. Второй вариант более понятен. Точки перестают лежать на вертикали, и есть шанс построить параболу. Составляется система уравнений, куда входит произвольный угол поворота, а также столько уравнений y=ax^2+bx+c с подставленной точкой, сколько задано точек. Но обычно ученикам дают задачи, где точки не надо поворачивать и надо найти a, b, c -параметры кривой. У Вас эти параметры заданы, но если бы были заданы и точки, о которых Вы умолчали, то не о чем и говорить, ибо всё известно) ) ) . Особенность Вашей функции только в том, что под корнем всегда положительное выражение и аргумент х ограничен диапазоном p=(-x^2+6х-5) > 0, что представляет по вертикали верхнюю часть параболы, но вертикаль — это аргумент p для y=y(p)=V(-x^2+6х-5). Обратите внимание, что при p=1 y=1 (x=3±V3), то есть кривые аргумента p (парабола) и функции y(x,p) — окружность пересекаются в двух точках, равны. Та часть параболы, что выше 1, сплющивается к окружности, когда из большого числа извлекается корень, а нижняя часть от 0 до 1 по вертикали, стремится приподняться к окружности по извлечении корня из р<1. Теперь ясно, как из параболы получается полуокружность ! Из значений ординат параболы извлекать квадратные корни. А если бы был дан эллипс, то значения ординат эллипса измеренные относительно его оси надо делить на коэффициент его растяжения, и получим окружность <img src=»//otvet.imgsmail.ru/download/8d68cac4d4749772d5e55e1a44fe3672_i-66.jpg»>
touch.otvet.mail.ru
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида  , где
, где 
 называется квадратичной функцией.
называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:
имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции  , составим таблицу:
, составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент  , то график квадратичной функции имеет ровно такую же форму, как график функции
, то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.
при любых значениях остальных коэффициентов.
График функции  имеет вид:
имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции  симметричен графику функции
симметричен графику функции  относительно оси ОХ.
относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции
— это точки пересечения графика функции  с осью ОХ.
с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции  с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение  .
.
В случае квадратичной функции  нужно решить квадратное уравнение
нужно решить квадратное уравнение  .
.
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант:  , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если 
 ,то уравнение
,то уравнение  не имеет решений, и, следовательно, квадратичная парабола
не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если
не имеет точек пересечения с осью ОХ. Если 
 ,то график функции выглядит как-то так:
,то график функции выглядит как-то так:

2. Если 
 ,то уравнение
,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола
имеет одно решение, и, следовательно, квадратичная парабола  имеет одну точку пересечения с осью ОХ. Если
имеет одну точку пересечения с осью ОХ. Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

3. Если 
 ,то уравнение
,то уравнение  имеет два решения, и, следовательно, квадратичная парабола
имеет два решения, и, следовательно, квадратичная парабола  имеет две точки пересечения с осью ОХ:
имеет две точки пересечения с осью ОХ:
 ,
, 
Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:



Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.
с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль:
с осью OY, нужно в уравнение параболы вместо х подставить ноль:  .
.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой  .
.
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 
1. Направление ветвей параболы.
Так как 
 ,ветви параболы направлены вверх.
,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 



Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение: 
 ,
, 
3. Координаты вершины параболы:


4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы


Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид  — в этом уравнении
— в этом уравнении  — координаты вершины параболы
— координаты вершины параболы
или в уравнении квадратичной функции 
 , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Построим для примера график функции  .
.
Вспомним линейные преобразования графиков функций. Чтобы построить график функции  , нужно
, нужно
- сначала построить график функции
 ,
, - затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции  . В уравнении этой функции
. В уравнении этой функции  , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат: 
Следовательно, координаты вершины параболы:  . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда 
2. Координаты вершины параболы: 

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.
Перед вами график квадратичной функции вида  .
.
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции  от значения коэффициента
от значения коэффициента  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения 
— направления ветвей параболы от знака коэффициента 
— координат вершины параболы  от значений
от значений  и
и  :
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Квадратичная функция в задачах с параметром. Видеоурок. Алгебра 11 Класс
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Квадратичная функция в задачах с параметром
Напомним смысл выражения «решить с параметром» – можно решать уравнения, неравенства, системы с параметром.
Решить задачу, например, уравнение  или неравенство
или неравенство  с параметром а – означает «перебрать» все значения параметра и для каждого из них указать ответ.
с параметром а – означает «перебрать» все значения параметра и для каждого из них указать ответ.
Применительно к данной теме все преобразования будут выполняться с учетом свойств квадратичной функции.
Напомним основные сведения о квадратичной функции.
Определение:
Квадратичной функцией называется функция вида 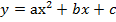 , где
, где 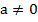
Здесь х – зависимая переменная, а, b, с – тройка чисел, которые определяют данную квадратичную функцию, у – зависимая переменная;
Чтобы найти корни квадратичной функции, игрек приравнивают к нулю, и если корни существуют, то они вычисляются по формуле:
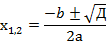
 – дискриминант квадратного уравнения;
– дискриминант квадратного уравнения;
График квадратичной функции – это парабола, причем если 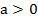 , то ветви параболы направлены вверх.
, то ветви параболы направлены вверх.
У каждой параболы есть вершина. Координаты вершины (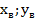 ) вычисляются по формулам:
) вычисляются по формулам:
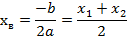

При работе с квадратичной функцией необходимо выделять полный квадрат. После выделения полного квадрата квадратичная функция выглядит следующим образом:

Теорема Виета (прямая):
Если  и
и 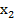 – корни квадратного уравнения, то они связаны с коэффициентами квадратного уравнения следующим образом:
– корни квадратного уравнения, то они связаны с коэффициентами квадратного уравнения следующим образом:
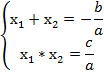
Если известны корни квадратного уравнения, то квадратный трехчлен можно следующим образом разложить на множители:
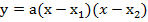
Кроме того, существуют интервалы знакопостоянства функции. Внутри интервала корней функция одного знака, вне интервала корней функция другого знака.
Пример 1 – решить уравнение с параметром:
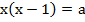
Раскроем скобки и перенесем все члены в левую часть уравнения:
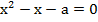
Корни данного квадратного уравнения:
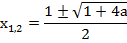
Корни квадратного уравнения существуют, когда подкоренное выражение неотрицательно, т. е. когда дискриминант больше либо равен нулю.
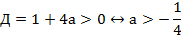
Когда дискриминант положителен, уравнение имеет два различных корня.

Когда дискриминант равен нулю, уравнение имеет два совпадающих корня, которые совпадают с вершиной параболы: 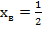
Ответ: при 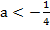 уравнение не имеет решений; при
уравнение не имеет решений; при 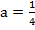
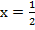 ; при
; при 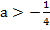
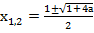
Итак, мы видим специфику квадратного уравнения: оно может иметь один корень, два корня или не иметь корней.
Квадратичную функцию с параметром можно представить в следующем виде:
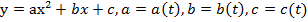
Здесь t – параметр. Если мы зададим конкретное значение параметра t, то мы зададим тройку чисел, определяющих конкретную квадратичную функцию. Как мы видим, параметр – это управление, он управляет всей кривой, в частности, расположением корней.
Пример 2 – решить уравнение с параметром:
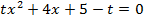
В данном случае при 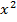 стоит параметр t, значит, заданное уравнение может быть как квадратным, так и линейным. Рассмотрим два случая:
стоит параметр t, значит, заданное уравнение может быть как квадратным, так и линейным. Рассмотрим два случая:
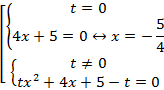
Теперь рассмотрим квадратное уравнение с параметром:
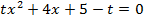
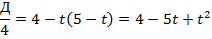
Получили квадратное уравнение. Решаем его любым способом и получаем корни: 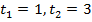
Таким образом, имеем:

Наличие корней в квадратном уравнении зависит от знака дискриминанта, мы выяснили, что в данном случае дискриминант есть квадратичная функция от t. Данную функцию легко исследовать. Проиллюстрируем:
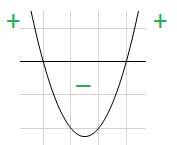
Рис. 1. Интервалы знакопостоянства функции 
Очевидно, что внутри интервала корней дискриминант отрицателен, вне интервала корней – положителен. Теперь легко можем дать ответ к поставленной задаче.
Ответ: при 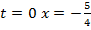 ; при
; при 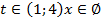 ; при
; при  ; при
; при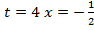 : при
: при 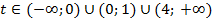

Пример 3 – найти значения параметра, при которых неравенство выполняется при любых значениях х:
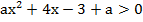
Решение основано на свойствах функции, стоящей в левой части, данная функция зависит от х и от параметра а.
Поведение функции зависит от старшего коэффициента а. Рассмотрим возможные варианты:
1. 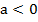 . Имеем параболу, направленную ветвями вниз. В зависимости от значения дискриминанта заданного квадратного уравнения, парабола может находиться полностью под осью х (неравенство не выполняется ни при каких х), касаться ее в вершине (неравенство не выполняется ни при каких х), или пересекать в корнях уравнения, в этом случае внутри интервала корней функция положительна и неравенство выполняется, но вне интервала корней функция отрицательна и неравенство не выполняется.
. Имеем параболу, направленную ветвями вниз. В зависимости от значения дискриминанта заданного квадратного уравнения, парабола может находиться полностью под осью х (неравенство не выполняется ни при каких х), касаться ее в вершине (неравенство не выполняется ни при каких х), или пересекать в корнях уравнения, в этом случае внутри интервала корней функция положительна и неравенство выполняется, но вне интервала корней функция отрицательна и неравенство не выполняется.
2. 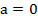 . Подставив в заданное неравенство, получаем:
. Подставив в заданное неравенство, получаем: 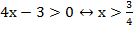 , поставленная задача не выполняется.
, поставленная задача не выполняется.
3. 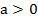 . Имеем параболу, направленную ветвями вверх. В зависимости от значения дискриминанта заданного квадратного уравнения, парабола может находиться полностью над осью х (неравенство выполняется всегда), касаться ее в вершине (неравенство не выполняется в вершине параболы), или пересекать в корнях уравнения, в этом случае внутри интервала корней функция отрицательна и неравенство не выполняется.
. Имеем параболу, направленную ветвями вверх. В зависимости от значения дискриминанта заданного квадратного уравнения, парабола может находиться полностью над осью х (неравенство выполняется всегда), касаться ее в вершине (неравенство не выполняется в вершине параболы), или пересекать в корнях уравнения, в этом случае внутри интервала корней функция отрицательна и неравенство не выполняется.
Таким образом, нас удовлетворят положительные значения параметра, при которых уравнение не имеет корней, т. е. его дискриминант отрицателен:
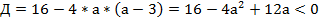
Имеем квадратное неравенство:

Исследуем полученное квадратное уравнение:
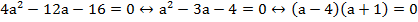
Имеем параболу, направленную ветвями вверх, ее значения положительны вне интервала корней: 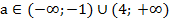 . Нас интересуют только положительные значения параметра.
. Нас интересуют только положительные значения параметра.
Ответ: при 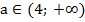 неравенство выполняется при любых значениях х.
неравенство выполняется при любых значениях х.
Итак, мы рассмотрели решение различных задач с параметром и квадратичной функцией, привели примеры и показали технику решения.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Tutoronline.ru (Источник).
2. Параметры (Источник).
Домашнее задание
1. Решить уравнение с параметром:
а) 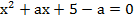 ;
;
б) 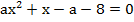 ;
;
в) 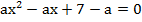 ;
;
г)
interneturok.ru