| 1. |
Табличные интегралы
Сложность: лёгкое |
1 |
| 2. |
Определённый интеграл степенной функции
Сложность: лёгкое |
2 |
3.
|
Основной интеграл тригонометрической функции
Сложность: лёгкое |
3 |
| 4. |
Неопределённый интеграл от дробной функции
Сложность: среднее |
4 |
5.
|
Неопределённый интеграл от дробной тригонометрической функции
Сложность: среднее |
3 |
| 6. |
Неопределённый интеграл от показательной функции
Сложность: среднее |
4 |
7.
|
Неопределённый интеграл, метод замены переменной, натуральный логарифм
Сложность: среднее |
4 |
| 8. |
Неопределённый интеграл, метод замены переменной, тригонометрические функции
Сложность: среднее |
4 |
9.
|
Определённый интеграл, функция, содержащая квадратный корень
Сложность: среднее |
4 |
| 10. |
Определённый интеграл, тригонометрическая функция
Сложность: среднее |
4 |
11.
|
Определённый интеграл, геометрический смысл
Сложность: сложное |
4 |
| 12. |
Вычисление силы сжатия пружины
Сложность: сложное |
4 |
13.
|
Физический смысл определённого интеграла
Сложность: сложное |
5 |
1.3. Простейшие определённые интегралы
Начинаем:
Пример 1
Вычислить определенный интеграл
Сначала решение, затем комментарии:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице (см. Приложения) с помощью самой популярной формулы . Появившуюся константу целесообразно сразу отделить от и вынести за скобку (кстати, ещё одно свойство). Делать это не обязательно, но желательно – зачем лишние вычисления?
Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Это пример для самостоятельного решения. ОБЯЗАТЕЛЬНО прорешиваем все предлагаемые мной примеры от руки!! Ручка и тетрадь под рукой? Отлично. Кроме того, открываем и освежаем в памяти Таблицу интегралов и Таблицу производных (см. приложения к курсу).
…всё получилось? Свериться с решениями можно в конце книги.
Также проверьте, есть ли у вас калькулятор.
Хотя бы самый простой. Но лучше с функциями (логарифмами, синусами и т.д.). На всякий бедственный случай прилагаю к курсу  Потому что с дробовиком всё нипочём.
Потому что с дробовиком всё нипочём.
…оружие под рукой? Продолжаем!
Пример 3
Вычислить определенный интеграл
Сначала решение, затем комментарии:
(1) Используем свойство линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений,
в частности, часто встречающаяся ПУТАНИЦА В ЗНАКАХ.
Поэтому будьте внимательны! Особое внимание заостряю на 3-м слагаемом: – первое место в хит-параде ошибок по невнимательности, здесь очень часто теряют минус: (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается подробно).
Следует заметить, что рассмотренный способ решения – не единственный, и при определенном опыте его можно значительно сократить. Примерно так:
Здесь устно используем правила линейности, устно интегрируем по таблице и в результате получаем всего лишь одну скобку с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). Далее в «цельную» первообразную функцию, сначала подставляем 4, затем –2, опять же выполняя все действия в уме.
Какие достоинства у «короткого» способа решения? Быстрота и компактность записи. А недостатки? Повышенный риск допустить ошибку. Поэтому «чайникам» я рекомендую подробное решение. А лучше оба. Для сверки.
Кстати, о сверках и проверках. Запомните красное правило:
Перед тем, как использовать формулу Ньютона-Лейбница,
полезно провести проверку: а сама-то первообразная найдена правильно?
Ибо, если она найдена неверно, то и всё остальное тоже будет неправильным.
Так, применительно к рассмотренному примеру: перед тем, как в первообразную функцию подставлять верхний и нижний пределы, желательно на черновике проверить, а правильно ли вообще найден неопределенный интеграл? Дифференцируем:
– получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.
Пример 4
Вычислить определенный интеграл
Решаем самостоятельно. И коротко, и подробно.
1.4. Замена переменной в определенном интеграле
1.2. Некоторые свойства определённого интеграла
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
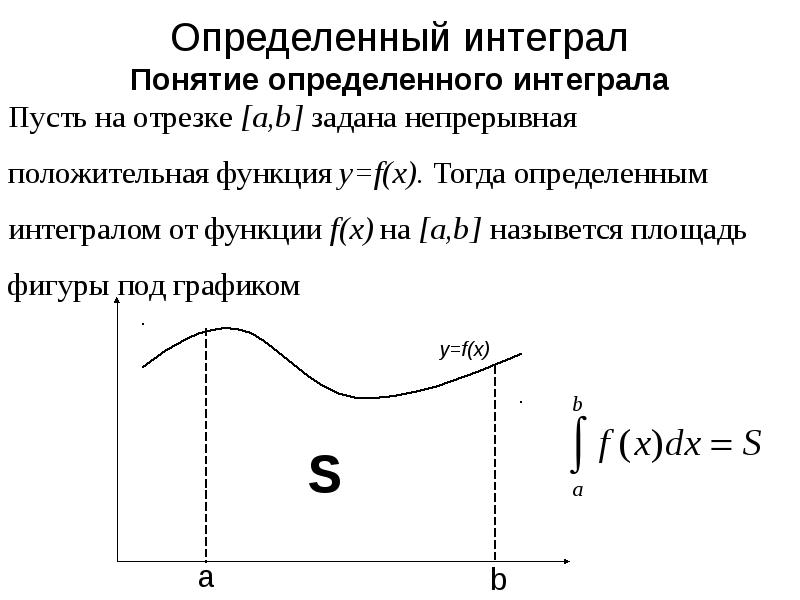
Определение определенного интеграла.
 Объем конуса интеграл. Объем тела вращения интеграл. Определение определенного интеграла римана.
Объем конуса интеграл. Объем тела вращения интеграл. Определение определенного интеграла римана.Функция определенного интеграла тесно связана с первообразной и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, то есть входит в область определения подынтегральной функции, является вещественным числовым значением, в то время как первообразная и неопределенный интеграл представляют собой бесконечное число функций, отличающихся только константой. Развитие определенного интеграла начинается с функции \(f( x) \) на замкнутом интервале \([ a, b]\). Данный интервал разбивается на ” \(n\) » подинтервалов, которые могут, хоть и не обязательно, быть равными длинами \((Δ x)\). В каждом подинтервале выбирается произвольное значение интервала и определяется его последующее значение функции. Произведение каждого значения функции умножается на соответствующую длину подинтервала и эти ” \(n\)» продуктов добавляются для определения их суммы. 2}d\theta\)
2}d\theta\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
5.16. Вычисление определенных интегралов (приближенное и точное). Форму
Определенный интеграл , согласно его математическому определению (4.2), представляет собой сумму бесконечно большого числа бесконечно малых слагаемых, образованных по схеме рисунка 5.5. Для непрерывной подынтегральной функции F(X) и конечных пределов интегрирования A и B этот интеграл, как было показано выше, заведомо существует (представляет собой некоторое число). Но найти его напрямую, следуя указанной на рис. 5.5 схеме, очевидно, невозможно. По этой схеме его можно найти лишь приближенно.
Для этого промежуток интегрирования [A; B] следует разбить не на бесконечно малые участки Dx, которых будет бесконечно много, а на конечное число (скажем, на 100) частичных промежутков одинаковой (или не одинаковой) конечной длины . Затем на каждом выбрать некоторую точку Х (скажем, середину) и подсчитать сумму
Из уже конечного числа (из 100) слагаемых. Эта сумма будет Приближенным значением определенного интеграла . Если нужно получить более точный результат, то нужно сделать более мелкое разбиение промежутка интегрирования (скажем, разбить его не на 100 частичных промежутков, а на 200, 300, и т. д.). Собственно, таким путем (с некоторыми непринципиальными усовершенствованиями указанной схемы) и вычисляют приближенно определенные интегралы на ЭВМ. ЭВМ умеют, кстати, оценивать точность полученного результата, и при вычислении определенных интегралов за счет своего быстродействия способны достигать любой разумной точности (до нескольких тысяч десятичных знаков после запятой). Но вычисляя таким путем определенные интегралы, абсолютно точного результата, тем не менее, ЭВМ дать не в состоянии.
Но вычисляя таким путем определенные интегралы, абсолютно точного результата, тем не менее, ЭВМ дать не в состоянии.
И тут возникает вопрос: а нельзя ли все-таки вычислять определенные интегралы абсолютно точно? Ответ на это вопрос такой: можно, хотя далеко и не всегда. Для точного подсчета определенных интегралов, если оно возможно, применяется знаменитая формула Нютона-Лейбница.
Суть ее в следующем. Пусть F(X) – непрерывная на [A; B] функция, так что заведомо существует. И пусть вычислен неопределенный интеграл от функции F(x):
(4.19) |
Тогда Точное значение можно найти по формуле:
(4.20) |
Здесь F(X) – любая первообразная для функции F(X). Формула (4.20) называется Формулой Ньютона-Лейбница.
Формула (4.20) называется Формулой Ньютона-Лейбница.
Для доказательства формулы Ньютона-Лейбница докажем сначала, что функция
(4.21) |
То есть определенный интеграл с переменным верхним пределом, имеет на [A; B] производную Ф΄(X), совпадающую с F(X) (Ф΄(X) = F(X)).
Действительно,
(4.22) |
Но
(4.23) |
В последнем интеграле интегрирование происходит на бесконечно малом промежутке [X; X+Dx] оси T длиной Dx. На нем, при его разбиении на бесконечно малые промежутки Dt, уместится лишь один такой промежуток Dt = Dx
(см. рис. 5.11). Выбирая на нем в качестве произвольно выбираемой точки T точку X и следуя схеме (4.2) вычисления определенного интеграла, получим по этой схеме лишь одно слагаемое:
рис. 5.11). Выбирая на нем в качестве произвольно выбираемой точки T точку X и следуя схеме (4.2) вычисления определенного интеграла, получим по этой схеме лишь одно слагаемое:
(4.24) |
А значит, согласно (4.22), получаем:
(4.25) |
Отметим, что заодно мы доказали следующий принципиальный факт, который мы обещали доказать в конце §2: у любой непрерывной на [A; B] функции F(X) имеется первообразная F(X). Ею, в частности, является функция Ф(х). А значит, для любой непрерывной на [A; B] функции F(X) существует для X Î [A; B] и неопределенный интеграл (4.19). Хотя, как мы уже замечали в §1, он далеко не всегда может быть выражен через элементарные функции (может оказаться неберущимся). Найдя приближенно (машинным путем) функцию Ф(х), мы тем самым найдем приближенно и .
Найдя приближенно (машинным путем) функцию Ф(х), мы тем самым найдем приближенно и .
А теперь перейдем непосредственно к доказательству формулы Ньютона-Лейбница (4.20). Пусть F(X) – любая первообразная для функции F(X) на [A; B]. Так как она может отличаться от указанной выше первообразной Ф(х) лишь на константу, то
(4.26) |
Полагая в этом равенстве Х = а, получаем:
(4.27) |
Значит, равенство (4.26) принимает вид:
(4.28) |
А теперь, полагая в (4.28) Х = B, получим:
(4. |
Но это, по сути, это и есть формула (4.20) Ньютона-Лейбница.
Пример 3. Вычислить .
Решение. Вычислим сначала
(значит, )
А тогда
Геометрическая иллюстрация полученного результата изображена ниже:
(4.30)
Формула Ньютона-Лейбница (4.20) принадлежит к числу важнейших формул высшей математики. Она позволяет просто, а главное, точно вычислять определенные интегралы. А значит, позволяет находить точные значения многих нужных для практики величин (площадей криволинейных фигур; помещений тел при переменных скоростях их движения; работ переменных сил и многое другое). Но она может быть использована, если только соответствующий неопределенный интеграл – из берущихся. В противном случае неизвестна первообразная F(X) для функции F(X), а значит, нечего подставлять и в формулу (4.20) Ньютона-Лейбница.
Если неопределенный интеграл неберущийся, то соответствующий ему определенный интеграл может быть найден лишь приближенно. Например, с помощью ЭВМ – так, как об этом говорилось выше, перед выводом формулы Ньютона-Лейбница.
Упражнения
1. На основании формулы (4.18) (формулы грубой оценки определенных интегралов) оценить величину следующих интегралов:
А); б).
Ответ: а); б).
2. Сравнив подынтегральные функции интегралов и , выяснить, какой из них больше.
Ответ: > .
3. Доказать, что для всех справедливо неравенство , и с его помощью доказать, что
4. Доказать, что заключен между и .
5. Найти площадь S, заключенную между параболой и осью оХ.
Ответ:
6. Найти работу А, которую нужно затратить, чтобы растянуть пружину на 6 см, если для ее растяжения на 1 см необходима сила в 20 н.
Указание. При решении задачи использовать закон Гука: величина удлинения пружины пропорциональна растягивающей ее силе.
При решении задачи использовать закон Гука: величина удлинения пружины пропорциональна растягивающей ее силе.
Ответ: .
7. Производительность труда Z = F(T) среднестатистического рабочего на некотором предприятии представляет собой функцию
Найти объем Q продукции, производимой рабочим за смену (8 часов).
Ответ:
| < Предыдущая | Следующая > |
|---|
5.2 Определенный интеграл — Исчисление Том 1
Цели обучения
- 5.2.1 Сформулируйте определение определенного интеграла.
- 5.2.2 Объясните термины подынтегральное выражение, пределы интегрирования и переменная интегрирования.
- 5.2.3 Объясните, когда функция интегрируема.
- 5.2.4 Опишите взаимосвязь между определенным интегралом и чистой площадью.

- 5.2.5 Используйте геометрию и свойства определенных интегралов для их вычисления.
- 5.2.6. Вычислить среднее значение функции.
В предыдущем разделе мы определили площадь под кривой в терминах сумм Римана:
A = limn → ∞∑i = 1nf (xi *) Δx.A = limn → ∞∑i = 1nf (xi *) Δx.Однако это определение имело ограничения. Мы потребовали, чтобы f (x) f (x) была непрерывной и неотрицательной. К сожалению, реальные проблемы не всегда соответствуют этим ограничениям. В этом разделе мы рассмотрим, как применить концепцию площади под кривой к более широкому набору функций с помощью определенного интеграла.
Определение и обозначения
Определенный интеграл обобщает понятие площади под кривой. Мы снимаем требования о непрерывности и неотрицательности функции f (x) f (x) и определяем определенный интеграл следующим образом.
Определение
Если f (x) f (x) — функция, определенная в интервале [a, b], [a, b], определенный интеграл f от a до b задается как
Abf (x) dx = limn → ∞∑i = 1nf (xi *) Δx, ∫abf (x) dx = limn → ∞∑i = 1nf (xi *) Δx, 5. 8
8
при наличии ограничения. Если этот предел существует, функция f (x) f (x) называется интегрируемой на [a, b], [a, b] или интегрируемой функцией.
Знак интеграла в предыдущем определении должен показаться знакомым. Мы видели аналогичные обозначения в главе «Применение производных», где мы использовали символ неопределенного интеграла (без a и b сверху и снизу) для представления первообразной. Хотя обозначения для неопределенных интегралов могут выглядеть аналогично обозначениям для определенного интеграла, они не совпадают.Определенный интеграл — это число. Неопределенный интеграл — это семейство функций. Позже в этой главе мы исследуем, как связаны эти концепции. Однако всегда следует уделять пристальное внимание обозначениям, чтобы мы знали, работаем ли мы с определенным интегралом или с неопределенным интегралом.
Интегральная система обозначений восходит к концу семнадцатого века и является одним из вкладов Готфрида Вильгельма Лейбница, которого часто считают соавтором исчисления вместе с Исааком Ньютоном.Символ интегрирования ∫ представляет собой удлиненную букву S, обозначающую сигму или суммирование. На определенном интеграле выше и ниже символа суммирования находятся границы интервала, [a, b]. [A, b]. Числа a и b являются значениями x и называются пределами интегрирования; в частности, a — это нижний предел, а b — верхний предел. Чтобы уточнить, мы используем слово limit двумя разными способами в контексте определенного интеграла.Сначала поговорим о пределе суммы при n → ∞.n → ∞. Во-вторых, границы области называются пределами интеграции .
Мы называем функцию f (x) f (x) подынтегральным выражением, а dx указывает, что f (x) f (x) является функцией по отношению к x , называемой переменной интегрирования. Обратите внимание, что, как и индекс в сумме, переменная интегрирования является фиктивной переменной и не влияет на вычисление интеграла. В качестве переменной интегрирования мы можем использовать любую понравившуюся переменную:
Abf (x) dx = ∫abf (t) dt = ∫abf (u) du∫abf (x) dx = ∫abf (t) dt = ∫abf (u) duРанее мы обсуждали тот факт, что если f (x) f (x) непрерывна на [a, b], [a, b], то предел limn → ∞∑i = 1nf (xi *) ∆xlimn → ∞∑ i = 1nf (xi *) Δx существует и единственно.Это приводит к следующей теореме, которую мы сформулируем без доказательства.
Теорема 5.1
Непрерывные функции интегрируемы
Если f (x) f (x) непрерывна на [a, b], [a, b], то f интегрируемо на [a, b]. [A , б].
Функции, которые не являются непрерывными на [a, b] [a, b], могут быть интегрируемыми, в зависимости от характера разрывов. Например, функции с конечным числом скачков на отрезке интегрируемы.
Здесь также стоит отметить, что мы сохранили использование регулярного разбиения в суммах Римана.Это ограничение не является строго необходимым. Любое разбиение можно использовать для образования суммы Римана. Однако, если для определения определенного интеграла используется нерегулярное разбиение, этого недостаточно, поскольку количество подынтервалов стремится к бесконечности. Вместо этого мы должны принять предел, поскольку ширина самого большого подынтервала стремится к нулю. Это вводит немного более сложные обозначения в наши пределы и усложняет вычисления без особого дополнительного понимания, поэтому мы придерживаемся регулярных разбиений для сумм Римана.
Пример 5.7
Вычисление интеграла по определению
Используйте определение определенного интеграла для вычисления ∫02x2dx.∫02x2dx. Используйте аппроксимацию правой конечной точки, чтобы получить сумму Римана.
Решение
Сначала мы хотим установить сумму Римана. Исходя из пределов интегрирования, имеем a = 0a = 0 и b = 2.b = 2. Для i = 0,1,2,…, n, i = 0,1,2,…, n, пусть P = {xi} P = {xi} — регулярное разбиение [0,2]. [0, 2]. Тогда
Δx = b − an = 2n.Δx = b − an = 2n.Поскольку мы используем аппроксимацию правой конечной точки для генерации сумм Римана, для каждого i нам нужно вычислить значение функции на правом конце интервала [xi − 1, xi]. [Xi − 1, xi] . Правая конечная точка интервала — xi, xi, и поскольку P является обычным разделом,
xi = x0 + iΔx = 0 + i [2n] = 2in.xi = x0 + iΔx = 0 + i [2n] = 2in.Таким образом, значение функции на правом конце интервала составляет
f (xi) = xi2 = (2in) 2 = 4i2n2.f (xi) = xi2 = (2in) 2 = 4i2n2.Тогда сумма Римана принимает вид
∑i = 1nf (xi) Δx = ∑i = 1n (4i2n2) 2n = ∑i = 1n8i2n3 = 8n3∑i = 1ni2.∑i = 1nf (xi) Δx = ∑i = 1n (4i2n2) 2n = ∑i = 1n8i2n3 = 8n3∑i = 1ni2.Используя формулу суммирования для ∑i = 1ni2, ∑i = 1ni2, получаем
∑i = 1nf (xi) Δx = 8n3∑i = 1ni2 = 8n3 [n (n + 1) (2n + 1) 6] = 8n3 [2n3 + 3n2 + n6] = 16n3 + 24n2 + 8n6n3 = 83 + 4n + 86n2.∑i = 1nf (xi) Δx = 8n3∑i = 1ni2 = 8n3 [n (n + 1) (2n + 1) 6] = 8n3 [2n3 + 3n2 + n6] = 16n3 + 24n2 + 8n6n3 = 83 + 4n + 86n2.Теперь, чтобы вычислить определенный интеграл, нам нужно перейти к пределу при n → ∞.n → ∞. Получаем
∫02x2dx = limn → ∞∑i = 1nf (xi) ∆x = limn → ∞ (83 + 4n + 86n2) = limn → ∞ (83) + limn → ∞ (4n) + limn → ∞ (86n2) = 83 + 0. + 0 = 83. 02x2dx = limn → ∞∑i = 1nf (xi) ∆x = limn → ∞ (83 + 4n + 86n2) = limn → ∞ (83) + limn → ∞ (4n) + limn → ∞ (86n2 ) = 83 + 0 + 0 = 83.КПП 5,7
Используйте определение определенного интеграла, чтобы вычислить ∫03 (2x − 1) dx.∫03 (2x − 1) dx. Используйте аппроксимацию правой конечной точки, чтобы получить сумму Римана.
Вычисление определенных интегралов
Вычисление определенных интегралов таким способом может быть довольно утомительным из-за сложности вычислений. Позже в этой главе мы разработаем методы вычисления определенных интегралов без , взяв пределы сумм Римана. Однако на данный момент мы можем полагаться на тот факт, что определенные интегралы представляют площадь под кривой, и мы можем вычислить определенные интегралы, используя геометрические формулы для вычисления этой площади.Мы делаем это, чтобы подтвердить, что определенные интегралы действительно представляют собой площади, поэтому мы можем обсудить, что делать в случае, если кривая функции опускается ниже оси x .
Пример 5.8
Использование геометрических формул для вычисления определенных интегралов
Используйте формулу площади круга, чтобы вычислить ∫369− (x − 3) 2dx.369− (x − 3) 2dx.
Решение
Функция описывает полукруг с радиусом 3. Найти
∫369− (x − 3) 2dx, ∫369− (x − 3) 2dx,мы хотим найти площадь под кривой на интервале [3,6].[3,6]. Формула площади круга: A = πr2.A = πr2. Площадь полукруга составляет половину площади круга, или A = (12) πr2.A = (12) πr2. Заштрихованная область на рис. 5.16 покрывает половину полукруга, или A = (14) πr2.A = (14) πr2. Таким образом,
∫369− (x − 3) 2 = 14π (3) 2 = 94π≈7,069. 369− (x − 3) 2 = 14π (3) 2 = 94π≈7,069. Рис. 5.16. Значение интеграла функции f (x) f (x) на интервале [3,6] [3,6] представляет собой площадь заштрихованной области.КПП 5.8
Используйте формулу площади трапеции, чтобы вычислить ∫24 (2x + 3) dx.∫24 (2x + 3) dx.
Площадь и определенный интеграл
При определении определенного интеграла мы сняли требование неотрицательности f (x) f (x). Но как мы интерпретируем «площадь под кривой», когда f (x) f (x) отрицательно?
Чистая подписанная площадь
Вернемся к сумме Римана. Рассмотрим, например, функцию f (x) = 2−2x2f (x) = 2−2×2 (показанную на рисунке 5.17) на интервале [0,2]. [0,2]. Используйте n = 8n = 8 и выберите {xi *} {xi *} в качестве левой конечной точки каждого интервала.Постройте прямоугольник на каждом подынтервале высотой f (xi *) f (xi *) и шириной Δ x . Когда f (xi *) f (xi *) положительно, произведение f (xi *) Δxf (xi *) Δx, как и раньше, представляет площадь прямоугольника. Однако, когда f (xi *) f (xi *) отрицательно, произведение f (xi *) Δxf (xi *) Δx представляет отрицательных площади прямоугольника. Сумма Римана тогда становится
∑i = 18f (xi *) Δx = (Площадь прямоугольников над осью x) — (Площадь прямоугольников ниже оси x) ∑i = 18f (xi *) Δx = (Площадь прямоугольников над осью x) — ( Площадь прямоугольников ниже оси x)Рисунок 5.17 Для функции, которая частично отрицательна, сумма Римана — это площадь прямоугольников выше оси x минус площадь прямоугольников ниже оси x .
Принимая предел при n → ∞, n → ∞, сумма Римана приближается к площади между кривой выше оси x и осью x , за вычетом площади между кривой ниже оси x и ось x , как показано на рис. 5.18. Затем
∫02f (x) dx = limn → ∞∑i = 1nf (ci) Δx = A1 − A2.∫02f (x) dx = limn → ∞∑i = 1nf (ci) Δx = A1 − A2.Величина A1-A2A1-A2 называется чистой подписанной областью.
Рисунок 5.18 В пределе определенный интеграл равен площади A 1 за вычетом площади A 2 или чистой подписанной площади.
Обратите внимание, что чистая подписанная площадь может быть положительной, отрицательной или нулевой. Если область над осью x больше, чистая подписанная область положительна. Если область под осью x больше, чистая подписанная область отрицательна.Если области выше и ниже оси x равны, чистая подписанная область равна нулю.
Пример 5.9
Поиск чистой подписанной области
Найдите чистую площадь со знаком между кривой функции f (x) = 2xf (x) = 2x и осью x на интервале [−3,3]. [- 3,3].
Решение
Функция создает прямую линию, которая образует два треугольника: один от x = −3x = −3 до x = 0x = 0, а другой от x = 0x = 0 до x = 3x = 3 (рисунок 5.19). Используя геометрическую формулу для площади треугольника, A = 12bh, A = 12bh, площадь треугольника A 1 над осью равна
, где 3 — основание, а 2 (3) = 62 (3) = 6 — высота. Площадь треугольника A 2 ниже оси равна
A2 = 12 (3) (6) = 9, A2 = 12 (3) (6) = 9,, где 3 — это основание, а 6 — высота. Таким образом, чистая площадь составляет
∫ − 332xdx = A1 − A2 = 9−9 = 0. − 332xdx = A1 − A2 = 9−9 = 0.Рис. 5.19. Площадь над кривой и под осью x равна площади под кривой и над осью x .
Анализ
Если A 1 — это область над осью x , а A 2 — это область под осью x , то чистая площадь равна A1 − A2.A1 − A2. Поскольку площади двух треугольников равны, чистая площадь равна нулю.
КПП 5.9
Найдите чистую знаковую площадь f (x) = x − 2f (x) = x − 2 на интервале [0,6], [0,6], как показано на следующем рисунке.
Общая площадь
Одно из применений определенного интеграла — определение смещения при заданной функции скорости.Если v (t) v (t) представляет скорость объекта как функцию времени, тогда площадь под кривой сообщает нам, насколько далеко объект от своего исходного положения. Это очень важное применение определенного интеграла, и мы рассмотрим его более подробно позже в этой главе. А пока мы просто рассмотрим некоторые основы, чтобы понять, как это работает, изучая постоянные скорости.
Когда скорость постоянна, площадь под кривой равна скорости, умноженной на время. Эта идея уже хорошо знакома.Если автомобиль удаляется от исходного положения по прямой со скоростью 70 миль в час в течение 2 часов, то он находится на расстоянии 140 миль от исходного положения (рис. 5.20). Используя интегральные обозначения, имеем
∫0270dt = 140.∫0270dt = 140. Рис. 5.20. Площадь под кривой v (t) = 75v (t) = 75 показывает, как далеко автомобиль находится от начальной точки в данный момент времени.В контексте смещения чистая подписанная площадь позволяет нам учитывать направление. Если автомобиль движется прямо на север со скоростью 60 миль в час в течение 2 часов, он находится в 120 милях к северу от своей начальной позиции.Если после этого автомобиль развернется и поедет на юг со скоростью 40 миль в час в течение 3 часов, он вернется в исходное положение (рис. 5.21). Опять же, используя интегральные обозначения, имеем
∫0260dt + ∫25−40dt = 120−120 = 0. 0260dt + ∫25−40dt = 120−120 = 0.В данном случае смещение равно нулю.
Рис. 5.21. Площадь над осью и площадь под осью равны, поэтому чистая подписанная площадь равна нулю.
Предположим, мы хотим знать, как далеко автомобиль проехал в целом, независимо от направления.В этом случае мы хотим знать область между кривой и осью x , независимо от того, находится эта область выше или ниже оси. Это называется общей площадью.
С графической точки зрения проще всего рассчитать общую площадь, добавив области над осью и области под осью (вместо вычитания областей под осью, как мы это делали с чистой подписанной областью). Чтобы достичь этого математически, мы используем функцию абсолютного значения. Таким образом, общее расстояние, пройденное автомобилем, составит
∫02 | 60 | dt + ∫25 | −40 | dt = ∫0260dt + ∫2540dt = 120 + 120 = 240.∫02 | 60 | dt + ∫25 | −40 | dt = ∫0260dt + ∫2540dt = 120 + 120 = 240.Объединяя эти идеи формально, мы даем следующие определения.
Определение
Пусть f (x) f (x) — интегрируемая функция, определенная на интервале [a, b]. [A, b]. Пусть A 1 представляет область между f (x) f (x) и осью x , которая лежит на выше оси , а A 2 представляет область между f (x) f. (x) и ось x , которая находится на ниже оси .Тогда чистая подписанная область между f (x) f (x) и осью x задается как
Abf (x) dx = A1 − A2. Abf (x) dx = A1 − A2.Общая площадь между f (x) f (x) и осью x определяется как
Ab | f (x) | dx = A1 + A2. Ab | f (x) | dx = A1 + A2.Пример 5.10
Определение общей площади
Найдите общую площадь между f (x) = x − 2f (x) = x − 2 и осью x в интервале [0,6]. [0,6].
Решение
Вычислите точку пересечения x как (2,0) (2,0) (установите y = 0, y = 0, найдите x ).Чтобы найти общую площадь, возьмите область ниже оси x на подынтервале [0,2] [0,2] и добавьте ее к области над осью x на подынтервале [2,6] [2,6] (Рисунок 5.22).
Рис. 5.22. Общая площадь между линией и осью x на [0,6] [0,6] составляет A 2 плюс A 1 .У нас
∫06 | (x − 2) | dx = A2 + A1. 06 | (x − 2) | dx = A2 + A1.Тогда, используя формулу площади треугольника, получим
A2 = 12bh = 12 · 2 · 2 = 2 A2 = 12bh = 12 · 2 · 2 = 2 A1 = 12bh = 12 · 4 · 4 = 8.A1 = 12bh = 12 · 4 · 4 = 8.Таким образом, общая площадь составляет
A1 + A2 = 8 + 2 = 10. A1 + A2 = 8 + 2 = 10.КПП 5.10
Найдите общую площадь между функцией f (x) = 2xf (x) = 2x и осью x в интервале [−3,3]. [- 3,3].
Свойства определенного интеграла
Свойства неопределенных интегралов применимы также к определенным интегралам. Определенные интегралы также имеют свойства, относящиеся к пределам интегрирования. Эти свойства вместе с правилами интегрирования, которые мы рассмотрим далее в этой главе, помогают нам манипулировать выражениями для вычисления определенных интегралов.
Правило: свойства определенного интеграла
-
∫aaf (x) dx = 0∫aaf (x) dx = 05,9
Если пределы интегрирования одинаковы, интеграл представляет собой просто линию и не содержит области. -
∫baf (x) dx = −∫abf (x) dx∫baf (x) dx = −∫abf (x) dx5.10
Если пределы поменяны местами, поставьте знак минус перед интегралом . -
ab [f (x) + g (x)] dx = ∫abf (x) dx + ∫abg (x) dx∫ab [f (x) + g (x)] dx = ∫abf (x) dx + ∫abg (x) dx5.11
Интеграл от суммы — это сумма интегралов. -
ab [f (x) −g (x)] dx = ∫abf (x) dx − ∫abg (x) dx∫ab [f (x) −g (x)] dx = ∫abf (x) dx − ∫abg (x) dx5,12
Интеграл разности — это разность интегралов. -
∫abcf (x) dx = c∫abf (x) ∫abcf (x) dx = c∫abf (x)5.13
для константы c . Интеграл от произведения константы и функции равен константе, умноженной на интеграл функции. -
∫abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx∫abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx5.14
Хотя эта формула обычно применяется, когда c находится между a и b , формула верна для всех значений a , b и c , при условии, что f (x) f (x ) интегрируемо на наибольшем интервале.
Пример 5.11
Использование свойств определенного интеграла
Используйте свойства определенного интеграла, чтобы выразить определенный интеграл от f (x) = — 3×3 + 2x + 2f (x) = — 3×3 + 2x + 2 в интервале [−2,1] [- 2,1] как сумму трех определенных интегралов.
Решение
В интегральных обозначениях имеем ∫ − 21 (−3×3 + 2x + 2) dx.∫ − 21 (−3×3 + 2x + 2) dx. Применяем свойства 3. и 5., чтобы получить
. ∫ − 21 (−3×3 + 2x + 2) dx = ∫ − 21−3x3dx + ∫ − 212xdx + ∫ − 212dx = −3∫ − 21x3dx + 2∫ − 21xdx + ∫ − 212dx.∫ − 21 (−3×3 + 2x + 2) dx = ∫ − 21−3x3dx + ∫ − 212xdx + ∫ − 212dx = −3∫ − 21x3dx + 2∫ − 21xdx + ∫ − 212dx.КПП 5.11
Используйте свойства определенного интеграла, чтобы выразить определенный интеграл от f (x) = 6×3−4×2 + 2x − 3f (x) = 6×3−4×2 + 2x − 3 на интервале [1,3] [1,3] как сумму четырех определенных интегралов.
Пример 5.12
Использование свойств определенного интеграла
Если известно, что ∫08f (x) dx = 10∫08f (x) dx = 10 и ∫05f (x) dx = 5, ∫05f (x) dx = 5, найдите значение ∫58f (x) dx.∫58f (x) dx.
Решение
По собственности 6.,
Abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx.∫abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx.Таким образом,
∫08f (x) dx = ∫05f (x) dx + ∫58f (x) dx10 = 5 + ∫58f (x) dx5 = ∫58f (x) dx.∫08f (x) dx = ∫05f (x) dx + ∫ 58f (x) dx10 = 5 + ∫58f (x) dx5 = ∫58f (x) dx.КПП 5.12
Если известно, что ∫15f (x) dx = −3∫15f (x) dx = −3 и ∫25f (x) dx = 4, ∫25f (x) dx = 4, найдите значение ∫12f ( x) dx.∫12f (x) dx.
Сравнительные свойства интегралов
Изображение иногда может рассказать нам о функции больше, чем результаты вычислений. Сравнение функций по их графикам, а также по их алгебраическим выражениям часто может дать новое понимание процесса интеграции. Интуитивно можно сказать, что если функция f (x) f (x) находится над другой функцией g (x), g (x), то область между f (x) f (x) и осью x больше площади между g (x) g (x) и осью x .Это верно в зависимости от интервала, в течение которого производится сравнение. Свойства определенных интегралов действительны независимо от того, a
Теорема 5.2
Теорема сравнения
- Если f (x) ≥0f (x) ≥0 для a≤x≤b, a≤x≤b, то
Abf (x) dx≥0.∫abf (x) dx≥0. - Если f (x) ≥g (x) f (x) ≥g (x) для a≤x≤b, a≤x≤b, то
Abf (x) dx≥∫abg (x) dx.Abf (x) dx≥∫abg (x) dx. - Если m и M — константы такие, что m≤f (x) ≤Mm≤f (x) ≤M для a≤x≤b, a≤x≤b, то
m (b − a) ≤∫abf (x) dx≤M (b − a). m (b − a) ≤∫abf (x) dx≤M (b − a).
Пример 5.13
Сравнение двух функций за заданный интервал
Сравните f (x) = 1 + x2f (x) = 1 + x2 и g (x) = 1 + xg (x) = 1 + x в интервале [0,1]. [0,1].
Решение
Построение графиков этих функций необходимо, чтобы понять, как они сравниваются в интервале [0,1].[0,1]. Изначально при построении графика на графическом калькуляторе f (x) f (x) оказывается везде выше g (x) g (x). Однако на интервале [0,1], [0,1] графики кажутся поверх друг друга. Нам нужно увеличить масштаб, чтобы увидеть, что на интервале [0,1], g (x) [0,1], g (x) находится выше f (x) .f (x). Две функции пересекаются в точках x = 0x = 0 и x = 1x = 1 (рисунок 5.23).
Рисунок 5.23 (a) Функция f (x) f (x) появляется над функцией g (x) g (x) за исключением интервала [0,1] [0,1] (b) Просмотр того же графика с больший масштаб показывает это более четко.Из графика видно, что на интервале [0,1] g (x) ≥f (x). [0,1], g (x) ≥f (x). Сравнивая интегралы по заданному интервалу [0,1], [0,1], мы также видим, что ∫01g (x) dx≥∫01f (x) dx∫01g (x) dx≥∫01f (x) dx ( Рисунок 5.24). Тонкая заштрихованная область показывает, насколько велика разница между этими двумя интегралами в интервале [0,1]. [0,1].
Рисунок 5.24 (a) График показывает, что на интервале [0,1] g (x) ≥f (x), [0,1], g (x) ≥f (x), где равенство выполняется только на конечные точки интервала.(b) Просмотр того же графика с большим увеличением показывает это более четко.Среднее значение функции
Нам часто требуется найти среднее значение набора чисел, например средней оценки за тест. Предположим, вы получили следующие результаты тестов в своем классе алгебры: 89, 90, 56, 78, 100 и 69. Ваша семестровая оценка — это ваши средние результаты тестов, и вы хотите знать, какую оценку ожидать. Мы можем найти среднее значение, сложив все оценки и разделив их на количество оценок. В этом случае есть шесть результатов теста.Таким образом,
89 + 90 + 56 + 78 + 100 + 696 = 4826≈80,33,89 + 90 + 56 + 78 + 100 + 696 = 4826≈80,33.Таким образом, ваша средняя оценка за тест составляет примерно 80,33, что в большинстве школ соответствует B-.
Однако предположим, что у нас есть функция v (t) v (t), которая дает нам скорость объекта в любой момент времени t , и мы хотим найти среднюю скорость объекта. Функция v (t) v (t) принимает бесконечное количество значений, поэтому мы не можем использовать только что описанный процесс. К счастью, мы можем использовать определенный интеграл, чтобы найти среднее значение такой функции, как эта.
Пусть f (x) f (x) непрерывна в интервале [a, b] [a, b] и пусть [a, b] [a, b] разделен на n подинтервалов шириной Δx = (b −a) /n.Δx= (b − a) / n. Выберите представителя xi * xi * в каждом подынтервале и вычислите f (xi *) f (xi *) для i = 1,2,…, n.i = 1,2,…, n. Другими словами, рассматривайте каждый f (xi *) f (xi *) как выборку функции на каждом подынтервале. Среднее значение функции может быть приблизительно равно
. f (x1 *) + f (x2 *) + ⋯ + f (xn *) n, f (x1 *) + f (x2 *) + ⋯ + f (xn *) n,, которое по сути является тем же выражением, которое используется для вычисления среднего дискретных значений.
Но мы знаем Δx = b − an, Δx = b − an, поэтому n = b − aΔx, n = b − aΔx, и мы получаем
f (x1 *) + f (x2 *) + ⋯ + f (xn *) n = f (x1 *) + f (x2 *) + ⋯ + f (xn *) (b − a) Δx.f (x1 *) + f (x2 *) + ⋯ + f (xn *) n = f (x1 *) + f (x2 *) + ⋯ + f (xn *) (b − a) Δx.После алгебры числитель представляет собой сумму, которая представлена как i = 1nf (xi *), ∑i = 1nf (xi *), и мы делим на дробь. Чтобы разделить на дробь, переверните знаменатель и умножьте. Таким образом, приблизительное значение среднего значения функции составляет
∑i = 1nf (xi *) (b − a) Δx = (Δxb − a) ∑i = 1nf (xi *) = (1b − a) ∑i = 1nf (xi *) Δx.∑i = 1nf (xi *) (b − a) Δx = (Δxb − a) ∑i = 1nf (xi *) = (1b − a) ∑i = 1nf (xi *) Δx.Это сумма Римана. Затем, чтобы получить точное среднее значение , возьмите предел, поскольку n стремится к бесконечности. Таким образом, среднее значение функции равно
1b − alimn → ∞∑i = 1nf (xi) Δx = 1b − a∫abf (x) dx. 1b − alimn → ∞∑i = 1nf (xi) Δx = 1b − a∫abf (x) dx.Определение
Пусть f (x) f (x) непрерывна на интервале [a, b]. [A, b]. Тогда среднее значение функции f (x) f (x) (или f ave ) на [a, b] [a, b] равно
fave = 1b − a∫abf (x) dx.fave = 1b − a∫abf (x) dx.Пример 5.14
Нахождение среднего значения линейной функции
Найдите среднее значение f (x) = x + 1f (x) = x + 1 на интервале [0,5]. [0,5].
Решение
Сначала изобразите функцию на указанном интервале, как показано на Рисунке 5.25.
Рисунок 5.25 На графике показана площадь под функцией f (x) = x + 1f (x) = x + 1 над [0,5]. [0,5].Область представляет собой трапецию, лежащую на боку, поэтому мы можем использовать формулу площади для трапеции A = 12h (a + b), A = 12h (a + b), где h представляет высоту, а a и b представляют две параллельные стороны.Затем
∫05x + 1dx = 12h (a + b) = 12 · 5 · (1 + 6) = 352. 05x + 1dx = 12h (a + b) = 12 · 5 · (1 + 6) = 352.Таким образом, среднее значение функции составляет
. 15−0∫05x + 1dx = 15 · 352 = 72,15−0∫05x + 1dx = 15 · 352 = 72.КПП 5.13
Найдите среднее значение f (x) = 6−2xf (x) = 6−2x в интервале [0,3]. [0,3].
Раздел 5.2. Упражнения
В следующих упражнениях пределы выражаются в виде интегралов.
60.limn → ∞∑i = 1n (xi *) Δxlimn → ∞∑i = 1n (xi *) Δx по [1,3] [1,3]
61.limn → ∞∑i = 1n (5 (xi *) 2−3 (xi *) 3) Δxlimn → ∞∑i = 1n (5 (xi *) 2−3 (xi *) 3) Δx над [0, 2] [0,2]
62.limn → ∞∑i = 1nsin2 (2πxi *) Δxlimn → ∞∑i = 1nsin2 (2πxi *) Δx на [0,1] [0,1]
63.limn → ∞∑i = 1ncos2 (2πxi *) Δxlimn → ∞∑i = 1ncos2 (2πxi *) Δx на [0,1] [0,1]
В следующих упражнениях, учитывая L n или R n , как указано, выразите их пределы при n → ∞n → ∞ как определенные интегралы, определяя правильные интервалы.
64.Ln = 1n∑i = 1ni − 1nLn = 1n∑i = 1ni − 1n
65.Rn = 1n∑i = 1ninRn = 1n∑i = 1nin
66.Ln = 2n∑i = 1n (1 + 2i − 1n) Ln = 2n∑i = 1n (1 + 2i − 1n)
67.Rn = 3n∑i = 1n (3 + 3 дюйма) Rn = 3n∑i = 1n (3 + 3 дюйма)
68.Ln = 2πn∑i = 1n2πi − 1ncos (2πi − 1n) Ln = 2πn∑i = 1n2πi − 1ncos (2πi − 1n)
69.Rn = 1n∑i = 1n (1 + дюйм) журнал ((1 + дюйм) 2) Rn = 1n∑i = 1n (1 + дюйм) журнал ((1 + дюйм) 2)
В следующих упражнениях вычислите интегралы функций, изображенных на графике, с помощью формул для площадей треугольников и кругов и вычитания площадей ниже оси x .
70. 72. 74.В следующих упражнениях вычислите интеграл, используя формулы площади.
76.∫03 (3 − x) dx∫03 (3 − x) dx
77.∫23 (3 − x) dx∫23 (3 − x) dx
78.∫ − 33 (3− | x |) dx∫ − 33 (3− | x |) dx
79.∫06 (3− | x − 3 |) dx∫06 (3− | x − 3 |) dx
80.∫ − 224 − x2dx∫ − 224 − x2dx
81.∫154− (x − 3) 2dx∫154− (x − 3) 2dx
82.∫01236− (x − 6) 2dx∫01236− (x − 6) 2dx
83.∫ − 23 (3− | x |) dx∫ − 23 (3− | x |) dx
В следующих упражнениях используйте средние значения в левой ( L ) и правой ( R ) конечных точках, чтобы вычислить интегралы кусочно-линейных функций с графиками, которые проходят через данный список точек через указанные интервалы.
84.{(0,0), (2,1), (4,3), (5,0), (6,0), (8,3)} {(0,0), (2,1) , (4,3), (5,0), (6,0), (8,3)} больше [0,8] [0,8]
85.{(0,2), (1,0), (3,5), (5,5), (6,2), (8,0)} {(0,2), (1,0) , (3,5), (5,5), (6,2), (8,0)} больше [0,8] [0,8]
86.{(−4, −4), (- 2,0), (0, −2), (3,3), (4,3)} {(- 4, −4), (- 2,0 ), (0, −2), (3,3), (4,3)} над [−4,4] [- 4,4]
87.{(−4,0), (- 2,2), (0,0), (1,2), (3,2), (4,0)} {(- 4,0), (- 2,2), (0,0), (1,2), (3,2), (4,0)} над [−4,4] [- 4,4]
Предположим, что ∫04f (x) dx = 5∫04f (x) dx = 5 и ∫02f (x) dx = −3, ∫02f (x) dx = −3 и ∫04g (x) dx = −1 ∫04g (x) dx = −1 и ∫02g (x) dx = 2.∫02g (x) dx = 2. В следующих упражнениях вычислите интегралы.
88.∫04 (f (x) + g (x)) dx∫04 (f (x) + g (x)) dx
89.∫24 (f (x) + g (x)) dx∫24 (f (x) + g (x)) dx
90.∫02 (f (x) −g (x)) dx∫02 (f (x) −g (x)) dx
91.∫24 (f (x) −g (x)) dx∫24 (f (x) −g (x)) dx
92.∫02 (3f (x) −4g (x)) dx∫02 (3f (x) −4g (x)) dx
93.∫24 (4f (x) −3g (x)) dx∫24 (4f (x) −3g (x)) dx
В следующих упражнениях используйте тождество ∫ − AAf (x) dx = ∫ − A0f (x) dx + ∫0Af (x) dx∫ − AAf (x) dx = ∫ − A0f (x) dx + ∫0Af (x) dx для вычисления интегралов.
94.∫ − ππsint1 + t2dt∫ − ππsint1 + t2dt (Подсказка: sin (−t) = — sin (t)) (Подсказка: sin (−t) = — sin (t))
95.∫ − ππt1 + costdt∫ − ππt1 + costdt
В следующих упражнениях найдите чистую зону со знаком между f (x) f (x) и осью x.
96.∫13 (2 − x) dx∫13 (2 − x) dx ( Подсказка: Посмотрите на график f .)
97.∫24 (x − 3) 3dx∫24 (x − 3) 3dx ( Подсказка: Посмотрите на график f .)
В следующих упражнениях, учитывая, что ∫01xdx = 12, ∫01x2dx = 13, ∫01xdx = 12, ∫01x2dx = 13 и ∫01x3dx = 14, ∫01x3dx = 14, вычислите интегралы.
98.∫01 (1 + x + x2 + x3) dx∫01 (1 + x + x2 + x3) dx
99.∫01 (1 − x + x2 − x3) dx∫01 (1 − x + x2 − x3) dx
100.∫01 (1 − x) 2dx∫01 (1 − x) 2dx
101.∫01 (1-2x) 3dx∫01 (1-2x) 3dx
102.∫01 (6x − 43×2) dx∫01 (6x − 43×2) dx
103.∫01 (7−5×3) dx∫01 (7−5×3) dx
В следующих упражнениях используйте теорему сравнения.
104.Покажите, что ∫03 (x2−6x + 9) dx≥0.∫03 (x2−6x + 9) dx≥0.
105.Покажите, что ∫ − 23 (x − 3) (x + 2) dx≤0.∫ − 23 (x − 3) (x + 2) dx≤0.
106.Покажите, что ∫011 + x3dx≤∫011 + x2dx.∫011 + x3dx≤∫011 + x2dx.
107.Покажите, что ∫121 + xdx≤∫121 + x2dx.∫121 + xdx≤∫121 + x2dx.
108.Покажите, что ∫0π / 2sintdt≥π4.∫0π / 2sintdt≥π4. (Подсказка: sint≥2tπ (Подсказка: sint≥2tπ над [0, π2]) [0, π2])
109.Покажите, что ∫ − π / 4π / 4costdt≥π2 / 4.∫ − π / 4π / 4costdt≥π2 / 4.
В следующих упражнениях найдите среднее значение f ave из f между a и b и найдите точку c , где f (c) = fave.f (c) = любимый.
110.f (x) = x2, a = −1, b = 1 f (x) = x2, a = −1, b = 1
111.f (x) = x5, a = −1, b = 1 f (x) = x5, a = −1, b = 1
112.f (x) = 4 − x2, a = 0, b = 2f (x) = 4 − x2, a = 0, b = 2
113.f (x) = (3− | x |), a = −3, b = 3f (x) = (3− | x |), a = −3, b = 3
114.f (x) = sinx, a = 0, b = 2πf (x) = sinx, a = 0, b = 2π
115.f (x) = cosx, a = 0, b = 2πf (x) = cosx, a = 0, b = 2π
В следующих упражнениях аппроксимируйте среднее значение, используя суммы Римана L 100 и R 100 .Как ваш ответ соотносится с точным данным ответом?
116.[T] y = ln (x) y = ln (x) в интервале [1,4]; [1,4]; точное решение ln (256) 3−1.ln (256) 3−1.
117.[T] y = ex / 2y = ex / 2 в интервале [0,1]; [0,1]; точное решение 2 (e − 1) .2 (e − 1).
118.[T] y = tanxy = tanx в интервале [0, π4]; [0, π4]; точное решение 2ln (2) π.2ln (2) π.
119.[T] y = x + 14 − x2y = x + 14 − x2 в интервале [−1,1]; [- 1,1]; точное решение — π6.π6.
В следующих упражнениях вычислите среднее значение, используя левую сумму Римана L N для N = 1,10,100.N = 1,10,100. Как точность соотносится с заданным точным значением?
120.[T] y = x2−4y = x2−4 в интервале [0,2]; [0,2]; точное решение -83.-83.
121.[T] y = xex2y = xex2 в интервале [0,2]; [0,2]; точное решение — 14 (e4−1) .14 (e4−1).
122.[T] y = (12) xy = (12) x в интервале [0,4]; [0,4]; точное решение — 1564ln (2).1564ln (2).
123.[T] y = xsin (x2) y = xsin (x2) в интервале [−π, 0]; [- π, 0]; точное решение — cos (π2) −12π.cos (π2) −12π.
124.Предположим, что A = ∫02πsin2tdtA = ∫02πsin2tdt и B = ∫02πcos2tdt.B = ∫02πcos2tdt. Покажем, что A + B = 2πA + B = 2π и A = B.A = B.
125.Предположим, что A = ∫ − π / 4π / 4sec2tdt = πA = ∫ − π / 4π / 4sec2tdt = π и B = ∫ − π / 4π / 4tan2tdt.B = ∫ − π / 4π / 4tan2tdt. Покажем, что A − B = π2.A − B = π2.
126.Покажите, что среднее значение sin2tsin2t на [0,2π] [0,2π] равно 1/2 Без дальнейших вычислений определите, равно ли среднее значение sin2tsin2t на [0, π] [0, π] до 1/2.
127.Покажите, что среднее значение cos2tcos2t на [0,2π] [0,2π] равно 1 / 2,1 / 2. Без дополнительных вычислений определите, равно ли среднее значение cos2 (t) cos2 (t) по [0, π] [0, π] 1 / 2,1 / 2.
128. Объясните, почему графики квадратичной функции (параболы) p (x) p (x) и линейной функции ℓ (x) ℓ (x) могут пересекаться не более чем в двух точках. Предположим, что p (a) = ℓ (a) p (a) = ℓ (a) и p (b) = ℓ (b), p (b) = ℓ (b), и что ∫abp (t) dt> Abℓ (t) dt.∫abp (t) dt> ∫abℓ (t) dt. Объясните, почему ∫cdp (t)> ∫cdℓ (t) dt∫cdp (t)> ∫cdℓ (t) dt, когда a≤c Предположим, что парабола p (x) = ax2 + bx + cp (x) = ax2 + bx + c открывается вниз (a <0) (a <0) и имеет вершину y = −b2a> 0. y = — b2a> 0. Для какого интервала [A, B] [A, B] ∫AB (ax2 + bx + c) dx∫AB (ax2 + bx + c) dx максимально велико? Предположим, что [a, b] [a, b] можно разделить на подинтервалы a = a0 Предположим, что f и g — непрерывные функции, такие что ∫cdf (t) dt≤∫cdg (t) dt∫cdf (t) dt≤∫cdg (t) dt для каждого подынтервала [c, d] [c , d] из [a, b]. [a, b]. Объясните, почему f (x) ≤g (x) f (x) ≤g (x) для всех значений x . Предположим, что среднее значение f по [a, b] [a, b] равно 1, а среднее значение f по [b, c] [b, c] равно 1, где a Предположим, что [a, b] [a, b] можно разделить. взяв a = a0 Предположим, что для каждого i такого, что 1≤i≤N1≤i≤N, имеет место ∫i − 1if (t) dt = i.∫i − 1if (t) dt = i. Покажем, что ∫0Nf (t) dt = N (N + 1) 2. 0Nf (t) dt = N (N + 1) 2. Предположим, что для каждого i такого, что 1≤i≤N1≤i≤N, выполняется ∫i − 1if (t) dt = i2.∫i − 1if (t) dt = i2. Покажем, что ∫0Nf (t) dt = N (N + 1) (2N + 1) 6. 0Nf (t) dt = N (N + 1) (2N + 1) 6. [T] Вычислите левую и правую суммы Римана L 10 и R 10 и их среднее значение L10 + R102L10 + R102 для f (t) = t2f (t) = t2 за [0, 1]. [0,1]. Учитывая, что ∫01t2dt = 0,33–, ∫01t2dt = 0,33–, до скольки десятичных знаков точность L10 + R102L10 + R102? [T] Вычислите левую и правую суммы Римана, L 10 и R 10 , и их среднее значение L10 + R102L10 + R102 для f (t) = (4 − t2) f (t ) = (4 − t2) над [1,2]. [1,2]. Учитывая, что ∫12 (4 − t2) dt = 1.66–, ∫12 (4 − t2) dt = 1.66–, до скольки десятичных знаков точность L10 + R102L10 + R102? Если ∫151 + t4dt = 41.7133 …, ∫151 + t4dt = 41.7133 …, что такое ∫151 + u4du? ∫151 + u4du? Оцените ∫01tdt∫01tdt, используя суммы левой и правой конечных точек, каждая с одним прямоугольником.Как соотносится среднее этих сумм левой и правой конечных точек с фактическим значением ∫01tdt? ∫01tdt? Оцените ∫01tdt∫01tdt путем сравнения с площадью одиночного прямоугольника с высотой, равной значению t в средней точке t = 12.t = 12. Как эта средняя оценка соотносится с фактическим значением ∫01tdt? ∫01tdt? Из графика sin (2πx) sin (2πx) показано: Если f является 1-периодическим (f (t + 1) = f (t)), (f (t + 1) = f (t)), нечетным и интегрируемым по [0,1], [0 , 1], всегда ли верно, что ∫01f (t) dt = 0? ∫01f (t) dt = 0? Если f является 1-периодическим и ∫01f (t) dt = A, ∫01f (t) dt = A, обязательно ли, что ∫a1 + af (t) dt = A∫a1 + af (t) dt = A для всех A ? Несомненно, некоторые термины в области математики могут быть немного пугающими.Однако, как только вы перестанете использовать имена, то, как работает фактическая математика, будет довольно просто. Понимание интеграции Интеграция — это метод, используемый для добавления фрагментов для поиска целого. Его можно использовать для определения центральных точек, объемов и площадей нескольких полезных вещей. Однако проще всего начать с области под кривой функции. Пока можно вычислить функцию в нескольких точках и сложить срезы шириной Δx; однако ответ, к которому вы придете, не будет очень точным.Лучший способ — уменьшить Δx и сложить более мелкие срезы, что даст более точный ответ. По мере того, как срезы становятся ближе к нулю по ширине, вы приближаетесь к истинному ответу. В этот момент вы можете подумать: «Вау, это много добавлений». Не волнуйтесь! Их не нужно складывать, потому что есть ярлык, который вы можете использовать. Нахождение интеграла обратное нахождению производной. Например, что такое интеграл от 2x? Вы уже знаете, что производная от x 2 равна 2x, поэтому интеграл от 2x равен x 2 . Символ, используемый для интеграла, — это «причудливая S», обозначающая сумму для сложения ваших срезов. После символа интеграла вставьте функцию, для которой вы хотите найти интеграл, а затем закончите с dx, что означает, что срезы перемещаются в направлении x. Вот как написать ответ: ᶴ 2x dx = x 2 + C Что такое C? Это «постоянная интегрирования», которая присутствует в уравнении, потому что все функции имеют производную 2x. Производная уравнения x 2 + 4 равна 2x, а производная x 2 +99 равна 2x, и это продолжается и продолжается, потому что производная любой константы равна нулю.В результате, когда для определения интеграла выполняется обратная операция, вы знаете, что только в 2 раза константа могла иметь любое значение. В результате идея завершается простым написанием + C в. Более простой способ понять — просто согласиться! С помощью этого уравнения вы теперь готовы найти определенные интегралы триггерных функций. Все, что вам нужно сделать, это указать соответствующие значения. Производные триггерных функций В тригонометрии функции — полезная часть повседневной жизни.Однако вы можете задаться вопросом, как найти производные триггерной функции. Для этого необходимо использовать лимиты. Понимание ограничений может занять время, но если вы действительно хотите определить производные триггерной функции, вам нужно углубиться в этот навык. Если у вас кружится голова, не волнуйтесь, вы не одиноки. Хорошая новость в том, что чем больше вы практикуетесь, тем лучше вы будете работать с этими числами и уравнениями. Плохая новость — это математика. Еще хорошие новости — калькуляторы! Модуль 5: Раздел 4, Часть 2 В последнем разделе мы познакомились с определенным интегралом и основной теоремой исчисления, которая дает нам способ вычислить определенный интеграл.В этом разделе мы более подробно обсудим концепцию определенного интеграла, рассмотрим некоторые приложения и теоремы, касающиеся определенного интеграла, и применим наши техники первообразных для вычисления определенных интегралов. Для начала вспомним, что мы получаем из определенного интеграла: Щелкните здесь, если хотите просмотреть короткое видео с графическим представлением определения определенного интеграла. Основная теорема исчисления Хорошо, теперь, когда у нас есть эти напоминания, давайте оценим несколько определенных интегралов. Напомним, что основная теорема исчисления гласит, что мы можем вычислить определенный интеграл, если найдем первообразную подынтегрального выражения. Рассмотрим шаг за шагом следующий пример. Попробуйте вычислить следующие определенные интегралы, а затем несколько видеороликов LiveScribe, чтобы проверить свои ответы: LiveScribe PDF-версия В этом видео инструктор вычисляет основной определенный интеграл. Перейдите по этой ссылке. В этом видео инструктор вычисляет определенный интеграл, используя подстановку на . Перейдите по этой ссылке. Теперь, если у нас есть определенные интегралы, у нас также есть неопределенные интегралы (или общие первообразные). Давайте посмотрим, чем отличаются характеристики двух интегралов: В последнем разделе мы кратко рассмотрели две теоремы.Давайте вернемся к ним, но на этот раз для определенных интегралов. В следующем видео обсуждается, почему эти две теоремы верны с точки зрения персонала. Если вы хотите увидеть доказательства некоторых из этих свойств, перейдите по этой ссылке. Используйте следующие два определенных интеграла, чтобы ответить на вопросы В предыдущем разделе мы видели, что если мы интегрируем функцию скорости за интервал времени, мы получаем расстояние, пройденное за этот интервал. Давайте рассмотрим еще пару сценариев.
131.
142. Определенные интегралы | Блог по математике ∞
Модуль 5: Раздел 4, Часть 2
Модуль 5: Раздел 4, Часть 2
Определенный интеграл Определенный интеграл
Примеры.
Пример 1.
Пример 2.
Видео примеры вычисления определенных интегралов
Видео Пример 1.
Видео, пример 2.
Определенные интегралы и неопределенные интегралы
Теоремы, связанные с определенными интегралами
 29)
29)