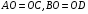Решение задач по теме «Параллелограмм и трапеция». Видеоурок. Геометрия 8 Класс
На этом уроке мы рассмотрим комплекс задач на параллелограмм и трапецию. Для этого мы сначала повторим основные связанные с ними факты. Сначала мы вспомним свойства параллелограмма, а затем его признаки, потом уделим внимание свойствам равнобедренной трапеции. Основная часть урока будет посвящена рассмотрению примеров.
Тема: Четырехугольники
Урок: Решение задач по теме «Параллелограмм и трапеция»
Очевидно, что для решения задач на тему «Параллелограмм и трапеция», необходимо повторить основные понятия, связанные с этими фигурами. Вспомним их свойства и признаки.
Рассмотрим сначала параллелограмм.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

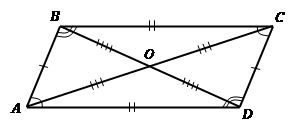
Рис. 1. Параллелограмм
Основные свойства параллелограмма:

Чтобы иметь возможность при решении задач пользоваться указанными свойствами, нам необходимо понимать, является ли указанный четырехугольник параллелограммом или нет. Для этого необходимо знать признаки параллелограмма.
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. 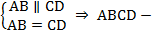 параллелограмм.
параллелограмм.

Рис. 2. Первый признак параллелограмма
Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм. 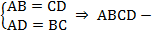 параллелограмм.
параллелограмм.
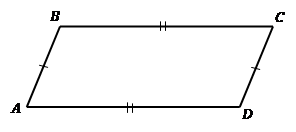
Рис. 3. Второй признак параллелограмма
Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. 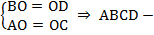
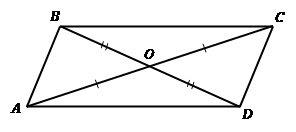
Рис. 4. Третий признак параллелограмма
Теперь рассмотрим такую фигуру, как трапеция. Отдельным ее видом является равнобедренная трапеция, имеющая важные свойства.
Определение. Равнобедренная трапеция – это трапеция, в которой боковые стороны равны (см. Рис. 5).

Рис. 5. Равнобедренная трапеция
Теперь сформули
Презентация к уроку решения задач «Свойства и признаки параллелогрмма»

Свойства и признаки параллелограмма.
(решение задач)

Свойства параллелограмма используем, если известно, что четырехугольник-параллелограмм.
Признаки параллелограмма используем, если доказываем, что четырехугольник –параллелограмм.
У параллелограмма : 1.противолежащие стороны равны;
2.противолежащие углы равны;
Четырехугольник-параллелограмм
2.противолежащие углы равны;
3.диагонали пересекаются и точкой пересечения делятся пополам
3.диагонали пересекаются и точкой пересечения делятся пополам;
4.противолежащая пара сторон одновременно параллельна и равна

Задача № 1
B
C
Дано: ABCD – параллелограмм
Найди: С, В, D,
AB, BC
19м
51 °
A
D
15м

C
D
E
Задача № 2
«
Дано: BCEF – параллелограмм
Найди : E, F
=
34°
F
B

Задача № 3
D
Е
30°
11см
7см
F
Дано: CDEK – параллелограмм, DF-
высота
Найди: СК, ЕК
K
C

Задача № 4
F
E
K
Дано: DEKN — параллелограмм
R
N
D
O

Задача № 5
В
С
⁽
2
«
О
Дано: АО=ОС,
Доказать: АВСD–
параллелограмм
«
1
⁾
D
A

Задача № 6
B
D
C
«
Дано: ABDE – параллелограмм
Доказать: АСDF — параллелограмм
A
E
«
F

Задача №7
B
C
«
Дано: ABCD – параллелограмм
Доказать: EBF D — параллелограмм
F
E
«
A
D

Самостоятельная работа
Вариант 1
Вариант 2
1. Периметр параллелограмма равен 46 см. Найдите стороны параллелограмма, если сумма трех его сторон равна 42 см.
1. Периметр параллелограмма равен 56 см. Найдите стороны параллелограмма, если сумма двух его сторон равна 20 см.
2. Сумма двух углов параллелограмма равна 84 °. Найдите углы параллелограмма.
2. Сумма трех углов параллелограмма равна 254 °. Найдите углы параллелограмма.

Автор шаблона и презентации Конева Н. А., учитель математики МБОУ БГО СОШ №4
г. Борисоглебск
Урок обобщения знаний по геометрии по теме «Параллелограмм». 7-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Класс:
8Тип урока: обобщение и систематизация знаний.
УМК: “Геометрия 7-9” Учебник для общеобразовательных учреждений, автор Атанасян Л.С., Бутузов В.Ф., М: Просвещение, 2006г
Цели урока:
образовательная:
- организовать деятельность учащихся по обобщению и систематизации знаний по теме “Параллелограмм и его свойства” при подготовке к контрольной работе;
- решить типовые задачи для подготовки к контрольной работе;
развивающая:
- развитие логического мышления, творческого мышления, умения анализировать, сравнивать, делать выводы;
- развитие пространственных представлений, математической речи;
воспитательная:
- воспитать уважение к предмету, умение видеть математические фигуры в окружающем мире.
- воспитание чувства прекрасного,
- воспитание интереса к предмету,
- воспитание умения контроля и самоконтроля.
Методы обучения:
- репродуктивный,
- частично-поисковый,
- проблемный.
Средства обучения:
- планшет с презентацией PowerPoint;
- инструменты: транспортиры, угольники, линейки, циркули,
- обобщающая таблица;
- программа для рисования Paint.
В результате урока учащиеся должны:
понимать
- как используются знания для решения математических и практических задач;
- смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
- распознавать геометрические фигуры, различать их взаимное расположение;
- изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
- решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, идеи симметрии;
- проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
- пользоваться языком геометрии для описания предметов окружающего мира;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- описания реальных ситуаций на языке геометрии;
- решения практических задач, связанных с нахождением геометрических величин.
Ход урока
I. Организационный момент.
Задача этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока.
Сообщить тему урока “Параллелограмм и его свойства”.
Составим кластер данного урока (слайд 2).
В информационных технологиях этот термин объясняется так: “Кластер это подмножество результатов поиска, связанных единством темы”.
Какие темы мы изучили в пятой главе учебника геометрии и повторяли к этому уроку?
Ответ: Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
Сформулируйте цели урока: повторить и обобщить знания и умения по теме при подготовке к контрольной работе.
II. Актуализация опорных знаний учащихся. Разминка (слайд 3, 4).
Задача этапа: актуализировать знания учащихся по изученным темам, подготовка следующего этапа – настроить учащихся на самостоятельную работу.
Фронтальный опрос.
- Является ли прямоугольником параллелограмм, у которого есть прямой угол?
- Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
- Верно ли, что любой квадрат является ромбом?
- Верно ли, что любой параллелограмм является ромбом?
- Диагонали четырехугольника равны. Обязательно ли этот четырехугольник – прямоугольник?
- Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм?
- Верно ли, что каждый квадрат является прямоугольником?
- Верно ли, что любой ромб является параллелограммом?
- Может ли один угол параллелограмма быть равным 40?, а другой 80??
III. Обобщение и систематизация всех изученных определений и свойств параллелограммов.
Задача этапа: проверка изучения наиболее важных видов четырехугольников — параллелограмма, прямоугольника, ромба, квадрата, трапеции.
Задание (слайд 5). Заполнить таблицу “Параллелограммы”, которая имеет 5столбцов (виды параллелограмма, параллелограмм, прямоугольник, ромб, квадрат) и 6 строк (название параллелограмма, определение, построение параллелограмма, стороны, углы, диагонали) (см. приложение №1).
Таблицу сильные учащиеся заполнят быстро, поэтому для них приготовлено дополнительное задание. Слабые учащиеся могут заполнять таблицу с помощью учебника или учителя. Можно организовать работу в парах, где сильные учащиеся помогают слабым. Можно таблицу использовать для проверки знаний на зачете.
В любом случае после заполнения такой таблицы у ученика появляется полная картина всех определений и свойств параллелограммов. Таблица емкая, несет много информации, которая легко запоминается. Такую таблицу каждый ученик вставляет в папку для подготовки к ГИА (см приложение №2).
Учитель проверяет заполнение таблицы у каждого ученика (если позволяет количество обучаемых) или организует взаимопроверку или самопроверку выполненной работы (слайды 6-8).
Дополнительное задание для сильных учащихся:
Задачи с практическим содержанием:
1. Из медной проволоки, длиной 30 см, изготовить параллелограмм, стороны которого относятся как 2:3.
Ответ: 30 : (2 + 3) = 6 см – одна часть. Стороны параллелограмма: 12 см и 18 см.
2. Как построить, используя свойства параллелограмма, через пункт С дорогу, параллельную дороге, соединяющую пункты А и В?
Ответ: проведем перпендикуляр СМ к АВ, а затем еще один перпендикуляр CN к прямой СМ. Получим два перпендикуляра в прямой СМ, которые параллельны между собой. CN – искомая дорога.
IV. Применение знаний при решении типовых задач по готовым чертежам.
Задача этапа: решить типовые задачи для подготовки к контрольной работе.
| Чертеж | Подсказка | |
| Слайд 9 | Определите вид треугольника АВК. Определите угол ВАК. Определите угол АВС. Как называется отрезок ВК для угла АВС? | |
| Слайд 10 | Как называется отрезок DE? Определите вид треугольника CDE. Длина СЕ. | |
| Слайд 11 | Определите вид треугольника ABD. Сравните углы ADВ и MBD. Определите их. | |
| Слайд 12 | Определите вид треугольника ABО. Как называются углы АОВ и СОD? Определите угол ОСD. | |
| Слайд 13 | Определите вид четырехугольника BCDE. Определите угол ABC. Определите угол CBE. Определите угол BCD. | |
| Слайд 14 | Докажите, что АА1D1 = С1D1D. Найдите сумму углов АD1А1 и С1D1D. Определите угол А1D1С1. |
V. Практическое применение параллелограммов в жизни.
Задача этапа: научить видеть математические фигуры в окружающем мире и показать межпредметные связи математики с другими наукам.
Беседа “Параллелограммы в жизни”.
Слайд 8. Параллелограммы в жизни.
В жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жесткости проведена диагональ.
Реечный домкрат для легковых автомобилей имеет форму ромба.
Слайд 9. Параллелограммы в строительстве.
Плиточники укладывают плитки в виде ромба, квадрата – из них получаются красивые узоры.
Прямоугольник несет красоту, стройность, четкость. Это стены домов, пол, потолок, грани карандашей.
Слайд 10. Параллелограммы в народном хозяйстве.
В сельском хозяйстве применяют квадратно – гнездовой способ посадки культур – урожай при этом лучше, этот способ хорош тем, что можно применять механизированную обработку.
Квадрат стальной горячекатаный используется для производства деталей машин и механизмов, для строительства зданий и сооружений, для изготовления декоративных элементов, а также для производства заборов и ограждений.
Слайд 11. Параллелограммы в физике.
В физике применяют параллелограмм при изучении разложения сил, при нахождении равнодействующей силы.
Равнодействующая силы тяжести и силы нормального давления, действующих на лыжника на гладкой горе.
А воз и ныне там! Из басни И. А. Крылова “Лебедь, Щука и Рак” (1816).
Слайд 12. Параллелограммы в быту.
Интересное решение вязание пледов разноцветными мотивами. На рисунках бабушкин или африканский квадрат.
Задание:
- Приведите примеры, где вы встречались с параллелограммами в жизни?
- Нарисуйте рисунок или орнамент, используя параллелограммы, осевую или центральную симметрию.
VI. Итог урока. Выставление оценок. Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, систематизированном на уроке. Сформулировать домашнее задание для учащихся.
Итоги урока:
- Обобщили знания о параллелограммах.
- Решили типовые задачи.
- Подготовились к контрольной работе.
- Оценка и самооценка работы учащихся на уроке.
Домашнее задание. Нарисовать рисунок или орнамент, используя параллелограммы.
Урок по теме: Свойства и признаки параллелограмма.
Название работы: урок с использованием презентации.
Предмет: геометрия, урок закрепления знаний.
Тема: Решение задач по теме: «Свойства и признаки параллелограмма».
Продолжительность: 45 минут
Класс : 8 класс
Технологии: презентации PowerPoint, текстовый документ Word.
Текст работы:
Тема: Решение задач по теме «Свойства и признаки параллелограмма»
Урок № 3 в разделе «Параллелограмм».
Тип урока: урок закрепления знаний.
Оборудование: интерактивная доска (или любое другое оборудование для показа презентаций), распечатка заданий для работы в группах.
Цель урока:
Образовательная: контроль уровня усвоения теоретических знаний по теме, создание условий для формирования навыков применения свойств и признаков параллелограмма к решению задач;
Воспитательная: воспитание этических норм поведения при работе в группе, умения слушать, настойчивости и воли для достижения результата;
Развивающая: развитие умений выдвигать гипотезы, анализировать, делать выводы, выделять существенные признаки, развитие математической речи, мышления, умений самостоятельной работы;
План урока:
1. Организация начала урока.
2. Проверка выполнения домашнего задания.
3. Подготовка к основному этапу урока (математический диктант)
4. Закрепление знаний и способов действия (работа по готовым чертежам)
5. Контроль и самопроверка знаний (работа в группах)
6. Подведение итогов урока.
7. Информация о домашнем задании.
Ход урока.
1. Здравствуйте, ребята! Эпиграфом нашего урока будут слова Н. Г. Чернышевкого «Незнанием никогда не следует хвалиться: незнание есть бессилие». Так давайте же сегодня покажем прочные знания по теме урока, усердие и настойчивость к достижению цели. Итак, запишите тему урока.
2. Мы изучили свойства и признаки параллелограмма, сегодня на уроке проверим, насколько хорошо вы усвоили свойства и признаки параллелограмма, будем формировать умения применять знания при решении задач.
Какие вопросы возникли при выполнении домашнего задания? (задание, вызвавшее затруднения решить на доске, вызвать ученика, справившегося с заданием).
3. А со всеми остальными проведем математический диктант. (Приложение 1). (Примечание: диктант можно диктовать самому учителю, но если в классе есть слабослышащие ученики, или ученики с задержкой психического развития, то возможно его спроектировать на доску).
Диктант выполняется в тетради под копирку, затем верхние листы сдаются, и учащиеся проверяют правильность выполнения работы. На доску проецируются верные ответы. (Приложение 1). Оценки за диктант можно поставить выборочно.
Ученик, записывающий задание из домашней работы, рассказывает ход решения, отвечает на вопросы учащихся.
4. Итак, попрошу еще раз сформулировать свойства и признаки параллелограмма (фронтальный опрос). На доске представлены задания, которые содержат готовые чертежи, поработаем устно (Приложение 2). Какие теоретические сведения мы повторили, решая задания? (Ребята формулируют свойства и признаки).
Физкультминутка (зарядка для глаз).
5. Мы повторили весь необходимый материал по теме, поэтому можем перейти к решению задач. Вы сидите в мини группах (предварительно разделить учащихся на 6 мини групп (группы формируются по уровню усвоения: 1, 2, 3 уровень), по 4 человека в каждой, в которых выбран председатель (организатор), секретарь (ученик, который будет оформлять запись задания)). Для каждой мини группы предлагаю по 3 задания (Приложение 3), которые расположены в порядке увеличения уровня сложности. На всю работу отводится 20 минут. Затем обсуждаем, анализируем решения, делаем выводы. Фронтально опросить каждую группу, например, первую группу – решение 1 задачи, 2 группу – второй и т.д., выполнение остальных заданий собрать на проверку.
6. Подведение итогов урока. Собрать листы с решением заданий в группах. Оценки учащимся за проверку домашней работы, отвечавшим в группе.
7. Домашнее задание: № 374, 377. На доске рисунки к домашней работе, кратко обсудить ход решения.
«Параллелограмм и его свойства»,
Умарова М.К Украинская средняяя школа
Урок по теме «Параллелограмм и его свойства», 8 класс
Тип урока: Урок формирования новых знаний.
Цель урока: Введение нового понятия – параллелограмма
Задачи:
1. Образовательные: дать определение параллелограмма. Вывести свойства параллелограмма и применять при решений задач.
2. Развивающие: формировать навыки и умения решения геометрических задач, творческое мышление, умение анализировать задачи.
3.Воспитательные: Формирование трудолюбия, взаимовыручки, коллективизма, развитие культуры математической речи, аккуратность.
Оборудование: интерактивная доска ,карточки с заданиями.
Ход урока:1. Организационный момент.
Ученикам сообщается цели урока. 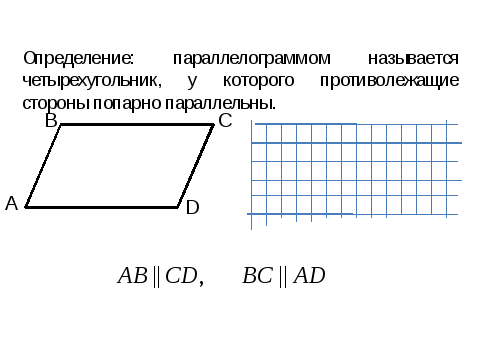 Слайд 4
Слайд 4
На слайде вводится определение параллелограмма, на клетчатой части слайда с помощью маркера ученикам показывается, как чертить параллелограмм;
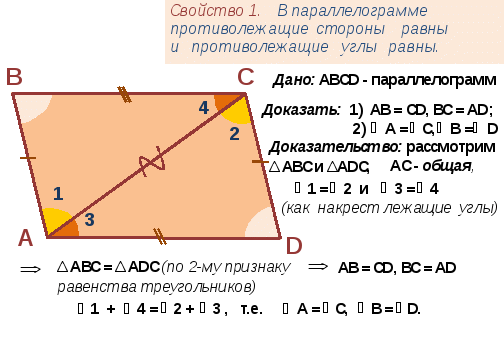
Слайд 5
2)Вводится свойство параллелограмма: в параллелограмме противоположные углы и противоположные стороны равны.
На слайде появляются основные «узлы» доказательства. Ученикам предлагается самостоятельно определить, что надо доказать, а также доказать равенство треугольников.
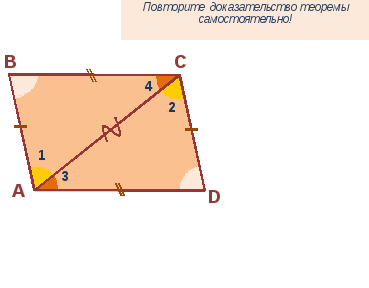
Слайд 6
3)Вводится свойство параллелограмма: Диагонали параллелограмма точкой пересечения делятся пополам. Слайд 7

На слайде появляются основные «узлы» доказательства. Ученикам предлагается самостоятельно определить, что надо доказать, а также доказать равенство треугольников.
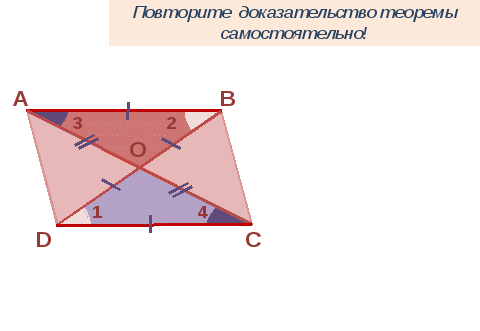 Слайд 8
Слайд 8
4) Вводится свойство параллелограмма: В параллелограмме сумма углов, прилежащих к одной стороне, равна 180o.
Данное свойство предлагается ученикам доказать самостоятельно. Устно.
 Слайд 9
Слайд 9
5)После доказательства свойства, ученикам предлагается заполнить схему «Паучок», используя арабскую грамотность.
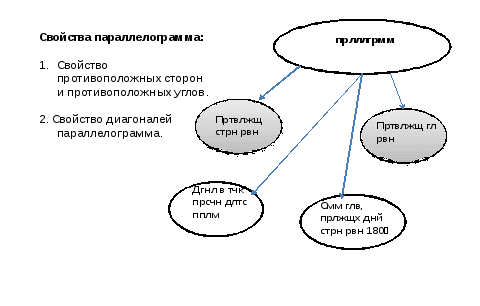 Слайд 10
Слайд 10
6)Устная работа
а) Из перечисленных четырехугольников укажи параллелограмм.  Слайд 11
Слайд 11
б) Установи соответствие.
В параллелограмме противолежащие стороны делятся пополам
В параллелограмме противолежащие углы 180º
Диагонали пересекаются и в точке пересечения параллельны и равны
Сумма углов прилежащих к одной стороне равны равны
в) В параллелограмме стороны 7см и 4см. Найди периметр параллелограмма
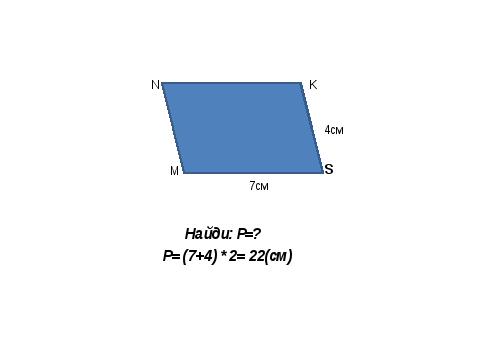
Слайд 12
.
г) В параллелограмме один угол 70ᵒ. Найди остальные углы параллелограмма.
Слайд 13
7) Работа в тетрадях. Задача 1: В параллелограмме АВСД диагонали АС и ВД 20см и 16см. Сторона АВ=10см. Найдите периметр ∆СОД. 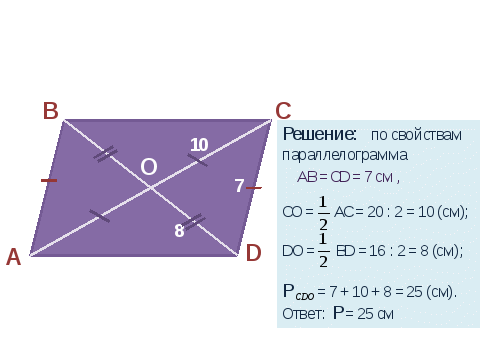 Слайд 14
Слайд 14
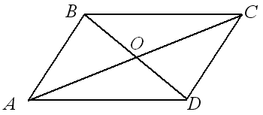
Задача2: В параллелограмме АВСД, О — точка пересечения диагоналей, отрезок МК проходит через эту точку. Докажите, что
∆ОМВ=∆ОКД
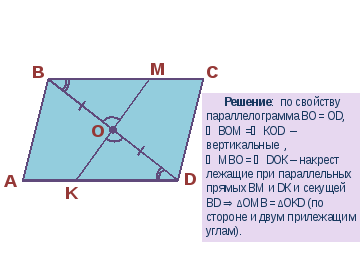 Слайд 15
Слайд 15
Решение задач рассматриваются у доски, после ученики записывают решение в тетрадях.
8)Творческая работа: Как провести через пункт N дорогу, чтобы расстояние по ней от этого пункта до железной дороги и до канала были равны?
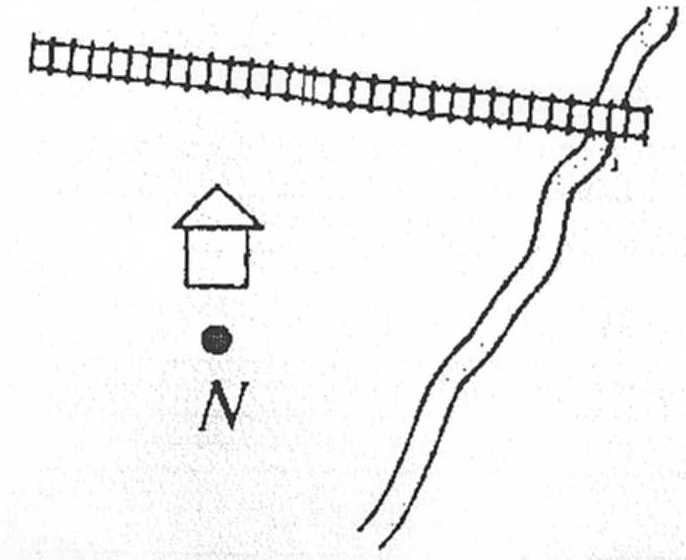 Слайд 16
Слайд 16
Решение:
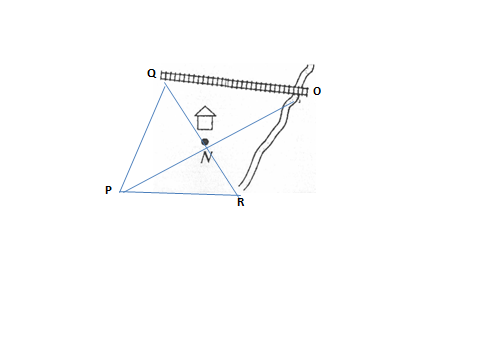
На луче ОN отложим отрезок NP=ON, проведем прямые PQ ǁOR, PR ǁ OQ. ORPQ-параллелограмм, значит NQ= NR. Прямая RQ-искомая.
9) Домашняя работа (раздать карточки)

10) Рефлексия урока.
Вопросы для проверки усвоения материала:
— Что такое выпуклый четырехугольник?
— Как найти сумму углов произвольного выпуклого
n – угольника?
— Что такое параллелограмм?
— Каковы свойства параллелограмма?
Составьте «Синквейн»
1.Существительное
2.Два прилагательных
3.Три глагола
4. Фраза из четырех слов.
5. Синоним
Самостоятельная работа по геометрии №2 в 8 классе ( с решением) по теме: Параллелограмм и его свойства
ГЕОМЕТРИЯ 8 класс
Тема: ПАРАЛЛЕЛОГРАММ И ЕГО СВОЙСТВА С-2 Вариант 1
В четырехугольнике ABCD AB||CD, BC||AD. AC=20 см, BD=10 см, АВ= 13 см. Диагонали четырехугольника пересекаются в точке О. Найдите периметр треугольника СОD.
Т.к. в четырёхугольнике ABCD по условию задачи противоположные стороны параллельны (AB||CD, BC||AD ), значит он является параллелограммом. О — точка пересечения диагоналей. Диагональ АС пересекает диагональ BD в точке О, значит AO = OC, BO = OD (по второму свойству параллелограмма) BD=BO+OD=10 см, OD=5см АС=АО+ОС=20 см, ОС=10 см.
Периметр треугольника СOD равен сумме длин его сторон: Р=СО+ОD+DС
АВ =ДС=13 см, как противоположные стороны параллелограмма. Итак, получили , что периметр треугольника СОD равен 28 см.
Ответ: 28 см
Из вершины В параллелограмма АВСD с острым углом А проведен перпендикуляр ВК к прямой АD, ВК = 0,5 АВ . Найдите угол С , и угол D.
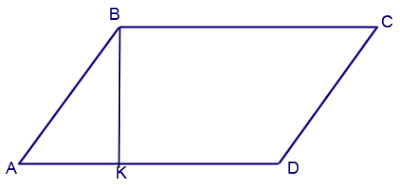
Пусть из вершины В параллелограмма АВСD с острым углом А проведен перпендикуляр ВК к прямой АD, тогда
∆АВК — прямоугольный и A = 30° (в прямоугольном треугольнике напротив катета, равного половине гипотенузы лежит угол в 30° ) C = A = 30° (противоположные углы у параллелограмма равны) D и C односторонние углы, значит их сумма равна 180⁰,поэтому D = 180 — C = 180 — 30 = 150°
Ответ : C = 30° , D = 150°
ГЕОМЕТРИЯ 8 класс
Тема: ПАРАЛЛЕЛОГРАММ И ЕГО СВОЙСТВА С-2 Вариант 2
В четырехугольнике АВСD АВ СD, ВС АD, О- точка пересечения диагоналей. Периметр треугольника АОD равен 25 см, АС=16 см, ВD= 14 см. Найдите ВС.
Решение

Исходя из условия задачи ясно, что данный четырехугольник АВСD — параллелограмм по определению. АС и ВD — его диагонали. По свойству диагоналей параллелограмма (диагонали параллелограмма пересекаются в одной точке и делятся в точке пересечения пополам) имеем: ВО = ОD = 0,5ВD =7 см; АО=ОС=0,5АС=8 см. Периметр треугольника АОD определим по формуле: S = АО+ОD+DА, 25=8+7+DА, DА=10 см Противоположные стороны параллелограмма равны, значит ВС = DА = 10 см.
Ответ : 10 см.
Дан параллелограмм АВСД с острым углом А. Из вершины в опущен перпендикуляр ВК к прямой АД, АК=ВК. Найдите С и Д.
Решение
Пусть в параллелограмме АВСД с острым углом А , из вершины В опущен перпендикуляр ВК к стороне АД. АK=KB, значит треугольник AKB равнобедренный прямоугольный, отсюда следует что KAB = ABK = 45⁰ как углы при основании АВ .
Углы A и С в параллелограмме равны, то есть угол С равен 45⁰
Известно, что cумма углов, прилежащих к одной стороне параллелограмма равна 180⁰: D + C = 180⁰,D+45⁰=180⁰, тогда D= 180⁰-45⁰ = 135⁰
Ответ:D =135⁰, C= 45⁰
Урок геометрии по теме «Параллелограмм и его свойства
Предмет: Геометрия
Урок №_____.
Дата проведения урока _______________. Проверено__________.
Класс 8 « »
Учитель: Борматов Виктор Николаевич
Тема : Параллелограмм и его свойства
Тип урока: Урок лекция
Оборудование урока : учебник, доска, мел
Цели урока :
Обучающая: дать понятие параллелограмма и свойства параллелограмма , научить применять полученные знания при решении задач.
Развивающая: развить мышление (способность анализировать, выделять главное), память и умения сравнительного анализа.
Воспитательная: воспитать уважительное отношение к предмету, средствами урока воспитать в учащихся уверенность в своих силах.
Методы: диалогический, фронтальной беседы, наглядно иллюстративный.
Ход урока
1. Организационный момент (проверка готовности учащихся к уроку, проверка присутствующих, общий настрой на урок).
2. Проверка домашнего задания №7, №8, №9: Выявления уровня знаний учащимися заданного на дом материала; определение типичных недостатков в знаниях и причин их появления; ликвидация обнаруженных недочетов.
3.Постановка цели: Подготовка учащихся к активному и сознательному усвоению знаний. Сообщение темы, цели и задачи изученного материала. Постановка перед учащимися цели урока.
4.Изложение нового материала
 Определение. Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Определение. Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
ABCD— параллелограмм,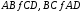 . Параллелограмм- есть выпуклый четырехугольник.
. Параллелограмм- есть выпуклый четырехугольник.
(почему?)
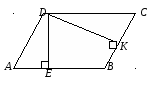 Перпендикуляр опущенный из вершины параллелограмма на противоположенную сторону называется его высотой а сторона на которую он опущен основанием
Перпендикуляр опущенный из вершины параллелограмма на противоположенную сторону называется его высотой а сторона на которую он опущен основанием
 .
.
Теорема 2. Противоположенные стороны параллелограмма равны
(Доказательство данной теоремы рассмотреть самостоятельно)
Из этой теоремы следуют три свойства параллелограмма
Противолежащие углы равны.

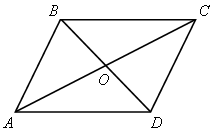
Диагонали параллелограмма делятся точкой пересечения пополам. т.к
 , то
, то 
Сумма углов, прилежащих одной стороне параллелограмма, равна

Теорема3. Если у выпуклого четырехугольника
Противолежащие стороны равны, то он является параллелограммом.
Противолежащие углы равны, то он является параллелограммом.
Диагонали пересекаются и точкой пересечения делятся пополам, то он является параллелограммом.
Сумма углов, прилежащих одной стороне равна
 , то он является параллелограммом.
, то он является параллелограммом.
Теорема4. Если у выпуклого четырехугольника две противолежащие стороны равны и попарно параллельны, то он является параллелограммом.
(Доказательство данной теоремы рассмотреть самостоятельно)
Пример. Найдем стороны параллелограмма периметр, которого равен 144дм, а одна из его сторон больше другой на 30дм.
Решение: Обозначим стороны параллелограмма через х,у . По условию задачи имеем
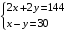 , Решая, данную систему имеем
, Решая, данную систему имеем 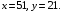
5.Домашнее задание §2 №13,№15+ доказательства теорем.
6. Итог урока Выставление оценок. Подведение итогов урока.
7. Этап рефлексии открытость учащихся в осмыслении своих действий.
Анкетирование учащихся.
УВАЖАЕМЫЕ РЕБЯТА!
Просим Вас ответить на данные вопросы.
 , то
, то