Квадрат, Ромб и их свойства

Еще одни представители класса параллелограммов — ромб и квадрат.

Параллелограмм, у которого все стороны равны, называется ромбом.

Свойства ромба:

• Противоположные углы ромба равны.
• В ромба сумма углов, прилегающих к одной стороне, равна 180°. Диагонали ромба пересекаются под прямым углом.
• Диагонали ромба являются биссектрисами его углов.
• Диагонали ромба пересекаются и точкой пересечения делятся пополам.

Признаки ромба:

• Если в параллелограмме диагонали пересекаются под прямым углом, то этот параллелограмм является ромбом.
• Если в параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм является ромбом.
• Если в параллелограмме две смежные стороны равны, то этот параллелограмм является ромбом.
• Если в четырехугольнике все стороны равны, то этот четырехугольник является ромбом.
• Если в параллелограмме одна из диагоналей является биссектрисой его угла, то этот параллелограмм является ромбом.
• Если в четырехугольнике диагонали являются биссектрисами его углов и пересекаются под прямым углом, то этот четырехугольник является ромбом.

Это интересно.

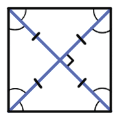
Если соединить отрезками середины сторон прямоугольника, то получим ромб.

Если соединить отрезками середины сторон ромба, то получим прямоугольник.

Если у параллелограмма все высоты равны, то этот параллелограмм является ромбом.

Прямоугольник, у которого все стороны равны, называется квадратом.

Свойства квадрата:

• Все углы квадрата — прямые.
• Диагонали квадрата пересекаются и точкой пересечения делятся пополам.
• Диагонали квадрата уровне.
• Диагонали квадрата пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами его углов.

Признаки квадрата:

• Если в прямоугольнике диагонали пересекаются под прямым углом, то этот прямоугольник является квадратом.
• Если ромба диагонали равны, то этот ромб является квадратом.
• Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник является квадратом.

 

xn—-7sbfhivhrke5c.xn--p1ai

Ромб и квадрат / Четырехугольники / Справочник по геометрии 7-9 класс

Частным видом параллелограмма является ромб.

Ромбом называется параллелограмм, у которого все стороны равны

ABCD — ромб.

Ромб обладает всеми свойствами параллелограмма.

Особое свойство ромба

Доказательство

Дано

: ABCD — ромб

Доказать: ACBD, ADO = CDO

Доказательство:

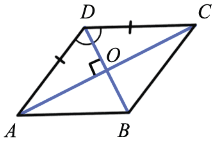
AD = DC (по определению ромба), значит, ADC — равнобедренный.

AO = OC (по свойству диагоналей параллелограмма), DO — медиана

ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,  ACBD, ADO = CDO, что и требовалось доказать.

---

Теорема

Доказательство

Дано: ABCD — параллелограмм, ACBD

Доказать: ABCD — ромб

Доказательство:

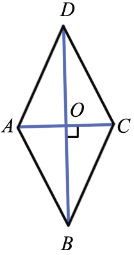
Рассмотрим AOВ и COВ:

Т.к. ACBD, тоAOВ = COВ = 90⁰;

AO = OC (по свойству диагоналей параллелограмма), ОВ — общий катет,

AOВ = COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны, ВС = ВА.

В параллелограмме противоположные стороны равны, AD = BC, AB = DC

Итак: ABCD — параллелограмм (по условию) AD = BC = AB = DC (по доказанному).

ABCD — ромб, что и требовалось доказать.

---

Теорема

Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб

Доказательство

Дано: ABCD — параллелограмм, АС — диагональ и биссектриса DAB иDCB

Доказать: ABCD — ромб

Доказательство:

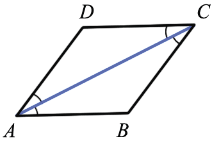
DAB =DCB (по свойству параллелограмма), а АС -биссектриса DAB иDCB (т.е. АС делит эти углы на два равных угла), DAC = BAC =DCA =

BCA

Рассмотрим ADC: DAC =DCA, ADC — равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны, AD = BC, AB = DC

Итак

: ABCD — параллелограмм (по условию) AD = BC = AB = DC (по доказанному). ABCD — ромб, что и требовалось доказать.

Две теоремы, доказанные выше, называют признаками ромба.

Основные свойства квадрата:

1. Все углы квадрата прямые.

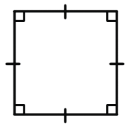
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

budu5.com

Свойства ромба | Треугольники

Свойства ромба — это свойства параллелограмма плюс собственные свойства.

Перечислим их.

Свойства ромба

1) Стороны ромба равны (по определению ромба).

2) Противолежащие углы ромба равны (по свойству параллелограмма).

3) Сумма углов, прилежащих к одной стороне ромба, равна 180º (по свойству параллелограмма).

4) Диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма).

5) Диагонали ромба взаимно перпендикулярны.

6) Диагонали ромба являются биссектрисами его углов.

7) Сумма квадратов диагоналей ромба равна сумме квадратов его сторон (по свойству параллелограмма).

8) Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба (по свойству параллелограмма).

9) Угол между высотами ромба, проведенными из вершины острого угла, равен тупому углу ромба.

 

Проиллюстрируем эти свойства для ромба ABCD:

 

1) AB=BC=CD=AD;

2) ∠A=∠C; ∠B=∠D;

3) ∠A+∠B=180º; ∠B+∠C=180º; ∠C+∠D=180º; ∠A+∠D=180º;

 

4) AC ∩ BD=O, AO=CO, BO=DO;

   

6) ∠ABO=∠CBO=∠ADO=∠CDO,

∠BAO=∠BCO=∠DAO=∠DCO;

   

 

 

 

8) ∠FBK=∠A;

 

 

 

 

 

9) ∠HAE=∠ABC.

www.treugolniki.ru

Опорный конспект «Ромб и его свойства»

«Ромб и его свойства»

---

---

Ромб — параллелограмму которого все стороны равны.
Слово «рoмб» греческого происхождения. Оно означало в давние времена любое круглое или вращающееся тело.

Свойства и признаки ромба

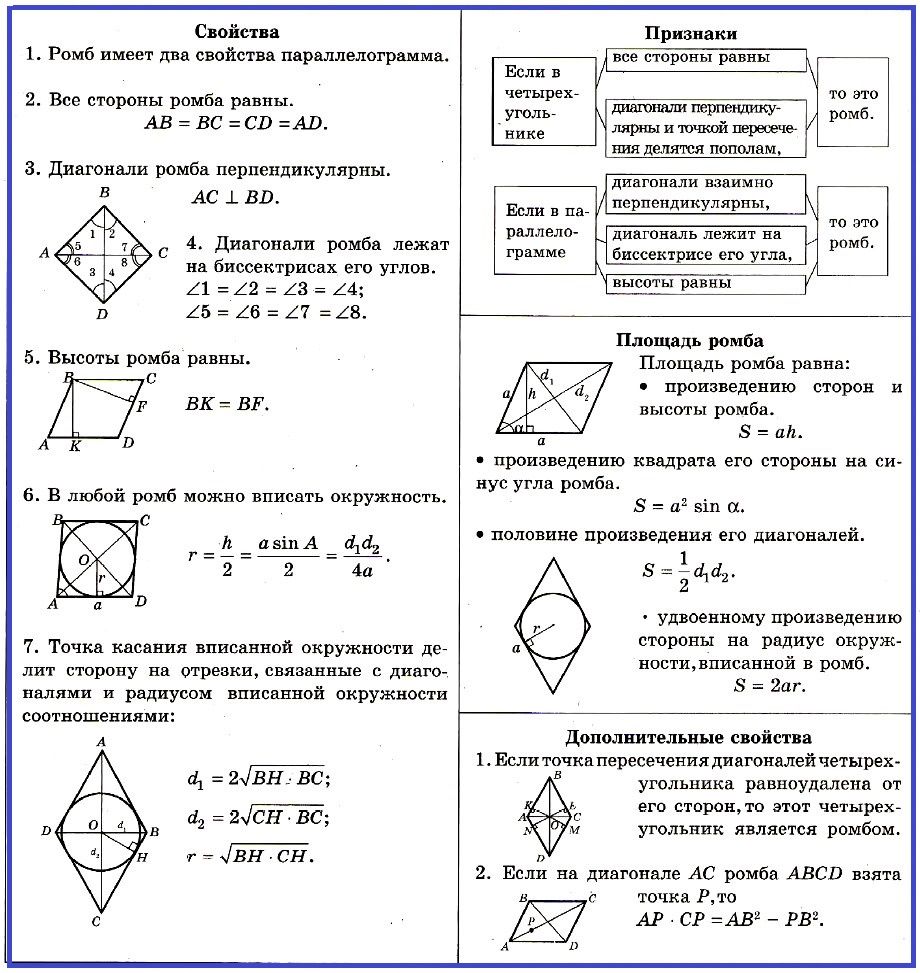
Свойства ромба:
1. Рoмб имеет два свойства параллелограмма.
2. Все стороны ромба равны.
3. Диагонали ромба перпендикулярны.
4. Диагонали ромба лежат на биссектрисах его углов.
5. Высоты ромба равны.
6. В любой рoмб можно вписать окружность.
7. Точка касания вписанной окружности делит сторону на отрезки, связанные с диагоналями и радиусом вписанной окружности соотношениями.

Признаки ромба:
Если в четырехугольнике все стороны равны
Если в четырехугольнике диагонали перпендикулярны и точкой пересечения делятся пополам,
Если в параллелограмме диагонали взаимно перпендикулярны,
Если в параллелограмме диагональ лежит на биссектрисе его угла,
Если в параллелограмме высоты равны.

---

Это конспект по теме «Ромб и его свойства». Выберите дальнейшие действия:

 

uchitel.pro

Диагонали ромба

Каким способом высчитать диагональ:

через сторону и другую диагональ

через сторону и угол

через вторую диагональ и угол

через площадь и диагональ

Введите размеры:

Результат:

Решение

Теория

Ромб — это параллелограмм у которого все стороны равны.

Свойства ромба:

• Диагонали ромба делят его углы пополам.
• Cумма углов прилежащих к одной стороне равна 180°.
• Диагонали ромба пересекаются под прямым углом (90°).
• Диагонали ромба в точке пересечения делятся попалам.
• Диагонали ромба являются биссектрисами его углов.

Формулы расчёта диагонали ромба

  Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:

Через сторону и другую диагональ

D = \sqrt{4a^2 — d^2}

d = \sqrt{4a^2 — D^2}

• D — большая диагональ ромба
• d — меньшая диагональ ромба
• a — сторона ромба

---

Через сторону и угол

• D — большая диагональ
• d — меньшая диагональ ромба
• a — сторона ромба
• α — острый угол ромба (от 0° до 90°)
• β — тупой угол ромба (от 90° до 180°)

D = a \sqrt{2 + 2 \cdot \cos \alpha}

D = a \sqrt{2 — 2 \cdot \cos \beta}

d = a \sqrt{2 — 2 \cdot \cos \alpha}

d = a \sqrt{2 + 2 \cdot \cos \beta}

---

Через угол и вторую диагональ

D = d \cdot \tg ( \dfrac{\beta}{2} )

d = D \cdot \tg ( \dfrac{\alpha}{2} )

• D — большая диагональ ромба
• d — меньшая диагональ ромба
• α — острый угол ромба (от 0° до 90°)
• β — тупой угол ромба (от 90° до 180°)

Через площадь и вторую диагональ

D = \dfrac{2 \cdot S}{d}

d = \dfrac{2 \cdot S}{D}

• D — большая диагональ ромба
• d — меньшая диагональ ромба
• S — площадь ромба

---

Похожие калькуляторы:

kalk.top

Ромб. Формулы, признаки и свойства ромба

Определение.

Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.

Ромбы отличаются между собой размером стороны и размером углов.

Рис.1		Рис.2

Признаки ромба

Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:

1. Две его смежные стороны равны (отсюда следует, что все стороны равны):

АВ = ВС = СD = AD

2. Его диагонали пересекаются под прямым углом:

AC┴BD

3. Одна из диагоналей (бисектрисса) делит содержащие её углы пополам:

∠BAC = ∠CAD или ∠BDA = ∠BDC

4. Если все высоты равны:

BN = DL = BM = DK

5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Если в параллелограмм можно вписать круг.

Основные свойства ромба

2. Диагонали перпендикулярны:

AC┴BD

3. Диагонали являются биссектрисами его углов:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:

AC² + BD² = 4AB²

5. Точка пересечения диагоналей называется центром симметрии ромба.

6. В любой ромб можно вписать окружность.

7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:

Диагонали ромба

Определение.

Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.

Ромб имеет две диагонали — длинную d₁, и короткую — d₂

Формулы определения длины диагонали ромба:

1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 — 2 · cosβ

2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₂ = a√2 + 2 · cosβ

d₂ = a√2 — 2 · cosα

3. Формулы большой диагонали ромба через сторону и половинный угол:

d₁ = 2a · cos(α/2)

d₁ = 2a · sin(β/2)

4. Формулы малой диагонали ромба через сторону и половинный угол:

d₂ = 2a · sin(α/2)

d₂ = 2a · cos(β/2)

5. Формулы диагоналей ромба через сторону и другую диагональ:

d₁ = √4a² — d₂²

d₂ = √4a² — d₁²

6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:

d₁ = d₂ · tg(β/2)

d₂ = d₁ · tg(α/2)

7. Формулы диагоналей через площадь и другую диагональ: 8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Определение.

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можна найти за формулами указанными выше.

Формула определения длины периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a

Площадь ромба

Определение.

Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.

Формулы определения площади ромба:

1. Формула площади ромба через сторону и высоту:

S = a · h_a

2. Формула площади ромба через сторону и синус любого угла:

S = a² · sinα

3. Формула площади ромба через сторону и радиус:

S = 2a · r

4. Формула площади ромба через две диагонали: 5. Формула площади ромба через синус угла и радиус вписанной окружности: 6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):

Окружность вписанная в ромб

Определение.

Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба: 2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба: 3. Формула радиуса круга вписанного в ромб через площадь и синус угла: 4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла: 5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла: 6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d1 · d2
	2√d12 + d22

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

math-public:romb [Президентский ФМЛ №239]

Определение

Ромб – это четырехугольник, у которого все стороны равны.

Замечание

Ромб является частным случаем параллелограмма, так как его противоположные стороны попарно равны (третий признак).

Замечание

Ромб наследует все свойства параллелограмма.

Свойства ромба

1. Диагонали ромба взаимно перпендикулярны.

2. Диагонали ромба являются биссектрисами его углов.

Доказательство

Рассмотрим ромб $ABCD$, в котором диагонали $AC$ и $BD$ пересекаются в точке $O$.

Докажем, что они перпендикулярны и являются биссектрисами углов ромба.

Действительно, так как $ABCD$ – частный случай параллелограмма, то диагонали точкой пересечения делятся пополам, то есть $AO=OC, BO=OD$.

Тогда, так как $AB=BC=CD=DA$, то $\triangle AOB=\triangle BOC=\triangle COD=\triangle AOD$ по третьему признаку равенства.

Тогда $\angle 1=\angle 2=90^\circ$, так как это смежные углы.

Кроме того, $\angle 3=\angle 4=\angle 5=\angle 6$, $\angle 7=\angle 8=\angle 9=\angle 10$.

Таким образом диагонали перпендикулярны и являются биссектрисами углов ромба.

Следствие

Диагонали ромба разбивают его на четыре равных прямоугольных треугольника.

Признаки ромба

1. Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб.

2. Если одна из диагоналей параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.

3. Если в четырёхугольнике $ABCD$ диагональ $AC$ является биссектрисой углов $\angle A$ и $\angle C$, а диагональ $BD$ является биссектрисой углов $B$ и $D$, то $ABCD$ – ромб.

Доказательство

Докажем первый пункт теоремы.

Рассмотрим параллелограмм $ABCD$, в котором $AC\perp BD$.

Докажем, что $ABCD$ – ромб.

В параллелограмме диагонали точкой пересечения делятся пополам, следовательно, $AO=OC, BO=OD$.

Кроме того, $\angle 1=\angle 2=90^\circ$.

Тогда $\triangle AOB=\triangle AOD$ по первому признаку равенства.

Следовательно $AB=AD$.

А так как $ABCD$ – параллелограмм, то $BC=AD=AB=CD$, то есть $ABCD$ – ромб.

Докажем второй пункт теоремы.

Рассмотрим параллелограмм $ABCD$, в котором диагональ $AC$ является биссектрисой угла $\angle A$, то есть $\angle 1=\angle 2$.

Докажем, что $ABCD$ – ромб.

$\angle 2=\angle 3$, как накрест лежащие, следовательно, $\angle 1=\angle 3$.

То есть $\triangle ABC$ – равнобедренный и $AB=BC$.

А так как $ABCD$ – параллелограмм, то $AB=CD, BC=AD$, то есть $AB=BC=CD=AD$, и $ABCD$ – ромб.

Докажем третий пункт теоремы

Заметим, что $\triangle ABC=\triangle ADC$ по второму признаку ($\angle 1=\angle 2, \angle 3=\angle 4$, $AC$ – общая).

Тогда $\angle B=\angle D$, а следовательно, равны и их половины: $\angle 5=\angle 6=\angle7=\angle 8$.

Но тогда треугольники $\triangle ABD$ и $\triangle BCD$ – равнобедренные: $AB=AD, BC=CD$.

Кроме того $\triangle ABD=\triangle BCD$ по второму признаку ($BD$ – общая, $\angle 5=\angle6, \angle 7=\angle 8$).

А значит $AB=BC$ и $AD=CD$.

Таким образом все стороны четырёхугольника равны между собой: $AB=BC=CD=DA$.

math-public/romb.txt · Последние изменения: 2016/04/17 00:55 — labreslav

wiki.sch239.net