Методическая разработка (4 класс) на тему: Внеклассное мероприятие «Решение стохастических и комбинаторных задач»

Внеклассное мероприятие «Решение стохастических и комбинаторных задач» (по мотивам мультфильма «Илья Муромец и Соловей-Разбойник»)

В ходе педагогической практики (МОУ Ясиновская Средняя общеобразовательная школа, с.Новая − Надежда, Куйбышевского района, Ростовской области) были разработаны и проведены с учащимися четвертого класса различные внеклассные мероприятия, посвященные решению вероятностных и комбинаторных задач по мотивам мультфильмов и сказок. Все подобранные задания были интересны и не вызывали особой трудности при решении. Приведем пример одного из таких внеклассных мероприятий по мотивам мультфильма «Илья Муромец и Соловей-Разбойник».

Тема: «Решение стохастических и комбинаторных задач».

Цели:

образовательные:

− закреплять умение решать комбинаторные и стохастические задачи;

− закреплять навыки использования специальных средств организации при решении стохастических задач.

развивающие:

− развивать логическое мышление;

− развивать внимание и наблюдательность;

− развивать математическую речь;

− развивать умение сравнивать, анализировать, делать выводы и выступать по результатам своей работы.

воспитательные:

− воспитывать самостоятельность;

− воспитывать усидчивость, трудолюбие, целеустремленность;

− воспитывать уважение к мнению других;

− воспитывать интерес к предмету.

Оборудование: телевизор, DVD, диск с мультфильмом «Илья Муромец и Соловей Разбойник», карточки, таблицы.

Ход занятия:

Организационный момент. 

Учитель: здравствуйте, ребята!

Ученик: здравствуйте!

Учитель: сегодня на нашем занятии мы еще раз повторим изученный материал, порешаем интересные задачки комбинаторного и стохастического характера. Чтобы вам не было скучно, в гости к нам я позвала наших любимых героев из мультфильма «Илья Муромец и Соловей-Разбойник».

Учитель: вы готовы отправиться в далекое путешествие по стране Стохастика?

Ученик: да!

Решение задач.

Задание №1: Для того чтобы узнать имя главного героя вам необходимо из цифр 3, 4, 1, 6 и 5 составить четные двузначные числа, так чтобы цифры в записи числа не повторялись. Расположить их в порядке возрастания.

Работа над заданием.

Учитель: прочитайте задание. Что требуется сделать?

Ученик: составить двузначные числа из цифр 3, 4, 1, 6 и 5.

Учитель: какими должны быть составленные нами числа?

Ученик: двузначными и четными.

Учитель: из каких разрядов состоят двузначные числа?

Ученик: десятков и единиц.

Учитель: какие двузначные числа являются четными?

Ученик: четными являются те числа, в разряде единиц которых находится четная цифра.

Учитель: среди предложенных нам цифр есть четные?

Ученик: да, это цифры 4 и 6.

Учитель: следовательно, какие цифры мы можем поставить в разряд единиц?

Ученик: цифры 4 и 6.

Учитель: какое значение может принимать количество десятков?

Ученик: 3, 1 и 5.

Учитель: составьте самостоятельно «дерево возможностей» (учащиеся выполняют задание в тетрадях самостоятельно).

Учитель: пользуясь «деревом возможностей», скажите, какие числа получим, если количество десятков будет равно 1?

Ученик: 14, 16 (на доске появляются карточки).

Рассуждая аналогично, получаем числа: 34, 36, 54 и 56.

Учитель: что в задании требуется сделать с полученными числами?

Ученик: расположить их в порядке возрастания.

Учитель: какое число будет первым в ряду: наибольшее или наименьшее?

Ученик: первым будет наименьшее число – 14.

Учитель: какие числа следующие?

Ученик: 26, 34, 36, 54 и 56.

Учитель: да, молодцы, правильно справились с заданием! На оборотной стороне каждой карточки находится буква. Перевернув карточки, получаем имя главного героя: Илья Муромец. Вместе с Ильей Муромцем с нами будут путешествовать: Аленушка, конь Бурушка, Соловей-Разбойник, князь.

Задание №2: (Показ фрагмента мультфильма).

У князя имеется 4 ключа, ему нужно положить свою казну в сейф, на котором 2 замка. Сколько попыток должен сделать князь, если он не знает, какой ключ подходит к каждому замку?

Работа над заданием.

Учитель: все внимательно прочитайте задачу. Сколько ключей у князя?

Ученик: у князя 4 ключа.

Учитель: сколько замков ему нужно открыть?

Ученик: нужно открыть два замка.

Учитель: что нам требуется узнать в задаче?

Ученик: сколько попыток должен сделать князь.

Во время опроса учащихся реализуется и начинает работать учебно-познавательная компетенция, а именно: учащиеся ставят цель своей работы, поясняют данную цель, задают вопросы к фактам и явлениям данной задачи, выдвигают гипотезы.

Учитель: решить эту задачу можно с помощью составления таблицы. Что мы можем отобразить в таблице?

Каждый предлагает свой вариант. На данном этапе реализуется как учебно-познавательная, так и ценностно-смысловая компетенции, а именно: владение учащимися различными способами самоопределения в ситуации выбора на основе собственных позиций, каждый высказывает свое личное мнение, учащиеся проводят эксперименты с предметами (ключи).

Учитель: отобразим номера замков, которые нужно открыть князю, и количество попыток, предпринятых для того, чтобы открыть каждый замок.

№ замка
Количество попыток

Учитель: сколько замков нужно открыть?

Ученик: нужно открыть два замка.

Учитель: значит, сколько столбцов мы должны внести в таблицу?

Учитель: мы должны внести в таблицу два столбца.

В процессе работы с таблицей свое дальнейшее развитие получают такие компетенции: учебно-познавательные, коммуникативные, информационные, социально-трудовые. Учащиеся работают в группах, взаимодействуют и сотрудничают между собой, самостоятельно получают определенную информацию, систематизируют её, овладевают навыками счета, необходимыми в жизни каждого человека, продолжают экспериментирование.

№ замка	1	2
Количество попыток

Учитель: сколько ключей у князя?

Ученик: у князя четыре ключа.

Учитель: подбирая ключ к первому замку, сколько попыток сделаем? Почему?

Ученик: подбирая ключ к первому замку, сделаем четыре попытки, так как у князя 4 ключа. Внесем число 4 в столбец № 1. Подобрав ключ, мы знаем, какой из четырех ключей подходит к первому замку.

Учитель: сколько ключей, не подобранных к «своему» замку осталось в связке?

Ученик: в связке осталось три не подобранных ключа.

Учитель: сколько попыток нужно сделать, чтобы наверняка подобрать ключ ко второму замку? Почему?

Ученик: чтобы наверняка подобрать ключ ко второму замку, нужно сделать три попытки, так как один ключ мы уже подобрали, а три ключа осталось.

Учитель: внесем цифру три в столбец № 2.

Учитель: пользуясь таблицей, посчитайте, сколько всего попыток нужно сделать князю, чтобы открыть все замки?

Ученик: для того чтобы открыть все замки, нужно сделать семь попыток.

Задание №3:Илья Муромец усердно трудиться на поле, чтобы выкупить своего коня Бурушку (показ фрагмента мультфильма). Если хотите узнать, кто же приедет в гости к князю, то решите следующую задачу: «Лиса, медведь и заяц неожиданно в лесу находят красивую поляну с огромным количеством цветов. Медведь решил сделать сюрприз лисе на день ее рожденья и отправился собирать букет. На поляне растут 5 желтых, 3 красных и 4 синих цветка. Медведь знал, что лиса любит только синие цветы. Какое количество цветов необходимо сорвать мишке, чтобы наверняка иметь синий цветок, если он не различает ни одного цвета?».

Работа над заданием.

Учитель: ребята внимательно прочитайте задачу. Какие цветы растут на поляне?

Ученик: на поляне растут желтые, красные и синие цветы.

Учитель: сколько красных цветов растет на поляне?

Ученик: на поляне растет 3 красных цветка.

Учитель: сколько желтых цветов растет на поляне?

Ученик: на поляне растет 5 желтых цветов.

Учитель: сколько цветов синего цвета растет на поляне?

Ученик: на поляне растет 4 цветка синего цвета.

Учитель: о чем еще говорится в задаче?

Ученик: мишка не различает никакие цвета.

Учитель: каков вопрос задачи?

Ученик: сколько цветков нужно сорвать медведю, чтобы наверняка иметь синий цветок?

Учитель: вдруг наш мишка сорвет один цветок, обязательно ли он будет иметь синий цветок? Почему?

Ученик: нет, не обязательно, так как он может взять красный или желтый цветок.

Учитель: а если мишка сорвет с поляны два каких-либо цветка, обязательно ли среди них окажется синий цветок? Почему?

Ученик: синий цветок может оказаться у мишки, но не обязательно, так как у него может быть и 1 красный, а 1 желтый, и 2 красных, и 2 желтых цветы, а синего не быть вовсе.

Учитель: наш мишка решил сорвать девять цветов, может ли среди них наверняка оказаться синий цветок?

Ученик: если мишка сорвет девять цветков, то среди них наверняка окажется синий цветок: у него из 9 цветков могут оказаться 3 красных и 5 желтых цветков, тогда 1 цветок будет наверняка синим. Такие рассуждения можно продолжать и дальше, вводя при этом новые числа.

Учитель: молодцы, ребята, ну а теперь посмотрим, кто же приехал в гости к Илье Муромцу (показ фрагмента мультфильма).

Задание №4: Вот наши путешественники отправляются в лес, где князь был схвачен и привязан вокруг дерева (показ фрагмента). Интересно, убьют князя или нет? Узнаем, решив следующую задачу: «В мешке имеется 3 красных, 3 белых и 3 зелёных шара. Сколько шаров нужно вытянуть из мешка, чтобы наверняка иметь шары трёх цветов?».

Работа над заданием.

Учащиеся путем длительного экспериментирования должны прийти к следующим выводам:

Ученик: если вынуть 7, 8, 9 шаров, наверняка будут шары трёх цветов.

Ученик: если вынуть 3, 4, 5 или 6 шаров, то возможно, но необязательно будут шары трёх цветов.

Ученик: если вынуть 1 или 2 шара, то невозможно получить шары трёх цветов.

Учитель: молодцы, справились и с этим заданием, теперь мы сможем посмотреть, что же будет с князем (показ фрагмента).

Задание №5:А в это время на корабле Соловей-Разбойник играет в кубики с купцом на похищенную Бурушку (показ фрагмента). Если сумма выпавших очков будет четной, выигрывает Соловей-Разбойник, а если же сумма выпавших очков окажется нечетной, выигрывает купец и забирает лошадь. Кубики решили подбросить 11 раз. У кого шансов выиграть больше?

Работа над заданием.

Учитель: прочитайте задачу еще раз. Во что играли купец и Соловей-Разбойник?

Ученик: они подбрасывали два игральных кубика и подсчитывали сумму выпавших очков.

Учитель: для чего они это делали?

Ученик: чтобы узнать, кому достанется конь.

Учитель: в каком случае победит купец?

Ученик: если сумма выпавших очков будет нечетной.

Учитель: при каких условиях победителем становится Соловей-Разбойник?

Ученик: когда количество очков будет четным.

Учитель: что нам требуется узнать в задаче?

Ученик: у кого больше шансов выиграть?

Учитель: чтобы ответить на вопрос задачи, что нам нужно знать?

Ученик: число событий, удовлетворяющих условиям, при которых выигрывает купец и Соловей-Разбойник.

Учитель: когда количество выигрышных вариантов будет известно, как узнаем, у кого больше шансов выиграть?

Ученик: шансов больше у того, у кого количество выигрышных вариантов будет больше.

Учитель: чему может равняться сумма выпавших очков?

Ученик: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Учитель: почему мы не включаем 1?

Ученик: так как подбрасывают два игральных кубика. На каждом кубике самое меньшее количество очков – 1. Если на каждом кубике выпадет по 1, их сумма будет равна 2. Значит, самое меньшее количество очков в сумме равно 2, а 1 подбрасывая два игральных кубика получить нельзя.

Учитель: каким будет событие − сумма выпавших очков равна 1− достоверным или невозможным?

Ученик: невозможным.

Учитель: какие еще события невозможны при подбрасывании двух игральных кубиков? Почему?

Ученик: количество выпавших очков больше 12. Это событие невозможно, потому что 12 – это наибольшее количество очков, которые могут выпасть при подбрасывании двух игральных кубиков.

Учитель: подсчитаем количество событий, при которых выиграет Соловей-Разбойник. Какое условие должно выполняться?

Ученик: количество выпавших очков будет четным.

Учитель: какое количество очков удовлетворяет этому условию?

Ученик: 2, 4, 6, 8, 10, 12.

Учитель: подсчитаем количество способов, которыми можно получить четную сумму очков. Заполним таблицу на доске.

Сумма выпавших                                                                                                                                                                                                                                         очков

2

4

6

8

10

12

Количество способов

1 кубик

2 кубик

1 кубик

2 кубик

1 кубик

2 кубик

1 кубик

2 кубик

1 кубик

2 кубик

1 кубик

2 кубик

1

1 и 1

1 и 3

1 и 5

2 и 6

4 и 6

6 и 6

2

2 и 2

2 и 4

3 и 5

5 и 5

3

3 и 1

3 и 3

4 и 4

6 и 4

4

4 и 2

5 и 3

5

5 и 1

6 и 2

6

Учитель: подсчитаем число событий, при которых выиграет Соловей. Чему оно равно?

Ученик: ответ 18.

Учитель: итак, существует 18 выигрышных комбинаций для Соловья-Разбойника. Подсчитаем количество событий, при которых победителем окажется купец. Какое условие должно выполняться?

Ученик: сумма выпавших очков должна быть нечетной.

Учитель: какие значения суммы удовлетворяют заданному условию?

Ученик: 3, 5, 7, 9, 11.

Учитель: заполним таблицу.

Сумма выпавших очков	3		5		7		9		11
Количество способов	1 кубик	2 кубик	1 кубик	2 кубик	1 кубик	2 кубик	1 кубик	2 кубик	1 кубик	2 кубик
1	1 и 2		1 и 4		1 и 6		3 и 6		5 и 6
2	2 и 1		2 и 3		2 и 5		4 и 5		6 и 5
3			3 и 2		3 и 4		5 и 4
4			4 и 1		4 и 3		6 и 3
5					5 и 2
6					6 и 1

Учитель: пользуясь таблицей, подсчитаем количество событий, при которых выигрывает купец. Чему оно равно?

Ученик: 18 способов.

Учитель: итак, количество выигрышных комбинаций для Соловья-Разбойника равно 18, и для купца тоже 18. У кого же больше шансов выиграть? Почему?

Ученик: шансы на выигрыш у них равны, потому что количество выигрышных комбинаций равно.

Ответ: шансы равны.

Задание №6:Соловей-Разбойник сидит в тюрьме и пытается угадать, кто же выиграет в этой схватке? Могучий богатырь или его противники? (показ фрагмента). Если хотите узнать, кто же победит в этой жестокой схватке, то решите следующую задачу: «На середину класса выходят три ученика, например, Даша, Леша, Оксана, которые садятся на три стула в любом порядке. Учитель предлагает им поменяться местами и задает вопрос: как вы думаете, смогут ли Оксана, Леша и Даша каждый раз меняться своими местами так, чтобы их новое расположение оказывалось всё время отличным от предыдущих?».

Работа над заданием.

Учащиеся предлагают различные варианты расположения у доски и записывают ответы. Данный перебор осуществляется учащимися случайным образом, хаотично. Всеми вместе было найдено шесть различных вариантов расположения.

Учитель: а можно ли найти седьмой вариант? Давайте запишем все получившиеся варианты на доске (Даша − Оксана − Леша; Даша − Леша − Оксана; Леша − Даша − Оксана; Леша − Оксана − Даша; Оксана − Даша − Леша; Оксана − Леша − Даша).

Учитель: вот мы с вами и убедились, что других вариантов быть не может. Теперь посмотрим, чем же закончилась схватка Ильи и его противников (показ фрагмента мультфильма).

Илья Муромец возвращает золото и своего любимого коня.

Итог урока:

Учитель: сегодня мы помогли героям преодолеть разнообразные препятствия, какие задания нам пришлось выполнить?

Ученик: задания комбинаторного и стохастического характера.

Учитель: что мы делали при этом?

Ученик: мы составляли графы и таблицы, «дерево возможностей», пользовались методом систематического перебора.

Учитель: какие правила мы использовали при решении комбинаторных задач?

Учитель: правило произведения.

Учитель: какие задания вам больше всего понравились? (Варианты учеников.)

Учитель: вот и закончилось наше с вами путешествие по стране Стохастика. Спасибо за активность и прекрасную работу (показ финала мультфильма).

Комбинаторные задачи по математике для 4-6 класса — Колпаков Александр Николаевич

Небольшая подборка занимательных комбинаторных задач для работы репетитора по математике с младшими школьниками. Номера расположены по возрастанию уровня сложности и соответствуют способностям сильного (среднего) ученика. Репетитор найдет в списке несколько уникальных задач

1) В магазине «Планета чая» продаются 6 чашек разной высоты 4 блюдца разной ширины. Миша решил купить одну чашку и одно блюдце. Сколькими способами он может этот сделать?

2) В магазине «планета чая» еще продаются 5 чайных ложек. Сколькими способами Миша может купить чайный комплект из одного блюдца, одной чашки и одной ложки?

3) В волшебной стране есть 3 города: Мудрый, Светлый и Чудный. Из Мудрого в Светлый ведут 5 дорог, из Светлого в Чудный 6 дорог. Сколькими способами Миша может проехать из города Мудрый в город Чудный?

4) В той же волшебной стране еще 4 города: Красный, Синий, Серый и Зеленый. Город Красный и город Синий связывают 5 дорог, города Синий и Серый связывают 7 дорог. Из Красного в Зеленый ведут две дороги, из Зеленого в Серый три дороги. Сколькими способами Миша может проехать из города Красный в город Зеленый?

5) В магазин «Планета Чая» привезли для продажи 5 чашек, 4 блюдца и 3 ложки. Сколькими способами Миша может купить два разных предмета?

6) Миша решил называть числа «приятными», если в их записи участвуют только четные цифры. Помогите ему сосчитать количество 4-значных «приятных» чисел.

7) Буратино три раза бросил монету. Сколько различных последовательностей выпадения орлов и решек он мог при этом получить?

8) Миша решить разделить огород на 4 части на каждой посадить или картофель или свеклу. Сколько различных вариантов посадок существует?

9) Номер телефона репетитора по математике 756-93-95. Миша запомнил только первые 5 его цифр и то, что какие-то две цифры повторяются дважды. Он выписал все возможные комбинации окончаний и позвонил на каждый из номеров. Правильным оказался последний вариант. Какое количество звонков сделал Миша?

10) Миша захотел предсказать итог проведения пяти товарищеских матчей двух баскетбольных команд. Итогом каждой встречи может быть или победа первой команды или поражение. Сколько разных прогнозов Миша мог бы сделать?

11) Алфавит жителей другой планеты состоит из трех разных букв. Словом является любая их последовательность, состоящая не более чем из 4 букв. Сколько слов в языке инопланетян.

Указание репетитора по математике: считайте отдельно количество слов с одной буквой, потом с двумя буквами, потом с тремя и четырьмя.

12) В футбольной команде имеются семь игроков, которые удачно пробивают пенальти. Тренеру нужно выбрать пятерку пенальтистов для выяснения победителя матча. Сколько разных составов могут пробить серию пенальти. Порядок в котором они пробиваются не учитывается.

13) На горку ведут 7 дорог. Сколько существует маршрутов, которыми можно подняться на горку, а затем спуститься с нее? Решите эту же задачу при условии, что нельзя спускаться и подниматься по одной и той же дороге.

Простейшие комбинаторные задачи, представленные на этой странице, все-таки относятся к категории олимпиадных, однако даже в работе с сильным учеником 4-6 класса репетитор по математике не часто их разбирает. Причина в содержаниях большинства олимпиад и экзаменов в математические школы (классы). Больший упор делается на логигику и поиск особого подхода к решению, а не на простой перебор вариантов. Однако не стоит забывать о предстоящем изучении теории вероятности (в 7-9 классе), которая полностью держится на комбинаторных правилах. Репетитору математики лучше заняться подготовкой к их восприятию с раннего возраста. Главное не утомлять ребенка подсчетом большого количества варинтов и не затрагивать комбинаторные формулы.

А.Н. Колпаков. Репетитор по математике

Метки: Комбинаторика

Конспект по логике на тему «Решение комбинаторных задач» (4 класс)

Тема: Решение комбинаторных задач методом с помощью таблиц и графов

Цель урока: формировать навыки решения комбинаторных задач с помощью таблиц и графов.

Приведение в систему умения решать комбинаторные задачи методом графов.

Формировать умение точно и грамотно выражать свои мысли, поддерживать инициативное сотрудничество в поиске и сборе информации, осознавать учащимся уровень и качество усвоения результата, осуществлять выбор наиболее эффективных способов решения задач.

Формирование навыков сотрудничества индивидуального и коллективного выполнения творческих задач.

Научиться решать комбинаторные задачи, применяя метод графов.

Осознанно владеть приемом решения комбинаторных задач .

Уметь точно и грамотно выражать свои мысли, ориентироваться на разнообразие способов решения задач.

Готовность к выполнению задачи, достижению цели в решении задач.

Этапы

урока

Действия учителя

Деятельность обучающихся

Формируемые результаты

Предметные

Метапредметные

личностные

1.Организационный момент.

(1мин)

Игра «Черный ящик» СЛАЙД 1

— Кому нужны эти предметы: лупа, перчатки, фотографии ,фотоаппарат, папка «Дело № 1»

— Вы сегодня посвящаетесь в учеников ШЮД СЛАЙД 2

— Как расшифруете данную аббревиатуру?

Детективу

Школа юных детективов

Готовность принять урок и его задачи.

2. Мотивация к учебной деятельности.

(10 мин)

— Поработайте в паре и определите, в чём заключается основной метод дедукции Шерлока Хомса

КАРТОЧКИ

— Подведем итог СЛАЙД 3

1. Умение видеть улики

2. Умение составлять факты в единую цепочку

3. Умение предугадывать

4. Умение рассуждать

5. Умение быстро находить ответ или решение

— Готовы проявлять все указанные качества?

— Тогда сверим часы

Мои часы показывают 12 ч 50 мин., но они отстают на 25 минут. Какое время покажут ваши часы, если они спешат на 15 мин?

Наблюдательность

Анализ

Интуиция

Логика

Сообразительность

12 час 50 мин+25 мин= 13 часов15 мин

13 часов 15 мин+15 мин=13 часов 30мин

Общеучебные и логические действия.

Регулятивные: планирование и прогнозирование своей деятельности.

Познавательные: ориентироваться в разнообразии способов решения задач.

Коммуникативные:

вступают в диалог.

Формирование устойчивой мотивации к обучению.

3.Формулирование темы и цели урока.

(3 мин)

— Проверим вашу наблюдательность юные детективы СЛАЙД 4

ДЕЛО №1 Загадочное письмо СЛАЙД 5

— Какое слово у вас получилось?

— Какую задачу можно назвать комбинаторной?

— Какие способы решения комбинаторных задач вы знаете?

комбинаторика

задача, требующая осуществления перебора всех возможных вариантов или подсчета их числа.

Организованный перебор вариантов, таблица, графы

Коммуникативные: диалог с учителем.

4.Актуализация знаний

(10 мин)

— Проверим ваше умение решать комбинаторные задачи с помощью анализа, юные детективы СЛАЙД 6

— Перед вами очень запутанное дело

ДЕЛО №2 Что в коробке? СЛАЙД 7

В каждой из четырёх коробок лежит один из фруктов: апельсин, лимон, зелёное яблоко и ананас. Цвет коробки не совпадает с цветом фрукта. Известно, что зелёное яблоко лежит в коричневой коробке, а лимон не лежит в зелёной коробке. В коробке какого цвета лежит каждый фрукт?

— Какой цвет соответствует каждому фрукту?

— Дополните таблицу

— Заполните таблицу и ответьте на вопрос :»В коробке какого цвета лежит каждый фрукт»

— Проверим вашу логику юные детективы СЛАЙД 8

ДЕЛО №3 Во что одет доктор Ватсон? СЛАЙД 9

Доктор Ватсон ходит в брюках или джинсах, к ним подбирает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве обуви носит туфли или мокасины

а) Сколько дней доктор Ватсон сможет выглядеть по-новому?

б) Сколько дней при этом он будет ходить в мокасинах?

в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

Решение. Построим дерево возможных вариантов, обозначив Б — брюки, Д — джинсы, С — серая рубашка, Г — голубая рубашка, З — зеленая рубашка, Р — рубашка в клетку, Т — туфли, М — мокасины

Ответ: а) 16 дней; б) 8 дней; в) 2 дня.

— Проверим вашу сообразительность, юные детективы

— Перед вами ДЕЛО №4 СЛАЙД 10,11

Однажды вечером к Шерлоку Холмсу пришла вдова Андерсон вся в слезах. Она забыла код от сейфа. Единственное, что она помнила, что код составлен из нулей и единиц и имеет ровно 4 цифры

Сколько вариантов комбинаций цифр Шерлок Холмс, предложит вдове, чтобы она смогла открыть сейф?

Общие подходы к решению задач.

Коммуникативные:

Формулирование собственного мнения и позиции, аргументирование их.

Регулятивные:

Адекватное оценивание своих возможностей в достижении цели.

Познавательные:

уметь осуществлять анализ объектов.

Готовность к принятию задач и их выполнению.

5.Самостоятельное выполнение заданий под контролем учителя.

(15 мин)

ДЕЛО №5 Где чей щенок?

СЛАЙД 12,13,14

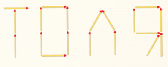
Из спичек выложено мужское имя Толя. Переложите 1 спичку так, чтобы получить женское имя.

Детективная история:

«Инспектор и два его помощника гнались за преступниками. Следы привели их к подвалу. Укрепив на выступе стены канат, сыщики опустились в подвал. Но не успели они осмотреться, как преступник вытянул веревку, свисавшую из окна. Как же выбраться из подвала? Решили выстроить пирамиду: внизу стал самый высокий сыщик, затем сыщик пониже и, наконец, самый низкорослый сыщик. До окна не хватало каких-то 5 см. Что делать?»

(Следует поменяться местами. Если высокий сыщик станет вверху пирамиды, то он сможет достать до окна, так как у высоких людей длиннее руки.)

Понимание условия текстовой задачи, установление причинно-следственных связей.

Выбор наиболее эффективного способа решения задач.

Коммуникативные:

развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений.

Регулятивные:

Планирование, прогнозирование, действие по алгоритму.

Познавательные:

уметь осуществлять анализ объектов с выделением существенных и несущественных признаков.

Планирование учебного сотрудничества, управление поведением партнера, умение выражать четко свои мысли.

4. Рефлексия деятельности.

(3 мин)

Предлагает ученикам обвести ладонь руки на бумаге.

Написать пять прилагательных, определяющих чувства, которые учащиеся испытывали сегодня на уроке.

Выберите для себя пословицу которая отражает состояние вашей работы на уроке.

Зачитывают слова с нарисованной ладони.

Выбирают и зачитывают пословицы.(по желанию)

Умение выразить свое отношение к результату собственной деятельности на уроке.

Информирование о домашнем задании.

(1 мин)

Показывает книги занимательной математики в библиотеке.

Читать книги занимательной математики.

Разработка урока по математике на тему «Задачи на перебор вариантов» (4 класс)

Конспект урока по математике для 4 класса

на тему «Задачи на перебор вариантов»

Цель: научиться решать и записывать задачи на перебор вариантов.

Задачи:

Образовательные:

• понаблюдать за методом полного перебора вариантов при решении комбинаторных задач;

• вырабатывать умения применять математическую теорию в конкретных ситуациях;

• способствовать владению интеллектуальными умениями и мыслительными операциями.

Развивающая:

• формировать умения самостоятельно выбирать способ решения и умения обосновать выбор;

• формировать умения решать задачи путём логических рассуждений.

Воспитательные:

• воспитывать чувство ответственности за качество и результат выполняемой работы;

• прививать сознательное отношение к труду; учить работать в парах, в группе, создавать условия для воспитания чувств, взаимовыручки, дружбы.

Формы работы: фронтальная, самостоятельная работа, самопроверка, работа в парах, работа в группе, взаимопроверка.

В процессе работы формируются:

Регулятивные УУД: формировать умение планировать, предвидеть полученный результат, контролировать и оценивать свои действия; умение высказывать свои предположения на основе работы с материалом учебника; принимать и сохранять учебную задачу.

Познавательные: выполнять перебор всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям; развивать мыслительную деятельность.

Коммуникативные: формировать умение работать в парах, в группе, умение высказывать свои суждения, умение слушать и понимать других; договариваться о совместной деятельности.

Личностные: развивать учебно-познавательный интерес к учебному материалу и способам решения задач; ориентировать в нравственных нормах и правилах, вырабатывать свою жизненную позицию.

Ход урока

I Мотивация к учебной деятельности

Сегодня у нас не совсем обычный урок. У нас присутствуют гости. Поприветствуйте их. Садитесь.

Ребята, готовы к уроку?

На вас надеюсь я, друзья.

Мы хороший дружный класс

Все получится у нас!

А что необходимо для успешной работы?

Девиз урока: «Учимся не для школы, а для жизни»(Сенека) (слайд 2).

Как понимаете эти слова? (ответы детей)

II Актуализация знаний

Начнем работу с устного счета. (слайд 3)

— Какие из чисел 300, 27, 108, 25, 36, 909, 350, 40, 99, 72, 450, 75 делятся на 5? Делятся на 3, на 2?

— Какое число лишнее и почему? 46, 82, 504, 227, 24, 668, 754, 56, 312 (слайд 4)

— На кормушке сидело 5 воробьёв и 2 синицы. Улетели 3 птицы. Был ли среди них хотя бы один воробей? (слайд 5)

— Дима моет 4 тарелки за то же время, что и 6 чашек. Что он моет быстрее — тарелку или чашку? (слайд 6)

— Истинное или ложное высказывание (слайд 7)

Число 5200 содержит 2 десятка.

Неверно, что 10 км 50 м = 1050 м.

В марте 31 день и в апреле 31 день.

Если 9 * 8 = 72, то 72 : 8 = 9.

Тонна – единица длины или скорости.

— Придумайте числа, которые делились бы на 2, на 5 и на 8 одновременно. (40, 80, 160, 240, 360…) (слайд 8)

III Постановка учебной задачи

Работа в паре

А сейчас я поставлю перед вами задачу. (на столе листочки, на которых записаны цифры 2, 5, 8)

Работая в паре, запишите все трёхзначные числа, используя цифры 2, 5, 8 так, чтобы в записи числа цифры не повторялись. (слайд 9)

Сколько чисел получилось? (спрашиваю несколько человек)

Записать на доске (3-5 человек)

Кто записал все числа и не пропустил ни одного?

Кто испытывал затруднение? В чём? (запутались, повторили числа, некоторые не назвали)

Как вы нашли решение этой задачи? (перебирали варианты, записывали те числа, которых ещё не было)

Мы учились решать такие задачи?

А вы хотите научиться?

Значит чему будет посвящен наш урок? (открытию нового знания)

Сформулируем тему урока (дети стараются назвать тему урока)

Тема урока «Задачи на перебор вариантов» (слайд 10)

Чему мы будем учиться на уроке? (Учиться решать и записывать задачи на перебор вариантов)

IV Проблемное объяснение нового знания

Какая проблема у нас возникла? (не знали, как записать решение)

Почему нужно научиться записывать? (чтобы не повторить дважды вариант или не пропустить).

Задачи, которые мы сегодня будем решать, в математике ещё называют – комбинаторикой. Найдем определение этого слова в толковом словаре.

Комбинаторикой — это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо правилам или условиям.(слайд 12)

Как вы поняли это определение? (чтобы решить задачи на перебор вариантов нужно знать правило, чтобы их решить)

Да, должен быть какой-то способ перебора вариантов.

Я предлагаю найти этот способ записи, работая в группе. Вспомните правила работы в группе.

Запомни и соблюдай простые правила:

1. Уважай своего товарища.

2. Умей каждого выслушать.

3. Не согласен – предлагай!

Подсказка. Вспомним, как мы записываем задачу(условие)? (таблица, схема)

Итак, что вы должны сделать? (перебрать всевозможные варианты, придумать определенный способ записи).

(Слайд 13). Папа купил три книги. В каком порядке эти книги можно поставить на книжную полку? (у каждой группы альбомный лист, фломастеры)

Ученики каждой группы выходят к доске и рассказывают, как они решали задачу, какой способ записи выбрали.

Какой сделаем вывод (при решении задачи лучше сделать таблицу)

Сравниваем свой вывод с авторским

А сейчас откроем учебник стр. 46 прочитаем правило.

Как записано решение задачи в учебнике.

— Рассмотрите таблицу и объясните, как выполнен перебор вариантов.

По таблице дети самостоятельно объясняют способы перебора вариантов.

— Для чего использовали таблицу при решении данной задачи? (Для упорядочивания вариантов)

Соответствует ли наш способ со способом в учебнике?(Да)

Работа с таблицей (слайд 14)

Продолжение работы по таблице по заданиям учебника на с. 47

— Прочитайте высказывания. Используя таблицу, определите, в каких случаях каждое высказывание истинно и в каких – ложно.

Физминутка

V Первичное закрепление

Задача на экране (слайд 15)

Попробуем применить новое знание на практике. (фронтально)

У Васи в тетради нарисован прямоугольник, разделенный на три равные части. Он должен закрасить каждую из этих частей в один из трех цветов: красный, желтый, зеленый. Нельзя окрашивать разные части одинаковым цветом. Сколько вариантов рисунка может получить Вася?

(ученик у доски)

Работа идет фронтально, дети предлагают свои варианты, изображают на доске с помощью наглядности.

Можно ли это задание упорядочить(записать) в таблицу? Как?(заготовки)

Как нужно разместить данные в таблицу?

VI Самостоятельная работа с взаимопроверкой

№ 91 с. 31 в рабочей тетради. Работа в парах.

Выполнить самостоятельно, проверить с другом по парте. Если всё правильно показывают (берутся за руки), если есть ошибки, помогите их друг другу исправить. Не забудьте поблагодарить за помощь.

Проверка. Учитель спрашивает 2 -3 х учеников о работе напарника.

— Что ты можешь сказать о работе напарника?

— Молодцы, ребята.

Обратимся ещё раз к эпиграфу нашего урока. «Учимся не для школы, а для жизни» (Сенека).(слайд 16)

— А где в жизни мы можем столкнуться с решением таких задач? Так ли уж нам нужны эти знания?

– Подумайте и приведите примеры.

(При составлении расписания уроков, при составлении меню, подбор гардероба, при шифровании и кодировке информации, комбинация грядок с посевами на огороде, на спортивных соревнованиях при расчёте количества игр между командами, комбинации расположения звёзд и планет и т. д.)

Задачи на перебор вариантов или комбинаторные задачи играют большую роль в практической деятельности человека.

— Я хочу вам предложить решить ещё одну задачу данного вида и записать решение в тетрадь.

— Как вы будите записывать решение? (С помощью таблицы.)

— В субботу по расписанию три урока: Математика, Русский язык, Литературное чтение. Сколько можно составить вариантов расписания на день?

— Проверим. (самопроверка)

VII Итог урока. Рефлексия (слайд 17)

— Какую цель мы ставили на уроке (Учиться решать и записывать задачи на перебор вариантов)

Мы научились записывать задачи на перебор вариантов?

— Какой способ мы использовали?(таблица)

Закончите предложения

Я сегодня узнал(а) …
Я научился(лась)…
Мне было интересно …
Я понял(а), что …
Мне было трудно …
Материал урока мне …
Свою работу я оцениваю …

— Чьи идеи вам больше всего понравились?

— Что вам помогало на уроке получить новые знания?

Мне на уроке понравилось, как вы все высказывали свои мысли, работали.

Оценки за урок

Д/з №2 с. 47 (1,2,3,4)

Спасибо вам, ребята, за работу.

Задачи на перебор всех возможных вариантов

ФИО: Тютюгина Н. А.

Место работы: ГБУ РК «КСС «Симеиз»

Должность: учитель математики

Предмет: математика

Класс: 6

Тема и номер урока в теме : гл. 1 , уроки № 29, 30 Тип урока: комбинированный (изучение нового материала; закрепление знаний и умений).

Конспект урока по теме «Задачи на перебор всех возможных вариантов»

Цель: научиться решать комбинаторные задачи на перебор всех возможных вариантов.

План урока

1. Организационный момент.

2. Актуализация опорных знаний.

3. Примеры решения задачи на перебор всех возможных вариантов (без таблицы).

4. Решение задач с помощью схем, таблиц.

5. Решение задачи обучающимися (самостоятельно).

6. Рефлексия.

7. Подведение итогов, домашнее задание.

Ход урока

3. Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

1) Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

2) В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

Ответ:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.

3) В кружок бального танца записались: Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

Ответ:
1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег.

4. Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.

Решить комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
В разделе представлены комбинаторные задачи на размещение, сочетание, перестановки с повторением и без повторения элементов. Используется естественный, доступный детям всех возрастов метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций).

Решение задач методом полного перебора всех возможных вариантов:

4) Какие трехзначные числа можно составить из цифр 0, 2, 4?

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.

5. Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?

Решение: Для того чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)
71; 74; 77; (начали с 7)

Ответ: 9 чисел.

5. На обед в школьной столовой предлагается 2 супа,3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?

Суп х2, вторые блюда х3, сок х4

Решение: 2 x 3 x 4 = 24

Ответ: Можно составить 24 варианта различных обедов.

5. Андрей, Борис и Василий входят в комнату по одному. Сколько у них есть способов это сделать?

Решение. Пусть первым войдёт Андрей, но тогда вторым может войти Борис или Василий, то есть имеются две возможности. Аналогично есть две возможности, если первым войдёт Борис и если первым войдёт Василий.

2 x 3 =6. Таким образом, 6 возможностей.

Ответ: 6 способов.

5. Решение задач самостоятельно.

1) На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?

2) Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Конспект внеурочного занятия «Комбинаторные задачи на образование перестановок»

Конспект внеурочного занятия

Направление внеурочной деятельности: общеинтеллектуальное.

Тема: «Комбинаторные задачи на образование перестановок»

Цель: формирование умения решать простейшие комбинаторные задачи.

Задачи:

образовательные: решать простейшие комбинаторные задачи;

развивающие: развивать логическое мышление;

воспитательные: воспитывать уважительное отношение к своим товарищам; учить работать в группе.

Планируемые результаты занятия:

Познавательные: умение добывать новые знания.

Регулятивные: планирование свои действия в соответствии с задачей; оценивание результатов познавательной деятельности.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; владение монологической и диалогической формами речи.

Личностные результаты: способность к самооценке; познавательный интерес к новым понятиям.

Средства обучения (в том числе и интернет-ресурсы): интерактивная доска, презентация, раздаточный материал.

ХОД ЗАНЯТИЯ

-Здравствуйте, ребята. Сегодня мы с вами отправимся в небольшое путешествие в страну Комбинаторию, где живут комбинаторные задачи. А передвигаться мы будем по морю.

— Как вы думаете, на каком транспорте мы можем совершить это путешествие?

Приветствуют

Воспринимают

Корабль

II. ОСНОВНАЯ ЧАСТЬ

-Но для того чтобы отправиться в путь, нам необходимо собрать корабль. Для этого 1 группа будет собирать кораблик, а 2 группа – составлять программу на компьютере. У каждой команды есть своя инструкция.

-Итак, мы отправляемся в путь.

-Вот мы и прибыли в страну комбинаторных задач. И нас в гости уже ждет хозяин первого острова.

— Используя карточки с цифрами, составьте все трехзначные числа из цифр 1, 2, 3 так, чтобы цифры в числе не повторялись .

— Второй остров нам тоже приготовил задание. Слушайте внимательно.

— Ребята сделали из бумаги новогодние снежинки разного цвета : желтый, красный и зеленый. Покажите, в каком порядке они могут располагаться в альбоме. У каждого из вас есть три снежинки. На доске — альбомные листы. По очереди расположите снежинки на альбомные листы так, чтобы комбинация нигде не повторилась.

— Раскрасьте каждую шапочку с помпоном в три цвета: красный, желтый и зеленый так, чтобы шапочки отличались друг от друга.

Моделируют корабль с помощью лего-конструктора

Работа в группах

Воспринимают

Используя карточки, составляют все трехзначные числа так, чтобы цифры в числах не повторились.

123, 132, 213, 231, 312, 321

Располагают листы

По очереди со своим комплектом снежинок каждый ребенок подходит к доске, на которой находится альбомный лист, и располагает снежинки так, чтобы не повторилась комбинация.

Раскрашивают так, чтобы комбинация не повторилась.

III. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ, РЕФЛЕКСИЯ

— Ребята, в какую страну мы сегодня путешествовали?

-Кто живет в этой стране?

-Чем сегодня на занятии мы занимались?

-Спасибо вам за хорошую работу и увлекательное путешествие.

-Комбинаторию

—Комбинаторные задачи

-Учились решать простейшие комбинаторные задачи