Урок 15. пирамида — Геометрия — 10 класс

Геометрия, 10 класс

Урок № 15. Пирамида

Перечень вопросов, рассматриваемых в теме:

• Понятие пирамиды;
• Виды пирамид;
• Элементы пирамиды: вершина, ребра, грани, основание;
• Площадь боковой поверхности и полной поверхности пирамиды.

Глоссарий по теме

Пирамида – многогранник, составленный из n-угольника и n треугольников

Основание пирамиды – грань пирамиды, являющаяся n-угольником

Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.

Боковая грань – грань пирамиды, являющаяся треугольником

Боковые ребра – общие отрезки боковых граней

Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание

Апофема – высота боковой грани правильной пирамиды

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой

Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).

Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды

Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды

Основная литература:

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Образовательный портал «Решу ЕГЭ». https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

Определение пирамиды

Рассмотрим многоугольник A₁A₂…A_n и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA₁A₂, PA₂A₃,…, PA_nA₁.

Многогранник, составленный из n-угольника A₁A₂…A_n и n треугольников, называется пирамидой. Многоугольник A₁A₂…A_n называется основанием, а треугольники PA₁A₂, PA₂A₃,…, PA_nA₁ – боковые грани пирамиды, отрезки PA

1, PA₂,…, PA_n – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A₁A₂…A_n и вершиной Р называют n-угольной пирамидой и обозначают PA₁A₂…A_n.

Рисунок 1 — пирамида

Высота пирамиды

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).

Рисунок 3 – высота вне пирамиды

Рисунок 4 – Высота пирамиды — боковое ребро

Правильная пирамида

Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).

Рисунок 5 – Правильная пирамида

Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.

Рассмотрим правильную пирамиду PA₁A₂…A_n (рис. 5).

Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А

1О, А₂О,…А_nО.

Образованные высотой и радиусами треугольники являются прямоугольными. Причем, эти треугольники имеют общий катет – РО и равные катеты А₁О, А₂О,…А_nО (равны как радиусы). Значит, треугольники РОА₁, РОА₂,…РОА_n равны по двум катетам, значит равны гипотенузы PA_{1 ,} РA₂… РA_n, которые являются боковыми ребрами правильной пирамиды.

Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.

Таким образом, верны следующие утверждения:

• Все боковые ребра правильной пирамиды равны.
• Боковые ребра правильной пирамиды являются равными равнобедренными треугольниками.

Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.

Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.

Усеченная пирамида

Возьмем произвольную пирамиду PA₁A₂…A_n и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В₁,В₂,…В_n (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A₁A₂…A_n и В₁В₂…В_n (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A

3B₃B₂, … A₁A_nB_nB₁(боковые грани), называется усеченной пирамидой.

Рисунок 6 – Усеченная пирамида

Отрезки A₁B₁, A₂B₂, … A_nB_n называют боковыми ребрами усеченной пирамиды.

Усеченную пирамиду с основаниями A₁A₂…A_n и В₁В₂…В_n обозначают следующим образом: A₁A₂…A_nВ₁В₂…В_n.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH₁ и В1O –высоты усеченной пирамиды.

Рисунок 7 – Высота усеченной пирамиды

Площадь поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

Докажем теорему для площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Для площади боковой поверхности усеченной пирамиды верна следующая теорема

Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Примеры и разбор решения заданий тренировочного модуля

Задание 1.

В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?

Решение

Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.

Ответ: 177

Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?

Решение

Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.

Ответ: 80

resh.edu.ru

5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида

Видеоурок 1: Задачи на пирамиду. Основные формулы

Видеоурок 2: Задача на пирамиду. Объем пирамиды

Видеоурок 3: Задача на пирамиду. Правильная пирамида

Лекция: Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида

Пирамида, её свойства

Пирамида – это объемное тело, которое имеет в основании многоугольник, а все её грани состоят из треугольников. 

Частным случаем пирамиды является конус, в основании которого лежит окружность.

Рассмотрим основные элементы пирамиды:

Апофема – это отрезок, который соединяет вершину пирамиды с серединой нижнего ребра боковой грани. Иными словами, это высота грани пирамиды.

На рисунке можно увидеть треугольники ADS, ABS, BCS, CDS. Если внимательно посмотреть на названия, можно увидеть, что каждый треугольник имеет в своем названии одну общую букву – S. То есть это значит, что все боковые грани (треугольники) сходятся в одной точке, которая называется вершиной пирамиды.

Отрезок ОS, который соединяет вершину с точкой пересечения диагоналей основания (в случае с треугольников – в точке пересечения высот), называется высотой пирамиды.

Диагональным сечением называют плоскость, которая проходит через вершину пирамиды, а также одну из диагоналей основания.

Так как боковая поверхность пирамиды состоит из треугольников, то для нахождения общей площади боковой поверхности необходимо найти площади каждой грани и сложить их. Количество и форма граней зависит от формы и размеров сторон многоугольника, который лежит в основании.

Единственная плоскость в пирамиде, которой не принадлежит её вершина, называется основанием пирамиды. 

На рисунке мы видим, что в основании лежит параллелограмм, однако, может быть любой произвольный многоугольник.

Свойства:

Рассмотрим первый случай пирамиды, при котором она имеет ребра одинаковой длины:

• Вокруг основания такой пирамиды можно описать окружность. Если спроецировать вершину такой пирамиды, то её проекция будет находится в центре окружности.
• Углы при основании пирамиды у каждой грани одинаковы.
• При этом достаточным условием к тому, что вокруг основания пирамиды можно описать окружность, а так же считать, что все ребра разной длины, можно считать одинаковые углы между основанием и каждым ребром граней.

Если Вам попалась пирамида, у которой углы между боковыми гранями и основанием равны, то справедливы следующие свойства:

• Вы сможете описать окружность вокруг основания пирамиды, вершина которой проецируется точно в центр.
• Если провести у каждой боковой грани высоты к основанию, то они будут равной длины.
• Чтобы найти площадь боковой поверхности такой пирамиды, достаточно найти периметр основания и умножить его на половину длины высоты.
• S_бп = 0,5P_ocH.
• Виды пирамиды.
• В зависимости от того, какой многоугольник лежит в основании пирамиды, они могут быть треугольными, четырехугольными и др. Если в основании пирамиды лежит правильный многоугольник (с равными сторонами), то такая пирамида будет называться правильной.

Правильная треугольная пирамида

Хотелось бы обратить особое внимание на правильную треугольную пирамиду.

Свойства:

• Такая пирамида имеет равные боковые грани, а также равные боковые ребра.
• Боковые грани такой пирамиды являются равнобедренными треугольниками.
• Вокруг основания такой пирамиды можно вписать окружность с центром в месте пересечения высот треугольника, а так же в месте проецирования вершины. Более того, в основание такой пирамиды можно списать окружность, которая будет иметь аналогичными характеристики, описанные ранее.

Формула объема правильной пирамиды:

cknow.ru

Боковая грань — пирамида — Большая Энциклопедия Нефти и Газа, статья, страница 1

Боковая грань — пирамида

Cтраница 1

Боковые грани пирамиды, описанной около конуса, лежат в касательных плоскостях к этому конусу.  [1]

Боковые грани пирамиды, проходящие через катеты АВ и ВС, перпендикулярны плоскости основания, а третья боковая грань образует с плоскостью основания угол у.  [2]

Боковые грани пирамиды, проходящие через катеты [ АС ] и [ ВС ], перпендикулярны к плоскости основания, а третья боковая грань образует с основанием угол а.  [3]

Боковые грани пирамиды SABC равны между собой.  [4]

Боковая грань SAB пирамиды SABC перпендикулярна плоскости основания. Треугольники SAB и ABC являются прямоугольными и AC BC SA SB.  [5]

Боковыми гранями пирамиды называются треугольники ASB, BSC, CSD, DSE, ESA с общей вершиной S, которая называется вершиной пирамиды.  [6]

Боковыми гранями пирамиды являются треугольники, для построения которых достаточно определить истинные длины их сторон — ребер пирамиды.  [7]

Все боковые грани пирамиды образуют с плоскостью основания один и тот же угол. При каких значения k задача имеет решение.  [8]

Все боковые грани пирамиды образуют с плоскостью основания один и тот же угол. Найти этот угол, если отношение полной поверхности пирамиды к площади основания равно Те. При каких значениях k задача имеет решение.  [9]

Все боковые грани пирамиды образуют с плоскостью основания один и тот же угол. При каких значениях k задача имеет решение.  [10]

Все боковые грани пирамиды образуют с плоскостью основания один и тот же угол. При каких значениях k задача имеет решение.  [11]

Площадь боковой грани правильной двенад-цатиугольной пирамиды равна S. Плоский угол при вершине равен а.  [12]

Если все боковые грани пирамиды имеют одинаковый наклон к плоскости основания, то высота пирамиды проектируется в центр круга, вписанного в основание пирамиды.  [13]

Они пересекают левые боковые грани пирамиды по фронталям — прямым линиям, параллельным левому ребру пирамиды.  [14]

Основанием и боковыми гранями пирамиды служит равнобедренный треугольник с острым углом а при вершине.  [15]

Страницы:      1    2    3

www.ngpedia.ru

Площадь боковой поверхности пирамиды — формула, пример расчета

Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.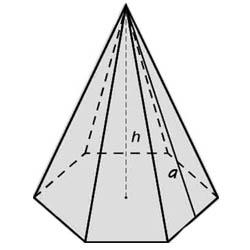

Если в основании лежит квадрат, то пирамиду называется четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:

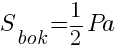
Рассмотрим пример расчета площади боковой поверхности пирамиды.

Пусть дана пирамида с основанием ABCDE и вершиной F. AB=BC=CD=DE=EA=3 см. Апофема a = 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:

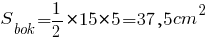
Площадь правильной треугольной пирамиды

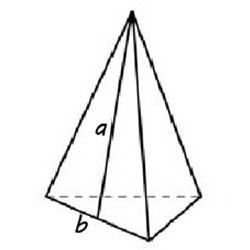
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.

Площадь усеченной пирамиды

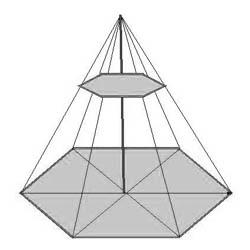
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:

Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.

Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь:

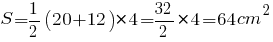
Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.

2mb.ru

Решение задач с использованием свойств различных видов пирамид

Изучение пирамиды и ее элементов представляет широкие возможности для составления и решения задач на различных видах пирамид по следующим темам:

• Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.
• Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.
• Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Действующие учебники геометрии либо не содержат , либо содержат в недостаточном количестве задачи по этим темам.

Как показала практика, учащиеся с большим интересом принимают участие не только в решении данных задач, но и в их составлении. Они с удовольствием предлагают различные решения придуманных ими задач.

К этому учащихся необходимо подводить хорошо продуманной системой теоретических положений и практических упражнений.

Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и А.В.Погорелова “Геометрия 10–11” содержат опорный теоретический материал по теме “Пирамида и ее элементы”.

В дополнение к нему можно рассмотреть следующие свойства часто встречающихся видов пирамид.

Справочный материал.

Теория.

Теоремы о пирамидах, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

• Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды равны между собой.

• Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то:

а) все боковые ребра пирамиды образуют с плоскостью основания равные углы;

в) все боковые ребра пирамиды равны между собой.

• Если все боковые ребра пирамиды равны, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.

• Если высота пирамиды пересекает ее основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в ее основание.
• Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
• Если у треугольной пирамиды все боковые ребра равны, а в основании лежит прямоугольный треугольник, то грань, содержащая его гипотенузу, перпендикулярна основанию. Основание высоты данной пирамиды является середина гипотенузы.

Теоремы о пирамидах, в которых одна или две боковые грани перпендикулярны плоскости основания.

• Если пирамида содержит ровно одну боковую грань, которая перпендикулярна плоскости основания, то высота такой пирамиды лежит в этой боковой грани.
• Если пирамида содержит две смежные боковые грани, перпендикулярные плоскости основания, то высотой такой пирамиды является боковое ребро, общее для этих граней.
• Если в пирамиде две не смежные боковые грани перпендикулярны плоскости основания, то высота такой пирамиды лежит на прямой пересечения плоскостей этих граней.
• Если боковое ребро пирамиды перпендикулярно основанию, то и боковые грани, содержащие это ребро, перпендикулярны основанию.
• Если в четырехугольной пирамиде в основании ромб, и две смежные боковые грани перпендикулярны основанию, то боковые грани данной пирамиды – две пары равных треугольников.

Задачи для решения.

Задания из книги “Самостоятельные и контрольные работы по геометрии для 11-го класса” Ершовой А.П., Голобородько В.В.

Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

Вариант А.

1. Основание пирамиды SABCD – прямоугольник АВСД со сторонами 6 и 8 см. Все боковые ребра пирамиды равны 13 см.

а) Опишите построение высоты пирамиды SO.

б) Докажите равенство отрезков АО, ВО, СО и ДО.

в) Обоснуйте положение точки О в прямоугольнике АВСД и найдите длину высоты SO.

2.  Основание пирамиды – равнобедренный треугольник с основанием а и углом при вершине . Все двугранные углы при основании пирамиды равны .

а) Опишите построение высоты пирамиды, высот боковых граней и их проекций на плоскость основания. Обоснуйте двугранные углы при основании пирамиды.

б) обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

в) Найдите высоту пирамиды.

 Вариант Б.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при основании . Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

б) Определите, при каких значениях ? высота пирамиды будет находиться вне пирамиды.

в) Найдите высоту пирамиды.

2. Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны .

а) Обоснуйте данные двугранные углы и положение основания высоты пирамиды в ромбе.

б) Найдите высоту пирамиды.

в) Двумя способами – путем вычисления площадей боковых граней и с помощью теоремы об ортогональной проекции многоугольника – найдите боковую поверхность пирамиды. Сравните полученные результаты.

Вариант В.

1. Основание пирамиды – треугольник с углами и . Точка высоты пирамиды, удаленная от плоскости основания на расстояние d, равноудалена от концов бокового ребра. Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды.

б) При каких условиях высота пирамиды лежит внутри пирамиды?

в) Найдите высоту пирамиды.

г) Найдите площадь основания пирамиды.

2. В основании пирамиды лежит равнобокая трапеция с острым углом . Высота пирамиды равна Н, а все двугранные углы при основании равны .

а) обоснуйте положение основания высоты пирамиды.

б) Найдите высоту трапеции, лежащей в основании пирамиды.

в) Не вычисляя площадей боковых граней, найдите боковую поверхность пирамиды.

Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.

Вариант А.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при вершине . Боковые грани пирамиды, содержащие стороны данного угла перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте угол .

в) Найдите площадь третьей боковой грани.

г) Найдите боковую поверхность пирамиды.

2. Основание пирамиды – правильный треугольник со стороной а. Одна из боковых граней пирамиды перпендикулярна плоскости основания, а две другие – наклонены к ней под углом .

а) Из вершины пирамиды в плоскости грани, перпендикулярной основанию, проведите перпендикуляр к ребру основания и обоснуйте, почему он будет высотой пирамиды.

б) Обоснуйте углы наклона, равные .

в) Докажите, что основание высоты пирамиды равноудалено от двух сторон правильного треугольника, и обоснуйте положение основания высоты на стороне правильного треугольника.

г) Найдите боковую поверхность пирамиды.

Вариант Б.

1. Основание пирамиды – квадрат со стороной а, две смежные боковые грани пирамиды перпендикулярны плоскости основания, а две другие – наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б ) Обоснуйте углы, равные .

в ) Докажите, что боковые грани пирамиды попарно равны.

г ) Найдите боковую поверхность пирамиды.

2. Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковая грань, содержащая катет, противолежащий данному углу , перпендикулярна плоскости основания, а две другие грани наклонены к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите высоту пирамиды.

г) Найдите боковую поверхность пирамиды.

Вариант В.

1. Основание пирамиды – ромб с тупым углом . Две боковые грани, содержащие стороны этого угла, перпендикулярны плоскости основания, а две другие – наклонены к ней под углом . Высота пирамиды равна Н.

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте углы, равные .

в) Найдите боковую поверхность пирамиды.

2. Основание пирамиды – прямоугольная трапеция с острым углом ? и прилежащей к нему боковой стороной . Боковая грань, содержащая большее основание трапеции, перпендикулярна плоскости основания, а три другие грани наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите площадь основания пирамиды.

г) Найдите боковую поверхность пирамиды.

Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Вариант А.

1. В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом . Расстояние от середины высоты пирамиды до середины бокового ребра равно d.

а ) Найдите высоту пирамиды.

б ) Найдите площадь основания пирамиды.

2. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от середины высоты пирамиды до ее апофемы равно l . Найдите боковую поверхность пирамиды.

Вариант Б.

1. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от основания высоты пирамиды до середины апофемы равно l . Найдите полную поверхность пирамиды.
2. Основание пирамиды – равнобедренный треугольник с углом при вершине. Все боковые ребра пирамиды наклонены к плоскости основания под углом . Биссектриса этого угла пересекает высоту пирамиды в точке, удаленной от бокового ребра на расстояние d.

а ) Найдите высоту пирамиды.

б ) Найдите площадь основания пирамиды.

Вариант В.

1. Основание пирамиды – равнобедренный треугольник с углом при основании . Все двугранные углы при основании пирамиды равны . Отрезок, соединяющий точки пересечения медиан боковых граней, содержащих боковые стороны треугольника, равен m. Найдите боковую поверхность пирамиды.
2. Основание пирамиды – прямоугольный треугольник с острым углом . Боковые грани пирамиды, содержащие катеты треугольника, перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом . Расстояние от основания высоты пирамиды до этой грани равно l. Найдите боковую поверхность пирамиды.

Указанный в статье перечень задач может быть расширен Вами и вашими учениками.

Желаем успеха!

urok.1sept.ru