Производная функции — Википедия
У этого термина существуют и другие значения, см. Производная.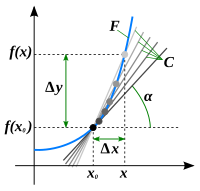 Иллюстрация понятия производной
Иллюстрация понятия производнойПроизво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
В классическом дифференциальном исчислении производная чаще всего определяется через понятие предела, однако исторически теория пределов появилась позже дифференциального исчисления. Исторически производная вводилась кинематически (как скорость) или геометрически (определяясь по сути наклоном касательной, в разных конкретных формулировках). Ньютон называл производную
Русский термин в форме «производная функция» впервые употребил В. И. Висковатов, переведя на русский язык соответствующий французский термин dérivée, используемый Лагранжем[2].
Пусть в некоторой окрестности точки x0∈R{\displaystyle x_{0}\in \mathbb {R} } определена функция f:U(x0)⊂R→R.{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .} Производной функции называется такое число A{\displaystyle A}, что функцию в окрестности U(x0){\displaystyle U(x_{0})} можно представить в виде
- f(x0+h)=f(x0)+Ah+o(h){\displaystyle f(x_{0}+h)=f(x_{0})+Ah+o(h)}
если A{\displaystyle A} существует.
Определение производной функции через предел[править | править код]
Пусть в некоторой окрестности точки x0∈R{\displaystyle x_{0}\in \mathbb {R} } определена функция f:U(x0)⊂R→R.{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .} Производной функции f{\displaystyle f} в точке x0{\displaystyle x_{0}} называется предел, если он существует,
- f′(x0)=limx→x0f(x)−f(x0)x−x0=limΔx→0f(x0+Δx)−f(x0)Δx=limΔx→0Δf(x)Δx.{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim \limits _{{\Delta x}\to 0}{\frac {\Delta {f(x)}}{\Delta x}}.}
Общепринятые обозначения производной функции y=f(x){\displaystyle y=f(x)} в точке x0{\displaystyle x_{0}}[править | править код]
- f′(x0)=fx′(x0)=Df(x0)=dfdx(x0)=dydx|x=x0=y˙(x0).{\displaystyle f'(x_{0})=f’_{x}(x_{0})=\mathrm {D} \!f(x_{0})={\frac {df}{dx}}(x_{0})=\left.{\frac {dy}{dx}}\right\vert _{x=x_{0}}={\dot {y}}(x_{0}).}
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике и физике, исторически часто тоже).
(c)=(const){\displaystyle \left(c\right)=\left(\mathrm {const} \right)}
Производная f′(x0){\displaystyle f'(x_{0})} функции f{\displaystyle f} в точке x0{\displaystyle x_{0}}, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f{\displaystyle f} является дифференцируемой в точке x0{\displaystyle x_{0}} тогда и только тогда, когда её производная в этой точке существует и конечна:
- f∈D(x0)⇔∃f′(x0)∈(−∞;∞).{\displaystyle f\in {\mathcal {D}}(x_{0})\Leftrightarrow \exists f'(x_{0})\in (-\infty ;\infty ).}
Для дифференцируемой в x0{\displaystyle x_{0}} функции f{\displaystyle f} в окрестности U(x0){\displaystyle U(x_{0})} справедливо представление
- f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0){\displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})} при x→x0.{\displaystyle x\to x_{0}.}
- Назовём Δx=x−x0{\displaystyle \Delta x=x-x_{0}} приращением аргумента функции, а Δy=f(x)−f(x0){\displaystyle \Delta y=f(x)-f(x_{0})} или Δy=f(x0+Δx)−f(x0){\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})} приращением значения функции в точке x0.{\displaystyle x_{0}.} Тогда
- f′(x0)=limΔx→0ΔyΔx.{\displaystyle f'(x_{0})=\lim \limits _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}.}
- Пусть функция f:(a,b)→R{\displaystyle f\colon (a,b)\to \mathbb {R} } имеет конечную производную в каждой точке x0∈(a,b).{\displaystyle x_{0}\in (a,b).} Тогда определена произво́дная фу́нкция
- f′:(a,b)→R.{\displaystyle f’\colon (a,b)\to \mathbb {R} .}
- Функция, имеющая производную в точке, непрерывна в ней. Обратное не всегда верно.
- Если производная функция сама является непрерывной, то функцию f{\displaystyle f} называют непреры́вно дифференци́руемой и пишут: f∈C(1)((a,b)).{\displaystyle f\in C^{(1)}{\bigl (}(a,b){\bigr )}.}
Геометрический и физический смысл производной[править | править код]
Тангенс угла наклона касательной прямой[править | править код]
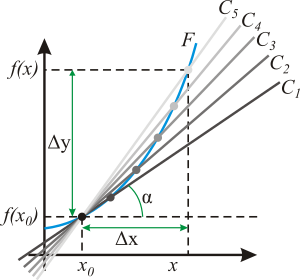 Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.Если функция f:U(x0)→R{\displaystyle f\colon U(x_{0})\to \mathbb {R} } имеет конечную производную в точке x0,{\displaystyle x_{0},} то в окрестности U(x0){\displaystyle U(x_{0})} её можно приблизить линейной функцией
- fl(x)≡f(x0)+f′(x0)(x−x0).{\displaystyle f_{l}(x)\equiv f(x_{0})+f'(x_{0})(x-x_{0}).}
Функция fl{\displaystyle f_{l}} называется касательной к f{\displaystyle f} в точке x0.{\displaystyle x_{0}.} Число f′(x0){\displaystyle f'(x_{0})} является угловым коэффициентом (угловым коэффициентом касательной) или тангенсом угла наклона касательной прямой.
Скорость изменения функции[править | править код]
Пусть s=s(t){\displaystyle s=s(t)} — закон прямолинейного движения. Тогда v(t0)=s′(t0){\displaystyle v(t_{0})=s'(t_{0})} выражает мгновенную скорость движения в момент времени t0.{\displaystyle t_{0}.} Вторая производная a(t0)=s″(t0){\displaystyle a(t_{0})=s»(t_{0})} выражает мгновенное ускорение в момент времени t0.{\displaystyle t_{0}.}
Вообще производная функции y=f(x){\displaystyle y=f(x)} в точке x0{\displaystyle x_{0}} выражает скорость изменения функции в точке x0{\displaystyle x_{0}}, то есть скорость протекания процесса, описанного зависимостью y=f(x).{\displaystyle y=f(x).}
Анимация, дающая первоначальное интуитивное представление о производной, как «размах» изменения функции при изменении аргумента (нажмите для воспроизведения).Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
- f(0)(x0)≡f(x0).{\displaystyle f^{(0)}(x_{0})\equiv f(x_{0}).}
Если функция f{\displaystyle f} дифференцируема в x0{\displaystyle x_{0}}, то производная первого порядка определяется соотношением
- f(1)(x0)≡f′(x0).{\displaystyle f^{(1)}(x_{0})\equiv f'(x_{0}).}
Пусть теперь производная n{\displaystyle n}-го порядка f(n){\displaystyle f^{(n)}} определена в некоторой окрестности точки x0{\displaystyle x_{0}} и дифференцируема. Тогда
- f(n+1)(x0)=(f(n))′(x0).{\displaystyle f^{(n+1)}(x_{0})=\left(f^{(n)}\right)'(x_{0}).}
Если функция u=f(x,y,z){\displaystyle u=f(x,y,z)} имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от x,y,z,{\displaystyle x,y,z,} может иметь в некоторой точке (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})} частные производные по той же или по любой другой переменной. Для исходной функции u=f(x,y,z){\displaystyle u=f(x,y,z)} эти производные будут частными производными второго порядка (или вторыми частными производными).
- ux2″=fx2″(x0,y0,z0){\displaystyle u»_{x^{2}}=f»_{x^{2}}(x_{0},y_{0},z_{0})} или ∂2u∂x2=∂2f(x0,y0,z0)∂x2{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x^{2}}}}
- uxy″=fxy″(x0,y0,z0){\displaystyle u»_{xy}=f»_{xy}(x_{0},y_{0},z_{0})} или ∂2u∂x∂y=∂2f(x0,y0,z0)∂x∂y{\displaystyle {\frac {\partial ^{2}u}{\partial x\partial y}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x\partial y}}}
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
- uxy″=fxy″(x0,y0,z0){\displaystyle u»_{xy}=f»_{xy}(x_{0},y_{0},z_{0})}
Класс функций, у которых производная n{\displaystyle n}-порядка является непрерывной, обозначается как C(n){\displaystyle C^{(n)}}.
В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:
- Лагранжа f(n)(x0){\displaystyle f^{(n)}(x_{0})}, при этом для малых n часто используют штрихи и римские цифры:
- f(1)(x0)=f′(x0)=fI(x0),{\displaystyle f^{(1)}(x_{0})=f'(x_{0})=f^{I}(x_{0}),}
- f(2)(x0)=f″(x0)=fII(x0),{\displaystyle f^{(2)}(x_{0})=f»(x_{0})=f^{II}(x_{0}),}
- f(3)(x0)=f‴(x0)=fIII(x0),{\displaystyle f^{(3)}(x_{0})=f»'(x_{0})=f^{III}(x_{0}),}
- f(4)(x0)=fIV(x0),{\displaystyle f^{(4)}(x_{0})=f^{IV}(x_{0}),} и т. д.
Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.
- Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если x{\displaystyle x} — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):
- dnfdxn(x0){\displaystyle {\frac {d^{n}\!f}{dx^{n}}}(x_{0})}
- Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:
- x˙(t0){\displaystyle {\dot {x}}(t_{0})} — производная первого порядка x{\displaystyle x} по t{\displaystyle t}
Найти производную: алгоритм и примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
 .
.
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
 .
.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
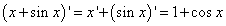 .
.
Пример 2. Найти производную функции
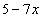 .
.
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Правило 1. Если функции
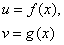
дифференцируемы в некоторой точке 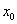 , то в той же точке дифференцируемы и функции
, то в той же точке дифференцируемы и функции
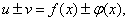
причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие.
Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.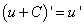
Правило 2. Если функции

и
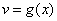
дифференцируемы в некоторой точке 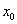 , то в то же точке дифференцируемо и их произведение
, то в то же точке дифференцируемо и их произведение
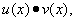
причём
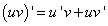
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
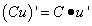
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
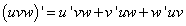
Правило 3. Если функции

и

дифференцируемы в некоторой точке  и
и  , то в этой точке дифференцируемо и их частное u/v , причём
, то в этой точке дифференцируемо и их частное u/v , причём
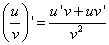
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье
Здесь же (далее) — более простые примеры на производную произведения и частного, на которых Вы увереннее освоите алгоритмы вычислений.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v, в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде 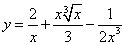 , то
следуйте на занятие «Производная суммы дробей со степенями и корнями».
, то
следуйте на занятие «Производная суммы дробей со степенями и корнями».
Если же перед Вами задача вроде 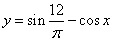 ,
то Вам на занятие «Производные простых тригонометрических функций».
,
то Вам на занятие «Производные простых тригонометрических функций».
Пример 3. Найти производную функции
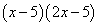 .
.
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
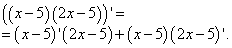
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

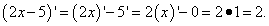
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
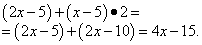
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
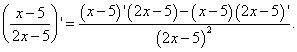
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, 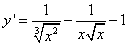 ,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями».
,
то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями».
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других
тригонометрических функций, то есть, когда функция имеет вид вроде 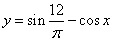 ,
то Вам на урок «Производные простых тригонометрических функций».
,
то Вам на урок «Производные простых тригонометрических функций».
Пример 5. Найти производную функции
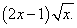
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
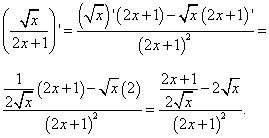
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на 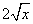 :
:

Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Ещё больше домашних заданий на нахождение производных
Пример 12. Найти производную функции
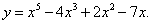 .
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим
 .
.
Пример 13. Найти производную функции

Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
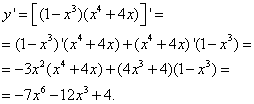
Пример 14. Найти производную функции

Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:

Теперь вычислим производные в числителе и перед нами уже требуемый результат:

Пример 15.Найти производную функции

Шаг1. Применяем правило дифференцирования суммы:
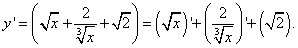
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):

Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
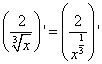
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя — это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
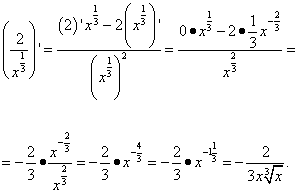
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
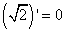 ,
,
а производная, требуемая в условии задачи:

Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях «Производная произведения и частного функций» и «Производная суммы дробей со степенями и корнями».
Также настоятельно рекомендуем изучить производную сложной функции.

Поделиться с друзьями
Весь блок «Производная»
Онлайн калькулятор: Производная функции
Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.
Калькулятор производных

Производная функции
Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Производная функции
Показать детали вычисления
Показать шаги вычисления производной и упрощения формулы
save Сохранить share Поделиться extension Виджет
Синтаксис описания формул
В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, — — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

Таблица синтаксиса математических выражений
ГруппаКонстанты и переменныеОперацииТригонометрические функцииОбратные тригонометрические функцииГиперболические функцииsave Сохранить share Поделиться extension Виджет
Вычисление производной
Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…
Правила дифференцирования
1) производная суммы:
2) производная произведения:
3) производная частного:
4) производная сложной функции равна произведению производных:
Таблица производных
Производная степенной функции:
Производная показательной функции:
Производная экспонециальной функции:
Производная логарифмической функции:
Производные тригонометрических функций:
,
,
,
Производные обратных тригонометрических функций:
,
,
,
Производные гиперболических функций:
Производная по определению (через предел). Примеры решений
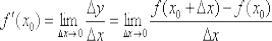
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на свет таблицы производных и правил дифференцирования. Начало положено в статье о смысле производной, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную? и Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это без пределов функций. Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, что производная
функции  в точке
в точке  определяется формулой:
определяется формулой:
Напоминаю обозначения и термины: 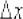 называют приращением аргумента;
называют приращением аргумента;
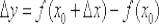 – приращением функции;
– приращением функции;

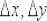 – это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что  является «динамической» переменной,
является «динамической» переменной,  – константой и результат вычисления предела
– константой и результат вычисления предела  – числом (иногда – «плюс» либо «минус» бесконечностью).
– числом (иногда – «плюс» либо «минус» бесконечностью).
В качестве точки 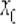 можно рассмотреть ЛЮБОЕ значение
можно рассмотреть ЛЮБОЕ значение  , принадлежащее области определения функции
, принадлежащее области определения функции 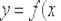 , в котором существует производная.
, в котором существует производная.
! Примечание: оговорка «в котором существует производная» – в общем случае существенна! Так, например, точка 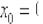 хоть и входит в область определения функции
хоть и входит в область определения функции  , но производной
, но производной
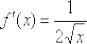 там не существует. Поэтому формула
там не существует. Поэтому формула
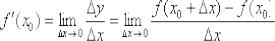 не применима в точке
не применима в точке 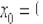 ,
,
и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены 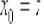 , получаем вторую рабочую формулу:
, получаем вторую рабочую формулу:
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение  . Результатом вычисления предела
. Результатом вычисления предела
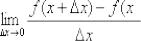 является производная функция
является производная функция 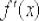 .
.
Исходя из вышесказанного, сформулируем условия двух типовых задач:
–Найти производную в точке, используя определение производной.
–Найти производную функцию, используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность), а во втором –
функцию. Кроме того, производной может и вовсе не существовать.
Как найти производную по определению?
Составить отношение  и вычислить предел
и вычислить предел 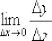 .
.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу
 . Кажется волшебством, но в
. Кажется волшебством, но в
действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
Пример 1
Найти производную функции 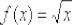 , пользуясь определением производной
, пользуясь определением производной

По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице:  .
.
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку 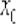 , принадлежащую области определения функции
, принадлежащую области определения функции  , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение  (разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
(разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим
числитель и знаменатель на сопряженное выражение 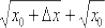 :
:
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак, 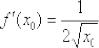 .
.
Поскольку в качестве  можно выбрать ЛЮБУЮ точку
можно выбрать ЛЮБУЮ точку  интервала
интервала

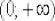 , то, осуществив замену
, то, осуществив замену 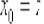 , получаем:
, получаем:
Ответ: по определению производной: 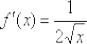
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции 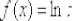 , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от
подстрочного индекса и вместо буквы  использовать букву
использовать букву  .
.
Рассмотрим произвольную точку 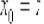 , принадлежащую области определения функции
, принадлежащую области определения функции 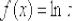 (интервалу
(интервалу  ), и зададим в ней приращение
), и зададим в ней приращение  . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может

возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому:  – античная статуя, а
– античная статуя, а 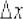 – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости  закомментирую пошагово:
закомментирую пошагово:
(1)Используем свойство логарифма  .
.
(2)В скобках почленно делим числитель на знаменатель.
(3)В знаменателе искусственно домножаем и делим на «икс» чтобы
воспользоваться замечательным пределом 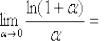 , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает 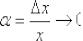 .
.
Ответ: по определению производной: 
Или сокращённо: 
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
Найти производную  по определению
по определению

тоже вполне конкретное число | и так же подставляем его в | |
функцию | вместо «икса»: | |
|
| . Записываем разность |
| , при этом | необходимо полностью взять в |
скобки. |
|
|
Составленное приращение функции  бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы 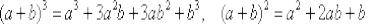 , раскрываем скобки и сокращаем всё, что можно сократить:
, раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
В итоге: 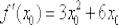
Поскольку в качестве  можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену 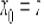 и получим
и получим  .
.
Ответ: 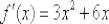 по определению.
по определению.
В целях проверки найдём производную с помощью правил

дифференцирования и таблицы:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции 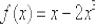 по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Вернёмся к стилю №2: Пример 7
Пользуясь определением, найти производную функции
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции:
Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую 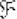 , зададим в ней приращение аргумента
, зададим в ней приращение аргумента 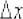 и составим приращение
и составим приращение
функции:
Найдём производную:

(1) Используем тригонометрическую формулу
.
(2)Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3)Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4)В силу нечётности синуса выносим «минус». Под косинусом
указываем, что слагаемое  .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел  . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ:  по определению Как видите, основная трудность рассматриваемой задачи упирается в
по определению Как видите, основная трудность рассматриваемой задачи упирается в

сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Пример 9
Найти производную функции 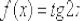 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число Вычислим ответ стандартным способом:
Решение: с точки зрения наглядности это задание значительно проще, так как в формуле  вместо
вместо 
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция  в точке
в точке  ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке 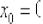 , но будет ли она там дифференцируема?
, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1)Находим левостороннюю производную в данной точке:  .
.
2)Находим правостороннюю производную в данной точке: 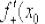 .
.
3)Если односторонние производные конечны и совпадают:
 , то функция
, то функция 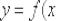 дифференцируема в точке
дифференцируема в точке 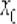 и
и
геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной).
Если получены два разных значения: 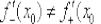 (одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке
(одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке  .
.
Если же обе односторонние производные равны бесконечности
(пусть даже разных знаков), то функция  не
не
дифференцируема в точке 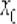 , но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
, но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
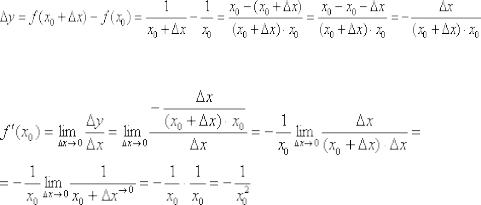
Ответ:  по определению производной
по определению производной

Ответ: 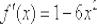 по определению.
по определению.
Пример 8: Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую  , зададим в ней приращение
, зададим в ней приращение  и составим приращение функции:
и составим приращение функции:
Найдём производную:
Используем тригонометрическую формулу
и первый замечательный
предел:
Ответ:  по определению
по определению
Пример 10: Решение: Зададим приращение 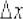 в точке
в точке  . Тогда приращение функции:
. Тогда приращение функции:
Вычислим производную в точке:

Умножим числитель и знаменатель на сопряженное выражение:
Ответ: 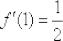 по определению производной в точке
по определению производной в точке
Как найти производную по определению?
Составить отношение  и вычислить предел
и вычислить предел  .
.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу 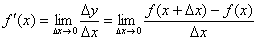 . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
. Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
Пример 1
Найти производную функции 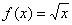 , пользуясь определением производной
, пользуясь определением производной
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице:  .
.
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку 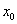 , принадлежащую области определения функции
, принадлежащую области определения функции 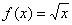 , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение  (разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
(разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции: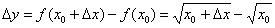
Вычислим предел: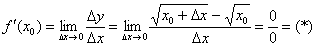
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение 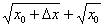 :
:

Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак,  .
.
Поскольку в качестве 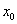 можно выбрать ЛЮБУЮ точку
можно выбрать ЛЮБУЮ точку  интервала
интервала  , то, осуществив замену
, то, осуществив замену  , получаем:
, получаем: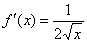
Ответ: по определению производной: 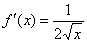
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции 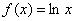 , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы 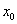 использовать букву
использовать букву  .
.
Рассмотрим произвольную точку  , принадлежащую области определения функции
, принадлежащую области определения функции 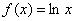 (интервалу
(интервалу  ), и зададим в ней приращение
), и зададим в ней приращение  . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому:  – античная статуя, а
– античная статуя, а  – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости 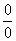 закомментирую пошагово:
закомментирую пошагово:
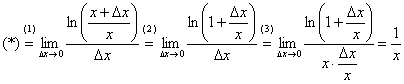
(1) Используем свойство логарифма  .
.
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом  , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает  .
.
Ответ: по определению производной: 
Или сокращённо: 
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
Найти производную  по определению
по определению
В данном случае составленное приращение  сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 3:Решение: рассмотрим некоторую точку 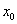 , принадлежащую области определения функции
, принадлежащую области определения функции  . Зададим в данной точке приращение
. Зададим в данной точке приращение  и составим соответствующее приращение функции:
и составим соответствующее приращение функции:
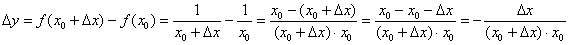
Найдём производную в точке 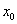 :
:
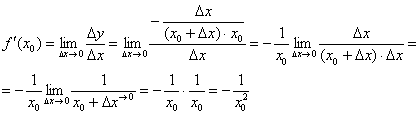
Так как в качестве 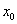 можно выбрать любую точку
можно выбрать любую точку  области определения функции
области определения функции  , то
, то  и
и 
Ответ:  по определению производной
по определению производной
Пример 4
Найти производную 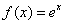 по определению
по определению
А тут всё необходимо свести к замечательному пределу 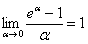 . Решение оформлено вторым способом.
. Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных. Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой 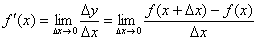 .
.
Пример 4:Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую  , и зададим в ней приращение
, и зададим в ней приращение  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:

Найдём производную:

Используем замечательный предел 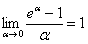

Ответ:  по определению
по определению
Пример 5
Найти производную функции  , используя определение производной
, используя определение производной
Решение: используем первый стиль оформления. Рассмотрим некоторую точку 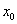 , принадлежащую
, принадлежащую  , изададим в ней приращение аргумента
, изададим в ней приращение аргумента  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции: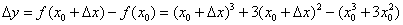
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение  . Берём точку
. Берём точку 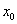 (число) и находим в ней значение функции:
(число) и находим в ней значение функции: 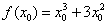 , то есть в функцию
, то есть в функцию  вместо «икса» следует подставить
вместо «икса» следует подставить 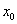 . Теперь берём тоже вполне конкретное число
. Теперь берём тоже вполне конкретное число  и так же подставляем его в функцию
и так же подставляем его в функцию  вместо «икса»:
вместо «икса»:  . Записываем разность
. Записываем разность 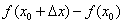 , при этом
, при этом 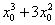 необходимо полностью взять в скобки.
необходимо полностью взять в скобки.
Составленное приращение функции  бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы 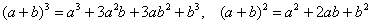 , раскрываем скобки и сокращаем всё, что можно сократить:
, раскрываем скобки и сокращаем всё, что можно сократить: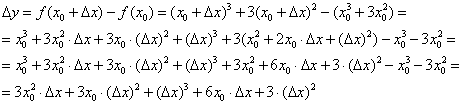
Индейка выпотрошена, с жаркое никаких проблем: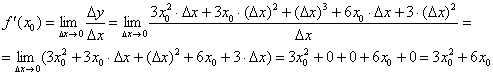
В итоге: 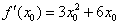
Поскольку в качестве 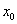 можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену  и получим
и получим  .
.
Ответ:  по определению.
по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы: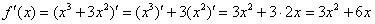
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции 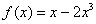 по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Пример 6:Решение: рассмотрим некоторую точку 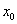 , принадлежащую
, принадлежащую  , и зададим в ней приращение аргумента
, и зададим в ней приращение аргумента  . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
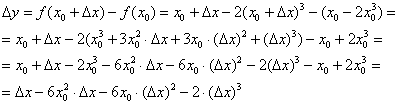
Вычислим производную:
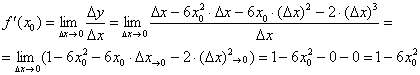
Таким образом: 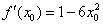
Поскольку в качестве 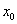 можно выбрать любое действительное число, то
можно выбрать любое действительное число, то  и
и 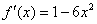
Ответ: 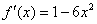 по определению.
по определению.
Вернёмся к стилю №2:
Пример 7
Пользуясь определением, найти производную функции
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции: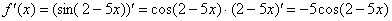
Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую  , зададим в ней приращение аргумента
, зададим в ней приращение аргумента  и составим приращение функции:
и составим приращение функции:
Найдём производную: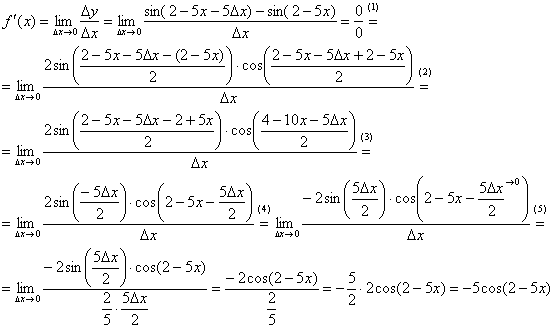
(1) Используем тригонометрическую формулу 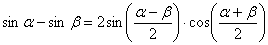 .
.
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое 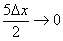 .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел 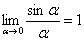 . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ:  по определению
по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Пример 8:Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую  , зададим в ней приращение
, зададим в ней приращение  и составим приращение функции:
и составим приращение функции:

Найдём производную:

Используем тригонометрическую формулу 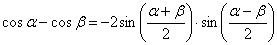 и первый замечательный предел:
и первый замечательный предел:

Ответ:  по определению
по определению
Разберём более редкую версию задачи:
Пример 9
Найти производную функции 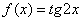 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Вычислим ответ стандартным способом: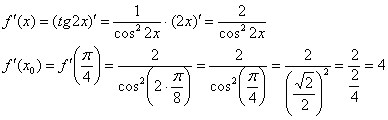
Решение: с точки зрения наглядности это задание значительно проще, так как в формуле 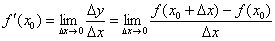 вместо
вместо 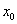 рассматривается конкретное значение.
рассматривается конкретное значение.
Зададим в точке  приращение
приращение  и составим соответствующее приращение функции:
и составим соответствующее приращение функции: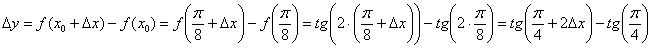
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов 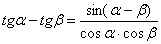 и в который раз сведём решение к первому замечательному пределу:
и в который раз сведём решение к первому замечательному пределу:
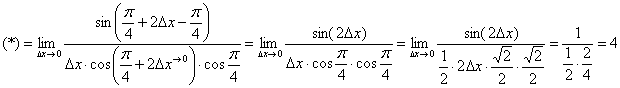
Ответ: 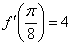 по определению производной в точке.
по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить 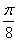 на
на 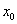 или просто
или просто  в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
в зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10
Используя определение, найти производную функции 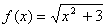 в точке
в точке 
Пример 10:Решение: Зададим приращение  в точке
в точке  . Тогда приращение функции:
. Тогда приращение функции:

Вычислим производную в точке:
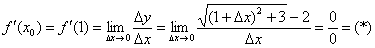
Умножим числитель и знаменатель на сопряженное выражение:

Ответ: 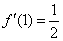 по определению производной в точкеЗаключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
по определению производной в точкеЗаключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция  в точке
в точке  ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке  , но будет ли она там дифференцируема?
, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1) Находим левостороннюю производную в данной точке: 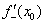 .
.
2) Находим правостороннюю производную в данной точке:  .
.
3) Если односторонние производные конечны и совпадают:  , то функция
, то функция  дифференцируема в точке
дифференцируема в точке 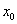 и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения:
и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения: 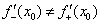 (одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке
(одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке 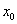 .
.
Если же обе односторонние производные равны бесконечности (пусть даже разных знаков), то функция  не дифференцируема в точке
не дифференцируема в точке 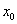 , но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
, но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
! Примечание: таким образом, между вопросами «Будет ли дифференцируема функция в точке?» и «Существует ли производная в точке?» есть разница!
Всё очень просто!
1) При нахождении левосторонней производной приращение аргумента отрицательно: 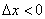 , а слева от точки
, а слева от точки  расположена парабола
расположена парабола 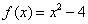 , поэтому приращение функции равно:
, поэтому приращение функции равно: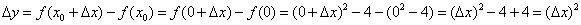
И соответствующий левосторонний предел численно равен левосторонней производной в рассматриваемой точке: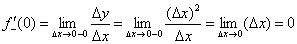
2) Справа от точки  находится график прямой
находится график прямой  и приращение аргумента положительно:
и приращение аргумента положительно: 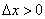 . Таким образом, приращение функции:
. Таким образом, приращение функции: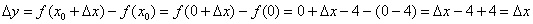
Правосторонний предел и правосторонняя производная в точке:
3) Односторонние производные конечны и различны: 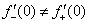
Ответ: функция не дифференцируема в точке  .
.
Ещё легче доказывается книжный случай недифференцируемости модуля 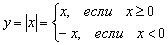 в точке
в точке  , о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
, о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс  обладает общей производной и общей касательной (ось абсцисс) в точке
обладает общей производной и общей касательной (ось абсцисс) в точке  . Кривой, да дифференцируемый на
. Кривой, да дифференцируемый на  ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
О производных / Habr
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я «предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения. Казалось бы, и что статья с таким началом может делать в этом блоге?
А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.
Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.
Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.
Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.
Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
И, конечно же, опять — нифига подобного!
Глянем вот на этот график:
Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.
К чему это я?
1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:
- А где работаешь?
- А кем?
- Сколько получаешь?
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.
2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?
Каков знак Вашей производной?
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Выпуклые вверх функции
Определение 1. Функцию y = f (x) называют выпуклой вверх на интервале (a, b), если для любых двух точек 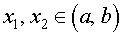 таких, что x1 x2 , график функции y = f (x) расположен выше отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
таких, что x1 x2 , график функции y = f (x) расположен выше отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
Функция, график которой изображен на рисунке 1, выпукла вверх на интервале (a, b) .
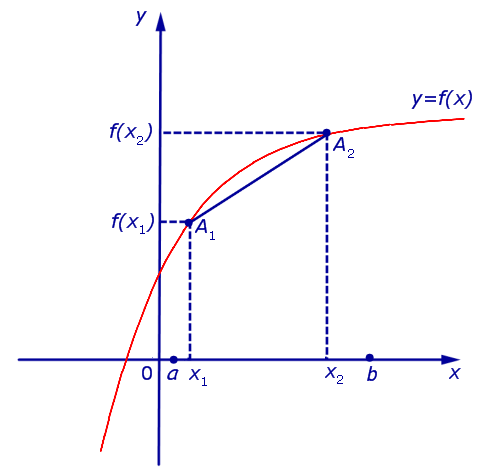
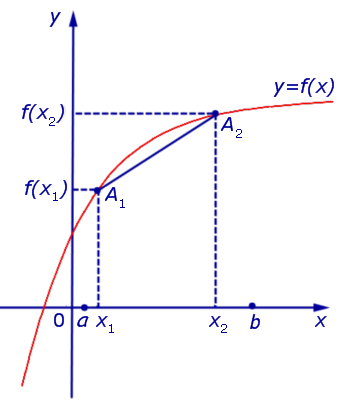
Рис.1
Пример 1. Примером функции, выпуклой вверх на 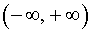 , является функция y = – x2 (рис. 2).
, является функция y = – x2 (рис. 2).
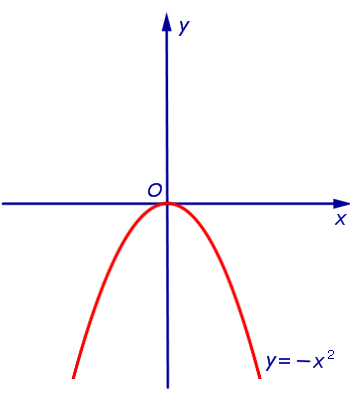
Рис.2
Выпуклые вниз функции
Определение 2. Функцию y = f (x) называют выпуклой вниз на интервале (a, b), если для любых двух точек 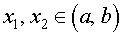 таких, что x1 x2 , график функции y = f (x) расположен ниже отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
таких, что x1 x2 , график функции y = f (x) расположен ниже отрезка, соединяющего точки A1 = (x1; f (x1)) и A2 = (x2; f (x2)) .
Функция, график которой изображен на рисунке 3, выпукла вниз на интервале (a, b) .
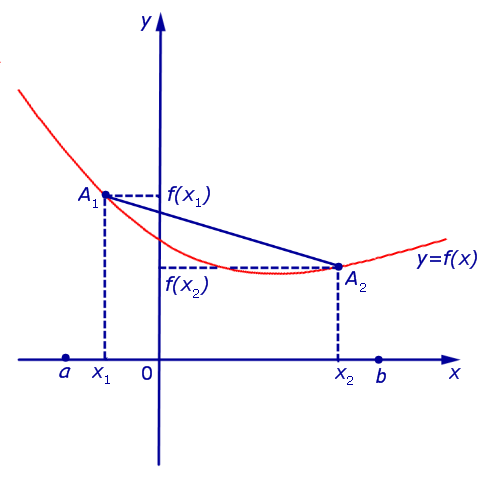
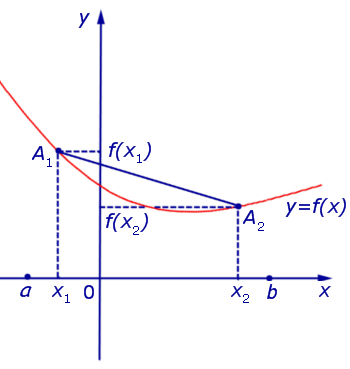
Рис.3
Пример 2. Примером функции, выпуклой вниз на 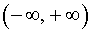 , является функция y = x2 (рис. 4).
, является функция y = x2 (рис. 4).
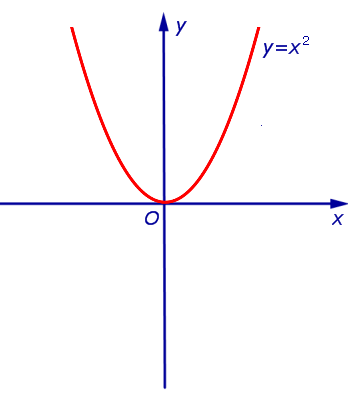
Рис.4
Вторая производная функции
Определение 3. Если у функции y = f (x) существует производная в некоторой точке x0 , то эту производную часто называют первой производной или производной первого порядка функции y = f (x) в точке x0 .
Пусть у функции y = f (x) существует производная во всех точках 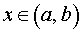 . Тогда, вычисляя в каждой точке
. Тогда, вычисляя в каждой точке 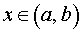 производную f ‘ (x), мы получим функцию y = f ‘ (x). Если у функции y = f ‘ (x) существует производная в некоторой точке x0 интервала (a, b), то эту производную называют второй производной или производной второго порядка функции y = f (x) в точке x0 .
производную f ‘ (x), мы получим функцию y = f ‘ (x). Если у функции y = f ‘ (x) существует производная в некоторой точке x0 интервала (a, b), то эту производную называют второй производной или производной второго порядка функции y = f (x) в точке x0 .
Для производной второго порядка y = f (x) используются обозначения:
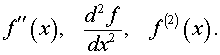
Например,
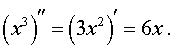
Точно так же, как это было сделано при определении второй производной функции f (x), можно определить и производные более высоких порядков: третью производную, четвертую производную и т.д. (конечно же, при условии, что они существуют).
Достаточные условия выпуклости вверх и выпуклости вниз функции
При исследовании направления выпуклости функции (выпуклость вверх или выпуклость вниз) важную роль играет вторая производная этой функции.
Утверждение 1. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 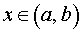 выполнено условие
выполнено условие
f » (x) > 0 ,
то функция f (x) выпукла вниз на интервале (a, b).
Утверждение 2. Если функция f (x) имеет на интервале (a, b) вторую производную, причем для всех 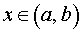 выполнено условие
выполнено условие
f » (x) < 0 ,
то функция f (x) выпукла вверх на интервале (a, b).
Доказательства утверждений 1 и 2 выходят за рамки школьного курса математики и здесь не приводятся.
Пример 3. Функция y = ln x на интервале 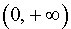 удовлетворяет условию
удовлетворяет условию
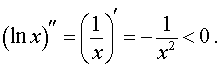
В силу утверждения 2 отсюда следует, что функция y = ln x выпукла вверх (рис. 5) на всей своей области определения 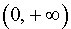 .
.
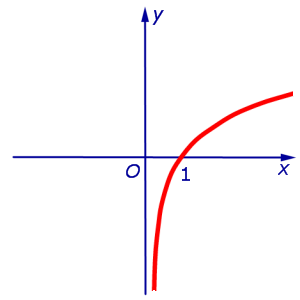
Рис.5
Пример 4. Функция y = e x на интервале  удовлетворяет условию
удовлетворяет условию
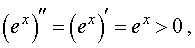
и, в силу утверждения 1, функция y = e x выпукла вниз (рис. 6) на всей своей области определения  .
.
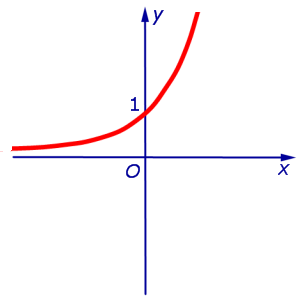
Рис.6
Точки перегиба
Определение 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 . Говорят, что при переходе через точку x0 функция f (x) меняет направление выпуклости, если на одном из интервалов
(a, x0) и (x0, b)
функция выпукла вверх, а на другом – выпукла вниз.
Определение 5. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 , а у графика функции в точке (x0; f (x0)) существует касательная. Если функция f (x) при переходе через точку x0 меняет направление выпуклости, то точку x0 называют точкой перегиба функции f (x) .
Замечание 1 . Если x0 – точка перегиба функции y = f (x), то график функции y = f (x) при переходе через точку x0 переходит с одной стороны от касательной в точке (x0; f (x0)) на другую сторону от касательной, то есть «перегибается» через касательную.
Пример 5. Рассмотрим функцию y = x3, график которой изображен на рисунке 7.
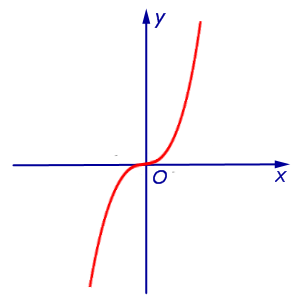
Рис.7
Поскольку
y (0) = 0, y’ (0) = 0,
то прямая y = 0 (ось абсцисс Ox ) является касательной к графику функции y = x3 в точке (0; 0).
Кроме того,
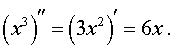
Поэтому y» > 0 при x > 0 и y» < 0 при x < 0 . Таким образом, функция y = x3 выпукла вверх при x < 0 и выпукла вниз при x > 0 , и точка x = 0 является точкой перегиба графика функции y = x3. График функции y = x3 при переходе через точку x = 0 переходит из нижней полуплоскости в верхнюю полуплоскость, то есть «перегибается» через касательную y = 0 .
Необходимые условия для существования точки перегиба
Утверждение 3. Если точка x0 является точкой перегиба графика функции f (x), то в точке x0 либо вторая производная f » (x) = 0 , либо f » (x) не существует.
Замечание 2. Условия существования точки перегиба, сформулированные в утверждении 3, являются необходимыми, но не являются достаточными.
Действительно, рассмотрим функцию y = x4, график которой изображен на рисунке 8.
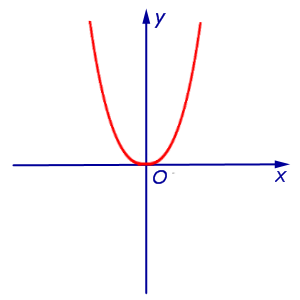
Рис.8
Вычисляя вторую производную этой функции
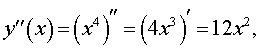
замечаем, что y » (0) = 0 , однако точка x = 0 не является точкой перегиба графика функции y = x4, так как функция y = x4 выпукла вниз, как при x < 0 , так и при x > 0 .
Достаточные условия для существования точки перегиба
Утверждение 4. Пусть функция y = f (x) определена на некотором интервале (a, b) , содержащем точку x0 , имеет первую производную в каждой точке интервала (a, b) и имеет вторую производную в каждой точке интервала (a, b) за исключением, быть может, самой точки x0 .
Если для точек 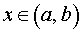 выполнено условие:
выполнено условие:
f » (x) > 0 при x < x0 и f » (x) < 0 при x > x0 ,
либо выполнено условие:
f » (x) < 0 при x < x0 и f » (x) > 0 при x > x0 ,
то точка x0 является точкой перегиба графика функции f (x).
Другими словами, точка x0 является точкой перегиба графика функции f (x), если при переходе через точку x0 вторая производная функции меняет свой знак.
Пример 6. Найти интервалы, на которых функция
y (x) = x4 – 6x3 + 12x2
выпукла вверх, а также интервалы, на которых эта функция выпукла вниз. Определить точки перегиба.
Решение. Вычислим вторую производную функции:
y’ (x) = 4x3 – 18x2 + 24x ,
y» (x) = 12x2 – 36x + 24 = 12(x2 – 3x + 2) = 12(x – 1) (x – 2) .
y» (x) = 12x2 – 36x + 24 =
= 12(x2 – 3x + 2) =
= 12(x – 1) (x – 2) .
Отсюда вытекает, что вторая производная существует во всех точках  и обращается в нуль в точках x = 1 и x = 2 . Воспользуемся методом интервалов и изобразим на рисунке 9 диаграмму знаков второй производной y» (x)
и обращается в нуль в точках x = 1 и x = 2 . Воспользуемся методом интервалов и изобразим на рисунке 9 диаграмму знаков второй производной y» (x)
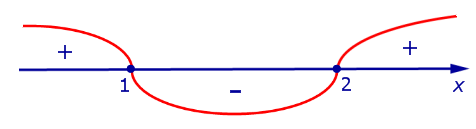

Рис.9
При переходе через точку x = 1 вторая производная функции y» (x) меняет знак с «+» на «–» . Следовательно, x = 1 – точка перегиба графика функции.
При переходе через точку x = 2 вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, x = 2 также является точкой перегиба графика функции.
При 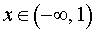 и при
и при  вторая производная функции y» (x) > 0, следовательно, функция y (x) выпукла вниз на этих интервалах.
вторая производная функции y» (x) > 0, следовательно, функция y (x) выпукла вниз на этих интервалах.
При 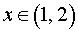 вторая производная функции y» (x) < 0, следовательно, функция y (x) выпукла вверх на интервале (1, 2) .
вторая производная функции y» (x) < 0, следовательно, функция y (x) выпукла вверх на интервале (1, 2) .

  ;На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.