Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х). Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2 и осуществим преобразование
2 и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0.
2+x-6=0.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см2.
Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х2-18х+77=0.
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11, то 18-х=7, наоборот тоже справедливо (если х=7 , то 21-х=9).
Задача 6. Разложить квадратное 10x2-11x+3=0 уравнения на множители.
Решение: Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество.
Квадратное уравнение с параметром
Пример 1. При каких значениях параметра а, уравнение (а-3)х2+(3-а)х-1/4=0 имеет один корень?
Решение: Прямой подстановкой значения а=3 видим, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант
упростим его и приравняем к нулю
Получили квадратное уравнение относительно параметра а, решение которого легко получить по теореме Виета. Сумма корней равна 7, а их произведение 12. Простым перебором устанавливаем, что числа 3,4 будут корнями уравнения. Поскольку решение а=3 мы уже отвергли в начале вычислений, то единственным правильным будет — а=4. Таким образом, при а=4 уравнение имеет один корень. 2+(2а+6)х-3а-9=0 имеет более одного корня?
2+(2а+6)х-3а-9=0 имеет более одного корня?
Решение:Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3. При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0.
Вычислим дискриминант
и найдем значения а при котором оно положительно
С первого условия получим а>3. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0. Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0, которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
|
Умение решать квадратные уравнения и неравенства очень важны для решения более сложных математических задач. Также, начиная именно с квадратичной функции, учащиеся впервые знакомятся с понятиями промежутков возрастания и убывания, нулями функции, приобретают первичные навыки по исследованию функций. Поэтому нами были разработаны виджеты, дающие пошаговое объяснение решению типичных задач, связанных с квадратичной функцией и квадратными уравнениями. Установите себе на сайт наши виджеты, объясняющие решения типичных математических задач на квадратный трехчлен: решение квадратных уравнений по формуле корней и методом выделения квадрата двучлена, разложение квадратного трехчлена на множители, исследование квадратичной функции (промежутки возрастания и убывания, координаты вершины параболы и т.д.). Сделайте Ваш сайт более востребованным с помощью бесплатных виджетов. Пользуйтесь нашими сервисами без установки. |
|
Уравнения.
 Квадратные уравнения | Математика, которая мне нравится
Квадратные уравнения | Математика, которая мне нравитсяОпределение. Уравнение с одним неизвестным — это высказывание с одной переменной, имеющее вид , где и — функции. Те значения , при которых определены обе эти функции, образуют область определения уравнения.
Примеры.
1) , — вещественное число;
2) , ;
3) , .
Определение. Значение , при котором уравнение обращается в верное равенство, называется корнем, или решением уравнения.
Определение. Пусть даны два уравнения (1) и (2). Уравнение (2) называется следствием уравнения (1), если множество корней уравнения (1) содержится в множестве корней уравнения (2).
Обозначение. .
Пример.
1)
2)
3)
Теорема. Пусть — функции. Рассмотрим уравнения
Пусть — функции. Рассмотрим уравнения
Если область определения функции содержит область определения уравнения (1), то уравнения (2), (3), (4) являются следствиями уравнения (1). Если, кроме того, функция не обращается в нуль ни в одной точке области определения уравнения (1), то уравнение (5) является следствием уравнения (1).
Доказательство. 1) .
Пусть — корень уравнения (1). Тогда и — это одно и то же число. Тогда и — одно и то же число. Следовательно, — корень уравнения (2). Аналогично доказываются остальные утверждения.
Пример.
Докажем, что .
Разобьем область определения уравнения (1) на два множества и . На первом множестве уравнение корней не имеет (убеждаемся в этом проверкой). Поэтому достаточно рассмотреть уравнение (1) на множестве . Теперь на этом множестве . Значит, .
Теперь на этом множестве . Значит, .
, так как числа вида не являются корнями уравнения (1).
, так как число является корнем уравнения (1), но не входит в область определения уравнения (8).
Пусть, решая уравнение (1), получили
Предположим, что известны все корни уравнения . Чтобы решить уравнение (1), достаточно подставить в него поочередно все корни уравнения .
Определение. Два уравнения называются равносильными, если каждое из них является следствием другого, т.е. множества их корней совпадают.
Применяя теорему, можно показать, что уравнение (1) является следствием каждого из уравнений (2), (3), (5) и, следовательно, равносильно им. Уравнения (1) и (4) равносильны, если потребовать, чтобы функция не обращалась в нуль на области определения уравнения (1).
Решая уравнение, можно прибавлять к обеим частям одну и ту же функцию (вычитать, умножать, делить) при условии, что область определения этой функции содержит область определения уравнения, а в случае умножения и деления не обращается в нуль в точках этой области. В этих случаях мы будем получать уравнение, равносильное данному, если из его корней выбирать только те, которые входят в область определения исходного уравнения.
В этих случаях мы будем получать уравнение, равносильное данному, если из его корней выбирать только те, которые входят в область определения исходного уравнения.
Теорема. Пусть — функции, причем область определения функции содержит множества значения функций и . Рассмотрим уравнения
Тогда .
Если функция при этом обратима, то уравнения (1) и (6) равносильны.
Квадратные уравнения
Определение. Квадратным называется уравнение вида
где — вещественные числа, .
Решим квадратное уравнение. Разделим обе части на
Число называется дискриминантом данного уравнения.
Если , то уравнение вещественных корней не имеет. Если , то уравнение имеет единственный корень . Если , то уравнение можно представить в виде
или
или
Уравнение имеет два корня
Если , то формулу для корней можно переписать в таком виде
— корень в том и только в том случае, если .
— корень в том и только в том случае, если .
Теорема Виета
Замечательный математик французского Ренессанса Франсуа Виет (1540–1603) ввел коренные улучшения в алгебраическую символику. Среди многих своих открытий он особенно ценил установление зависимости между корнями и коэффициентами уравнений. Виет много занимался алгебраическими уравнениями, соответствующими делению угла на три, пять и семь равных частей. Он нашел разложение и по степеням и . Это позволило ему сразу же решить в октябре 1594 г. уравнение 45-й степени с числовыми коэффициентами, предложенное как вызов всем математикам мира голландским ученым Андриеном ван Роуменом (1561–1615). Виет разработал оригинальное исчисление прямоугольных треугольников и впервые рассмотрел бесконечные произведения.
Теорема. Если и — корни квадратного уравнения и других корней у этого уравнения нет, то
Доказательство. Можно считать, что
Обратная теорема Виета
Теорема.
Если числа и таковы, что
то и — корни уравнения , и других корней это уравнение не имеет.
Таким образом,
и — корни этого уравнения, и других корней это уравнение не имеет.
Следствие. Попутно доказано, что если и — корни уравнения и других корней у него нет, то левая часть представляется в виде
Задачи.
1. При каких значениях параметра уравнение
имеет два корня, один из которых меньше , а другой больше ?
2. Какие из уравнений
равносильны уравнению
Решение квадратных уравнений через производные / Хабр
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?».
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим

Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика
можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль». Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Функции Квадратные функции
Мы знаем, что такое квадратные уравнения. Теперь мы собираемся изобразить их на графике. Вот как мы катимся. Всякий раз, когда мы узнаем, что такое лотерейные номера Mega Millions, мы также наносим их на график. То же самое касается результатов баскетбольных матчей, результатов выборов и кассовых сборов за первые выходные. У нас могут быть проблемы.
То же самое касается результатов баскетбольных матчей, результатов выборов и кассовых сборов за первые выходные. У нас могут быть проблемы.
Чтобы получить функции, нарисуем квадратные уравнения вида
y = ax 2 + bx + c .
Это гарантирует, что у нас будет только одно значение y для каждого значения x .
Пример задачи
Нарисуйте уравнение y = x 2 .
Это простейшее квадратное уравнение. Это тоже отношение, так что мы уже знаем, как изобразить его на графике. Возможно, мы забыли об этом, но знание где-то там.
Сначала мы делаем таблицу значений, чтобы мы могли изобразить некоторые точки, а затем мы видим фигуру, которую мы получаем, и соединяем точки.Вот выборка точек:
Теперь давайте изобразим их на графике:
Это образует своего рода U-образную форму, вот как мы соединяем точки:
Единственный корень многочлена x 2 равно x = 0. Таким образом, 0 является единственным значением x , которое мы можем подставить в уравнение Неслучайно единственная точка на графике y = x 2 с координатой y -0 — это точка (0, 0).
Таким образом, 0 является единственным значением x , которое мы можем подставить в уравнение Неслучайно единственная точка на графике y = x 2 с координатой y -0 — это точка (0, 0).
И снова появление вечно популярного 0. Этот парень в последнее время повсюду. Должно быть, он продвигает новый фильм.
Давайте сделаем несколько более интересных, хотя и более сложных примеров. Конечно, мы могли бы просто изобразить их на калькуляторе, но мы хотели бы понять, почему мы получаем именно такие изображения. Так что, если у вас нет одного из тех калькуляторов, которые постоянно болтают о том, как они «попали туда», давайте продолжим и сделаем работу сами.
Иногда нас просят нарисовать график.Не напрягайтесь; никакие баллы не будут сняты за менее чем идеально прямые линии или полное отсутствие художественных способностей. Идея состоит в том, чтобы нарисовать грубую форму графика и обозначить пару простых значений, но не беспокоиться о точности. Сохраните высочайшую точность для практики стрельбы из лука.
Сохраните высочайшую точность для практики стрельбы из лука.
Пример задачи
Начертите график функции без использования калькулятора мы получаем график y = x 2 сдвинутый вверх на 1 единицу.Единственное значение, которое нам нужно обозначить на эскизе, это y = 1.
Примеры, которые мы делали до сих пор, были довольно простыми, но теперь мы перейдем к некоторым примерам, которые прямо противоположны. Графики в наших предыдущих примерах выглядели так, как будто график x 2 немного сдвинулся вверх или вниз. Однако для построения общих квадратных уравнений нам нужно действовать по-другому.
Сначала нам нужно несколько новых определений, так что расслабьтесь и расчистите место…
График любого квадратного уравнения представляет собой параболу . Парабола будет выглядеть как перевернутая U:
… или перевернутая U:
Места, где парабола пересекает ось x , называется x -перехватами , как и в случае с линейными уравнениями. Место, где парабола пересекает ось y , является точкой пересечения y . Самая низкая или самая высокая точка параболы, в зависимости от того, в какую сторону она раскрывается, называется вершиной параболы.Это не вихрь, так что не нужно беспокоиться о том, что вас поглотит крутящаяся спираль, похожая на торнадо… если только вы не живете в Канзасе.
Место, где парабола пересекает ось y , является точкой пересечения y . Самая низкая или самая высокая точка параболы, в зависимости от того, в какую сторону она раскрывается, называется вершиной параболы.Это не вихрь, так что не нужно беспокоиться о том, что вас поглотит крутящаяся спираль, похожая на торнадо… если только вы не живете в Канзасе.
Чтобы нарисовать график общего квадратного уравнения, нам нужно знать три вещи.
- Пересечения
- Вершина
- Открыт ли график вверх («U») или вниз (перевернутая «U»)
Давайте рассмотрим пример, чтобы увидеть, как найти все эти вещи, и как собрать их вместе в графике.Это будет приятная, расслабляющая прогулка. Вы даже можете делать это сидя; вот как это расслабляет.
Пример задачи
Нарисуйте график y = x 2 + 3 x + 2.
Нам нужно найти точки пересечения, вершину и направление параболы вверх или вниз. Мы также должны выяснить, до какого числа он будет открыт, на случай, если нам понадобится пробежаться поздно ночью.
Мы также должны выяснить, до какого числа он будет открыт, на случай, если нам понадобится пробежаться поздно ночью.
1. Где парабола пересекает оси?
Во-первых, где парабола пересекает ось x ? Точка пересечения x — это точка формы (что-то, 0).
Таким образом, x пересечений нашего графика будут происходить при любых значениях x , делающих y нулевыми; другими словами, в корнях многочлена x 2 + 3 x + 2. Чтобы найти корни, мы факторизируем полином, приравниваем его к нулю и находим x .
x 2 + 3 x + 2 = 0
( x + 2) ( x + 1) = 0
x = -2, x = -1
Это корни многочлена, и в качестве бонуса они также являются точками пересечения параболы размером x .Не проблема, что они оба отрицательные. Это график равных возможностей.
Теперь мы знаем, что точки (-2, 0) и (-1, 0) находятся на графике:
Где парабола пересекает ось y ? Чтобы найти y -intercept, мы подставим 0 вместо x и посмотрим, что получится. В этом случае мы находим:
В этом случае мы находим:
y = (0) 2 + 3(0) + 2 = 2
Таким образом, точка пересечения y равна 2. У нас также есть точка (0, 2) на графике:
Теперь у нас есть две точки.Если бы это была НФЛ, это было бы безопасно.
2. Что такое вершина?
Вершина параболы находится на полпути между корнями, по крайней мере, когда корни существуют. Через мгновение мы будем беспокоиться о том, что происходит, когда они этого не делают. Ну, вы можете беспокоиться об этом сейчас, но, пожалуйста, держите это при себе, пока мы не доберемся до этого. Нет ничего хорошего в том, чтобы тем временем портить его всем остальным.
Таким образом, для этой параболы вершина возникает, когда x находится на полпути между -2 и -1 или в точке .Мы находим y -значение, подставляя в квадратное уравнение:
Отлично. Точка тоже на нашей параболе.
3. График раскрывается вверх или вниз?
Вы когда-нибудь пытались толкнуть «тянущую» дверь? Потому что мы, гм, нет. Важно знать, как открываются вещи. Парабола ничем не отличается.
Важно знать, как открываются вещи. Парабола ничем не отличается.
Когда x находится за пределами x -перехватов, чем дальше x от нуля, тем больше становится y , и он даже не принимает гормоны роста.Когда х = 5, y = 42; когда х = 100, y = 10302. Мы можем представить, что если бы мы нанесли на график больше точек, то увидели бы, что график открывается вверх.
Соединяя все части вместе, мы соединяем наши точки в форме буквы «U», вот так:
Теперь, когда мы прошли пример задачи, и вам это так понравилось, что ваш рот приобрел форму y = ax 2 + bx + c.
1. Нахождение перехватов.
Здесь есть два шага: найти точки пересечения x и найти точки пересечения y . Это похоже на охоту за пасхальными яйцами снова и снова. Отрезки x — это значения x , которые делают y нулем. Другими словами, решения квадратного уравнения
Другими словами, решения квадратного уравнения
0 = x 2 + bx + c .
Это может включать использование квадратичной формулы.Поскольку не все квадратные уравнения имеют решения, на графике может не быть x -пересечений. Это может выглядеть, например, так:
y -значение, которое мы получим, если подставим x = 0 в уравнение ax 2 + bx 909 c +9 . Когда мы это сделаем, мы найдем
a (0) 2 + b (0) + c = c .
Таким образом, пересечение y равно y = c .Парабола всегда будет иметь точку пересечения и , поскольку c всегда будет некоторым числом (возможно, 0). Со всем этим x -перехватом в воздухе приятно осознавать, что мы все еще можем полагаться на c и y -intercept. Они останутся с нами, несмотря ни на что.
2. Нахождение вершины.
Когда парабола имеет x точек пересечения, вершина оказывается на полпути между ними. Число на полпути между двумя числами также известно как их среднее.Точно так же, как вы находитесь на полпути между возрастом вашего старшего брата и младшей сестры, что делает вас совершенно средним. Подождите…
Среднее между 4 и 10 равно , что является числом на полпути между 4 и 10. Если мы используем квадратичную формулу, чтобы найти x -отрезков, мы получим значения
.
Число на полпути между этими двумя значениями равно
Это означает, что вершина находится в .
Но подождите, что происходит, когда квадратичная формула не дает нам никаких решений? Достаточно скрытно, вершина все еще будет в .Значение будет существовать всегда, потому что если a = 0, у нас вообще не будет квадратной формулы. О, алгебра. Всегда пытается проскользнуть мимо нас. Не в этот раз, приятель.
3. Принятие решения о том, открывается ли график вверх («U») или вниз (перевернутый «U»»).
Коэффициент a при члене x 2 говорит нам, открывается ли график вверх или вниз. Если и положительны, график открывается вверх. Если и отрицательные, график открывается вниз.Это должно быть легко запомнить, потому что, когда вы настроены позитивно, ваш рот образует букву «U», а когда вы настроены отрицательно, он образует перевернутую букву «U». Если только вы не один из тех людей, которые всегда могут оставаться совершенно невозмутимыми, в этом случае вы сами по себе с этим.
В любом случае, причина этого в том, что по мере удаления x от 0, y будет становиться все более и более отрицательным.
Как писать квадратичные функции — видео и стенограмма урока
Дан график
Давайте начнем с записи квадратичной функции по графику.2+ k
Где a — константа, а h и k — значения x и y вершины (h,k). Помните, что наше «f(x)» такое же, как «y». Шаги следующие:
Помните, что наше «f(x)» такое же, как «y». Шаги следующие:
1. Подставьте вершинные значения h и k в вершинную форму квадратичной функции и упростите
2. Теперь подставьте значения x и y другой точки в упрощенную квадратичную функцию из шага 1
3. Найдите
4. Теперь подставьте значение a в упрощенную квадратичную функцию из шага 1.2 + bx + c
Где a, b и c — константы. Опять же, помните, что наша f(x) такая же, как y. Что мы собираемся сделать, так это создать систему из трех уравнений, которые мы будем использовать для решения наших трех неизвестных констант, a, b и c. Шаги следующие:
1. Подставьте значения x и y в общую форму квадратичной функции и упростите. Итак, это для всех трех точек, поэтому вы получаете одно уравнение для каждой точки. У вас должно получиться три уравнения.
2. Решите эту систему из трех уравнений либо с заменой, либо с исключением.2 + b(2) + c, что упрощается до:
1 = 4a + 2b + c
Теперь, взяв эти три уравнения и решив систему методом исключения, мы получим следующее:
Мы можем вычесть 1 = 4a — 2b + c из 4 = 16a — 4b + c, чтобы исключить переменную c. Получаем:
Получаем:
4 = 16a — 4b + c — 1 = 4a — 2b + c =
3 = 12a — 2b
Используя другую пару уравнений, мы снова исключим переменную c. На этот раз мы вычтем:
1 = 4a + 2b + c из 1 = 4a — 2b + c.Получаем:
1 = 4a — 2b + c — 1 = 4a + 2b + c =
(0 = 0a — 4b) Это упрощает до:
0 = -4b
Так как последнее уравнение, которое мы получили 0 = -4b имеет только одну переменную, мы можем решить это уравнение для этой переменной. Если бы это уравнение имело две переменные, мы использовали бы другое уравнение, 3 = 12a — 2b, в сочетании с этим уравнением, чтобы помочь нам найти a и b.
Поскольку это не так, мы можем продолжить и решить 0 = -4b для переменной b.Получаем:
b = 0
Теперь мы знаем, чему равно b. Теперь мы можем подставить это значение в уравнение 3 = 12a — 2b и найти a. Мы получаем:
3 = 12a — 2(0)
3 = 12a
a = 3/12
a = 1/4
Теперь мы имеем a = 1/4 и b = 0. Теперь мы можем использовать эти два значения. и подставьте их в любое из трех уравнений, которые мы сначала написали. Подставим эти значения a и b в уравнение:
и подставьте их в любое из трех уравнений, которые мы сначала написали. Подставим эти значения a и b в уравнение:
1 = 4a + 2b + c
Получим:
1 = 4 (1/4) + 2(0) + c
1 = 1 + c
c = 0
Теперь мы решили для всех наших переменных.2
Пример
Рассмотрим еще один пример. Напишите квадратичную функцию для графика, проходящего через точки (-1,0), (0,-1) и (1,0), где (0,-1) — вершина. Читая эту задачу, мы видим, что нам даны три точки, и это также говорит нам, что -1 является вершиной. Хм… мы можем использовать любой метод. Давайте сделаем метод, использующий вершинную форму квадратичной функции. В нем меньше шагов, и решение будет короче и быстрее.
Поскольку наша вершина (0,-1), h = 0 и k = -1, мы можем использовать любую другую точку в качестве второй точки.2 + k , где a — константа, а h и k — значения x и y вершины (h,k).
Чтобы записать квадратичную функцию, зная вершину и еще одну точку, выполните следующие действия:
1. Подставьте вершинные значения h и k в вершинную форму квадратичной функции и упростите
Подставьте вершинные значения h и k в вершинную форму квадратичной функции и упростите
2. Теперь подставьте значения x и y другой точки в упрощенную квадратичную функцию из шага 1
3. Найдите
4. Теперь подставьте значение a в упрощенную квадратичную функцию из шага 1.2 + bx + c, где a, b и c — константы.
Чтобы записать квадратичную функцию по трем точкам, выполните следующие действия:
1. Подставьте значения x и y в общую форму квадратичной функции и упростите. Сделайте это для всех трех точек, чтобы получить одно уравнение для каждой точки. У вас должно получиться три уравнения.
2. Решите эту систему из трех уравнений либо с заменой, либо с исключением.
3. Подставьте найденные значения a, b и c в общую форму квадратичной функции.Упростите, чтобы найти нашу квадратичную функцию, которая проходит через все три заданные точки.
квадратное уравнение | математика | Британика
квадратное уравнение , в математике, алгебраическое уравнение второй степени (с одной или несколькими переменными, возведенными во вторую степень). Древневавилонские клинописные тексты, датируемые временем Хаммурапи, свидетельствуют о знании того, как решать квадратные уравнения, но, похоже, древнеегипетские математики не знали, как их решать.Со времен Галилея они играли важную роль в физике ускоренного движения, такого как свободное падение в вакууме. Общее квадратное уравнение с одной переменной имеет вид ax 2 + bx + c = 0, в котором a, b, и c — произвольные константы (или параметры), а a — произвольные константы (или параметры). равно 0. Такое уравнение имеет два корня (не обязательно различных), что определяется квадратичной формулой ).Если вместо приравнивания вышеприведенного к нулю построить кривую x 2 + bx + c = y , то видно, что действительными корнями являются координаты x точек в кривая пересекает ось x . Форма этой кривой в евклидовом двумерном пространстве — парабола; в евклидовом трехмерном пространстве это параболическая цилиндрическая поверхность, или параболоид.
Древневавилонские клинописные тексты, датируемые временем Хаммурапи, свидетельствуют о знании того, как решать квадратные уравнения, но, похоже, древнеегипетские математики не знали, как их решать.Со времен Галилея они играли важную роль в физике ускоренного движения, такого как свободное падение в вакууме. Общее квадратное уравнение с одной переменной имеет вид ax 2 + bx + c = 0, в котором a, b, и c — произвольные константы (или параметры), а a — произвольные константы (или параметры). равно 0. Такое уравнение имеет два корня (не обязательно различных), что определяется квадратичной формулой ).Если вместо приравнивания вышеприведенного к нулю построить кривую x 2 + bx + c = y , то видно, что действительными корнями являются координаты x точек в кривая пересекает ось x . Форма этой кривой в евклидовом двумерном пространстве — парабола; в евклидовом трехмерном пространстве это параболическая цилиндрическая поверхность, или параболоид.
в двух переменных, общее квадратичное уравнение AX 2 + BXY + CY 2 + DX + EY + F = 0, в котором A, B, c, d, e, и f — произвольные константы, а a, c ≠ 0.Дискриминант (обозначается греческой буквой дельта, Δ) и инвариант ( b 2 − 4 ac ) вместе дают информацию о форме кривой. Геометрическое место в евклидовом двумерном пространстве любого общего квадратичного уравнения от двух переменных является коническим сечением или его вырожденным.
Более общие квадратные уравнения с переменными x, y, и z, приводят к порождению (в евклидовом трехмерном пространстве) поверхностей, известных как квадрики или квадратичные поверхности.
Эта статья была недавно пересмотрена и обновлена Уильямом Л. Хошем.Как найти уравнение квадратичной функции по ее графику
Недавно один читатель спросил:
Я хотел бы знать, как найти уравнение квадратичной функции по ее графику, в том числе, когда он не пересекает ось x .
Спасибо.
Моделирование
Это хороший вопрос, потому что он лежит в основе «настоящей» математики. Часто у нас есть набор точек данных из наблюдений, скажем, в эксперименте, но мы не знаем функцию, которая проходит через наши точки данных.(Большая часть математики из «учебников» работает неправильно: сначала выдается функция, а затем предлагается подставить значения в эту функцию.)
График квадратичной функции представляет собой параболу
График квадратичной функции представляет собой параболу. Парабола может быть направлена либо «ногами вверх», либо «ногами вниз».
Мы знаем, что квадратное уравнение будет иметь вид:
у = ах 2 + бх + с
Наша задача состоит в том, чтобы найти значения a , b и c после первого просмотра графика . Иногда легко определить точки, через которые проходит кривая, но часто нам нужно оценить точки.
Начнем с самого простого случая. (Мы будем считать, что ось данной параболы вертикальна.)
Парабола разрезает график в 2 местах
На графике видно, что корни квадратного числа равны:
x = -2 (поскольку график пересекает ось x на x = — 2); и
x = 1 (поскольку график пересекает ось x на уровне x = 1.)
Теперь мы можем написать нашу функцию для квадратного числа следующим образом (поскольку, если мы решим следующее для 0, мы получим наши 2 точки пересечения):
f ( х ) = ( х + 2)( х — 1)
Мы можем расширить это, чтобы получить:
f ( х ) = х 2 + х — 2
Это квадратичная функция, которая проходит через ось x в нужных точках.
Но правильный ли это ответ?
Обратите внимание, что мой график проходит через -3 по оси y . Давайте подставим x = 0 в уравнение, которое я только что получил, чтобы проверить его правильность.
Давайте подставим x = 0 в уравнение, которое я только что получил, чтобы проверить его правильность.
f (0) = 0 2 + 0 — 2 = -2
Это неправильно!
Оказывается, через точки (−2,0) и (1,0) проходит бесконечных парабол.
Вот некоторые из них (зеленым цветом):
И не забудьте про параболы в положении «ногами вниз»:
Итак, как нам найти правильную квадратичную функцию для нашего первоначального вопроса (тот, что в синем)?
Метод системы уравнений
Чтобы найти уникальную квадратичную функцию для нашей синей параболы, нам нужно использовать 3 точки на кривой.Затем мы можем составить 3 уравнения с 3 неизвестными и решить их, чтобы получить требуемый результат.
На исходной синей кривой видно, что она проходит через точку (0, −3) на оси y . Мы будем использовать это как нашу 3-ю известную точку.
Используя нашу общую форму квадрата, y = ax 2 + bx + c , мы подставляем известные значения для x и y , чтобы получить:
Замена (−2,0):
0 = а (−2) 2 + b (−2) + c = 4 a − 2 b + c
Замена (1,0):
0 = a (1) 2 + b (1) + c = a + b + c
Замена (0,−3):
− 3 = a (0) 2 + b (0) + c = c
Получаем c = − 3.
Подстановка c = − 3 в первой строке дает:
4 а − 2 б = 3; и подстановка во вторую строку дает:
а + б = 3
Умножение последней строки на 2 дает:
2 а + 2 б = 6
Прибавляя это к 4 a − 2 b = 3, получаем:
6 a = 9
Это дает = 1.5.
Подставляя а = 1,5 в а + Ь = 3, мы получаем Ь = 1,5.
Таким образом, правильная квадратичная функция для синего графика равна
.f ( х ) = 1,5 х 2 + 1,5 х — 3
Заметим, что значение « a » положительное, что приводит к ориентации «ноги вверх», как и ожидалось.
Вершинный метод
Еще один способ сделать это — наблюдать вершину («заостренный конец») параболы.
Мы можем написать параболу в «вершинной форме» следующим образом:
y = a ( x − h ) 2 + k
Вершина этой параболы находится в точке ( h, k ).
В нашем примере выше мы не можем точно сказать, где находится вершина. Это около (-0,5, -3,4), но «близко» не даст нам правильного ответа. (Если нет других «хороших» точек, через которые мы можем видеть прохождение графика, то нам придется использовать нашу оценку.)
В следующем примере показано, как мы можем использовать метод вершин для нахождения нашей квадратичной функции.
Одна точка касается оси
xЭта парабола касается оси x только в точке (1, 0).
Если мы используем y = a ( x − h ) 2 + k , мы можем видеть из графика, что h = 1 и Это дает нам y = a ( x − 1) 2 .Каково значение « a «? Но, как и в предыдущем случае, мы имеем бесконечное число парабол, проходящих через (1, 0). Вот некоторые из них: В этом примере синяя кривая проходит через (0, 1) на оси y , поэтому мы можем просто заменить x = 0, y = 1 на y = a ( x − 1) 2 следующим образом: 1 = a (− 1) 2 Это дает нам = 1. Итак, наша квадратичная функция для этого примера равна f ( х ) = ( х — 1) 2 = х 2 — 2 х + 1 Примечание: Мы могли бы также использовать тот факт, что x -значение вершины параболы y = ax 2 + bx + c определяется как: Вот пример, где нет x -intercept. Мы видим, что вершина находится в точке (-2, 1), а точка пересечения и находится в точке (0, 2). Просто подставляем, как и раньше, в вершинную форму нашей квадратичной функции. Имеем ( ч , к ) = (-2, 1) и при х = 0, у = 2. Так y = a ( x − h ) 2 + k становится 2 = a (0 − (−2)) 2 + 1 2 = 4 a +1 и = 0. Итак, наша квадратичная функция: F ( x ) = 0.25 ( x — (- 2)) 2 + 1 = 0.25 ( x + 2) 2 + 1 = 0,25 ( x 2 + 4 х + 4) + 1 f ( х ) = 0,25 х 2 + х + 2 а. Вольфрам|Альфа Этот поиск Wolfram|Alpha дает ответ на мой последний пример. б. Эксель Вы можете использовать MS Excel, чтобы найти уравнение. Введите точки в ячейки, как показано, и заставьте Excel построить график, используя «диаграмму рассеяния X-Y». Это дает показанную черную кривую. Затем щелкните правой кнопкой мыши на кривой и выберите «Добавить линию тренда». Выберите «Полиномиальный» и «Порядок 2». (Это дает синюю параболу, как показано ниже). Во вкладке «Параметры» выберите «Отображать уравнение на графике». Получаем следующий результат. в.GeoGebra GeoGebra не был так полезен для этой задачи. GeoGebra даст нам уравнение параболы, но сначала вам нужно знать фокус и директрису. Это не так просто из наблюдений над графиком. Нахождение уравнения параболы с заданными точками данных — полезный навык в математике. Параболы очень полезны для математического моделирования из-за их простоты. Все еще нужна помощь? Найти репетитора См. 82 комментария ниже. Квадратичная функция также называется квадратичным многочленом или квадратичной функцией, и это многочлен с одной или несколькими переменными, где член высшей степени имеет вторую степень. Если квадратичная функция принимается равной нулю, она называется квадратным уравнением. В алгебре важно понимать квадратичные функции и то, как их идентифицировать. Если у вас есть квадратичная функция, у вас может быть одна переменная, например x, или несколько переменных, включая x, y и z.Самое главное, что следует отметить, это то, что никакая переменная не может быть выше второй степени. Это относится к показателям в функции. Например, если одна из переменных равна x в третьей степени, то у вас будет многочлен третьей степени, и это не будет квадратичной функцией. Независимо от того, сколько переменных в вашей функции, вам нужно проверить каждую из них. Если вы обнаружите, что самый высокий показатель степени равен двум, то у вас есть квадратичная функция.Вы можете использовать квадратичные функции для решения задач, связанных с измерениями с неизвестными переменными. Например, если вы строите забор, вы можете использовать квадратное уравнение для определения длины забора, нанеся самую длинную и самую короткую возможные секции забора. Это один из способов применения квадратичной функции. Независимо от того, как представлены переменные, вы можете переписать их в стандартном формате для квадратичной функции.2 + x + 9. Поскольку старший показатель, также называемый степенью многочлена, равен 2, это квадратичная функция. Квадратичная функция имеет область определения, полностью состоящую из действительных чисел, поэтому вы можете построить график этой функции, чтобы определить, является ли она квадратичной функцией. Кроме того, он создаст на графике параболу, которая представляет собой U-образную фигуру. Парабола может раскрываться вверх или вниз. Вы можете взять действительные числа, подставить их вместо х и найти у. Когда вы рисуете график, координата x будет падать вдоль оси x, которая проходит слева направо.Координата y будет соответствовать оси y, которая движется вверх и вниз. После того, как вы начертите несколько точек, проверьте, есть ли у вас парабола. Понимание квадратичных функций имеет решающее значение в алгебре и используется во многих приложениях в реальном мире, особенно в инженерии, науке и бизнесе. Например, если вы хотите узнать траекторию прыгающего мяча, вы будете использовать квадратичную функцию. Предприятия используют их для прогнозирования прибыли и убытков.Они также полезны в любой области, где вам нужно определить минимальные или максимальные значения. Самый простой пример — бросание мяча, потому что гравитация заставляет мяч подниматься, а затем опускаться, образуя дугу. Эта дуга представляет собой параболу. Есть точка, в которой мяч поднимается настолько высоко, насколько это возможно, прежде чем он повернется и полетит обратно вниз. Это называется вершиной параболы. Парабола начинается с человека, бросающего мяч, достигает вершины и затем направляется вниз. Квадратное уравнение скажет вам траекторию этого мяча.2} + bx + c, нам нужно положить y = 0. Это означает, что у нас есть ax 2 + bx + c = 0 Отсюда я собираюсь применить обычные шаги, связанные с завершением квадрата, чтобы получить квадратичную формулу. Я надеюсь, что вы найдете пошаговое решение полезным для выяснения того, как формула квадратного уравнения выводится с использованием метода завершения квадрата. Вы можете заинтересованы в: квадратичная квадратичная формула квадратичная функция (также называется квадратичным полиномом , квадратный полиномиал , или полином степени 2 ) является особым типом полиномиальной функции, в которой член высшей степени является второй степенью. Общая форма квадратичной функции: График квадратичной функции представляет собой параболу, двумерную кривую, которая выглядит либо как чашка (∪), либо как шапка (∩). Квадратный многочлен с двумя действительными корнями (пересечениями оси x), что означает отсутствие комплексных корней. Квадратичная функция, имеющая минимум над осью x, не имеет действительных корней и имеет два комплексных корня. Переменная «а» квадратичной функции сообщает вам, открывается ли парабола вверх (более формально называется вогнутой вверх) или открывается вниз (называется вогнутой вниз).На графике выше переменная x 2 положительна, поэтому парабола раскрывается. Если бы переменная x 2 была отрицательной, например -3x 2 , парабола развернулась бы вниз. Квадратичная функция является примером полинома второй степени.Это означает, что наивысшая степень, которую может иметь переменная в функции, равна 2. Один из способов запомнить это — помнить, что термин «квадратный» происходит от слова «квадратный », что означает «квадрат» (мы ищем функцию где квадрат — самая высокая переменная). Квадратичная функция — это тип полиномиальной функции. Вы можете использовать следующую блок-схему, чтобы найти домен и диапазон: Посмотрите это короткое видео о том, как найти домен и диапазон квадратичной функции, используя блок-схему и график: Квадратичная функция или уравнение имеет вид f(x) = ax 2 + bx + c. Например, для функции f(x) = 5x 2 + 4x – 2 квадратичный член равен 5x 2 . В выражении f(x) = x 2 + 2 это x 2 . На форму параболы влияет знак старшего коэффициента: Положительный коэффициент (красный) и отрицательный (синий). Графика с Desmos.com. Это называется квадратичным членом, потому что это член делает выражение квадратичной функцией: уберите «ax 2 », и у вас останется линейная функция, bx + c. Движение снаряда можно частично описать квадратичным термином. Например, на следующем графике показана траектория бейсбольного мяча: Выражение, необходимое для полного объяснения траектории бейсбольного мяча, состоит из трех частей: В исчислении нас больше всего интересуют функции. Уравнение — это просто выражение с двумя равными членами. Например: Квадратное уравнение всегда имеет два решения, так как оно является полиномом второго порядка. Эти два решения могут быть как действительными, так и комплексными числами. Вы можете найти корни (или нули), разложив на множители или дополнив квадрат. Иногда может быть целесообразно изобразить уравнение в виде графика; Часто самый простой способ найти корни — это использовать квадратную формулу , которая, когда вы подставите a, b и c вашего конкретного квадратного уравнения, даст вам корни. Эту формулу можно получить, заполнив квадрат обобщенного уравнения ax 2 + bx + c = 0. Заполнение квадрата означает, что вы переписываете полином как величину, возведенную в степень «2». Квадратные уравнения часто встречаются в алгебре, и квадратную формулу стоит запомнить. Квадратная формула — это способ найти решение для любого многочлена в виде ax 2 + bx + c = 0.Вам нужно будет использовать квадратичную формулу, чтобы найти решения многочленов во многих местах; например, вы можете использовать решения для полиномов, чтобы найти полное расстояние для уравнений скорости. Это работает, когда факторинг не работает или когда факторинг слишком сложен. На самом деле формула всегда даст вам решение, в то время как факторинг иногда работает, а иногда нет. Квадратичная формула формулируется как: «a», «b» и c просто числа или числовые коэффициенты.Формула получается из заполнения квадрата. Пример задачи: Решите x 2 + 3x + 4 по квадратичной формуле. Шаг 1: Определите a, b и c в своей функции. Шаг 2: Подставьте числа a, b и c в квадратную формулу: Это еще больше упрощает до -8/2, 2/2 или -4, 1, что является решением для этого конкретного квадратного уравнения. Совет: Чтобы формула работала, ваша функция должна иметь вид ax 2 + bx + c = 0. Вам может понадобиться немного алгебры, чтобы получить вашу функцию в правильной форме. Обратите внимание, что «2a» в знаменателе находится под всем , а не только квадратным корнем.Большинство ошибок совершается из-за того, что случайно отбрасывают квадратный корень, ставят «а» в знаменателе вместо «2а» или опускают «плюс/минус». График параболической функции — это любой график, имеющий U-образную (или перевернутую U-образную) форму. Другими словами, это график квадратичной функции. График параболической функции имеет базовую форму: f(x) = c(x – a) 2 + b Константы a, b и c говорят вам кое-что о: Вершина — это самая низкая точка параболы (или, если парабола перевернута, самая высокая точка). Например, функция f(x) = 5(x – 2) 2 + 1 имеет вершину в точке (2, 1). Знак «с» говорит вам, открывается ли парабола вверх или вниз. На следующем графике показана функция f(x) = 5(x – 2) 2 + 1 (показана красным).Изменение знака первого члена на -5 переворачивает график вверх ногами: Значение «c» изменяет крутизну графика. В приведенном ниже примере одна и та же функция изображена с тремя разными значениями c. Чем дальше от нуля, тем круче график параболической функции: Влияние изменения константы c на 1 (красный), 5 (зеленый) и 20 (синий) на графике параболической функции для той же функции. Чтобы сравнить крутизну графиков с разными знаками для c (e.г. -10 и 4), сначала возьмите абсолютные значения. В этом примере вам останется сравнить 10 и 4, поэтому 10 — более крутой график. Калькулятор Десмос. Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Нет точек, соприкасающихся с осью
x 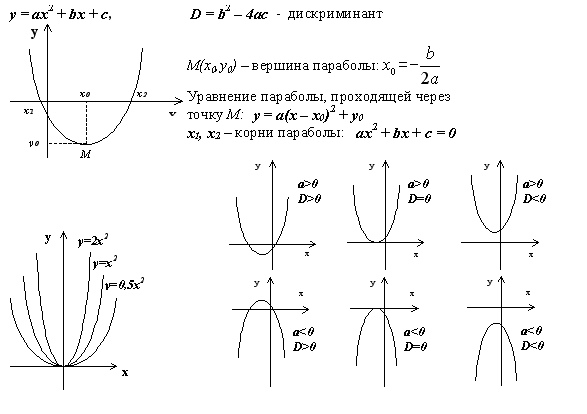 25
25 Использование математического программного обеспечения для нахождения функции

Заключение
Как узнать, является ли функция квадратичной

Проверка показателей каждой переменной
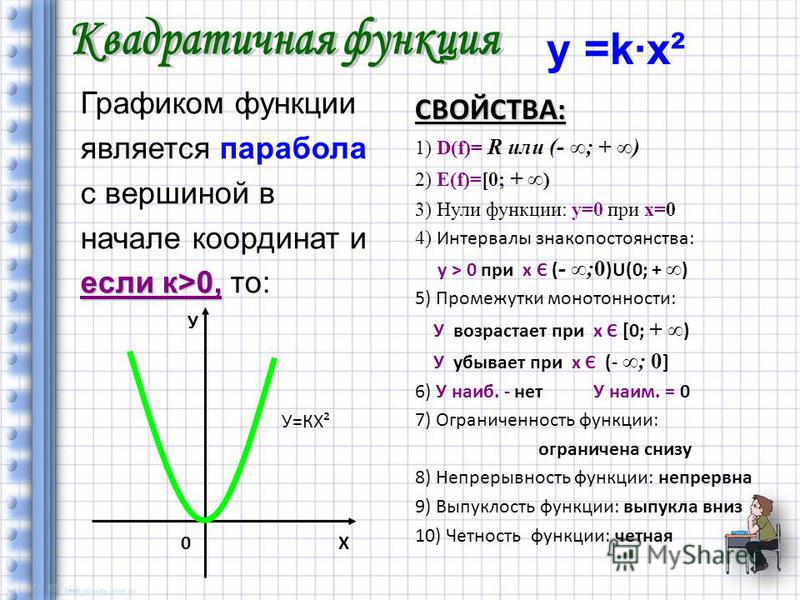
Перепишите уравнение в стандартной квадратичной форме
График уравнения
 Если да, то это квадратичная функция.
Если да, то это квадратичная функция. 2} + bx + c, где a, b и c — действительные числа, но a \ne 0.
2} + bx + c, где a, b и c — действительные числа, но a \ne 0.
квадратичная функция (полиномиальная), уравнение и формула

f(x) = ax 2 + bx + c (или y = ax 2 + bx + c) ,
, где a, b и c — все действительные числа, а и не могут быть равны 0. Развернутая парабола имеет вершину, являющуюся точкой минимума. Парабола, обращенная вниз, имеет вершину, являющуюся точкой максимума. Квадратичные функции полезны при решении задач, связанных с величинами с неизвестными переменными.
Развернутая парабола имеет вершину, являющуюся точкой минимума. Парабола, обращенная вниз, имеет вершину, являющуюся точкой максимума. Квадратичные функции полезны при решении задач, связанных с величинами с неизвестными переменными.
 Он содержит три члена :
Он содержит три члена : Пример квадратичного члена
 е. горбатую) форму: ускорение замедляется по мере того, как гравитация притягивает мяч.В конце концов мяч достигает своей максимальной высоты, затем гравитация еще больше замедляет мяч, пока он не упадет на землю.
е. горбатую) форму: ускорение замедляется по мере того, как гравитация притягивает мяч.В конце концов мяч достигает своей максимальной высоты, затем гравитация еще больше замедляет мяч, пока он не упадет на землю.
y = ax 2 + bx + c
Если квадратное уравнение удовлетворяет требованиям к функциям (каждый вход соответствует не более чем одному выходу), то оно называется квадратичной функцией. Обычно этой функции дают имя:
f(x) = ax 2 + bx + c.
Это соглашение об именах, где «f» — отношение функций, означает, что проще разделить квадратичные функции и квадратные уравнения. Решение квадратного уравнения
 Они также имеют множество приложений в геометрии, инженерии и биологии.
Они также имеют множество приложений в геометрии, инженерии и биологии.
Для любой функции вида ax 2 + bx + c = 0 значение x определяется как: Пример квадратичной формулы

Мы знаем, что квадратичная формула имеет вид: ax 2 + bx + c = 0. Итак, в этом примере a = 1, b = 3 и c = 4. Обратите внимание, что перед x 2 нет числа. , поэтому мы ставим «1». Это потому, что 1 * х 2 = х 2 . Кроме того, когда вы вычисляете «b 2 », ответ всегда будет положительным, даже если перед b стоит отрицательный. Не забывайте включать знаки при работе с уравнением.
Кроме того, когда вы вычисляете «b 2 », ответ всегда будет положительным, даже если перед b стоит отрицательный. Не забывайте включать знаки при работе с уравнением. Базовая форма графика параболической функции
A и B: расположение вершины квадратичной функции

C: Направление и крутизна
Каталожные номера
Колумбийский университет. Предварительное исчисление: нелинейные функции. Получено 6 декабря 2019 г. с: http://ci.columbia.edu/ci/premba_test/c0331/s4/s4_3.html
Получено 6 декабря 2019 г. с: http://ci.columbia.edu/ci/premba_test/c0331/s4/s4_3.html
Applications of Squared Equations. Получено с https://www.cos.edu/Faculty/jonb/Documents/10.6.pdf 13 января 2019 г.
Подготовка к экзамену по математике THEA: решение квадратичных уравнений.Колледж Сан-Хасинто, подготовительное отделение колледжа. Получено с http://stufiles.sanjac.edu/THEA/THEAMathReviewforWebsite/THEAMathReviewforWebsite15.html 13 января 2019 г.
Савельев, П. (2019). Иллюстрированное исчисление: Том 1: Предварительное исчисление.
Общественный колледж Whatcom. Решение уравнений путем заполнения квадрата. Получено 21 января 2019 г. с http://whatcom.edu/home/showdocument?id=1766
.
 В случае, если Вы просто хотите разобраться, как решается та или иная математическая задача, Вы можете никуда не устанавливать виджет: просто зайдите на нужную страницу и введите там необходимые данные. Программа сама посчитает решение и выдаст ответ.
В случае, если Вы просто хотите разобраться, как решается та или иная математическая задача, Вы можете никуда не устанавливать виджет: просто зайдите на нужную страницу и введите там необходимые данные. Программа сама посчитает решение и выдаст ответ. Спасибо.
Спасибо.