Карл Фридрих Гаусс: восхождение на престол

С первых лет Гаусс отличался феноменальной памятью и выдающимися способностями к точным наукам. Всю свою жизнь он совершенствовал свои познания и систему счета, что принесло человечеству множество великих изобретений и бессмертных трудов.

Маленький принц математики

Карл родился в Брауншвейге, в Северной Германии. Это событие произошло 30 апреля 1777 года в семье бедного рабочего Герхарда Дидериха Гаусса. Хотя Карл был первым и единственным ребенком в семье, у отца редко находилось время на воспитание мальчика. Чтобы как-то прокормить семью, ему приходилось хвататься за любую возможность заработать: обустройство фонтанов, садовничество, каменные работы.

Большую часть своего детства Гаусс провел вместе с матерью Доротеей. Женщина души не чаяла в своем единственном сыне и, в дальнейшем, безумно гордилась его успехами. Она была веселой, умной и решительной женщиной, но, в силу своего простого происхождения, — неграмотной. Поэтому, когда маленький Карл, попросил научить его писать и считать, помочь ему оказалось нелегкой задачей.

Впрочем, мальчик не потерял энтузиазма. При любой удобной возможности он расспрашивал взрослых: «Что это за значок?», «Какая это буква?», «Как это прочитать?». Таким нехитрым способом он смог выучить весь алфавит и все цифры уже в трехлетнем возрасте. Тогда же ему поддались и самые простые операции счета: сложение и вычитание.

Как-то раз, когда Герхард снова снял подряд на каменные работы, он расплачивался с рабочими в присутствии маленького Карла. Внимательный ребенок в уме успел пересчитать все озвученные отцом суммы, и тут же нашел ошибку в его подсчетах. Герхард усомнился в правоте своего трехлетнего сына, но, пересчитав, действительно, обнаружил неточность.

Пряники вместо кнута

Когда Карлу исполнилось 7, родители отдали его в народную Екатерининскую школу. Всеми делами здесь заведовал немолодой и строгий учитель Бюттнер. Главным методом воспитания у него были телесные наказания (впрочем, как и везде в то время). В устрашение при себе Бюттнер носил внушительный хлыст, которым первое время попадало и маленькому Гауссу.

Сменить гнев на милость Карлу удалось достаточно быстро. Как только прошел первый урок по арифметике, Бюттнер кардинально изменил отношение к смышленому мальчику. Гауссу удавалось решать сложные примеры буквально на лету, используя оригинальные и нестандартные методы.

Так на очередном уроке Бюттнер задал задачу: сложить все числа от 1 до 100. Как только учитель закончил объяснять задание, Гаусс уже сдал свою табличку с готовым ответом. Позже он пояснил: «Я не складывал числа по порядку, а разделил их попарно. Если сложить 1 и 100 – получим 101. Если сложить 99 и 2 – тоже 101, и так далее. Я умножил 101 на 50 и получил ответ». После этого Гаусс стал любимым учеником.

Таланты мальчика заметил не только Бюттнер, но и его помощник – Христиан Бартельс. На свое небольшое жалование он покупал учебники по математике, по которым занимался сам и учил десятилетнего Карла. Эти занятия привели к ошеломительным результатам – уже в 1791 году мальчика представили герцогу Брауншвейгскому и его приближенным особам, как одного из самых талантливых и перспективных учеников.

Циркуль, линейка и Геттинген

Герцог был в восторге от юного дарования и пожаловал Гауссу стипендию в размере 10 талеров в год. Только благодаря этому, мальчику из бедной семьи удалось продолжить обучение в самой престижной школе – Каролинской коллегии. Там он получил необходимую подготовку и в 1895 году с легкостью поступил в Геттингенский университет.

Здесь Гаусс совершает одно из своих величайших открытий (по мнению самого ученого). Юноше удалось рассчитать построение 17-угольника и воспроизвести его с помощью линейки и циркуля. Другими словами, он решил уравнение х17- 1 = 0 в квадратичных радикалах. Это показалось Карлу настолько значимым, что в этот же день он начал вести дневник, в котором завещал начертить 17-угольник на своем надгробии.

Работая в этом же направлении, Гауссу удается построить правильный семи- и девятиугольник и доказать, что возможно построение многоугольников с 3, 5, 17, 257 и 65337 сторонами, а также с любым из этих чисел, умноженным на степень двойки. Позже эти числа нарекут «простыми гауссовыми».

Звезды на кончике карандаша

В 1798 году Карл покидает университет по неизвестным причинам и возвращается в родной Брауншвейг. При этом свою научную деятельность молодой математик и не думает приостанавливать. Наоборот, время, проведенное в родных краях, стало самым плодотворным периодом его работы.

Уже в 1799 году Гаусс доказывает основную теорему алгебры: «Количество действительных и комплексных корней многочлена равно его степени», исследует комплексные корни из единицы, квадратичные корни и вычеты, выводит и доказывает квадратичный закон взаимности. С этого же года он становится приват-доцентом университета Брауншвейга.

В 1801 году увидела свет книга «Арифметические исследования», где почти на 500 страницах ученый делится своими открытиями. В нее не вошло ни одного незаконченного исследования или сырого материала – все данные максимально точны и доведены до логического вывода.

В это же время он увлекается вопросами астрономии, а точнее математическими приложениями в этой области. Благодаря одному только правильному расчету, Гаусс нашел на бумаге то, что потеряли на небе астрономы – малую планету Цирреру (1801г, Дж. Пиацци). Этим методом было найдено еще несколько планет, в частности, Паллада (1802г, Г.В. Ольберс). Позже Карл Фридрих Гаусс станет автором бесценного труда под название «Теория движения небесных тел» (1809г) и множества исследований в области гипергеометрической функции и сходимости бесконечных рядов.

Браки без расчета

Здесь же, в Брауншвейге, Карл знакомится со своей первой женой – Иоанной Остгоф. Они поженились 22 ноября 1804 года и счастливо прожили на протяжении пяти лет. Иоанна успела родить Гауссу сына Иосифа и дочь Минну. При родах третьего ребенка – Луи – женщина скончалась. Вскоре погиб и сам младенец, и Карл остался один с двумя детьми. В письмах своим товарищам математик не раз утверждал, что эти пять лет в его жизни были «вечной весной», которая, к сожалению, закончилась.

Это несчастье в жизни Гаусса не стало последним. Примерно в то же время от смертельных ран погибает друг и наставник ученого – герцог Брауншвейгский. С тяжелым сердцем Карл покидает родину и возвращается в университет, где принимает кафедру математики и пост директора астрономической лаборатории.

В Геттингене он сближается с дочерью местного советника – Минной, которая была хорошей подругой его покойной жены. 4 августа 1810 года Гаусс женится на девушке, но их брак с самого начала сопровождают ссоры и конфликты. Из-за бурной личной жизни Карл даже отказался от места в Берлинской академии наук Минна родила ученому троих детей – двух сыновей и дочь.

Новые изобретения, открытия и ученики

Высокий пост, который Гаусс занимал в университете, обязывал ученого к преподавательской карьере. Его лекции отличались свежестью взглядов, а сам он был добрым и отзывчивым, что вызывало отклик у студентов. Тем не менее, сам Гаусс преподавать не любил и считал, что, уча других, он тратит свое время попусту.

В 1818 году Карл Фридрих Гаусс одним из первых начинает работу, связанную с неевклидовой геометрией. Побоявшись критики и насмешек, он так и не печатает свои открытия, тем не менее, яро поддерживает Лобачевского. Такая же участь постигла кватернионы, которые первоначально исследовал Гаусс под названием «мутации». Открытие приписали Гамильтону, который опубликовал свои труды, спустя 30 лет после смерти немецкого ученого. Эллиптические функции впервые появились в работах Якоби, Абеля и Коши, хотя основной вклад принадлежал именно Гауссу.

Спустя несколько лет Гаусс увлекается геодезией, проводит съемку Ганноверского королевства с помощью метода наименьших квадратов, описывает действительные формы земной поверхности и изобретает новый прибор – гелиотроп. Несмотря на простоту конструкции (зрительная труба и два плоских зеркала), это изобретения стало новым словом в геодезических измерениях. Результатом исследований в этой области стали труды ученого: «Общие исследования о кривых поверхностях» (1827г) и «Исследования о предметах высшей геодезии» (1842-47гг), а также понятие «гауссовой кривизны», которое дало начало дифференциальной геометрии.

В 1825 году Карл Фридрих совершает еще одно открытие, которое увековечило его имя – гауссовы комплексные числа. Он успешно использует их для решения уравнений высоких степеней, что позволило провести ряд исследований в области вещественных чисел. Основным результатом стал труд «Теория биквадратичных вычетов».

К концу жизни Гаусс изменил свое отношение к преподаванию и стал уделять своим ученикам не только лекционные часы, но и свободное время. Его работы и личный пример оказали огромное влияние на молодых математиков: Римана и Вебера. Дружба с первым привела к созданию «римановой геометрии», а со вторым – к изобретению электромагнитного телеграфа (1833 г).

В 1849 году за заслуги перед университетом, Гаусс был удостоен звания «почетный гражданин Геттингена». К этому времени в круг его друзей уже входят такие известные ученые, как Лобачевский, Лаплас, Ольберс, Гумбольд, Бартельс и Баум.

С 1852 года крепкое здоровье, которое досталось Карлу от отца, дало трещину. Избегая встреч с представителями медицины, Гаусс рассчитывал сам справиться с болезнью, но на этот раз его расчет оказался неверным. Он умер 23 февраля1855 года, в Геттингене, окруженный друзьями и единомышленниками, которые позже наградят его титулом короля математики.

calculator888.ru

Гаусс, Карл Фридрих, подробная биография

(1777-1855) немецкий математик и астроном

Карл Фридрих Гаусс родился 30 апреля 1777 года в Германии, в городе Брауншвейге, в семье ремесленника. Отец, Герхард Дидерих Гаусс, имел много различных профессий, поскольку из-за нехватки денег ему приходилось заниматься всем, начиная от устройства фонтанов и кончая садоводством. Мать Карла, Доротея, была также из простой семьи каменотесов. Ее отличал веселый характер, она была женщина умная, веселая и решительная, любила своего единственного сына и гордилась им.

В детстве Гаусс очень рано научился считать. Однажды летом отец взял трехлетнего Карла на работу в каменоломню. Когда рабочие закончили работу, Герхард, отец Карла, стал производить расчеты с каждым работником. После утомительных расчетов, где учитывалось количество часов, выработка, условия работы и т.п., отец зачитал ведомость, из которой следовало, кому сколько причитается. И вдруг маленький Карл произнес, что счет неверен, что имеется ошибка. Проверили, и мальчик оказался прав. Стали говорить, что маленький Гаусс научился считать раньше, чем говорить.

Когда Карлу исполнилось 7 лет, его определили в Екатерининскую школу, которой заведовал Бюттнер. Он сразу обратил внимание на мальчика, который быстрее всех решал примеры. В школе Гаусс познакомился и подружился с молодым человеком, помощником Бюттнера, которого звали Иоганн Мартин Христиан Бартельс. Вместе с Бартельсом 10-летний Гаусс занялся математическим преобразованием, изучением классических трудов. Благодаря Бартельсу на юное дарование обратили внимание герцог Карл Вильгельм Фердинанд и знатные особы Брауншвейга. Иоганн Мартин Христиан Бартельс в дальнейшем учился в Гельмштедтском и Гёттингенском университетах, а впоследствии приехал в Россию и был профессором Казанского университета, его лекции слушал Николай Иванович Лобачевский.

Тем временем Карл Гаусс в 1788 году поступил учиться в Екатерининскую гимназию. Бедный мальчик никогда бы не смог учиться в гимназии, а потом и в университете без помощи и покровительства герцога Брауншвейгского, которому Гаусс был предан и благодарен в течение всей жизни. Герцог всегда помнил о застенчивом юноше необыкновенных способностей. Карл Вильгельм Фердинанд отпустил необходимые средства для продолжения образования юноши уже в Каролинской Коллегии, которая готовила к поступлению в университет.

В 1795 году Карл Гаусс поступил учиться в Гёттингенс-кий университет. Среди университетских друзей молодого математика был Фаркаш Бойяи, отец Яноша Бойяи, великого венгерского математика. В 1798 году он закончил университет и возвратился на родину.

В родном Брауншвейге в течение десяти лет Гаусс переживает своеобразную «болдинскую осень» — период кипучего творчества и великих открытий. Область математики, где он работает, называется «три великих А»: арифметика, алгебра и анализ.

Началось все с искусства счета. Гаусс считает постоянно, он проводит вычисления с десятичными числами с невероятным количеством знаков после запятой. В течение жизни он становится виртуозом в численных расчетах. Гаусс накапливает информацию о различных суммах чисел, расчетах бесконечных рядов. Это похоже на игру, где гений ученого приходит к гипотезам и открытиям. Он подобен гениальному старателю, чувствует, когда его кирка попадет в золотой самородок.

Гаусс составляет таблицы обратных величин. Он решил проследить, как изменяется период десятичной дроби в зависимости от натурального числа р.

Он доказал, что правильный семнадцатиугольник может быть построен с помощью циркуля и линейки, т.е. что уравнение:

или уравнение

разрешимо в квадратичных радикалах.

Он дал полное решение задачи построения правильных семиугольников и девятиугольников. Ученые трудились над этой задачей 2000 лет.

Гаусс начинает вести дневник. Читая его, мы видим, как начинает разворачиваться завораживающее математическое действо, рождается шедевр ученого, его «Арифметические исследования».

Он доказал основную теорему алгебры, в теории чисел доказал закон взаимности, который был открыт великим Леонардом Эйлером, но тот не смог его доказать. Карл Гаусс занимается в геометрии теорией поверхностей, из которой следует, что геометрия строится на любой поверхности, а не только на плоскости, как в планиметрии Евклида или сферической геометрии. Ему удалось построить на поверхности линии, которые играют роль прямых, удалось измерять расстояния на поверхности.

Прикладная астрономия прочно входит в сферу его научных интересов. Это экспериментально-математическая работа, состоящая из наблюдений, исследований экспериментальных точек, математических методов обработки результатов наблюдений, численных расчетов. Известен интерес Гаусса к практической астрономии, а утомительные вычисления он никому не доверял.

Славу самого знаменитого астронома Европы ему принесло открытие малой планеты Цереры. А дело было так. Сначала Д. Пиацци открыл малую планету и назвал ее Церерой. Но определить ее точное местоположение ему не удалось, поскольку небесное тело скрылось за плотными облаками. Гаусс же «на кончике пера», за письменным столом вновь открыл Цереру. Он рассчитал орбиту малой планеты и в письме к Пиацци указал, где и когда можно наблюдать Цереру. Когда астрономы направили свои телескопы в указанную точку, они увидели Цереру, которая вновь появилась. Их изумлению не было конца.

Молодого ученого прочат в директора Гёттингенской обсерватории. О нем писали следующее: «Слава Гаусса вполне заслужена, и молодой 25-летний человек идет уже впереди всех современных математиков…».

22 ноября 1804 года Карл Гаусс женился на Иоанне Ост-гоф из Брауншвейга. Он писал своему другу Бойяи: «Жизнь представляется мне вечной весной со всеми новыми яркими цветами». Он счастлив, но это длится недолго. Через пять лет Иоанна умирает после рождения третьего ребенка, сына Луи, который, в свою очередь, прожил недолго, всего полгода. Карл Гаусс остается один с двумя детьми — сыном Иосифом и дочерью Минной. А следом произошло другое несчастье: внезапно умирает герцог Брауншвейгский, влиятельный друг и покровитель. Герцог умер от ран, полученных в боевых сражениях, причем им проигранных, при Ауерштедте и Иене.

Тем временем ученого приглашает Гёттингенский университет. Тридцатилетний Гаусс получает кафедру математики и астрономии, а затем и должность директора Гёттингенской астрономической обсерватории, которую занимал до конца жизни.

4 августа 1810 года он женился на любимой подруге своей покойной жены, дочери гёттингенского советника Валь-дека. Звали ее Минной, она родила Гауссу дочь и двух сыновей. В домашней обстановке Карл был строгим, не терпящим никаких нововведений консерватором. Он обладал железным характером, а выдающиеся способности и гениальность сочетались в нем с истинно детской скромностью. Был он глубоко религиозен, твердо верил в загробную жизнь. Обстановка его маленького кабинета в течение всей жизни ученого говорила о непритязательных вкусах его хозяина: небольшой рабочий стол, конторка, выкрашенная белой масляной краской, узкая софа и единственное кресло. Тускло горит свеча, в комнате весьма умеренная температура. Это обитель «короля математиков», как называли Гаусса, «гёттингенского колосса».

В творческой личности ученого очень сильна гуманитарная составляющая: он интересуется языками, историей, философией и политикой. Он выучил русский язык, в письмах друзьям в Петербург просил прислать ему книги и журналы на русском языке и даже «Капитанскую дочку» Пушкина.

Карлу Гауссу предлагают занять кресло в Берлинской академии наук, но его так захлестнула личная жизнь, ее проблемы (ведь только что состоялась помолвка с его второй женой), что он отказался от заманчивого предложения. Уже после непродолжительного пребывания в Гёттингене у Гаусса образовался круг учеников, они боготворили своего учителя, преклонялись перед ним и впоследствии сами стали знаменитыми учеными. Это Шумахер, Герлин, Николаи, Мёбиус, Струве и Энке. Дружба возникла на ниве прикладной астрономии. Все они становятся директорами обсерваторий.

Работа Карла Гаусса в университете, конечно, была связана с преподаванием. Как ни странно, отношение его к этой деятельности весьма и весьма негативное. Он считал, что это потеря времени, которое отнимается от научной работы, от исследований. Однако при этом все отмечали высокое качество его лекций и их научную ценность. А так как по своей натуре Карл Гаусс был человеком добрым, отзывчивым и внимательным, то студенты платили ему почтением и любовью.

Исследования по диоптрике и практическая астрономия привели его к практическим приложениям, в частности, к тому, как усовершенствовать телескоп. Он провел необходимые расчеты, но никто не обратил на них внимания. Прошло полстолетия, и Штейнгель воспользовался расчетами и формулами Гаусса и создал улучшенную конструкцию телескопа.

В 1816 году была построена новая обсерватория, и Гаусс переехал в новую квартиру как директор Гёттингенской обсерватории. Теперь у руководителя важные заботы — нужно заменить инструменты, которые давно морально устарели, особенно телескопы. Гаусс заказывает знаменитым мастерам Рейхенбаху, Фрауенгоферу, Утцшнейдеру и Эртелю два новых меридианных инструмента, которые были готовы в 1819 и 1821 годах. Гёттингенская обсерватория под руководством Гаусса начинает производить самые точные измерения.

Ученый изобрел гелиотрон. Это несложный и дешевый прибор, состоящий из зрительной трубы и двух плоских зеркал, поставленных нормально. Говорят, что все гениальное просто, это касается и гелиотрона. Прибор оказался совершенно необходимым при геодезических измерениях.

Гаусс рассчитывает влияние силы тяжести на поверхности планет. Оказывается, что на Солнце могут жить только существа очень маленького роста, так как сила тяжести там в 28 раз превышает земную.

В физике он интересуется магнетизмом и электричеством. В 1833 году был продемонстрирован электромагнитный телеграф, изобретенный им. Это был прообраз современного телеграфа. Проводник, по которому шел сигнал, был выполнен из железа толщиной в 2 или 3 миллиметра. На этом первом телеграфе сначала передавались отдельные слова, а потом и целые фразы. Общественный интерес к электромагнитному телеграфу Гаусса был весьма велик. Герцог Кембриджский специально приезжал в Гёттинген, чтобы познакомиться с ним.

«Если бы были деньги, — писал Гаусс Шумахеру, — то электромагнитная телеграфия могла бы быть приведена к такому совершенству и к таким размерам, перед которыми фантазия просто приходит в ужас». После успешных опытов в Гёттингене саксонский государственный министр Линденау предложил лейпцигскому профессору Эрнсту Генриху Веберу, который вместе с Гауссом продемонстрировал телеграф, представить доклад об «устройстве электромагнитного телеграфа между Дрезденом и Лейпцигом». В докладе Эрнста Генриха Вебера прозвучали пророческие слова: «…если когда-нибудь земля покроется сетью железных дорог с телеграфными линиями, то это будет напоминать нервную систему в человеческом теле…». Вебер принял активное участие в проекте, внес много усовершенствований, и первый телеграф Гаусса-Вебера просуществовал десять лет, пока 16 декабря 1845 года после сильной молнии не сгорела большая часть его проволочной линии. Оставшийся кусок провода стал музейным экспонатом и хранится в Гёттингене.

Гаусс и Вебер провели знаменитые эксперименты в области магнитных и электрических единиц, измерения магнитных полей. Результаты их исследований легли в основу теории потенциала, в основу современной теории ошибок.

Когда Гаусс занимался кристаллографией, он изобрел приспособление, с помощью которого можно было с высокой точностью измерять 12-дюймовым рейхенбаховским теодолитом углы кристалла, при этом он изобрел новый способ обозначения кристаллов.

Интересна страница его наследия, связанная с основаниями геометрии. Говорили, что великий Гаусс занимался теорией параллельных прямых и пришел к новой, совершенно другой геометрии. Постепенно вокруг него образовалась группа математиков, которые обменивались идеями в этой области. Началось все с того, что молодой Гаусс, так же как и другие математики, пытался доказать теорему о параллельных исходя из аксиом. Отвергнув все псевдодоказательства, он понял, что на этом пути ничего создать не удастся. Неевклидова гипотеза его испугала. Публиковать эти мысли нельзя — ученого предали бы анафеме. Но мысль остановить нельзя, и гауссова неевклидова геометрия — вот она перед нами, в дневниках. Это его тайна, скрытая от широкой публики, но известная его ближайшим друзьям, так как у математиков существует традиция переписки, традиция обмениваться мыслями и идеями.

Фаркаш Бойяи, профессор математики, друг Гаусса, воспитывая сына Яноша, талантливого математика, уговаривал его не заниматься в геометрии теорией параллельных, говорил, что эта тема проклята в математике и, кроме несчастия, она ничего не принесет. И то, чего не сказал Карл Гаусс, сказали в дальнейшем Лобачевский и Бойяи. Поэтому абсолютная неевклидова геометрия названа их именами.

С годами у Гаусса исчезает нерасположенность к педагогической деятельности, к чтению лекций. К этому времени его окружают ученики и друзья. 16 июля 1849 года в Гёттингене праздновали пятидесятилетний юбилей получения Гауссом докторской степени. Собрались многочисленные ученики и почитатели, коллеги и друзья. Ему вручили дипломы почетного гражданина Гёттингена и Брауншвейга, ордена различных государств. Состоялся торжественный обед, на котором он сказал, что в Гёттингене существуют все условия для развития таланта, здесь помогают и в житейских трудностях, и в науке, и еще, что «…банальные фразы никогда не имели силы в Гёттингене».

Карл Гаусс постарел. Теперь он работает менее интенсивно, но круг его занятий по-прежнему широк: сходимость рядов, практическая астрономия, физика.

Зима 1852 года была для него очень тяжелой, резко ухудшается его здоровье. Он никогда не обращался к врачам, так как ие доверял медицинской науке. Его друг, профессор Баум, осмотрел ученого и сказал, что положение очень тяжелое и это связано с сердечной недостаточностью. Здоровье великого математика неуклонно ухудшается, он перестает ходить и 23 февраля 1855 года умирает.

Современники Карла Гаусса чувствовали превосходство гения. На медали, отчеканенной в 1855 году, выгравировано: Mathematicorum princeps (Принцепс математиков). В астрономии память о нем осталась в названии одной из фундаментальных постоянных, система единиц, теорема, принцип, формулы — все это носит имя Карла Гаусса.

biografiivsem.ru

Биография Карла Фридриха Гаусса

История жизни Карла Фридриха Гаусса.

Детство

30 апреля 1777 года в Брауншвейге появился на свет Карл Гаусс. У него была малообеспеченная семья. Папа трудился садовником и водопроводчиком в герцогстве. А мать не имела никакого образования. Любопытно в этом случае то, что даты рождения своего ребёнка родители не знали. Гаусс сам вычислил дату спустя несколько лет. Когда малышу было всего два года, родственники уже называли Карла уникальным ребёнком. А в три года маленький Гаусс умел читать, писать и даже исправлял счетные ошибки собственного отца
Когда Карл Гаусс пошёл в школу, один из преподавателей, Мартин Бартельс, назвал мальчика одаренным. В школе его возможности отметил педагог, когда дал задание вычислить сумму чисел от 1 до 100. Гауссу моментально понял, что все крайние числа в паре составляют 101, и за пару секунд он решил это уравнение, умножив 101 на 50. Мартин помог Карлу получить стипендию в самом крупном техническом университете в Германии.

Студенческие годы

В 1792 году Карл Гаусс приступает к своей научной подготовки Брауншвейгском университете. Многие биографы писали о том, что данный промежуток времени в жизни был самым плодотворным для математика. В это время Карл доказывает, что начертить семнадцатиугольник, применяя только циркуль, очень даже возможно. Удивительно то, что секрет такого черчения Карл так и не открыл. Здесь он изучал труды великих людей: Лагранжа, Ньютона и Эйлера. Когда Карл учился на втором курсе, он начал вести собственный дневник наблюдения. Позже этот дневник поможет ученым со многими открытиями, о которых Гаусс не решился рассказать. Его друзья рассказывали, что Гаусс не афишировал собственные открытия, если не был в них уверен на 100%.

Научная деятельность

В 1798 году Карл заканчивает обучение и возвращается домой. В это же время заканчивает свою первую работу «Арифметические исследования». Карл Гаусс был первым арифметиком, который умел считать дроби и выражать их в функции. Герцог Брауншвейгский оплатил публикацию докторской диссертации, а также выплачивал юному гению стипендию. В 1801 году работал корреспондентом в Санкт-Петербургском университете. Круг интересов у Карла не ограничивался только математикой, особенно после открытия планеты незначительных размеров. Карл сделал много попыток узнать точное местонахождение данной планеты, но безуспешно. В 1801 году впервые было найдено новое небесное тело. Это случилось случайно и неожиданно, точно таким же образом планета была утеряна. Гаусс предпринял попытку выявить ее, используя математические способы, и, как ни странно, она была непосредственно там, куда показал ученный.
Астрономией Гаусс занимался более двадцати лет. Метод Гаусса, с помощью которого определили орбиты, получил всемирную известность. Карл Гаусс открыл две планеты, а в честь математика назвали астероид, который вращается вокруг Марса.
В 1805 году Гаусс впервые женится на Иоганне Остгоф. В браке рождается трое прекрасных детей, но к сожалению, младший сын погибает в раннем возрасте. На этом трагедии в их семьей не заканчиваются. В 1809 году погибает Иоганна.
В 1806 году в военной борьбе погибает человек, на которого хотел быть похож Гаусс. К этому времени Карл Гаусс уже известен всему миру. На работу его зовут все страны Европы, но он едет на работу в Германию.
Спустя какое-то время математик заполучает здесь должность профессора и становится директором обсерватории.
Широкое принятие у людей Карл Гаусс получил не после смерти, а ещё при жизни. Карл являлся участником АН в Петербурге, а также был награжден премией Парижской АН и золотой медалью Лондонского королевского общества. В конце своего жизненного пути стал лауреатом медали Колли и одним из членов Шведской АН.
Карл Фридрих Гаусс не спешил публиковать свои работы. Он проверял свои работы тщательно и кропотливо, начиная от самих формул, заканчивая формулировкой теоремы. Карл преуспел во многих науках: физике, астрономии, механике и геодезии. Но математика занимала в его сердце особенное место. Находясь в пожилом возрасте, Гаусс продолжать делать все вычисления, даже самые сложные, в уме. Также Карл выучил многие иностранные языки за свою жизнь. Математик легко мог общаться на нескольких языках. Карл Гаусс декламировал обыкновенную художественную литературу, а не только книги с научным уклоном. В особенности ему нравились работы Диккенса, Свифта и Вальтера Скотта. Позже Гаусс стал проявлять интерес к американскими литературным авторам, это было связано с переездом его сыновей в Соединенные Штаты Америки. Со временем пристрастился к датским, шведским, итальянским и испанским книжкам. Все без исключения произведения арифметик обязательно прочитывал в оригинале.
В последние года собственного существования великий ученый много болел. Доктора зафиксировали заболевание сердца и нервозное истощение. Медицинские препараты оказывали минимальную помощь, организм их не принимал.
Гаусс умер 23 февраля 1855 года. Математик похоронен в Геттингене.

www.istmira.com

Биография Карла Фридриха Гаусса

История исследования космоса > Великие астрономы > Карл Фридрих Гаусс

Биография Карла Фридрих Гаусса (1777-1855 гг.)

---

Краткая биография:

Имя: Карл Фридрих Гаусс

Дата рождения: 30 апреля 1777 г.

Дата смерти: 23 февраля 1855 г.

Образование: Гёттингенский университет

Место рождения: Брауншвейг

Место смерти: Гёттинген

---

Карл Фридрих Гаусс – немецкий астроном, математик и физик: биография с фото, открытия, интересные факты, пояс астероидов между Марсом и Юпитером, орбита Цереры.

Карл Фридрих Гаусс, одаренный невероятными математическими способностями, знаменитый ученый и астроном, родился в маленьком герцогстве Брауншвейг 30 апреля 1777 г. В детстве его учителя  называли  вундеркиндом, мальчик отличался большими способностями в учебе, его успехи превосходили  сверстников  в изучении точных наук. Один из его учителей, Мартин Бартельс, оценил научный потенциал Карла Фридриха и помог ему получить дальнейшее образование. В 1795 году юный Гаусс успешно окончил колледж и поступил в Геттингенский университет. Во время дальнейшего обучения в университете молодой человек проявлял необыкновенные способности в изучении, как точных наук, так и иностранных языков.

Одним из первых громких успехов Карла Фридриха Гаусса было доказательство построения при помощи циркуля и линейки правильного семнадцатиугольника. В университете в 1801 году преуспевающий в математике студент закончил свою первую серьезную работу под названием «Арифметические исследования».

После окончания университета некоторое время Гауссу пришлось пожить дома, а затем, по рекомендации выдающегося ученого Александра Гумбольдта, его приняли на работу в Геттинген, где он до конца жизни проработал директором обсерватории.

Гаусс проявлял себя в математике главным образом, но его достижения коснулись и астрономии. Так, с помощью него был открыт пояс астероидов, который находится между Марсом и Юпитером. Гаусс рассчитал параметры орбиты планеты Церера, вследствие чего было установлено, что она относится к абсолютно новому виду небесных тел.

Самым знаменитым трудом, проделанным Карлом Фридрихом Гауссом, была работа под названием «Теория движения небесных тел». Именно в ней ученый предложил теорию возмущения орбит. С помощью него он и его последователи могли с точностью вычислять орбиты небесных тел. Так, Гаусс, после публикования своей работы, вычислил орбиту кометы, а на следующий год вычислил орбиту другой.

В математике достижения Гаусса оказались невероятно ценными. Он запомнился в истории как величайший математик, двигатель прогресса и развития науки. Знаменитая теорема алгебры, термин  «гауссова кривизна», основы дифференциальной геометрии вошли в основу фундаментальных математических законов. «Исследования относительно кривых поверхностей» были оценены при жизни ученого и стали классикой в математике. «Теория биквадратичных вычетов» и открытие комплексных чисел также стали научным достоянием Гаусса.

Отличился Карл Фридрих Гаусс и в области физики. Его интересовала электромагнитная индукция, магнитные поля и электричество. Даже единица измерения в физике названа в его честь, магнитная индукция стала измеряться в гауссах. Вместе со своим коллегой Вильгельмом Вебером, он изобрел электрический телеграф. Это изобретение было первым в своем роде и было представлено публике в 183 году.

Карл Фридрих Гаусс был известен во всем мире, его талант и научные достижения признавали в разных странах. В России, Англии и Франции ученый был удостоен различными медалями и наградами за свои достижения. Кроме того, ученый превосходно владел языками, свободно говорил на английском, французском языках и даже латыни.

Карл Гаусс был великим ученым, который проявил свои математические таланты в разных областях науки. Он прожил долгую жизнь, за которую получил призвание и внес огромный вклад в развитие науки. Умер ученый в 1855 году.

---

v-kosmose.com

Карл Гаусс краткая биография | Kratkoe.com

Карл Гаусс краткая биография немецкого математика, механика, физика, астронома и геодезиста изложены в этой статье.

Карл Гаусс биография кратко

Карл Фридрих Гаусс появился на свет 30 апреля 1777 года в бедной семье. Его родители были необразованными, но у мальчика с детства проявились признаки гениальности. Об этом говорит написанный им труд «Арифметические исследования», который он закончил в 1798 году. В возрасте 21-го года книга увидела мир, и его способности настолько поразили герцога Брауншвейгского, что тот отправил юношу в Карлов коллегиум учиться. Здесь он обучался до 1795 года, а после перевелся в Геттингский университет, который окончил в 1798 году. Уже в студенческие годы он доказал и опровергнул большое количество теорем.

1796 год стал самым удачным для него. В марте Карл Гаусс открыл правила построения семнадцатиугольника, усовершенствовал модулярную арифметику и упростил манипуляции в теории чисел. В апреле ученый доказал закон взаимности квадратичных вычетов. Через месяц уже предложил другим математикам свою теорему простых чисел, а в июле сделал очередное открытие – всякое положительное целое число может выражаться суммой не больше 3-ех треугольных чисел.

Карл Гаусс интересные факты

В 1799 году Карл Гаусс заочно защитил научную диссертацию. В 1807 году он получил должность профессора астрономии, а также директора астрономической обсерватории Геттингена.

Познакомившись в 1831 году с Вильгельмом Вебером, профессором физики они начинают сотрудничать, причем плодотворно. Они установили правила Кирхгофа в сфере электричества. В 1833 году ученые изобрели первый электромеханический телеграф.   Умер ученый в Геттингене в 1855 году.

kratkoe.com

Карл Фридрих Гаусс — кратко

Ранние годы, образование, карьера

Иоганн Карл Фридрих Гаусс (кратко), родился 30 апреля 1777 года в городе Брауншвейг, Нижняя Саксония, Германия. Отец Гебхард Дитрих Гаусс каменщик, садовник. Мать Доротея Бенце домохозяйка. В 1782 году, поступил в государственную школу Святой Екатерины. Маленький Карл с легкостью решал математические задачи, чем поразил своего учителя господина Бюттнера. Именно Бюттнер первым обнаружил математический талант у Карла. Он настоял на том, чтобы мальчик ни в коем случае не бросал учебу, а поступил в дальнейшем в университет. Карл начал обучаться у Мартина Бартельса, его старшего на восемь лет, талантливого математика. В 10 лет, Карл самостоятельно вывел теорему о биноме. В 1788 году, начал учиться в гимназии Мартино-Катаринеум, где он преуспел в математике, древнегреческом, латинском, английском языках. В 1792 году, он поступил в Кэролайн-колледж, по завершению получив степень по математике. В 1795 года, Гаусс поступил в Геттингенский университет. Спустя всего шесть месяцев Гаусс вывел математическую формулу, чтобы найти все правильные многоугольники, которые могут быть построены, используя только линейку и компас. В 1807 году, Гаусс принял кафедру астрономии в Геттингене, которую он занимал до конца своей жизни.

Научные достижения

Теория чисел была его любимым математическим занятием. В 1801 году, он опубликовал одну из величайших работ в истории математики – «Disquisitiones Arithmeticae», эта книга написана на латыни. В нем он записал формальные доказательства многих своих ранних открытий, здесь начинается современная теория чисел. Гаусс задокументировал значительные прорывы, такие как закон квадратичной взаимности, его формулировку современной модульной арифметики и конгруэнтность — идею, которая легла в основу его единого подхода к теории чисел. Почитатели таланта ученого, говорили, что Гаусс сделал для теории чисел то же, что Евклид сделал для геометрии. Он также очень глубоко изучал теорию потенциала и решению уравнений с частными производными — эти уравнения имеют многочисленные приложения в физике, включая электромагнетизм и гравитацию. В 1809 году он опубликовал важную двухтомную работу по движению небесных тел — Теорию движения небесных тел. В 1821 году, он изобрел гелиотроп это зеркало, которое отражает солнечные лучи на очень большие расстояния. Гелиотропы использовались в геодезических работах в Германии более 150 лет. Он стал участвовать в геодезических работах для составления карт и увидел важность записи удаленных позиций с большой точностью. В 1832 году при содействии Вебера, Гаусс провел эксперименты, результаты которых позволили ему определить магнитное поле Земли, используя единицы миллиметров, граммов и секунд. Другими словами, он показал, что магнитное поле Земли можно определить, используя чисто механические измерения — массу, длину и время. В 1833 году Гаусс и Вебер изобрели одну из первых в мире телеграфных систем. Они также изобрели двоичный алфавитный код, обеспечивающий связь между зданием Вебера и астрономической обсерваторией Гаусса на расстоянии около 1,5 миль. К 1835 году их телеграфные линии были проложены рядом с первой железной дорогой Германии.
Гаусс использовал свой огромный математический арсенал для анализа поведения электрических и магнитных полей, он сформулировал два закона: Закон Гаусса, который связывает электрическое поле с распределением электрических зарядов, вызывающих его. Закон Гаусса о магнетизме, который гласит, что магнитные монополи не существуют.

Он открыл теорему Egregium, связывающую кривизну поверхности с расстояниями и углами.

Семья и последние годы

Гаусс терпеть не мог путешествовать и покинул Геттинген только один раз в 48 лет — чтобы поехать на конференцию в Берлин. Он был увлечен литературой, его библиотека, насчитывала 6000 книг, написанных на разных языках. В 1805 году, он женился на Джоанне Остхофф, у них было трое детей. К сожалению, жена Гаусса Иоганна умерла в октябре 1809 года. В 1810 году Гаусс женился на Йоханне Вильгельмине, у них также было трое детей. Карл Фридрих Гаусс мирно скончался во сне в Геттингене 23 февраля 1855 года. Он был похоронен без мозга на Геттингенском кладбище Альбанифридхоф, недалеко от университета. Его мозг был сохранен и хранится в физиологическом отделении Геттингена. Гаусс так гордился своим молодым достижением в виде семиугольника, что он попросил вырезать фигуру на его надгробии. Его желание не было выполнено — каменщик сказал, что будет слишком трудно вырезать семиугольник, который не напоминает круг.

www.istmira.com

Карл Фридрих Гаус – Уикипедия

Тази статия е за германския математик и физик. За мерната единица вижте Гаус (единица).

---

Карл Фридрих Гаус Carl Friedrich Gauss
германски учен
Фрагмент от картина на Gottlieb Biermann, 1887
Роден
Починал
Погребан	Гьотинген, Германия
Националност	Германия
Религия	Лутеранство
Образование	Гьотингенски университет
Научна дейност
Област	Математика, физика, астрономия, геодезия
Образование	Брауншвайгски технически университет, Гьотингенски университет
Работил в	Гьотингенски университет
Видни студенти	Фридрих Вилхелм Бесел, Кристоф Гудерман, Рихард Дедекинд, Йохан Енке, Бернхард Риман
Известен с	Метод на най-малките квадрати, Гаусов интеграл, Гаусова функция, Теорема на Гаус — Остроградски и много други
Семейство
Съпруга	Йохана Елизабет Розина Остхоф (1780 – 1809)
Деца	Йозеф Гаус (1806 – 1873) Мина Евалд (1808 – 1840) Луис Гаус (1809 – 1810)
Подпис
Карл Фридрих Гаус в Общомедия

Йохан Карл Фридрих Гаус (на немски: 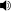 Johann Carl Friedrich Gauß) е германски математик и физик със значителен принос в различни области като теория на числата, статистика, математически анализ, диференциална геометрия, геодезия, геофизика, електростатика, астрономия и оптика.

Понякога наричан Princeps mathematicorum^[1] („Принц на математиците“) и „най-великият математик след Античността“, Гаус има забележителен принос към много области на математиката и природните науки и се нарежда сред най-влиятелните математици в историята.^[2] Той е автор на определението за математиката като „царица на науките“.^[3]

Произход и младежки години[редактиране | редактиране на кода]

Домът, в който се е родил Гаус (не е запазен)

Гаус е роден на 30 април 1777 г. в Брауншвайг в херцогството Брауншвайг, днес част от Долна Саксония, Германия, като единствен син на бедно семейство.^[4] Баща му работи като градинар, зидар, помощник на търговец, както и касиер на застрахователно дружество. Кръстен е и получава първо причастие в църква, разположена близо до училището, което посещава като дете.^[5]

Още от ранна възраст Гаус проявява математически способности, с което привлича вниманието на херцог Карл Вилхелм Фердинанд.^[6] Той поема разноските по обучението му в Каролинския колеж (днес Брауншвайгски технически университет), където Гаус учи от 1792 до 1795 г., както и в Гьотингенския университет, който той посещава от 1795 до 1798 г. Това става с помощта на учителя на Гаус Мартин Бартелс, който по стечение на обстоятелствата по-късно е учител и на Лобачевски.

Първия си значим успех Карл Фридрих Гаус постига през 1796 г., когато демонстрира, че всеки правилен многоъгълник с брой на страните, равен на някое число на Ферма, може да бъде построен с линийка и пергел. Това е важно откритие в основен раздел на математиката, възникнал още през Древността, и то изиграва решаваща роля за насочването на Гаус към математиката, вместо към филологията.

През същата година Гаус въвежда използването на модулна артиметика, която силно опростява преобразуванията в теорията на числата. По същото време доказва квадратичния закон за реципрочност, който дава възможност за определяне на решимостта на всяко квадратно уравнение в дадена модулна аритметика, както и закона за разпределението на простите числа. Той установява също, че всяко цяло положително число може да се представи като сбор от най-много три триъгълни числа. През октомври публикува резултатите си за броя на решенията на полиномни уравнения с коефициенти в крайни полета.

Семейство[редактиране | редактиране на кода]

Дъщерята на Гаус Терезе (1816 – 1864)

През ноември 1804 година Гаус се сгодява за Йоана Елизабет Розина Остхоф от Брауншвайг и се жени за нея на 9 октомври 1805 г. През 1806 г. се ражда първото им дете, Йозеф. След това семейството се премества в Гьотинген. Там първо се ражда дъщеря им Вилхелмина, а през 1809 година – синът им Луис. На 11 октомври 1809 година първата жена на Гаус, Йоана, умира като следствие от усложнения при раждането. На 1 март 1810 г. умира и едва шестмесечното момченце Луис. Като следствие от тези събития Гаус изпада в депресия. На 4 август 1810 година се жени за Фредерика Вилхелмина Валдек, която е дъщеря на учения в областта на правото Йохан Петер Валдек. Тя е била и най-добрата приятелка на първата жена на Гаус. От нея той има три деца: двама сина, които заминават съответно през 1830 и 1837 година за Америка и се занимават успешно с търговия. Най-малката му дъщеря, Терезе, води домакинството при баща си след смъртта на втората му съпруга до неговата смърт.

Гаус е бил член на лутеранската протестантска църква Свети Албан в Гьотинген.^[7]

Зрели години[редактиране | редактиране на кода]

След внезапната смърт на херцога на Брауншвайг след битка при Йена и Ауерщед през ноември 1807 г. Гаус става професор в Гьотингенския университет и директор на местната астрономическа обсерватория, и като такъв работи до края на дните си. Налага му се да обучава, макар че няма склонност към това. Много от неговите студенти по това време стават известни математици, като Рихард Дедекинд и Бернхард Риман. Отклонява всички предложения за работа в Берлинската академия на науките. През 1838 г. той получава Медал-Копли. През 1845 г. той става таен дворцов съветник, а през 1846 г. става за трети път декан на философския факултет. През 1849 г. празнува своя златен докторски юбилей и става почетен гражданин на Брауншвайг и Гьотинген. През 1852 г. започва своята последна научна работа, а именно, повторение на опитите с махалото на Фуко за доказване на въртенето на Земята.

Гаус се интересува от музика, посещава концерти и пее. Няма данни да свири на музикален инструмент. Събира цифрови и статистически данни от всякакъв вид и прави списък например за очакванията за продължителността на живота на известни хора в дни. Занимава се със спекулации на пазара с акции. След смъртта си оставя значително състояние от около 170 000 талера по време, когато заплатата на професор е 1000 талера годишно. Това са основно ценни книжа, главно от железниците. Във връзка с това са намерени негови критични изказвания за политиката и свързаните с нея банки във връзка с това, че придобити от него акции на железницата в Хесен-Дармщат са загубили драстично от стойността си поради информация, че ще бъде национализирана.

Последните години от живота си страда от сърдечна недостатъчност и безсъние. През юни 1854 година заедно със своята дъщеря Тереза, пътувайки за строителството на железница от Хановер за Гьотинген, претърпява нещастен случай, при който изплашените от влака коне обръщат каретата и е тежко наранен кочияшът. Гаус и дъщеря му остават невредими. След като участва в освещаването на железницата по-късно, поради заболяване той остава все по-често в дома си. Умира на 23 февруари 1855 г. сутринта в дома си в Гьотинген в креслото си. На паметната му плоча е изобразен по негова молба правилен 17-оъгълник.

В математиката[редактиране | редактиране на кода]

Гаус през 1828 г.

Основните му приноси в математиката са в областите висша алгебра, теория на числата, теория на редовете, диференциална геометрия и неевклидова геометрия. Гаус е освен това един от хората с най-голям принос в областта на теория на грешките.

Гаус започва научната си дейност през 1791 г. с изследвания върху средното аритметично, средното геометрично, върху разпределението на простите числа. През 1792 г. се заема с основите на геометрията. През 1794 г. открива метода на най-малките квадрати. Първата си научна работа публикува през 1796 г. Тя съдържа прочутото доказателство, че правилен n-ъгълник може да се построи с линийка и пергел, когато n е просто число на Ферма. Особено много време Гаус посвещава на правилния 17-оъгълник. Не случайно той пожелава на паметника му да бъде изобразен правилен 17-оъгълник. През 1799 г. дава първото строго доказателство на основната теорема на алгебрата. Първото голямо негово съчинение са прочутите „Disquisitiones arithmeticae“ („Аритметични изследвания“), което съдържа теорията на квадратичните конгруенции и доказателство на квадратичния закон за реципрочност – „theorema aureum“ („златната теорема“), както и теорията за деленето на окръжността. През 1812 г. той публикува първото системно изследване върху сходимостта на хипергеометричния ред. През 1825 г. излизат от печат работите му върху биквадратичните остатъци. През 1832 г. Гаус публикува геометричното представяне на комплексните числа и нова теория на простите числа. Най-забележителните му научни постижения са създаването на теорията на повърхнините и „theorema egregium“ („превъзходната теорема“).

За много резултати на Гаус математиците научават от дневника и писмата му. Забележително е, че още през 1816 г. той владее основите на неевклидовата геометрия, но не публикува нищо на тази тема, за да избегне очакваните конфликти. Не публикува и други важни свои резултати поради строгите си научни критерии. Голям брой трудове и записки остават недоразвити от него. Част от тях са довършени десетки години след смъртта му.

Освен това той открива бърз и лесен начин за пресмятане на някои суми: ако имаме n брой последователни естествени числа, първото от които е a, а последното – b, то тогава сборът им е:

• ако n = k*2 (четно число), сумата =n2×(a+b){\displaystyle ={n \over 2}\times {({a}+{b})}}. Например сборът на числата от 5 до 20 = 16/2*(5+20) = 8*25 = 200. Ето защо се получава така:

5+6+7+8+…+17+18+19+20. Можем да забележим, че сборът на крайните числа е 5+20=25. Следващите числа – 6 и 19, също сборът им е 6+19=25. За следващите числа важи същото. Следователно можем да разделим числата от 5 до 20 на 8 групи (16 числа делено 2 числа в група) със сбор на всяка група 25. Имаме 8 групи по 25, Следователно сборът на тези числа е 8*25 = 200. От тук извеждаме формулата n/2*(a+b).

• ако n = k*2+1 (нечетно число), сумата

=n−12×(a+(b−1))+b{\displaystyle ={n-1 \over 2}\times {({a}+({b}-{1}))}+b}. Например сборът на числата от 5 до 21 е равен на 17−12×(5+(21−1))+21=8×25+21=200+21=221{\displaystyle {17-1 \over 2}\times {({5}+({21}-{1}))}+21={8}\times {25}+21=200+21=221}. Можем да проверим верността: 5+6+7+..+20+21 = (5+6+..+19+20)+21 = 200+21 = 221.

Въведение в елиптичните функции[редактиране | редактиране на кода]

Като 19-годишен Гаус през 1796 г. при наблюдение на дължината на дъгата върху една лемниската въвежда с лемнискатната синусна функция исторически първата елиптична функция. Той не публикува нищо от своите записки. Фактическото развитие на теорията на елиптичните функции се извършва от Нилс Абел (1827 г.) и Карл Якоби.

Неевклидова геометрия[редактиране | редактиране на кода]

Трима големи математици се занимават активно с неевклидовата геометрия: това са Гаус, Янош Бояй и Николай Лобачевски. Когато бащата на Янош Фаркаш Бояй моли своя приятел Гаус за мнение по труда на Янош, Гаус високо го оценява, но оспорва първенството на научните му резултати. Самият Гаус бил достигнал до тези резултати още в началото на века, но така и не се осмелил да ги публикува, „защото повечето хора няма да разберат за какво става дума“,^[8] Отговорът на Гаус предизвиква силно разочарование и гняв у Бояй. Известно време той дори вярва, че великият математик си приписва заслугите му, и това личи от неговата кореспонденция и архиви. Паралелно и Николай Лобачевски разработва идеите на неевклидовата геометрия. Първите му публикации се посрещат с насмешка от математици като Михаил Остроградски. По-късно, през 1841 година и Гаус се запознава с труда на Лобачевски, издаден на немски език. В писма до приятел Гаус изразява признание за разработката на Лобачевски. Той препоръчва избирането му за чуждестранен член кореспондент на Академията на науките в Гьотинген като един от най-добрите математици на руската държава. Започва изучаването на руски език, за да се запознае с неговата работа по-подробно. Приоритетът на публикациите на Лобачевски обаче е безспорен и затова неевклидовата геометрия носи и неговото име.

В астрономията[редактиране | редактиране на кода]

Причината за започване на изследвания от страна на Гаус е откриването на планетата Церера от Джузепе Пиаци на 1 януари 1801 година, малко след което тя отново е загубена. Резултат от изследванията на Гаус в тази област са пресмятането на орбитата на планетата-астероид Церера. Гаус успява да направи това посредством помощта на индиректен метод за определяне на орбитата и пресмятане на уравненията на базата на метода на най-малките квадрати. Хайнрих Вилхелм Олберс и Франц Ксавер фон Цах наблюдават независимо един от друг новото положение на планетата една година по-късно. Гаус се занимава и с орбитата на астероида 2 Палада, но не намира решението. Неговият опит в изследванията на орбитите на небесните тела завършват с публикуването на съчинението „Теория на движението на небесните тела“.

Проблемът с повторното откриване на планетата е в това, че нито мястото, нито част от орбитата, нито разстоянието до планетата са известни. Известна е само посоката на наблюдение. Това води до търсенето на една елипса, единият фокус на която е Слънцето. Освен това е известно, че дъгите на орбитата на Церера преминават съгласно втория закон на Кеплер.

Тези дейности правят Гаус известен в Европа и водят между другото до поканата му от страна на Академията в Санкт Петербург, чийто член той става през 1802 година.

Геодезия[редактиране | редактиране на кода]

Занимава се и с практическа геодезия и получава първите си познания между 1797 и 1801 година, когато е съветник при френския генерал-квартирмайстер при неговите измервания на територията на Херцогство Вестфалия. През 1816 година на неговия бивш ученик Хайнрих Шумахер е възложено от краля на Дания извършването на едно измерване на дължини и широчини в Дания. Във връзка с това Гаус получава между 1820 и 1826 година ръководството по измерването на географските дължини и широчини в кралство Хановер област. При това отчасти му помага и синът му Йозеф, който е действащ артилерийски офицер в армията на Хановер. Използвайки открития от него метод на най-малките квадрати и решаването на системи от линейни уравнения, той успява да постигне значително повишаване на точността на измерване и създава висшата геодезия. За практическите си измервания той създава като измервателен инструмент хелиотроп, инструмент, който използва чрез огледало светлината на слънцето.

През тези години той се занимава, вследствие на интереса си, предизвикан от геодезията и теорията за картите, с теорията за диференциалната геометрия на повърхнините, въвежда гаусовото изкривяване и доказва своята Theorema Egregium. Именно резултатите на Гаус вдъхновяват Бернхард Риман за създадената от него класическа дисертация за Римановата геометрия.

Към края на живота си проявява интерес и към физически въпроси. Заедно с Вилхелм Вебер създават системата на електромагнитните единици. Конструира и първия в Германия електромагнитен телеграф. Работите му в областта на физиката се отнасят към теорията на потенциала, учението за капилярността и теоретичната оптика.

Универсалните способности на Карл Фридрих Гаус му позволяват да остави следи в почти всички основни дялове на чистата и приложната математика. Гьотингенската академия на науките издава (след 1908 г.) единадесет тома негови съчинения. При това всичко, написано от Гаус, е подчинено на девиза му: „Не много, но зряло.“

Магнетизъм, електричество и телеграфия[редактиране | редактиране на кода]

Гаус и Вебер. Скулптура в Гьотинген.

Заедно с Вилхелм Вебер от 1831 година работи в областта на магнетизма. Заедно с Вебер създава магнитометъра и свързва през 1833 година своята обсерватория с института по физика. В двора на обсерваторията е построена сграда, изработена изцяло от немагнитни материали с цел извършване на магнитни измервания. При това те успяват да обменят определени съобщения между две точки. Това става чрез управлявана по електромагнитен път намагнитена компасна игла. Това представлява и първата телеграфна връзка в света. Използва се подобие на морзовата азбука.

Заедно с Вебер, той разработва системата за измерване сантиметър-грам-секунда, която е определена за основа при електротехническите измервания на международен конгрес в Париж през 1881 година. Тази система и сега се използва основно за изчисления във физиката. Той организира също така създаването на една разположена в целия свят мрежа от измервателни станции в така наречено магнитно обединение (немски:Magnetischer Verein), което се занимава с измервания на земното магнитно поле. По-късно тези измервания са обобщени и анализирани.

Въз основа на отношенията на Гаус с Александър фон Хумболт и във връзка с тези измервания, през 2005 година в Германия излиза романът на Даниел Келман „Измерването на света“, който става бестселър. През 2012 година е заснет и филмът („Die Vermessung der Welt“).

При своите експерименти за електричеството Гаус открива през 1833 г. преди Густав Кирхоф (1845 г.) законите на Кирхоф за токовите кръгове.^[9]

Гаус работи в много области, но публикува своите резултати едва след като е напълно е убеден, че, по негово мнение, една теория е напълно завършена. Вследствие на това, той често обръща внимание на свои колеги, че даден резултат вече е доказан, но не го е представил поради незавършеност на теорията или недостатъчна сигурност в разработките си. Това му е спестявало време за основните разработки, като не е губил време за странични теми в този момент.

Той говори добре английски и френски и заедно с класическите древни езици чете модерните европейски езици като испански, италиански, датски, шведски и учи по-късно руски, за да чете трудове на Лобачевски. В тази връзка през 1839 г. 62-годишният Гаус в писмо до Петербургската академия моли да му се изпратят руски списания и книги, включително „Капитанската дъщеря“ на Пушкин. През 1842 г. Лобачевски е избран за чуждестранен член-кореспондент на Гьотингенското кралско дружество по предложение на Гаус. Също така започва да се занимава със санскрит. През по-късните години от живота си започва да чете все повече художествена литература. Любими автори са му Уолтър Скот и Жан Паул.

Когато бил малък, учителят, за да си освободи малко време, поставил задача на децата да съберат числата от 1 до 100. Той започнал да пише на дъската всички числа, но през това време Гаус притичал при учителя и му казал отговора, който самият учител не бил открил. Накрая след събирания се оказало, че единственият верен отговор е на Гаус. Така възниква немного известният „Метод на Гаус“. Той пресметнал сумата от 1 до 100 така:

S=1+2+3+…+98+99+100{\displaystyle S=1+2+3+…+98+99+100}.

Забелязал, че всеки две числа, които са на равни разстояния от двата края, имат равни суми:

1+100=99+2=3+98{\displaystyle 1+100=99+2=3+98} и т.н.

Групирал стоте събираеми в 50 групи по две и получил

S=(1+100)+(2+99)+(3+98)+…+(50+51)=100.(100+1)2=50.101=5050{\displaystyle S=(1+100)+(2+99)+(3+98)+…+(50+51)={100.(100+1) \over 2}=50.101=5050}

Виж повече в раздел „Научни изследвания и открития“.

След неговата смърт е взет неговият главен мозък за изследвания. Той е изследван с различни методи многократно, последно през 1998 година. При това не са открити особености, които да обясняват неговите изключителни математически способности.^[10] Той се намира отделно, консервиран във формалин в медицинския факултет на университета в Гьотинген.

През есента на 2013 година в университета е открито, че има объркване и всъщност два препарата с мозъка на Гаус и на лекаря Конрад Фукс са подменени, и в надписаната с неговото име стъкленица не се съдържа истинския препарат. С това правените до момента изследвания се оказват напълно неверни.

Отляво надясно: повърхност с отрицателна Гаусова кривина (хиперболоид), повърхност с нулева Гаусова кривина (цилиндър), и повърхност с положителна Гаусова кривина (сфера).

Редица методи в математиката носят изцяло или частично името на Гаус:

• Гаусов метод за елиминация, използван за решаване на система линейни уравнения.
• Гаусов интеграл на грешките: интеграл за нормално разпределение.
• Интегрална теорема на Гаус-Остроградски, представляваща резултат от векторния анализ, който представя зависимостта между дивергенцията на едно векторно поле и потока на полето през затворена повърхност. Теоремата следва от един специален случай на теоремата на Стокс, която от своя страна обобщава основния израз в интегралното и диференциално смятане.
• Гаусов закон за електростатиката, съгласно който електрическият поток през една затворена повърхност е пропорционален на затворения в повърхността електрически товар. Представлява практическо приложение на интегралната теорема на Гаус-Остроградски.
• Гаусовата система единици, наричана още система сантиметър-грам-секунда
• Гаусова кривина, представляваща основно понятие в диференциалната геометрия.
• Гаусова квадратура представлява числено интегриране за пресмятане на квадратури.
• Гаусово разпределение или Нормално разпределение в теорията на вероятностите и статистиката е закон за разпределението на непрекъсната случайна величина. Графиката на функцията е камбановидна крива, наречена Гаусова крива.
• Гаусова числова равнина е равнина на комплексните числа или комплексна равнина.
• Функция скобка, или Гаусови скоби, по дефиниция означаващи за едно реално число, че е най-голямото цяло число, което е по-малко или равно на x.
• Теорема на Гаус-Боне в диференциалната геометрия.
• Метод на Гаус-Жордан, представляващ развитие на Гаусовия метод за елиминация.
• Метод на Гаус-Зайдел за решаване на линейни уравнения.
• Алгоритъм на Гаус-Нютон, който е модификация на метода на Нютон, разработена от Карл Фридрих Гаус за решаване на нелинейни задачи за най-малките квадрати.
• Гаусово диференциално уравнение или хипергеометрично диференциално уравнение, представляващо обикновено линейно диференциално уравнение от втори ред.
• Проекция на Гаус-Крюгер: Представлява наклонена цилиндрична проекция, използвана в топографските карти. При нея меридианните ивици, при които контурните меридиани сключват на върха ъгъл 6°, се изобразяват върху околната повърхнина на цилиндър, която от своя страна се развива върху равнината.
• Гаусов принцип на най-малката принуда или Принцип на Гаус е предложен от Гаус през 1829 г. в разработката му „За един нов общ закон на механиката“.
• Гаусова формула на трапеца за пресмятане на повърхнини чрез разлагането на триъгълници и трапеци.
• На името на Гаус са наречени формули, създадени за пресмятане на Великден, Пасха, както и дните на седмицата. С промяната на календара се променят и формулите.
• Гаусово оръдие: Нарича се на името на Гаус, който е поставил основите на математическата теория на електромагнетизма. По своя принцип на работа е подобен на линейните двигатели.

1. ↑ Zeidler, Eberhard. Oxford User’s Guide to Mathematics. Oxford, UK, Oxford University Press, 2004. ISBN 0198507631. p. 1188. (на английски)
2. ↑ Dunnington, G. Waldo. The Sesquicentennial of the Birth of Gauss. // Scientific Monthly XXIV (402 – 414). May 1927. (на английски)
3. ↑ Waltershausen, W Sartorius von. Gauss zum gedächtniss. Leipzig, S. Hirzel, 1856. (на немски)
4. ↑ Wichita State University .
5. ↑ Chambless .
6. ↑ Dunnington 2000.
7. ↑ Guy Waldo Dunnington (1955). Carl Friedrich Gauss, Titan of Science: A Study of His Life and Work.
8. ↑ „Лексикон Математика“, Георги Симитчиев, Георги Чобанов, Иван Чобанов, ИК Абагар, С., 1995, ISBN 954-584-146-Х
9. ↑ Dunnington: Gauss – Titan of Science. American Mathematical Society, S. 161.
10. ↑ Wolfgang Hänicke, Jens Frahm und Axel D. Wittmann: Magnetresonanz-Tomografie des Gehirns von Carl Friedrich Gauß. In: MPI News 5. Heft 12 (1999). Архив на оригинала от 2011-07-19 в Wayback Machine.

Цитирани източници

bg.wikipedia.org