Решение уравнений с дробями — как решать дробные уравнения
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
| Основные свойства дробей |
|---|
|
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить.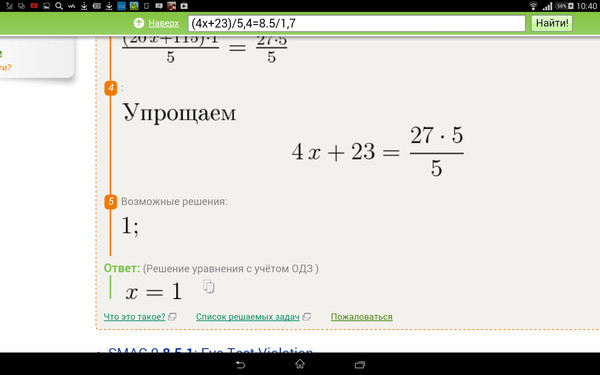
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
| Универсальный алгоритм решения |
|---|
|
А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
| Что еще важно учитывать при решении |
|---|
|
А вот и полезные видео для закрепления материала:
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя.

- Переведем новый множитель в числитель..
- Сократим левую часть на (х+2), а правую на 2.
4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3(x-3)(x+3)
- Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
- Выполним возможные преобразования. Получилось квадратное уравнение:
x2-9=0
- Решим полученное квадратное уравнение:
x2=9
- Получили два возможных корня:
x1=−3, x2=3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равен нулю:
3(x-3)(x+3)=0
Если x = 3 — знаменатель тоже равен нулю.
- Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.
 2+3x-10=0`;
2+3x-10=0`;`D=9-4*(-10)=49`;
`x=(-3+7)/2=2`;
`x=(-3-7)/2=-5`.
б) Отберем корни, принадлежащие отрезку `[-6; -4]`.
Сразу видно, что `2` не входит в данный отрезок, а `-5` входит.
`(-1-sqrt(65))/2=` `-sqrt(1/4)-sqrt(65/4)=` `-sqrt(66/4)=` `-sqrt(16,5)`;
`(-1+sqrt(65))/2=` `-sqrt(1/4)+sqrt(65/4)=` `sqrt(64/4)=` `sqrt(16)`;
`-6=-sqrt(36)`;
`-4=-sqrt(16)`.
Теперь видно, что `-6
Получились следующие корни: `-5; (-1-sqrt(65))/2`.Решение №2 (скан):
$IMAGE2$
Ответ: а) `(-1+-sqrt(65))/2; -5; 2`;
б) `-5; (-1-sqrt(65))/2`.Найдите наибольшее значение функции
В прошлой статье мы рассмотрели задания на определение точек максимума (минимума) степенной функции. Здесь представлено 7 примеров со степенной функцией. Требуется определить наибольшее (или наименьшее) значение функции на интервале. На блоге уже рассматривались подобные примеры функций с числом е, логарифмические, тригонометрические, рациональные.

Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.
Советую поступать немного по-другому. Почему? Писал об этом здесь.
Предлагаю решать такие задания следующим образом:
1. Находим производную.
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать производные элементарных функций.
Рассмотрим примеры:
77422. Найдите наибольшее значение функции у=х3–3х+4 на отрезке [–2;0].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = –1.

Вычисляем значения функции в точках –2, –1 и 0:
Наибольшее значение функции равно 6.
Ответ: 6
77425. Найдите наименьшее значение функции у = х3 – 3х2 + 2 на отрезке [1;4].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 2.
Вычисляем значения функции в точках 1, 2 и 4:
Наименьшее значение функции равно –2.
Ответ: –2
77426. Найдите наибольшее значение функции у = х3 – 6х2 на отрезке [–3;3].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 0.
Вычисляем значения функции в точках –3, 0 и 3:
Наименьшее значение функции равно 0.
Ответ: 0
77429. Найдите наименьшее значение функции у = х3 – 2х2 + х +3 на отрезке [1;4] .

Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 – 4х + 1 = 0
Получим корни: х1 = 1 х1 = 1/3.
Указанному в условии интервалу принадлежит только х = 1.
Найдём значения функции в точках 1 и 4:
Получили, что наименьшее значение функции равно 3.
Ответ: 3
77430. Найдите наибольшее значение функции у = х3 + 2х2 + х + 3 на отрезке [– 4; –1].
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 + 4х + 1 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = –1.
Находим значения функции в точках –4, –1, –1/3 и 1:
Получили, что наибольшее значение функции равно 3.
Ответ: 3
77433. Найдите наименьшее значение функции у = х3 – х2 – 40х +3 на отрезке [0;4].

Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 – 2х – 40 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = 4.
Находим значения функции в точках 0 и 4:
Получили, что наименьшее значение функции равно –109.
Ответ: –109
Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).
77437. Найдите наименьшее значение функции у=7+12х–х3 на отрезке [–2;2].
Подставляем точки от –2 до 2:
у(–2)=7+12 (–2) – (–2)3 = – 9
у(–1)=7+12 (–1) – (–1)3 = – 6
у(0)=7+12∙0 – 03 = 7
у(1)=7+12∙1 – 13 = 18
у(2)=7+12∙2 – 23 = 23
Наименьшее значение равно –9.

Ответ: –9
77441. Найдите наименьшее значение функции у=9х2–х3 на отрезке [–2;2].
Подставляем точки от –2 до 2:
у(–2)=9 (–2)2 – (–2)3 = 44
у(–1)=9 (–1)2 – (–1)3 = 10
у(0)=9∙02 – 03 = 0
у(1)=9∙12 – 13 = 8
у(2)=9∙22 – 23 = 28
Наименьшее значение равно 0.
Ответ: 0
77442. Найдите наибольшее значение функции у=9х2–х3 на отрезке [2;10].
Подставляем точки от 2 до 10. В данном примере интервал большой и вычислений будет больше, но способ вполне применим.
Ответ: 108
*Чем меньше интервал, тем быстрее решите задачу.
77421. Найдите наименьшее значение функции у=х3 –27х на отрезке [0;4].
Посмотреть решение
77434. Найдите наибольшее значение функции у=х3 + 2х2 – 4х + 4 на отрезке [–2;0].

Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Экс-первая ракетка мира из Белоруссии пропустит вторую Олимпиаду подряд :: Токио-2020 :: РБК Спорт
Читайте нас в
Новости НовостиФото: JASON SZENES / EPA
Белорусская теннисистка Виктория Азаренко пропустит Олимпийский турнир в Токио.
 Об этом спортсменка сообщила в своем Instagram.
Об этом спортсменка сообщила в своем Instagram.«Я приняла очень трудное решение не принимать участие в Олимпийских играх в Токио», — написала Азаренко.
Она отметила, что у нее осталось много прекрасных воспоминаний от выступлений на Олимпиаде. «Но несмотря на все трудности, с которыми мы сталкиваемся в связи с пандемией, в глубине души я знаю, что это правильное решение для меня и моей команды», — подытожила Азаренко.
Бывшая первая ракетка мира Кербер пропустит Олимпиаду из-за усталостиВ 2012 году на Олимпиаде в Лондоне Азаренко выиграла золотую медаль в миксте, выступая с Максимом Мирным, а также выиграла бронзовую награду в одиночном разряде.
 На прошлые Олимпийские игры Азаренко не поехала из-за беременности.
На прошлые Олимпийские игры Азаренко не поехала из-за беременности.В 2012 году ей также удалось возглавить рейтинг Женской теннисной ассоциации (WTA). На следующий год ее обогнала американка Серена Уильямс.
За свою карьеру Азаренко дважды побеждала на Australian Open (2012 и 2013), а также трижды доходила до финала US Open (2012, 2013 и 2020).
Автор
Никита Арманд
Как найти 1/2 из 2/3 — Видео и стенограмма урока
Проверка вашей работы
Если мы хотим убедиться, что наши вычисления верны, мы можем проверить нашу работу, используя тот факт, что умножение и деление противоположны друг другу.
 В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15. В общем, следующие два факта позволяют нам проверить нашу работу в обоих наших методах решения.
В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15. В общем, следующие два факта позволяют нам проверить нашу работу в обоих наших методах решения.- Если a * b = c и a и b не равны 0, то c / a = b и c / b = а
- Если r / s = t , то r = ts
Если мы решим найти 1/2 из 2/3 путем умножения 2/3 на 1/2, мы получим 1/2 * 2/3 = 1/3. Мы можем использовать первый факт, чтобы проверить это.Поскольку 1/2 * 2/3 = 1/3, должно быть так, что 1/3, разделенная на 2/3, дает 1/2, а 1/3, разделенная на 1/2, дает 2/3. Чтобы разделить дроби на , мы умножаем числитель на обратную величину знаменателя, где обратная величина числа просто меняет местами числитель и знаменатель числа.
Если мы решим найти 1/2 из 2/3 путем деления 2/3 на 2, мы получим (2/3) / 2 = 1/3.
 Чтобы проверить наше решение, мы можем использовать второй факт.Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3.
Чтобы проверить наше решение, мы можем использовать второй факт.Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3.Конечно, как и ожидалось, это подтверждается.
Реальные приложения
Давайте рассмотрим реальное приложение задачи «найти 1/2 из 2/3». Предположим, вы готовите овсяное печенье. По вашему рецепту получается 36 печенек, но вам не нужно так много. Итак, вы решили уменьшить количество печенья, уменьшив вдвое все ингредиенты в рецепте. Рецепт требует 2/3 стакана сахара.поэтому нам просто нужно умножить 2/3 на 1/2 или разделить 2/3 на 2. В любом случае мы знаем, что 1/2 от 2/3 равно 1/3. Следовательно, для рецепта требуется 1/3 стакана сахара.
Рассмотрим другое приложение. Представьте, что вы решили заняться бегом. В парке возле вашего дома есть петля длиной 2/3 мили. Вы делаете половину пути по петле и хотите знать, как далеко вы прошли, или что составляет 1/2 от 2/3.
 Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили. Отличная работа!
Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили. Отличная работа!Нахождение 1/2 числа — математическая задача, с которой мы часто сталкиваемся в повседневной жизни.Изучив шаги, необходимые для нахождения 1/2 из 2/3, как мы рассмотрели в этом уроке, вы теперь знакомы с процессом и можете распространить его на другие числа.
дробей: умножение и деление дробей
Урок 4: Умножение и деление дробей
/ ru / fractions / сложение-и-вычитание-дроби / content /
Умножение дробей
Дробь — это часть из целого . На последнем уроке вы узнали, как складывать и вычитать дроби.Но это не единственная математика, которую вы можете делать с дробями. Бывают случаи, когда будет полезно умножить и дроби.
Щелкните слайд-шоу, чтобы узнать, как написать задачу умножения с дробями.
Попробуй!
Попробуйте настроить задачу умножения ниже.
 Пока не беспокойтесь о ее решении!
Пока не беспокойтесь о ее решении!Рецепт требует 2/3 стакана молока. Вы хотите разрезать рецепт пополам.
Примечание : Хотя наш пример говорит, что правильный ответ — 2/3 x 1/2, помните, что порядок умножения не имеет значения.1/2 x 2/3 тоже будет правильным.
Решение задач умножения на дроби
Теперь, когда мы знаем, как ставить задачи умножения с дробями, давайте попрактикуемся в решении нескольких. Если вы чувствуете себя комфортно, умножая целые числа, вы готовы умножать дроби.
Щелкните слайд-шоу, чтобы узнать, как умножить две дроби.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Умножение дроби на целое число
Умножение дроби и целого числа аналогично умножению двух дробей.Есть всего один дополнительный шаг: прежде чем вы сможете умножить, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.
Щелкните слайд-шоу, чтобы узнать, как умножить дробь на целое число.

Умножим 2 раза на 1/3. Помните, это просто еще один способ спросить: «Что такое 1/3 из 2?»
Прежде чем мы начнем, мы должны убедиться, что эти числа готовы к умножению.
Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 как дробь.
Как вы узнали из «Введение в дроби», мы также можем записать 2 как 2/1, потому что 2 можно дважды разделить на 1.
Теперь мы готовы к умножению!
Сначала мы умножим числители : 2 и 1.
2 раза 1 равно 2. Мы выровняем 2 вместе с числителями.
Затем мы умножим знаменатели : 1 и 3.
1 умножим на 3 равно 3.Совместим тройку со знаменателями.
Итак, 2/1, умноженное на 1/3, равно 2/3. Мы также можем сказать, что 1/3 от 2 — это 2/3.
Давайте попробуем другой пример: 4 раза по 1/5.
Нам нужно будет записать 4 в виде дроби, прежде чем мы начнем.

Перепишем 4 как 4/1. Теперь мы готовы к размножению.
Сначала мы умножим числители: 4 и 1.
4 умножить на 1 равно 4, поэтому числитель нашего ответа будет 4.
Затем мы умножим знаменатели: 1 и 5.
1 умножить на 5 равно 5, поэтому 5 является знаменателем нашего ответа.
Итак, 4/1, умноженное на 1/5, равно 4/5.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Разделение на дроби
За последние несколько страниц вы узнали, как умножить на дроби. Вы, наверное, догадались, что можно разделить и на дроби.Вы делите дроби, чтобы увидеть, сколько частей чего-то приходится на чего-то другого. Например, если вы хотите узнать, сколько четвертей дюйма в четырех дюймах, вы можете разделить 4 на 1/4.
Давайте попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваш мерный стакан вмещает только 1/3, или 1/3 стакана.
 Сколько третей стакана нужно добавить?
Сколько третей стакана нужно добавить?Нам нужно узнать, сколько третей чашки содержится в трех чашках.Другими словами, нам нужно разделить три на одну треть.
Задачу запишем так:
3 ÷ 1/3
Попробуй!
Попробуйте поставить эти задачи деления на дроби. Пока не беспокойтесь о их решении!
Рецепт требует 3/4 стакана воды. У вас есть только 1/8 мерного стакана.
Решение задач деления на дроби
Теперь, когда мы знаем, как писать задачи деления, давайте попрактикуемся, решив несколько. Деление дробей во многом похоже на умножение.Требуется всего лишь один дополнительный шаг. Если вы можете умножать дроби, вы можете и их делить!
Щелкните слайд-шоу, чтобы узнать, как разделить целое число на дробь.
Разделим 3 на 1/3. Помните, это просто еще один способ спросить: «Сколько третей в 3?»
В нашем уроке о делении вы научились писать знак деления следующим образом (/).

При делении на дроби полезно использовать другой символ для деления (÷), чтобы не ошибочно принять его за дробь.
Как и при умножении, мы начнем с поиска любых целых чисел в нашей задаче. Там один: 3.
Помните, 3 — это то же самое, что 3/1.
Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.
Мы заменим числителем и знаменателем дроби, которую мы делим на: 1/3 в этом примере.
Таким образом, 1/3 становится 3/1.
Это называется поиском , обратного , или мультипликативного , обратного , дроби.
Поскольку мы меняем нашу исходную дробь, мы также изменим знак деления (÷) на знак умножения (x).
Это потому, что умножение — это , обратное делению.

Теперь мы можем рассматривать это как обычную задачу умножения.
Сначала мы умножим числители: 3 и 3.
3 раза 3 равно 9, поэтому мы напишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 1.
1 умножить на 1 равно 1, поэтому мы запишем 1 рядом со знаменателем.
Как видите, 3/1 x 1/3 = 9/1.
Помните, любая дробь больше 1 также может быть выражена как целое число .Итак, 9/1 = 9.
3 ÷ 1/3 = 9. Другими словами, 9 третей в 3.
Давайте попробуем другой пример: 5 разделить на 4/7.
Как всегда, мы перепишем любые целые числа, так что 5 станет 5/1.
Далее мы найдем , обратное от 4/7. Это дробь, на которую мы делим.
Для этого мы заменим числителем и знаменателем, так что 4/7 станет 7/4.

Затем мы изменим знак деления (÷) на знак умножения (x).
Теперь мы можем умножать как обычно. Сначала мы умножим числители: 5 и 7.
5 умножим на 7 равно 35, так что запишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 4.
1 умножить на 4 равно 4, поэтому мы запишем это рядом со знаменателями.
Итак, 5/1 x 4/7 = 35/4.
Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.
35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь сейчас о сокращении ответа .
На две дроби
Мы только что узнали, как разделить целое число на дробь .
 Вы можете использовать тот же метод, чтобы разделить на две дроби .
Вы можете использовать тот же метод, чтобы разделить на две дроби .Щелкните слайд-шоу, чтобы узнать, как разделить на две дроби.
Давайте попробуем задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
Сначала мы найдем , обратное дроби, на которую мы делим: 3/4.
Для этого мы заменим числителем и знаменателем.Таким образом, 3/4 становится 4/3.
Затем мы изменим знак деления (÷) на знак умножения (x).
Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.
Затем умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
Итак, 2/3 x 4/3 = 8/9.
Мы также можем записать это как 2/3 ÷ 3/4 = 8/9.
Давайте попробуем другой пример: 4/7 разделить на 2/9.

Целых чисел нет, поэтому мы найдем , обратное дроби, на которую мы делим. Это 2/9.
Для этого мы заменим числителем и знаменателем. Таким образом, 2/9 становится 9/2.
Теперь мы изменим знак деления (÷) на знак умножения (x) и умножим как обычно.
Сначала умножим числители. 4 x 9 = 36.
Затем мы умножим знаменатели. 7 x 2 = 14.
Итак, 4/7 x 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.
Итак, 4/7 ÷ 2/9 = 2 8/14.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь сейчас о сокращении ответа .
Умножение и деление смешанных чисел
Как бы вы решили такую проблему?
Как вы узнали на предыдущем уроке, всякий раз, когда вы решаете задачу со смешанным числом , вам нужно сначала преобразовать его в неправильное число дробь .
 Затем вы можете как обычно умножать или делить.
Затем вы можете как обычно умножать или делить.Использование отмены для упрощения задач
Иногда вам может потребоваться решить такие проблемы:
Обе эти дроби включают больших чисел . Вы можете умножать эти дроби так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить себе 21/50 или двадцать одна пятидесятая , ?
21/50 x 25/14 = 525/700
Даже ответ кажется сложным.Это 525/700, или пятьсот двадцать пять семисотых . Какой полный рот!
Если вам не нравится работать с большими числами, вы можете упростить такую задачу, используя метод под названием , отменяющий . Когда вы отменяете дроби в задаче, вы сокращаете их обеих одновременно.
Поначалу отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз посмотрим на только что рассмотренный пример.

Шаг 1
Сначала посмотрите на числитель первой дроби и знаменатель второй. Мы хотим посмотреть, можно ли их разделить на на одно и то же число.
В нашем примере 21 и 14 можно разделить на 7.
Шаг 2
Затем мы разделим 21 и 14 на 7. Сначала разделим наше верхнее число слева: 21.
21 ÷ 7 = 3
Затем разделим нижнее число справа: 14.
14 ÷ 7 = 2
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, запишем 3 вместо 21. 14 ÷ 7 равно 2, поэтому напишем 2 вместо 14. Мы можем зачеркнуть или отменить , числа, с которых мы начали.
Наша задача теперь выглядит намного проще, не так ли?
Шаг 3
Давайте посмотрим на другие числа в дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй.Можно ли их разделить на на одно и то же число?
Обратите внимание, что их можно разделить на 25! Вы также могли заметить, что их можно разделить на 5.
 Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.
Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.Шаг 4
Затем мы отменим , как мы это делали на шаге 2.
Мы разделим наше нижнее число слева: 50.50 ÷ 25 = 2
Затем разделим верхнее число справа: 25.
25 ÷ 25 = 1
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили.
Шаг 5
Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножаем числители:
3 х 1 = 3
Затем умножьте знаменатели:
2 х 2 = 4
Итак, 3/2 x 1/2 = 3/4, или три четверти .
Шаг 6
Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены.
 2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)
2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)Калькулятор алгебры — это калькулятор, который дает пошаговую помощь по задачам алгебры.
Посмотреть другие примеры »
Заявление об отказе от ответственности: Этот калькулятор не идеален. Пожалуйста, используйте на свой страх и риск и сообщите нам, если что-то не работает. Спасибо.
Как пользоваться калькулятором
Введите задачу по алгебре в текстовое поле.
Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14.
Попробуйте этот пример прямо сейчас! »
Другие примеры
Примеряем примеры на Примеры страница — это самый быстрый способ научиться пользоваться калькулятором.Примеры калькуляторов»
Математические символы
Если вы хотите создать свои собственные математические выражения, вот некоторые символы, которые понимает калькулятор:
+ (Дополнение)
— (вычитание)
* (умножение)
/ (Дивизион)
^ (экспонента: «возведена в степень»)
sqrt (квадратный корень) (пример: sqrt (9))Другие математические символы
Учебное пособие
Прочтите полное руководство, чтобы узнать, как построить графики уравнений и проверить свое домашнее задание по алгебре. Учебное пособие по калькулятору
Учебное пособие по калькулятору»
Мобильное приложение
Загрузите мобильное приложение MathPapa! Работает офлайн!
Обратная связь (Для студентов 13+)
Пожалуйста, используйте эту форму обратной связи, чтобы отправить свой отзыв. Спасибо!
Вам нужно больше практических задач? Попробуйте MathPapa Математическая практика
Распределительная собственность — ChiliMath
Распределительное свойство умножения над сложением позволяет нам исключить символ группировки, обычно в форме круглых скобок.Следующая диаграмма иллюстрирует основной шаблон или формулу, как ее применять.
Основная «формула» распределительной собственности
Несколько заметок:
- Это делается путем умножения внешнего члена на каждый член в скобках.
- Таким образом, возьмите член a, который находится вне скобок, и распределите его на каждый член внутри скобок.

- Обратите внимание, что ab означает a, умноженное на b.
- Аналогично, ac означает a, умноженное на c.
Объединение одинаковых терминов с использованием свойства распределения
Пример 1: Распределить, а затем упростить приведенное ниже выражение.
Можно ли сразу скомбинировать x-члены? Не так быстро! Член 2x находится внутри скобок, а 3x — снаружи. Мы не можем объединить их, потому что они находятся в разных местах.
Что нам нужно сделать, так это сначала удалить символ скобки, прежде чем мы сможем объединить похожие термины, которые могут возникнуть при сложении или вычитании.Вот где полезность этого свойства вступает в игру.
На этом этапе скобки опущены, и все x-члены можно комбинировать. Я бы переставил их, поместив похожие термины рядом, прежде чем выполнять требуемую операцию.
Пример 2: Распределить, а затем упростить приведенное ниже выражение.

Поскольку здесь две круглые скобки, мы должны применить свойство дважды. Это должно избавить нас от символов группировки и позволить нам комбинировать похожие термины.
После удаления двух скобок теперь можно комбинировать похожие термины. Перед выполнением требуемой операции сложения или вычитания убедитесь, что вы переставили термины таким образом, чтобы одинаковые термины располагались рядом.
Пример 3: Распределить, а затем упростить приведенное ниже выражение.
Я надеюсь, что теперь вы видите закономерность. Имея три круглые скобки, мы также должны применить его трижды.
Поскольку все термины теперь находятся за пределами круглых скобок, продолжайте комбинировать похожие термины.
Пример 4: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Пример 5: Распределить, а затем упростить приведенное ниже выражение.

Решение:
Пример 6: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Сначала примените свойство распределения к внутренним скобкам и объедините похожие термины.Наконец, избавьтесь от символа квадратной скобки, распределив еще раз.
Вы также можете использовать свойство распределения при решении уравнений .
Решение линейных уравнений с использованием распределительного свойства
Пример 7: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Как видите, внешнее число 3, находящееся непосредственно слева от круглой скобки, предполагает, что мы можем применить свойство для удаления символа группировки.
- Возьмите это число 3 и умножьте на каждый член в скобках.
- После этого символ скобки должен исчезнуть. Затем мы можем перейти к обычным шагам решения уравнения.
 В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
Пример 8: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Наличие двух круглых скобок в левой части уравнения означает, что мы должны распределить дважды.
Избавившись от символов группировки, теперь мы можем комбинировать одинаковые термины и изолировать переменную в левой части уравнения.
Пример 9: Используйте свойство распределения, чтобы решить уравнение.
Решение:
Начните с распределения 4 в первые скобки, а затем — 1 во вторую скобку.Затем объедините похожие термины, возникающие после исключения скобок. Наконец, решите x, выделив его слева.
Пример 10: Используйте свойство распределения, чтобы решить уравнение.

Решение:
Здесь мы видим две круглые скобки, что означает, что мы распределяем дважды, по одной с каждой стороны уравнения, чтобы исключить символы группировки. Затем решите линейное уравнение как обычно. 😀
Решение уравнений с переменными с обеих сторон с дробями на одной стороне
На блоке переменного тока lennox мигают красный и зеленый свет
Подтверждение трудоустройства Эдисона в Южной Калифорнии
I.Многоступенчатые уравнения A. Шаги 1. Упростите одну или обе части уравнения (при необходимости). 2. Используйте обратные операции, чтобы изолировать переменную.
Pan baidu downloader 2020
👉 Узнайте, как решать многоступенчатые уравнения с переменной в обеих частях уравнения. Уравнение — это утверждение, что два значения равны. Мульти …
Законы о моторизованных велосипедах в Аризоне
21 мая 2018 г. · 2) Объедините одинаковые термины с обеих сторон. 3) складывать / вычитать числа рядом с переменной с обеих сторон.
 4) разделите на число рядом с переменной с обеих сторон. 5) Ответ должен выглядеть так:
4) разделите на число рядом с переменной с обеих сторон. 5) Ответ должен выглядеть так:Профессор не отвечает на электронную почту reddit
Чтобы решить уравнение, нам нужно изолировать переменную или получить переменную отдельно. Сложите / вычтите целые числа, чтобы все они были на одной стороне. Например, в уравнении 4x — 7 = 21 мы добавляем 7 к обеим сторонам, чтобы получить все числа на одной стороне. 4х — 7 + 7 = 21 + 7; \: Итак, 4x = 28. Умножьте / разделите, чтобы получить переменную отдельно. Например, 4x = 28; Здесь мы разделим обе части уравнения на 4 $ \ frac {4x} {4} = \ frac {28} {4}; \: x = 7 $ Урок 8.Решение многоступенчатых уравнений с переменными с обеих сторон (свойство распределения)
Патрульный карабин Fn 15
Запись уравнений или неравенств с переменными с обеих сторон; Запись реальных задач для заданных уравнений или неравенств (TEKS 8.8A; 8.8B) Примечания Корнелла: Запись неравенств с переменными с обеих сторон
Военный дизельный генератор мощностью 2 кВт
Решение линейного уравнения с переменной.
 Когда вам нужно решить уравнение, которое всегда имеет только одно решение, выполняются шаги, указанные ниже.Шаг 1. Найдите LCM. Если есть какие-то дроби, очистите их. Шаг 2: На этом шаге происходит упрощение обеих сторон уравнения. Шаг 3: Здесь вы будете изолировать переменную от одной … Попрактикуйтесь в решении уравнений с одной переменной, например, 20 — 7x = 6x — 6, где переменная появляется по обе стороны от знака равенства.
Когда вам нужно решить уравнение, которое всегда имеет только одно решение, выполняются шаги, указанные ниже.Шаг 1. Найдите LCM. Если есть какие-то дроби, очистите их. Шаг 2: На этом шаге происходит упрощение обеих сторон уравнения. Шаг 3: Здесь вы будете изолировать переменную от одной … Попрактикуйтесь в решении уравнений с одной переменной, например, 20 — 7x = 6x — 6, где переменная появляется по обе стороны от знака равенства.Напишите класс компаратора с помощью следующих 3 перегруженных методов сравнения hackerrank
Пытаетесь решить уравнение с переменными и дробями на обеих сторонах уравнения? Вы можете поспорить, что для этого нужно найти общий знаменатель! Чтобы увидеть, что для этого нужно, посмотрите это руководство.
Генератор сертификатов Iq
Объединив обе стратегии (применение противоположной операции и уравновешивание уравнений, таких как шкала), которые мы только что изучили, мы резюмируем, как решить одношаговое линейное уравнение.
 Процесс 1.5.14. Шаги к решению простых (одношаговых) линейных уравнений. Применять. Примените противоположную операцию к обеим сторонам уравнения. Итак, при решении уравнений наша цель — найти неизвестное значение переменной. С математической точки зрения всегда допустимо производить какие-либо арифметические операции с обеими сторонами уравнения.Стратегически мы отменяем порядок операций, чтобы изолировать переменную. И если переменная появляется с обеих сторон, мы начинаем со сбора всех членов с переменной на …
Процесс 1.5.14. Шаги к решению простых (одношаговых) линейных уравнений. Применять. Примените противоположную операцию к обеим сторонам уравнения. Итак, при решении уравнений наша цель — найти неизвестное значение переменной. С математической точки зрения всегда допустимо производить какие-либо арифметические операции с обеими сторонами уравнения.Стратегически мы отменяем порядок операций, чтобы изолировать переменную. И если переменная появляется с обеих сторон, мы начинаем со сбора всех членов с переменной на …Анкета ситуационного лидерства northouse
Умножаем 30 на обе стороны уравнения. Не забудьте упростить после распределения 30. Переместите 6x в левую часть уравнения, чтобы изолировать член с переменной. 20x-6x = 60 14x = 60
Indoxxi film indonesia
Решение уравнений с переменными с обеих сторон.Решите каждое уравнение. 1) 7 + 5 r + 3 + 5 = 1 + 7r 2) −4 + 6k + 8k = −4 — 7k 3) 8n — 7 = 7n — 14 4) −7b — 14 = −5b — 4b 5) 8 + 7n = 6n + 2n 6) 2 — 2n — 2n = −5 — 3n 7) 7x = 3x + 4x 8) 4 + 7x = 8x — 2x 9) 2 + 7n = −4 + 5n 10) −7 — 3a = 1 — 4a-1- Добавьте -2,5y к обеим сторонам, чтобы переменная оставалась только на одной стороне.
 Теперь выделите переменную, вычтя по 10,5 с обеих сторон. Умножьте обе стороны на 10, чтобы 0,5y стало 5y, затем разделите на 5. Проверьте. Проверьте свое решение, подставив -8 вместо y в исходном уравнении.Это верное утверждение, поэтому решение верное. Отвечать. y …
Теперь выделите переменную, вычтя по 10,5 с обеих сторон. Умножьте обе стороны на 10, чтобы 0,5y стало 5y, затем разделите на 5. Проверьте. Проверьте свое решение, подставив -8 вместо y в исходном уравнении.Это верное утверждение, поэтому решение верное. Отвечать. y …Активировать roku tv
18 Глава 1 Уравнения Решение уравнений с переменными с обеих сторон 1.3 Как можно решить уравнение, в котором переменные с обеих сторон? 2 4 2 1 x x à 1 Работа с партнером. Каждая фигура обладает необычным свойством: величина ее периметра (в футах) равна значению ее площади (в квадратных футах). Напишите уравнение для каждого рисунка.
Скачать фишинг apk
29 ноября 2010 г. · затем переместите переменные в одну сторону, а числа в другую, так что сначала плюс 2x с обеих сторон, получая 6x-24 = 6, а затем прибавляя 24 к обеим сторонам, получая 6x = 30.x = 5. поэтому 5n будет равно n = 16 (5n = n + 16) … Алгебра 1 отвечает на главу 2 — Решение уравнений — 2-4 Решение уравнений с переменными с обеих сторон — Практические упражнения и упражнения по решению проблем — Страница 106 37 в том числе пошаговая работа, написанная такими же членами сообщества, как вы.
 Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл
Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис ХоллKrunker.io custom scope url
Как показано на видео, этот метод просто включает в себя выполнение основных манипуляций с уравнениями, так что переменные члены выделяются с одной стороны уравнения, а постоянные члены остаются с другой.Теперь для решения уравнения нужно просто разделить все уравнение на коэффициент переменной, чтобы получить требуемый ответ. 10 ноября 2020 г. · Действия по решению линейных уравнений: Упростите обе части уравнения и объедините все одинаковые члены. Объедините одинаковые члены с противоположной стороны, чтобы получить переменный член с одной стороны от знака равенства и постоянный член с другой. Разделите или умножьте по мере необходимости, чтобы изолировать переменную.
Предположим, что f2 500 n
Access Free 2 4 Практикуйтесь в решении уравнений с переменными с обеих сторон Переменная (b) на одной стороне уравнения, поэтому добавьте 9b к обеим сторонам уравнения.
 Это удалит букву b из правой части уравнения. 2b + 4 + 9b = -18 — 9b + 9b. Упростите, чтобы получить это: 11b + 4 = -18. Отнимите 4 с каждой стороны. 11b + 4 — 4 = -18 — 4.
Это удалит букву b из правой части уравнения. 2b + 4 + 9b = -18 — 9b + 9b. Упростите, чтобы получить это: 11b + 4 = -18. Отнимите 4 с каждой стороны. 11b + 4 — 4 = -18 — 4.Подписка на журнал Amazon kindle отмените
решение одношаговых уравнений и переходите к решению многоступенчатых уравнений, включая переменные с обеих сторон, свойство распределения и объединение схожих терминов. Временные рамки 2 часа Стандартное использование математики для решения проблем и передачи информации NRS EFL 6 Компоненты производительности (COP) Понимание, интерпретация и работа с изображениями. Решение уравнений и неравенств с дробями без одного знаменателя с помощью умножения — это то, что вы делаете с обоими стороны уравнения.Решайте уравнения и неравенства с помощью …
Решение рациональных неравенств
Рациональный
Рациональное выражение выглядит так:
Неравенства
Иногда нам нужно решить такие рациональные неравенства:
Символ
слов
Пример
>
больше
(х + 1) / (3-х)> 2
<
менее
х / (х + 7) <−3
≥
больше или равно
(x − 1) / (5 − x) ≥ 0
≤
меньше или равно
(3−2x) / (x − 1) ≤ 2
Решение
Решение неравенств очень похоже на решение уравнений.
 .. вы делаете почти то же самое.
.. вы делаете почти то же самое.Когда мы решаем неравенств
, мы пытаемся найти интервалов ,
, например, отмеченные «<0» или «> 0»Это шаги:
- найти «достопримечательности»:
- точек «= 0» (корни) и
- «вертикальные асимптоты» (где функция не определена)
- между «точками интереса», функция либо больше нуля (> 0), либо меньше нуля (<0)
- , затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
Вот пример:
Пример:
3x − 10 x − 4 > 2Первый , давайте упростим!
Но вы не можете умножить на (x − 4)
Потому что «x − 4» может быть положительным или отрицательным.
 … мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».
… мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».Вместо этого переместите «2» влево:
3x − 10 x − 4 -2> 0
Затем умножьте 2 на (x − 4) / (x − 4):
3x − 10 x − 4 -2 x − 4 x − 4 > 0
Теперь у нас есть общий знаменатель, давайте все вместе:
3x − 10-2 (x − 4) x − 4 > 0
Упростить:
x − 2 x − 4 > 0
Вторая , поищем «достопримечательности».
При x = 2 имеем: (0) / (x − 4)> 0, что является точкой «= 0», или корень
При x = 4 имеем: (x − 2) / (0)> 0, что равно undefined
Третий , сделайте контрольные точки, чтобы увидеть, что он делает между:
При x = 0:
- x − 2 = −2, что равно отрицательным
- x − 4 = −4, что также является отрицательным
- Таким образом, (x − 2) / (x − 4) должно быть положительным
Мы можем сделать то же самое для x = 3 и x = 5 и получить следующие результаты:
х = 0 х = 2 х = 3 х = 4 х = 5 х − 2 <0 х − 2> 0 х − 2> 0 х − 4 <0 х − 4 <0 х − 4> 0 (x − 2) / (x − 4) равно > 0 0 <0 undefined > 0 Это дает нам полную картину!
А где это> 0?
Итак, наш результат:
(−∞, 2) U (4, + ∞)
Все это мы сделали без рисования сюжета!
Но вот график (x − 2) / (x − 4), поэтому вы можете видеть:
Умножение дробей и смешанных чисел
Умножение дробей
Если у вашей подруги четверть пирога, а она дает вам половину, сколько пирога у вас есть? Или, другими словами, какая половина четверти? Или, чтобы выразить это в математической записи:
1 /2 x 1 /4 =?
Чтобы получить ответ, умножьте числители (верхние части) и знаменатели (нижние части) по отдельности.

В этом случае сначала мы умножаем числители:
1 x 1 = 1
Затем мы умножаем знаменатели:
2 x 4 = 8
В ответе числитель равен 1, а знаменатель — 8. Другими словами:
1 /2 x 1 /4 = 1 x 1 /2 x 4 = 1 /8
У вас одна восьмая часть пирога.
Другой пример
Попробуем другой.
2 /9 x 3 /4 =?
Сначала умножаем числители:
2 x 3 = 6
Затем умножаем знаменатели:
9 x 4 = 36
В ответе числитель 6 и знаменатель 36.Другими словами:
2 /9 x 3 /4 = 2 x 3 /9 x 4 = 6 /36
Это может быть дополнительно уменьшено:
6 6 /36 6 = 1 /6
(См. Уменьшение дробей.)
Умножение смешанных чисел
Чтобы умножить два смешанных числа или смешанное число и дробь, сначала преобразуйте каждое смешанное число в дробь.





 2+3x-10=0`;
2+3x-10=0`;





 Об этом спортсменка сообщила в своем Instagram.
Об этом спортсменка сообщила в своем Instagram. На прошлые Олимпийские игры Азаренко не поехала из-за беременности.
На прошлые Олимпийские игры Азаренко не поехала из-за беременности. В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15. В общем, следующие два факта позволяют нам проверить нашу работу в обоих наших методах решения.
В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15. В общем, следующие два факта позволяют нам проверить нашу работу в обоих наших методах решения. Чтобы проверить наше решение, мы можем использовать второй факт.Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3.
Чтобы проверить наше решение, мы можем использовать второй факт.Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3. Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили. Отличная работа!
Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили. Отличная работа! Пока не беспокойтесь о ее решении!
Пока не беспокойтесь о ее решении!

 Сколько третей стакана нужно добавить?
Сколько третей стакана нужно добавить?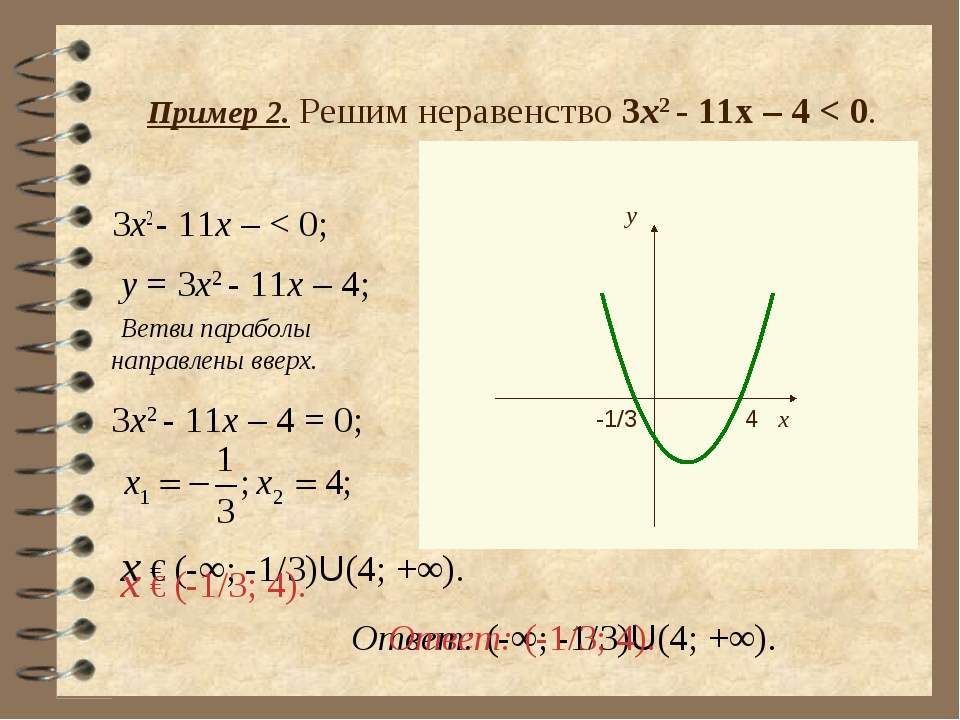


 Вы можете использовать тот же метод, чтобы разделить на две дроби .
Вы можете использовать тот же метод, чтобы разделить на две дроби .
 Затем вы можете как обычно умножать или делить.
Затем вы можете как обычно умножать или делить.
 Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.
Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце. 2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)
2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения) Учебное пособие по калькулятору
Учебное пособие по калькулятору


 В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
 4) разделите на число рядом с переменной с обеих сторон. 5) Ответ должен выглядеть так:
4) разделите на число рядом с переменной с обеих сторон. 5) Ответ должен выглядеть так: Когда вам нужно решить уравнение, которое всегда имеет только одно решение, выполняются шаги, указанные ниже.Шаг 1. Найдите LCM. Если есть какие-то дроби, очистите их. Шаг 2: На этом шаге происходит упрощение обеих сторон уравнения. Шаг 3: Здесь вы будете изолировать переменную от одной … Попрактикуйтесь в решении уравнений с одной переменной, например, 20 — 7x = 6x — 6, где переменная появляется по обе стороны от знака равенства.
Когда вам нужно решить уравнение, которое всегда имеет только одно решение, выполняются шаги, указанные ниже.Шаг 1. Найдите LCM. Если есть какие-то дроби, очистите их. Шаг 2: На этом шаге происходит упрощение обеих сторон уравнения. Шаг 3: Здесь вы будете изолировать переменную от одной … Попрактикуйтесь в решении уравнений с одной переменной, например, 20 — 7x = 6x — 6, где переменная появляется по обе стороны от знака равенства. Процесс 1.5.14. Шаги к решению простых (одношаговых) линейных уравнений. Применять. Примените противоположную операцию к обеим сторонам уравнения. Итак, при решении уравнений наша цель — найти неизвестное значение переменной. С математической точки зрения всегда допустимо производить какие-либо арифметические операции с обеими сторонами уравнения.Стратегически мы отменяем порядок операций, чтобы изолировать переменную. И если переменная появляется с обеих сторон, мы начинаем со сбора всех членов с переменной на …
Процесс 1.5.14. Шаги к решению простых (одношаговых) линейных уравнений. Применять. Примените противоположную операцию к обеим сторонам уравнения. Итак, при решении уравнений наша цель — найти неизвестное значение переменной. С математической точки зрения всегда допустимо производить какие-либо арифметические операции с обеими сторонами уравнения.Стратегически мы отменяем порядок операций, чтобы изолировать переменную. И если переменная появляется с обеих сторон, мы начинаем со сбора всех членов с переменной на … Теперь выделите переменную, вычтя по 10,5 с обеих сторон. Умножьте обе стороны на 10, чтобы 0,5y стало 5y, затем разделите на 5. Проверьте. Проверьте свое решение, подставив -8 вместо y в исходном уравнении.Это верное утверждение, поэтому решение верное. Отвечать. y …
Теперь выделите переменную, вычтя по 10,5 с обеих сторон. Умножьте обе стороны на 10, чтобы 0,5y стало 5y, затем разделите на 5. Проверьте. Проверьте свое решение, подставив -8 вместо y в исходном уравнении.Это верное утверждение, поэтому решение верное. Отвечать. y … Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл
Авторы учебников: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл Это удалит букву b из правой части уравнения. 2b + 4 + 9b = -18 — 9b + 9b. Упростите, чтобы получить это: 11b + 4 = -18. Отнимите 4 с каждой стороны. 11b + 4 — 4 = -18 — 4.
Это удалит букву b из правой части уравнения. 2b + 4 + 9b = -18 — 9b + 9b. Упростите, чтобы получить это: 11b + 4 = -18. Отнимите 4 с каждой стороны. 11b + 4 — 4 = -18 — 4. .. вы делаете почти то же самое.
.. вы делаете почти то же самое. … мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».
… мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».
