`D=9-4*(-10)=49`;
`x=(-3+7)/2=2`;
`x=(-3-7)/2=-5`.
б) Отберем корни, принадлежащие отрезку `[-6; -4]`.
Сразу видно, что `2` не входит в данный отрезок, а `-5` входит.
`(-1-sqrt(65))/2=` `-sqrt(1/4)-sqrt(65/4)=` `-sqrt(66/4)=` `-sqrt(16,5)`;
`(-1+sqrt(65))/2=` `-sqrt(1/4)+sqrt(65/4)=` `sqrt(64/4)=` `sqrt(16)`;
`-6=-sqrt(36)`;
`-4=-sqrt(16)`.
Теперь видно, что `-6
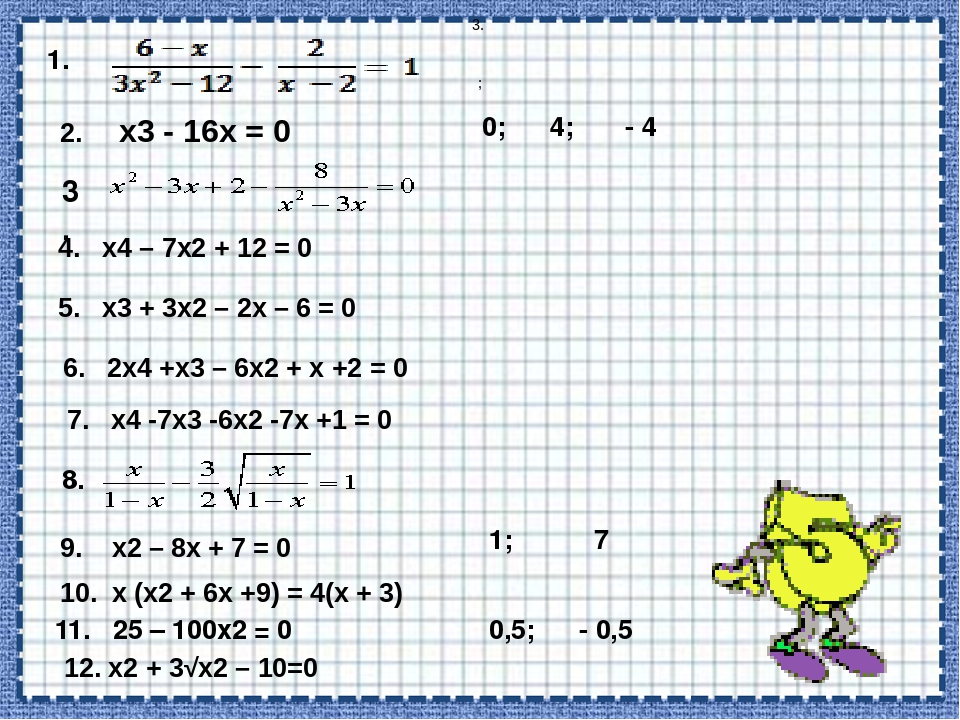
Получились следующие корни: `-5; (-1-sqrt(65))/2`.Решение №2 (скан):
$IMAGE2$Ответ: а) `(-1+-sqrt(65))/2; -5; 2`;
б) `-5; (-1-sqrt(65))/2`.
АПКШ «Континент», цена на официальном сайте Store.Softline.ru
Аппаратно-программный комплекс шифрования «Континент» обеспечивает криптографическую защиту информации (в соответствии с ГОСТ 28147–89), передаваемой по открытым каналам связи, между составными частями VPN, которыми могут являться локальные вычислительные сети, их сегменты и отдельные компьютеры. Современная ключевая схема «Континент», реализуя шифрование каждого пакета на уникальном ключе, предлагает гарантированную защиту от возможности дешифрации перехваченных данных.
Для защиты от проникновения со стороны сетей общего пользования комплекс «Континент» обеспечивает фильтрацию принимаемых и передаваемых пакетов по различным критериям (адресам отправителя и получателя, протоколам, номерам портов, дополнительным полям пакетов и т.д.). Решение осуществляет поддержку VoIP, видеоконференций, ADSL, Dial-Up и спутниковых каналов связи, технологии NAT/PAT для сокрытия структуры сети.
Область применения:
- Защита внешнего периметра сети от вредоносного воздействия со стороны сетей общего пользования.
- Создание отказоустойчивой VPN-сети между территориально распределенными сетями.
- Защита сетевого трафика в мультисервисных сетях (VoIP, Video conference).
- Разделение сети на сегменты с различным уровнем доступа.

- Организация защищенного удаленного доступа к сети для мобильных сотрудников.
- Защита беспроводных сегментов сетей.
- Организация защищенного межсетевого взаимодействия между конфиденциальными сетями.
Эффективная защита корпоративных сетей
- Безопасный доступ пользователей VPN к ресурсам сетей общего пользования
- Криптографическая защита передаваемых данных в соответствии с ГОСТ 28147–89.
- Межсетевое экранирование – защита внутренних сегментов сети от несанкционированного доступа.
- Безопасный доступ удаленных пользователей к ресурсам VPN-сети.
- Создание информационных подсистем с разделением доступа на физическом уровне.
- Возможность идентификации и аутентификации пользователей, работающих на компьютерах в защищаемой сети криптошлюзов.
Основные характеристики и возможности
- Поддержка распространенных каналов связи.
- Прозрачность для любых приложений и сетевых сервисов.
- Работа с высокоприоритетным трафиком.
- Резервирование гарантированной полосы пропускания за определенными сервисами.
- Поддержка VLAN.
- Скрытие внутренней сети. Поддержка технологий NAT/PAT.
- NAT внутри VPN-связей.
- Интеграция с внешними системами анализа событий безопасности.
- L2VPN.
- Поддержка NTP на ЦУСе.
- АРМ генерации ключей.
- Поддержка протокола IPv6.
- Режим повышенной безопасности.
- Возможность удобного защищенного взаимодействия между сетями разных организаций.
- Возможность интеграции с системами обнаружения атак.
- Защита от DoS-атак типа SYN-flood.
- Поддержка внешних 3G-модемов (USB).
- Функционал DHCP сервера на КШ.
✅ Купите Код безопасности АПКШ «Континент» 3 7, Отказоустойчивый, HA кластер 2-х Криптошлюзов, КШ СКЗИ КС3 (включена ТП уровня Базовый, срок 1 год ), Платформа IPC-100 на официальном сайте
✅ Лицензия Код безопасности АПКШ «Континент» 3 7, Отказоустойчивый, HA кластер 2-х Криптошлюзов, КШ СКЗИ КС3 (включена ТП уровня Базовый, срок 1 год ), Платформа IPC-100 по выгодной цене
✅ Код безопасности АПКШ «Континент» 3 7, Отказоустойчивый, HA кластер 2-х Криптошлюзов, КШ СКЗИ КС3 (включена ТП уровня Базовый, срок 1 год ), Платформа IPC-100, лицензионное программное обеспечение купите в Москве и других городах России
Предлагаем также:КОНТРОЛЬНАЯ РАБОТА 7 — НЕРАВЕНСТВА
Рекомендации по оцениванию.
Для получения отметки “3” достаточно выполнить первые два задания. Для получения отметки “5” необходимо выполнить любые четыре задания. Если выполнены все пять заданий, учащийся может получить дополнительную оценку.
Вариант 1
1. Докажите неравенство:
2. Известно, что а < b. Сравните:
Результат сравнения запишите в виде неравенства.
3. Известно, что 2,6 < √7 < 2,7. Оцените:
4. Оцените периметр и площадь прямоугольника со сторонами а см и b см, если известно, что 2,6 < а < 2,7, 1,2 < b < 1,3.
5. К каждому из чисел 2, 3, 4 и 5 прибавили одно и то же число а. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.
Вариант 2
1. Докажите неравенство:
2. Известно, что а > b. Сравните:
Результат сравнения запишите в виде неравенства.
3. Известно, что 3,1 < √10 < 3,2. Оцените:
4. Оцените периметр и площадь прямоугольника со сторонами а см и 6 см, если известно, что 1,5 < а < 1,6, 3,2 < b < 3,3.
5. Даны четыре последовательных натуральных числа. Сравните произведение первого и последнего из них с произведением двух средних чисел.
Вариант 3
1. Докажите неравенство:
2. Известно, что x < у. Сравните:
Результат сравнения запишите в виде неравенства.
3. Известно, что 3,6 < √13 < 3,7 . Оцените:
4. Оцените периметр и площадь прямоугольника со сторонами x см и у см, если известно, что 1,1 < x < 1,2, 1,5 < у < 1,6.
5. Даны три последовательных натуральных числа. Сравните квадрат среднего из них с произведением двух других.
Вариант 4
1. Докажите неравенство:
2. Известно, что x > y. Сравните:
Результат сравнения запишите в виде неравенства.
3. Известно, что 3,3 < √11 <3,4 .
4. Оцените периметр и площадь прямоугольника со сторонами с см и b см, если известно, что 4,6 < с < 4,7, 6,1 < b < 6,2.
5. К каждому из чисел 6, 5, 4 и 3 прибавили одно и то же число m. Сравните произведение средних членов получившейся последовательности с произведением крайних членов.
Решение вариантов контрольной работы
Вариант 1
5. Пусть 2 + а, 3 + а, 4 + а, 5 + а — полученная последовательность.
значит, произведение крайних членов последовательности меньше произведения её средних членов.
Вариант 2
5. n, n + 1, n + 2, n + 3 — последовательные натуральные числа, значит, произведение первого и последнего числа меньше произведения двух средних чисел.
Вариант 3
5. n, n + 1, n + 2 — последовательные натуральные числа.
значит, квадрат среднего числа больше произведения двух других чисел.
Вариант 45. 6 + m, 5 + m, 4 + m, 3 + m — полученная последовательность.
значит, произведение средних членов последовательности больше произведения её крайних членов.
Порядок выполнения действий: правила, примеры.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их.
Порядок вычисления простых выражений
Определение 1В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1Условие: вычислите, сколько будет 7−3+6
.Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7−3+6=4+6=10
Ответ: 7−3+6=10.
Пример 2Условие: в каком порядке нужно выполнять вычисления в выражении 6:2·8:3?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3Условие: подсчитайте, сколько будет 17−5·6:3−2+4:2.
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
17−5·6:3−2+4:2=17−10−2+2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17−10−2+2=7−2+2=5+2=7
Ответ: 17−5·6:3−2+4:2=7.
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Определение 3Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Проиллюстрируем нашу мысль примером.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 4Условие: вычислите, сколько будет 5+(7−2·3)·(6−4):2.
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7−2·3=7−6=1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5+(7−2·3)·(6−4):2=5+1·2:2
Начнем с умножения и деления, потом выполним вычитание и получим:
5+1·2:2=5+2:2=5+1=6
На этом вычисления можно закончить.
Ответ: 5+(7−2·3)·(6−4):2=6.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).
Решение
У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.
Ответ: 4+(3+1+4·(2+3))=28.
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4+(4+(4−6:2))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−6:2=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам: 4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6Условие: найдите, сколько будет (3+1)·2+62:3−7.
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+36:3−7.
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
(3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13
Ответ: (3+1)·2+62:3−7=13.
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Пансионат в Алуште, Крым — официальный сайт пансионата НЕВА
«Нева» — пансионат в Алуште с питанием
Завтраки, обеды и ужины по системе «шведский стол» проходят в уютной столовой пансионата – отдельном здании из экологического деревянного сруба с открытой террасой. Меню состоит из разнообразных горячих блюд, свежей домашней выпечки, свежих овощей и сочных фруктов, собранных в крымских садах. Широкий выбор блюд русской, украинской, восточно-европейской, грузинской и татарской кухни. Столь насыщенный ассортимент подобран для того, чтобы каждый гость остался предельно довольным.
Столь насыщенный ассортимент подобран для того, чтобы каждый гость остался предельно довольным.
Пансионат на берегу моря с собственным пляжем
Всласть поплавать в теплых водах Черного моря, принять солнечные ванны и получить крымский бронзовый загар, вы сможете на нашем пляже. Здесь вы найдете все для комфортного времяпрепровождения: чистый берег, мелкая галька, широкие навесы и зонты, удобные шезлонги и лежаки, мягкий заход в воду по ортопедическим деревянным дорожкам. Всегда дежурят спасатели и медработник.
Дорога до пляжа Невы занимает 5 минут пешком: весь путь вы преодолеете, находясь в прохладе тоннеля и раскидистых крон деревьев вечнозеленого парка.
Отдых с детьми в Крыму, Алуште
Наши аниматоры подготовили насыщенные развлекательные программы, наполненные увлекательными приключениями, детективными квестами и, конечно, зажигательными играми с водой. Разнообразят отдых занятия по лепке, рисованию и скрапбукингу.
Если интересно детям, то родителям наслаждаться отпуском гораздо легче. Для юных постояльцев «Невы» — игровая площадка, одна из лучших в Алуште, с лабиринтами, лестницами, качелями, горками, мини-тренажерами.
Для удобства гостей с малышами мы предлагаем детское питание, аренду детской кроватки, коляски, а также велосипедов и самокатов.
Развлечения во время отдыха
Взрослым также скучать не придется. Отдых в Алуште раскрывает широкие возможности для увлекательных экскурсий.
Специально для вас мы подготовили конные прогулки по живописным маршрутам, поездку в уникальный историко-культурный центр «Викинг», посещение местного аквапарка, аквариума, многочисленных музеев и других примечательных мест.
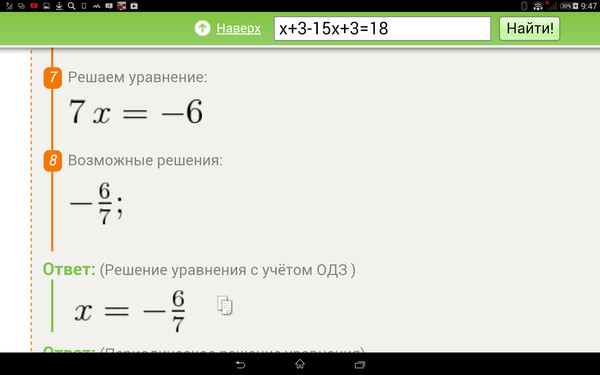
Учебное пособие по калькулятору алгебры — MathPapa
Это руководство по использованию калькулятора по алгебре , пошагового калькулятора для алгебры.
Решение уравнений
Сначала перейдите на главную страницу Калькулятора алгебры. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить.
Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле.
После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14.
Примеры
Чтобы увидеть больше примеров задач, которые понимает калькулятор алгебры, посетите Страница примеров.2.Вычисление выражений
Алгебра Калькулятор может вычислять выражения, содержащие переменную x.
Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x. Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6.
Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).
Проверка ответов для решения уравнений
Так же, как калькулятор алгебры можно использовать для вычисления выражений, Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x.
В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, калькулятор алгебры показывает зеленый знак равенства.
Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно».
Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y.Пример: x + y = 7; х + 2у = 11 @ (3,4).
Режим планшета
Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру.
Похожие статьи
Назад к калькулятору алгебры »
Решите линейные уравнения с одним неизвестным x-3/2 = 2x + 7/7 Решатель алгебры тигра
Переставьте:
Переставьте уравнение, вычитая то, что находится справа знака равенства с обеих сторон уравнения:
x-3 / 2- (2 * x + 7/7) = 0
Пошаговое решение:
Шаг 1:
1
Упростить -
1
Уравнение в конце шага 1:
3
(х - -) - (2x + 1) = 0
2
Шаг 2:
3
Упростить -
2
Уравнение в конце шага 2:
3
(х - -) - (2x + 1) = 0
2
Шаг 3:
Переписывание целого как эквивалентной дроби:
3.1 Вычитание дроби из целого
Перепишем целое как дробь, используя 2 в качестве знаменателя:
x x • 2
x = - = —————
1 2
Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целая
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель.
Добавление дробей с общим знаменателем:
3.2 Сложение двух эквивалентных дробей
Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель
Объедините числители, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если возможно:
x • 2 - ( 3) 2х - 3
знак равно
2 2
Уравнение в конце шага 3:
(2x - 3)
———————— - (2x + 1) = 0
2
Шаг 4:
Переписывание целого как эквивалентной дроби:
4. 1 Вычитание целого из дроби
1 Вычитание целого из дроби
Перепишем целое как дробь, используя 2 в качестве знаменателя:
2x + 1 (2x + 1) • 2
2x + 1 = —————— = ————————————
1 2
Сложение дробей с общим знаменателем:
4.2 Сложение двух эквивалентных дробей
(2x-3) - ((2x + 1) • 2) -2x - 5
знак равно
2 2
Шаг 5:
Вытягивание аналогично терминам:
5.1 Коэффициенты вытягивания:
-2x — 5 = -1 • (2x + 5)
Уравнение в конце шага 5:
-2x - 5
——————— = 0
2
Шаг 6:
Когда дробь равна нулю:
6.1 Когда дробь равна нулю ...
Если дробь равна нулю, ее числитель, часть, которая находится над линией дроби, должна равняться нулю.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
-2x-5
————— • 2 = 0 • 2
2
Теперь, с левой стороны, 2 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
Уравнение теперь принимает форму:
-2x-5 = 0
Решение уравнения с одной переменной:
6.2 Решите: -2x-5 = 0
Добавьте 5 к обеим сторонам уравнения:
— 2x = 5
Умножьте обе части уравнения на (-1): 2x = -5
Разделите обе части уравнения на 2:
x = -5/2 = -2.500
Было найдено одно решение:
x = -5/2 = -2,500Уравнения абсолютного значения
Уравнения абсолютного значения Уравнения абсолютных значенийВыполните следующие действия, чтобы найти абсолютное значение равенства который содержит одно абсолютное значение:
- Выделите абсолютное значение на одной стороне уравнения.
- Число на другой стороне уравнения отрицательное?
Если вы ответили утвердительно, то уравнение не имеет решения.Если вы ответили
нет, переходите к шагу 3.

- Напишите два уравнения без абсолютных значений. Первое уравнение установит количество внутри столбцов, равное количеству на другом сторона знака равенства; второе уравнение установит количество внутри столбцы равны противоположному числу на другой стороне.
- Решите два уравнения.
Выполните следующие действия, чтобы найти равенство абсолютного значения
который содержит два абсолютных значения (по одному с каждой стороны уравнения):
- Напишите два уравнения без абсолютных значений.Первое уравнение установит количество внутри столбцов с левой стороны равным количество внутри полос с правой стороны. Второе уравнение установит количество внутри столбцов с левой стороны равным противоположному количества внутри полос с правой стороны.
- Решите два уравнения.
Давайте рассмотрим несколько примеров.
Пример 1: Решить | 2x — 1 | + 3 = 6
| Шаг 1: Изолировать абсолютное значение | | 2x — 1 | + 3 = 6 | 2x — 1 | = 3 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 3, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 2x — 1 = 3 | 2х — 1 = -3 |
| Шаг 4: Решить оба уравнения | 2x — 1 = 3 2x = 4 х = 2 | 2х — 1 = -3 2x = -2 х = -1 |
Пример 2: Решить | 3x — 6 | — 9 = -3
| Шаг 1: Изолировать абсолютное значение | | 3х — 6 | — 9 = -3 | 3x — 6 | = 6 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 6, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 3х — 6 = 6 | 3х — 6 = -6 |
| Шаг 4: Решить оба уравнения | 3х — 6 = 6 3x = 12 х = 4 | 3х — 6 = -6 3x = 0 х = 0 |
Пример 3: Решить | 5x + 4 | + 10 = 2
| Шаг 1: Изолировать абсолютное значение | | 5x + 4 | + 10 = 2 | 5x + 4 | = -8 |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Да, это отрицательное число, -8. Нет решения
к этой проблеме. Нет решения
к этой проблеме. |
Пример 4: Решить | x — 7 | = | 2x — 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 7 = 2х — 2 | х — 7 = — (2х — 2) |
| Шаг 4: Решить оба уравнения | х — 7 = 2х — 2 -x — 7 = -2 -x = 5 х = -5 | х — 7 = -2x + 2 3x — 7 = 2 3x = 9 х = 3 |
Пример 5: Решить | x — 3 | = | x + 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = х + 2 | х — 3 = — (х + 2) |
| Шаг 4: Решить оба уравнения | х — 3 = х + 2 — 3 = -2 ложное заявление Нет решения из этого уравнения | х — 3 = -x — 2 2х — 3 = -2 2x = 1 x = 1/2 |
Итак, единственное решение этой проблемы — x = 1/2
Пример 6: Решить | x — 3 | = | 3 — x |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = 3 — х | х — 3 = — (3 — х) |
| Шаг 4: Решить оба уравнения | х — 3 = 3 — х 2x — 3 = 3 2x = 6 х = 3 | х — 3 = — (3 — х) х — 3 = -3 + х -3 = -3 Все действительные числа являются решениями этого уравнения |
Так как 3 входит в набор действительных чисел, мы просто скажем, что решение этого уравнения — все действительные числа
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. 1/2
1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи с дробями:
следующие математические задачи »
Решение простых абсолютных уравнений | Purplemath
Purplemath
Когда мы берем абсолютное значение числа, мы всегда получаем положительное число (или ноль).Независимо от того, был ли вход положительным или отрицательным (или нулевым), выход всегда положительный (или нулевой). Например, | 3 | = 3 и | –3 | = 3 тоже.
Это свойство — положительное и отрицательное превращение в положительное — делает решение уравнений абсолютного значения немного сложным. Но как только вы усвоите «трюк», они не так уж и плохи. Начнем с простого:
Но как только вы усвоите «трюк», они не так уж и плохи. Начнем с простого:
MathHelp.com
Я уже решил это в своем обсуждении выше:
Значит, x должно быть равно 3 или равно –3.
Но как мне решить эту проблему, если я еще не знаю ответа ? Я буду использовать свойство положительного / отрицательного абсолютного значения, чтобы разделить уравнение на два случая, и я буду использовать тот факт, что знак «минус» в отрицательном случае означает «противоположный знак», а не «отрицательное число».
Например, если у меня x = –6, то «- x » означает «противоположность x » или, в данном случае, — (- 6) = +6, положительное число. Знак «минус» в «- x » просто указывает на то, что я меняю знак на x . Это означает, что , а не , означает отрицательное число. Это различие очень важно!
Каким бы ни было значение x , взятие абсолютного значения x делает его положительным.Поскольку x изначально могло быть положительным, а может быть отрицательным, я должен признать этот факт, когда удаляю столбцы абсолютных значений. Я делаю это, разбивая уравнение на два случая. Для этого упражнения это следующие случаи:
а. Если значение x было неотрицательным (то есть, если оно было положительным или нулевым) для начала, то я могу вывести это значение из столбцов абсолютного значения, не меняя его знака, давая мне уравнение x = 3.
г. Если значение x изначально было отрицательным, то я могу вывести это значение из столбцов абсолютного значения, изменив знак на x , получив уравнение — x = 3, которое решает как х = –3.
Тогда мое решение —
Мы, кстати, можем проверить это решение графически. Когда мы пытаемся решить уравнение абсолютных значений | x | = 3, мы, по сути, приравниваем два линейных уравнения друг к другу и находим, где они пересекаются.Например:
Выше я построил график y 1 = | x | (синяя линия, которая выглядит как «V») и y 2 = 3 (зеленая горизонтальная линия). Эти два графика пересекаются при x = –3 и x = +3 (две красные точки).
Если вы хотите проверить свои ответы на тесте (перед тем, как сдать его), может быть полезно подключить каждую сторону исходного уравнения абсолютного значения в ваш калькулятор как их собственные функции; затем спросите у калькулятора точки пересечения.
Конечно, любое решение также можно проверить, вставив его обратно в исходное упражнение и подтвердив, что левая часть (LHS) уравнения упрощается до того же значения, что и правая часть (RHS). уравнение. Вот мой чек для приведенного выше уравнения:
Если вы когда-либо сомневаетесь в своем решении уравнения, попробуйте построить график или попробуйте снова вставить свое решение в исходный вопрос. Проверяю свою работу всегда нормально!
Шаг, описанный выше, где уравнение абсолютного значения было переформулировано в двух формах, одна со знаком «плюс», а другая со знаком «минус», дает нам удобный способ упростить ситуацию: когда мы изолировали абсолютное значение и перейти к снятию стержней, мы можем разделить уравнение на два случая; мы обозначим эти случаи, поставив «минус» на противоположной стороне уравнения (для одного случая) и «плюс» на противоположной стороне (для другого).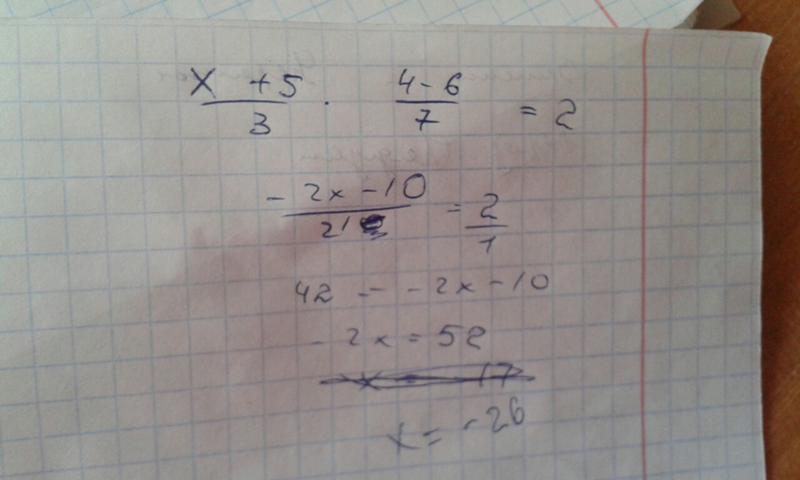 Вот как это работает:
Вот как это работает:
Решить |
x + 2 | = 7 и проверьте свое решение (я).
Абсолютное значение выделено в левой части уравнения, поэтому я уже настроил его, чтобы разделить уравнение на два случая. Чтобы очистить столбцы абсолютного значения, я должен разделить уравнение на два возможных случая, по одному для каждого случая, если содержимое столбцов абсолютного значения (то есть, если «аргумент» абсолютного значения) отрицательное, и если он неотрицательный (то есть положительный или нулевой).Для этого я создаю два новых уравнения, единственное различие между которыми — это знак в правой части. Сначала сделаю «минусовый» случай:
x + 2 = –7
x + 2 = –7
x = –9
Теперь я займусь неотрицательным случаем, когда я могу просто опустить столбцы и решить:
Теперь мне нужно проверить свои решения.Я сделаю это, вставив их обратно в исходное уравнение, поскольку оценщик не видит, как я проверяю графики на моем графическом калькуляторе.
Оба решения проверяют, поэтому мой ответ:
Решить | 2
x — 3 | — 4 = 3 9 10 17
Во-первых, я выделю часть уравнения, относящуюся к абсолютным значениям; то есть, я получу само выражение абсолютного значения с одной стороны от знака «равно», а все остальное — с другой стороны:
| 2 x — 3 | — 4 = 3
| 2 x — 3 | = 7
Теперь я очищу столбцы абсолютных значений, разделив уравнение на два случая, по одному для каждого знака аргумента. Сначала сделаю отрицательный случай:
Сначала сделаю отрицательный случай:
2 x — 3 = –7
2 x = –4
x = –2
А затем сделаю неотрицательный случай:
2 x — 3 = 7
2 x = 10
x = 5
В упражнении мне не сказано проверять, поэтому я не буду.(Но, если бы я хотел, я мог бы вставить «abs (2X – 3) –4» и «3» в свой калькулятор (как Y1 и Y2, соответственно), и увидеть, что точки пересечения были на моем x -значения.) Мой ответ:
URL: https://www.purplemath.com/modules/solveabs.htm
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 ломтиками. 1 из этих 8 кусочков будет составлять числитель дроби, а всего 8 кусочков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
1 из этих 8 кусочков будет составлять числитель дроби, а всего 8 кусочков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Вычитание:
Вычитание фракции по сути то же самое, что и сложение фракции. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к уравнениям ниже для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Дивизион:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , — это просто
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите. Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму с использованием тех же принципов. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.Преобразование общей инженерной дроби в десятичную дробь
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 th | 32 th | 16 th | 8 th | 4 th | 2 nd | 000000 (десятичное)|||||||||
| 1/64 | 0,015625 | 0,396875 | ||||||||||||
| 2/64 | 1/32 | 03125 | 0,79375 | |||||||||||
| 3/64 | 0,046875 | 1,1 | ||||||||||||
| 4/64 | 000 | 2/64000 | 2/64000 | 2/640,0625 | 1,5875 | |||||||||
| 5/64 | 0,078125 | 1.984375 | ||||||||||||
0. 09375 09375 | 2.38125 | |||||||||||||
| 7/64 | 0.109375 | 2.778125 | ||||||||||||
| 0004 8/64 | 000 9/64000 9/640000,125 | 3,175 | ||||||||||||
| 9/64 | 0,140625 | 3,571875 | 0000 | 000007500050000.15625 | 3.96875 | |||||||||
| 11/64 | 0.171875 | 4.365625 | ||||||||||||
| 12/64 | 000 | 000 | 000 | 000 | 000 3/9 | 0,1875 | 4,7625 | |||||||
| 13/64 | 0.203125 | 5,159375 | ||||||||||||
| 0.21875 | 5.55625 | |||||||||||||
| 15/64 | 0.234375 | 5.953125 | ||||||||||||
| 16/64 | 000 9/640000001/4 | 0,25 | 6,35 | |||||||||||
| 17/64 | 0,265625 | 6.74685000 9325000 | 0006.74685000 | 0000000.28125 | 7.14375 | |||||||||
| 19/64 | 0,296875 | 7,540625 | ||||||||||||
| 20/64 | 000 9/640000,3125 | 7,9375 | ||||||||||||
| 21/64 | 0,328125 | 8,334375 | ||||||||||||
0. 34375 34375 | 8,73125 | |||||||||||||
| 23/64 | 0,359375 | 9.128125 | ||||||||||||
| 24/64 | 0000,375 | 9,525 | ||||||||||||
| 25/64 | 0,3 | 9. | 5400000000040000004000 | 0.40625 | 10.31875 | |||||||||
| 27/64 | 0.421875 | 10.715625 | ||||||||||||
| 28/64 | 000000 | 000 | 000 | 000 | 00028/64 | 0000000,4375 | 11,1125 | |||||||
| 29/64 | 0,453125 | 11.509375 | ||||||||||||
| 0.46875 | 11. | |||||||||||||
| 31/64 | 0.484375 | 12.303125 80005 | ||||||||||||
| 32/64 | 000 | 000 | 0005000 | 32/64 | 000 | 000 | 2/4 | 1/2 | 0,5 | 12,7 | ||||
| 33/64 | 0,515625 | 13.0 | 5 | 0000000.53125 | 13.49375 | |||||||||
| 35/64 | 0.546875 | 13.8 | ||||||||||||
| 36/64 | 000000000 | 000 | 0000000,5625 | 14,2875 | ||||||||||
| 37/64 | 0,578125 | 14. 684375 684375 | ||||||||||||
| 0.59375 | 15.08125 | |||||||||||||
| 39/64 | 0.609375 | 15.478125 | ||||||||||||
| 40/64 | 00000000040/64 | 000000|||||||||||||
| 40/64 | 0000000,625 | 15.875 | ||||||||||||
| 41/64 | 0,640625 | 16.2718754000 9325000 9325000 | 00016.2718754000 | 0000000.65625 | 16.66875 | |||||||||
| 43/64 | 0.671875 | 17.065625 | ||||||||||||
| 44/64 | 000000000 | 000 | 000000 | 000 | 0000000,6875 | 17,4625 | ||||||||
| 45/64 | 0.703125 | 17.859375 | 0004 17.859375 | |||||||||||
| 000 | 0.71875 | 18.25625 | ||||||||||||
| 47/64 | 0.734375 | 18.653125 | ||||||||||||
| 48/64 | 00000048/64 | 0003/4 | 0,75 | 19,05 | ||||||||||
| 49/64 | 0,765625 | 19.4114685000 9325000 | 00019.4114685000 | 0000000.78125 | 19.84375 | |||||||||
| 51/64 | 0,796875 | 20. |

