Способы изменения внутренней энергии тела
Внутренняя энергия тела не является какой-то постоянной величиной: у одного и того же тела она может изменяться. При повышении температуры тела внутренняя энергия тела увеличивается, так как увеличивается средняя скорость, а значит, и кинетическая энергия, молекул этого тела. С понижением же температуры, наоборот, внутренняя энергия тела уменьшается. Таким образом, внутренняя энергия тела изменяется при изменении скорости движения его молекул. Какими же способами можно увеличить или уменьшить эту скорость? Обратимся к опыту.
На подставке (рис. 181) укреплена тонкостенная латунная трубка, в которую налито немного эфира, трубка плотно закрыта пробкой. Трубку обвивают веревкой и быстро двигают веревку то в одну, то в другую сторону. Через некоторое время эфир закипит и его пар вытолкнет пробку. Этот опыт показывает, что внутренняя энергия эфира, увеличилась: ведь он нагрелся и даже закипел. Увеличение внутренней энергии произошло в результате работы, совершенной при натирании веревкой трубки.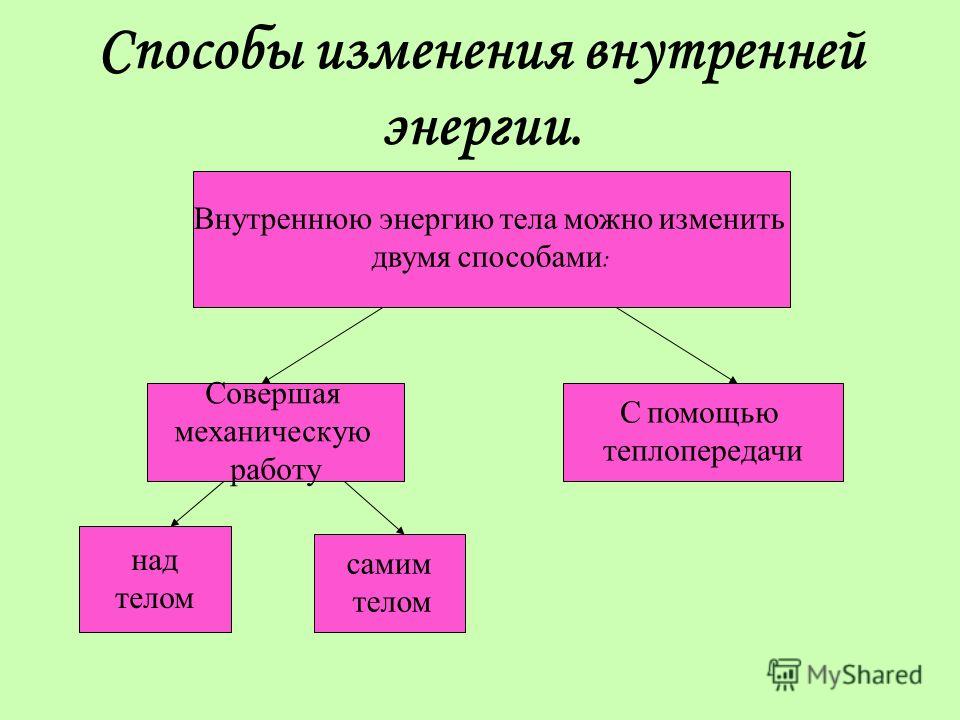
Тела нагреваются также при ударах, разгибании и сгибании, вообще при деформации. Во всех этих случаях за счет совершенной работы увеличивается внутренняя энергия тел.
Итак, внутреннюю энергию тела можно увеличить путем совершения работы над телом. Если работу совершает само тело, то внутренняя энергия его при этом уменьшается. Это можно наблюдать на следующем опыте.
Берут толстостенный стеклянный сосуд, закрытый пробкой. Через специальное отверстие в сосуд накачивают воздух, в котором содержится водяной пар. Через некоторое время пробка выскакивает из сосуда (рис. 182). В тот момент, когда пробка выскакивает, в сосуде появляется туман. Его появление означает, что воздух в сосуде стал холоднее (вспомните, что и на улице туман появляется во время похолодания).
Находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счет своей внутренней энергии, которая при этом уменьшается. Об уменьшении энергии мы судим по охлаждению воздуха в сосуде.
Внутреннюю энергию тела можно изменить и другим способом.
Известно, что чайник с водой, стоящий на плите, металлическая ложка, опущенная в стакан с горячим чаем, печь, в которой разведен огонь, крыша дома, освещаемая солнцем, нагреваются. Во всех случаях повышается температура тел, а значит, увеличивается и их внутренняя энергия. Как объяснить ее увеличение?
Как, например, нагревается холодная металлическая ложка, опущенная в горячий чай? Сначала скорость и кинетическая энергия молекул горячей воды больше скорости и кинетической энергии частиц холодного металла. В тех местах, где ложка соприкасается с водой, молекулы горячей воды передают часть своей кинетической энергии частицам холодного металла. Поэтому скорость и энергия молекул воды в среднем уменьшается, а скорость и энергия частиц металла увеличивается: температура воды уменьшается, а температура ложки увеличивается — температуры их постепенно выравниваются. С уменьшением кинетической энергии молекул воды уменьшается и внутренняя энергия всей воды, находящейся в стакане, а внутренняя энергия ложки, увеличивается.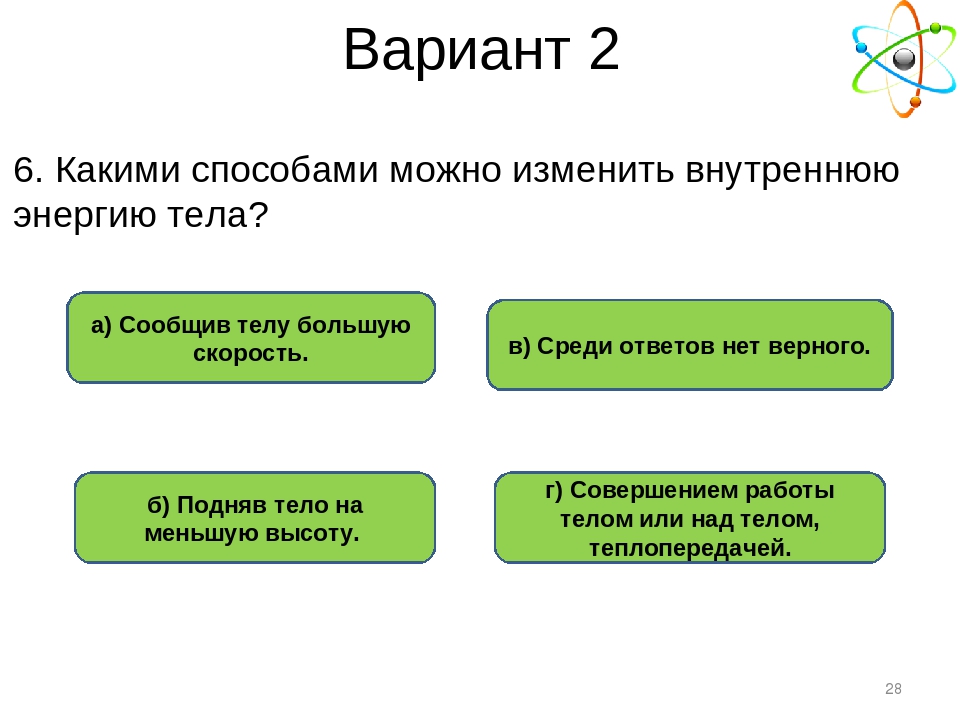
Процесс изменения внутренней энергии, при котором над телом не совершается работа, а энергия передается от одних частиц к другим, называют теплопередачей. Итак, внутреннюю энергию тела можно изменить двумя способами: совершением механической работы или теплопередачей.
Когда тело уже нагрето, мы не можем указать, каким из двух способов это было сделано. Так, держа в руках нагретую стальную спицу, мы не можем сказать, каким способом ее нагрели — натирая ее или помещая в пламя.
Вопросы. 1. Приведите примеры, показывающие, что внутренняя энергия тела увеличивается при совершении над телом работы. 2. Опишите опыт, показывающий, что за счет внутренней энергии тело может совершить работу. 3. Приведите примеры увеличения внутренней энергии тела способом теплопередачи. 4. Объясните на основе молекулярного строения вещества теплопередачу. 5. Какими двумя способами можно изменить внутреннюю энергию тела?
Задание.
Положите пятикопеечную, монету на лист фанеры или деревянную доску. Прижмите монету к доске и двигайте ее быстро, то в одну, то в другую сторону. Заметьте, сколько раз надо передвинуть монету, чтобы она стала теплой, горячей. Сделайте вывод о связи между проделанной работой и увеличением внутренней энергии тела.
Прижмите монету к доске и двигайте ее быстро, то в одну, то в другую сторону. Заметьте, сколько раз надо передвинуть монету, чтобы она стала теплой, горячей. Сделайте вывод о связи между проделанной работой и увеличением внутренней энергии тела.
Внутренняя энергия тела и способы её изменения
Вы знаете, что существует два вида механической энергии — кинетическая и потенциальная. Давайте вспомним, что кинетической энергией обладает всякое движущееся тело: .
Потенциальная энергия определяется взаимным положением взаимодействующих тел или отдельных частей тела: Eп = mgh.
Изучая механические явления, вы узнали, что кинетическая и потенциальная энергии могут превращаться друг в друга таким образом, что их сумма остаётся постоянной величиной: E = Ek + Eп = const.
В этом
заключается один из наиболее общих и фундаментальных законов природы — закон
сохранения и превращения энергии.
Однако, вы знаете, что в реальных опытах закономерности превращения энергии выглядят гораздо сложнее.
Например, возьмём гирю из какого-либо мягкого металла, например, из свинца, и стальную плиту. Поднимем гирю вверх на какую-либо высоту, тем самым сообщив ей некоторый запас потенциальной энергии. А затем отпустим. Во время полёта гири её потенциальная энергия уменьшается, а кинетическая, наоборот, увеличивается. После падения, гиря остановится. Её потенциальная энергия относительно плиты равна нулю, как равна нулю и кинетическая энергия, поскольку гиря неподвижна. Означает ли это, что нарушился основной закон природы, и энергия бесследно исчезла?
Конечно
же нет. Механическая энергия перешла в другой вид энергии. Если внимательно
посмотреть на гирю после удара, то мы обнаружим, что она, как и плита, слегка
сплющилась, то есть деформировалась. А если мы измерим её температуру до и
после падения, то окажется, что она увеличилась.
Мы уже знаем, что при изменении температуры тела, изменяется скорость движения его молекул. Помимо этого, в результате деформации гири, изменилось и взаимное расположение молекул друг относительно друга. Значит изменилась и их потенциальная энергия.
Следовательно, механическая энергия, которой обладала гиря в начале опыта, не исчезла: она перешла в потенциальную и кинетическую энергию её молекул.
Сумма кинетической энергии теплового движения частиц, из которых состоит тело, и потенциальной энергии их взаимодействия, называется внутренней энергией тела.
Обозначают внутреннюю энергию буквой U. А измеряют её в тех же единицах, что и механическую энергию: [U] = [Дж].
Возникает логичный вопрос: а каково значение внутренней энергии какого-либо тела?
Для
примера рассмотрим какой-нибудь газ, например, кислород. Потенциальная энергия
взаимодействия его молекул между собой практически отсутствует.
Кто-то скажет, что это очень маленькая величина, и будет прав. Но, например, в 1 м3 газообразного кислорода содержится примерно 2,7 ∙ 1025. А их общая энергия равна почти 100 кДж. А это значение энергии уже весьма значительно. Такой энергией, например, будет обладать одна тонный бизон, если его поднять на высоту десяти метров.
Теперь выясним, от чего зависит внутренняя энергия тела?
Вы уже знаете, что чем больше температура тела, тем быстрее движутся молекулы. Чем больше скорость движения, тем больше их кинетическая энергия. Значит, внутренняя энергия тела зависит от его температуры.
Также вам
должно быть известно, что для перевода вещества из жидкого состояния в
газообразное, например, чтобы превратить воду в пар, нужно подвести энергию. Следовательно, пар будет обладать большей внутренней энергией, чем вода той же
массы. Значит, внутренняя энергия тела при неизменной массе зависит от его
агрегатного состояния.
Следовательно, пар будет обладать большей внутренней энергией, чем вода той же
массы. Значит, внутренняя энергия тела при неизменной массе зависит от его
агрегатного состояния.
Т. к. масса тела равна сумме масс составляющих его частиц, то внутренняя энергия зависит и от массы тела.
Но внутренняя энергия тела не зависит от его механического движения и от его взаимодействия с другими телами. Так, например, внутренняя энергия мяча, лежащего на полу и поднятого на некоторую высоту от пола, одинакова, так же, как и мяча, неподвижного и катящегося по полу (если, конечно, пренебречь силами сопротивления его движению).
Возникает вопрос, а может ли у тела отсутствовать внутренняя энергия?
Чтобы
правильно на него ответить, достаточно вспомнить, что движение частиц, из
которых состоит тело, никогда не прекращается, даже при очень низких
температурах. Поэтому тело всегда обладает внутренней энергией.
Как правило, значение внутренней энергии в большинстве случаев вычислить очень трудно, поскольку каждое тело состоит из огромного числа частиц. Однако нас чаще будет интересовать не само значение внутренней энергии, а её изменение. А о нём можно судить, в частности, по значению совершённой работы.
Вот мы и подошли ко второй важной проблеме — можно ли как-то изменить внутреннюю энергию тела?
Рассуждаем последовательно. Внутренняя энергия определяется энергией движения и энергией взаимодействия частиц. Следовательно, если мы сможем изменить скорость движения частиц, либо усилить или ослабить их взаимодействие друг с другом, то мы сможем изменить и внутреннюю энергию тела.
Рассмотрим каждую из возможностей изменения внутренней энергии отдельно.
Мы уже знаем, что изменить кинетическую энергию частиц тела можно путём увеличения или уменьшения температуры тела.
Существует
два способа это сделать. Рассмотрим их на конкретных примерах. И так, возьмём
закрытый сосуд с воздухом, к которому присоединим манометр. И начнём натирать
сосуд с помощью тряпочки или сукна.
Рассмотрим их на конкретных примерах. И так, возьмём
закрытый сосуд с воздухом, к которому присоединим манометр. И начнём натирать
сосуд с помощью тряпочки или сукна.
Уровень жидкости в левом колене манометра начинает понижаться. Это обусловлено тем, что воздух в колбе начинает нагреваться, вследствие чего, увеличивается его давление. Значит увеличивается и кинетическая энергия молекул воздуха. Таким образом, совершив механическую работу (трение сукна о колбу) мы смогли увеличить кинетическую энергию молекул находящегося в колбе воздуха.
Проделаем ещё один опыт. Возьмём толстостенный стеклянный сосуд, на дне которого находится небольшое количество воды. Закроем его пробкой с пропущенной через неё трубкой. Соединим трубку с насосом и начнём накачивать в сосуд воздух. Через некоторое время пробка из сосуда вылетит и в нём образуется туман.
Туман — это превратившийся в воду водяной пар.
Подумайте,
когда образуется туман? Наверняка каждый из вас замечал, что чаще всего туман
образуется тогда, когда после тёплого дня, наступает прохладная ночь, т. е. при
значительном понижении температуры.
е. при
значительном понижении температуры.
Следовательно, температура воздуха в сосуде понизилась. А понизилась она из-за того, что воздух, находящийся в сосуде, совершил работу. Вследствие чего, внутренняя энергия молекул воздуха в сосуде уменьшилась.
Таким образом, мы с вами можем сделать важный вывод о том, что внутренняя энергия тела изменяется при совершении работы. При этом если тело совершает работу, то его внутренняя энергия уменьшается. А если над телом совершают работу, то его внутренняя энергия увеличивается.
Теперь подумаем, можно ли изменить внутреннюю энергию тела, без совершения механической работы?
Вернёмся
к опыту с колбой и манометром. Теперь не будем натирать колбу, а нагреем в ней
воздух при помощи спиртовки. И опять через небольшой промежуток времени уровень
жидкости в левом колене манометра начнёт понижаться. Что свидетельствует о том,
что опять происходит изменение внутренней энергии воздуха в колбе.
Теперь обратимся к ситуации, с которой вы сталкиваетесь в жизни постоянно. Возьмём стакан с горячим чаем и металлическую ложку. Вы хорошо знаете, что если ложку опустить в стакан с чаем, то она через некоторое время тоже становится горячей.
В этом случае, как и в предыдущем, работа не совершается, но внутренняя энергия ложки увеличивается, о чём и свидетельствует повышение её температуры.
Поскольку вначале температура воды выше, чем температура ложки, то и средняя скорость молекул воды больше. А это значит, что молекулы воды обладают большей кинетической энергией, чем частицы металла, из которого сделана ложка. При столкновении с частицами металла молекулы воды передают им часть своей энергии, и кинетическая энергия частиц металла увеличивается. А кинетическая энергия молекул воды при этом уменьшается.
В
рассмотренных нами примерах внутренняя энергия тел изменялась путём теплопередачи.
Теплопередача — способ изменения внутренней энергии тела, при котором энергия передаётся от одной части тела к другой или от одного тела к другому без совершения работы.
Стоит обратить внимание на то, что процесс теплопередачи происходит в определённом направлении — от более нагретых тел к менее нагретым, но не наоборот. А когда температуры тел выравниваются, теплопередача прекращается.
Таким образом, возможны два способа изменения внутренней энергии —совершение механической работы и теплопередача.
Существует три вида теплопередачи — теплопроводность, конвекция и излучение. Но о них мы с вами поговорим на следующих занятиях.
Способы изменения внутренней энергии тела
Способы изменениявнутренней энергии
тела
8 класс
Шашунькина Наталья Павловна
Тема урока: «Способы изменения внутренней энергии тела».
Цель урока: выяснить, какими способами можно изменить внутреннюю

Образовательные задачи:
Выяснить зависимость внутренней энергии тела от изменения
температуры тела и агрегатного состояния вещества;
Рассмотреть способы изменения внутренней энергии;
Уметь объяснять изменение внутренней энергии тела с точки зрения
молекулярного строения вещества;
Уметь приводить примеры изменения внутренней энергии разными
способами;
Научить решать задачи с применением новых знаний.
Развивающие задачи:
развитие и совершенствование умения проводить эксперимент,
выдвигать гипотезы, планировать эксперимент, проводить эксперимент,
формулировать выводы;
развитие познавательного интереса к физике и способностей к физике;
развитие мышления, памяти, речи, внимания, воображения.
Воспитательные задачи:
формирование научного мировоззрения;
формирование силы воли и умения контролировать свои эмоции;
формирование эстетического восприятия мира;
формирование представлений о роли физики в жизни общества.

Тип урока: комбинированный урок:
Методическая структура урока:
Актуализация опорных знаний и умений;
Формирование новых знаний и способов деятельности;
Применение сформированных знаний и способов деятельности.
Методы обучения:
Проблемный метод;
Частично- поисковый метод;
Объяснительно-иллюстративный;
Метод контроля.
Средства обучения:
Компьютер, мультимедиа проектор, стеклянная колба, гибкая трубка ,
сосуд с холодной водой, манометр
Формы организации работы обучающихся:
Фронтальная форма организации;
Групповая форма;
Индивидуальная форма.
1.
Организационный момент (2 минуты):
Приветствие, сообщение об отсутствующих
2.
Актуализация знаний(12 минут):
Фронтальный опрос
Решение качественных задач
3.
Изучение нового материала (20 минут):
Проводят эксперимент, делают выводы
Наблюдают демонстрационный эксперимент, делают выводы
Отвечают на вопросы учителя
Заполняют таблицу
4.

Исторические сведения (1 минута)
5.
Закрепление знаний (5 минут):
Работа с тестом.
6.
Контроль и оценивание, домашнее задание (2 минуты):
Записывают в дневники домашнее задание; Слушают пояснение учителя
7.
Рефлексия (3минуты):
Отвечают на вопросы итоговой рефлексии;
Подведение итогов урока
Фронтальный опрос:
1.Какое движение называется тепловым?
2.Как связана скорость движения молекул и
температура тела?
3.Опишите характер движения молекул в
твердых телах, жидкостях и газах.
4.Что называется внутренней энергией тела?
5.Зависит ли внутренняя энергия тела от того,
движется тело или покоится?
6.Зависит ли внутренняя энергия тела от
положения тела относительно других тел?
Решение качественных задач:
1.
Бросим свинцовый шар на свинцовую плиту. Потенциальная энергия
превратилась в кинетическую, затем исчезла. Сможете ли вы
опровергнуть это утверждение?
2.

Выведем из положения равновесия шар, подвешенный на нити.
Через некоторое время он остановится. Куда исчезла его
механическая энергия?
3.
В один стакан налита холодная вода, в другой – горячая такой же
массы. Одинакова ли внутренняя энергия в этих стаканах?
4.
На столе стакан и графин с водой одинаковой температуры.
Одинакова ли внутренняя энергия воды в этих сосудах?
Проведите экспериментальное исследование темы:
1.Зажгите свечу и подержите ладонь над свечой.
2.Зажгите одну спичку о коробок, а другую спичку внесите в пламя свечи. В чем
различие причин, приведших к воспламенению спички?
3.Потрите ладони друг о друга. Каков результат эксперимента? Каким способом
изменилась внутренняя энергия ладоней в первом и во втором случаях?
4.Согните алюминиевую проволоку несколько раз. Затем аккуратно исследуйте
сгиб проволоки. Изменилась ли внутренняя энергия сгиба? Каким способом?
Демонстрационный эксперимент:
Стеклянную колбу с помощью резинового шланга соединяем
с манометром.
 Осторожно опускаем колбу в сосуд с холодной
Осторожно опускаем колбу в сосуд с холоднойводой. Проводим наблюдение за уровнями жидкости манометре.
Определите:
1.
В каком случае внутренняя энергия воздуха
увеличивается, а в каком– уменьшается?
2.
Каким способом была изменена внутренняя энергия
воздуха?
3.
За счёт какой энергии совершилась механическая работа
по подъему
жидкости
в манометре?
Внутренняя
энергия
изменилась
Внутренняя энергия изменилась
способом теплопередачи
способом совершения
Заполнитемеханической
таблицу: работы
1. Наши предки добывали огонь, изменяя внутреннюю энергию куска
дерева путем трения.
2. Римляне стучали камнем о камень и пытались
высеченной искрой поджечь лучину, покрытую серой.
3. В 1861 году англичанин Роберт Бойл изобрел первые,
легко зажигающиеся спички – лучины, покрытые серой.
4. Английский аптекарь Джон Уокер изобрел первые практические
спички, которые зажигались о бумагу с нанесенным на неё
толченым стеклом.

5. Первые безопасные спички были изобретены в Швеции в
1855 году.
Работа с тестом
1. В каком из приведенных случаев внутренняя энергия тела изменяется?
а) камень, сорвавшись с утеса, падает всё быстрее и быстрее.
б) гантели подняты с пола и положены на полку.
в) электроутюг включили в сеть и начали гладить бельё.
г) соль пересыпали из пакета в солонку.
2.
Какими способами можно изменить внутреннюю энергию тела?
а) приведением его в движение.
б) совершением телом или над ним работы.
в) подняв его на некоторую высоту.
г) путем теплопередачи
3.
Изменение внутренней энергии какого тела происходит в результате теплопередачи
названных ситуациях?
а) Нагревание сверла, когда делают отверстие с помощью дрели.
б) Понижение температуры газа при его расширении.
в) Охлаждение пачки масла в холодильнике.
г) Нагревание колес движущегося поезда
4. В каком примере внутренняя энергия тела изменяется в результате совершения
механической работы?
а) Чайная ложка опущена в стакан с горячей водой.

б) При резком торможении грузовика от тормозов пошел запах гари.
в) В электрочайнике закипает вода.
г) Замерзшие руки человека согревает, прижав их к теплому радиатору.
5. Металлические бруски (см. рис.) имеют разную температуру. Два из них надо
соединить торцами так, чтобы их внутренняя энергия не изменилась. Какие это должны
быть бруски?
50°С
100°С
№1
№2
50°С
№3
10°С
а) № 1 и № 2
в) № 3 и № 4
б) № 1 и № 3
г) № 2 и № 4
№4
6. В контакт с каким бруском следует привести брусок №1, чтобы возникла теплопередача,
при которой его внутренняя энергия уменьшится?
40°С
100°С
№1
№2
40°С
30°С
№3
№4
а) №2
в) №4
б) №3
г) с любым
7. При соединении с каким из приведенных на рисунке в предыдущем задании брусков
возникает процесс теплопередачи, при котором внутренняя энергия бруска №2 будет
возрастать?
а) №1
б) №3
в) №4
г) такого бруска на рисунке нет.

Оценки обучающиеся получают:
За ответы на вопросы;
За решение качественных задач;
За проведение экспериментального исследования темы и
объяснение полученных результатов;
За заполнение таблицы;
За работу с тестовыми материалами.
Домашнее задание:
§3, № 932, 933, 934.
На этапе «Подведение итогов. Рефлексия» применяется прием
«для меня сегодняшний урок…».
Учащимся выдается индивидуальная карточка, в которой нужно
подчеркнуть фразы, характеризующие работу ученика на уроке.
На уроке я
работал
Своей
работой на
уроке я
Урок для
меня
показался
За урок я
Моё настроение
1. Активно
1. Доволен
1. Коротким
1. Устал
1. Стало лучше
2. Пассивно
2. Недоволен
2. Длинным
2. Не устал
2. Стало хуже
Урок физики по теме «Способы изменения внутренней энергии тела». 8-й класс
Цели урока:
1. Образовательная:
– выяснить условия, при которых внутренняя энергия тела изменяется,
– дать понятие теплопередачи;
2. Развивающая:
Развивающая:
– развивать правильную речь, логическое мышление;
3. Воспитательная:
– достигать внимания, сосредоточение внимания на изучение новой темы, активности
класса.
Ход урока
1. Актуализация знаний.
2. Проверка усвоения изученного материала (проверка домашнего задания).
(Работа по карточкам, 8 карточек по 2 варианта.)
Вариант № 1.
- Дайте определение внутренней энергии тела.
- Почему при малых значениях кинетической и потенциальной энергии одной молекулы внутренняя энергия тела достаточно большая величина?
- Камень лежал на земле, его подняли и положили на скамейку, а затем подбросили вверх. Изменилась ли внутренняя энергия камня при таких изменениях его положения?
Вариант № 2.
- Почему внутренняя энергия тела увеличивается с увеличением средней скорости движения молекул тела?
- Почему внутренняя энергия тела изменяется при деформации тела?
- Укажите, в каком из перечисленных ниже случаев, внутренняя энергия воды
не изменяется:
а) воду переливают из ведра в чайник;
б) её нагревают до кипения;
в) оставляют кипящей на плите.
3. Изучение нового теоретического материала.
Изменение внутренней энергии тела при повышении его температуры или при её понижении.
Опыт: на подставке укреплена тонкостенная латунная трубка, в которую налито немного эфира, трубка плотно закрыта пробкой. Трубку обвивают верёвкой и быстро двигают верёвку то в одну, то в другую сторону. Через некоторое время эфир закипает и пар вытолкнет пробку.
Внутренняя энергия тела увеличивается за счёт работы, совершённой над ним другими телами.
Увеличение внутренней энергии тела при его деформации; уменьшение внутренней энергии тела в случае, если тело совершает работу над другими телами.
Опыт: берут толтостенный стеклянный сосуд, закрытый пробкой. Через
специальное отверстие в сосуд накачивают воздух, в котором содержится водяной
пар. Через некоторое время пробка выскакивает из сосуда. В тот момент, когда
пробка выскакивает, в сосуде появляется туман. Появление тумана означает, что
воздух в сосуде стал холоднее, следовательно, его внутренняя энергия
уменьшилась.
Появление тумана означает, что
воздух в сосуде стал холоднее, следовательно, его внутренняя энергия
уменьшилась.
Объясняется это тем, что находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счёт своей внутренней энергии, которая при этом уменьшается. Об уменьшении энергии мы судим по охлаждению воздуха в сосуде.
Выяснение физической сути процесса нагревания холодной металлической ложки, опущенной в горячую воду. Постепенное выравнивание температур ложки и воды.
Понятие процесса теплопередачи.
Процесс изменения внутренней энергии без совершения работы над телом или самим телом называется теплопередачей.
Два способа изменения внутренней энергии:
- совершение над телом механической работы,
- теплопередача.
4. Закрепление изученного материала.
Задача № 1.
Растяните слегка резиновую нить. Как надо поступить (отпустить нить или растянуть сильнее), чтобы ее внутренняя энергия увеличилась?
Задача № 2.
Кусок сахара раздробили на мелкие кусочки, а потом растёрли в порошок. В каком случае внутренняя энергия сахара больше?
Задача № 3.
Каким способом и как изменяется внутренняя энергия пилы при распиливании бревна? На основании чего вы об этом судите?
Задача № 4.
Каким способом и как изменяется внутренняя энергия продуктов, положенных в холодильник? Объясните это на основе МКТ.
Задача № 5.
Почему при обработке детали напильником деталь и напильник нагреваются?
5. Подведение итогов.
– Как изменяется внутренняя энергия тела, когда над ним совершают работу.
– Приведите примеры увеличения внутренней энергии тела способом теплопередачи.
– Что такое теплопередача?
– Объясните на основе молекулярного строения вещества нагревание ложки,
опущенной в горячую воду.
– Какими двумя способами можно изменить внутреннюю энергию тела?
6. Домашнее задание. § 3, задание № 1 с.10, рабочая тетрадь: урок № 2 (2 часть).
Физика — 10
7.1
ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА.
ВНУТРЕННАЯ ЭНЕРГИЯ.
Дополните предложения, используя данные ключевые слова (ключевые слова можно использовать несколько раз; окончания предложений завершите соответствующим суффиксом ), на основании известных знаний (см.: Физика-8, стр. 20-26).
С ростом … тела, его … … увеличивается, так как увеличивается … … движения молекул и атомов, из которых
состоит тело. Это означает, что также увеличивается …
… молекул этого тела. С понижением … тела его . .. …
уменьшается. При совершении … над телом или при …тела его … … изменяется — увеличивается.
.. …
уменьшается. При совершении … над телом или при …тела его … … изменяется — увеличивается.
- скорость
- механическая работа
- температура
- излучение
- атом и молекула
- средняя кинетическая
энергия - внутренняя энергия
- Что подразумевают под выражением “внутренняя энергия тела”?
- Какими способами можно изменить внутреннюю энергию тела?
- Как изменится внутренняя энергия тела, например газа, при действии на него внешних сил, под действием которых он сжимается или расширяется?
 За счет чего изменилась внутренняя энергия системы?
За счет чего изменилась внутренняя энергия системы?Оборудование: тонкостенная бронзовая трубка, запаянная с одного конца, пробка, эфирный спирт, шнурок, подставка для штатива.
Ход исследования:
- Налейте в закрепленную на подставке трубку 3 — 4 см3 спирта. Подождав 1-2 минуты, плотно закройте пробкой открытый конец трубки.
- Оберните один раз шнурок вокруг трубки и, взявшись за его концы, тяните то в одну, то в другую сторону, создавая скольжение шнура по поверхности трубки (a). Продолжайте этот процесс до возникновения “необычного” явления в системе.
- Какое “необычное” явление наблюдалось в системе при непрерывном трении шнура о поверхность трубки? Как можно объяснить причину возникновения этого явления?
- Какова связь этого явления с изменением внутренней энергии системы?
Термодинамическая система. Раздел физики, изучающий тепловые явления в макроскопических системах, называется термодинамикой. В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос “как?”, например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамичекие системы.
Раздел физики, изучающий тепловые явления в макроскопических системах, называется термодинамикой. В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос “как?”, например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамичекие системы.
Тема №7553 Ответы к тестам по физике 8 класс 769874 (Часть 1)
Тема №7553
ТЕПЛОВЫЕ ЯВЛЕНИЯ
(Часть Тепловое движение. 5. В одном стакане находится теплая вода (№ 1), в другом —
5. В одном стакане находится теплая вода (№ 1), в другом —
горячая (№ 2), в третьем — холодная (№ 3). В каком из них
температура воды самая высокая, в каком — молекулы воды
движутся с наименьшей скоростью?
1) № 2; № 3 3) № 1; № 2) № 3; № 2 4) № 2; № 6. Чем отличаются молекулы горячего чая от молекул этого же
чая, когда он остыл?
1) Размером
2) Скоростью движения
3) Числом атомов в них
4) Цветом
7. Какие из перечисленных явлений тепловые?
1) Падение на пол ложки
2) Разогревание на плите супа
3) Таяние на солнце снега
4) Купание в бассейне
8. Какое движение называют тепловым?
1) Движение тела, при котором оно нагревается
2) Постоянное хаотическое движение частиц, из которых состоит тело
3) Движение молекул в теле при высокой температуре
9. Какие молекулы тела участвуют в тепловом движении? При
какой температуре?
1) Находящиеся на поверхности тела; при комнатной температуре
2) Все молекулы; при любой температуре
3) Расположенные внутри тела; при любой температуре
4) Все молекулы; при высокой температуре
10. Тепловые явления (Часть 2. Какими способами можно изменить внутреннюю энергию
Тепловые явления (Часть 2. Какими способами можно изменить внутреннюю энергию
тела?
1) Приведением его в движение
2) Совершением телом или над ним работы
3) Подняв его на некоторую высоту
4) Путем теплопередачи
3. Изменение внутренней энергии какого тела происходит в результате теплопередачи в названных ситуациях?
1) Нагревание сверла, когда делают отверстие с помощью
дрели
2) Понижение температуры газа при его расширении
3) Охлаждение пачки масла в холодильнике
4) Нагревание колес движущегося поезда
4. В каком примере внутренняя энергия тела изменяется в результате совершения механической работы?
1) Чайная ложка опущена в стакан с горячей водой
2) При резком торможении грузовика от тормозов пошел запах гари
3) В электрочайнике закипает вода
4) Замерзшие руки человек согревает, прижав их к теплому
радиатору
5. Металлические бруски (см. рис.) имеют разную температуру. Два из них надо соединить торцами так, чтобы их
внутренняя энергия не изменилась. ■ . Почему для возникновения конвекции в жидкости ее надо
■ . Почему для возникновения конвекции в жидкости ее надо
подогревать снизу?
1) Иначе жидкость не прогреется
2) Потому что нагретые верхние слои жидкости, как более
легкие, останутся наверху
3) Потому что подогревать сверху неудобно
. На какую полку — самую верхнюю или самую нижнюю —
надо поставить банку с вареньем в комнате-кладовке, чтобы
оно лучше сохранялось?
1) На самую верхнюю
2) На самую нижнюю
3) Все равно
. Какие существуют виды конвекции?
1) Естественная и свободная
2) Естественная и вынужденная
3) Только свободная
4) Только вынужденная
. В каком случае происходит вынужденная конвекция?
1) Согревание помещения электронагревателем с вентилятором
2) Нагревание воздуха стоящим на полу баком с кипятком
3) Обогревание северных районов Европы Гольфстримом
4) Образование прохладного ветерка вблизи водоема
Естественная конвекция наблюдается
1) в воде, когда ее греют в котелке над костром
2) в бульоне при размешивании в нем соли
3) в воздухе при работе вентилятора
4) в воде, когда от брошенного в нее камня расходятся круги
1Излучение
Излучение
1. 6. Выразите количества теплоты, равные 6000 Дж и 10 000 кал,
6. Выразите количества теплоты, равные 6000 Дж и 10 000 кал,
в килоджоулях.
1) 6 кДж и 4,2 кДж
2) 60 кДж и 42 кДж
3) 6 кДж и 42 кДж
4) 60 кДж и 4,2 кДж
7. Переведите количества теплоты, равные 7,5 кДж и 25 кал, в
джоули.
1) 750 Дж и 10,5 Дж
2) 7500 Дж и 105 Дж
3) 750 Дж и 105 Дж
4) 7500 Дж и 10,5 Дж
8. Чтобы нагреть чашку воды, потребовалось количество теплоты, равное 600 Дж. На сколько и как изменилась внутренняя
энергия воды?
1) На 600 Дж; уменьшилась
2) На 300 Дж; увеличилась
3) На 300 Дж; уменьшилась
4) На 600 Дж; увеличилась
9. При нагревании воды ей передано 400 Дж энергии. Какое
количество теплоты выделится при ее охлаждении до первоначальной температуры?
1) 100 Дж
2) 200 Дж
3) 400 Дж
4) Для ответа нужны дополнительные данные
10. Одинаковые шары нагреты до указанных на рисунке температур. Какому из них надо сообщить наименьшее количество
теплоты, чтобы довести температуру до 300 °С?
1№ 1 № 2 № 1) № 2) № 3) № Удельная теплоемкость
11. 4. Какое количество теплоты потребуется для повышения температуры на 1 °С кусков олова и меди массой по 1 кг?
4. Какое количество теплоты потребуется для повышения температуры на 1 °С кусков олова и меди массой по 1 кг?
1) 230 Дж и 400 Дж
2) 23 Дж и 40 Дж
3) 230 Дж и 40 Дж
4) 23 Дж и 400 Дж
5. Одинаково нагретые металлические бруски равной массы
внесены в холодное помещение. Какой из них выделит наибольшее количество теплоты?
1) № 2) № 3) № 4) Для ответа нет нужных данных
6. В сосуды налиты имеющие одинаковые температуры жидкости равной массы: подсолнечное масло, вода и керосин. Какая из них нагреется меньше всего, если им сообщить одинаковые количества теплоты?
1) Масло 2) Вода 3) Керосин
7. В три сосуда налит кипяток порциями равной массы. В один
из них опустили стальной шар (№ 1), в другой — медный (№
2) , в третий — железный (№ 3). В каком из сосудов температура воды при этом понизится больше? (Начальные температуры и массы шаров одинаковы.)
1) № 1 2) № 2 3) № 8. Для нагревания куска цинка массой 5 кг на 10 °С необходимо количество теплоты, равное 20 кДж. Расчет количества теплоты,
Расчет количества теплоты,
необходимого для нагревания тела
или выделяемого им при охлаждении
1. Если на нагревание 1,5 кг воды на 10 °С потребовалось 63 кДж,
то какое количество теплоты будет необходимо для нагревания
на то же число градусов 7,5 кг воды?
1) 31,5 кДж 3) 840 Дж
2) 315 кДж 4) 75 кДж
— £ Г 2. При остывании на 15 °С тело потеряло количество теплоты,
равное 2500 Дж. Сколько теплоты оно потеряет, остывая на
45 °С?
1) 75 Дж 3) 7500 Дж
2) 750 Дж 4) 75 кДж
— £ Г 3. Медный и стальной шары массой по 0,5 кг, находившиеся
при комнатной температуре (20 °С), опущены в кипяток. На
нагревание какого из них будет затрачено большее количество теплоты? Во сколько раз?
1) Стального; в 1,25 раза 3) Стального; в 1,5 раза
2) Медного; в 1,25 раза 4) Медного; в 1,5 раза
HD
та
sn
4. По какой формуле рассчитывают количество теплоты, которое необходимо передать телу для его нагревания и которое
оно передает окружающим телам при остывании?
1) F = gph 2) Q = cm(t2 — 3) F = gpV
^ HD
HD
2Тепловые явления (Часть •е?5. 10.* Когда в бак горячей воды массой 10 кг с температурой 90 °С
10.* Когда в бак горячей воды массой 10 кг с температурой 90 °С
налили холодную воду с температурой 10 °С и, перемешав,
измерили температуру, она оказалась равной 35 °С. Сколько
холодной воды было налито в бак?
1) 22 кг 3) « 25,7 кг
2) 36 кг 4) ж 16 кг
2Энергия топлива. Удельная теплота сгорания
Энергия топлива.
Удельная теплота сгорания
1. Источник энергии топлива —
1) движение его молекул
2) взаимодействие его молекул
3) соединение при его горении атомов в молекулы
jgs’lZf
ED2. Удельная теплота сгорания топлива — это физическая величина, показывающая
1) какое количество теплоты выделяется при полном сгорании 1 кг топлива
2) сколько энергии выделяется при сгорании топлива
3) какое количество теплоты можно получить, сжигая
имеющееся топливо
3. Удельная теплота сгорания топлива измеряется в
1) джоулях
Дж
кг • °С
3 )
Дж
с
Дж
кг
4. По какой формуле вычисляют количество теплоты, выделяющееся при сгорании топлива?
1) F = gm
2) Q = qm
3) Q — cm(t2 — П)
4) A = Nt
5. . При забивании молотом в грунт сваи произведена работа
. При забивании молотом в грунт сваи произведена работа
12 кДж. Какая энергия и на сколько изменилась при этом?
1) Внутренняя энергия сваи; на 12 кДж
2) Внутренняя энергия сваи и молота; на 12 кДж
3) Механическая энергия молота и сваи; на 6 кДж каждого
из этих тел
4) Внутренняя энергия сваи, молота и грунта; в сумме на
12 кДж
1. ИТОГОВЫЙ ТЕСТ (темы: «Внутренняя
энергия», «Количество теплоты»)
I вариант
1. Температура тела зависит от
1) количества в нем молекул
2) скорости движения частиц, из которых состоит тело
3) их размеров
4) расположения молекул в теле
. В пробирках находится ртуть во всех трех состояниях: в одной — в жидком, в другой — газообразном (пар), в третьей —
твердом. Чем отличаются частицы ртути в этих пробирках?
1) Ничем 2) Размером
3) Скоростью движения и расположением
. Какую энергию называют внутренней энергией тела?
1) Энергию теплового движения частиц тела
2) Кинетическую и потенциальную энергию всех частиц тела
3) Энергию их взаимодействия
. j£ T 3. Внутренняя энергия тела зависит от
j£ T 3. Внутренняя энергия тела зависит от
1) теплового движения частиц, из которых состоит тело
2) его внутреннего строения
3) количества молекул, входящих в состав тела
4) потенциальной и кинетической энергий всех частиц тела
4. Температуру тела повысили с 20 °С до 60 °С. Какая энергия и
как изменилась при этом?
1) Кинетическая энергия частиц тела — одна из составляющих его внутренней энергии; повысилась
2) Кинетическая энергия тела; повысилась
3) Внутренняя энергия; уменьшилась
4) Потенциальная энергия частиц тела — другая составляющая внутренней энергии; увеличилась
5. Массы одного и того же газа в сосудах одинаковы. В каком
сосуде внутренняя энергия газа наименьшая?
№ 1 № 2 № 1) № 1 2) № 2 3) № 3Итоговый тест. II вариант
6. Какими двумя способами можно изменить внутреннюю энергию тела?
1) Сообщив телу большую скорость
2) Подняв тело на меньшую высоту
3) Теплопередачей
4) Совершением работы телом или над телом
-£$»7. 10. По какой формуле рассчитывают количество теплоты, полученное нагреваемым телом или выделенное остывающим
10. По какой формуле рассчитывают количество теплоты, полученное нагреваемым телом или выделенное остывающим
телом?
1) Q = qm 3) Q = cm(t2 — Ч)
2) F = k(l2 ~ It) 4) = gph
j£$»11. В каких единицах измеряют удельную теплоемкость веществ?
3явления (Часть 12. Какое количество теплоты потребуется для нагревания 10 кг
меди на 1 °С?
1) 40 Дж
2) 400 Дж
3) 4000 Дж
13. Ведро горячей воды, температура которой 100 °С, а масса
10 кг, остывает до комнатной температуры (20 °С). Какое количество теплоты вода отдает окружающим телам и воздуху?
1) 3360 кДж 3) 33,6 кДж
2) 336 кДж 4) 3360 Дж
14. Алюминиевая кастрюля массой 100 г с 2 л воды нагрета от
10 °С до 90 °С. Какое количество теплоты затрачено на это?
1) 679360 Дж
2) 745600 Дж
3) 67936 Дж
4) 74560 Дж
15. Остывая, медный цилиндр массой 3 кг отдал окружающей
среде количество теплоты, равное 54 кДж. На сколько градусов понизилась его температура?
1) 4,5 °С 3) 18 °С
2) 45 °С 4) 135 °С
д ж
16. Г 0 5. В сосуде находятся равные массы одного и того же газа при
Г 0 5. В сосуде находятся равные массы одного и того же газа при
комнатной температуре. В каком из них его внутренняя
энергия наибольшая?
№ 2 № 1) № 1 2) № 2 3) № 2 ? 6. В каких приведенных здесь случаях внутренняя энергия тела
изменяется?
1) Ведро с водой поднимают и ставят на табуретку
2) Чайник с водой подогревают на плите
3) Кусок резины сжимают
4) Камешек забрасывают на крышу j£T37. В теплоизолированную камеру помещены два стальных бруска. Один имеет температуру -2 5 °С, другой -30 °С. У какого
из них внутренняя энергия больше? Выше какой температуры не может установиться температура бруска, получающего
теплоту?
Итоговый тест. Ill вариант
1) Первого; -25 °С
2) Второго; -25 °С
3) Первого; теплообмен при
происходить не будет
4) Второго; -30 °С
отрицательных температурах
8. Наименьшей теплопроводностью вещество обладает в
1) твердом состоянии
2) жидком состоянии
3) газообразном состоянии
4) Теплопроводность каждого вещества во всех состояниях
одинакова
9. ЮП
ЮП
1П
20. Закон сохранения и превращения энергии говорит о том, что
1) во всех явлениях, происходящих в природе, энергия не
возникает и не исчезает, а превращается из одного вида в
другой
2) внутренней энергией обладают все тела
3) полная механическая энергия в отсутствие сил трения постоянна
jg f! □
IV вариант
1. Температура тела понизится, если
1) уменьшить скорость его движения
2) молекулы расположатся в теле на меньших расстояниях
3) уменьшится скорость хаотического движения частиц тела
2. В тепловом движении участвуют
1) молекулы нагретого тела
2) частицы тела, когда оно находится в покое
3) молекулы движущегося тела
4) все частицы, из которых состоит тело, при любом его состоянии
3. Внутренняя энергия тела изменяется при изменении
1) его положения в пространстве
2) его взаимодействия с другими телами
3) потенциальной и кинетической энергий составляющих его
частиц
4) Ее вообще изменить нельзя
3Тепловые явления (Часть i£Tш
34. Внутренняя энергия тела возросла. Изменение какой физической величины позволяет судить об этом?
Внутренняя энергия тела возросла. Изменение какой физической величины позволяет судить об этом?
1) Давления 3) Силы
2) Температуры 4) Мощности
5. Газ помещен в сосуды, где он находится при разных температурах. В каком из них внутренняя энергия газа (его массы
одинаковы) наибольшая?
1) № 2) № 3) № 6. В каком случае внутренняя энергия тела не изменяется?
1) Лодка качается на волнах
2) Катящийся по полу мяч останавливается
3) Лейка с водой стоит на солнце
7. Из кастрюли с горячей водой, имеющей температуру 100 °С,
вынули нагревшиеся в ней диски — медный и бронзовый —
и положили их друг на друга. Какой из них будет передавать
другому внутреннюю энергию?
1) Бронзовый
2) Медный
3) Теплопередача происходить не будет
8. Наибольшей теплопроводностью вещество обладает в
1) твердом состоянии
2) жидком состоянии
3) газообразном состоянии
9. В вакууме энергия передается
1) излучением
2) конвекцией
3) теплопроводностью
4) всеми тремя способами
70°С
• • «
*20°С * • • *90°С •
№ 1 № 2 № Итоговый тест. IV вариант
IV вариант
10. Нагревая воду, ей передали 1000 Дж энергии. Какое количество теплоты выделит эта вода, остывая до своей первоначальной температуры?
1) 500 Дж
2) 1000 Дж
3) Чтобы ответить, нужны дополнительные данные
11. Какое количество теплоты выделит свинцовая плитка массой
1 кг, остывая на 7 °С?
1) 200 Дж
2) 400 Дж
3) 490 Дж
4) 980 Дж
12. По какой формуле определяют количество теплоты, необходимой для нагревания тела или выделяющейся при его охлаждении?
1) Р = mg 3)F = Щ2 — 1г)
2) Q = qm 4) Q = cm(t2 — tx)
13. Раскаленный до 450 °C медный шарик массой 100 г остывает
до 50 °С. Какое количество теплоты выделяет он при этом?
1) 160 Дж
2) 1600 Дж
3) 16000 Дж
4) 16 • 104 Дж
14. Стальной бак массой 500 г и вместимостью 40 л наполнен водой и нагрет до 70 °С. Какое количество теплоты потребовалось для этого? Начальная температура воды и бака 20 °С.
1) 8412,5 кДж 3) 841,25 кДж
2) 84125 кДж 4) 841250 кДж
15. полученное
полученное
20. Закон сохранения и превращения энергии устанавливает
1) превращение механической энергии во внутреннюю энергию и внутренней в механическую
2) постоянство общего значения энергии при всех ее превращениях и передачах от одного тела к другому
3) постоянство энергии при ее переходах из механической во
внутреннюю
4) равенство при теплообмене полученной одним телом энергии и отданной другим телам
4ТЕПЛОВЫЕ ЯВЛЕНИЯ
(Часть Агрегатные состояния вещества.
Плавление и отвердевание
кристаллических тел
1. Агрегатное состояние вещества — это его пребывание в виде
1) твердого тела
2) жидкого тела
3) газообразного тела
4) какого-либо из этих трех тел
2. В каком агрегатном состоянии могут находиться железо и
ртуть?
1) Железо в твердом, ртуть в жидком
2) И железо, и ртуть в жидком
3) И железо, и ртуть в твердом
4) Оба вещества могут находиться в любом агрегатном состоянии
3. От чего зависит, в каком именно агрегатном состоянии находится вещество?
1) От числа и состава молекул
2) От расположения, взаимодействия и движения молекул
3) От расположения и состава молекул
4) От взаимодействия и числа молекул
4. j2S»4Тепловые явления (Часть _□
j2S»4Тепловые явления (Часть _□
шш
_ш
5. Плавление — это
1) таяние снега или льда
2) разжижение вещества, когда оно получает теплоту
3) переход при получении веществом энергии из твердого состояния в жидкое
6. Температура, при которой вещество плавится, называется
1) температурой перехода в жидкое состояние
2) температурой плавления
3) температурой таяния
7. Температура плавления цинка 420 °С. В каком состоянии находится этот металл, если его температура 410 °С (№ 1)?
430 °С (№ 2)?
1) № 1 — твердом, № 2 — жидком
2) № 1 — жидком, № 2 — твердом
3) № 1 и № 2 — жидком
4) № 1 и № 2 — твердом
8. Отвердевание — это
1) отдача веществом энергии и превращение в другое вещество
2) переход вещества из жидкого состояния в твердое
3) замерзание воды
9. Как изменяется внутренняя энергия вещества при плавлении? При отвердевании?
1) При плавлении уменьшается, при отвердевании увеличивается
2) Не изменяется
3) В том и другом случае возрастает
4) При плавлении увеличивается, при отвердевании уменьшается
10. Температура плавления стали 1500 °С. При какой температуре она отвердевает?
Температура плавления стали 1500 °С. При какой температуре она отвердевает?
1) При температурах ниже 1500 °С
2) При 1500 °С
3) При температурах выше 1500 °С
4) При любой температуре, если отдает энергию
4Агрегатные состояния вещества. Плавление и отвердевание
11. Из какого металла — алюминия, меди или стали — нужно изготовить плавильный сосуд, чтобы расплавить в нем свинец?
1) Из алюминия
2) Из меди
3) Из стали
4) Из любого названного
12. В сосуд с расплавленным алюминием упали цинковая и железная пластинки. Какая из них расплавится?
1) Цинковая
2) Железная
3) Никакая
4) Обе
13. В каком состоянии будут находиться ртуть и натрий при
комнатной температуре (20 °С)?
1 ) В твердом
2) В жидком
3) Ртуть — в жидком, натрий в твердом
4) Ртуть в твердом, натрий в жидком
14. На рисунке изображен график нагревания и таяния снега и
нагревания полученной из него воды. Какой участок графика соответствует таянию снега? Сколько примерно времени оно длилось? До какой температуры нагрелась вода за
5 мин?
1) ВС; 3,5 мин; 30 °С 3) АВ; 1,5 мин; 30 °С
2) ВС; 2 мин; 30 °С 4) ВС; 3,5 мин; 40 °С
^ * Г * Г 4Тепловые явления (Часть ^ ! □
та
^ 15. Воду из комнаты с температурой 25 °С вынесли на 30-градусный мороз, где она превратилась в лед. График изменения ее
Воду из комнаты с температурой 25 °С вынесли на 30-градусный мороз, где она превратилась в лед. График изменения ее
температуры и льда показан на рисунке. Какой его участок соответствует отвердеванию воды? О чем свидетельствует участок
DE1) ВС; о достижении льдом температуры окружающего воздуха и прекращении ее изменения
2) АВ; о выравнивании температур льда и воздуха
3) CD; о том, что температура льда стала равной 30 °С
16. Что происходит с температурой вещества во время его плавления?
1) Она понижается
2) Повышается
3) Остается постоянной
17. Какой из приведенных графиков изменения температуры вещества соответствует процессу его отвердевания, какой нагреванию без перехода в другое агрегатное состояние?
41) № 3; № 2) № 2; № 3) № 1; № 4) № 2; № Удельная теплота плавления
18. Какой участок изображенных здесь графиков № 1 и № изменения температуры вещества соответствует его отвердеванию?
t,°С А
№ _ в Д D
t, мин
1) АВ
2) FK
3) EF
4) CD
Удельная теплота плавления
1. HD
HD
HD
>efHD
HD
0 П
4i) 2,1 •105 Дж 0,25 • 10!5 ДЖ
кг К Г
2) 2,3 108 Дж 8,2 •106 Дж
кг кг
3) 2,1 •105 Дж 8,2 •106 Дж
кг кг
4) 2,3 •108 Дж 0,25 • 10;i Дж
КГ КГ
4. На плавление какого из кубиков — медного или алюминиевого — пойдет меньше энергии и во сколько раз, если плавить эти металлы будут при температуре плавления каждого
из них?
1) Медного в * 4 раза
2) Алюминиевого в ~ 4 раза
3) Медного в * 2 раза
4) Алюминиевого в ~ 2 раза
5. Почему во время плавления температура нагреваемого вещества не повышается?
1) Потому что оно уже достигло температуры плавления
2) Потому что идет переход из твердого состояния в жидкое
3) Потому что получаемая твердым веществом энергия расходуется на разрушение его кристаллического строения
6. Нагретый до температуры плавления лед частично растаял.
Оставшийся лед или вода имеет большую внутреннюю
энергию?
1) Лед
2) Вода
3) Их внутренние энергии одинаковы
7. 9. Известно, что на плавление куска меди при температуре
9. Известно, что на плавление куска меди при температуре
плавления израсходовано 6,3 • 105 Дж энергии. Какова его
масса? Какое количество теплоты выделится при отвердевании жидкой меди этой массы?
1) 3 кг; 6,3 • 105 Дж 3) 1 кг; 6,3 • 105 Дж
2) 1 кг; 2,1 • 105 Дж 4) 3 кг; 2,1 • 105 Дж
ir<HD
Внутренняя энергия тел. Два способа изменения внутренней энергии — ОСНОВЫ ТЕРМОДИНАМИКИ — УРОКИ ФИЗИКИ В 10 КЛАССЕ. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
ОСНОВЫ ТЕРМОДИНАМИКИ*
Урок № 1
Тема. Внутренняя энергия тел. Два способа изменения внутренней энергии
Цель: дать молекулярно-кинетическое трактовка понятия внутренней энергии и способов изменения внутренней энергии; развивать логическое мышление, умение анализировать, делать выводы.
Тип урока: урок изучения нового материала.
Демонстрации: зависимость между объемом, давлением и температурой; изменение внутренней энергии тела в результате выполнения работы.
ХОД УРОКА
И. Актуализация опорных знаний
Работа с научным текстом
Более 200 лет назад М. В. Ломоносов в работе «Размышления о причине теплоты и холода» писал: «Так как тела могут двигаться двойным движением — общим, при котором все тело непрерывно меняет свое положение при неподвижных друг относительно друга частиц, и внутренним, которое является изменением места нечувствительных частиц материи, и так как при самом быстром общем движении не наблюдается теплоты, а при его отсутствии наблюдается теплота, то очевидно, что теплота состоит во внутреннем движении материи».
— О какие два разные типы движения идет речь?
— Какие виды механической энергии тела вы знаете?
— Что можно сказать о относительную скорость движения молекул при рассмотрении механической и внутренней энергии?
— Изменение параметров приводит к изменению механической, а какие к изменению внутренней энергии?
II. Постановка учебной проблемы
Постановка учебной проблемы
На стол с определенной высоты падает пластилиновая шарик. Ответьте на вопросы:
1. Какую энергию имела шарик на начало движения?
2. Происходил переход энергии во время падения? Какой именно?
3. Какую энергию имела шарик непосредственно перед ударом? Куда делась эта энергия?
4. Что случилось с шариком и плитой?
Если тереть лед при температуре 0 °С, он будет превращаться в воду, температура которой 0 °С. На что же превращается в этом эксперименте механическая энергия?
III. Изучение нового материала
Внутренняя энергия — это сумма кинетической энергии хаотического движения молекул и потенциальной энергии взаимодействия молекул друг с другом. Внутренняя энергия — функция состояния U = f(T).
В термодинамике рассматривают изменение внутренней энергии при переходе из одного состояния в другое. Величины, определяющие состояние газа: Р, Т, V.
Проще всего можно вычислить внутреннюю энергию идеального одноатомного газа, потому что его молекулы совершают только поступательное движение.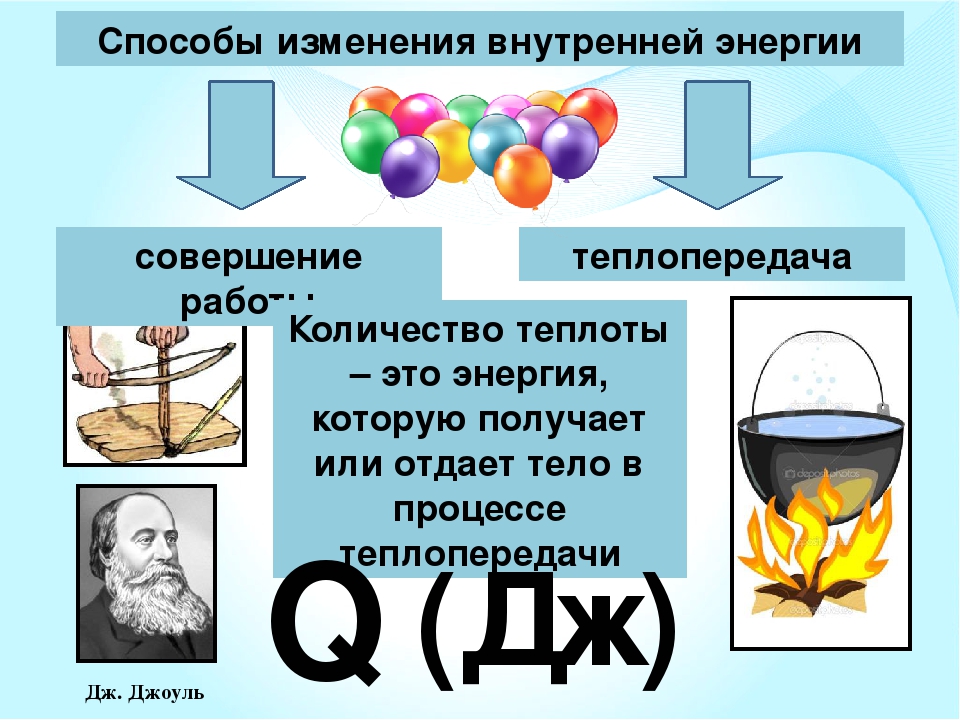 Изменение внутренней энергии данной массы идеального газа происходит только за изменения его температуры:
Изменение внутренней энергии данной массы идеального газа происходит только за изменения его температуры:
Какими способами можно изменить внутреннюю энергию тела? Обсуждение опытов.
Выводы обобщаем в виде таблицы.
IV. Закрепление изученного материала
Решение задач
1. Вычислите внутреннюю энергию одноатомного газа с количеством вещества 5 моль при температуре 27 °С.
2. На сколько изменится внутренняя энергия 200 г гелия при увеличении температуры на 20 К?
V. Обобщение знаний
Составление ОК.
• Внутренняя энергия макроскопического тела (U) является суммой кинетической энергии хаотического движения молекул (атомов) и потенциальной энергии их взаимодействия.
• Внутренняя энергия одноатомного идеального газа:
где m — масса газа; М — молярная масса газа; R — универсальная газовая постоянная; NA — постоянная Авогадро.
• Способы изменения внутренней энергии:
1. Выполнения работы.
2. Теплообмен.
• Виды теплообмена — процесс передачи энергии от более нагретых тел к менее нагретым:
— теплопроводность;
— конвекция;
— излучения
VI. Итоги урока
Упражнение «Микрофон». Закончи предложения.
1. Энергию хаотического движения молекул и их взаимодействия называют…
2. Она обозначается буквой…, а количество теплоты обозначается буквой… .
3. Количество теплоты и внутреннюю энергию измеряют в… .
4. Внутреннюю энергию тела можно уменьшить, если… .
5. Внутреннюю энергию можно увеличить, если… .
VII. Домашнее задание
1. Проработать соответствующий раздел учебника.
2. Выполнить № 3.1,416-Г из сборника задач под редакцией И. М. Гельфгата.
____________________________________________________________________
*Пишінська Валентина Анатольевна — учитель физики Новогребельської общеобразовательной школы Жашковской районного совета, высшая категория
6.
 3: Первый закон термодинамики: внутренняя энергия
3: Первый закон термодинамики: внутренняя энергияЦели обучения
- Для расчета изменений внутренней энергии
Чтобы изучить поток энергии во время химической реакции, нам нужно различать систему, небольшую, четко определенную часть вселенной, которая нас интересует (например, химическая реакция), и ее окружение, остальную часть Вселенная, включая контейнер, в котором происходит реакция (Рисунок \ (\ PageIndex {1} \)).В последующем обсуждении смесь химических веществ, которая вступает в реакцию, всегда является системой, а поток тепла может исходить от системы к окружающей среде или наоборот.
Рисунок \ (\ PageIndex {1} \): Система и ее окружение. Система — это та часть вселенной, которую мы интересуемся изучением, например химическая реакция внутри колбы. Окружающая среда — это остальная часть Вселенной, включая контейнер, в котором происходит реакция. В химии важны три типа систем.Открытая система может обмениваться материей и энергией с окружающей средой. Кастрюля с кипящей водой — это открытая система, потому что горелка подает энергию в виде тепла, а вещество в виде водяного пара теряется при кипении воды. Замкнутая система может обмениваться энергией, но не веществом, с окружающей средой. Запечатанный пакет готового обеда, брошенный в кастрюлю с кипящей водой, представляет собой закрытую систему, потому что тепловая энергия передается системе от кипящей воды, но не происходит обмен веществ (если пакет не протекает, и в этом случае он больше не закрытая система).Изолированная система не обменивается ни энергией, ни материей с окружающей средой. Между системой и ее окружением всегда происходит обмен энергией, хотя этот процесс может происходить очень медленно. По-настоящему изолированной системы на самом деле не существует. Изолированный термос с горячим кофе похож на изолированную систему, но в конечном итоге кофе остывает, поскольку тепло передается в окружающую среду. Во всех случаях количество тепла, теряемого системой, равно количеству тепла, полученного ее окружением, и наоборот.
Кастрюля с кипящей водой — это открытая система, потому что горелка подает энергию в виде тепла, а вещество в виде водяного пара теряется при кипении воды. Замкнутая система может обмениваться энергией, но не веществом, с окружающей средой. Запечатанный пакет готового обеда, брошенный в кастрюлю с кипящей водой, представляет собой закрытую систему, потому что тепловая энергия передается системе от кипящей воды, но не происходит обмен веществ (если пакет не протекает, и в этом случае он больше не закрытая система).Изолированная система не обменивается ни энергией, ни материей с окружающей средой. Между системой и ее окружением всегда происходит обмен энергией, хотя этот процесс может происходить очень медленно. По-настоящему изолированной системы на самом деле не существует. Изолированный термос с горячим кофе похож на изолированную систему, но в конечном итоге кофе остывает, поскольку тепло передается в окружающую среду. Во всех случаях количество тепла, теряемого системой, равно количеству тепла, полученного ее окружением, и наоборот. То есть полная энергия системы плюс ее окружение постоянна , что должно быть истинным, если энергия сохраняется .
То есть полная энергия системы плюс ее окружение постоянна , что должно быть истинным, если энергия сохраняется .
Состояние системы — это полное описание системы в данный момент времени, включая ее температуру и давление, количество вещества, которое она содержит, ее химический состав и физическое состояние вещества. Функция состояния — это свойство системы, величина которого зависит только от текущего состояния системы, а не от ее предыдущей истории.Температура, давление, объем и потенциальная энергия — все это функции состояния. Например, температура духовки не зависит от того, сколько шагов она могла предпринять для достижения этой температуры. Точно так же давление в шине не зависит от того, как часто воздух нагнетается в шину для достижения этого давления, как и конечный объем воздуха в шине. С другой стороны, тепло и работа не являются функциями состояния, потому что они зависят от пути . Например, автомобиль, стоящий на верхнем уровне гаража, имеет одинаковую потенциальную энергию независимо от того, был ли он поднят краном, установлен там вертолетом, поднят или поднят группой студентов (Рисунок \ (\ PageIndex) {2} \)). Однако объем работы, затраченной на его получение, может сильно различаться в зависимости от выбранного пути. Если бы ученики решили довести машину до вершины пандуса, они бы выполнили гораздо больше работы, чем если бы они просто подтолкнули машину вверх по пандусу (если, конечно, они не забыли отпустить стояночный тормоз, и в этом случае Затраченные работы существенно увеличились бы!). Однако потенциальная энергия автомобиля одинакова, независимо от того, какой путь они выберут.
Однако объем работы, затраченной на его получение, может сильно различаться в зависимости от выбранного пути. Если бы ученики решили довести машину до вершины пандуса, они бы выполнили гораздо больше работы, чем если бы они просто подтолкнули машину вверх по пандусу (если, конечно, они не забыли отпустить стояночный тормоз, и в этом случае Затраченные работы существенно увеличились бы!). Однако потенциальная энергия автомобиля одинакова, независимо от того, какой путь они выберут.
Направление теплового потока
Реакция порошкообразного алюминия с оксидом железа (III), известная как термитная реакция, генерирует огромное количество тепла — фактически достаточного для плавления стали (рис. \ (\ PageIndex {3} \)).Сбалансированное химическое уравнение реакции выглядит следующим образом:
\ (\ PageIndex {3} \)).Сбалансированное химическое уравнение реакции выглядит следующим образом:
\ [\ ce {2Al (s) + Fe_2O_3 (s) -> 2Fe (s) + Al_2O_3 (s)} \ label {5.2.1} \]
Рисунок \ (\ PageIndex {3} \): Реакция термитов выделяет столько тепла, что производимое ею железо выходит расплавленным, что делает эту реакцию полезной при сварке. Изображение предоставлено Kingfisher [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)], из Wikimedia Commons.Мы также можем записать это химическое уравнение как
\ [\ ce {2Al (s) + Fe_2O_3 (s) \ rightarrow 2Fe (s) + Al_2O_3 (s)} + \ text {heat} \ label {5.2.2} \]
, чтобы указать, что тепло является одним из продуктов. Химические уравнения, в которых тепло отображается как реагент или продукт, называются термохимическими уравнениями . В этой реакции система состоит из атомов алюминия, железа и кислорода; все остальное, включая контейнер, составляет окружение. Во время реакции выделяется столько тепла, что железо разжижается.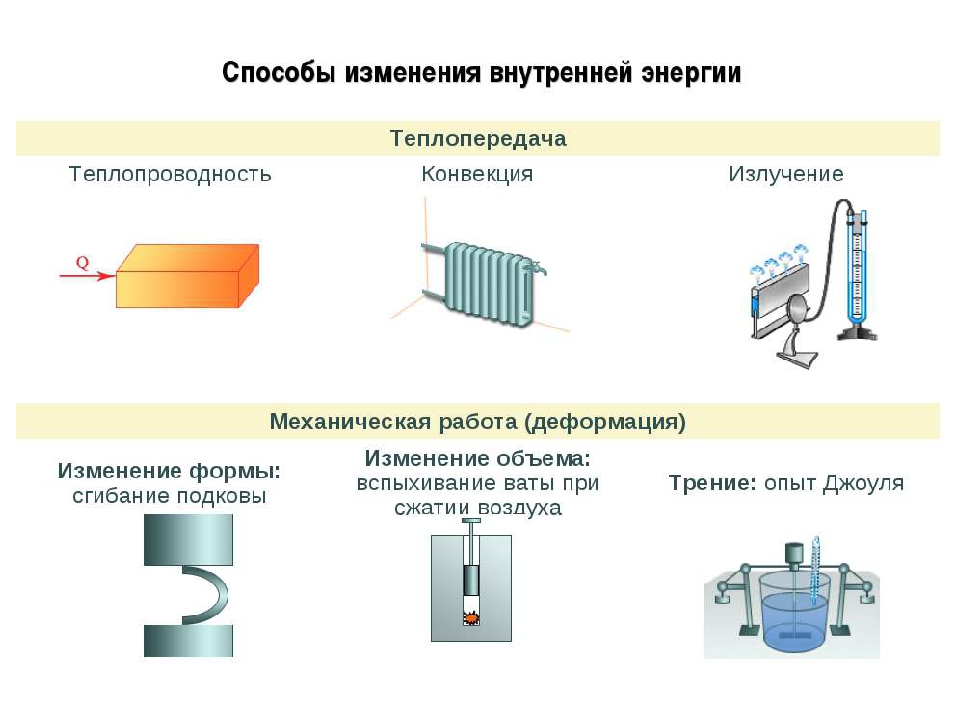 В конце концов, система остывает; железо затвердевает, когда тепло передается в окружающую среду.Процесс, в котором тепло ( q ) передается от системы к ее окружению, описывается как экзотермический. По соглашению \ (q <0 \) для экзотермической реакции.
В конце концов, система остывает; железо затвердевает, когда тепло передается в окружающую среду.Процесс, в котором тепло ( q ) передается от системы к ее окружению, описывается как экзотермический. По соглашению \ (q <0 \) для экзотермической реакции.
Когда вы держите кубик льда в руке, тепло из окружающей среды (включая вашу руку) передается в систему (лед), в результате чего лед тает, а ваша рука становится холодной. Мы можем описать этот процесс следующим термохимическим уравнением:
\ [\ ce {heat + H_2O (s) \ rightarrow H_2O (l)} \ label {5.2.3} \]
Когда тепло передается с на системе из ее окружения, процесс является эндотермическим. По соглашению \ (q> 0 \) для эндотермической реакции.
Тепло технически не является компонентом химических реакций
Технически, наличие члена \ (тепло \) в химической реакции, как в Уравнениях \ (\ ref {5.2.2} \) и \ (\ ref {5.2.3} \), является плохой формой, поскольку это не настоящий вид в реакции. Однако это удобный подход для представления экзотермического и эндотермического поведения, который обычно используется химиками.
Однако это удобный подход для представления экзотермического и эндотермического поведения, который обычно используется химиками.
Первый Закон
Связь между изменением энергии системы и ее окружением задается первым законом термодинамики , который гласит, что энергия Вселенной постоянна. Математически этот закон можно выразить следующим образом:
\ [U_ {univ} = ΔU_ {sys} + ΔU_ {surr} = 0 \ label {5.2.4a} \]
\ [\ Delta {U_ {sys}} = — ΔU_ {surr} \ label {5.2.4b} \]
, где индексы univ, sys и surr относятся к вселенной, системе и окружению соответственно.Таким образом, изменение энергии системы идентично по величине, но противоположно по знаку изменению энергии ее окружения.
Все системы, химические или другие, имеют тенденцию двигаться к состоянию с наименьшей возможной энергией.
Важным фактором, определяющим исход химической реакции, является тенденция всех систем, химических или иных, двигаться к наиболее низкому возможному общему энергетическому состоянию. Когда кирпич падает с крыши, его потенциальная энергия преобразуется в кинетическую; когда он достигает уровня земли, он достигает состояния с более низкой потенциальной энергией.Любой, кто находится поблизости, заметит, что энергия передается в окружающую среду, поскольку шум от удара отражается, и пыль поднимается, когда кирпич падает на землю. Точно так же, если искра воспламеняет смесь изооктана и кислорода в двигателе внутреннего сгорания, диоксид углерода и вода образуются спонтанно, в то время как потенциальная энергия (в виде относительного положения атомов в молекулах) выделяется в окружающую среду в виде тепла и Работа. Содержание внутренней энергии смеси продуктов \ (CO_2 / H_2O \) меньше, чем у смеси реагентов изооктан / \ (O_2 \).Однако эти два случая различаются по форме передачи энергии в окружающую среду. В случае падающего кирпича энергия передается как работа, выполняемая над всем, что оказывается на пути кирпича; в случае сжигания изооктана энергия может выделяться исключительно в виде тепла (если реакция осуществляется в открытом контейнере) или в виде смеси тепла и работы (если реакция осуществляется в цилиндре двигателя внутреннего сгорания.
Когда кирпич падает с крыши, его потенциальная энергия преобразуется в кинетическую; когда он достигает уровня земли, он достигает состояния с более низкой потенциальной энергией.Любой, кто находится поблизости, заметит, что энергия передается в окружающую среду, поскольку шум от удара отражается, и пыль поднимается, когда кирпич падает на землю. Точно так же, если искра воспламеняет смесь изооктана и кислорода в двигателе внутреннего сгорания, диоксид углерода и вода образуются спонтанно, в то время как потенциальная энергия (в виде относительного положения атомов в молекулах) выделяется в окружающую среду в виде тепла и Работа. Содержание внутренней энергии смеси продуктов \ (CO_2 / H_2O \) меньше, чем у смеси реагентов изооктан / \ (O_2 \).Однако эти два случая различаются по форме передачи энергии в окружающую среду. В случае падающего кирпича энергия передается как работа, выполняемая над всем, что оказывается на пути кирпича; в случае сжигания изооктана энергия может выделяться исключительно в виде тепла (если реакция осуществляется в открытом контейнере) или в виде смеси тепла и работы (если реакция осуществляется в цилиндре двигателя внутреннего сгорания. ). Поскольку тепло и работа — единственные два способа передачи энергии между системой и ее окружением, любое изменение внутренней энергии системы представляет собой сумму переданного тепла (q) и проделанной работы (w):
). Поскольку тепло и работа — единственные два способа передачи энергии между системой и ее окружением, любое изменение внутренней энергии системы представляет собой сумму переданного тепла (q) и проделанной работы (w):
\ [ΔU_ {sys} = q + w \ label {5.2.5} \]
Хотя \ (q \) и \ (w \) сами по себе не являются функциями состояния, их сумма (\ (ΔU_ {sys} \)) не зависит от пройденного пути и, следовательно, является функцией состояния. Основная задача разработчиков любой машины, преобразующей энергию в работу, состоит в том, чтобы максимально увеличить объем получаемой работы и минимизировать количество энергии, выделяемой в окружающую среду в виде тепла. Примером может служить сжигание угля для производства электроэнергии. Хотя максимальное количество энергии, доступное в процессе, фиксируется содержанием энергии в реагентах и продуктах, доля этой энергии, которая может быть использована для выполнения полезной работы, не является фиксированной.
Поскольку мы фокусируемся почти исключительно на изменениях энергии системы, мы не будем использовать «sys» в качестве индекса, если нам не нужно явно различать систему и ее окружение.
Хотя \ (q \) и \ (w \) не являются функциями состояния, их сумма (\ (ΔU_ {sys} \)) не зависит от пройденного пути и, следовательно, является функцией состояния.
Таким образом, согласно первому закону, мы можем определить \ (ΔU \) для любого процесса, если мы можем измерить как \ (q \), так и \ (w \). Теплота \ (q \) может быть рассчитана путем измерения изменения температуры окружающей среды.Работа, \ (w \), может иметь разные формы, но ее тоже можно измерить. Одной из важных форм работы в области химии является работа с объемом давления , выполняемая расширяющимся газом. При постоянном внешнем давлении (например, атмосферном)
\ [w = −PΔV \ label {5.2.6} \]
Отрицательный знак, связанный с выполненной работой \ (PV \), указывает на то, что система теряет энергию при увеличении объема. То есть расширяющийся газ действительно воздействует на свое окружение, в то время как газ, который сжимается, воздействует на него окружением.
Пример \ (\ PageIndex {1} \)
Проба идеального газа в цилиндре двигателя сжимается от 400 мл до 50,0 мл во время такта сжатия при постоянном давлении 8,00 атм. В то же время 140 Дж энергии передается от газа окружающей среде в виде тепла. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
В то же время 140 Дж энергии передается от газа окружающей среде в виде тепла. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
Дано : начальный объем, конечный объем, внешнее давление и количество энергии, переданной в виде тепла
Запрошено: общее изменение внутренней энергии
Стратегия:
- Определите знак \ (q \) для использования в уравнении \ (\ ref {5.2.5} \).
- По формуле \ (\ ref {5.2.6} \) вычислите \ (w \) по заданным значениям. Подставьте это значение в уравнение \ (\ ref {5.2.5} \), чтобы вычислить \ (ΔU \).
Решение
A Из уравнения \ (\ ref {5.2.5} \) мы знаем, что ΔU = q + w. Нам дана величина q (140 Дж), и нам нужно только определить ее знак. Поскольку энергия передается от системы (газа) в окружающую среду, q по соглашению отрицательно.
B Поскольку газ сжимается, мы знаем, что в системе проводятся работы, поэтому \ (w \) должно быть положительным.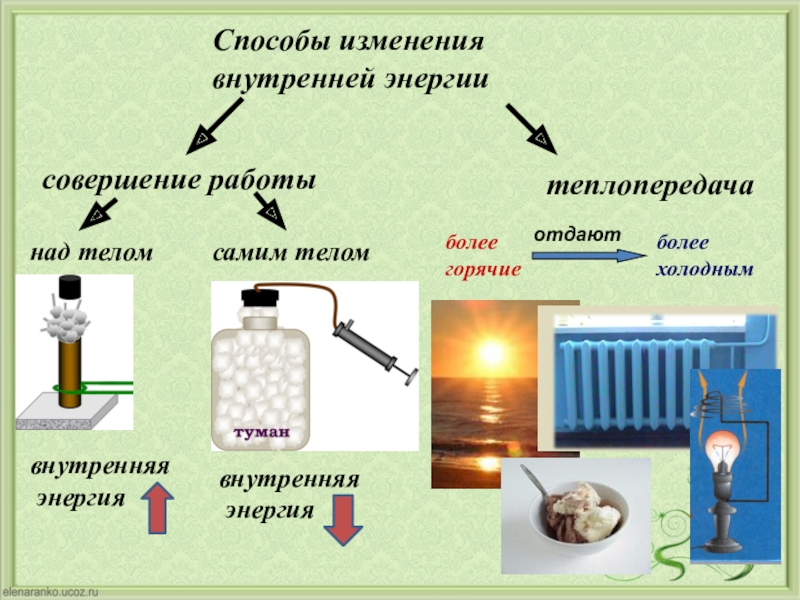 Из уравнения \ (\ ref {5.2.5} \),
Из уравнения \ (\ ref {5.2.5} \),
\ [w = -P _ {\ textrm {ext}} \ Delta V = -8.00 \ textrm {atm} (\ textrm {0.0500 L} — \ textrm {0.400 L}) \ left (\ dfrac {\ textrm {101.3 J}} {\ mathrm {L \ cdot atm}} \ right) = 284 \ textrm {J} \]
Таким образом,
\ [\ begin {align *} ΔU & = q + w \\ [4pt] & = −140 \, J + 284 \, J \\ [4pt] & = 144 \, J \ end {align *} \ ]
В этом случае, хотя работа выполняется с газом, увеличивая его внутреннюю энергию, тепло течет из системы в окружающую среду, уменьшая его внутреннюю энергию на 144 Дж.Проделанная работа и переданное тепло могут иметь противоположные знаки.
Упражнение \ (\ PageIndex {1} \)
Образец идеального газа расширяется от начального объема 0,200 л до конечного объема 3,50 л при постоянном внешнем давлении 0,995 атм. При этом 117 Дж тепла передается от окружающей среды к газу. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
- Ответ
−216 Дж
По соглашению (для химиков) и тепловой поток, и работа имеют отрицательный знак, когда энергия передается от системы к ее окружению и наоборот.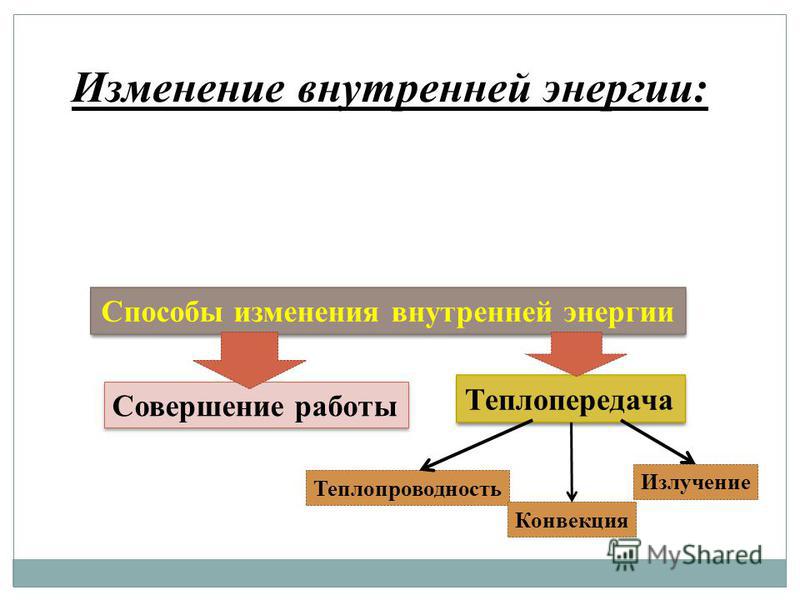
Сводка
В химии небольшая часть Вселенной, которую мы изучаем, — это система , а остальная часть Вселенной — это окружение . Открытые системы могут обмениваться как веществом, так и энергией со своим окружением, закрытые системы могут обмениваться энергией, но не веществом со своим окружением, а изолированные системы не могут обмениваться ни материей, ни энергией со своим окружением. Функция состояния является свойством системы, которое зависит только от ее текущего состояния , а не от ее истории.Реакция или процесс, в котором тепло передается от системы к ее окружению, — это экзотермический . Реакция или процесс, в котором тепло передается системе из окружающей среды, — это эндотермический . Первый закон термодинамики гласит, что энергия Вселенной постоянна. Изменение внутренней энергии системы — это сумма переданного тепла и проделанной работы. Тепловой поток равен изменению внутренней энергии системы плюс проделанная работа фотоэлектрических модулей.Когда объем системы постоянен, изменения ее внутренней энергии можно рассчитать, подставив закон идеального газа в уравнение для ΔU.
Тепловой поток равен изменению внутренней энергии системы плюс проделанная работа фотоэлектрических модулей.Когда объем системы постоянен, изменения ее внутренней энергии можно рассчитать, подставив закон идеального газа в уравнение для ΔU.
2.1: Внутренняя энергия — Chemistry LibreTexts
Определение системы
Химики интересуются системами, содержащими материю — материю, имеющую массу и занимающую физическое пространство. Классическая термодинамика рассматривает макроскопических аспектов материи. Он имеет дело со свойствами совокупностей огромного количества микроскопических частиц (молекул, атомов и ионов).Фактически, макроскопическая точка зрения рассматривает материю как непрерывную материальную среду , а не как набор дискретных микроскопических частиц, которые, как мы знаем, действительно присутствуют. Хотя эта электронная книга представляет собой описание классической термодинамики, время от времени она будет указывать на связи между макроскопическими свойствами и молекулярной структурой и поведением.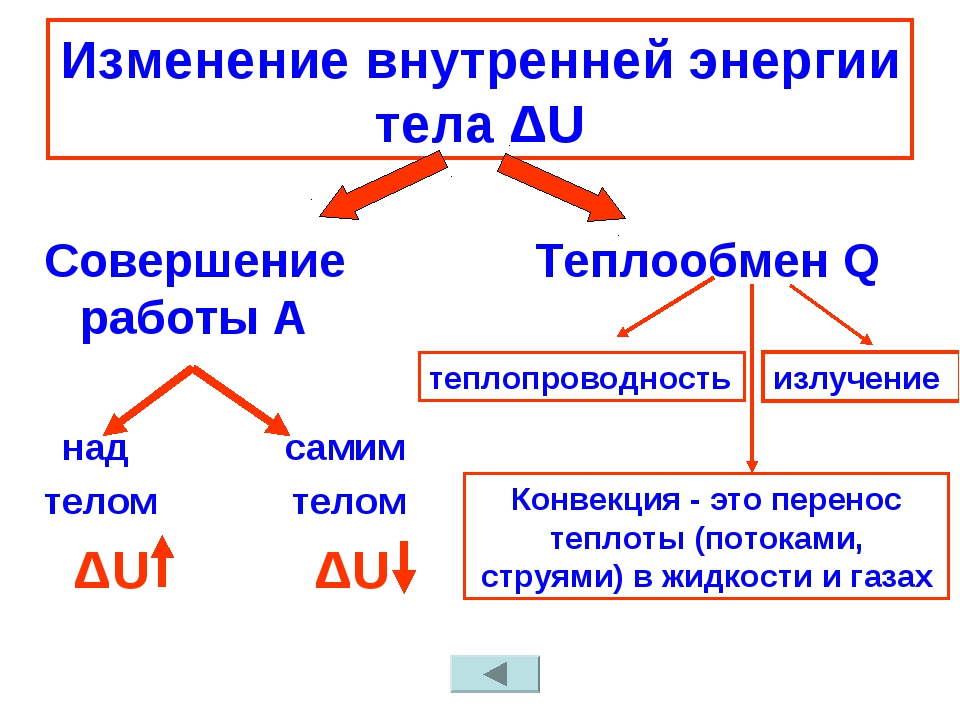
Термодинамическая система — это любая трехмерная область физического пространства, на которой мы хотим сосредоточить свое внимание.Обычно мы рассматриваем только одну систему за раз и называем ее просто «системой». Остальная часть физической вселенной составляет , окружение системы.
Граница — это замкнутая трехмерная поверхность, которая охватывает систему и отделяет ее от окружающей среды. Граница может (и обычно совпадает) с реальными физическими поверхностями: границей между двумя фазами, внутренней или внешней поверхностью стенки колбы или другого сосуда и так далее.В качестве альтернативы, часть или вся граница может быть воображаемой нематериальной поверхностью в пространстве, не связанной с какой-либо физической структурой. Размер и форма системы, определяемые ее границами, могут изменяться со временем. Короче говоря, наш выбор трехмерной области, составляющей систему, является произвольным, но важно, чтобы мы точно знали, что это за выбор.
Обычно мы думаем о системе как о части физической вселенной, на которую мы можем влиять только косвенно, через ее взаимодействие с окружающей средой, а окружение — как часть вселенной, которой мы можем напрямую манипулировать с помощью различных физических устройств, находящихся под ее воздействием. наш контроль.То есть мы (экспериментаторы) являемся частью окружения, а не системой.
Для некоторых целей мы можем рассматривать систему как разделенную на подсистем, или рассматривать комбинацию двух или более систем как суперсистему .
Если с течением времени материя передается в любом направлении через границу, система будет открыта . Если неважно передается в систему или из нее, система закрывается .Если система открыта, материя может проходить через неподвижную границу, или граница может перемещаться через материю, которая закреплена в пространстве.
Примечание
Одна из трудностей в описании обмена энергией состоит в том, что тепло не является объектом; это процесс передачи энергии из-за разницы температур. Однако часто бывает трудно сформулировать такие слова, чтобы тепло не походило на сущность. Итак, хотя предпочтительно писать, что система «нагрелась», вы часто будете читать, что система «набрала тепло» или «получила энергию в виде тепла».
Однако часто бывает трудно сформулировать такие слова, чтобы тепло не походило на сущность. Итак, хотя предпочтительно писать, что система «нагрелась», вы часто будете читать, что система «набрала тепло» или «получила энергию в виде тепла».
И открытые, и закрытые системы могут передавать энергию в любом направлении через границу, если граница допускает такую передачу энергии. Граница, которая обеспечивает теплообмен , называется диатермическим или диатермическим . Адиабатическая граница (по-гречески: непроходимая ), с другой стороны, является границей, не допускающей теплопередачи. В принципе, мы можем гарантировать, что граница является адиабатической, окружив систему адиабатической стенкой — стенкой с идеальной теплоизоляцией и идеальной защитой от излучения.Изолированная система — это система, которая не обменивается веществом, теплом или не работает с окружающей средой, так что масса и общая энергия системы остаются постоянными во времени. Замкнутая система с адиабатической границей, вынужденная не выполнять никакой работы и не выполняющая никаких действий над ней, является изолированной системой.
Замкнутая система с адиабатической границей, вынужденная не выполнять никакой работы и не выполняющая никаких действий над ней, является изолированной системой.
В химии системы могут претерпевать изменения тепла из-за изменений количества и типов связей, а также изменений типа и эффективности межмолекулярных сил. Любой процесс, который приводит к нагреванию системы, называется экзотермическим процессом .Эти процессы происходят, когда энергия, выделяемая при образовании новых связей и межмолекулярных сил, превышает энергию, потребляемую при разрыве существующих связей и межмолекулярных сил. Когда система подвергается экзотермическому процессу, ее температура повышается. При хранении в адиабатическом контейнере система будет поддерживать эту повышенную температуру неограниченно долго. При хранении в диатермическом контейнере система будет терять тепло в окружающую среду до тех пор, пока температуры снова не достигнут теплового равновесия.
Любой процесс, который приводит к охлаждению системы, называется эндотермическим процессом . Эти процессы происходят, когда энергия, выделяемая при образовании новых связей и межмолекулярных сил, меньше энергии, получаемой при разрыве существующих связей и межмолекулярных сил. Когда система подвергается эндотермическому процессу, ее температура понижается. При хранении в адиабатическом контейнере система будет поддерживать эту пониженную температуру неопределенно долго. При хранении в диатермическом контейнере система будет получать тепло от окружающей среды до тех пор, пока температуры снова не достигнут теплового равновесия.
Эти процессы происходят, когда энергия, выделяемая при образовании новых связей и межмолекулярных сил, меньше энергии, получаемой при разрыве существующих связей и межмолекулярных сил. Когда система подвергается эндотермическому процессу, ее температура понижается. При хранении в адиабатическом контейнере система будет поддерживать эту пониженную температуру неопределенно долго. При хранении в диатермическом контейнере система будет получать тепло от окружающей среды до тех пор, пока температуры снова не достигнут теплового равновесия.
Ограничения, необходимые для предотвращения работы, обычно включают силы между системой и окружающей средой. В этом смысле система может взаимодействовать с окружающей средой, даже если она изолирована. Например, газ, содержащийся в жестких теплоизолированных стенах, представляет собой изолированную систему. Однако газ воздействует на каждую стенку с силой, и стенки оказывают на газ равную и противоположную силу. Изолированная система также может испытывать постоянное внешнее поле, такое как гравитационное поле.
Тепло
Тепловая энергия — это кинетическая энергия, связанная со случайным движением атомов и молекул.Температура — это количественная мера «горячего» или «холодного». Когда атомы и молекулы в объекте быстро движутся или вибрируют, они имеют более высокую среднюю кинетическую энергию (KE), и мы говорим, что объект «горячий». Когда атомы и молекулы движутся медленно, у них более низкий KE, и мы говорим, что объект «холодный» (рисунок \ (\ PageIndex {1} \)). Если предположить, что никаких химических реакций или фазовых изменений (таких как плавление или испарение) не происходит, увеличение количества тепловой энергии в образце вещества приведет к повышению его температуры.И, если предположить, что не происходит никаких химических реакций или фазовых изменений (таких как конденсация или замерзание), уменьшение количества тепловой энергии в образце вещества приведет к снижению его температуры.
‘
Рисунок \ (\ PageIndex {1} \) : (а) Молекулы в образце воды при более высокой температуре движутся быстрее, чем (б) молекулы в образце воды при более низкой температуре.
Работа
Работа — это целенаправленная или организованная передача энергии, связанная с неслучайным движением атомов и молекул.В макроскопическом масштабе мы описываем работу как результат силы, перемещающей объект. Другими словами, энергия расходуется организованным, скоординированным образом, чтобы заставить объект двигаться. Эту же концепцию можно применить на молекулярном уровне, чтобы описать скоординированное движение молекул и атомов как работу.
Рисунок \ (\ PageIndex {2} \) : Давление · Объемная работа газовых частиц. При использовании поршня без трения, если внешнее давление меньше P int (a), молекулы газа с восходящей составляющей своего движения будут сталкиваться с поршнем, в совокупности заставляя поршень двигаться вверх.Конечный объем (V f ) будет больше, чем V i . В качестве альтернативы, если внешнее давление больше, чем P int (b), поршень будет выполнять работу с частицами газа, поскольку он заставляет их коллективно усиливать нисходящую составляющую их движения. Окончательный объем (V f ) будет быть меньше V i .
Окончательный объем (V f ) будет быть меньше V i .
Внутренняя энергия
Закон Первый, часть 1
Состояние системы — это полное описание системы в данный момент времени, включая ее температуру и давление, количество вещества, которое она содержит, ее химический состав и физическое состояние вещества.Функция состояния — это свойство системы, величина которого зависит только от текущего состояния системы, а не от ее предыдущей истории. Температура, давление, объем и потенциальная энергия — все это функции состояния. Например, температура духовки не зависит от того, сколько шагов она могла предпринять для достижения этой температуры. Точно так же давление в шине не зависит от того, как часто воздух нагнетается в шину для достижения этого давления, как и конечный объем воздуха в шине.С другой стороны, тепло и работа не являются функциями состояния, потому что они зависят от пути . Например, автомобиль, стоящий на верхнем уровне гаража, имеет одинаковую потенциальную энергию независимо от того, был ли он поднят краном, установлен там вертолетом, поднят или поднят группой студентов (Рисунок \ (\ PageIndex) {3} \)). Однако объем работы, затраченной на его получение, может сильно различаться в зависимости от выбранного пути. Если бы ученики решили довести машину до вершины пандуса, они бы выполнили гораздо больше работы, чем если бы они просто подтолкнули машину вверх по пандусу (если, конечно, они не забыли отпустить стояночный тормоз, и в этом случае Затраченные работы существенно увеличились бы!).Однако потенциальная энергия автомобиля одинакова, независимо от того, какой путь они выберут.
Однако объем работы, затраченной на его получение, может сильно различаться в зависимости от выбранного пути. Если бы ученики решили довести машину до вершины пандуса, они бы выполнили гораздо больше работы, чем если бы они просто подтолкнули машину вверх по пандусу (если, конечно, они не забыли отпустить стояночный тормоз, и в этом случае Затраченные работы существенно увеличились бы!).Однако потенциальная энергия автомобиля одинакова, независимо от того, какой путь они выберут.
Рисунок \ (\ PageIndex {3} \): Высота как пример функции состояния. Изменение высоты между состоянием 1 (внизу гаража) и состоянием 2 (на верхнем уровне гаража) одинаково для обоих путей A и B; это не зависит от того, какой путь идет снизу вверх. Напротив, пройденное расстояние и работа, необходимая для достижения вершины, действительно зависят от выбранного пути.Высота — это функция состояния, но расстояние и работа — это функции состояния , а не .
Связь между изменением энергии системы и ее окружением определяется первым законом термодинамики, который гласит, что энергия Вселенной постоянна. Математически этот закон можно выразить следующим образом:
Математически этот закон можно выразить следующим образом:
\ [U_ {univ} = ΔU_ {sys} + ΔU_ {surr} = 0 \ label {2.1.1} \]
\ [\ Delta {U_ {sys}} = — ΔU_ {surr} \ label {2.1.2} \]
, где индексы univ, sys и surr относятся к вселенной, системе и окружению соответственно.Таким образом, \ (ΔU_ {sys} \), изменение внутренней энергии системы, идентично по величине, но противоположно по знаку изменению энергии окружающей среды.
(\ (ΔU_ {sys} \)) не зависит от пройденного пути и, следовательно, является функцией состояния. Таким образом, \ (ΔU_ {sys} \) также можно выразить как:
\ [ΔU_ {sys} = U_ {final} — U_ {initial} \ label {2.1.3} \]
Поскольку мы фокусируемся почти исключительно на изменениях энергии системы, мы не будем использовать «sys» в качестве индекса, если нам не нужно явно различать систему и ее окружение.Также следует отметить, что \ (ΔU_ {sys} \) — это обширное свойство, которое изменяется в зависимости от количества присутствующего вещества. Связанное с этим интенсивное свойство — это молярная внутренняя энергия \ (U_m \), определяемая как
Связанное с этим интенсивное свойство — это молярная внутренняя энергия \ (U_m \), определяемая как
\ [U_m = \ dfrac {U} {n} \ label {2.1.4} \]
Вклад во внутреннюю энергию
Внутренняя энергия может быть объяснена на молекулярном уровне, принимая во внимание различные члены, которые могут вносить вклад в эту общую энергию. Этот процесс учета проще всего выполнить для идеальной пробы газа, поскольку частицы не взаимодействуют друг с другом.Таким образом, внутренняя энергия идеального газа может быть аппроксимирована добавлением энергии нулевой точки, поступательной энергии, вращательной энергии, колебательной энергии и электронной энергии. Вклады поступательной и вращательной энергии требуют самых простых вычислений, потому что для этих членов каждая степень свободы вносит вклад \ (\ dfrac {1} {2} RT \) в молярную внутреннюю энергию согласно теореме об уравновешивании. Таким образом, трансляционный вклад для всех частиц равен \ (\ dfrac {3} {2} RT \) для движения в направлениях x, y и z. Вращательный вклад зависит от числа атомов в частице. Одиночные атомы не имеют вращательных степеней свободы. Линейные молекулы имеют 2 степени свободы (по двум осям, перпендикулярным оси связи. Многоатомные нелинейные молекулы имеют три степени свободы вращения.
Вращательный вклад зависит от числа атомов в частице. Одиночные атомы не имеют вращательных степеней свободы. Линейные молекулы имеют 2 степени свободы (по двум осям, перпендикулярным оси связи. Многоатомные нелинейные молекулы имеют три степени свободы вращения.
Важно отметить, что внутренняя энергия образца идеального газа не зависит от объема, занимаемого частицами газа. Между частицами нет межмолекулярного притяжения, поэтому нет разницы в потенциальной энергии, если частицы расположены очень близко друг к другу в маленьком контейнере или очень далеко друг от друга в большом контейнере.
Внутренняя энергия реальных газов, жидкостей и твердых тел не может быть описана так просто, потому что частицы действительно испытывают межмолекулярные силы притяжения, и, таким образом, их потенциальная энергия вносит вклад в общую внутреннюю энергию. Тем не менее, по-прежнему верно, что с увеличением температуры внутренняя энергия увеличивается, потому что вероятность наличия более высоких уровней поступательной и вращательной энергии увеличивается.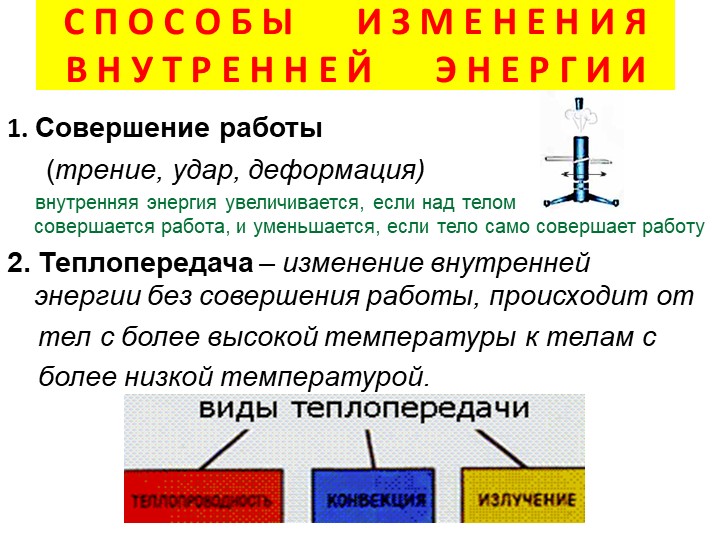
Закон Первый, часть 2
Поскольку тепло и работа — это единственные два способа передачи энергии между системой и ее окружением, любое изменение внутренней энергии системы является суммой переданного тепла (q) и проделанной работы (w):
\ [ΔU_ {sys} = q + w \ label {2.1.5} \]
Если предположить, что Вселенная представляет собой изолированную систему, второй закон можно переформулировать как:
Определение
Внутренняя энергия изолированной системы постоянна. Таким образом, q = 0 и w = 0 для изолированной системы, как того требует определение.
Для закрытой системы энергия может передаваться в систему и из нее. По соглашению, членам \ (q \) и \ (w \) в уравнении \ (\ ref {2.1.5} \) присваиваются отрицательные значения, если энергия покидает систему (экзотермический процесс или работа выполняется посредством система) и присвоены положительные значения, если энергия поступает в систему (эндотермический процесс, или работа выполняется на системе. )
)
Пример \ (\ PageIndex {1} \):
Предположим, что на сжатие пружины затрачено 150 кДж работы и 25 кДж тепла отводится пружиной во время этого сжатия. Как меняется внутренняя энергия пружины в процессе?
Стратегия : Используйте \ (ΔU_ {sys} = q + w \), чтобы найти \ (\ Delta U_ {sys} \), понимая, что работа выполняется в системе (+ w) и тепло теряется из система (- q).
Ответ : \ (\ Delta U_ {sys} \) = 150 кДж — 25 кДж = + 125 кДж.
Упражнение \ (\ PageIndex {1} \)
Предположим, что двигатель выполняет 100 кДж работы, но он также выделяет 10 кДж тепла при выполнении этой работы. Как изменяется внутренняя энергия мотора во время процесса?
Ответ : \ (\ Delta U_ {sys} \) = -100 кДж — 10 кДж = — 110 кДж.
Работа по расширению / сжатию
Работа в целом определяется как произведение силы \ (\ textbf {F} \) и элемента пути \ (\ textbf {ds} \). Оба являются векторами, и работа вычисляется путем интегрирования по их произведению
Оба являются векторами, и работа вычисляется путем интегрирования по их произведению
\ [w = \ int \ textbf {F} \ cdot \ textbf {ds} \ label {2.1.6} \]
Перемещение объекта против силы трения — лишь один из примеров работы.
\ [w_ {трение} = \ int \ textbf {F} _ {трение} \ cdot \ textbf {ds} \ label {2.1.7} \]
Мы могли бы также подумать о электрических работах. В этом случае мы будем перемещать заряд e (например, отрицательный заряд электрона) против электрического (векторного) поля \ (\ textbf {E} \). Работа будет:
\ [w_ {electical} = \ int e \ textbf {E} \ cdot \ textbf {ds} \ label {2.1.8} \]
Другими примерами являются растяжение резиновой ленты против силы упругости или перемещение магнита в магнитном поле и т. Д. И т. Д.
В случае цилиндра, заполненного идеальным газом, мы можем ввести площадь поршня A и забыть о векторности. Движение поршня ограничено одним направлением, в котором мы прикладываем внешнее давление, P ex . Напомним, что P — это сила (F) на площадь (A). Мы также можем предположить, что молекулы газа быстро уравновешиваются приложенным давлением и превращаются во всестороннее явление.
Напомним, что P — это сила (F) на площадь (A). Мы также можем предположить, что молекулы газа быстро уравновешиваются приложенным давлением и превращаются во всестороннее явление.
\ [w_ {volume} = \ int \ left (\ dfrac {F} {\ cancel {A}} \ right) (\ cancel {A} \, ds) = \ int P_ {ex} \, dV \ label {2.1.9} \]
Эта конкретная форма работы называется объемная работа и будет играть важную роль в развитии нашей теории. Обратите внимание, однако, что объемная работа составляет всего на одну форму работы.
условных обозначений
На этом этапе важно создать знаковое соглашение: положительное тепло и положительная работа — это всегда то, что вы вкладываете в систему.Если система выделяет тепло или выполняет работу, эти события получают знак минус.
Другими словами: вы оплачиваете счет .
Чтобы соответствовать этому соглашению, нам нужно переписать объемную работу (Уравнение \ (\ ref {2. 1.9} \)) как
1.9} \)) как
\ [w_ {volume} = — \ int \ left (\ dfrac {F} {\ cancel {A}} \ right) (\ cancel {A} \, ds) = — \ int P_ {ex} \, dV \ label {2.1.10} \]
Следовательно, чтобы уменьшить объем газа (\ (\ Delta V \) отрицательно), мы должны выполнить работу с газом.Это набор энергии системой, поэтому знак работы положительный. Если объем газа увеличивается, газ должен выполнять работу по перемещению поршня. Это потеря энергии системой, поэтому знак работы отрицательный.
Необратимое расширение / сжатие против постоянного давления
Когда система далека от равновесия, бесконечно малое изменение любой переменной будет незначительным, потому что по крайней мере одна переменная в системе будет претерпевать относительно большие изменения по мере того, как система движется к равновесию.Поскольку система далека от равновесия, значительные изменения, которые происходят по мере того, как система достигает равновесия, считаются необратимыми изменениями , не только потому, что их нелегко отменить, но также потому, что их отмена приведет к отклонению системы от равновесия.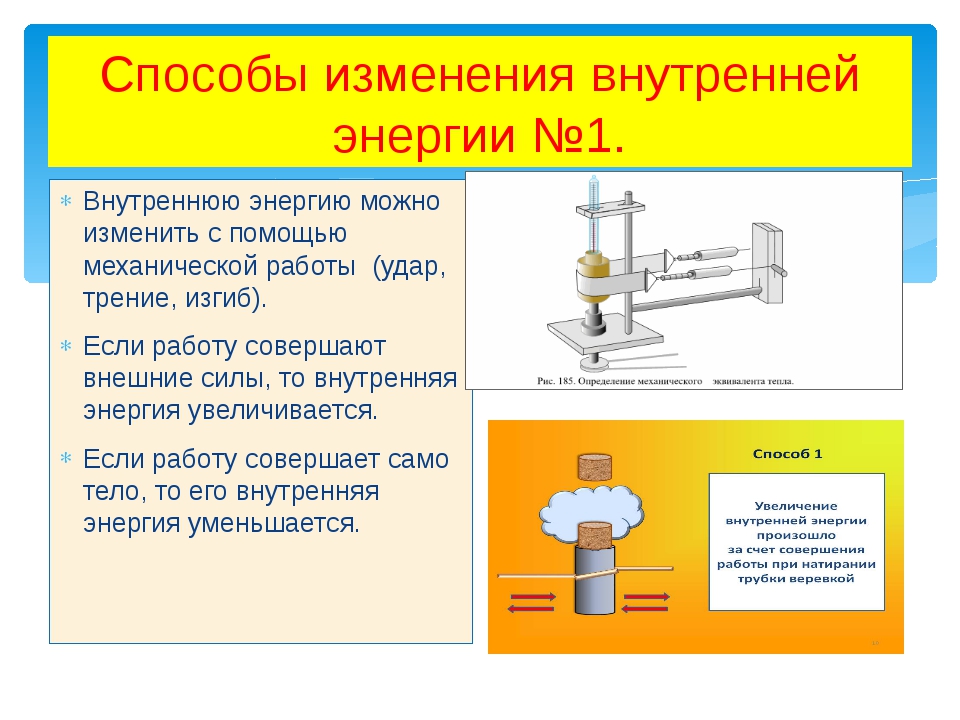 . Такая ситуация возникает, когда исходные материалы в химической реакции смешиваются вместе, когда очень горячий объект ставится рядом с холодным объектом, и когда на поршень помещается 50-килограммовая масса, находящаяся в равновесии с пробой газа, находящейся на давление в одну атмосферу.
. Такая ситуация возникает, когда исходные материалы в химической реакции смешиваются вместе, когда очень горячий объект ставится рядом с холодным объектом, и когда на поршень помещается 50-килограммовая масса, находящаяся в равновесии с пробой газа, находящейся на давление в одну атмосферу.
Если газ расширяется против постоянного давления (атмосферного давления или постоянной массы, установленной на поршне), уравнение \ (\ ref {2.1.10} \) может быть упрощено до
\ [w = -P_ {ex} \, \ int dV = -P_ {ex} (V_ {final} — V_ {initial}) = -P_ {ex} \ Delta V \ label {2.1.11} \]
Поскольку интегралы можно интерпретировать как площадь под кривой, значение \ (w \) равно площади под линией постоянного давления \ (P = P_ {ex} \) между \ (V_ {initial} \ ) и \ (V_ {final} \). На рисунке \ (\ PageIndex {4} \) показан график PV (известный как индикаторный график ) постоянного расширения давления.
Рисунок \ (\ PageIndex {4} \): Индикаторная диаграмма расширения при постоянном давлении
Индикаторный график такого типа может быть получен путем добавления энергии к пробе газа, удерживаемой в цилиндре поршнем, который оказывает постоянное давление.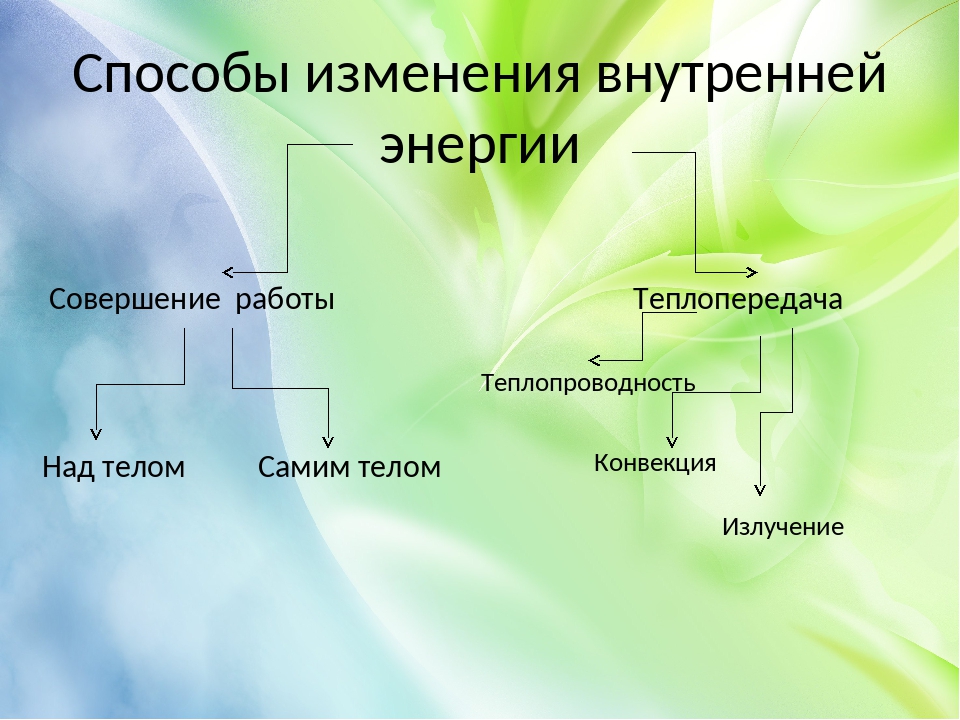 Цилиндр должен иметь диатермические стенки и должен быть окружен ванной с постоянной температурой. Начальное состояние этого расширения нестабильно, потому что давление газа, P , газа , должно сильно отличаться от внешнего давления, P ex .Если вы хотите, чтобы газ подвергался расширению, P газ > P ex . Если вы хотите, чтобы газ подвергался сжатию, используйте P gas
Цилиндр должен иметь диатермические стенки и должен быть окружен ванной с постоянной температурой. Начальное состояние этого расширения нестабильно, потому что давление газа, P , газа , должно сильно отличаться от внешнего давления, P ex .Если вы хотите, чтобы газ подвергался расширению, P газ > P ex . Если вы хотите, чтобы газ подвергался сжатию, используйте P gas
ex . В обоих процессах поршень необходимо удерживать на месте до тех пор, пока вы не будете готовы начать процесс. Верно также, что как при сжатии, так и при расширении процесс будет продолжаться до тех пор, пока P газ = P ex . Для изотермического расширения энергия, необходимая для работы расширения, будет доставляться в систему окружающей ванной с постоянной температурой.При изотермическом сжатии тепло, создаваемое при выполнении работы в системе, будет рассеиваться в окружающую ванну с постоянной температурой.
Рисунок \ (\ PageIndex {5} \): Система, подвергающаяся расширению при постоянном давлении. Масса, оказывающая давление, является фиксированной величиной, поэтому P ex является постоянной величиной.
Масса, оказывающая давление, является фиксированной величиной, поэтому P ex является постоянной величиной.
Если газ расширяется без противодействующей силы, то P ex должно быть 0 и, следовательно, \ (w \) должно быть 0.Этот частный случай расширения называется свободным расширением и происходит всякий раз, когда газ расширяется в вакуум.
Пример \ (\ PageIndex {2} \):
Предположим, что 3,00 моля идеального газа, содержащегося в контейнере 4,00 л при 20,0 бар, претерпевают необратимое изотермическое расширение при постоянном внешнем давлении 5,00 бар. Сколько работы проделал газ?
Стратегия : Для решения уравнения необходимо использовать уравнение \ (\ ref {2.1.11} \). Вы знаете P ex и \ (V_i \), поэтому сначала вы должны найти \ (V_f \) газа.3 Дж \)
Упражнение \ (\ PageIndex {2} \)
A. Предположим, что 2,50 моля идеального газа, содержащегося в контейнере на 2,00 л при давлении 10,0 бар, претерпевают необратимое изотермическое расширение при постоянном внешнем давлении 2,00 бар. Сколько работы проделал газ?
Сколько работы проделал газ?
B. Предположим, что 2,50 моля идеального газа, содержащегося в контейнере на 2,00 л при давлении 10,0 бар, претерпевают три отдельных необратимых изотермических расширения. Первый шаг включает расширение по сравнению с P ex из 6.00 бар. Второй этап включает расширение по сравнению с P ex на 3,00 бар. Третий шаг включает расширение по сравнению с P ex на 2,00 бар. Какой общий объем работы был проделан газом за три комбинированных этапа?
Ответ : A. -1,60 x 10 3 J B. -2,47 x 10 3 J
Обратите внимание, что конечное состояние в части B такое же, как конечное состояние в части A. Однако работа, выполняемая газом, увеличивается, когда увеличивается количество необратимых шагов.
Пример \ (\ PageIndex {3} \)
Проба идеального газа в цилиндре двигателя сжимается от 400 мл до 50,0 мл во время такта сжатия при постоянном давлении 8,00 атм. В то же время 140 Дж энергии передается от газа окружающей среде в виде тепла. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
В то же время 140 Дж энергии передается от газа окружающей среде в виде тепла. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
Дано : начальный объем, конечный объем, внешнее давление и количество энергии, переданной в виде тепла
Запрошено: общее изменение внутренней энергии
Стратегия:
- Определите знак \ (q \) для использования в уравнении \ (\ ref {2.1.5} \).
- По формуле \ (\ ref {2.1.11} \) вычислите \ (w \) по заданным значениям. Подставьте это значение в уравнение \ (\ ref {2.1.5} \), чтобы вычислить \ (ΔU \).
Решение
A. Из уравнения \ (\ ref {2.1.5} \) мы знаем, что ΔU = q + w. Нам дана величина q (140 Дж), и нам нужно только определить ее знак. Поскольку энергия передается от системы (газа) в окружающую среду, q по соглашению отрицательно.
B Поскольку газ сжимается, мы знаем, что в системе проводятся работы, поэтому \ (w \) должно быть положительным. Из уравнения \ (\ ref {2.1.11} \),
Из уравнения \ (\ ref {2.1.11} \),
\ (w = -P _ {\ textrm {ext}} \ Delta V = -8.00 \ textrm {atm} (\ textrm {0.0500 L} — \ textrm {0.400 L}) \ left (\ dfrac {\ textrm {101.3 J}} {\ mathrm {L \ cdot atm}} \ right) = 284 \ textrm {J} \)
Таким образом,
ΔU = q + w = −140 Дж + 284 Дж = 144 Дж
В этом случае, хотя работа выполняется с газом, увеличивая его внутреннюю энергию, тепло течет из системы в окружающую среду, уменьшая его внутреннюю энергию на 144 Дж. Выполненная работа и переданное тепло могут иметь противоположные знаки.
Упражнение \ (\ PageIndex {3} \)
Образец идеального газа расширяется от начального объема 0,200 л до конечного объема 3,50 л при постоянном внешнем давлении 0,995 атм. При этом 117 Дж тепла передается от окружающей среды к газу. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
Ответ :
−216 Дж
Обратимое расширение / сжатие
Когда система находится в состоянии равновесия, бесконечно малое изменение любой переменной заставит систему измениться бесконечно малым образом, чтобы достичь нового равновесия. Из этого нового равновесия дальнейшее бесконечно малое изменение заставило бы систему снова измениться бесконечно малым образом, чтобы достичь нового равновесия, которое фактически могло бы быть исходным состоянием равновесия. Поскольку система всегда находится в равновесии или бесконечно близка к нему, все бесконечно малые изменения считаются обратимыми изменениями , потому что любое данное изменение может быть отменено одним или несколькими дополнительными бесконечно малыми изменениями. Такая ситуация может иметь место для реакции при химическом равновесии, для объекта, находящегося в тепловом равновесии с окружающей средой, и для газа, удерживаемого в цилиндре поршнем, находящимся в механическом равновесии с внешним давлением.Совершенно обратимый процесс, также известный как квазистатический процесс , никогда не завершится, но мы можем использовать эту концепцию для определения предельного результата для многих термодинамических процессов.
Из этого нового равновесия дальнейшее бесконечно малое изменение заставило бы систему снова измениться бесконечно малым образом, чтобы достичь нового равновесия, которое фактически могло бы быть исходным состоянием равновесия. Поскольку система всегда находится в равновесии или бесконечно близка к нему, все бесконечно малые изменения считаются обратимыми изменениями , потому что любое данное изменение может быть отменено одним или несколькими дополнительными бесконечно малыми изменениями. Такая ситуация может иметь место для реакции при химическом равновесии, для объекта, находящегося в тепловом равновесии с окружающей средой, и для газа, удерживаемого в цилиндре поршнем, находящимся в механическом равновесии с внешним давлением.Совершенно обратимый процесс, также известный как квазистатический процесс , никогда не завершится, но мы можем использовать эту концепцию для определения предельного результата для многих термодинамических процессов.
Как было только что отмечено, обратимое расширение можно аппроксимировать, если проба газа удерживается в цилиндре поршнем. Если давление газа равно внешнему давлению на поршень, система находится в механическом равновесии с окружающей средой. Если давления равны, то P ex = P gas , и уравнение \ (\ ref {2.1.10} \) можно выразить как
Если давление газа равно внешнему давлению на поршень, система находится в механическом равновесии с окружающей средой. Если давления равны, то P ex = P gas , и уравнение \ (\ ref {2.1.10} \) можно выразить как
\ [w = — \ int P_ {gas} \, dV \ label {2.1.12} \]
Изотермическое обратимое расширение / сжатие
Предположим, у нас есть образец идеального газа, удерживаемый под давлением в цилиндре поршнем, который может перемещаться с бесконечно малыми шагами с помощью двигателя. Цилиндр имеет диатермические стенки и погружен в ванну с постоянной температурой. Как будет показано в следующем разделе этой главы, если нет изменения температуры для идеального газа, не может быть изменения внутренней энергии.Таким образом, для изотермического процесса, проводимого на / с помощью идеального газа:
\ [\ Delta U = 0 = q + w \ label {2.1.13} \]
Внутри цилиндра находится змеевик, который нагревает пробу газа. Ванна с постоянной температурой поддерживает постоянную температуру образца газа, поэтому добавленное тепло не может поднять температуру газа. Если температура газа не меняется, внутренняя энергия не изменяется. Если нет изменений во внутренней энергии, даже если тепло добавляется, тогда газ должен использовать все тепло, добавляемое к газу, для работы с окружающей средой.Другими словами:
Если температура газа не меняется, внутренняя энергия не изменяется. Если нет изменений во внутренней энергии, даже если тепло добавляется, тогда газ должен использовать все тепло, добавляемое к газу, для работы с окружающей средой.Другими словами:
\ [w_ {done \, by \, gas} = — q_ {added \, to \, gas} \ label {2.1.14} \]
Работа, которую газ выполняет с окружающей средой, заключается в том, чтобы надавить на поршень, чтобы увеличить объем содержащегося в нем газа. Если змеевик подводит тепло к газу бесконечно малыми приращениями, тогда объем газа будет увеличиваться бесконечно малыми приращениями по мере того, как он отталкивается от P ex . Однако по мере увеличения объема газ P будет бесконечно уменьшаться. Чтобы поддерживать (или оставаться очень близким к этому) механическое равновесие между газом P и P ex , двигатель должен будет уменьшить давление, оказываемое поршнем.Когда давление, оказываемое поршнем, уменьшается, P gas снова будет равным P ex , и оба давления будут бесконечно меньше, чем они были до того, как змеевик добавил бесконечно малое количество тепла к газу. Таким образом, у нас есть процесс, отвечающий требованиям обратимого расширения. Если мы проведем процесс нагрева до такой степени, что мы изменим объем газа на значительную величину, мы можем предположить, что процесс действительно происходил путем бесконечного числа обратимых расширений, в которых давление газа всегда равнялось внешнему давлению. давление.Общую работу для такого процесса можно рассчитать, если выразить P как функцию от V:
Таким образом, у нас есть процесс, отвечающий требованиям обратимого расширения. Если мы проведем процесс нагрева до такой степени, что мы изменим объем газа на значительную величину, мы можем предположить, что процесс действительно происходил путем бесконечного числа обратимых расширений, в которых давление газа всегда равнялось внешнему давлению. давление.Общую работу для такого процесса можно рассчитать, если выразить P как функцию от V:
\ [P = \ dfrac {nRT} {V} \ label {2.1.15} \]
, а затем подставьте в уравнение \ (\ ref {2.1.12} \), чтобы получить
\ [w = — \ int \ dfrac {nRT} {V} \, dV = -nRT \ int \ dfrac {dV} {V} = -nRT \ ln \ dfrac {V_f} {V_i} \ label {2.1. 16} \]
Поскольку \ (V_f \) больше, чем \ (V_i \), работа будет отрицательной, как ожидается, когда работа будет выполнена на в системе.
(Точно такой же результат можно получить, уменьшив давление, оказываемое поршнем, на бесконечно малую величину. После каждого постепенного уменьшения P ex , газ будет реагировать расширением, выполняя работу против поршня, пока его объем не увеличится до точки, в которой P gas будет равен новому, более низкому P ex . Змеевик нагревателя должен отреагировать, передав соответствующее количество тепла газу для поддержания постоянной температуры.)
После каждого постепенного уменьшения P ex , газ будет реагировать расширением, выполняя работу против поршня, пока его объем не увеличится до точки, в которой P gas будет равен новому, более низкому P ex . Змеевик нагревателя должен отреагировать, передав соответствующее количество тепла газу для поддержания постоянной температуры.)
Рисунок \ (\ PageIndex {5} \) представляет собой индикаторную диаграмму для этого обратимого процесса, начиная с состояния высокого давления, низкого объема и заканчивая состоянием низкого давления и большого объема.
Рисунок \ (\ PageIndex {6} \) сравнивает индикаторную диаграмму обратимого расширения от V i до V f с индикаторной диаграммой необратимого расширения от V i до V f относительно постоянной давление, равное конечному P ex , достигаемому обратимым процессом.
Легко видеть, что площадь под кривой обратимого расширения больше, чем площадь под кривой постоянного давления, необратимого расширения. Эта дополнительная область представляет собой дополнительную работу, которую может выполнить система, если процесс выполняется обратимо, а не необратимо. Тот факт, что обратимые процессы обеспечивают максимальную работу, будет подробно рассмотрен в главе 3, раздел A.
Эта дополнительная область представляет собой дополнительную работу, которую может выполнить система, если процесс выполняется обратимо, а не необратимо. Тот факт, что обратимые процессы обеспечивают максимальную работу, будет подробно рассмотрен в главе 3, раздел A.
Примечание
В этом примере мы утверждаем, что тепло, добавляемое к газу змеевиком, никогда не могло поднять температуру газа, а вместо этого использовалось газом для выполнения работы. Мы также утверждаем, что система всегда находилась в механическом равновесии с P = P ex , хотя каждое бесконечно малое изменение могло произойти, только если P \ (\ ne \) P ex .Эти параметры невозможно удовлетворить, но, приняв их, мы можем рассчитать максимальную работу, которую может выполнить процесс.
Пример \ (\ PageIndex {4} \):
Предположим, что 3,00 моля идеального газа, содержащегося в контейнере 4,00 л при 20,0 бар, претерпевают обратимое изотермическое расширение до конечного давления 5,00 бар. Сколько работы проделал газ?
Сколько работы проделал газ?
Стратегия : Как и в примере 2.1.2, вам необходимо рассчитать температуру и конечный объем пробы газа.4 Дж \)
Обратите внимание, что обратимый процесс выполняет примерно в два раза больше работы, чем одноэтапный необратимый процесс!
Упражнение \ (\ PageIndex {4} \)
Предположим, что 2,50 моля идеального газа, содержащегося в контейнере на 2,00 л при давлении 10,0 бар, претерпевают необратимое изотермическое расширение при постоянном внешнем давлении 2,00 бар. Сколько работы проделал газ?
Ответ : -3,22 x 10 3 J
Теплообмен
Некоторые системы не работают.Если система является газовой, это будет означать, что емкость, в которой находится газ, имеет постоянный объем. Поскольку никакая работа не может быть выполнена, единственный способ, которым система может изменить внутреннюю энергию, — это набирать или терять тепло. Для такой системы первый закон будет
.
\ [\ Delta U = q_V \ label {2.1.17} \]
, где нижний индекс «V» указывает, что объем системы постоянный.
Калориметрия
Калориметрия — это экспериментальное измерение тепловых изменений.Основная предпосылка калориметрического эксперимента состоит в том, что всегда будет соблюдаться первый закон; тепло не может быть ни создано, ни уничтожено:
\ [q_ {system} = — q_ {окружение} \ label {2.1.18} \]
Калориметрия постоянного объема, также известная как калориметрия бомбы, используется для измерения \ (q_V \) для многих экзотермических процессов, таких как реакции горения. В состав калориметра бомбы входят:
- Стальной внутренний контейнер («бомба») с реагентами
- Водяная баня, в которую погружена бомба
- Термометр
- Мешалка с электроприводом
- Провод зажигания
Все эти компоненты находятся внутри двустенной внешней части калориметра (рис. 1).Поскольку процесс происходит при постоянном объеме, реакционный сосуд должен быть сконструирован таким образом, чтобы выдерживать высокое давление, возникающее в результате процесса горения, которое представляет собой ограниченный взрыв. Судно обычно называют «бомбой», а методика известна как калориметрия бомбы .
Судно обычно называют «бомбой», а методика известна как калориметрия бомбы .
Рисунок 1 : Упрощенный калориметр бомбы
В адиабатическом калориметре постоянного объема весь эксперимент изолирован или изолирован от остальной части комнаты, так что тепло не поступает и не покидает «вселенную» калориметра.В этих условиях изменение теплоты реакции будет равно, но противоположно изменению теплоты окружающей среды, которое ограничивается водой и другими компонентами калориметра.
\ [q_ {response} = — q_ {калориметр} \ label {2.1.19} \]
Значение \ (q_ {калориметр} \) фактически зависит от двух членов
\ [q_ {калориметр} = q_ {вода} + q_ {бомба} \ label {2.1.20} \]
, но если для каждого эксперимента используется одинаковое количество воды, то уравнение \ (\ ref {2.1.19} \) действительно для всех экспериментов.
После измерения начальной температуры воды в калориметре нагретая проволока внутри бомбы используется для запуска реакции. Температура внутри калориметра повышается из-за преобразования химической энергии в тепловую, которое происходит в результате реакции горения. Для обеспечения полного сгорания эксперимент проводят в присутствии кислорода выше атмосферного. После сгорания измеряется конечная температура воды в калориметре.Однако тепло, выделяемое реакцией, не только нагревает воду калориметра; он также нагревает сам калориметрический прибор. Таким образом, необходимо определить постоянную калориметра , \ (C \), которая представляет собой фиксированное количество энергии, необходимое для повышения температуры калориметрического устройства на 1 кельвин.
Температура внутри калориметра повышается из-за преобразования химической энергии в тепловую, которое происходит в результате реакции горения. Для обеспечения полного сгорания эксперимент проводят в присутствии кислорода выше атмосферного. После сгорания измеряется конечная температура воды в калориметре.Однако тепло, выделяемое реакцией, не только нагревает воду калориметра; он также нагревает сам калориметрический прибор. Таким образом, необходимо определить постоянную калориметра , \ (C \), которая представляет собой фиксированное количество энергии, необходимое для повышения температуры калориметрического устройства на 1 кельвин.
\ [C = \ dfrac {q_ {калориметр}} {\ Delta T} \ label {2.1.21} \]
Значение C обычно определяется одним из двух методов. В калориметре можно проводить химическую реакцию с известной тепловой мощностью.Вы знаете значение \ (q_ {response} \) и, следовательно, значение \ (q_ {calorimeter} \) для известного количества воды в вашем калориметре. Вы также знаете \ (\ Delta T \) для реакции, поэтому можете рассчитать значение \ (C \).
Вы также знаете \ (\ Delta T \) для реакции, поэтому можете рассчитать значение \ (C \).
Второй метод включает добавление тепла к калориметрическому устройству с помощью электрического нагревателя. Если вы пропустите постоянный электрический ток (\ (I \)) через нагреватель с известным падением напряжения (\ (\ Delta \ phi \)) в течение известного времени (\ (t \)), вы можете рассчитать тепло, добавляемое к калориметрическому устройству, потому что тепло = (ток) (время) (разность потенциалов):
\ [q = \ Delta \ phi · I · t \ label {2.1.22} \]
Пример \ (\ PageIndex {5} \):
Температура калориметра повышается на 6,00 K, когда источник питания 12,0 В используется для пропускания тока 17,0 А через нагревательную катушку в течение 200 секунд. Какое значение C для калориметра?
Стратегия :
Шаг 1: Используйте уравнение \ (\ ref {2.1.19} \) для вычисления \ (q_ {response} \) (поскольку нагреватель является источником дополнительного тепла). Помните, что \ (1 \, Volt = 1 \ dfrac {Joule} {Coulomb} = 1 \ dfrac {J} {C} \) и что \ (1 \, ampere = 1 \ dfrac {Coulomb} {second} = 1 \ dfrac {C} {s} \).
Помните, что \ (1 \, Volt = 1 \ dfrac {Joule} {Coulomb} = 1 \ dfrac {J} {C} \) и что \ (1 \, ampere = 1 \ dfrac {Coulomb} {second} = 1 \ dfrac {C} {s} \).
Шаг 2: Используйте уравнение \ (\ ref {2.1.21} \) для вычисления \ (C \).
Ответ :
Шаг 1: \ (q_ {response} = \ Delta \ phi · I · t = (12.0 \ dfrac {J} {C}) (17.0 \ dfrac {C} {s}) (200. S) (\ dfrac {1 \, кДж} {1000 \, Дж)} = 40,8 \, кДж \)
Шаг 2: \ (C = \ dfrac {40.8 \, кДж} {6.00 \, K} = 6.80 \ dfrac {kJ} {K} \)
Упражнение \ (\ PageIndex {5} \)
Температура калориметра повышается на 8,00 К, когда источник питания 12,0 В пропускает ток 20,0 А через нагревательную катушку на 150.секунд. Какое значение C для калориметра?
Ответ : 4.50 \ (\ dfrac {kJ} {K} \)
Другие калориметры
Существует много других типов калориметров, помимо бомбовых калориметров, включая изобарные калориметры (пример: кофейная чашка, открытая в атмосферу), калориметры адиабатического пламени (калориметры постоянного давления, используемые для реакций горения), дифференциальные сканирующие калориметры (DSC, калориметр, который сравнивает количество энергии, необходимое для поддержания температуры образца и температуры стандартного эталонного материала на одном уровне, когда энергия добавляется к обоим веществам), и калориметры изотермического титрования (калориметр, подобный DSC, но который снижает энергию, необходимую для поддержания равных температур эталона и химической реакции, поскольку к реакционной смеси добавляются точно измеренные объемы реагента. )
)
Тепловая мощность
Как отмечалось ранее, внутренняя энергия системы увеличивается с увеличением температуры системы. Если мы работаем с чистым веществом, которое поддерживается в постоянном объеме, мы можем получить как интенсивное, так и экстенсивное свойство вещества из графика зависимости внутренней энергии от температуры. Наклон касательной к кривой \ (U \) vs \ (T \) при любой температуре известен как теплоемкость при постоянном объеме \ (C_v \) для этого вещества:
\ [C_V = \ left (\ dfrac {\ partial U} {\ partial T} \ right) _V \ label {2.1.23} \]
Это частная производная, потому что внутренняя энергия системы обычно зависит как от объема, так и от температуры, но мы сохраняем объем постоянным и позволяем изменяться только температуре.
Поскольку \ (C_V \) сообщает нам количество тепла, необходимое для изменения температуры образца вещества при постоянном объеме, мы также можем сказать, что бесконечно малое изменение внутренней энергии равно бесконечно малому изменению температуры, умноженному на теплоемкость при постоянном объеме
\ [dU = C_V \, dT \ label {2. 1.24} \]
1.24} \]
Если теплоемкость при постоянном объеме вещества не сильно меняется при изменении температуры, то наклон графика \ (U \) в зависимости от \ (T \) будет довольно постоянным. В данном случае
\ [\ Delta U = \ int C_V \, dT \, = \, C_V · (T_2 — T_1) = C_V · \ Delta T \ label {2.1.25} \]
Как указано в уравнении \ (\ ref {2.1.17} \),
\ [\ Delta U = q_V \ tag {2.1.17} \]
, так что
\ [q_V = C_V · \ Delta T \ label {2.1.26} \]
Уравнение \ (\ ref {2.1.26} \) показывает нам, что мы можем довольно легко экспериментально определить постоянную объемную теплоемкость вещества, измеряя изменение температуры вещества при добавлении к нему тепла.
Значение \ (C_V \) является обширным свойством, потому что оно говорит нам, сколько тепла необходимо для изменения температуры этого конкретного образца чистого вещества. Мы можем определить интенсивное свойство этого чистого вещества, молярную теплоемкость при постоянном объеме, \ (C_ {V, m} \), если разделим экспериментально полученное \ (C_V \) на количество молей используемого вещества. в эксперименте:
в эксперименте:
\ [C_ {V, m} = \ dfrac {C_V} {n} \ label {2.1.27} \]
Мы также можем вычислить второе интенсивное свойство, удельную теплоемкость, \ (C_ {V, s} \), которая представляет собой теплоемкость на массу образца:
\ [C_ {V, s} = \ dfrac {C_V} {mass} \ label {2.1.28} \]
Пример \ (\ PageIndex {6} \):
Когда 18,9 кДж передается на пробу газа в адиабатическом контейнере постоянного объема с постоянной калориметра 2,22 \ (\ dfrac {kJ} {K} \), температура газа (и калориметра) увеличивается на 8,06 К.
А.Какова теплоемкость образца?
B. Если образец имеет массу 0,500 кг, какова удельная теплоемкость вещества?
C. Если образец представляет собой криптон, какова молярная теплоемкость криптона при постоянном объеме?
Стратегия :
A. Используйте модифицированную версию Equation \ (\ ref {2.1.18} \),
\ [q_ {added} = — (q_ {калориметр} + q_ {V \, gas}) \ label {2. 1.29} \]
1.29} \]
и замените в уравнениях \ (\ ref {2.1.21} \) и \ (\ ref {2.1.26} \), чтобы получить
\ [q_ {added} = — (C_ {калориметр} \ Delta T + C_ {V \, gas} \ Delta T) \ label {2.1.30} \]
Затем решите относительно \ (C_ {V \, gas} \).
B. Используйте уравнение \ (\ ref {2.1.28} \), чтобы найти удельную теплоемкость.
C. Определите количество присутствующих молей криптона, а затем используйте уравнение \ (\ ref {2.1.27} \), чтобы найти молярную теплоемкость при постоянном объеме.
Ответ :
A. \ (- 18 900 Дж = — [(2,220 \ dfrac {J} {K}) (8.06 K) + (C_ {V \, газ}) (8.06 K)] \)
\ (\ dfrac {18 900 Дж — 17 893 Дж} {8,06 К} = C_ {V \, газ} \)
\ (125 \ dfrac {J} {K} = C_ {V \, gas} \)
B. \ (C_ {V, s \, gas} = \ dfrac {C_ {V \, gas}} {mass} = \ dfrac {125 \ dfrac {J} {K}} {0,500 кг} = 250. \ dfrac {J} {кг · K} \)
C. \ (моль Kr = \ dfrac {граммы Kr} {83,8 \ dfrac {граммы} {моль}} = \ dfrac {500. Грамм} {83,8 \ dfrac {граммы} {моль}} = 5,97 моль \)
Грамм} {83,8 \ dfrac {граммы} {моль}} = 5,97 моль \)
\ (C_ {V, m \, gas} = \ dfrac {C_ {V \, gas}} {моль} = \ dfrac {125 \ dfrac {J} {K}} {5.97 моль} = 20,9 \ dfrac {J} {моль · K} \)
Упражнение \ (\ PageIndex {6} \)
Когда 20,3 кДж переносится на образец газа массой 253 грамма в адиабатическом контейнере постоянного объема с константой калориметра 4,30 \ (\ dfrac {kJ} {K} \), температура газа (и калориметра) увеличивается на 4,50 К. Какова удельная теплоемкость вещества?
Ответ : \ (C_ {V, s} = 834 \ dfrac {J} {kg · K} \)
Примечание
Следует отметить, что температура чистого вещества не изменяется при фазовых переходах.Добавляемое тепло разрушает электростатические взаимодействия, удерживающие частицы вместе. При \ (\ Delta T = 0 \) уравнение \ (\ ref {2.1.26} \) говорит нам, что \ (C_V \) при фазовых изменениях должен приближаться к бесконечности:
\ [C_V = \ dfrac {q_V} {\ Delta T} = \ dfrac {q_V} {0} \ label {2. 1.31} \]
1.31} \]
Список литературы
- Чанг, Раймонд. Физическая химия для биологических наук. Саусалито, Калифорния: Университетская наука, 2005.
Энергия, энтальпия и первый закон термодинамики
Энергия, энтальпия и первый закон Термодинамика
Химическая термодинамика
Термодинамика определяется как отрасль науки, которая занимается взаимосвязь между теплом и другими формами энергии, например работой.Это часто обобщены в виде трех законов, которые описывают ограничения на то, как различные формы энергии могут быть взаимопревращенными. Химическая термодинамика — это раздел термодинамики, относится к химическим реакциям.
Законы термодинамики Первый закон: Энергия сохраняется; его нельзя ни создать, ни уничтожить. Второй закон: В изолированной системе естественные процессы являются спонтанными, когда они приводят к увеличение беспорядка или энтропии. Третий закон: энтропия идеального кристалла равна нулю, когда температура кристалл равен абсолютному нулю (0 К).
Было много попыток построить устройство, нарушающее законы термодинамика. Все потерпели неудачу. Термодинамика — одна из немногих областей науки в мире. для которых нет исключений.
Система и окружение
Одно из основных предположений термодинамики — это идея, что мы можем
произвольно разделите вселенную на систему и ее окружение .В
граница между системой и ее окружением может быть такой же реальной, как стенки стакана
который отделяет решение от остальной Вселенной (как на рисунке ниже).
Или это может быть так же воображаемо, как набор точек, которые просто разделяют воздух. над поверхностью металла от остальной атмосферы (как на рисунке ниже).
Внутренняя энергия
Одним из термодинамических свойств системы является ее внутренняя энергия , E , который представляет собой сумму кинетической и потенциальной энергий частиц, которые образуют систему.Внутреннюю энергию системы можно понять, исследуя простейшая из возможных систем: идеальный газ. Поскольку частицы в идеальном газе не взаимодействуют, эта система не имеет потенциальной энергии. Внутренняя энергия идеального газа равна следовательно, сумма кинетических энергий частиц в газе.
Кинетическая молекулярная теория предполагает, что температура газа равна
прямо пропорциональна средней кинетической энергии его частиц, как показано на
рисунок ниже.
Следовательно, внутренняя энергия идеального газа прямо пропорциональна температура газа.
E sys = 3 / 2 RT
В этом уравнении R — постоянная идеального газа в джоулях на моль. кельвин (Дж / моль-К), а T — температура в кельвинах.
Внутренняя энергия систем более сложных, чем идеальный газ нельзя измерить напрямую. Но внутренняя энергия системы по-прежнему пропорциональна его температура. Таким образом, мы можем отслеживать изменения внутренней энергии системы с помощью наблюдая, что происходит с температурой системы. Когда температура системы увеличивается, мы можем сделать вывод, что внутренняя энергия системы также вырос.
Предположим на время, что термометр, погруженный в стакан с водой
на плите — 73. 5 o C, как показано на рисунке ниже. Это измерение может
описывать только состояние системы в данный момент времени. Он не может сказать нам,
воду нагревали непосредственно от комнатной температуры до 73,5 o C или нагревали из комнаты
температура до 100 o C, а затем дают остыть.
5 o C, как показано на рисунке ниже. Это измерение может
описывать только состояние системы в данный момент времени. Он не может сказать нам,
воду нагревали непосредственно от комнатной температуры до 73,5 o C или нагревали из комнаты
температура до 100 o C, а затем дают остыть.
Температура является функцией состояния . Это зависит только от состояние системы в любой момент времени, а не путь, по которому система государство.Поскольку внутренняя энергия системы пропорциональна ее температуре, внутренняя энергия также является функцией состояния. Любое изменение внутренней энергии системы равна разнице между его начальным и конечным значениями.
E sys = E f — E i
Первый закон термодинамики
Первый закон термодинамики можно выразить в следующем уравнении:
который утверждает, что энергия Вселенной постоянна. Энергию можно передавать от
систему в ее окружение или наоборот, но она не может быть создана или уничтожена.
Энергию можно передавать от
систему в ее окружение или наоборот, но она не может быть создана или уничтожена.
Первый закон термодинамики : E унив = E sys + E surr = 0
Более полезная форма первого закона описывает, как сохраняется энергия.Это говорит, что изменение внутренней энергии системы равно сумме тепла полученные или утраченные системой, а также работа, выполненная системой или в ней.
Первый закон термодинамики : E sys = q + w
Знаковое соглашение о соотношении внутренней энергии
систему и тепло, получаемое или теряемое системой, можно понять, подумав о
конкретный пример, такой как стакан с водой на горячей плите. Когда плита повернута
при включении система получает тепло от окружающей среды. В результате и температура, и
внутренняя энергия системы увеличивается, а E составляет положительный . Когда конфорка выключена,
вода теряет тепло в окружающую среду при охлаждении до комнатной температуры, а E — отрицательное значение .
Когда плита повернута
при включении система получает тепло от окружающей среды. В результате и температура, и
внутренняя энергия системы увеличивается, а E составляет положительный . Когда конфорка выключена,
вода теряет тепло в окружающую среду при охлаждении до комнатной температуры, а E — отрицательное значение .
Связь между внутренней энергией и работой можно понять Рассмотрим другой конкретный пример: вольфрамовая нить внутри лампочки.Когда работаешь осуществляется в этой системе путем пропускания электрического тока через вольфрамовую проволоку, система нагревается, и E , следовательно, положительный . (В конце концов, проволока становится достаточно горячей светиться.) И наоборот, E отрицательное значение , когда система работает со своим окружением.
Условные обозначения для тепла, работы и внутренней энергии кратко изложены в
рисунок ниже. Внутренняя энергия и температура системы уменьшаются ( E <0), когда система
либо теряет тепло, либо работает со своим окружением. Наоборот, внутренняя энергия и
повышение температуры ( E > 0), когда система получает тепло от окружающей среды или когда она работает
в системе.
Наоборот, внутренняя энергия и
повышение температуры ( E > 0), когда система получает тепло от окружающей среды или когда она работает
в системе.
Система и работа
Система обычно определяется как химическая реакция, а граница контейнер, в котором протекает реакция.В ходе реакции тепло либо испускается или поглощается системой. Кроме того, система либо работает на нем. окружение или какие-то работы, сделанные в его окрестностях. Любое из этих взаимодействий может влияют на внутреннюю энергию системы.
E sys = q + w
С химической реакцией обычно связаны два вида работы: электрическая
работа и работа расширения . Химические реакции могут повлиять на их
окружение, пропуская электрический ток по внешнему проводу. Реакции тоже делают
работать с их окружением, когда объем системы увеличивается в течение
реакция Количество работы расширения, совершаемой реакцией, равно произведению
давление, против которого система расширяется, умноженное на изменение объема
система.
Химические реакции могут повлиять на их
окружение, пропуская электрический ток по внешнему проводу. Реакции тоже делают
работать с их окружением, когда объем системы увеличивается в течение
реакция Количество работы расширения, совершаемой реакцией, равно произведению
давление, против которого система расширяется, умноженное на изменение объема
система.
w = — PV
Знаковое соглашение для этого уравнения отражает тот факт, что внутреннее энергия системы уменьшается, когда система действительно работает со своим окружением.
Энтальпия относительно внутренней энергии
Что произойдет, если мы создадим набор условий, при которых работа не будет
что делает система в своем окружении или, наоборот, во время химической реакции? Под
В этих условиях тепло, выделяемое или поглощаемое реакцией, будет равно
изменение внутренней энергии системы.
E sys = q (тогда и только тогда, когда w = 0)
Самый простой способ достичь этих условий — запустить реакцию при постоянный объем, при котором работа расширения невозможна.При постоянном объеме тепло выделяется или поглощается реакцией, равно изменению внутренней энергии, которая происходит во время реакции.
E sys = q v (при постоянном объеме)
На рисунке ниже показан калориметр, в котором реакции могут проводиться при постоянный объем. Однако большинство реакций проводят в открытых колбах и лабораторных стаканах. Когда это сделано, объем системы не является постоянным, потому что газ может входить или выходить из контейнер во время реакции.Однако система находится под постоянным давлением, поскольку общее давление внутри контейнера всегда равно атмосферному давлению.
Если во время реакции из колбы выходит газ, система
работать над его окрестностями. Если в результате реакции в колбу втягивается газ, окружающая среда
работать над системой. Мы все еще можем измерить количество тепла, выделяемого или поглощаемого во время
реакции, но она больше не равна изменению внутренней энергии
система, потому что часть тепла была преобразована в работу.
Если в результате реакции в колбу втягивается газ, окружающая среда
работать над системой. Мы все еще можем измерить количество тепла, выделяемого или поглощаемого во время
реакции, но она больше не равна изменению внутренней энергии
система, потому что часть тепла была преобразована в работу.
E sys = q + w
Мы можем обойти эту проблему, введя понятие энтальпии ( H ), который представляет собой сумму внутренней энергии системы плюс произведение давление газа в системе, умноженное на объем системы.
H sys = E sys + PV
Для простоты индекс «sys» будет опущен. символ внутренней энергии системы и энтальпии системы из сейчас на.Поэтому мы будем сокращать соотношение между энтальпией системы и внутренняя энергия системы следующим образом.
H = E + PV
Изменение энтальпии системы во время химической реакции равно
равна изменению его внутренней энергии плюс изменение произведения давления
раз больше объема системы.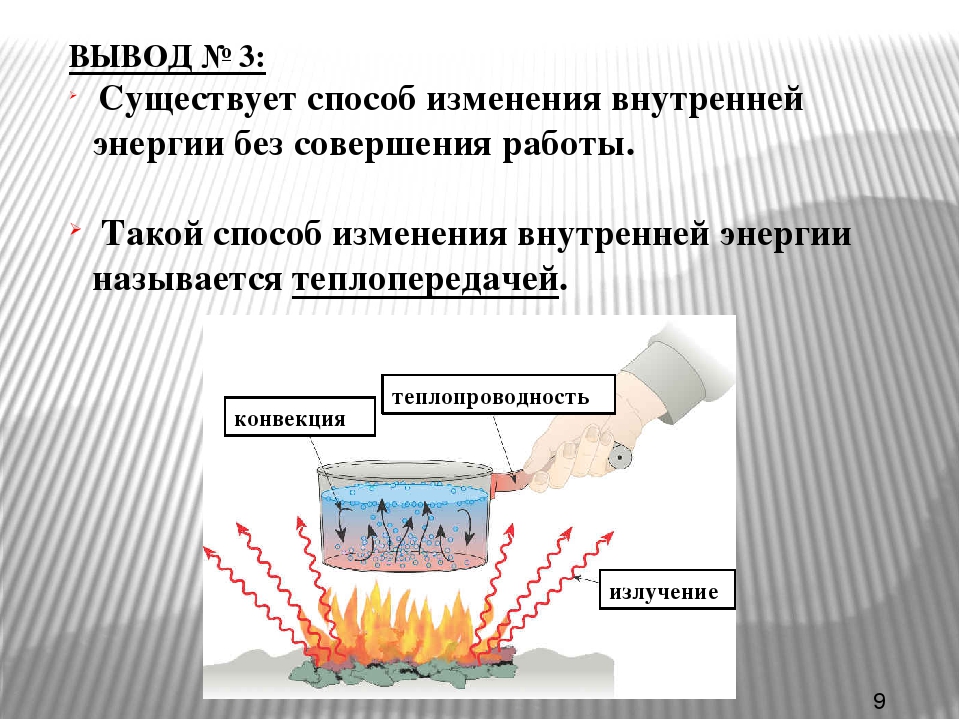
H = E + ( PV )
Предположим, что реакция протекает в стакане из пенополистирола, как показано на рисунок ниже.
Поскольку реакция протекает при постоянном давлении, изменение энтальпия, возникающая во время реакции, равна изменению внутренней энергии система плюс произведение постоянного давления на изменение объема система.
H = E + PV (при постоянном давлении)
Подстановка первого закона термодинамики в это уравнение дает следующий результат.
H = ( q p + w ) + PV
Предполагая, что единственная работа, совершаемая реакцией, — это работа расширения дает уравнение, в котором члены PV сокращаются.
H = ( q p — PV ) + PV
Таким образом, тепло, выделяемое или поглощаемое во время химической реакции при
постоянное давление равно изменению энтальпии системы.
H = q p (при постоянном давлении)
Связь между изменением внутренней энергии системы во время химической реакции и энтальпию реакции можно резюмировать следующим образом.
1. Тепло, выделяемое или поглощаемое при протекании реакции при константе . объем равен изменению внутренней энергии системы.
E sys = q v
2.Тепло, выделяемое или поглощаемое при протекании реакции при константе давление равно изменению энтальпии системы.
H sys = q p
3. Изменение энтальпии системы во время химической реакции равно равна изменению внутренней энергии плюс изменение произведения давления количества газа в системе и его объема.
H sys = E sys + ( PV )
4. Разница между E и H для системы небольшая
для реакций, в которых участвуют только жидкости и твердые вещества, поскольку изменения практически отсутствуют
в объеме системы во время реакции. Разница может быть относительно большой,
однако для реакций, в которых участвуют газы, при изменении количества молей
газ в процессе реакции.
Разница между E и H для системы небольшая
для реакций, в которых участвуют только жидкости и твердые вещества, поскольку изменения практически отсутствуют
в объеме системы во время реакции. Разница может быть относительно большой,
однако для реакций, в которых участвуют газы, при изменении количества молей
газ в процессе реакции.
| Практическая задача 1: Какая из следующих процессы выполняются при постоянном объеме, а какие — при постоянном давлении? (а) кислотно-основное титрование (б) разложение CaCo 3 путем нагревания известняка в тигле с бунзеном. горелка (c) реакция между металлическим цинком и водным раствором ионов Cu 2+ до образуют металлическую медь и ионы Zn 2+ (d) измерение калорий в 1 унции.подача хлопьев для завтрака путем сжигания хлопьев в калориметре бомбы Нажмите здесь, чтобы проверить свой ответ на «Практика»
Задача 1. |
Работа, тепло и внутренняя энергия — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Опишите работу, выполняемую системой, теплопередачу между объектами и изменение внутренней энергии системы
- Расчет работы, теплопередачи и изменения внутренней энергии в простом процессе
Мы обсуждали концепции работы и энергии ранее в механике.Примеры и связанные с ними вопросы теплопередачи между различными объектами также обсуждались в предыдущих главах. Здесь мы хотим расширить эти концепции до термодинамической системы и окружающей ее среды. В частности, мы подробно остановились на концепциях теплопередачи и теплопередачи в предыдущих двух главах. Здесь мы хотим понять, как работа выполняется термодинамической системой или с ней; как тепло передается между системой и окружающей средой; и как общая энергия системы изменяется под влиянием проделанной работы и теплопередачи.
Работа, выполненная системой
Сила, созданная из любого источника, может выполнять работу, перемещая объект посредством смещения. Тогда как же работает термодинамическая система? (Рисунок) показывает газ, заключенный в цилиндр с подвижным поршнем на одном конце. Если газ расширяется относительно поршня, он передает силу на расстояние и воздействует на поршень. Если поршень сжимает газ при движении внутрь, работа также выполняется — в данном случае с газом. Работу, связанную с такими изменениями объема, можно определить следующим образом: Пусть давление газа на торец поршня будет p .Тогда сила, действующая на поршень от газа, составляет па, , где А, — площадь торца. Когда поршень выталкивается наружу на бесконечно малое расстояние dx , величина работы, совершаемой газом, составляет
.Так как объем газа изменяется, это становится
.
Для конечного изменения объема от мы можем проинтегрировать это уравнение от, чтобы найти чистую работу:
Работа, совершаемая ограниченным газом при перемещении поршня на расстояние dx , определяется выражением Этот интеграл имеет смысл только для квазистатического процесса, что означает процесс, который происходит бесконечно малыми шагами, поддерживая систему в тепловом равновесии.(Мы рассмотрим эту идею более подробно позже в этой главе.) Только тогда существует четко определенная математическая связь (уравнение состояния) между давлением и объемом. Эту зависимость можно изобразить на диаграмме pV зависимости давления от объема, где кривая представляет собой изменение состояния. Мы можем аппроксимировать такой процесс как процесс, который происходит медленно, через серию состояний равновесия. Интеграл интерпретируется графически как площадь под кривой pV (заштрихованная область на (Рисунок)).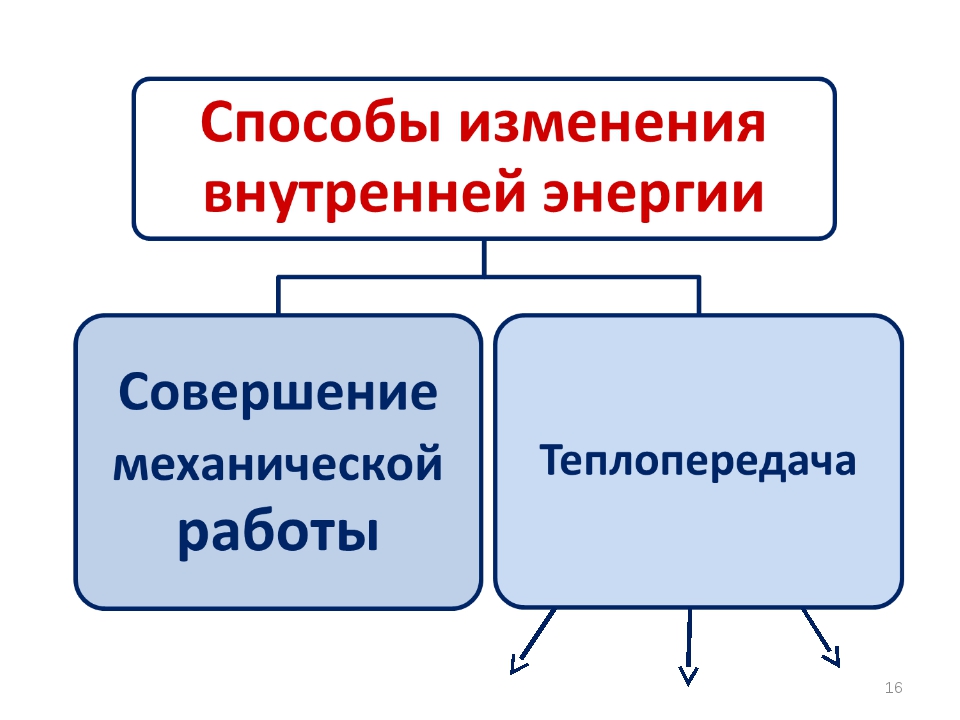 Работа, совершаемая газом, положительна для расширения и отрицательна для сжатия.
Работа, совершаемая газом, положительна для расширения и отрицательна для сжатия.
Рассмотрим два процесса с участием идеального газа, которые представлены путями AC и ABC на (рисунок). Первый процесс — это изотермическое расширение, при котором объем газа изменяется от. Этот изотермический процесс представлен кривой между точками A и C .Газ поддерживается при постоянной температуре T , поддерживая его в тепловом равновесии с резервуаром тепла при этой температуре. Из (Рисунок) и закона идеального газа,
Пути ABC , AC и ADC представляют три различных квазистатических перехода между состояниями равновесия A и C .
Расширение изотермическое, поэтому T остается постоянным на протяжении всего процесса. Поскольку n и R также являются постоянными, единственная переменная в подынтегральном выражении — В , поэтому работа, совершаемая идеальным газом в изотермическом процессе, составляет
.Обратите внимание, что if (расширение), W положительное значение, как и ожидалось.
Прямые линии от A до B и затем от B до C представляют собой другой процесс. Здесь газ под давлением сначала расширяется изобарно (постоянное давление) и квазистатически, а затем охлаждается квазистатически при постоянном объеме, пока его давление не упадет до. От A до B давление постоянно на уровне p , поэтому работа на этом участке пути составляет
Объем с B до C не изменился, поэтому работы не выполнялись. Тогда сеть на пути ABC равна
Тогда сеть на пути ABC равна
Сравнение выражений для работы, совершаемой газом в двух процессах (рисунок), показывает, что они совершенно разные. Это иллюстрирует очень важное свойство термодинамической работы: путь зависимый . Мы не можем определить работу, совершаемую системой при переходе из одного состояния равновесия в другое, если не знаем ее термодинамический путь. Разные ценности работы связаны с разными путями.
Проверьте свое понимание Сколько работы совершает газ, как показано на (Рисунок), когда он квазистатически расширяется по пути ADC ?
Внутренняя энергия
Внутренняя энергия термодинамической системы — это, по определению, сумма механических энергий всех молекул или объектов в системе. Если кинетическая и потенциальная энергии молекулы и равны и соответственно, то внутренняя энергия системы является средним значением полной механической энергии всех сущностей:
, где суммирование ведется по всем молекулам системы, а столбцы над K и U указывают средние значения. Кинетическая энергия отдельной молекулы включает вклады из-за ее вращения и вибрации, а также ее поступательную энергию, где скорость молекулы измеряется относительно центра масс системы. Потенциальная энергия связана только с взаимодействиями между молекулой и и другими молекулами системы. Фактически, ни расположение системы, ни ее движение не имеют никакого значения с точки зрения внутренней энергии. На внутреннюю энергию системы не влияет ее перемещение из подвала на крышу 100-этажного дома или установка на движущийся поезд.
Кинетическая энергия отдельной молекулы включает вклады из-за ее вращения и вибрации, а также ее поступательную энергию, где скорость молекулы измеряется относительно центра масс системы. Потенциальная энергия связана только с взаимодействиями между молекулой и и другими молекулами системы. Фактически, ни расположение системы, ни ее движение не имеют никакого значения с точки зрения внутренней энергии. На внутреннюю энергию системы не влияет ее перемещение из подвала на крышу 100-этажного дома или установка на движущийся поезд.
В идеальном одноатомном газе каждая молекула представляет собой отдельный атом. Следовательно, нет вращательной или колебательной кинетической энергии и. Кроме того, нет межатомных взаимодействий (несмотря на столкновения), поэтому мы устанавливаем его равным нулю. Следовательно, внутренняя энергия обусловлена только поступательной кинетической энергией и
Из обсуждения в предыдущей главе мы знаем, что средняя кинетическая энергия молекулы в идеальном одноатомном газе равна
.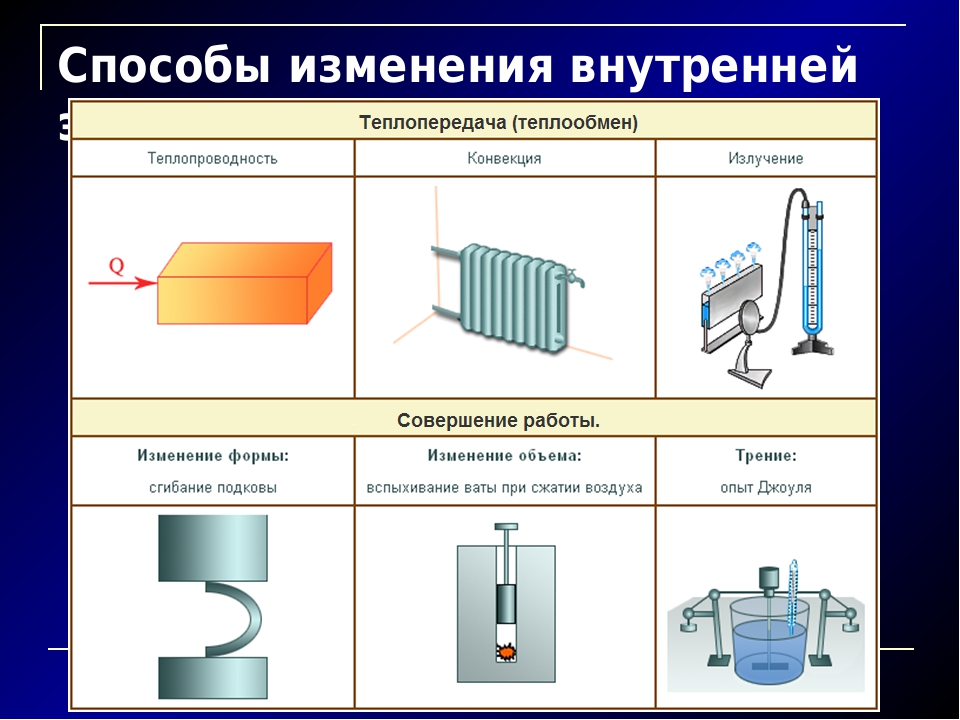
, где T — температура газа по Кельвину.Следовательно, средняя механическая энергия, приходящаяся на молекулу идеального одноатомного газа, также равна
.Внутренняя энергия — это просто количество молекул, умноженное на среднюю механическую энергию на молекулу. Таким образом, для n моль идеального одноатомного газа
Обратите внимание, что внутренняя энергия данного количества идеального одноатомного газа зависит только от температуры и полностью не зависит от давления и объема газа. Для других систем внутреннюю энергию нельзя выразить так просто.Однако увеличение внутренней энергии часто может быть связано с повышением температуры.
Из нулевого закона термодинамики мы знаем, что, когда две системы находятся в тепловом контакте, они в конечном итоге достигают теплового равновесия, при котором они имеют одинаковую температуру. В качестве примера предположим, что мы смешиваем два одноатомных идеальных газа. Теперь энергия, приходящаяся на молекулу идеального одноатомного газа, пропорциональна его температуре. Таким образом, когда два газа смешиваются, молекулы более горячего газа должны терять энергию, а молекулы более холодного газа должны получать энергию.Это продолжается до тех пор, пока не будет достигнуто тепловое равновесие, после чего температура и, следовательно, средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу, одинаковы для обоих газов. Подход к равновесию для реальных систем несколько сложнее, чем для идеального одноатомного газа. Тем не менее, мы все же можем сказать, что между системами происходит обмен энергией до тех пор, пока их температуры не станут одинаковыми.
Теперь энергия, приходящаяся на молекулу идеального одноатомного газа, пропорциональна его температуре. Таким образом, когда два газа смешиваются, молекулы более горячего газа должны терять энергию, а молекулы более холодного газа должны получать энергию.Это продолжается до тех пор, пока не будет достигнуто тепловое равновесие, после чего температура и, следовательно, средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу, одинаковы для обоих газов. Подход к равновесию для реальных систем несколько сложнее, чем для идеального одноатомного газа. Тем не менее, мы все же можем сказать, что между системами происходит обмен энергией до тех пор, пока их температуры не станут одинаковыми.
Сводка
- Положительная (отрицательная) работа совершается термодинамической системой, когда она расширяется (сжимается) под действием внешнего давления.
- Тепло — это энергия, передаваемая между двумя объектами (или двумя частями системы) из-за разницы температур.

- Внутренняя энергия термодинамической системы — это ее полная механическая энергия.
Концептуальные вопросы
Можно ли определить, вызвано ли изменение внутренней энергии теплопередачей, выполненной работой или их комбинацией?
Когда жидкость испаряется, ее внутренняя энергия не равна добавленному теплу.Почему?
Часть энергии уходит на преобразование фазы жидкости в газ.
Почему при накачивании шины велосипедный насос нагревается?
Возможно ли, чтобы температура системы оставалась постоянной, когда тепло поступает в нее или из нее? Если да, то приведите примеры.
Да, до тех пор, пока проделанная работа равна добавленному теплу, внутренняя энергия не изменится, а следовательно, и температура не изменится. Когда вода замерзает или когда лед тает при отводе или добавлении тепла, соответственно, температура остается постоянной.
Проблемы
Газ под давлением 2,00 атм подвергается квазистатическому изобарическому расширению с 3,00 до 5,00 л. Сколько работы совершает газ?
Сколько работы совершает газ?
Для квазистатического сжатия 0,50 моль идеального газа до одной пятой его первоначального объема требуется 500 Дж работы. Рассчитайте температуру газа, предполагая, что она остается постоянной во время сжатия.
Установлено, что при квазистатическом расширении разреженного газа от 0,50 до 4,0 л он совершает 250 Дж работы.Если предположить, что температура газа остается постоянной на уровне 300 К, сколько молей газа присутствует?
При квазистатическом изобарическом расширении 500 Дж работы совершает газ. Если давление газа составляет 0,80 атм, каково частичное увеличение объема газа, если исходное значение составляло 20,0 л?
Когда газ претерпевает квазистатическое изобарическое изменение объема от 10,0 до 2,0 л, требуется 15 Дж работы от внешнего источника. Какое давление газа?
Идеальный газ квазистатически и изотермически расширяется из состояния с давлением p и объемом V в состояние с объемом 4V. Покажите, что работа, совершаемая газом при расширении, равна pV (ln 4).
Покажите, что работа, совершаемая газом при расширении, равна pV (ln 4).
Как показано ниже, рассчитайте работу, совершаемую газом в квазистатических процессах, представленных путями (a) AB; (б) АБР; (c) ACB; и (d) ADCB.
(a) Рассчитайте работу, совершаемую газом по замкнутому пути, показанному ниже. Изогнутая часть между R и S полукруглая. б) Если процесс осуществляется в обратном направлении, какую работу выполняет газ?
Идеальный газ квазистатически расширяется до трехкратного первоначального объема.Какой процесс требует большей работы от газа, изотермический или изобарический? Определите соотношение проделанной работы в этих процессах.
Разбавленный газ под давлением 2,0 атм и объемом 4,0 л проходит следующие квазистатические этапы: (а) изобарическое расширение до объема 10,0 л, (б) изохорическое изменение до давления 0,50 атм, (в) изобарическое сжатие до объема 4,0 л, и (г) изохорическое изменение до давления 2,0 атм. Покажите эти шаги на диаграмме pV и определите по вашему графику чистую работу, выполненную газом.
Покажите эти шаги на диаграмме pV и определите по вашему графику чистую работу, выполненную газом.
Какова средняя механическая энергия атомов идеального одноатомного газа при 300 К?
Какова внутренняя энергия 6,00 моль идеального одноатомного газа?
Рассчитайте внутреннюю энергию 15 мг гелия при температуре
Два одноатомных идеальных газа A и B имеют одинаковую температуру. Если 1,0 г газа A имеет ту же внутреннюю энергию, что и 0,10 г газа B, каково (а) соотношение количества молей каждого газа и (б) соотношение атомных масс двух газов?
Коэффициенты Ван-дер-Ваальса для кислорода равны и.Используйте эти значения, чтобы построить изотерму Ван-дер-Ваальса кислорода при 100 К. На том же графике изотермы одного моля идеального газа.
Найдите работу, выполненную в квазистатических процессах, показанных ниже. Состояния представлены как значения (p, V) для точек в плоскости pV: 1 (3 атм, 4 L), 2 (3 атм, 6 L), 3 (5 атм, 4 L), 4 (2 атм. , 6 л), 5 (4 атм, 2 л), 6 (5 атм, 5 л) и 7 (2 атм, 5 л).
, 6 л), 5 (4 атм, 2 л), 6 (5 атм, 5 л) и 7 (2 атм, 5 л).
а. 600 Дж; б. 0; c. 500 Дж; d. 200 Дж; е. 800 Дж; f. 500 Дж
Глоссарий
- внутренняя энергия
- среднее значение полной механической энергии всех молекул или объектов в системе
- квазистатический процесс
- эволюция системы, которая идет так медленно, что вовлеченная система всегда находится в термодинамическом равновесии
Первый закон термодинамики — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Изложите первый закон термодинамики и объясните, как его применять
- Объясните, как теплопередача, выполненная работа и изменение внутренней энергии связаны в любом термодинамическом процессе
Теперь, когда мы увидели, как рассчитать внутреннюю энергию, тепло и работу, проделанную для термодинамической системы, претерпевающей изменения во время некоторого процесса, мы можем увидеть, как эти величины взаимодействуют, чтобы повлиять на величину изменения, которое может произойти.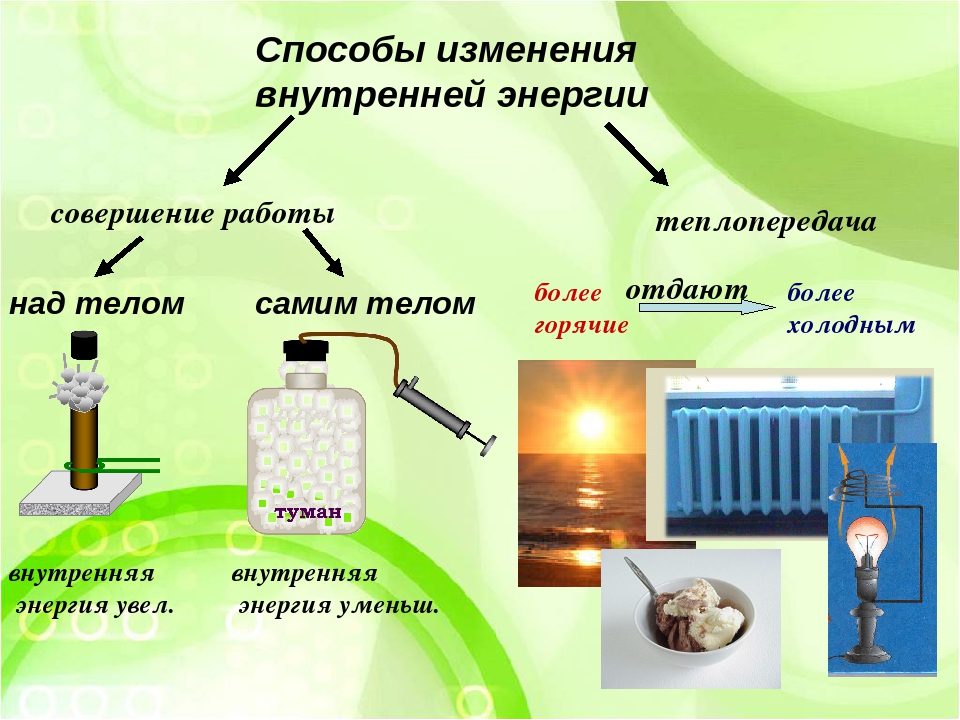 Это взаимодействие задается первым законом термодинамики. Британскому ученому и писателю К. П. Сноу (1905–1980) приписывают шутку о четырех законах термодинамики. Его юмористическое заявление о первом законе термодинамики гласит: «Вы не можете выиграть», или, другими словами, вы не можете получить больше энергии из системы, чем вложили в нее. В этой главе мы увидим, как внутренняя энергия, тепло и работа играют роль в первом законе термодинамики.
Это взаимодействие задается первым законом термодинамики. Британскому ученому и писателю К. П. Сноу (1905–1980) приписывают шутку о четырех законах термодинамики. Его юмористическое заявление о первом законе термодинамики гласит: «Вы не можете выиграть», или, другими словами, вы не можете получить больше энергии из системы, чем вложили в нее. В этой главе мы увидим, как внутренняя энергия, тепло и работа играют роль в первом законе термодинамики.
Предположим, что Q представляет собой теплообмен между системой и окружающей средой, а Вт, — это работа, выполняемая системой или над ней.Первый закон гласит, что изменение внутренней энергии этой системы определяется величиной. Поскольку добавленное тепло увеличивает внутреннюю энергию системы, Q является положительным, когда оно добавляется в систему, и отрицательным, когда оно удаляется из системы.
Когда газ расширяется, он работает, и его внутренняя энергия уменьшается.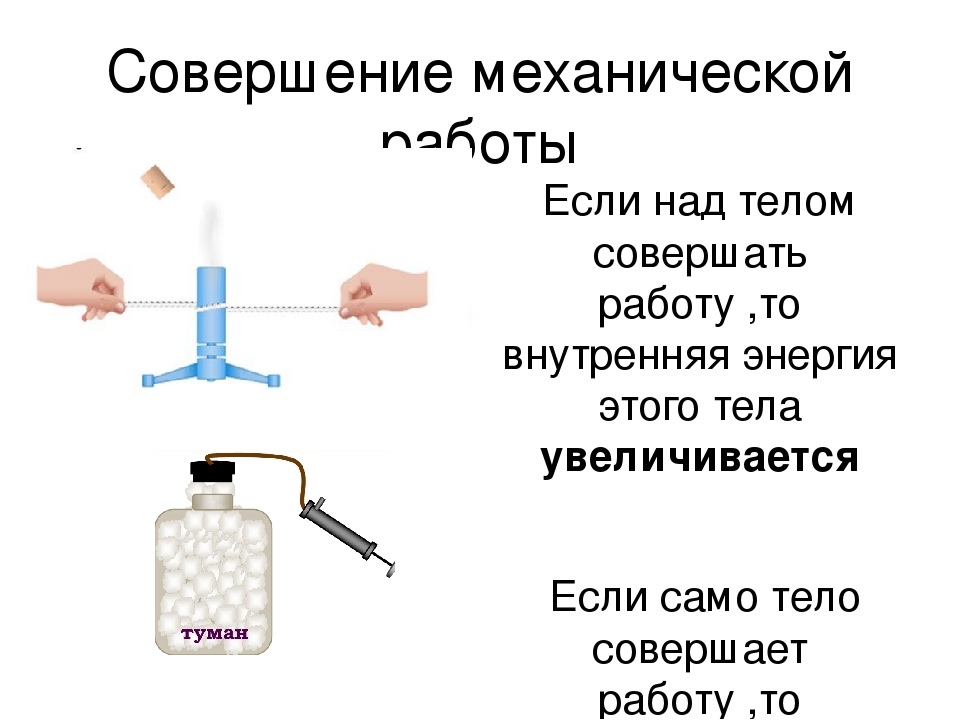 Таким образом, Вт, является положительным, когда работа выполняется системой, и отрицательным, когда работа выполняется в системе. Это соглашение о знаках кратко изложено на (Рисунок). Первый закон термодинамики сформулирован следующим образом:
Таким образом, Вт, является положительным, когда работа выполняется системой, и отрицательным, когда работа выполняется в системе. Это соглашение о знаках кратко изложено на (Рисунок). Первый закон термодинамики сформулирован следующим образом:
Первый закон термодинамики
С каждым состоянием равновесия системы связана ее внутренняя энергия. Изменение для любого перехода между двумя состояниями равновесия равно
., где Q и W представляют, соответственно, тепло, передаваемое системой, и работу, выполняемую системой или над ней.
Первый закон — это закон сохранения энергии. Он говорит нам, что система может обмениваться энергией с окружающей средой за счет передачи тепла и выполнения работы. Таким образом, обменная чистая энергия равна изменению полной механической энергии молекул системы (то есть внутренней энергии системы). Таким образом, если система изолирована, ее внутренняя энергия должна оставаться постоянной.
Он говорит нам, что система может обмениваться энергией с окружающей средой за счет передачи тепла и выполнения работы. Таким образом, обменная чистая энергия равна изменению полной механической энергии молекул системы (то есть внутренней энергии системы). Таким образом, если система изолирована, ее внутренняя энергия должна оставаться постоянной.
Хотя Q и W оба зависят от термодинамического пути, взятого между двумя состояниями равновесия, их разница не зависит.(Рисунок) показывает диаграмму pV системы, которая многократно совершает переход от A к B по различным термодинамическим путям. По пути 1 система поглощает тепло и работает по пути 2, поглощает тепло и выполняет работу и так далее. Значения и могут варьироваться от пути к пути, но у нас
или
То есть изменение внутренней энергии системы между A и B не зависит от пути. В главе о потенциальной энергии и сохранении энергии мы столкнулись с другой величиной, не зависящей от пути: изменением потенциальной энергии между двумя произвольными точками в пространстве.Это изменение представляет собой отрицательный результат работы, проделанной консервативной силой между двумя точками. Потенциальная энергия является функцией пространственных координат, тогда как внутренняя энергия является функцией термодинамических переменных. Например, мы могли бы написать для внутренней энергии. Такие функции, как внутренняя энергия и потенциальная энергия, известны как функций состояния , потому что их значения зависят исключительно от состояния системы.
В главе о потенциальной энергии и сохранении энергии мы столкнулись с другой величиной, не зависящей от пути: изменением потенциальной энергии между двумя произвольными точками в пространстве.Это изменение представляет собой отрицательный результат работы, проделанной консервативной силой между двумя точками. Потенциальная энергия является функцией пространственных координат, тогда как внутренняя энергия является функцией термодинамических переменных. Например, мы могли бы написать для внутренней энергии. Такие функции, как внутренняя энергия и потенциальная энергия, известны как функций состояния , потому что их значения зависят исключительно от состояния системы.
Часто первый закон используется в его дифференциальной форме, то есть
.
Вот бесконечно малое изменение внутренней энергии, когда бесконечно малое количество тепла dQ обменивается с системой и бесконечно малое количество работы dW выполняется (положительный знак) или (отрицательный знак) системой.
Изменения состояния и первый закон Во время термодинамического процесса система переходит из состояния A в состояние B , она получает 400 Дж тепла и выполняет 100 Дж работы.(а) Каково изменение внутренней энергии системы при этом переходе? (b) Если затем система переходит из состояния B обратно в состояние A , каково изменение ее внутренней энергии? (c) Если при перемещении от A к B по другому пути, работа выполняется в системе, сколько тепла она поглощает?
Стратегия Первый закон термодинамики связывает изменение внутренней энергии, работу, выполняемую системой, и тепло, передаваемое системе, в простом уравнении. Внутренняя энергия является функцией состояния и поэтому фиксируется в любой заданной точке независимо от того, как система достигает состояния.
Внутренняя энергия является функцией состояния и поэтому фиксируется в любой заданной точке независимо от того, как система достигает состояния.
Решение
- Из первого закона изменение внутренней энергии системы составляет
- Рассмотрим замкнутый путь, который проходит через состояния A и B . Внутренняя энергия — это функция состояния, поэтому для замкнутого пути она равна нулю. Таким образом,
и
Это дает - Изменение внутренней энергии одинаково для любого пути, поэтому
и теплообменник
Знак минус указывает на то, что при этом переходе система теряет тепло.
Значение Когда замкнутый цикл рассматривается в качестве первого закона термодинамики, изменение внутренней энергии на всем пути равно нулю. Если бы трение играло роль в этом примере, добавление тепла привело бы к меньшему объему работы. (Рисунок) учитывает, что происходит, если трение играет роль.
(Рисунок) учитывает, что происходит, если трение играет роль.
Обратите внимание, что на (Рисунок) мы не предполагали, что переходы были квазистатическими. Это потому, что первый закон не подлежит такому ограничению.Он описывает переходы между состояниями равновесия, но не касается промежуточных состояний. Система не должна проходить только через состояния равновесия. Например, если газ в стальном контейнере при четко определенной температуре и давлении взорвется с помощью искры, часть газа может конденсироваться, различные молекулы газа могут объединиться, чтобы образовать новые соединения, и могут быть все своего рода турбулентность в контейнере, но в конечном итоге система придет к новому состоянию равновесия.Эта система явно не находится в равновесии во время своего перехода; однако его поведение по-прежнему определяется первым законом, потому что процесс начинается и заканчивается, когда система находится в состоянии равновесия.
Полировка фитинга Машинист полирует медный фитинг весом 0,50 кг с помощью куска наждачной бумаги в течение 2,0 мин. Он перемещает ткань по фитингу с постоянной скоростью 1,0 м / с, прикладывая силу 20 Н, касательную к поверхности фитинга. (а) Какая общая работа, проделанная механиком по установке, составляет? (б) Каково увеличение внутренней энергии фитинга? Предположим, что изменение внутренней энергии ткани незначительно и что между фитингом и окружающей средой не происходит теплообмена.(c) Каково повышение температуры арматуры?
Он перемещает ткань по фитингу с постоянной скоростью 1,0 м / с, прикладывая силу 20 Н, касательную к поверхности фитинга. (а) Какая общая работа, проделанная механиком по установке, составляет? (б) Каково увеличение внутренней энергии фитинга? Предположим, что изменение внутренней энергии ткани незначительно и что между фитингом и окружающей средой не происходит теплообмена.(c) Каково повышение температуры арматуры?
Стратегия Сила машиниста на расстоянии, которую можно рассчитать по заданной скорости и времени, — это работа, проделанная в системе. Работа, в свою очередь, увеличивает внутреннюю энергию системы. Эту энергию можно интерпретировать как тепло, которое повышает температуру системы за счет ее теплоемкости. Будьте осторожны со знаком каждого количества.
Решение
- Мощность, создаваемая силой, действующей на объект, или скорость, с которой механик выполняет работу трения с фитингом, равна.Таким образом, за истекшее время (2,0 мин) на фитинге проделано
работ.
- Предполагается, что между фитингом и окружающей средой не происходит теплообмена, поэтому первый закон дает изменение внутренней энергии фитинга:
- Так как не зависит от пути, эффект работы такой же, как если бы он подавался при атмосферном давлении путем передачи тепла. Таким образом,
и повышение температуры штуцера
, где мы использовали значение удельной теплоемкости меди.
Значение Если выделялось тепло, изменение внутренней энергии было бы меньшим и вызвало бы меньшее изменение температуры, чем то, что было рассчитано в задаче.
Проверьте свое понимание г Приведенные ниже величины представляют четыре различных перехода между одним и тем же начальным и конечным состоянием. Заполнить бланки.
Проверьте свое понимание Почему было необходимо утверждать, что процесс (рисунок) является квазистатическим?
Итак, процесс представлен кривой на графике pV для оценки работы.
Проверьте свое понимание Когда 1,00 г аммиака закипает при атмосферном давлении и его объем изменяется от 1,47 до. Его теплота испарения при этом давлении равна. Каково изменение внутренней энергии аммиака при его испарении?
Сводка
- Внутренняя энергия термодинамической системы является функцией состояния и, следовательно, уникальна для каждого состояния равновесия системы.
- Увеличение внутренней энергии термодинамической системы дается за счет тепла, добавляемого к системе, за вычетом работы, выполняемой системой в любом термодинамическом процессе.
Концептуальные вопросы
Что первый закон термодинамики говорит нам об энергии Вселенной?
Всегда ли добавление тепла к системе увеличивает ее внутреннюю энергию?
Если в системе выполняется больше работы, чем добавляется тепла, внутренняя энергия системы фактически уменьшается.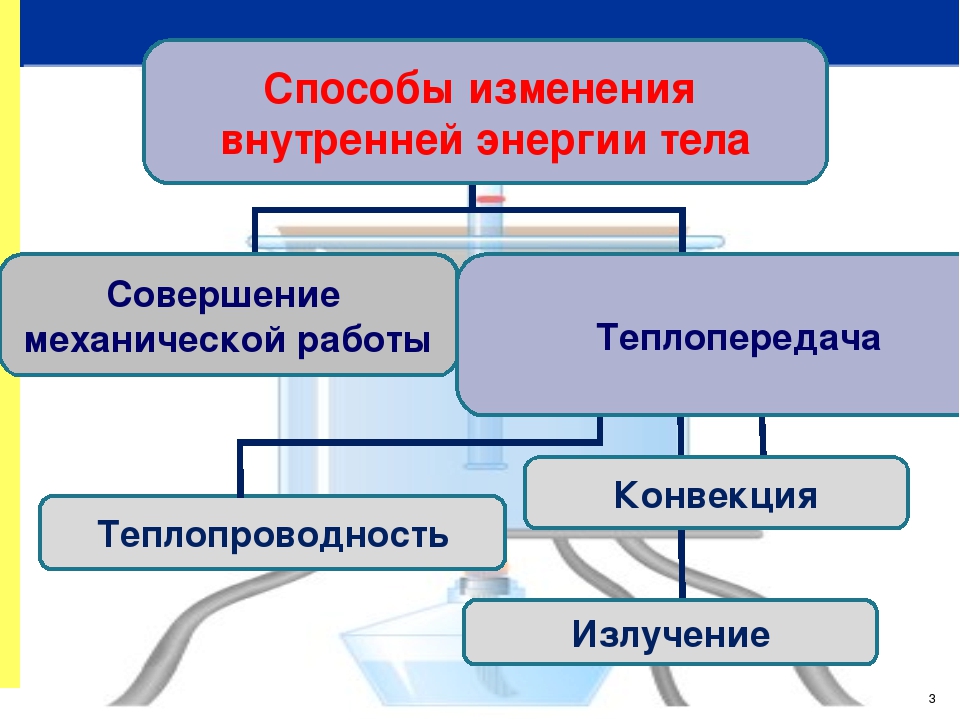
Много усилий, времени и денег было потрачено на поиски так называемой машины с вечным двигателем, которая определяется как гипотетическая машина, которая работает или производит полезную работу бесконечно долго, и / или гипотетическую машину, которая производит больше работы или энергии, чем потребляет.Объясните в терминах первого закона термодинамики, почему или почему не может быть построена такая машина.
Проблемы
Когда разбавленный газ квазистатически расширяется от 0,50 до 4,0 л, он совершает 250 Дж работы. Если предположить, что температура газа остается постоянной на уровне 300 К, (а) каково изменение внутренней энергии газа? б) Сколько тепла поглощается газом в этом процессе?
При квазистатическом изобарическом расширении 500 Дж работы совершает газ.Давление газа составляет 0,80 атм, и первоначально оно составляло 20,0 л. Если внутренняя энергия газа увеличилась на 80 Дж при расширении, сколько тепла газ поглотит?
Идеальный газ квазистатически и изотермически расширяется из состояния с давлением p и объемом V в состояние с объемом 4V.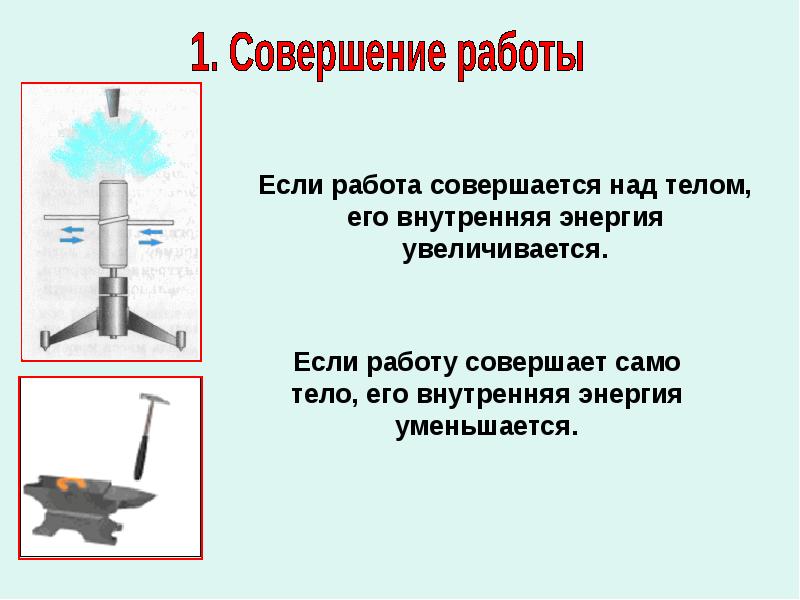 Сколько тепла добавляется расширяющемуся газу?
Сколько тепла добавляется расширяющемуся газу?
Как показано ниже, если тепло, поглощаемое газом вдоль AB, составляет 400 Дж, определите количество тепла, поглощенного вдоль (a) ADB; (б) ACB; и (c) ADCB.
а. 600 Дж; б. 600 Дж; c. 800 Дж
Во время изобарного расширения от A до B, представленного ниже, из газа отводится 130 Дж тепла. Как изменилась его внутренняя энергия?
(a) Каково изменение внутренней энергии процесса, представленного замкнутым путем, показанным ниже? б) Сколько тепла передается? (c) Если путь проходит в противоположном направлении, сколько тепла передается?
а.0; б. 160 Дж; c. –160 Дж
Когда газ расширяется по пути AC, показанному ниже, он выполняет 400 Дж работы и поглощает 200 или 400 Дж тепла. (a) Предположим, вам сказали, что на пути ABC газ поглощает 200 или 400 Дж тепла. Какое из этих значений правильное? (б) Дайте правильный ответ из части (а), сколько работы выполняет газ вдоль линии ABC? (c) Вдоль CD внутренняя энергия газа уменьшается на 50 Дж. Сколько тепла передается газом на этом пути?
Сколько тепла передается газом на этом пути?
Когда газ расширяется вдоль AB (см. Ниже), он совершает 500 Дж работы и поглощает 250 Дж тепла.Когда газ расширяется вдоль AC , он выполняет 700 Дж работы и поглощает 300 Дж тепла. (а) Сколько тепла обменивается газом в районе г. до н.э. г.? (b) Когда газ переходит от C к A по CDA , на нем выполняется 800 Дж работы от C до D . Сколько тепла передает CDA ?
Разбавленный газ хранится в левой камере контейнера, стенки которого идеально изолируют (см. Ниже), а правая камера откачивается.Когда перегородка снимается, газ расширяется и заполняет всю емкость. Посчитайте работу, проделанную газом. Меняется ли при этом внутренняя энергия газа?
Идеальные газы A и B хранятся в левой и правой камерах изолированного контейнера, как показано ниже. Перегородка снимается и газы смешиваются. Выполняется ли какая-либо работа в этом процессе? Если температуры A и B изначально равны, что произойдет с их общей температурой после их смешивания?
Перегородка снимается и газы смешиваются. Выполняется ли какая-либо работа в этом процессе? Если температуры A и B изначально равны, что произойдет с их общей температурой после их смешивания?
Никаких работ не выполняется, и они достигают одинаковой общей температуры.
Идеальный одноатомный газ при давлении и температуре 300 K претерпевает квазистатическое изобарическое расширение из (а) Какую работу совершает газ? б) Какова температура газа после расширения? (c) Сколько там молей газа? (г) Как изменяется внутренняя энергия газа? (e) Сколько тепла добавляется к газу?
Рассмотрим процесс для пара в цилиндре, показанный ниже. Предположим, изменение внутренней энергии в этом процессе составляет 30 кДж.Найдите тепло, попадающее в систему.
Состояние 30 моль пара в цилиндре изменяется циклически от abca, где давление и объем состояний равны: a (30 атм, 20 л), b (50 атм, 20 л) и c. (50 атм, 45 л). Предположим, что каждое изменение происходит вдоль линии, соединяющей начальное и конечное состояния в плоскости pV.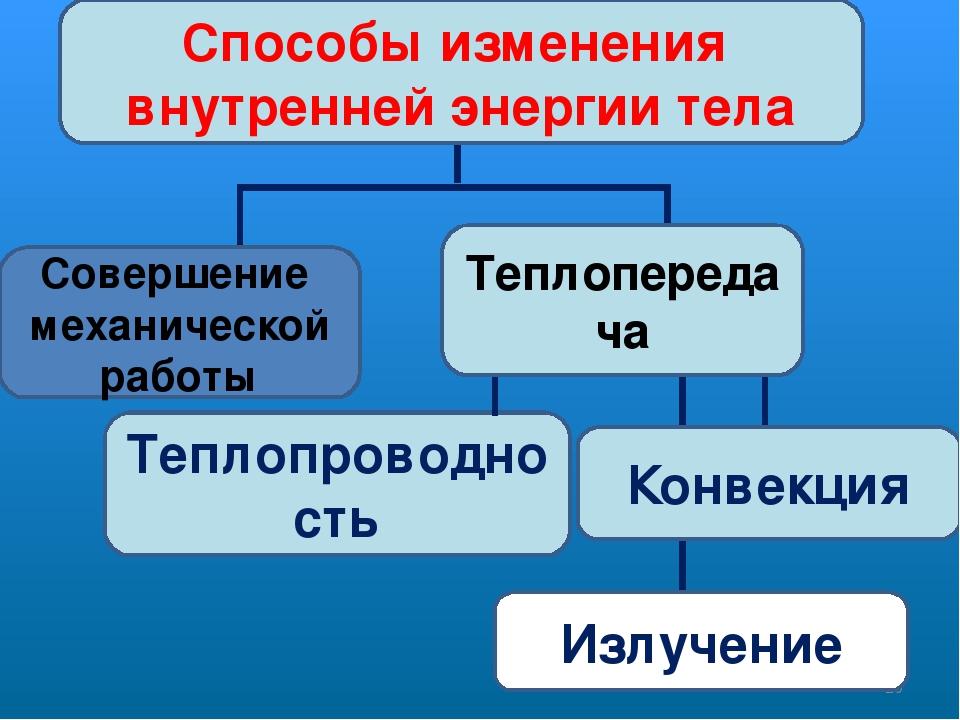 (а) Отобразите цикл в плоскости pV. (б) Найдите чистую работу, выполненную паром за один цикл. (c) Найдите чистое количество теплового потока в паре в течение одного цикла.
(а) Отобразите цикл в плоскости pV. (б) Найдите чистую работу, выполненную паром за один цикл. (c) Найдите чистое количество теплового потока в паре в течение одного цикла.
Металлический контейнер фиксированного объема, погруженный в большой резервуар с температурой, содержит два отсека, разделенных свободно подвижной стенкой. Первоначально стенка удерживается на месте пробкой, так что 0,02 моль газообразного азота с одной стороны и 0,03 моль газообразного кислорода с другой стороны, каждый из которых занимает половину объема. Когда стопор снимается, стена перемещается и принимает окончательное положение. Движение стены контролируется так, что стена движется бесконечно малыми квазистатическими шагами.(a) Найдите окончательные объемы двух сторон, принимая идеальное поведение газов для двух газов. б) Сколько работы каждый газ выполняет над другим? (c) Как изменяется внутренняя энергия каждого газа? (d) Найдите количество тепла, которое входит или выходит из каждого газа.
Газ в цилиндрическом закрытом контейнере адиабатически и квазистатически расширяется от состояния A (3 МПа, 2 л) до состояния B с объемом 6 л вдоль пути (a) Постройте путь в пВ самолет. (б) Найдите количество работы, совершаемой газом, и изменение внутренней энергии газа во время процесса.
(б) Найдите количество работы, совершаемой газом, и изменение внутренней энергии газа во время процесса.
а.
;
г.
Глоссарий
- первый закон термодинамики
- изменение внутренней энергии для любого перехода между двумя состояниями равновесия равно
Какая связь между теплом и изменением внутренней энергии в адиобатической системе?
Важно понимать, что адиабатический процесс не означает отсутствия изменения температуры.Изотермический процесс — это процесс, в котором нет изменения температуры. Процесс является адиабатическим, , если он происходит так быстро (или так медленно), что подвод энергии (в систему) за счет нагрева равен нулю, или, другими словами, система не теряет и не получает тепла.
Есть компонент, о котором вы забываете: работа .
# цвет (синий) (Q = W + DeltaE) #
, где # Q # — энергия, потребляемая нагревом, # W # — проделанная работа, а # DeltaE # — изменение внутренней энергии.
# цвет (синий) (0 = W + DeltaE) #
Это говорит нам о том, что работа , выполненная (системой или средой, в зависимости от того, как вы структурируете свои знаки), равна изменению внутренней энергии .
Давайте, например, рассмотрим адиабатическое расширение газа. Здесь газ действительно воздействует на окружающую среду, поскольку он расширяется, поэтому # W # является положительной величиной. Тогда:
# W = -DeltaE #
Мы знаем, что работа положительна, поэтому у нас должно быть отрицательное изменение внутренней энергии (чтобы отменить отрицательное), что означает, что # E_f-E_i # является отрицательной величиной. Это говорит нам о том, что начальная энергия системы была больше, чем конечная энергия.
- Один из способов определения внутренней энергии (средняя поступательная кинетическая энергия # N # молекул / атомов / частиц):
# цвет (синий) (E = 3 / 2Nk_bT) #
где # k_b # — постоянная Больцмана, а # T # — температура системы
Потому что количество молекул / частиц / пр.
 остается постоянным, а # k_b # по определению является постоянным, единственный фактор, который может изменить , — это температура.
остается постоянным, а # k_b # по определению является постоянным, единственный фактор, который может изменить , — это температура.Мы должны иметь внутреннюю энергию , убывающую в этом адиабатическом процессе. Это не остается неизменным .
12.2 Первый закон термодинамики: тепловая энергия и работа
Биология: биологическая термодинамика
Мы часто думаем о термодинамике, как о полезной для изобретения или тестирования оборудования, такого как двигатели или паровые турбины.Однако термодинамика также применима к живым системам, таким как наши собственные тела. Это составляет основу биологической термодинамики (рис. 12.7).
Рис. 12.7 (a) Первый закон термодинамики применим к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, тогда как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую организмом. ) (Б) Растения преобразуют часть лучистой энергии солнечного света в запасенную химическую энергию, процесс, называемый фотосинтез .
) (Б) Растения преобразуют часть лучистой энергии солнечного света в запасенную химическую энергию, процесс, называемый фотосинтез .
Сама жизнь зависит от биологической передачи энергии. Посредством фотосинтеза растения поглощают солнечную энергию и используют эту энергию для преобразования углекислого газа и воды в глюкозу и кислород. Фотосинтез принимает одну форму энергии — свет — и преобразует ее в другую форму — химическую потенциальную энергию (глюкозу и другие углеводы).
Метаболизм человека — это преобразование пищи в энергию, выделяемую теплом, работой, выполняемой клетками тела, и накопленным жиром.Метаболизм — интересный пример действия первого закона термодинамики. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии; это неромантичный взгляд на хороший буррито.
Организм усваивает всю пищу, которую мы потребляем. По сути, метаболизм — это процесс окисления, в котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы. Упражнения помогают вам похудеть, поскольку они обеспечивают передачу энергии от вашего тела как за счет тепла, так и за счет работы, и повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.
Это означает, что питание осуществляется в форме работы. Упражнения помогают вам похудеть, поскольку они обеспечивают передачу энергии от вашего тела как за счет тепла, так и за счет работы, и повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.
Биологическая термодинамика также включает изучение трансдукции между клетками и живыми организмами. Трансдукция — это процесс, при котором генетический материал — ДНК — передается от одной клетки к другой. Это часто происходит во время вирусной инфекции (например, гриппа), и именно так вирус распространяется, а именно путем передачи своего генетического материала все большему количеству ранее здоровых клеток. Когда инфицировано достаточное количество клеток, вы начинаете ощущать воздействие вируса (симптомы гриппа — мышечная слабость, кашель и заложенность носа).
Энергия передается вместе с генетическим материалом и, таким образом, подчиняется первому закону термодинамики. Энергия передается — а не создается и не уничтожается — в процессе. Когда с элементом выполняется работа или тепло передает энергию ячейке, внутренняя энергия ячейки увеличивается. Когда клетка работает или теряет тепло, ее внутренняя энергия уменьшается. Если количество работы, выполняемой ячейкой, такое же, как количество энергии, передаваемой теплом, или количество работы, выполняемой ячейкой, совпадает с количеством энергии, передаваемой теплом, чистого изменения внутренней энергии не будет. .
Когда с элементом выполняется работа или тепло передает энергию ячейке, внутренняя энергия ячейки увеличивается. Когда клетка работает или теряет тепло, ее внутренняя энергия уменьшается. Если количество работы, выполняемой ячейкой, такое же, как количество энергии, передаваемой теплом, или количество работы, выполняемой ячейкой, совпадает с количеством энергии, передаваемой теплом, чистого изменения внутренней энергии не будет. .
Проверка захвата
Исходя из того, что вы знаете о теплопередаче и о первом законе термодинамики, нужно ли вам есть больше или меньше, чтобы поддерживать постоянный вес в холодную погоду? Объяснить, почему.
- еще
- ; поскольку в холодную погоду организм теряет больше энергии, потребность в еде увеличивается, чтобы поддерживать постоянный вес Еще
- ; употребление большего количества пищи означает накопление большего количества жира, что защитит организм от холодной погоды и уменьшит потерю энергии На
- меньше; поскольку в холодную погоду организм теряет меньше энергии, потребность в еде уменьшается, чтобы поддерживать постоянный вес На
- меньше; употребление меньшего количества пищи означает накопление меньшего количества жира, поэтому для сжигания жира потребуется меньше энергии, и, как следствие, вес останется постоянным



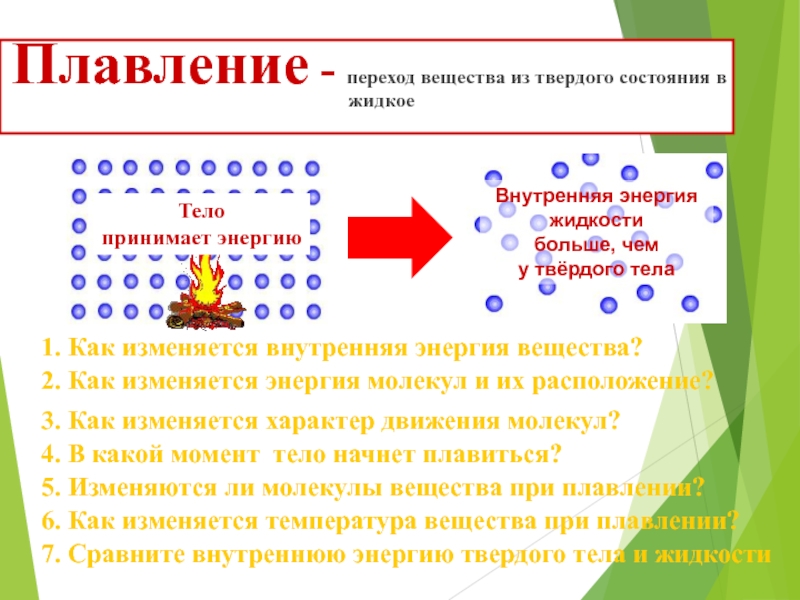



 остается постоянным, а # k_b # по определению является постоянным, единственный фактор, который может изменить , — это температура.
остается постоянным, а # k_b # по определению является постоянным, единственный фактор, который может изменить , — это температура.