2+n-72)=1/(n+9)| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | ||
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| Найти точное значение | cos((7pi)/6) | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
РАЗНИЦА МЕЖДУ SIN 2X И 2 SIN X | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — НАУКА
Грех 2x против 2 Греха x Функции — это один из важнейших классов математических объектов, которые широко используются почти во всех областях математики.
Синусоидальная функция, обозначаемая как ж(Ик
Грех 2x против 2 Греха x
Функции — это один из важнейших классов математических объектов, которые широко используются почти во всех областях математики. Синусоидальная функция, обозначаемая как ж(Икс) = грех Икс — тригонометрическая функция, определенная из множества действительных чисел на интервале [-1, 1] и периодическая с периодом 2ᴫ.
Основное определение синуса острого угла выполняется с помощью прямоугольного треугольника. Синус угла равен отношению длины стороны, противоположной углу, к длине гипотенузы. Это определение можно распространить на все углы, используя тождества sin (-Икс) = — грех Икс и грех (ᴫ + Икс) = — грех Икс и грех (2пᴫ + Икс) = грех Икс.
В следующих двух разделах рассмотрим ж(Икс) = грех Икс и грамм(Икс) = 2Икс.
Что такое грех 2х?
Рассмотрим составную функцию f o g данный f o g (Икс) = ж (грамм(Икс)) = ж(2Икс) = грех 2Икс. Эта функция очень похожа на sin Икс с доменом как набор действительных чисел и диапазоном как интервал [-1, 1]. Эта функция периодическая с периодом (в отличие от периода 2ᴫ функции sin Икс). Грех 2Икс может быть расширен тождеством Sin 2Икс = 2 греха Икспотому чтоИкс слишком.
Что такое 2 Sin x?
Рассмотрим составную функцию g o f данный g o f (Икс) = грамм (ж(Икс)) = грамм (грех Икс) = 2 греха Икс. Это также периодическая функция с тем же периодом, что и sin Икс, но в два раза больше его амплитуды, поскольку -1 ≤ sin Икс ≤ 1 означает -2 ≤ 2 греха Икс ≤ 2. Его доменом является набор действительных чисел, а диапазон — интервал [-2, 2]
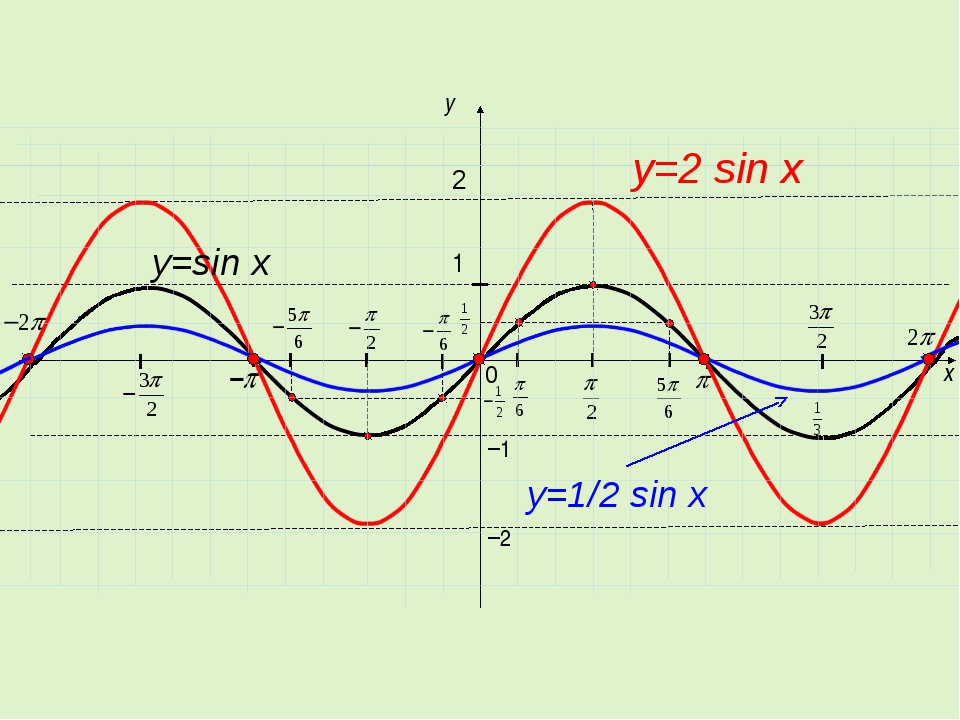
В чем разница между Sin 2x и 2 Sin x? • Sin 2x определяется из набора действительных чисел на интервале [-1, 1], тогда как 2Sin x определяется из набора действительных чисел на интервале [-2, 2]. • Sin 2x периодичен с периодом, но 2 Sin x периодичен с периодом 2ᴫ. |
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙРЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Примечание: Если вы хотите ознакомиться с обзором тригонометрии, нажмите на тригонометрия.
Пример 1: Найдите x в следующем уравнении.
Существует бесконечное множество решений этой проблемы.
Выделите синусоидальный член. Для этого перепишем левую часть уравнения в эквивалентная факторизованная форма.
Произведение двух множителей равно нулю, если хотя бы один из множителей равен нули. Это означает, что если или
Мы просто превратили сложную задачу в две более простые. Найти решения исходного уравнения, , находим решения уравнений и
и
Как мы изолируем x? Мы могли бы взять арксинус обеих сторон.
Однако функция синуса не является однозначной функцией.
Давайте ограничим домен, чтобы функция была взаимно однозначной на ограниченном домен с сохранением исходного диапазона.График синусоидальной функции один к одному на интервале Если мы ограничим область определения функции синуса этим интервалом, мы можем взять арксинус обеих частей каждого уравнения.
Мы знаем это Следовательно, если , тогда
Завершим задачу, найдя второй множитель.
С периода
равно ,
эти решения будут повторяться
каждый
единицы. Точные решения
где n — целое число.
Приближенные значения этих решений равны
где n — целое число.
Каждое решение можно проверить алгебраически, подставив каждое решение в исходное уравнение. Если после подстановки левая часть исходное уравнение равно правой части исходного уравнения, решение в силе.
Можно также проверить решения графически, построив график функции, образованной левой частью исходного уравнения, и график функции, образованной правой частью исходного уравнения.
Координаты x точек пересечения являются решениями. Правая часть уравнения равна 0, а f ( x )=0 — это ось x. Так что на самом деле то, что вы ищете, это
x-пересекает функцию, образованную левой частью уравнения.
Алгебраическая проверка:
Проверить решение
Левая сторона:
Правая сторона: 0
Так как левая часть исходного уравнения равна правой части исходное уравнение при замене -0.52359878 для х, тогда -0,52359878 — это решение.
Проверить решение
Левая сторона:
Правая сторона: 0
Так как левая часть исходного уравнения равна правой части исходное уравнение, когда вы заменяете x на 3,665191, тогда 3,665191 является решением.
Проверить решение
Левая сторона:
Правая сторона: 0
Так как левая часть исходного уравнения равна правой части
исходное уравнение при подстановке 1.5707963 для x, тогда 1,5707963 является решением.
Мы только что убедились, что точные решения , и являются решениями, и эти решения повторяются каждые единицы. Приближенные значения этих решений равны и 1,5707963, и эти решения повторяются каждые единицы.
Графическая проверка:
Нарисуйте уравнение Обратите внимание, что график пересекает ось x много раз, что указывает на решения.
График пересекает ось x в точке -0,52359878. Так как период , вы можете убедиться, что график также пересекает ось x снова в -0.52359878+6,2831853=5,7595865 и в , и Т. Д.
График пересекает ось x в точке . Так как период , график также снова пересекает ось x в точке tex2 html c комментарий m ark > 3,665191+6,2831853=9,9483763 и при , и т.д..
График пересекает ось x в точке .
Так как период ,
график также снова пересекает ось x в точке tex2 html c комментарий m ark >
1.
5707963+6,2831853=7,8539816 и в ,
и Т. Д.
Примечание. Если задача состоит в том, чтобы найти решения в интервале , затем вы выбираете эти решения из множества бесконечных решения, принадлежащие множеству , и 5.7595865.
Если вы хотите работать с другим примером, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой например, щелкните Проблема.
Если вы хотите перейти к следующему разделу, нажмите далее.
Если вы хотите вернуться к предыдущему разделу, нажмите . предыдущий .
Если вы хотите вернуться к оглавлению уравнения, нажмите на Содержание.
[Алгебра] [Тригонометрия] [Геометрия] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра]
Домашняя страница S.O.S MATHematics
Автор: Нэнси МаркусCopyright 1999-2022 MathMedics, LLC.Все права защищены.
Связаться с нами
Математика Медикс, ООО.
— П.О. Box 12395 — Эль-Пасо, Техас 79913 — США пользователей онлайн за последний час
| Уравнения триггера могут быть квадратными, например: 2 sin²x – sin x – 1 = 0 К квадратным триггерным уравнениям применяются те же правила, что и с регулярными квадратными уравнениями. Решите их факторингом или используя квадратное уравнение. Решить:
При факторинге убедитесь, что каждое квадратное уравнение имеет только одну триггерную функцию i. 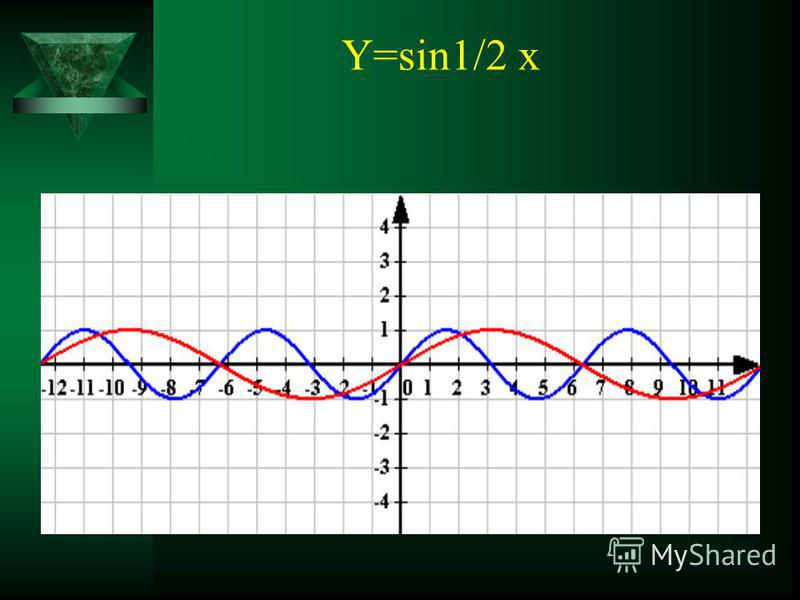 е. синус, косинус и т.д. Если
у него нет только одной функции, используйте базовый триггер
тождества, чтобы изменить уравнение. 3 сек² x – 2 тангенс² x – 4 = 0 3 (тангенс² х + 1) – 2 тангенс² х – 4 = 0 тангенс² х – 1 = 0 тангенс² х = =1 тангенс х = ± 1 х = /4 + п х = 3/4 + п Иногда уравнение не может быть решено как есть и должно быть возведено в квадрат, чтобы сделать его квадратичным.Дополнительный решения, вероятно, станут очевидными, которые могут не применимы к исходному уравнению. sin x + 1 = cos x
Поскольку исходное уравнение было возведено в квадрат, каждое решение должны быть проверены и подтверждены исходным уравнением.  Значение
не подходит для x, потому что: грех + 1 ? 0 + 1 ? – 1 Следовательно, единственные решения в интервале [0, 2), единственные решения: x = 0, 3/2. |
Интеграл от 2sinx — формула, доказательство, примеры
Интеграл от 2sinx равен -2cosx + C.Этот интеграл можно вычислить, используя формулу для интеграла от sin x. Мы знаем, что интегрирование — это процесс, обратный дифференцированию, и поэтому интеграл от 2sinx также называется первообразной от 2sinx. Мы знаем, что интеграл от sinx равен -cosx + C. Следовательно, интегрирование 2sinx равно -2cosx + C, где C — постоянная интегрирования.
В этой статье мы вычислим интеграл от 2sinx и выведем его формулу. Мы также оценим определенную интеграцию 2sinx с различными ограничениями и рассмотрим несколько решенных примеров, основанных на аналогичной концепции, для лучшего понимания.
Что такое интеграл от 2sinx?
Интеграл от 2sinx можно вычислить, используя формулу для интеграла от sinx, которая определяется как ∫sin x dx = -cos x + C, где C — постоянная интегрирования. Теперь, чтобы найти интегрирование 2sinx, мы используем эту формулу и математически запишем интеграл от 2sinx как ∫2sinx dx = -2cosx + C, где C — константа интегрирования. Давайте теперь рассмотрим формулу для того же самого в следующем разделе.
Интеграл 2sinx Formula
Поскольку мы знаем, что ∫sin x dx = -cos x + C, поэтому формула для интеграла от 2sinx записывается как ∫2sinx dx = -2cosx + C, где символ ∫ обозначает интегрирование 2sinx, dx обозначает, что переменная – x, а C – постоянная интегрирования.На изображении ниже показан интеграл формулы 2sinx:
.
Интеграл от 2sinx Доказательство
Теперь, когда мы знаем, что интеграл от 2sinx равен -2cosx + C, далее в этом разделе мы докажем этот результат, используя различные формулы интегрирования.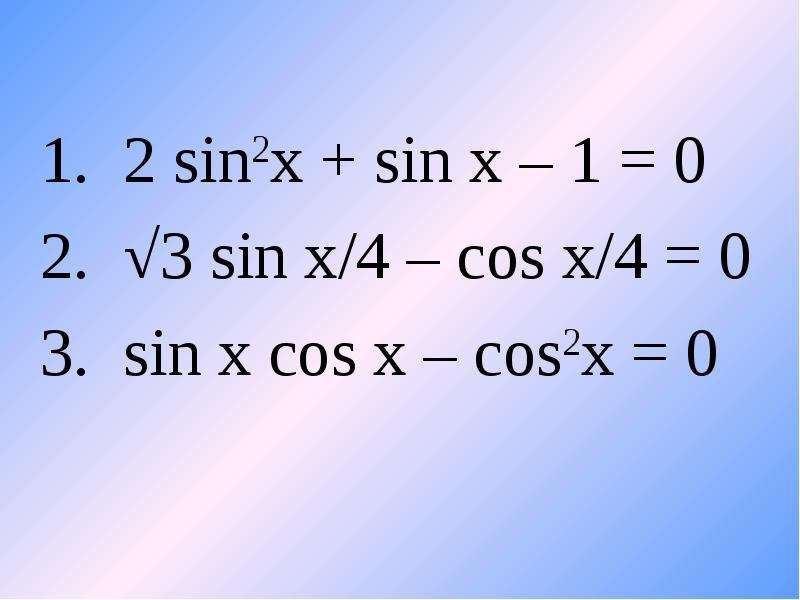
Мы будем использовать следующие первообразные правила и формулы:
- ∫sinxdx = -cosx + C
- ∫kf(x) dx = k ∫f(x) dx
Используя приведенные выше формулы, мы имеем
∫2sinx дх = 2 ∫sinx дх
= 2[-cosx + К]
= -2cosx + 2К
= -2cosx + C, где C = 2K — постоянная интегрирования.
Таким образом, мы доказали, что интеграл от 2sinx равен -2cosx + C.
Чтобы убедиться, что интегрирование 2sinx равно -2cosx + C, мы можем взять производную от -2cosx + C. Мы знаем, что производная от cos x равна -sin x, то есть d(cos x)/dx = -sin x и производная постоянной функции равна нулю. Следовательно, имеем d(-2cosx + C)/dx = d(-2cosx)/dx + dC/dx = -2d(cosx)/dx + 0 = -2(-sinx) = 2sinx. Значит проверено.
Определенная интеграция 2sinx
Мы знаем, что формула интегрирования 2sinx равна -2cosx + C.{\pi}\\&=(-2\cos\pi+C)-(-2\cos0 + C)\\&=-2\times (-1)+C+2\times1-C\\ &=2+2\\&=4 \end{align}\)
Следовательно, значение определенного интеграла от 2sinx в пределах от 0 до π равно 4.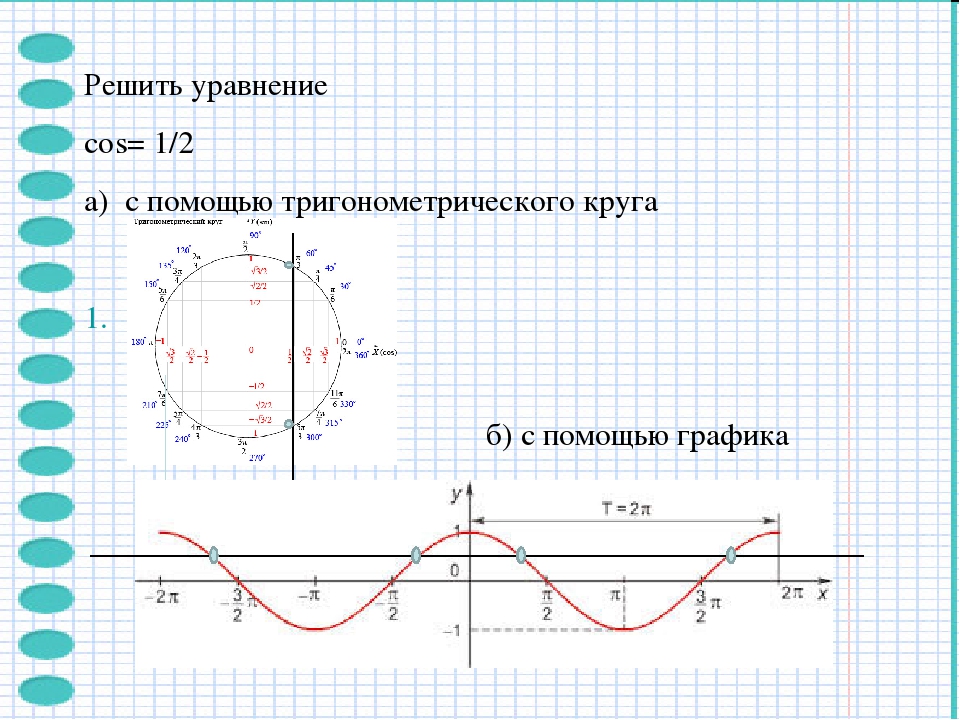
Важные замечания по интегралу от 2sinx
- Интеграл от 2sinx математически записывается как ∫2sinx dx = -2cosx + C.
- Мы можем найти интегрирование 2sinx, используя интеграл от sinx.
☛ Похожие темы:
Часто задаваемые вопросы по интегралу 2sinx
Что такое интеграл от 2sinx?
Интеграл от 2sinx равен -2cosx + C, где C — постоянная интегрирования.Этот интеграл можно вычислить, используя формулу для интеграла от sin x.
Какова формула интеграции 2sinx?
Интеграл от 2sinx можно вычислить, используя формулу для интеграла от sinx, которая определяется как ∫2sin x dx = -2cos x + C, где C — постоянная интегрирования.
Как найти интеграл от 2sinx?
Мы можем найти интеграл от 2sinx, используя следующие правила и формулы первообразных:
- ∫sinxdx = -cosx + C
- ∫kf(x) dx = k ∫f(x) dx
Используя приведенные выше формулы, мы получаем, что интеграл от 2sinx равен -2cosx + C, где C является константой интегрирования.
Чему равен неопределенный интеграл от 2sinx по отношению к cosx?
Неопределенный интеграл от 2sinx относительно cosx определяется как ∫2sinx d(cosx) = ∫2sinx (-sinx) dx = ∫-2sin 2 x dx = — ∫(1 — cos2x) dx = -(x — sin2x/2) + C = -x + (1/2)sin2x + C. Следовательно, интеграл от 2sinx по cosx равен -x + (1/2)sin2x + C, где C — константа интеграция.
Чему равно значение интеграла от 2sinx от 0 до pi?
Значение определенного интеграла от 2sinx в пределах от 0 до π равно 4.Это интегральное значение определяется путем подстановки пределов в формулу интеграла от 2sinx и вычитания двух.
BestMaths
Тригонометрические уравнения — это уравнения, содержащие такие члены, как sin x, cos x и tan x.
Их можно решить с помощью тригонометрических графиков и, при необходимости, калькулятора. Можно использовать другой метод, использующий общие решения.
Поскольку тригонометрические функции являются периодическими и продолжаются вечно, эти тригонометрические уравнения часто имеют бесконечное число решений, если область определения (значения x) не фиксирована.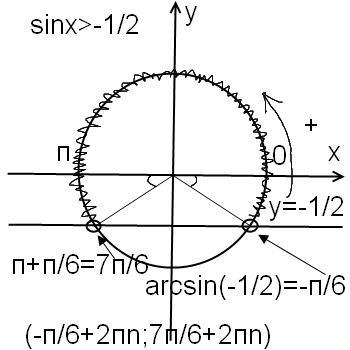
Обычно домен предоставляется.
Для иллюстрации различных методов, которые можно использовать, будет приведено несколько различных типов примеров. Решения даны в тех же единицах, в которых написан вопрос. Градусы или радианы.
Углы, используемые в особых треугольниках, часто встречаются в тригонометрических уравнениях и снова показаны ниже в качестве напоминания.
Особые треугольники
Углы, такие как 30 ° ( ), 45 ° ( ) и 60 ° ( ), используются часто, а тригонометрические отношения этих углов получаются из двух специальных треугольников (см. Раздел 38, 12-й класс).Они приведены ниже:
sin 30° | cos 30° | желтовато-коричневый 30° | sin 45° | cos 45° | желтовато-коричневый 45° | sin 60° | cos 60° | желтовато-коричневый 60° |
1 | √3 |
Если ответы могут быть даны с использованием точных значений из специальных треугольников, они должны быть даны.
Калькулятор следует использовать только в том случае, если не используются специальные углы треугольника.
Тригонометрические уравнения
Пример 1
Решите sin x = 0,5 для 0° ≤ x ≤ 360°. Дайте ответы в градусах.
Рассмотрим функции y = sin x и прямую y = 0,5. Там, где встречаются линия и кривая, и будут решения. Чтобы найти первое значение, можно использовать калькулятор, найдя sin -1 (0,5)
.
Калькулятор можно использовать для первого решения 30° и второго решения, найденного из симметрии графа (180 ° — 30° = 150°).
Набор решений {30°, 150°}
Аналогичные методы можно использовать для уравнений, содержащих косинус и тангенс.
Пример 2
Решите 2sin 2 x + sin x = 0 для 0 ≤ x ≤ 2π .
Дайте ответы в радианах.
Это квадратное уравнение, поэтому, если возможно, разложите его на множители.
sin x(2sin x + 1) = 0
Существует два набора решений:
sin x = 0 и 2sin x + 1 = 0, что дает sin x = -0.5Решения sin x = 0 равны 0, 3,14π и 2π
Решения sin x = -0,5 равны 7π/6 и 11π/6
Набор решений {0, π, 7π/6, 11π/6, 2π}
Пример 3
Решите √ 2cos 2x = 1 для 0 ≤ x ≤ 2π . Дайте ответы в терминах π .
Функция косинуса изолируется делением обеих частей на √2. Поскольку требуется cos 2 x, необходимо будет изучить график cos x от 0 до 4π, чтобы найти все корни.
√ 2, потому что 2x = 1
cos 2x = 1 / √ 2
Первое решение можно найти с помощью специальных треугольников выше или с помощью калькулятора.
Остальные решения находятся из симметрии графа:
Остальные решения находятся из симметрии графа:
Набор решений: {, ,, }
Пример 4
Решите sin 3x + sin x = 0 для 0 ≤ x ≤ 2π . Дайте ответы в терминах π .
Здесь используется формула суммы в произведение.
Набор решений равен {0, , π , , 2π }2sin 2x cos x = 0
Следовательно, sin 2x = 0 или cos x = 0
2x = {0, π, 2π, 3π, 4π} или x = { , }
Разница между Sin 2x и 2 Sin x
Опубликовано Admin
Sin 2x vs 2 Sin x
Функции — один из наиболее важных классов математических объектов, которые широко используются почти во всех разделах математики.
Функция синуса, которая обозначается как f ( x ) = sin x , представляет собой тригонометрическую функцию, определяемую набором действительных чисел на интервале [-1, 1] и является периодической с периодом 2ᴫ.
Основное определение синуса острого угла выполняется с помощью прямоугольного треугольника. Синус угла равен отношению длины стороны, противолежащей углу, к длине гипотенузы. Это определение можно распространить на все углы, используя тождества sin (- x ) = — sin x и sin (ᴫ + x ) = — sin x и sin (2 n ᴫ + х ) = грех х .
Для следующих двух секций рассмотрим f ( x ) = sin x и g ( x ) = 2 x .
Что такое Sin 2x?
Рассмотрим композитную функцию F O G , заданный F o G ( x ) = F ( г ( x ) = F (2 x ) = SIN 2 x .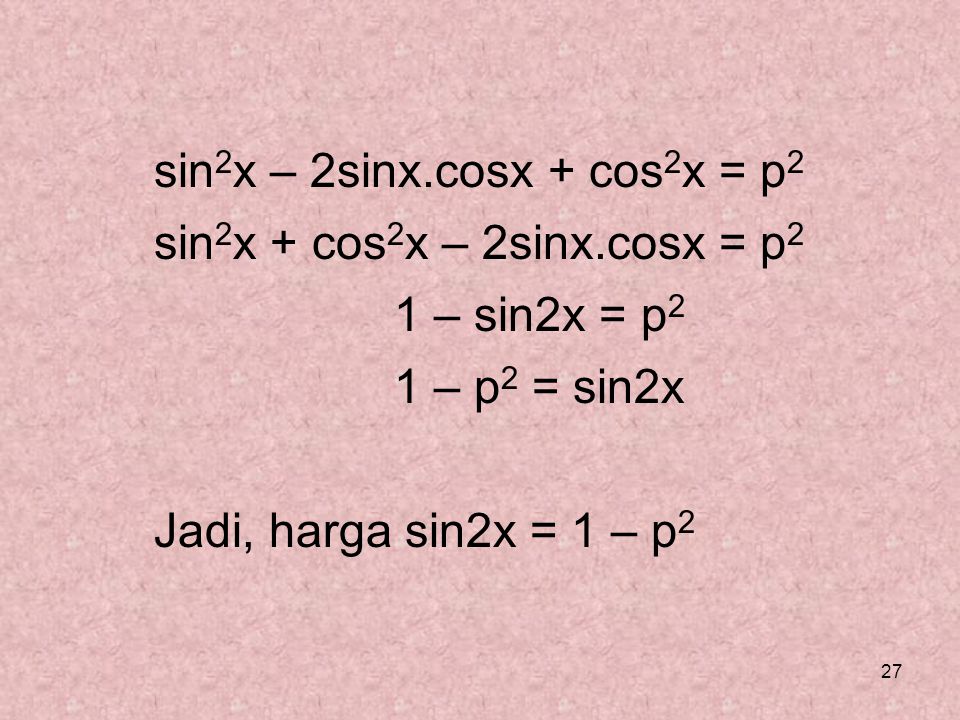
Эта функция очень похожа на sin x с доменом в виде набора действительных чисел и диапазоном в виде интервала [-1, 1].Эта функция является периодической с периодом ᴫ (в отличие от периода 2ᴫ sin x ). Sin 2 90 567 x 90 568 можно расширить тождеством Sin 2 90 567 x 90 568 = 2 sin 90 567 x 90 568, потому что 90 567 x 90 568 тоже.
Что такое 2 Sin x?
Рассмотрим композитную функцию г o F , заданный г o F ( x ) = г ( F ( x ) = г (sin x ) = 2 sin x .Это также периодическая функция с тем же периодом, что и sin 90 567 x 90 568, но в два раза больше его амплитуды, поскольку -1 ≤ sin 90 567 x 90 568 ≤ 1 подразумевает -2 ≤ 2 sin 90 567 x 90 568 ≤ 2. Ее областью определения является множество действительные числа, а диапазон — это интервал [-2, 2]
В чем разница между Sin 2x и 2 Sin x? • Sin 2x определяется набором действительных чисел на интервале [-1, 1], тогда как 2Sin x определяется набором действительных чисел на интервале [-2, 2]. • Sin 2x периодичен с периодом ᴫ, но 2 Sin x периодичен с периодом 2ᴫ. |
тригонометрических тождеств
Тригонометрические тождества — это уравнения, содержащие тригонометрические функции которые верны для каждого значения вовлеченных переменных.
Некоторые из наиболее часто используемых тригонометрических тождеств получены из Теорема Пифагора , как показано ниже:грех 2 ( Икс ) + потому что 2 ( Икс ) знак равно 1
1 + загар 2 ( Икс ) знак равно сек 2 ( Икс )
1 + детская кроватка 2 ( Икс ) знак равно csc 2 ( Икс )
Есть также взаимные тождества :
грех ( Икс ) знак равно 1 csc ( Икс ) потому что ( Икс ) знак равно 1 сек ( Икс ) загар ( Икс ) знак равно 1 детская кроватка ( Икс )
csc ( Икс ) знак равно 1 грех ( Икс ) сек ( Икс ) знак равно 1 потому что ( Икс ) детская кроватка ( Икс ) знак равно 1 загар Икс
То частные тождества :
загар ( ты ) знак равно грех ( ты ) потому что ( ты )
детская кроватка ( ты ) знак равно потому что ( ты ) грех ( ты )
То кофункциональные тождества :
грех ( π 2 − Икс ) знак равно потому что ( Икс ) потому что ( π 2 − Икс ) знак равно грех ( Икс ) загар ( π 2 − Икс ) знак равно детская кроватка ( Икс )
csc ( π 2 − Икс ) знак равно сек ( Икс ) сек ( π 2 − Икс ) знак равно csc ( Икс ) детская кроватка ( π 2 − Икс ) знак равно загар ( Икс )
То четно-нечетные тождества :
грех ( − Икс ) знак равно − грех ( Икс ) потому что ( − Икс ) знак равно потому что ( Икс ) загар ( − Икс ) знак равно − загар ( Икс )
csc ( − Икс ) знак равно − csc ( Икс ) сек ( − Икс ) знак равно сек ( Икс ) детская кроватка ( − Икс ) знак равно − детская кроватка ( Икс )
То Бхаскарачарья формулы суммы и разности :
грех ( ты ± в ) знак равно грех ( ты ) потому что ( в ) + потому что ( ты ) грех ( в )
потому что ( ты ± в ) знак равно потому что ( ты ) потому что ( в ) ∓ грех ( ты ) грех ( в )
загар ( ты ± в ) знак равно загар ( ты ) ± загар ( в ) 1 ∓ загар ( ты ) загар ( в )
То формулы двойного угла :
(Это всего лишь частные случаи формул Бхаскарачарьи, когда
ты
знак равно
в
.
)
грех ( 2 ты ) знак равно 2 грех ты потому что ты
потому что ( 2 ты ) знак равно потому что 2 ( ты ) − грех 2 ( ты )
знак равно 2 потому что 2 ( ты ) − 1
знак равно 1 − грех 2 ( ты )
загар ( 2 ты ) знак равно 2 загар ( ты ) 1 − загар 2 ( ты )
То формулы половинного угла или уменьшения мощности :
(Опять же, частный случай Бхаскарачарьи.
)
грех 2 ( ты ) знак равно 1 − потому что ( 2 ты ) 2
потому что 2 ( ты ) знак равно 1 + потому что ( 2 ты ) 2
загар 2 ( ты ) знак равно 1 − потому что ( 2 ты ) 1 + потому что ( 2 ты )
То формулы суммы к произведению :
грех ( ты ) + грех ( в ) знак равно 2 грех ( ты + в 2 ) потому что ( ты − в 2 )
грех ( ты ) − грех ( в ) знак равно 2 потому что ( ты + в 2 ) грех ( ты − в 2 )
потому что ( ты ) + потому что ( в ) знак равно 2 потому что ( ты + в 2 ) потому что ( ты − в 2 )
потому что ( ты ) − потому что ( в ) знак равно − 2 грех ( ты + в 2 ) грех ( ты − в 2 )
И формулы произведения на сумму :
грех ( ты ) грех ( в ) знак равно 1 2 [ потому что ( ты − в ) − потому что ( ты + в ) ]
потому что ( ты ) потому что ( в ) знак равно 1 2 [ потому что ( ты − в ) + потому что ( ты + в ) ]
грех ( ты ) потому что ( в ) знак равно 1 2 [ грех ( ты + в ) + грех ( ты − в ) ]
4.
2(α/2) = (1 − cos α)/2`Решение дает нам следующий синус полуугла тождество:
`sin (альфа/2)=+-sqrt((1-cos альфа)/2`
Знак (положительный или отрицательный) `sin(alpha/2)` зависит от квадранта в котором лежит `α/2`.
Если `α/2` находится в первом или втором квадрантах , формула использует положительный регистр:
`sin (альфа/2)=sqrt(1-cos альфа)/2`
Если `α/2` находится в третьем или четвертом квадрантах , формула использует отрицательный регистр:
`sin (альфа/2)=-sqrt(1-cos альфа)/2`
Формула половинного угла — косинус
Используя аналогичный процесс, с той же заменой `theta=alpha/2` (таким образом, 2 θ = α ) мы подставляем в личность
cos 2 θ = 2cos 2 θ − 1 (см.
2(alpha/2)=(1+cos alpha)/2`Решая `cos(α/2)`, получаем:
`cos (альфа/2)=+-sqrt((1+cos альфа)/2`
Как и прежде, нужный нам знак зависит от квадранта.
Если `α/2` находится в первом или четвертом квадрантах , формула использует положительный регистр:
`cos (альфа/2)=sqrt((1+cos альфа)/2`
Если `α/2` находится в втором или третьем квадрантах , формула использует отрицательный регистр:
`cos (альфа/2)=-sqrt((1+cos альфа)/2`
Формула половинного угла — касательная
Тангенс половинного угла определяется по формуле:
`tan (альфа/2)=(1-cos альфа)/(sin альфа)`
Доказательство
Сначала вспомним `tan x = (sin x) / (cos x)`.2а))`
Затем мы находим квадратный корень:
`=(1-cos a)/(sin a)`
Конечно, нам нужно было бы учитывать положительные и отрицательные знаки, в зависимости от рассматриваемого квадранта.
@`, используя приведенное выше отношение синуса половинного угла.(текст(о)))/2)`
`=+-sqrt(((1+0.866))/2)`
`=0,9659`
Первый квадрант, так что положительный.
2. Найдите значение `sin(alpha/2)`, если `cos alpha=12/13`, где 0° < α < 90°.
Ответить
`sin (альфа/2)=+-sqrt((1-cos альфа)/2)`
`= кв.((1-12/13)/2)`
`=кв.((1/13)/2)`
`= кв.(1/26)`
`=0,1961`
Мы выбираем положительное, потому что находимся в первом квадранте.2сек\ тета`
`=(1+cos тета)сек\ тета`
`=(1+cos тета)1/(cos тета)`
`=сек\тета+1`
`=»RHS»`
.