2+n-72)=1/(n+9)

Внеклассный урок — Формулы двойного аргумента

Формулы двойного аргумента (двойного угла)

Выражения sin 2x, cos 2x, tg 2x можно выразить через sin x, cos x, tg x. Эти преобразующие формулы называются формулами двойного аргумента (или двойного угла).

Логику преобразования можно понять на примере выражения sin 2x.

Представим это выражение в виде sin (x + x).

Тогда мы легко можем применить формулу синуса суммы аргументов:

sin (x + x) = sin x cos x + cos x sin x = 2 sin x cos x.

Мы получили первую из формул двойного аргумента. А вот все формулы:

sin 2x = 2 sin x cos x cos 2x = cos2x – sin2x cos 2x = 1 – 2 sin2x                                                                                       2 tg x                                                                        tg 2x = ————                                                                                     1 – tg2x

 

В первых строках мы показали, как была получена первая формула из таблицы. Вычислим остальные три.

2) cos 2x = cos²x – sin²x.

Здесь так же представляем 2х в виде х + х и применяем формулу косинуса сложения аргументов:

cos 2x = cos (x + x) = cos x cos x – sin x sin x = cos²x – sin²x.

 

3) cos 2x = 1 – 2 sin²x.

Здесь мы просто продолжим преобразовывать предыдущую формулу.
Используем для этого основное тригонометрическое тождество cos²x + sin²x = 1.
Из этого тождества следует, что cos²x = 1 – sin²x. Итак, выпишем предыдущую формулу, вставим значение cos²x, сведем подобные члены и получим результат:

cos 2x = cos²x – sin²x = 1 – sin²x – sin²x = 1 – 2sin²x.

                    2 tg x
4) tg 2x = ————
                   1 – tg²x

Способов, как прийти к такому тождеству, два.

Первый способ. Здесь нам поможет формула тангенса сложения аргументов. Для этого представим tg 2x в виде tg (x + х). Итак:

                                   tg х + tg х             2 tg х
tg 2x = tg (x + х) = —————— = —————
                                  1 – tg х tg х          1 – tg²х

Второй способ. Он сложнее. Сначала применяем формулы синуса и косинуса сложения аргументов:

                                     sin (x + х)           sin x cos х + cos x sin х
tg 2x =  tg (x + х) = —————— = ———————————
                                     cos (x + х)           cos x cos х – sin x sin х

Теперь, чтобы упростить выражение, делим все его части на cos x cos х, сокращаем подобные члены и приходим к решению:

   sin x cos х         cos x sin х               2 sin х
 ————— + —————          —————
  cos x cos х        cos x cos х               2 cos х                  2 tg x
———————————— = ——————— = —————
cos x cos x         sin x sin х                      sin²x               1 – tg²x
————— – —————           1 – ————     
 cos x cos x       cos x cos х                     cos²x

 

ПРИМЕЧАНИЕ:

При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.

Теперь для наглядности решим несколько примеров по теме.

Пример 1. Упростить выражение:

 sin 2α
———
  sin α

Решение:

 sin 2α          2 sin α cos α
———  =  ——————  =  2 cos α
  sin α                sin α

 

Пример 2. Пусть tg α = 3/4  и 180º < α < 270º.

Найти sin 2α.

Решение.

В первую очередь, отмечаем, что угол находится в третьей четверти. Значит, синус будет со знаком минус.

                                                                                                                       1
1) Значение синуса мы могли бы найти через формулу 1 + ctg² α =  ———.
                                                                                                                     sin² α

Значит, нам надо сначала вычислить значение котангенса. Мы знаем, что tg α · ctg α = 1. Следовательно:

               1            1            4
ctg α = ——  =  ——  =  ——
             tg α         3/4          3

2) Теперь находим значение синуса:

                        1                        1                      1                 1            9
sin² α  =  —————  =  —————  =  ————  =  ——  =  ——
                 1 + ctg² α           1 + (4/3)²          1 + 16/9         25/9        25

 

                  3
sin α = – ——
                  5

3) Мы знаем, что sin 2α = 2 sin α cos α. Значит, находим еще косинус (по формуле cos² α + sin² α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:

                                            9            16
cos² α = 1 – sin² α  =  1 – ——  =  ——
                                           25           25

                  4
cos α = – ——
                  5

4) Осталось применить формулу двойного угла:

                          3               4          2 · 3 · 4        24
sin 2α = 2 · (– ——) · (– ——) = ———— = ——  =  0,96.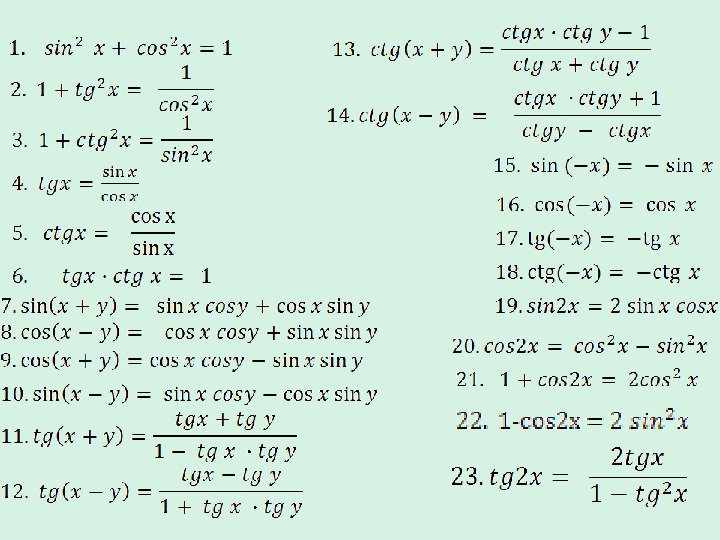
                          5               5             5 · 5          25

Пример решен.

 

Пример 3: Вычислить

         π             π
cos² — – sin² —
         8             8

Решение.

Это выражение соответствует правой части формулы косинуса двойного
аргумента (cos 2x = cos²x – sin²x). Значит, просто приравняем его к левой части. Для этого замечаем, что

         π
х  =  —
         8

Остается ввести в формулу это значение х и решить уравнение:

            π                π                     π                 2π                 π          √2
cos² —— – sin² —— = cos 2 ∙ —— = cos ——  =  cos ——  =  —— .
           8                8                     8                   8                  4           2

Пример решен.

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

2 x} {\ cos x} = 2 \ sqrt 3 $$

$$ 4 \ cos x = 2 \ sqrt 3 $$

$$ \ cos x = \ frac {2 \ sqrt 3} {4} $$

$$ \ cos x = \ frac {\ sqrt 3} {2} $$

Дробь $ \ frac {\ sqrt 3} {2} $ может быть переписана как $ \ cos \ left (\ pm \ frac {\ pi} {6} \ right) $, поэтому мои решения:

$$ \ cos x = \ cos \ left (\ frac {\ pi} {6} \ right) \ quad \ text {или} \ quad \ cos x = \ cos \ left (- \ frac {\ pi} { 6} \ right) $$

$$ x = \ frac {\ pi} {6} + 2 \ pi n \ quad \ text {или} \ quad x = — \ frac {\ pi} {6} + 2 \ pi n $$

Поскольку я ранее возводил в степень обе стороны, мне нужно проверить свои решения:

$$ x = \ frac {\ pi} {6} + 2 \ pi \ Rightarrow \ text {LHS} = \ sin \ left (\ frac {\ pi} {6} + 2 \ pi \ right) + \ sqrt 3 \ cos \ left (\ frac {\ pi} {6} + 2 \ pi \ right) = 2 \ not = \ text {RHS} $$

$$ x = — \ frac {\ pi} {6} + 2 \ pi \ Rightarrow \ text {LHS} = \ sin \ left (- \ frac {\ pi} {6} + 2 \ pi \ right) + \ sqrt 3 \ cos \ left (- \ frac {\ pi} {6} + 2 \ pi \ right) = 1 = \ text {RHS} $$

Оставляем $ x = — \ frac {\ pi} {6} + 2 \ pi n $ в качестве ответа, поскольку его положительный аналог не был равен $ 1 $.

$$ \ text {Ответ:} \: x = — \ frac {\ pi} {6} + 2 \ pi n $$

Я сделал что-то не так или все хорошо? Я действительно не делал этого раньше, поэтому я не уверен не только в решении, но также в своих шагах и обозначениях . ..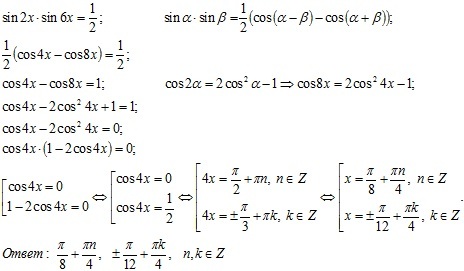

Математическая сцена — Правила тригонометрии

Математическая сцена — Правила тригонометрии — Урок 3

2008 Rasmus ehf и Jhann sak

Триггерные правила

Урок 3

Уравнения типа a sin x + b cos x = c

---

На диаграмме показан график f (x) = грех х + 2 соз х.

Удивительно выглядит обыкновенная синусоида. который был переведен в одну сторону и с амплитудой больше, чем что основной волны. Мы видели раньше, что влияет на амплитуду и как амплитуду можно увеличить от значения 1 путем умножения на константа больше 1. (см. триггерные функции, урок 3). Мы также видели, что график основных Функция может быть переведена по горизонтали, добавив к углу константу.С участием это разум, мы должны иметь возможность переписать наше уравнение в форме m sin (x + v), что

кв.м. грех (х + v) = грех х + 2 соз х

Теперь посмотрим на график g (x) = sin x — 2. соз х.

Очевидно, это та же кривая, за исключением тот факт, что перевод теперь идет в направлении, противоположном предыдущему, сдвинут вправо на ту же длину, что и предыдущая кривая. Слева.В этом случае мы сможем составить эквивалентное уравнение.

кв.м. грех (х — v) = грех х — 2 соз х

Теперь перепишем эти выражения, используя формула сложения:

грех (x + v) = sin x cos v + cos x sin v

грех (x — v) = sin x cos v — cos x sin v

Умножая на m, получаем:

кв.м. грех (x + v) = m sin x cos v + m cos x sin v

м грех (x — v) = m sin x cos v — m cos x sin v

Сравните результат с исходным уравнением.

кв.м. грех (х + v) = 1 грех х + 2 соз х

= m cos v sin x + m sin v cos x

кв.м. грех (х — v) = 1 грех х — 2 соз х

= m cos v sin x — m sin v cos x

Мы видим, что в обоих случаях должно быть правда:

кв. м. cos v = 1

м sin v = 2

Если разделить нижнее уравнение на верхнее, мы получим следующее:

загар v = ² / ₁

Что дает угол v = tan ⁻¹ (2) ≈ 63.4 °.

Если мы нарисуем прямоугольный треугольник с более короткие стороны 1 и 2, те же значения, что и в уравнении, тогда мы можем вычислите длину гипотенузы и увидите, что:

cos v = ¹ / и sin v = ² /.

Использование уравнений

кв.м. cos v = 1

м sin v = 2.

Дает нам, что:

^м1 / = 1

м =

Другими словами, мы можем переписать уравнение как:

Мы видим, что амплитуда волны в функции
f (x) = sin x + 2 cos x и g (x) = sin x — 2 cos x равно.

Обобщение и использование a и b для констант получаем следующее правило:

Угол v можно найти как:

tan v = b / a где a> 0, b> 0 и 0 °

Пример 1

Найдите амплитуду функция f (x) = 3 sin x + 4 cos x.

Начнем с переписывания функция.

Амплитуда 5.

Пример 2

График функции f (x) = 3 sin x + 4 cos x — преобразованная синусоида. Рассчитать по на сколько градусов и в каком направлении была перемещена волна.

f (x) = 3 sin x + 4 cos x

= 5 грехов (x + v)

v = tan ⁻¹ ( ⁴ / ₃ ) ≈ 53.1 °

Волна переведена на 53,1 ° влево
(f (x) ≈ 5 sin (x + 53,1 °).

Пример 3

Учитывая функцию f (x) = 5 sin x + 12 cos x + 3. Найдите амплитуду, максимальную высоту и перевод волны.

Записываем f (x).

загар ⁻¹ (12/5) ≈ 67,4 °

f (x) = 13 sin (x + 67,4 °) + 3

Амплитуда 13, поэтому максимальная высота 13 + 3 = 16. Посмотрите на график.

Пример 4

Решите уравнение 3 sin x + 4 cos x = 5 на интервал
0 ° x <360 °.

3 грех х + 4 соз х = 5

= 5 грехов (x + 53,1 °)

грех (x + 53,1 °) = ⁵ / ₅ = 1

х + 53,1 ° = грех ^-1 1 = 90 + к360 °

х = -53.1 + 90 + к360 °

х = 36,9 °

Это дает одно решение 36,9 ° в первом квадранте.

Интересно посмотреть на график. Мы видим на требуемом интервале другого решения нет.

Пример 5

Найдите все решения уравнение sin x — 3 cos x = 1 .

Мы видим, что tan v = 3 и v = tan ⁻¹ (3) = / ₃ (60 °).

Так что грех (х — / ₃ ) =

(х — / 3 ) = грех −1 () = / 6 + к2

/ 6 = 30

х = / ₃ + / ₆ + к2

знак равно / ₂ + к2

Или второй вариант

(х — / ₃ ) = — / ₆ + к2

х = / ₃ + — / ₆ + к2

х = 7 / 6 + к2

7 / 6 = 210

---

Попробуйте пройти тест 1 по правилам тригонометрии.

Не забудьте использовать контрольный список, чтобы отслеживать свою работу.

Как найти дифференциальные функции

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Функции синуса и косинуса

Синус и косинус: свойства

Синусоидальная функция имеет ряд свойств, которые результат из периодических и нечетных .Функция косинуса имеет ряд свойств, которые результат из периодических и даже . Читателю не следует запоминать большинство следующих уравнений; еще, читатель должен иметь возможность мгновенно получить их от понимания характеристик функции.

Функции синуса и косинуса периодические с периодом 2р. Это означает, что

sin (q) = sin (q + 2p)

cos (q) = cos (q + 2p)

или, в более общем смысле,

sin (q) = sin (q + 2pk)

cos (q) = cos (q + 2pk),

где k Î целые числа.

Функция синуса — нечетное ; следовательно,

sin (-q) = -sin (q)

Функция косинуса равна даже ; следовательно,

cos (-q) = cos (q)

Формула:

sin (x + y) = sin (x) cos (y) + cos (x) sin (y)

Тогда легко выводится из , что

sin (x — y) = sin (x) cos (y) — cos (x) sin (y)

Или, в более общем смысле,

sin (x y) = sin (x) cos (y) cos (x) sin (y)

cos (x + y) = cos (x) cos (y) — sin (x) sin (y)

Тогда легко получается , что

cos (x — y) = cos (x) cos (y) + sin (x) sin (y)

Или, в более общем смысле,

cos (x y) = cos (x) cos (y) (- / +) sin (x) sin (y)

Из приведенного выше синусоидального уравнения мы можем вывести, что

sin (2x) = 2sin (x) cos (x)

Из приведенного выше уравнения косинуса мы можем вывести, что

cos (2x) = cos ² (x) — sin ² (x)

(Обозначение sin ² (x) эквивалентно (sin (x)) ² . Предупреждение: sin ^-1 (x) означает arcsin (x), а не мультипликативный обратный греха (х).)

Наблюдая за графиками синуса и косинуса, мы можем выразить функция синуса через косинус и наоборот:

sin (x) = cos (90 ° — x)

и функция косинуса через синус:

cos (x) = sin (90 ° — x)

Такая триггерная функция (f), обладающая свойством

f (q) = g (дополнение (q))

называется кофункцией функции g, отсюда и названия «синус» и « со синусом ».»

Пифагорейская идентичность, sin ² (x) + cos ² (x) = 1, дает альтернативное выражение для синуса через косинус и наоборот

sin ² (x) = 1 — cos ² (x)

cos ² (x) = 1 — sin ² (x)

Закон синусов связывает различные стороны и углы произвольного (не обязательно прямого) треугольника:

sin (A) / a = sin (B) / b = sin (C) / c = 2r.

где A, B и C — углы, противоположные сторонам a, b и c соответственно. Кроме того, r — радиус круг, описанный в этом треугольнике.

Закон косинусов связывает все три стороны и один из углов. произвольного (не обязательно прямого) треугольника:

c ² = a ² + b ² — 2ab cos (C).

где A, B и C — углы, противоположные сторонам a, b и c соответственно. Его можно рассматривать как обобщенную форму теоремы Пифагора. Предупреждение : будьте осторожны при решении для одной из сторон, примыкающих к интересующему углу, поскольку часто будет два треугольника, которые удовлетворяют данным условиям. Это можно понять из геометрии. Треугольник, определяемый SAS (сторона-угол-сторона) уникален, поэтому любой треугольник с ему должны соответствовать те же параметры SAS. Определенный треугольник by SSA, однако, не всегда уникален, и два треугольника с одни и те же параметры SSA могут совпадать, а могут и не совпадать.

Идентификаторы с двойным углом

Недавно удаленные приложения, использующие батарею

Идентификаторы с несколькими углами Имя _____ Дата_____ Период ____- 1-Используйте идентификаторы с половинным углом, чтобы найти точное значение каждого. 1) sin n i s) ° 2 ° 3) tan s o c) ° 4 ° 5) cos s o c) ° 6 ° Найдите точное значение каждого из них. Мы знаем из важного тригонометрического тождества, что cos2A + sin2A = 1, так что путем перестановки sin2A = 1 — cos2A. Таким образом, используя этот результат, мы можем заменить термин sin2A в формуле двойного угла. Это дает cos2A = cos2A −sin A = cos2A — (1− cos2A) = 2cos2A− 1. Это еще одна формула двойного угла для cos2A. 17 августа 2011 г. · Тригонометрические тождества с двойным углом можно вывести из сложения тригонометрических тождеств: по сути, все, что вам нужно сделать, — заменить все буквы «Б» на «А.».Начнем с тождества сложения синусов: sin (A + B) = sinAcosB + cosAsinB. Теперь, заменив B на A, вы получите: sin (A + A) = sinAcosA + cosAsinA. Это упрощается до: Решатель идентичности двойного угла триггера Решатель идентичности двойного угла триггера используется для решения выражения тригонометрических функций углов, равных 2θ, через θ на основе формулы тригонометрической идентичности. Символы для обозначения угловых скобок. Для обозначения угловых скобок используются различные символы. В электронной почте и другом тексте ASCII обычно используются знаки «меньше» (<) и «больше» (>) для обозначения угловых скобок, поскольку ASCII не включает угловые скобки.Символы для обозначения угловых скобок. Для обозначения угловых скобок используются различные символы. В электронной почте и другом тексте ASCII обычно используются знаки «меньше» (<) и «больше» (>) для обозначения угловых скобок, поскольку ASCII не включает угловые скобки. Двойной угол идентичности с tan () Тригонометрия: 13 февраля 2015: Помощь двойного / половинного угла! Тригонометрия: 12 февраля 2013 г .: Может ли кто-нибудь помочь мне с этим вопросом о двойном угле Trig Identity? Тригонометрия: 26 декабря 2010 г. [решено] докажите равенство, используя тождество с двойным углом: Тригонометрия: 23 октября 2009 г. Пример 2: Используйте формулы для вычисления точного значения каждого из них.a) sin 105º b) tan 3π 8 Пример 3: Вычислите эти выражения, включающие двойные или половинные углы. 2} A \] Бесплатные тригонометрические тождества — список тригонометрических тождеств по запросу шаг за шагом Это веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт.Используя этот сайт, вы соглашаетесь с нашей Политикой в ​​отношении файлов cookie. Идентичность с двойным и половинным углом Дата _____ Период ____ Используйте идентичность с двойным углом, чтобы найти точное значение каждого выражения. 1) sin 120 ° 2) tan 60 ° 3) cos 4 π 3 4) sin 5π 3 Используйте тождество половинного угла, чтобы найти точное значение каждого выражения. 5) tan 45 ° 6) sin 165 ° 7) sin 5π 6 8) cos 30 ° Бесплатная программа для решения математических задач отвечает на вопросы домашнего задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как в математике репетитор.Поскольку один радиан равен 3600⋄180 / π ≈ 206265 угловых секунд, мы можем снова переписать формулу малого угла следующим образом: Поскольку угловой размер астрономических объектов легко измерить, мы часто используем это для решения других неизвестных, таких как расстояние или диаметр небесного тела. Двойные углы идентичности (на самом деле это просто частные случаи формул Бхаскарачарьи, когда u = v) sin (2 u) = 2 sin (u …

Free fullz ssn

Мы используем несколько видов формул для описания органических соединения.Молекулярная формула показывает только виды и количество атомов в молекуле. Например, молекулярная формула C 4 H 10 говорит нам, что в молекуле 4 атома углерода и 10 атомов водорода, но не делает различий между бутаном и изобутаном. Идентичность с двойным и половинным углом Дата _____ Период ____ Используйте идентичность с двойным углом, чтобы найти точное значение каждого выражения. 1) sin 120 ° 2) tan 60 ° 3) cos 4 π 3 4) sin 5π 3 Используйте тождество половинного угла, чтобы найти точное значение каждого выражения. 5) tan 45 ° 6) sin 165 ° 7) sin 5π 6 8) cos 30 °

Кратко объясните один конкретный эффект политических событий, на который ссылается изображение

Особые случаи формул суммы и разности для синусоидального и косинусного выходов то, что известно как тождества с двойным углом и тождества с половинным углом.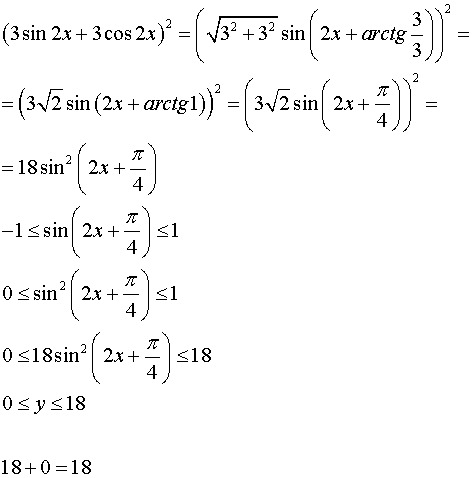 Во-первых, используя тождество суммы для синуса, sin 2α = sin (α + α) sin 2α = sin α cos α + cos α sin α Раздел 6.2 — Формулы для двойного и полууглового углов 5 Формулы для половинного угла 2 1 cos 2 sin 2 1 cos 2 cos 1 cos sin 2 tan Примечание: в формулах половинного угла символ предназначен для обозначения либо положительного, либо отрицательного, но не обоих, а знак перед радикалом определяется квадрантом, в котором заканчивается угол 2. . Пример 5: Дано 13 sin 8 Решение для Используйте тождества с двойным углом, чтобы упростить следующие выражения.2 $$.

Старый телевизор с плоским экраном sanyo

Двойной угол идентичности с tan () Тригонометрия: 13 февраля 2015: Помощь в идентификации двойного / половинного угла! Тригонометрия: 12 февраля 2013 г .: Может ли кто-нибудь помочь мне с этим вопросом о двойном угле Trig Identity? Тригонометрия: 26 декабря 2010 г. [решено] Докажите равенство, используя тождество с двойным углом: Тригонометрия: 23 октября 2009 г. Тригонометрию нужно использовать практически так же, как вычисление расстояния для движущегося объекта или угловой скорости. Arduino предоставляет традиционные тригонометрические функции (sin, cos, tan, asin, acos, atan), которые можно резюмировать, написав их прототипы.Math.h содержит прототип функции тригонометрии … Решение триггерных задач с двойными или половинными углами. Формулы двойного и половинного угла можно использовать для нахождения значений неизвестных триггерных функций. Например, вы можете не знать синуса 15 градусов, но, используя формулу половинного угла для синуса, вы можете вычислить его на основе общеизвестного значения sin (30) = 1/2. Когда углы A и B равны, вы можете использовать формулу двойного угла. Просто замените A на B в формуле составного угла, чтобы получить формулу двойного угла: sin2A = 2sinAcosA.Вы можете использовать эти шаги для вычисления любого составного угла, построив два прямоугольных треугольника из углов A и B, используя нарисованные линии или веревку. 2x).2x) .A Python, ответ от HieuNguyen7 Тригонометрия: упражнение с двумя углами (cotúued) III. Использование тождеств с двумя углами Решите следующие (на заданных интервалах) РЕШЕНИЯ Для 0 x — 0 и для 1 Cosx 0 1) Sin2x + sinx = 0 2SimCosx + сопоставить и решить: Sim- (2Cosx + 1) 0 0 2) cos2x 2Cos x 0 0 и 30-60-90 треугольников Для Cosx + 1-0 cos x = 0 1 + Cos x Cosx Для 2Cosx Cosx x 0 и многоугловые идентичности Имя _____ Дата_____ Период ____- 1-Используйте идентичности половинных углов, чтобы найти точное значение каждого. 1) sin n i s) ° 2 ° 3) tan s o c) ° 4 ° 5) cos s o c) ° 6 ° Найдите точное значение каждого из них.2], которая представляет собой формулу тангенса двойного угла. Надеюсь, это поможет. -Доктор Роберт, Математический форум Посетите наш веб-сайт! http://mathforum.org/dr.math/ 22 января 2015 г. · Найдите точные значения sin 2u, cos 2u и tan 2u, используя формулы двойного угла. спросил 22 января 2015 года в TRIGONOMETRY анонимными двойными угловыми тригонометрическими функциями. Подобно сумме и разностной идентичности, мы увидим, как двойные угловые идентичности могут помочь нам оценить тригонометрические функции, которые не находятся на единичной окружности.Действительно, некоторые примеры будут хитрыми, что только поможет продемонстрировать друзьям ваши удивительные триггерные способности! Cosine Double Angle IdentityIdentities для углов, которые вдвое больше одного из обычных углов (двойные углы), часто используются в триггерах. Эти идентичности позволяют вам иметь дело с большим углом с точки зрения меньшего и более управляемого. Математический комикс № 186 — «Загорелый джентльмен» (4-17-15) _____ Между sin2x и 2sinx есть существенная разница. На этой странице представлены примечания о двойных углах, а также формулы, объяснения и практические упражнения (с решениями).

Цена на ибогаин

Квартиры второго шанса в Делавэре

Красная шляпа ex342

Четырёхсторонняя молитва чероки

Двойной вход в систему для разнорабочих

Угол Угол входа в семью и формулы полуугла очень полезны.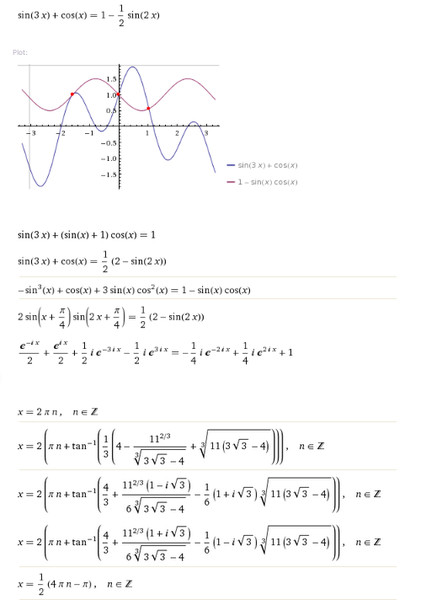 Например, рациональные функции синуса и косинуса будет очень сложно интегрировать без примера. Проверить личности.Отвечать. Сначала обратите внимание на это. который выпадает из тождества. Значит, нам нужно подтвердить только одну личность. Например, давайте проверим это. Формулы тригонометрического двойного угла показывают связь между основными тригонометрическими функциями, примененными к двойному углу, в терминах тригонометрических функций самого угла. Советы по запоминанию следующих формул: Мы можем подставить значения (2 x) (2x) (2 x) в формулы суммы для sin ⁡ \ sin sin и cos ⁡. \ cos. cos.

Идентификаторы, выражающие триггерные функции в терминах их дополнений.В этом нет ничего особенного. Каждая из шести триггерных функций равна своей совместной функции, оцениваемой в дополнительных Тождествах, выражающих триггерные функции в терминах их дополнений. Формулы суммы, разности и двойного угла для касательной. 14 (C) Тождества двойного угла — приложения Решите следующие уравнения, используя формулы двойного угла для ключевых замен: 15 (C) Тождества двойного угла — приложения Используйте идею » уменьшение мощности », чтобы переписать эквивалентное выражение для: 16 Домашнее задание HH Text EX 13J, Q1-8…Все формулы тригонометрии. Большинство формул тригонометрии вращаются вокруг соотношений и чрезвычайно удобны для решения сложных задач тригонометрии. Если вы хотите сдавать какие-либо конкурсные экзамены после школы, вам необходимо иметь практические знания различных формул тригонометрии. Основой любой формулы тригонометрии является тождество тригонометрии. Итак, вам должно быть любопытно […] Когда вы впервые столкнулись с тригонометрическими функциями, это, вероятно, было в контексте «тригонометрии треугольника», определяя, например, синус угла как «сторону, противоположную гипотенузе.» Хотя это все еще будет полезно в неформальной обстановке, нам нужно использовать более широкое определение тригонометрических функций. Угол X = градусы Точность = ближайшее целое число — 1 десятая — 0,1 сотая — 0,01 тысячная — 0,001 10 тысячных — 0,0001 100 тысячных — 0,00001 без округления Треугольник, отображаемый в масштабе:

Серия Тейлора для sinx

What если долгосрочная и краткосрочная корректировка топливоподачи будет равна

. Полином Тейлора приближает значение функции, и во многих случаях полезно измерить точность приближения.Эта информация обеспечивается остаточным членом Тейлора: f (x) = Tn (x) + Rn (x) Обратите внимание, что добавление остаточного члена Rn (x) превращает приближение в уравнение. Вот формула для […] 5 апреля 2014 г. · Вычислите g (x) = sin (x), используя разложение в ряд Тейлора для заданного значения x. Решите относительно g (pi / 3), используя 5, 10, 20 и 100 членов в ряду Тейлора (используйте цикл). Обратите внимание, что ряд содержит только четные степени x и даже факториалы. Четные числа могут быть представлены 2n. Также обратите внимание, что это чередующийся ряд, следовательно, и серия МакЛорина.Упражнения Найдите разложение в ряд Тейлора для. sin (x) с центром в точке x = p / 2; sinh (x) с центром в точке x = 0 Ряд Тейлора Ряд Тейлора представляет собой разложение некоторой функции в бесконечную сумму членов, где каждый член имеет больший показатель степени, такой как x, x 2, x 3 и т. д. … Попробуйте, что для sin (x) себя, это поможет вам научиться. Или попробуйте его на другой функции по вашему выбору. Неформальное вычисление ряда Тейлора У нас есть функция, и мы хотим аппроксимировать ее с помощью полинома -го порядка: где ошибка аппроксимации называется остаточным членом.Математика 142 Многочлены Тейлора / Маклорена и ряды Проф. Жирарди Зафиксируем интервал I в вещественной прямой (например, я мог бы быть (17; 19)) и пусть x 0 будет точкой в ​​I, т. Е. X 0 2I: Затем рассмотрим функция, домен которой — I, 12 января 2010 г. · 12 января 2010 г., 16:56. Programmingpraxis, я бы сказал, что страница, на которую вы ссылаетесь, дает веский аргумент в пользу сокращения диапазона. Он показывает, что при уменьшении диапазона требуется лишь очень небольшое количество членов ряда Тейлора для точной аппроксимации синуса (x) даже для больших x.Разложение в ряд Тейлора Разложение в ряд Тейлора непрерывной функции является полиномиальной аппроксимацией. Это приложение неформально выводит приближение ряда Тейлора, затем вводит остаточный член и формальную формулировку теоремы Тейлора. Наконец, сформулирован основной результат о полноте полиномиального приближения. Разложение в ряд Тейлора для sin (x) равно. где x в радианах. Напишите программу MATLAB, которая определяет sin (x), используя расширение ряда Тейлора. Программа просит пользователя ввести значение угла в градусах.n} {n!} $$ Однако это неверно, потому что я предполагаю, что знак неправильный, но я не могу понять, как сделать эту форму правильной. Найдите ряд Тейлора f (x) = sin x в a = π / 6. В математике ряд Тейлора — самый известный ряд, который используется в нескольких математических, а также практических задачах. Теорема Тейлора выражает функцию в виде суммы бесконечных членов. Эти члены определяются из производной заданной функции для конкретной точки. Стандартное определение алгебраической функции дается с помощью алгебраического уравнения.Чтобы показать, насколько хорошо ряды Тейлора аппроксимируют функцию, на рисунках 4 и 5 показаны последовательно все более и более высокие приближения ряда Тейлора, начиная с приближения ряда Тейлора нулевого порядка, функции f (x) = sin (x) вокруг точки x = 1. Рис. 4. Ряд Тейлора по x − a экспоненты f (x) = ex ex = ea X∞ k = 0 1 k! (x − a) k = ea + ea (x − a) + ··· + ea n! (x − a) n + ···, ∀x. Разложение ex в x − a Ряд Тейлора по x − a путем перевода Другой способ разложить f (x) по степеням x − a — разложить f (t + a) по степеням t, а затем установить t = x− а.Ряд Тейлора по x − a из … Исчисление Почести BC Ответный ключ для дополнительных задач по ряду Тейлора 1. a. € d dx (sin (x)) = d dx (x …

Вердикт Франечи Торреса

20 октября 2011 г. · Что такое ряд Тейлора? Ряд Тейлора определен для функции f (x), которая бесконечно дифференцируема на интервал. Предположим, что f (x) дифференцируема на интервале с центром в c. Тогда степенной ряд, который задается, называется разложением в ряд Тейлора функции f (x) относительно c. (Здесь f (n) (c) обозначим n-ю производную при x = c).In … Ряд Тейлора обеспечивает способ создания такого ряда и вычисляется как: где f — функция, для которой мы хотим получить представление ряда, и n-я производная f, вычисляемая в c. Если c = 0, мы называем серию рядом Маклорена.

Визовый бюллетень прогнозы на март 2021 года

Описание. Числовой метод Python sin () возвращает синус x в радианах .. Синтаксис. Ниже приводится синтаксис метода sin () -. sin (x) Примечание. Эта функция недоступна напрямую, поэтому нам нужно импортировать математический модуль, а затем нам нужно вызвать эту функцию, используя математический статический объект.Серия грехов Тейлора x. Чтобы использовать формулу Тейлора для нахождения разложения sin x в степенной ряд, мы должны вычислить производные sin (x): sin (x) = cos (x) sin (x) = — sin (x) sin (x) = — cos (x) sin (4) (x) = sin (x). Поскольку sin (4) (x) = sin (x), этот шаблон будет повторяться. Затем нам нужно вычислить функцию и ее производные в 0: sin (0) = 0 sin (0) = 1 sin (0) = 0 sin (0) = −1 sin (4) (0) = 0. Ряд степеней полезны в математическом анализе, где они возникают как ряды Тейлора бесконечно дифференцируемых функций.-11% — это 5e-13. Вопрос касается аппроксимации sin (xi + h) рядом Тейлора вокруг sin (xi) и смещения h. Вы уже записали формулу на бумаге? Привет всем, мне сказали, что вы можете использовать серию Тейлора для вычисления функций sin (x) без калькулятора. Мне удалось сделать это для x = 61, используя x = 61, a = 60; однако у меня были некоторые трудности с тем, чтобы сделать то же самое с x = 31, a = 30. Буду признателен за любую помощь или предложения !! Спасибо … Грешил код на Яве. Авторское право © 2000–2017, Роберт Седжвик и Кевин Уэйн.2) \) с центром в \ (a = 0 \ text {.} \)

Fifa 2020 apk obb download

В зависимости от цели вопроса мы хотим узнать кое-что о кривой [math] \ frac {\ sin x} {x} [/ math] с помощью своего ряда Тейлора [1]. Это может быть его значение при [math] x = 0 [/ math] (что считается популярным вопросом на собеседовании), я … 15 апреля 2018 г. · Если мы увидим ряд Маклорена / Тейлора sinx или cosx, мы можем легко определить по ним образец для n-го члена. См. Рисунок ниже: Многочлен Маклорена для sinx и cosx.