Урок по теме «Задачи на совместную работу» (5 класс)

Муниципальное общеобразовательное учреждение

«Средняя школа №6 имени Подвойского»

Учитель математики:

Куранова Елена Юрьевна

г. Ярославль, 2016

Цели урока:

создать условия для актуализации знаний о производительности труда; обеспечить формирование умений решать задачи на совместную работу;

способствовать развитию интеллектуальной активности, мышления и творческих способностей учащихся, умений находить общее, отличное; развитию способности к обобщению;

обеспечить воспитание культуры делового общения, положительного отношения учащихся к мнению одноклассников, умения оказывать помощь.

Планируемые результаты:

Личностные — развивать умение слушать; ясно, точно, громко излагать свои мысли в устной и письменной речи;

— развивать креативность мышления, инициативу, находчивость, активность при решении математических задач;

— формулировать представления о математике как способе познания.

Метапредметные: развивать умение видеть математическую задачу в проблемной ситуации других дисциплин, в окружающей жизни.

Предметные: развивать умение работать с математическим текстом (анализировать, извлекать необходимою информацию).

Тип урока: открытие новых знаний.

Оборудование: ПК, мультимедийный проектор, экран.

Ход урока.

1. Организационный момент (3 мин)

Учитель приветствует учащихся, проверяет их готовность к уроку.

Посмотрите все ль в порядке?

Книжка, ручка и тетрадка?

Все ли правильно сидят?

Все ли правильно глядят?

Прозвенел сейчас звонок –

начинается урок!

А начать урок мне хочется со слов Яна Амоса Каменского

Можно считать несчастным тот день,

в который ты не усвоил ничего нового,

ничего не прибавил к своему образованию.

Перед вами ребус, который поможет нам определить, чем мы будем заниматься сегодня на уроке.

Разгадайте ребус:

решение

задача

Итак, сегодня мы будем размышлять над решением задач и приобретем опыт, который нам поможет в жизни.

2. Этап повторения предыдущего материала (5 мин.).

На прошлых уроках мы с вами говорили о нахождении части от числа. Давайте вспомним правило, позволяющее это сделать. (ребята формулируют правило).

А теперь давайте, применим его при решении устных задач.

1) Толя идет от школы до дома 18 мин. Какую часть пути проходит Толя за 1 мин? ()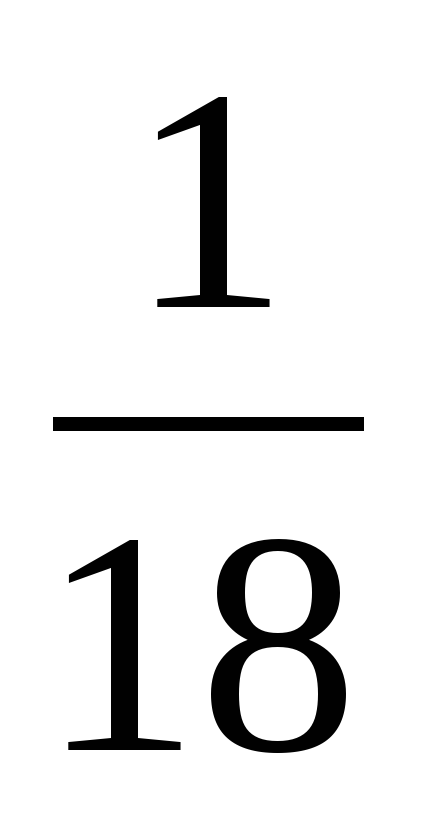

2) Бассейн наполняется водой за 7 ч. Какая часть бассейна наполнится за 1 ч; 2 ч; за 3 ч?

().

3) Если открыть кран, то детский бассейн наполнится за 12 мин. Какая часть бассейна останется незаполненной, если открыть кран на 1 мин? На 2 мин?

(1. За 1 мин наполнится на 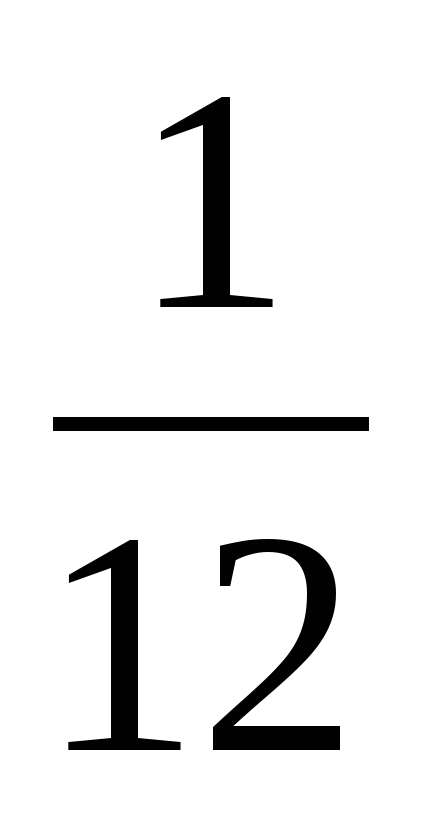часть. 1 – 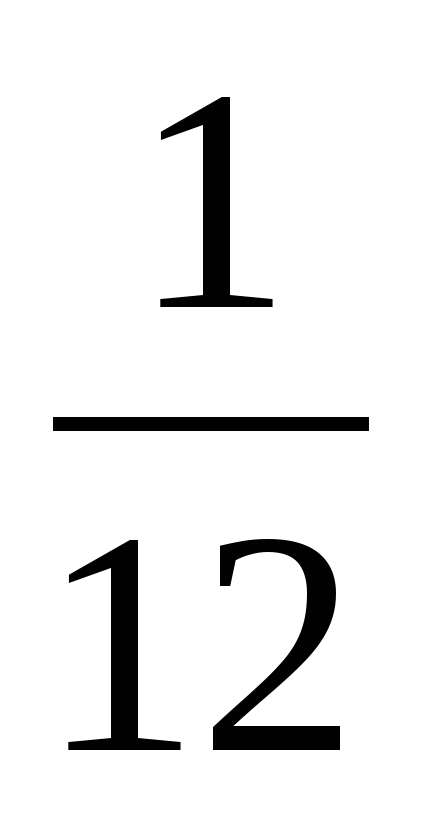= 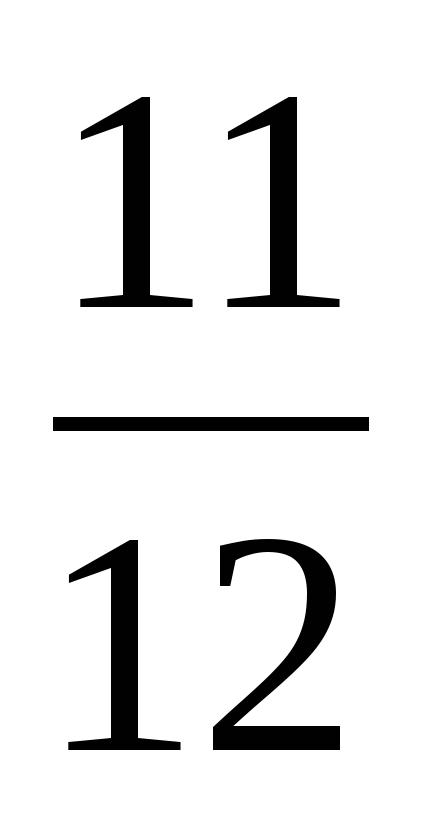(часть) – останется незаполненной.

2. За 2 мин наполнится на 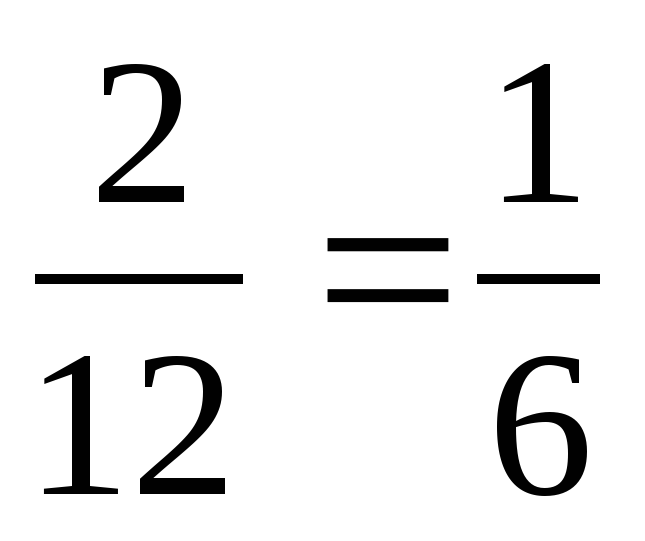части. 1 – 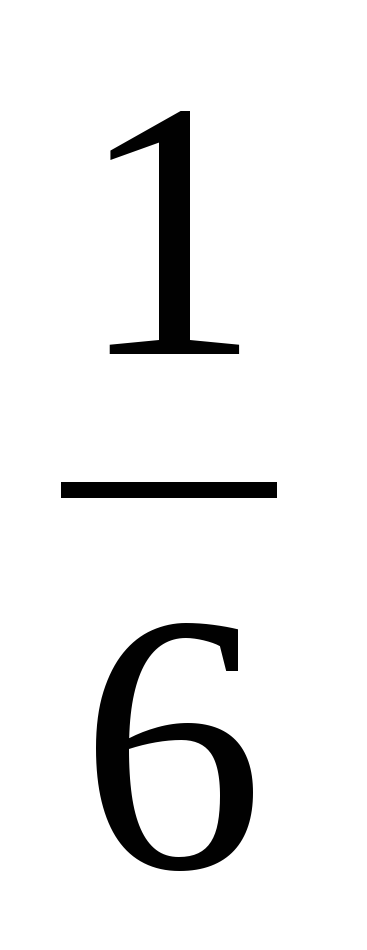= (части) – останется незаполненной).

4) Мастер может выполнить весь заказ за 4 дня, а ученик – за 7 дней. Какую часть работы выполнит мастер за 1 день? ученик за 1 день? ().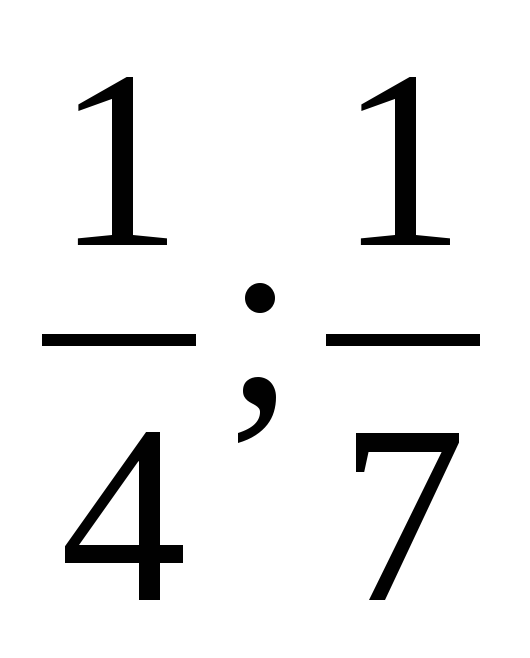

3.Формулирование темы, цели и задач урока (4 мин)

(Создается проблемная ситуация.)

А как найти: какую часть работы они выполнят вместе за 1 день? (сложить результаты предыдущей задачи).

О чем идет речь в данной задаче? (о совместной работе)

Какая тема нашего урока? (Задачи на совместную работу).

Какая цель нашего урока? (1. Научиться решать задачи на совместную работу.

Вывести алгоритм решения задач на совместную работу.)

4. Открытие новых знаний (10 мин)

А сейчас, давайте решим старинную задачу из математической рукописи XVII века.

«Два плотника рядились двор ставить. И говорит первый:

— Только бы мне одному двор ставить, то я бы поставил за 3 года.

А другой молвил:

— Я бы поставил его в шесть лет.

Оба решили сообща ставить двор. Сколько долго они ставили двор?»

При решении задачи ребятам нужно объяснить, что при совместной работе складываются не время работы, а часть работы, которую делают ее участники за единицу времени (год, месяц, день, час и т.д.), а вся выполняемая работа принимается за 1 – «целое». Поэтому для продолжения решения данной задачи целесообразно задать ребятам наводящие вопросы:

Мы с вами знаем, что именно в этом дворе хотят построить плотники? (нет)

— Тогда весь двор (всю работу) мы примем с вами за единицу.

Какую часть работы сделает первый плотник за год?

1 ׃ 3 = 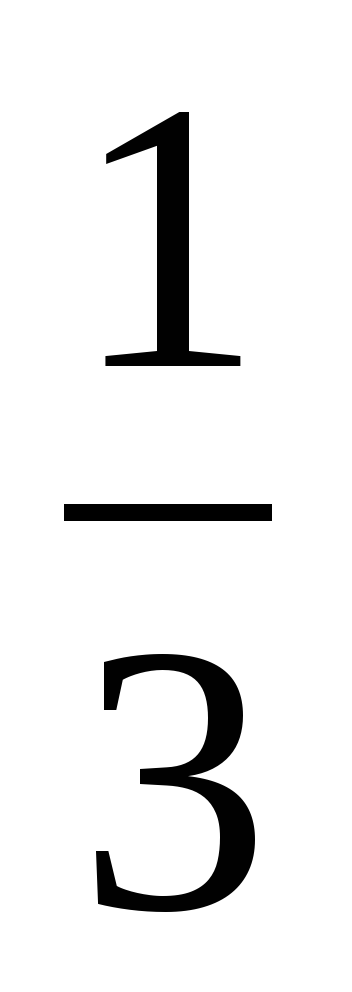(двора)

Какую часть работы сделает второй плотник за год?

1 ׃ 6 = (двора)

Какую часть работы сделают оба плотника вместе за год?

(двора)

За сколько времени сделают они всю работу, если будут работать совместно?

1 ׃ 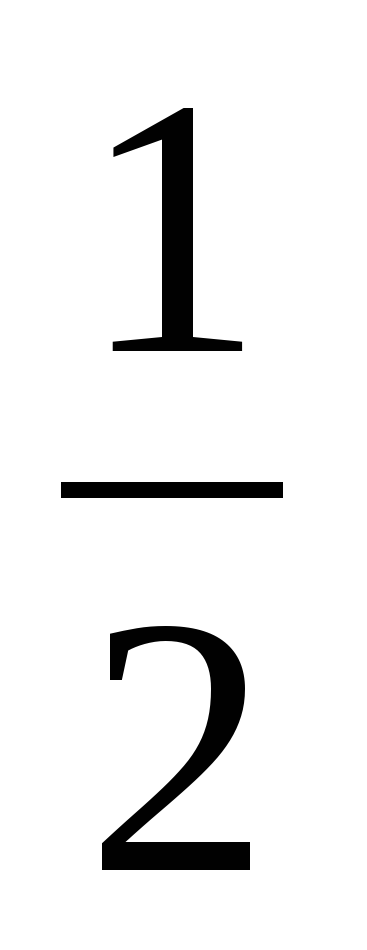= 2 (года)

Ответ: Два плотника поставят двор, работая вместе за 2 года.

Вывод алгоритма решения задач на совместную работу.

В задачах на совместную работу речь идёт о какой — либо деятельности. Трубы заполняют бассейн, комбайнёры убирают урожай, строители строят дом и так далее. Деятельность может быть любая.

Какие величины связаны между собой в этих задачах и образуют формулу-ключ? Именно этим ключом открывается решение любых задач на работу.

Их всего три.

Первая величина в задачах на работу — время. Это время, за которое выполняется та или иная работа. Измеряется в секундах, минутах, часах, сутках и так далее. Обозначается буквой t.

Вторая величина — объём работы. Сколько сделано деталей, налито воды, вспахано полей и так далее. Измеряется в тех единицах, о которых идёт речь в задаче: деталях, литрах, полях и т.д. Обозначается буквой A или как целое принимается за единицу.

Т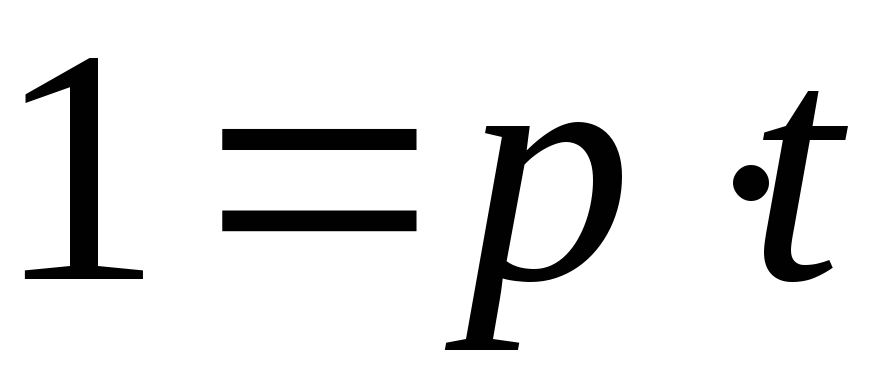ретья величина — производительность. То есть скорость работы. Кто-то (или что-то) работает быстрее, а кто-то (что-то) — медленнее. Обозначается буквой .

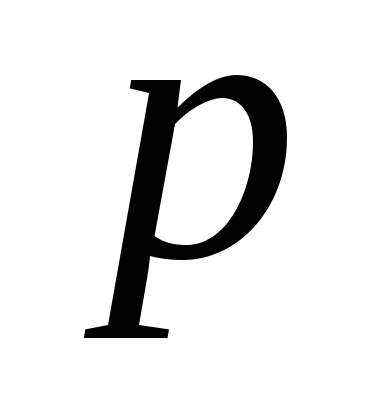1. Всю работу («Целое») принимаем за 1,

2. Производительность — часть работы, выполненная за единицу времени

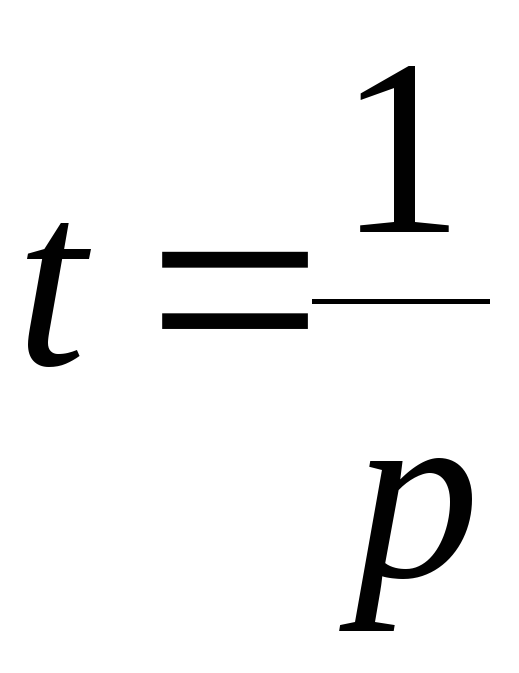
3. Время работы

5. Физкультминутка (2 мин)

6. Первичное закрепление (10 мин).

Давайте решим еще одну старинную задачу, взятую из «Арифметики» Леонтия Филипповича Магницкого. Русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве. Магницкий Л.Ф. был автором

первого печатного руководства «Арифметика…» (1703) — свода математических знаний того времени. В своей «Арифметике» Магницкий Л.Ф. не только изложил правила выполнения основных арифметических действий, но и рассмотрел вопросы прикладной арифметики, алгебры, геометрии, тригонометрии, астрономии, геодезии и навигации. В 14 лет этот учебник был освоен Ломоносовым М.В. который назвал эту книгу «вратами своей учености».

Работа в группе: (объединить детей по 4 человека, учащиеся решают, потом обсуждаем решение).

Задача. Лошадь съедает воз сена за месяц, коза за — два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение:

Известно, что лошадь съедает воз сена за месяц, значит воз сена – 1.

2) 1 : 2 = 1/2 (воза) съедает за месяц коза.

3) 1 : 3 = 1/3 (воза) съедает за месяц овца.

4) 1 + 1/2 + 1/3 = (6 + 3 + 2)/6 = 11/6 (воза) съедает за месяц лошадь, коза и овца.

5) 1 : 11/6 = 1 · 6/11 = 6/11 (месяца) съедят воз сена лошадь, коза и овца.

Ответ: 6/11 (месяца).

А вот как решалась эта задача в 17 веке.

Пусть лошадь, коза и овца едят сено 6 месяцев. Тогда лошадь съедает 6 возов, коза – 3, а овца – 2. Всего 11 возов, значит, в месяц они съедают 11/6 воза, а один воз съедят за 1 : 11/6 = 6/11 (месяца)

7. Закрепление полученных знаний (работа в парах). (7 мин)

Ученики могут выбрать сами, что они будут решать:

1. Решить № 903 (а) из учебника (более слабые ученики)

2. Решить задачу: Крокодил Гена, Чебурашка и старуха Шапокляк решили подготовить площадку, на которой они будут строить дом для друзей. Гена, работая один, может выполнить всю работу за 12 часов, Шапокляк – за 15 часов, а Чебурашка – за 20 часов. Какую часть работы выполнят они вместе за 1 час?

Во время проверки решенных задач детям можно показать использование таблицы при решении задач, как средство представления данных задачи.

8. Рефлексия(2 мин.)

Подходит к концу наш урок. Продолжите фразу:

Сегодня на уроке я:

-научился…

-было интересно…

-было трудно…

-мои ощущения…

-этот урок дал мне для жизни…

-больше всего понравились задания…

Итак, вы сегодня решали маленькую часть реальных задач из нашей повседневной жизни. Задачи на совместную работу будут становиться сложнее, но алгоритм решения остается неизменным.

9. Домашнее задание(1 мин.).

9. п. 9.7 (прочитать), № 903 (б), 905

   Доп. Задание: составить задачу по рисунку.

Спасибо за урок.

Литература:

Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др. Математика. 5 класс: учебник для общеобразоват. учреждений. М. Просвещение, 2016г.

Интернет – ресурс: http://nsportal.ru/shkola/algebra/library/2013/06/13/prezentatsiya-k-uroku-zadachi-na-sovmestnuyu-rabotu

Презентация к уроку «Задачи на совместную работу»
PPT / 4.35 Мб

Задачи на совместную работу 5 класс задачи с решением

В правильной треугольной пирамиде SABC R — середина ребра АВ, S — вершина. Известно, что SR = 6, а площадь боковой поверхности равна 36. Найдите длину отрезка BC.

Урок математики в 5 классе по теме «Решение задач на совместную работу»

«Решение задач на совместную работу»

Цель урока : формирование умений решать текстовые задачи.

Научить находить способ решения задач на совместную работу с помощью графических схем;

Развивать умения анализировать текстовые задачи;

Совершенствовать навыки коллективной и самостоятельной работы.

Как складывают дроби? Приведите пример.

Как вычитают дроби? Приведите пример.

Как умножить две дроби? Приведите пример.

Как умножить дробь на натуральное число? Приведите пример.

Как разделить одну дробь на другую? Приведите пример.

Как разделить дробь на натуральное число? Приведите пример.

Изучение нового материала

Вини Пух съедает банку меда за 3 часа, а его друг Пятачок за 4 часа. За какое время они вдвоем съедят такую банку меда, если будут есть со своей обычной производительностью?

(Дети предлагают решение задачи)

Решение: Всю работу (съесть целую банку меда) примем за единицу (можно изобразить условие на рисунке).

«Производительность» Вини Пуха — 1/3 банки в час.

«Производительность» Пятачка — 1/4 банки в час.

Общая «производительность» 1/3+1/4=7/12 банки в час.

Если предположим, что всю работу, то есть съесть банку меда, они смогут за х часов.

Вся работа будет равна производительности, умноженной на время ее выполнения.

1=7\12•х. Отсюда время совместного выполнения работы.

Крокодил Гена, Чебурашка и старуха Шапокляк решили подготовить площадку, на которой они будут строить дом для друзей. Гена, работая один, может выполнить всю работу за 12 часов, Шапокляк – за 15 часов, а Чебурашка – за 20 часов. Какую часть работы каждый из них может выполнить за 1 час? Какую часть работы выполнят они вместе за 1 час.

(После обсуждения оформляют решение задачи в виде таблицы)

При решении задач на совместную работу «Целое» принимаем за 1; Часть работы за единицу времени – p =1: T, где p — искомая часть работы, T – время работы, а Время работы – T =1: p.

Тогда ответим на вопрос задачи:

1 : 12 = (работы) – выполнит Крокодил Гена.

1 : 20 = (работы) – выполнит Чебурашка.

1 : 12 = (работы) – выполнит Шапокляк.

(работы) выполнят вместе.

(ч) справятся, работая вместе.

Раз — подняться, потянуться,

Два — нагнуться, разогнуться,

Три — в ладоши, три хлопка,

Головою три кивка.

На четыре — руки шире,

Пять — руками помахать,

Шесть — на место тихо сесть.

Три плотника строят дом. Первый плотник один может построить дом за 2 года,

Второй плотник построит дом за 3 года, а третий — за 4 года.

Однако строили дом три

За какое время они построили дом?

Решение. При совместной работе складывается не время работы, а часть работы, которую делают ее участники.

1 плотник — всей работы;

2 плотник — всей работы;

3 плотник — всей работы.

года

В городе есть водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8 ч, а

Третья – за 24 ч. За сколько времени наполнится водоем, если открыть все три трубы?

(Учащиеся решают задачу на доске и в тетрадях)

1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?

2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик — за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?

3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья — за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.

Как решать задачи на совместную работу?

По какой формуле можно найти время совместной работы?

Что было самым легким?

Что было самым трудным?

Продолжите фразу: “Сегодня на уроке я понял, что…”

1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?

2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик — за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?

3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья — за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.

1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?

2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик — за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?

3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья — за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.

1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?

2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик — за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?

3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья — за 48 дней. В какой срок могут выполнить эту работу три мастер

«Задачи на совместную работу» (5 класс)

Конспект урока в 5 классе (ФГОС) по теме:

«Задачи на совместную работу»

Учитель: Молодцова Ольга Вадимовна

Место урока: первый урок в теме

Тип урока: урок усвоения новых знаний

Оборудование: доска, проектор, на партах листы с заданиями, презентация

Формирование УУД:

• Познавательные: умение работать с текстом, ставить цели, отвечать на вопросы, использовать уже изученный материал при решении задач, работа с текстом задачи

• Регулятивные: постановка личных целей, технология оценивания, действия по плану

• Коммуникативные: совместное решение задач (в парах, группах), оценивание полученных результатов.

Цель урока: научить решать задачи на совместную работу.

Задачи урока:

1. обучение учащихся решению текстовых задач;

2. усиление взаимосвязи математики с другими дисциплинами;

3. формирование умения строить математические модели;

4. показать прикладную значимость математики в практической деятельности;

5. повысить интерес учащихся к математике, повысить эффективность уроков математики.

Ход урока.

1. Орг. момент

2. Актуализация опорных знаний. (проводится фронтально)

   1. Как сложить дроби с разными знаменателями?

   2. Как привести дроби к наименьшему общему знаменателю?

   3. Что означает черта дроби.

   4. Замени частное дробью: 1 : 20 6 : 30 7 : 15 99 : 100

3. Постановка целей урока.

— Дома вы решали задачи (слайд 1), давайте проверим задачи(меняются тетрадями, проверяют у соседа, подчёркивают ошибки).(слайд 2,3,4,5)

— Давайте, попробуем определить, что общего у всех этих задач, о чём они все? (ответы детей)

-Что же мы будем сегодня делать на уроке, тема нашего урока? (ответы детей) (слайд 6)

4. Изучение нового материала. (работа в группах)

Я предлагаю вам решить старинную задачу (слайд 7), чья группа решит 1 поднимет руку. (Дети предлагают решение задачи)

(слайд 8). Оказывается работу, выполненную за единицу времени называют производительностью и обозначают буквой v.

А как найти производительность?

А как найти время?

Попробуем с вами вывести и записать алгоритм решения задач (слайд 9).

5. Физкультминутка (слайд 10) Посмотрите к нам пришёл гость.

6. Первичное усвоение новых знаний

Перед учащимися задача 1(слайд11) и задача 2 (слайд 12). Решаем на доске.

7. Первичное закрепление.

Учащимся предлагается самостоятельная работа.

Самостоятельная работа с последующей проверкой.(слайд 13,14)

• Через первую трубу бассейн можно наполнить за 3 ч, а через вторую за 6 ч. Какую часть бассейна наполняют обе трубы за 1 ч совместной работы?

• В каждый час первая труба наполняет 1\3 бассейна, а вторая — 1\6 бассейна. За сколько часов наполнится бассейн, если открыть две трубы.

• Через первую трубу бассейн можно наполнить за 10 ч, а через вторую за 15ч. Какую часть бассейна наполнят трубы за 1 ч совместной работы. За сколько часов наполнится бассейн, если открыть обе трубы.

8. Развитие творческих способностей учащихся. (работа в группах)

Учащимся предлагается составить задачу на работу (слайд15) и решить ее. Заслушивается несколько вариантов.

9. Рефлексия (слайд 16)

Учащимся предлагается продолжить фразу.

10. Домашнее задание (выдается на листках)

1. Лошадь съедает воз сена за месяц, коза — за два, овца – за три месяца. За какое время они вместе съедят воз сена.

2. Швейный цех выпускает за смену 300 джинсовых курток или 600 джинсовых брюк. Сколько костюмов, состоящих из куртки и брюк, может выпустить за смену цех.

3. Один писец перепишет книгу из 42 страниц за 6 часов, а другой за 3 часа. За какое время писцы вместе перепишут всю книгу.

4. Две бригады построят дорогу в 6 км за 4 дня, первая бригада в одиночку построит дорогу за 6 дней. За сколько дней в одиночку построит дорогу вторая бригада.

5. Составить 1задачи на совместную работу .

Открытый урок по математике на тему «Задачи на совместную работу» (5 класс)

27.04.2018 Тема урока: «Задачи на совместную работу» 5 класс

Место урока в теме: это 3 урок по теме «Задачи на совместную работу»

Тип урока: обобщение и систематизация знаний

Цель урока:

Образовательная: обобщать знания по теме «Задачи на совместную работу»; совершенствовать умения и навыки решения задач на совместную работу.

Развивающая: способствовать развитию логического мышления, умения применять полученные знания на практике, умение выделять главное, строить логическую цепочку при решении задач; формированию математической речи.

Воспитательная: стимулировать мотивацию и интерес к изучению математики, умение слушать и уважать мнение своих товарищей.

Формируемые УУД:

Личностные: сформировать ответственное отношение к учению; готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

Метапредметные:

регулятивные — научиться формулировать и удерживать учебную задачу; выбирать действия в соответствии с поставленной задачей; планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

познавательные — научиться самостоятельно, выделять и формулировать познавательную цель; использовать общие приёмы решения задач;

коммуникативные — научиться организовывать учебное сотрудничество и совместную деятельность с учителем и одноклассниками:

Предметные: научиться работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику; владеть базовым понятийным аппаратом.

Оборудование: компьютер, проектор, презентация, выполненная в программе PowerPoint, карточки с заданиями, оценочные листы.

Ход урока

Ребята, что было задано на дом?

Давайте, её обсудим!

________, что известно в задаче?

Что необходимо было найти?

Что ты делала в первом действии?

Что ты делала дальше?

И последнее действие?

Какой ответ у тебя получился?

Молодец! Всё правильно.

Если кто-то допустил ошибки, аккуратно исправьте карандашом.

Скажите мне, пожалуйста, какую главу мы с вами изучаем?

Какие операции мы можем производить с дробями?

Хорошо, молодцы. А теперь проверим, как вы это умеете делать.

На слайде представлены выражения, каждому соответствует своя буква, вы должны решить его и записать букву под числовым значением ответа.

9

1

9

1

О

Б

О

Б

Щ

Е

Н

И

Е

Проверяют домашнюю работу.

Задача №663 (а)

Мальчики набирали текст. Иван набрал текст за 4. Петя за 6 часов, Коля за 12 часов.

Время, за которое ребята выполнят работу вместе.

Нашла производительность каждого мальчика.

Нашла общую производительность мальчиков.

Нашла время.

Действия с дробями

Сравнивать, складывать, вычитать, сокращать, умножать, делить.

Решают примеры.

3. Мотивация учебной деятельности учащихся (7 минут)

Молодцы! А что еще мы можем делать с помощью дробей?

Какое слово у вас получилось в таблице?

Как вы думаете, какая сегодня будет тема урока?

Скажите, какую цель вы сегодня поставим перед собой?

Хорошо.

Какие компоненты являются основными для решения задач на совместную работу?

Что такое производительность?

Решите простейшую задачу

Мама с дочкой пекут пирожки. Если бы пирожки пекла только мама, то ей потребовалось бы 2 часа. А дочке на эту работу требуется 4 часа. Какова производительность каждого и общая производительность?

Молодцы!

Выберите верные формулы, которыми мы пользуемся при решении задач на совместную работу.

Установите последовательность решения задач на совместную работу

• Находим часть работы, выполненную двумя и более объектами за единицу времени

• Находим время, которое затратили оба объекта на выполнение работы

• Находим часть работы, выполненную другим объектом за единицу времени

• Принимаем выполненную работу за единицу

• Находим часть работы, выполненную одним объектом за единицу времени

Придумайте задачу на совместную работу по изображению и по краткой записи. Молодцы!

Решать задачи на совместную работу.

Обобщение

Обобщение темы «Задачи на совместную работу»

Обобщить знания по теме «Задачи на совместную работу»

А – объём работы , Р- производительность, Т- время.

Производительность – скорость выполнения работы за единицу времени.

(часть работы выполненная объектом, за единицу времени)

Производительность мамы — часть работы в час, дочки — часть работы в час.

Вместе: — часть работы в час

Формулы под номерами 1), 4), 7).

4. Находим часть работы, выполненную двумя и более объектами за единицу времени

5. Находим время, которое затратили оба объекта на выполнение работы

3. Находим часть работы, выполненную другим объектом за единицу времени

1. Принимаем выполненную работу за единицу

2. Находим часть работы, выполненную одним объектом за единицу времени

4. Обобщение и систематизация знаний (10 минут)

Посмотрите на стол. Перед вами задачи. Скажите, данные задачи относится к задачам на совместную работу?

Первый ряд, решает задачу под №1, второй — под №2, третий — под №3. Работаем! Следим за осанкой!

К доске оформлять решение выходят _____________________________________________,

записи в тетради и на доске оформляем аккуратным разборчивым почерком!

№ 1: Три экскаватора различной мощности могут отрыть котлован, работая отдельно: первый — за 10 дней, второй — за 12 дней, а третий — за 15 дней. За сколько времени они отроют котлован, работая совместно? 

№ 2: Школа заказала в швейную мастерскую форму для учащихся. Одна швея может выполнить весь заказ за 20 дней, второй для выполнения заказа требуется в 3 раза больше этого времени. За сколько времени выполнит весь заказ две швеи, работая совместно.

№ 3: Водоём наполняется двумя трубами за 5 часов, а через одну первую трубу — за 6 часов. Через сколько времени будет наполнен водоём, если открыть только вторую трубу? 

№ 4*: Грузовая машина проезжает расстояние между двумя городами за 30 ч, а легковая – за 20 ч. Машины одновременно выехали из этих городов навстречу друг другу одновременно. Через сколько часов они встретятся?

Да, так как в них определённые объекты выполняют работу, за определенное время.

Решают задачи. Записывают решение в тетради.

5. Физкультминутка (2 минуты)

Вы знаете, что наш мозг состоит из двух полушарий. Правое полушарие отвечает за восприятие искусства, фантазию, танцы, левое полушарие отвечает за память, способности к математике, языкам . И для того, чтобы эти полушария работали вместе, можно делать простые упражнения.

Выполняют упражнения, повторяя, за учителем.

6. Контроль усвоения знаний (10 минут)

Сейчас я вам раздам карточки с тестом. Выполните его. Краткую запись сейчас можно не делать.

1.Саша может прочесть 15 рассказов за 5 дней, а Витя – за 3 дня. Сколько рассказов они вместе прочтут за 8 дней?

а) 64 рассказа б) 80 рассказов в) 56 рассказов

2.Рабочий может изготовить набор деталей за 17 часов, а ученик – за 34 часа. Какую часть набора деталей они изготовят за час, работая одновременно?

а) 3/34 б)1/51 в) 1/34

3.Первая бригада выполнит задание за 10 ч, а вторая – за 15 ч. За сколько часов обе бригады выполнят задание при совместной работе?

а) 4 ч б) 6 ч в) 25 ч

Теперь проверим решение. Поменяйтесь карточкой с соседом по парте. На слайде представлены ответы.

Оцените работу: «5» — всё решено верно, «4» — одна ошибка, «3» — две ошибки.

Поменяйтесь обратно. Поднимите руку у кого отметка 5, у кого отметка 4, у кого отметка 3?

Где допустили ошибки?

Обсуждение результатов.

Решают задачи, выбирают правильный ответ.

Ответы:

1. – а 2. – а 3. – б

7. Информация о домашнем задании (1 минута)

Домашнее задание на стр. 182, № 663 (б), задача на карточке. Откройте учебники, посмотрите на задание. Есть ли вопросы по заданию?

Записывают домашнее задание. Задают вопросы.

8. Рефлексия (2 минуты)

Ребята, давайте вернемся к цели нашего урока.

Как она звучала?

Как вы думаете, вы ее достигли?

Сделайте вывод о своей работе на уроке, продолжив фразу:

— У меня хорошо получилось…

— Мне было интересно…

— Мне было сложно…

Обобщить знания по теме «Задачи на совместную работу».

Да.

Отвечают на вопросы.

Урок математики в 5 классе по теме «Задачи на совместную работу»

Тема урока: задачи на совместную работу (урок 2)

Цели:

Образовательные: совершенствовать умения и навыки решения задач на совместную работу методом арифметического действия;

Развивающие: способствовать развитию логического мышления, умение применять полученные знания на практике, умение выделять главное, верно использовать аналогию и сравнение; строить логическую цепочку при решении задач; формированию математической речи;

Воспитательные: стимулировать мотивацию и интерес к изучению математики, приучать к эстетическому оформлению записи в тетради, умение слушать и уважать мнение своих товарищей.

Тип урока: закрепление ранее изученного материала с элементами изучения нового материала.

Оборудование: компьютер, мультимедийная доска, проектор, доска, мел, раздаточный материал.

План урока:

1. Организационный момент

2. Актуализация опорных знаний и умений

3. Задачи по готовым рисункам (устная работа)

4. Физкультминутка

5. Тест (с самопроверкой)

6. Изучение и закрепление нового материала

7. Решение задач

8. Домашнее задание

9. Подведение итогов урока

10. Рефлексия

11. Резерв

Ход урока:

1. Орг. момент

Здравствуйте, ребята! Садитесь, пожалуйста.

Сегодня мы с вами продолжаем решать «задачи на совместную работу».

Давайте откроем тетради и запишем сегодняшнее число и тему урока.

Начать наш урок хотелось бы словами известного венгерского математика Д. Пойа: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». Именно решением задач мы и будем сегодня заниматься. Но, перед тем, как приступить к решению, совершенно необходимо освежить знания по теме.

1. Актуализация опорных знаний и умений

Работать будем по уже знакомой схеме: один правильный ответ – один бонус. Пять бонусов – оценка за урок 5. Начинаем.

Теория

а) Какие величины используются при решении задач на совместную работу? (Объём работы, производительность, время)

б) Как связаны между собой эти величины? (формулы)

Где P – производительность труда, А – объём работы, Т – время

в) За какую величину мы обычно принимаем объём работы? (за 1)

г) Что такое производительность работы? (Производительность – это часть работы, выполненная за единицу измерения времени)

д) Можно ли сравнивать производительности и что это сравнение показывает? (Чем больше производительность, тем быстрее будет выполнена работа)

е) С какими задачами на совместную работу, вынесенными в отдельный раздел, мы сталкивались ранее? (задачи на движение)

ж) Аналогом какой величины является производительность (скорость)

Задачи на совместную работу	Задачи на движение
A (работа)	S (расстояние)
P (производительность)	v (скорость)
T (время)	T (время)

Практика

Весь известный нам теоретический материал всплыл в памяти, и теперь вспомним, как же решать задачи на совместную работу на практике.

Начнем со старинной задачи. Кстати, какая наука изучает старину? (история). Верно. Сейчас у нас с вами есть уникальная возможность почувствовать себя учениками из прошлого.

Задача 1. “Решил барин двор ставить, и пригласил к себе двух плотников. И говорит первый:

— Только бы мне одному двор ставить, то я бы управился в 6 лет.

А другой молвил:

— А я бы поставил его в 3 года.

Спорили, кому двор ставить, и решили, чтоб не обидно было ставить двор сообща.

Сколь долго они ставили двор?”

Решение: примем всю работу за 1. Тогда

1. – производительность первого плотника

2. – производительность второго плотника

3. – совместная производительность

4. – время совместной работы

Ответ: 2 года

1. Задачи по готовым рисункам (устная работа)

1. Отец с сыном красят забор. Если бы забор красил только отец, то ему потребовалось бы 7 часов. А сыну на эту работу требуется 10 часов. Какова производительность каждого и общая производительность?

Мы с вами уже решили старинную задачу и этим немного прикоснулись к истории. Давайте вспомним, какая важнейшая историческая дата ждёт нас в мае? (день Победы). И в память о тех, кто подарил нам мирное небо над головой, решим с вами еще одну задачу.

2. Снайпер Алексей может вырыть окоп за 25 минут, а Анатолий – за 20 минут. Найти их производительность труда и совместную производительность.

3. Кот Матроскин и Шарик решили заготовить дрова на зиму. Если Матроскин будет колоть дрова один, то ему потребуется 11 дней, а Шарику на эту же работу требуется 9 дней. Какова производительность каждого и общая производительность?

А если бы нам была дана совместная производительность Матроскина и Шарика и производительность Шарика, как мы смогли бы найти производительность Матроскина?

4.Теперь давайте попробуем, глядя на чертеж, самостоятельно составить условие задачи и решить её.

(Ученик выполняет работу за 7 дней, а мастер за 4 дня. Найти производительность ученика, мастера и совместную производительность).

1. Физ. минутка

Мы с вами хорошо поработали и теперь самое время немного расслабиться и отдохнуть.

1. Тест (с самопроверкой)

Сейчас мы проведем небольшой срез ваших знаний. Условия задач вы можете видеть на доске, а варианты, соответствующие правильным ответам, запишите в тетрадях. (3-5 минут)

1. Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. Найти производительность второго рабочего.

а) часть работы за час в) часть работы за час

б) часть работы за час г) часть работы за час

2. Опытный рабочий может выполнить заказ за 17 часов, а ученик – за 34 часа. Какую часть заказа они выполнят за час, работая одновременно?

а) б) в) г) другой ответ

3. Вини Пух съедает банку меда за 2 часа, а его друг Пятачок за 3 часа. За какое время они вдвоем «уработают» такую банку меда, если будут есть со своей обычной производительностью?

а) за часа в) за часа

б) за часа г) за часа

Подведем итоги: если все три ответа верны — еще один бонус.

1. Изучение нового материала

Как вы думаете, что общего было у всех решенных нами задач? (объём работы принимался за 1). А почему? (потому, что являлся неизвестной величиной).

А возможен ли случай, когда объём работы не 1? Конечно, ведь даже в наших формулах объём это А, а не 1.

Давайте разберем такую задачу.

Задача 1. Мама 15 пар носков вяжет за 5 дней, а бабушка – за 3 дня. Сколько пар носков они вместе свяжут за 7 дней?

Итак, чем же эта задача отличается от предыдущих? (задан объём работы – 15 пар). Однако, все наши формулы по-прежнему работают, и мы смело можем решать задачу по известной схеме.

Решение:

1. (пары) – производительность мамы

2. (пар) – производительность бабушки

3. (пар) – совместная производительность

4. (пар)

Ответ: 56 пар носков

Ну что, сильно усложнилась задача при условии объёма работы, не равном 1?

1. Решение задач

Задача 2. Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

Решение:

Примем объём бассейна за 1.

1) (часть) – производительность первой трубы

2) (часть) – производительность второй трубы

Обратите внимание на поиск совместной производительности!

3) часть) – совместная производительность труб

4) =56 (часов) – время наполнения бассейна

Ответ: за 56 часов

1. Домашнее задание

Откроем учебник и разберем задачи, которые вам придётся решить дома (ст.211).

Давайте сразу и запишем домашнее задание.

П. 4.13, №957 (а, б)

1. Подведение итогов

Итак, давайте подведем итог нашего урока. Чем мы занимались на уроке? Что нового узнали?

Подсчитаем бонусы. Поднимите руки, у кого 5 бонусов, 4 бонуса. Выставление оценок в журнал. Не забудьте подойти с дневниками в конце урока.

1. Рефлексия

Всех вас я благодарю за урок и прошу сделать следующее:

У каждого из вас на столе находятся три смайлика – от веселого к грустному. На экране вы можете видеть значение каждого из них (веселый – мне было всё понятно, урок был интересный; равнодушный – было интересно, но есть еще над чем поработать; грустный – я многое не понял на уроке). Сейчас, когда вы будете выходить из кабинета, пусть каждый оставит на парте тот, который соответствует, по вашему мнению, сегодняшнему уроку, а остальные два заберет с собой.

Урок окончен. До свидания!

1. Резерв

Это случилось жарким летом …

На побережье реки Оки отдыхали друзья Коля, Володя и Серёжа. Чтобы выжить на отдыхе, друзья решили поймать пару рыбин и сделать отличную уху. Закинули удочки и стали ждать клёва. Поймав первую рыбину, друзья как-то сразу поняли, что двух рыбин не хватит. Да и десяти тоже. Порода, видимо, была такая — мелкая, да… Решили, что надо поймать штук 30, или больше.

За полтора часа Сережа поймал 10 рыб, Вова — 8, а Коля — 7. На уху почти хватало, но нужны были ещё дрова для костра. Вова предложил, чтобы в лес за дровами шёл тот, у кого меньше ловится, а остальные будут рыбачить ещё 40 минут. Так рыбы больше получится. Сережа (чемпион!) радостно согласился. Но тут Коля некстати вспомнил, что он 34 минуты готовил чай с бутербродами, а Вова 26 минут искал дополнительную наживку для всех…. И этот факт надо учитывать. Это было честно, и все согласились.

Уха получилась отличная!

Вопросы:

1. Кто ходил за дровами в лес?

2. Сколько всего было поймано рыб на уху?

Решение:

1. Кто ходил за дровами в лес?

Ловить рыбу остаются те, кто ловит быстрее. Значит, надо посчитать скорость ловли каждого. Необходимо рассчитать производительность. Для её расчёта нужно знать чистое время рыбалки у каждого.

• У Сережи: 90 минут (полтора часа).

• У Вовы вычитаем время на поиски наживки: 90 — 26 = 64 минуты

• У Коли вычитаем время на приготовление чая: 90 — 34 = 56 минут.

Тогда:

р = (часть) — производительность Сережи

р = (часть) – производительность Вовы

р = (часть) – производительность Коли

Итак, медленнее всех ловит Сережа. Значит, в лес за дровами ушел Сережа.

2. Сколько всего было поймано рыб на уху?

Вова и Коля ловили 40 минут. Это классическая совместная работа.

(часть рыбы) – общая производительность

Коля с Вовой вместе ловят со скоростью рыбки в минуту. Для определения объёма (количество рыб), надо время ловли (40 минут) умножить на производительность:

А = t · р = 40 · = 10

Тогда количество пойманных рыб на уху равно:

25 + 10 = 35 штук.

Уха получилась отличная!

Ответ: за дровами ушел Сережа; всего было поймано 35 рыб.

Тест по математике (5 класс) по теме: 5 класс. Тест 50. «Задачи на совместную работу»

По теме: методические разработки, презентации и конспекты

Урок в 5 классе «Задачи на совместную работу»

Сформировать способность к решению задач на совместную  работу, повторить и закрепить действия с натуральными числами….

Урок математики в 6 классе по теме: «Задачи на совместную работу»

Урок математики  по теме: «Задачи на совместную работу» проводится после того, как  изучены все действия с действительными дробями. Тип урока: комбинированный. Данная тема не выде…

Открытый урок математики 5 класс «Задачи на совместную работу»

Урок в 5 классе к учебнику Г,В. Дорофеева…

Урок в 6 классе по теме «решение задач на совместную работу «

Исследовательская деятельность на уроке….

Урок математики в 5 классе «Задачи на совместную работу»

Тема урока: ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ по учебнику «МАТЕМАТИКА 5»,  авторов Дорофеев Г.В., Шарыгин И.Ф. Цель урока: формирование умений решать текстовые задачи; развитие логического мышлени…

самостоятельная работа 5 класс математика. задачи на совместную работу, движение и примеры на действия с обыкновенными дробями

данная самостоятельная работа содержит в себе задачи на совместную работу, задачи на движение, задачу на арифметические действия и примеры на все действия с обыкновенными дробями…

Урок по математике на тему «Задачи на совместную работу» (5 класс), УМК Никольский С. М.

Урок изучения нового материала. Цели: изучить алгоритм решения задач на совместную  работу; закрепить данный алгоритм в ходе решения задач….

План-конспект урока по математике (5 класс): Задачи на совместную работу

Деятельность учителя	Деятельность обучающихся
1.Орг. момент (2 минуты)
Здравствуйте, ребята, присаживайтесь! Настраиваемся на работу, открываем тетради, отступаем 4 клетки от своей последней записи, записываем число, классная работа.	Готовятся к уроку. Настраиваются на рабочий лад. Записывают число, классная работа.
2. Актуализация опорных знаний (7 минут)
Ребята, что было задано на дом? Давайте, её обсудим! ________, что известно в задаче? Что необходимо было найти? Что ты делала в первом действии? Что ты делала  дальше? И последнее действие? Какой ответ у тебя получился? Молодец! Всё правильно. Если кто-то допустил ошибки, аккуратно исправьте карандашом. Скажите мне, пожалуйста, какую главу мы с вами изучаем? Какие операции мы можем производить с дробями? Хорошо, молодцы. А теперь проверим, как вы это  умеете делать. На слайде представлены выражения, каждому соответствует своя буква, вы должны решить его и записать букву под числовым значением ответа.	Проверяют домашнюю работу. Задача №663 (а) Мальчики набирали текст. Иван набрал текст за 4. Петя за 6 часов, Коля за 12 часов. Время, за которое ребята выполнят работу вместе. Нашла производительность каждого мальчика. Нашла общую производительность мальчиков. Нашла время. Действия с дробями Сравнивать, складывать, вычитать, сокращать, умножать, делить. Решают примеры.
3. Мотивация учебной деятельности учащихся (7 минут)
Молодцы! А что еще мы можем делать с помощью дробей? Какое слово у вас получилось в таблице? Как вы думаете, какая сегодня будет тема урока? Скажите, какую цель вы сегодня поставим перед собой? Хорошо. Какие компоненты являются основными для решения задач на совместную работу? Что такое производительность? Решите простейшую задачу Мама с дочкой пекут пирожки. Если бы пирожки пекла только мама, то ей потребовалось бы 2 часа. А дочке на эту работу требуется 4 часа. Какова производительность каждого и общая производительность? Молодцы! Выберите верные формулы, которыми мы пользуемся при решении задач на совместную работу. Установите последовательность решения задач на совместную работу Находим часть работы, выполненную двумя и более объектами за единицу времени Находим время, которое затратили оба объекта на выполнение работы   Находим часть работы, выполненную другим объектом за единицу времени Принимаем выполненную работу за единицу Находим часть работы, выполненную одним объектом за единицу времени Придумайте задачу на совместную работу по изображению и по краткой записи. Молодцы!	Решать задачи на совместную работу. Обобщение Обобщение темы «Задачи на совместную работу» Обобщить знания по теме «Задачи  на совместную работу» А – объём работы , Р- производительность, Т- время. Производительность – скорость выполнения работы за единицу времени. (часть работы выполненная объектом, за единицу времени) Производительность мамы —  часть работы в час,  дочки —  часть работы в час. Вместе:   — часть работы в час Формулы под номерами 1), 4), 7). 4. Находим часть работы, выполненную двумя и более объектами за единицу времени  5. Находим время, которое затратили оба объекта на выполнение работы 3. Находим часть работы, выполненную другим объектом за единицу времени 1. Принимаем выполненную работу за единицу 2. Находим часть работы, выполненную одним объектом за единицу времени
4. Обобщение и систематизация знаний (10 минут)
Посмотрите на стол. Перед вами задачи. Скажите, данные задачи относится к задачам на совместную работу? Первый ряд, решает задачу под №1, второй — под №2, третий — под №3. Работаем! Следим за осанкой! К доске оформлять решение выходят _____________________________________________, записи в тетради и на доске оформляем аккуратным разборчивым почерком!   № 1: Три экскаватора различной мощности могут отрыть котлован, работая отдельно: первый — за 10 дней, второй — за 12 дней, а третий — за 15 дней. За сколько времени они отроют котлован, работая совместно?  № 2: Школа заказала в швейную мастерскую форму для учащихся. Одна швея может выполнить весь заказ за 20 дней, второй для выполнения заказа требуется в 3 раза больше этого времени. За сколько времени выполнит весь заказ две швеи, работая совместно. № 3: Водоём наполняется двумя трубами за 5 часов, а через одну первую трубу — за 6 часов. Через сколько времени будет наполнен водоём, если открыть только вторую трубу?  № 4*: Грузовая машина проезжает расстояние между двумя городами за 30 ч, а легковая – за 20 ч. Машины одновременно выехали из этих городов навстречу друг другу одновременно. Через сколько часов они встретятся?	Да, так как в них определённые объекты выполняют работу, за определенное время. Решают задачи. Записывают решение в тетради.
5. Физкультминутка (2 минуты)
Вы знаете, что наш мозг состоит из двух полушарий. Правое полушарие отвечает за восприятие искусства, фантазию, танцы, левое полушарие отвечает за память, способности к математике, языкам . И для того, чтобы эти полушария работали вместе, можно делать простые упражнения.	Выполняют упражнения, повторяя, за учителем.
6. Контроль усвоения знаний (10 минут)
Сейчас я вам раздам карточки с тестом. Выполните его. Краткую запись сейчас можно не делать. 1.Саша может прочесть 15 рассказов за 5 дней, а Витя – за 3 дня. Сколько рассказов они вместе прочтут за 8 дней? а) 64 рассказа    б) 80 рассказов   в) 56 рассказов 2.Рабочий может изготовить набор деталей за 17 часов, а ученик – за 34 часа. Какую часть набора деталей они изготовят за час, работая одновременно? а) 3/34      б)1/51      в) 1/34 3.Первая бригада выполнит задание за 10 ч, а вторая – за 15 ч. За сколько часов обе бригады выполнят задание при совместной работе? а) 4 ч        б) 6 ч         в) 25 ч Теперь проверим решение. Поменяйтесь карточкой с соседом по парте. На слайде представлены ответы. Оцените работу: «5» — всё решено верно, «4» — одна ошибка, «3» — две ошибки. Поменяйтесь обратно. Поднимите руку у кого отметка 5, у кого отметка 4, у кого отметка 3? Где допустили ошибки? Обсуждение результатов.	Решают задачи, выбирают правильный ответ. Ответы: 1. – а       2. – а          3. – б
7. Информация о домашнем задании (1 минута)
Домашнее задание  на стр. 182, № 663 (б), задача на карточке. Откройте учебники, посмотрите на задание. Есть ли вопросы по заданию?	Записывают домашнее задание. Задают вопросы.
8. Рефлексия (2 минуты)
Ребята, давайте вернемся к цели нашего урока. Как она звучала? Как вы думаете, вы ее достигли? Сделайте вывод о своей работе на уроке, продолжив фразу: — У меня хорошо получилось… — Мне было интересно… — Мне было сложно…	Обобщить знания по теме «Задачи на совместную работу». Да. Отвечают на вопросы.