Линейные уравнения – примеры с объяснением (7 класс, математика)
Линейные уравнения это первый шаг на пути изучения огромного количества самых разных уравнений. Именно в этой теме ученики усваивают важнейшие приемы решения. Чтобы не упустить ни одну из мелочей курса математики 6 класса, разберемся в вопросе подробнее.


Что такое уравнение?
В общем случае, уравнением называется тождество с одной неизвестной.
Тождеством зовется равенство. То есть уравнение это два равных между собой выражения, одно из которых или оба содержат неизвестное. Важным является условие присутствия только одной неизвестной в одном уравнении.
Можно написать уравнение с двумя и большим количеством переменных, но такое выражение решить не получится. Запомните, даже в системах уравнений, количество переменных должно равняться количеству уравнений. Например, система:
х+3=2
у+х=3
Z+у=4 – имеет решение. А вот уравнение:
Х+у=12 – однозначных решений не имеет. Почему?
Решением называется строго определенные числа, которые удовлетворяю требованиям равенства. То есть:
Х+3=5
Неизвестная имеет только одно решение. В уравнении х+у=12 – решений бесконечно много. Число х может быть любым, как только мы выберем и подставим любое число, изменится в соответствии с нашим выбором и у. Поэтому и говорят, что у такого уравнения нет определенных решений.
Виды уравнений
Выделяют следующие виды уравнений:
Выделяют так же системы уравнений, где несколько тождеств имеют одинаковые значения переменных. В таких уравнениях часто используют способ подстановки, заменяя одну переменную другой.
Способы решения линейного уравнения
Любое уравнение можно решить двумя способами:
- Аналитическим, то есть с помощью математических вычислений. Этот способ хорош своей точностью
- Графическим, то есть с помощью построения на графике. Этот способ хорош возможностью использования практически в любой ситуации. К нему прибегают, когда найти корень с помощью вычислений невозможно.
Рассмотрим каждый из способов.
Графический способ
Для понимания графического способа нужно вспомнить, что такое функция. Функция это зависимость одной переменной от другой. Выражение, которое мы записали в начале: х+у=12 – как раз является функцией. Перенесем х в левую сторону выражения и запишем функцию в классическом виде.
у=12-х – функция имеет форму линии, откуда и название функции и соответствующего ей уравнения. Значение корня любого уравнения это одна или несколько точек на графике функции. Точки эти задаются пересечением с графиком другой функции.
Например, уравнение х+7=13 можно разбить на две функции:
у=х+7
у=13 – в первом случае это прямая линия. Во втором, прямая линия, которая проходит параллельно оси Оу через точку 13 на оси Ох. Точка пересечения двух графиков и будет решением уравнения.
Аналитический способ
Аналитический способ решения линейных уравнений подразумевает перенос величин из одной части выражения в другую с заменой знака. Смысл переноса в том, чтобы собрать все неизвестные в одной части уравнения, а все числа в другой.
Приведем пример линейного уравнения: 2х-7х+15=0
2х-7х+15=0 – соберем все значения х в правой части, а числа в левой
2х-7х=-15
-5х=-15 – теперь поделим обе части выражения на коэффициент при неизвестном, т. е. на число -5
х=3
Что мы узнали?
Мы поговорили о видах уравнений. Разобрали, какие уравнения нельзя решить и привели объяснение. Выделили и разобрали на примерах два способа решений линейных уравнений.
ПредыдущаяАлгебраДействительные числа – примеры, определение, символ (6 класс, математика)
СледующаяАлгебраДискриминант квадратного уравнения – нахождение по формуле
sprint-olympic.ru
Практикум «Решение линейных уравнений», 7 класс
Материал опубликовалФайл загрузился с искажением, просьба смотреть его, скачав по ссылке: Практикум по решению линейных уравнений.
Решите уравнения:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 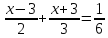
9.  10.
10. 
Ответы
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
12 | 0,6 | 1 | -2 | Решений нет | Любое число | 0.9 | 0,8 | -1 | 0.5 |
Решите уравнения
1) (х – 3)2 = (х – 6)(х + 6) 2) 4∙(х + 2)2 = 3(х2 – 3)+(х – 3)(х + 3) + 2
3) (х – 5)2 – (х + 5)2 = 20 4) 3х(х – 3) = 3(х + 2)2 – 75
5) (х – 2)(х2 + 2х + 4) = х(х – 1)2 + 2х2 6) х2 + 9 = х2 – 81 + 6х
7) 2х(2х – 1) = 3х2 – (3 – х)(3+х) 8) х2 – 25 = 2∙(х – 4)(х +4) – х(х–7)
9) (х + 1)2 = 3х + 1 10) (х – 3)2 = 6∙(15 – х)
Ответы
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
7,5 | -2 | -1 | -3 | -8 | 15 | 4,5 | 1 | 0 и 1 | -9 и 9 |

![]()
![]()
![]()
![]()
xn--j1ahfl.xn--p1ai
Решение линейных уравнений — Математика
Решение линейных уравнений, 7 класс
Разноуровневые карточки для проверки знаний учащихся по теме: «Линейные уравнения» содержат 5 уравнений разного уровня сложности. Их можно применять не только на уроках в данной теме, но и при повторении материала.
|
Вариант I (Уровень А) |
|
Вариант II (Уровень В)
|
|
Вариант III (Уровень С)
|
|
Вариант I (Уровень А) |
|
Вариант II (Уровень В) |
|
Вариант III (Уровень С)
|
|
Вариант I (Уровень А) |
|
Вариант II (Уровень В)
|
|
Вариант III (Уровень С)
|
Просмотр содержимого документа
«Решение линейных уравнений»
multiurok.ru
Теста по теме «Линейные уравнения», 7 класс
Таблица 1. Обоснование спецификации теста по теме «Линейные уравнения», 7 класс, УМК Мордкович А Г.
Диагностируемая учебная цель
Уровень
Кол-во заданий в тесте
Тип (типы) тестовых заданий
Примечания (например, содержание)
1.
Понятие уравнения и корня уравнения
Знание
1
Выбор нескольких правильных ответов
Уравнение вида (где x – переменная, a и b – некоторые числа) называется линейным уравнением с одной переменной. В линейном уравнении переменная x обязательно в первой степени.
Значения неизвестных, при которых равенство уравнения достигается, называются решениями или корнями данного уравнения.
Знание
1
Подстановка пропущенного слова
Применение
2
Выбор одного правильного ответа
2.
Представление о равносильности уравнений.
Применение
1
Выбор нескольких правильных ответов
Два уравнения называются равносильными, если множества их корней совпадают (в том числе, уравнения, не имеющие корней, считаются равносильными).
1
Выбор одного правильного ответа
3.
Алгоритм решения линейных уравнений.
Знание
1
Выбор одного правильного ответа
Алгоритм решения линейных уравнений:
Раскрыть скобки
Перенести слагаемые содержащие переменную в одну часть, а не содержащие – в другую.
Привести подобные слагаемые.
Разделить обе части уравнение на коэффициент при переменной.
Если a = b = 0, то решением уравнения ax + b = 0 является любое число.
Если a = 0 и b 0, то уравнение корней не имеет.
Если a 0, то уравнение ax + b = 0 называется линейным и имеет ровно одно решение x = − b/a
1
Последовательность
Применение
1
Соответствие
1
Краткий ответ
1
Выбор одного правильного ответа
4.
Процесс решения задач с помощью линейных уравнений.
Применение
1
Краткий ответ.
Ввести неизвестную величину.
Составить уравнение.
Найти корни уравнения.
1
Выбор одного правильного ответа
Таблица 2. Сводка по уровню контроля и представленности содержания (репрезентативности) в тесте
Понятие уравнения и корня уравнения
2
2
4
2
Представление о равносильности уравнений.
2
2
3
Алгоритм решения линейных уравнений.
2
3
5
4
Процесс решения задач с помощью линейных уравнений.
2
2
ИТОГО ПО ТЕСТУ
4
9
13
Таблица 3. Тестовые задания
А.
Б.
В. (х-2)(х+4)=18
Г. 5х + 3 = 2х – 7
1 балл – правильно указаны два уравнения
0 балл – правильно указано одно уравнение или не указано ни одного
ответ: б, г
2
Вставьте пропущенное слово.
Уравнение вида (где x – переменная, a и b – некоторые числа) называется ……. уравнением с одной переменной.
Верно выполненное задание – 1 балл
Линейное
3
Какому неравенству удовлетворяет корень уравнения -15x -7 = 0?
А.
Б.
В.
Г.
Верно выполненное задание – 3 балла
Ответ: Б
4
Из множества чисел выберите то число, которое будет корнем уравнения: 2х + 1 = -5
А. – 3
Б. – 2
В. 3
Г. 0
Верно выполненное задание – 2 балла
Ответ: А.
5
Найдите пары равносильных уравнений:
А. 3х – 6 = 0; 3х = 6
Б. 5(х + 2) = 20; х + 2 = 5
В. ; 5 + 2х = 5
Г. 2х + 4 = 7; 5 + 2х = 8.
3 балла – правильно указаны все уравнения
2 балл – правильно указано одно уравнение
0 балл –не указано ни одного
Ответ: А, Г.
6
Какие уравнения являются равносильными:
А. 2х – 7 = 3 и 2х = –4;
Б. 3х-7=2 и 3х+6=1
В. 3(х – 2) = –6 и 3х – 6 = –6;
Г. –0,1х + 0,1х = 0 и 0,2х = 0?
Верно выполненное задание – 3 балла
Ответ: В.
7
Какое действие не принадлежит к основным свойствам уравнений:
А. приведение подобных слагаемых в обеих частях уравнения;
Б. умножение двух частей уравнения на одно и то же число, отличное от нуля;
В. прибавление некоторого числа к одной части уравнения;
Г. перенесение некоторого члена уравнения из одной части уравнения в другую?
Верно выполненное задание – 1 балл
Ответ: В
8
Укажите верный порядок действий при решении линейных уравнений
А. Перенести слагаемые содержащие переменную в одну часть, а не содержащие — в другую.
Б. Разделить обе части уравнение на коэффициент при переменной
В. Привести подобные слагаемые.
Г. Раскрыть скобки
Верно выполненное задание – 1 балл
Ответ: Г, А, В, Б
9
После решения уравнения коэффициент при х оказался стертым, восстановите его.
…х = 27 , х=9
Верно выполненное задание – 2 балла
Ответ: 3
10
Выберите уравнения, корнем которых является число 5.
А. 3х + 1 = 16
Б. 5(2 – х) = 4 + х
В. 7 + х = 2х – 22
Г. (х + 2)+(х – 2) =21
Верно выполненное задание – 3 балла
Ответ: А.
11
Решите уравнения и установите соответствия:
А. 6у – (у – 1) = 2(3у – 4)
Б. 6у – (у + 1) = 2(2у – 4)
В. 6у – (2у – 1) = 2(у – 4)
Г. 6у – (у + 1) = 2(2у + 4)
1. -7
2. 9
3. 7
4. -3,5
Правильно указаны все соответствия – 4 балла;
Правильно указаны 3 соответствия – 3 балла;
Правильно указаны 2 соответствия – 2 балла;
Правильно указано 1 соответствие – 1 балл;
Соответствия указаны неверно – 0 баллов.
Ответ: А3, Б1, В4, Г2.
12
Решите задачу и запишите ответ. Катер за 2 часа по озеру и за 3 часа против течения реки проплывает такое же расстояние, что и за 3 ч 24 мин по течению реки. Найдите собственную скорость катера, если скорость течения реки равна 3 км/ч.
Задача решена верно – 3 балла.
Задача решена неверно – о баллов.
Ответ: 12
13
Выберете правильный вариант ответа.
У меня в холодильнике в общей сложности 19 куриных и
перепелиных яиц. После приготовления яичницы из 2 куриных и
5 перепелиных яиц, перепелиных стало в два раза больше, чем куриных.
Сколько куриных яиц было в холодильнике изначально?
А. 7
Б. 5
В. 6
Г. 4
Верно выполненное задание – 3 балла
Ответ: В.
Подход к измерению – субъективно-центрированный, поскольку проверяются знания каждого субъекта, и нам необходимо распределить учащихся на группы.
Тип итоговой шкалы измерений – интервальная шкала.
Подход к начислению тестовых баллов – не дихотомический
Максимальное количество набранных баллов – 12.
Алгоритм перехода от тестовых баллов к оценке по итоговой шкале:
infourok.ru