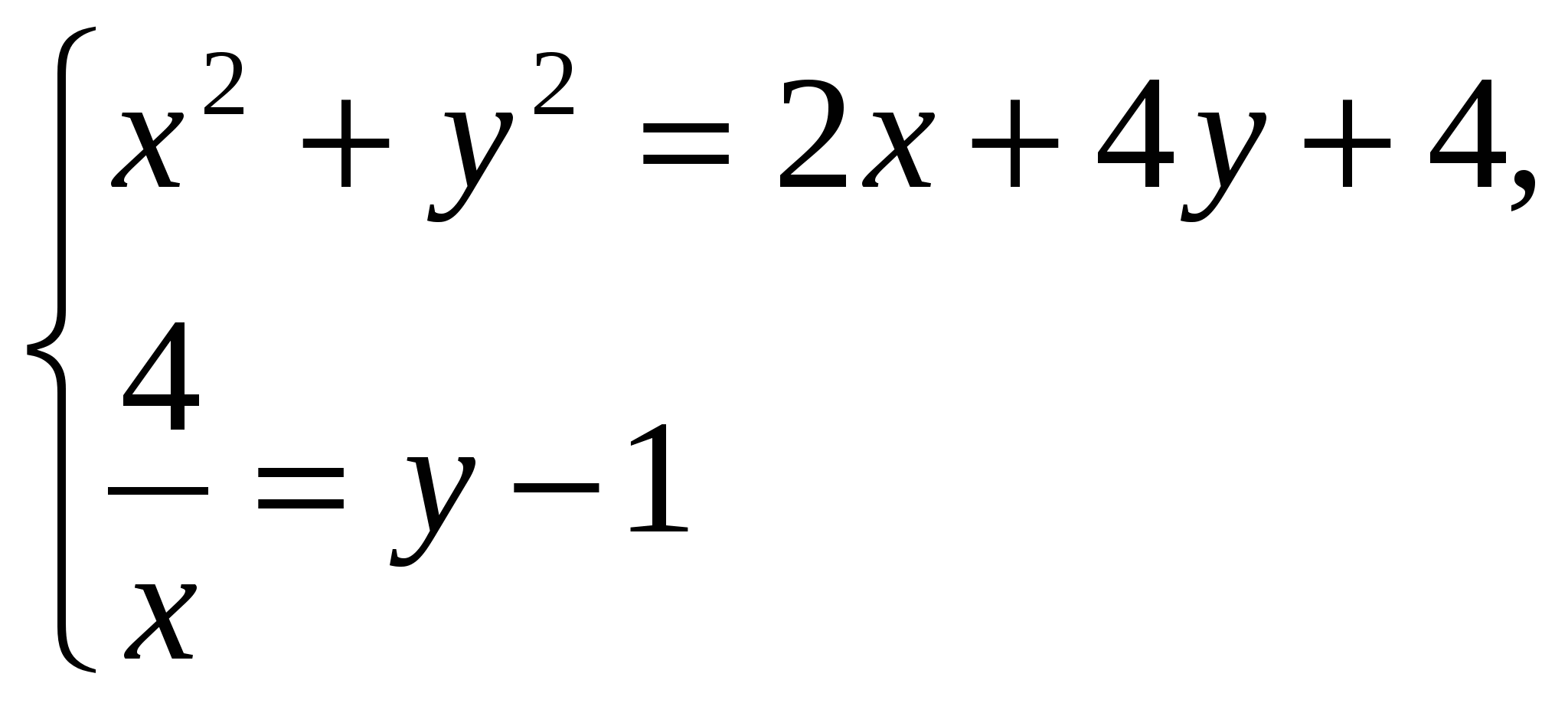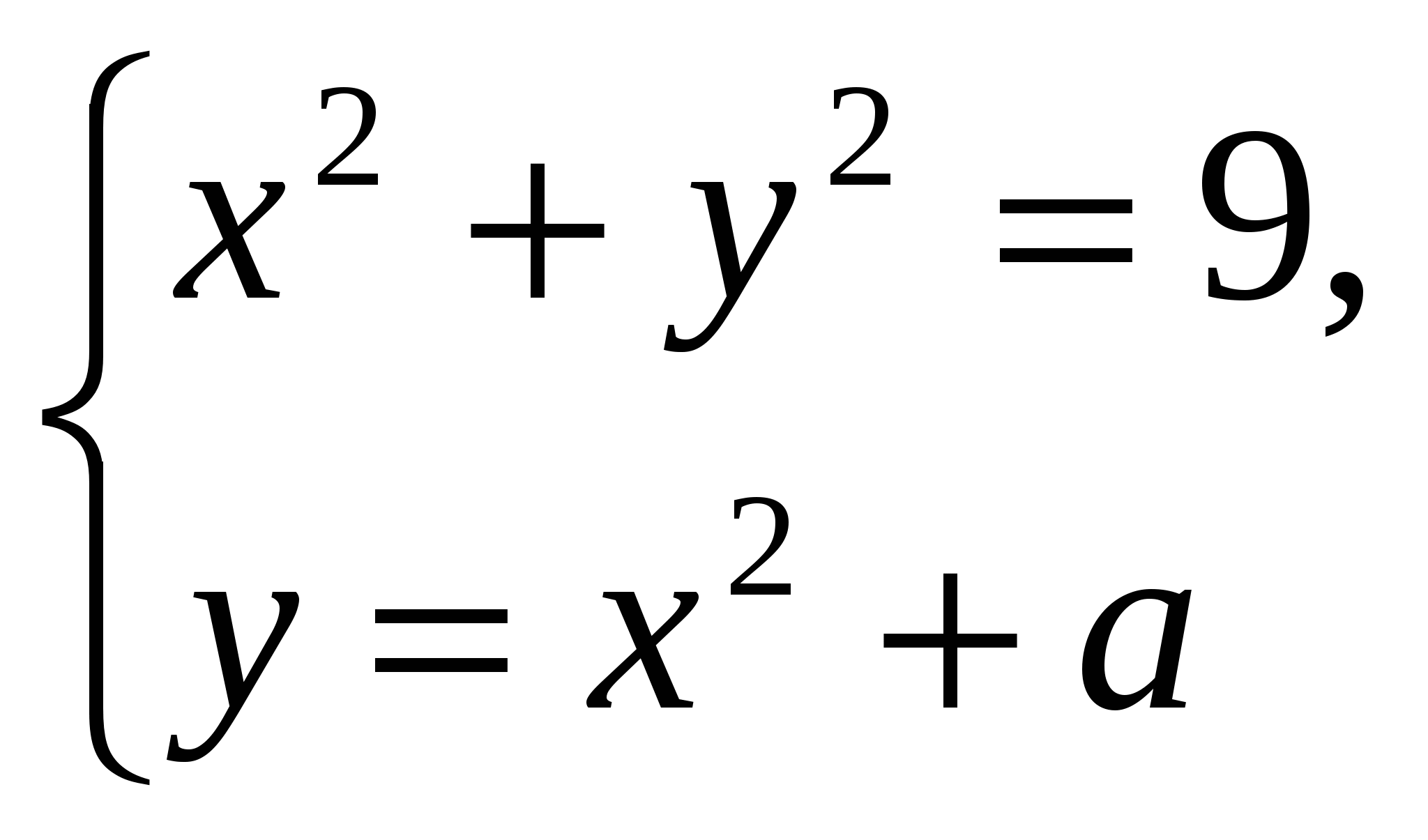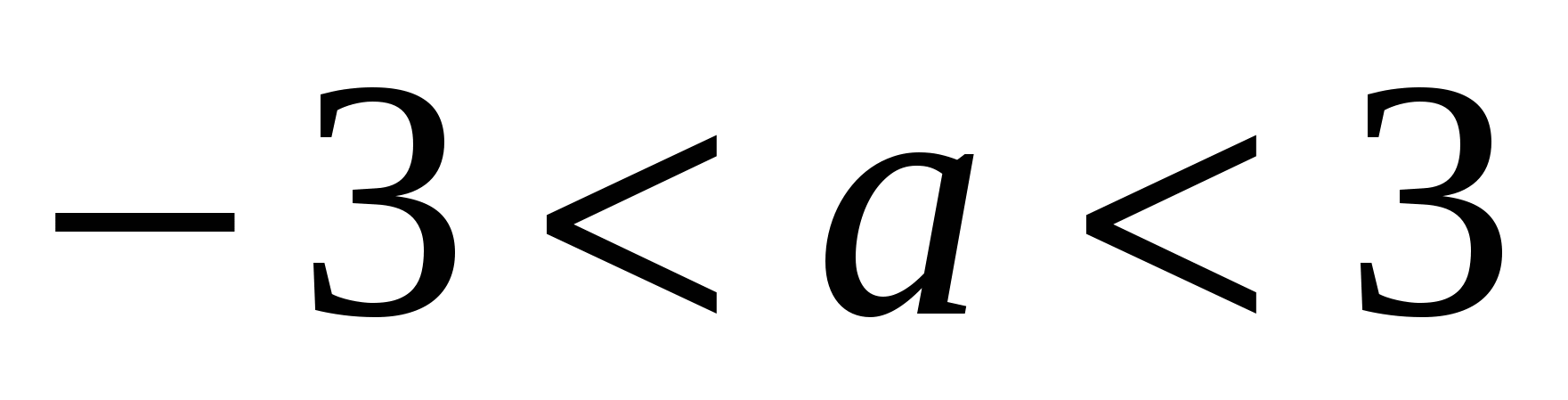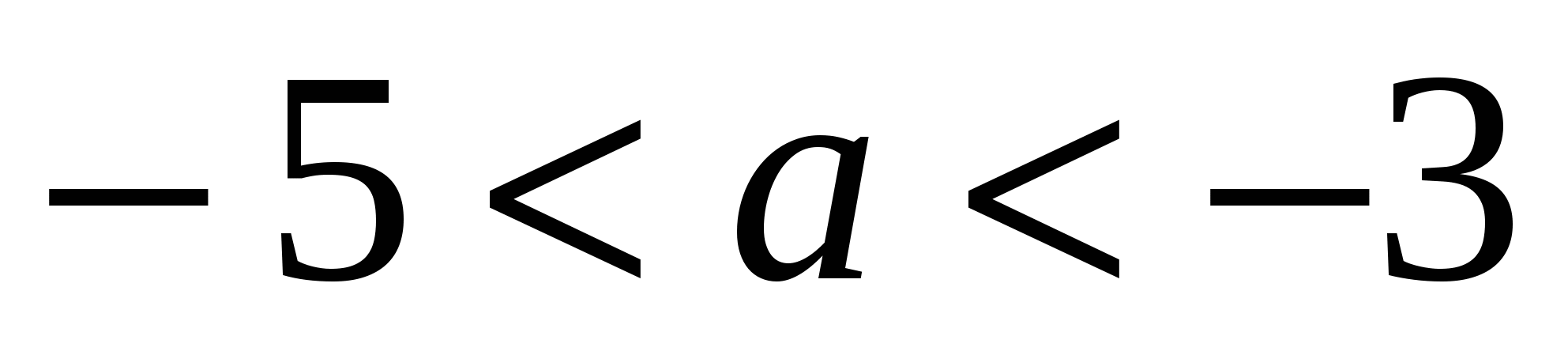Системы уравнений в текстовых задачах с алгебраическим или геометрическим содержанием
На этом уроке мы продолжим решение текстовых задач на алгебраическую или геометрическую тему методом математического моделирования. Подробно рассмотрим составление математических моделей и три этапа его решения. Решим ряд задач на данную тему.
Тема: Системы уравнений
Урок: Системы уравнений в текстовых задачах с алгебраическим или геометрическим содержанием
На этом уроке мы продолжим решение текстовых задач методом математического моделирования. Здесь требуется перевести задачу на математический язык, получить математическую модель – систему уравнений – и решить ее.
Задача 1. Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
Решение:
Пусть 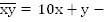
(Например, 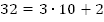 ).
).
Мы записали искомое число с помощью двух неизвестных.
Что нам известно, чтобы найти x и y?
1. 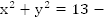 сумма квадратов цифр равна 13.
сумма квадратов цифр равна 13.
2. 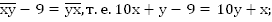
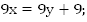
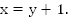
Мы получили математическую модель – систему двух уравнений с двумя неизвестными.
Далее следует работа с математической моделью, нужно решить систему:
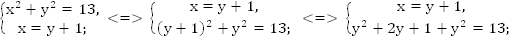
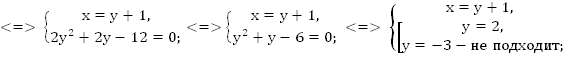
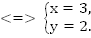
Ответ: 32.
Задача 2. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 секунд быстрее другой. При этом совпадение точек происходит каждый раз через 1 минуту. Определите скорости движения точек.
Решение:
Пусть x м/с, y м/с – искомые скорости точек, и пусть 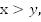
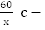 время прохождения одного оборота первой точкой,
время прохождения одного оборота первой точкой, 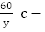 время прохождения одного оборота второй точкой.
время прохождения одного оборота второй точкой.По условию 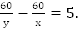
Упростив это выражение, получим 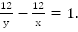
По условию совпадения происходят через 1 минуту, это значит, что за время 1 мин = 60 с между соседними совпадениями точек первая точка пройдет на один круг – 60 м – больше, чем вторая. Со скоростью сближения 
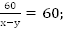

Мы получили второе уравнение.
Мы получили математическую модель, теперь переходим ко второму этапу – р
Примеры. Видеоурок. Алгебра 9 Класс
Тема: Системы уравнений
Урок: Примеры
Ранее мы уже составляли математические модели реальных ситуаций, но только те, которые описывались линейными системами. Сейчас мы научились решать нелинейные системы. Наша задача – научиться составлять математические модели с помощью нелинейных систем уравнений.
Задача 1. Сумма двух чисел равна 12, а их произведение равно 35. Найти эти числа.
Решение:
Первый этап – переведем словесную модель на математический язык. Пусть x и y – искомые числа. По условию 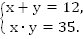
Эта нелинейная система представляет собой математическую модель реальной ситуации.
Второй этап – работа с математической моделью.

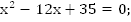
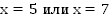 ;
;
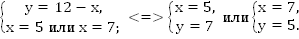
Ответ: 
Обсудим связь полученной системы с квадратным уравнением. Воспользуемся теоремой Виета:
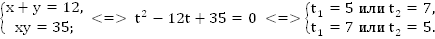
Это еще один способ решения системы.
Задача 2. Какое двузначное число в 4 раза больше суммы своих цифр и в 3 раза больше их произведения?
Решение:
Получим математическую модель. Пусть 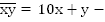 искомое число, x и y его цифры.
искомое число, x и y его цифры. 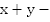 сумма цифр искомого числа,
сумма цифр искомого числа, 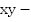
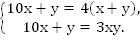
Число двузначное, т.е. 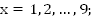

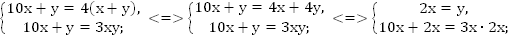


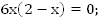
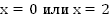 ;
;

Ответ: 24.
Задача 3. Если к числителю и знаменателю дроби прибавить по единице, то дробь станет равна 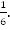 А если сложить квадраты числителя и знаменателя исходной дроби, то получится 122. Найдите эту дробь.
А если сложить квадраты числителя и знаменателя исходной дроби, то получится 122. Найдите эту дробь.
Решение:
Пусть x – числитель дроби, y – знаменатель дроби,  – искомая дробь.
– искомая дробь.
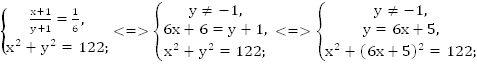
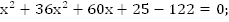
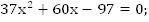
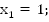 (методом подбора)
(методом подбора)
 ( по т.Виета) – не подходит по условию задачи.
( по т.Виета) – не подходит по условию задачи.
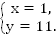
Ответ:  .
.
Задача 4. Периметр прямоугольного треугольника равен 84 см. Его гипотенуза равна 37 см. Найти площадь прямоугольного треугольника.
Решение:
Дан прямоугольный 
Пусть x, y – катеты прямоугольного треугольника.
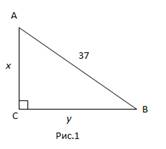
Тогда по условию задачи
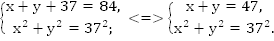
Нам необходимо найти 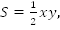 поэтому отдельно находить x и y не нужно.
поэтому отдельно находить x и y не нужно.
Возведем в квадрат обе части первого уравнения:


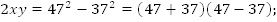
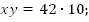
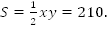
Ответ: 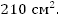
Задача 5. Сумма катетов прямоугольного треугольника равна 49 м, гипотенуза – 41 м. Найти площадь прямоугольного треугольника.
Решение:
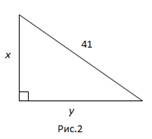
Пусть x, y – катеты прямоугольного треугольника. Тогда
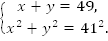
Возведем в квадрат обе части первого уравнения, получаем:
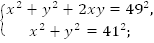
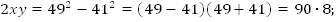
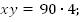

Ответ: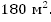
Мы решили текстовые задачи, перевели русский язык на математический, получили нелинейные математические модели, решили их, и получили решения исходных задач. На следующем уроке мы рассмотрим задачи на движение.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 143, 146, 152, 164.
| 1. |
Переход от математической модели к словесной
Сложность: лёгкое |
1 |
| 2. |
Составление словесной модели по математической (действия с числами)
Сложность: лёгкое |
1 |
| 3. |
От математической модели к словесной
Сложность: лёгкое |
1 |
| 4. |
Составление математической модели по словесной (прямоугольный треугольник)
Сложность: среднее |
3 |
| 5. |
От словесной модели к математической (прямоугольник)
Сложность: среднее |
2 |
| 6. |
Переход от словесной модели к математической (на движение)
Сложность: среднее |
4 |
| 7. |
Составление системы уравнений (школа)
Сложность: среднее |
4 |
| 8. |
Решение текстовой задачи (зрительный зал)
Сложность: сложное |
8 |
| 9. |
Решение текстовой задачи (числа)
Сложность: сложное |
7 |
| 10. |
Решение текстовой задачи (на работу)
Сложность: сложное |
9 |
| 1. |
Условие, когда пара чисел является или не является решением системы
Сложность: лёгкое |
1 |
| 2. |
Преобразования, которые являются / не являются равносильными
Сложность: лёгкое |
3 |
| 3. |
Пара чисел, которая является решением системы уравнений
Сложность: лёгкое |
2 |
| 4. |
Является ли пара чисел решением системы уравнений?
Сложность: среднее |
4 |
| 5. |
Выбор пары чисел, которая является решением системы уравнений
Сложность: среднее |
4 |
| 6. |
Выбор пар чисел
Сложность: среднее |
4 |
| 7. |
Пары чисел, которые не являются решением системы уравнений
Сложность: среднее |
2 |
| 8. |
Число решений системы уравнений
Сложность: среднее |
3 |
| 9. |
Определение названия графика по уравнению (квадрат суммы)
Сложность: сложное |
5 |
| 10. |
График уравнения (квадрат разности)
Сложность: сложное |
5 |
Урок по теме «Решение систем уравнений» (9 класс)
ЧИКРИН ЕВГЕНИЙ АЛЕКСАНДРОВИЧ
План- конспект открытого урока по алгебре,
проведенного в 9 А классе гимназии № 125
Советского района города Казани
на тему «Решение систем уравнений»
Урок был и остается основным элементом образовательного процесса, но в системе личностно-ориентированного обучения существенно меняется его функция, форма организации. В этом случае урок подчиняется не сообщению и проверке знаний, хотя и такие уроки тоже нужны, а выявлению опыта учеников по отношению к излагаемому учителем содержанию. Математикой нельзя овладеть путем простого заучивания отдельных фактов. Для устранения затруднений при усвоении математики большое значение имеет воспитание любознательности и интереса к предмету. Чтобы увлечь детей математикой, урок должен быть интересным и запоминающимся. Повторение учебного материала с использованием элементов новизны дает возможность переосмыслить известные понятия, факты, закономерности. Использование новых информационных технологий позволяет успешно решать поставленные задачи, способствует развитию творческой активности школьников.
Содержание урока подбиралось таким образом, чтобы вовлечь каждого учащегося в активную и посильную деятельность. Новые подходы, используемые в разработке урока — идея сотрудничества и применение элементов личностно-ориентированного обучения, что позволяет заботиться о развитии и поддержке индивидуальности каждого ученика.
Тип урока. Комплексный урок
Урок проводится в форме презентации с использованием интерактивной доски.
Цели урока.
Познавательные цели — обеспечить мотивацию и принятия учащимися цели учебно-познавательной деятельности, провести актуализацию опорных знаний и умений, развивать готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний и их способность к самостоятельному выполнению заданий, требующих применения знаний в знакомой и измененной ситуации, проверить качество и уровня овладения знаниями и способами действий.
Развивающие цели – формировать у учащихся умения анализировать, учить выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, ставить и разрешать проблемы.
Воспитывающие цели — формировать гуманных отношений на уроке, воспитывать у учащихся дисциплинированность, аккуратность, добросовестность, ответственность и честность, любовь к предмету и гордость за свою Родину.
Ход урока.
Организация начала урока. Постановка целей и задач урока
(3 минуты).
Эпиграфом к уроку послужили слова великого татарского поэта Габдуллы Тукая: «Можно стать и слоном, если тело раскармливать в тушу. Можно ангелом стать, возвышая учением душу»


Совместное решение задачи на составление систему уравнений
(3 минуты).
Учащимся предлагается решить задачу, содержание которой связано с историей Казанского императорского университета.
Лобачевский Николай Иванович российский математик, создатель неевкли-довой геометрии, с 1827 года шесть раз избирался ректором Казанского университета. В каком году был создан Казанский императорский университет и в каком году родился Николай Иванович Лобачевский, если в год избрания ректором он был старше своего «детища» на 12 лет, а на двоих им в этом году исполнилось 58 лет?


Решение задачи напоминает детям о славной истории родного города, которой можно и нужно гордиться.
Всесторонняя проверка знаний. Устная работа в виде соревнования
(7 минут.).
1 этап. Найди правильное решение.
Перед учащимся появляются пять систем уравнений
1.
2.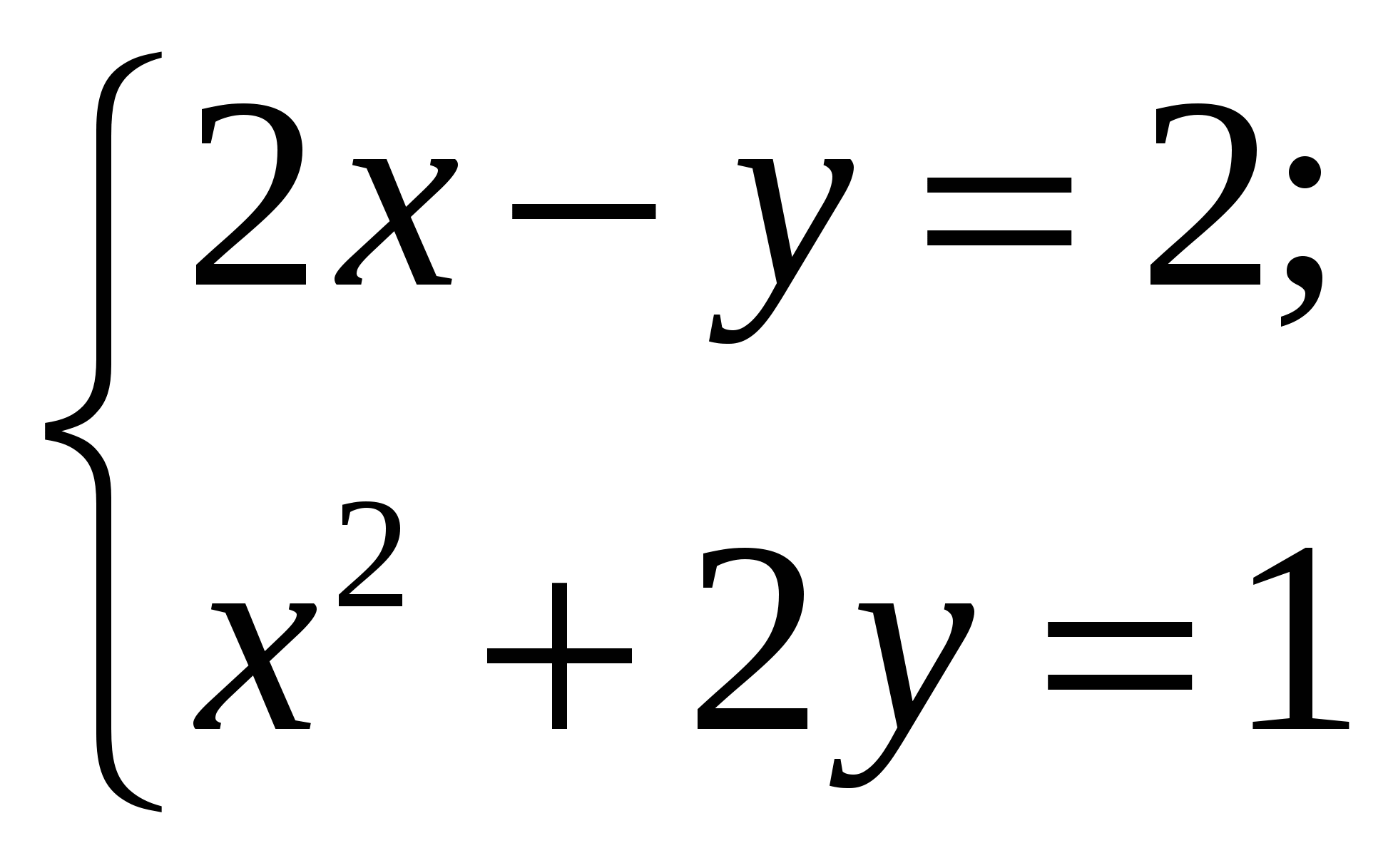
3.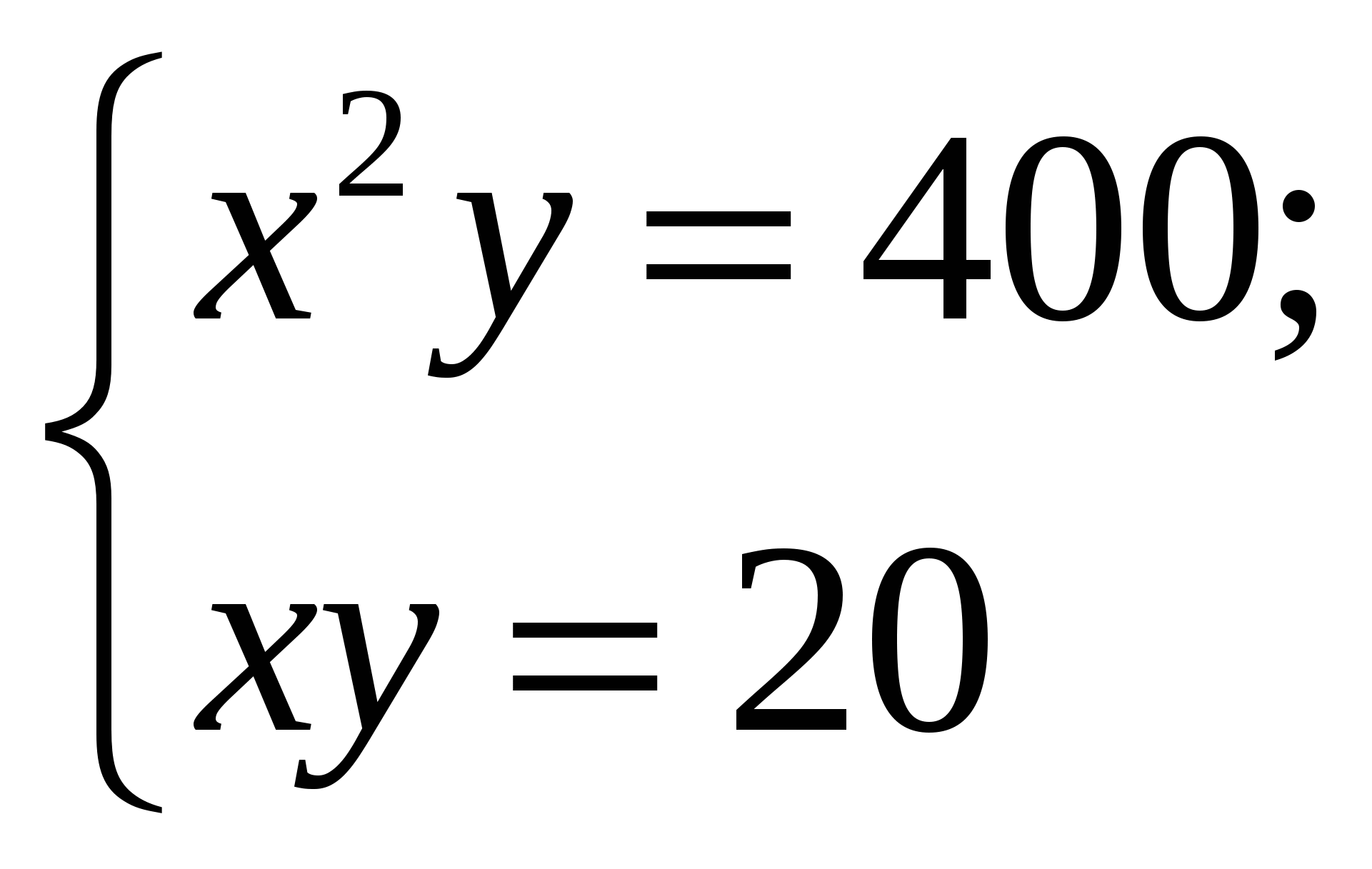
4.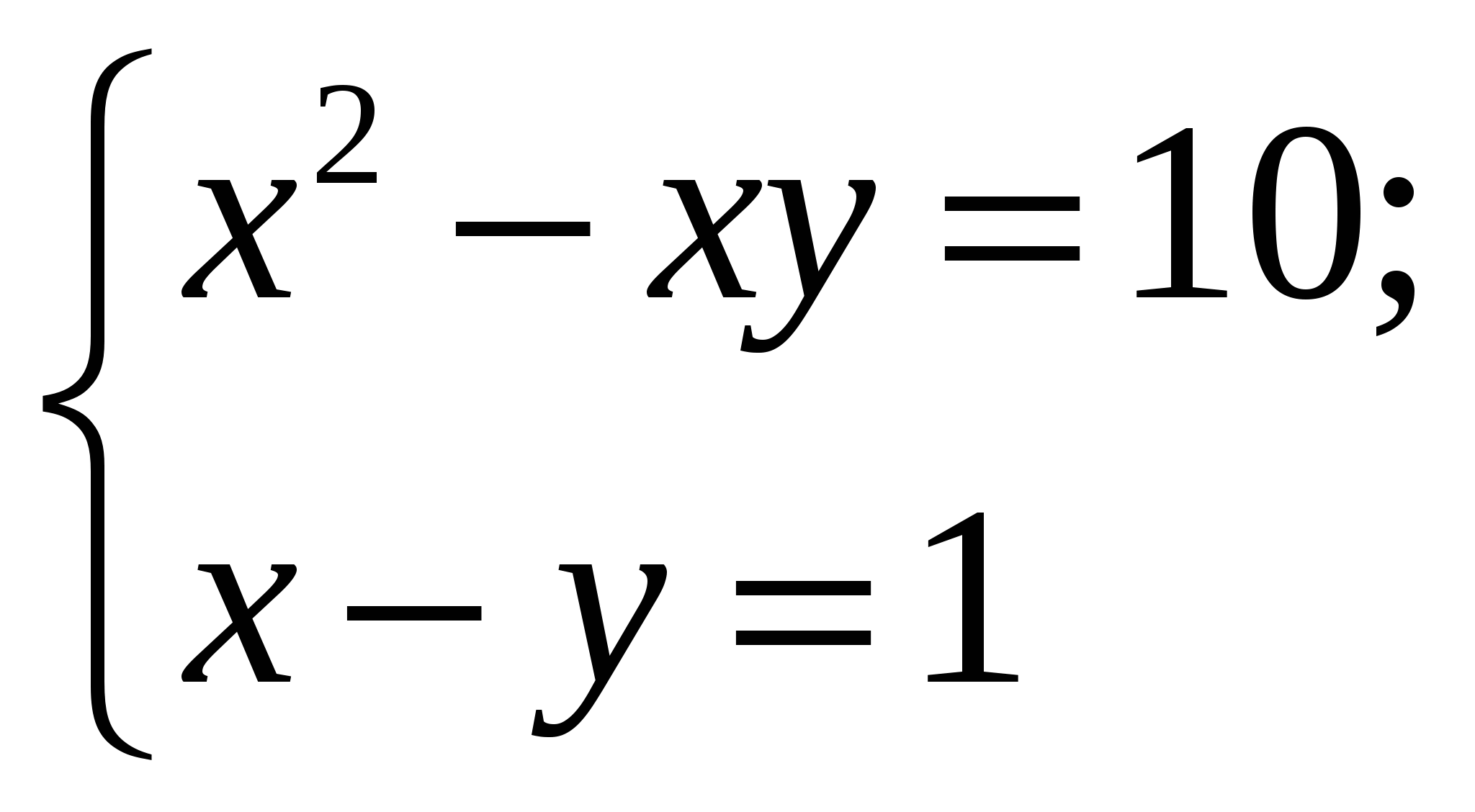
5.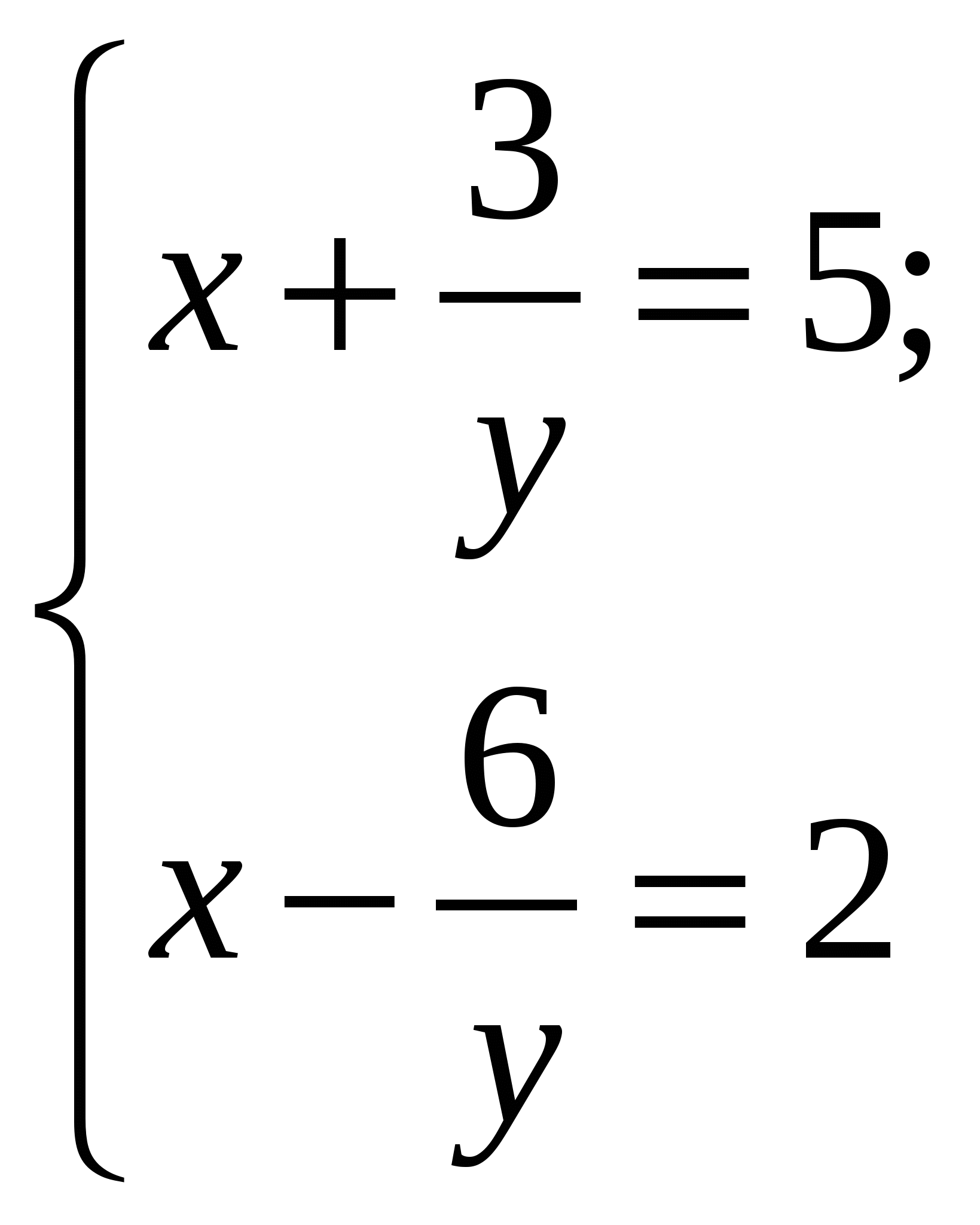
Необходимо найти решения этих систем среди восьми предложенных и получить фамилию великого немецкого математика, внесшего фундаментальный вклад в развитие математики, астрономии и геодезии, именем которого назван метод решения систем линейных уравнений путем исключения неизвестных.
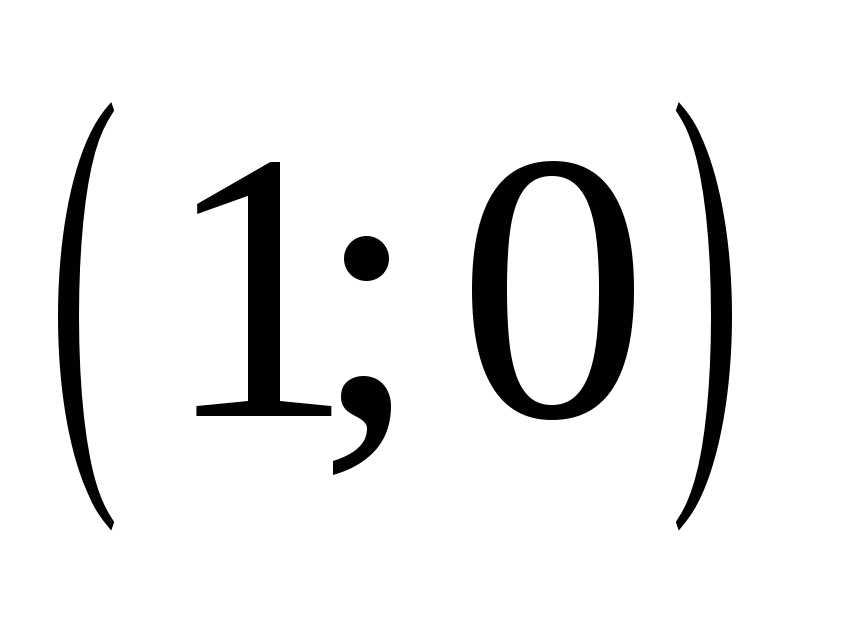
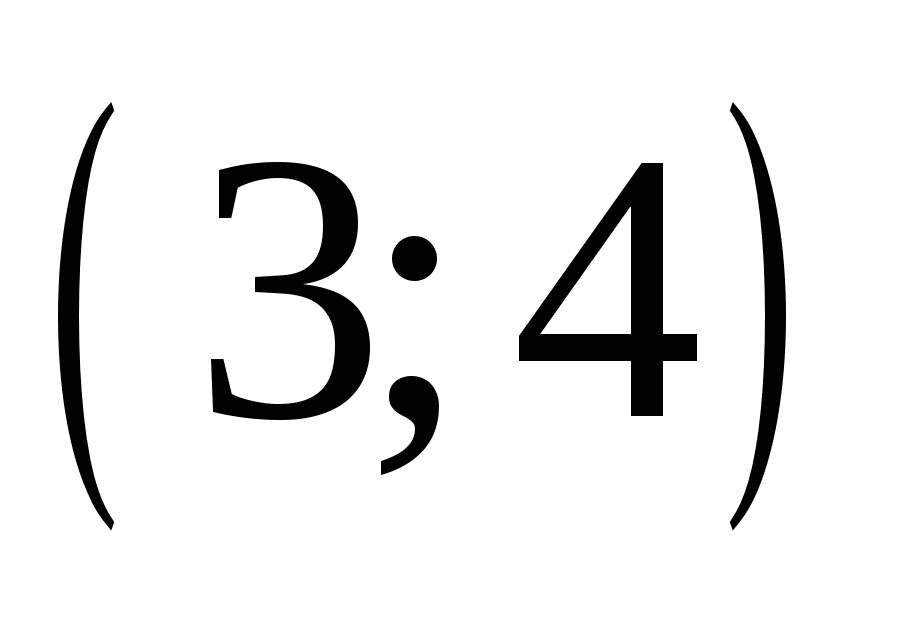
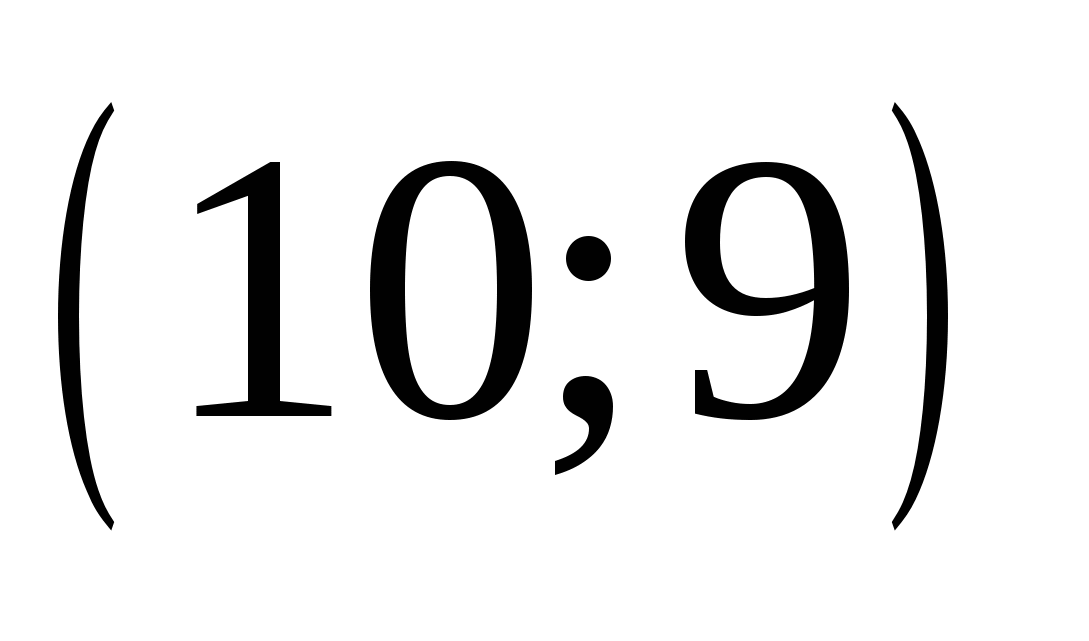
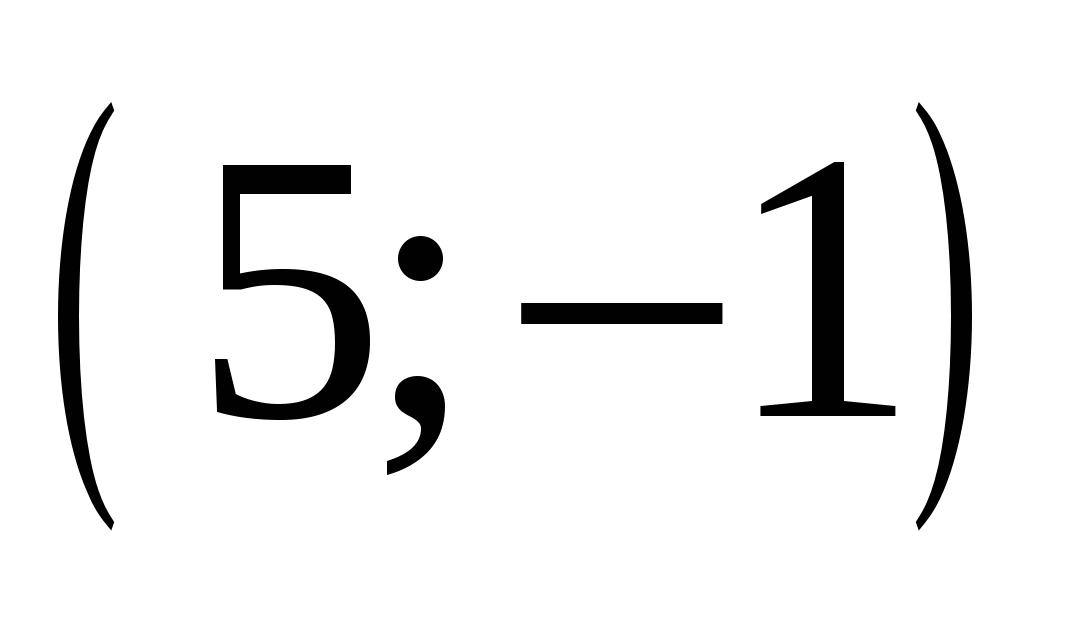
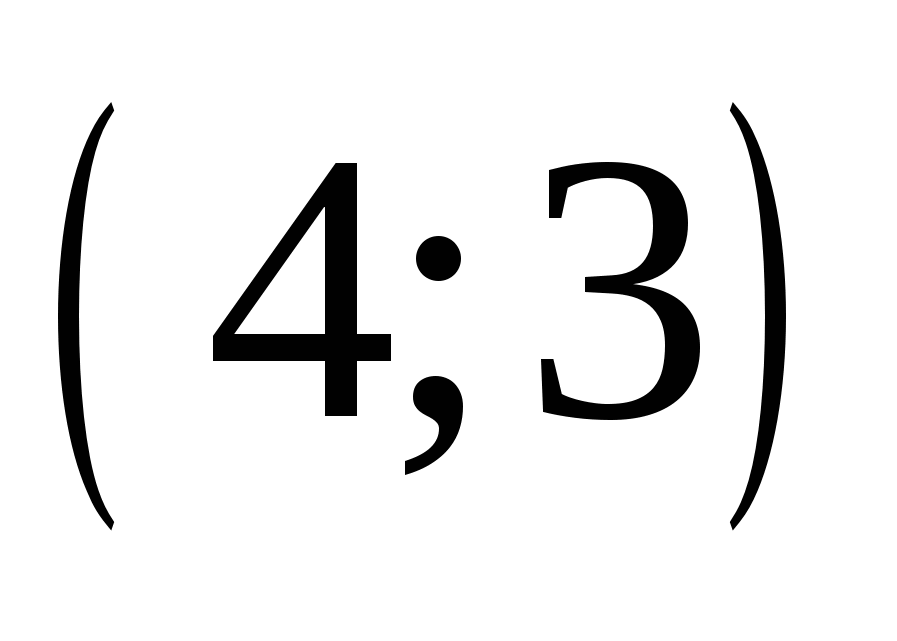
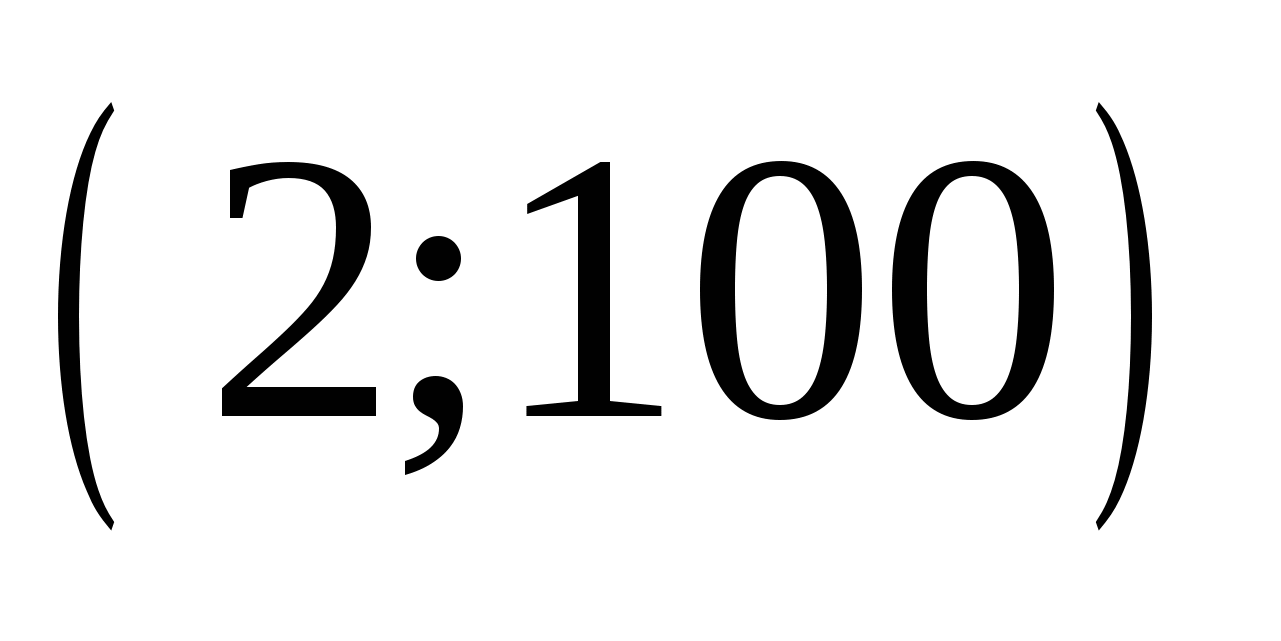

А
Н
С
Г
С
О
У
Впишите полученное слово
1.
2.
3.
4.
5.

Гаусс (Gauss) Карл Фридрих (30.04.1777, Брауншвейг, – 23.02.1855, Геттинген),
немецкий математик, внесший фундаментальный вклад также в астрономию и геодезию, почетный член Петербургской Академии Наук.
В ходе работы над этим заданием дети учатся сопоставлять системы уравнений с возможными вариантами решения, сравнивать и анализировать
2 этап 
Учащимся предлагаются шесть систем уравнений
1. 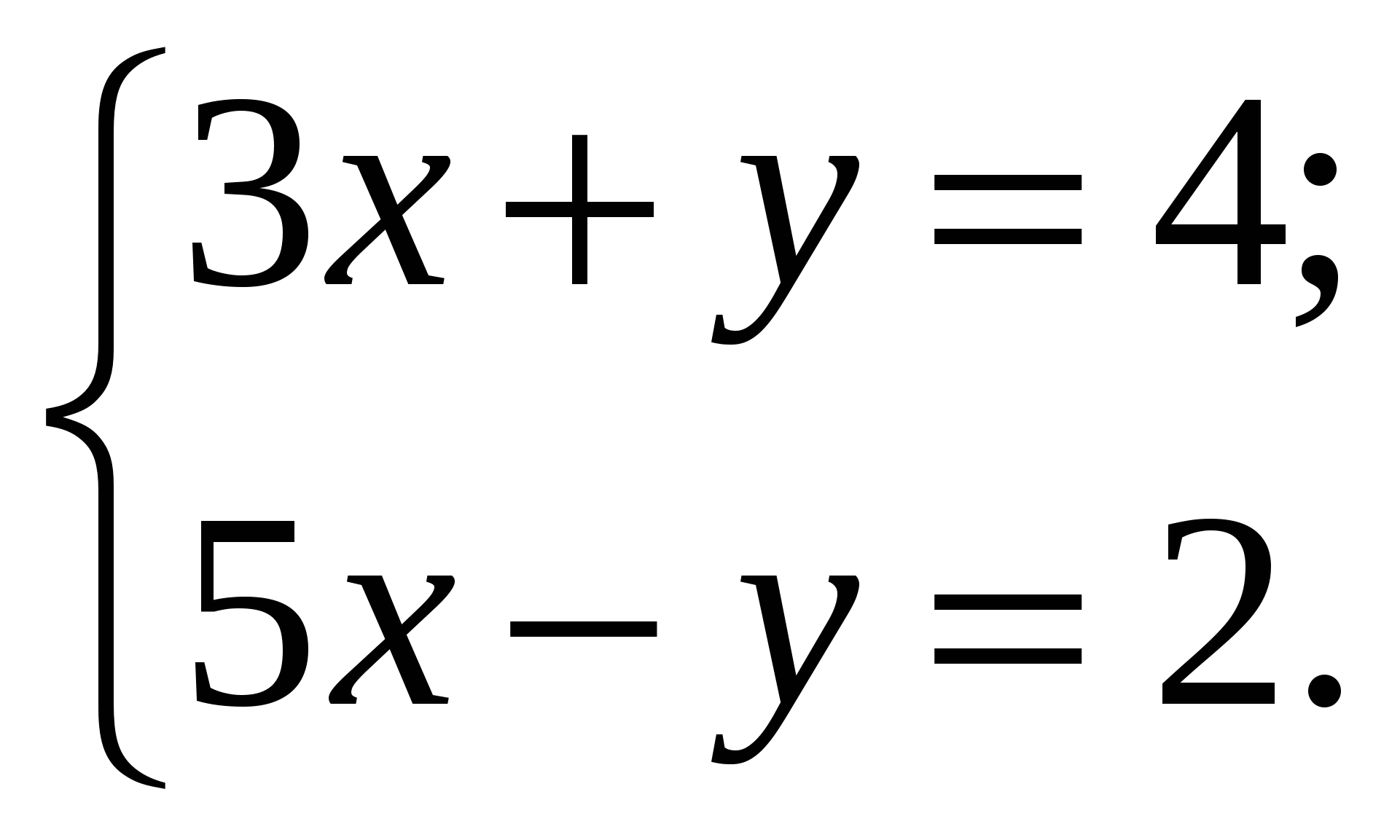
2. 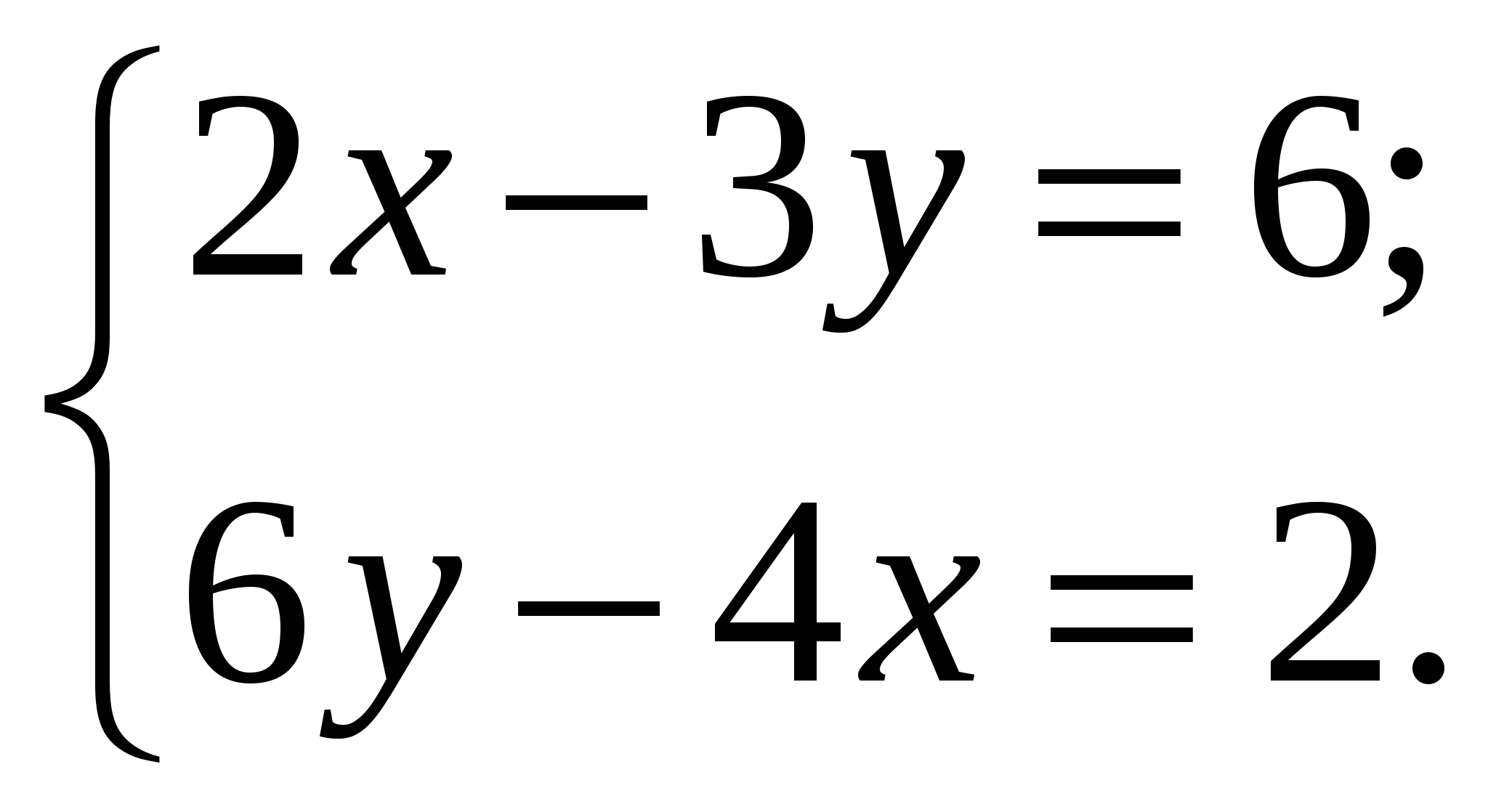
3. 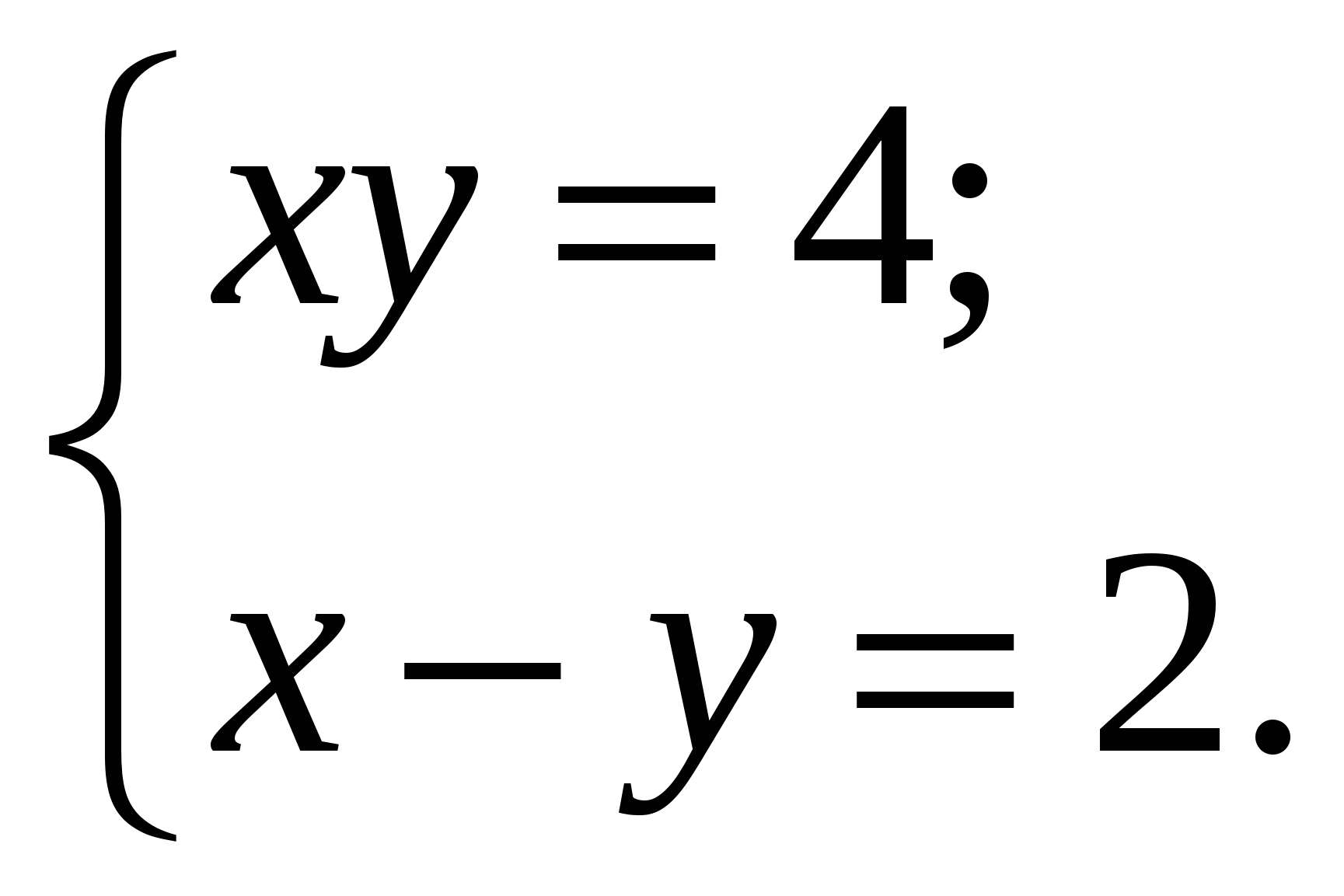
4. 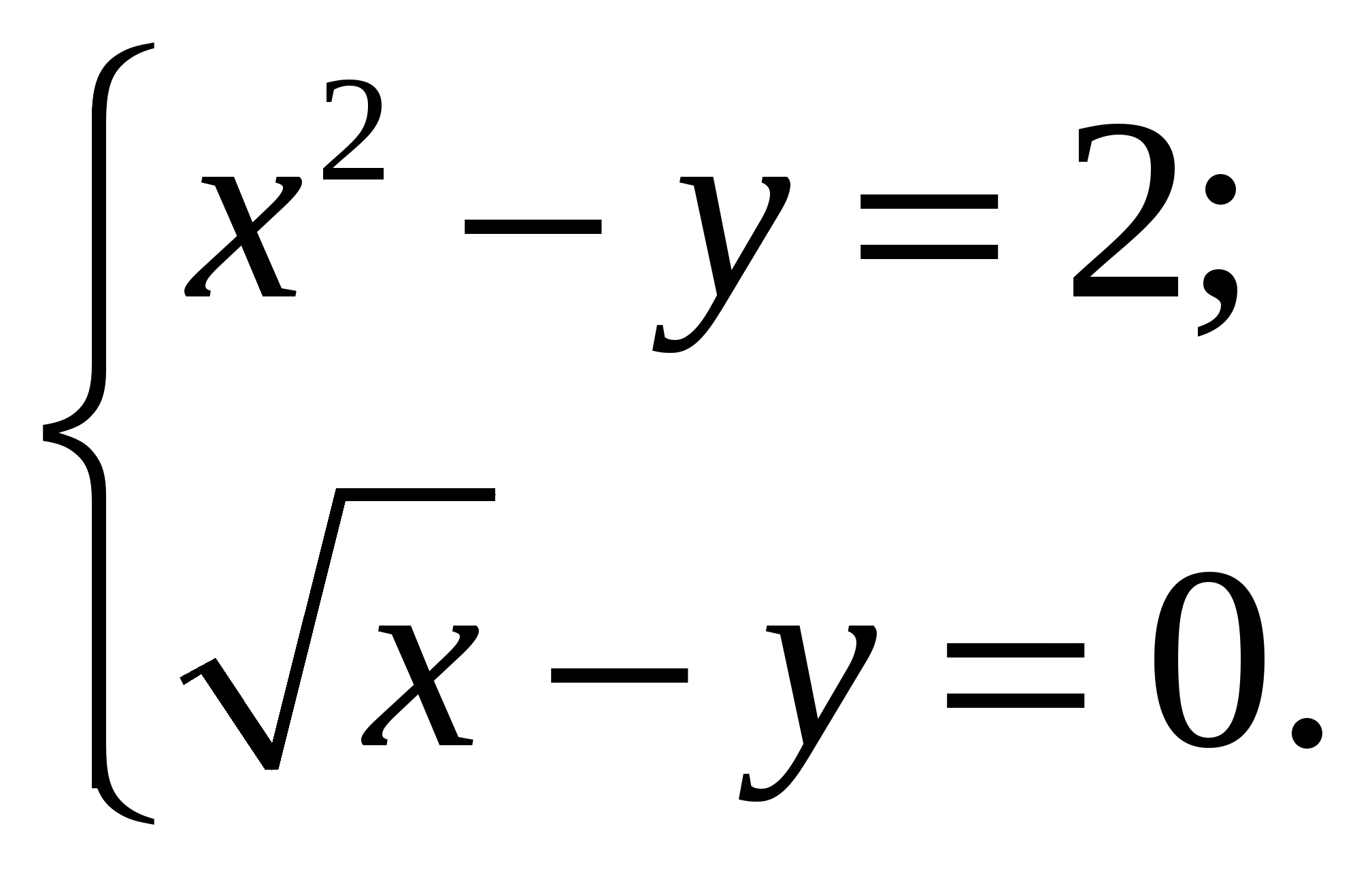
5. 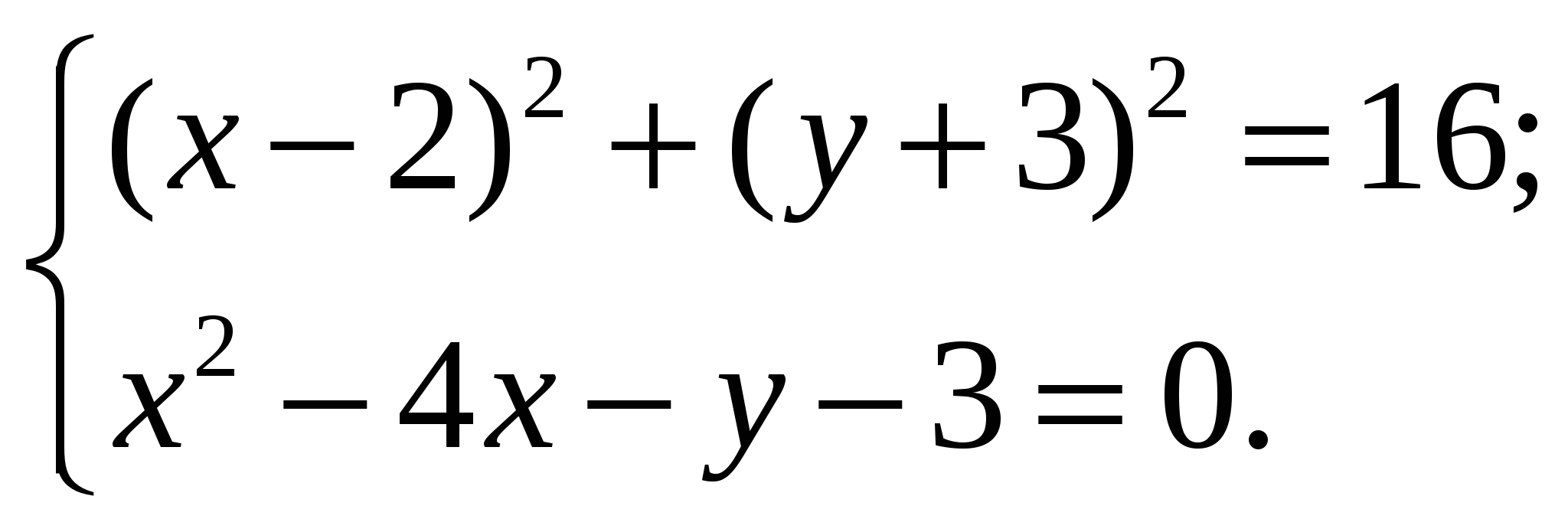
6. 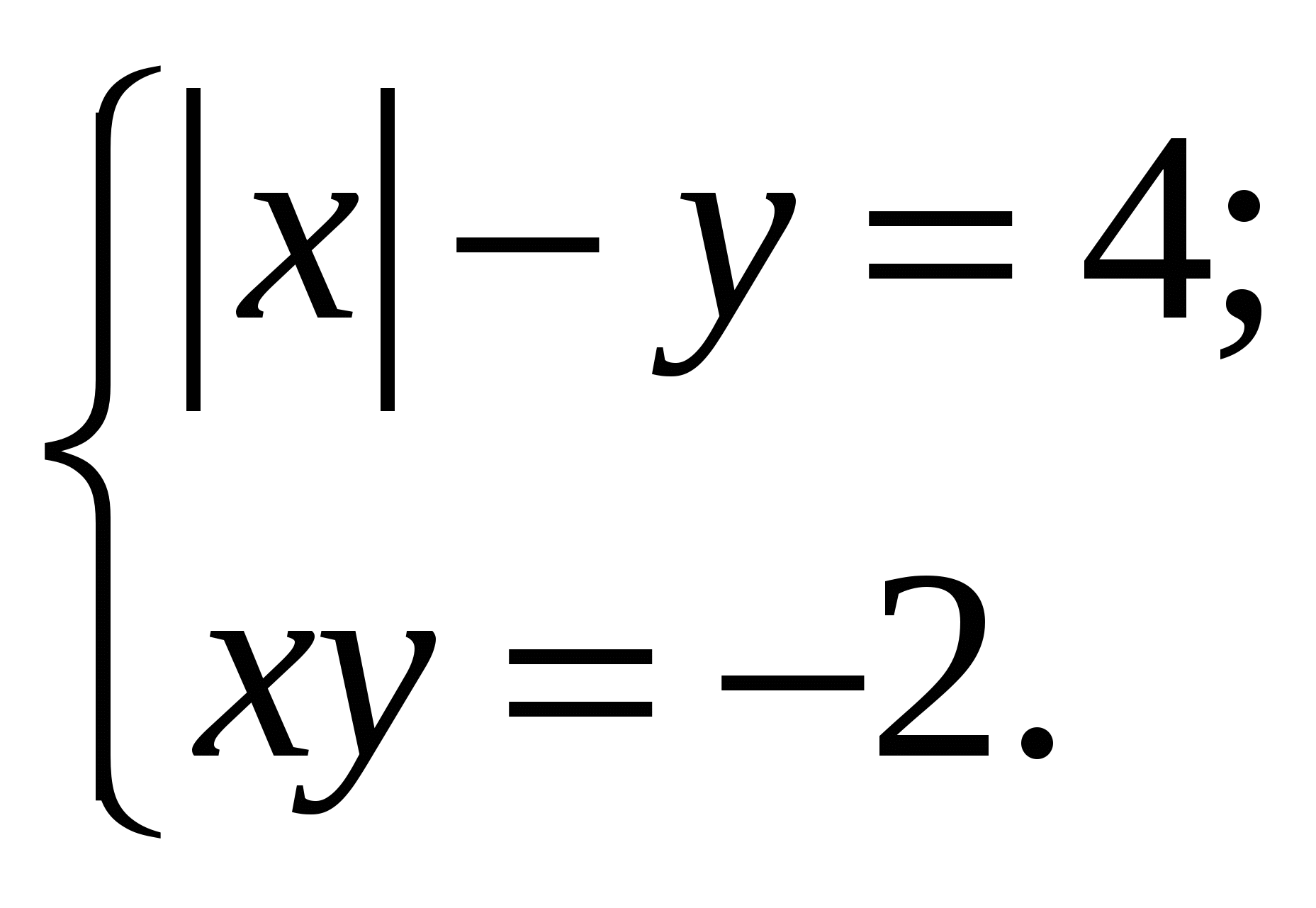
Необходимо сопоставить эти системы с их графическим решением и получить фамилию швейцарского математика, установившего и опубликовавшего в 1750 году правило решения систем линейных уравнений с буквенными коэффициентами.
Поставьте в соответствие указанным системам их графические решения и разгадайте загаданное слово.
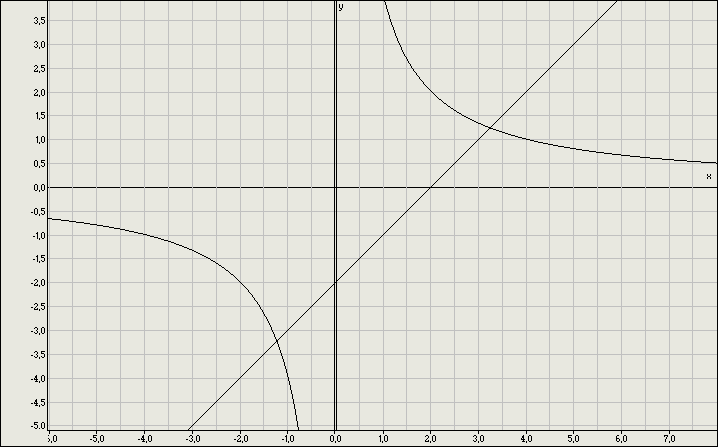
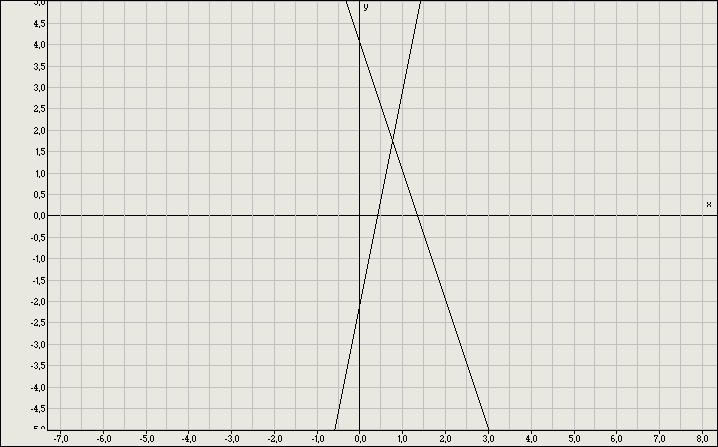
А К
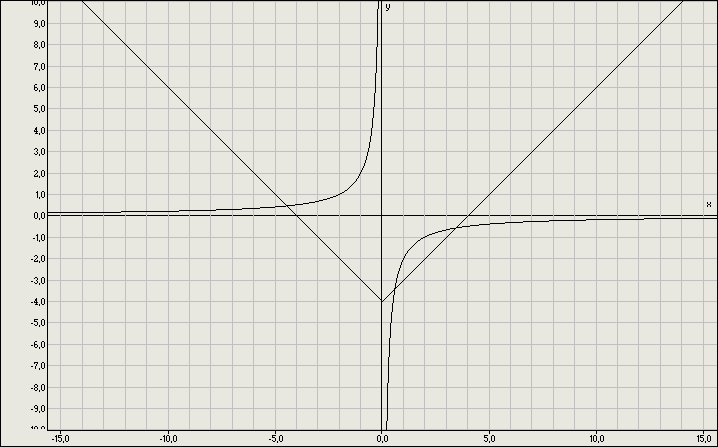
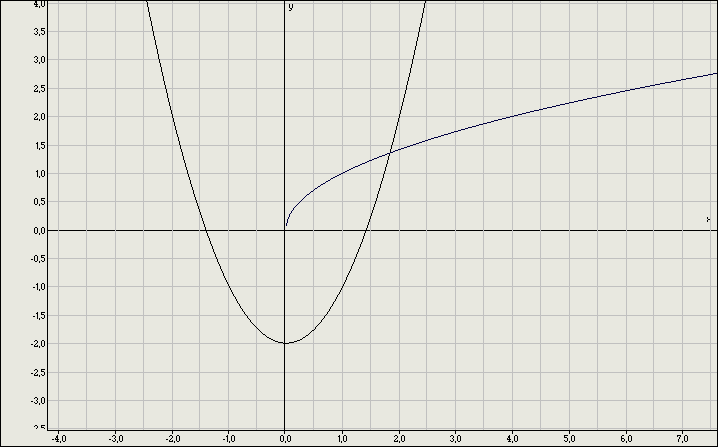
Р М

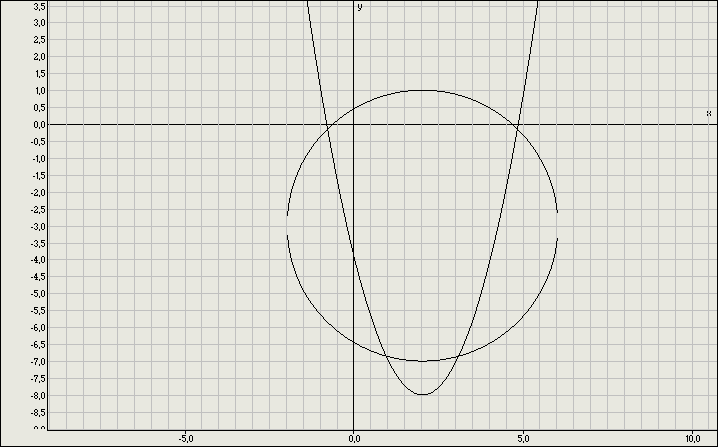
Р Е
Впишите отгаданные буквы:
1
2
3
4
5
6
1. 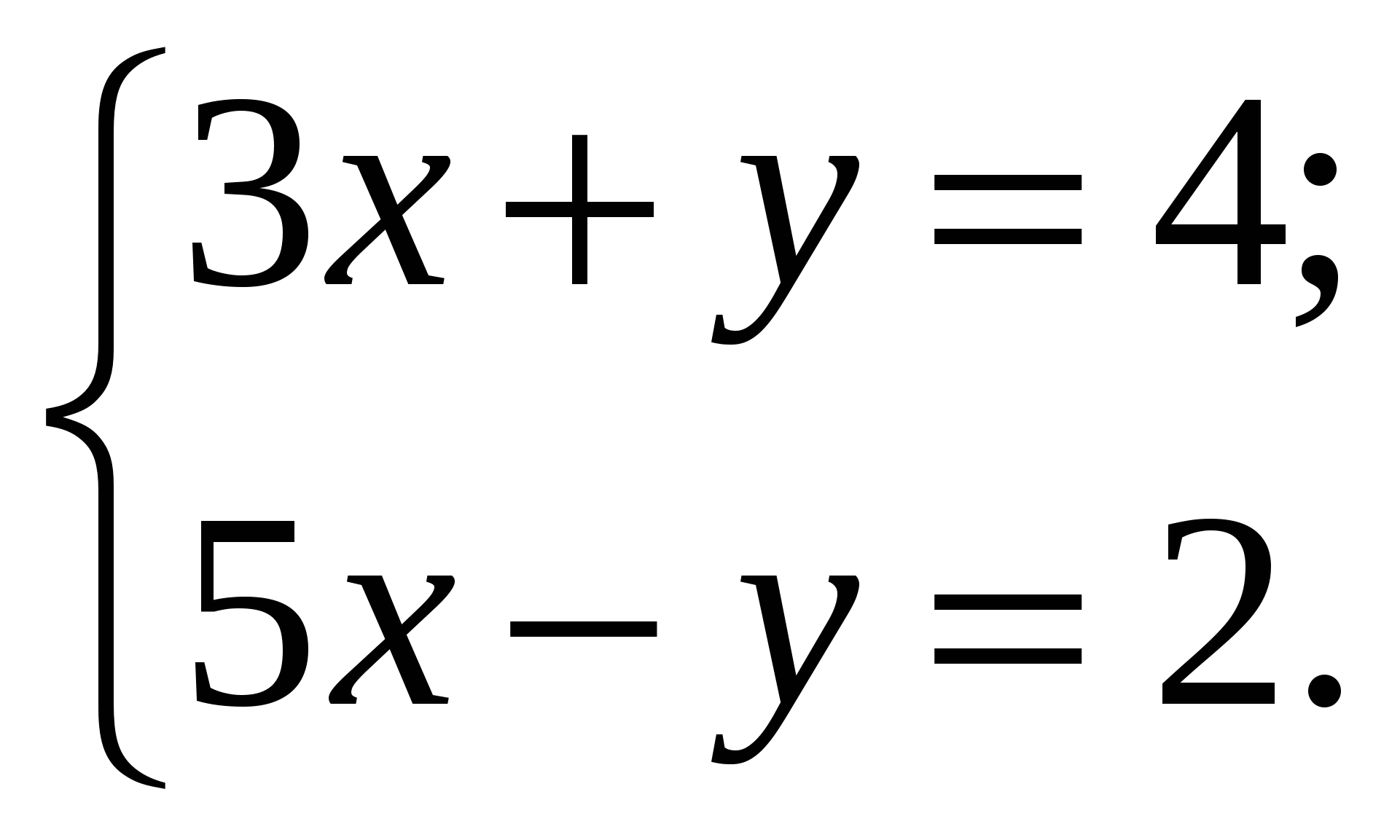
2. 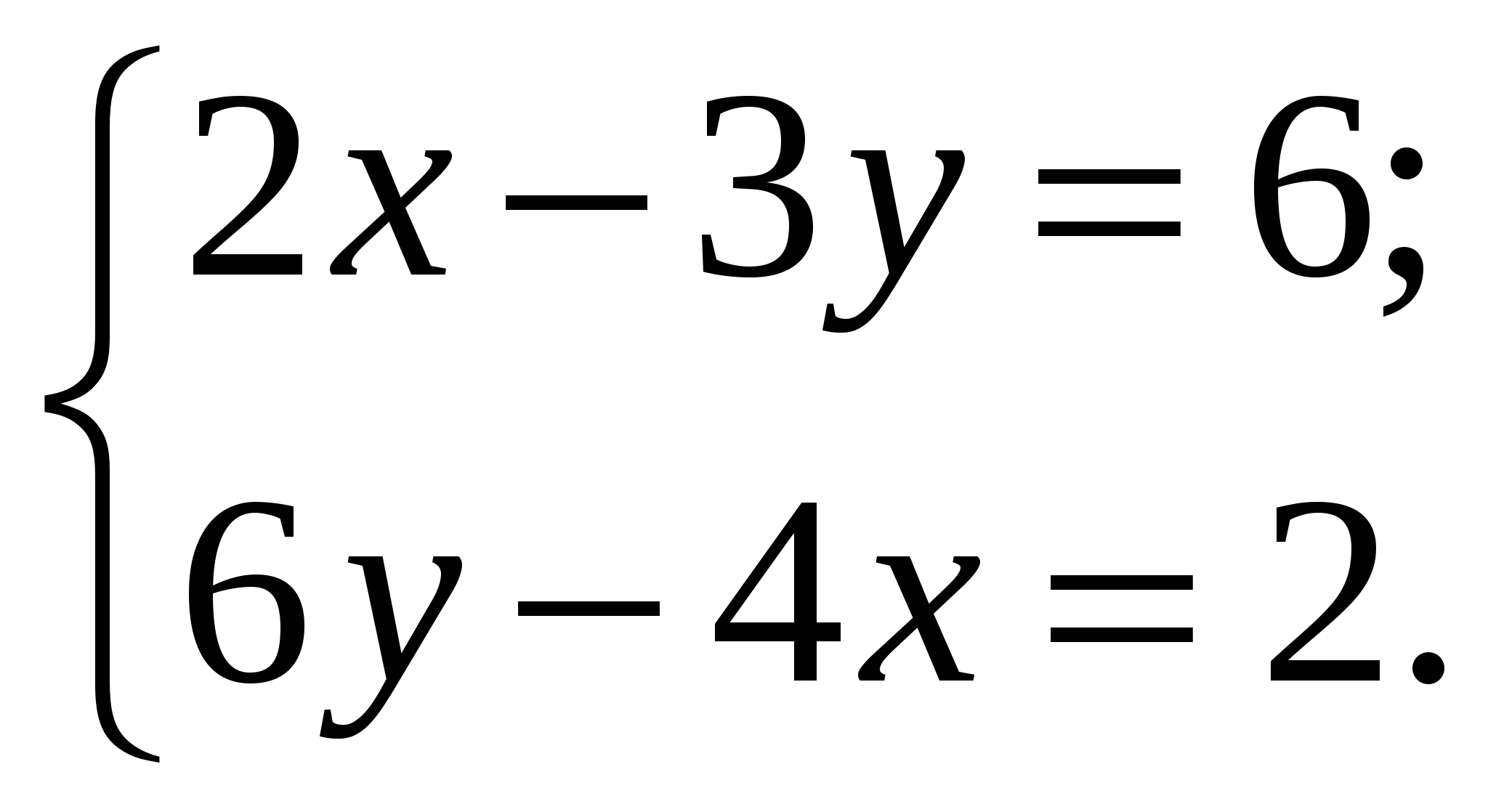
3. 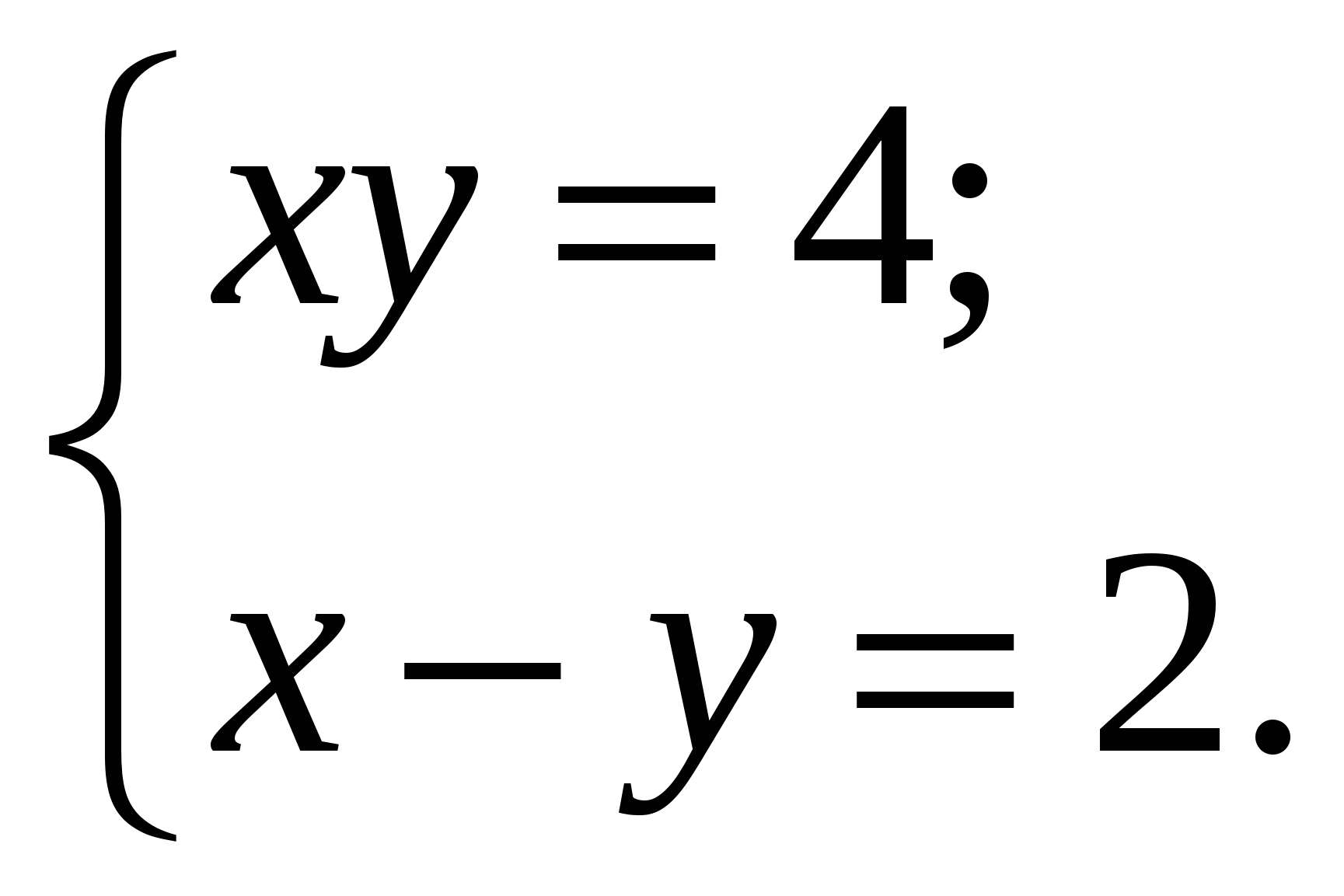
4. 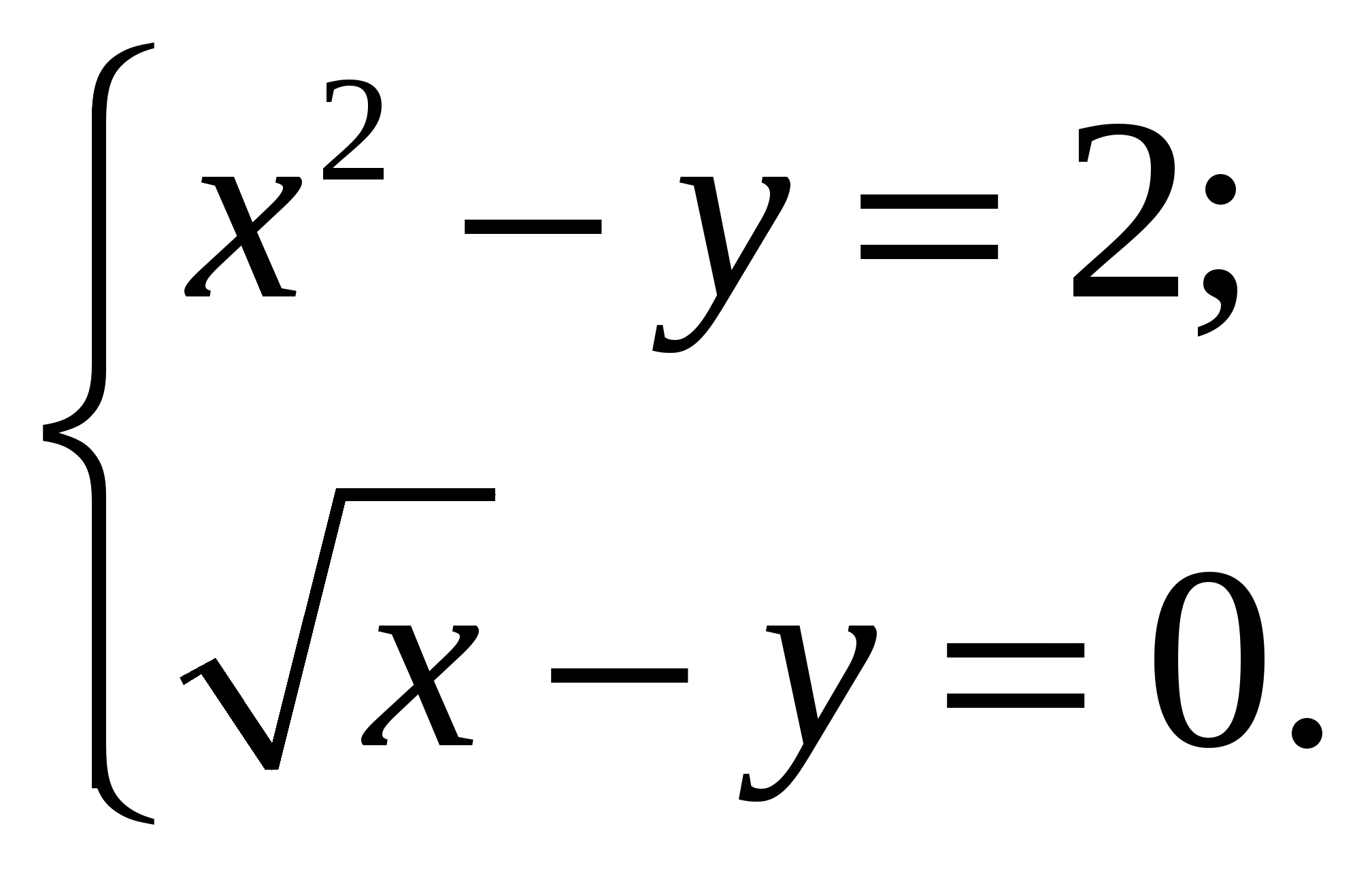
5. 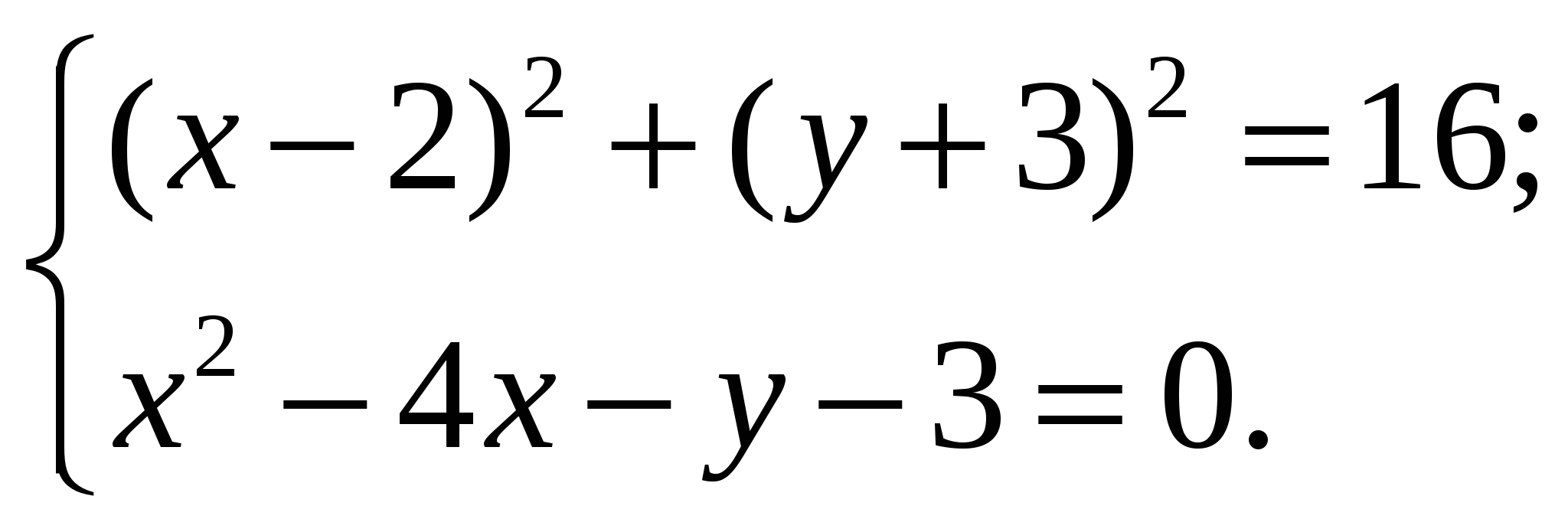
6. 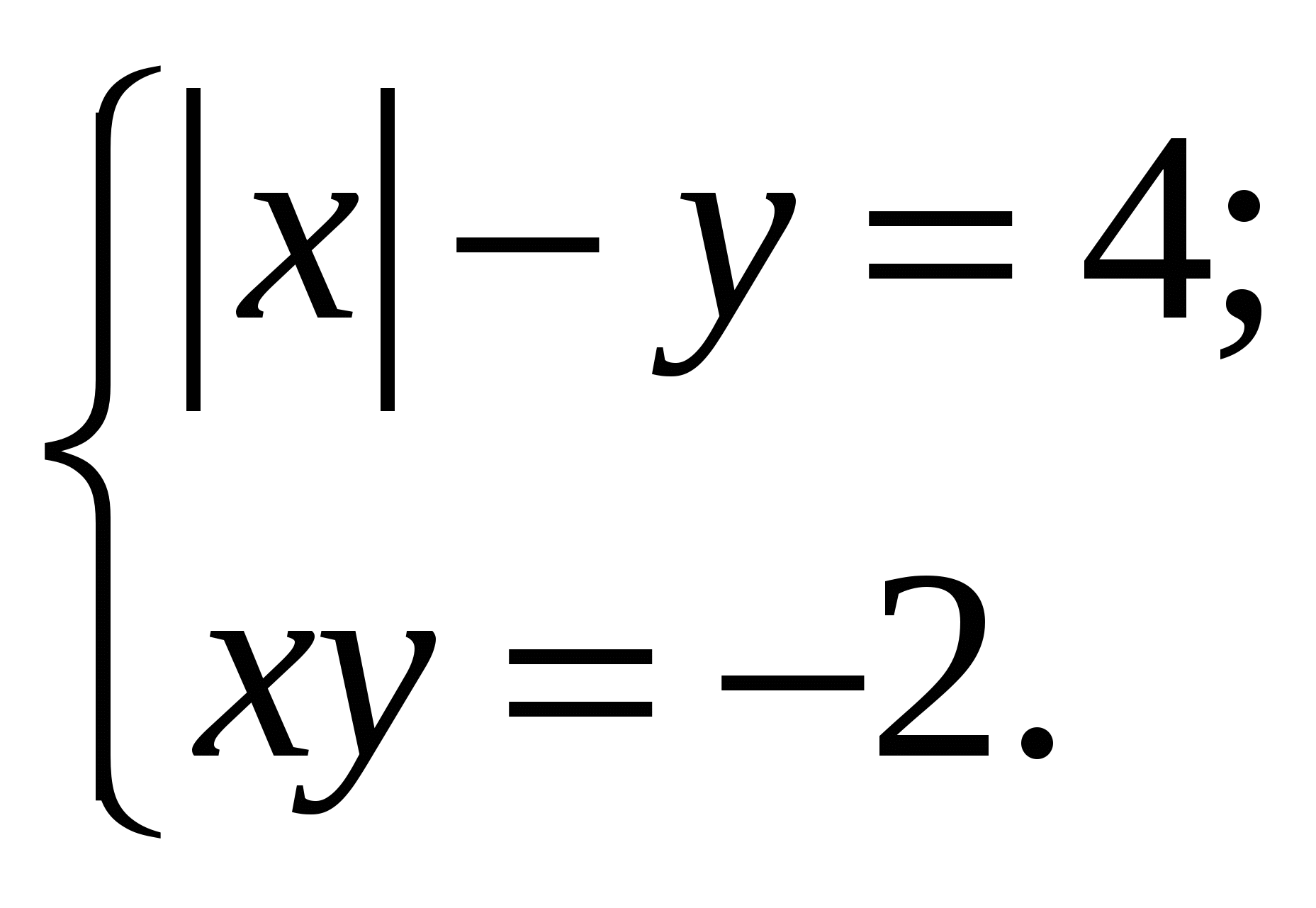

Крамер Габриель (31.7.1704-1752)- швейцарский математик. Родился в Женеве. Был учеником и другом Иоганна Бернулли. Издатель трудов Иоганна и Якова Бернулли, переписки Г. Лейбница с И. Бернулли.Учился и работал в Женеве. Основные труды по высшей алгебре и аналитической геометрии. Установил и опубликовал (1750г.) правила решения систем  линейных уравнений с
линейных уравнений с  неиз-вестными с буквенными коэффициентами (правило Крамера), заложил основы теории определителей.
неиз-вестными с буквенными коэффициентами (правило Крамера), заложил основы теории определителей.
По ходу выполнения данного задания ученики учились «видеть» системы уравнений, понимать их графический смысл.
Примечание. Победители каждого этапа были отмечены оценками.
4. Совместное решение и обсуждение систем уравнений
(15 минут)
Пример 1. Решить систему уравнений 

До этого урока дети уже решали системы однородных уравнений, а на данном этапе они столкнулись с проблемой сведения приведенной системы неоднородных уравнений к системе с однородными уравнениями. В ходе оживленного обсуждения выход был найден.

Пример 2. Выяснить при каких положительных значениях параметра  система уравнений
система уравнений 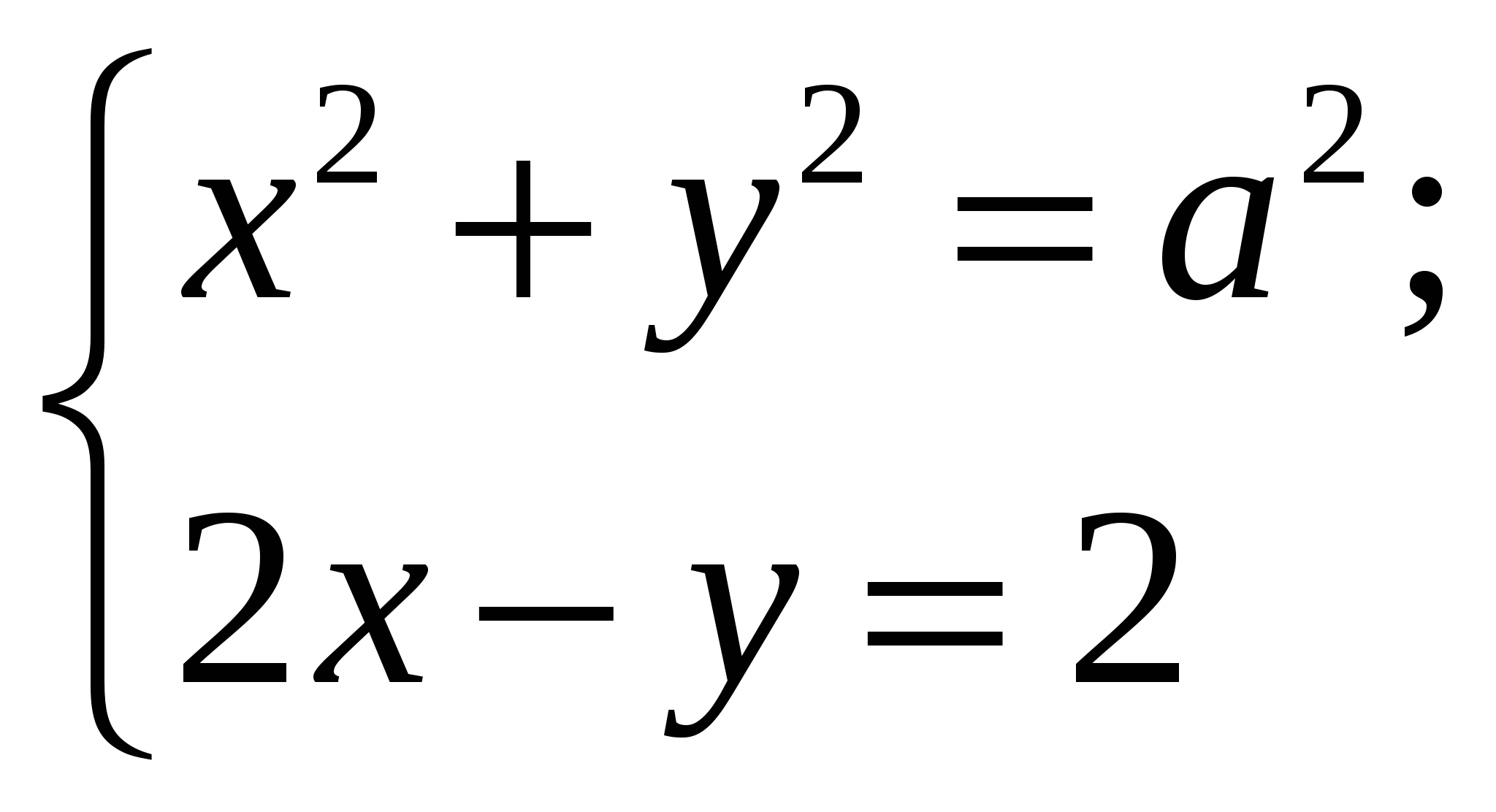 имеет два решения.
имеет два решения.
Задания с параметрами традиционно вызывают много вопросов у школьников, требуют исследовательского подхода к решению, развивают умение мыслить и проводить анализ выполненных действий.

Следует отметить, что, в общем и целом, дети успешно справились с поставленными перед ними задачами, следовательно, выбор уровня трудности заданий оказался оправданным.
5. Самостоятельная работа в форме тестов-6 вариантов
(15 минут).
Каждый ученик на заключительной стадии урока получил карточку с заданиями в тестовой форме, содержание которой перекликается с вопросами, рассмотренными на уроке. Такой вид самостоятельной работы актуален на сегодняшний день, так как позволяет нарабатывать навыки работ с тестами, загодя готовит школьников к ЕГЭ.
В1
Задание
Ответы
1.
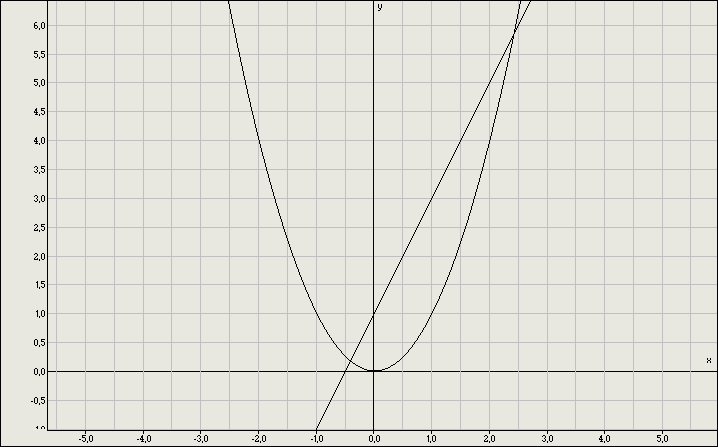
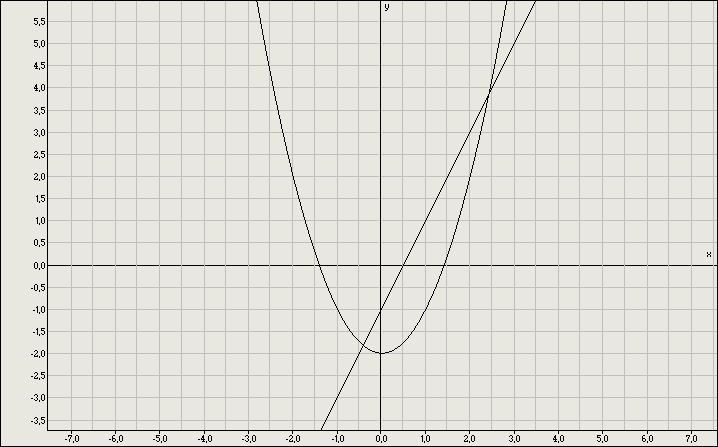
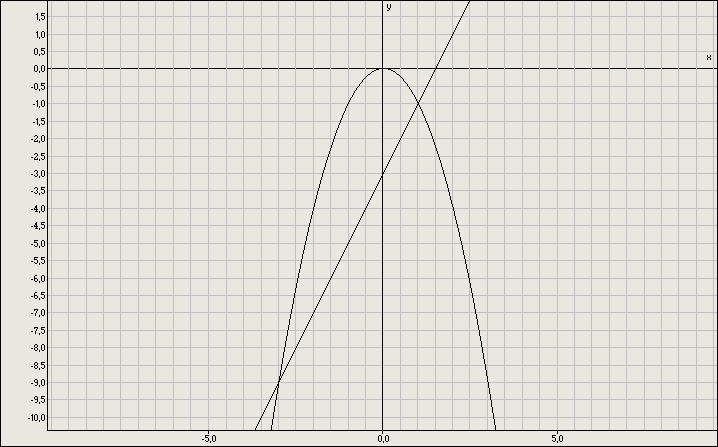
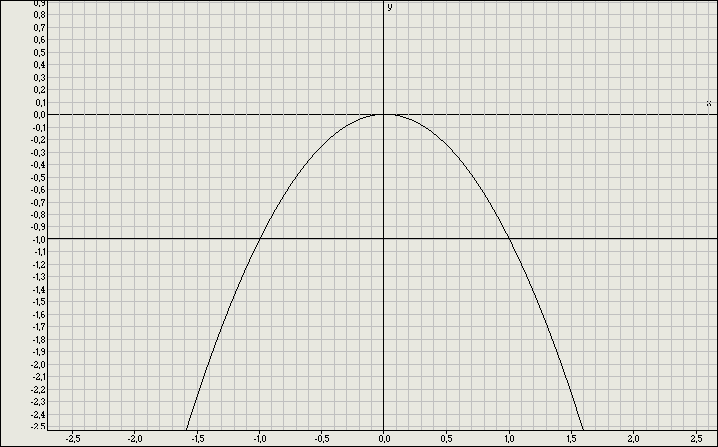
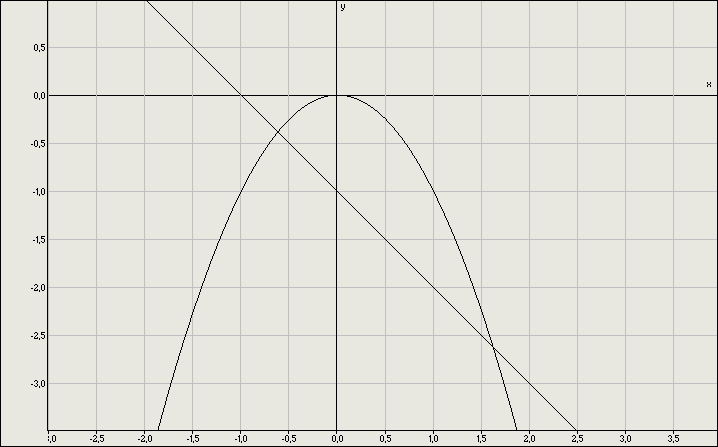
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 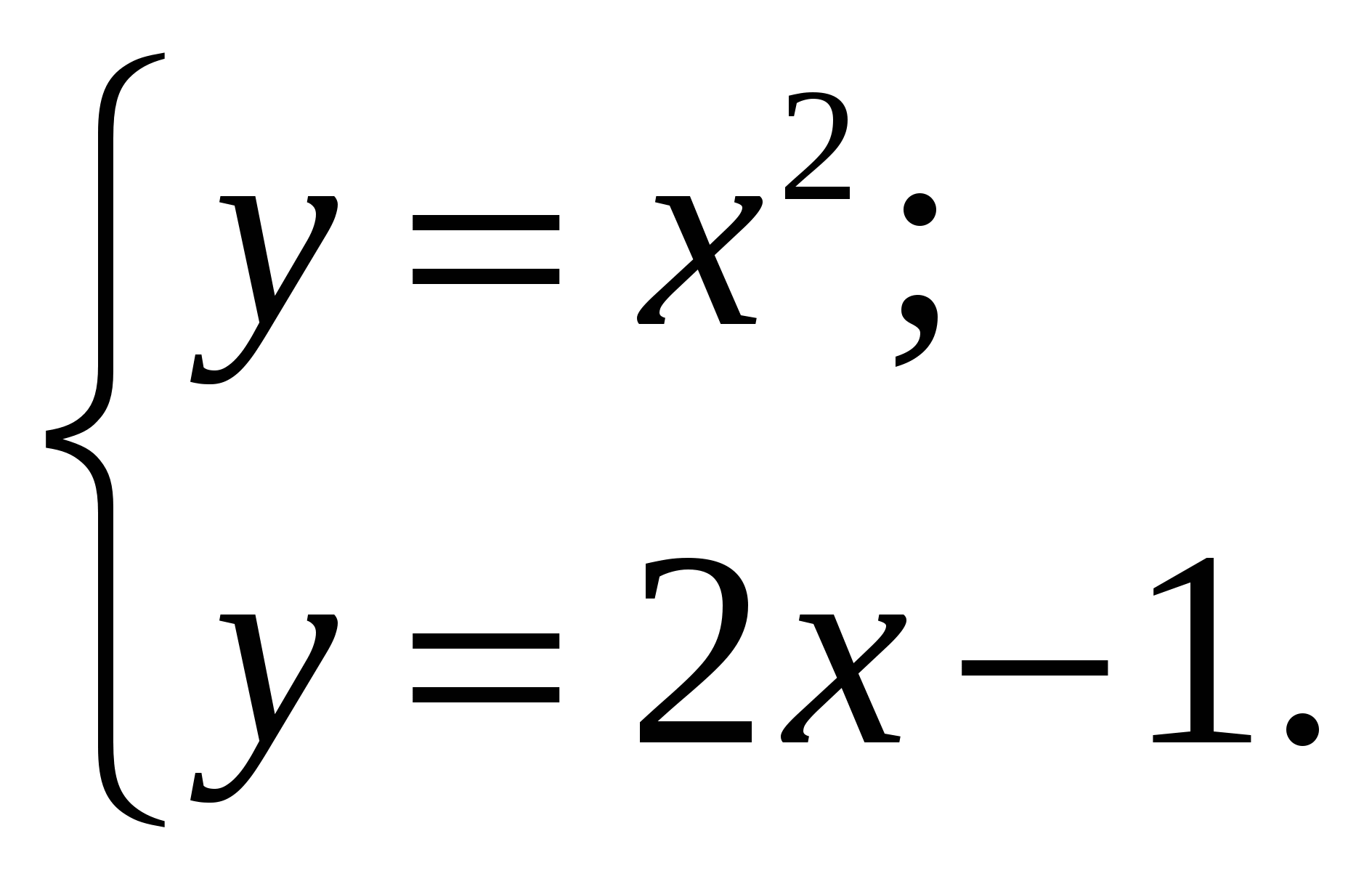
1) 1
2) 2
3) 3
4) 4
1. 
2.
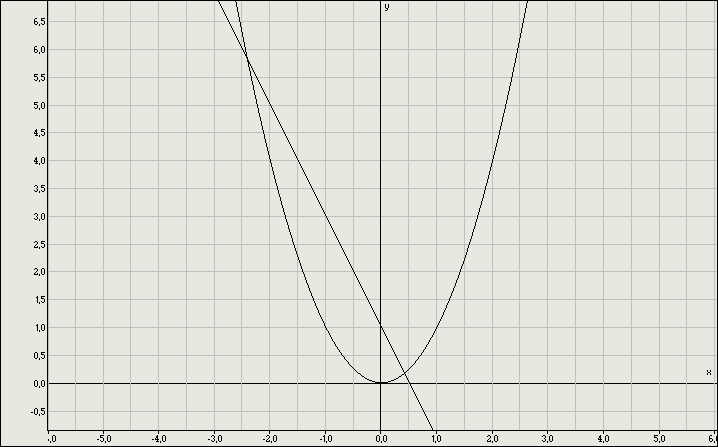
3. 
4. 
2.
Найдите пару чисел, являющуюся решением системы уравнений 
1) 1
2) 2
3) 3
4) 4
1. 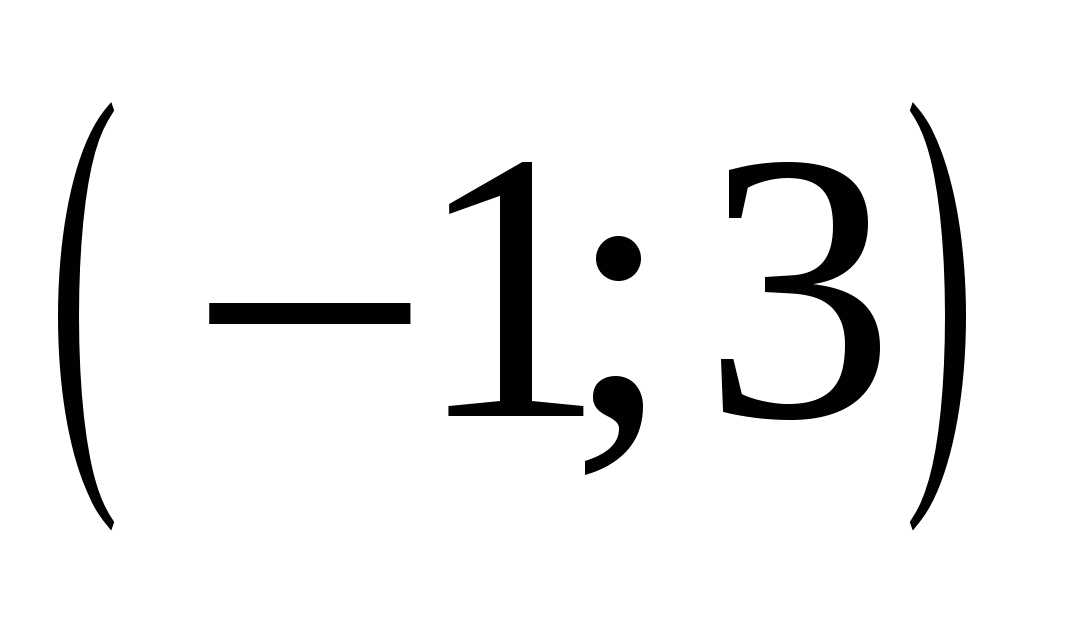
2. 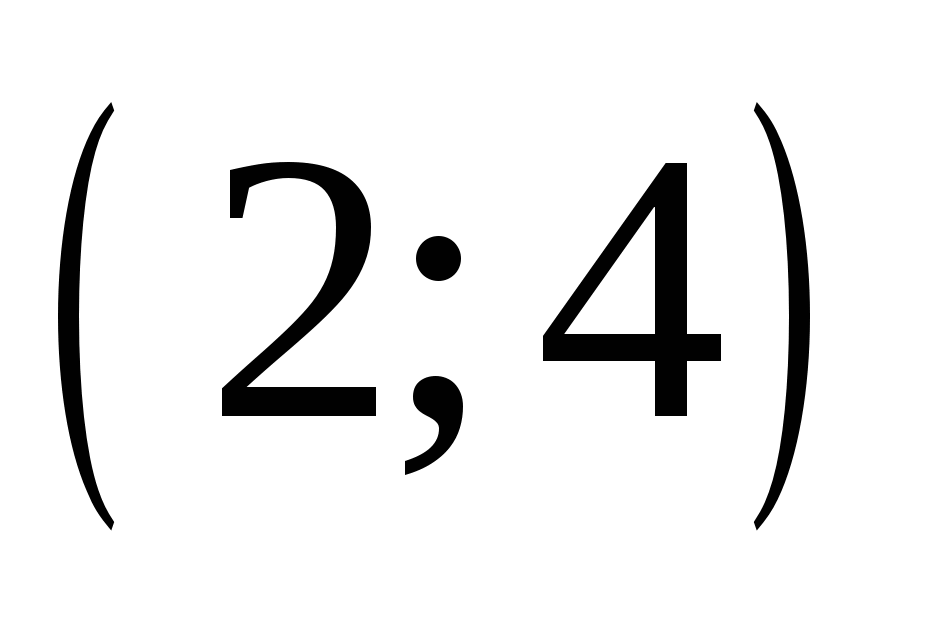
3. 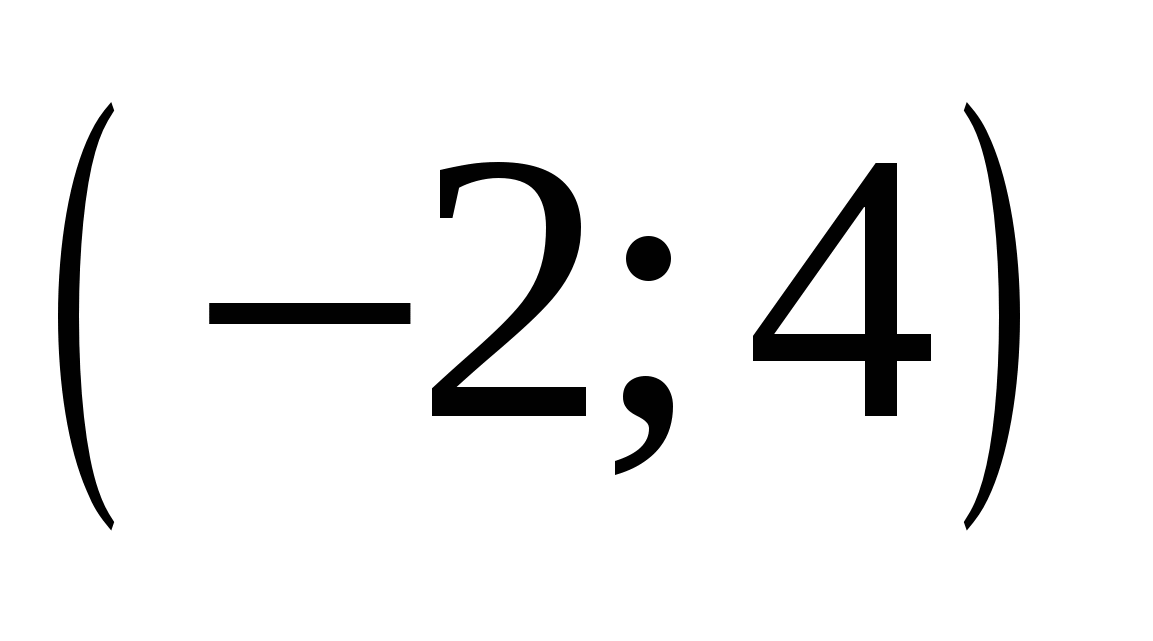
4. 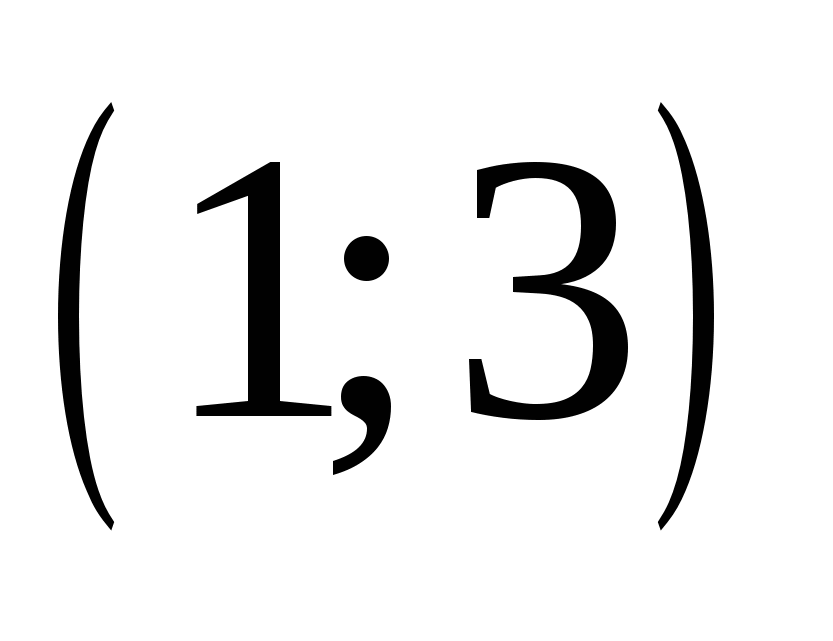
3.
Если 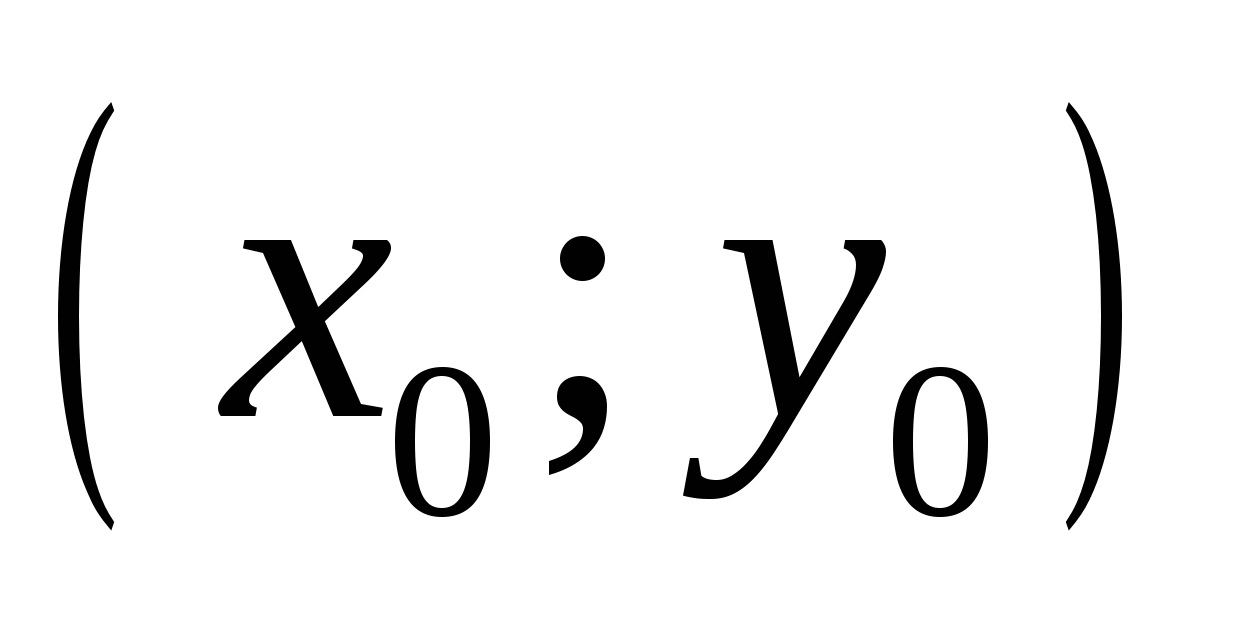 -решение системы уравнений
-решение системы уравнений 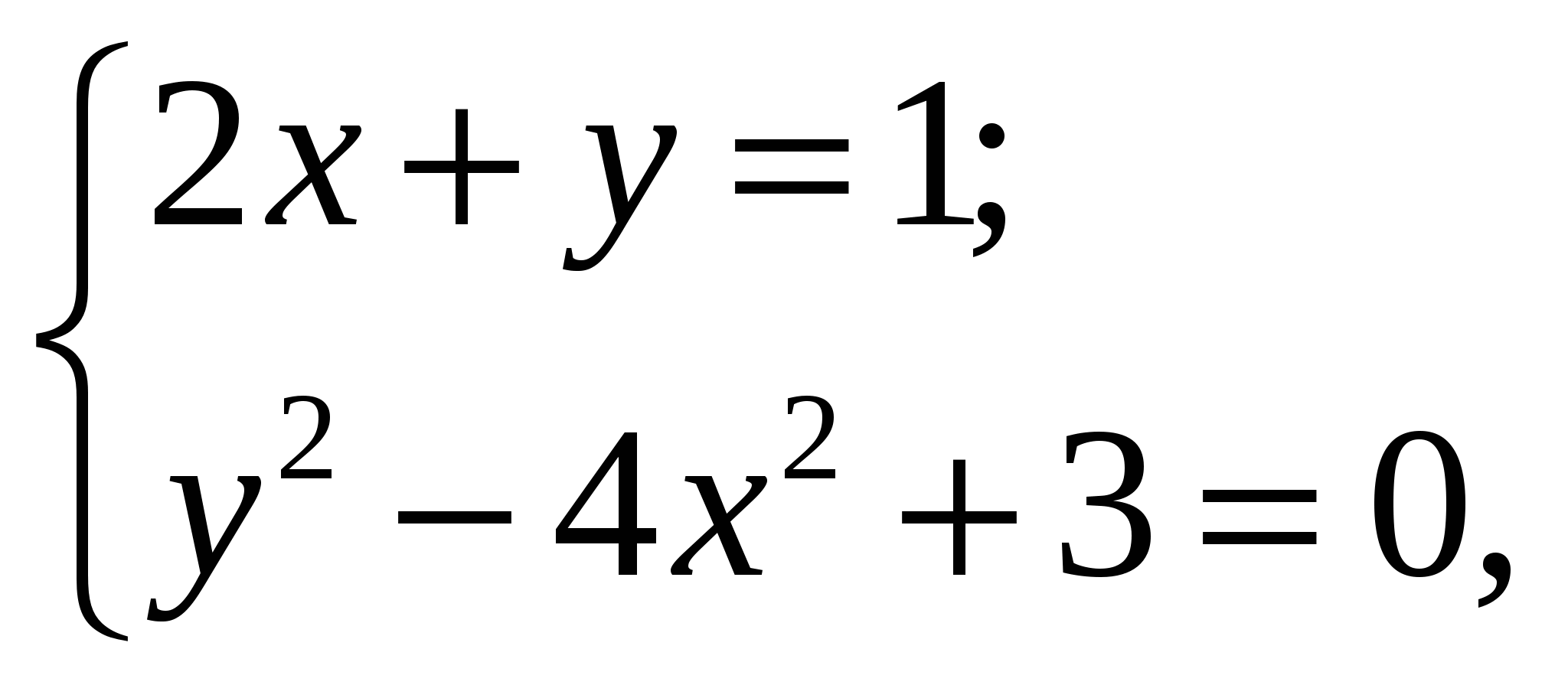
то значение  равно
равно
1) -1
2) 0
3) 1
4) 4
4.
Если 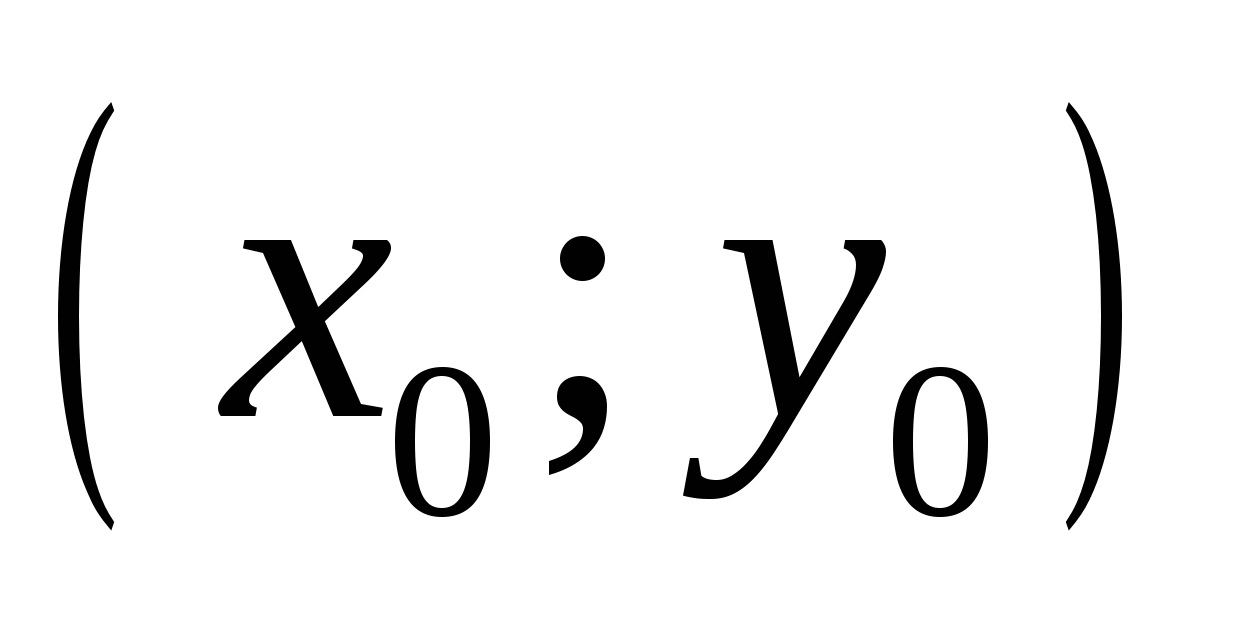 -решение системы уравнений
-решение системы уравнений 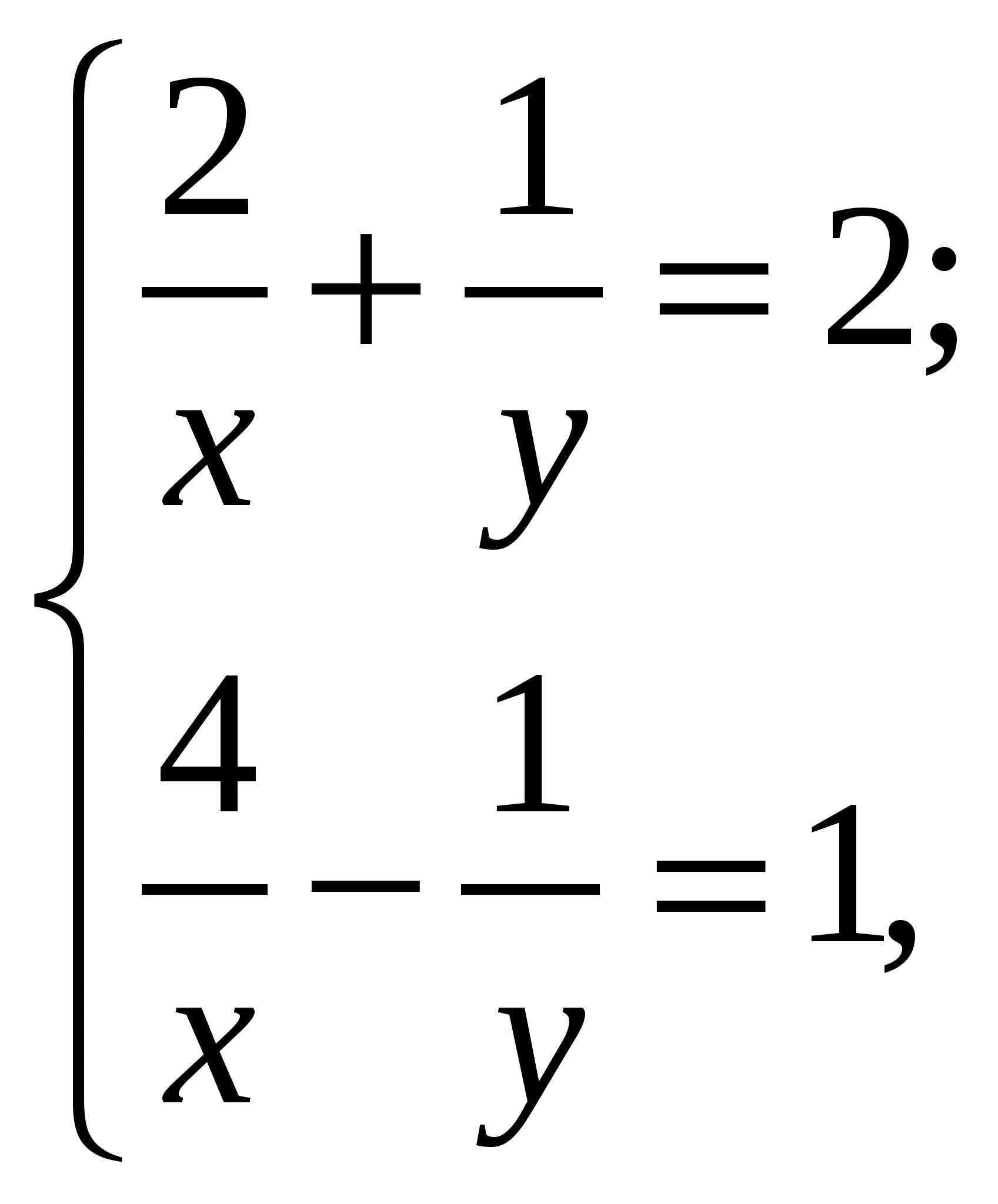 то значение
то значение 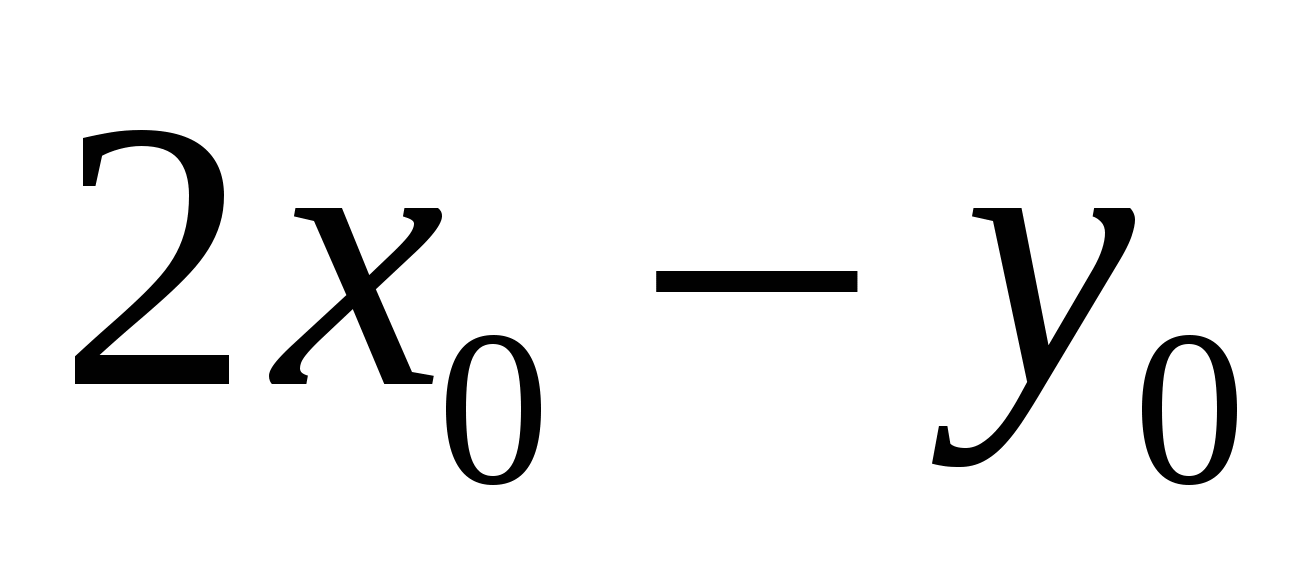 равно
равно
1) 3
2) 2
3) 4
4) 1
5.
При каком наименьшем целом значении параметра  система уравнений
система уравнений 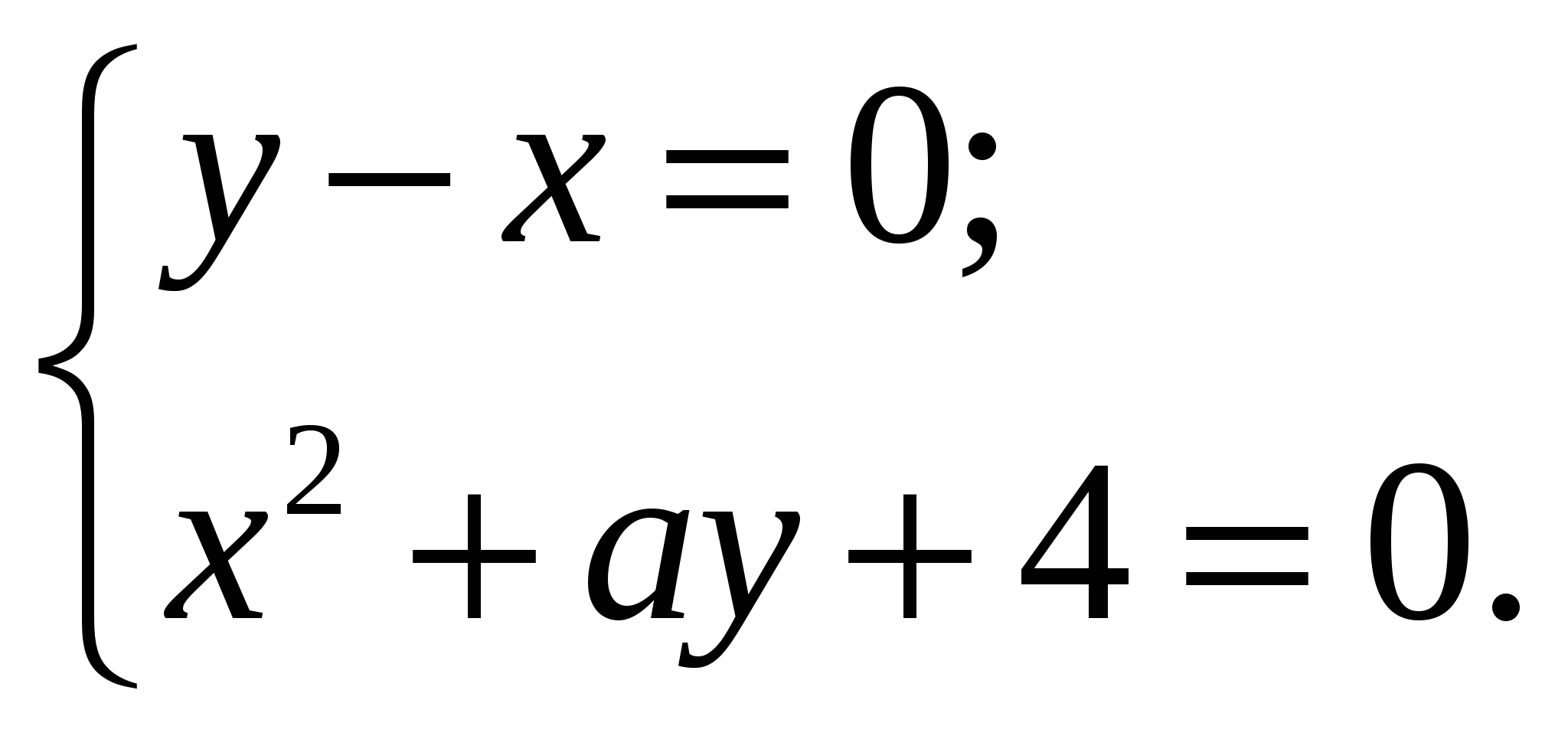 не имеет решений?
не имеет решений?
1) -4
2) -3
3) 0
4) 2
В2
Задание
Ответы
1.
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 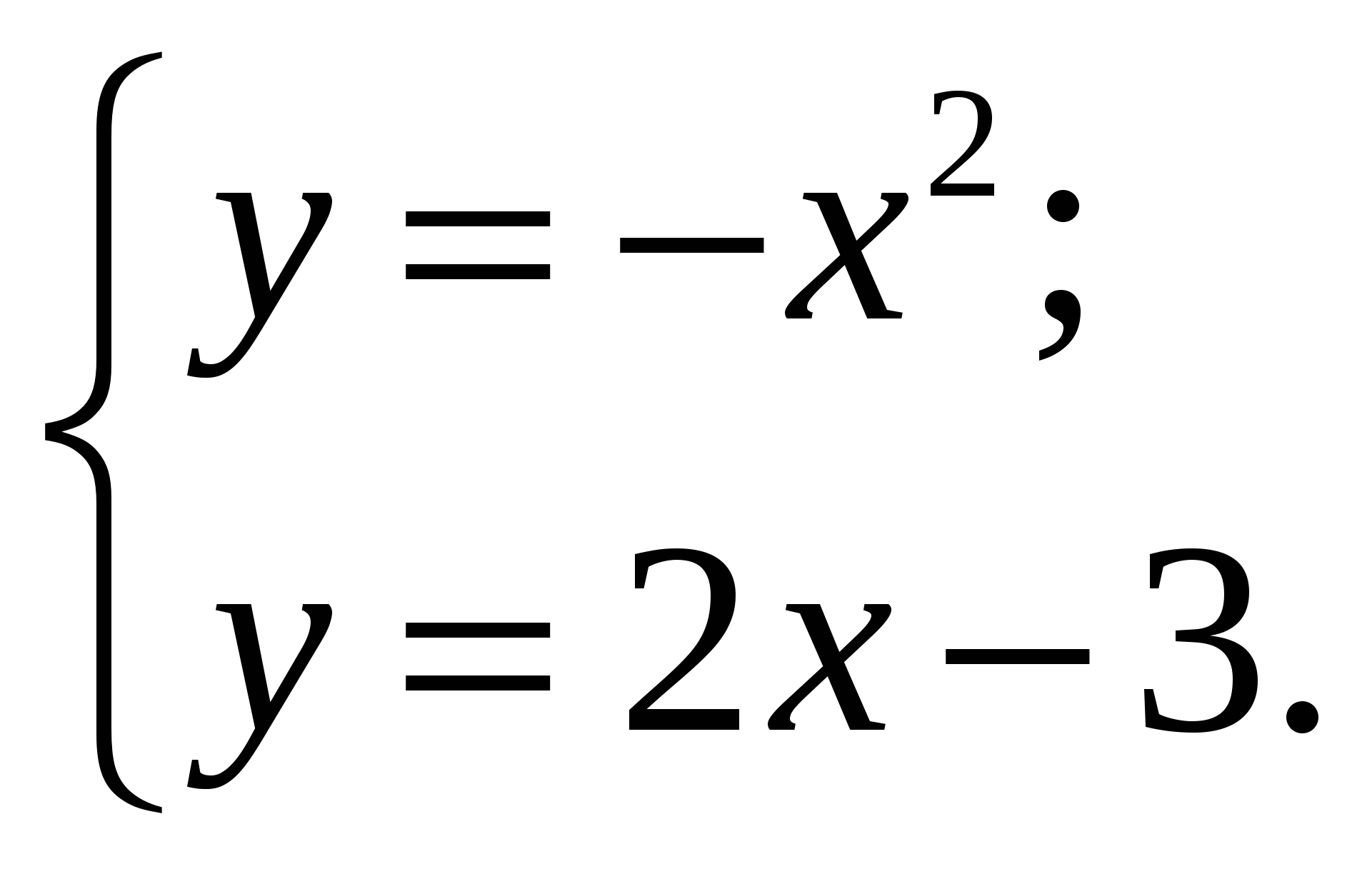
1) 1
2) 2
3) 3
4) 4
1.
2.

3.
4.
2.
Найдите пару чисел, являющуюся решением системы уравнений 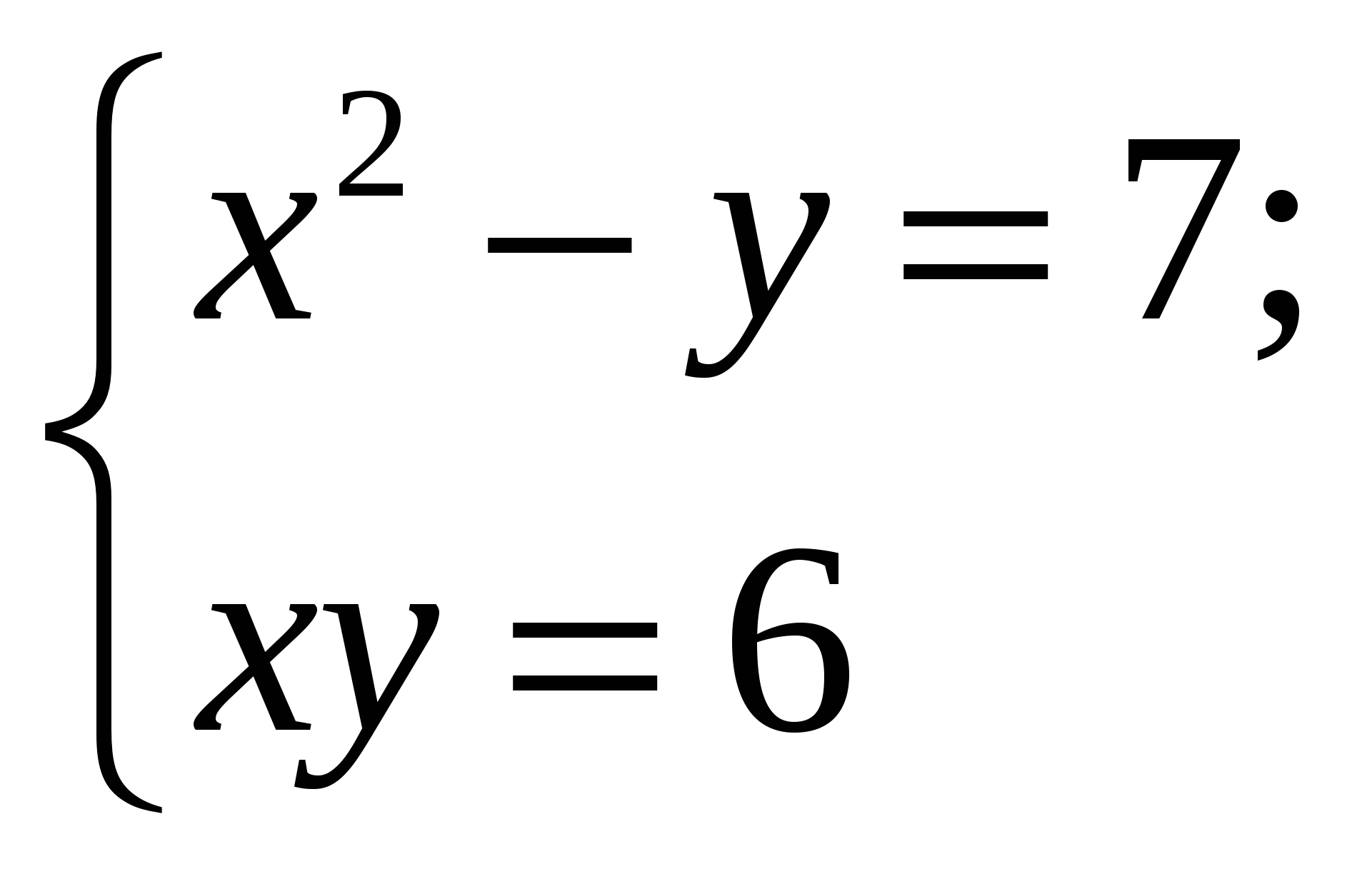
1) 1
2) 2
3) 3
4) 4
1. 
2. 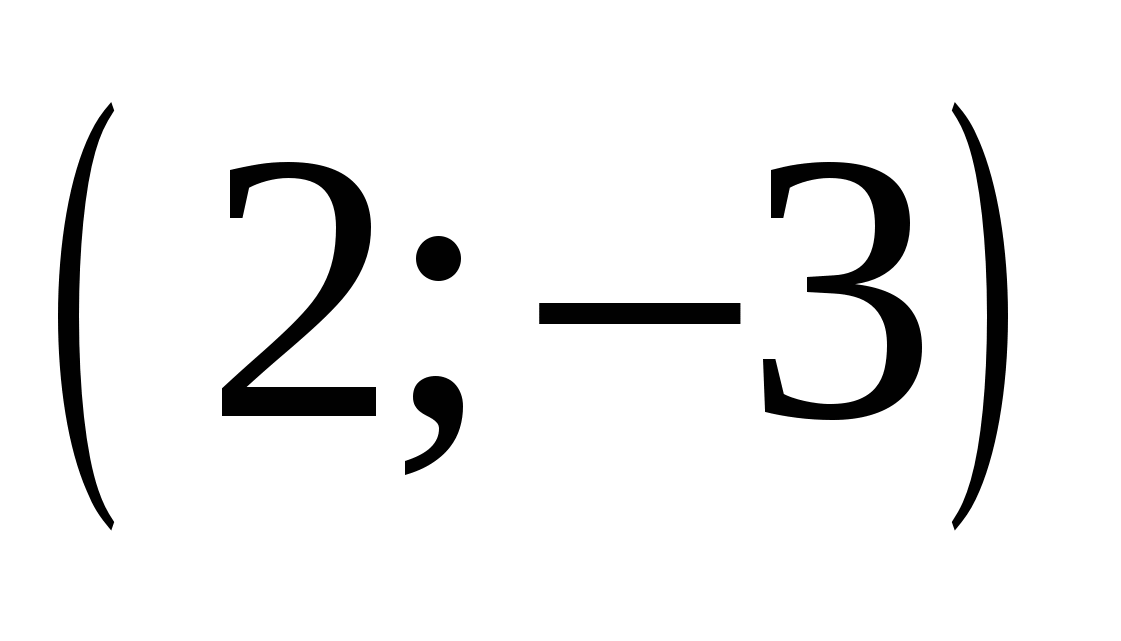
3. 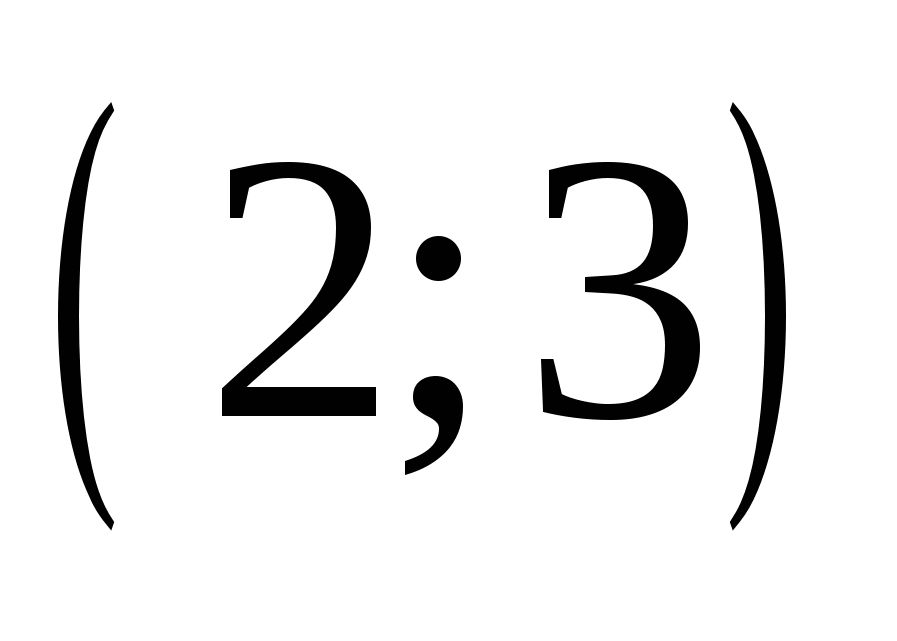
4. 
3.
Если 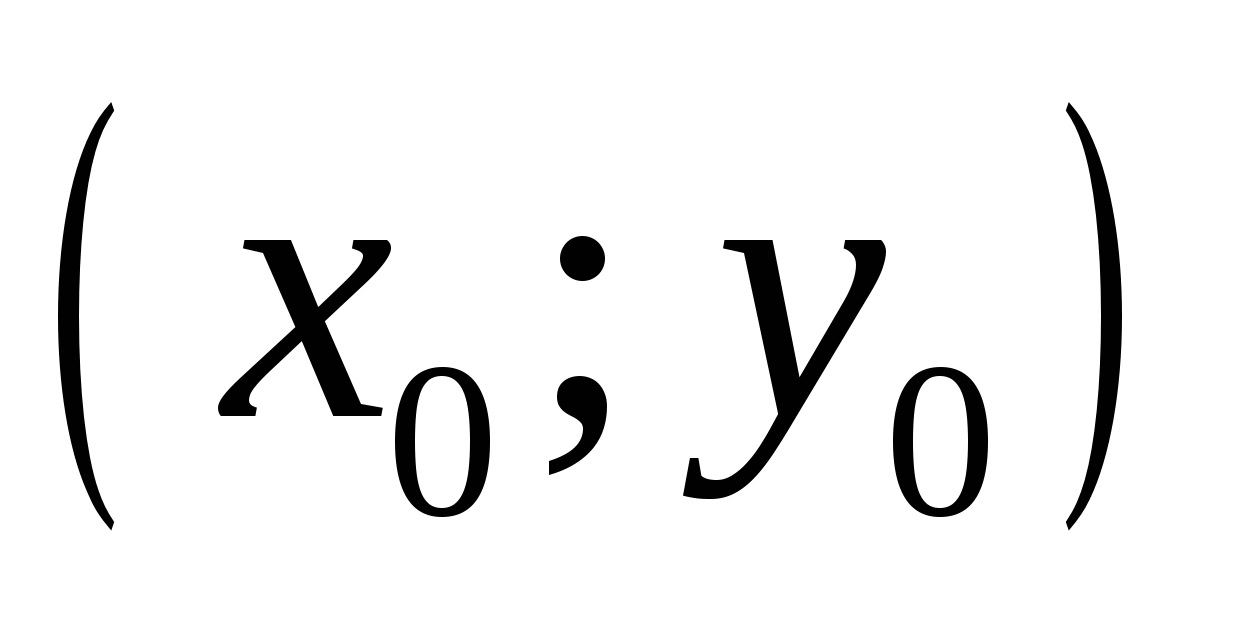 -решение системы уравнений
-решение системы уравнений 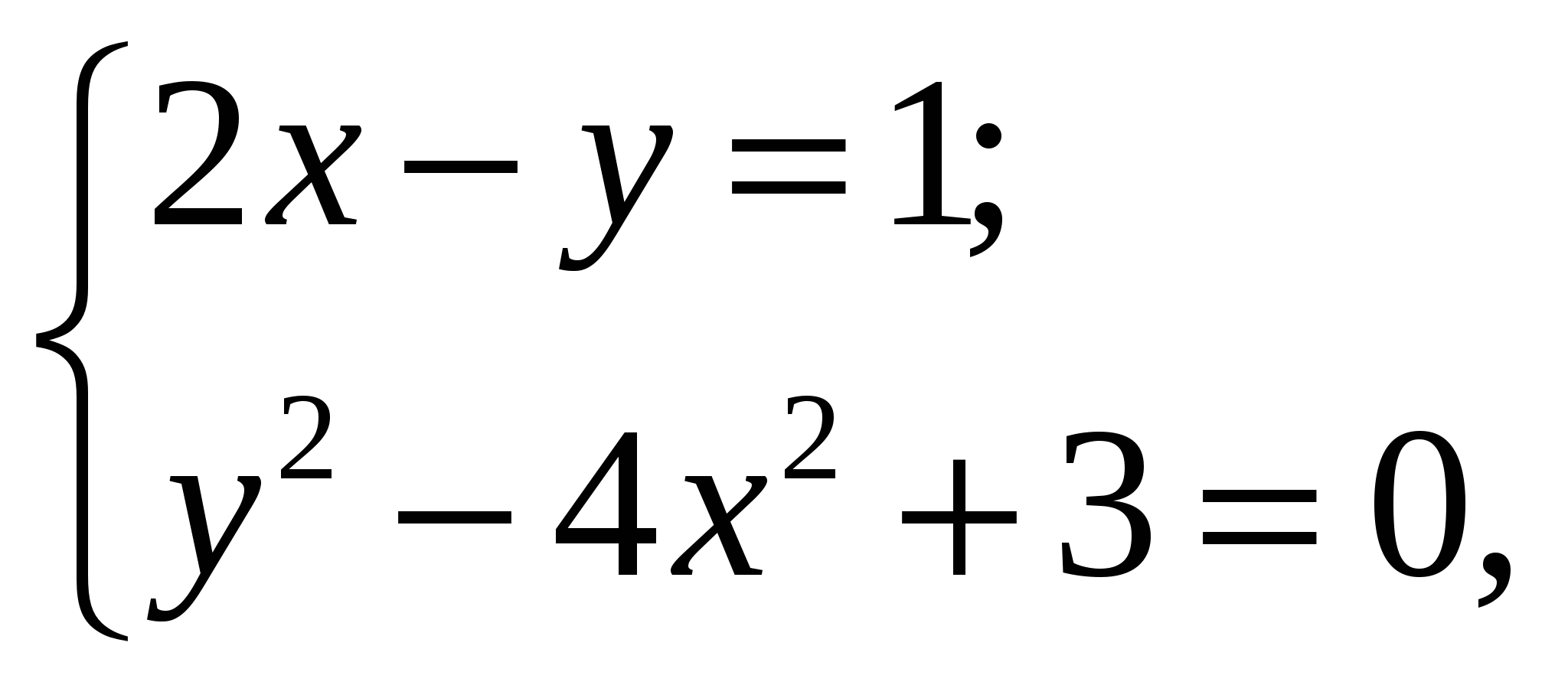
то значение  равно
равно
1) -2
2) 0
3) 2
4) -1
4.
Если 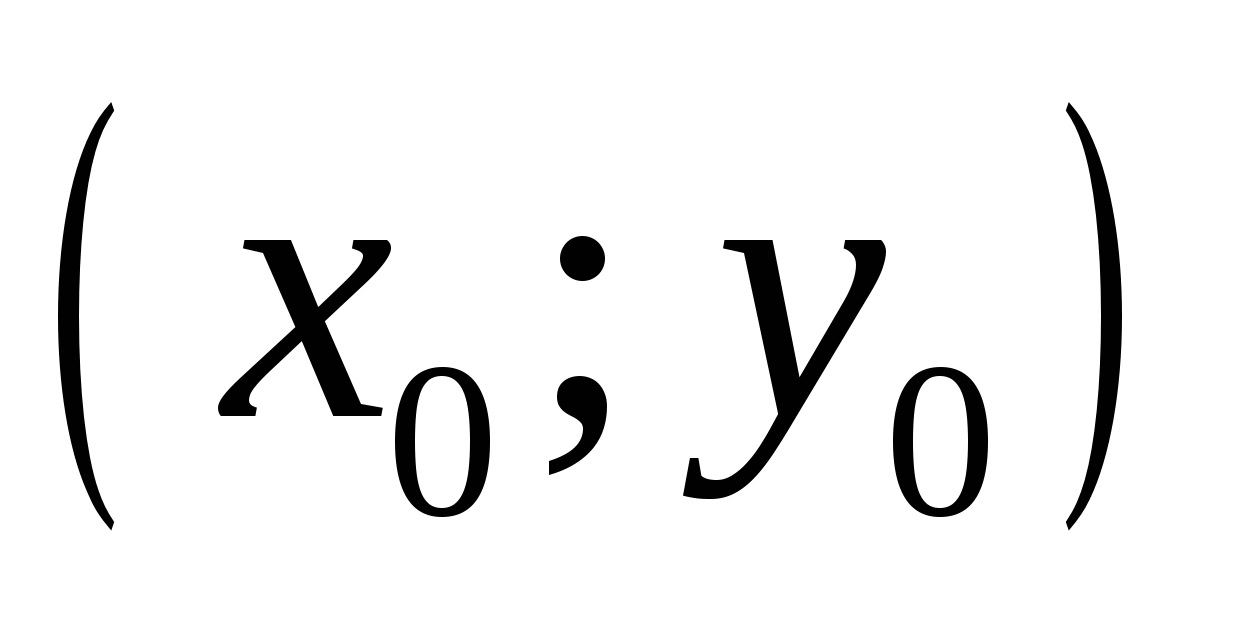 -решение системы уравнений
-решение системы уравнений 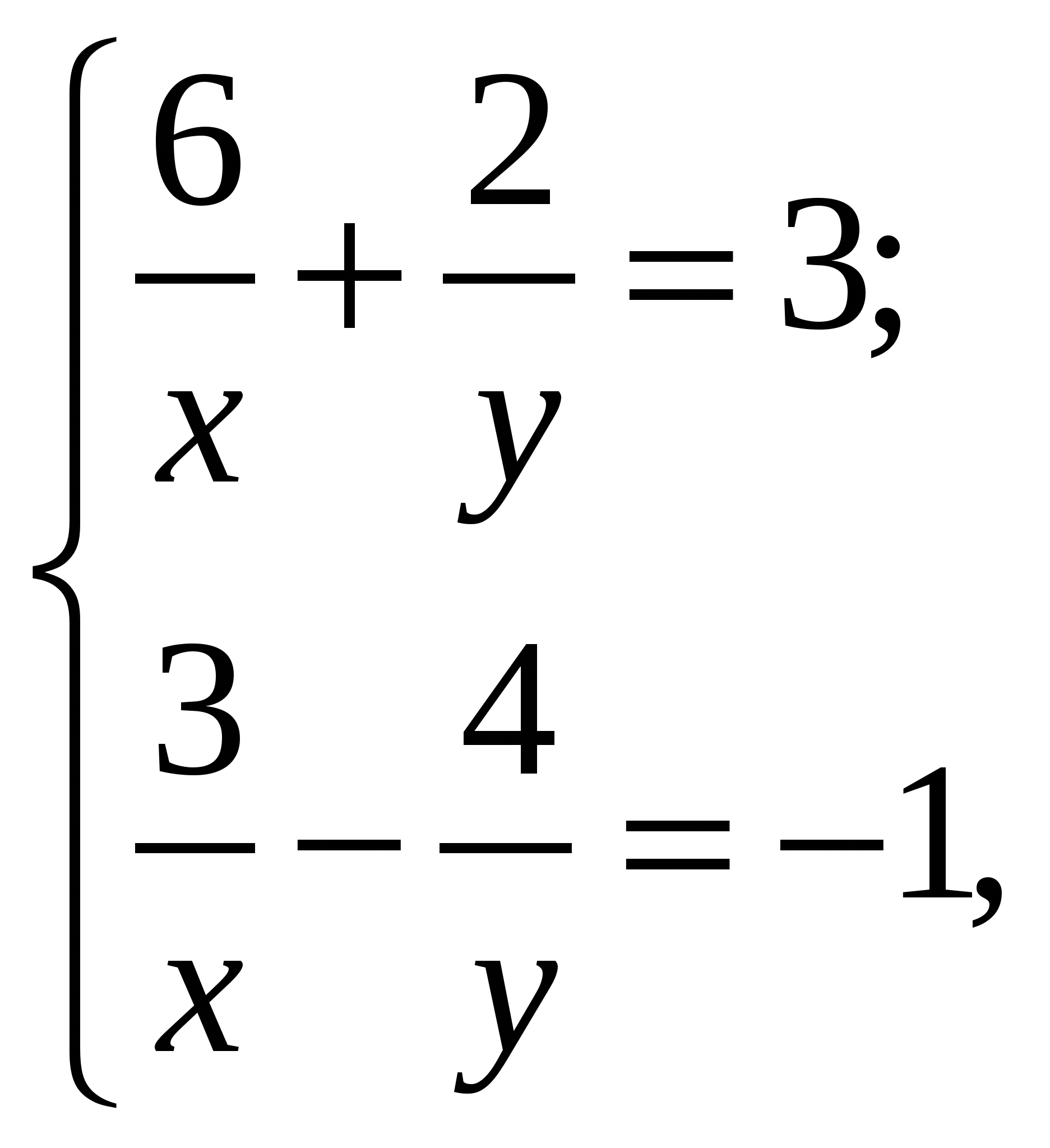 то значение
то значение 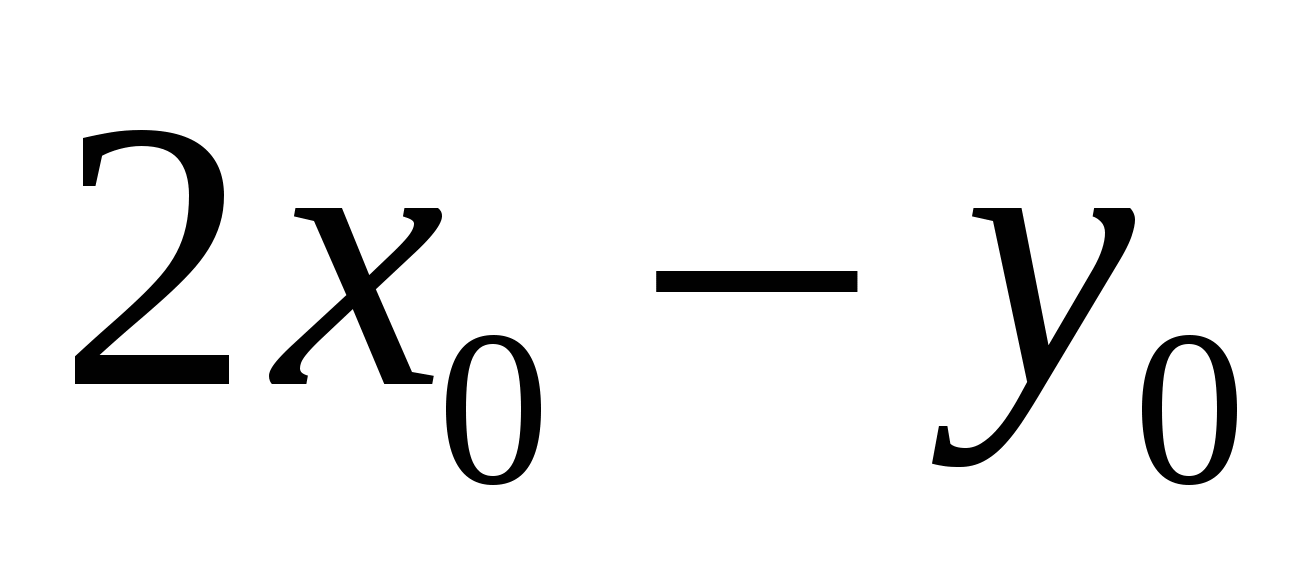 равно
равно
1) 3
2) 2
3) 4
4) 1
5.
При каком наибольшем целом значении параметра  система уравнений
система уравнений 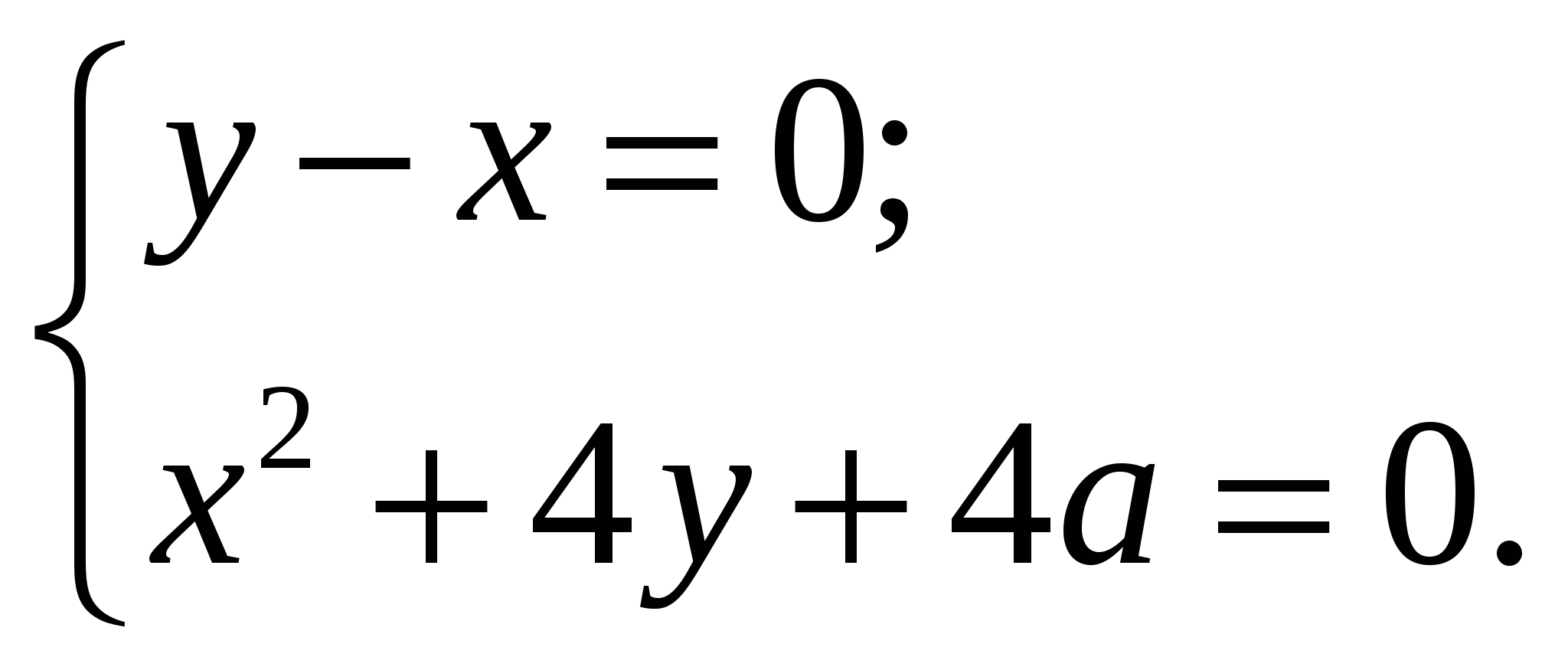 имеет два решения?
имеет два решения?
1) -4
2) -3
3) 0
4) 2
В3
Задание
Ответы
1.
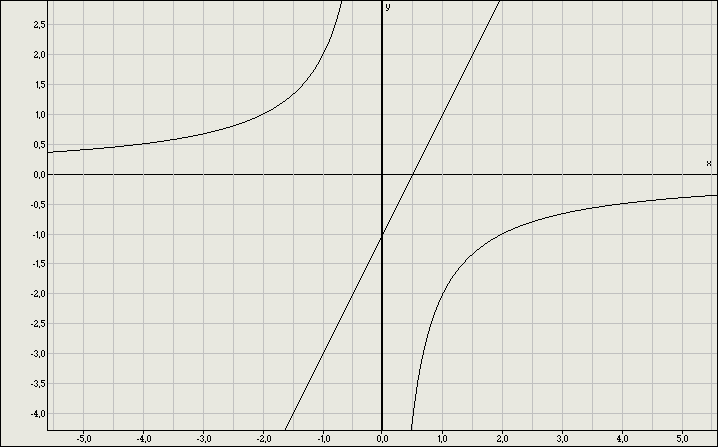
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 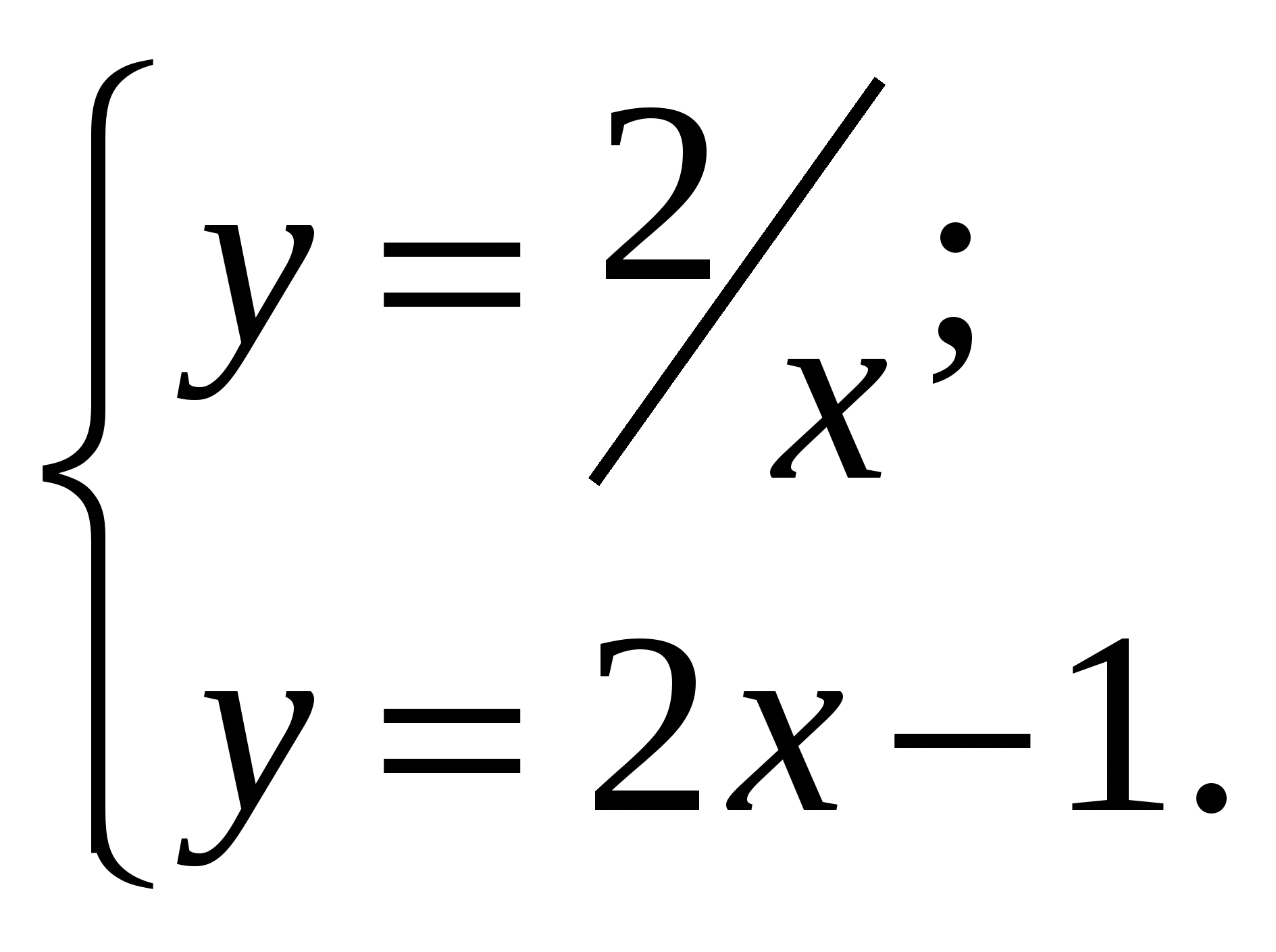
1) 1
2) 2
3) 3
4) 4
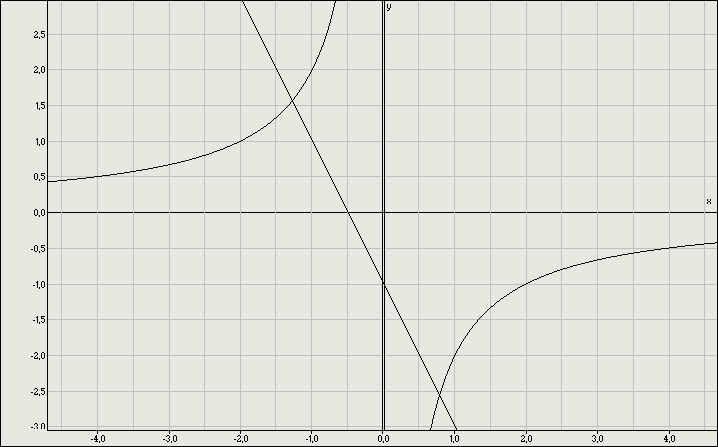
1. 
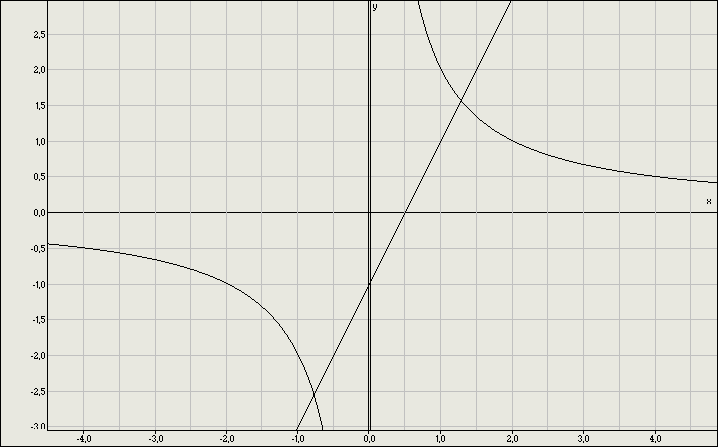
2. 
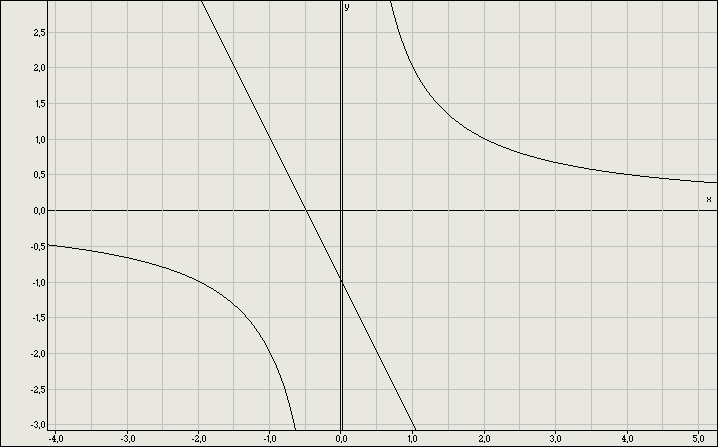
3. 
4. 
2.
Найдите пару чисел, являющуюся решением системы уравнений 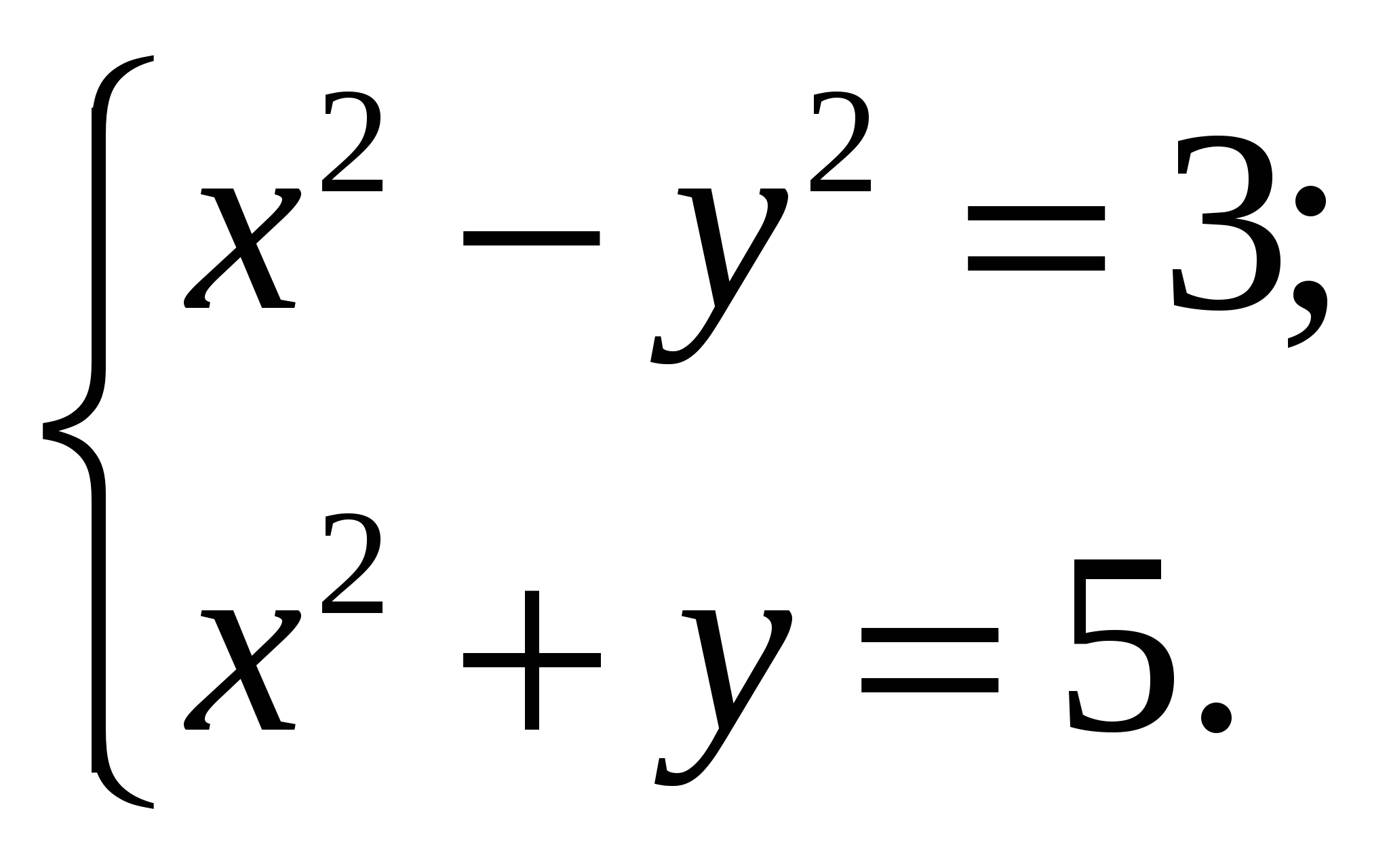
1) 1
2) 2
3) 3
4) 4
1. 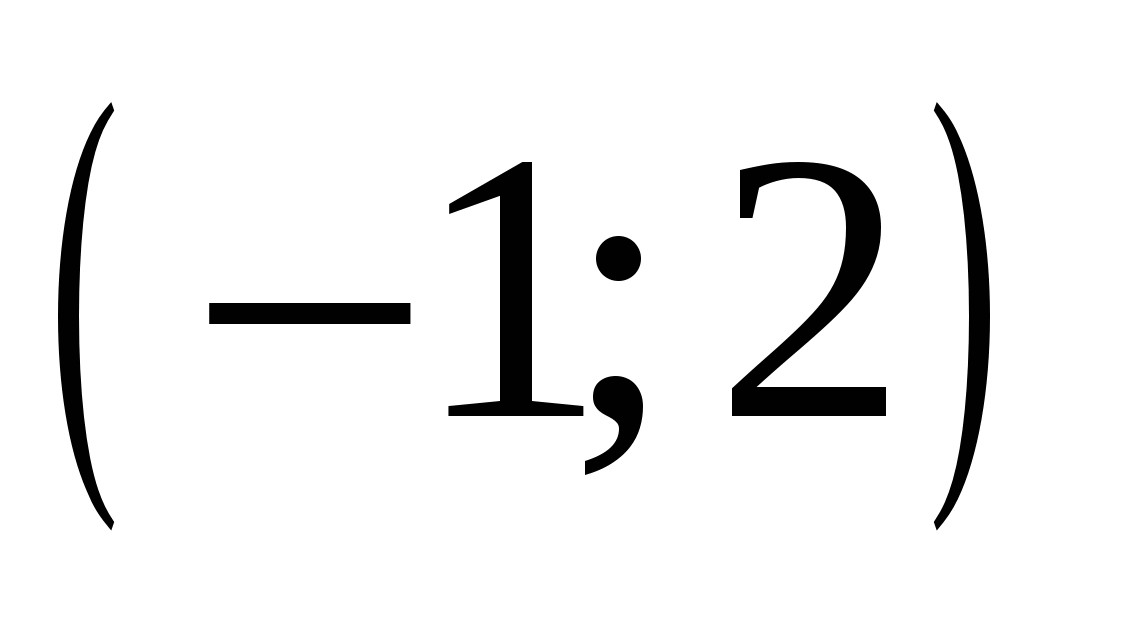
2. 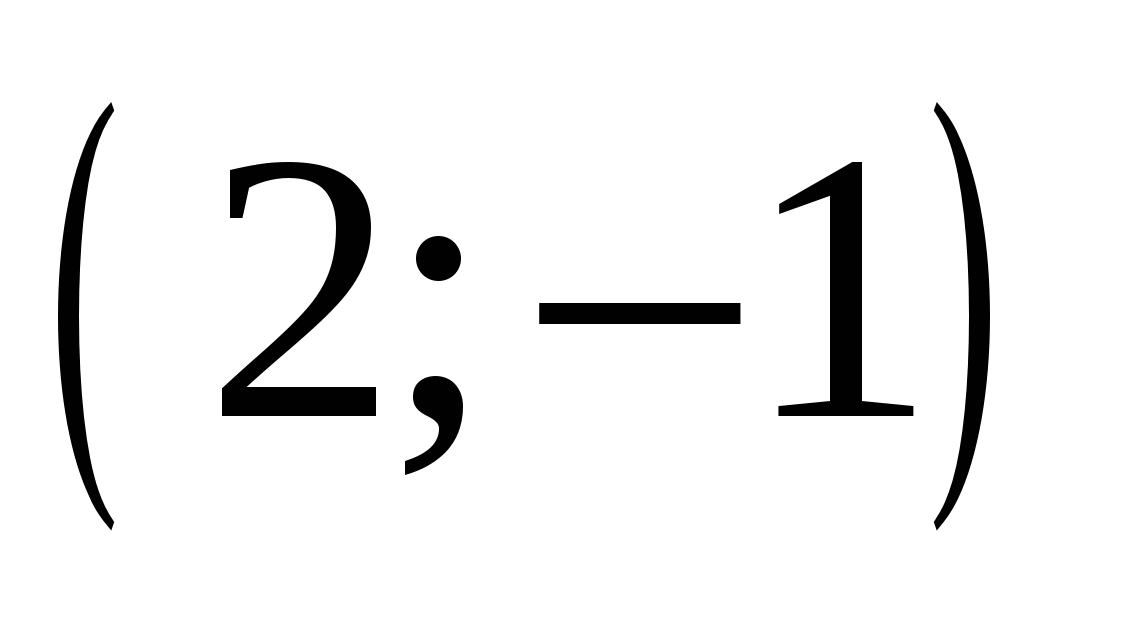
3. 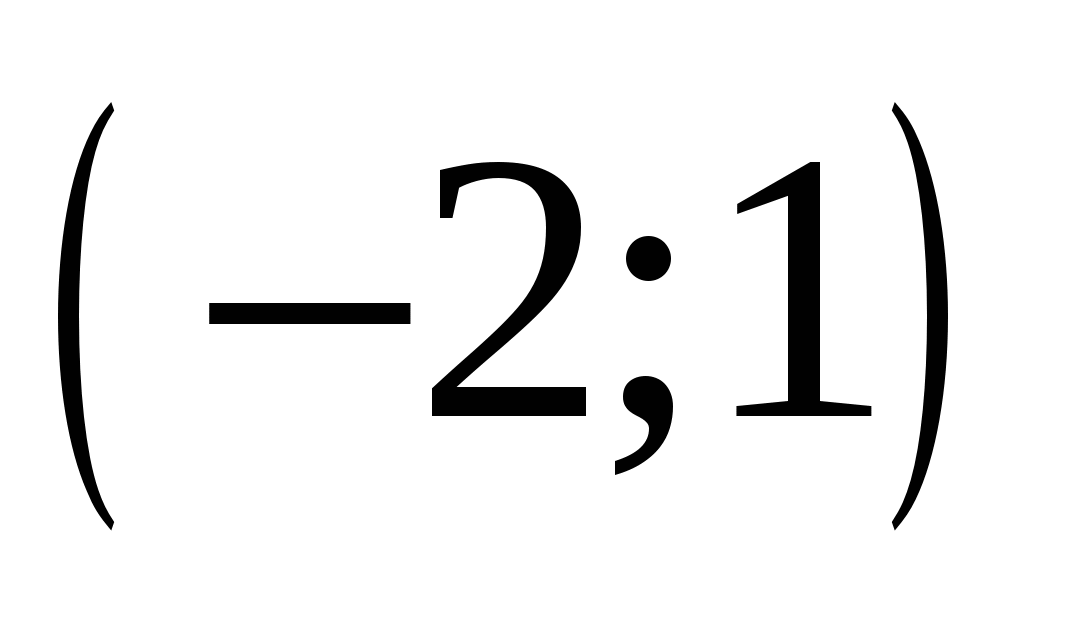
4. 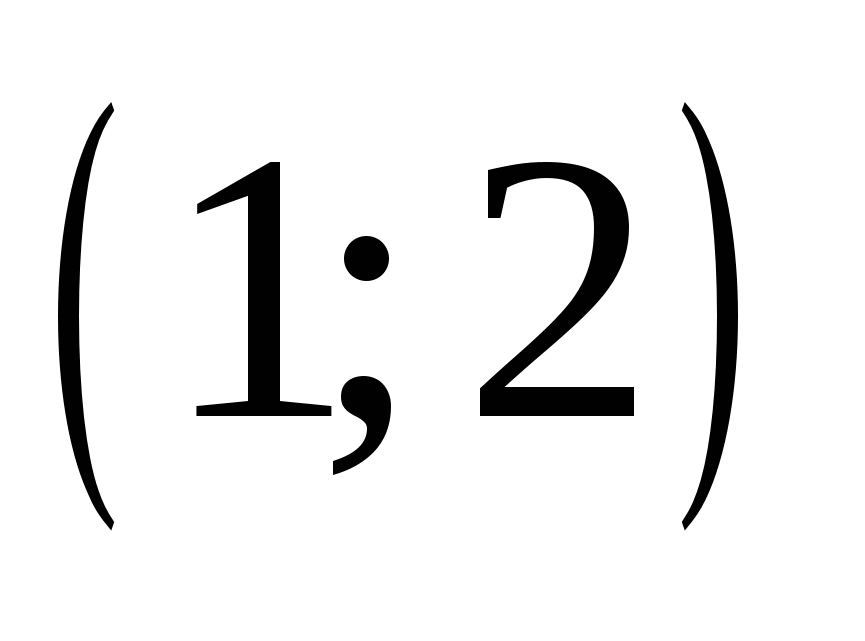
3.
Если 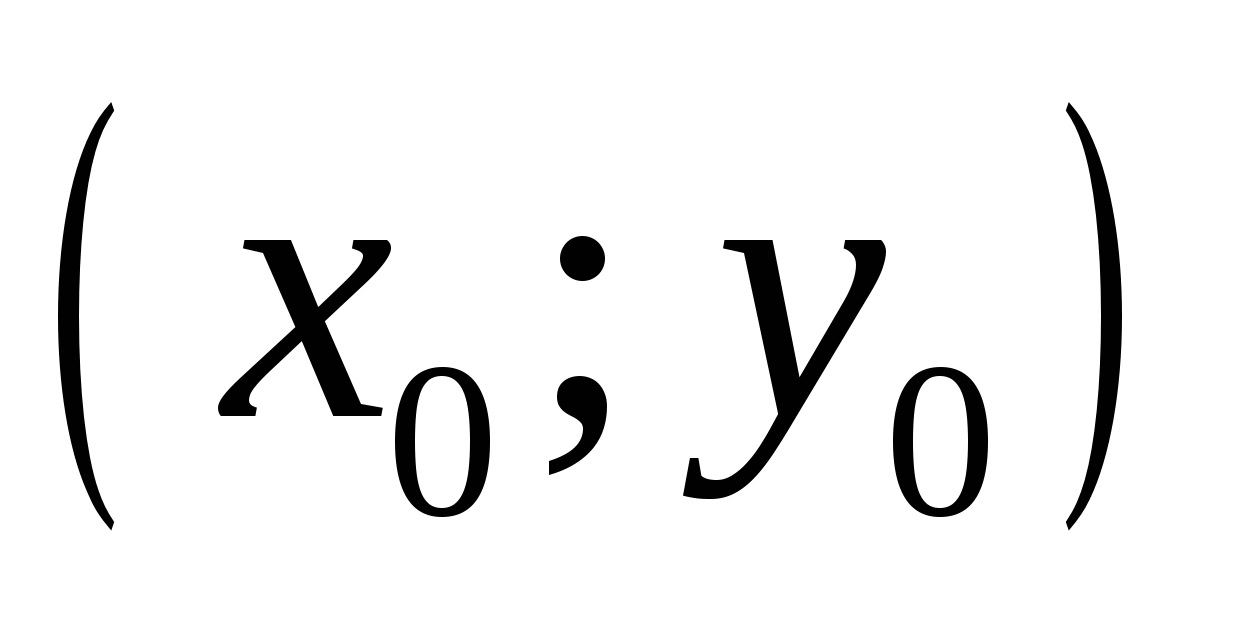 -решение системы уравнений
-решение системы уравнений 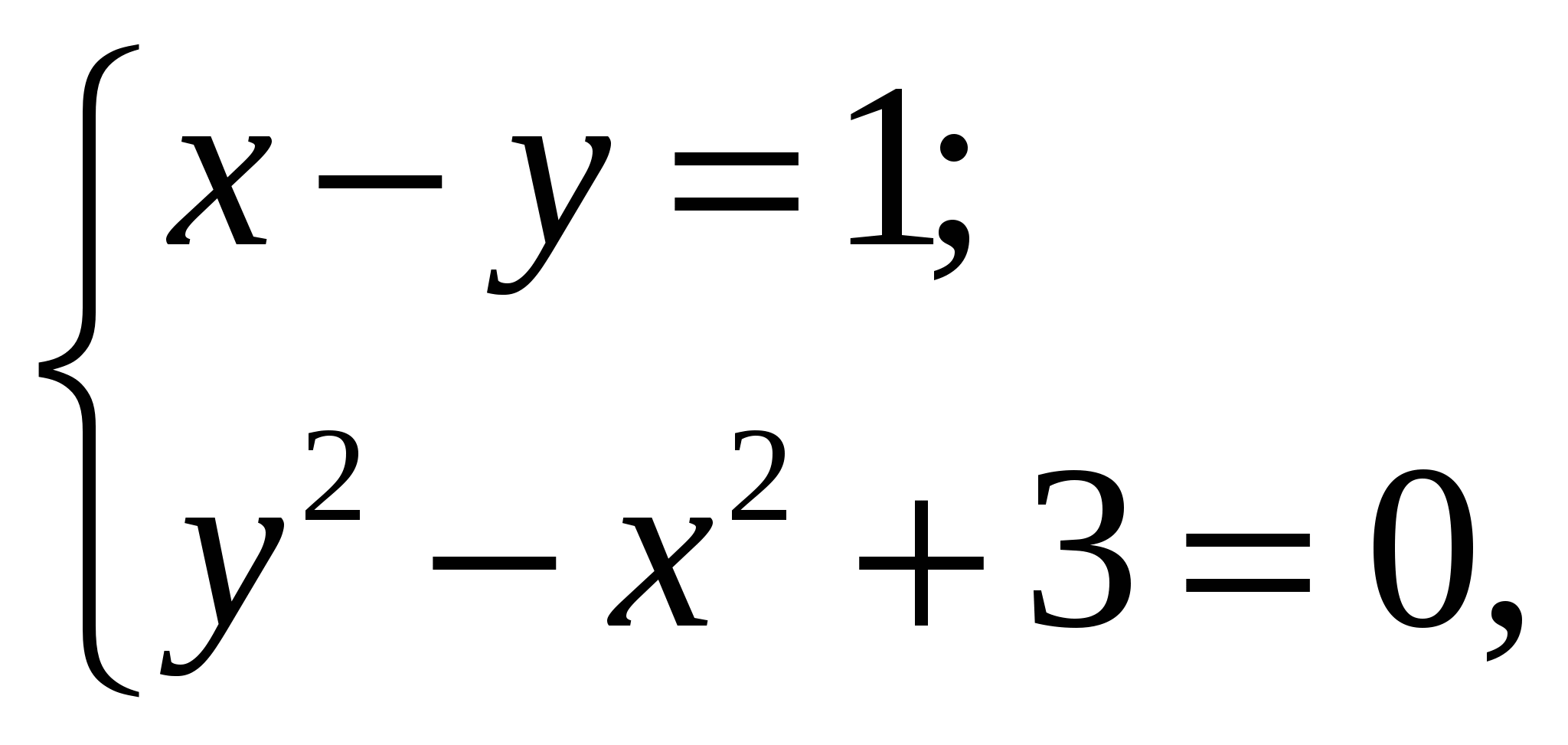
то значение  равно
равно
1) 3
2) 0
3) -2
4) 1
4.
Если 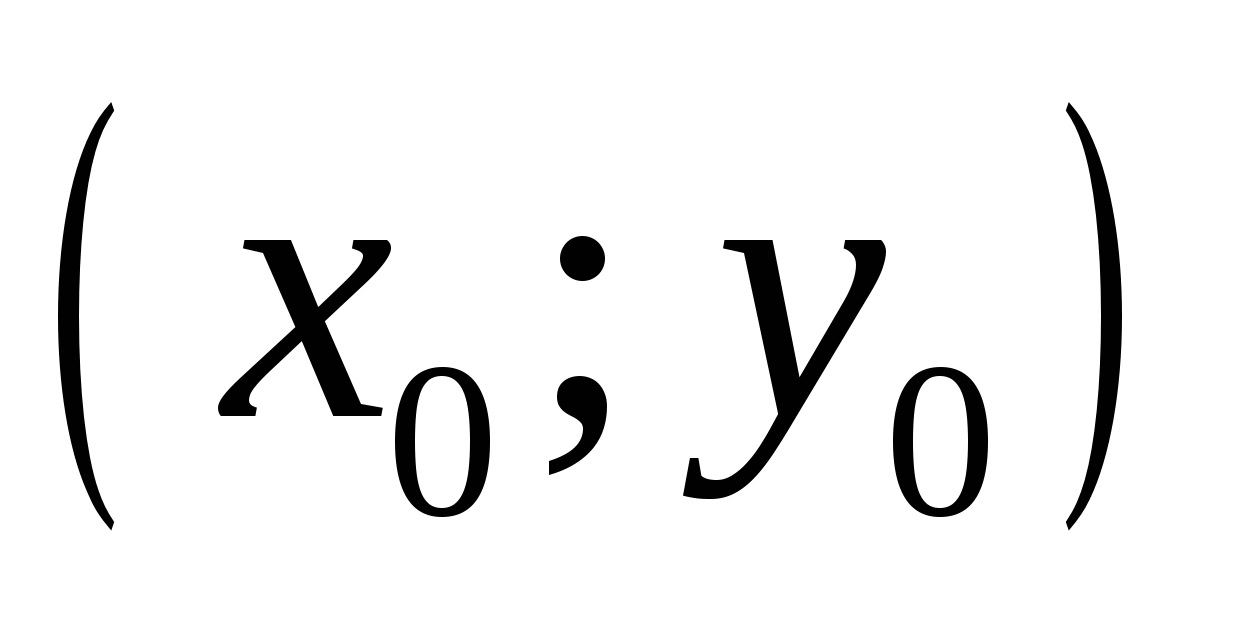 -решение системы уравнений
-решение системы уравнений 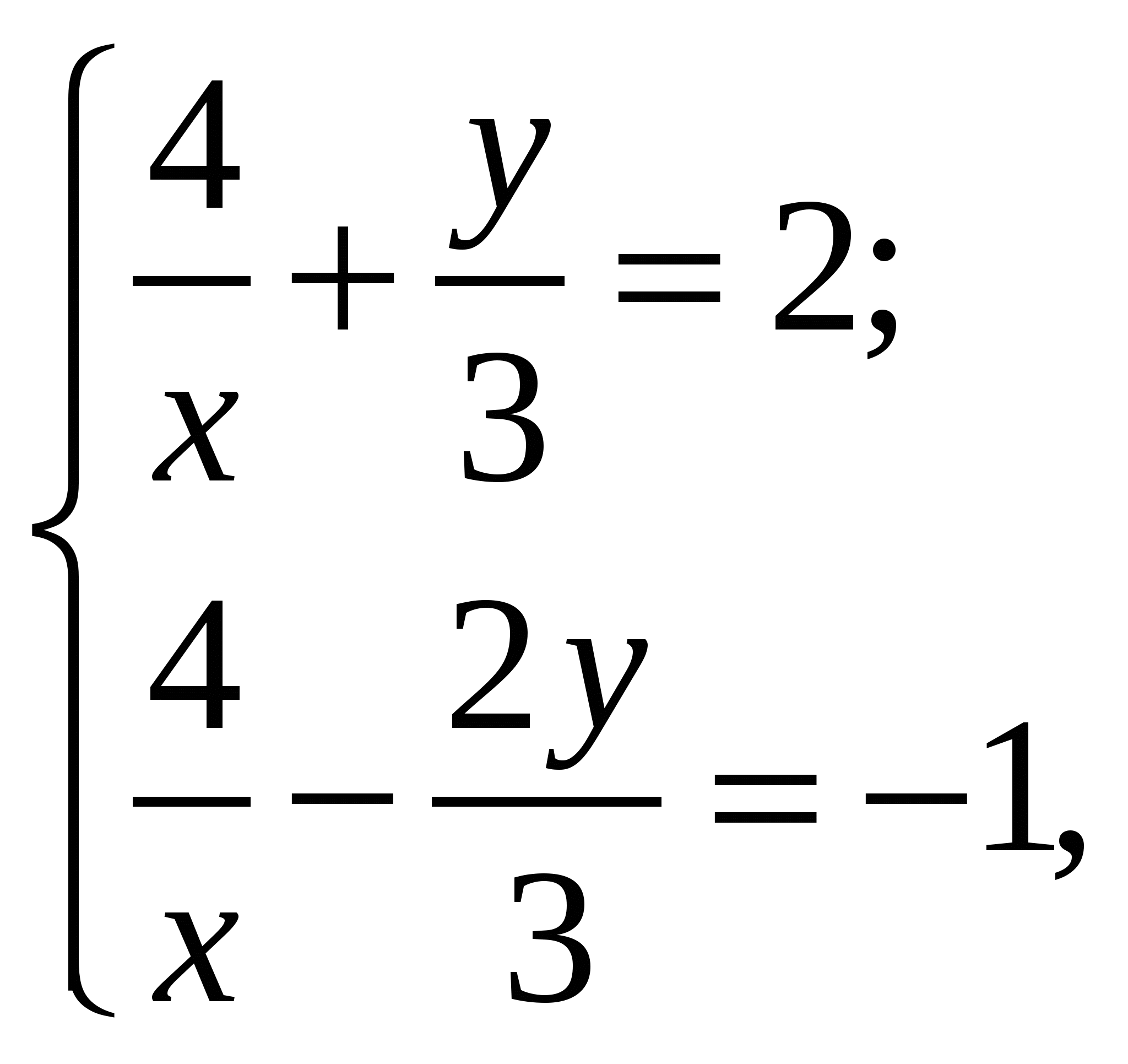 то значение
то значение 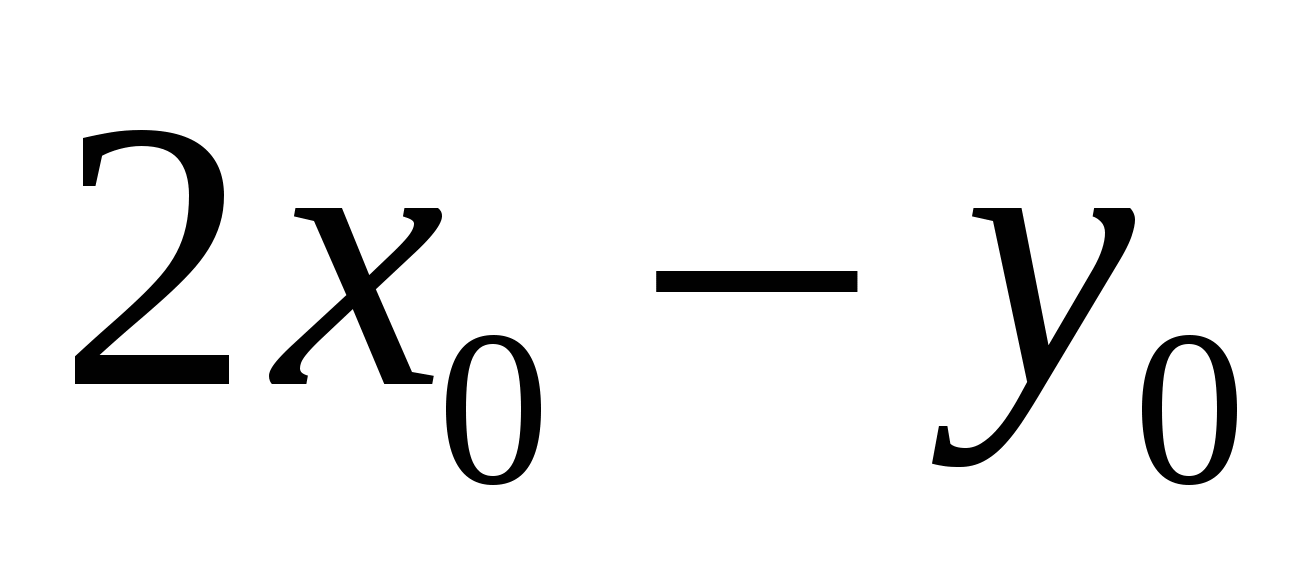 равно
равно
1) -2
2) 3
3) 4
4) 5
5.
При каком наименьшем натуральном значении параметра  система уравнений
система уравнений 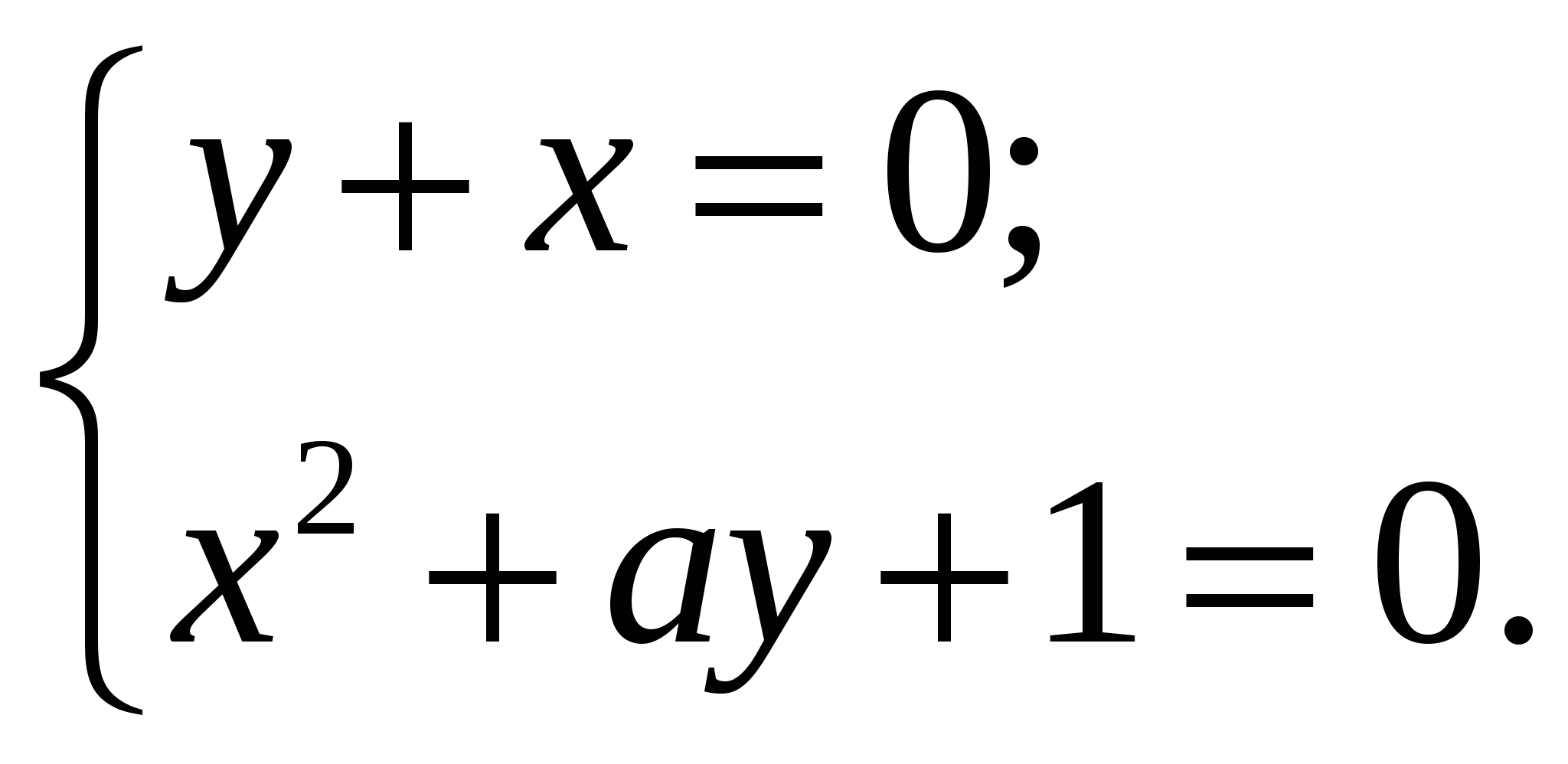 имеет два решения?
имеет два решения?
1) 1
2) 2
3) 3
4) 4
В4
Задание
Ответы
1.
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 
1) 1
2) 2
3) 3
4) 4
1. 
2. 
3. 
4. 
2.
Найдите пару чисел, являющуюся решением системы уравнений 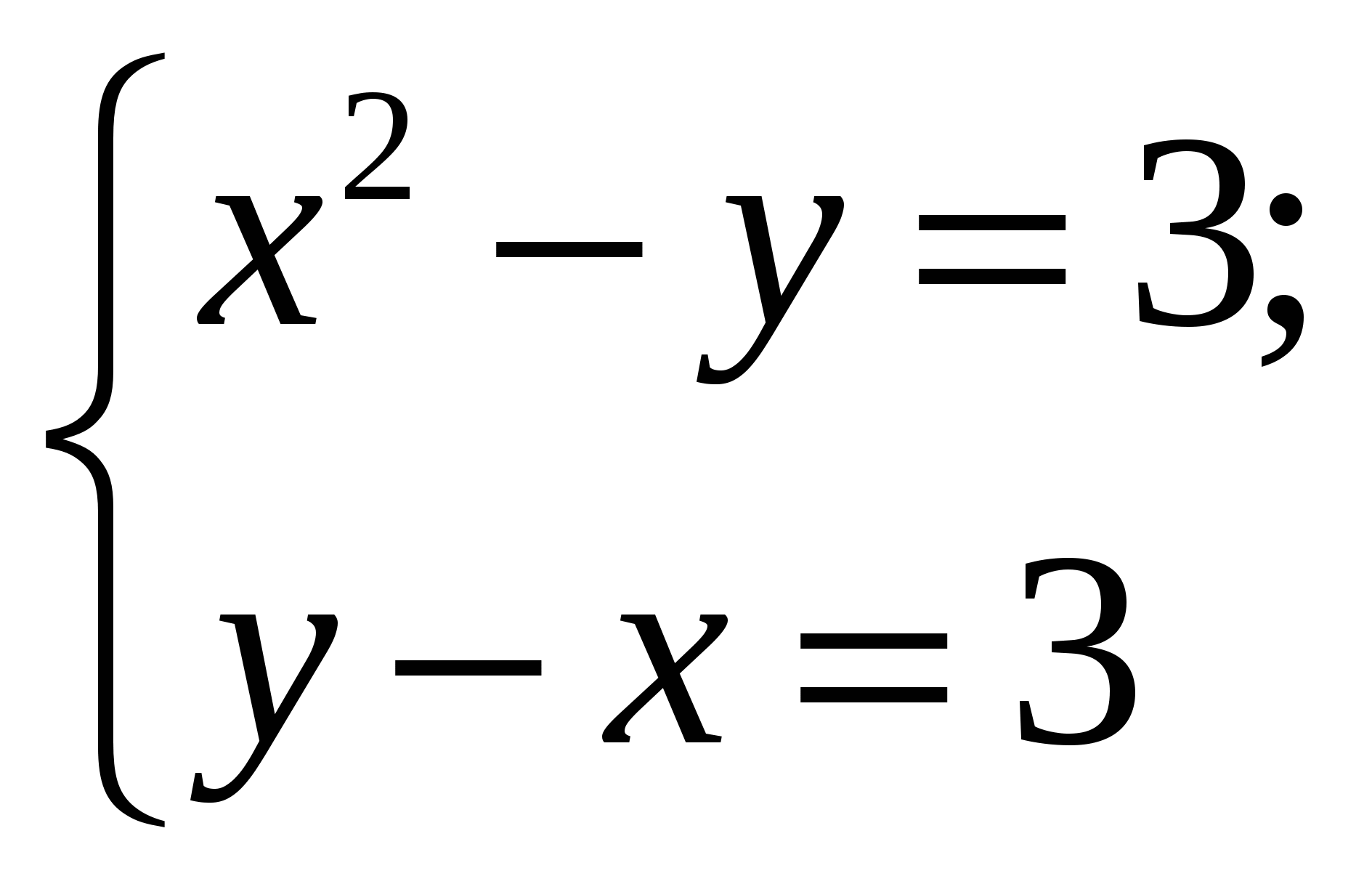
1) 1
2) 2
3) 3
4) 4
1. 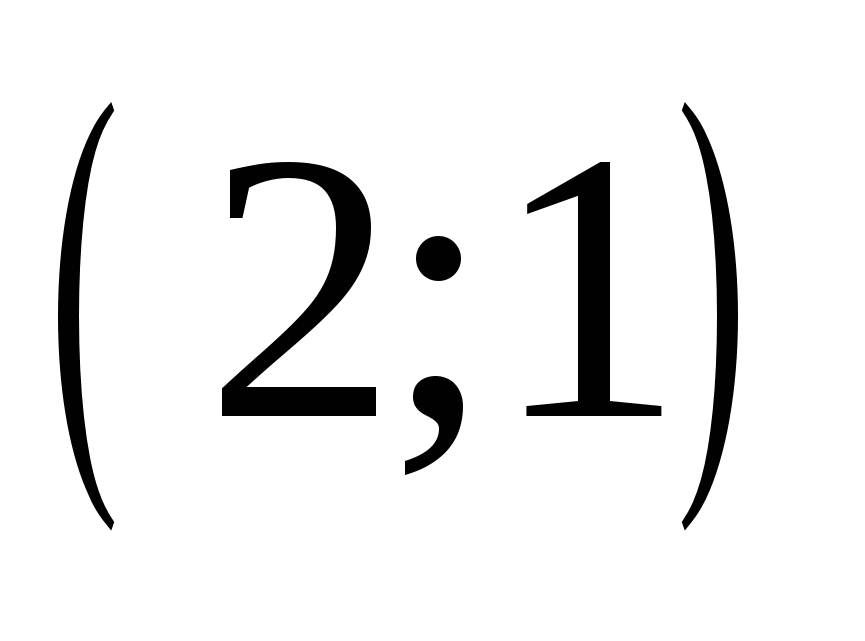
2. 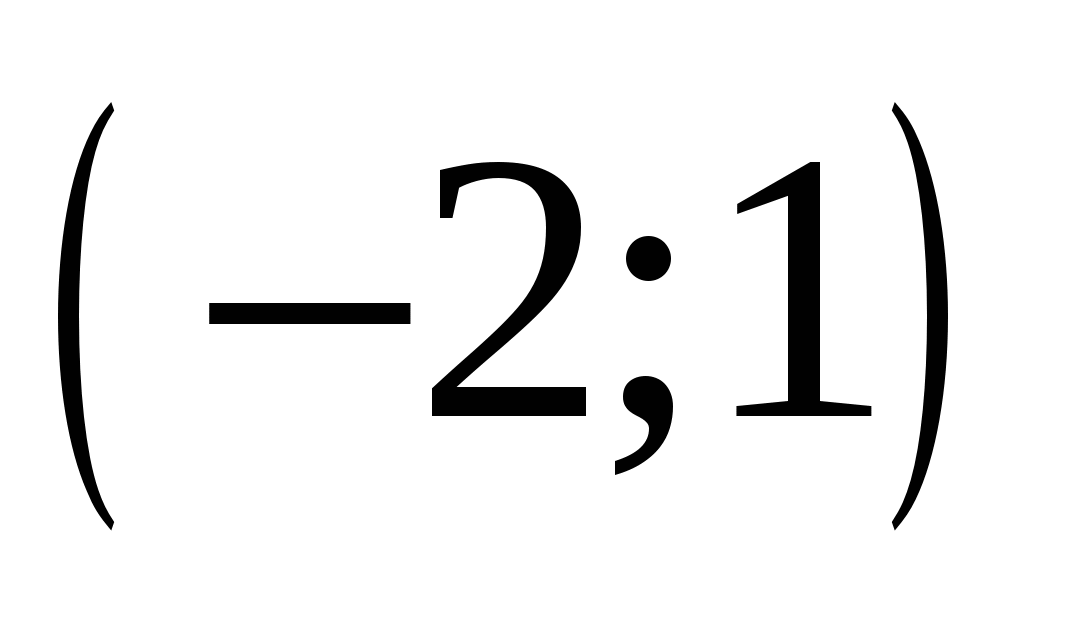
3. 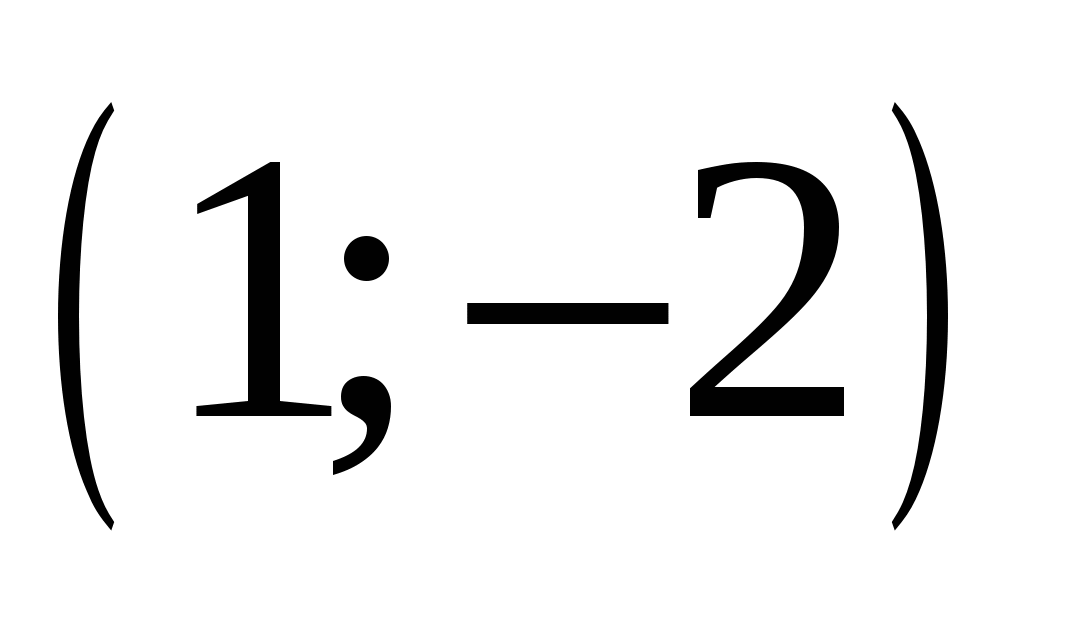
4. 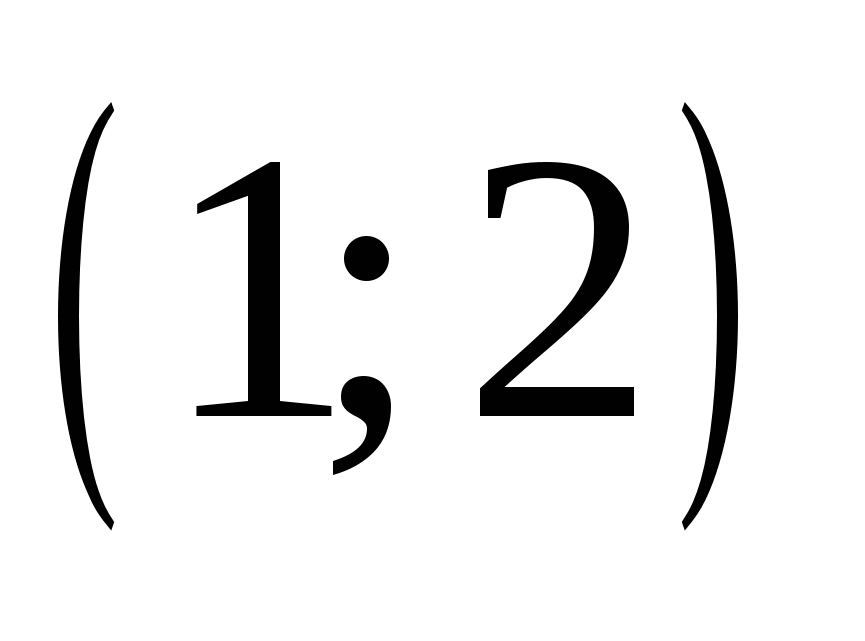
3.
Если 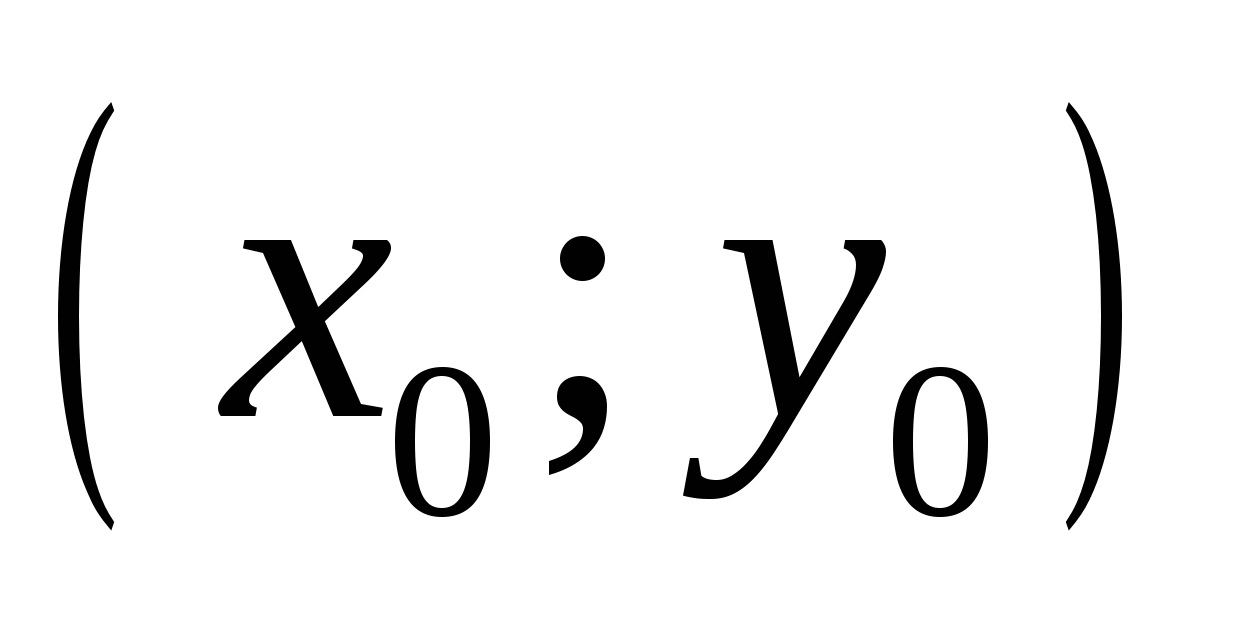 -решение системы уравнений
-решение системы уравнений 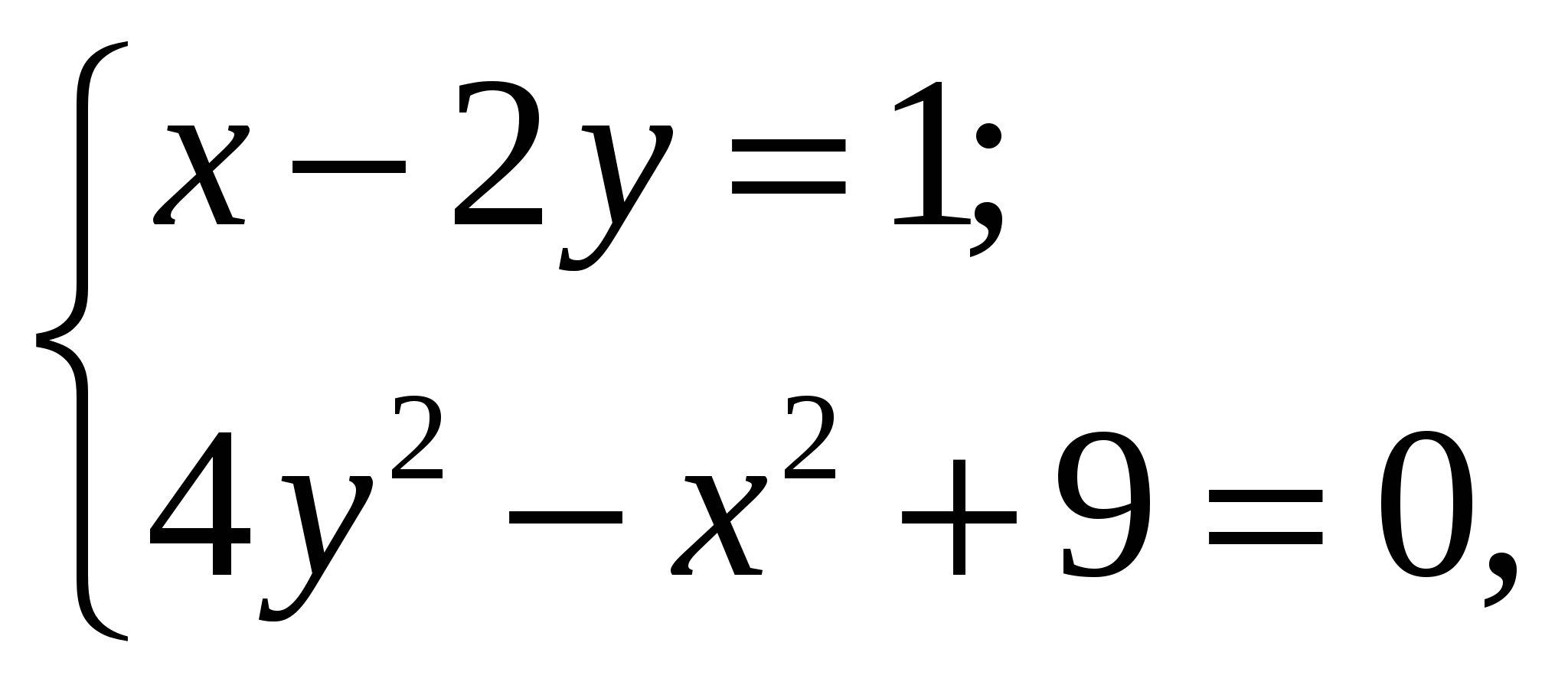
то значение  равно
равно
1) 7
2) 5
3) —2
4) -4
4.
Если 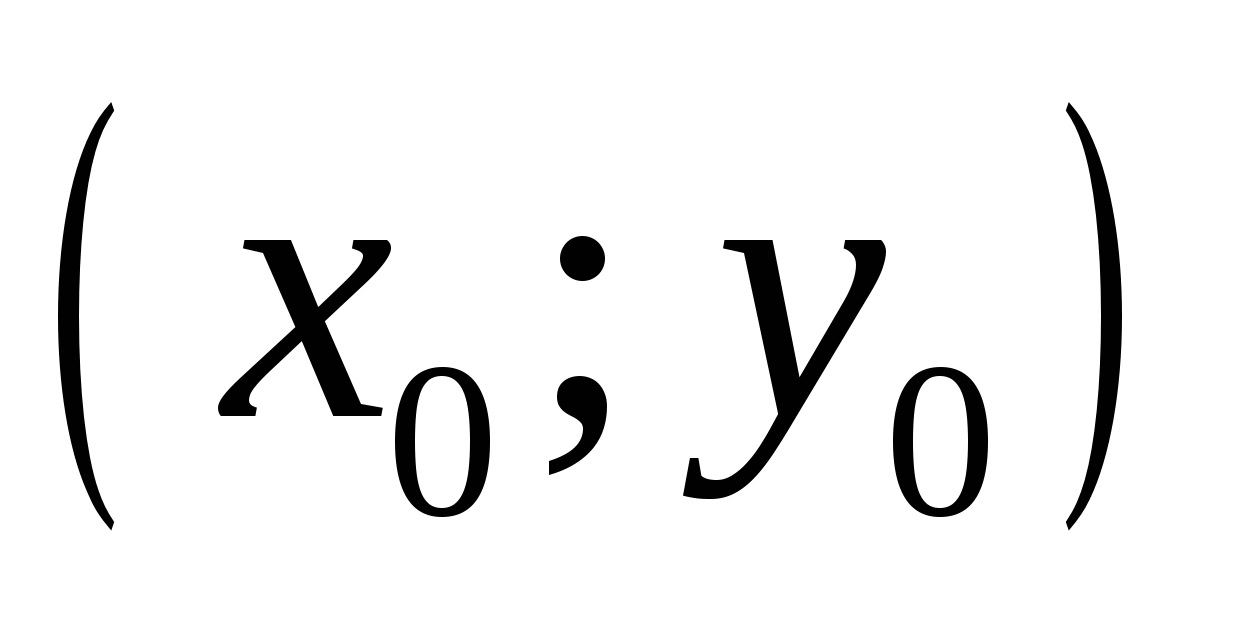 -решение системы уравнений
-решение системы уравнений 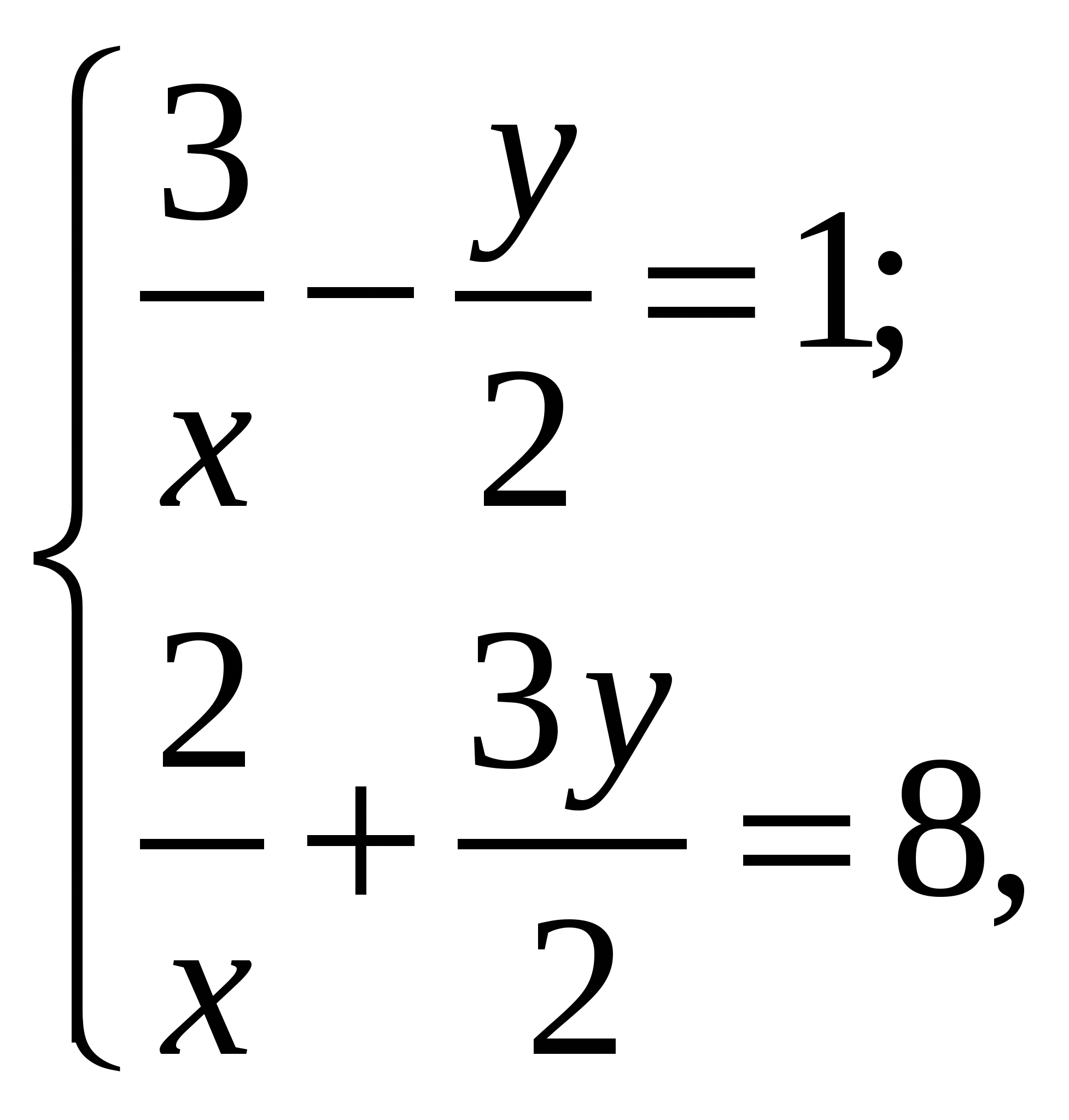 то значение
то значение 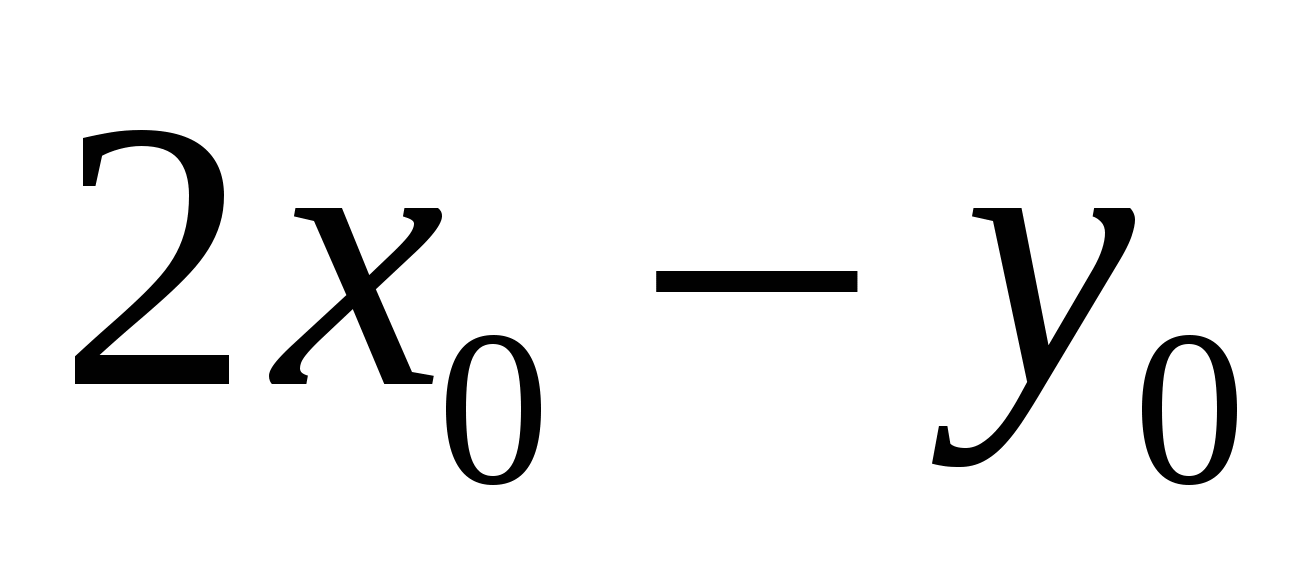 равно
равно
1) 3
2) 2
3) -2
4) -3
5.
При каком значении параметра  система уравнений
система уравнений 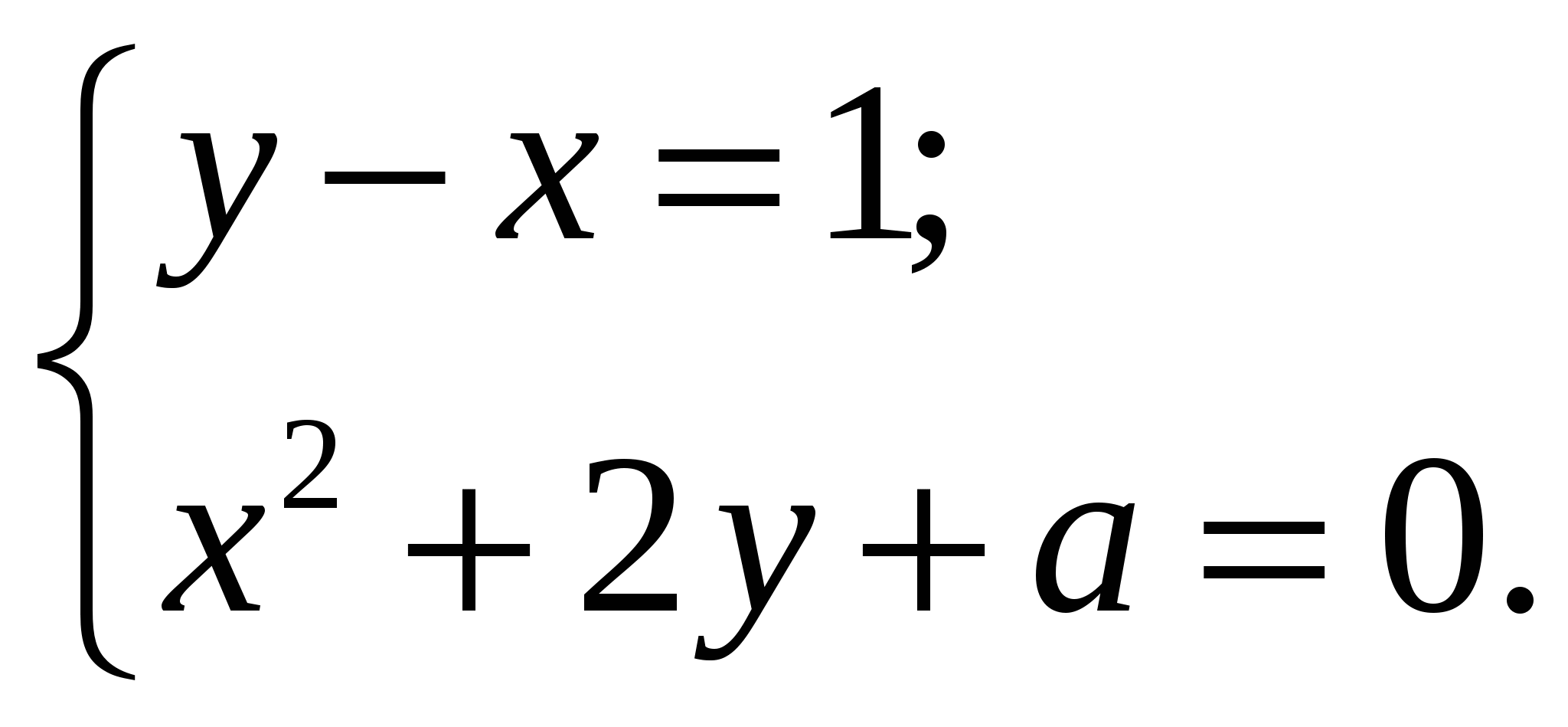 имеет единственное решение?
имеет единственное решение?
1) -2
2) -1
3) 0
4) 1
В5
Задание
Ответы
1.
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 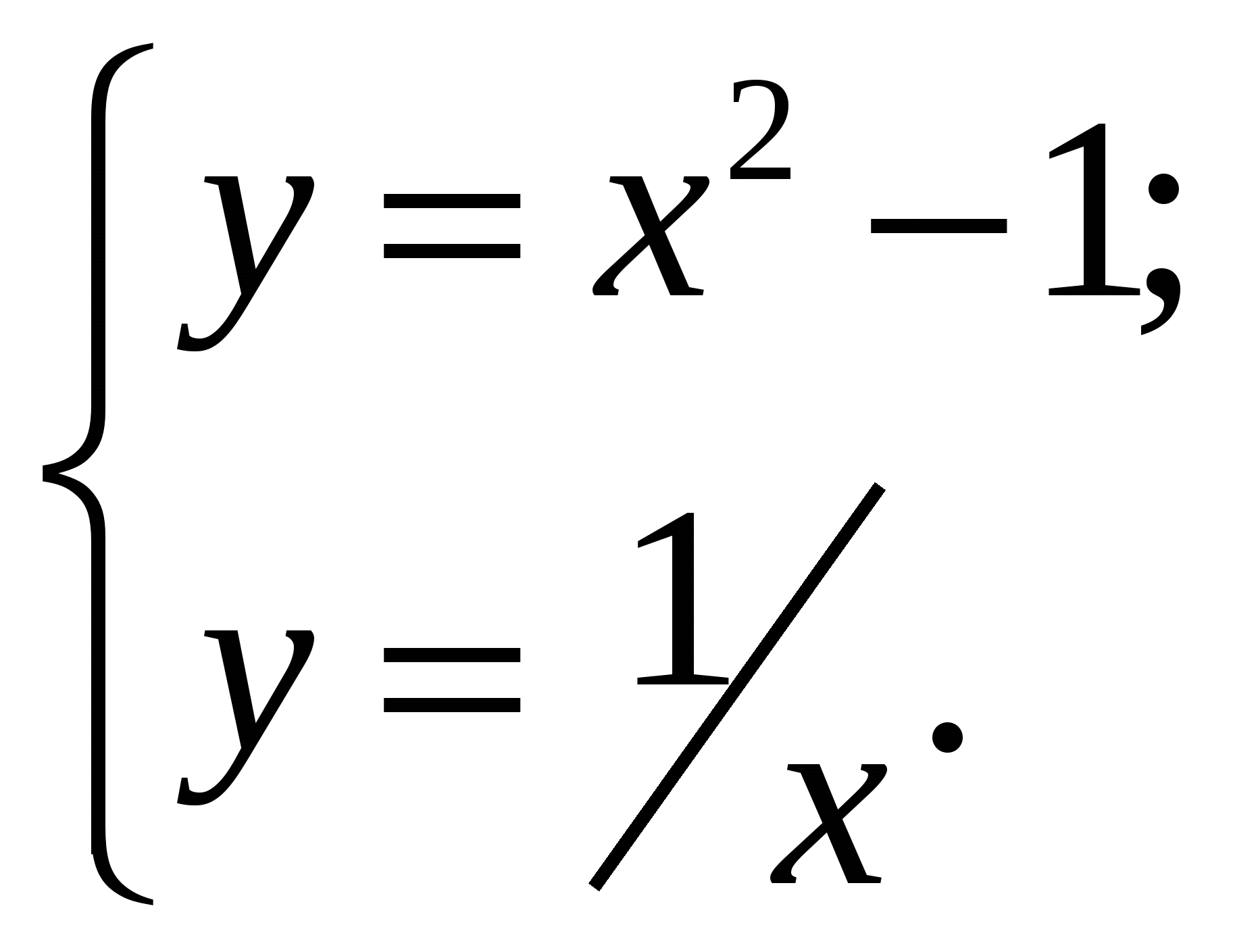
1) 1
2) 2
3) 3
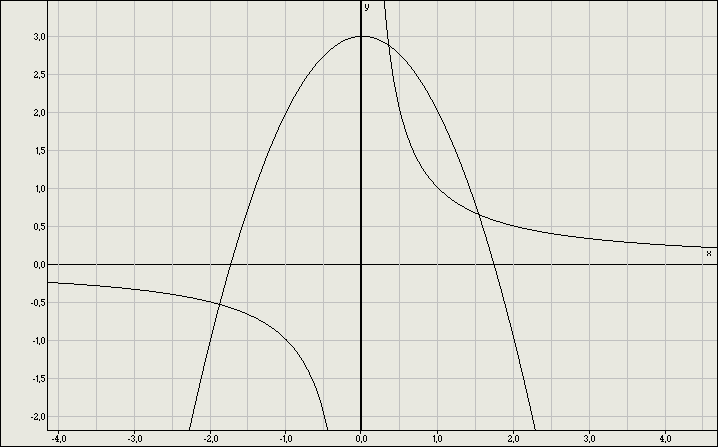
4) 4
1. 
2. 
3. 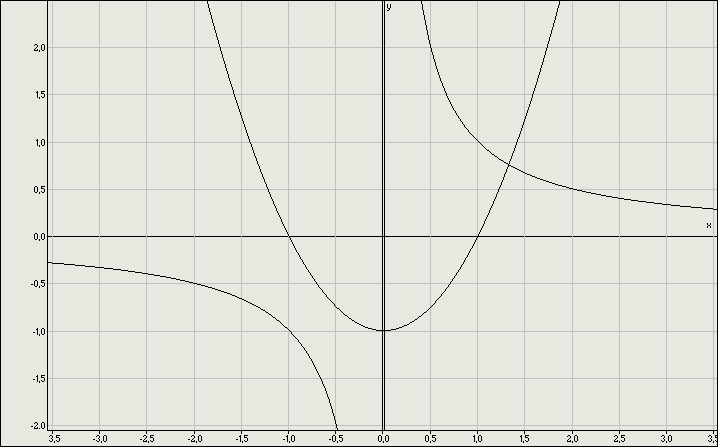
4. 
2.
Найдите пару чисел, являющуюся решением системы уравнений 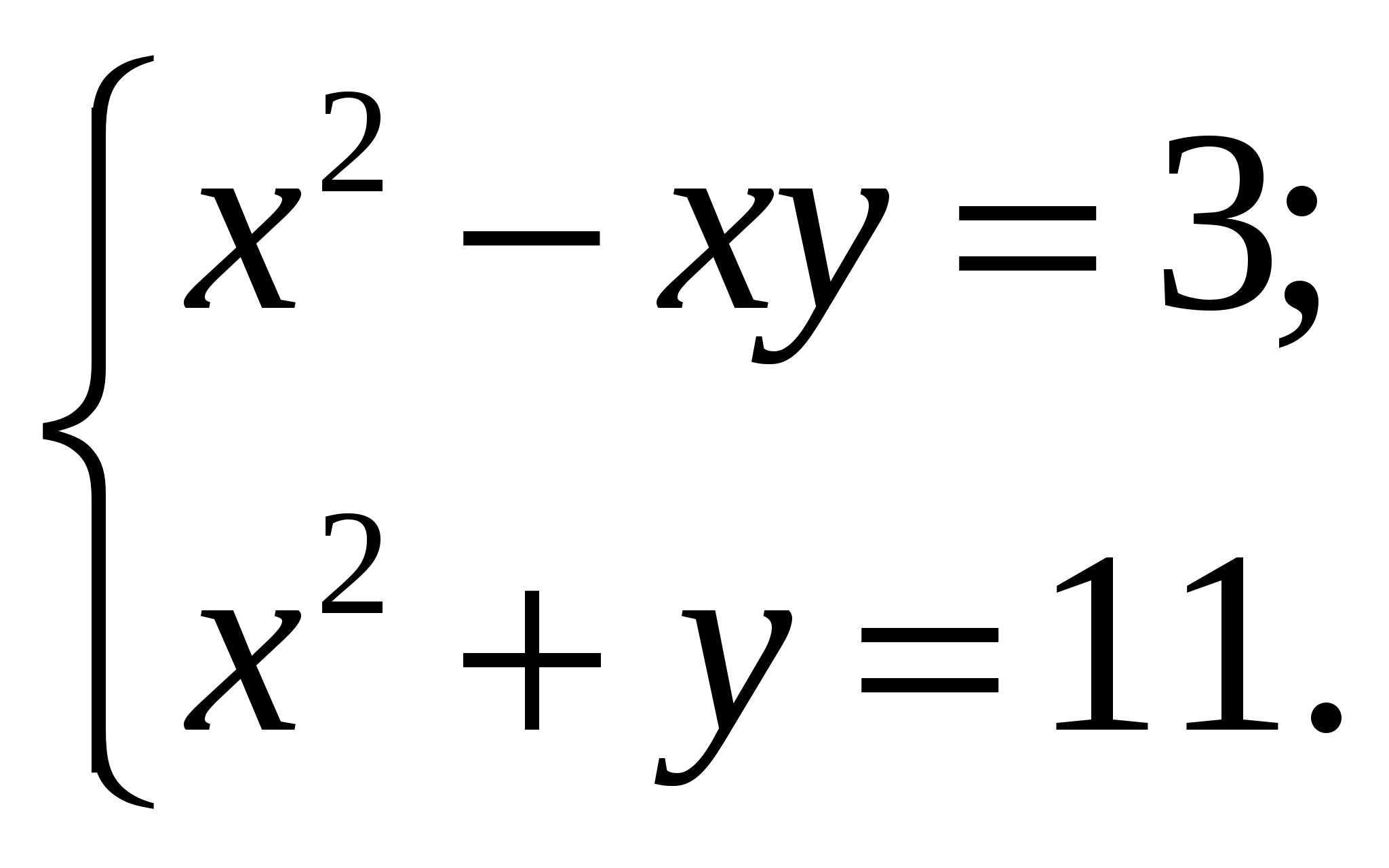
1) 1
2) 2
3) 3
4) 4
1. 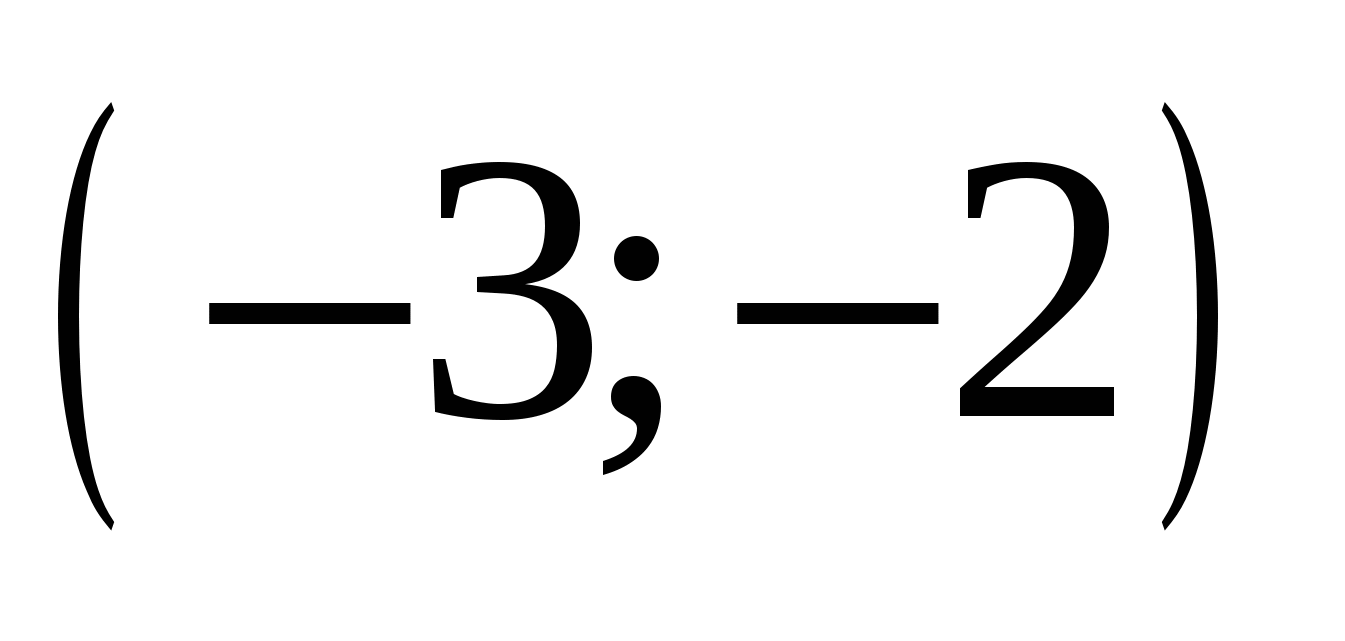
2. 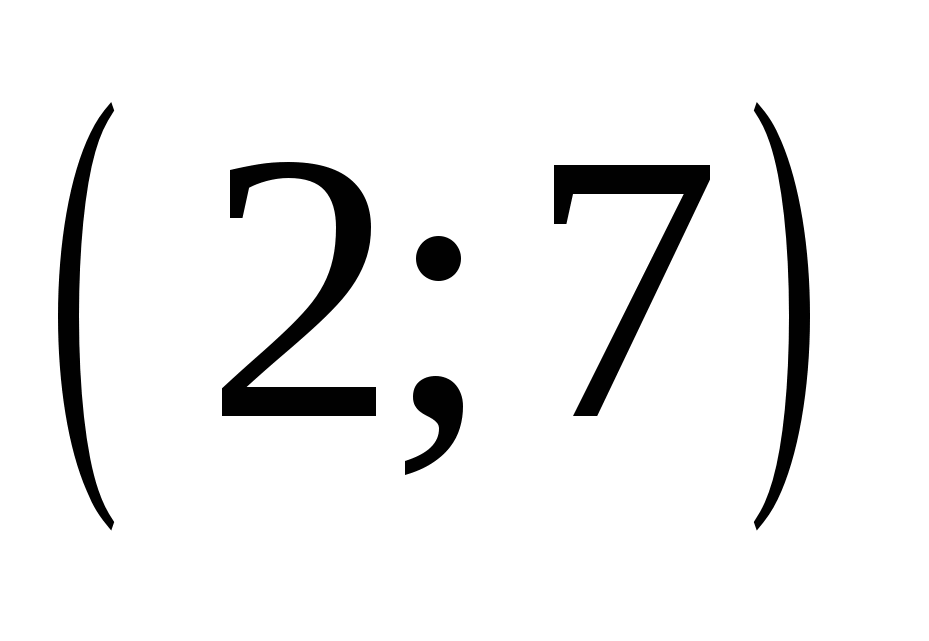
3. 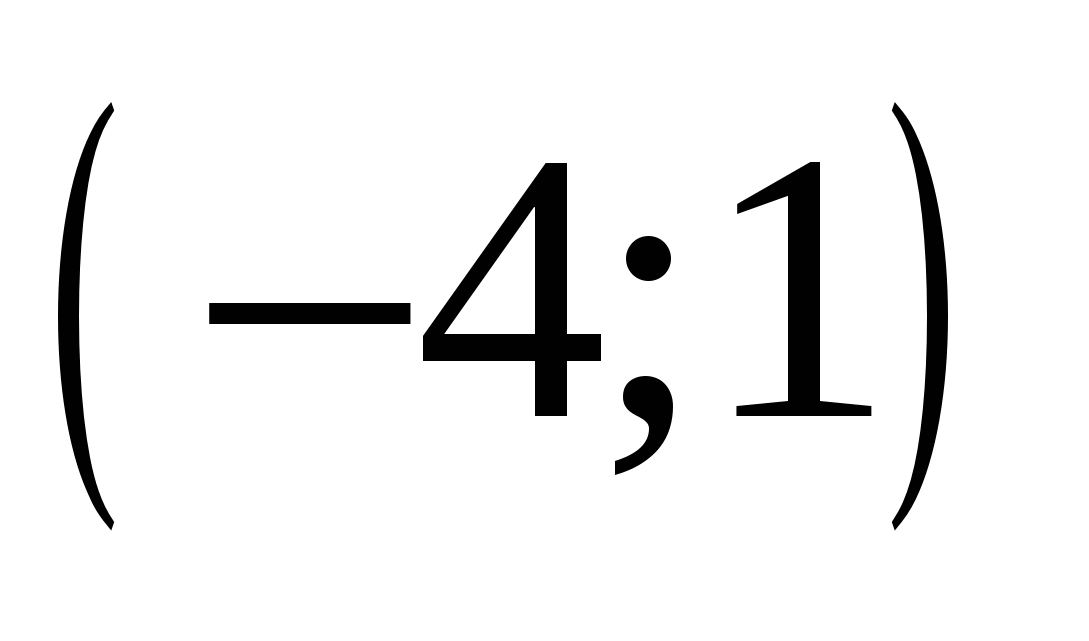
4. 
3.
Если 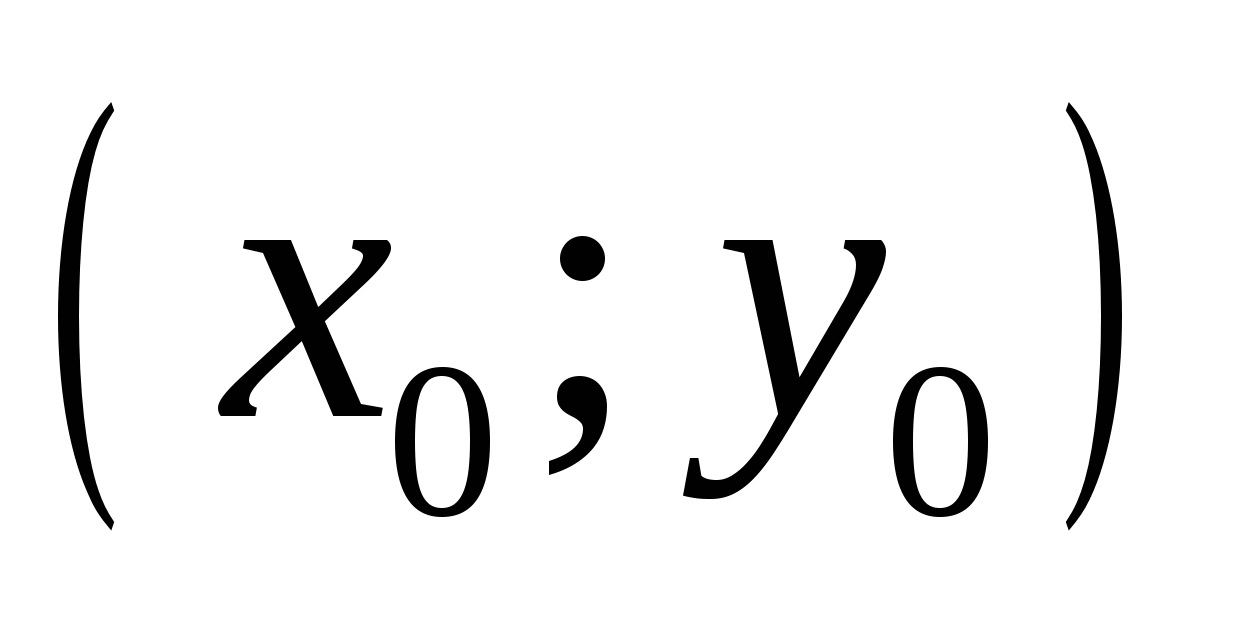 -решение системы уравнений
-решение системы уравнений 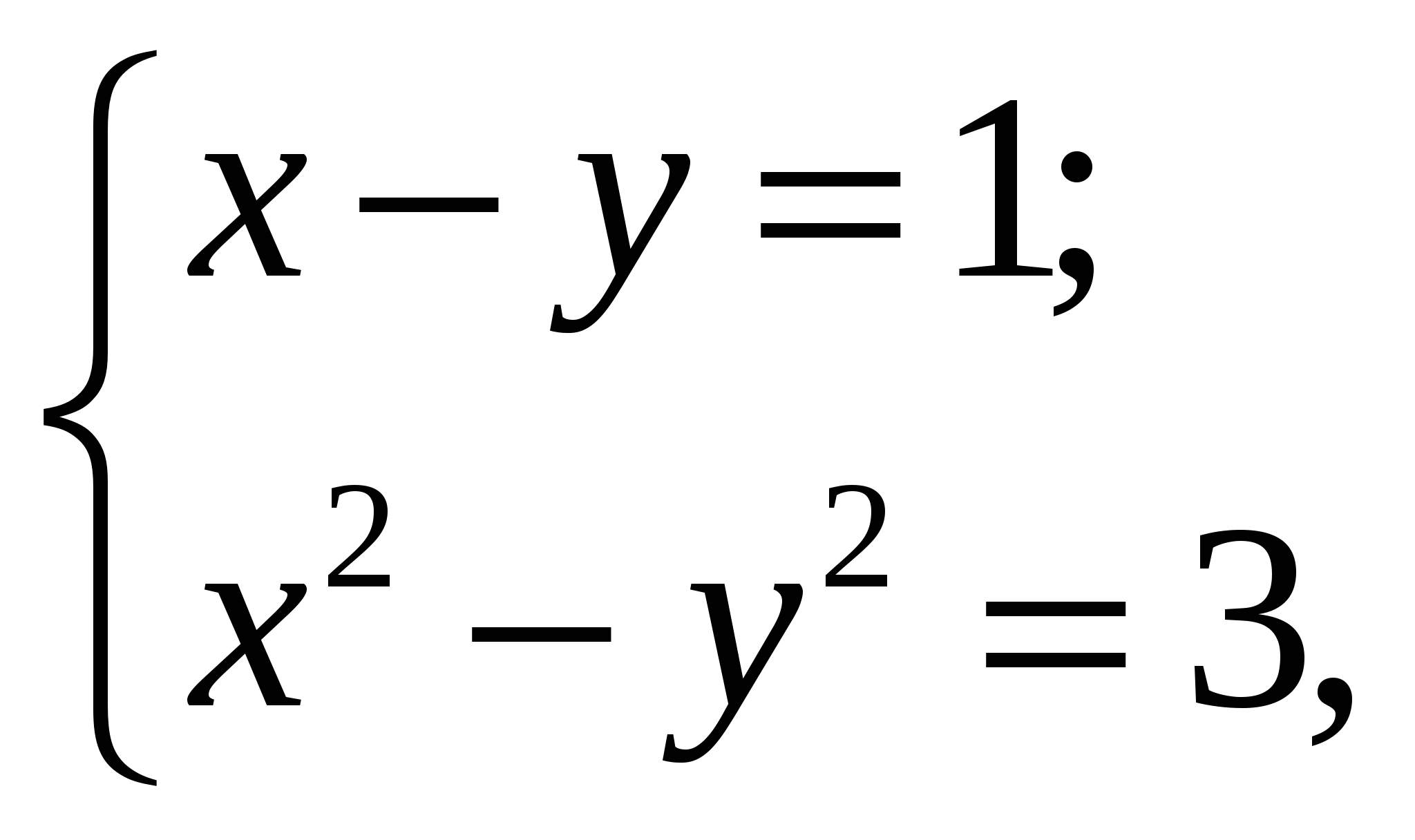
то значение  равно
равно
1) 1
2) 3
3) -2
4) 0
4.
Если 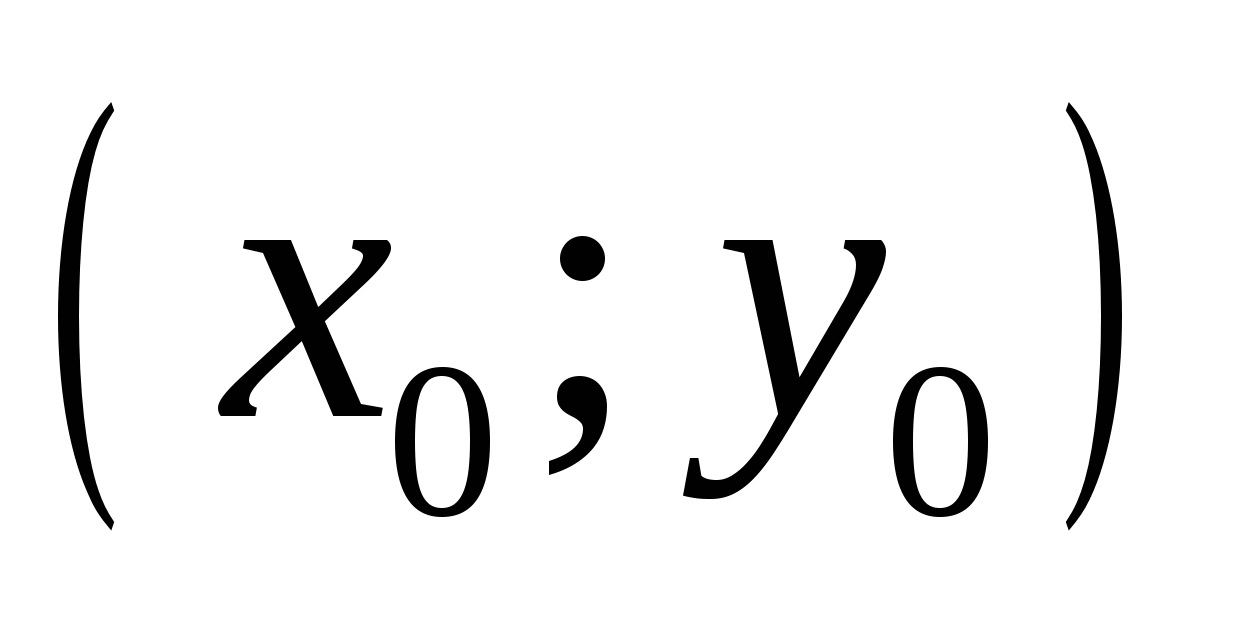 -решение системы уравнений
-решение системы уравнений 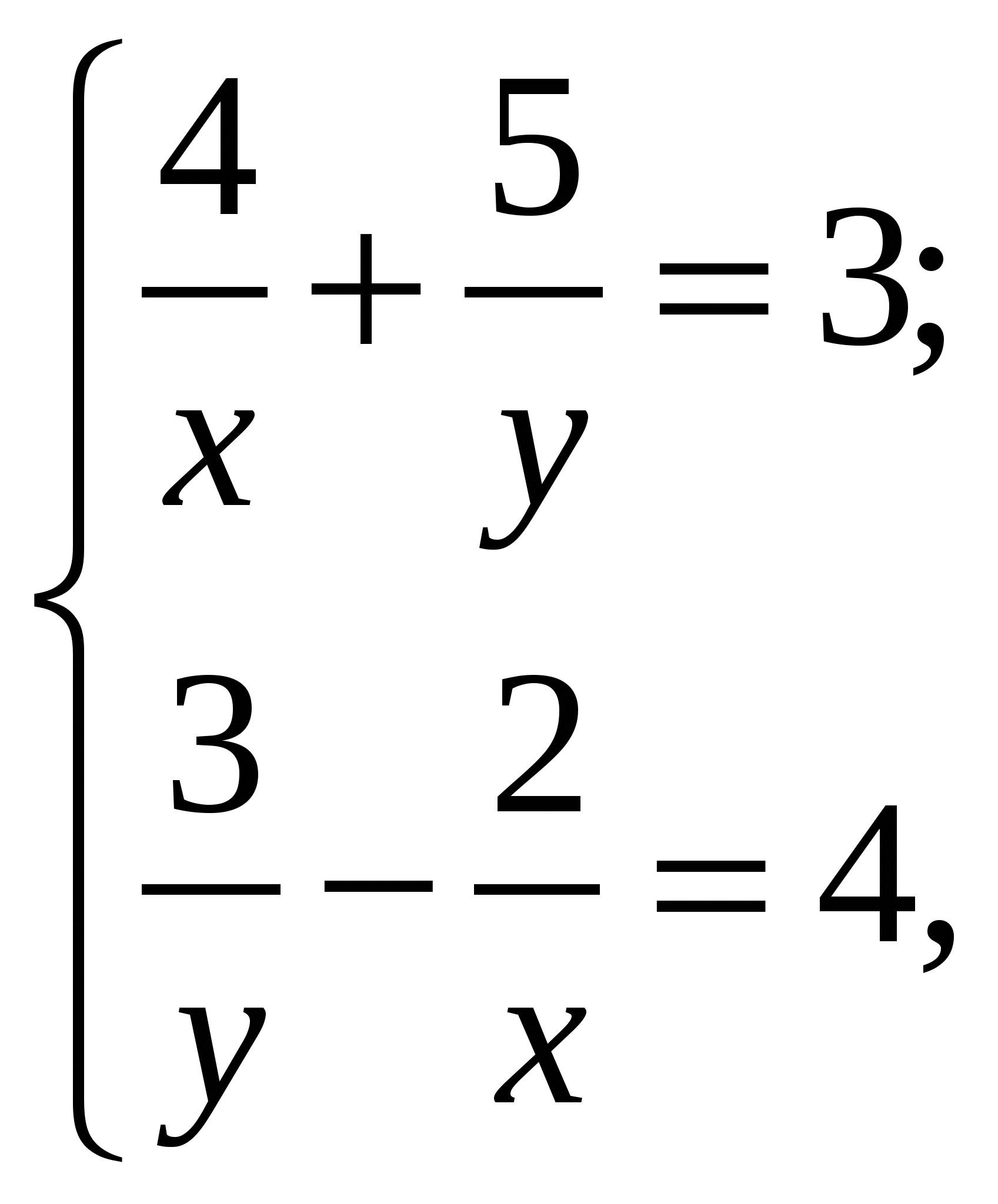 то значение
то значение 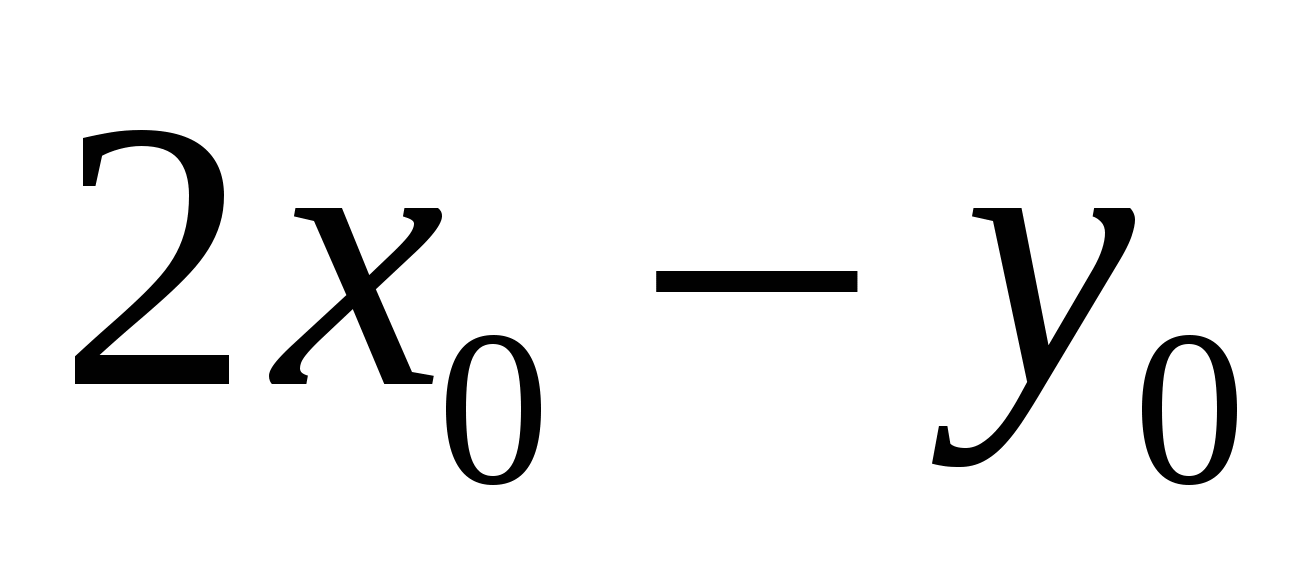 равно
равно
1) -5
2) —3
3) 1
4) 3
5.
При каком наибольшем целом значении параметра  система уравнений
система уравнений 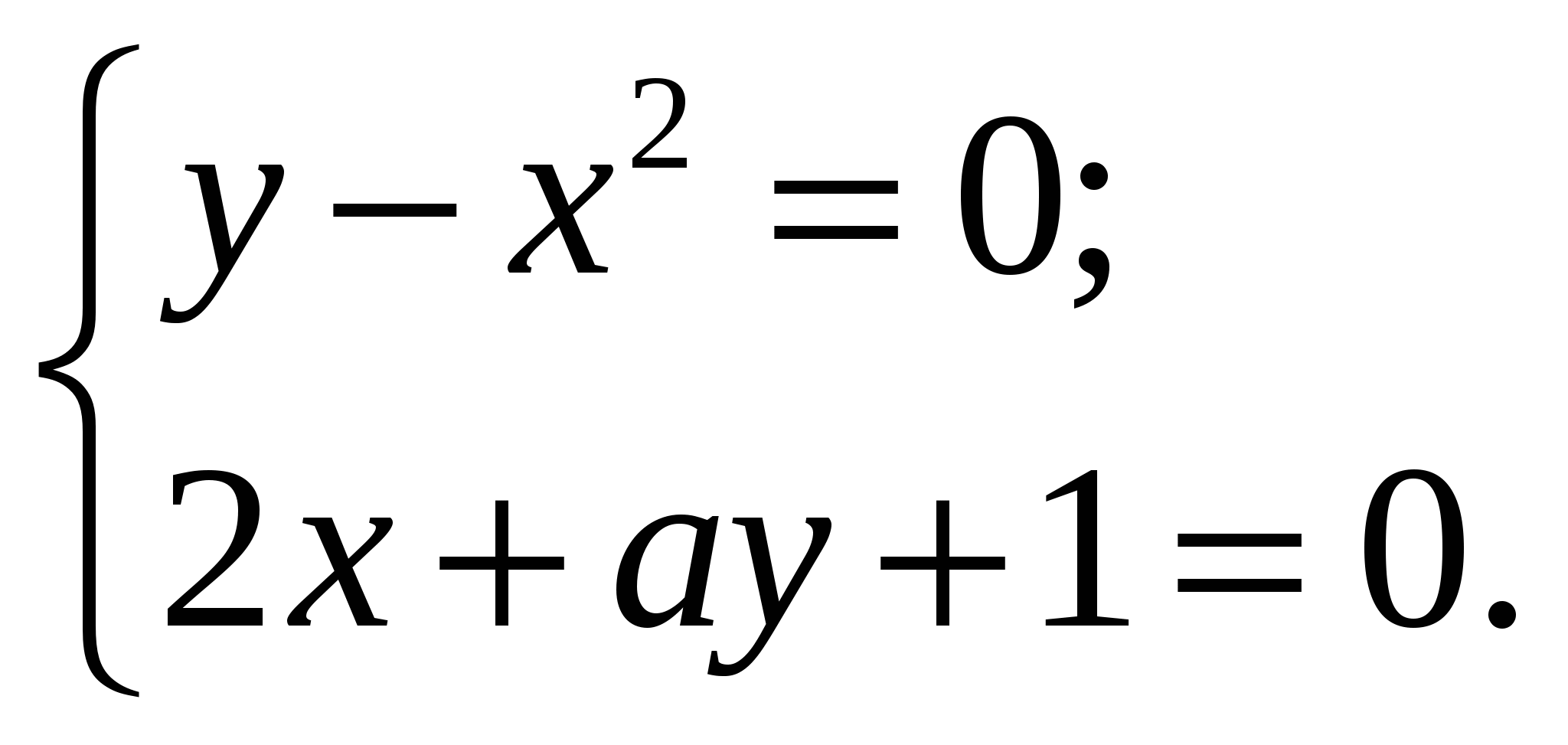 имеет два решения?
имеет два решения?
1) 0
2) 1
3) -1
4) -2
В6
Задание
Ответы
1.
Укажите рисунок на котором приведена графическая иллюстрация решения системы уравнений 
1) 1
2) 2
3) 3
4) 4
1. 
2. 
3. 
4. 
2.
Найдите пару чисел, являющуюся решением системы уравнений 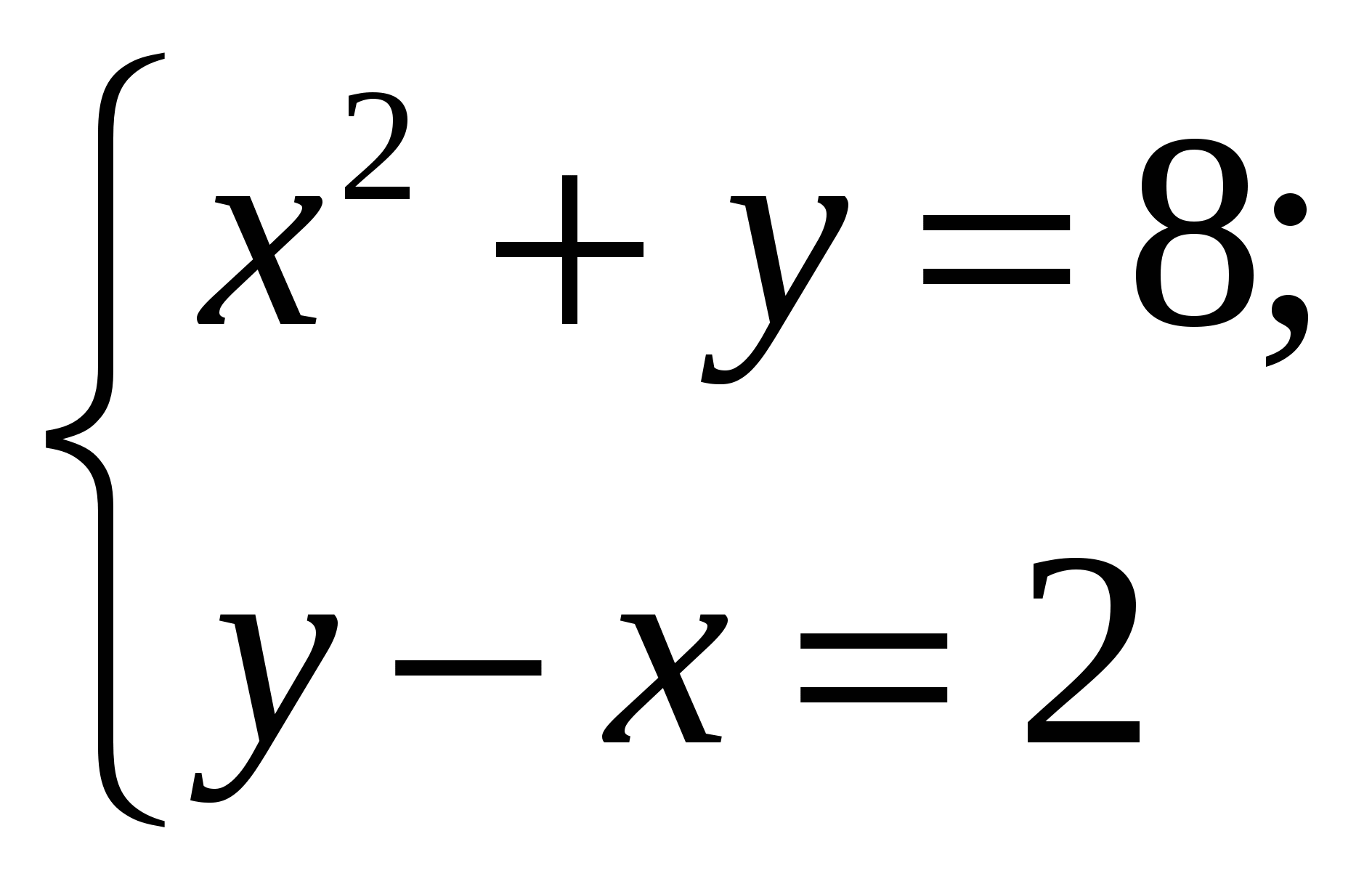
1) 1
2) 2
3) 3
4) 4
1. 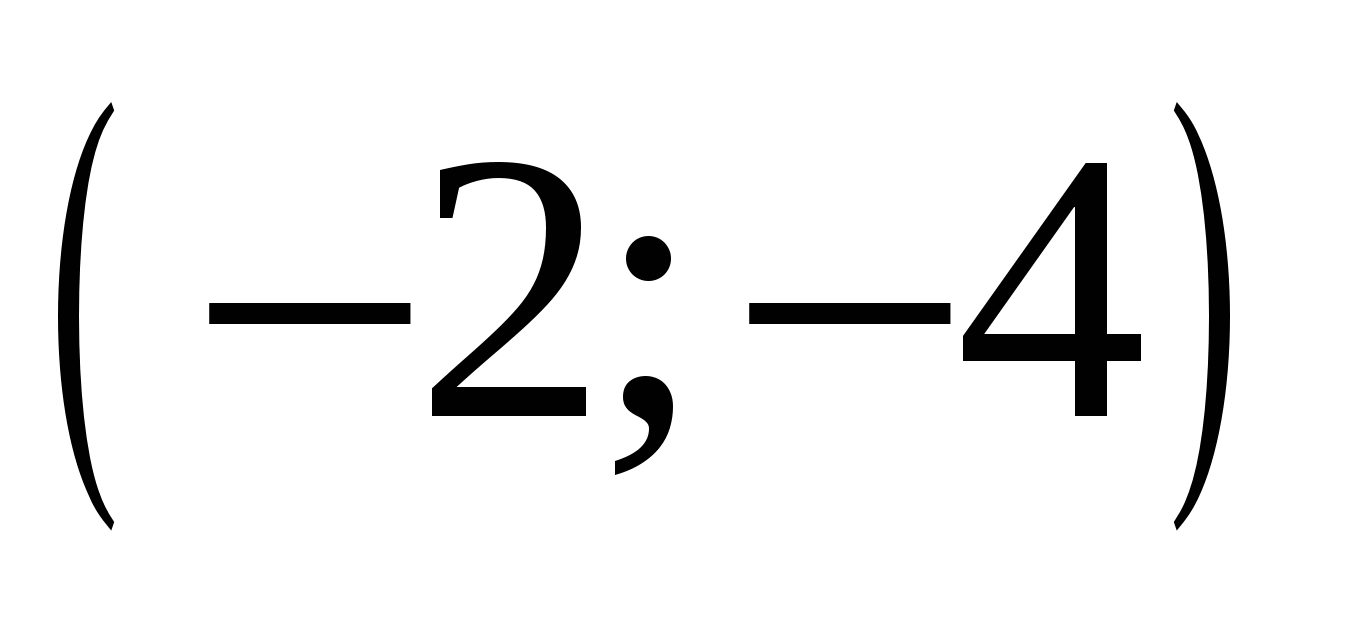
2. 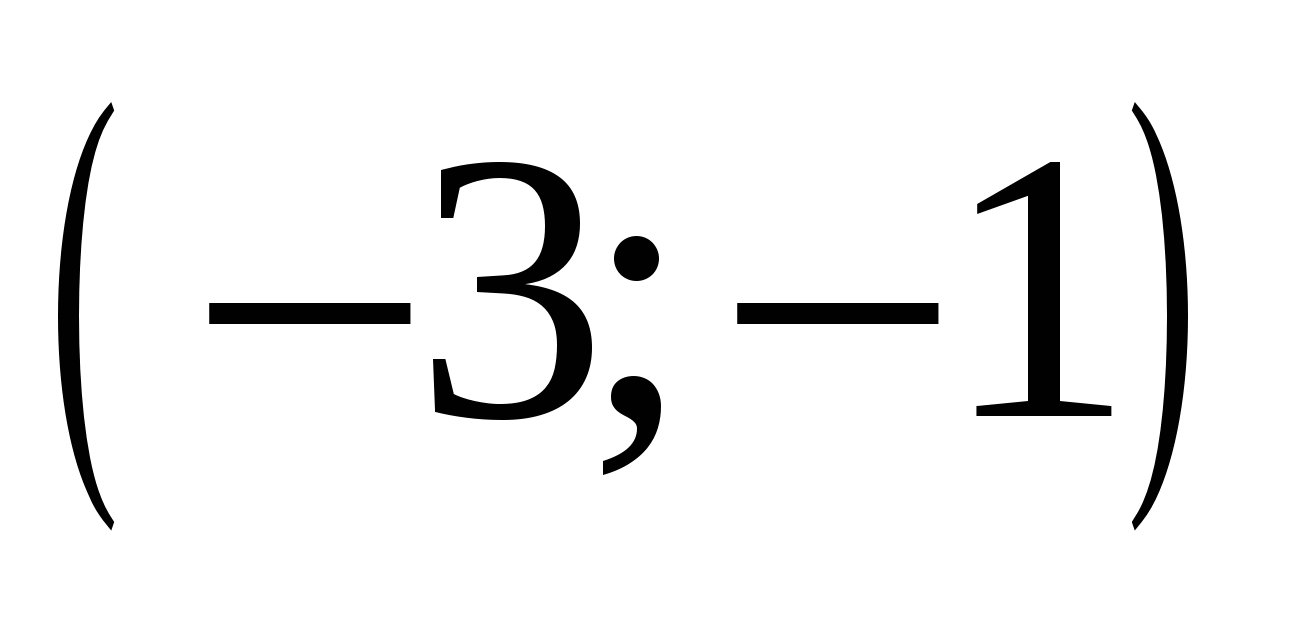
3. 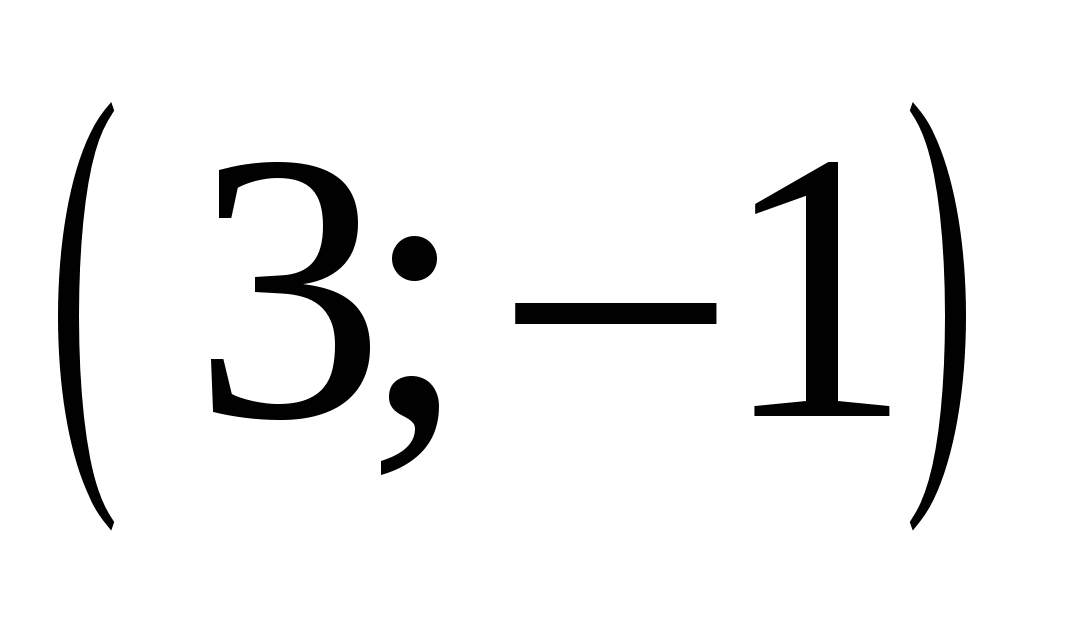
4. 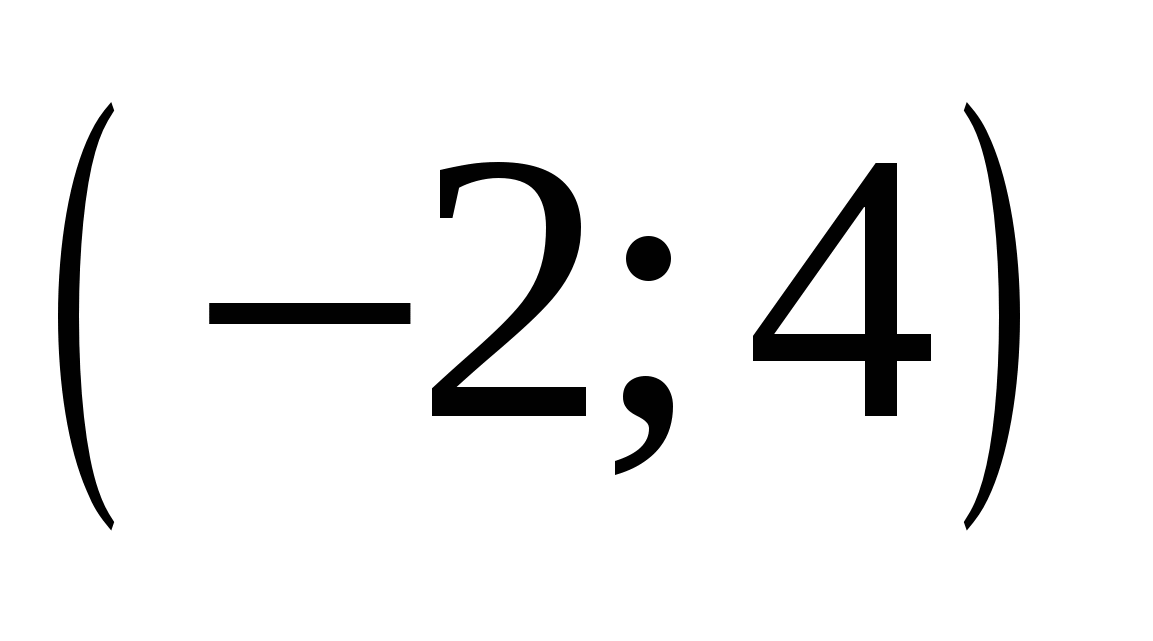
3.
Если 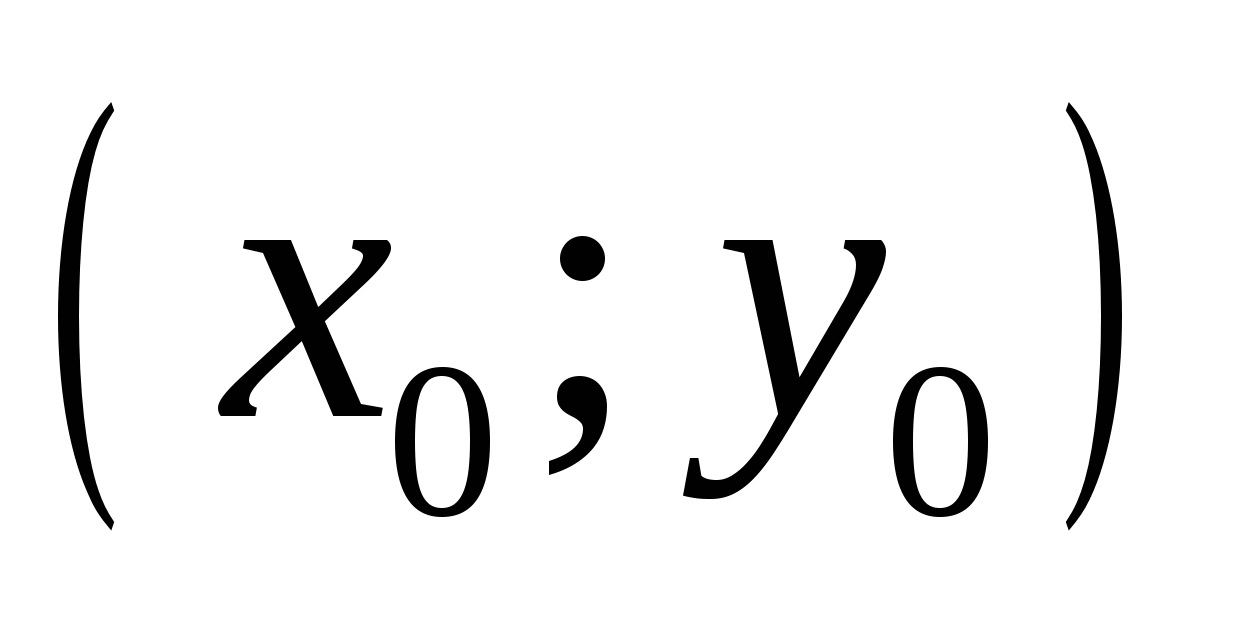 -решение системы уравнений
-решение системы уравнений 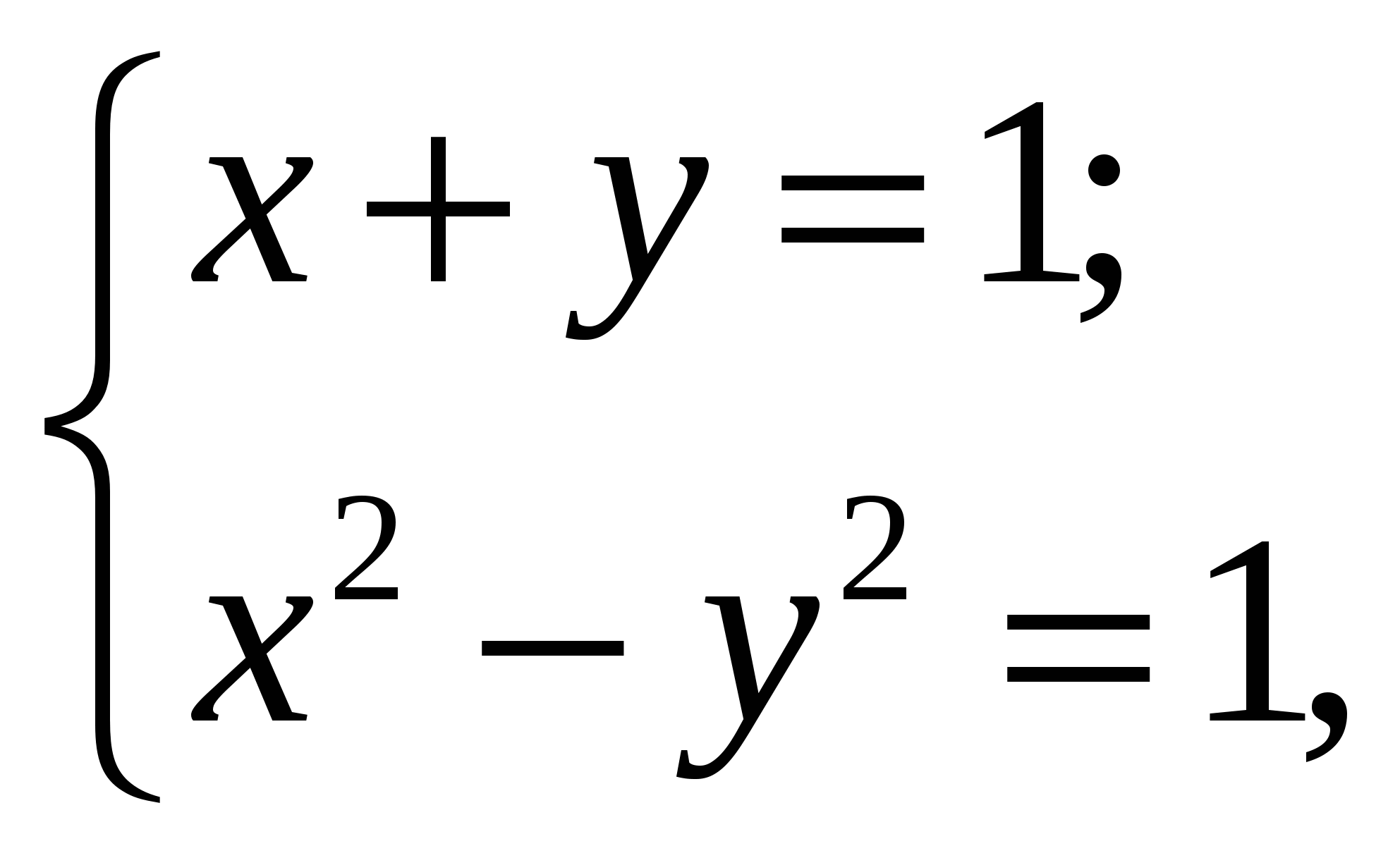
то значение  равно
равно
1) 1
2) -1
3) —2
4) 3
4.
Если 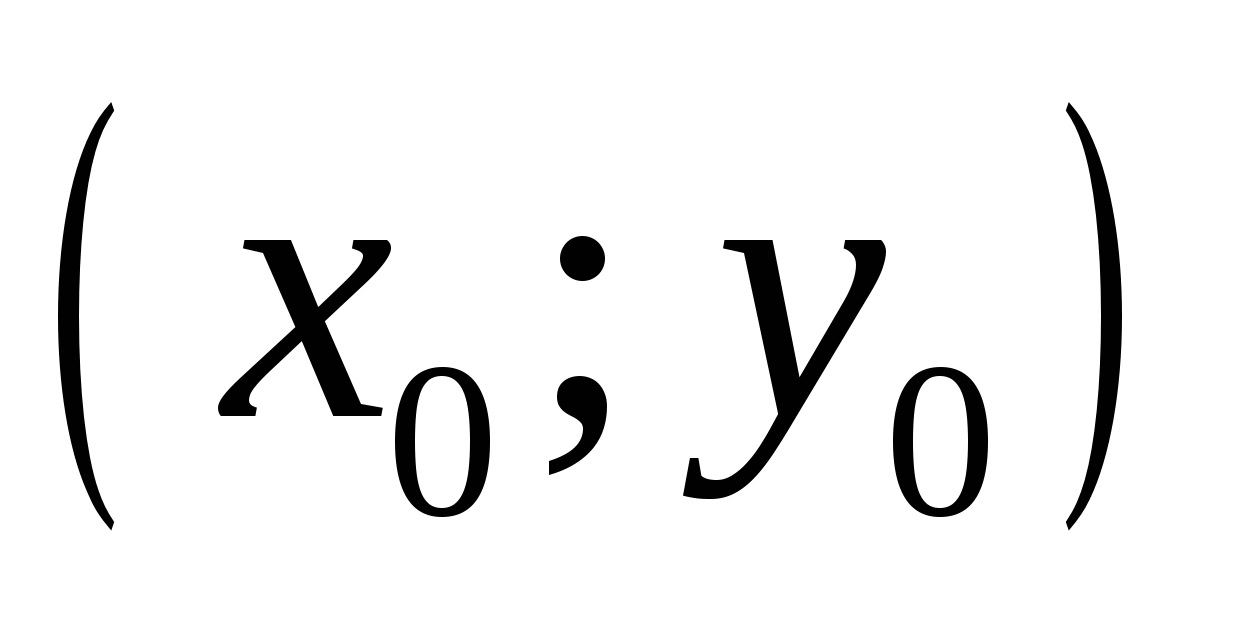 -решение системы уравнений
-решение системы уравнений 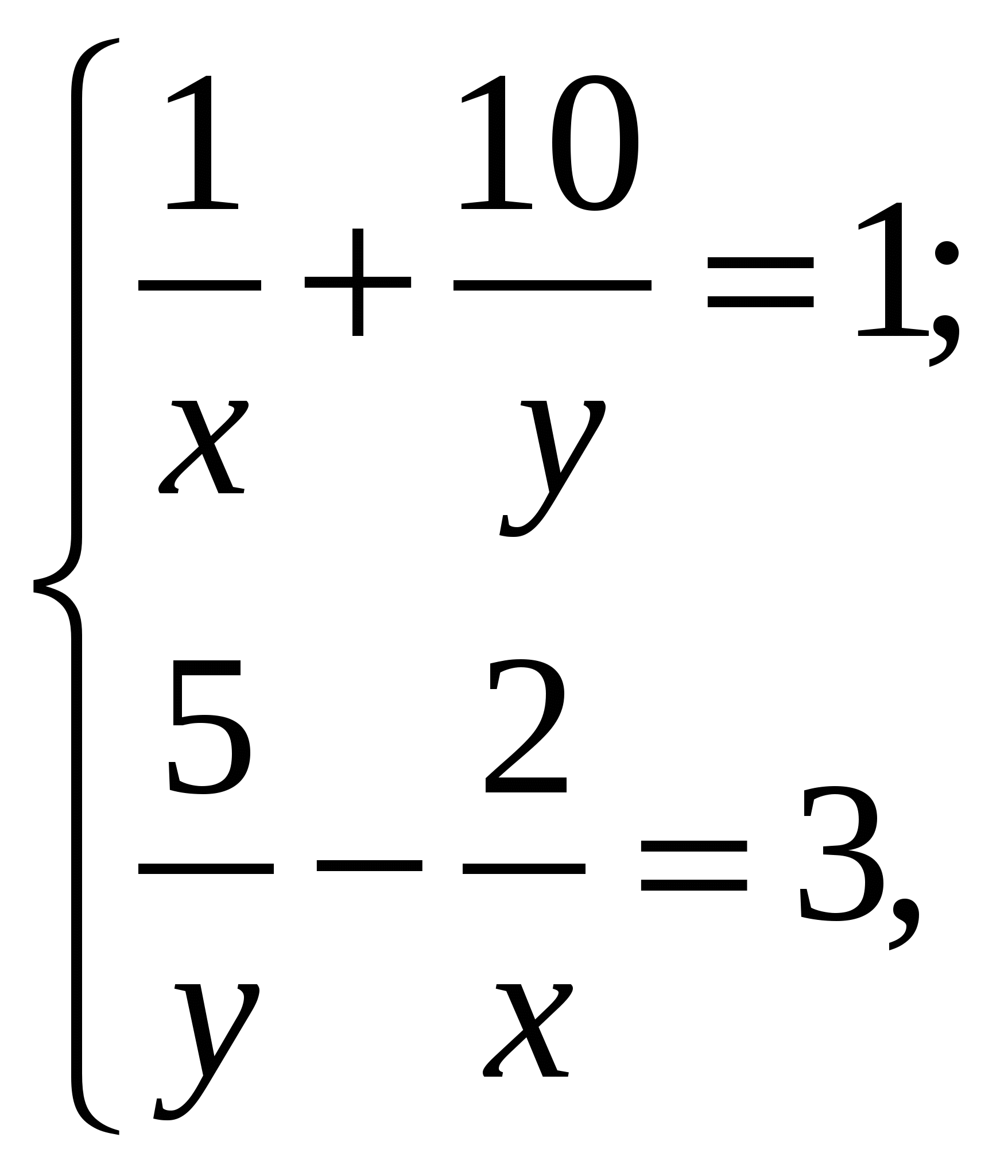 то значение
то значение 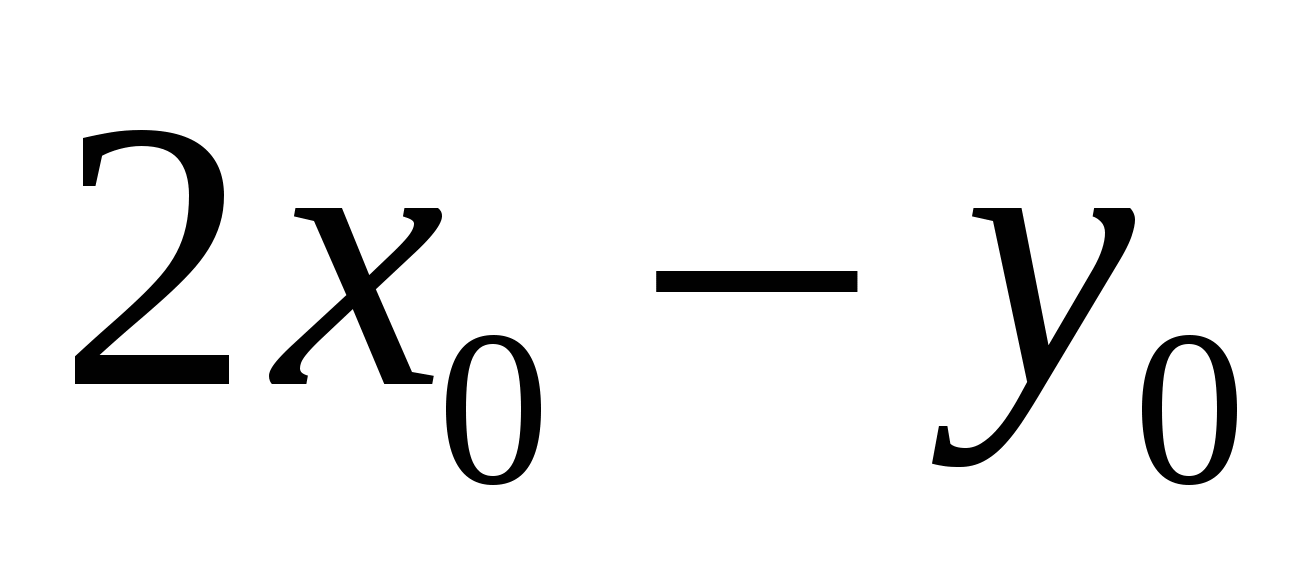 равно
равно
1) 7
2) 1
3) -1
4) -7
5.
При каком наименьшем целом значении параметра  система уравнений
система уравнений 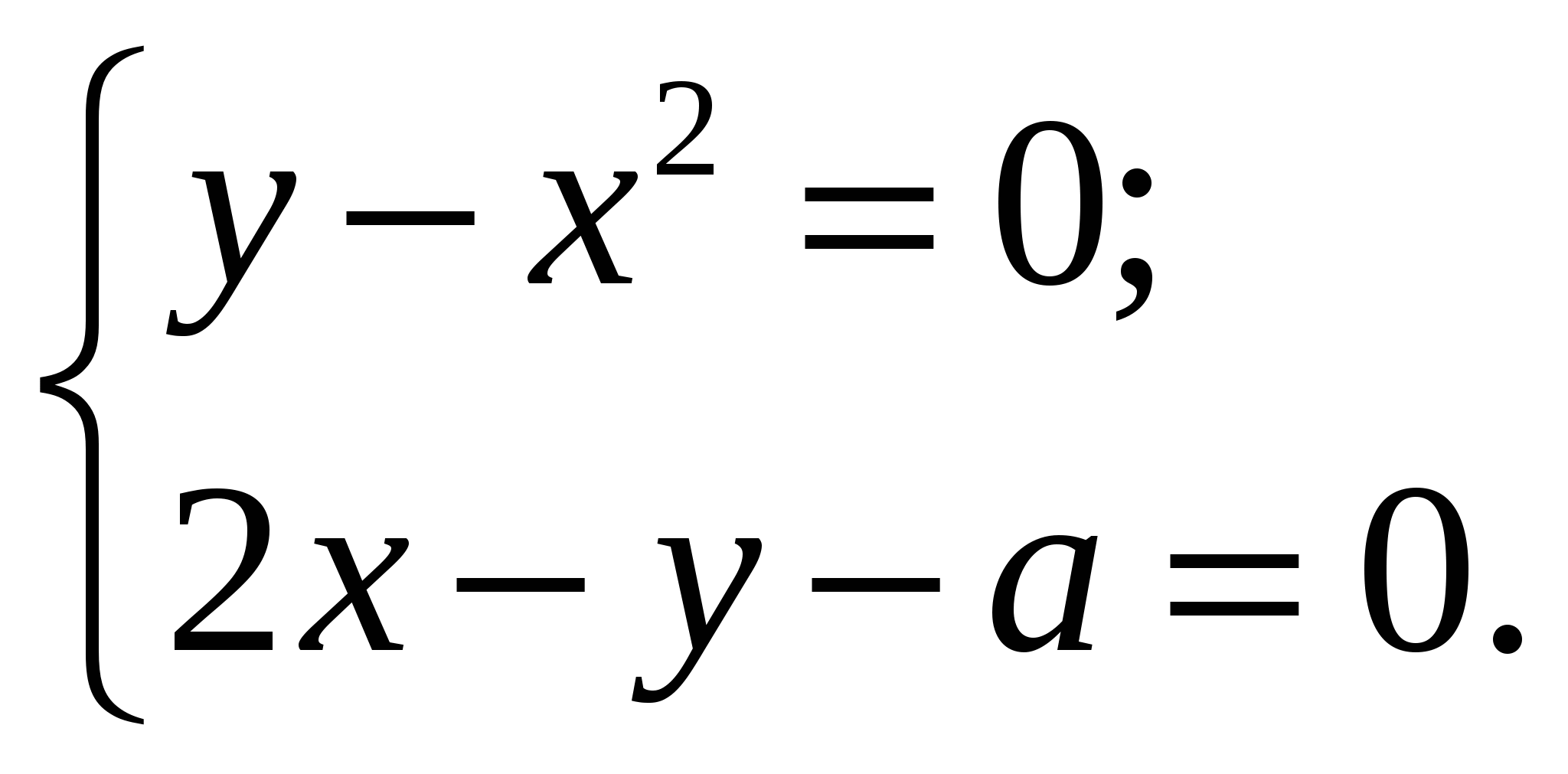 не имеет решений?
не имеет решений?
1) 0
2) 1
3) 2
4) 4
Ответы к тесту
Вариант
1
2
3
4
5
1
3
4
2
1
2
2
1
4
3
3
3
3
2
3
1
4
3
4
4
2
1
3
2
5
3
4
2
1
1
6
2
2
1
4
3
Подведение итогов урока (2 минуты).
Домашнее задание.
Придумать и решить задачу при помощи системы уравнений.

Урок состоялся и прошел живо и интересно. Присутствующие на нем учителя отмечали располагающую к сотрудничеству атмосферу, открытость и расположенность детей, их готовность преодолевать трудности и желание учиться.
Урок алгебры в 9 класса по теме: Методы решения системы уравнений
Урок алгебры в 9 классе по теме:
Методы решения систем уравнений.
Цели:
обучающая: повторение ранее изученного материала; закрепить умения учащихся решать системы уравнений; проверить уровень сформированности навыков решения системы уравнений;
развивающая: развить познавательную активность, самостоятельность учащихся; развить логическое мышление, память, учащихся;
воспитательная: воспитание внимательности, аккуратности при выполнении письменных заданий, воспитание трудолюбия, инициативности
Ход урока.
Организационный момент.Эпиграф:
Скажи мне, и я забуду,
покажи мне, и я, может быть, запомню,
вовлеки меня, и я пойму.
Конфуций (450г. до н.э.)
«Быть сильным хорошо, быть умным лучше вдвое»
(пословица)
Устная работа.
Фронтальный опрос класса (Слайд №2-4).
Фронтальный опрос класса (Презентация учащегося, гиперссылка с 4 слайда).
Актуализация знаний.
Сегодня на уроке мы продолжаем рассматривать примеры решения системы двух уравнений с двумя неизвестными.
Какие способы решения системы уравнения Вам известны?
Первый способ решения системы уравнений. (Слайд № 5). Дополни рассуждения:
Способ подстановки.
Решение.
Первое уравнение системы – уравнение ____ степени, второе уравнение системы – уравнение _______ степени.
1.Выразим из ________________ переменную x через переменную y: x=4-2y
2.Подставим ____________ вместо x в __________, получим ______________:
3. __________________ уравнение.
4. Подставим в выражение x=4-2y _________, и найдем ____
5. Система уравнений имеет решения:
Ответ.
Рассмотрим второй способ решения системы уравнений.
Решение.
Данная система уравнений содержит уравнения первой и второй степени.
Обращаем внимание на то, что коэффициенты при одном из неизвестных, y, противоположны по знаку. Поэтому здесь удобно воспользоваться способом _____________.
1. Складывая ____________, мы получим уравнения с одним неизвестным.
+
__________________________
2._______________________
Найдем его корни:_____________
3. _______________ значения x1,x2 в любое уравнение системы:
Найдем значения ______________
Ответ.
3.Рассмотрим третий способ решения системы уравнений.
Графический способ

4.Рассмотрим четвертый способ решения системы уравнений.
Метод введения новой переменной
Слайд
Закрепление материала.
Тесовые задания на 2 варианта
Домашнее задание.
1.
Итог урока.
Выбери пословицу, которая тебе ближе и запиши ее на обратной стороне тестового листа:
— Набирайся ума в ученье, храбрости в сраженье.
— Без муки нет науки.
— Была бы охота — заладится всякая работа.
— Математика – гимнастика ума.
Проверки выполнения тестирования
-Чему научились на уроке?
-Какие затруднения у вас были?
-Какой материал из пройденного вам понадобился сегодня на уроке?
-Как выбрать способ решения системы уравнений? Что при этом необходимо учитывать?
Проверка готовности учащихся к уроку.
Сообщение целей урока.
Проверка знания теоретического материала. Выражение одной переменной через другую, графики уравнений
Ответы учащихся.
Ученики выполняют тесты
Комментарий выполнения домашнего задания.
Выставление оценок учащимся за работу на уроке, комментирование работы учащихся.
«Решение систем уравнений» (9 класс)
 Министерство образования и науки Республики Бурятия
Министерство образования и науки Республики Бурятия
Средняя общеобразовательная школа №49
План – конспект открытого урока по алгебре в 9 политехническом классе
Тема: «Решение систем уравнений»
Учитель математики: Цыдендоржиева В.А.
г. Улан – Удэ
2012 – 2013 учебный год
План-конспект открытого урока по алгебре в 9 «политехн» классе.
Тема: «Решение систем уравнений».
Цель урока:
Обобщить и систематизировать знания о способах решения систем уравнений;
Закрепить навыки и умения решения систем уравнений.
Проверка домашнего задания.
Решите системы уравнений:
а) 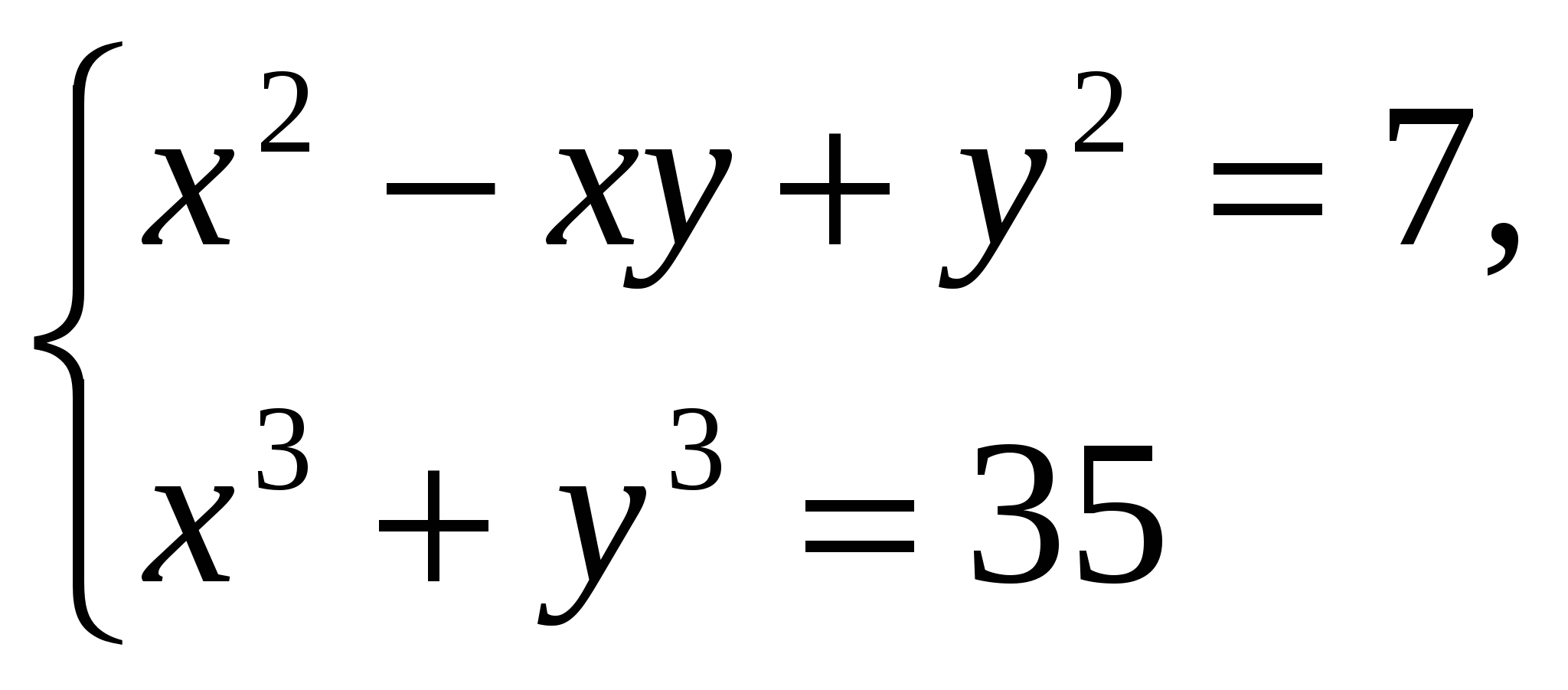
б) 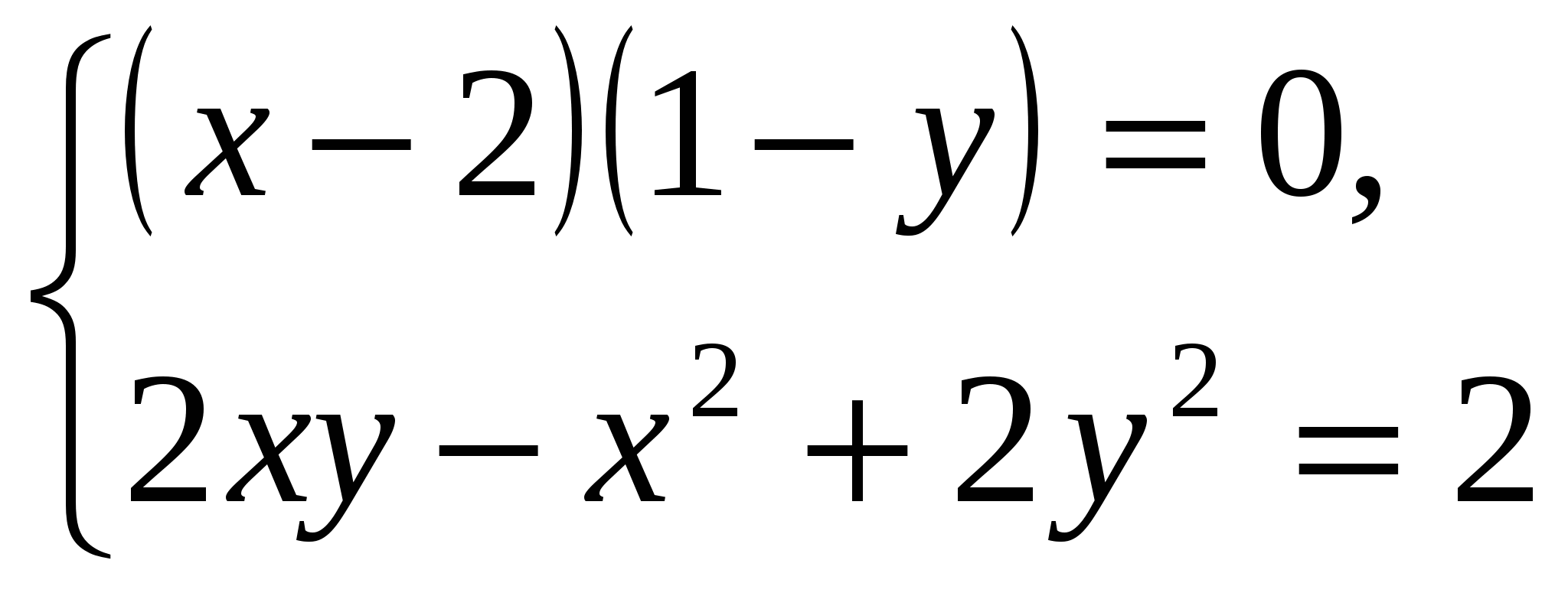
2. При каких значениях  система уравнений имеет одно решение?
система уравнений имеет одно решение?
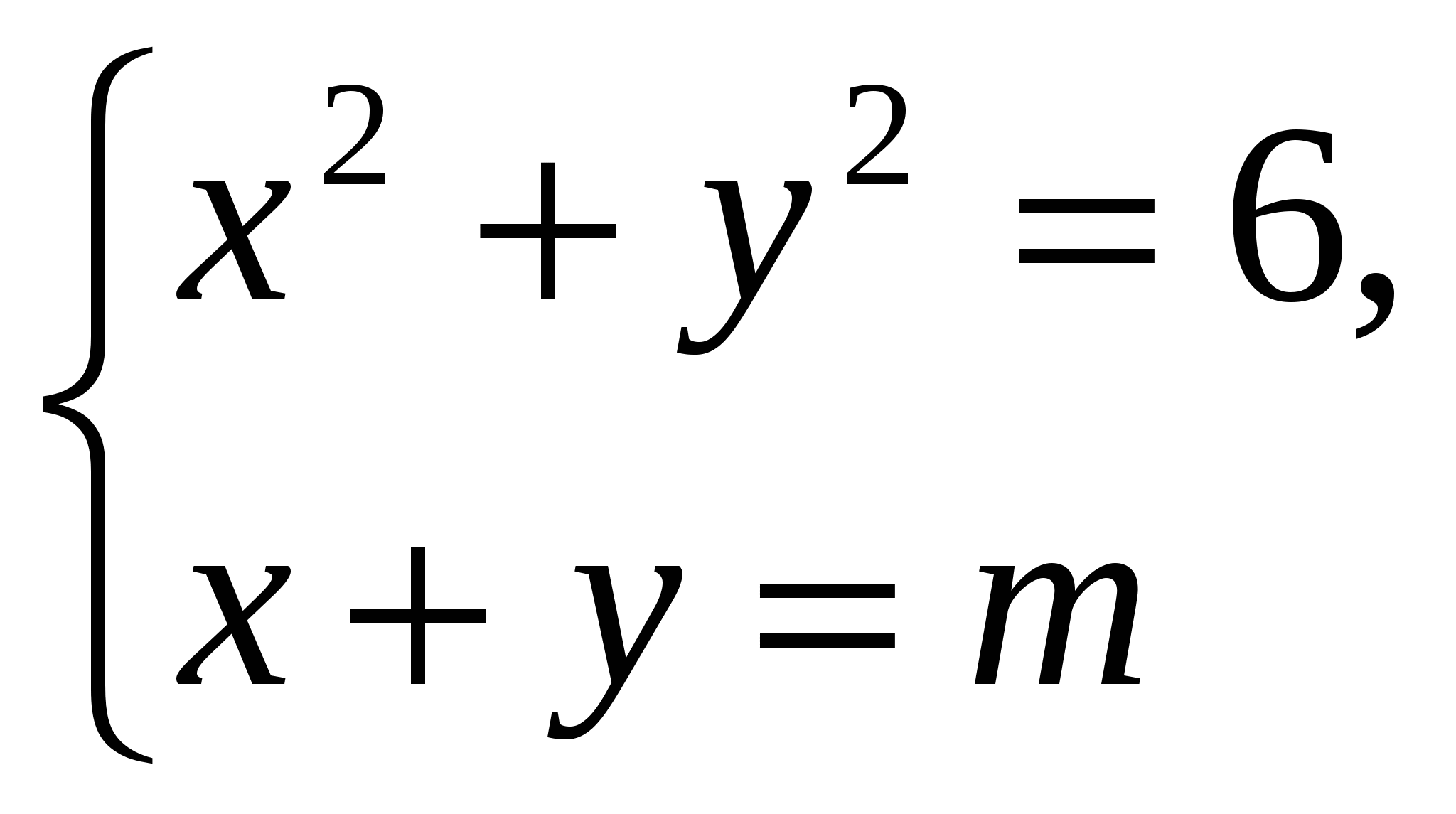
Решение: 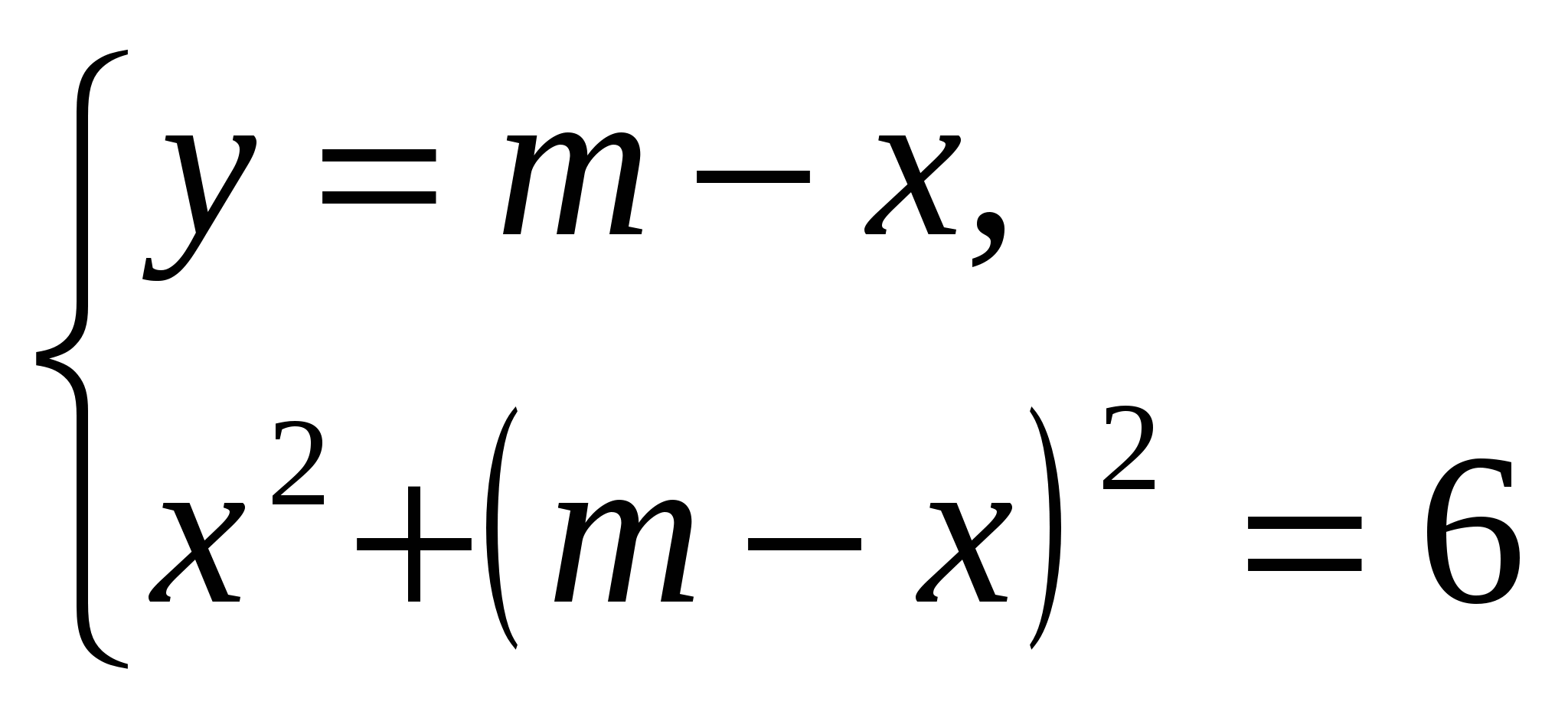
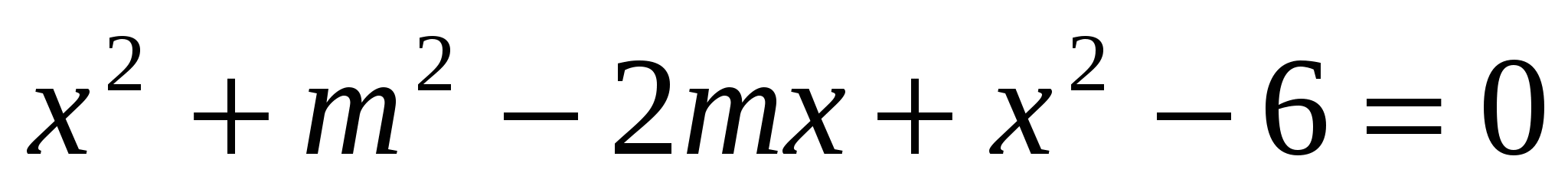
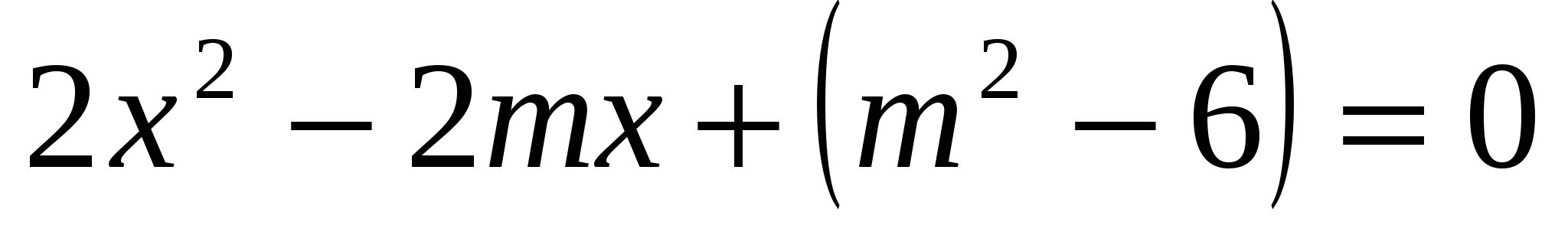

Чтобы система имела одно решение, уравнение должно иметь одно решение, значит 
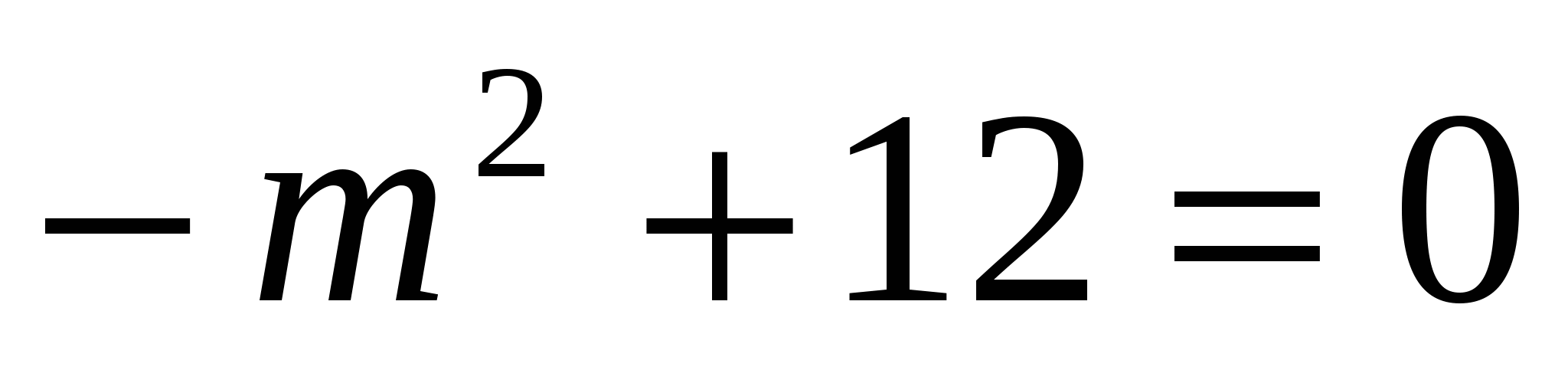
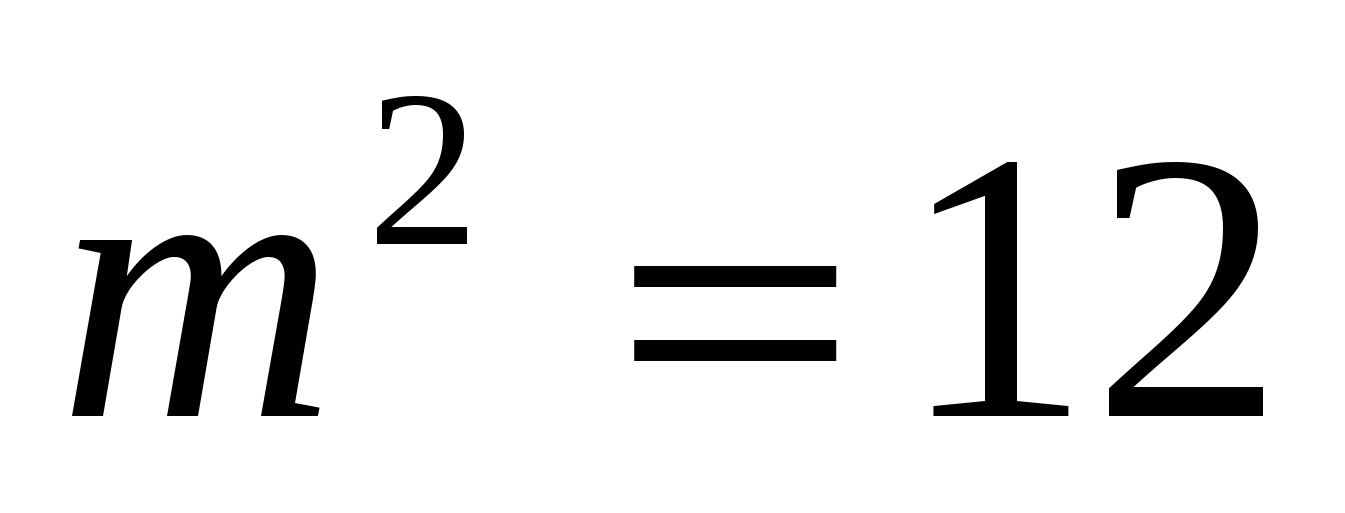
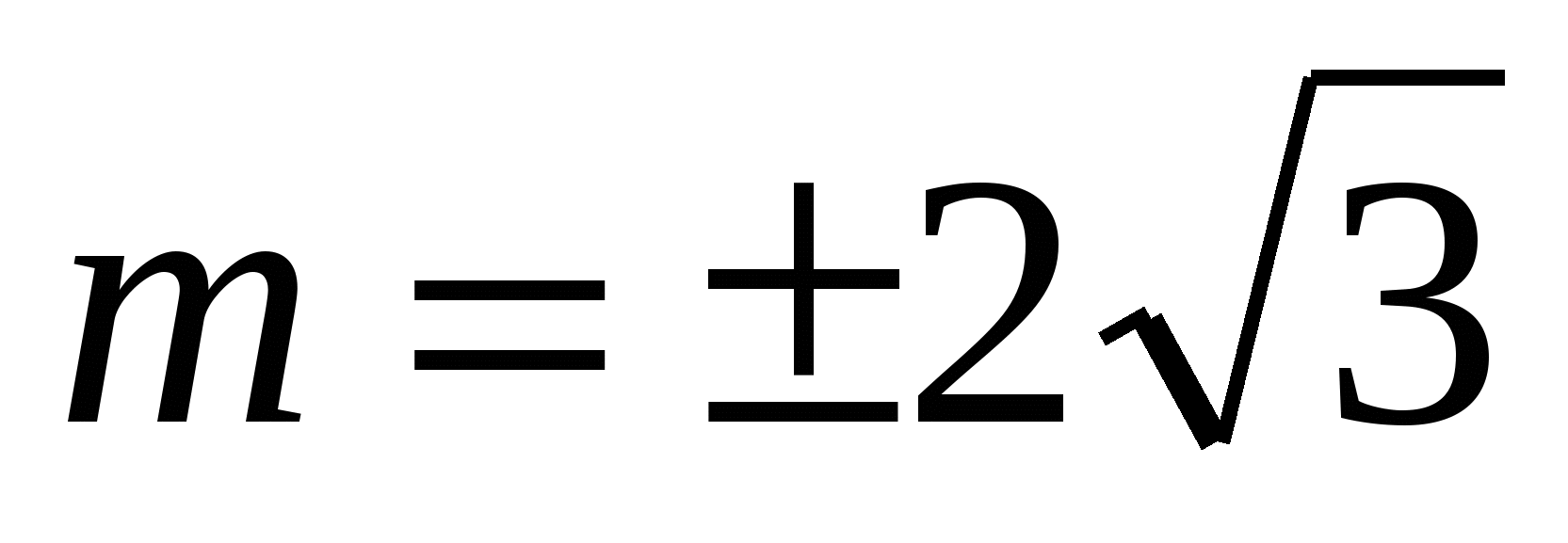
Ответ: система уравнений имеет одно решение при 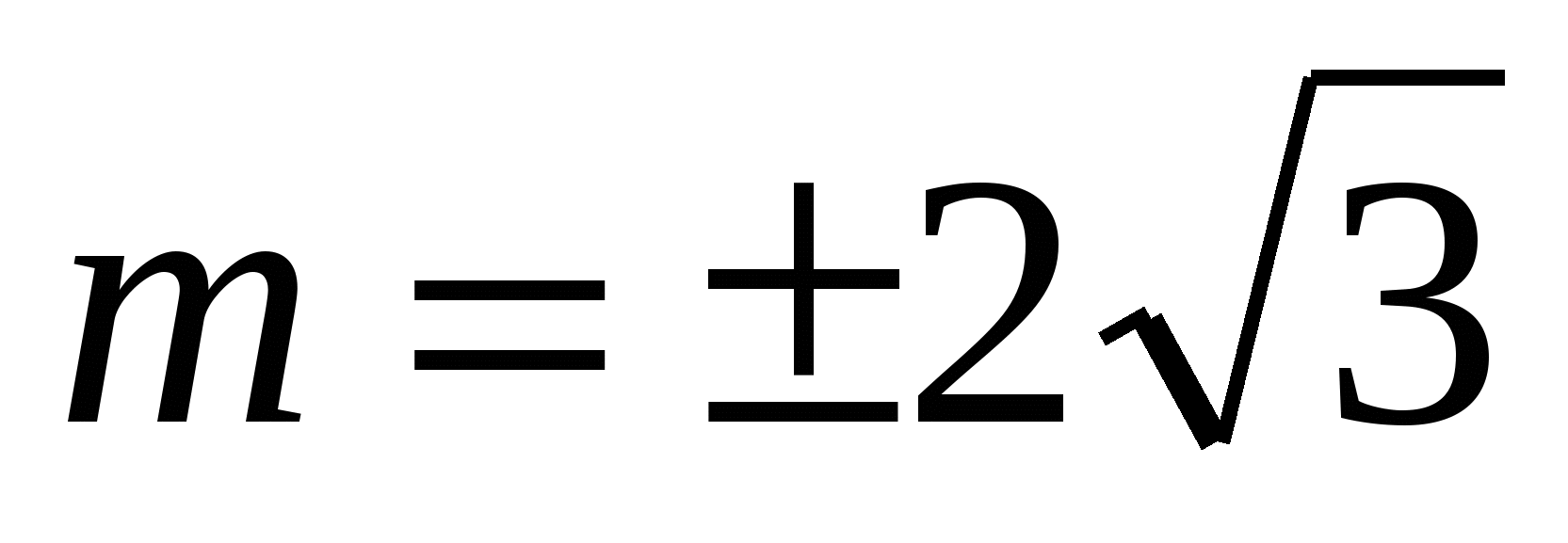 .
.
А может ли система иметь два решения? При каком условии?
Ответ: если 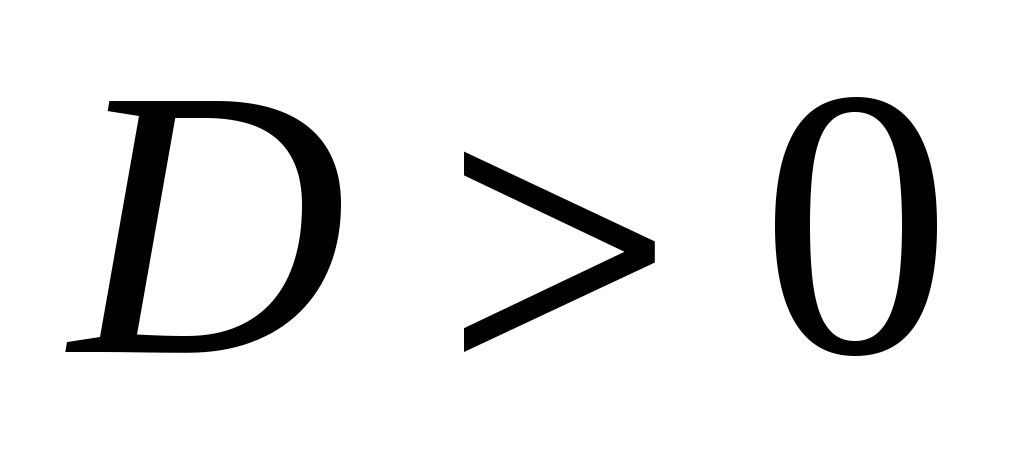 , т.е.
, т.е. 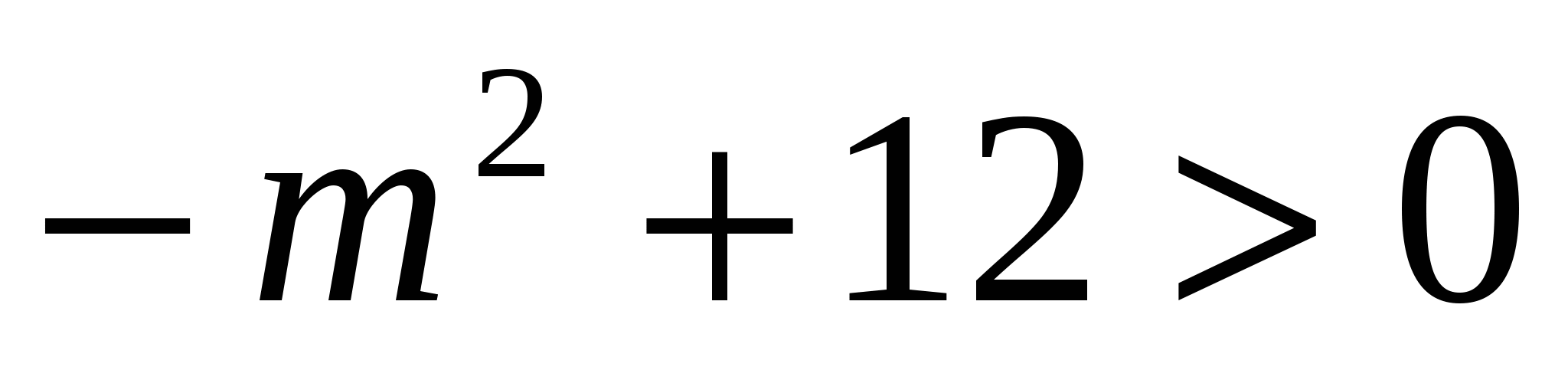
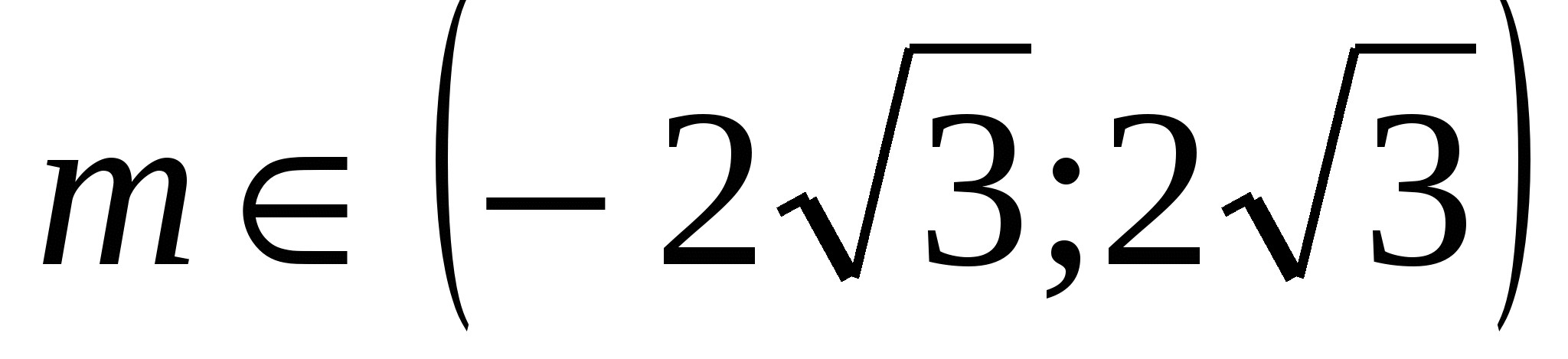 .
.
Устные упражнения:
1. Приготовьте черновики для кратких записей при решении систем уравнений.
Определите, сколько решений имеет система уравнений.
а) 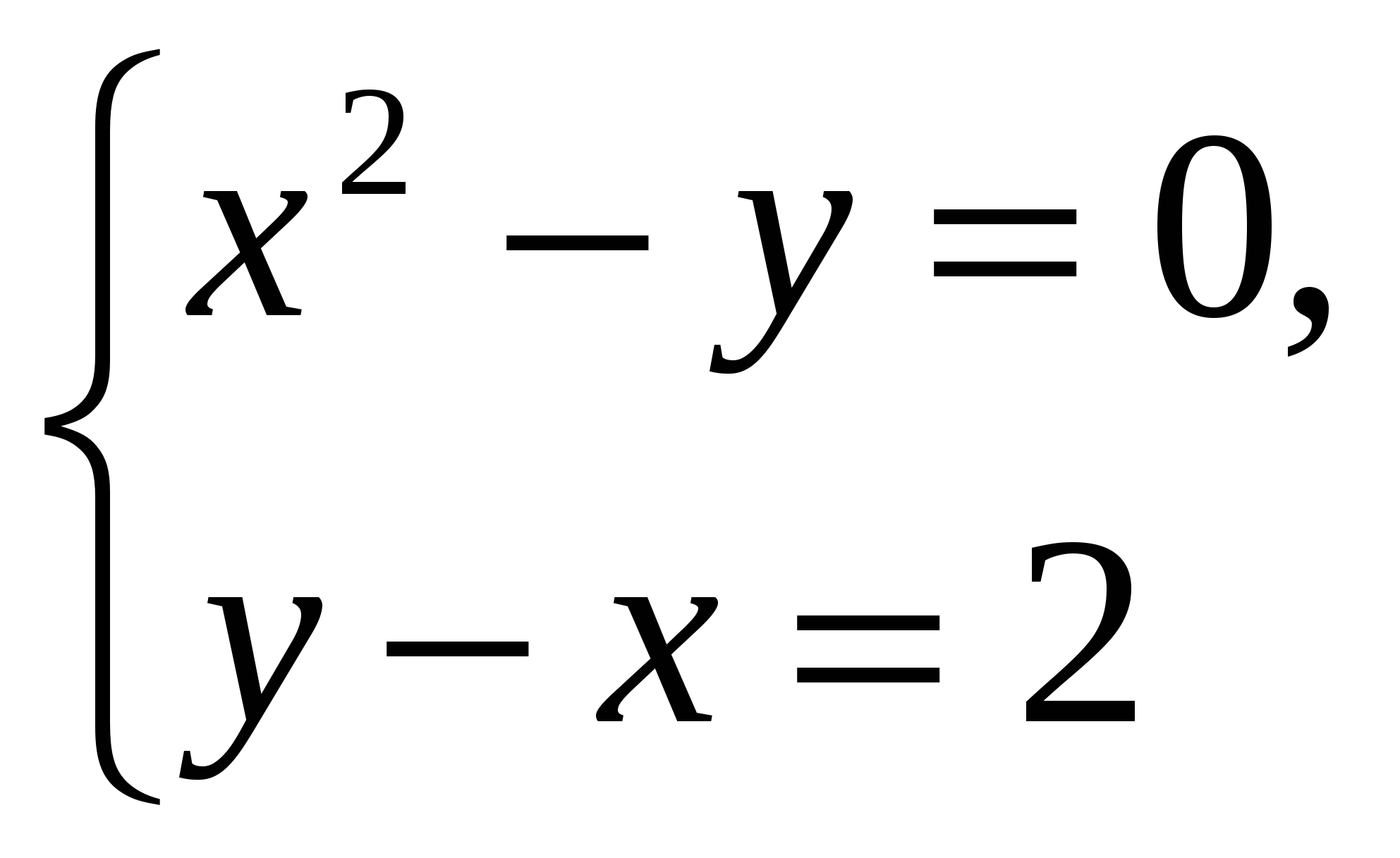 Ответ: 2
Ответ: 2
б)  Ответ: 2
Ответ: 2
в) 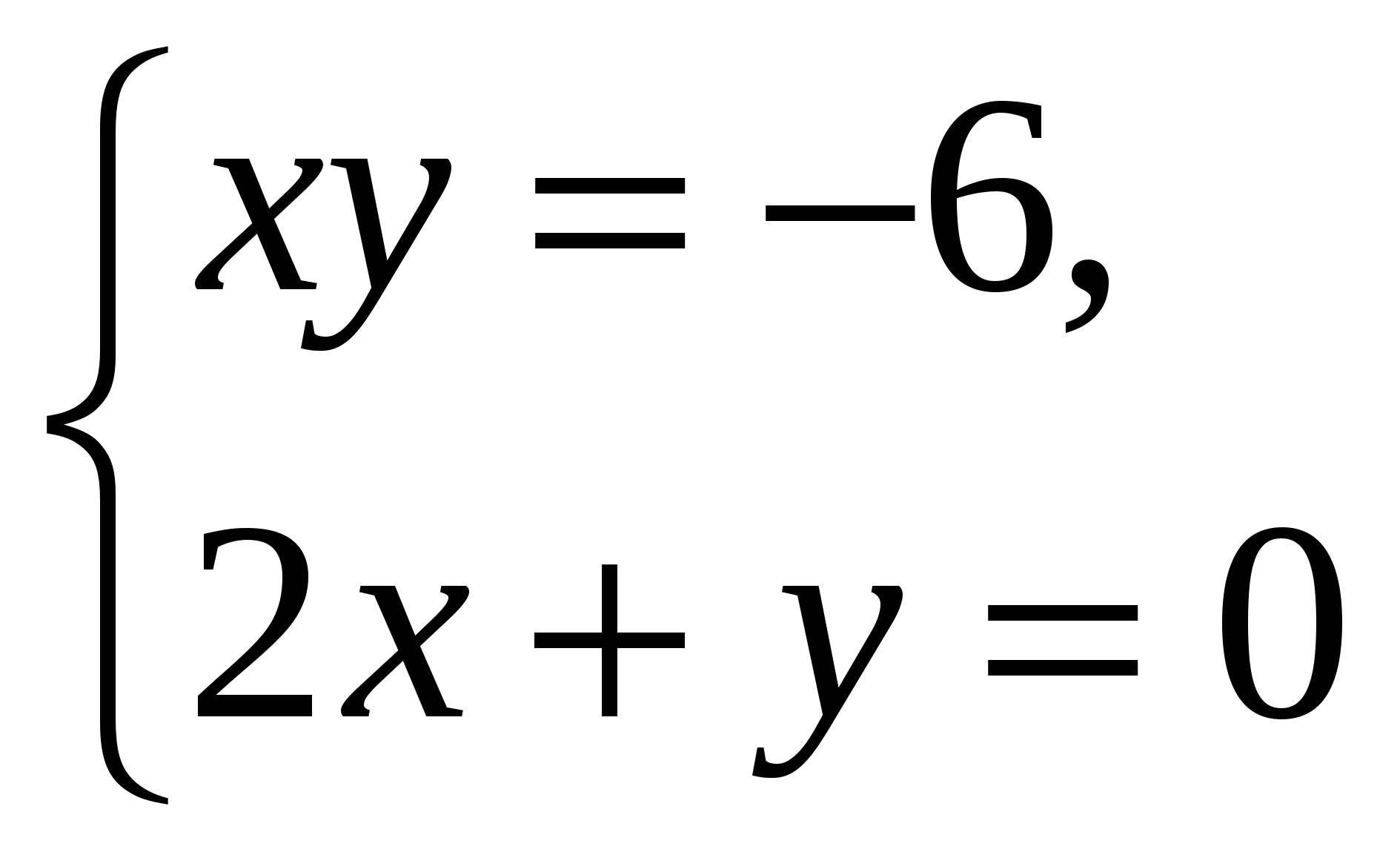 Ответ: 2
Ответ: 2
г) 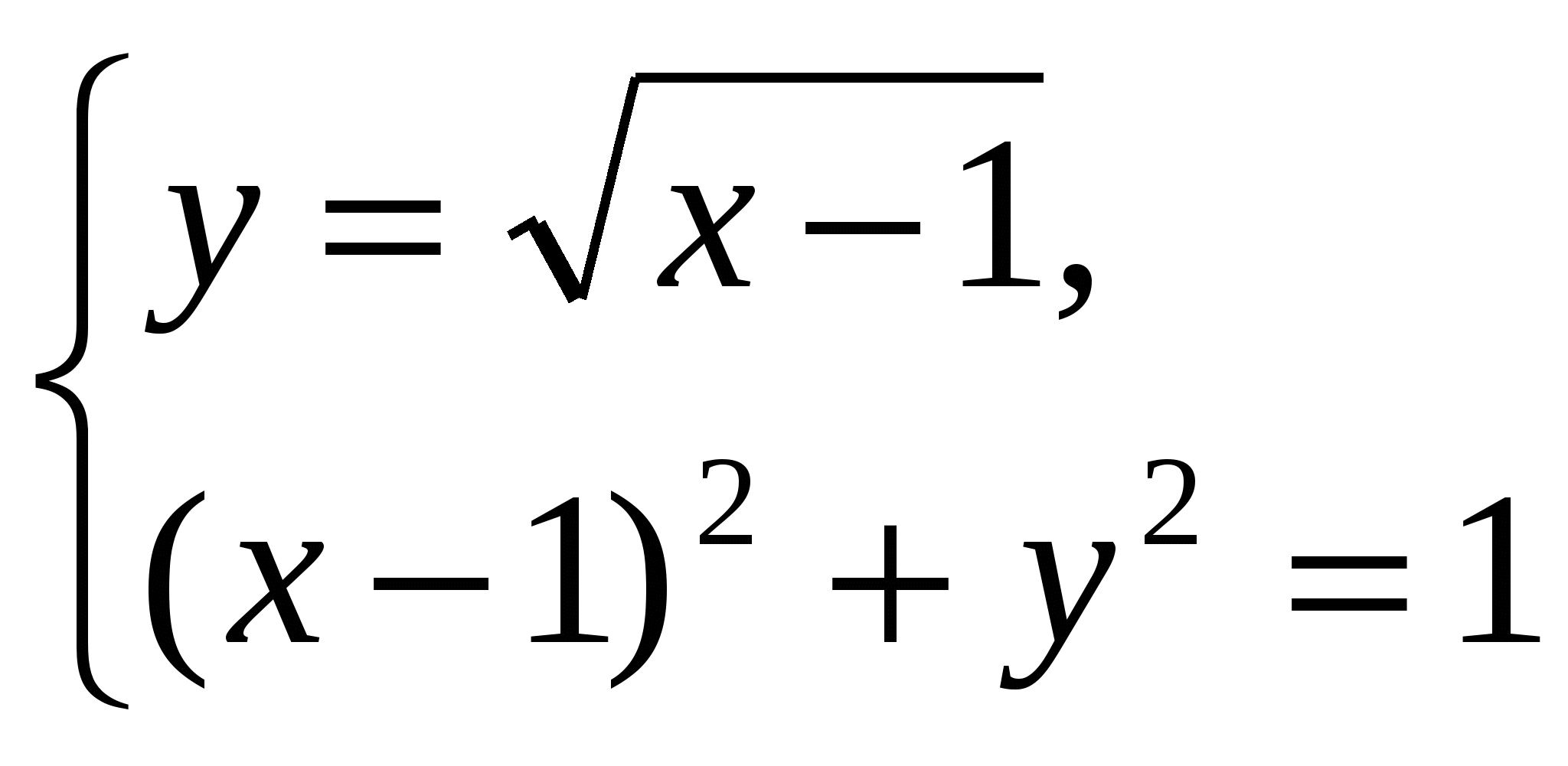 Ответ: 1
Ответ: 1
д) 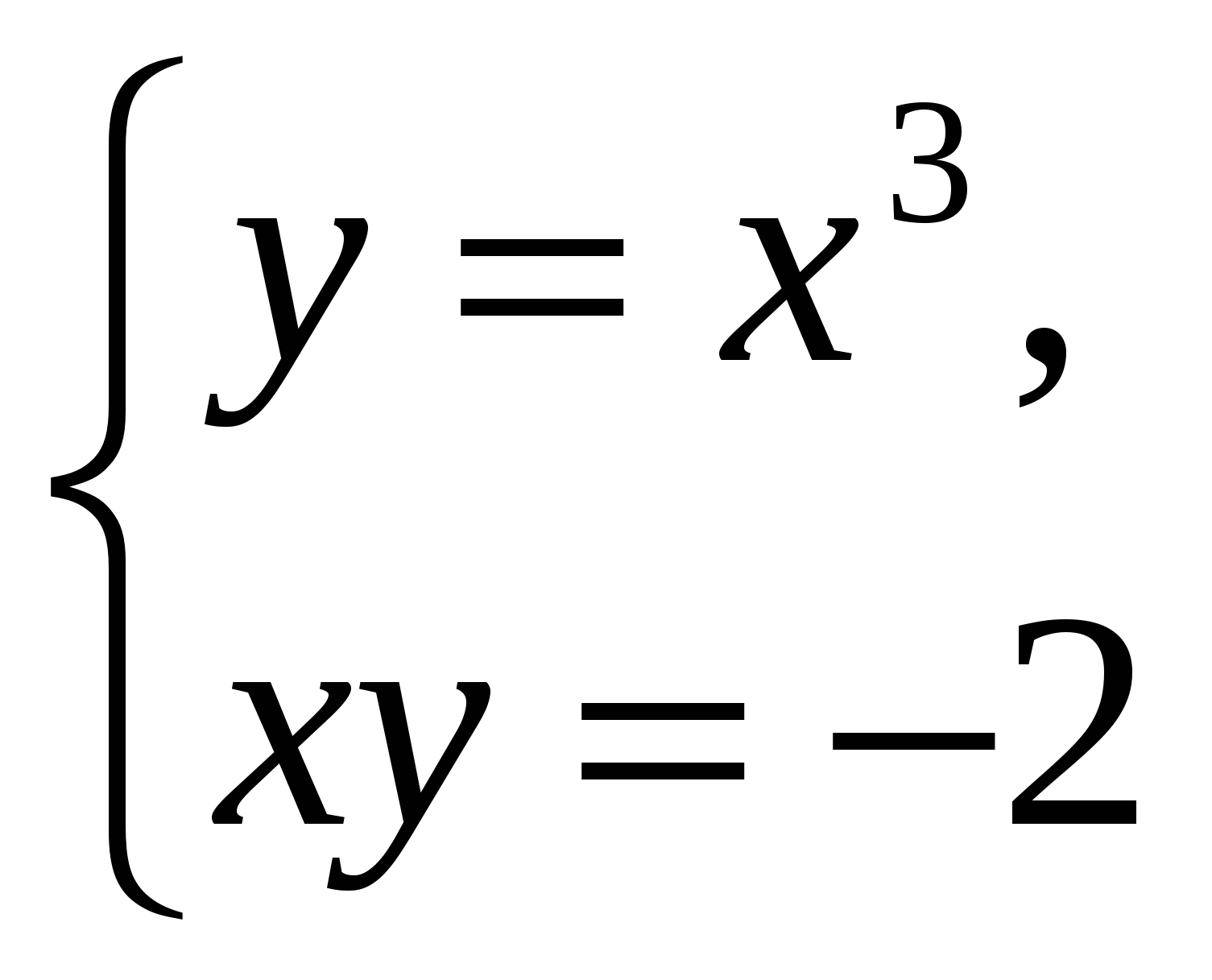 Ответ: решений нет
Ответ: решений нет
е) 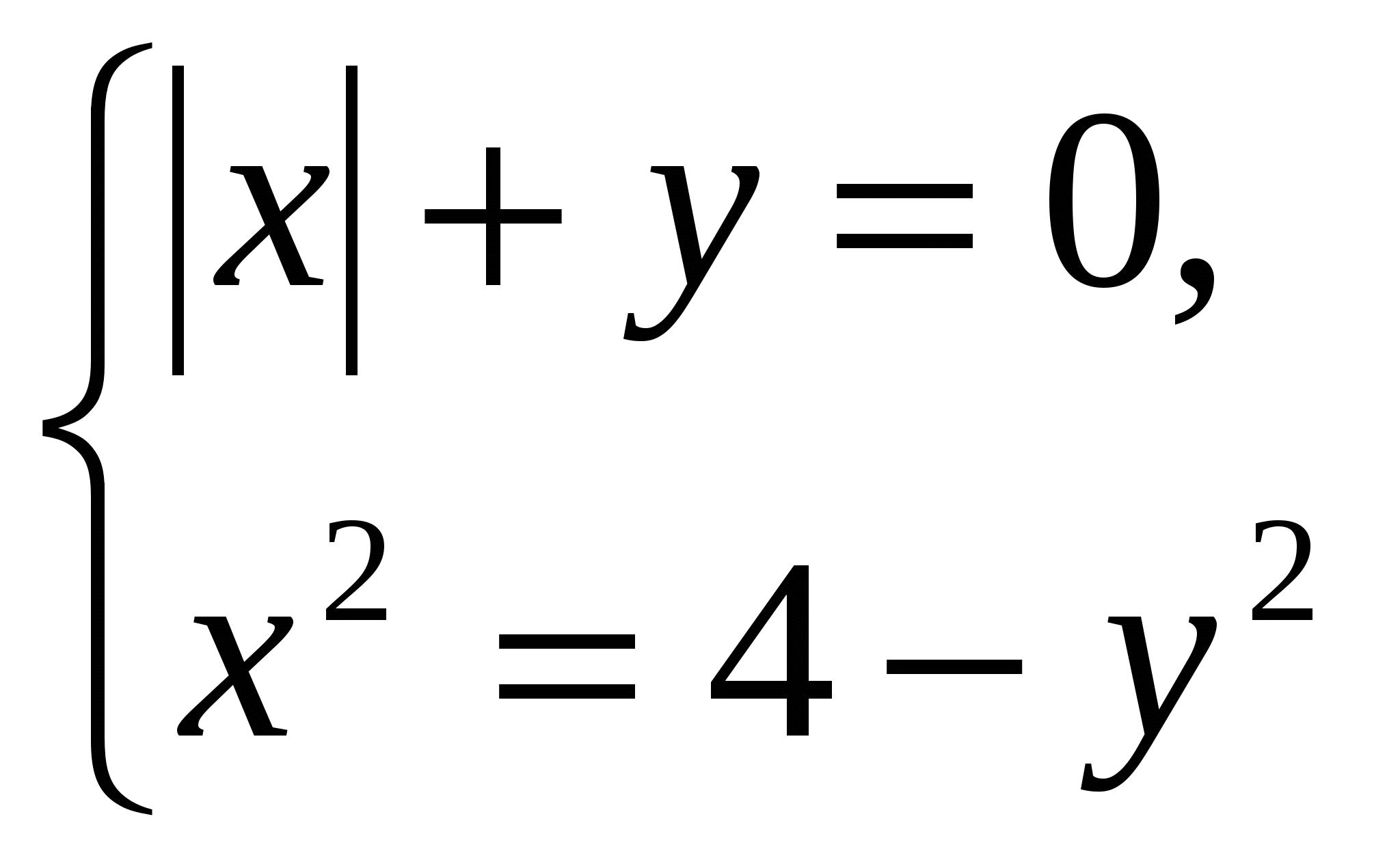 Ответ: 2
Ответ: 2
ж) 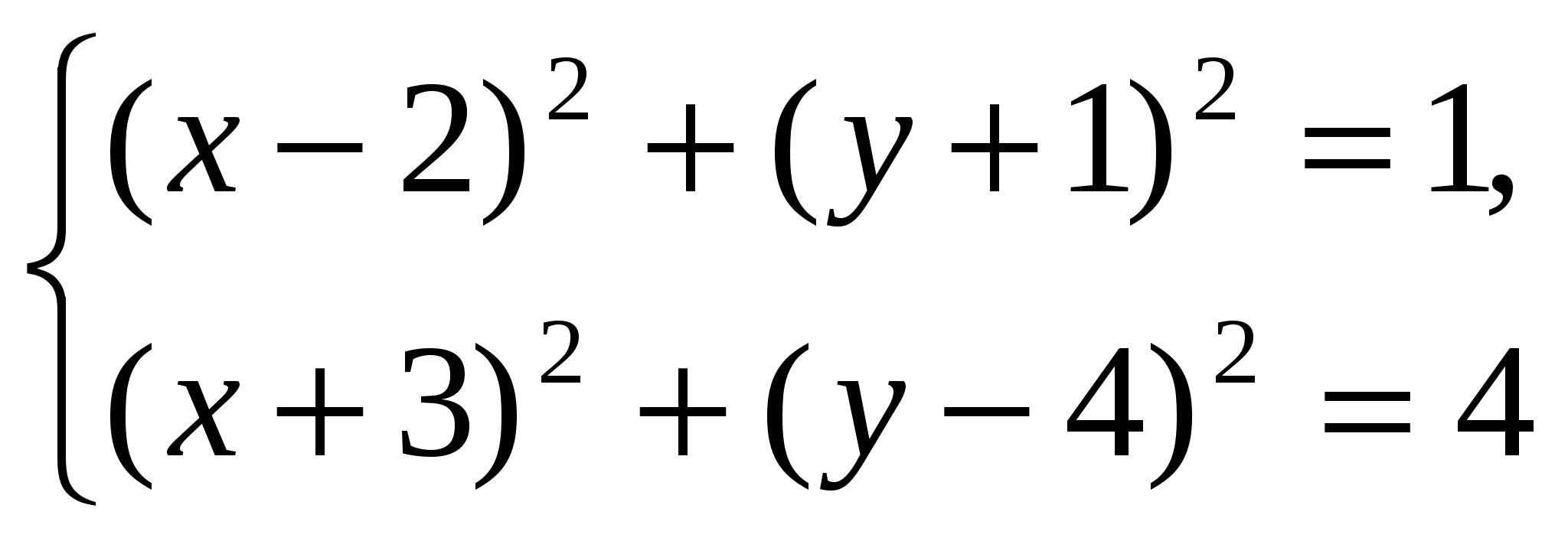 Ответ: решений нет
Ответ: решений нет
з) 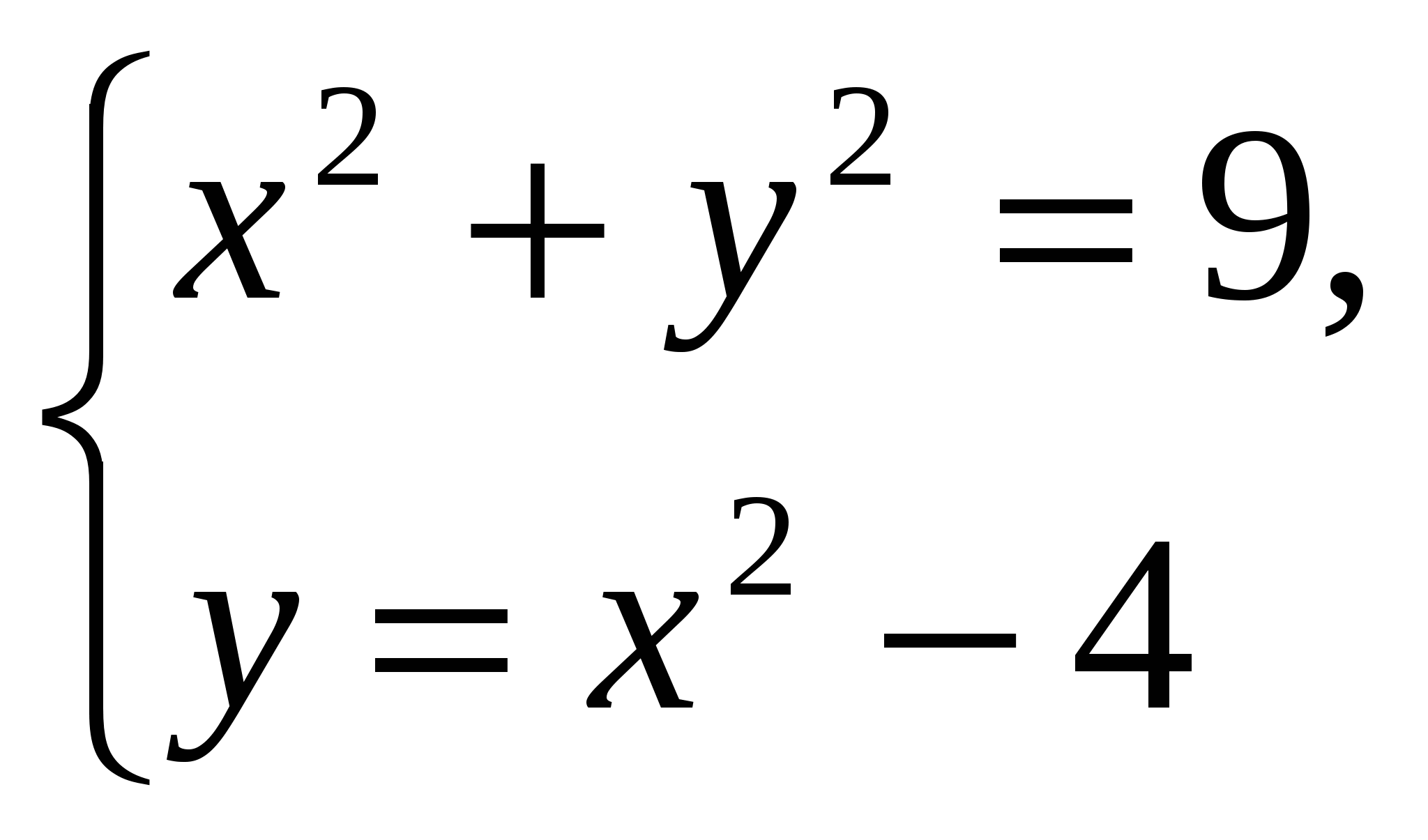 Ответ: 4
Ответ: 4
и) 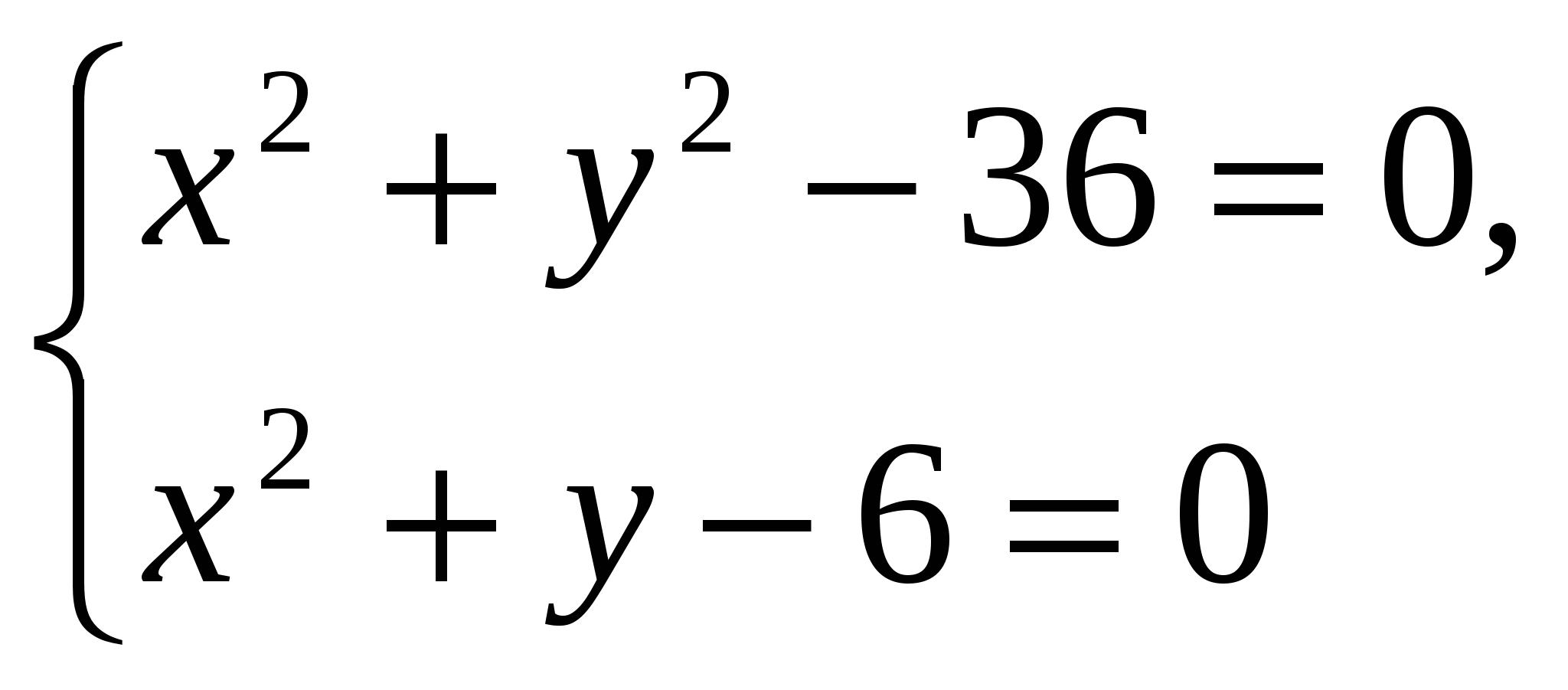 Ответ: 3
Ответ: 3
к) 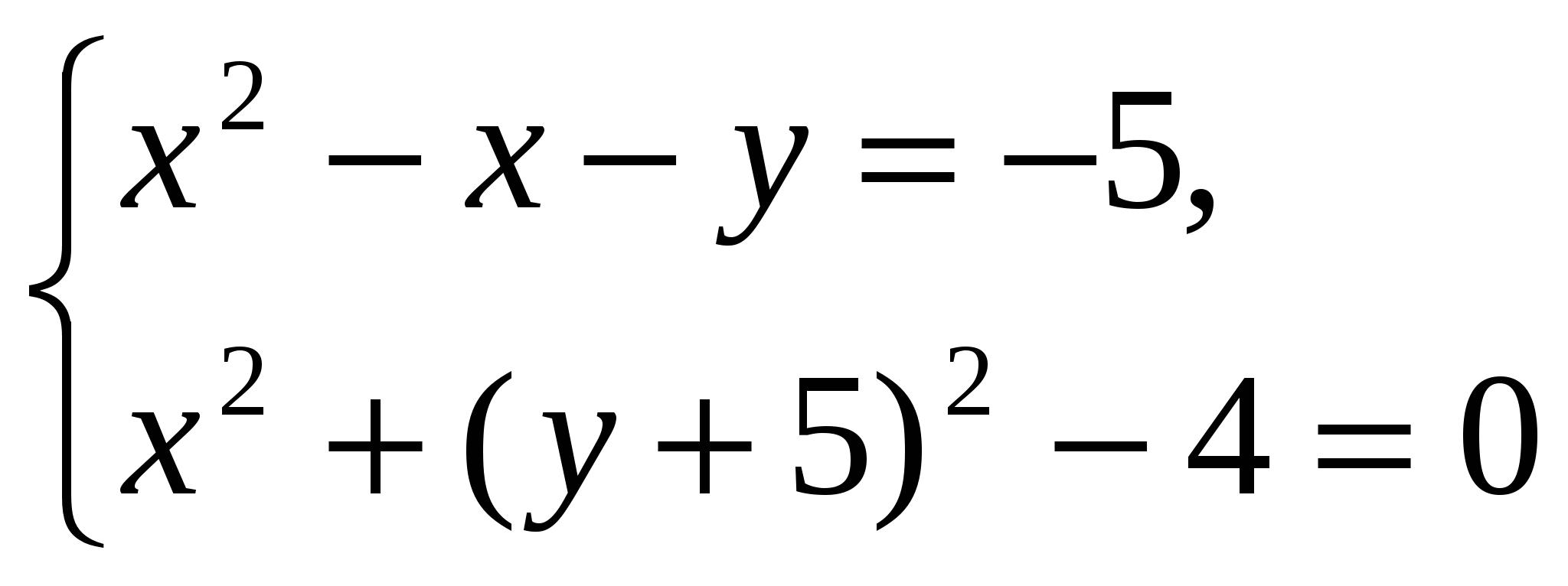 Ответ: решений нет
Ответ: решений нет
Дана система уравнений:

Сколько решений может иметь система, при условии, что 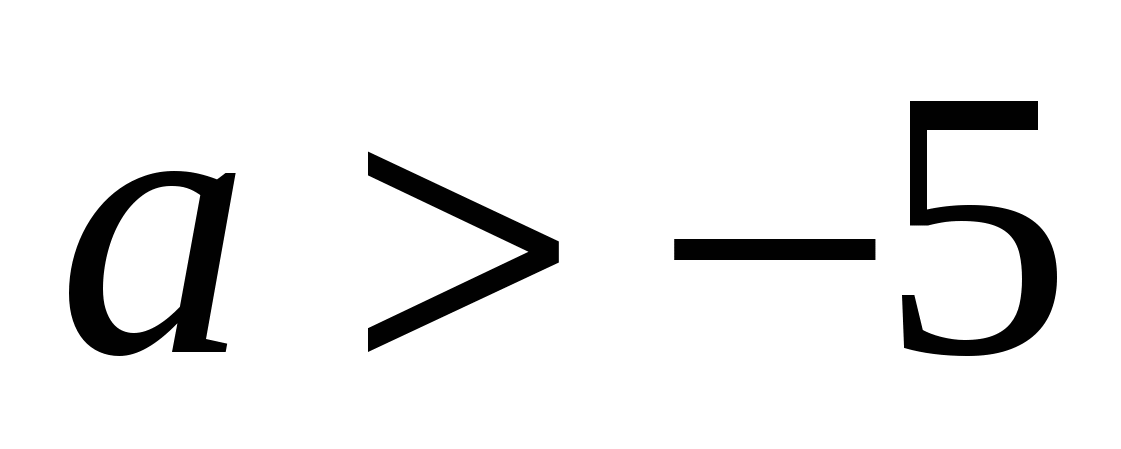 ?
?
При каких значениях 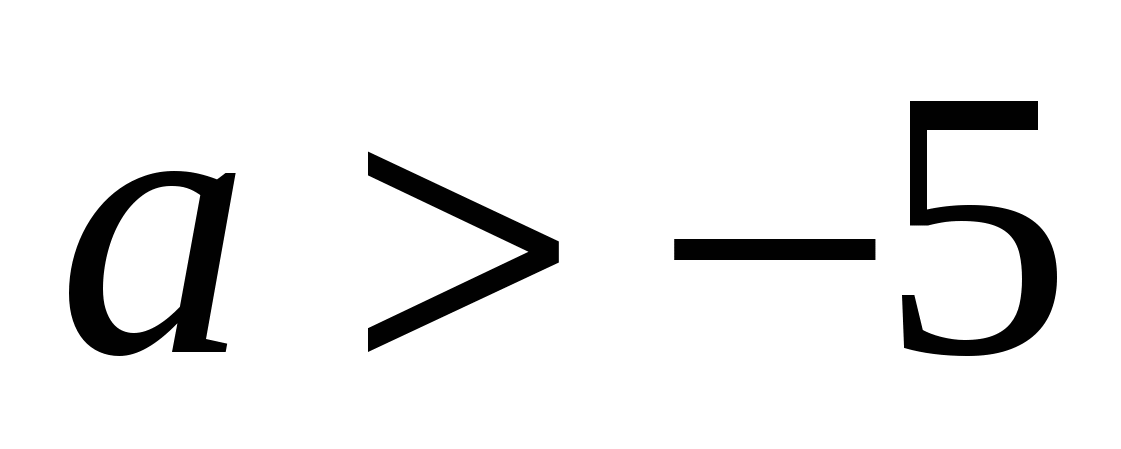 система уравнений будет иметь:
система уравнений будет иметь:
одно решение? При

три решения? При

два решения? При

четыре решения? При

И чтобы система не имела решений, какие значения  может принимать?
может принимать? 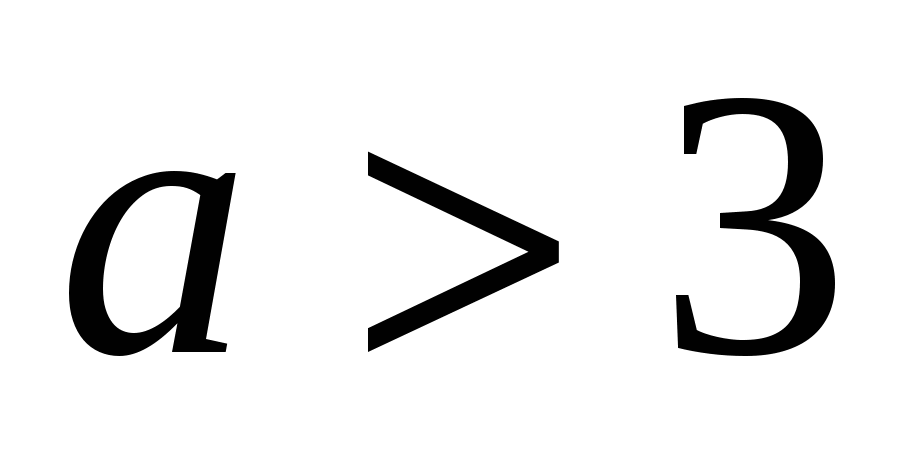 .
.
Продолжим работу над решениями более сложных систем уравнений.
Возьмите карточку №1.
Даны системы уравнений. Подумайте и запишите способы решения напротив системы уравнений. (2мин)
Предложите свои способы решения систем уравнений.
1. 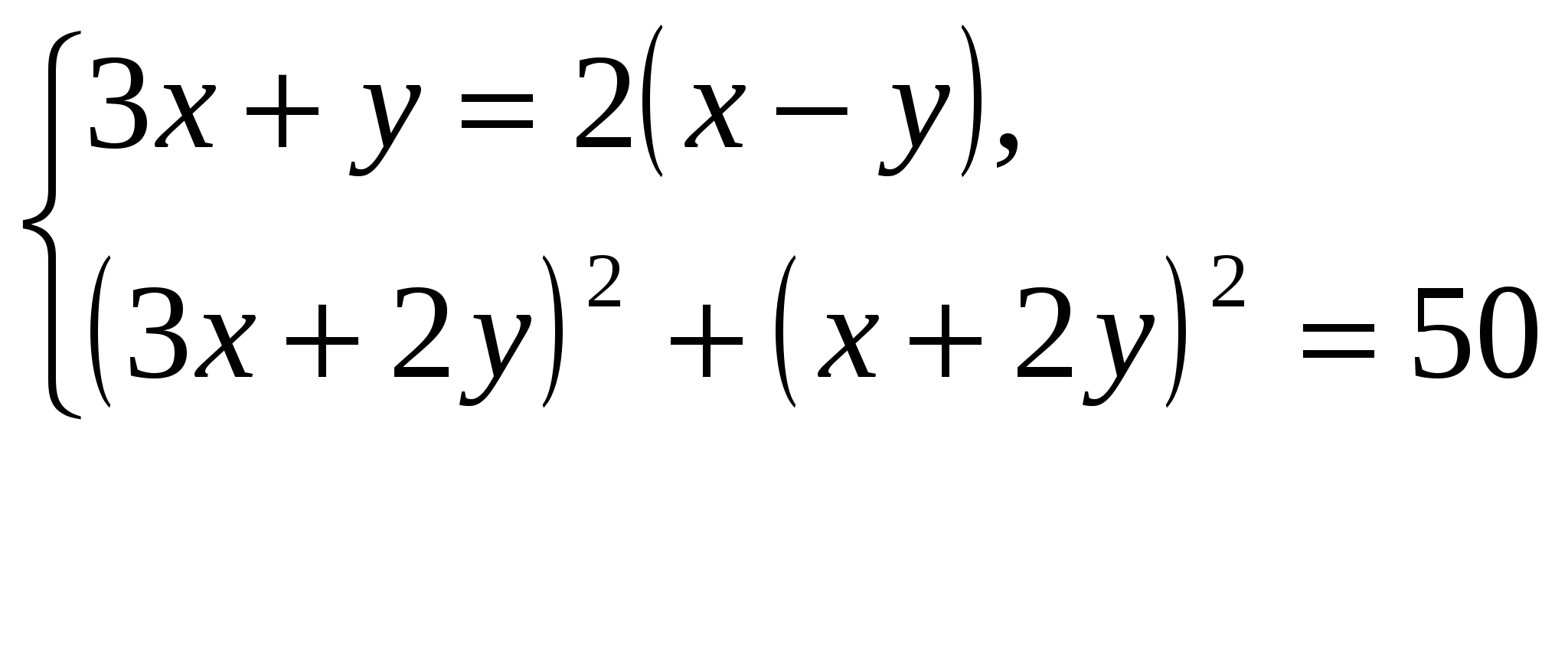 т.к. I уравнение – линейное, то метод подстановки.
т.к. I уравнение – линейное, то метод подстановки.
2. 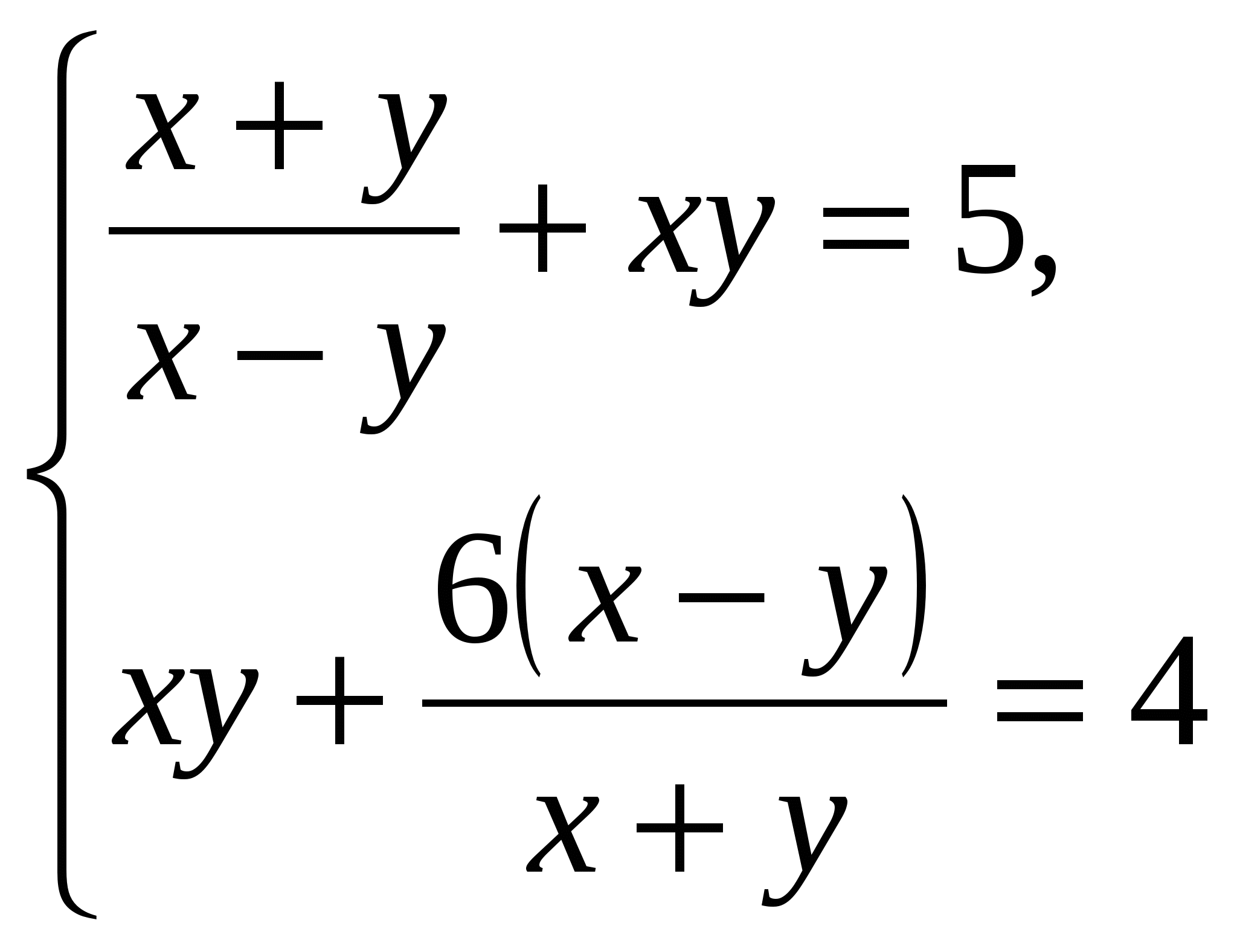 метод замены:
метод замены: 
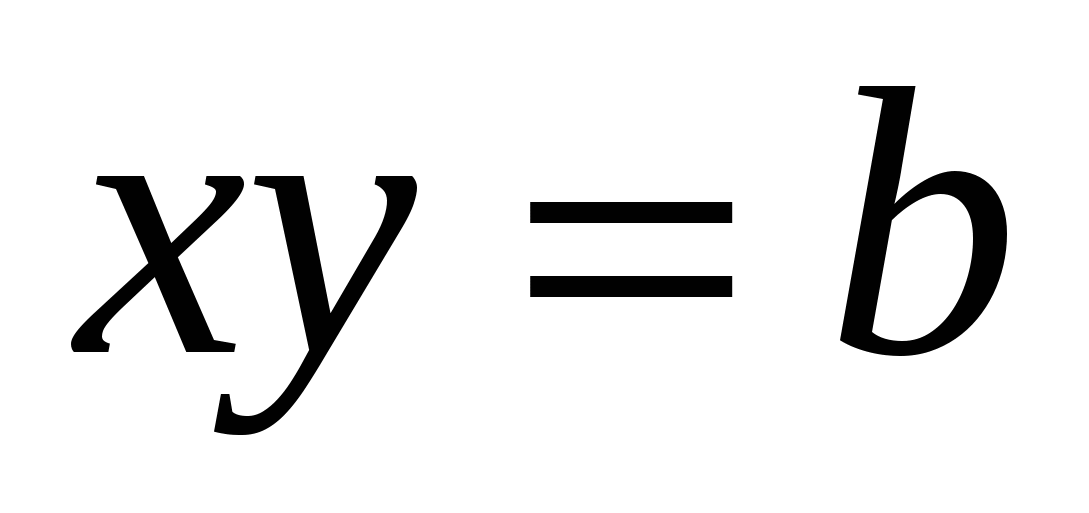 . ОДЗ:
. ОДЗ: 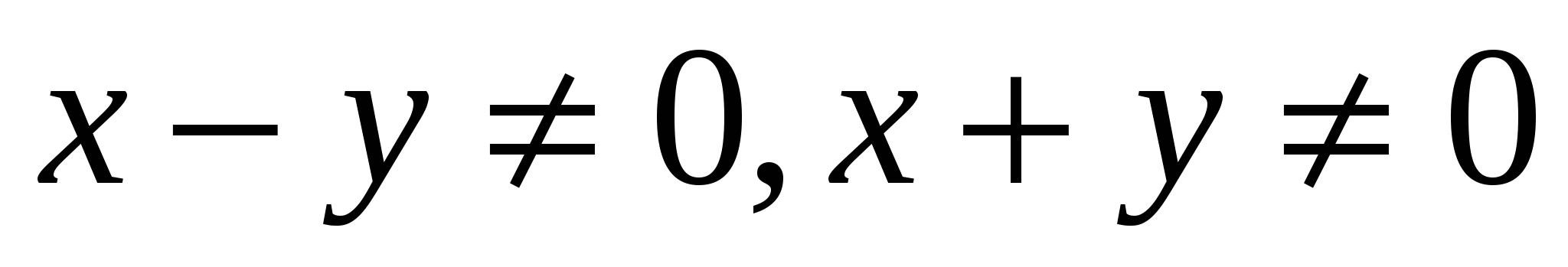
3. 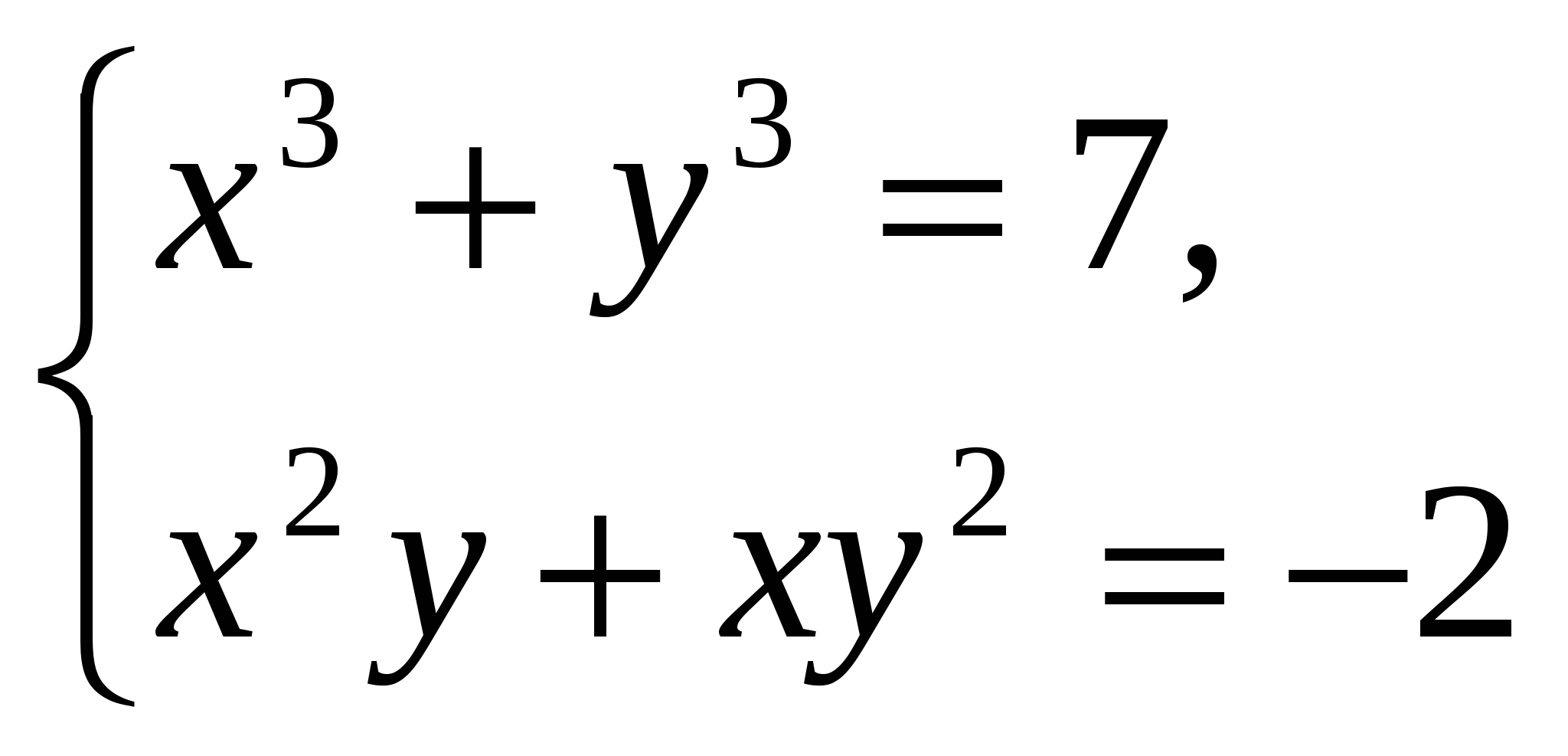 симметрическая система или II уравнение умножить на 3 и
симметрическая система или II уравнение умножить на 3 и
применить формулу: 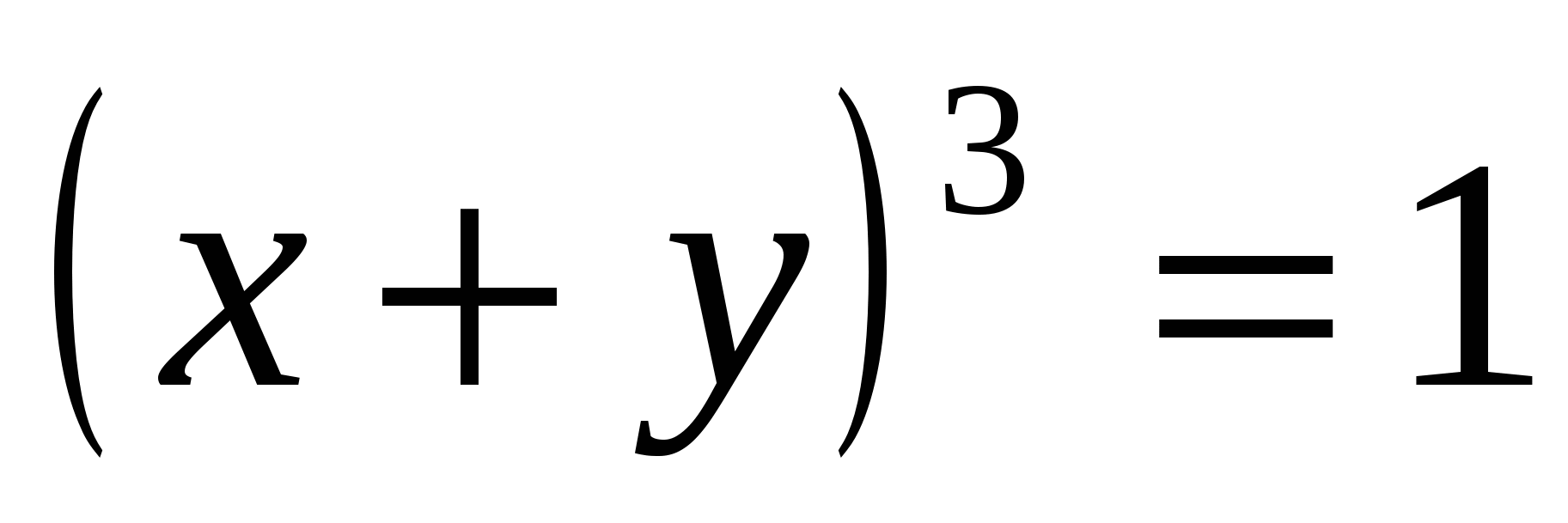
4. 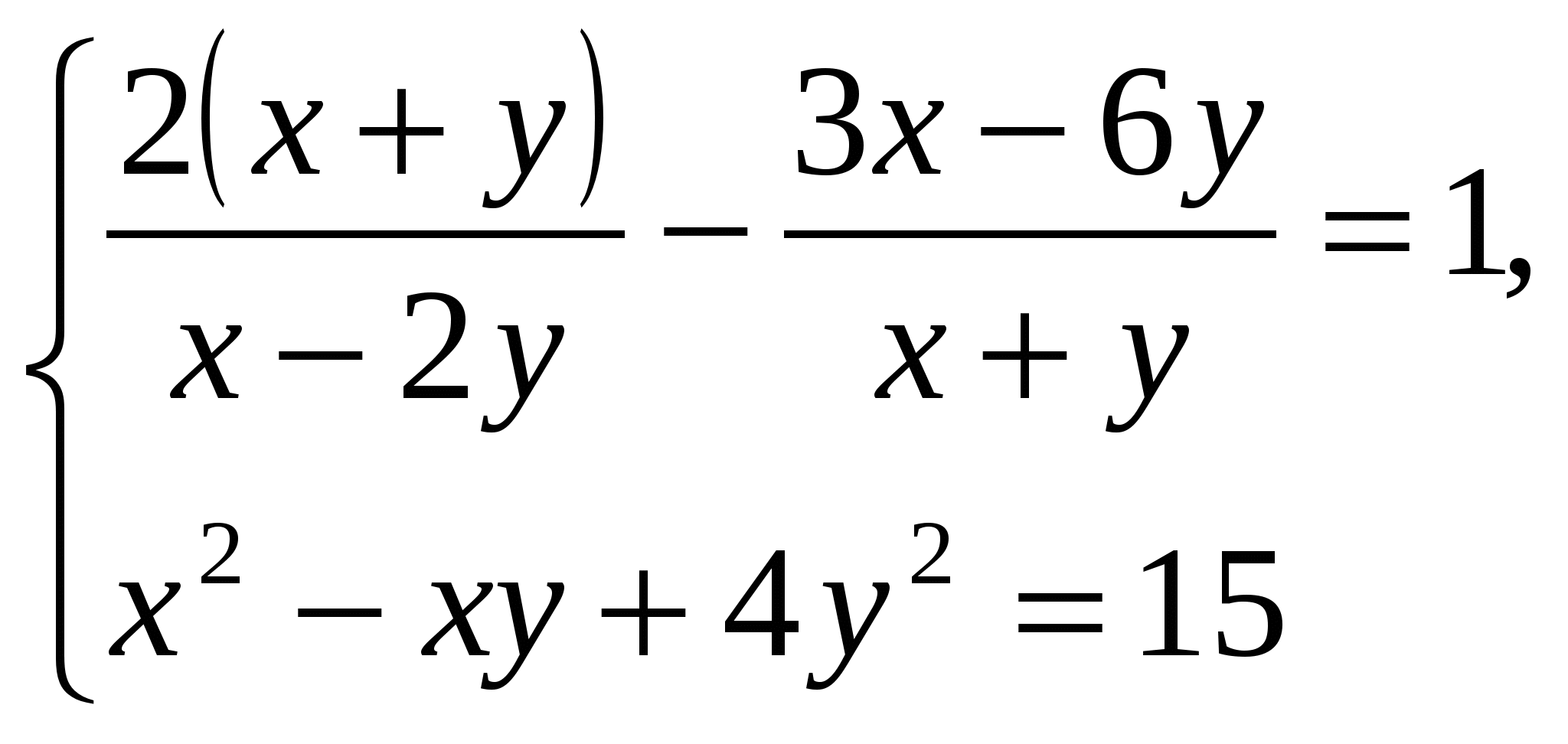 замена:
замена: 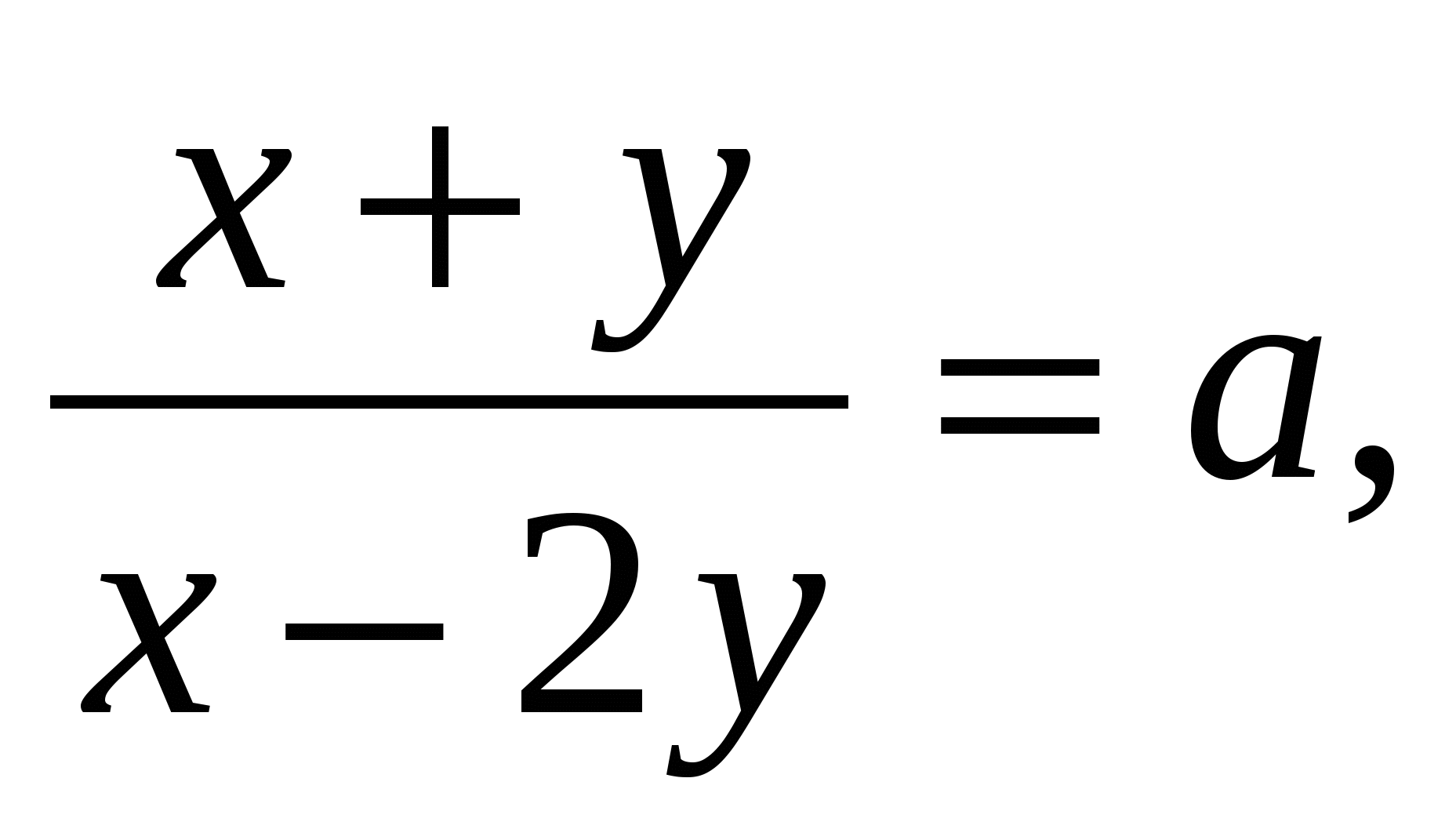
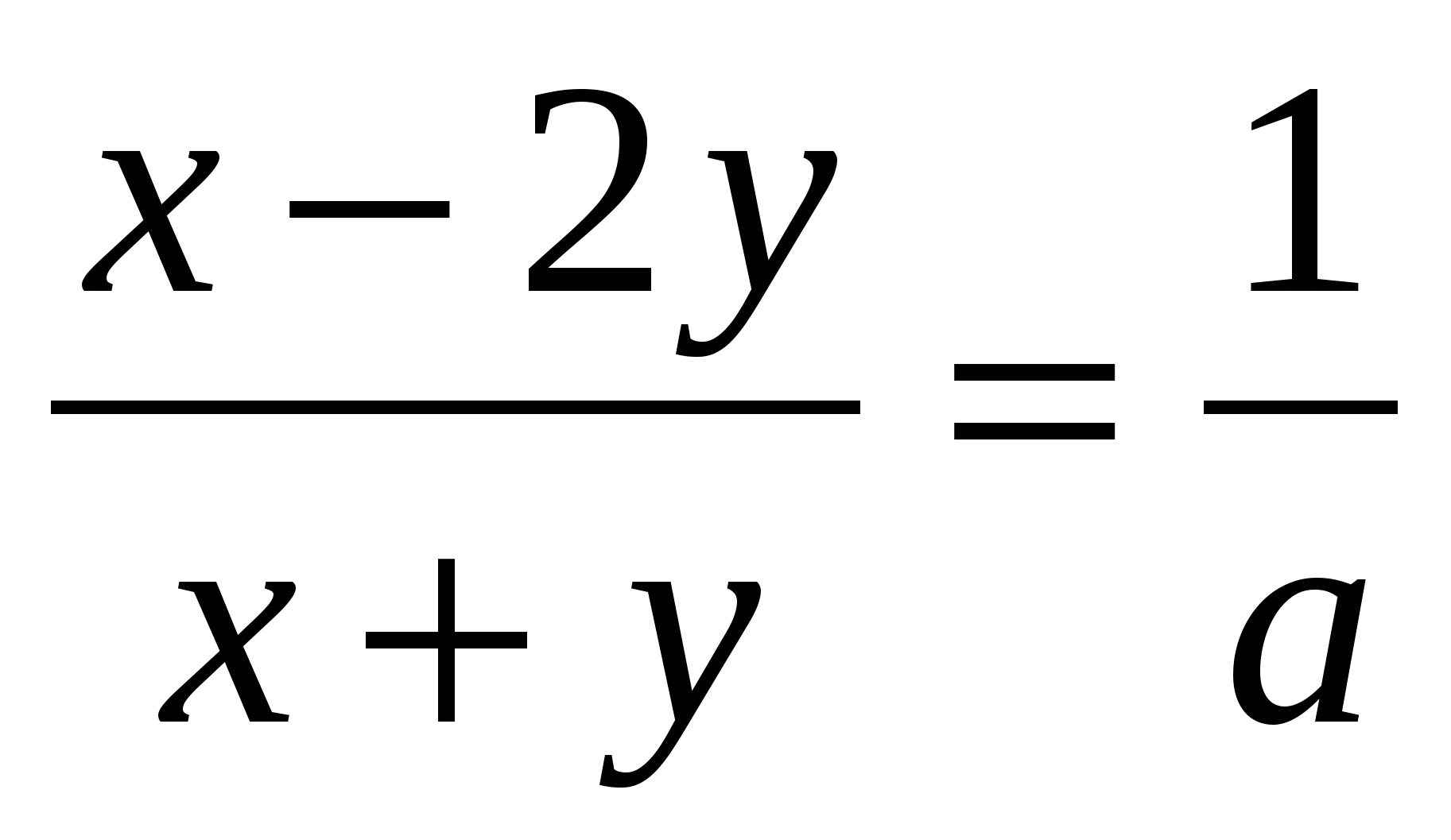
5. 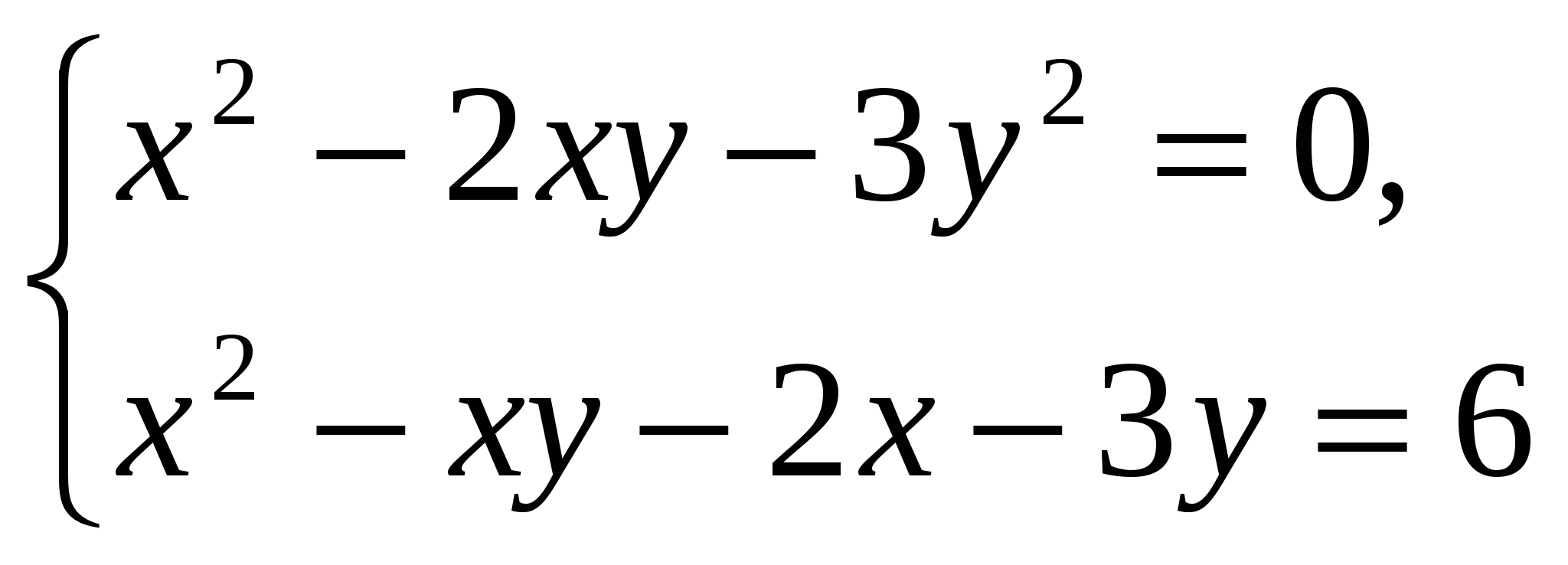 I уравнение – однородное, из него получить более
I уравнение – однородное, из него получить более
простые уравнения
6. 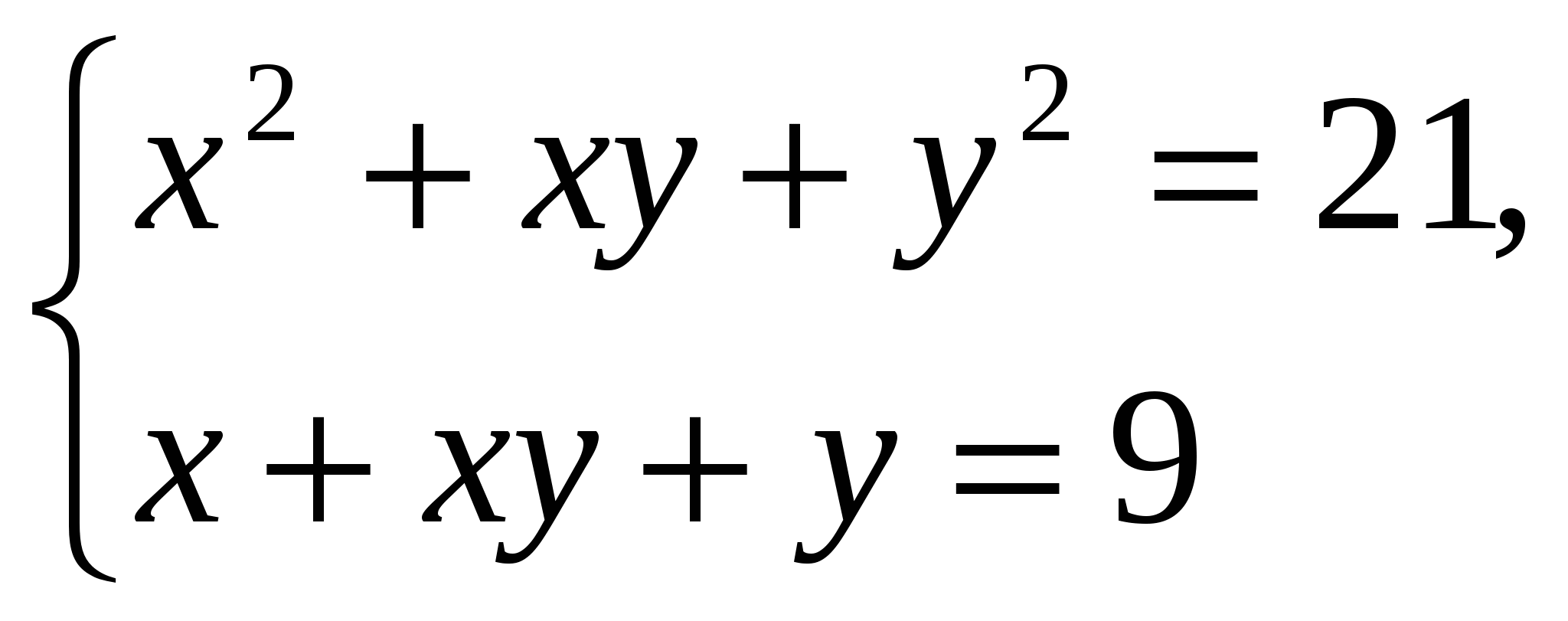 симметрическая система
симметрическая система
7. 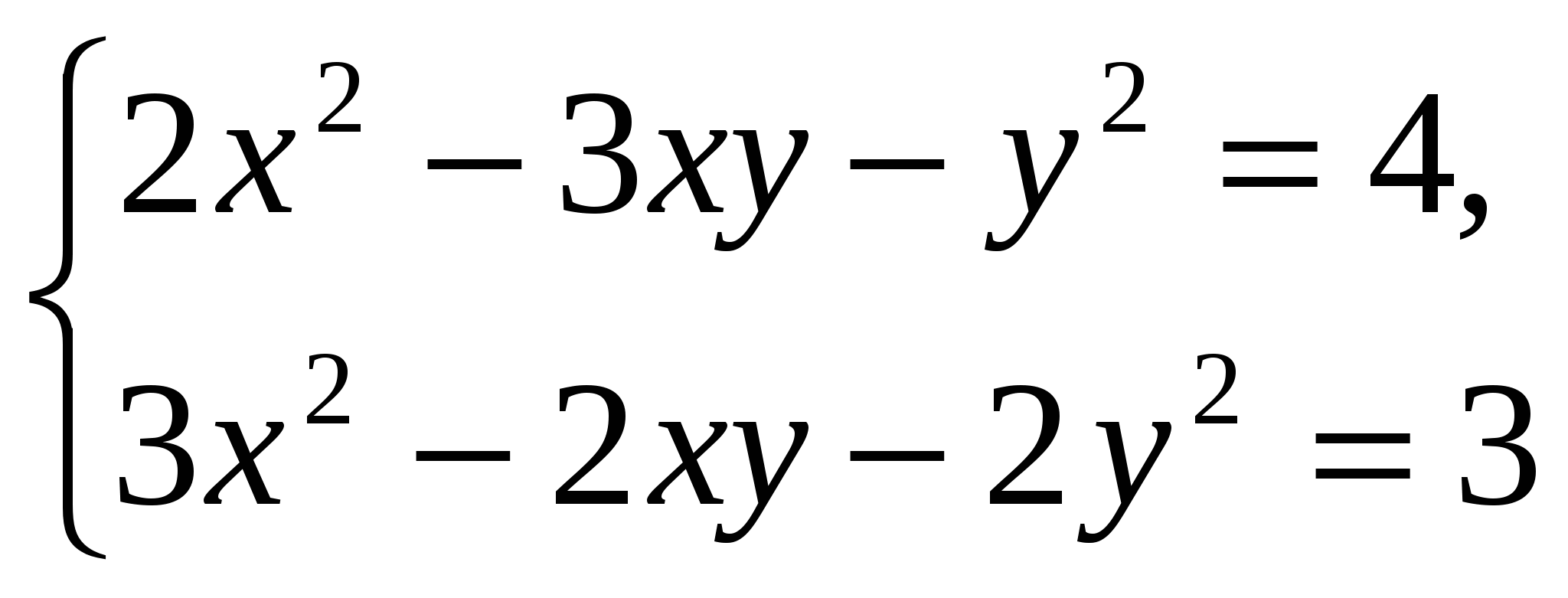 система уравнений, левые части которых являются
система уравнений, левые части которых являются
однородными многочленами. Применив метод деления,
получим однородное уравнение. (или умножив I уравнение на
3, II – на -4 и сложив эти уравнения, получим однородное
уравнение).
8. 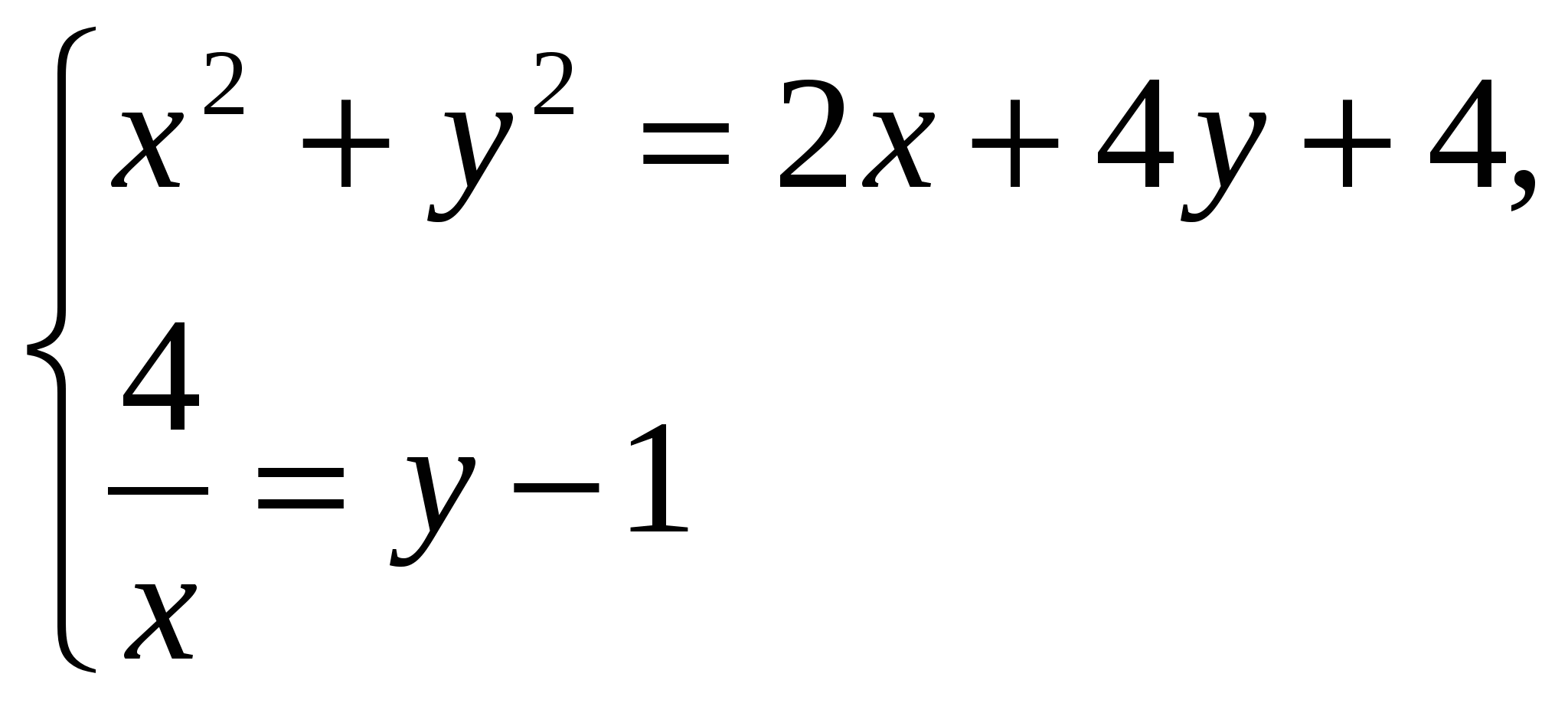 графический способ.
графический способ.
Готовясь к занятиям по подготовке к олимпиадам по математике, Ходошкинова Надя нашла интересную задачку, решение которой хотела бы нам предложить.
Известно, что существуют два прямоугольных треугольника с целочисленными сторонами, примечательные тем, что площадь каждого численно равна его периметру. Найти длины сторон этих треугольников. И определить, есть ли еще прямоугольные треугольники с этой же особенностью.
Пусть натуральные числа x, y, z выражают длины соответственно катетов и гипотенузы треугольника. Тогда по теореме Пифагора 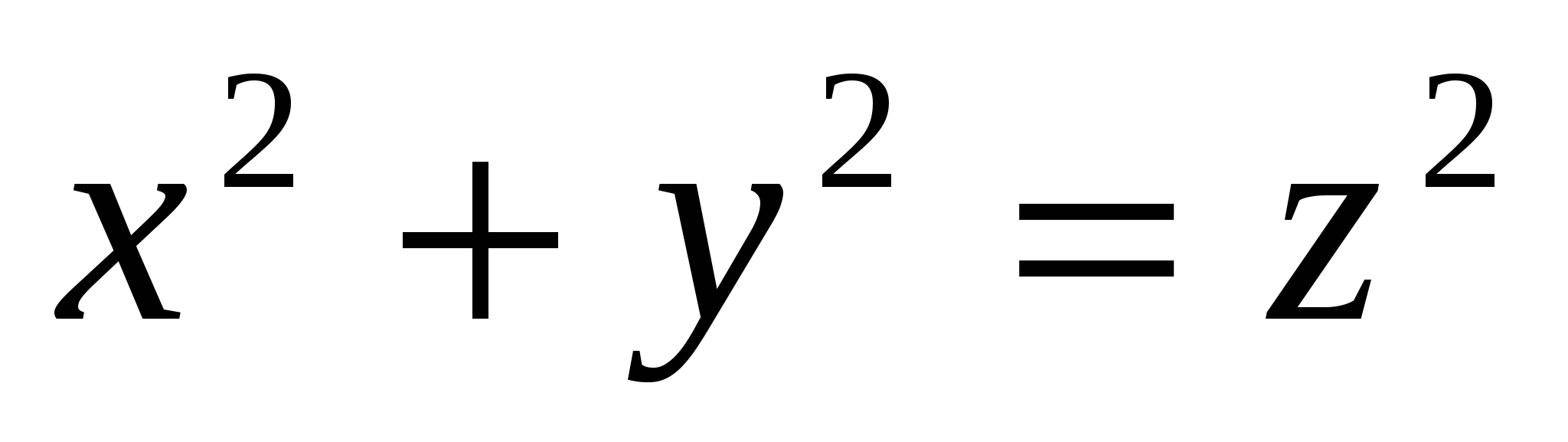 и т.к. площадь треугольника равна периметру этого же треугольника, то
и т.к. площадь треугольника равна периметру этого же треугольника, то 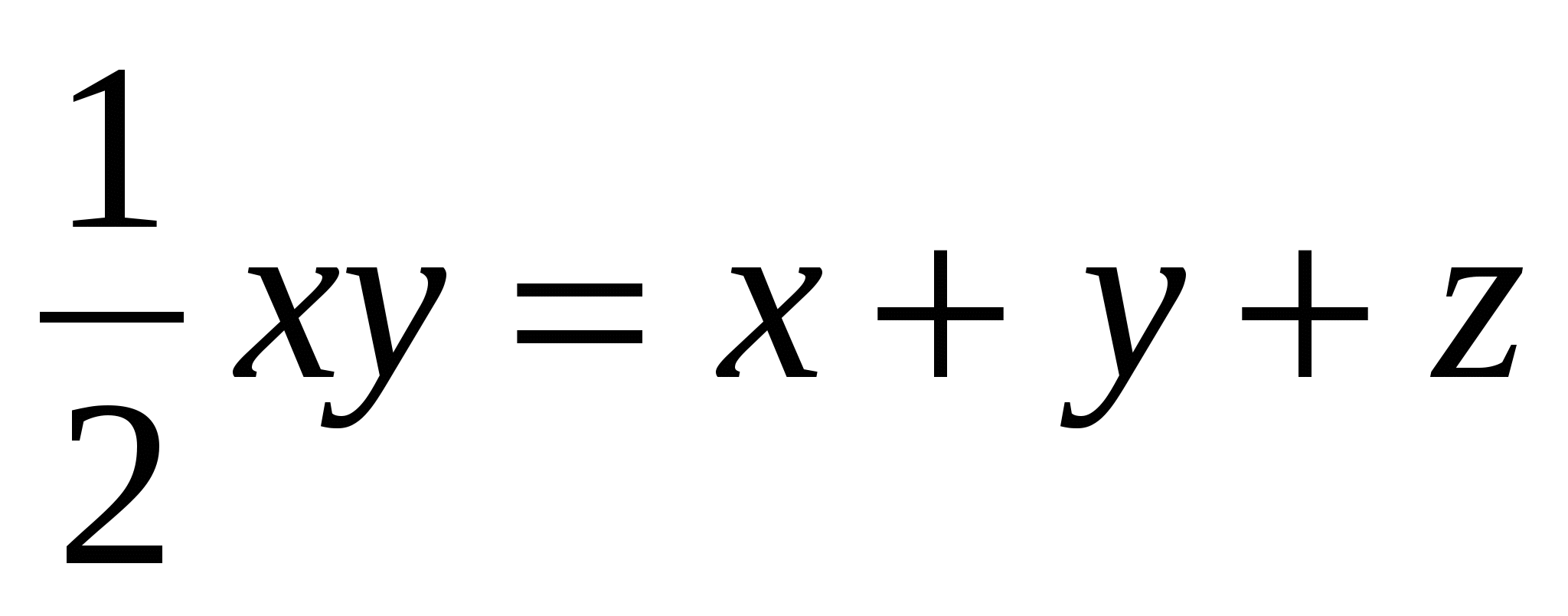 .
.
Составим систему уравнений: 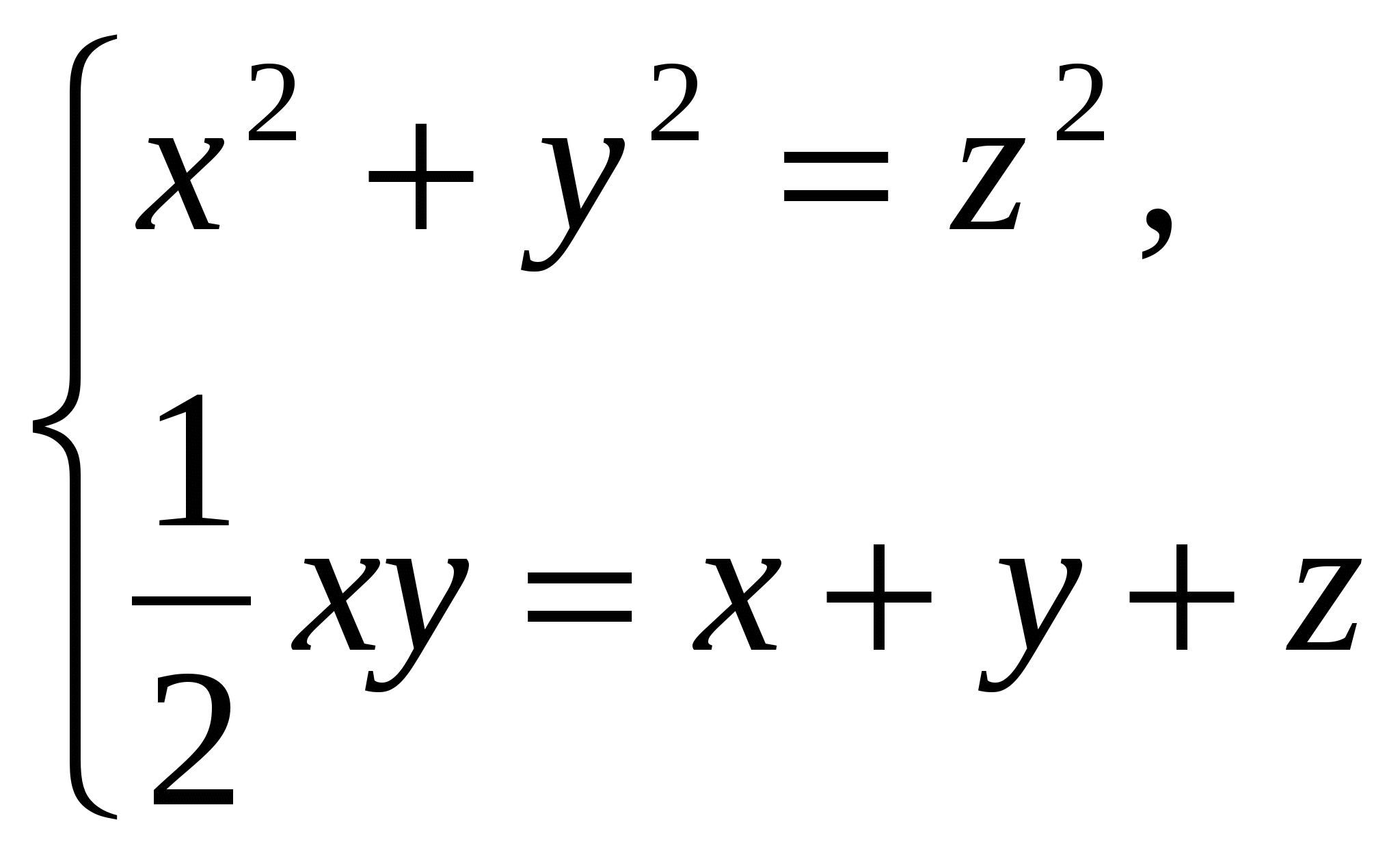
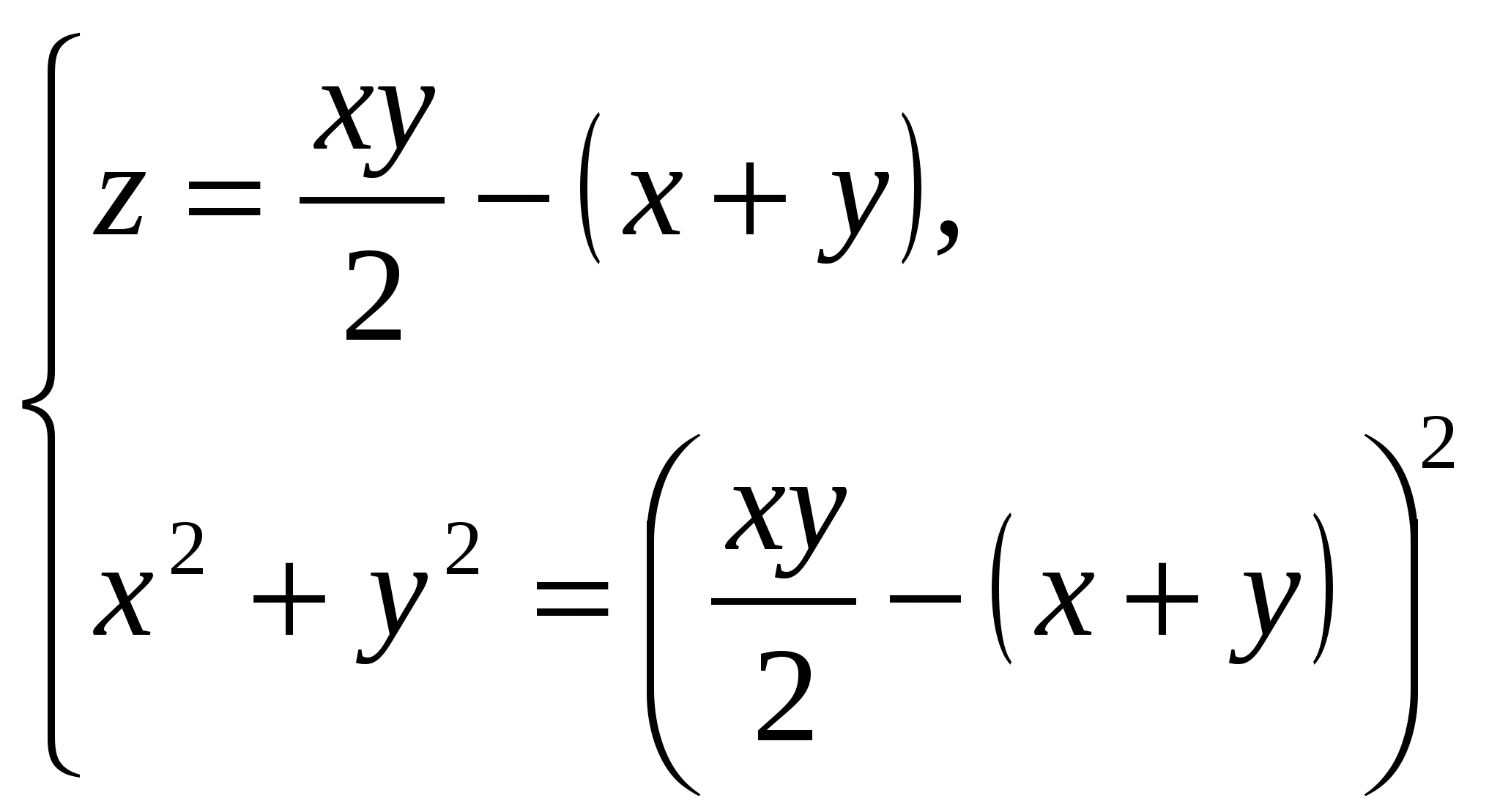
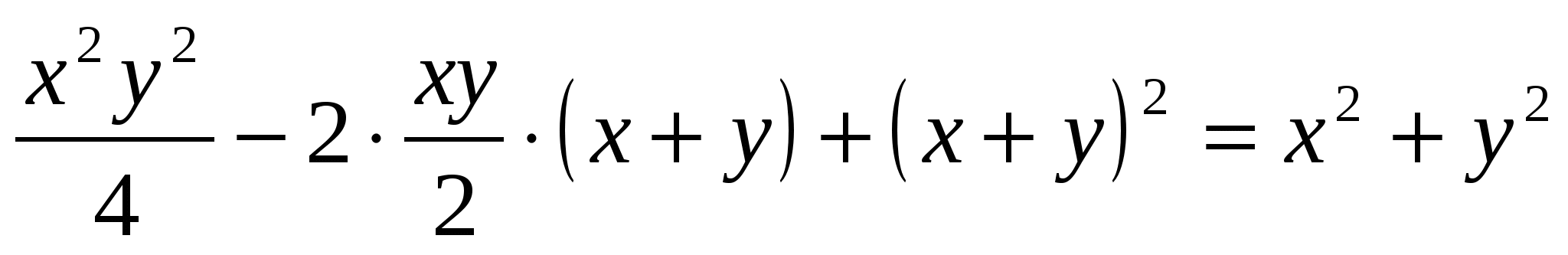
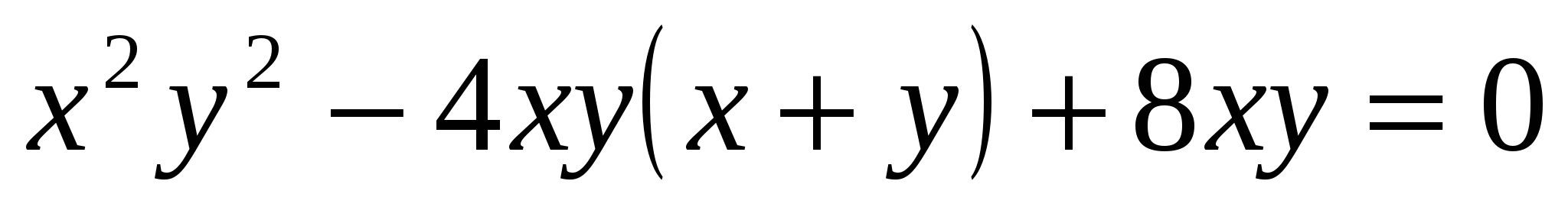
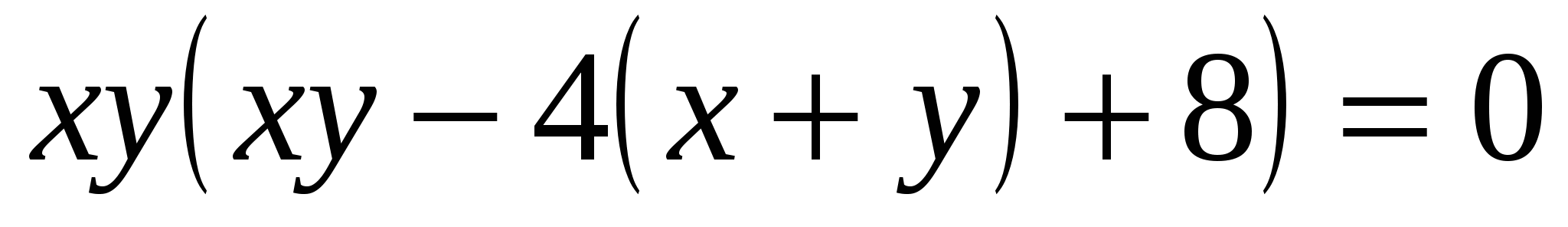
 или
или 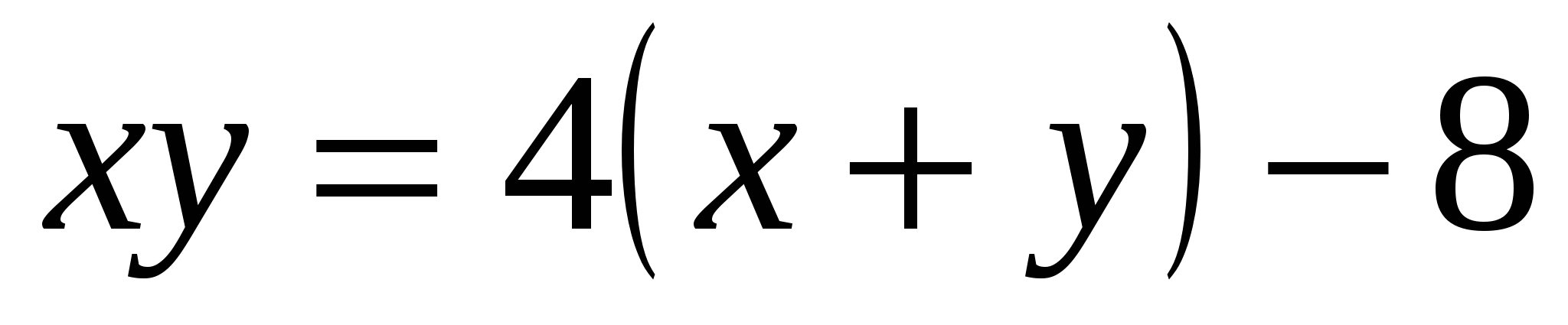
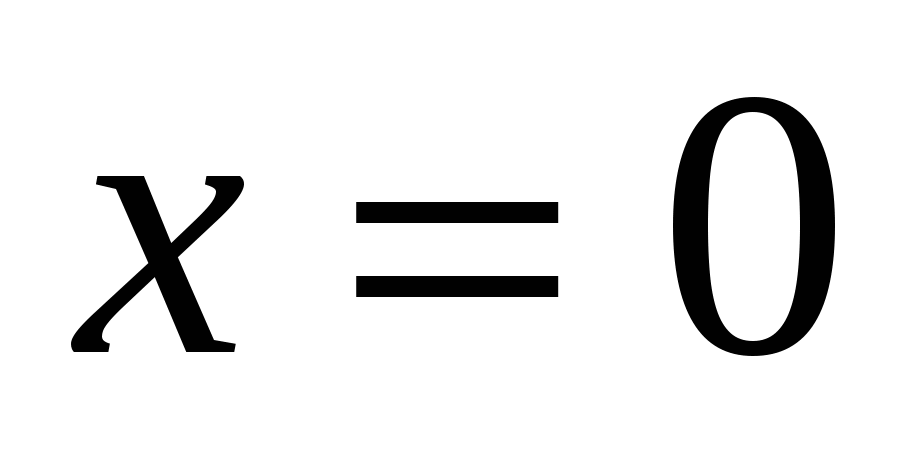 ,
, 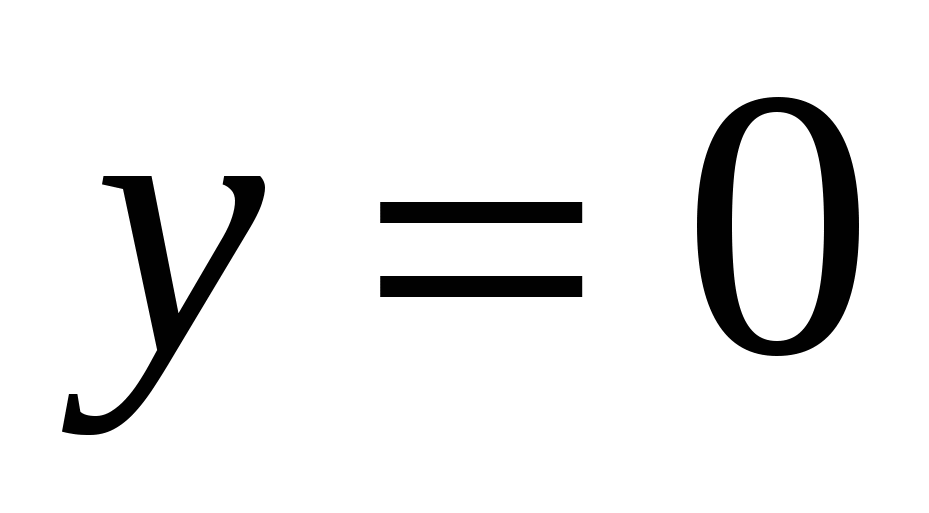 или
или 
не удовл усл задачи это означает, что, либо 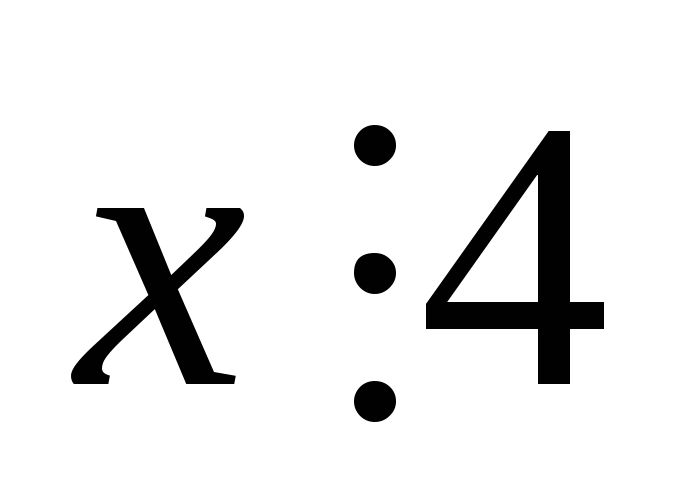 , либо
, либо 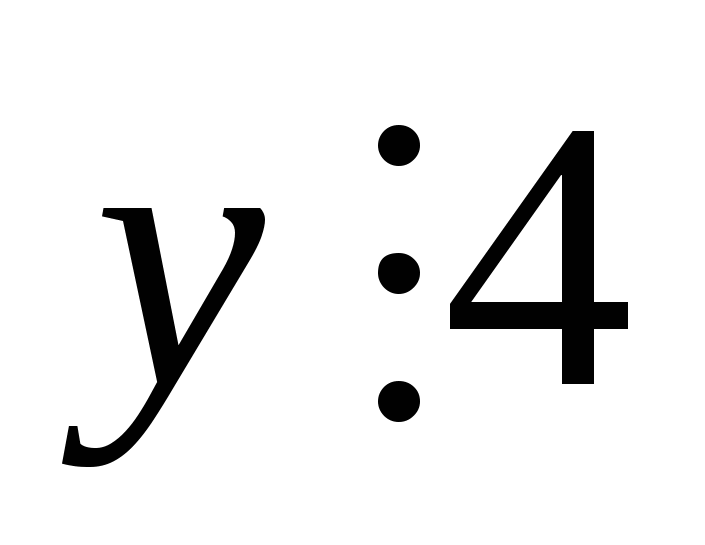 .
.
Пусть 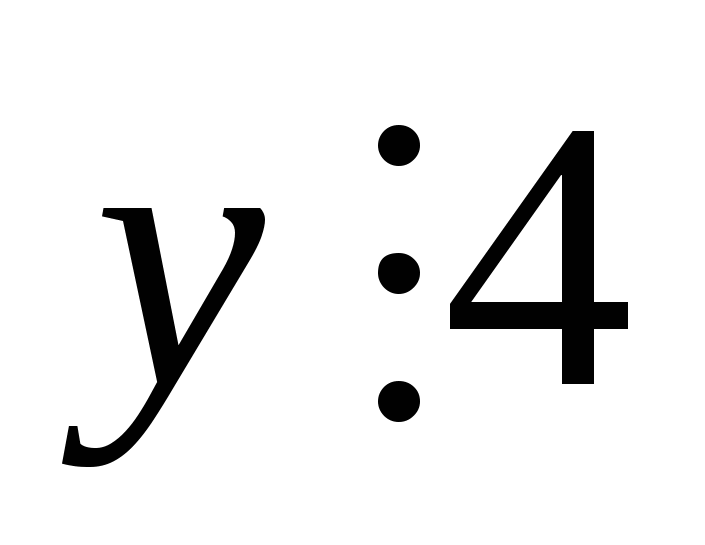 , т.е.
, т.е. 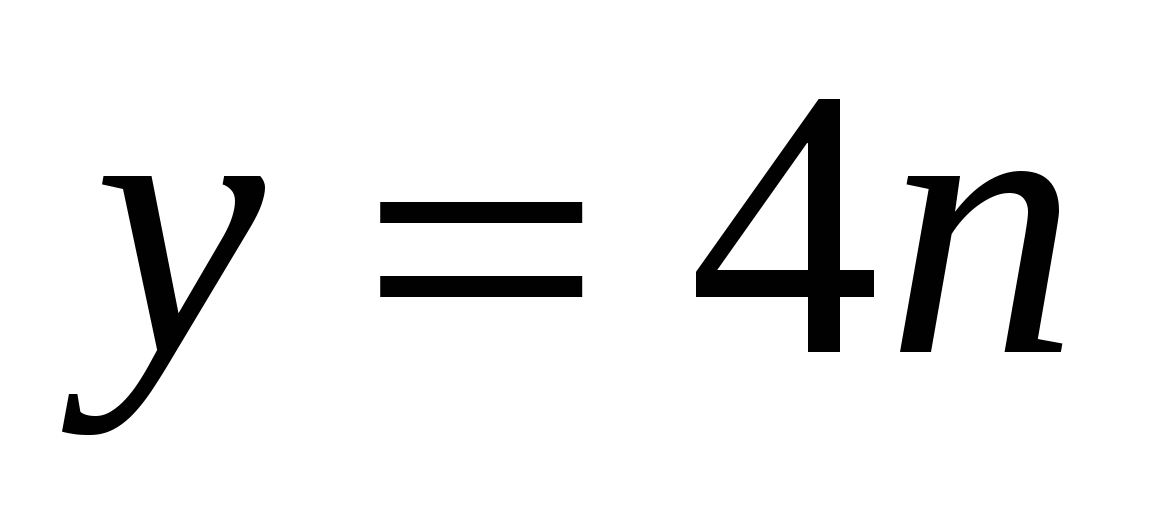 ,
, 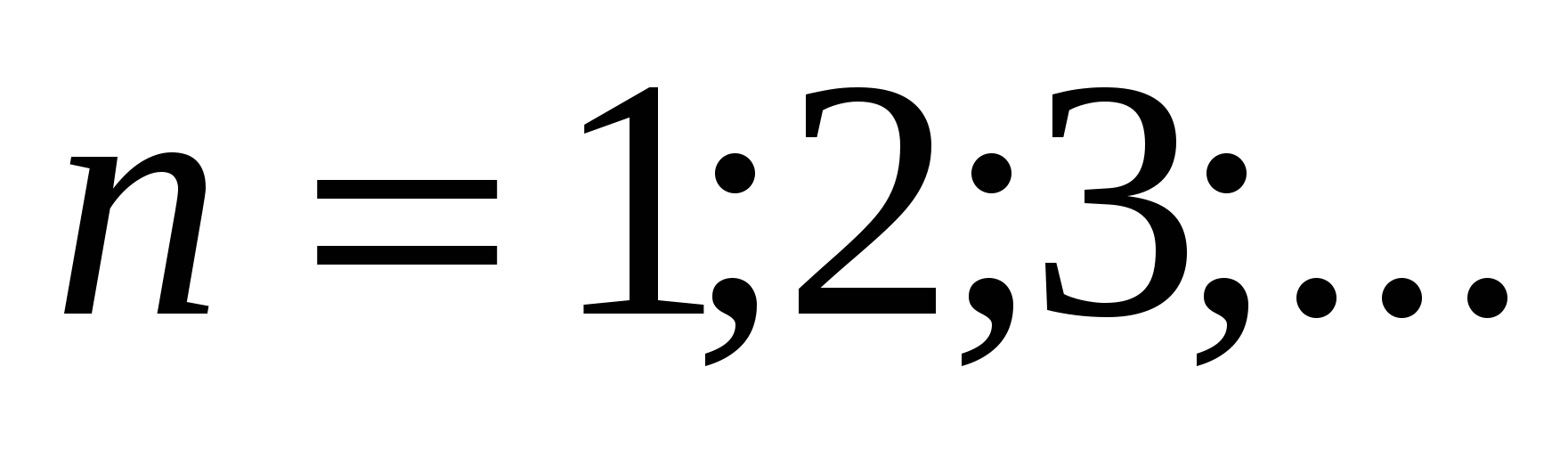
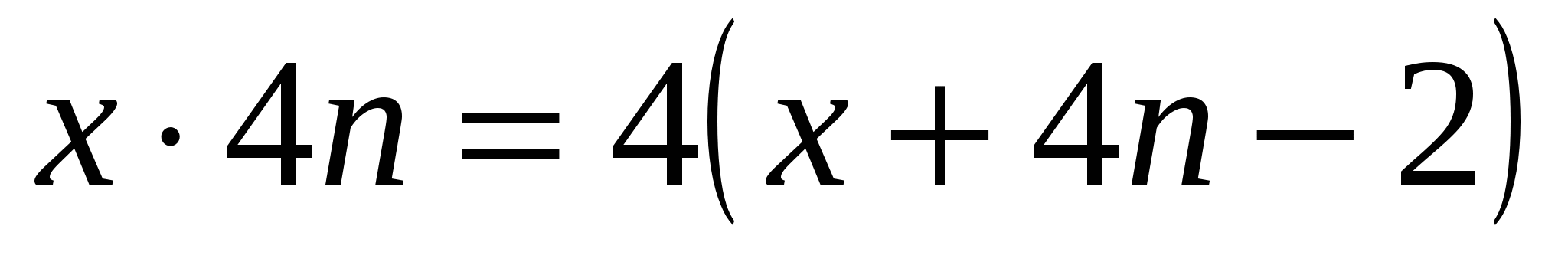 │:4
│:4
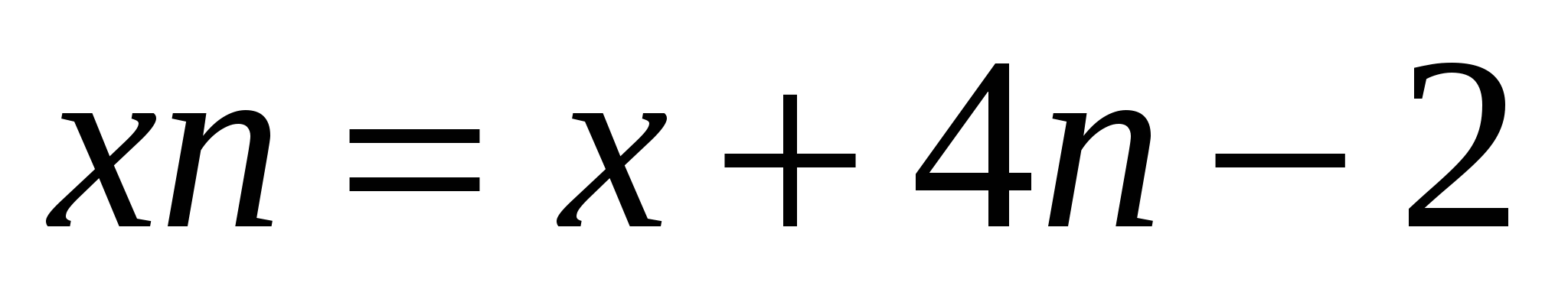

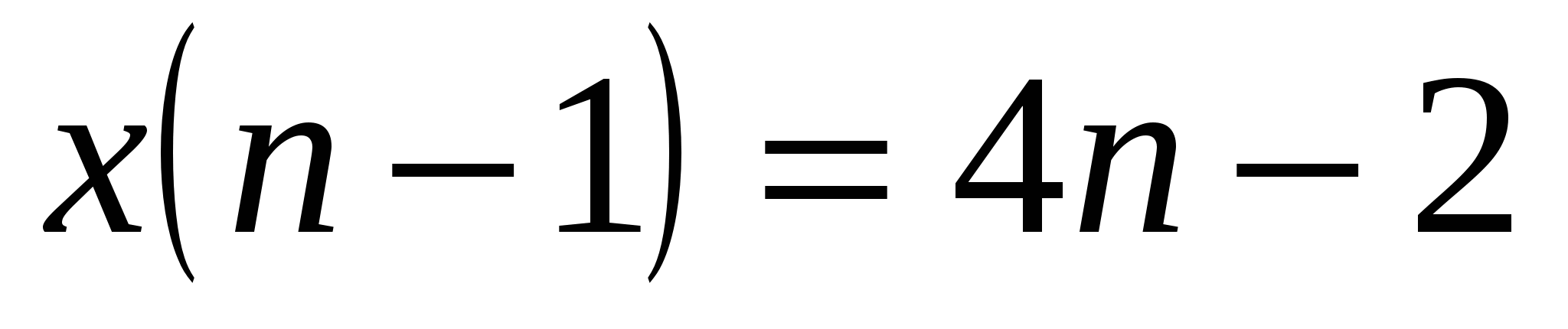
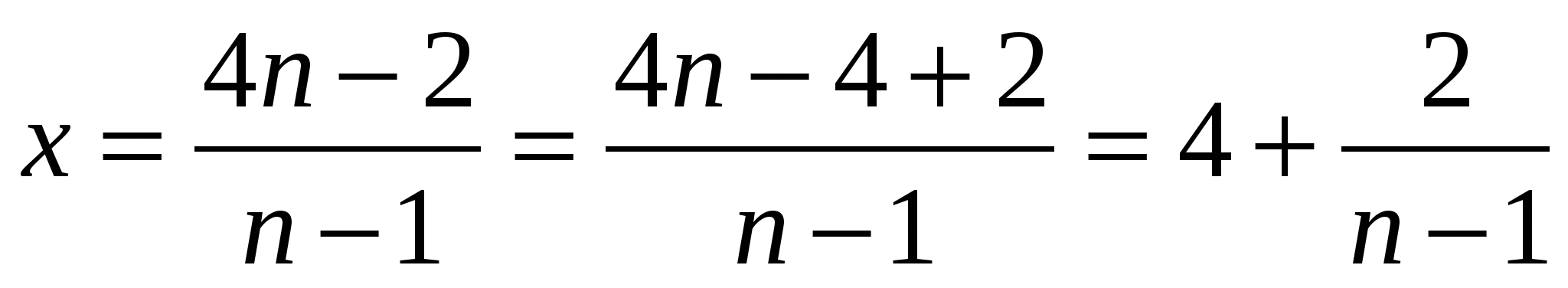
 будет натуральным числом
будет натуральным числом  число 2 нацело делится на
число 2 нацело делится на 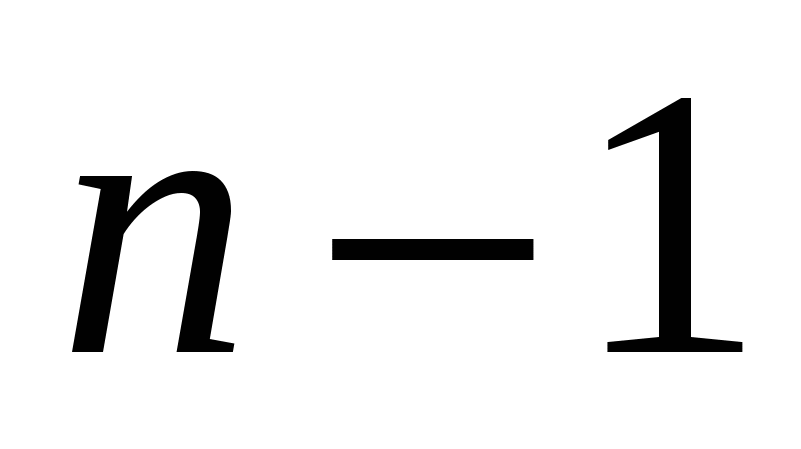 , т.е.
, т.е.
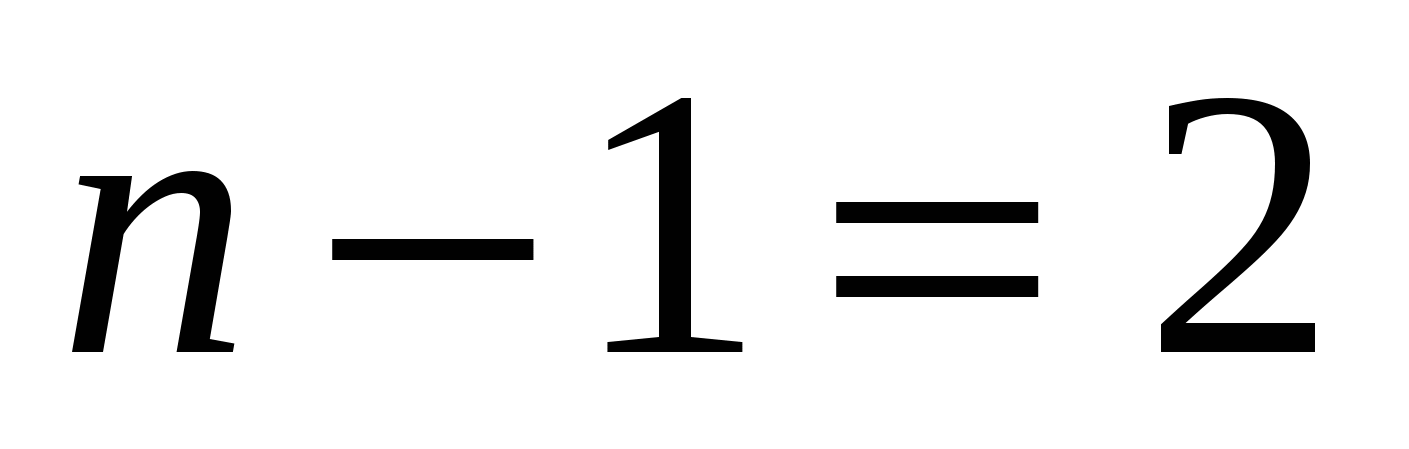 или
или 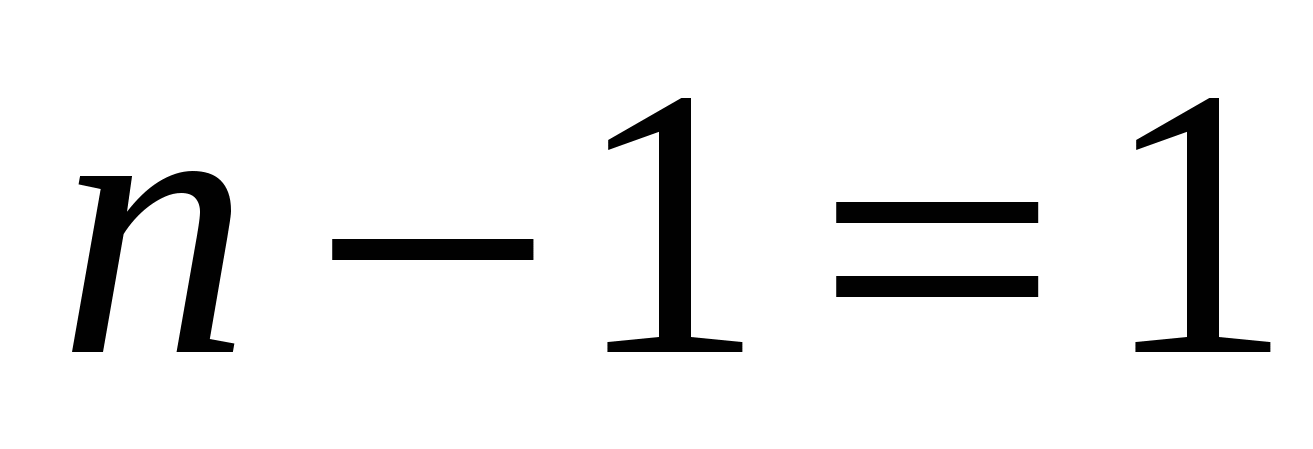
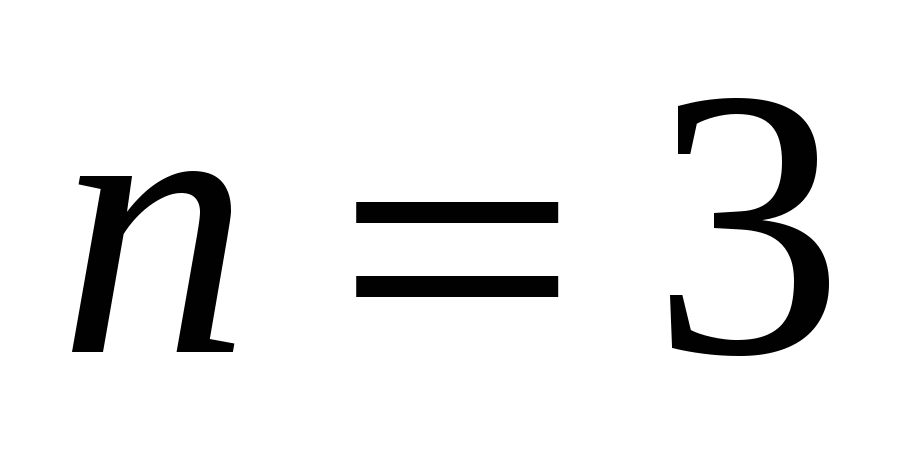
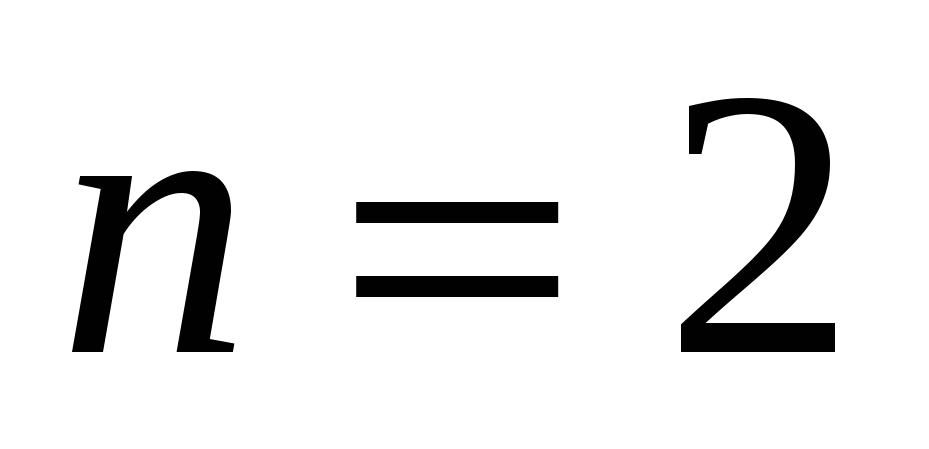
Если 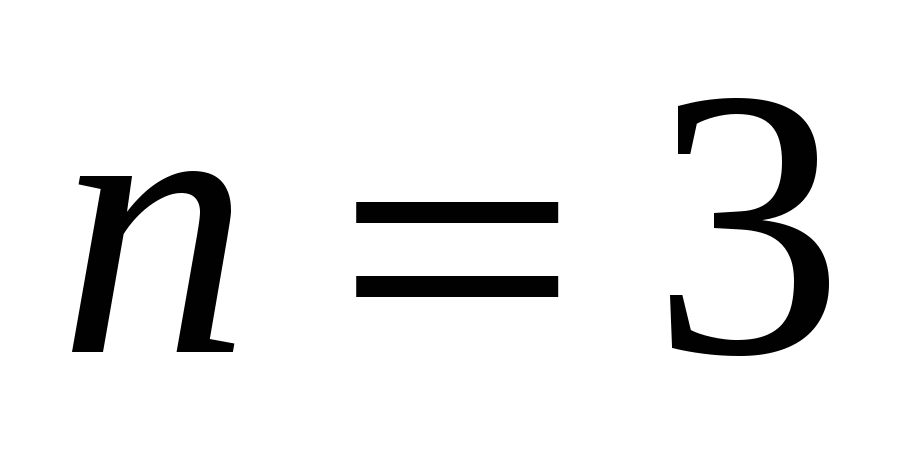 , то
, то 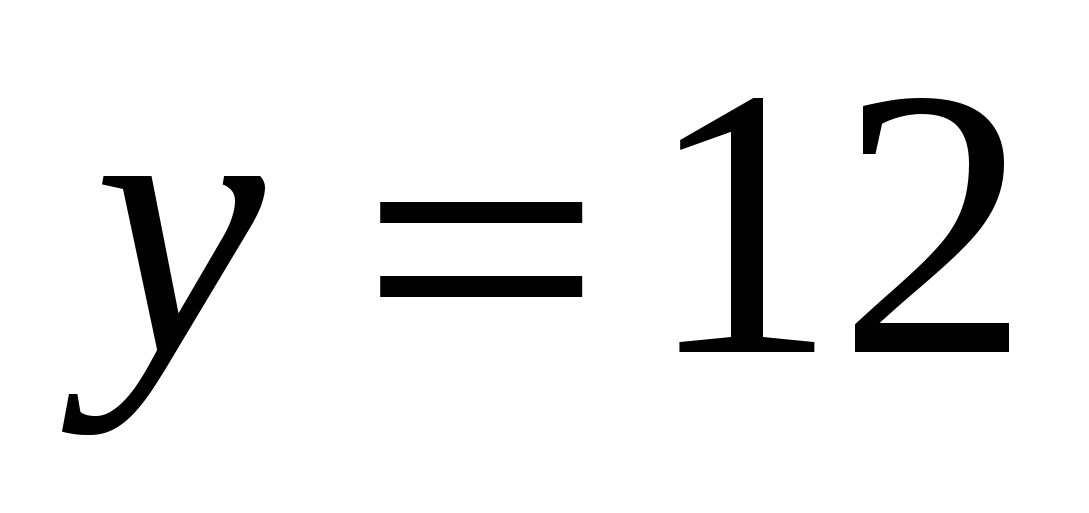 ,
, 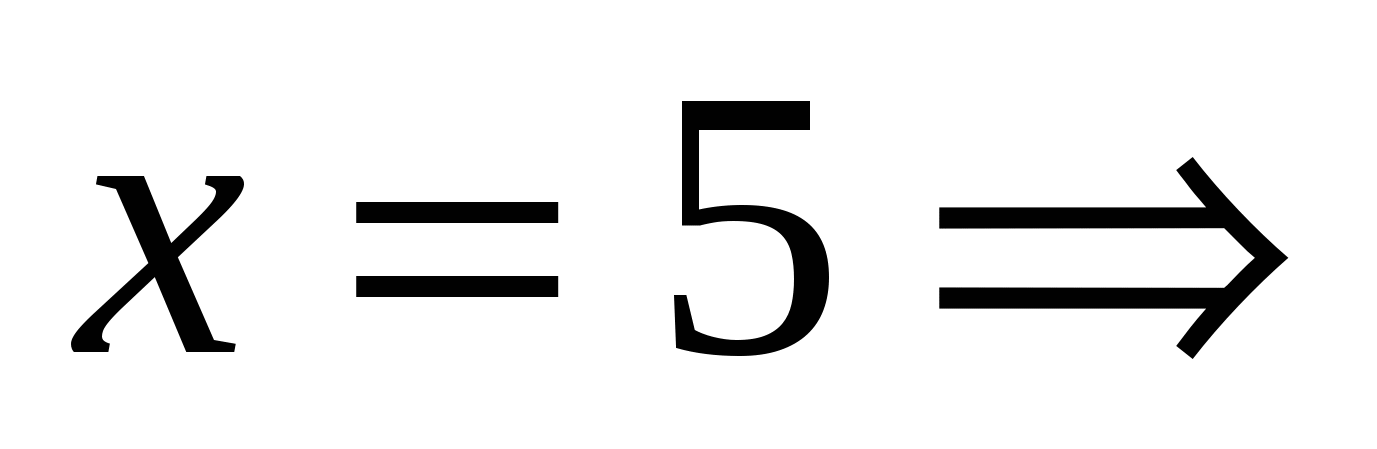
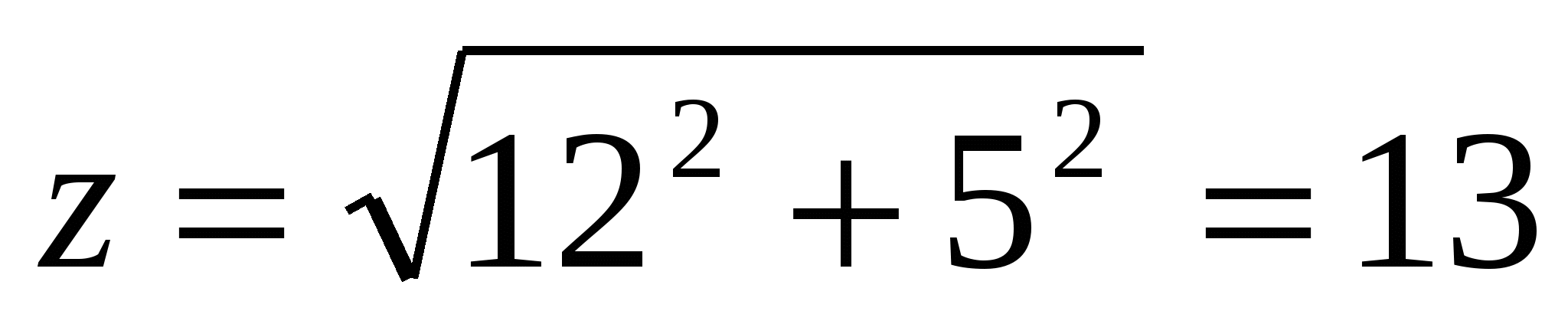 ;
;
Если 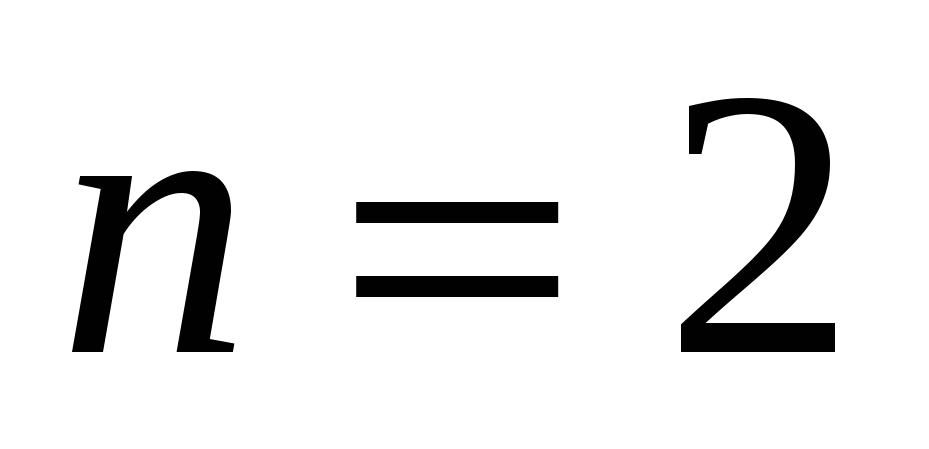 , то
, то 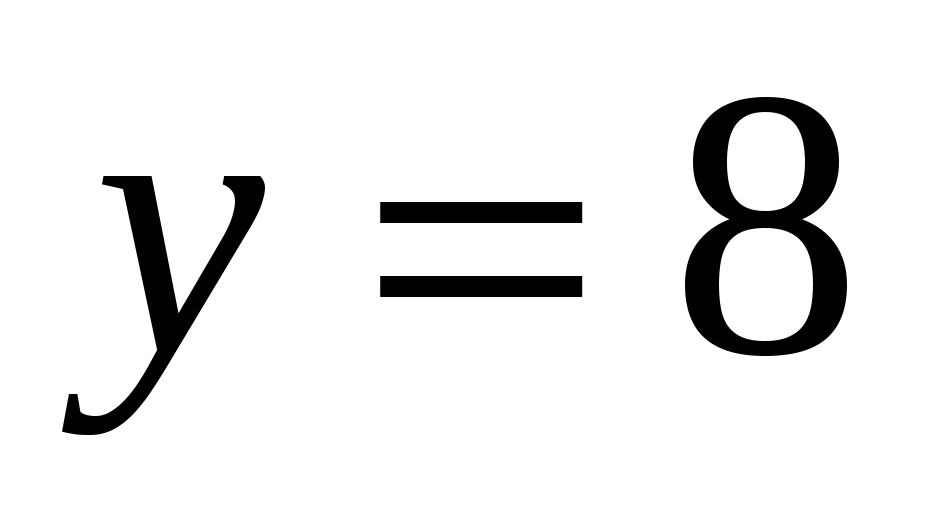 ,
, 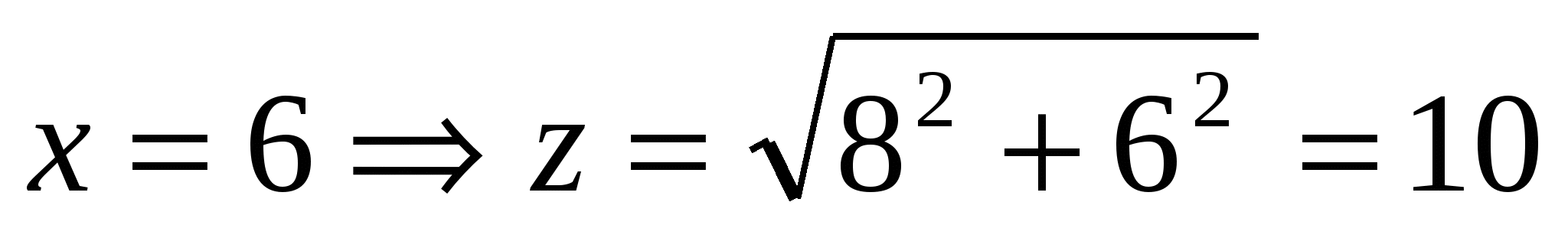 .
.
Ответ: существует только два таких треугольника, со сторонами 5; 12; 13 и 6;8;10.
А я тоже приготовила вам интересное задание, которое было предложено абитуриентам для поступления в МГУ:
Решите системы уравнений с тремя неизвестными:
а) 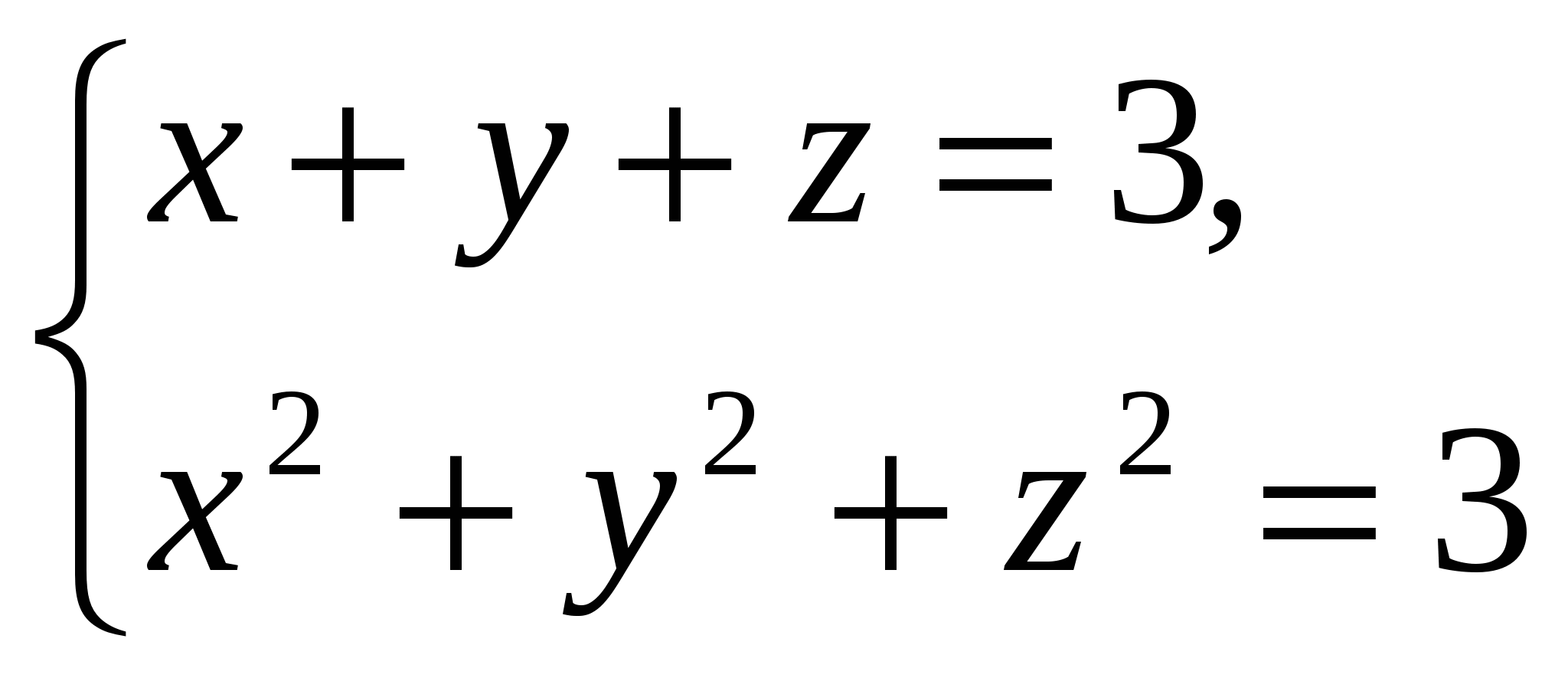 б)
б) 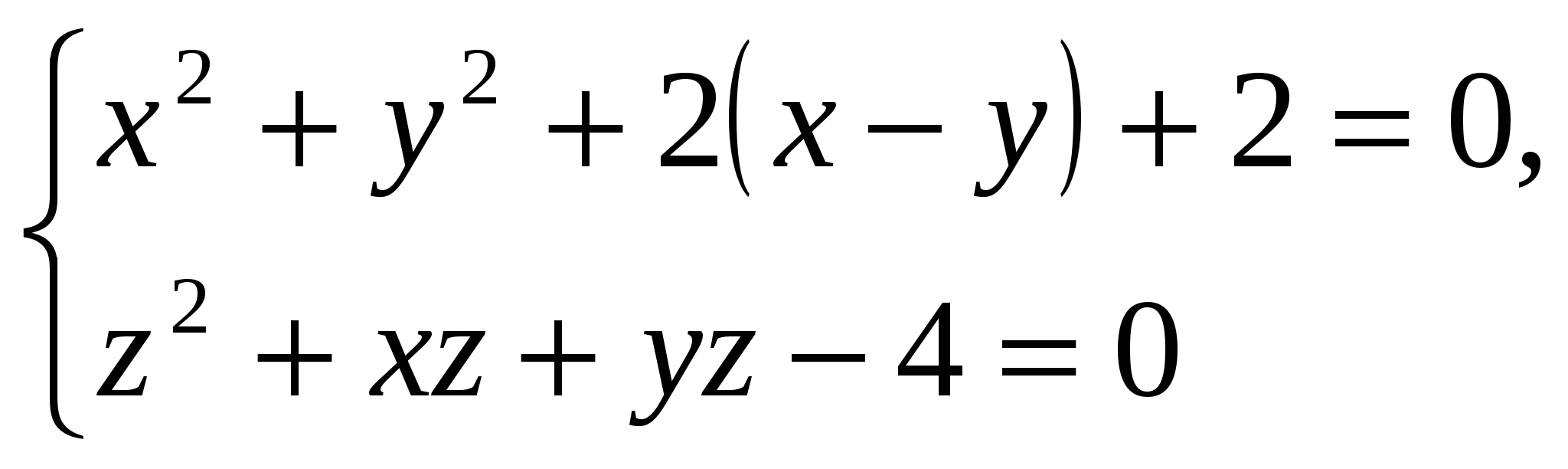
Умножим обе части I уравнения на 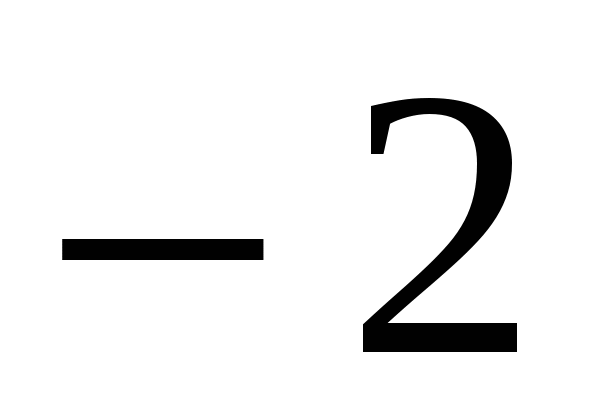 и сложим его со II уравнением. Получим:
и сложим его со II уравнением. Получим:

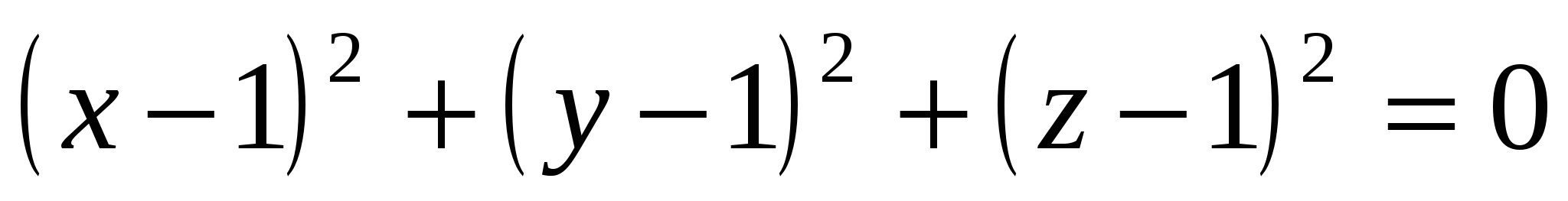
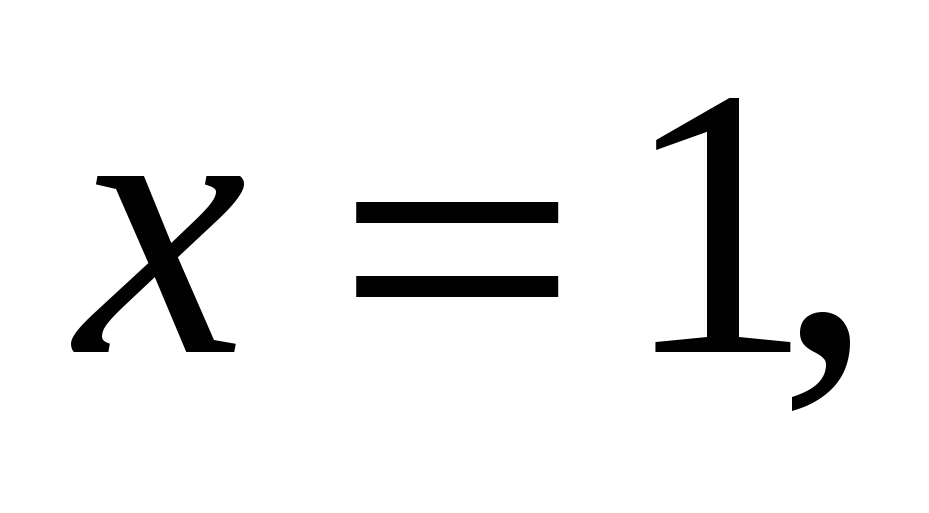
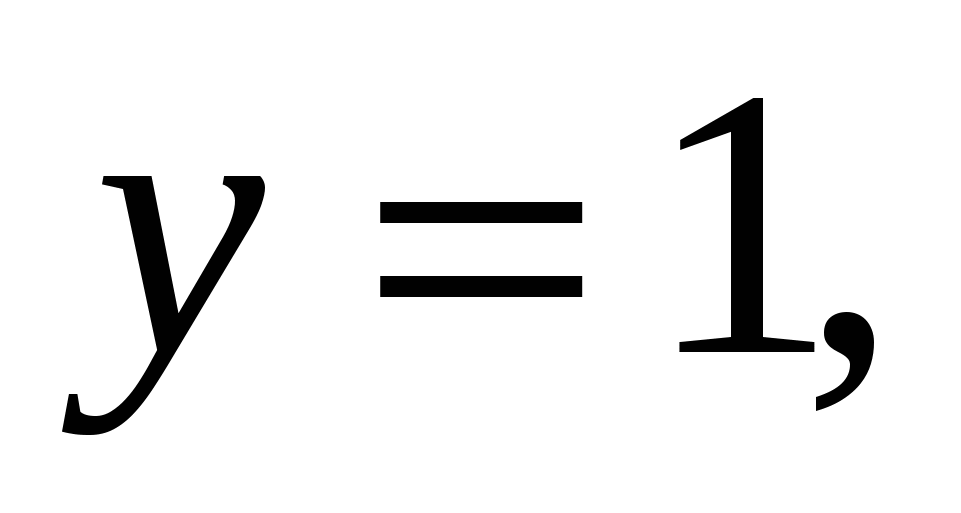
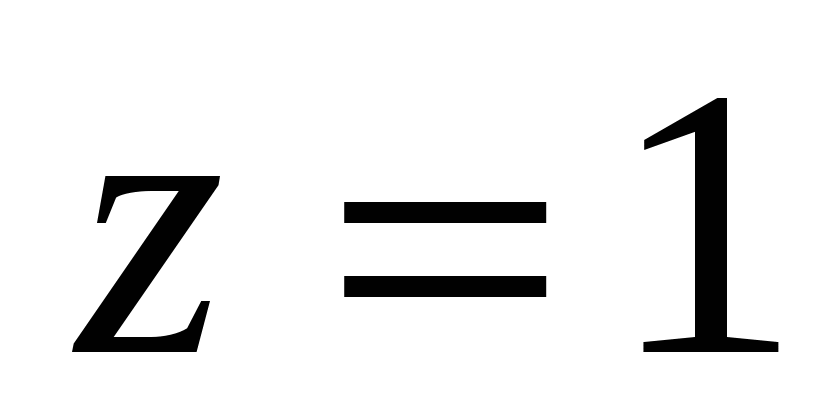
Ответ: (1;1;1)
б) 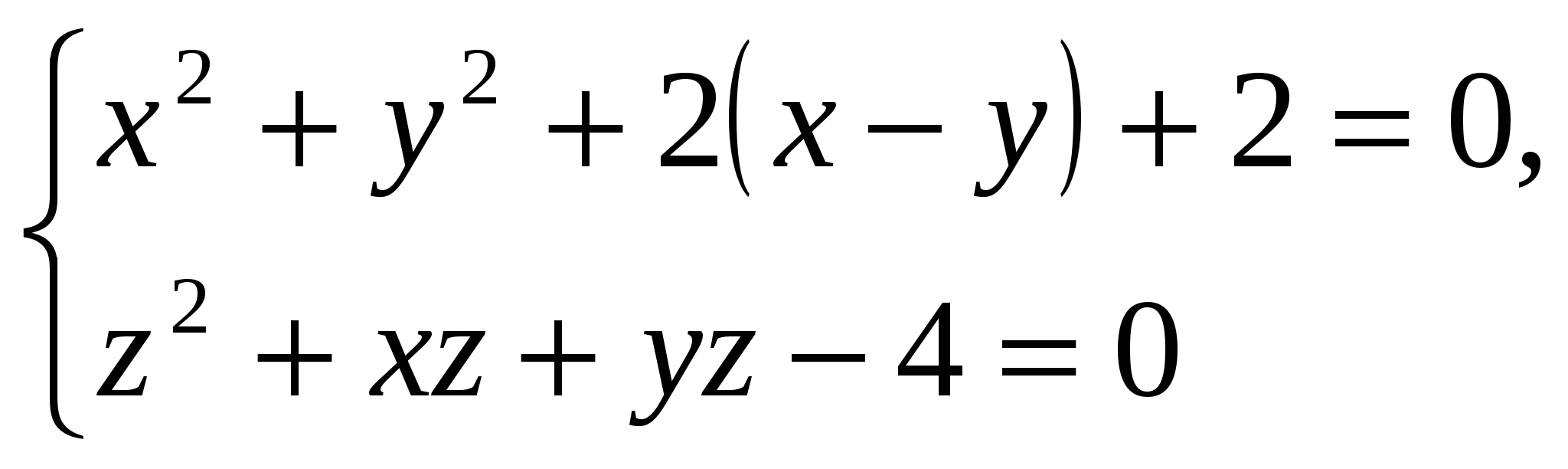

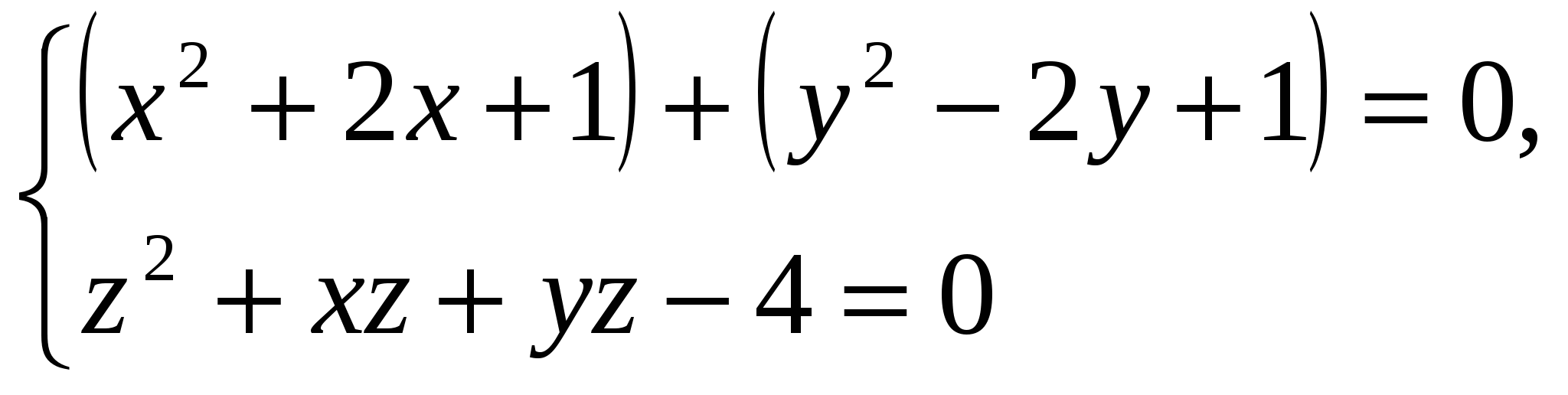
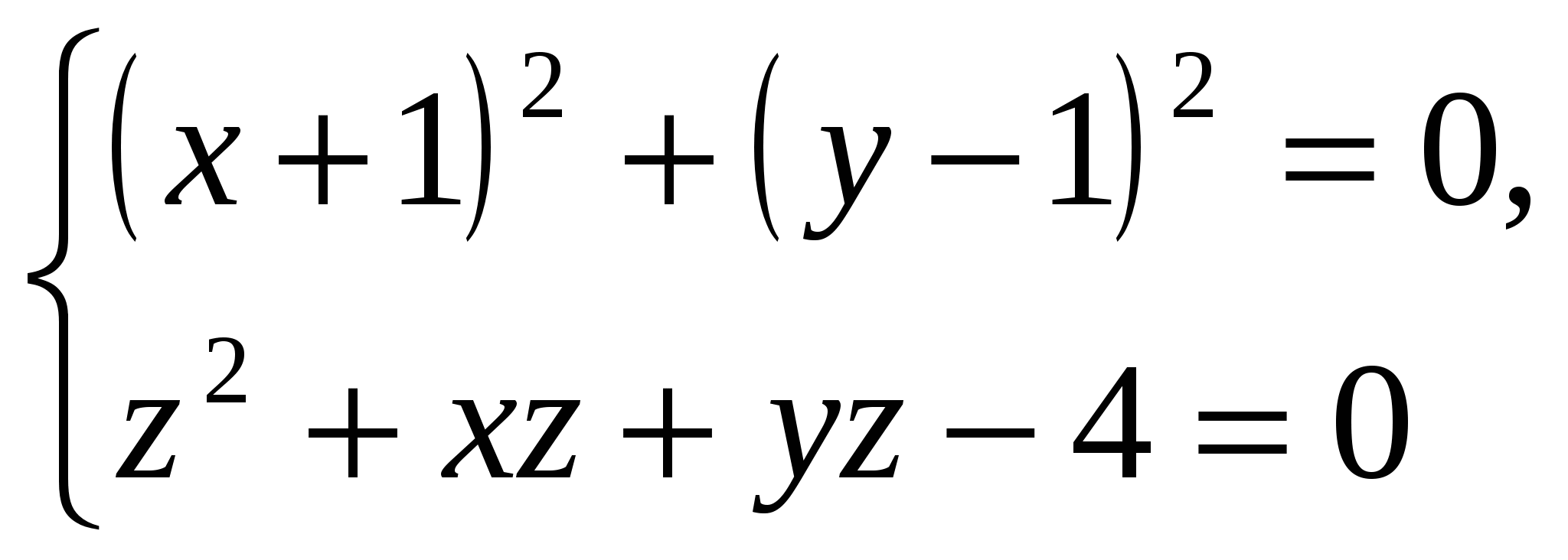
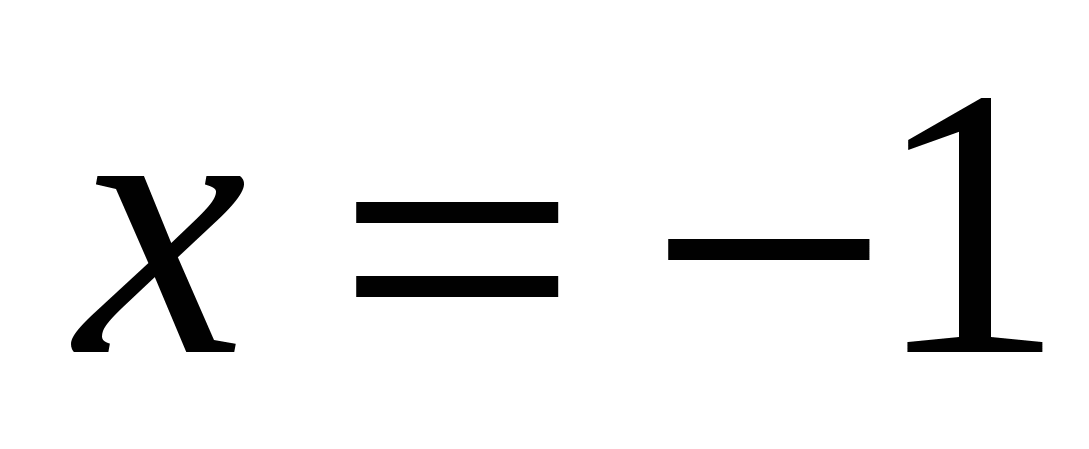 и
и 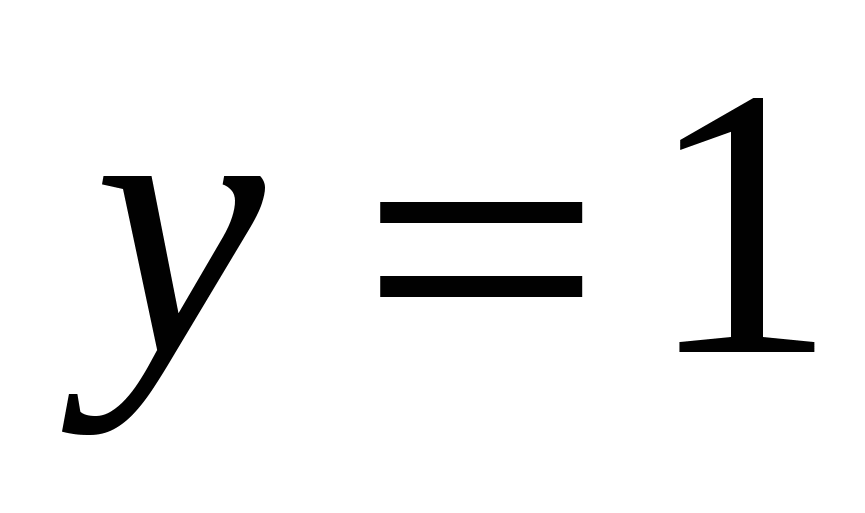
Тогда 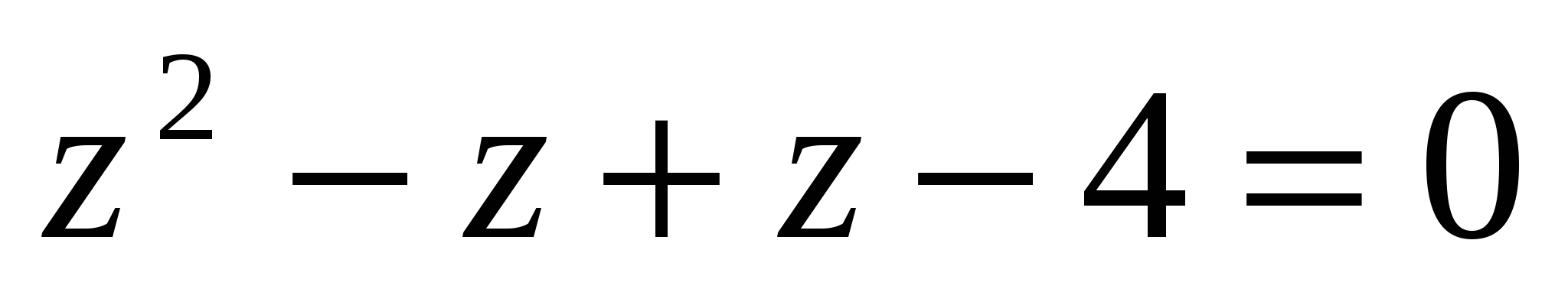

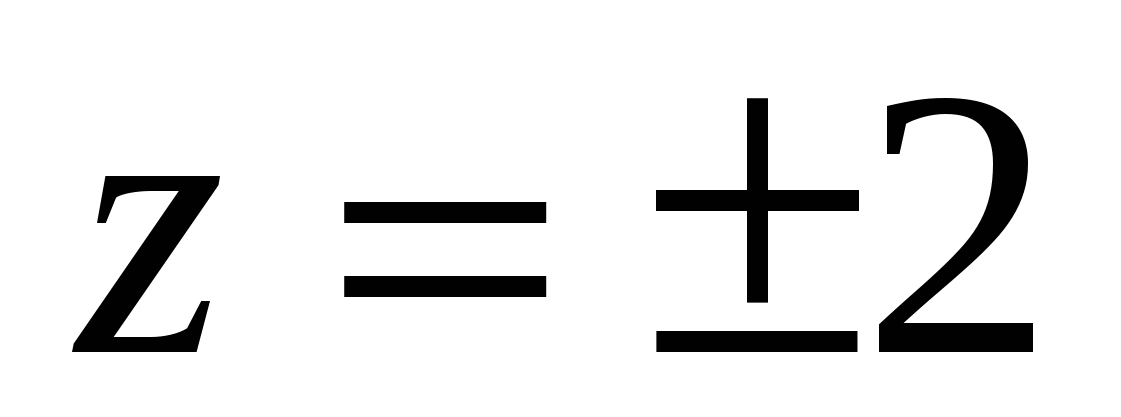 .
.
Ответ: 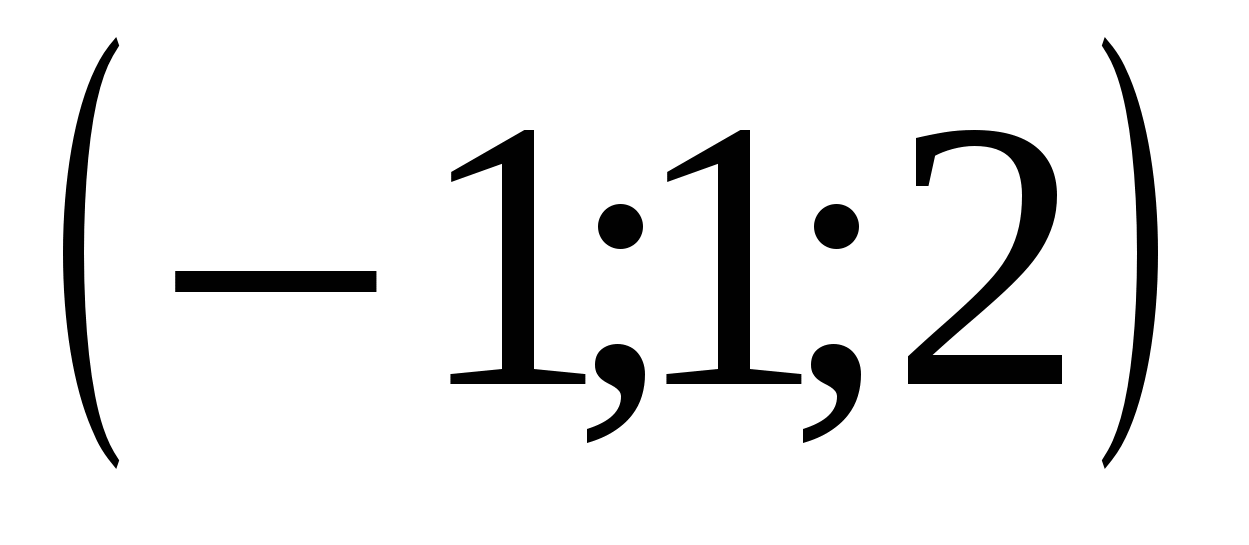 ;
;  .
.
карточка №1.
Даны системы уравнений. Подумайте и запишите способы решения напротив системы уравнений.
1. 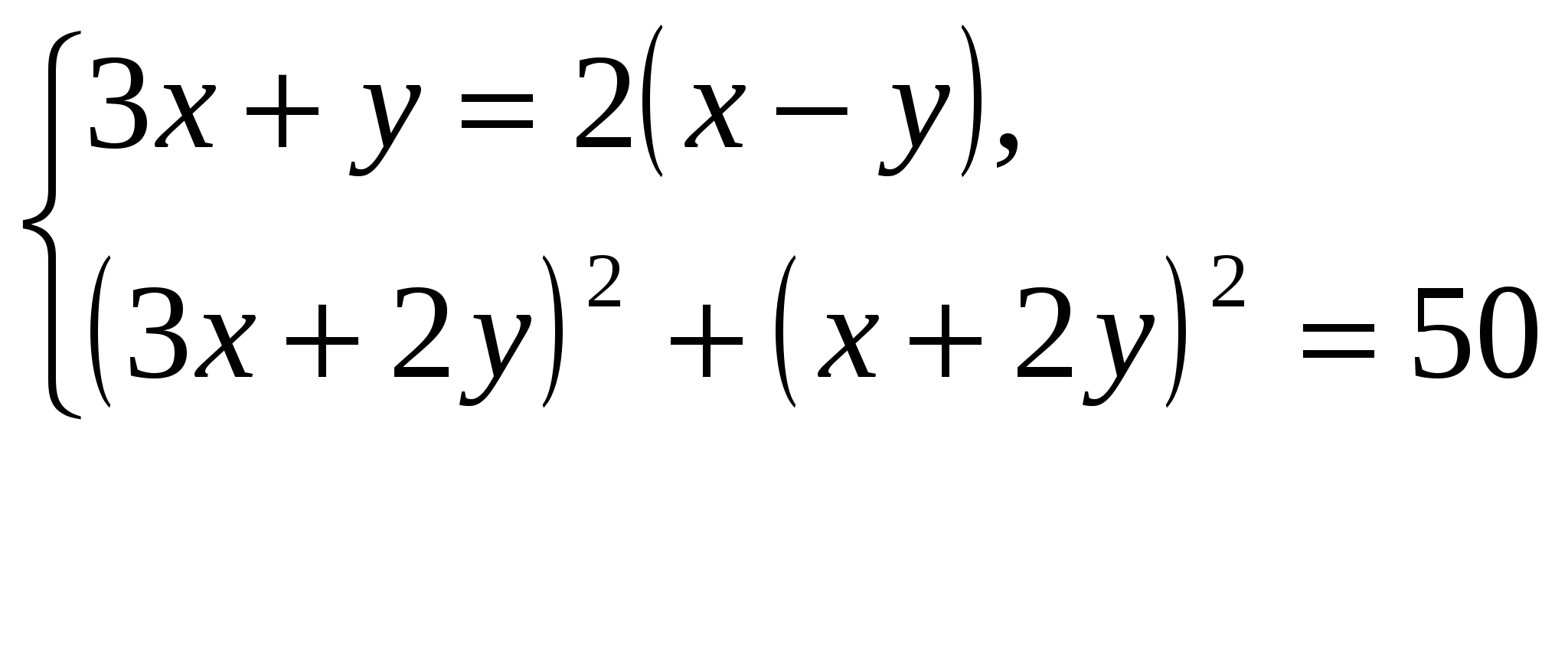
2. 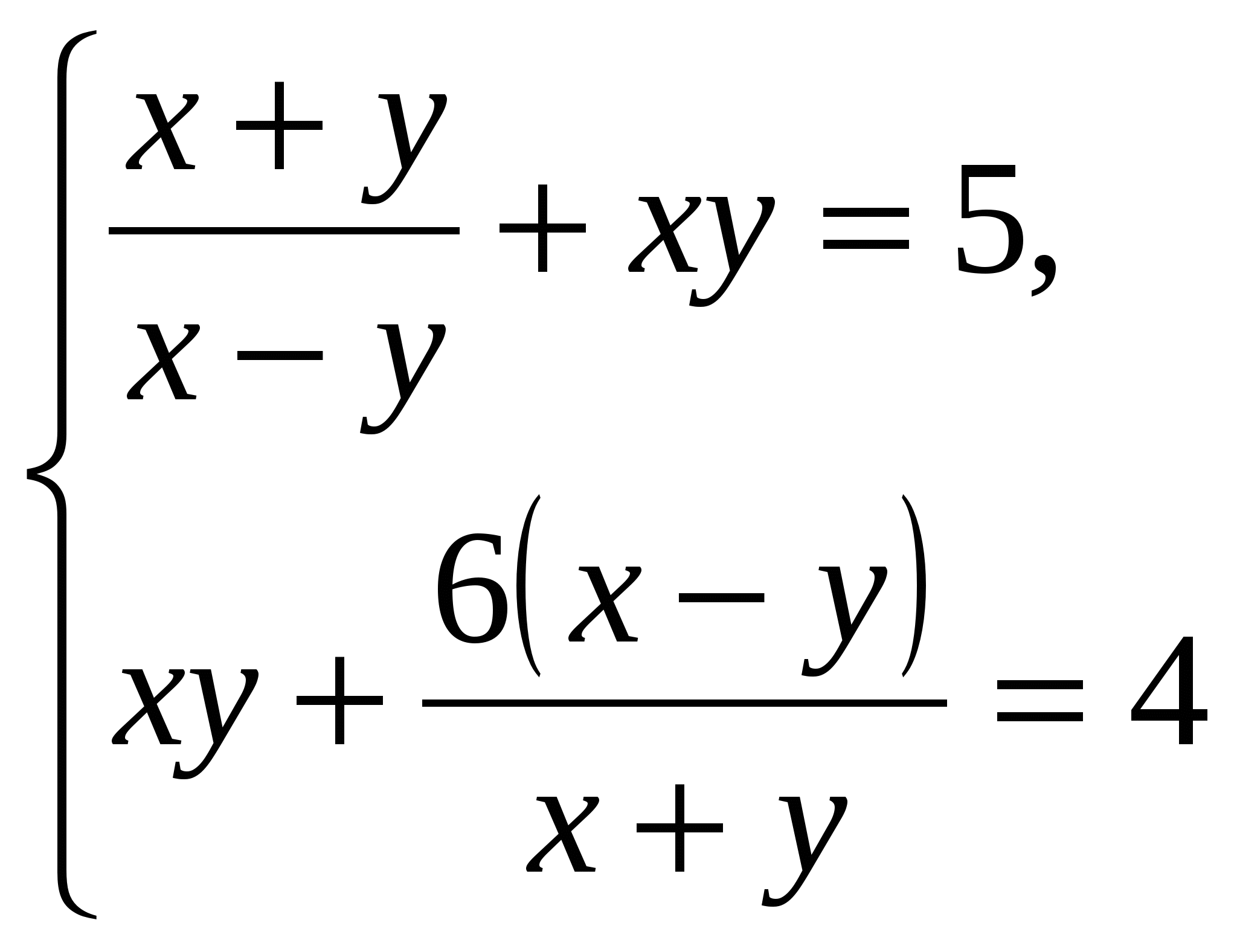
3. 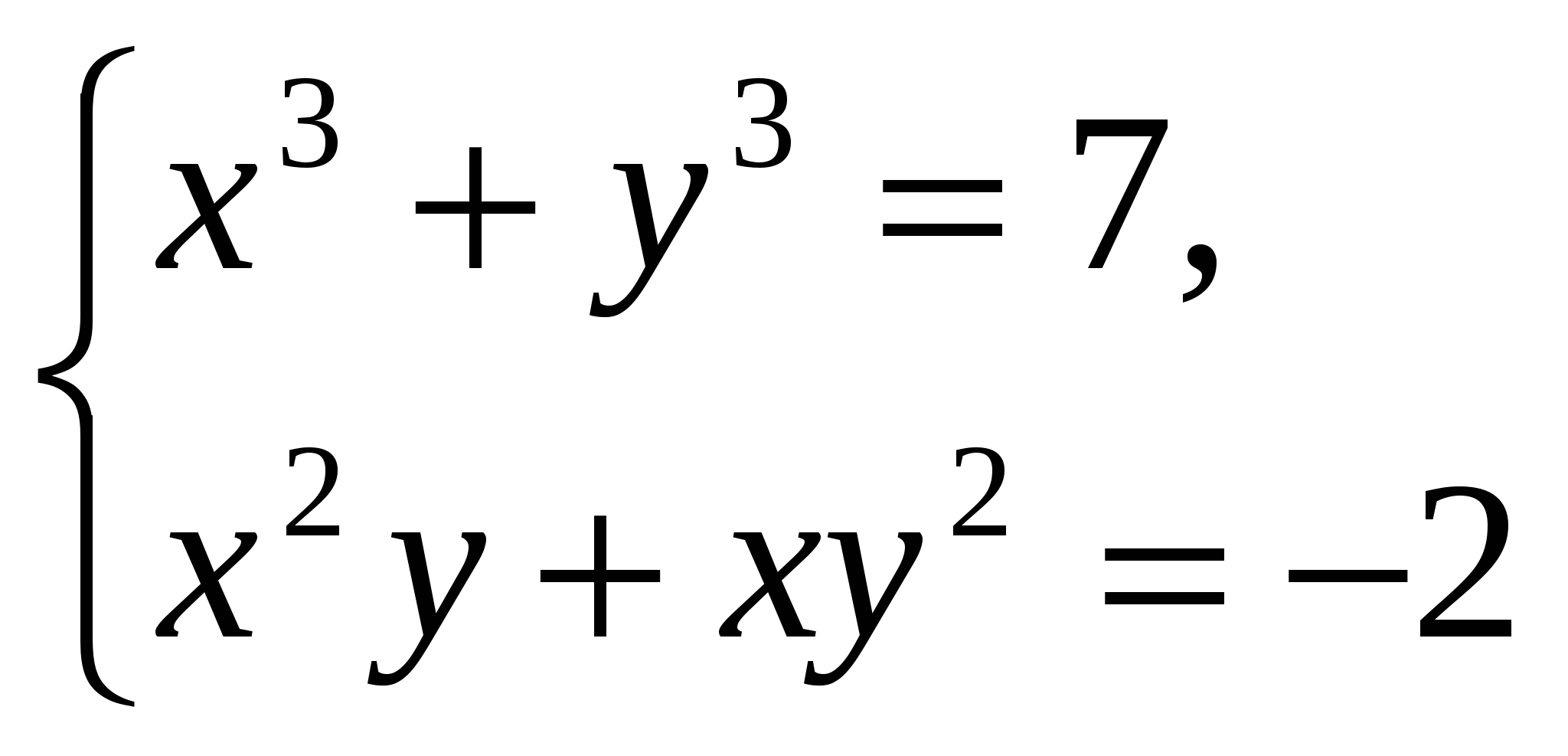
4. 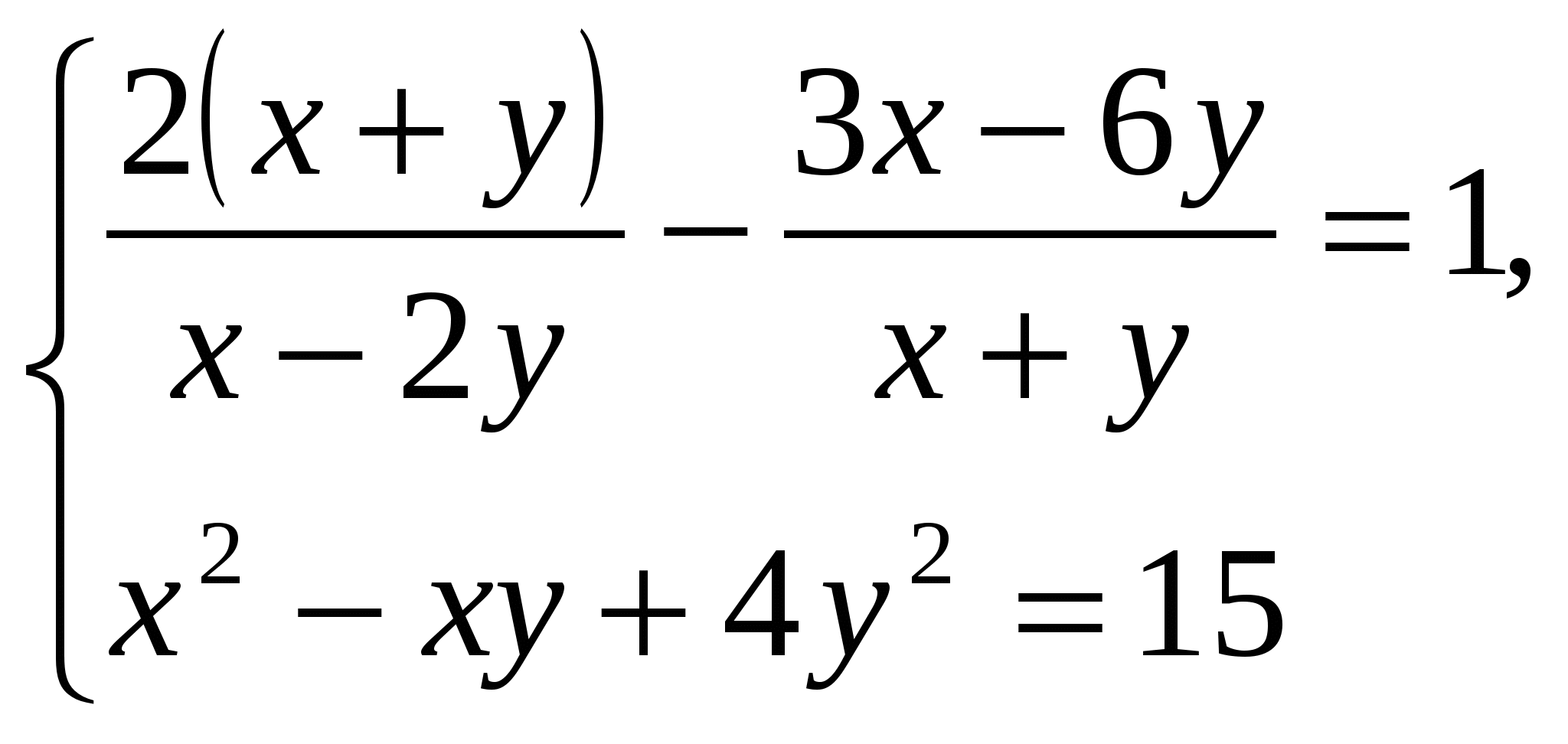
5. 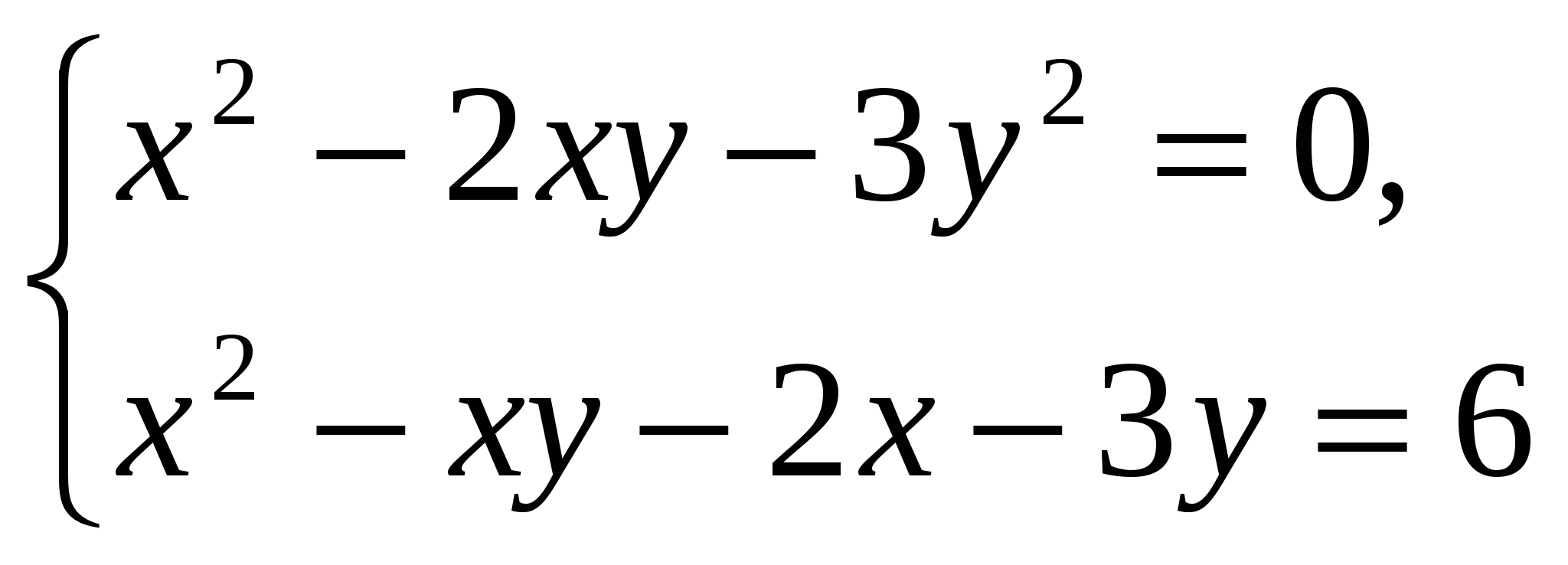
6. 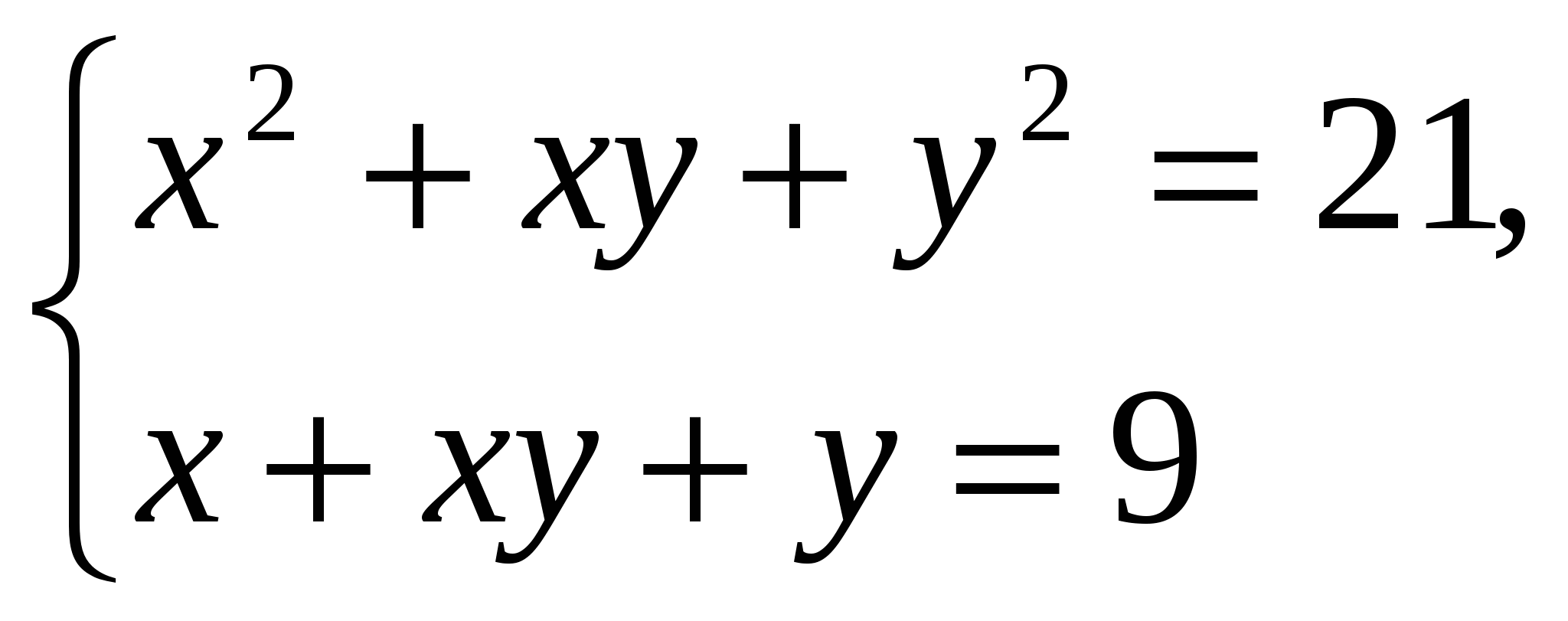
7. 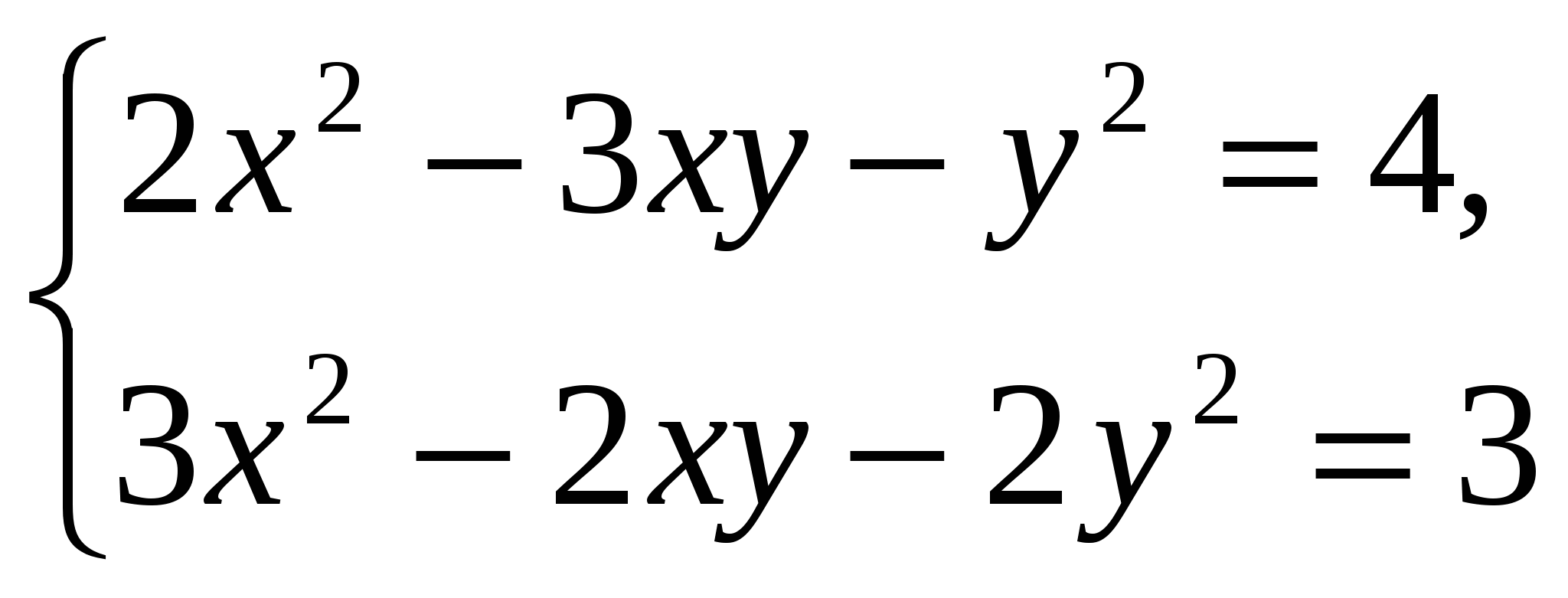
8.