Открытый урок в 9 классе по теме»Решение уравнений»

Открытый урок по алгебре в 9 классе

«Уравнения с одной переменной и

методы их решения»

Учитель математики МБОУ СОШ № 32 Маланичева

Татьяна Александровна

Дата проведения: 18 апреля 2015 года

Тип урока: урок повторения и систематизации ЗУН

Вид урока: повторительно-обобщающий

Оборудование:

• карточки с заданиями,

• проектор,

• компьютеры для индивидуальной работы с электронным справочником.

Формы работы: 

• коллективная,

• индивидуальная,

• фронтальная.

Методы обучения: 

Технологии: 

• развивающее обучение,

• дифференциация и индивидуализация обучения,

• здоровьесберегающие технологии,

• ИКТ.

Оборудование урока:

• Алгебра.7-11 класс. Электронный учебник-справочник. Обучающая программа для школьников и абитуриентов. ЗАО КУДИЦ и ООО Кордис &Медиа, 2007 г.,

• доска,

• компьютеры,

• мультимедийный проектор,

• презентация.

Цель урока:

Повторить и систематизировать знания, умения и навыки учащихся при решении уравнений с одной переменной.

Задачи урока:

Образовательные:

• повторение основных понятий по теме «Уравнения с одной переменной»,

• обобщение и систематизация способов решения уравнений разных видов,

• восполнение пробелов в знаниях, умениях и навыках учащихся.

Воспитательные:

• воспитание интереса к предмету через содержание учебного материала; умения работать в коллективе, взаимопомощь, культуры общения,

• воспитание настойчивости в достижении цели, умения не растеряться в проблемных ситуациях.

Развивающие:

• развитие умения применять знания в конкретной ситуации,

• развитие логического мышления,

• развитие умения работать в проблемной ситуации,

• развитие умения обобщать, конкретизировать, грамотно излагать свои мысли,

• развитие умения работать самостоятельно.

Ход урока.

I. Организационный момент.

1. Приветствие.

2. Проверка готовности рабочих мест.

II. Проверка домашнего задания.

III.Сообщение темы и цели урока.

Ребята, в свое время современный польский математик Станислав Коваль сказал: «Уравнение — это золотой ключ, открывающий все математические сезамы». Сегодня на уроке мы продемонстрируем умение пользоваться этим ключом.

Тема сегодняшнего урока: «Уравнения с одной переменной и его корни».

Цель нашего урока – повторение видов уравнений с одной переменной и закрепление умений и навыков решения уравнений различными способами.

IV. Актуализация опорных знаний и умений. Повторение основных понятий, связанных с уравнениями:

1. Что называется уравнением?

2. Что бывает и у дерева, и у уравнения?

3. Что называется корнем уравнения?

4. Сколько корней может иметь уравнение?

5. Как определить степень уравнения?

6. Какие виды уравнений с одной переменной вы знаете?

V. Основная часть урока.

Чтобы проверить, как вы усвоили понятие видов уравнений, давайте выполним такое задание:

Задание 1: С помощью компьютера учитель выводит на доске уравнения и обращается к классу: «Ребята, вам необходимо сказать, под какими номерами находятся следующие уравнения: линейные, квадратные, уравнения третьей степени, биквадратные, дробные рациональные и рассказать о методах их решения рассказать кратко алгоритм решения».

1. 

2. х³ – 16х = 0;

4. х⁴ — 7х² +12 = 0;

5. х³ + 3х² – 2х – 6 = 0;

6. 2 – 3(х + 2)=5-2х;

8. х² -8х + 7=0;

9. (х² +4х)( х² +4х — 17)= -60.

10. 25-100х² = 0

Задание 2: Ребята, какие уравнения вы можете решить устно и без особого затруднения. Решите эти уравнения:

• линейные №6, №7

• квадратные №8, №10.

• кубическое №2.

А остальные уравнения нам придётся решать с подробным объяснением, чтобы не допустить вычислительных ошибок.

Физкультминутка.

  Упражнения для глаз с использованием геометрических фигур, расположенных на стене классной комнаты.

Цель: расширение зрительной активности, снятие утомления на уроке.

В кабинете на стене размещены различные цветные фигуры (квадрат, круг, ромб и т.д.). Во время физминутки дается задание последовательно перемещать взгляд с одной фигуры на другую (самостоятельно) или по названию фигуры (цвета) учителем. Упражнение можно выполнять сидя и стоя.

Продолжаем урок.

Ребята, а какой ещё существует способ решения уравнений? (

графический). Почему этот способ применяется при решении уравнений крайне редко?

Задание 3: Перед вами графики какой функции? (квадратичной). Назовите число корней уравнения ax²+bx+c=0 и знак коэффициента а, если график соответствующей квадратичной функции расположен следующим образом:

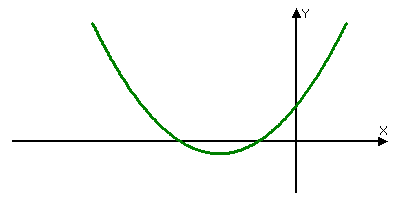
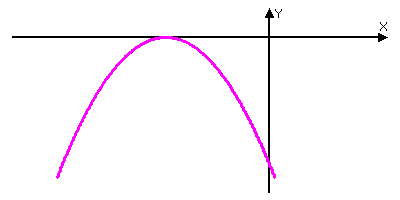
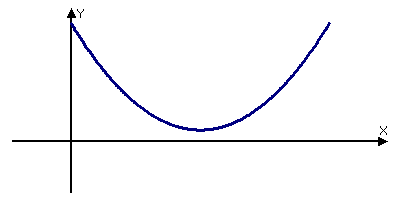
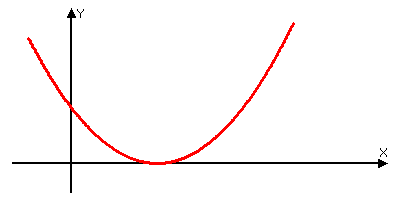
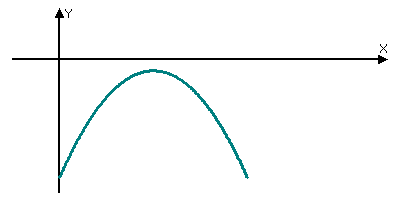
Вопрос классу: Ребята, знаете ли вы ученых-математиков, которые занимались изучением уравнений, их классификацией, способами решения?

После ответов учащихся учитель, используя презентацию, показывает портреты великих математики и кратко рассказывает об их вкладе в изучение уравнений [Приложение 1,2].

VI. Самостоятельная работа (работа с электронным справочником).

Ребята, давайте обратимся к электронному справочнику [Приложение 3].

Ещё два выдающихся итальянских математика XVI века Сципион дель — Ферро (1465 -1526) и его ученик Фиоре Николо Тарталья (ок. 1499 -1557) внесли огромный вклад в развитие науки алгебры, в том числе в решение уравнений 3-й и 4-й степени.

Однажды между ними состоялся научный поединок, на котором Тарталья одержал блестящую победу. Он за 2 часа решил 30 задач, предложенных Ферро, а сам Ферро не решил ни одной задачи.

Итак, Тарталья за 2 часа решил 30 задач.

Вопрос классу: Сколько уравнений вы сможете решить за 10 минут урока? Какие способы решения уравнений при этом изберете?

Учащимся предлагается поработать с электронным справочником в рубрике «Проверь себя» с 5-ю уравнениями разными по уровню сложности, которые можно решить разными способами [Приложение 4,5]. Учащиеся работают каждый за своим компьютером, решают уравнения в тетрадях, проверяют ответы на экране. Если ученик справился с уравнением правильно, продолжает решать следующее, если неверно, то он поднимает руку и разбирает решение вместе с педагогом. Учащиеся сами оценивают себя в самостоятельной работе согласно критериям оценки.

Критерии оценок:

«3» — 2 уравнения

«4» — 3 уравнения

«5»- 4 уравнения

VII. Подведение итогов урока

Учитель рассказывает ученикам притчу:

Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма».

Ребята, давайте попробуем с вами оценить каждый свою работу за урок:

• Кто работал так, как первый человек? (поднимают руки)

• Кто работал добросовестно?

• Кто принимал участие в строительстве храма?

Выставление оценок и их комментирование. Дается оценка работы класса, отдельных учащихся.

VIII. Домашнее задание:

Карточки с заданиями. Решите уравнения:

1. (2х + 7)(3х – 1) – (5х – 1)(х + 3) = (х + 1)²

2. =

3. 16х² — 40х + 25 = 0

4. (3х + 4 )( 11х – 6 ) = 0

5. + = 2

6. =

7. = 7 – х

Творческое задание:

Составить кроссворд по теме «Уравнения с одной переменной и методы их решения».

Презентация к уроку по алгебре (9 класс) на тему: Презентация «Решение линейных уравнений с одной переменной»

Слайд 1

Решение линейных уравнений с одной переменной Кузнецова Валентина Константиновна, учитель математики ГБОУ “ Школа № 329 “ г . Москвы Готовимся к ОГЭ

Слайд 2

Линейным уравнением с одной переменной называется уравнение вида a х + b = с , где а, в, с – числа, х – переменная. Например: 3х + 8 = 0, 1 4 – 2х =9; – 4х = 10. Определение

Слайд 3

Решить уравнение – это значит найти все его корни или доказать, что корней нет. Корнем уравнения с одной переменной называется значение переменной, при котором уравнение обращается в верное равенство.

Слайд 4

При решении уравнений с одной переменной используются следующие свойства: Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; Если обе части уравнения умножить или разделить на одно и то же число, то получится уравнение, равносильное данному .

Слайд 5

Алгоритм решения уравнения Раскрыть скобки . Перенести слагаемые, содержащие переменную, в одну часть уравнения, а числа без переменной – в другую часть . Упростить, привести подобные слагаемые . Найти корень уравнения . Сделать проверку.

Слайд 6

Раскрытие скобок Если перед скобками стоит знак « + », то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки. Пример: (25 –3х) + (–2х + 6) = 25 – 3х – 2х + 6 = 31 – 5х.

Слайд 7

Раскрытие скобок Если перед скобками стоит знак « — », то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки. ( 6х – 3) – ( 14 – 2х) = 6х – 3 –14 + 2х = = 8х – 17; 12 + ( х – 3) – (– 3х + 1) = =12 + х – 3 +3х – 1 = 8 + 4х.

Слайд 8

Распределительное свойство умножения а(в + с) = ав +ас а(в – с) = ав – ас Примеры: 6 ( 3 – 2х) = 18 – 12х – 5 ( а + 3) = – 5а –15.

Слайд 9

Примеры решения уравнений Пример 1. 4(х + 5) = 12; 4х + 20 = 12; 4х =12 – 20; 4х = — 8; х = — 8 : 4; х = — 2 Ответ: -2.

Слайд 10

Пример 2 5х = 2х + 6; 5х – 2х = 6; 3х =6; х = 6 : 3; х = 2 Ответ: 2.

Слайд 11

Пример 3 3 (х + 6) + 4 = 8 – ( 5х + 2) 3х + 18 + 4 = 8 – 5х – 2 3х + 5х = — 18 – 4 + 8 — 2 8х = — 16 х = — 16 : 8 х = — 2 Ответ: -2.

Слайд 12

Задания для самостоятельного решения Решить уравнени е: 1). 2х + 5 = 2 (- х + 1) + 11 2). 6у – 3(у – 1) = 4 + 5у 3). 4 ( х – 1) – 3 = — (х + 7) + 8 4). – 2(5 у – 9) + 2 = 15 + 7(- х + 2) 5). 12 + 4(х – 3) – 2х = (5 – 3х) + 9

Слайд 13

Ответы 1) 2 2) — 0,5 3) 1,6 4) — 3 5) 2,8

Слайд 14

Удачи на экзамене !

Контрольная работа по алгебре 9 класс «Уравнение с одной переменной»

Контрольная работа № 4

по теме «Уравнения с одной переменной»

Вариант 1

1. Решите уравнение:

а) ; б) 3(х – 1,5) + 2х = 5(2,5 + 2х).

2. Решите уравнение:

а) х³ – 4х² – 9х + 36 = 0; б) х⁶ + 4х⁴ – х² – 4 = 0.

3. Решите биквадратное уравнение:

а) х⁴ — 10х² + 9 = 0; б) х⁴ +6х² — 27 = 0.

4. Решите дробное рациональное уравнение:

а) += 5; б) += .

Контрольная работа № 4

по теме «Уравнения с одной переменной»

Вариант 2

1. Решите уравнение:

а) ; б) 5(х – 2,5) — 4х = 3(2,5 + 3х).

2. Решите уравнение:

а) 16х³ – 32х² – х + 2 = 0; б) х⁶ — х⁴ + 5х² – 5 = 0.

3. Решите биквадратное уравнение:

а) х⁴ — 5х² + 4 = 0; б) х⁴ + 15х² + 54 = 0.

4. Решите дробное рациональное уравнение:

а) 2 + = ; б) + =

Контрольная работа № 4

по теме «Уравнения с одной переменной»

Вариант 1

1. Решите уравнение:

а) ; б) 3(х – 1,5) + 2х = 5(2,5 + 2х).

2. Решите уравнение:

а) х³ – 4х² – 9х + 36 = 0; б) х⁶ + 4х⁴ – х² – 4 = 0.

3. Решите биквадратное уравнение:

а) х⁴ — 10х² + 9 = 0; б) х⁴ +6х² — 27 = 0.

4. Решите дробное рациональное уравнение:

а) += 5; б) += .

Контрольная работа № 4

по теме «Уравнения с одной переменной»

Вариант 2

1. Решите уравнение:

а) ; б) 5(х – 2,5) — 4х = 3(2,5 + 3х).

2. Решите уравнение:

а) 16х³ – 32х² – х + 2 = 0; б) х⁶ — х⁴ + 5х² – 5 = 0.

3. Решите биквадратное уравнение:

а) х⁴ — 5х² + 4 = 0; б) х⁴ + 15х² + 54 = 0.

4. Решите дробное рациональное уравнение:

а) 2 + = ; б) + =

Презентация урока алгебра 9 класса по теме «Уравнения с одной переменной»

Обобщающий урок в 9 классе «Уравнения с одной переменной»

Учитель математики Бодякшин И.С.

МБОУ «Апраксинская основная школа»

Задание №1

Укажите номера целых уравнений:

а) х 2 (5х 3 – 2х 2 )+8-5х 5 + х 3 =0

б) х 2 + 2х = х 3 -8х 2

2 5

в) 3х + 2 = 4

х-2 х+3

г) 8 = 0

2-13с – 7с 2

Задание №2

Число 6 является корнем какого уравнения?

а) х+8=х+7

 

б) х 2 -6х =х-6

6

в) 6х-1=0

 

г) 1 + 1 = 1 + 1

х+6 х-6

Задание №3

 

Сколько корней имеет уравнение 5х 2 +75=0 ?

а) один корень

б) два корня

в) не имеет корней

г) имеет бесконечное множество корней

Задание №4

Найдите корни уравнения

5х 2 — х =0

а) 0 ; 5

б) -5 ; 0

в) 0 ; 0,2

г) Нет корней

Задание №5

Сколько корней может иметь уравнение

х 3 +х 2 -9х-9=0

а) 5 или менее

б) не более трех

в) не менее трех

г) не имеет корней

Задание №6

Найдите общий знаменатель дробного рационального уравнения

х 2 +2х = х 3 -8х 2

3(х-1) (х+1)

а) (х-1) 2

б) 3(х-1)(х+1)

 

в) 3(х 2 — 1)

 

г) (х-1)(х+1)

Проверь себя

Номера

заданий

1

Правильные ответы

2

а,б

3

б

4

в

5

в

6

б

б,в

Уравнения с одной переменной

Дробные рациональные уравнения P n (х)/Q n (х)=0

Целые уравнения P n (х)=0

• Найти ОДЗ уравнения
• Найти общий знаменатель дробей, входящих в уравнение
• Умножить обе части уравнения на общий знаменатель

4) Решить полученное целое уравнение

5)Исключить из его корней те, которые обращают в нуль знаменатель .

5)Исключить из его корней те, которые обращают в нуль знаменатель.

Уравнения n-х степеней

Уравнения 4 степени ах 4 +вх 3 +сх 2 +dx+e=0 (в том числе биквадратные

Квадратные ах 2 + вх+с=0 полные , не приведенные ( в том числе неполные ах 2 + вх=0 , ах 2 + с=0 , ах 2 =0 ; приведенные х 2 + вх+с=0 ) . Имеют 2,1, 0 корней

Линейные ах+в=0 Имеют не более одного корня

Уравнения 3 степени например ах 3 + вх 2 +сх+d =0

ах 4 +вх 2 +с=0 ). Имеют не более 4,3,2,1,0 корней

Имеет 3,2,1,0

корней

2 основных метода решения уравнений выше второй степени

Метод разложения  на множители

Метод введения  новой переменной

С помощью какого метода можно решить уравнения:  

а) х 5 -4х 3 =0

б) 9 х 4  – 10 х 2  + 1 = 0

в) х-4 = 2

х+3

Решение:

  а) х 5 -4х 3 =0

х 3 (х 2 -4)=0

х 3 =0 ( х 2 -4 ) = 0

х 1 =0 ( х-2 )( х+2) = 0

х 2 =2 х 3 =-2

Ответ: х 1 =0 х 2 =2 х 3 =-2

Уравнение решили методом разложения на множители

б) 9 х 4  – 10 х 2  + 1 = 0.

-Если обозначить х 2 переменной у, то получится квадратное уравнение

9 у 2  – 10у + 1 = 0.

Д=(-10) 2 — 4 . 9 . 1= 100-36=64=8 2

у 1 = 10+8 = 1 у 2 = 10-8 = 1

18 18 9

Возвращаемся к переменной х.

х 2 =1 х 2 = 1

9

х 1 =1 х 2 =-1 х 3 =1/3 х 4 =-1/3

Ответ:х 1 =1 х 2 =-1 х 3 =1/3 х 4 =-1/3

В уравнении 4 степени получили 4 корня. Решили методом введения новой переменной у.

в) х-4 = 2

х+3

 

ОДЗ: Х не равен -3 (иначе знаменатель превращается в 0)

х-4 -2 = 0 / . ( х+3)

х+3

(х-4)- 2( х+3) =0

-х-10=0

х=-10 Ответ: х=-10

При решении уравнения использовали алгоритм для дробно-рациональных уравнений и решили целое линейное уравнение

Физкультминутка

Повторим с помощью физкультминутки,как строится график линейной функции.

Если график параллелен оси ОХ — разводим руки в стороны;

Проходит через начало координат — руки на пояс;

Пересекает ось ОУ в точке, отличной от начала координат- руки вверх;

параллелен оси ОУ- одна рука вверх, другая-вниз.

у=2х х=3 у=-2х у=4 у=х/2 х=-5 у=-8 у=7х

Самостоятельная работа

В а р и а н т — образец

• Решите уравнение:

• а)  х 3  – 4 х 2  – 9 х  + 36 = 0; б)  х 4  + 6 х 2  – 27 = 0;
• в) ( х 2  +  х  + 6) ( х 2  +  х  – 4) = 144

В а р и а н т -1 (на карточке)

• Решите уравнение:

• а) 16 х 3  – 32 х 2  –  х  + 2 = 0; б)  х 4  + 7 х 2  – 44 = 0;
• в) ( х 2  –  х  + 1) ( х 2  –  х  – 7) = 65.

Решение варианта – образца (самопроверка)

 

• в) ( х 2  +  х  + 6) ( х 2  +  х  – 4) = 144.

Вводим новую переменную у = х 2  +  х

• а)   х 3  – 4 х 2  – 9 х  + 36 = 0

 

х 2 (х – 4 )  – 9( х  — 4) = 0

(у+6)(у-4)=144

(х – 4 )  ( х 2 — 9) = 0

у 2  + 6у-4у-24-144=0

(х – 4 )  ( х — 3) ( х — 3) = 0

  у 2  + 2у-168=0

х 1 =4 х 2 =3 х 3 =-3

Ответ: х 1 =4 х 2 =3 х 3 =-3

Д=4+4 . 168=676=26 2

 

у 1 = -2+26 ; у 2 = -2-26

• б)   х 4  + 6 х 2  – 27 = 0;

2 2

Вводим новую переменную х 2 =у у 2  + 6у – 27 = 0; Д= 36+4 . 27=144=12 2

у 1 =12 у2=-14 Ответ: у 1 =12 у 2 =-14

у 1 = -6+12 ; у 2 = -6-12 ; у 1 =3 ; у 2 =9

Возвращаемся к переменной х

2 2

х 2  +  х  =12 х 2  +  х  =-14

Возвращаемся к переменной х 2 =у

х 2 =у 1 ; х 2 =3 ; х 1 =- х 2=

х 2  +  х  -12 =0 х 2  +  х  +14=0

х 2 = у 2 ; х 2 = 9 ; х 3 =- 3 ; х 4 = 3

Д=1+4 . 12=49=7 2 Д=1-4 . 14=-55

Ответ: х 1 =- ; х 2= ; х 3 =- 3 ; х 4 = 3 .

х 1 = -1+7 х 2 = -1-7

2 2

х 1 =3 х 2 =-4

Ответ:х 1 =3 х 2 =-4

• б) х 4 +7х 2 -44=0 Введем новую переменную у=х 2

• а)16 х 3 -32 х 2 -х+2=0

Решение: выделим одинаковый множитель

• 16 х 2 (х-2) – (х-2)=0

• у 2 +7у-44=0 ; Д=в 2 -4ас =7 2 -4 (-44)=49+176=225=15 2

(х-2)(16х 2 -1)=0

у 1 = -7+15 у 2 = -7-15 у 1 = 4; у 2 = -11

(х-2)(4х-1) (4х+1)=0

2 2

Вернемся к переменной х. х 2 =у 1 = 4 х 1 =2; х 2 = -2

х-2=0; 4х-1=0 ; 4х+1=0

х 1 =2 ; 4х=1 ; 4х=-1

х 2 = у 2 = -11 уравнение не имеет смысла

Ответ: х 1 =2; х 2 = -2

х 2 =1/4; х 3 =-1/4

Ответ: х 1 =2; х 2 =1/4; х 3 =-1/4

• в)(х 2 -х+1)(х 2 -х-7)=65 Вводим новую переменную у= х 2 -х (у+1)(у-7)=65 у 2 +у-7у-7-65=0 у 2 -6у-72=0 Д=36+ 4 . 72=324=18 2 у 1 = 6+18 ; у 2 = 6-18 2 2 у 1 =12; у 2 = -6 Возвращаемся к переменной х , т.к. у= х 2 -х 12= х 2 -х ; -6= х 2 -х х 2 -х -12=0; х 2 -х+6=0 Д=1+ 4 . 12=49=7 2 ; Д=1- 4 . 6=-23-1+7 ; х 2 = -1-7 2 2 х 1 =3; х 2 = -4 Ответ: х 1 =3; х 2 = -4

Дополнительно, для тех, кто справился раньше с самостоятельной работой задание из учебника, стр.100 №371(а), 372(а) Задание на дом №371(б),№372(б)

Заполните листы самооценки

Скажи про себя «Какой я молодец потому, что ___________________________________________________»

Например, какой я молодец, я сам решил уравнение методом подстановки или

какой я молодец, я правильно и быстро решил самостоятельную работу .

Алгебра 7-9 классы. 2. Решение уравнений с одной переменной

Алгебра 7-9 классы. 2. Решение уравнений с одной переменной

Подробности

Категория: Алгебра 7-9 классы

 

 

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЯ

 

При решении задач с помощью уравнений поступают следующим образом. Обозначают некоторое неизвестное число буквой x, используя условие задачи, составляют уравнение. Затем решают это уравнение и найденное значение неизвестного истолковывают в соответствии с условием задачи.

Задача 1. В корзине было в 2 раза меньше яблок, чем в ящике. После того как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?

Решение. Пусть в корзине было х яблок, тогда в ящике было 2х яблок. После того как из корзины переложили в ящик 10 яблок, в корзине стало (х—10) яблок, а в ящике (2х +10) яблок. По условию задачи в ящике стало в 5 раз больше яблок, чем в корзине. Значит,

Решим составленное уравнение:

 

Следовательно, в корзине было 20 яблок. Так как 2х  = 2 • 20 = 40, то в ящике было 40 яблок.

Задача 2. Предназначенные Для обработки 67 деталей решили распределить между тремя рабочими так, чтобы первый получил на 5 деталей больше второго и на 7 деталей меньше третьего. Сколько деталей надо выделить первому рабочему?

Пусть первому рабочему следует выделить х деталей, тогда второму рабочему надо выделить х — 5 Деталей, а третьему х + 7 деталей. По условию задачи рабочие должны обработать всего 67 деталей, т. е.

Отсюда

По смыслу задачи неизвестное значение х не может быть дробным числом. Значит, распределить детали указанным способом нельзя.

Конспект урока по теме «Уравнения и неравенства с одной переменной», алгебра 9 класс

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ КРАСНОДАРСКОГО КРАЯ

Государственное казенное специальное УЧЕБНО-ВОСПИТАТЕЛЬНОЕ учреждение закрытого типа специальная общеобразовательная школа Краснодарского края для детей с девиантным (общественно опасным) поведением

(Спецшкола)

Октябрьская ул., д.14, станица Переясловская, Брюховецкий район, Краснодарский край, 352762, тел.: (86156) 6-10-54 ИНН 2327005040 ОКПО 34992545

Открытый урок

«Уравнения и неравенства с одной переменной»

Учитель математики:

Зиненко Нина Александровна

ст. Переясловская

2016 — 2017 уч. г.

Урок по теме «Уравнения и неравенства с одной переменной».

Тип урока: урок обобщения и закрепления знаний.

Используемые технологии:

• информационно-коммуникативные;

• педагогика сотрудничества;

• дифференцированное обучение;

• игровые.

Формы работы:

Цели урока:

образовательные: обобщить знания учащихся по теме урока; подготовиться к написанию контрольной работы;

развивающие: развитие познавательного интереса учащихся; развитие интеллектуальной сферы личности, развитие умений сравнивать и обобщать;

воспитательные: прививать навыки графической культуры, воспитывать аккуратность и внимательность при решении.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

На слайде открывается правильно выполненное домашнее задание (самопроверка).

3. Актуализация знаний.

Разминка. 1. Запишите интервал.

2. Задание № 5 (подготовка к ГВЭ).

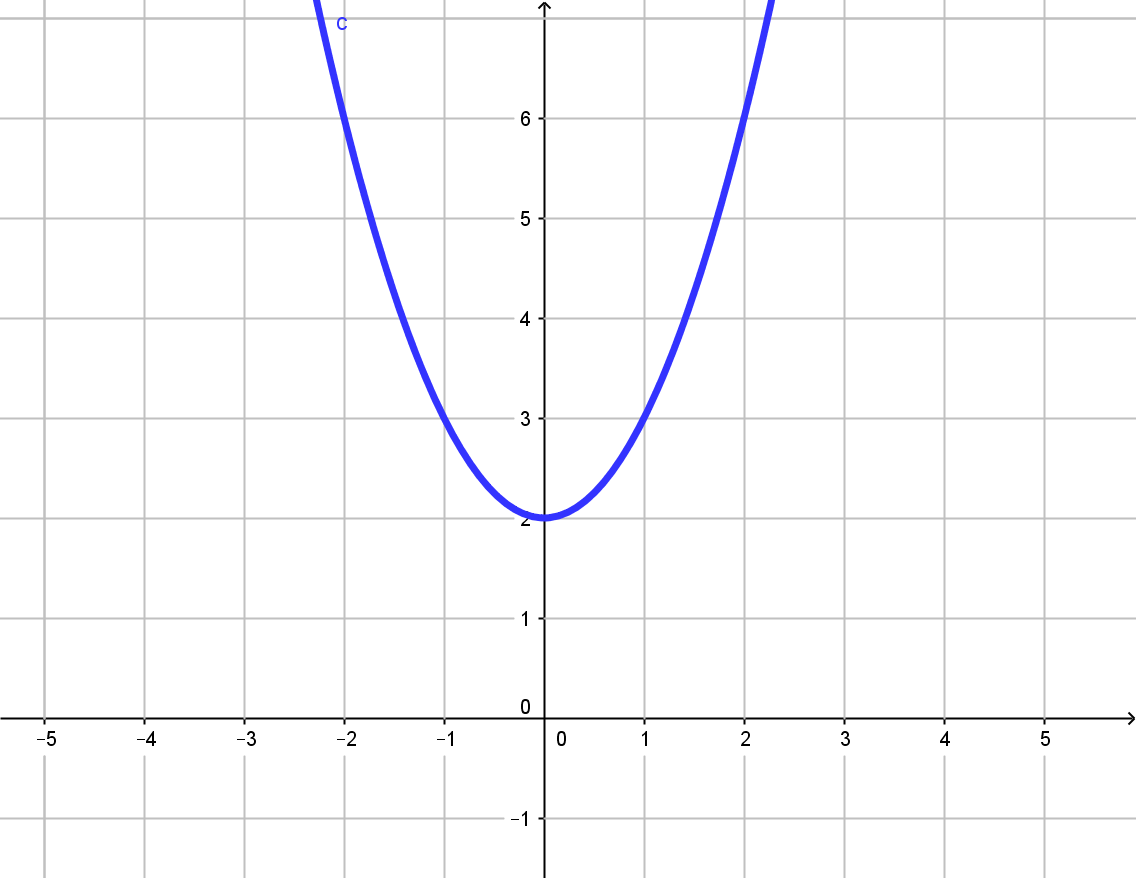
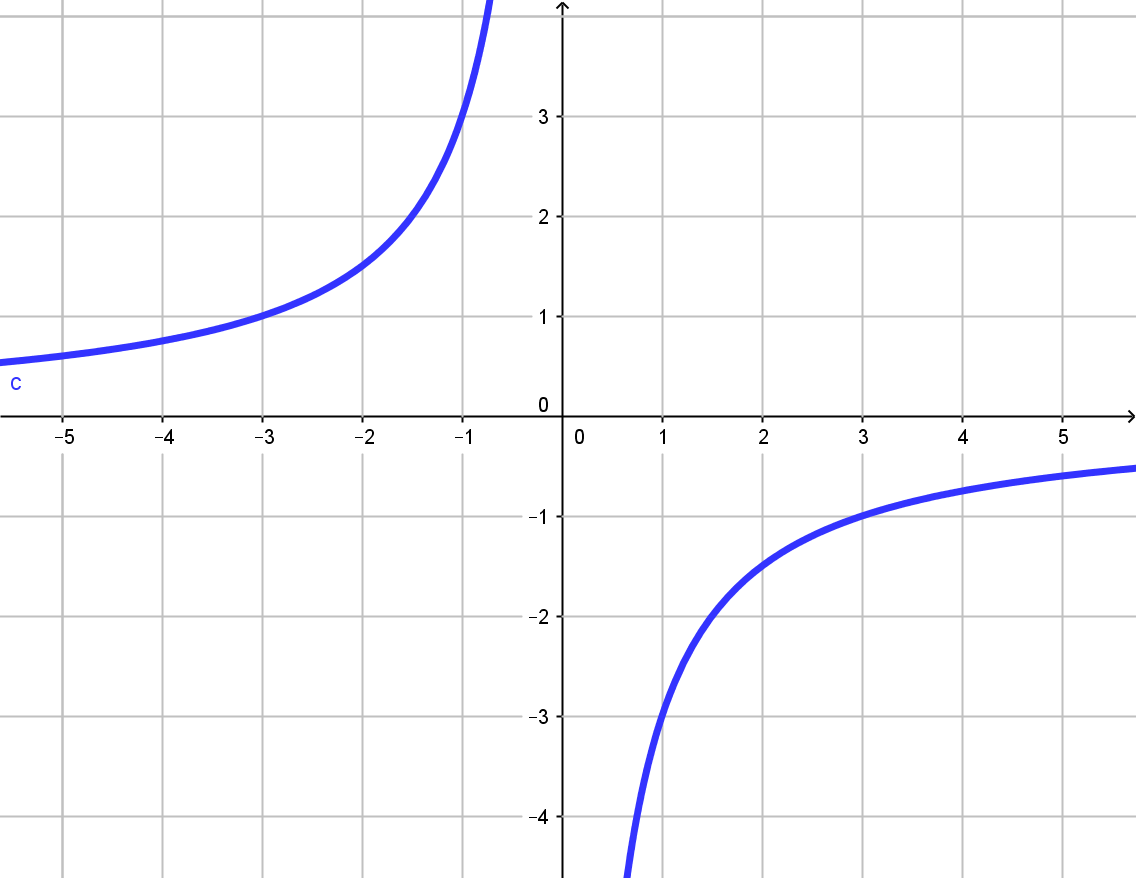
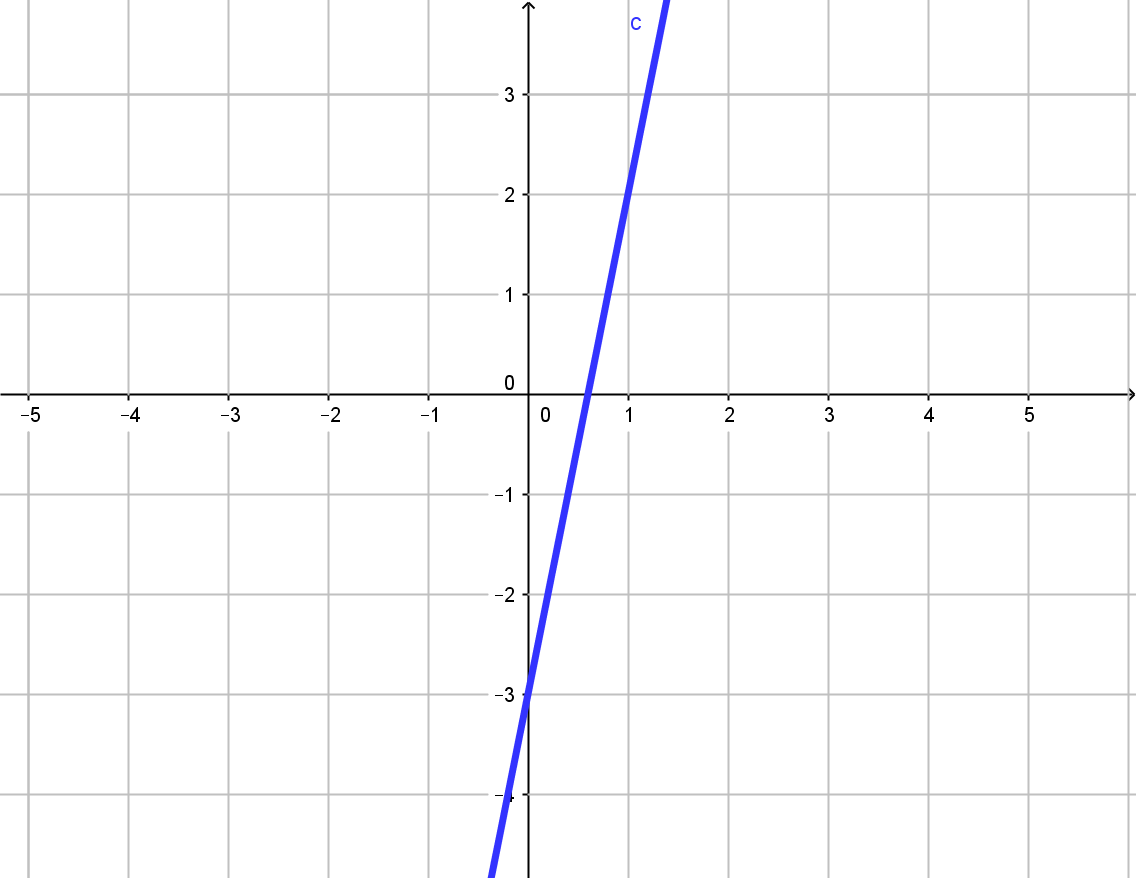Установите соответствие между графиками функций и формулами, которые их задают.

3. Для каждого графика запишите функцию.

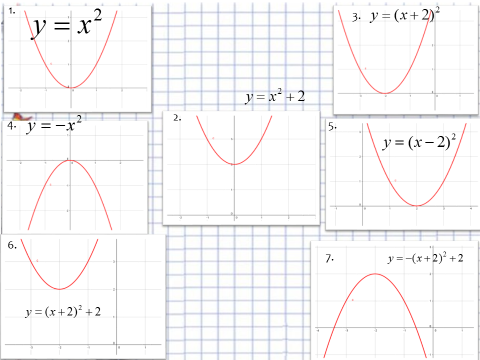
4. Повторим теорию.

4. Закрепление и обобщение знаний.

Класс делится на две команды. Право первого хода определяется по конкурсу капитанов.

1. Конкурс капитанов.

Задание для капитана первой команды:

Задание для капитана второй команды:

2. Игра «Морской бой».

Правила игры. У каждой команды есть игровое поле, на котором размещены по четыре “однопалубных корабля”. За каждой клеткой поля закреплено задание. Если команда делает выстрел и попадает в корабль, то ей засчитывается 1 балл, а за выполненное задание обе команды могут получить дополнительные баллы (в зависимости от сложности задания). Право выстрела переходит ко второй команде, не зависимо от попадания в корабль.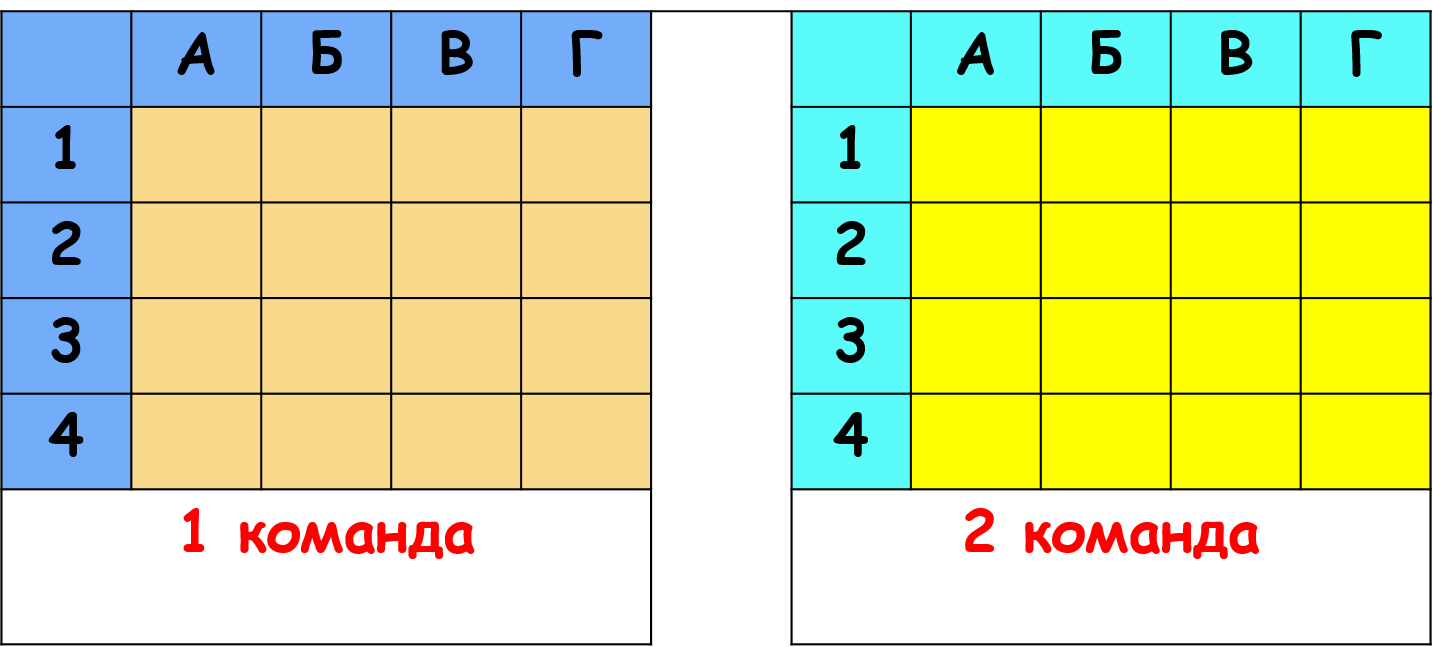

Задания для игры:

1а. 2х² +5х — 7

1б. х² — 25 > 0; (2) Ответ:

(- ∞; — 5) U (5; + ∞)

1в. -5х² + 4х — 21< 0; (2) Ответ: (- ∞; + ∞)

1г. х² — 18х ≥ 0; (2) Ответ:

(- ∞; 0] U [18; + ∞)

2а. Найти область определения функции (1 б) Ответ:

(- ∞; — 9]U[5; + ∞)

2б. (х — 3)(х+6)<0; (1) Ответ: (- 6; 3)

2в. х(х+10)(х – 3) ≤ 0; (1) Ответ:

(- ∞; — 10]U[0; 3]

2г. – (х – 1)(5 – х) > 0; (1) Ответ:

(- ∞; 1)U(5; +∞)

3а. х³ – 4х = 0; (3) Ответ: -2; 0; 2.

3б. 10х³ –3х² – х = 0; (3) Ответ: -0,2; 0; 0,5.

3в. х⁶ – 4х⁴ = 0; (3) Ответ: -2; 0; 2

3г. х³ + 9х = 0; (3) Ответ: 0.

4а. (2х² +3)² – 12(2х² +3)+11=0; (3) Ответ: -2; 2.

4б. х⁴ – 5х² + 4 = 0; (3) Ответ:±1; ±2.

4в. х⁴ – 4х² + 4 = 0; (3) Ответ:

4г. 7х⁴ – 5х² + 1 = 0. (3) Ответ: корней нет

1а. 5х² +3х – 8 ≥ 0; (2) Ответ:

(- ∞; — 1,6]U[1; + ∞)

1б. х² — 49 < 0; (2) Ответ: (- 7; 7)

1в. 4х² — 2х + 13< 0; (2) Ответ: решений нет

1г. 2х — х² > 0; (2) Ответ: (0;2)

2а. Найти область определения функции (1 б) Ответ: (-∞; -12]U[7; + ∞)

2б. (х — 10)(х+5) > 0; (1) Ответ: (-∞; -5)U(10; + ∞)

2в. х(х+7)(х – 4) ≤ 0; (1) Ответ: (-∞; -7]U[0; 4]

2г. – (х – 2)(9 – х) > 0; (1) Ответ: (-∞; 2)U(9; + ∞)

3а. х³ – 9х = 0; (3) Ответ: -3; 0; 3

3б. 2х³ – 7х² +6х = 0; (3) Ответ: 0; 1,5; 2.

3в.х⁵ – х³ = 0; (3) Ответ: 0; ±1.

3г. 4х + х³ = 0; (3) Ответ: 0.

4а. (х² +3)² – 11(х² +3)+28=0; (3) Ответ:±1; ±2

4б. х⁴ – х² – 12 = 0; (3) Ответ: ±2

4в. х⁴ + 10х² + 25 = 0; (3) Ответ: корней нет

4г. х⁴ – 5х² – 36 = 0. (3) Ответ: ±3.

5. Итоги урока.

Подсчет баллов и определение команды-победителя, выставление оценок.

6. Домашнее задание.

№ 393 (а – в)

Тест по алгебре (9 класс) по теме: Уравнение с одной переменной.

Уравнения с одной переменной.

 

                               

1.  3(х – 1,5) + 2х  = 5(2,5 + 2х)                                  2.   4х – 5(3х – 0,5) = 3(7 – 3х)

 

 3.   5(х – 2,5) — 4х  = 3(2,5 + 3х)                                  4.  7х  — 3(2х – 1,5)   = 4(3 + х)

   

 5.   -=                                                   6.   -=

 

 7.   3х2 – 21 = 0                                                              8.   75 – 3х2 = 0                                                                    

 9.  18х – 8х2 = 0                                                             10.    8х – 2х2 = 0                                                                                                                              

 

11.  8х2 + 6х = 2                                                             12.  6х2 — 8х = -2

13. — 4х2 + 10х + 6 = 0                                                    14.   -3х2 — 5х + 2 = 0

 15. х2 — х — 1 = 0                                                         16.   х2 — х – 0,5 = 0

17.  2 –  =                                                      18.   2х –  = 4

19.  х3 – 25х = 0                                                              20.   х4 – 4х2 = 0

21.   2х4  — 2х = 0                                                              22.   х3  — 81х = 0

 

23.   х3 – 4х2 – 9х + 36 = 0                                               24.  16х3 – 32х2 – х + 2 = 0

 

25.   х6 + 4х4 – х2 – 4 = 0                                                 26.   х6 — х4 + 5х2 – 5 = 0                                            

 

27.   у3 – 2у2 = у – 2                                                         28.  у6 + 4у4 = у2 + 4

29.    3(х + 4)2 – 9(х + 4) = 0                                            30.  5(х — 6)2 + 11(х — 6) = (х — 6)

31.   += 5                                                          32.   2 + =

33.   +=                                                34.   + =

35.     х4  — 10х2 + 9 = 0                                                    36.    х4  — 5х2 + 4 = 0

37.    х4 +6х2 — 27 = 0                                                        38.  х4  + 15х2 + 54 = 0

39.    2(х2 — 1)2 + 6(х2 — 1) = 0                                           40.  (х2 — 4)2 + 5(х2 — 4) = 0

41.  (х2 +2х)2 — 2(х2 +2х) – 3 = 0                                       42.  (х2 +х)2 — 5(х2 +х) +6 = 0