«Уравнение с одной переменной». 9-й класс
Используемая технология: Блочно-модульное обучение.
Для средней общеобразовательной школы.
Автор учебника Макарычев Ю.Н., 3 часа в неделю.
- Информационный блок : выдержка из КТП
№ |
Содержание учебного материала |
Кол-во часов |
Тип урока |
Планируемый результат |
|
базовый |
повышенный |
||||
| §5. Уравнения с одной переменной, 6 часов. | |||||
| 1. | Целое уравнение и его корни. | 1 |
Урок-лекция (формирование понятий). | Формирование понятия уравнение высших степеней, умение решать биквадратные уравнения. |
Формирование понятия уравнения высших степеней, их типы; умение безошибочно находить способ решения уравнения, определяя для этого его тип. |
| 2. | Решение уравнений высших степеней. | 1 |
Урок-отработка лекции. | ||
2 |
Урок-диагностика знаний (с\р). | ||||
| 3. | Решение целых уравнений с параметрами. | 1 |
Урок-коррекция ( РНО). |
||
| 4. | Проверочная работа. | 1 |
Урок- контроля ЗУН | ||
Образовательные |
Развивающие |
Воспитывающие |
Сформировать понятие и закрепить знания учащихся по теме “Уравнения с одной переменной”; Умения составлять алгоритм решения уравнения; Закрепить умения и навыки решать уравнения высших степеней с использованием разных приемов, в нестандартных ситуациях. |
Развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения; Развивать внимательность, собранность и аккуратность; Развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления |
Чувство ответственности; Умение работать в микро группе; Культура труда, аккуратность. |
- Дидактические разработки урока.
1. Урок-лекция. На этом уроке обзорно рассматриваются следующие вопросы:
- Понятие целого уравнения, корни уравнения, повторить способы решения уже известных уравнений;
- Рассмотреть все виды уравнений высших степеней, уметь определять количество корней уравнения;
- Разобрать алгоритмы решения уравнений высших степеней.
- Составить опорный конспект урока. (д\з)
2. Урок-отработка лекции
.На этом уроке разбираются и отрабатываются основные понятия, приемы и способы, о которых говорилось на первом уроке (пошаговая отработка лекции). Привожу пример лучшего опорного конспекта, составленного учащимися.
Опорный конспект урока по теме:
“Целое уравнение. Уравнения высших степеней”.
Основные методы решений уравнений. |
|
Разложение на множители. |
Введение новой переменной. |
Ключевые понятия:
уравнение, корень уравнения, решить уравнение, равносильные уравнение.Виды уравнений:
№ |
Название уравнения |
Общий вид |
пример |
1. |
Биквадратное |
ах4+ вх2 + с = 0 замена х2=t обратная замена переменных |
3х4— 5х2 + 8=0 замена х2 = t 3 t2— 5 t +8=0 |
2. |
Уравнение, сводящееся к квадратному с помощью замены выражения. |
(х2— 3х)2 + 5(х2— 3х) = 2 замена (х2 а2 + 5а = 2 а2 + 5а — 2 = 0 |
|
3. |
Уравнение, решая которое используем метод группировки слагаемых. |
Прием группировки 3(х-5) –х(х-5)=(х-5)(3-х) |
3х-15-х2+5х=0 3(х-5) + х(-х+5)=0 3(х-5) – х(х-5)=0 (х-5)(3-х)=0 х — 5=0 или 3 — х=0 |
4. |
Симметрическое (возвратное) |
а х4+вх3+сх2+вх+а=0 сгруппируема х4+ а +вх3+ вх+ с=0а(х4+1) + в(х3+х) + с=0 делим все уравнение на х2 а(х2+) + в(х+)+с=0 замена х += к ; х2+= к – 2 а(к-2) + вк + с = 0 найдем к обратная замена |
х4+5х3+4х2-5х-1=0 |
5. |
Уравнение с использованием способа деления углом многочлена на одночлен (т.Безу) |
Любой многочлен. Если не удалось решить перечисленными способами, тогда применяем данный прием. |
х3 +6х +4х2+3=0 подробно рассмотреть решение в конспекте. |
Задание 1: Определить вид уравнения.
№ |
пример |
Вид уравнения |
1. |
(х-2)6— 19(х-2)3= 216 |
|
2. |
3х3— 7х2-7х +3 =0 |
|
3. |
2х4-х3-9х2+13х -5=0 |
|
4. |
х(х+1)(х+2)(х+3)=0,5625 |
|
5. |
6х4-5х3-38х2-5х + 6 = 0 |
|
6. |
(х2+5)2 – 36 = 0 |
|
7. |
х4 + 2х2 – 24 = 0 |
|
8. |
||
9. |
а2х4— (а2 + 1)х2 + 1 = 0 |
Задание 2: Решить уравнения.
Оценка |
Вариант 1 |
Вариант 2 |
“3” |
№7 |
№6 |
“4” |
№1 |
№2 |
“5” |
№5 |
№8 |
Проверка решений у учителя. Выставление оценок.
Домашнее задание.
Уровень |
Решить уравнение. |
“3” |
По учебнику, авторы Ю.Н.Макарычев и др. №234(а,б),247а,248а |
“4” |
№3,№4,№5 |
“5” |
№9,№4,№6 |
3. Урок-диагностика знаний
.На этом уроке учащимся предлагается самостоятельно выполнить работу с целью определения уровня владения новым материалом. Каждому выдается разработка модуля урока, учащийся сам выбирает темп работы и по окончанию урока (2 часа) получает оценку.
Комментарий: У учителя разработка с ответами, учащимся же выдается без ответов.
Разработка модуля урока по теме: ” Решение уравнений высших степеней”, 9 класс.
ДЛЯ УЧИТЕЛЯ
Для успешного освоения данной темы:
На ”3” нужно выполнить таблицы №1,№2,№3
На “4” нужно выполнить таблицы №1- 4
На “5” нужно выполнить все задания.
Желаю УДАЧИ всем!!!
Блок №1. Решить различные уравнения уже известными способами.
Цель: Закрепить знания и умения, полученные ранее.
Таблица №1 служит разминкой для дальнейшего решения уравнений более высокой степени. Следует решить два уравнения из таблицы, проверить результат и если вы успешно справились, то перейти к следующему заданию.
ТАБЛИЦА №1
| 1. (х+5)(3х-6) = 0 2. х2— 6х = 0 3. (8х –1)2— х(64х + 1) = 12 4. х –5 + 4х-1 = 1 2 3 5. 0.5х2— х2 = 0 |
Блок №2. Решить уравнения, сделав замену переменных.
Цель: Закрепить способ решения уравнений, используя замену переменных.
Пример- образец №1. Решить уравнение (х2+2х)2 — 2(х2+ 2х) = 3
Решение: Запишем равносильное данному уравнение (х2+ 2х)2 – (х2+ 2х) –3 =0, сделаем замену переменных, выражения в скобках одинаковые, поэтому можно записать:
Замена: х2 + 2х =у
Перепишем получившееся уравнение и решим его.
у2— 2у – 3= 0
Д= в2— 4ас= (-2)2— 4·1·(-3)= 16
у= 3, у= -1
Вернемся теперь к переменной х, сделаем обратную замену и решим два уранения.
Обратная замена:
Ответ: 1, -3, -1.
ТАБЛИЦА №2
Вариант 1 |
Вариант 2 |
| 1. (х2 +6х)2 –5 (х2 +6х) = 24 2. (х2+2)2– (х2+2) = 12 |
1. (х2 –5)2 –5 (х2 –5) – 36 =0 2. (х2 –4х)2 + 9(х2-4х) = — 20 |
Блок №3. Решение биквадратных уравнений.
Цель: Закрепить способ решения биквадратных уравнений.
| Уравнение вида ах4+вх2+с=0, где а,в,с – числа, х – неизвестная переменная называется биквадратным уравнением. Решение биквадратного уравнения с помощью замены переменной сводится к решению квадратного уравнения. |
Пример-образец №2 Решить биквадратное уравнение х4 – 5х2 +4 = 0
Решение: х4 –5х2 +4 =0, биквадратное уравнение, сделаем замену переменной и решим получившееся квадратное уравнение.
Замена: х2= t >= 0
t2-5t +4 = 0
D= 9
t= 4, t= 1
Оба корня положительные, поэтому удовлетворяют условию t >= 0.
Обратная замена:
Ответ: ± 2, ± 1.
ТАБЛИЦА №3
Вариант 1 |
Вариант2 |
| 1. х4 – 2х2— 3 =0 2. 5у4 – 5у2 + 2 = 0 3. х4 –4х2 + 4 = 0 |
1. х4 – 5х2 — 36 = 0 2. у4 – 6у2 + 8 = 0 3. 2х4 – 9х2 + 4 = 0 |
Блок №4. Решить уравнения высшей степени.
Цель: Закрепить разные способы решения уравнений высших степеней.
Если ребята вы добрались до 4 блока, поздравляю вас, вы делаете успехи. Сейчас вам предстоит самостоятельно выбирать способ решения, переменную, которую нужно заменить.
КАРТОЧКА №4
Вариант 1 |
Вариант 2 |
| 1. (х2 +2х)(х2 +2х +2)
= 3 2. х4 – 9х2 + 18 =0 3. (х2 –х-16)(х2-х+2) =88 |
1. (х2 +х)(х2 +х — 5)
= 84 2. х4 – 20х2 +100 =0 3. (2х2 +7х –8)(2х2 +7х – 3) –6 =0 |
Блок №5.
Указания учителя. Молодцы!!! Вы ребята освоили решение уравнений высших степеней. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
КАРТОЧКА №5
| 1. (х2 –1)(х2 +1) – 4(х2 – 11)
= 0 2. х5 + х4 – 6х2 – 6х2 + 5х +5 = 0 3. При каких с не имеет корней уравнение х4 – 12х2 +с = 0 |
Указания учителя: В случае затруднений воспользуйтесь подсказками, данными ниже.
Подсказки.
1. Воспользуйтесь формулой (а-в)(а+в)=а2-в2, преобразуйте данное уравнение в биквадратное.
2. Сгруппируйте первое слагаемое со вторым, третье с четвертым и пятое с шестым, примените способ группировки и разложите на множители.
3. Сделайте замену и запишите условие, при котором уравнение не имеет корней, решите получившееся неравенство.
ОТВЕТЫ: (только у учителя)
ОТВЕТЫ |
|||
| № таблицы | № задания |
вариант |
|
I |
II |
||
1 |
1 |
— 5; 2. |
|
2 |
0, -v6, v6. |
||
3 |
— 11/17 |
||
4 |
23/11 |
||
5 |
0; 2. |
||
2 |
1 |
— 3±v6; — 3 ± v17 |
±2, ± 1. |
2 |
±v2 |
2 |
|
3 |
1 |
±v3 |
± 3 |
2 |
Нет корней |
±v2, ± 2 |
|
3 |
± v2 |
± 0.5; ± 2. |
|
4 |
1 |
— 1, 3. |
— 3, 4. |
2 |
±v3, ± v6. |
±v10 |
|
3 |
— 4, 5. |
-4,5; 1; (-7± v65)· 0,25 |
|
5 |
1 |
Нет корней |
|
2 |
±1, ±v5 |
||
3 |
с > 36 |
||
4. Урок-коррекция ЗУН.
На этом уроке разбираются у доски задания, которые вызвали затруднения на самостоятельной работе, вторая часть урока посвящена решению задач повышенного уровня, заданиям с параметрами. “Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы”,9 класс, издательство “Дрофа”. Л.В.Кузнецова и др.
5. Урок контроля ЗУН.
Проводится проверочная или контрольная работа. Предлагаю провести проверочную работу в форме ЕГЭ с целью подготовки учащихся 9-х классов к выпускным экзаменам в форме ЕГЭ.
Цель проверки: 1. Проверка ЗУН по основным разделам курса алгебры по теме “Уравнения”; 2. Корректировка учебной программы, с целью ликвидации пробелов в ЗУН учащихся.
Время проведения работы – 1 урок (40 минут).
Бланк для ответов: Часть А, часть В.
Ответы к тесту Ф.И. _______________________________________________ класс ______________
№ вопроса |
А1 |
А2 |
А3 |
urok.1sept.ru
План-конспект урока (алгебра, 9 класс) по теме: конспект урока по теме «Уравнения с одной переменной»
Тема урока: «Уравнение с одной переменной». 9-й класс
Используемая технология: Блочно-модульное обучение.
По учебнику Макарычев Ю.Н.
Цели:
Образовательные:
Сформировать понятие и закрепить знания учащихся по теме “Уравнения с одной переменной”;
Умения составлять алгоритм решения уравнения;
Закрепить умения и навыки решать уравнения высших степеней с использованием разных приемов, в нестандартных ситуациях.
Развивающие:
Развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения;
Развивать внимательность, собранность и аккуратность;
Развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления
Воспитывающие:
Чувство ответственности;
Умение работать в микро группе;
Культура труда, аккуратность.
На этом уроке учащимся предлагается самостоятельно выполнить работу с целью определения уровня владения новым материалом. Каждому выдается разработка модуля урока, учащийся сам выбирает темп работы и по окончанию урока (2 часа) получает отметку.
Комментарий: У учителя разработка с ответами, учащимся же выдается без ответов.
Разработка модуля урока по теме: ” Решение уравнений высших степеней”, 9 класс.
ДЛЯ УЧИТЕЛЯ
Для успешного освоения данной темы:
На ”3” нужно выполнить таблицы №1,№2,№3
На “4” нужно выполнить таблицы №1- 4
На “5” нужно выполнить все задания.
Желаю УДАЧИ всем!!!
Блок №1. Решить различные уравнения уже известными способами.
Цель: Закрепить знания и умения, полученные ранее.
Виды уравнений:
№ | Название уравнения | Общий вид | пример |
1. | Биквадратное | ах4+ вх2 + с = 0 замена х2=t обратная замена переменных | 3х4- 5х2 + 8=0 замена х2 = t 3 t2- 5 t +8=0 |
2. | Уравнение, сводящееся к квадратному с помощью замены выражения. |
| (х2- 3х)2 + 5(х2- 3х) = 2 замена (х2- 3х) = а а2 + 5а = 2 а2 + 5а — 2 = 0 |
3. | Уравнение, решая которое используем метод группировки слагаемых. | Прием группировки 3(х-5) –х(х-5)=(х-5)(3-х) | 3х-15-х2+5х=0 3(х-5) + х(-х+5)=0 3(х-5) – х(х-5)=0 (х-5)(3-х)=0 х — 5=0 или 3 — х=0 |
Блок №1. Решить различные уравнения уже известными способами.
Таблица №1 служит разминкой для дальнейшего решения уравнений более высокой степени. Следует решить два уравнения из таблицы, проверить результат и если вы успешно справились, то перейти к следующему заданию.
ТАБЛИЦА №1
1. (х+5)(3х-6) = 0 2. х2- 6х = 0 3. (8х –1)2- х(64х + 1) = 12 4. х –5 + 4х-1 = 1 5. 0.5х2- х2 = 0 |
Блок №2. Решить уравнения, сделав замену переменных.
Цель: Закрепить способ решения уравнений, используя замену переменных.
Пример- образец №1. Решить уравнение (х2+2х)2 — 2(х2+ 2х) = 3
Решение: Запишем равносильное данному уравнение (х2+ 2х)2 – (х2+ 2х) –3 =0, сделаем замену переменных, выражения в скобках одинаковые, поэтому можно записать:
Пусть х2 + 2х =у, тогда
Перепишем получившееся уравнение и решим его.
у2 — 2у – 3= 0
Д= в2- 4ас= (-2)2- 4·1·(-3)= 16
у= 3, у= -1
Вернемся теперь к переменной х, сделаем обратную замену и решим два уранения.
Обратная замена:
Ответ: 1, -3, -1.
ТАБЛИЦА №2
Вариант 1 | Вариант 2 |
1. (х2 +6х)2 –5 (х2 +6х) = 24 2. (х2+2)2– (х2+2) = 12 | 1. (х2 –5)2 –5 (х2 –5) – 36 =0 2. (х2 –4х)2 + 9(х2-4х) = — 20 |
Блок №3. Решение биквадратных уравнений.
Цель: Закрепить способ решения биквадратных уравнений.
Уравнение вида ах4+вх2+с=0, где а,в,с – числа, х – неизвестная переменная называется биквадратным уравнением. Решение биквадратного уравнения с помощью замены переменной сводится к решению квадратного уравнения.
Пример-образец №2 Решить биквадратное уравнение х4 – 5х2 +4 = 0
Решение: х4 –5х2 +4 =0, биквадратное уравнение, сделаем замену переменной и решим получившееся квадратное уравнение.
Пусть х2= t , тогда
t2-5t +4 = 0
D= 9
t= 4, t= 1
Оба корня положительные, поэтому удовлетворяют условию t >= 0.
Обратная замена:
Ответ: ± 2, ± 1.
ТАБЛИЦА №3
Вариант 1 | Вариант 2 |
1. х4 – 2х2- 3 =0 2. 5у4 – 5у2 + 2 = 0 3. х4 – 4х2 + 4 = 0 | 1. х4 – 5х2 — 36 = 0 2. у4 – 6у2 + 8 = 0 3. 2х4 – 9х2 + 4 = 0 |
Блок №4. Решить уравнения высшей степени.
Цель: Закрепить разные способы решения уравнений высших степеней.
Если ребята вы добрались до 4 блока, поздравляю вас, вы делаете успехи. Сейчас вам предстоит самостоятельно выбирать способ решения, переменную, которую нужно заменить.
Таблица №4
Вариант 1 | Вариант 2 |
1. (х2 +2х)(х2 +2х +2) = 3 2. х4 – 9х2 + 18 =0 3. (х2 –х-16)(х2-х+2) =88 | 1. (х2 +х)(х2 +х — 5) = 84 2. х4 – 20х2 +100 =0 3. (2х2 +7х –8)(2х2 +7х – 3) –6 =0 |
Блок №5.
Указания учителя. Молодцы!!! Вы ребята освоили решение уравнений высших степеней. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Таблица №5
1. (х2 –1)(х2 +1) – 4(х2 – 11) = 0 2. х5 + х4 – 6х2 – 6х2 + 5х +5 = 0 3. При каких с не имеет корней уравнение х4 – 12х2 +с = 0 |
Указания учителя: В случае затруднений воспользуйтесь подсказками, данными ниже.
Подсказки.
1. Воспользуйтесь формулой (а-в)(а+в)=а2-в2, преобразуйте данное уравнение в биквадратное.
2. Сгруппируйте первое слагаемое со вторым, третье с четвертым и пятое с шестым, примените способ группировки и разложите на множители.
3. Сделайте замену и запишите условие, при котором уравнение не имеет корней, решите получившееся неравенство.
ОТВЕТЫ: (только у учителя)
ОТВЕТЫ | |||
№ таблицы | № задания | вариант | |
I | II | ||
1 | 1 | — 5; 2. |
|
2 | 0, -v6, v6. | ||
3 | — 11/17 | ||
4 | 23/11 | ||
5 | 0; 2. | ||
2 | 1 | — 3±v6; — 3 ± v17 | ±2, ± 1. |
2 | ±v2 | 2 | |
3 | 1 | ±v3 | ± 3 |
2 | Нет корней | ±v2, ± 2 | |
3 | ± v2 | ± 0.5; ± 2. | |
4 | 1 | — 1, 3. | — 3, 4. |
2 | ±v3, ± v6. | ±v10 | |
3 | — 4, 5. | -4,5; 1; (-7± v65)· 0,25 | |
5 | 1 | Нет корней |
|
2 | ±1, ±v5 | ||
3 | с > 36 |
nsportal.ru
Математика. 9-й класс. Обобщающий урок по теме блока «Уравнения с одной переменной. Методы решения»
Пояснительная записка
На современном этапе развития общество предъявляет определённые требования к системе математических знаний, которые международная общественность считает необходимыми для формирования так называемого «человеческого капитала». Элементами общей человеческой культуры являются определённый объём математических знаний, владение характерными для математики методами, знакомство с ее специфическим языком. Помимо этого, все большую актуальность приобретает проблема оценки качества обучения математике.
Одним из важнейших направлений модернизации системы образования является совершенствование контроля и управления качеством образования. Цель государственного контроля качества заключается в обеспечении стабильного соответствия качества образования потребностям человека, общества и государства. Фундаментальной составляющей школьного образования является математическая подготовка учащихся. Актуальность исследования обусловлена, с одной стороны, новыми государственными требованиями, к математической подготовке школьников, сформулированными в стандарте образования, а с другой, сложившейся системой оценивания учебных достижений в каждом образовательном учреждении.
Изменения в сфере образования, произошедшие за последнее время (введение ЕГЭ и др.), привели к противоречию между наличием разработанной теории и методике использования тестов в оценке качества знаний и их эффективным применением в практике преподавания математике.
Процесс обучения – двусторонний процесс. Для успеха обучения требуется не только высокое качество работы учителя, но и активная деятельность учащихся, их интерес к обучению, сосредоточенная и вдумчивая работа под руководством учителя. Для этого нужно строить процесс обучения так, чтобы широко вовлекать учащихся в самостоятельную творческую деятельность по усвоению новых знаний и успешному применению их на практике. На мой взгляд, наиболее соответствует этому блочное преподавание математики, которое характеризуется опережающим изучением теоретического материала укрупнёнными блоками, алгоритмизацией учебной деятельности завершённостью и согласованностью циклов познания. Использование блочной технологии обучения математике даёт возможность больше внимания уделять основным понятиям математики, материал выступает не отдельной единицей, а в качестве выделенного из той структурной единицы, к которой он тяготеет. Важно также, что блочное обучение преследует цель – формирование у детей навыка самообразования, весь процесс строится на основе осознанного целеполагания, а уровневая дифференциация учебной деятельности создаёт ситуацию выбора для ученика, его следование собственной программе развития.
Опыт высшей школы показывает, что усвоение взаимосвязанного материала более успешно при его изложении крупными порциями (блоками), позволяющими установить различные отношения нового понятия с известными. При этом автоматически происходит выделение основного и второстепенного в изучаемом материале. Резко возрастающий объем материала, подлежащий усвоению, компенсируется увеличением времени на решение задач по данному материалу. При таком подходе несколько удлиняется период освоения новых понятий и фактов, но освоение их — вполне сознательное, разностороннее и активное.
Необходимо учитывать возрастные особенности учащихся и значительно более неоднородный состав учащихся в школе по сравнению с вузом, т.к. многие учащиеся имеют склонность к гуманитарным наукам и изучение математики им даётся не так легко, следовательно, на школьном уроке-лекции необходимо давать более подробные комментарии. С учетом разной способности учеников к усвоению новой информации лекция учителя должна сопровождаться необходимым повторением узловых моментов рассуждения, для того чтобы ученики запоминали основные моменты и видели их значимость. Лекция в школе должна быть более короткой и чередоваться в отдельных случаях с другими формами учебной работы, потому что психологические исследования показывают, что в ученики при длительной однообразной работе быстро утомляются и не могут удерживать внимание. Объяснение учителя должно сопровождаться контрольными вопросами к классу, но в минимально необходимом объеме, не нарушающем логику рассуждений, это делается, для того чтобы ученики четко представляли изучаемый материал и одновременно поддерживает внимание и диагностирует уровень понимания данного материала. Контроль над усвоением знаний должен быть более частым и разнообразным по форме, опираться на индивидуальные и коллективные формы работы учащихся. Лекции в блочной системе обучения имеют свою особенность: в начале лекции проводиться диагностирующий тест, который помимо основной диагностирующей функции помогает актуализировать знания учащихся.
До блока практических занятий проводится урок-зачет, на котором проверяются и закрепляются теоретические знания учеников. Основная цель урока-зачета заключается в том, чтобы выяснить, соответствуют ли знания и умения каждого школьника по изученной теме уровню обязательных результатов для продолжения занятий. Обычно учителя перед проведением таких уроков заранее сообщают круг теоретических вопросов, выносимых на зачет, что позволяет ученикам ответственно подготовиться к уроку.
Следующий этап: уроки-практикумы, где в различных формах идёт закрепление практических умений и навыков по теме блока.
При блочном изучении учебного материала можно достичь гораздо лучших результатов, чем при традиционном обучении. Высвобождается много времени на действенное применение изучаемой теории к решению разнообразнейших задач, выработку самостоятельных умений и навыков учащихся. Успеху дела способствует и то, что внимание учащихся постоянно и целиком сконцентрировано на материале всей темы и они с каждым днём всё с большим интересом и пониманием участвуют в работе, повторяют самое главное, делают обобщения.
Далее представлен обобщающий урок по теме блока «Уравнения с одной переменной»
Основные цели урока:
Образовательные:
обобщение и систематизация знаний учащихся по теме блока, закрепление умений и навыков по решению уравнений с одной переменной, самостоятельного выбора способа решения, закрепить умения и навыки решать уравнения высших степеней с использованием разных приемов, в нестандартных ситуациях.
Развивающие:
развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения, развивать внимательность, собранность и аккуратность, развивать умения работать самостоятельно и в микрогруппах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления.
Воспитательные: чувство ответственности, умение работать в микрогруппе, культура труда, аккуратность.
План урока:
- Организационный момент
- Повторение теоретического материала блока через многократное повторение и примеры теста
- Работа с опорным конспектом в парах
- Практикум по решению уравнений (3 уровня сложности, работа в микрогруппах)
- Итоги урока, постановка домашнего задания
Ход урока
1. Организационный момент
Сегодня у нас обобщающий урок по теме блока «Уравнения с одной переменной. Способы решения»
Н.Е.Жуковский сказал: “В математике есть своя красота, как в живописи и поэзии”. Сегодня на уроке мы ещё раз увидим всю красоту такой математической структуры как уравнения. Ведь уравнения — одна из сквозных тем всего курса математики, проходящая красной линией с 1 по 11 класс. И нет в математике ничего изящнее, чем красиво решённое уравнения.
2. Повторение теоретического материала блока через многократное повторение и примеры теста
Устно повторим основные понятия блока по нарастающей схеме (появляются в презентации)
- целое уравнение
- корень уравнения
- решить уравнение
- равносильные уравнение
- степень уравнения
- основные способы решения целых уравнений
(оценку за знание теории получают последние два, проговоривших определения)
Но знания теории теряет свою силу, если они не находят своего применения на практике. Первая индивидуальная работа на сегодня – это тестовая работа на знание теории с самооценкой. (работа с презентацией, ученики заполняют бланк ответа № 1 в индивидуальном листе) (приложение 1, слайды 1-6)
Тест № 1.
1. Укажите номера целых уравнений:
2. Определите степень уравнения:
1) 4-я степень
2) 5-я степень
3) 1-я степень
4) степень уравнения определить невозможно
3. Корнями какого уравнения являются числа -2; 0; 2:
1) х³ – 4х = 0
2) х (х² – 4х + 4) = 0
3) х³ – 2х = 0
4) х³ – 4х + 4 = 0
4. Для уравнения (х + 3)² – 6х + 5х² = 1 выберите ему равносильное:
1) 6х² + 12х + 8 = 0
2) 6х² – 8 = 0
3) 6х² + 8 = 0
4) 6х² – 6х + 8 = 0
4. Для уравнения (х + 3)² – 6х + 5х² = 1 выберите ему равносильное:
1) 6х² + 12х + 8 = 0
2) 6х² – 8 = 0
3) 6х² + 8 = 0
4) 6х² – 6х + 8 = 0
5. Определите вид уравнения:
1) квадратное
2) биквадратное
3) кубическое
4) нельзя определить, не хватает данных
3. Работа с опорным конспектом в парах
Прежде чем перейти к практикуму по решению целых уравнений, используя опорный конспект и уравнения, представленные на слайде, нужно определить способ решения этого уравнения. Работать будем в парах, обсуждая способ решения. Время – 2 минуты, затем общее обсуждение.
(на слайде предлагаются 10 уравнений) (приложение 1,слайды 7-8)
Определить способ решения уравнения:
4. Практикум
Математика похожа на мельницу: если вы засыплете в неё зёрна пшеницы, то получите муку, если же засыплете отруби, то отруби и получите.
Андру Филлинг Хаксли
Практикум по отработке умений и навыков проведём, используя работу в микрогруппах (группы сформированы по технологии дифференцированного обучения). Он включает в себя 4 основных обязательных уровня и один дополнительный, задания в которых идут по нарастающей. Цели дойти до конца всем нет. У каждого своя программа развития. И для кого – то успешный 2 уровень – это уже очень хорошо, а для какого – то – это только ступенька, чтобы подняться ещё выше. (приложение 1, слайды 9-14)
Уровень № 1 служит своеобразной стартовой площадкой для дальнейшего решения уравнений более высокой степени. Следует решить уравнения из таблицы, проверить результат и если вы успешно справились, то перейти к следующему заданию.
| уравнение | задание |
ответ |
(х+5)(3х-6) = 0 |
решить уравнение |
-5; 2 |
х³- 6х = 0 |
указать количество корней |
3 корня |
(8х –1)²- х(64х + 1) = 12 |
решить уравнение |
— 11/17 |
Уровень №2 Решить уравнения, сделав замену переменных.
Цель: Закрепить способ решения уравнений, используя замену переменных. Если группа затрудняется в решении уравнений, она может взять задание-образец.
| уравнение | задание |
ответ |
(х² +6х)² –5 (х² +6х) = 24 |
найти количество корней уравнения |
4 корня: |
(х²- 5х)(х²-5х+10) + 24=0 |
найти произведение корней уравнения |
1•2•3•4=24 |
Уровень №3. Решение биквадратных уравнений.
Цель: Закрепить способ решения биквадратных уравнений. Если возникла сложности на этом этапе, можно обратиться к примеру-образцу.
Уровень №4. Решить уравнения высшей степени.
Цель: Закрепить разные способы решения уравнений высших степеней. Если вы добрались до 4 этапа, это очень хорошо, вы делаете успехи. Сейчас вам предстоит самостоятельно выбирать способ решения уравнения.
Задания-подсказки на данном этапе отсутствуют.
Уровень № 5
Цель: рассмотреть нестандартные задания, в т.ч. задачи с параметром.
Итак, сегодня на уроке мы обобщили такую важную тему, как решение уравнений. Конечно, школьная линия уравнений на этом не заканчивается, но полученные на этом блоке знания найдут своё применение и при сдаче ЕГЭ, и в дальнейшем при изучении математики.
Домашнее задание: тесты тематического контроля, тест № 5, свой вариант.
А закончить урок мне хочется афоризмом Ж.Даламбера:
«Алгебра щедра. Зачастую она даёт человеку больше, чем он у неё спрашивает».
Всего хорошего! Урок закончен.
urok.1sept.ru
Конспект урока по математике на тему «Уравнения с одной переменной»(9 класс)
Графический способ решения уравнений не обеспечивает …?
Каким способом можно решить уравнение х3+х-4=0?
Полное квадратное, старший коэффициент которого равен 1, называется … квадратным уравнением?
Задание 2. Выпишите буквы обозначенные цифрами в кружках.
Ученики получают фамилию известного математика Виета. После этого заслушивается сообщение ученика по теме «Великий математик Франсуа Виет».
Франсуа Виет (1540-1603)
Знаменитый математик Франсуа Виет родился в 1540 году в небольшом городке Фантанеле-Конт на юге Франции. Юрист по образованию, Виет служил при дворе Генриха IX. Математикой занимался в часы отдыха. Франсуа Виет обладал огромной трудоспособностью, он мог работать по трое суток без отдыха, многие его результаты и открытия достойны восхищения. Во время войны с Франции с Испанией Виет оказал большую услугу родине – он расшифровал весьма важное письмо испанского двора. Правители Испании, письмо которых было перехвачено, не допускали мысли, что такой сложный шифр может быть раскрыт. Впоследствии они приписали раскрытие их шифра волшебству чародея.
Его знаменитой теоремой, которая известна под названием теорема Виета, люди пользуются уже пятое столетие.
Теорема Виета.
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни – и дробь уж готова:
В числителе c, в знаменателе a,
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта,
Что за беда –
В числителе b, в знаменателе а.
(На магнитной доске висит плакат).
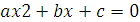
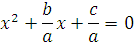
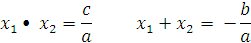
— Сформулируйте теорему, обратную теореме Виета.
— Для решения каких квадратных уравнений ее удобно применять?
Задание 3. На доске висят 4 карточки.
x2-6x+5=0
3x2-4x+7=0
x2-10x+9=0
7x2-3x+5=0
Какие уравнения удобно решить по теореме, обратной теореме Виета?
Если вы найдете корни этих уравнений, пользуясь данной теоремой, то сможете узнать, в каком году Ф. Виет доказал ее. (Ответ: в 1591 г.)
Задание 4. Самостоятельно ответьте на вопросы теста, букву правильного ответа занесите в таблицу в конце теста.
Функция у=х2 задается графиком изображенным на рисунке.
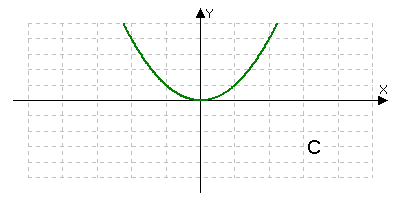
Уравнение х2=а при а>0 имеет
у) 1 корень; а) 2 корня; т) нет корней.
Сколько точек пересечения имеют графики функций, изображенных на рисунке?
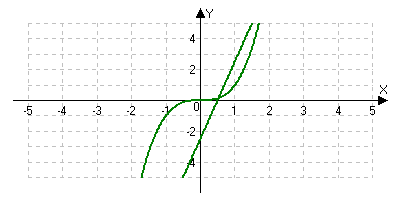
н) одну; а) две; т) три.
Чтобы построить график линейной функции, сколько точек достаточно отметить?
а) одну; ю) две; к) как можно больше, чтобы график был точнее.
Функция y=kx+b, если k>0
т) возрастает; у) убывает.
В каких четвертях расположен график функции у=2х2-3х+15 (D<0)?
а) III и IV четверти; у) I и II четверти.
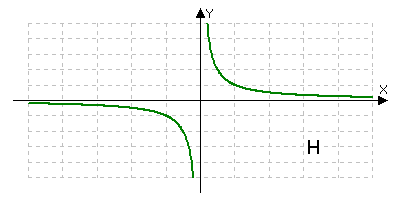
График какой функции изображен на рисунке?
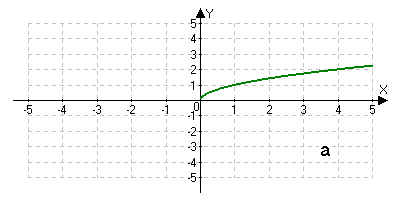
б) y=kx; р) у=1/х; и) у=√х.
В каких четвертях расположен график функции y=kx, если k<0?
и) I и III; д) II и IV.
Когда вершина параболы находится на оси Ох?
а) D<0; в) D=0; н) D>0.
Задание 5. Как бы Вы могли окончить фразу «Статую красит вид, а …»?
(«… человека его деяния.»)
— Чьи это слова? (Пифагора).
Пифагор (справка)
В Древней Греции жил ученый Пифагор. О жизни этого ученого известно немного, зато с его именем связано много легенд. Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимали после долгих испытаний. Каждый вступивший в кружок отрекался от своего имущества. Ими было сделано множество открытий. В школе существовал обычай, по которому авторство всех работ приписывалось Пифагору. После его смерти ученики окружили имя своего учителя множеством легенд.
Задание 6. Решите уравнения:
x3=4-3x;
 .
.
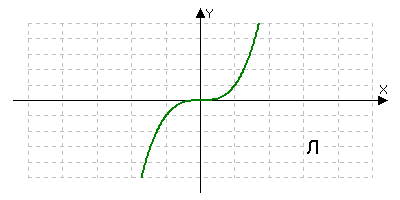
На столах лежат таблицы. Назовите букву рисунка, на котором график соответствует графику функции y=x3. Назовите букву рисунка, на котором график соответствует графику функции y=4-3x.
Если мы изобразим графики данных функций в одной системе координат, то мы узнаем, есть ли точки пересечения, сколько их и какие у них абсциссы.
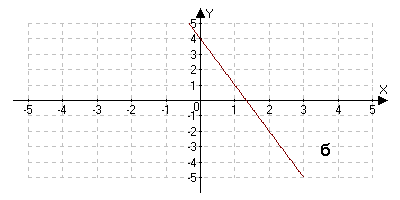

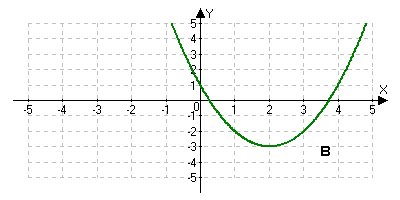
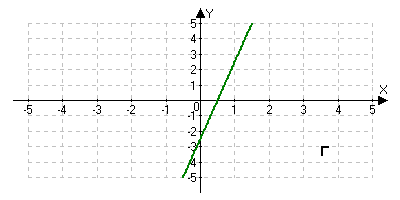
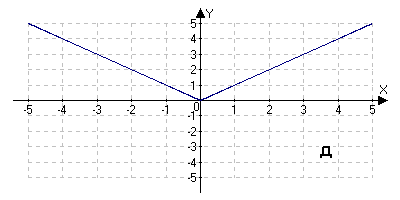
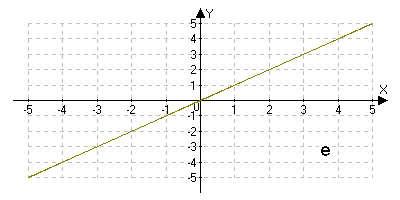
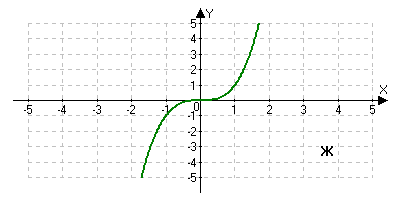
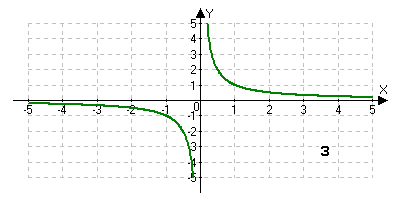
Решение задач.
Задание 7. На доске вывешиваются карточки с правильными и неправильными ответами, на которых с одной стороны варианты ответов, с другой обрывки фразы «Ты лучше голодай, чем что попало ешь». Ученикам предлагается решить шесть уравнений. Ученик, решивший уравнение, выходит к доске и переворачивает карточку с правильным ответом. В результате должна получиться фраза.
Уравнения, предлагаемые ученикам:
Решить уравнение

Ответ: 0;6.
Решить уравнение (6-х)(6+х)-х(х-11)=36.
Ответ: 0; 5,5.
Решить уравнение х3+4х=5х2.
Ответ: 0; 4; 1.
Решить уравнение 3х3-х2+18х-6=0.
Ответ: 1/3.
I Вариант. Решить уравнение х4-5х2-36=0.
Ответ: ±3.
II Вариант. Решить уравнение x4-7x2+12=0.
Ответ: 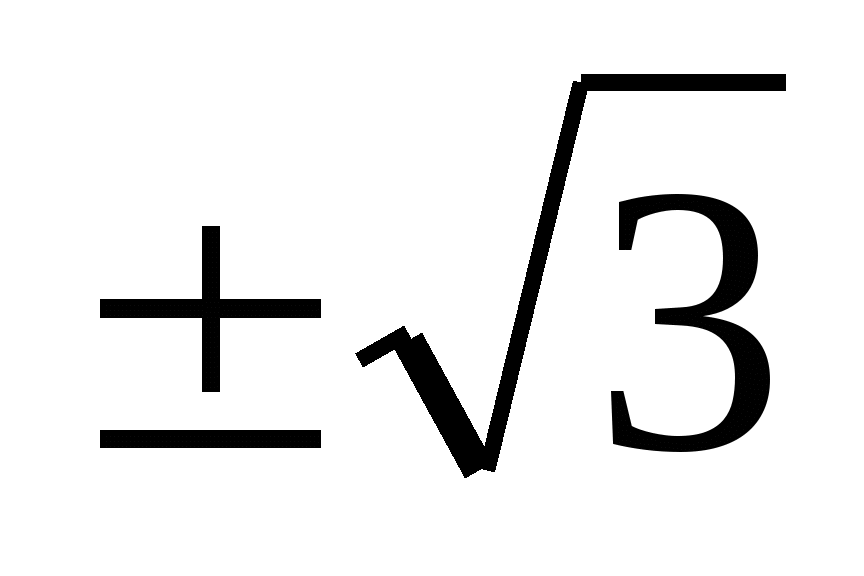 , ±2.
, ±2.
№5 и №6 ученикам предлагается решить самостоятельно, с последующей проверкой при помощи плаката с правильными ответами.
— Получена строка из стихотворения поэта и математика Омара Хаяма.
Омар Хаям (справка)
Омар Хаям жил в Северной Персии. Он написал «Алгебру» (полное название «Трактат о документах алгебры и алмукабалы»), выдающееся произведение, так как в ней содержится систематическое исследование уравнений третьей степени.
Чтоб мудро жизнь прожить
Знать надобно не мало
Ты лучше голодай, чем что попало ешь
И лучше будь один, чем вместе с кем попало.
Человек — это истина мира, венец,
Знает это не каждый, а только мудрец.
Закрепление пройденного за урок в форме игры.
Задание. Ученик решил уравнения и получил следующие ответы. Вам нужно оставить только те карточки, на которых корни найдены правильно.
После выполнения задания учитель переворачивает оставшиеся карточки и если задание выполнено верно, то получится слово Фалес.
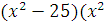 +4)=0
+4)=0
x = ±5
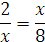
x = ±8
Сообщение
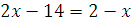
x = 5
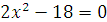
x = ±3
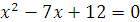
x = 3, =4
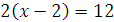
x = 8
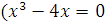
x=0, x = ±2
Фалес (справка)
Отцом греческой математики является милетский купец Фалес. Среди семи известных мудрецов, живших в VII—VI вв. до н. э. в Греции, он занимал первое место. Фалес ставил перед собой не только вопрос «как?», но и современный научный вопрос «почему?». Он разделил год на 365 дней, объяснил причину солнечных затмений. Одна из теорем геометрии носит его имя.
VI. Подведение итогов урока.
VII. Домашнее задание. Повторить тему «Уравнения с одной переменной».
infourok.ru
«решение уравнений с одной переменной» (9 класс)
Открытый урок по алгебре в 9 классе
Учитель математики: Левченко Сталина Васильевна
МОБУ СОШ №17 г. Якутска
Тема: Целые уравнения с одной переменной в системе заданий второй части ГИА в 9 классе
Цели урока:
1) повторить определение целого уравнения;
2) дать определение степени уравнений;
3) способы решения уравнений второй, третьей, четвертой степени и т.д.;
4) решить квадратные уравнения с параметром;
5) повысить интерес к предмету через интеграцию с экологией.
Ход урока.
I. 1) Организационный момент.
2) Повторить:
а) определение целого уравнения
б) как определить степень уравнения
в) какие методы решения уравнений мы знаем?
(Решение квадратных уравнений – по формуле; уравнения приводимые к квадратным, уравнения третьей и четвертой степени – с помощью разложения на множители; метод введения вспомогательной переменной)
3) Устный счет.
Уравнение
Корни
1
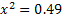
Корней нет
Т
2
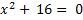
-2; -8
Х
3
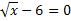
+0,7; -0,7
С
4
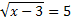
36
Е
5
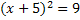
28
Р
Установить соответствие между уравнениями и их корнями. Прочитайте название птицы – символа якутов.
(сделать сообщение о птице стерх – заранее подготовлено одним из учащихся)
Область регулярного гнездования и летнего обитания стерха в Якутии располагается в тундре
Яно-Колымского междуречья на площади около 82 тыс. кв. км. На сильно увлажненных равнинных территориях, посреди топких болот, окруженных угнетенных лесом.
У Якутов исключительным уважением пользуется птица – кыталык (стерх). В древней мифологии стерх выступает в виде светлого начала, помощника и покровителя людей среднего мира. Она обитает в верхних небесах, является дочерью верховного божества Айыны Сиэр Тойон и величавой Айыы Ньуоралдъын Хотун. Появление летающих стерхов над какой-либо местностью порождает мысль о счастливой судьбе. А тому, кто увидит танец священных птиц, предвещается счастливое будущее.
Стерх олицетворяет светлое, доброе, счастливое начало во всей нашей многоликой и изменяющейся жизни. Стерх – символ вечности.
II. Основная часть.
1) Решаем у доски:
Пеликан:
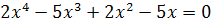
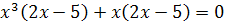
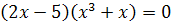
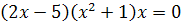
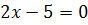
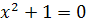
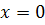
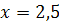 Решений нет
Решений нет
Ответ: 0; 2,5
Аист:
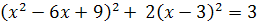
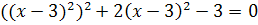
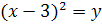
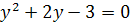
D = 4+12 = 16
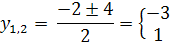
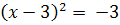
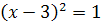
Решений нет 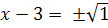
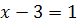
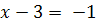
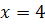
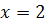
Ответ: 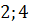 .
.
2) Решить самостоятельно:
Лебедь:
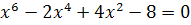
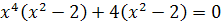
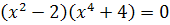
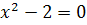
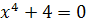
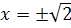 Корней нет
Корней нет
Ответ: 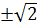
Сова:
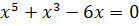
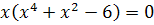
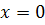
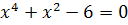 ,
, 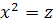
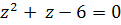
D = 1 + 24 = 25
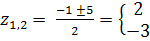
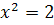
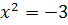
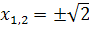 Решений нет
Решений нет
Ответ: 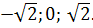
Вставить в таблицу название птицы, которой соответствует решение и рассказать о ней, что она символизирует.
Множество решений
Название птицы
Является символом
-√2, √2
Верность
-√2, 0, √2
Мудрость
2; 4
Счастье
0; 2,5
Жертвенность
3) Решение уравнений с параметрами. (Работаем фронтально)
а) Найдите все значения параметра «b», при которых уравнение: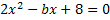
имеет два корня?
Решение:
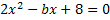
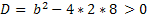
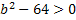
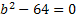
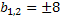
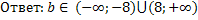
б) Найти «с» при которых квадратное уравнение будет иметь единственный корень.
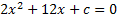
Решение: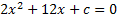
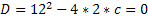
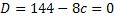
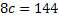
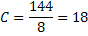
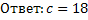
III. 1) Подведение итогов за урок.
а) Какие методы решения уравнений повторили?
б) Что интересного вы узнали на уроке из экологии?
в) Считаете ли вы нужным беречь и любить окружающую нас природу?
2)Задание на дом:
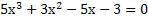
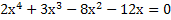
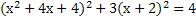
infourok.ru
Обобщающий урок по теме «Уравнения с одной переменной»
Тема урока « Обобщение по теме « Решение уравнений с одной переменной».
Цель урока: Обобщить знания учащихся о целых и дробных рациональных уравнениях.
Образовательные задачи: систематизировать знания и умения учащихся по применению методов решения целых и дробных рациональных уравнений, готовить учащихся к ОГЭ.
Развивающие: развивать умения наблюдать, сравнивать, обобщать, анализировать математические ситуации.
Воспитательные: воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели.
Тип урока: обобщающий
Наглядные пособия и оборудование урока: карточки -задания, учебник,компьютер. интерактивная доска, печатная основа для самостоятельной работы, лист самоконтроля.
Ресурсное обеспечение урока:
1.Программы общеобразовательных учреждений. Алгебра 7-9 классы под редакцией Т.А.Бурмистрова Москва «Просвещение»2018 г.
2.Алгебра 9 класс. Учебник для общеобразовательных учреждений под ред. С.А.Теляковского-16-е изд.-М.Просвещение,2010.
3. Алгебра поурочные планы 9 класс по учебнику Ю.Н.Макарычева, Н.Г.Миндюк и др. Издательство «Учитель».
3.Дидактические материалы 9 класс Москва «Просвещение»2013
4.Компьютер, мультимедийный проектор.
5.Презентация «Уравнения с одной переменной».
6. Интернет ресурсы: Презентация «Физкультминутка»
План урока.
I. Вводная часть
а) Организационный момент
Проверка готовности учащихся к уроку, проверка присутствующих, общий настрой на урок.
Учитель: -Добрый день! Тема, над которой мы будем работать с вами «Уравнения с одной переменной».
Давайте для начала за небольшой промежуток времени мы вспомним теоретический материал по данной теме и решим несколько заданий теста, используя различные методы и приемы.
б) Актуализация знаний, умений, навыков
1. Повторение теоретического материала по данной теме.
Учитель:
—Какие виды уравнений вы знаете? (Целые, биквадратные, линейные, квадратные, дробные рациональные,неполные квадратные,уравнения третьей степени …).
– Какое уравнение называется целым? (Целым называется уравнение с одной переменной, левая и правая части которого целые выражения).
—Какое уравнение называется дробным-рациональным?(Забыли? См.учебник страница 78)(Дробным рациональным уравнением называется уравнение ,обе части которого являются рациональными выражениями,причем хотя бы одно из них –дробным выражением).
Учитель:
—Тогда давайте выберем из предложенных уравнений номера тех, которые являются целыми уравнениями (и далее выполняются задания теста ) Номера ответов запишем в таблицу. Таблица заранее роздана ученикам.
Демонстрируются слайды с заданиями теста.
Задание №1
Укажите номера целых уравнений.
а) х2(5х3-2х2)+8=х3-5х2
б) х2 +2х = х3-8х2
2 5
в) 3х + 2 = 4
х-2 х+3
г) 8 = 0
2-13с-7с2
Учитель:
—Что называется корнем уравнения (корнем называется число, при котором уравнение превращается в верное равенство)
Задание №2
Число 6 является корнем какого уравнения?
а) х+8=х+7
б) х2-6х =х-6
6
в) 6х-1=0
с) 1+ 1 = 1 +1
х+6 х-6
Задание №3
Сколько корней имеет уравнение 5х2+75=0 ?
а) один корень
б) два корня
в) не имеет корней
с) имеет бесконечное множество корней
Задание №4
Найдите корни уравнения 5х2 –х=0
а) 0; 5
б) -5; 0
в) 0; 0,2
с) нет корней
Задание №5
Сколько корней может иметь уравнение х3+х2-9х-9=0
а) 5 или менее
б) не более трех
в) не менее трех
с) не имеет корней
Задание №6
Найдите общий знаменатель дробного рационального уравнения
х2 +2х = х3-8х2
3(х-1) (х+1)
а) (х-1)2
б) 3(х-1)(х+1)
в) 3(х2— 1)
г) (х-1)(х+1)
Учитель:
—Проверьте свои ответы.
Задание № | 1 | 2 | 3 | 4 | 5 | 6 |
Правильный ответ | а, б | б | в | в | б | б,в |
II. Основная часть
а) устная работа
Учитель:
—Итак, давайте подведем итог, какие две большие группы уравнений вы знаете. (Целые уравнения и дробные рациональные уравнения).
Демонстрируется слайд с таблицей обобщения .
—Чем они друг от друга отличаются ?(Наличием переменной в знаменателе)
—Каков алгоритм приведения дробного рационального уравнения к целому?(Найти ОДЗ, общий знаменатель, умножить обе части уравнения на дополнительные множители)
— А дальше решаем как обыкновенное целое уравнение.
– Вы знаете как решаются целые уравнения первой и второй степени? Это какие уравнения (Линейные и квадратные).
— Также мы уже решали уравнения третьей и четвертой степеней.
– Как решаются целые уравнения третьей и четвертой степени?
-Вспоминаем, что существуют 2 основных метода решения уравнений выше второй степени.
Метод разложения Метод введения
на множители новой переменной
б) Решение уравнений с использованием , имеющихся знаний.
Слайд. С помощью какого метода можно решить уравнения:
1) х5-4х3=0 2) 9х4 – 10х2 + 1 = 0.
3) х-4 = 2
х+3
Решение:
1) х5-4х3=0
х3(х2-4)=0
х3=0 ( х2-4 ) = 0
х=0 ( х-2 )( х+2) = 0
х=2 х=-2
Учитель:
—Каким методом решили уравнение?
( Уравнение решили методом разложения на множители.)
2) 9х4 – 10х2 + 1 = 0.
Учитель:
-Как называется это уравнение ? (Биквадратное)
—Если обозначить х2 переменной у, то получится квадратное уравнение
9 у2 – 10у + 1 = 0.
Д=(-10)2 — 4.9.1= 100-36=64=82
у= 10+8 =1 у= 10-8 = 1
18 18 9
Возвращаемся к переменной х.
х2=1 х2 = 1
9
Х1=1 х2=-1 х3=1/3 х4=-1/3
Учитель:
—Уравнение 4 степени, получили 4 корня. Решили методом введения новой переменной у.
х-4 = 2
х+3
ОДЗ: х не равен -3(иначе знаменатель превращается в 0)
х-4 — 2 =0 /.( х+3)
х+3
(х-4)- 2( х+3) =0
-х-10=0
х=-10
Учитель:
—При решении уравнения использовали алгоритм для дробно-рациональных уравнений. и решили целое линейное уравнение
III.Физкультминутка. (Слайд)
Повторим с помощью ФМ как строится график линейной функции.
Если график параллелен оси ОХ — разводим руки в стороны;
Проходит через начало координат — руки на пояс;
Пересекает ось ОУ в точке, отличной от начала координат- руки вверх, параллелен оси ОУ-одна рука вверх, другая-вниз.
у = 2х (Проходит через начало координат — руки на пояс), х =3 (параллелен оси ОУ-одна рука вверх, другая-вниз), у = -2х (Проходит через начало координат — руки на пояс) у = 4 (параллелен оси ОХ — разводим руки в стороны), у = х /2(Проходит через начало координат — руки на пояс), у = 6х2 (Проходит через начало координат — руки на пояс), у = -8(параллелен оси ОХ — разводим руки в стороны), у=7х(Проходит через начало координат — руки на пояс),
IV. Закрепление умений и навыков решать целые уравнения, используя при этом различные приемы и методы.
Самостоятельная работа.
Слайд 4
В а р и а н т 1 (на карточке)
Решите уравнение:
а) 16х3 – 32х2 – х + 2 = 0;
б) х4 + 7х2 – 44 = 0;
в) (х2 – х + 1) (х2 – х – 7) = 65.
В а р и а н т -образец
Решите уравнение:
а) х3 – 4х2 – 9х + 36 = 0;
б) х4 + 6х2 – 27 = 0;
в) (х2 + х + 6) (х2 + х – 4) = 144.
Решение варианта-образца. (самопроверка).
а) х3 – 4х2 – 9х + 36 = 0
х2(х – 4) – 9(х — 4) = 0
(х – 4) (х2— 9) = 0
(х – 4) (х— 3) (х— 3) = 0
Х1=4 х2=3 х3=-3
б) х4 + 6х2 – 27 = 0;
Вводим новую переменную у = х2
у2 + 6у – 27 = 0;
Д= 36+4.27=144=122
у= -6+12 у = -6-12
2 2
У1=3 у2=9
в) (х2 + х + 6) (х2 + х – 4) = 144.
Вводим новую переменную у = х2 + х
(у+6)(у-4)=144
у2 + 6у-4у-24-144=0
у2 + 2у-168=0
Д=4+4 . 168=676=262
У1 = -2+26 ; у2 = -2-26
2 2
У1=12 ; у2=-14
Возвращаемся к переменной х
х2 + х =12 х2 + х =-14
х2 + х -12 =0 х2 + х +14=0
Д=1+4 . 12=49=72 Д=1-4 . 14=-55
х1= -1+7 х2=-1-7
2 2
Х1=3 х2=-4
(уравнение 4 степени ,корней получилось 2,т.е. не больше 4-х)
Решение самостоятельной работы Вариант -1(карточка)
Вариант 1 (карточка)
а)16 х3-32 х2-х+2=0
Решение: выделим одинаковый множитель
16 х2(х-2) – (х-2)=0
(х-2)(16х2-1)=0
(х-2)(4х-1) (4х+1)=0
х-2=0; 4х-1=0 ; 4х+1=0
4х=1 ; 4х=-1
х1=2 х2=1/4; х3=-1/4
Ответ: х1=2; х2=1/4; х3=-1/4
б) х4+7х2-44=0 Введем новую переменную у=х2
у2+7у-44=0
Д=в2-4ас =72-4 (-44)=49+176=225=152
у1= -7+15 у2= -7-15
2 2
у1= 4; у2= -11
Вернемся к переменной х.
х2=у1= 4; х2 = у2= -11 уравнение не имеет смысла
х1=2; х2= -2
Ответ: х1=2; х2= -2
в)(х2-х+1)(х2-х-7)=65
Вводим новую переменную у= х2-х
(у+1)(у-7)=65
у2+у-7у-7-65=0
у2-6у-72=0
Д=36+ 4 . 72=324=182
у1= 6+18 ; у2= 6-18
2 2
у1=12; у2= -6
Возвращаемся к переменной х , т.к. у= х2-х
12= х2-х ; -6= х2-х
х2-х -12=0; х2-х+6=0
Д=1+ 4 . 12=49=72; Д=1- 4 . 6=-23
х1= -1+7 ; х2= -1-7
2 2
х1=3; х2= -4
Ответ: х1=3; х2= -4
Дополнительно, для тех, кто справился раньше с самостоятельной работой
задание из учебника, стр.100 №371(а), 372(а)
IV. Заключительная часть. Рефлексия.
Оценивание работы учащихся на уроке.
Учитель:
Уроку подошел конец.
Заполняем лист самоконтроля.
Лист самооценки
Вид работы | Критерий оценивания | Баллы | |||||||||||||||
Тест | Задания выполнил : правильно 6 заданий — 3 балла правильно 4-5 заданий — 2 балла правильно 2-3 заданий — 1 балл | ||||||||||||||||
| |||||||||||||||||
Устная работа со схемой | Работал активно сам -3 балла Отвечал на вопросы учителя-2 балла | ||||||||||||||||
Решение уравнений | Решил правильно 1 уравнение-1балл Решил правильно 1 и 2 уравнение -2 балла Решил правильно все три уравнения -3 балла | ||||||||||||||||
Физкультминутка | Все графики определил правильно-3 балла Ошибся 2-3 раза- 2 балла; Определил правильно 1-2 графика-1 балл | ||||||||||||||||
Самостоятельная работа | Решил 1-ое уравнение сам-3 балла Решил 1-ое уравнение с помощью образца-2 балла Не решил-0 баллов | ||||||||||||||||
Решил 2-ое уравнение сам-3 балла Решил 2-ое уравнение с помощью образца-2балла Не решил-0 баллов | |||||||||||||||||
Решил 3-ое уравнение сам-3 балла Решил 3-ое уравнение с помощью образца-2балла Не решил-0 баллов | |||||||||||||||||
Дополнительное задание из учебника | Решил правильно №371(а) — 3 балла | ||||||||||||||||
Решил правильно №и372 (а) — 3 балла | |||||||||||||||||
Оценка за урок | 13-21 баллов-получи оценку «5». 7-12 баллов –получи оценку «4» 4-5 баллов-получи оценку «3» | ||||||||||||||||
Скажи про себя «Какой я молодец потому, что___________________________________________________» Например, какой я молодец, я сам решил уравнение методом подстановки или какой я молодец, я правильно и быстро решил самостоятельную работу. | |||||||||||||||||
12
multiurok.ru
Опорный конспект по алгебре «Линейные уравнения» (9 класс)
Линейное уравнение с одним неизвестным
Определение.
Равенство, содержащее одну переменную, называется уравнением с одной переменной. Переменную в уравнении называют также неизвестным.
Значение переменной, при котором уравнение превращается в верное числовое равенство, называется корнем (или решением) уравнения.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Два уравнения называются равносильными, если каждый корень первого уравнения является корнем второго, и наоборот – каждый корень второго уравнения является корнем первого, то есть, оба уравнения имеют одни и те же корни.
Равносильными являются также уравнения, которые не имеют корней.
Например, уравнения

равносильны, так как оба имеют один корень, равный 3.
Основные свойства, которые используют при решении уравнений.
Первое свойство: если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится уравнение, равносильное данному.
Например,

Второе свойство: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнения, равносильное исходному.
Например,

Определение.
Линейным уравнением с одной переменной (с одним неизвестным) называется уравнение вида:

где 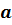 и
и 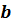 – постоянные,
– постоянные, 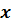 – переменная (неизвестное).
– переменная (неизвестное).
Если в уравнении 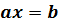 :
: 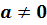 , то это уравнение называется уравнением первой степени.
, то это уравнение называется уравнением первой степени.
Задание.
Решить уравнения:
а) 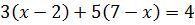 ; б)
; б) 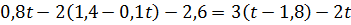 ; в)
; в) 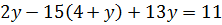 ; г)
; г) 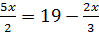 .
.
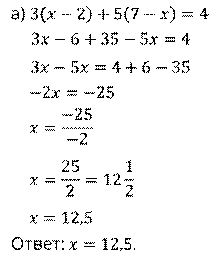
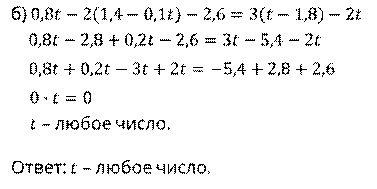

Обратите внимание, какое бы число мы не подставили вместо у, всегда будем получать неверное равенство. Следовательно, данное уравнение не имеет корней.
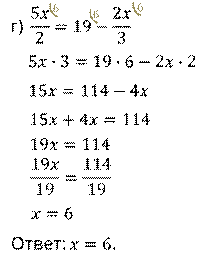
infourok.ru
 .
.