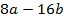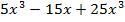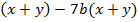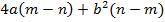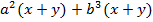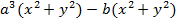Алгебра 7 класс. Преобразование выражений (подобные слагаемые, раскрытие скобок). Повторение

Алгебра 7 класс. Итоговое повторение

Тема: Преобразование выражений. Задания могут быть использованы для индивидуальной работы с учащимися при изучении данной темы и для итогового повторения .

4

4a + 3c – 3a – 4c

3(3k – c) – (3c – k)

4(y – a) – 5(2a – y)

5

2a – y – 3a + 2y

4(a – x) – 293a – x)

-(3a – c) + 3(3c – a)

6

a – 5p – 5a + 3p

-( 2a – p) – 3(a + 2p)

4y – 3 – 2(5 – y)

7

4k – 4y + 4a + y

3(k – 6) – (- 27 + k)

-2(k – a) – 3(a + 2k)

8

3y – (-4a) + 2y – 3a

3(14 – k) – 2(k + 2)

13(a – y) – 12(- y + a)

9

3k – 4y + 2b – (- y)

7( 1 – p) – 7(2p – 1)

-(-3y – a) + ( — a + 2y)

10

-6p + 2a + 4p – 6a

-(x – 4) – 2(6 – x)

-10(b – 3a) + 2(b – 15a)

11

-p – k – a + 2a + k

-(k – 2) – 2(2 – k)

4(3a – p) – (- 2a + 3p)

12

4h — 8f + 2f – 12h

3b – (- 2 + b) – 12

-( — 45k + 1) – 2(30k + 5)

13

5a – 4k – 10a – (- 2a)

-(4 – a) + 3(a – 3 )

-(- 23a + y) + 12(2a + y)

14

2y -12a – 14y + 10a

-( 3 – a) – 12(a + 12)

-12(y – 2a) + ( — 3y + 5a)

15

-p + 2y + 3p – (- 2y)

-2(d – 3) + 2(13 – d)

-2(3a – 4y) + 3(2y – 4a)

16

21a – 11p +a – p

-( -p) + 4k – 2(p – 2k)

21(- 2y – x) – 3(2x – 14y)

17

12y – 21x + 12x – 21y

2(c – 12) – 12(c – 1)

-2(k – 2y) + 3(3y – 4k)

18

2y – 6a – 12y + 12a

-(2 – a) – a + (2a + 1)

-21(- y – 2k) + 2(- y + 3K)

19

K – y – k – 2y + 2k

-(a + 31) + (30 – 3a)

21(- k – 4x) – 7(- 3k + 10x)

20

K – a – 2k – 2a + 3k

-2(a – 4) + 10(- 3a – 1 )

32(3a – y) – 21(5a + 2y)

21

2y – 32 + 12y +30 – y

2(y – 2) – (3y + 5)

12(- 2y + 4c) – 2(- 10y – 12c)

22

-Y – 2k + 3y + 3k — 10

-( 3 – k) + 2(k – 12 )

12(4a – 3y) – 4(12a – 9y)

23

10 – 2y – 12 – (-21y)

2(14 – y) – 14(2y – 1)

-2(3y + 2b) + 3(- 4b + 2y)

24

-23 – 2y + 13 + 3y

-(2 – y) + 3(3 – y)

-12(k – 2y) + 2(6k – 10y)

25

-2y – 4k – 3a + 4y + 3a

-3(1 – 3y) + 2(2y – 1)

2(2y – 3b + 1) – (2 – 4y +5b)

26

13y – 4a + 5k + a + 3a

-3(3c – 2) + 2(1 – c)

-(2a – 4p + 1) + 2(a – 2)

27

-4k – 5b – (-2b) + 3k

4(2 – x) – 12(1 – 2x)

-5(c – 2y) + 2(5c – 2y)

28

-2y + 3k + y – 2k + y

-2(3 – y) + (y – 2)

-3(2y +5c) + (3c – 2y)

Ответы . тема : Преобразование выражений.

4

A – c

10k – 6c

9y – 14a

5

Y – a

-2a – 2x

-6a + 10c

6

-4a – 2p

— 5a – 5p

6y – 22

7

4k + 4a – 3y

2k + 9

-8k –a

8

5y – a

2 – 5k

a – y

9

5k – 3y

14 – 21p

5y

10

-2p – 2a

X – 8

-8k

11

-p + a

K – 2

14k – 7p

12

-8h — 6f

2x — 10

15k – 11

13

-3a – 4k

4k – 13

47a + 11y

14

-2a — 12y

— 147 — 11k

-15y + 29a

15

2p + 4y

-4k + 22

-18k + 14y

16

22a – 12p

-p + 8k

-27x

17

-9y – 9x

-10k – 12

-14k + 13y

18

6a – 10y

-1 + 2a

19y + 48k

19

2k – 3y

-4k – 1

-151x

20

2k — 3a

-32a – 2

-9k – 74y

21

13y – 2

-y — 9

-4y + 72k

22

2y + k -10

-27 + 3k

0

23

19y — 2

42 – 30y

-16k

24

Y – 10

7 – y

4y

25

2y – 4k

13y – 1

8y – 11k

26

13y + 5k

-11c + 8

4p – 5

27

-k – 3b

-4 + 20x

5k + 6e

28

k

-12 — y

-8y – 12c

Математика . 7 класс. Тренажер.

Тема: «Решение линейных уравнений»

(Итоговое повторение)

2015 г.

Урок+презентация по математике для 7 класса на тему «Раскрытие скобок»

План-конспект урока в 7 классе по теме «Раскрытие скобок»

Цели урока:

Образовательные: обобщить и систематизировать ранее изученный материал, проверить усвоение учащимися изученного материала и формировать умение применять его; закрепить понятие раскрытие скобок; закрепить навыки по данной теме.

Развивающие: развивать познавательную активность, логическое мышление, творческие способности учащихся, навыки самоконтроля и взаимоконтроля, развивать творческие способности учащихся; развивать умение обобщать, классифицировать, строить умозаключения, делать выводы; развивать коммуникативные навыки; развивать умение сотрудничать при решении учебных задач.

Воспитательные: воспитывать интерес к предмету, культуру умственного труда; культуру коллективной работы;

воспитывать упорство в достижении цели.

Тип урока:  повторение, закрепления и систематизации полученных знаний.

Формы организации деятельности учащихся: фронтальная, парная, индивидуальная.

Тема урока: «Раскрытие скобок»

Цели деятельности учителя

создать условия для формирования представлений о распределительном законе умножения; умения решать сложные вычислительные примеры и уравнения, применяя правила раскрытия скобок

Задачи урока

– формировать умение раскрывать скобки, совершенствовать вычислительные навыки;
– тренировать умение ставить цель деятельности, фиксировать собственные затруднения;
– совершенствовать умение выражать свои мысли, обосновывать суждения

Тип урока:

урок закрепления новых знаний

Виды деятельности:

фронтальная работа с классом, работа в группах, использова­ние презентации, работа у доски и в те­традях

Решаемые проблемы:

как применяется распределительный закон умножения при раскрытии скобок в буквенных выражениях?

Технологии

здоровьесбережения, проблемного обуче­ния, индивидуально­го и коллективного проектирования

Оборудование

компьютер; мультимедийная установка; презентация

Планируемые результаты изучения темы:

Личностные: проявляют познавательный интерес к предмету.

Предметные: имеют представление о распределительном законе умножения, умеют раскрывать скобки, применяя правила.

Метапредметные результаты изучения темы (универсальные учебные действия):

познавательные: ориентируются на разнообразие способов решения задач; умеют работать с тестовыми заданиями;

регулятивные: учитывают правило в планировании и контроле способа решения;

коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; развернуто обосновывают суждения.

Ход урока:

1. Организационный момент

2. Вводная беседа. Актуализация знаний.

3. Устная работа (по слайдам презентации)

4. Правила раскрытия скобок

-Что значит раскрыть скобки?

5. Закрепление материала: (по слайдам презентации)

Отработка навыков Работа у доски «цепочкой»

6. Контроль полученных знаний.

Самостоятельная работа по карточкам (по слайдам презентации)

7. Взаимопроверка (по карточкам)

8. Подведение итогов урока

ОЦЕНКА МОЕЙ РАБОТЫ НА УРОКЕ

ФАМИЛИЯ ИМЯ…………………………………………………..

Этап

Вид работы

Оценка

Эмоциональное состояние

1

Устная работа

2

Знание правил

3

Умение применять правила

4

Самостоятельная работа

5

Итоговая оценка

1 2 3

Отличное настроение Хорошее настроение Грустно

Консультация по алгебре (7 класс) по теме: Карточки для коррекции знаний по алгебре 7кл

7 класс

---

Оглавление

Вычисление значений выражений        

Приведение подобных слагаемых        

Переместительный, сочетательный и распределительные свойства        

Преобразование выражений        

Решение линейных уравнений        

Нахождение x и y по формуле        

Сложение и вычитание многочленов        

Умножение одночлена на многочлен        

Преобразование выражений        

Решение уравнений вида )        

Вынесение общего множителя за скобку        

Умножение многочлена на многочлен        

Квадрат суммы, квадрат разности        

Сокращение дробей.        

Сложение и вычитание дробей с одинаковыми знаменателями        

Нахождение наименьшего общего знаменателя дробей        

Нахождение дополнительных множителей к дробям при приведении дробей к наименьшему общему знаменателю        

Приведение дробей к наименьшему общему знаменателю        

Сложение и вычитание дробей с разными знаменателями        

Умножение дробей        

Возведение в степень дроби        

Деление дробей        

Решение систем линейных уравнений с двумя переменными  способом подстановки        

Решение систем линейных уравнений с двумя переменными  способом сложения        

---

Правило	Примеры
	(3m+4x)y, при m=3, x=,y=
1. Подставить вместо всех переменных их значения
2. Выполнить действия

Правило	Примеры
	3х–7х+9х–15х	9х–4y+9+5x–3+3y–2x
1. Подчеркнуть одинаковыми черточками слагаемые с одинаковой буквенной частью.	3х–7х+9х–15х=	9х–4y+9+5x–3+3y–2x=
2. Сложить коэффициенты (вместе со знаками) одинаково подчеркнутых слагаемых.	=(3+(–7)+9+(–15))х= =(3–7+9–15)х=	=(9+5+(–2))x+((–4)+3)y+(9+(–3))= =(9+5–2)x+(–4+3)y+(9–3)=
3. Полученный в п.2 коэффициент умножить на общую буквенную часть.	= –10х	=12x+(–1)y+6=12x–y+6

Раскрытие скобок, если перед ними стоит знак + или –

Правило	Примеры
1а)Если перед скобкой стоит + или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих внутри скобок.	(a–b+c)= a–b+c +(x+y–z)= x+y–z +(–a+c–1)= –a+c–1
1б)Если перед скобкой стоит –, то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок, на противоположные (то есть + на –, а – на +)	–(a–x+c)= –a+x–c –(1–x+a)= –1+x–a
2. Если нужно привести подобные слагаемые.

Правило	Примеры
ab=ba (ab)c=a(bc)	–3,2a.5,6b=(–3,2.5,6)ab= –17,92ab
a(b+c)=ab+ac	1,3(4–3b)=1,3.4–1,3.3b=5,2–3,9b –4(3a–7b)= –4.3a–(–4).7b= –12a+28b

Правило	Примеры
	b–(4–2b)+(3b–1)	3(6–5x)+17x–10	12n+9–6(3n+1)
1. Раскрыть скобки	=b–4+2b+3b–1=	=3.6–3.5x+17x–10= =18–15x+17x–10=	=12n+9–6.3n+(–1).n= =12n+9–18n–6=
2. Привести подобные слагаемые.	=(1+2+3)b+(–4–1)= =6b–5	(18–10)+(–15+17)x= =8+2x	=(12–18)n+(9–6)= = –4n+4

Правило	Примеры
	–5х–150=0	15(х+2)–19=12х	6(1+5х)=5(1+6х)
1. Если нужно, раскрыть скобки.	––––––––––––	15(х+2)–19=12х 15х+15.2–19=12х 15х+30–19=12х	6(1+5х)=5(1+6х) 6.1+6.5х=5.1+5.6х 6+30х=5+30х
2. Перенести слагаемые с переменной в левую, а без переменной в правую часть уравнения, меняя их знаки на противоположные (+ на – , а – на +)	–5х–150=0 –5х=150	15х+30–19=12х 15х–12х= –30+19	6+30х=5+30х 30х–30х=5–6
3. Привести в обеих частях уравнения подобные слагаемые. Получится уравнение вида ax=b	––––––––––––	(15–12)х=–30+19 3х= –21	(30–30)х=5–6 0х= –1
4. Если а≠0, то  (x=b:a) Если a=0, b≠0, то уравнение не имеет корней Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения	а= –5≠0⇒ x=150:(–5) x= –30 Ответ: х= –30	а=3≠0⇒ x= –21:3 x= –7 Ответ: х= –7	а=0⇒ решений нет Ответ: решений нет

Правило	Примеры
	y=3x–5
	x	4
	y			–2
Дан х. Найти y. а) Подставить вместо х его значение	x=4 y=3.4–5=
б) Выполнить действия	=12–5=7
Дан y. Найти х. а) Подставить вместо y его значение	y= –2 –2=3x–5
б) Решить получившееся уравнение	–2=3x–5 –3x= –5+2 –3x= –3 x= –3:(–3) x=1		x		4	1
			y		7	–2

Нахождение координат точки пересечения графиков функций

Правило	Примеры
Функции заданы формулами. 1. Приравнять правые части данных формул	y=3x–5              y=4x+3 3x–5=4x+3
Решить получившееся уравнение. Получим х–координату точки пересечения	3x–4x=3+5 –x=8 x= –8
3. Подставить в одну из формул вместо х найденное в п.2 решение	y=3.(–8)–5=
4. Вычислить y	= –24–5= –29
5. Записать ответ в виде (х;y)	(–8;–29)

Правило	Примеры
Раскрыть скобки Привести подобные слагаемые, т.е. привести к стандартному виду.

Правило	Примеры
Умножить каждый член многочлена, записанного в скобках на одночлен, стоящий перед скобкой Сложить полученные произведения Получившийся многочлен привести к стандартному виду

Правило	Примеры
Раскрыть скобки Привести подобные слагаемые

Правило	Примеры
1. Найти наименьший общий знаменатель (НОЗ) всех дробей, входящих в уравнение	НОЗ знаменателей 5 и 3: 15	НОЗ знаменателей 7 и 1: 7	НОЗ знаменателей 4, 12 и 1: 12
2. Умножить каждую дробь уравнения на НОЗ
3. Если нужно, сократить дроби		4–3х= –14
4. Решить получившееся уравнение	9х+15= 5х+5 9х–5х= –15+5 4х= –10 х= –2,5	4–3х= –14 –3х= –4–14 –3х= –18 х= –18:(–3) х=6	18y+21–7+5y=60 18y+5y= –21+7+60 23y=46 y= 46:23 y=2
5. Записать ответ	Ответ: х= –2,5	Ответ: х=6	Ответ: y=2

Правило	Примеры
	4×2–12x+8a2x3	3(b–2c)+x(b–2c)	5(x–y)+a(y–x)
1. Представить каждое слагаемое в виде произведения	4×2–12x+8a2x3 = = 4xx–4.3x+4.2aaxxx=	3(b–2c)+x(b–2c)=	5(x–y)+a(y–x)= =5(x–y)–a(x–y)=
2. Подчеркнуть в каждом слагаемом одинаковые множители	= 4xx–4.3x+4.2aaxxx=	=3(b–2c)+x(b–2c)=	=5(x–y)–a(x–y)=
3.Записать подчеркнутый одинаковый множитель за скобками 4. В скобках записать слагаемые без подчеркнутого множителя	= 4x(x–3+2aaxx)= = 4x(x–3+2a2x2)	=(b–2c)(3+x)	=(x–y)(5–a)

Правило	Примеры
Умножить каждое слагаемое из 1–й скобки на каждое слагаемое из 2–й скобки Полученные произведения сложить Привести получившийся многочлен к стандартному виду	(2x–y)(4x+3y)= =2x.4x+2x.3y+(–y).4x+(–y).3y= =8×2+6xy –4xy–3y2=8×2+(6–4)xy–3y2= =8×2+2xy–3y2 (2a–3)(5–a)= =2a.5–2a.a+(–3).5–(–3).a= =10a–2a2–15+3a=(10+3)a–2a2–15= = –2a2+13a–15

Правило	Примеры
(I ± II)2 = I2 ±2. I . II + II2	(I ± II)2		I	II	I2 ±2. I . II + II2
	(3x+4)2		3x	4	(3x)2+2.3x.4+42
	(3x–4)2		3x	4	(3x)2–2.3x.4+42
Краткая запись	(3x+4)2=(3x)2+2.3x.4+42=9×2+24x+16 (3x–4)2=(3x)2–2.3x.4+42=9×2–24x+16
I2 ±2. I . II + II2 = (I ± II)2
25×2+10xy+y2 = ? I2 = 25×2 ⇒ I =5x II2 =y2 ⇒ II = y Проверяем, верно ли, что 2.(5x).y=10xy 10xy=10xy – верно ⇒ можно воспользоваться формулой 25×2+10xy+y2 = (5x+y)2 9×2+12x+16 = ? I2 = 9×2 ⇒ I =3x II2 =16 ⇒ II = 4 Проверяем, верно ли, что 2.(3x).4=12x 24x=12x – неверно ⇒  воспользоваться формулой нельзя		25×2–10xy+y2 = ? I2 = 25×2 ⇒ I =5x II2 =y2 ⇒ II = y Проверяем, верно ли, что 2.(5x).y=10xy 10xy=10xy – верно ⇒ можно воспользоваться формулой 25×2–10xy+y2 = (5x–y)2 9×2–12x+16 = ? I2 = 9×2 ⇒ I =3x II2 =16 ⇒ II = 4 Проверяем, верно ли, что 2.(3x).4=12x 24x=12x – неверно ⇒  воспользоваться формулой нельзя

Разложение многочленов на множители. Вынесение общего множителя за скобки

Что такое общий множитель, зачем его искать и с какой целью выносить за скобки? Ответим на эти вопросы, разобрав простейший пример.

Решим уравнение 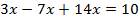. Левая часть уравнения является многочленом, состоящим из подобных членов. Буквенная часть  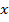является общей для данных членов, значит, она и будет общим множителем. Вынесем  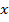за скобки:

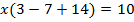
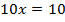
В данном случае вынесение за скобки общего множителя помогло нам преобразовать многочлен в одночлен. Таким образом, мы смогли упростить многочлен и его преобразование помогло нам решить уравнение.

В рассмотренном примере общий множитель был очевиден, но будет ли так просто найти его в произвольном многочлене?

Найдём значение выражения: .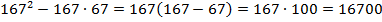

В данном примере вынесение общего множителя за скобки значительно упростило вычисление.

Решим еще один пример. Докажем делимость на 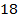 выражения .

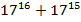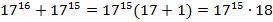
Полученное выражение делится на 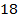, что и требовалось доказать. И снова вынесение общего множителя позволило нам решить задачу.

Решим еще один пример. Докажем, что выражение 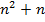 делится на  при любом натуральном : .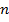

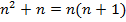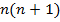 – выражение является произведением двух соседних чисел натурального ряда. Одно из двух чисел обязательно будет четным, значит, выражение будет делиться на .

Мы разобрали разные примеры, но применяли один и тот же метод решения: выносили общий множитель за скобки. Мы видим, что эта простая операция значительно упрощает вычисления. Было легко найти общий множитель для этих частных случаев, а что делать в общем случае, для произвольного многочлена?

Вспомним, что многочлен – сумма одночленов.

Рассмотрим многочлен 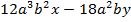. Данный многочлен является суммой двух одночленов. Одночлен – произведение числа, коэффициента, и буквенной части. Таким образом, в нашем многочлене каждый одночлен представлен произведением числа и степеней, произведение множителей. Множители могут быть одинаковыми для всех одночленов. Именно эти множители нужно определить и вынести за скобку. Сначала находим общий множитель для коэффициентов, причем целочисленных.

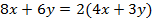
Было легко найти общий множитель, но давайте определим НОД коэффициентов: .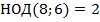

Рассмотрим ещё один пример: .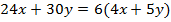

Найдем , что позволит нам определить общий множитель для данного выражения: .

Мы вывели правило для целых коэффициентов. Нужно найти их НОД и вынести за скобку. Закрепим это правило, решив ещё один пример.

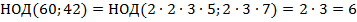
Мы рассмотрели правило вынесения общего множителя для целочисленных коэффициентов, перейдем к буквенной части. Сначала ищем те буквы, которые входят во все одночлены, а потом определяем наибольшую степень буквы, которая входит во все одночлены: .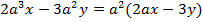

В этом примере была всего одна общая буквенная переменная, но их может быть несколько, как в следующем примере:

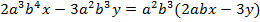
Усложним пример, увеличив количество одночленов:

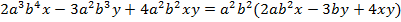
После вынесения общего множителя мы преобразовали алгебраическую сумму в произведение.

Мы рассмотрели правила вынесения для целых коэффициентов и буквенных переменных отдельно, но чаще всего для решения примера нужно применять их вместе. Рассмотрим пример:

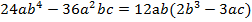
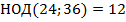
Иногда бывает сложно определить, какое выражение остается в скобках, рассмотрим легкий прием, который позволит вам быстро решить эту проблему.

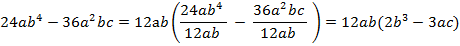
Общим множителем также может быть искомое значение :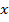

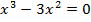
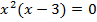
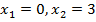
Общим множителем может быть не только число или одночлен, но и любое выражение, как, например, в следующем уравнении:

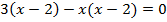
Обозначим выражение 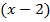 за 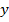 и вынесем его как общий множитель:

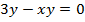
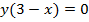
Вернемся к исходной переменной: 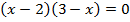. Получаем: .

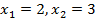Мы научились находить общий множитель и выносить его за скобки. Сформулировали соответствующие правила и закрепили их примерами.

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. School-assistant.ru (Источник).                
2. Mathematics-repetition.com (Источник).      
3. Edufuture.biz (Источник).            

 

Домашнее задание

1) Вынесите общий множитель за скобки:

1. 
2.  
3. 
4. 

2) Решите уравнение: .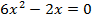    

3) Упростите выражения:

1.  
2. 

Разработка урока по алгебре в 7 классе «Раскрытие скобок»

Конспект урока математики в 7-м классе по теме «Раскрытие скобок»

Провела и подготовила учитель математики Шилыковской СОШ

Пухова Лариса Станиславовна

Тип урока:

Цели урока:

Обучающие:

• Сформировать способность к раскрытию скобок с учётом знака, стоящего перед скобками;

• Закрепить вычислительные навыки при работе с положительными и отрицательными числами;

Развивающие:

• Развивать аргументированную математическую речь, умение выполнять сравнение и анализ, делать выводы,

Воспитывающие:

• Воспитание навыков коммуникативности, культуру общения с товарищами, умение слушать и слышать других;

• Воспитание устойчивого интереса к предмету.

Оборудование урока:

Формы оценки знаний:

Устный опрос( фронтальный), письменный(самостоятельная работа), тестирование.

Формы работы:

Объяснение, самостоятельная работа.

Организация урока:

Индивидуальная, работа в парах.

Методы обучения:

Словесный, наглядный, практический

Проверка знаний:

самопроверка, взаимопроверка

ХОД УРОКА.

I этап урока – организационный

Учитель: Ребята! Проверьте, все ли у вас готово к уроку? На столе у вас должны лежать: учебник, дневник, тетрадь и ручка. Молодцы! Начнем наш урок. Запишем число « 24 октября. Классная работа.»

2. Мотивация урока.

Сегодня мы проведем урок под девизом:

«Математику уже затем учить следует, что она ум в порядок приводит». М. Ломоносов.(Слайд1)

— Кто такой Ломоносов?

-В ноябре исполняется 300 лет со дня рождения Михаила Васильевича Ломоносова, выдающегося ученого, который внес большой вклад в развитие математики.

3.Устный счет( фронтальная работа)

-Ребята, чем мы с вами занимались на прошлом уроке?

— Преобразованием буквенных выражений.

-Какие выражения мы называем буквенными?

-Выражения, записанные с помощью знаков арифметических действий, содержащие и числа и буквы.

-Что значит « преобразовать выражение?»

-Замена одного выражения другим, равным ему, называют преобразованием выражения.

Задание 1

Назовите каждое слагаемое в данном выражении(на доске)

а-в+с-d

-х-у-z-10

-Какие это выражения?

-Буквенные.

-Как еще можно назвать эти выражения?

-Алгебраическими суммами.

-Почему мы называем такие выражения алгебраическими суммами?

-Так как их можно представить в виде суммы, а алгебраическими, потому что в конечной записи они не являются чистыми суммами. В алгебраической сумме слагаемые путешествуют вместе со своими знаками.

— Запишите эти выражения в виде суммы (Дети по одному записывают на доске)

Задание 2

-Вычислите значения данных выражений наиболее удобным способом, применив известные вам основные свойства арифметических действий (записаны на доске) Дети выходят к доске по одному

Каждый пример ребенок поясняет

1

а) 69+37+31+23=100+60=160(меняем местами слагаемые, сочетательный)

б) 700-203=700-(200+30)=700-200-3=497 (вычитаем из числа разность двух чисел)

в) 453+299+=453+(300-1)= 453+(300-1)=453 +300-1=752( прибавляем к числу разность двух чисел)

2

а)97-38-12=97-(38+12)=97-50=47(заключили в скобки и вычли сумму из числа)

в)а+(3-а)=а+3-а=3 ( опустили скобки., поменяли местами слагаемые)

при сложении противоположных чисел=0

3

а)5+х+10-у-6=9+х-у( поменяли слагаемые местами, сгруппировали, упростили)

4.Актуализация опорных знаний.

Какие свойства мы использовали при выполнении этих заданий? В буквах эти свойства выглядят так

1)— В любой сумме слагаемые можно как угодно переставлять и произвольным образом объединять в группы. С помощью букв это запишем так:

а+в+с=(а+в)+с=а+(в+с) (Слайд2)

2)Чтобы вычесть из некоторого числа сумму двух чисел, вычитаем из него первое слагаемое, и из полученного результата вычитаем второе слагаемое

а-(в+с)=а-в-с (Слайд2)

3)Сумма противоположных чисел =0

а+(-а)=о (Слайд2)

-Как вы понимаете задание «Упростить выражение»?

— Упростить выражение- это значит привести его к более простому или более красивому виду.

-Что значит преобразовать выражение?

-Замена одного выражения другим равным ему называют преобразованием выражения

-Все что мы с вами сейчас делали- были различные способы упрощения выражений с помощью свойств арифметических действий.эти способы мы применили и для числовых и для буквенных выражений.

Одним из способов упрощения( преобразования ) выражения является раскрытие скобок.

5.Объяснение нового материала

Как вы думаете, чем же мы будем заниматься сегодня на уроке? (дети самостоятельно формулируют тему урока, которая высвечивается на слайде). (Слайд3)

Проблемная ситуация

В данном выражении расставить скобки произвольным образом( применяя свойства арифметических действий)(записано на доске)

Дети делают в тетрадях

5+7-2-1 (Слайд4)

4. 1. (5+7)-2-1

   2. 5+(7-2-1)

   3. 5+7-(2+1)

   4. 5+(7-2)-1

— Обратите внимание на скобки и знаки стоящие перед ними.

-Какие различные случаи можно выделить?

• Перед скобками не стоит никакого знака

• Перед скобками стоит знак(+)

• Перед скобками стоит знак (-)

Независимо от того , как мы расставили скобки, значение выражения не изменилось.

-Можно сказать, что мы заменили данное выражение выражениями тождественно равными?

-Да.

Примеры:

Записывают в тетради

Возьмем буквенные выражения , запишите без скобок

1)Какой знак стоит перед скобками?(Нет знака)

(37+5)+а=37+5+а

— Посмотрите, после раскрытия скобок выражения изменились или нет?

Запишем это в виде букв

(а+в)+с=а+в+с (Слайд5)

Это и есть свойство арифметических действий.

Вывод:

Если перед скобками не стоит никакого знака, то скобки можно опустить, а члены в скобках переписать без изменения. (Слайд6)

2)Какой знак стоит перед скобками? Знак +

83+(64-25)=83+64-25

— Посмотрите, после раскрытия скобок выражения изменились или нет? Запишем в виде букв

а+(в+с)=а+в=с (Слайд7)

Вывод:

Если перед скобками стоит знак «+», то при раскрытии скобок знаки слагаемых в скобках остаются без изменения (Слайд8)

3) Какой знак стоит перед скобками ?знак –

Примените свойство вычитания суммы из числа.

102-(80-4)=102-80+4

Что происходит со слагаемыми в скобках, если перед скобками стоит знак «-«? Слагаемые в скобках поменяли свои знаки на противоположные.

Запишем в виде букв

а-(в-с)=а-в+с (Слайд9)

Вывод:

Если перед скобками стоит знак «–»,то при раскрытии скобок знаки слагаемых в скобках изменяются на противоположные.) (Слайд10)

Правило раскрытия скобок (Слайд11)

( ) — знаки слагаемых в скобках не меняются;

+ ( ) — знаки слагаемых в скобках не меняются;

– ( ) — знаки слагаемых в скобках меняются на противоположные.

Первичное закрепление во внешней речи

Цель этапа:

1)зафиксировать изученное учебное содержание во внешней речи

Я несколько раз повторяю правила и дети повторяют (групповая работа)

Вернемся к устным упражнениям .Найдите подтверждающие примеры на каждое правило , раскройте скобки

4. 1. (5+7)-2-1 перед скобками нет знака =5+7-2-1

4. 2. 5+(7-2-1) перед скобками знак + 5+7-2-1

4. 3. 5+7-(2+1) перед скобками знак — 5=7-2-1

4. 4. 5+(7-2)-1 перед скобками знак + 5+7-2-1

Таким образом, правила раскрытия скобок помогут нам решать примеры, упрощать выражения. А для того чтобы вам легче было запомнить правило раскрытия скобок, предлагаю вам вот такое стихотворение: (Слайд12)

Если перед скобкой минус,
Он ведёт себя как вирус.
Скобки сразу все съедает,
Всем, кто в скобках, знак меняет.
Ну, а если плюс стоит,
Он все знаки сохранит!

Афтальмопауза

Закрепление

№282(у)

Далее учащимся предлагается работа в парах: необходимо стрелками соединить выражение, содержащее скобки с соответствующим нему выражением без скобок. ( Приложение 1)Проверка с помощью слайда13

Взаимопроверка Ставим напротив каждой строки + или — У кого правильно 1 задание? Встают

У кого второе, встают и т д.

Самостоятельная работа учащихся

Учащиеся выполняют тестовые задания .(Приложение 2). Выполнение данных заданий проверяется с помощью слайда14 , учащиеся самостоятельно проверяют и оценивают свои работы

Ставим напротив каждой строки + или — У кого правильно 1 задание? Встают

У кого второе, встают и т д.

Подведение итогов урока :выставление оценок, учащиеся отвечают на вопросы:

• Чем занимались на уроке?

• -Что значит раскрыть скобки?

• Повторим еще раз правила раскрытия скобок.(Слайд 15)

• С каким знаком при раскрытии скобок проблем больше? С каким меньше?

• Где нам потребуются правила раскрытия скобок?

-Вернемся к девизу урока.

-Этот урок помог нам привести наш ум в порядок?

Выставление оценок

Посчитаем свои + и – У кого все «+» ставим 5

У кого один и два «–« ставим 4

У кого 3 «-« ставим 3

Домашнее задание:

№284, 285, выучить правила раскрытия скобок

Для сильных учащихся решить уравнение, применив правило раскрытия скобок

Решите уравнение: 6,4 – ( 4,3 — х )= 2,5(Слайд16)

Вынесение общего множителя за скобки

Разложение многочлена на множители — это преобразование многочлена в произведение, равное данному многочлену.

Есть несколько способов разложения многочлена на множители. Один из них – вынесение общего множителя за скобки.

Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево:

ab + ac = a(b + c)

Определение общего множителя для всех членов многочлена производится пошагово:

1. Если у каждого члена есть коэффициент, то находим число, на которое делится коэффициент каждого члена, и выносим его за скобки.
2. Находим переменные, которые встречаются в каждом члене. Переменные выносятся за скобки в наименьшей встречающейся степени.
3. Определяем многочлен, который должен остаться в скобках. Обратите внимание, что многочлен в скобках должен иметь столько же членов, сколько было в исходном многочлене.

Рассмотрим разложение многочлена на множители методом вынесения общего множителя за скобки на примере многочлена:

20a²bc² — 10a³c + 15a²b²c

1. Рассматриваем коэффициенты 20, 10 и 15. Нам нужно найти для них наибольший общий делитель. Для данных чисел он равен 5. Число 5 и будет общим множителем для всех коэффициентов.
2. Буквенный множитель a есть во всех трёх членах. Возьмём его во второй степени (a²), так как это его наименьшая степень, встречающаяся в членах многочлена. По такому же принципу возьмём множитель c.
3. Множитель b встречается только в двух членах из трёх, поэтому его мы в общий множить включить не сможем.

В итоге мы получили следующие общие множители 5, a² и c. Их произведение 5a²c представляет наибольший общий множитель, который будет вынесен за скобки.

5a²c( … )

Теперь надо вычислить многочлен, который должен быть в скобках. Для этого надо разделить каждый член исходного многочлена на общий множитель, который мы нашли:

Следовательно:

20a²bc² — 10a³c + 15a²b²c = 5a²c(4bc — 2a + 3b²)

Обратите внимание, что вынесение общего множителя за скобки – это действие, обратное умножению одночлена на многочлен:

5a²c(4bc — 2a + 3b²) = 20a²bc² — 10a³c + 15a²b²c

Примеры разложения многочлена на множители

Пример 1. Вынесите общий множитель за скобки:

а) a — ab     б) 6xy + 2x

Решение:

а) a — ab = a · 1 — ab = a(1 — b)

б) 6xy + 2x = 6xy + 2x · 1 = 2x(3y + 1)

Пример 2. Сократите дробь:

а)	6x + 6y	б)	8b
	9x		4a — 4b

Решение:

а)	6x + 6y	=	6(x + y)	=	2(x + y)
	9x		9x		3x

б)	8b	=	8b	=	2b
	4a — 4b		4(a — b)		a — b