Что такое Функция в Алгебре?
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у.
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
- х ≠ 0 (потому что на ноль делить нельзя)
И записать это можно так: D (y): х ≠ 0.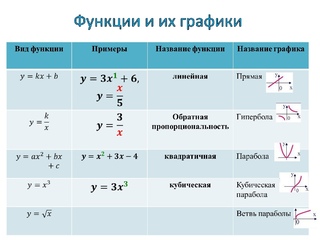
Область значений — множество у, то есть это значения, которые может принимать функция.
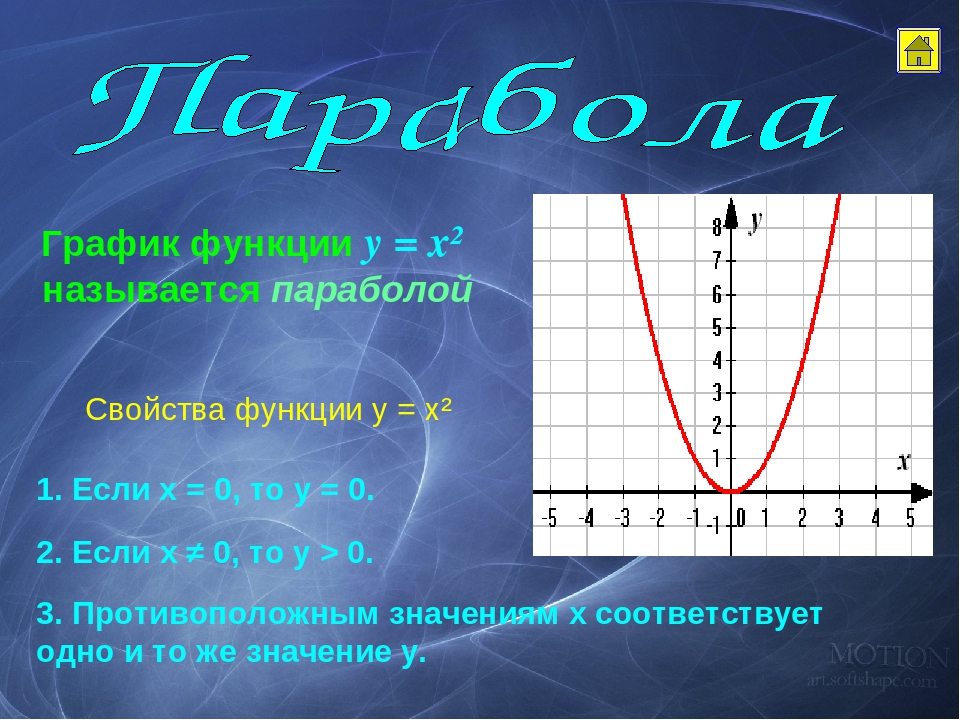
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение
х | -3 | -2 | -1 | 0 | 1 | 2 |
у = 3х +2 | -7 | -4 | -1 | 2 | 5 | 8 |
Рассмотрим другие типы соответствий между множествами.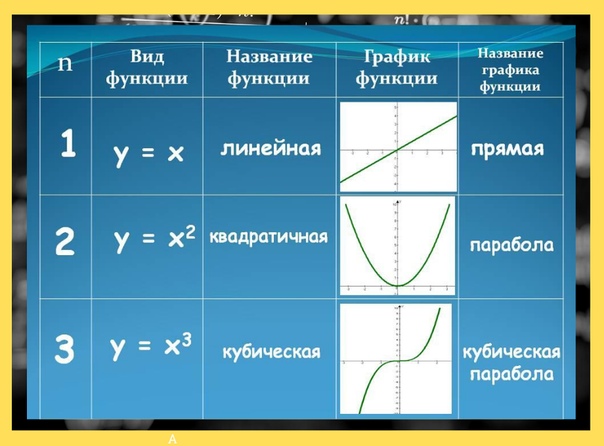
Например, фрукты и цвет каждого:
У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.
Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.
Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:
Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.
Способы задания функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения.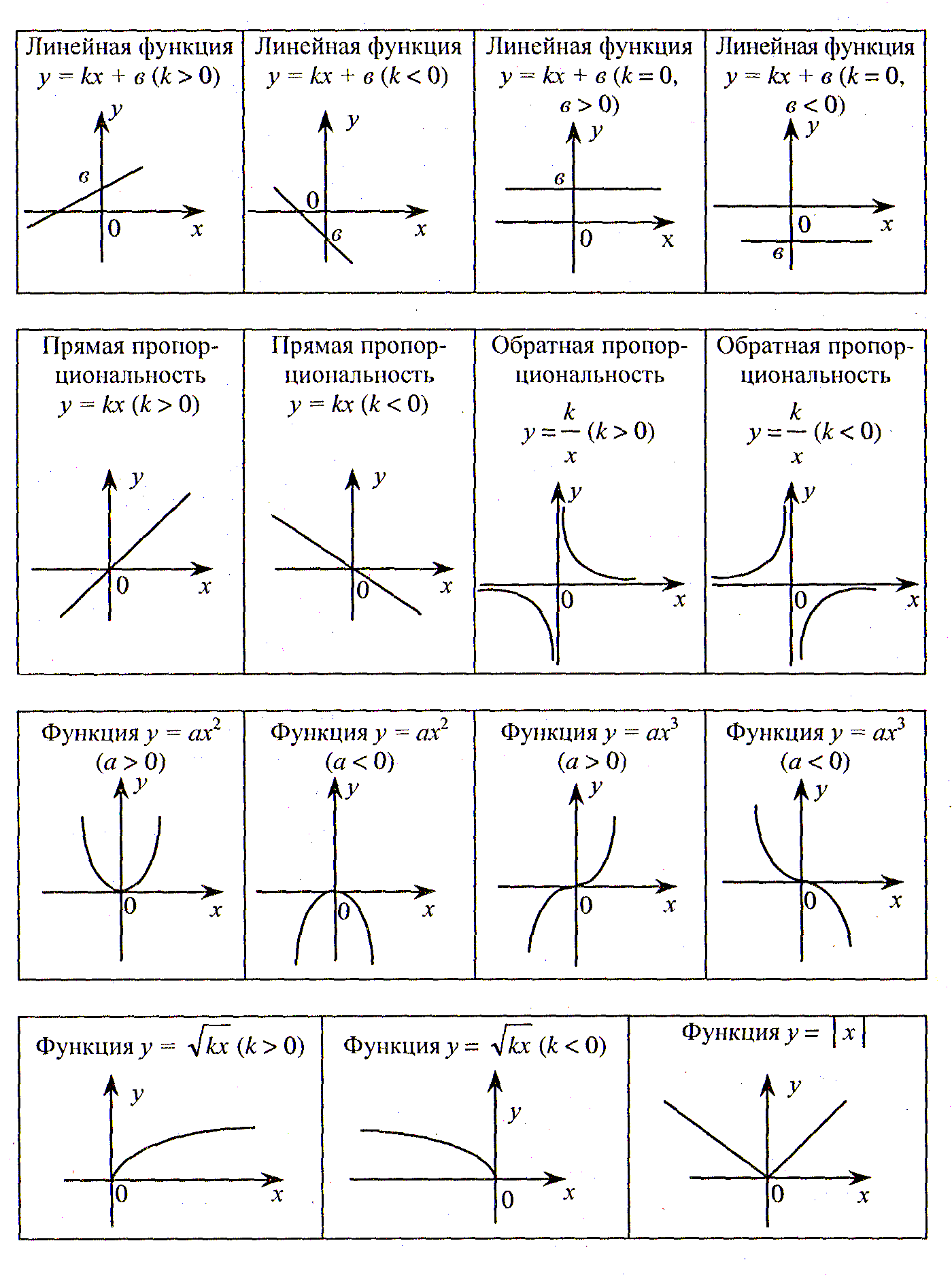 Вот, какими способами ее можно задать:
Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задать функцию формулой
Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».
Пример. Дана функция: y(x) = 32x + 5.
Найти: значения функции «y» при x = 0.
Как рассуждаем:
Подставим в формулу вместо «x» число «0». Запишем расчет.
y(0) = 32 * 0 + 5 = 5
Ответ: y = 5.
Задать функцию таблицей
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».
Пример. Дана функция: y(x) = −x + 4.
Найти: значения «y» при x = -1, x = 0 и x = 1.
Как рассуждаем:
1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.
2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3
Не путаем знаки!
Когда в функцию нужно подставить отрицательное число — включаем внимательность на максимум. Возьмите нужное число в скобки, чтобы точно не потерять знак минус.
3. Запишем полученные результаты в таблицу:
Так мы получили табличный способ задания функции y(x) = −x + 4.
Задать функцию графиком
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».
Пример. Дана функция: y(x) = −2x + 1.
Найти: значения «y» для произвольных «x», а именно −1, 0, 1.
Как рассуждаем:
1. Подставим данные значения х в функцию и запишем результаты:
x | Рассчет |
−1 | y(−1) = −2 * (−1) + 1 = 2 + 1 = 3 |
0 | y(0) = −2 * 0 + 1 = 0 + 1 = 1 |
1 | y(1) = −2 * 1 + 1 = −2 + 1 = −1 |
2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).
Дадим названия каждой точке и запишем их координаты:
Имя точки | x | y |
A | −1 | 3 |
B | 0 | 1 |
C | 1 | −1 |
3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.
Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.
4. Соединим отмеченные точки прямой.
Проведенная прямая будет графиком функции y(x) = −2x + 1.
Понятие функции | Алгебра
Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других.
Определение.
Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.
Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E.
«Поставлено в соответствие» — значит, указан определённый способ (правило), по которому для каждого x∈D находят y∈E. (∈ — знак принадлежности. Запись x∈D читают «икс принадлежит дэ»).
Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д.
Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией.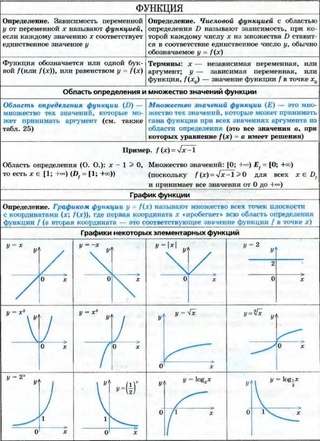
Множество значений D, которые может принимать x, называется областью определения функции.
Множество значений E, которые может принимать y, называется областью значений функции.
Функцию можно задать несколькими способами:
— аналитическим (с помощью формулы),
— графическим,
— табличным,
— описанием с помощью словесной формулировки).
Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. В курсе алгебры изучаются, в основном, числовые функции.
Примеры функций.
1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени .
Например, если автомобиль движется с постоянной скоростью 60 км/ч, зависимость пути от времени можно задать формулой s=60t, где s — пройденный путь (в километрах), t — время (в часах).
2) Периметр квадрата является функцией от его стороны.
Зависимость периметра от стороны квадрата можно задать формулой P=4a, где P — периметр, a — длина стороны.
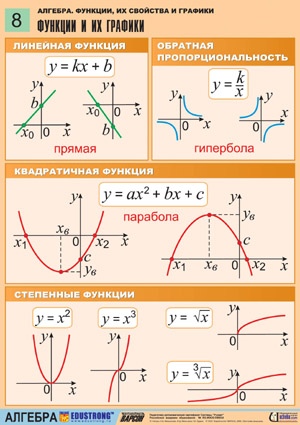
Тест по теме: «Функции и их графики»
Предмет: Алгебра
Класс: 8
Тема: Функции и их графики
Данная работа предложена в двух вариантах, они состоят из заданий базового уровня, а так же более высокого. В тесте дается краткая инструкция к каждой его части.
Время выполнения теста 45 минут.
Критерии оценивания:
Часть А: одно правильное задание оценивается в 1 балл.
Часть В: одно правильное задание оценивается в 2 балла.
Часть С: одно правильное решенное задание оценивается в 3 балла, при наличии развернутого математически грамотного решения на отдельном листе. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
Отметка по пятибалльной системе оценивания | «2» | «3» | «4» | «5» |
Первичный балл | 0-8 | 9-15 | 16-23 | 24-27 |
I вариант
Часть А
Запишите букву, которая обозначает выбранный Вами правильный ответ.
А1. Дана функции . Какая линия является ее графиком?
A) прямая, проходящая через начало координат
Б) прямая, не проходящая через начало координат
В) парабола
Г) гипербола
А2. Дана функция . Какое из нижеперечисленных значений функции является отрицательным числом?
А) f(1)
Б) f(−2)
В) f(2)
Г) f(5)
А3. Ветви какой параболы направлены вниз?
А)
Б)
В)
Г )
А4. График какой функции изображен на рисунке?
А)
Б)
В)
Г)
А5. Вершиной параболы, заданной формулой , является точка с координатами
А) (−1; −3)
Б) (1; −3)
В) (1; 3)
Г) (−1; 3)
Часть В
Запишите букву, которая обозначает выбранный Вами правильный ответ.
В1. Уравнение оси симметрии параболы имеет вид
А)
Б)
В)
Г)
В2. Дана функция . Укажите наименьшее значение данной функции на интервале [−1; 1).
А) −3
Б)
В)
Г) 3
В3. Даны функции:
1) 2) 3) 4) 5) 6) Выберите из них те функции, которые являются возрастающими.
А) 1,2,6
Б) 1,3,5
В) 1,5,6
Г) 1,2,4
В4. На рисунке приведены графики некоторых функций. Из приведенных ниже графиков выберете один, который соотв
Смещение графиков функций. Изменение графиков функций.
Смещение графика \(f(x)=|x|\) по вертикали
График функции \(f(x)=|x|\) и \(-f(x)=-|x|\):
Графики функций \(f(x)=x^3\) и \(f(-x)=(-x^3)\). Графики \(f(x)=\sqrt{x}\) и \(f(-x)=\sqrt{-x}\)
Графики \(f(x)=\sqrt{x}\) и \(f(-x)=\sqrt{-x}\)
Изменение графика параболы по мере увеличения и уменьшения числового коэффициента:
Если мы прибаляем к функции \(f(x)=|x|\) число \(f(x)=|x|+3\) , то график смещается по оси \(0Y\) на \(+3\) еденицы вверх, а если мы вычитаем число \(-4\)
\(f(x)=|x|-4\), то график сместиться вниз на 4 вниз:
То же самое с графиком \(f(x)=\sqrt{x}\):
\(f(-x)-\)отражение относительно \(OY\):
\(-f(x)- \)отражение относительно \(OX\) :
Изменение графиков функций
\(f(x)+c-\) сдвиг \(f(x)\) вверх относительно \(OY\)
\(f(x)-c-\) сдвиг \(f(x)\) вниз относительно \(OY\)
\(f(x+c)-\)сдвиг \(f(x)\) влево относительно \(OX\)
\(f(x-c)-\)сдвин \(f(x)\) вправо относительно \(OX\)
\(f(-x)-\) отражение относительно \(OY\)
\(-f(x)- \)отражение относительно \(OX\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Череповецкий государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-9 классов. Помощь в подготовке к ОГЭ. Задача математики привести ум в порядок, научить человека думать — она средство, а не самоцель. Люблю ее за постоянство, точность и краткость.
На занятиях отрабатываются теоретические знания и практические навыки.
Индивидуальный подход к каждому ученику в зависимости от уровня его подготовки, степени усвоения материала, особенностей мышления, программы обучения в школе. Сочетание традиционных и новых форм обучения.
Помощь в подготовке к ОГЭ. Задача математики привести ум в порядок, научить человека думать — она средство, а не самоцель. Люблю ее за постоянство, точность и краткость.
На занятиях отрабатываются теоретические знания и практические навыки.
Индивидуальный подход к каждому ученику в зависимости от уровня его подготовки, степени усвоения материала, особенностей мышления, программы обучения в школе. Сочетание традиционных и новых форм обучения.
Репетитор по математике
Омский государственный педагогический институт им. А.М.Горького
А.М.Горького
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-9 классов. Подготовка к ОГЭ.
Математика ум приводит в порядок. Развивает логическое мышление. Учит правильно выстраивать алгоритмы решения жизненных ситуаций и проблем. И у меня огромное желание и большой опыт работы в репетиторстве, чтобы помогать ученикам осваивать этот сложный и столь необходимый предмет. Каждый мой ученик — полноценная личность. И для работы с каждым из них я подбираю свои «ключики».
Подготовка к ОГЭ.
Математика ум приводит в порядок. Развивает логическое мышление. Учит правильно выстраивать алгоритмы решения жизненных ситуаций и проблем. И у меня огромное желание и большой опыт работы в репетиторстве, чтобы помогать ученикам осваивать этот сложный и столь необходимый предмет. Каждый мой ученик — полноценная личность. И для работы с каждым из них я подбираю свои «ключики».
Репетитор по математике
Удмуртский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 7-11 классов. Могу понятно и доступно объяснить материал любой сложности как успешным ученикам, так и тем, кто испытывает трудности в обучении. Имею большой опыт репетиторства, подготовки к ЕГЭ, ОГЭ, олимпиадам. Стремлюсь к тому, чтобы не просто научить составлять химические формулы и уравнения, но и формировать интерес к предмету, умение логически мыслить, самостоятельно делать выводы. Использую эффективные формы, методы и средства обучения, новые образовательные технологии.
Могу понятно и доступно объяснить материал любой сложности как успешным ученикам, так и тем, кто испытывает трудности в обучении. Имею большой опыт репетиторства, подготовки к ЕГЭ, ОГЭ, олимпиадам. Стремлюсь к тому, чтобы не просто научить составлять химические формулы и уравнения, но и формировать интерес к предмету, умение логически мыслить, самостоятельно делать выводы. Использую эффективные формы, методы и средства обучения, новые образовательные технологии.
Математика 11 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Что такое функция? Обозначение функций, область функции, диапазон функций
Здесь мы обсудим:- Что такое функция
- Обозначение функции
- область функции
- диапазон функции
Function
Если значение y зависит от другого значения x таким образом, что каждое значение x определяет только одно значение y, мы говорим, что y есть функцией x
y=4x+1 определяет y как функцию x потому что каждое значение x соответствует только одному значению y.
| x | Value of y = 4x + 1 |
| 2 | 9 |
| 1 | 5 |
| 0 | 1 |
| -1/4 | 0 |
| √3 | 4√3 + 1 |
В следующем примере y не есть функцией x, так как каждому значению x соответствует два значения y.
y = ± √x
if x = 4
y = ±√4
y = 2 и y = -2
Если мы используем букву f для обозначения функции, тогда уравнение
y = f(x)
y есть функцией x
Хотя f есть общепринятым символом для обозначения функции, любой символ может быть использован для обозначения функции. Тогда
y = F(x)
y = g(x)
y = h(x)
Пример
φ(x) = 1/(x3 — 1)
Then
φ( 3√7) = 1/(x3 = 1/( 3√7)3 — 1) = 1/(7 — 1) = 1/6
φ(1) = 1/[(1)3 — 1] = 1/0 Undefined
Пример
F(x) = 2x2 — 1
F(d) = 2(d)2 — 1
F(t — 1) = 2(t — 1)2 — 1
= 2(t2 -2t + 1) -1
= 2t2 — 4t + 1
g(c) = c2 — 4c
g(x) = x2 — 4x
Диапазон функции
Для каждого значения, данного независимой переменной из диапазона функции, мы получаем соответствующее значение y.

Множество всех таких значений y называется диапазоном функции
Пример
h(x) = 1/[(x — 1)/(x — 3)]
Область есть
(-∞, 1) ∪ (1, 3) ∪ (3, +∞)
Пример
h(x) = (x2 — 4)/(x — 2) = [(x — 2)(x + 2)]/(x — 2) = (x + 2) x ≠ 2
f(x) = x2
Записывается как:
y = x2
Естественная область
Если функция определена формулой, и явной области не определено, то понятно, что область состоит из всех действительных чисел, для которых формула имеет смысл, а функция имеет реальное значение. Такая область называется естественной областью функции.
Пример
y = (x + 1)/(x — 1) — Естественная область функции — все действительные числа кроме 1
Решите для y
x = (y + 1)/(y — 1) — Диапазон функции — все действительные числа кроме 1
Определение функций с разрывом
Математика — Алгебра Логики
Рассмотрим классы логических функций. Данная классификация не
является бессмысленным украшением, а необходима для теоремы Поста,
которая будет рассмотрена в следующей главе.
Данная классификация не
является бессмысленным украшением, а необходима для теоремы Поста,
которая будет рассмотрена в следующей главе.
Классы логических функций
Функция, «сохраняющая 0».
Это — такая логическая функция, значение которой равно 0, если все аргументы равны 0: f(0,0,…,0) = 0.
Примером функции, сохраняющей 0, является функция .
Функция, «сохраняющая 1».
Это — такая логическая функция, значение которой равно 1, если все аргументы равны 1: f(1,1,…,1) = 1.
Примером функции, сохраняющей 1, является функция &.
«Монотонная» функция.
Это — такая логическая функция, которую можно выразить через & и .
Монотонную функцию можно распознать по ее таблице истинности. Для этого нужно взять все пары строк в таблице, которые отличаются всего в одном столбце (не считая крайнего правого).
 Например: 0,0,0,0 и 0,0,0,1; 1,0,0,1 и 1,1,0,1.
Пусть в одной строке в некотором столбце стоит «0», а в
другой строке в этом же столбце стоит «1». Нельзя, чтобы
в крайнем правом столбце, где записано значение функции
было наоборот: «1», а потом «0». Если такая ситуация нигде
не встречается, то функция монотонная, и ее можно выразить
через и &. Пример монотонной функции: .
Например: 0,0,0,0 и 0,0,0,1; 1,0,0,1 и 1,1,0,1.
Пусть в одной строке в некотором столбце стоит «0», а в
другой строке в этом же столбце стоит «1». Нельзя, чтобы
в крайнем правом столбце, где записано значение функции
было наоборот: «1», а потом «0». Если такая ситуация нигде
не встречается, то функция монотонная, и ее можно выразить
через и &. Пример монотонной функции: .«Линейная» функция.
Это — такая логическая функция, которую можно выразить через , 0 и 1.
Чтобы узнать, линейна ли функция, надо выразить ее через полином Жегалкина и посмотреть, не встречается ли там операция &. Если нет, то функция линейна. Для функций от 1 и 2 переменных мы уже приводили формулы, выражающие их через &, и константы.
Двойственные функции.
Логические функции f и g называются двойственными, если
f(~x1, ~x2,. ..,~xN) = ~g(x1, x2,…, xN).
..,~xN) = ~g(x1, x2,…, xN).
Кратко это будем обозначать так: «f» * «g». Двойственные функции легко обнаружить с помощью простого приема. Надо заменить в таблице истинности все «0» на «1», а все «1» на «0». Полученная таблица истинности и будет таблицей двойственной функции. Ниже приведен список двойственных функций для всех унарных и бинарных операций.
«0» * «1»
«x» * «x»
«~» * «~»
«&» * «»
«» * «»
«|» * «»
«»
«>» * «»
«Самодвойственная» функция.
Это — логическая функция, которая двойственна самой себе:
f(~x1, ~x2,…,~xN) = ~f(x1, x2,…, xN).
Алгебраическая функция: определение и примеры — видео и стенограмма урока
Таблицы
Одним из способов идентификации алгебраической функции является использование таблицы, которая может показать нам, есть ли одна область и один диапазон. Иногда функции добавляются к домену, чтобы получить диапазон, например x + 2. Иногда функции умножают домен, чтобы получить диапазон, например 3 x .Функции также могут вычитать или делить домен или использовать комбинацию операций для получения диапазона. Пока действует правило «один вход/один выход», функция существует.
Иногда функции добавляются к домену, чтобы получить диапазон, например x + 2. Иногда функции умножают домен, чтобы получить диапазон, например 3 x .Функции также могут вычитать или делить домен или использовать комбинацию операций для получения диапазона. Пока действует правило «один вход/один выход», функция существует.
Если алгебраическая функция говорит добавить два к домену, мы можем создать таблицу, чтобы показать функцию:
Как видите, для каждого домена у нас есть один диапазон. Эти пары x значений и y значений называются упорядоченными парами , потому что мы расположили их по порядку ( x,y ).
Мы также можем превратить нашу таблицу в упорядоченные пары, чтобы показать функцию: (1,3), (4,6), (-2,0) и (-3,-1), где есть один x — значение для каждого y -значение.
Графики
Мы также можем использовать графики для определения функций, нанося упорядоченные пары на Декартову систему координат , где значения x находятся на горизонтальной линии, а значения y — на вертикальной линии. Там, где встречаются упорядоченные пары, и отображается точка.Если мы нанесем точки, то получим прямую линию, поэтому функция x + 2 считается линейной функцией и может быть записана в функциональной записи как f(x) = x + 2. f(x) — это просто другой способ записи y , который мы называем f-функцией . Это способ для нас идентифицировать различные функции вместо того, чтобы называть их все y = …
Там, где встречаются упорядоченные пары, и отображается точка.Если мы нанесем точки, то получим прямую линию, поэтому функция x + 2 считается линейной функцией и может быть записана в функциональной записи как f(x) = x + 2. f(x) — это просто другой способ записи y , который мы называем f-функцией . Это способ для нас идентифицировать различные функции вместо того, чтобы называть их все y = …
Тест вертикальной линии
Мы знаем, что график является функцией, если он может пройти тест вертикальной линии .В этом тесте, если мы поместим вертикальную линию в любом месте графика, она пересекутся только в одном месте. Если вертикальная линия пересекается в двух местах на графике, это противоречит правилу «один вход — один выход». Значит, это не функция.
Вот пример графика, который не является функцией.
Примеры функций
Как мы уже говорили в начале урока, существует много типов функций, таких как квадратичная функция и кубическая функция.2 — 3. Сначала создадим таблицу.
Домен может быть любым действительным числом, поэтому значение x или домен называется независимой переменной . Здесь мы будем использовать -2, -1, 0, 1 и 2 для домена.
Диапазон или y -значение называется зависимой переменной , поскольку он зависит от того, что мы используем для x -члена.
Записав числа в нашей таблице упорядоченными парами, мы имеем: (-2,1), (-1, -2), (0, -3), (1, -2), (2, 1 ).Вы заметили, как мы повторили некоторые значения диапазона? Это приемлемо? ДА, потому что каждая упорядоченная пара имеет одно значение x и одно значение y . 2.3 + x — 2 и используйте следующие значения для домена: -2, -1, 0, 1 и 2.
2.3 + x — 2 и используйте следующие значения для домена: -2, -1, 0, 1 и 2.
Записав эти значения в виде упорядоченных пар, мы получим: (-2, -12), (-1, -4), (0, -2), (1, 0), (2, 8).
На графике наши упорядоченные пары будут выглядеть так.
После применения теста вертикальной линии мы видим, что это действительно функция!
Резюме урока
Алгебраическая функция — это уравнение, которое позволяет ввести домен или x -значение и выполнить математические вычисления для получения результата, который является диапазоном , или , или y -значение, специфичное для данного конкретного значения x .
Между доменом и диапазоном существует отношение «один вход/один выход».
Есть несколько способов показать функцию:
- Используйте таблицу для расчета значений диапазона из случайно выбранных значений домена.
 Домен является независимой переменной. Диапазон является зависимой переменной.
Домен является независимой переменной. Диапазон является зависимой переменной. - Перечислите домен и диапазон в виде упорядоченных пар ( x , y ).
- Показать функцию в виде графика. Если вертикальная линия может проходить через любую часть графика и касаться только одной точки, то график является функцией.Если вертикальная линия пересекает две точки, то график не является функцией.
Определение функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне).Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-4: Определение функции
Теперь нам нужно перейти ко второй теме этой главы.Однако, прежде чем мы это сделаем, нам нужно позаботиться о быстром определении.
Определение отношения
Отношение представляет собой набор упорядоченных пар.
Это кажется странным определением, но оно понадобится нам для определения функции (что является основной темой этого раздела). Однако, прежде чем мы на самом деле дадим определение функции, давайте посмотрим, сможем ли мы понять, что такое отношение.
Вспомните пример 1 в разделе «Графика» этой главы.2}-4\). Вот упорядоченные пары, которые мы использовали.
\[\left( { — 2,5} \right)\,\,\,\,\left( { — 1,0} \right)\,\,\,\,\left( {0, — 3 } \right)\,\,\,\,\left( {1, — 4} \right)\,\,\,\,\left( {2, — 3} \right)\,\,\, \,\влево( {3,0} \вправо)\,\,\,\,\влево( {4,5} \вправо)\] Любое из следующего является отношениями, поскольку они состоят из набора упорядоченных пар.
Конечно, есть еще много отношений, которые мы могли бы сформировать из списка упорядоченных пар выше, но мы просто хотели перечислить несколько возможных отношений, чтобы привести несколько примеров.Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим.
Теперь, в этот момент вы, вероятно, спрашиваете, почему мы заботимся об отношениях, и это хороший вопрос. Некоторые отношения очень специфичны и используются почти на всех уровнях математики. Следующее определение говорит нам, какие именно отношения являются этими особыми отношениями.
Определение функции
Функция представляет собой отношение, для которого каждое значение из набора первых компонентов упорядоченной пары связано ровно с одним значением из набора вторых компонентов упорядоченной пары.
Ладно, это полный рот. Давайте посмотрим, сможем ли мы понять, что это значит. Давайте посмотрим на следующий пример, который, надеюсь, поможет нам во всем этом разобраться.
Пример 1 Следующее отношение является функцией. \[\left\{ {\left( { — 1,0} \right)\,\,\,\,\left( {0, — 3} \right)\,\,\,\,\left( {2, — 3} \right)\,\,\,\,\left( {3,0} \right)\,\,\,\,\left( {4,5} \right)} \right \}\] Показать решение Из этих упорядоченных пар мы имеем следующие наборы первых компонентов ( i. Для набора вторых компонентов обратите внимание, что «-3» встречается в двух упорядоченных парах, но мы указали его только один раз. Чтобы понять, почему это отношение является функцией, просто выберите любое значение из набора первых компонентов. Теперь вернитесь к отношению и найдите все упорядоченные пары, в которых это число является первым компонентом, и перечислите все вторые компоненты из этих упорядоченных пар.Список вторых компонентов будет состоять ровно из одного значения. Например, выберем 2 из набора первых компонентов. Из соотношения видно, что существует ровно одна упорядоченная пара с 2 в качестве первого компонента, \(\left( {2, — 3} \right)\). Следовательно, список вторых компонентов (, т. е. список значений из набора вторых компонентов), связанный с 2, представляет собой ровно одно число, -3. Обратите внимание, что нас не волнует, что -3 является вторым компонентом второй упорядоченной номинальной стоимости в отношении. Мы рассмотрели одно значение из набора первых компонентов для нашего быстрого примера, но результат будет таким же для всех других вариантов. Независимо от выбора первых компонентов, с ним будет связан ровно один второй компонент. Следовательно, это отношение является функцией. Чтобы действительно понять, что говорит нам определение функции, нам, вероятно, следует также проверить пример отношения, которое не является функцией. Не беспокойтесь о том, откуда взялась эта связь. Это всего лишь один, который мы составили для этого примера. Из набора первых компонентов выберем 6. Теперь, если мы подойдем к отношению, мы увидим, что есть две упорядоченные пары с 6 в качестве первого компонента: \(\left( {6,10} \right)\ ) и \(\left( {6, — 4} \right)\). Тогда список вторых компонентов, связанных с числом 6, будет следующим: 10, -4. Список вторых компонентов, связанных с 6, имеет два значения, поэтому это отношение не является функцией. Обратите внимание на тот факт, что если бы мы выбрали -7 или 0 из набора первых компонентов, то в списке вторых компонентов, связанных с каждым, будет только одно число. Это не имеет значения. Тот факт, что мы нашли хотя бы одно значение в наборе первых компонент с более чем одним вторым компонентом, связанным с ним, достаточен, чтобы сказать, что это отношение не является функцией. В качестве заключительного комментария к этому примеру отметим, что если бы мы удалили первую и/или четвертую упорядоченную пару из отношения, у нас была бы функция! Надеюсь, у вас есть хотя бы представление о том, что говорит нам определение функции. Теперь, когда мы заставили вас пройтись по фактическому определению функции, давайте дадим еще одно «рабочее» определение функции, которое будет гораздо полезнее для того, что мы здесь делаем. Фактическое определение работает с отношением. Однако, как мы видели, с четырьмя отношениями, которые мы дали до определения функции, и соотношением, которое мы использовали в примере 1, мы часто получаем отношения из некоторого уравнения. Важно отметить, что не все отношения вытекают из уравнений! Отношение из второго примера, например, было просто набором упорядоченных пар, которые мы записали для примера, а не из какого-либо уравнения. Тем не менее, все функции, которые мы будем использовать в этом курсе, основаны на уравнениях. Поэтому запишем определение функции, признающее этот факт. Прежде чем мы дадим «рабочее» определение функции, мы должны отметить, что это НЕ фактическое определение функции, данное выше. Это просто хорошее «рабочее определение» функции, которое связывает вещи с типами функций, с которыми мы будем работать в этом курсе. Функция — это уравнение, для которого любой \(x\), который можно подставить в уравнение, даст ровно один \(y\) из уравнения. Вот оно. Это определение функций, которое мы собираемся использовать, и, вероятно, будет легче расшифровать, что оно означает. Прежде чем мы рассмотрим это, еще немного отметим, что мы использовали фразу «\(x\), которую можно подключить» в определении. Далее, когда мы имеем дело с функциями, мы всегда будем предполагать, что и \(x\), и \(y\) будут действительными числами.Другими словами, мы ненадолго забудем, что знаем что-то о комплексных числах, пока занимаемся этим разделом. Хорошо, с этим покончено, давайте вернемся к определению функции и рассмотрим несколько примеров уравнений, являющихся функциями, и уравнений, не являющихся функциями. «Рабочее» определение функции гласит, что если мы возьмем все возможные значения \(x\), подставим их в уравнение и найдем \(y\), мы получим ровно одно значение для каждого значения \( Икс\).На этом этапе игры может быть довольно сложно показать, что уравнение является функцией, поэтому мы в основном будем обсуждать его. С другой стороны, часто довольно легко показать, что уравнение не является функцией. Итак, нам нужно показать, что независимо от того, какой \(x\) мы подставляем в уравнение и решим для \(y\), мы получим только одно значение \(y\). Также обратите внимание, что значение \(y\), вероятно, будет различным для каждого значения \(x\), хотя это и не обязательно. Давайте начнем с подстановки некоторых значений \(x\) и посмотрим, что произойдет. Итак, для каждого из этих значений \(x\) мы получили одно значение \(y\) из уравнения.Этого недостаточно, чтобы утверждать, что это функция. Чтобы официально доказать, что это функция, нам нужно показать, что она будет работать независимо от того, какое значение \(x\) мы подставим в уравнение. Конечно, мы не можем подставить все возможные значения \(x\) в уравнение. Это просто физически невозможно. Однако давайте вернемся и посмотрим на те, которые мы подключили. Для каждого \(x\) при подключении мы сначала умножили \(x\) на 5, а затем добавили к нему 1.2} + 1 = 9 + 1 = 10\end{выравнивание*}\] Теперь давайте немного подумаем о том, что мы делали с оценками. Во-первых, мы возвели в квадрат значение \(x\), которое мы подставили. Похоже, это уравнение тоже является функцией. Обратите внимание, что можно получить одно и то же значение \(y\) для разных \(x\).2} & = 10 + 1 = 11\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}y = \pm \sqrt {11} \end{align*}\] Теперь помните, что мы вычисляем \(y\), так что это означает, что в первом и последнем случаях мы фактически получим два разных значения \(y\) из \(x\), так что это уравнение НЕ является функцией. Обратите внимание, что у нас могут быть значения \(x\), которые дадут один \(y\), как мы видели выше, но это не имеет значения. Если хотя бы одно значение \(x\) дает более одного значения \(y\) при решении уравнения, оно не будет функцией.2} = 4\) Показать решение В этом случае мы воспользуемся уроком, полученным в предыдущей части, и посмотрим, сможем ли мы найти значение \(x\), которое даст более одного значения \(y\) при решении. Итак, это уравнение не является функцией. Напомним, что из предыдущего раздела это уравнение окружности. Круги никогда не являются функциями. Надеемся, что эти примеры помогли вам лучше понять, что такое функция на самом деле. Теперь нам нужно перейти к так называемой нотации функций . Обозначения функций будут активно использоваться в большинстве оставшихся глав этого курса, поэтому важно понимать их.2} — 5х + 3\] Буква, которую мы используем, не имеет значения. Что важно, так это часть «\(\left( x \right)\)». Буква в скобках должна соответствовать переменной, используемой справа от знака равенства. Очень важно отметить, что \(f\left( x \right)\) на самом деле не что иное, как действительно причудливый способ записи \(y\). Если вы помните об этом, вы можете обнаружить, что работа с обозначениями функций становится немного проще. Кроме того, это , а НЕ умножение \(f\) на \(x\)! Это одна из наиболее распространенных ошибок, которую люди совершают, когда впервые имеют дело с функциями.2} — 5х + 3\] и спросите, каково его значение для \(x = 4\). В терминах обозначения функций мы будем «спрашивать» об этом, используя обозначение \(f\left( 4 \right)\). Таким образом, когда в скобках есть что-то отличное от переменной, мы действительно спрашиваем, каково значение функции для этой конкретной величины. Теперь, когда мы говорим значение функции, мы на самом деле спрашиваем, каково значение уравнения для этого конкретного значения \(x\). Вот \(f\left( 4 \right)\).2} — 5} \справа)\) Показать все решения Скрыть все решения
a \(f\left( 3 \right)\) и \(g\left( 3 \right)\) Показать решение Хорошо, у нас есть две оценки функций, и у нас также есть две функции, поэтому нам нужно решить, какую функцию использовать для оценок. Убедитесь, что вы правильно обращаетесь с отрицательными знаками. Теперь второй. Теперь мы достигли разницы. Вспомните, когда мы впервые начали говорить об определении функций, мы заявили, что будем иметь дело только с действительными числами. Другими словами, мы подставляем только действительные числа и хотим, чтобы в качестве ответов возвращались только действительные числа.2} — 2\влево( 0 \вправо) + 8 = 8\] Опять же, не забывайте, что это не умножение! По какой-то причине ученикам нравится думать об этом как об умножении и получать нулевой ответ. Будь осторожен. Остальные оценки теперь будут немного другими. Обратите внимание, что в данном случае это почти то же самое, что и наша исходная функция, за исключением того, что на этот раз мы используем \(t\) в качестве переменной. Теперь давайте немного усложним, или, по крайней мере, они кажутся более сложными. Однако все не так плохо, как может показаться. Сначала мы оценим \(f\left({t + 1} \right)\). Работает точно так же, как и предыдущая часть.2} + 1} \end{выравнивание*}\] Оценка функции — это то, чем мы будем много заниматься в следующих разделах и главах, поэтому убедитесь, что вы можете это сделать. Вы обнаружите, что некоторые последующие разделы очень трудны для понимания и/или выполнения работы, если вы плохо понимаете, как работает вычисление функций. Раз уж мы заговорили о вычислении функций, теперь следует поговорить о кусочных функциях . На самом деле мы уже видели пример кусочной функции, даже если мы не называли ее функцией (или кусочной функцией) в то время.Вспомним математическое определение абсолютной величины. Это функция, и если мы используем обозначение функции, мы можем записать ее следующим образом: Это также пример кусочной функции. Кусочная функция — это не что иное, как функция, которая разбита на части, и какую часть вы используете, зависит от значения \(x\).2} + 4}&{{\mbox{if}}t \le — 4}\\{10}&{{\mbox{if}} — 4 15}\end{массив}} \right.\] оцените каждое из следующих действий. Прежде чем приступать к вычислениям, давайте заметим, что мы используем другие буквы для функции и переменной, чем те, которые мы использовали до этого момента. Теперь, чтобы выполнить каждую из этих оценок, первое, что нам нужно сделать, это определить, какому неравенству удовлетворяет число, а оно будет удовлетворять только одному неравенству. Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52\] В этом случае число 1 удовлетворяет среднему неравенству, поэтому мы будем использовать среднее уравнение для оценки. Эта оценка часто вызывает проблемы у студентов, несмотря на то, что на самом деле это одна из самых простых оценок, которые мы когда-либо делали. Мы знаем, что мы оцениваем функции/уравнения, подставляя число для переменной. В этом случае переменных нет. Это не проблема. Поскольку никаких переменных нет, это просто означает, что мы на самом деле ничего не подключаем, и мы получаем следующее: Опять же, как и во второй части, с этой нужно быть немного осторожнее. Не радуйтесь тому факту, что две предыдущие оценки были одинаковыми. Это будет происходить при случае. Для окончательной оценки в этом примере число удовлетворяет нижнему неравенству, поэтому мы будем использовать нижнее уравнение для оценки. Кусочные функции не так часто возникают на уроках алгебры, однако они возникают в нескольких местах на более поздних занятиях, поэтому вам важно понимать их, если вы собираетесь перейти к другим математическим занятиям. В качестве последней темы нам нужно вернуться и коснуться того факта, что мы не всегда можем подставлять каждый \(x\) в каждую функцию. Во-первых, нам нужно убрать пару определений. домен уравнения — это набор всех \(x\), которые мы можем подставить в уравнение и получить действительное число для \(y\). Диапазон уравнения — это набор всех \(y\), которые мы когда-либо можем получить из уравнения. Обратите внимание, что мы действительно хотели использовать уравнение в приведенных выше определениях вместо функций.Это действительно определения для уравнений. Однако, поскольку функции также являются уравнениями, мы можем использовать определения и для функций. Определение диапазона уравнения/функции может быть довольно сложным для многих функций, поэтому мы не будем вдаваться в подробности. Нас гораздо больше интересует здесь определение областей определения функций. Итак, мы получим деление на ноль, если подставим \(x = — 5\) или \(x = 2\). Это означает, что нам нужно избегать этих двух чисел. Однако все остальные значения \(x\) будут работать, так как они не дают деления на ноль. Тогда домен В этом случае у нас не будет проблем с делением на ноль, так как у нас нет дробей.У нас есть квадратный корень в задаче, поэтому нам нужно побеспокоиться о том, чтобы извлечь квадратный корень из отрицательных чисел. Эта часть будет работать немного иначе, чем предыдущая. В этой части мы определили значения \(x\), которых следует избегать. В этом случае так же просто будет напрямую получить домен. Чтобы избежать квадратных корней из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы Это довольно простое линейное неравенство, которое мы должны решить на данный момент.2} + 4}}\) Показать решение В этом случае у нас есть дробь, но обратите внимание, что знаменатель никогда не будет равен нулю для любого действительного числа, так как x 2 гарантированно будет положительным или равным нулю, и добавление 4 к этому будет означать, что знаменатель всегда не менее 4. Другими словами, знаменатель никогда не будет равен нулю. Итак, все, что нам нужно сделать, это побеспокоиться о квадратном корне в числителе. Для этого нам потребуется, Теперь мы можем подставить любое значение \(x\) в знаменатель, однако, поскольку у нас есть квадратный корень в числителе, мы должны убедиться, что все \(x\) удовлетворяют неравенство выше, чтобы избежать проблем. В этой заключительной части нам нужно побеспокоиться и о квадратном корне, и о делении на ноль. Давайте сначала позаботимся о квадратном корне, так как это, вероятно, наложит наибольшее ограничение на значения \(x\). Таким образом, чтобы получить квадратный корень (, т. е. без квадратного корня из отрицательных чисел), нам потребуется это, Так что, по крайней мере, нам нужно потребовать \(x \ge \frac{1}{2}\), чтобы избежать проблем с квадратным корнем.2} — 16 = \left( {x — 4} \right)\left( {x + 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in} x = — 4,\, \,х = 4\] Теперь обратите внимание, что \(x = — 4\) не удовлетворяет неравенству, которое нам нужно для квадратного корня, и поэтому значение \(x\) уже исключено квадратным корнем. С другой стороны, \(x = 4\) удовлетворяет неравенству. Тогда домен для этой функции В этом разделе вы: Реактивный лайнер меняет высоту по мере увеличения расстояния от начальной точки полета. Вес растущего ребенка со временем увеличивается. В каждом случае одна величина зависит от другой. Между двумя величинами существует взаимосвязь, которую мы можем описать, проанализировать и использовать для прогнозирования. Отношение представляет собой набор упорядоченных пар. Набор, состоящий из первых компонентов каждой упорядоченной пары, называется доменом , а набор, состоящий из вторых компонентов каждой упорядоченной пары, называется диапазоном . Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого. Домен: Диапазон Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто помечается строчной буквой Каждое значение в диапазоне также известно как выходное значение или зависимая переменная, и часто обозначается строчной буквой Функция — это отношение, которое присваивает один элемент диапазона каждому элементу домена . Теперь рассмотрим множество упорядоченных пар, связывающих термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как Обратите внимание, что каждый элемент в домене равен , а не в паре ровно с одним элементом в диапазоне. Например, термин «нечетный» соответствует трем значениям из домена, а термин «четный» соответствует двум значениям из диапазона. диапазон, Это нарушает определение функции, поэтому это отношение не является функцией. (рисунок) сравнивает отношения, которые являются функциями, а не функциями. Функция Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Входные значения составляют домен, а выходные значения составляют диапазон. Учитывая связь между двумя величинами, определите, является ли связь функцией. Определение того, являются ли прайс-листы меню функциями Меню кофейни, показанное на (Рисунок), состоит из позиций и их цен. Каждый пункт в меню имеет только одну цену, поэтому цена зависит от пункта. Таким образом, пункт не зависит от цены. Определение того, являются ли правила оценки класса функциями В конкретном математическом классе общая оценка в процентах соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? (Рисунок) показывает возможное правило для присвоения оценок. Для любого процента полученной оценки существует соответствующий средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл. В данной системе оценивания имеется диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, студенты, которые получают средний балл 3.0 может иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла. (Рисунок) 1 перечисляет пять величайших бейсболистов всех времен в порядке их ранга. а. Обычный способ представления функций — в виде таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях в таблице представлены несколько избранных примеров из более полных взаимосвязей. (рисунок) перечисляет входное число каждого месяца (январь = 1, февраль = 2 и т. д.) и выходное значение количества дней в этом месяце. Эта информация представляет собой все, что мы знаем о месяцах и днях для данного года (это не високосный год). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце, в которой месяцы идентифицируются целым числом, а не именем. (рисунок) определяет функцию Помните, это обозначение говорит нам, что это имя функции, которая принимает входные данные и дает выходные данные (Рисунок) отображает возраст детей в годах и их соответствующий рост.В этой таблице представлены лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет собой функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма Имея таблицу входных и выходных значений, определите, представляет ли таблица функцию. Идентификация таблиц, представляющих функции Какая таблица (рисунок), (рисунок) или (рисунок) представляет функцию (если есть)? (рисунок) и (рисунок) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. (Рисунок) не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям. Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции. Функция, представленная (Рисунок), может быть представлена записью Аналогично, операторы представляют функцию на (рис.). (рисунок) нельзя выразить подобным образом, потому что он не представляет функцию. Представляет ли (Рисунок) функцию? Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут дать одно и то же выходное значение. Когда у нас есть функция в форме формулы, обычно несложно вычислить функцию.Например, функцию можно вычислить, возведя входное значение в квадрат, умножив его на 3 и затем вычтя произведение из 5. Дана формула функции, вычислить. Учитывая функцию оценки Решающие функции Учитывая функцию решить для Как мы видели выше, мы можем представлять функции в виде таблиц. Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. (Рисунок). Иногда вычисление функции в виде таблицы может оказаться более полезным, чем использование уравнений. Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения. Оценка и решение табличной функции Использование (рисунок), Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как показано на (рис.). Эта система оценивания представляет собой функцию «один к одному», поскольку каждая введенная буква дает один конкретный средний балл успеваемости, а каждая средняя оценка соответствует одной введенной букве. Чтобы наглядно представить эту концепцию, давайте еще раз взглянем на две простые функции, показанные на (Рисунок) (a) и (Рисунок) (b) . Функция в части (а) показывает взаимосвязь, которая не является взаимно однозначной функцией, поскольку входные данные и оба дают выходные данные Функция в части (б) демонстрирует взаимосвязь, которая является взаимно однозначной функцией, поскольку каждый вход связан с одним вывод. Функция «один к одному» Функция «один к одному» — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.Нет повторяющихся значений x или y . Определение того, является ли отношение взаимно-однозначной функцией Является ли площадь круга функцией его радиуса? Если да, то функция один к одному? а. Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают большое количество пар вход-выход на небольшом пространстве. Наиболее распространенные графики называют входное значение и выходное значение, и мы говорим, что это функция или, когда функция названа График функции представляет собой набор всех точек на плоскости, которые удовлетворяют уравнению. Если функция определена только для нескольких входных значений, то график функции состоит всего из нескольких точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике (рисунок) говорят нам о том, что множество точек, удовлетворяющих условию, представляет собой кривую. Показанная кривая включает и потому, что кривая проходит через эти точки. Проверка вертикальной линии может использоваться для определения того, представляет ли график функцию. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию. Применение теста вертикальной линии Какой из графиков на (рисунке) представляет(ют) функцию Если любая вертикальная линия пересекает график более одного раза, отношение, представленное графиком, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку из двух графиков, показанных в частях (a) и (b) (Рисунок). Представляет ли график на (рисунке) функцию? После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — использовать тест горизонтальной линии.Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия. Применение теста горизонтальной линии Рассмотрим функции, показанные на (Рисунок) (a) и (Рисунок) (b) . Является ли какая-либо из функций взаимно однозначной? Функция на (Рисунок) (a) не является однозначной. Горизонтальная линия, показанная на (Рисунок), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках). Функция на (рис.) (b) является взаимно однозначной.Любая горизонтальная линия пересекает диагональную линию не более одного раза. Соответствует ли график, показанный на (Рисунок), один к одному? Нет, потому что он не проходит тест горизонтальной линии. В этом тексте мы будем изучать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними задач. Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге.Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной на (рис.). В чем разница между отношением и функцией? Отношение представляет собой набор упорядоченных пар. Функция — это особый вид отношения, в котором никакие две упорядоченные пары не имеют одинаковых первых координат. В чем разница между вводом и выводом функции? Почему тест вертикальной линии говорит нам, представляет ли график отношения функцию? Когда вертикальная линия пересекает график отношения более одного раза, это указывает на то, что для данного входа существует более одного выхода. Как определить, является ли отношение однозначной функцией? Почему тест горизонтальной линии говорит нам, является ли график функции взаимно однозначным? Когда горизонтальная линия пересекает график функции более одного раза, это означает, что для данного выхода имеется более одного входа. Функция является однозначной, если каждый выход соответствует только одному входу. Для следующих упражнений используйте графическое изображение в данном смотровом окне. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график. Для следующих упражнений используйте графическое изображение в данном смотровом окне. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график. Для следующих упражнений используйте графическое изображение в данном смотровом окне. Для следующих упражнений постройте график в заданном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график. Упорядоченная пара представляет собой набор входных и выходных данных и представляет отношение между двумя значениями. Некоторые отношения имеют смысл, а другие нет. Функции — это отношения, которые имеют смысл. Все функции являются отношениями , но не все отношения являются функциями. Функция — это отношение, согласно которому для каждого входа имеется только один выход. Вот отображения функций.Домен — это вход или x-значение , а диапазон — это выход или y-значение . Каждое значение x связано только с одним значением y. Хотя входы, равные -1 и 1, имеют одинаковый выход, это отношение по-прежнему является функцией, поскольку каждый вход имеет только один выход. Это сопоставление не является функцией. Вход для -2 имеет более одного выхода. Использование входных и выходных данных, перечисленных в таблицах, картах и списках, позволяет легко наносить точки на координатную сетку .Используя график точек данных, вы можете определить, является ли отношение функцией, используя тест вертикальной линии . Если вы можете провести вертикальную линию через график и коснуться только одной точки, отношение является функцией. Посмотрите на график этой карты отношений. Если бы вы провели вертикальную линию через каждую из точек на графике, каждая линия соприкасалась бы только в одной точке, поэтому это отношение является функцией. Специальные функции и их уравнения имеют узнаваемые характеристики. $f(x) = c$ Значение c может быть любым числом, поэтому график постоянной функции представляет собой горизонтальную линию. $f(x) = x$ Для функции идентификации значение x совпадает со значением y. График представляет собой диагональную линию, проходящую через начало координат. $f(x) = mx + b$ Уравнение, записанное в форме наклон-отрезок , является уравнением линейной функции , а график функции представляет собой прямую линию. Вот график $f(x)= 3x +4$ $f(x) = |x|$ Функцию абсолютного значения легко узнать по V-образному графику. График состоит из двух частей и является одной из кусочных функций. Это всего лишь пример наиболее распространенных специальных функций. Обратная функция меняет местами входы и выходы.{-1}(x) =\frac{x + 4}{3}$. Не всякая обратная функция является функцией, поэтому для проверки используйте тест вертикальной линии. Вы можете складывать, вычитать, умножать и делить функции . Посмотрите на два примера операций функции: Чему равна сумма этих двух функций? Просто добавьте выражения.{2} + 11х + 28
\end{выравнивание}$ Вы играли с » y =» уравнениями в течение некоторого времени. И вы видели, что «хорошие» уравнения (скажем, прямые линии, а не эллипсы) — это те, которые вы можете решить для « y =» и затем вставить в свой графический калькулятор. Вспомните себя в начальной школе. Ваш учитель дал вам рабочие листы, содержащие такие утверждения, как «[ ] + 2 = 4», и сказал вам заполнить поле. Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4», и сказал вам «решить для x ». Почему ваши учителя перешли с ящиков на переменные? Хорошо, подумайте об этом: сколько фигур вам нужно использовать для формул, подобных формуле для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? Формула выглядит следующим образом: Если вы попытаетесь выразить это или что-то более сложное, используя коробки различной формы, у вас быстро закончатся формы. Другими словами, они перешли от ящиков к переменным, потому что, хотя квадраты и буквы означают одно и то же (а именно, слот, ожидающий заполнения значением), переменные лучше.Переменные более гибкие, их легче читать, и они могут дать вам больше информации. То же самое верно для « y » и « f ( x )» (произносится как «eff-of-eks»). Для функций эти два обозначения означают одно и то же, но « f ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « х = 2 х + 3; найдите х , когда х = –1». Теперь вы говорите: « f ( x ) = 2 x + 3; найти f -отрицательного-один»). Но обозначение функций обеспечивает большую гибкость, чем простое использование « y » для каждой формулы. Например, ваш графический калькулятор будет отображать различные функции как y1, y2 и т. д., так что вы сможете различать уравнения, когда, скажем, просматриваете их значения в «TABLE». Точно так же в учебниках и при записи мы используем разные имена функций, такие как f ( x ), g ( x ), h ( x ), s ( x ), s ( t ) и т. д., чтобы отслеживать и работать с более чем одной формулой в любом отдельном контексте.Благодаря нотации функций мы теперь можем использовать более одной функции одновременно, не путая себя и не путая формулы, заставляя себя задаваться вопросом: «Хорошо, а какой ‘ y ‘ является этим ?» И обозначения могут быть полезными пояснениями. Из геометрии вы знаете, что « A ( r ) = π r 2 » указывает площадь круга, выраженную через значение радиуса r , а « C ( r ) = 2π r «обозначает длину окружности, выраженную в виде радиуса r .Обе функции имеют одну и ту же подключаемую переменную (« r »), но « A » напоминает вам, что первая функция — это формула «площади», а « C » напоминает вам, что вторая функция — это формула для «окружности». Помните: обозначение « f ( x )» точно такое же, как « y ». Вы даже можете обозначить ось y на своих графиках как « f ( x )», если хотите. Поясню еще один момент. В то время как круглые скобки до сих пор всегда указывали на умножение, это не относится к обозначению функций. Вопреки всему предыдущему опыту, круглые скобки для обозначения функции , а не указывают на умножение. Выражение « f ( x )» означает «формула с именем f имеет x в качестве входной переменной».Это означает, что , а не означает «умножить на и x »! Не смущайтесь, произнося (или думая) « f ( x )» как « f x x », и никогда не пытайтесь «умножить» имя функции с его скобками Вход. В обозначениях функций « x » в « f ( x )» называется «аргументом функции» или просто «аргументом».Так что, если вам дадут выражение « ф (2)» и спросят «аргумент», ответ будет просто «2». В сторону: Почему ввод называется «аргументом»? Термин «аргумент» имеет долгую историю. Первоначально это был логический термин, относящийся к заявлению, которое выдвигало доказательство или, в менее формальном смысле, к утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить. В двадцатом веке, когда компьютерное кодирование стало популярным, кодировщики приняли математический смысл для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» — это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а выход функции — это зависимая переменная (та, значение которой зависит от того, что было подключено). in, обычно это значение y ). Сначала я сделаю вторую часть.Аргумент — это то, что находится внутри круглых скобок, поэтому аргумент здесь s . Имя функции — это переменная, которая стоит перед круглыми скобками. В этом случае имя функции h . имя функции: ч аргумент: с Аргументом является то, что подключено.В этом конкретном (необычном) случае вставляется переменная « y ». (В конце концов, нет правила, говорящего, что и не могут быть независимой переменной.) Итак: Имя функции — это то, что стоит перед круглыми скобками, поэтому имя функции здесь — g . Во второй части вопроса от меня требуют аргумент. В первой части, где мне дали имя и аргумент функции (часть « g ( t )») и формулу (часть « t 2 + t «), аргумент был т . Но во второй части они подставили конкретное значение для t . Итак, во второй части аргументом является число –1. имя функции: г аргумент г (-1): -1 Вы оцениваете « f ( x )» точно так же, как вы всегда оценивали « y ».А именно, вы берете число, которое они вам дают в качестве входной переменной, подставляете его для переменной и упрощаете, чтобы получить ответ. Например: Чтобы оценить f ( x ) при x = 2, я подставлю 2 для каждого экземпляра x в правиле функции: ж (2) = (2) 2 +2(2) – 1 Чтобы все было ясно (и понятно в работе), я заключил в скобки каждый экземпляр аргумента 2 в формуле для f .Теперь я могу упростить: Тогда мой ответ: Чтобы оценить, я делаю то, что делал всегда. Я подставлю заданное значение (–3) для указанной переменной ( x ) в данную формулу: е (–3) = (–3) 2 + 2(–3) – 1 Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу. Тогда мой ответ: Если у вас возникают трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как, например, находится ли показатель степени на знаке «минус». И вообще это хорошая привычка, которую нужно развивать. Важный тип функции называется «кусочной» функцией, потому что она состоит из частей.Например, следующая функция является кусочной: Как видите, эта функция разделена на две половины: половина, предшествующая x = 1, и половина, идущая от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это: Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожным, чтобы вставить аргумент в правильную часть функции. Сначала они хотят, чтобы я оценил x = –1. Так как это меньше 1, то этот аргумент входит в первую часть функции. Для обновления функция такова: Затем я подставлю –1 в правило 2 x 2 – 1: е (–1) = 2(–1) 2 – 1 = 2(1) – 1 = 2 – 1 = 1 Затем они хотят, чтобы я нашел значение f (3).Поскольку 3 больше 1, мне нужно подключить вторую часть функции, поэтому: Наконец, они хотят, чтобы я оценил f ( x ) как x = 1. Внимательно изучив правила для функций, я вижу, что первая часть — это правило для x -значений, которые строго меньше 1; правило не применяется, когда x равно 1.С другой стороны, вторая часть применяется, когда x больше или равно 1. Поскольку я имею дело с x = 1, то применяется правило второй части. Тогда мой ответ: е (–1) = 1 ж (3) = 7 ж (1) = 5 Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в вычислении функций с заданным числовым значением.Попробуйте введенное упражнение или введите свое собственное упражнение. (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.) URL-адрес: https://www.purplemath.com/modules/fcnnot.htm {{\mbox{nd}}}}{\mbox{ компоненты : }}\left\{ {0, — 3,0,5} \right\}\]
{{\mbox{nd}}}}{\mbox{ компоненты : }}\left\{ {0, — 3,0,5} \right\}\]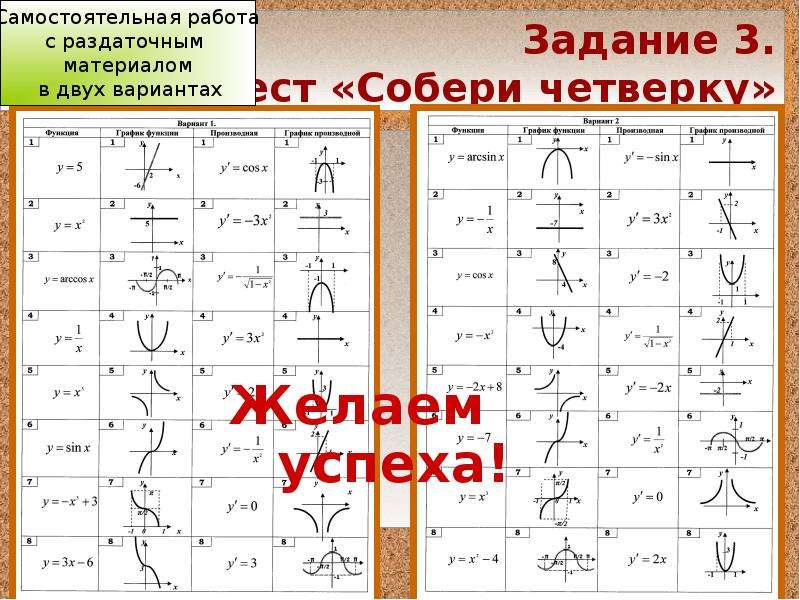 Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента.
Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента. {{\mbox{st}}}}{\mbox{ компоненты : }}\left\{ {6, — 7,0} \right\}\hspace{0.{{\mbox{nd}}}}{\mbox{ компоненты: }}\left\{ {10,3,4, — 4} \right\}\]
{{\mbox{st}}}}{\mbox{ компоненты : }}\left\{ {6, — 7,0} \right\}\hspace{0.{{\mbox{nd}}}}{\mbox{ компоненты: }}\left\{ {10,3,4, — 4} \right\}\]
 Это также может быть верно для отношений, которые являются функциями. Они не должны исходить из уравнений.
Это также может быть верно для отношений, которые являются функциями. Они не должны исходить из уравнений. «Рабочее определение» функции
 Это, как правило, означает, что не все \(x\) можно подставить в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако в этот момент просто помните, что мы не можем делить на ноль, и если мы хотим исключить из уравнения действительные числа, мы не можем извлечь квадратный корень из отрицательное число. Итак, из этих двух примеров ясно, что мы не всегда сможем подставить каждое \(x\) в какое-либо уравнение.
Это, как правило, означает, что не все \(x\) можно подставить в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако в этот момент просто помните, что мы не можем делить на ноль, и если мы хотим исключить из уравнения действительные числа, мы не можем извлечь квадратный корень из отрицательное число. Итак, из этих двух примеров ясно, что мы не всегда сможем подставить каждое \(x\) в какое-либо уравнение. 2} = 4\) Показать все решения Скрыть все решения
Показать обсуждение
2} = 4\) Показать все решения Скрыть все решения
Показать обсуждение
a \(y = 5x + 1\) Показать решение 25in} & y & = 5\left( { — 4} \right) + 1 = — 20 + 1 = — 19\\ x & = 0:\hspace{0.25in} & y & = 5\left( 0 \right) + 1 = 0 + 1 = 1\\ x & = 10:\hspace{0.25in} & y & = 5\left( { 10} \right) + 1 = 50 + 1 = 51\end{align*}\]
25in} & y & = 5\left( { — 4} \right) + 1 = — 20 + 1 = — 19\\ x & = 0:\hspace{0.25in} & y & = 5\left( 0 \right) + 1 = 0 + 1 = 1\\ x & = 10:\hspace{0.25in} & y & = 5\left( { 10} \right) + 1 = 50 + 1 = 51\end{align*}\] Когда мы возводим число в квадрат, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение.
Когда мы возводим число в квадрат, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение. 2} = 4\hspace{0.2} = 4\hspace{0,25 дюйма} \стрелка вправо \hspace{0,25 дюйма} y = \pm \,2\]
2} = 4\hspace{0.2} = 4\hspace{0,25 дюйма} \стрелка вправо \hspace{0,25 дюйма} y = \pm \,2\]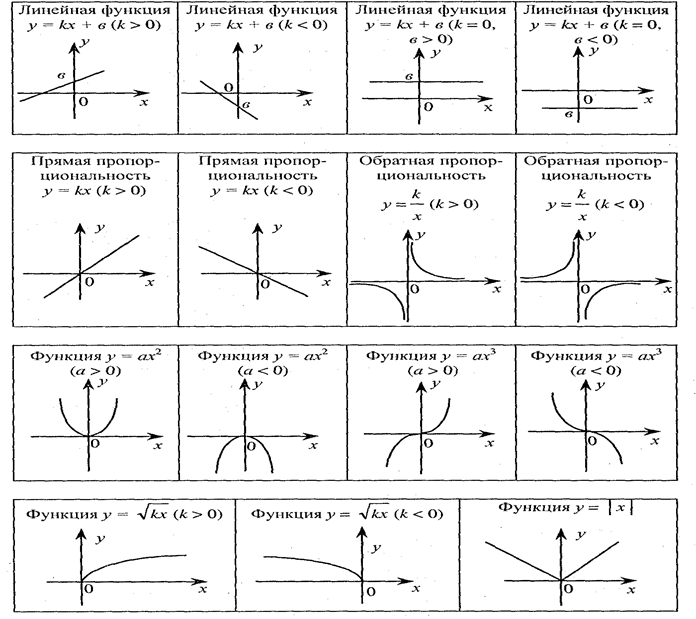
 Здесь важно обратить внимание на букву, которая стоит перед скобкой. Для \(f\left( 3 \right)\) мы будем использовать функцию \(f\left( x \right)\), а для \(g\left( 3 \right)\) мы будем использовать \(g \влево( х \вправо)\).2} — 2\влево( { — 10} \вправо) + 8 = 100 + 20 + 8 = 128\]
Здесь важно обратить внимание на букву, которая стоит перед скобкой. Для \(f\left( 3 \right)\) мы будем использовать функцию \(f\left( x \right)\), а для \(g\left( 3 \right)\) мы будем использовать \(g \влево( х \вправо)\).2} — 2\влево( { — 10} \вправо) + 8 = 100 + 20 + 8 = 128\]
d \(f\left( t \right)\) Показать решение Как показано на этом примере, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы подставляем в \(x\) справа от знака равенства то, что находится в скобках.2} — 2т + 8\]
Как показано на этом примере, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы подставляем в \(x\) справа от знака равенства то, что находится в скобках.2} — 2т + 8\]
e \(f\left( {t + 1} \right)\) и \(f\left( {x + 1} \right)\) Показать решение
Показать все решения Скрыть все решения
Показать обсуждение Это не изменит того, как работает оценка. Не зацикливайтесь на том, чтобы видеть \(f\) для функции и \(x\) для переменной, чтобы вы не могли решить задачу, в которой нет этих букв.
Это не изменит того, как работает оценка. Не зацикливайтесь на том, чтобы видеть \(f\) для функции и \(x\) для переменной, чтобы вы не могли решить задачу, в которой нет этих букв.
c \(g\left( 1 \right)\) Показать решение
d \(g\left( {15} \right)\) Показать решение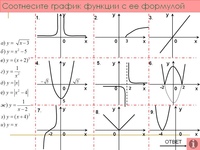 В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства. Затем, как и в предыдущей части, мы просто получаем
В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства. Затем, как и в предыдущей части, мы просто получаем
e \(g\left( {21} \right)\) Показать решение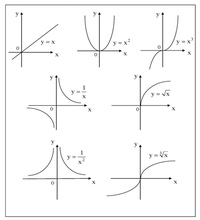 Мы кратко говорили об этом, когда давали определение функции, и видели пример этого, когда оценивали функции.Теперь нам нужно рассмотреть это немного подробнее.
Мы кратко говорили об этом, когда давали определение функции, и видели пример этого, когда оценивали функции.Теперь нам нужно рассмотреть это немного подробнее. Домен и диапазон
 Из определения домен — это набор всех \(x\), которые мы можем подставить в функцию и получить обратно действительное число. На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \left( {x + 5} \right)\left( {x — 2} \right) = 0\hspace{0.25in}x = — 5,\,\,x = 2\ ]
Из определения домен — это набор всех \(x\), которые мы можем подставить в функцию и получить обратно действительное число. На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \left( {x + 5} \right)\left( {x — 2} \right) = 0\hspace{0.25in}x = — 5,\,\,x = 2\ ]
b \(f\left( x \right) = \sqrt {5 — 3x} \) Показать решение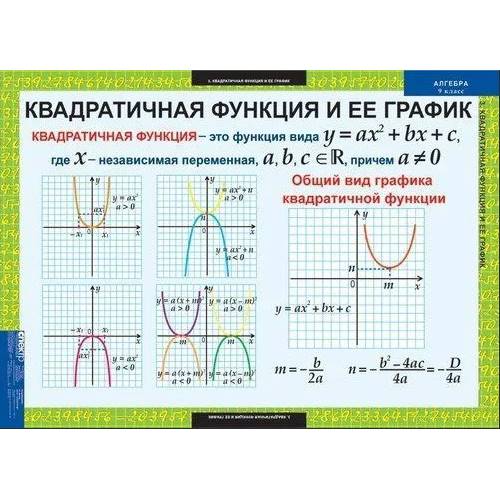
 2} — 16}}\) Показать решение
2} — 16}}\) Показать решение Это означает, что можно подставить \(x = 4\) в квадратный корень, однако, поскольку это приведет к делению на ноль, нам нужно будет этого избежать.
Это означает, что можно подставить \(x = 4\) в квадратный корень, однако, поскольку это приведет к делению на ноль, нам нужно будет этого избежать. функций и обозначение функций — College Algebra
Цели обучения
 В этом разделе мы проанализируем такие отношения.
В этом разделе мы проанализируем такие отношения. Определение того, представляет ли отношение функцию
 Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в домене связан ровно с одним элементом в диапазоне
Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в домене связан ровно с одним элементом в диапазоне Мы говорим, что «выход есть функция входа».
Мы говорим, что «выход есть функция входа».
«>
Процентное содержание 0–56 57–61 62–66 67–71 72–77 78–86 87–91 92–100 Средний балл 0,0 1,0 1.5 2,0 2,5 3,0 3,5 4,0 
Игрок Ранг Бейб Рут 1 Вилли Мейс 2 Тай Кобб 3 Уолтер Джонсон 4 Хэнк Аарон 5  да; б. да. (Примечание: если бы два игрока разделили, скажем, 4-е место, то имя не зависело бы от ранга.)
да; б. да. (Примечание: если бы два игрока разделили, скажем, 4-е место, то имя не зависело бы от ранга.) Представление функций с помощью таблиц
Reading the columns as ordered pairs, we have: (1, 31), (2, 28), (3, 31), (4, 30), (5, 31), (6, 30), (7, 31), (8, 31), (9, 30) , (10, 31), (11, 30), and (12, 31).»>
Номер месяца (ввод) 1 2 3 4 5 6 7 8 9 10 11 12 Дней в месяце,(выход) 31 28 31 30 31 30 31 31 30 31 30 31 «>
1 2 3 4 5 8 6 7 6 8 «>
Возраст в годах,(ввод) 5 5 6 7 8 9 10 Высота в дюймах (выход) 40 42 44 47 50 52 54 
Вход Выход –3 5 0 1 4 5 
Вход Выход 1 10 2 100 3 1000 Поиск входных и выходных значений функции
 Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению. Вычисление функций в алгебраических формах
Вычисление функции, заданной в табличной форме
 И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.
И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов. Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0,083 Кат 16 Золотая рыбка 2160 Бета-рыба 3600  Здесь давайте вызовем функцию. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых длится память питомца. Мы можем оценить функцию по входному значению «золотая рыбка». Мы бы написали Обратите внимание, что для оценки функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функций кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь давайте вызовем функцию. Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых длится память питомца. Мы можем оценить функцию по входному значению «золотая рыбка». Мы бы написали Обратите внимание, что для оценки функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функций кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
1 2 3 4 5 8 6 7 6 8 Определение того, является ли функция взаимно однозначной
 Например, на биржевой диаграмме, показанной в начале этой главы, цена акции составляла 1000 фунтов стерлингов в пять разных дат, а это означает, что было пять различных входных значений, которые все приводили к одному и тому же выходному значению в 1000 фунтов стерлингов.
Например, на биржевой диаграмме, показанной в начале этой главы, цена акции составляла 1000 фунтов стерлингов в пять разных дат, а это означает, что было пять различных входных значений, которые все приводили к одному и тому же выходному значению в 1000 фунтов стерлингов. Буквенный класс Средний балл А 4,0 Б 3,0 С 2,0 Д 1,0 
 да, потому что каждый банковский счет имеет единственный баланс в любой момент времени; б.нет, так как баланс на нескольких банковских счетах может быть одинаковым; в. нет, потому что один и тот же выход может соответствовать более чем одному входу.
да, потому что каждый банковский счет имеет единственный баланс в любой момент времени; б.нет, так как баланс на нескольких банковских счетах может быть одинаковым; в. нет, потому что один и тот же выход может соответствовать более чем одному входу. Использование теста вертикальной линии
 Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. (Рисунок).
Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. (Рисунок).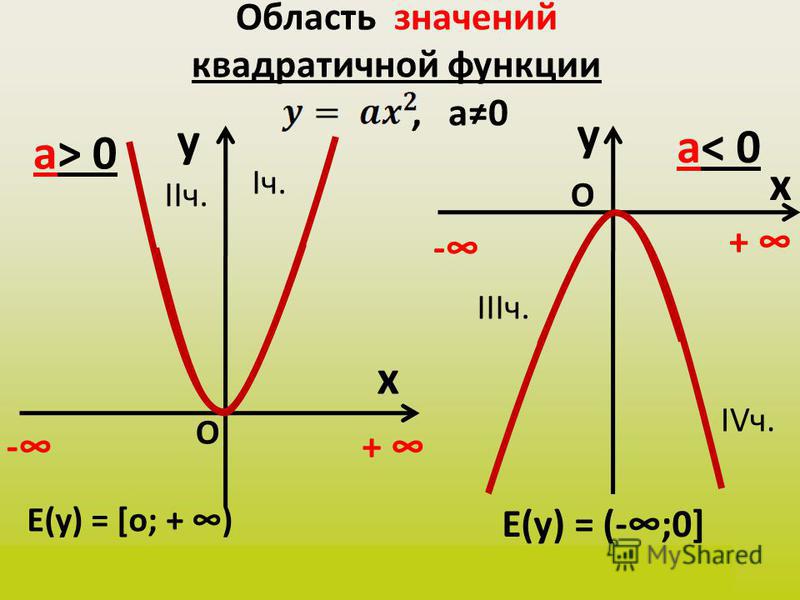 Отсюда можно сделать вывод, что эти два графика представляют собой функции. Третий график не представляет функцию, поскольку при максимальном разрешении x значений вертикальная линия будет пересекать график более чем в одной точке, как показано на (рис.).
Отсюда можно сделать вывод, что эти два графика представляют собой функции. Третий график не представляет функцию, поскольку при максимальном разрешении x значений вертикальная линия будет пересекать график более чем в одной точке, как показано на (рис.). Использование теста горизонтальной линии
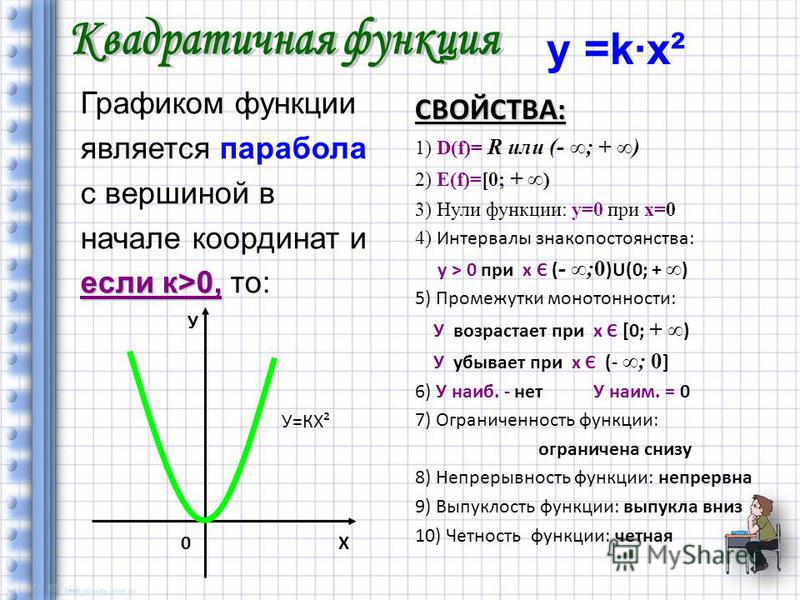
Определение основных функций инструментария
 При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел.При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать как входную переменную, так и выходную переменную.
При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел.При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать как входную переменную, так и выходную переменную. Ключевые понятия
 Функция — это особый тип отношения, в котором каждое значение домена или входные данные приводят ровно к одному значению диапазона или выходным данным. См. (Рисунок) и (Рисунок).
Функция — это особый тип отношения, в котором каждое значение домена или входные данные приводят ровно к одному значению диапазона или выходным данным. См. (Рисунок) и (Рисунок).
Секционные упражнения
Устный
 При любом конкретном входном значении может быть только один выход, если отношение должно быть функцией.
При любом конкретном входном значении может быть только один выход, если отношение должно быть функцией. Технология
 Определите соответствующий диапазон для каждого окна просмотра.Покажите каждый график.
Определите соответствующий диапазон для каждого окна просмотра.Покажите каждый график. Сноски
Глоссарий
функций и отношений — сделано проще
Содержание
Введение
 Отношение представляет собой набор входов и выходов, а функция представляет собой отношение с одним выходом для каждого входа.
Отношение представляет собой набор входов и выходов, а функция представляет собой отношение с одним выходом для каждого входа. Что такое функция?

Графические функции
Специальные функции
Постоянная функция
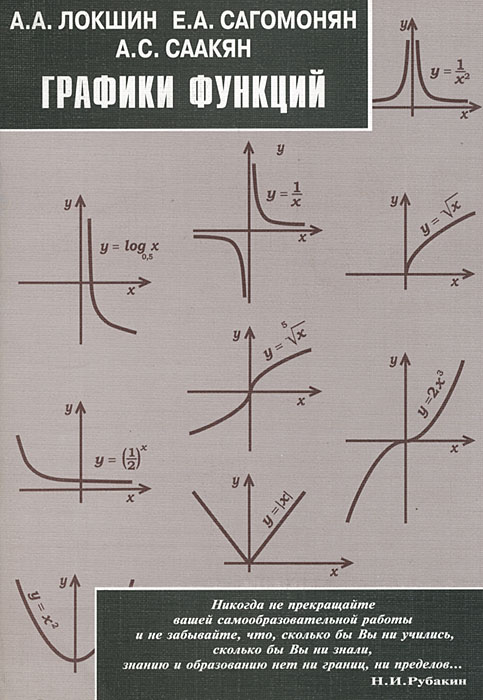 Вот график $f(x) = 4$
Вот график $f(x) = 4$ Функция идентификации
Линейная функция
Функция абсолютного значения
Обратные функции

Функциональные операции
: определения и оценка числа
Пурпурная математика
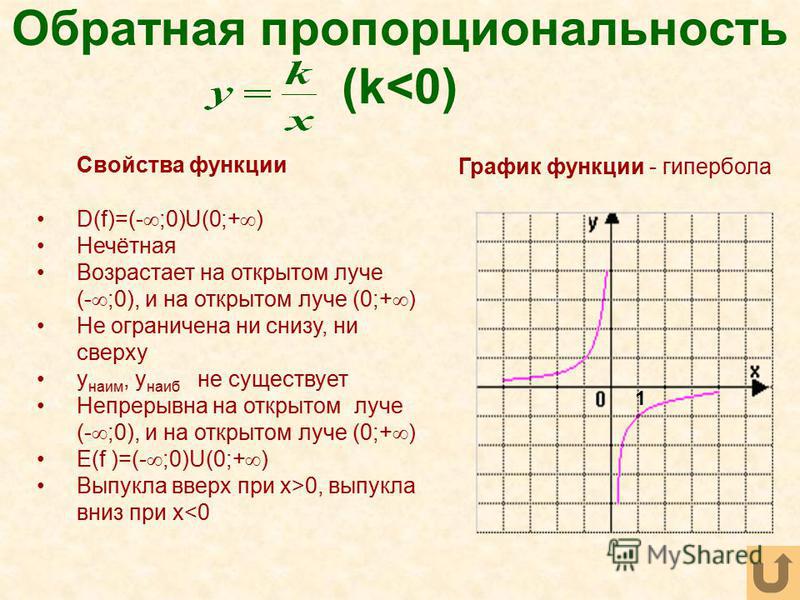 Эти « y =» уравнения являются функциями. Но вопрос, с которым вы столкнулись в данный момент: «Зачем мне нужна эта запись функций, особенно когда у меня есть прекрасное « y =» и как эта запись работает?»
Эти « y =» уравнения являются функциями. Но вопрос, с которым вы столкнулись в данный момент: «Зачем мне нужна эта запись функций, особенно когда у меня есть прекрасное « y =» и как эта запись работает?» MathHelp.com
 Кроме того, вы знаете из опыта, что « А » означает «площадь», « h » означает «высота», а « а » и « b » обозначают длины параллельных вершин и нижние стороны. Одному небу известно, что может означать квадратная коробка или треугольная коробка!
Кроме того, вы знаете из опыта, что « А » означает «площадь», « h » означает «высота», а « а » и « b » обозначают длины параллельных вершин и нижние стороны. Одному небу известно, что может означать квадратная коробка или треугольная коробка! В любой нотации вы делаете одно и то же: подставляете –1 для x , умножаете на 2, а затем добавляете 3, упрощая, чтобы получить окончательное значение +1.
В любой нотации вы делаете одно и то же: подставляете –1 для x , умножаете на 2, а затем добавляете 3, упрощая, чтобы получить окончательное значение +1.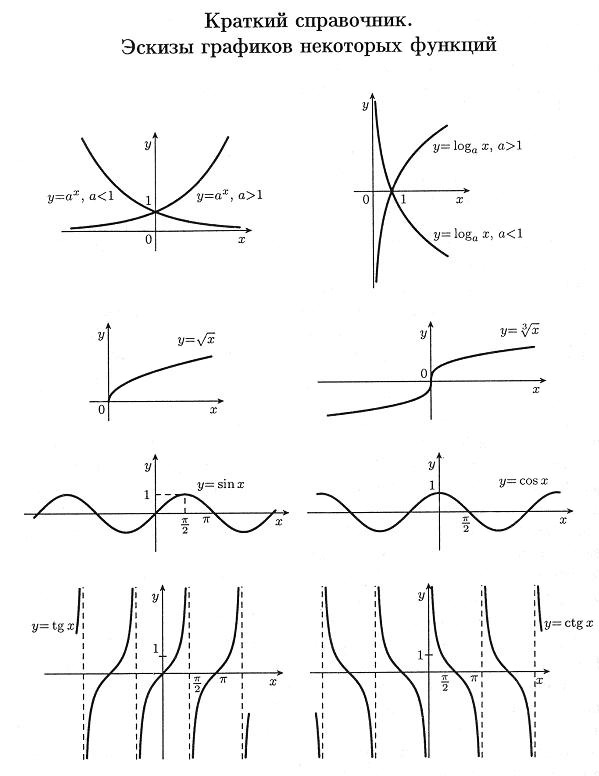

 В конце концов, в раннем научном контексте этот термин стал обозначать любое математическое значение, которое было необходимо в качестве исходных данных для других вычислений, или любое значение, от которого зависели более поздние результаты.
В конце концов, в раннем научном контексте этот термин стал обозначать любое математическое значение, которое было необходимо в качестве исходных данных для других вычислений, или любое значение, от которого зависели более поздние результаты. Учитывая
h ( s ), какое имя функции и каков аргумент?
Каков аргумент
f ( y )? Учитывая
г ( t ) = t 2 + t , как называется функция? В g (–1) какой аргумент?
Оценка по номеру Дано
f ( x ) = x 2 + 2 x – 1, найдите f (2).
Дано
f ( x ) = x 2 + 2 x – 1, найти f (–3).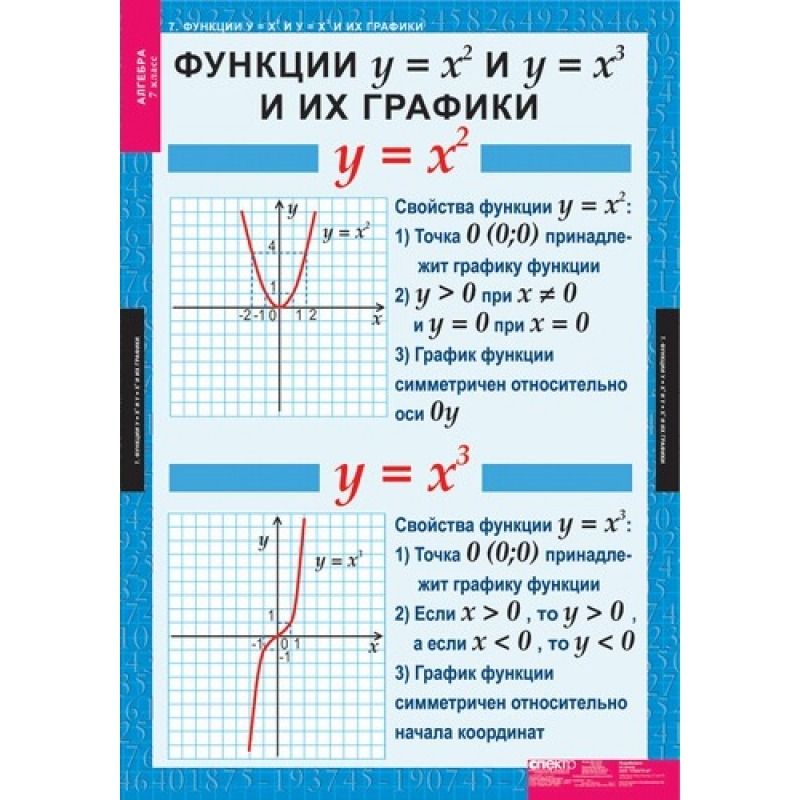 В этом случае скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:
В этом случае скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить: Учитывая функцию
f ( x ), определенную выше, оцените функцию при следующих значениях: x = –1, x = 3 и x = 1.
 Это единственное значение x , которое немного сложно. Какую половину я использую?
Это единственное значение x , которое немного сложно. Какую половину я использую? Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway. по алгебре I — проект Connected Mathematics
Цели по алгебре I — проект Connected Mathematics
Переключить инструменты специальных возможностей Думая математическими моделями
Линейные и нелинейные отношения:
Распознавание и моделирование закономерностей в двумерных данных. Анализ данных:
Измерение вариаций данных и силы связи в двумерных данных.
В поисках Пифагора
Теорема Пифагора:
Понимать и применять теорему Пифагора. Действительные числа:
Поймите, что множество действительных чисел состоит из рациональных и иррациональных чисел.
Растет, Растет, Растет
Экспоненциальные функции:
Исследуйте проблемные ситуации, в которых две или более переменных имеют экспоненциальную связь друг с другом.
Эквивалентность:
Развитие понимания эквивалентных экспоненциальных выражений.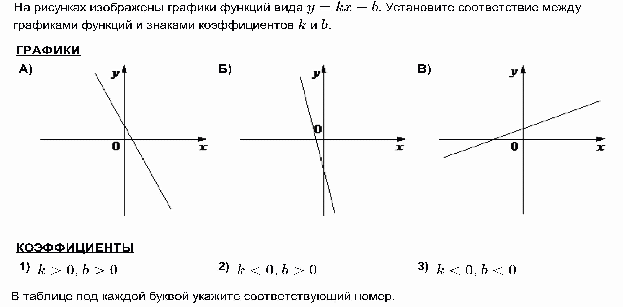
Лягушки, блохи и окрашенные кубики
Квадратичные функции:
Исследуйте проблемные ситуации, в которых две переменные находятся в квадратичной зависимости. Эквивалентность:
Развивать понимание эквивалентных квадратных выражений.
Бабочки, вертушки и обои
Преобразования:
Описать типы преобразований, которые связывают точки движениями отражений, вращений и перемещений; и методы определения и создания симметричных плоских фигур. Конгруэнтность и сходство:
Понимать конгруэнтность и сходство и изучать необходимые и достаточные условия для установления конгруэнтности и сходства форм.
Скажи это символами
Эквивалентность:
Развитие понимания эквивалентных выражений и уравнений.
Функции:
Развитие понимания конкретных функций, таких как линейные, экспоненциальные и квадратичные функции.
Это в системе
Линейные уравнения:
Развитие понимания линейных уравнений и систем линейных уравнений. 
Линейные неравенства:
Развивать понимание графических и символьных методов решения линейных неравенств с одной и двумя переменными.
Функциональное соединение
Функции:
Функция понимания. Эквивалентность:
Понимание эквивалентности алгебраических выражений и функций.
Quia — Глоссарий алгебры A-Z
A B абсолютное значение Расстояние от начала координат до координаты x. 
абсолютное значение комплексного числа абсолютное значение комплексного числа a + bi равно квадратному корню из квадрата плюс b квадрат. аддитивные обратные Пары действительных чисел, сумма которых равна 0. аддитивная обратная матрица A + (-A) = Z. алгебраические выражения Выражения, состоящие из переменных, чисел, группирующих символов, знаков операций и показателей степени. амплитуда Половина разницы между максимальным и минимальным значениями периодической функции. Угол или углубление Угол между 0′ и 90′, образованный горизонтальным лучом и лучом, идущим от наблюдателя к наблюдаемому внизу объекту. 
угол возвышения Угол между 0 и 90, образованный горизонтальным лучом и лучом от наблюдателя к объекту, наблюдаемому над ним. среднее арифметическое Сумма чисел в наборе, деленная на количество чисел в данном наборе. средние арифметические Члены арифметической последовательности, находящиеся между двумя заданными членами. arithmetic sequence Для каждого положительного целого числа n последовательность с первым членом a и n-м членом a является арифметической последовательностью тогда и только тогда, когда an = a1 + (n — 1)d. арифметический ряд Указанная сумма членов арифметического ряда. асимптоты (гиперболы) Линии, внутри которых лежат ветви гиперболы и к которым ветви приближаются при |x| увеличивается. 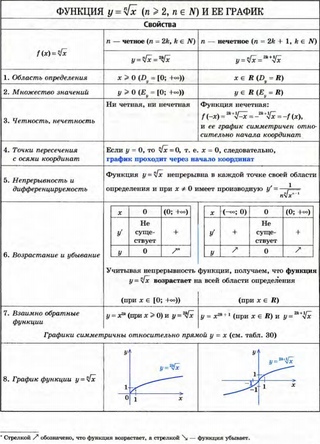
расширенная матрица Матрица коэффициентов для системы линейных уравнений с конечным столбцом, включенным для констант уравнений. ось симметрии Линия на плоскости графика, такая, что часть графика на одной стороне линии является отражением части на другой стороне. смещенная -выборка Неслучайная выборка. биномиальный Многочлен с двумя членами. граничное условие Экстремальное значение в задаче о неравенстве. Решения будут меньше или больше этого значения. центр окружности Точка на окружности, расстояние от которой до любой точки на окружности является постоянным. 
центр эллипса Пересечение осей симметрии. центральная тенденция набора чисел Число, считающееся наиболее типичным или репрезентативным для этого набора. окружность Множество всех точек на плоскости, для которых расстояние (радиус) от данной точки (центра окружности) постоянно. Круговые функции Периодические функции, относящиеся к единичному кругу. закрытие Набор чисел замыкается при выполнении операции, если объединение любых двух элементов в наборе с помощью этой операции дает число в наборе. коэффициент Постоянный множитель монома. обыкновенный коэффициент обыкновенный коэффициент является постоянной величиной. 
дополнение к событию Событие A является дополнением к событию B относительно выборочного пространства S тогда и только тогда, когда A и 8 включают все исходы S, а A и B не имеют общих исходов. завершение квадрата Метод, используемый для решения квадратного уравнения, в котором к обеим частям уравнения прибавляется число, так что одна сторона представляет собой идеальный квадрат. комплексное сопряжение Для всех действительных чисел a и b, a + bi и a — bi являются комплексно-сопряженными. сложная дробь Дробь, имеющая дроби либо в числителе, либо в знаменателе, либо в обоих. Комплексное число Число вида a + bi, где a и b — действительные числа, а i — мнимая единица. 
Компоненты или заказанная пара Отдельные номера в заказанной паре. составное неравенство Предложение, связывающее два условия с помощью «и» или «или». Хотя бы одно из условий является неравенством. коническое сечение Кривая, имеющая уравнение второй степени и определяемая расстоянием ее точек от фиксированных точек и/или линий. Сюда входят окружности, параболы. эллипсы и гиперболы. сопряженный Два двучлена вида (a + Nt/b) и (a — N/b).где а и b — рациональные числа. непротиворечивая система уравнений Система, имеющая хотя бы одно решение. 9000 Prontent Номер или полиномиальный уровень степени 0. 
Разница между последовательными условиями Разница между последовательными условиями в последовательности Константа обратного изменения Количество K в обратном вариация Y = K/X. постоянная линейная функция Функция, уравнение которой можно записать в виде y = b и график которой представляет собой горизонтальную линию. постоянный член многочлена Член а, который можно считать коэффициентом x. постоянный член квадратного уравнения Член c в виде V = ax- + bx + r. постоянная вариации Число k в прямой вариации y = kx или в обратной вариации Y = K/X. 
непрерывная Полиномиальная функция, график которой гладкий без «скачков». сходятся Если существует действительное число, являющееся значением бесконечного ряда, ряд сходится. Выпуклая многоугольная область Область, имеющая в качестве границы многоугольник без «углублений». координата Число, связанное с определенной точкой на числовой прямой. оси координат Две перпендикулярные линии, выбранные на плоскости. координаты точки Номера упорядоченной пары. коэффициент корреляции Число между — I и + I, которое является мерой разброса точек данных относительно линии регрессии. 
соответствующие элементы матриц Для двух матриц одинаковой размерности. элементы в одной строке и в одном столбце. Кубический многочлен Многочлен третьей степени. цикл График периодической функции через один фундаментальный период. убывающая функция функция такая, что для любых чисел a и b в области определения. если а > б. тогда f(a) степень монома Сумма показателей переменных. Степень полинома Степень члена (или членов) высшей степени. зависимые события Два события A и B зависимы тогда и только тогда, когда (A и затем B) * P(A) — P(B). 
зависимая система Система, граф-афы которой совпадают и которая имеет бесконечно много решений. зависимая переменная Если значение а зависит от значения b или если а обычно определяется через b, то а называется зависимой переменной. и откладывается по вертикальной оси. подавленное уравнение Уравнение Q(x) = 0, где Q(x) — частное от деления многочлена на множитель (x — r). в порядке убывания Многочлен записывается в порядке убывания, когда первым пишется член с наивысшей степенью, за ним следует член со следующей высшей степенью, и так далее. определитель Вещественное число, представленное квадратным массивом чисел. 
определитель матрицы Определитель матрицы – это определитель с одинаковыми соответствующими элементами. Размеры матрицы Количество строк и количество столбцов. прямая вариация Говорят, что две переменные изменяются прямо тогда и только тогда, когда существует константа вариации или (константа пропорциональности) k.k ¹ 0. такое, что y = kx. направленная сеть Сеть, указывающая направление потока на каждой дуге. направляющая Линия, используемая в определении конического сечения. Дискриминант Выражение b2 — 4ac квадратной формулы, определяющее некоторые характеристики корней квадратного уравнения. 
дисперсия Мера того, насколько близко набор данных сгруппирован относительно среднего значения.2. расходятся Если нет действительного числа, которое является значением бесконечного ряда, ряд расходится. домен отношения Набор первых компонентов упорядоченных пар в отношении. двойной корень Два одинаковых корня эксцентриситет Отношение, используемое в некоторых определениях конических сечений. эллипс Множество всех точек на плоскости, для которых сумма расстояний (радиусов фокуса) от двух заданных точек (фокусов) постоянна. многоточие Символ, указывающий, что шаблон продолжается в последовательности. 
эквивалентное преобразование Преобразование, результатом которого является уравнение, эквивалентное исходному. событие Подмножество демонстрационного пространства. явное определение Определение, используемое для определения отношения между термином t. последовательности и номер n этого члена. показательное уравнение Уравнение с переменной в показателе степени.x определяет экспоненциальную функцию с основанием b. факториал Для каждого положительного целого числа n, n! = n(n — 1)(n — 2) … 3 x 2 x 1. Кроме того, 0! = 1. поле Набор чисел с двумя операциями, обладающий замыкающими, коммутативными, ассоциативными, тождественными и обратными свойствами для сложения и умножения и распределительным для умножения на сложение. 
конечная последовательность Последовательность, имеющая последний член. подобранная линия Линия, которая наилучшим образом аппроксимирует график связи между двумя переменными, если эта связь близка к линейной. фокус Фиксированная точка или точки (фокусы), используемые для определения конического сечения. дробное уравнение Уравнение с переменной в знаменателе дроби. функция Отношение, в котором каждый элемент домена связан ровно с одним элементом диапазона. обозначение функции Представление любого числа в диапазоне функции f как f(x). где x — соответствующее число в домене. 
среднее геометрическое Квадратный корень из произведения двух чисел. Его также называют среднепропорциональным. средние геометрические Члены геометрической последовательности между двумя заданными членами. геометрическая последовательность Для каждого натурального числа n и для каждого действительного числа r, r ¹ 0, последовательность с первым членом a и n-м членом a.п-1. геометрический ряд Указанная сумма членов геометрического ряда. наибольший общий делитель Общий делитель, кратный каждому общему делителю. Функция наибольшего целого числа Ступенчатая функция, которая сопоставляет действительное число с наибольшим целым числом, которое меньше или равно действительному числу. 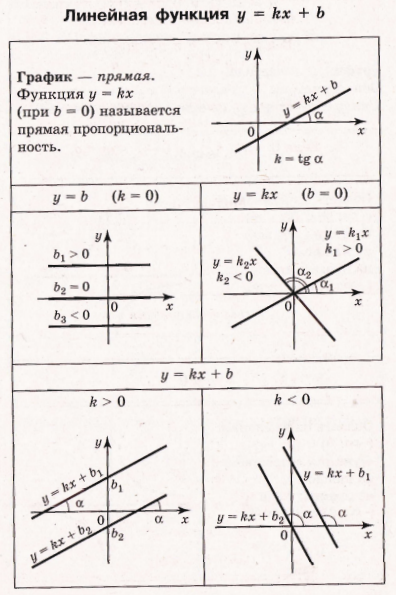
период полураспада Промежуток времени, в течение которого распадается половина количества радиоактивного материала. среднее гармоническое В наборе из n чисел. n разделить на сумму обратных чисел. гипербола Множество всех точек на этой плоскости, для которых абсолютная величина разности расстояний (фокальных радиусов) от двух заданных точек (фокусов) постоянна. гипотенуза Самая длинная сторона прямоугольного треугольника. Он находится напротив прямого угла. identity Уравнение, истинное для всех элементов своей области определения. элемент идентификации Число, которое при сложении или умножении на любое число в наборе дает то же самое число в наборе. 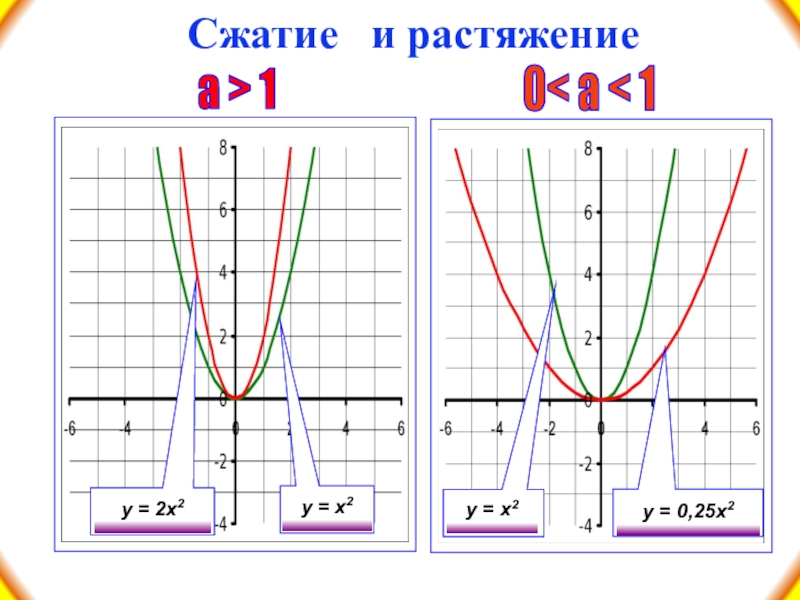
тождественные свойства Существуют действительные числа 0 и I такие, что для каждого действительного числа а, а + 0, 0 + а = а и а х 1 = 1 х а = а. мнимое число Комплексное число, которое не является реальным. несовместимая система уравнений Система без решения. Возрастающая функция Функция такая, что для любых чисел a и b в области определения. если а > b, то f(a) > f(b). независимые события Два события, не зависящие друг от друга. Два события A и B независимы тогда и только тогда, когда P(A и затем B) P(A) x P(B). независимая переменная Если значение a зависит от значения b или если a обычно определяется через b, b называется независимой переменной и отображается на горизонтальной оси. 
индекс Число, представленное буквой n в nÖb. индекс суммирования Переменная, используемая в сигма-нотации. бесконечный геометрический ряд Геометрический ряд с бесконечно большим числом членов. бесконечная последовательность Последовательность, не имеющая последнего члена. межквартильный диапазон Разница между верхним и нижним квартилями набора чисел. обратные функции Функции и g являются обратными функциями тогда и только тогда, когда f(g(x)) = g(f(x)) =x для всех чисел x в областях определения как f, так и 9. , обратное отношению Отношение B является обратным отношению A, если оно состоит из обратных значений отдельных упорядоченных пар в отношении A.  есть константа k. k ¹ 0, такое что Y = K/X.
есть константа k. k ¹ 0, такое что Y = K/X. иррациональное число Вещественное число, которое не является рациональным числом, т. е. не может быть выражено как частное двух целых чисел. широкая хорда Отрезок, концы которого лежат на параболе. которая проходит через фокус и параллельна директрисе. старший коэффициент Коэффициент члена полинома высшей степени. подобные термы Термы, которые содержат идентичные переменные с одинаковыми показателями степени. линейная комбинация Уравнение, которое получается путем сложения кратных двух уравнений. линейное уравнение с двумя переменными Уравнение вида y = mx + b. 
линейная функция Функция является линейной функцией тогда и только тогда, когда ее областью определения является множество всех действительных чисел и ее уравнение может быть записано в форме y = mx + b. линейный многочлен Многочлен первой степени.x младшие члены (простейшая форма) Дробь выражается младшими членами, если ее числитель и знаменатель не имеют общих делителей, кроме 1 или -1. главная диагональ квадратной матрицы диагональ из левого верхнего угла в правый нижний. большая ось Более длинная ось эллипса. сопоставление Связь элементов домена с элементами диапазона. 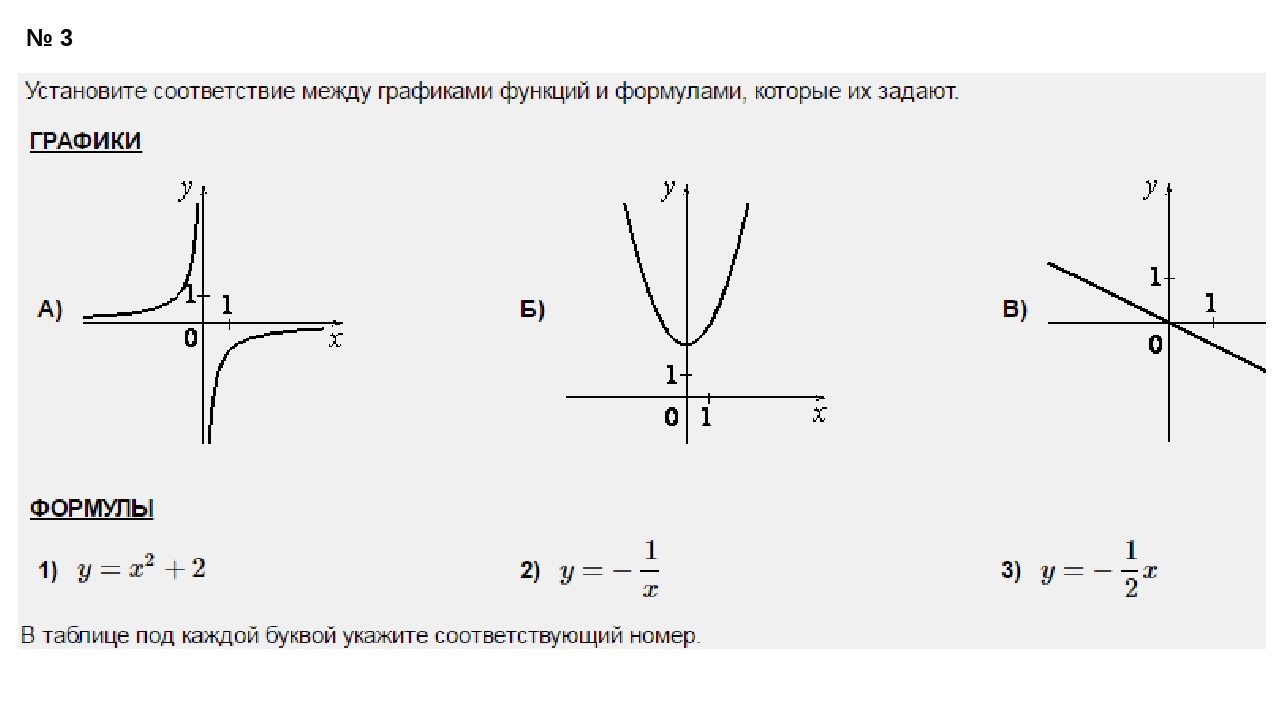
матричные матрицы Прямоугольный массив чисел, расположенных в столбцах и столбцах. максимальное значение Y-координата вершины графика квадратичной функции, обращенной вниз. среднее Сумма набора чисел, деленная на количество чисел в наборе. среднее абсолютное отклонение Среднее абсолютное отклонение от среднего для набора чисел. среднее пропорциональное Среднее геометрическое между двумя числами. медиана Среднее число в наборе чисел, расположенных по порядку. середина Точка на отрезке, равноудаленная от концов. 
формула средней точки Если координаты точки A равны (x1,y1), а координаты точки B равны (x2,y2), то координаты середины отрезка AB равны {(x1+x2)/ 2, (y1+y2)/2} минимальное значение Координата y вершины графика квадратичной функции, обращенного вверх. Минор элемента Определитель, который остается после удаления строки и столбца, содержащего элемент. Малая ось Короткая ось эллипса. режим Число, которое чаще всего встречается в наборе чисел. моном Константа (число), переменная или произведение констант и/или переменных. обратное мультипликативное (или обратное) Пары действительных чисел, произведение которых равно 1.  n.
n. отрицательные обратные числа Два числа, произведение которых равно 1. отрицательный квадратный корень Отрицательное значение главного квадратного корня. функция отрицательного квадратного корня Функция с уравнением y= -Öx сеть Набор точек (вершин), соединенных дугами. неэквивалентное преобразование Преобразование, результатом которого является уравнение, не эквивалентное исходному. нелинейная система Система двух или более уравнений, хотя бы одно из которых является нелинейным. нормальное распределение Специфическая колоколообразная алгебраическая функция, аппроксимируемая многими частотными распределениями. 
противоположности Два числа, сумма которых равна нулю. Также называется аддитивными инверсиями. упорядоченная пара Пара чисел, определяющая положение определенной точки на графике. упорядоченные тройки (X, Y, Z) Набор, являющийся решением уравнения с тремя переменными. начало координат (на графике) Точка пересечения осей координат. Обозначается (0.0). происхождение (на числовой прямой) Точка на числовой прямой, связанная с нулем. результат Результат эксперимента парабола Множество всех точек на плоскости, которые находятся на таком же расстоянии от точки (фокуса), как и от заданной линии (директрисы).  это график квадратичной функции, имеющий U-образную форму.
это график квадратичной функции, имеющий U-образную форму. параллельные линии Линии с одинаковым уклоном. частичная сумма ряда Сумма конечного числа членов ряда. треугольник Паскаля Треугольное расположение чисел, в котором каждое число является суммой двух чисел над ним в предыдущем ряду. идеальный квадрат трехчлена Квадрат двучлена.с видом a2 ± 2ab + b2. периодическая функция Функция y=f(x) является периодической тогда и только тогда, когда существует действительное число p такое, что для каждого x в области определения f. f (х + р) = f (х). перестановка Расположение ряда объектов в определенном порядке перпендикулярные линии Линии с отрицательными обратными наклонами. 
матрица точек Матрица 2 x 1, элементами которой являются координаты точки.n, где это положительное целое число. Разложение на простые множители Представление числа в виде произведения его простых множителей. основной кубический корень Кубический корень из одного действительного числа из действительного числа. главный квадратный корень Положительный квадратный корень, обозначаемый основная функция квадратного корня Функция с уравнением … вероятность события событие к количеству результатов в пространстве выборки. чисто мнимое число Любое число вида ai.  где а действительно.
где а действительно. чистое квадратное уравнение квадратное уравнение без x-члена. четырехугольник Четырехугольник — это многоугольник с четырьмя сторонами. рациональное число Число, которое можно представить как частное двух целых чисел. рационализация знаменателя Процесс замены иррационального знаменателя на рациональный. действительные числа Множество всех рациональных и иррациональных чисел. обратные числа Пары действительных чисел, произведение которых равно 1. Также известны как мультипликативные обратные числа. линия регрессии Подогнанная линия, определяемая специальным алгебраическим методом. 
отношение Набор упорядоченных пар. повторяющееся десятичное число Десятичное число, в котором цифра или группа цифр повторяются бесконечно, т.е.г. 0,66666 … или 0,846846846 … . repetend Повторяющаяся часть десятичной дроби. ограничения Набор возможных значений переменных, для которых выражение действительно или для которых оно определено. результирующий Сумма двух векторов. матрица строк Матрица с одной строкой. выборочное пространство Набор всех возможных исходов эксперимента. 
скалярное Вещественное число, являющееся коэффициентом скалярного умножения. скалярное умножение Для любого скаляра c, числа и любой матрицы размера m x n A с элементами aij произведение c и A представляет собой матрицу размера m x n, элементами которой являются caij. экспоненциальное представление Произведение степени 10 на число больше или равное 1 и меньше 10. определитель второго порядка Определитель с двумя строками и двумя столбцами. последовательность Функция, определенная для положительных целых чисел или подмножества последовательных положительных целых чисел, начинающихся с 1. ряд Указанная сумма членов последовательности. 
нотация построения множества Математическое предложение, которое «строит» множество путем выбора элементов, принадлежащих множеству. сигма-нотация Выражает сумму ряда. Форма пересечения наклона Форма Y = mx + b линейного уравнения с двумя переменными.2 = у. тогда x является квадратным корнем из y. Ступенчатая функция Функция, график которой напоминает лестницу. подмножество Набор, все элементы которого являются элементами большего набора. стандартные баллы (или —scores) Выражение для каждого значения частотного распределения в терминах количества стандартных отклонений, когда оно выше или ниже среднего. 
подстановка Способ решения систем уравнений путем замены одной переменной другой переменной или переменным выражением, равным ей. система Набор уравнений с одинаковыми переменными. члены последовательности Числа в последовательности. теорема Утверждение, истинность которого доказана. Определитель третьего порядка Определитель с тремя строками и тремя столбцами. матрица преобразования Матрица, используемая для умножения матрицы точек для получения новой матрицы точек. перевод Преобразование, осуществляемое путем подстановок, которые перемещают каждую точку данного графика в другое место без изменения формы графика. 
трехчленный Многочлен с тремя членами. единичная окружность Окружность с центром в начале координат и радиусом в одну единицу. значение ряда Упрощенная сумма ряда. переменная Символ, обычно буква, которая представляет любое число из определенного набора чисел и может быть заменена им. векторов Матрицы с одной строкой или одним столбцом. вершина параболы Точка на параболе посередине между фокусом и директрисой. проверка вертикальной линии Если ни одна вертикальная линия не пересекает график отношения более одного раза, то отношение является функцией. 
вершины эллипса Концы большой и малой осей. вершины гиперболы Две точки, в которых гипербола пересекается линией, проходящей через две фокусные точки. vinculum Бар над подкоренным числом. функция переноса Функция, которая отображает действительные числа в точках единичной окружности. ось x Горизонтальная ось. ось Y: Вертикальная ось. Y-пересечение графика Y-координата точки, в которой линия пересекает ось Y. нулевая матрица Матрица размера m x n, все элементы которой равны нулю. 
 Домен является независимой переменной. Диапазон является зависимой переменной.
Домен является независимой переменной. Диапазон является зависимой переменной.