Методическая разработка по алгебре (8 класс) на тему: открытый урок по математике на тему «Линейные уравнения с двумя переменными»
Содержание урока:
Организационный момент: здравствуйте, ребята.
Получать новые знания то же самое, что покорять горные вершины. Сегодня мы будем покорять вершину математических знаний [слайд 1].
В путешествии нам потребуется журнал маршрута [слайд 2].
Актуализация прежних знаний
Откроем его [слайд 3]. Что мы видим?
10+x=15, 2x=6, x2+4x=16, 3x-15=0, 5x+y=7, x2=9, 2×4+5×2-6=0, 0.5×3-4×2+2x-5=0.
-Уравнения.
— А что такое уравнение?
— Уравнение – это равенство, содержащее переменную.
Какие уравнения вам известны? Назовите.
Называют. Какое это уравнение?
Линейные, квадратные, кубические, биквадратные, и т. д.
Какое уравнение осталось? 5x+y=7, чем оно отличается?
Оно содержит две переменных.
На этом уроке мы рассмотрим уравнения с двумя переменными.
Запишите в тетрадях число и тему урока: «Линейные уравнения с двумя переменными» [слайд 4]
А теперь сформулируем цель урока.
Цель: узнать, что такое линейное уравнение с двумя переменными, найти способы его решения [слайд 5]
Перед нами первая ступень горной вершины знаний
На доске представлены задачи, [слайд 6]
1) Разность утроенного первого числа и удвоенного второго числа равна 12.
Найдите эти числа.
2) Площадь прямоугольника равна 36 см2. Каковы длины сторон?
3) Периметр равнобедренного треугольника равен 16 см. Чему равны длины его сторон?
4) Гипотенуза прямоугольного треугольника равна 5 см. Чему равны его катеты?
Нужно перевести их на математический язык. Обратите внимание на то, что для перевода этих задач на математический язык необходимо ввести две переменные, например, x и y. (пусть пробует дети без подсказки).
Разбор каждой задачи с записью на доске.
Сверим наши записи с журналом маршрута [слайд 7].
1) 3х – 2у=12
2) ху=36
3) 2х+у=16
4) x2+y2 =25
Если есть ошибки проанализировать и
Запишем в тетрадях результат.
Такие равенства называются уравнениями с двумя неизвестными.
Сформулируем определение уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала маршрута [слайд 8].
уравнением с двумя переменными называется равенство, содержащее две неизвестные величины.
Перед нами вторая ступень горной вершины и новое испытание.
Давайте к каждому из составленных уравнений подберём пару чисел, чтобы равенство было верным.
Учащиеся называют пары чисел, учитель записывает на доске.
Только ли положительные числа являются решением уравнений?
Записываем.
Полученные пары являются решениями данных уравнений с двумя переменными.
Сформулируем определение решения уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала нашего маршрута [слайд 9].
решением уравнения с двумя переменными называется всякая пара значений переменных, которая обращает это уравнение в верное числовое равенство
А сейчас перед нами третья ступень горной вершины.
Вспомним вторую задачу [слайд 10].
Обратите внимание на то, что отрицательные корни не являются решением этой задачи
[слайд 11]. Рассмотрим первое и третье уравнение, чем они похожи и чем отличаются от других.
Такие уравнения являются линейными.
Сформулируем определение линейного уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала маршрута [слайд 12].
линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c произвольные числа.
А вот и четвёртая ступень горной вершины.
Определите, какие из следующих уравнений являются линейными с двумя переменными [слайд 13].
- 2х – 10у = 3
- +3у = 1
- х + 0,5у = 4
- 5х – 2у2 =7
- 3х – у = 0
+ = -1
А сейчас попробуем решить линейное уравнение [слайд 14].
x+2y=4
Применим метод подбора.
Записать на доске.
Существует более простой способ решения линейных уравнений с двумя переменными. (варианты)
Посмотрим в журнал маршрута и запишем [слайд 15].
Для нахождения решений линейного уравнения с двумя переменными можно выражать одну переменную через другую.
Попробуем решить ещё одно уравнение [слайд 16]. Решите уравнение относительно Y.
Проверим по журналу маршрута [слайд 17].
Подберите несколько пар чисел, которые являются решением данного уравнения.
Минутка релаксации с цветотерапией
Перед самыми трудными испытаниями сделаем привал, отдохнём. [слайд 18].
Мы подошли к самым трудным ступеням, которые вы должны пройти самостоятельно. Решают номера [слайд 19]. №571 (а,в), 574.
[слайд 20] №575
Сравним ваши решения с журналом маршрута [слайд 21]
Подведение итогов.
Вот мы с вами и добрались до вершины [слайд 22]. Вспомните цель нашего урока, достигли ли мы её? Что помогло нам добиться успеха? С каким новым понятием мы познакомились? Что для вас было самым сложным на уроке? Какие качества характера помогли нам справиться с этими трудностями.
Выставление оценок.
Рефлексия «Плюс, минус»
Ребята заполните анкеты, в которых подчеркните тот вариант, который вам подходит для оценки нашего урока.
1.На уроке я работал | активно / пассивно |
Домашнее задание: А маршрут выполнения домашнего задания будет зависеть от того, какую оценку вы хотите получить. На 5, на 4 и на 3.
№ 572, 573, 577
На память о нашем восхождении к вершине примите в подарок фото, на котором есть определение линейного уравнения и алгоритм его решения. Вы можете им пользоваться при подготовке домашнего задания, а также заучить его в качестве основного правила.
План-конспект урока по алгебре (8 класс) по теме: «Линейное уравнение с двумя переменными»
Тема: «Линейное уравнение с двумя переменными»
Учитель математики Пестрова Е.А.
Цель:
1. Дать понятие линейного уравнения с двумя переменными,
решения уравнения с двумя переменными; познакомить со свойствами уравнений с двумя переменными; закрепить понятие линейного уравнения с одной переменной.
2. Развивать вычислительные навыки, речь, мышление, память.
3. Воспитывать самостоятельность активность, трудолюбие, любовь к математике.
Оборудование: Компьютер, проектор для просмотра презентации
Ход урока
Эта часть урока сопровождается презентацией
I Организационное начало урока.
-Здравствуйте, сегодня урок алгебры
II. Сообщение темы и цели.
-Сегодня, на уроке мы познакомимся с уравнениями нового вида — «Линейными уравнениями с двумя переменными».
III. Актуализация знаний учащихся.
-Посмотрите на доску. Какие из этих уравнений вам уже знакомы?
7х2+3х+5=0 5х+9=54
4х+9у=7 9(х2+6х+2)-8=30
x2/3+y2/2=1 4(х+2)+1=х+18.
-А как называются эти уравнения?
-Правильно это линейные уравнения с одной переменной.
-А кто скажет определение линейного уравнения с одной переменной?
-Уравнение вида ах = в, в котором x- переменная, а а и в – некоторые числа , называется линейным уравнением с одной переменной.
-Приведите примеры линейных уравнений с одной переменной.
-Посмотрите на доску, перед вами линейные уравнения. Давайте вспомним как они решаются.
-Все решают уравнения в тетрадях, а Оля пойдет к доске и решит с подробным объяснением первое уравнение: 2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе части уравнения на 2, получим х=2).
-Молодец. Садись.
-Второе уравнение пойдет решать Саша.
2(х+3)+4=х-1.
(Раскроем скобки, для этого умножим 2 на каждое слагаемое суммы (х+3), получим 2х+6+4=х-1. Перенесем слагаемые, содержащие х в левую часть уравнения, а не содержащие х – в правую часть, изменив при этом знаки на противоположные.
2х-х= -6-4-1.
Приведем подобные слагаемые : х = — 11.
Ребята , такие уравнения вы хорошо умеете решать.
А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак , то получится уравнение, равносильное данному.)
А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.)
IV. Изучение нового материала.
-Ребята, а сегодня мы познакомимся с уравнениями нового вида.
-Пусть известно , что одно их двух чисел на 5 больше другого. Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства х-у=5, содержащего 2 переменные. Такие уравнения называются уравнениями с двумя переменными или уравнениями с двумя неизвестными.
-Уравнениями с двумя переменными также являются уравнения:
5х+2у=10, -7х+у=5, х2+у2=20 , ху=12 (запись на доске).
-Из этих уравнений первые два имеют вид ах+ву=с, где а, в, с – числа. Такие уравнения называются линейными уравнениями с двумя переменными.
-Итак: Линейным уравнением с двумя переменными называется уравнение вида ах+ву=с где х и у – переменные, а, в, с, — некоторые числа .
-Откройте учебники на странице 188.Прочитайте определение про себя.
-Теперь прочитайте вслух.
-А кто из вас повторит его ?
-уравнение х-у=5, при х=8, у=3. Обращается в верное равенство 8-3=5. Говорят, что пара значений переменных х=8, у=3 является решением этого уравнения. Записываю на доске:
х-у=5, х=8, у=3
8-3=5 — верное равенство.
Определение: Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
-Прочитайте это определение на странице 188 про себя.
-Прочитайте его вслух. -Кто повторит?
-А какие еще пары чисел будут являться решениями уравнения х-у=5? (х=105, у=100; х=4, у= -1,…)
-Правильно решениями этого уравнения будут являться числа, разность которых равно 5.
-Иногда пары значений переменных записывают короче: (105; 100), (4;- 1). ( Запись на доске).
-При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором.
-в записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
-Уравнения с двумя переменными имеющие одни и те же решения, называют равносильными. уравнения с двумя переменными, не имеющие решений, также считают равносильными.
-Ребята, при решении линейных уравнений с одной переменной мы вспомним их свойства.
-Линейные уравнения с двумя переменными обладают такими же свойствами.
-Откройте учебники на стр. 189. Прочитайте эти свойства про себя.
-А теперь Таня , прочитай вслух. Повтори свойства.
-Рассмотрим уравнения 5х+2у=12.
-Воспользовались свойствами уравнений, выразим из этого уравнения одну переменную через другую , например у, через х. Для этого перенесем слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=2,5х+6, можно найти сколько угодно решений уравнения 5х+2у=12. Для этого достаточно взять произвольное х и вычислить соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12.
Это уравнение имеет бесконечно много решений.
V .Первичное закрепление.
-Что же называется линейным уравнением с двумя переменными?
-Выполним № 1092 на странице 190 устно.
-Прочитай задание.
-Является ли первое уравнение 3х-у=17 линейным? (Да).
-Почему? (Т.к. имеет вид ах+ву=с)
-А второе упражнение? (Нет).
-Почему? (Т.к. уравнение х2- 2у=5 не приводится к виду ах+ву=с, х имеет показатель степени 2).
(Далее аналогично).
-А теперь запишите № 1094.
-Читай задание .
-Как ответить на этот вопрос? (Поставить значение х и у в уравнение. Если получится верное равенство, то х и у является решением уравнения)
-Все решайте в тетрадях, а……. у доски.
х + у=6
6=6 – верное равенство.
Ответ: да.
-А какие еще числа могут быть решениями этого уравнения х+у=6. (Дающие в сумме 6: 4 и 2, 3 и 3 и т.д.).
-Запишите любые 2 решения этого уравнения.
-Не забывайте, что значение х пишется на первом месте а у – на втором месте.
Самостоятельная работа.
-А теперь выполним № 1096. запишите.
-Прочитай задание.
-Что нужно сделать, чтобы ответить на вопрос? (Подставить значения х и у в уравнение и посмотреть, получится ли верное равенство).
а) .Организация самостоятельной работы.
-Все решают в тетрадях, а к доске пойдут Лена и Оля.
-Саша проверит первые 2 пары, а Катя вторые 2 пары.
-А потом проверим.
б) Проведение самостоятельной работы.
(3; 1 ) (0; 10)
3*3+1>10 3*0+10=10.
10=10 – верное равенство 10=10 верное равенство
Ответ: является Ответ: является
(2; 4) (3; 2,5)
3*2+4=10 3*3+2.5=10
10=10 – верное равенство 11,5=10 – неверное равенство
Ответ: является Ответ: не является.
в) Проверка самостоятельной работы.
-Давайте проверим правильно ли выполнила Оля.
-У кого другой ответ? -А Лена?
-У кого другой ответ?
-Молодцы. Садитесь.
-А теперь выполним № 1099.
-Прочитай задание.
-Что нужно сделать, чтобы выразить у через х? (Представить, что х известное число и найти у )
-Пойди к доске реши с объяснением, а все решают в тетрадях.
4х-3у=12.
(Одночлен 3у является неизвестным вычитаемым. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность 3у=4х-12 .
Разделим обе части уравнения на 3, получим:
-Молодец. Садись.
А теперь выполним пункт б, Сережа иди к доске.
4х-3у=12.
(Одночлен 4х является неизвестным уменьшаемым, чтобы его найти, надо к разности прибавить вычитаемое: 4х=12+3у. Разделим обе части уравнения на 4 и получим:
-Правильно. Молодец. Садись .
VI. Подведение итогов.
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
VII.Домашнее задание: 1101(а,б), 1103, 1105(г,д),1107.
Презентация по алгебре (8 класс) на тему «Линейное уравнение с двумя переменными»
Линейное уравнение с двумя переменными.
Выполните задания.
1. Решите уравнение:
а) 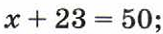 б)
б) 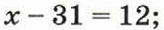 в)
в) 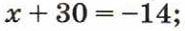
г) 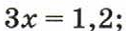 д)
д) 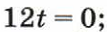 е)
е) 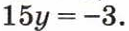
2. Сколько переменных содержится в уравнениях задания № 1.
3. Каким является уравнение вида ах = b? Чем являются а и b в данном уравнении? Как называют х в уравнении?
4. Что значит решить уравнение?
5. Сколько корней имеет уравнение вида ах = b?
6. Попробуйте подобрать два числа, сумма которых равна их удвоенной разности.
1. Обозначьте одно число за х, а другое число за у.
2. Запишите сумму этих чисел.
У вас получилось выражение х + у.
3. Запишите разность этих чисел. Запишите удвоенную разность.
У вас получилось выражение х – у, а затем выражение 2(х – у).
4. Составьте математическую модель (уравнение) по условию задания.
У вас получилось уравнение х + у = 2(х – у).
Такое равенство называют уравнением с двумя переменными.
5. Подберите пару чисел, которая обращает это уравнение в верное равенство.
Такими парами чисел являются:
х9
15
– 6
30
6
– 9
6
3
5
– 2
10
2
– 3
2
Часто пару чисел записывают в скобках (х; у), то есть (9; 3), (15; 5), (–6; –2) и так далее.
Каждую такую пару чисел называют решением уравнения с двумя переменными.
Определение.
Линейным уравнением с двумя переменными называется уравнение вида ах + bу = c, где а, b и с – произвольные числа.
Например, 6х – 5у = 7. Подберите пару чисел, которая является решением этого уравнения.
Вы убедились, что в таком виде подбирать решение очень не удобно.
Выразим из уравнения 3х + 5у = 10 переменную у через переменную х:
5у = –3х + 10 | :5
у = –0,6х + 2.
В данном случае говорят, что решили уравнение относительно переменной у.
В таком виде уравнение очень удобно использовать для нахождения его решения (пары чисел).
Возьмём значение х = 0 и подставим в уравнение:
у = –0,6 ∙ 0 + 2 = 0 + 2 = 2,
получаем решение (0; 2).
Возьмём значение х = –1 и подставим в уравнение:
у = –0,6 ∙ (–1) + 2 = 0,6 + 2 = 2,6,
получаем решение (–1; 2,6)
Как вы думаете, сколько существует таких пар чисел, которые являются решением уравнения 3х + 5у = 10.
Выполнить № 571 (б), 574 (2,4,6), 575, 576 (в), 577 (а), 579*(б,г)
Домашнее задание:
п. 4.1, № 571 (а,в), 574 (1,3,5), 576 (а), 577 (б), 579*(а,в)
План-конспект урока по алгебре (8 класс) на тему: конспект урока по алгебре «Линейное уравнение с одной переменной»
Тема: «Линейное уравнение с одной переменной»
Цели урока: 1) образовательная:
— закрепление умений и навыков решения уравнений с одной переменной;
— ознакомление с методикой решения уравнений с модулем;
-формирование у каждого ученика навыка самообучения и самоконтроля.
2) развивающая:
— развитие логики, умения анализировать;
— развитие вычислительных навыков.
3) коррекционная:
— развитие слухо-зрительного восприятия;
— привитие навыков соблюдения орфоэпических норм в самостоятельной речи;
— контроль над произношением учащихся.
4) воспитательная:
— развитие чувства товарищества, взаимопомощи;
-воспитание интереса к предмету;
— расширение кругозора учеников.
Оборудование: плакаты, индивидуальные карточки с тестовыми заданиями, проектор, ноутбук.
Тип урока: комбинированный
Формы работы учащихся: фронтальная, работа в парах, индивидуальная.
Словарь: уравнение, корень уравнения, решить уравнение, равносильные уравнения, линейные уравнения, переменная, раскроем скобки, перенесем слагаемые, изменим знаки, приведем подобные члены, разделим (умножим) обе части уравнения на.., модуль.
- Орг. Момент. Проверка слуховых аппаратов.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В алгебры мир отправимся смело,
В мир уравнений и разных задач. (Слайд 2)
— А девизом нашего урока будут такие слова:
Думать – коллективно!
Решать – оперативно!
Отвечать — доказательно!
Учиться – старательно!
— Давайте сегодня на уроке следовать этому совету. Будем активны. Желаю вам доброго дня и хорошего настроения.
2. Актуализация опорных знаний:
1) (Ответы на вопросы)
- Что такое числовое выражение?
- Что такое буквенное выражение?
- Что называется уравнением?
- Что значит «решить уравнение»?
- Что называется корнем уравнения?
6. Какие уравнения называются равносильными?
7. Какие уравнения называются линейными? (Слайд 4)
2) — Являются ли данные уравнения линейными? (Слайд 5)
3x = 9
(x -3)(y + 5)= 0
2 (3x -5) = x-3
3×2 + 6x +7 =0
3)Найдите все решения уравнения ax = b (Слайды 6,7)
4) Приведите уравнение к линейному виду ax = b: (Cлайд 8)
Исходное уравнение | результат |
5(x – 8) = 3 (x – 6 ) | 2x =22 |
— 3 x -5 = -5 | -3x= 0 |
5) Найдите корни уравнения: (x – 5) (x + 6) = 0 (Cлайд 9)
3 . Физминутка для глаз (Слайды 10, 11)
4. Выполнение уравнений у доски и в тетрадях (Слайд 12)
- 2(3х — 1) = 4(х + 3)
2(3х — 1) = 4(х + 3) + 2х
2(3х — 1) = 4(х + 3) – 14 +2x
2)Решите уравнение на скорость: (Слайд 13)
8 x + 5,9 = 5 x+ 20
5.Линейные уравнения с модулем (Слайд 14)
— Ребята, что такое модуль?
Модуль числа а – это расстояние (в единичных отрезках) от начала координат до точки А(а)
| 5 |= 5; | -5 |= 5;
— Что вы знаете о модуле? (Слайд 15)
Ответы учащихся.
— Модуль положительного числа равен самому этому числу.
— Модуль отрицательного числа равен противоположному числу.
— Модуль нуля равен нулю.
— Уравнение , содержащее переменную под знаком модуля, называется уравнением с модулем. (Слайд 16)
| x |= a, a > 0
x = a или x = -a
— Рассмотрим примеры: (Слайд 17)
| x -6|= 3
x-6 =3 или x-6 = -3
x=9 или x=3
Ответ . 9;3.
| x -6|= 0
x-6 = 0
x=6
Ответ. 6
| x -6|= -3
Корней нет.
— «Решите уравнения» (Слайд 18)
| 2 +x |= 4
| 2 +x |= 0
| 2 +x |= -7
- Динамическая пауза «Две сестрицы – две руки» (Слайды 19 -28)
- Выполнение теста. Взаимопроверка. (Слайды 29,30 )
- Подведение итогов. Рефлексия. (Слайд 31)
— Чему научил вас урок?
— Легко или трудно было вам?
— За что вы можете похвалить себя?
— Какую оценку поставите себе за урок?
- Домашнее задание.
Конспект урока по математике «Линейные уравнения с двумя переменными» (8 класс)
План-конспект урока
Линейные уравнения с двумя переменными
Предмет: математика
Класс: 8
Цель урока: создать условия для расширения понятийной базы по теме “Линейное уравнение с двумя переменными”, вывести алгоритм решения линейного уравнения с двумя переменными.
Задачи:
— обучающие: создать условия
— для формирования понятий: “уравнение с двумя переменными”, “решение уравнения с двумя переменными”, “линейное уравнение с двумя переменными”;
— для получения алгоритма решения линейного уравнения с двумя переменными.
— развивающие: создать условия
— для развития умения работать с новой информацией;
— для развития умения делать выводы, рассуждения;
— для развития способности к рефлексии.
— воспитательные: создать условия
-для воспитания познавательного интереса к открытию новых знаний и применения их практической деятельности.
Структура и ход урока:
№
Этап урока
Название используемого оборудования, программного обеспечения, информационных ресурсов
Деятельность учителя
Деятельность ученика
Время (в мин.)
1
Организационный
момент
1
Демонстрация презентации на интерактивной доске Педагог приветствует учащихся, проверяет готовность к уроку, обращает внимание на слайды 1,2 презентации
Ученики приветствуют учителя, проверяют готовность к уроку, видят горную вершину математических знаний и журнал маршрута, который будет помогать в пути.
1 мин.
2
Актуализация знаний (решение проблемной ситуации)
1
Предлагает обратить внимание на слайд 3, где изображены различные уравнения и через различные поисковые вопросы побуждает к решению проблемной ситуации
Учащиеся, отвечая на вопросы решают проблемную ситуацию и плавно подходят к теме урока
1 мин.
3
Формулирование темы и цели урока
2
Учитель предлагает сформулировать тему урока, а затем его цель.
Записывается тема и цель урока.
Формулируют тему и цель урока, записывают их в тетради.
3 мин
4
Ознакомление с новым материалом:
А) пробные учебные действия, приводящие к понятию уравнения с двумя переменными, решения уравнения с двумя переменными и линейного уравнения с двумя переменными.
Б) построение алгоритма решения линейного уравнения с двумя переменными и его первичное закрепление
1,2,3
Учитель обращает внимание детей на запись на интерактивной доске, где представлены задачи, условия которых необходимо перевести на математический язык.
Учитель предлагает сформулировать определение уравнения с двумя переменными.
Учитель говорит, что добрались до второй ступени горной вершины и предлагает к каждому из составленных уравнений подобрать пару чисел, чтобы равенство было верным.
Исходя из полученных результатов, педагог подводит детей к формулировке определения решения уравнения с двумя переменными.
Учитель сообщает о третьем испытании, в ходе, которого сравнивая уравнения, находя общее и различное между ними формулируется определение линейного уравнения с двумя переменными.
Учитель презентует четвёртое испытание
с помощью документ-камеры выводит на интерактивную доску различные уравнения, среди которых нужно найти линейные с двумя переменными
Там же демонстрируются два уравнения, которые необходимо решить различными способами и найти наиболее эффективный.
Ученики разбирают каждую задачу, один из учеников записывает её на интерактивной доске. Затем сверяют записи с журналом маршрута на слайде 7.
Ученики формулируют, затем записывают определение из журнала маршрута (слайд 8)
Учащиеся подбирают пары чисел, один записывает на доске, другие в тетради.
Ученики формулируют, затем записывают определение из журнала маршрута (слайд 9)
Учащиеся формулируют, затем записывают определение из журнала маршрута (слайд 12)
Учащиеся находят, доказывают свою точку зрения.
Учащиеся решают, записывают решение и проверяют по журналу маршрута (слайд 17)
15 мин.
5
Минутка релаксации с цветотерапией
4
Учитель через гиперссылку в презентации открывает видеоролик и предлагает отдохнуть перед трудными испытаниями.
Учащиеся снимают мышечное, эмоциональное и зрительное напряжение с помощью сочетания музыки, цвета
3 мин.
6
Осмысление и закрепление нового материала (самостоятельная работа с самопроверкой по эталону)
1,2
Учитель сообщает о том, что подошли к самым трудным ступеням, которые вы должны пройти самостоятельно и предлагает решить номера на слайдах 19,20.
Учащиеся самостоятельно выполняют задания, потом осуществляется самопроверка по журналу маршрута (слайд 21)
10 мин.
7
Подведение итогов.
2
Учитель задаёт вопросы:
Вспомните цель нашего урока, достигли ли мы её? Что помогло нам добиться успеха? С каким новым понятием мы познакомились? Что для вас было самым сложным на уроке? Какие качества характера помогли нам справиться с этими трудностями.
Выставление оценок.
Учащиеся отвечают.
1 мин.
8
Рефлексия «Плюс, минус» (самооценка результатов деятельности) с помощью интерактивного коммуникатора Enjoy
6
Учитель просит учеников отметить эффективность урока с помощью голосования, выводит результат на доске и анализирует
Ученики голосуют, обсуждают что получилось, что не удалось
3 мин.
9
Домашнее задание и стимулирование к его выполнению
5
Учитель даёт ученикам свой электронный адрес, предлагается решить задание на дополнительную оценку
Ученикам дома необходимо их решить и прислать решение на электронный адрес учителя
4 мин.
Перечень используемого на уроке учебного оборудования, программного обеспечения, информационных ресурсов.
№
Наименование
Назначение
1
На интерактивной доске размещена презентация, слайды которой будут сопровождать обучение
Наглядность материала с использованием современных возможностей активизирует интеллектуальные способности учащихся .
Интерактивное задание успешно решает проблему мотивации ученика на активное познание и достижение успеха в учебной деятельности
2
3
Интерактивное изучение нового материала с использованием возможностей интерактивной доски: тексты, уравнения можно скрыть, а затем показать в ключевые моменты урока, возможность вернуться к предыдущему этапу урока и повторить ключевые моменты занятия. Инструмент «прожектор» позволяет сфокусировать внимание на определенных участках экрана. Вариативность цветовых решений.
Использование документ-камеры для демонстрации уравнений
Эти возможности позволяют сделать изучение нового материала увлекательным восхождением на вершину математических знаний. Материал чётко структурирован, что улучшает темп и течение урока. Можно выделять важные области и привлекать внимание к ней, связывать общие идеи или показывать их отличие и демонстрировать ход размышления.
Экономит время на запись уравнения
4
Использование видеоролика для релаксации с цветотерапией
С помощью видео-ресурса можно снять мышечное и эмоциональное напряжение учащихся
Данный метод помогает осуществить взаимосвязанный переход к следующему виду работы.
5
Решение дополнительного задания с применением электронной почты учителя, учеников
Мотивированность учащихся на получение более высокого результата по предмету с помощью Интернет-ресурсов.
6
Электронное голосование Enjoy
Быстро и эффективно оценить работу, получить обратную связь, наметить новые учебные задачи.
Литература:
1. Дорофеев Г.В. и др. Алгебра. 8 класс: учебник для общеобразовательных организаций. — М.: Просвещение, 2010. – 288 с.
2. Дюмина Т.Ю.Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г.В. Дорофеева. II полугодие. – Волгоград: Учитель, 2011.- 253 с.
Презентация урока для интерактивной доски по алгебре (8 класс) на тему: Линейные уравнения
Слайд 1
Вводное повторение Светцова Валерия Валерьевна учитель математики МАОУ СОШ № 25 г.Владимир 2018Слайд 2
« Незнающие пусть научатся, знающие — вспомнят еще раз». ( Античный афоризм.)
Слайд 3
19 x -3 x +4 x =80 ( x +1)( x +2)-( x +3)( x +4)=0 9 x 2 -1-(3 x -2) 2 =0 Как мы называем данные равенства?
Слайд 4
Линейные уравнения
Слайд 5
Древнегреческий математик?
Слайд 6
Диофант
Слайд 7
Прах Диофанта гробница покоит; дивись ей и камень Мудрым искусством его скажет усопшего век. Волей богов шестую часть жизни он прожил ребенком. И половину шестой встретил с пушком на щеках. Только минула седьмая, с подругой он обручился. С нею, пять лет проведя, сына дождался мудрец; Только полжизни отцовской возлюбленный сын его прожил. Отнят он был у отца ранней могилой своей. Дважды два года родитель оплакивал тяжкое горе, Тут и увидел предел жизни печальной своей.
Слайд 8
(альфа) – 1 (бета) – 2 (гамма) – 3 ( эпсилон) – 5 ( дзета ) – 6 (эта) – 8 ( иота ) – 10 (сигма ) — 200 (ζ ) — «какое-то число», неизвестное число — квадрат неизвестного — свободный член Знак сложения Диофант не применял, просто записывал слагаемые друг за другом . Знаком вычитания служил символ ↑ . Равенство обозначалось буквой ι ( иота ) Символика Диофанта
Слайд 9
Уравнение 2 x +5=6 у Диофанта выглядело бы так : ζ ι
Слайд 10
1) Запишите уравнение 6x+3=8 , используя символику Диофанта . 2) Переведите уравнение ζ на современный язык . 3) Составьте своё уравнение в символике Диофанта . 4) Найдите ошибку в переводе уравнения 2𝑥+5𝑥=3 в символику Диофанта ζβ̅↑ ζε ̅ ιΜ ο γ ̅ ? 6) Найдите общие черты в записях между уравнением в символике Диофанта и уравнением в современных символах. Задание
Слайд 11
Выберите фразеологизм или пословицу которые характеризуют вашу работу сегодня на уроке. o Шевелить мозгами o Краем уха o Хлопать ушами
Слайд 12
Домашнее задание 1) Составьте своё уравнение в символике Диофанта . 2) Запишите уравнение 3x+2=6 , используя символику Диофанта . 3) Составьте брошюру о Диофанте, и его символике для записи уравнений.
Слайд 13
Благодарю за внимание!
Слайд 14
Вы можете использовать данное оформление для создания своих презентаций, но в своей презентации вы должны указать источник шаблона: Фокина Лидия Петровна учитель начальных классов МКОУ «СОШ ст. Евсино» Искитимского района Новосибирской области Сайт http://linda6035.ucoz.ru/ На момент создания ресурса ссылки являются активными Информационные источники Шаблон составлен из фигур программы PowerPoint Для ф она скрап-набор https:// photoshop-master.ru/adds/scrapbooking/20093-skrap-nabor-yarmarka-chast-2.html
Презентация к уроку по алгебре (8 класс) по теме: Презентация «Линейные уравнения» для подготовки к ГИА в 9 классе
Слайд 1
Уравнения.Слайд 2
Линейные уравнения Линейным уравнением с одной переменной х называют уравнение вида ах = b , где а – коэффициент при переменной, b – свободный член.
Слайд 3
Три случая для линейного уравнения. 1.а ≠ 0, в этом случае корень уравнения равен b /а; 2.а = о, b = 0, уравнение принимает вид 0х = 0,т.е. корнем уравнения служит любое действительное число; 3.а = о, b ≠ 0, уравнение принимает вид 0х = b корней не имеет.
Слайд 4
Пример линейного уравнения 3(2 +1,5х) = 0,5х + 24 6 + 4,5х = 0,5х + 24 4,5х – 0,5х = 24 – 6 4х = 18 х = 4,5 Ответ: х = 4,5
Слайд 5
Решите уравнение. 2х – 5,5 = 3(2х-1,5)
Слайд 6
Квадратное уравнение. Квадратным уравнением называется уравнение ах ² + b х + с = 0, где а, b ,с – заданные числа, а≠0, х- неизвестное.
Слайд 7
Корни уравнения Находят по формуле х = Выражение D = b² -4ас дискриминант квадратного уравнения. Если D 0, то уравнение имеет два корня. Если D= 0, то уравнение имеет один корень.
Слайд 8
Пример квадратного уравнения 2х ² – 5х + 2 = 0 D = b² – 4ас =25 – 4 · 2 · 2 =9 D>0 уравнение имеет два корня. х 1 = х 2 = Ответ:х 1 =1/2, х 2 =2
Слайд 9
Теорема Виета Если приведённое квадратное уравнение х ² + рх + q = 0 имеет действительные корни, то их сумма равна –р, а произведение равно q , х 1 + х 2 = -р х 1 · х 2 = q
Слайд 10
Решите квадратное уравнение х ² + 5х + 6 = 0
Слайд 11
Неполное квадратное уравнение. Если в квадратном уравнении ах ² + b х + с =0 второй коэффициент b или свободный член с равен нулю, то квадратное уравнение называют неполным. Решить такое уравнение проще методом разложения его левой части на множители.
Слайд 12
Пример неполного квадратного уравнения. 3х ² — 27 = 0 3(х ² -9) = 0 3(х + 3)(х — 3) = 0 (х + 3) = 0 или (х — 3) = 0 х =-3 х = 3 Ответ: х =-3 и х = 3.
Слайд 13
Решите неполное квадратное уравнение 2х ² +8х = 0
Слайд 14
Биквадратное уравнение. Биквадратным уравнением называется уравнение вида ах 4 + b х ² +с = 0, где а≠0. Биквадратное уравнение решается методом введения новой переменной.
Слайд 15
Пример биквадратного уравнения 3х 4 -13х ² +4 = 0 Обозначим х ² = у, у >0 получим квадратное уравнение 3у ² -13у + 4 = 0 D=b² -4ас= 13 ² -4 · 3 · 4 =121 D> 0 у 1 = =4 у 2 = =1/3 У 1 = 4, у 2 = 1/3 х ² = 4 имеет корни х 1 =-2, х 2 =2 х ² =1/3 имеет корни х 3 = х 4 = Ответ: х 1 =- 2, х 2 =2, х 3 = х 4 =
Слайд 16
Решите биквадратное уравнение. 2х 4 — 19х ² +9 = 0
Слайд 17
Проверьте. 2х – 5,5 = 3(2х-1,5) 2х – 5,5 = 6х – 4,5 2х – 6х = 5,5 – 4,5 -4х = 1 х = 1 : ( -4) х = -1/4 Ответ: х =-1/4 ( 1 бал) х ² + 5х + 6 = 0 D=b ² -4ас=25-4 · 6 · 1=1 D>0 Х 1 = = -2 Х 2 = =-3 Ответ:х 1 =-3 х 2 =-2 ( 1 бал) 2х ² +8х = 0 2х(х + 4) = 0 2х = 0 или х + 4 = 0 х = 0 х = -4 Ответ: х 1 =-4, х 2 =4 ( 1 бал) 2х 4 — 19х ² +9 = 0 Обозначим х ² =у, у > 0 получим квадратное уравнение 2у ² – 19у +9 = 0 D = b ² -4ас=19 ² -4 · 2 · 9=289 D> 0 у 1 = у 2 = У 1 =9, у 2 =1/2 х ² =9 х 1 = 3, х 2 =-3 х ² =1/2 х 3 = х 4 = Ответ: х 1 =-3, х 2 =3, х 3 = х 4 = (2 бала)