Предел числовой последовательности. Сумма бесконечной геометрической прогрессии
В этом уроке вы рассмотрите предел числовой последовательности, узнаете определение числовой последовательности. Познакомитесь с теоремой для вычисления пределов конкретных последовательностей, а также с суммой бесконечной геометрической прогрессии, разберете конкретные примеры. В заключение вспомните апории Зенона, согласно которой, как он доказывал, Ахиллес никогда не догонит черепаху
Числовая последовательность – частный случай функции, которая задана на множестве натуральных чисел. Некоторые числовые последовательности сходятся, то есть имеют предел, тогда пишут  либо по-иному:
либо по-иному:  когда
когда 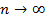 , это означает, что при достаточно больших
, это означает, что при достаточно больших 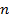 ,
,  .
.
Более точно, если у нас есть предел и его 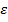
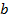 .
.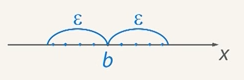
Рис. 1.Члены последовательности находятся в -окрестности точки 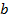
Пример 1
Последовательность 
 , это означает, что при достаточно больших
, это означает, что при достаточно больших  , все
, все  находятся вблизи от нуля. Может ли быть здесь два предела? Докажем, что если последовательность имеет предел, то он только один.
находятся вблизи от нуля. Может ли быть здесь два предела? Докажем, что если последовательность имеет предел, то он только один.Вот последовательность  и два предела (рис. 2).
и два предела (рис. 2).

Рис. 2.Последовательность  и два предела
и два предела 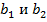
Что значит 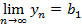 ? Это означает, что найдется такая малая окрестность точки
? Это означает, что найдется такая малая окрестность точки 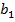
А что значит 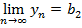 ? Это означает, что начиная с некоторого номера все члены последовательности находятся в -окрестности точки
? Это означает, что начиная с некоторого номера все члены последовательности находятся в -окрестности точки 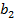 . Но возможно ли это? Между
. Но возможно ли это? Между 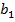 и
и 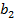
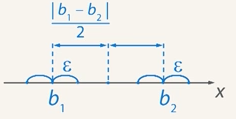
Рис. 3. Расстояние между 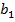 и
и 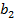
Выберем 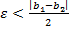
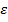 -окрестности не пересекаются. Начиная с некоторого номера все члены последовательности находятся в ε-окрестности одной точки и второй точки, но эти ε-окрестности не пересекаются. Таким образом, если у последовательности есть предел, то он один.
-окрестности не пересекаются. Начиная с некоторого номера все члены последовательности находятся в ε-окрестности одной точки и второй точки, но эти ε-окрестности не пересекаются. Таким образом, если у последовательности есть предел, то он один.Определение: число 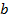 называется пределом последовательности
называется пределом последовательности  , если в любой заранее выбранной -окрестности точки
, если в любой заранее выбранной -окрестности точки 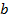 ,
, 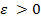
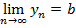
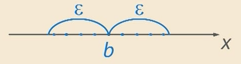
Рис. 4.
Число 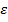
Если последовательность сходится, то:
- только к одному пределу;
- она ограничена.
Как узнать, что последовательности сходятся? Для некоторых последовательностей это можно сделать. Если последовательность монотонна и ограничена, то она сходится.
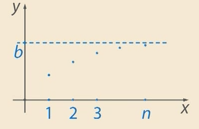
Рис. 5. Иллюстрация к теореме Вейерштрасса
Последовательность возрастает. Число точек не ограничено, последовательность ограничена числом 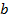 . Значит, к числу
. Значит, к числу 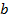
Даны две последовательности 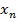 и
и  ,
, 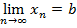 и
и 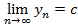
 – новая последовательность, ее предел
– новая последовательность, ее предел  . Предел суммы последовательностей, равен сумме пределов этих последовательностей.
. Предел суммы последовательностей, равен сумме пределов этих последовательностей. . Этот предел равен произведению
. Этот предел равен произведению 
 . Предел этой последовательности, то есть предел частного равен
. Предел этой последовательности, то есть предел частного равен  , где
, где  .
.
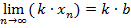 , где
, где  постоянный множитель, который можно вынести за знак предела.
постоянный множитель, который можно вынести за знак предела.
Пример 1
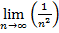 , мы знаем, что
, мы знаем, что 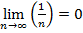 , отсюда
, отсюда 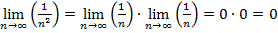 .
.
Пример 2
Найти предел последовательности 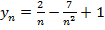 .
.
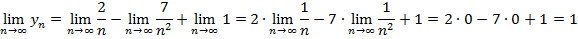
Последовательность, сходящаяся, имеет предел, равный 1.
Перейдем к следующей задаче.
Найдем сумму бесконечно убывающей геометрической прогрессии. Геометрическая прогрессия обозначается следующим образом: 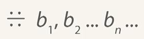 .
.
Второй член геометрической прогрессии 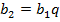 , где
, где 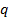 – знаменатель прогрессии, третий член
– знаменатель прогрессии, третий член 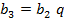 и т.д.
и т.д.
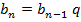 – определение геометрической прогрессии, членов у этой прогрессии бесчисленное множество.
– определение геометрической прогрессии, членов у этой прогрессии бесчисленное множество.
Прогрессия называется убывающей, если знаменатель по модулю меньше единицы:  .
.
Рассмотрим последовательность частичных сумм.
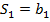
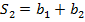
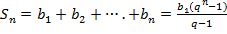 .
.
Если есть конечная геометрическая прогрессия, то сумма членов вычисляется по этой формуле. Необходимо знать первый член, знаменатель и число членов.
Бесконечная убывающая прогрессия
Если последовательность 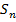 стремится к некоторому числу, то это число и будет называться суммой бесконечной геометрической убывающей прогрессии, если это число есть, то это сумма
стремится к некоторому числу, то это число и будет называться суммой бесконечной геометрической убывающей прогрессии, если это число есть, то это сумма 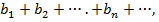 то есть это сумма беско
то есть это сумма беско
Бесконечная убывающая геометрическая прогрессия
Коротко о главном Начальный уровень
Геометрическая прогрессия. Коротко о главном.
Геометрическая прогрессия {} — это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число . Это число называют знаменателем геометрической прогрессии.
Знаменатель геометрической прогрессииможет принимать любые значения, кроме и .
- Если , то все последующие члены прогрессии имеют одинаковый знак – они положительны;
- если , то все последующие члены прогрессии чередуют знаки;
- при – прогрессия называется бесконечно убывающей.
Уравнение членов геометрической прогрессии — .
Сумма членов геометрической прогрессии вычисляется по формуле:
или
Если прогрессия является бесконечно убывающей, то:
Комментарии
Геометрическая прогрессия
Он называется геометрической прогрессией последовательность из ≥ нулевых чисел, причем каждый член начинается с другого, равного предыдущему выражению, умноженного на одно и то же число.
Таким образом, Геометрическая прогрессия числовая последовательность, определяемая соотношениями
bn + 1 = bn · q, где bn ≠ 0, q ≠ 0
q является знаменателем продвижения

Это геометрическая последовательность повышение, если b1 > 0, q > 1
Например, 1, 3, 9, 27, 81, ….
Это геометрическая последовательность уменьшается, если b1 > 0, 0 < Q < 1
К примеру, 
Формула n-го члена геометрической прогрессии
bn = b1 · qn-1
Характерная особенность геометрической прогрессии.
Численная последовательность представляет собой геометрическую прогрессию, только если квадрат каждого члена, за исключением первого (и, наконец, если конечная последовательность) равен произведению предыдущего и последующих членов.
BN2 = bn-1 · b n + 1
Сумма n первых членов Геометрическая прогрессия

Сумма n первых членов, то же самое бесконечно уменьшается геометрическая прогрессия

Основные определения и данные для геометрической прогрессии суммированы в одной таблице:
Определение геометрической прогрессии | bn + 1 = bn · q, где bn ≠ 0, q ≠ 0 |
Позиционер геометрической прогрессии |  |
| Формула n-го члена геометрической прогрессии | bn = b1 · qn-1 |
| Сумма первых выражений геометрической прогрессии |   |
| Характерная особенность геометрической прогрессии | bn2 = bn-1 · bn + 1 |
Пример 1.
Геометрическая прогрессия задается b1, b2, b3, …, bn, …
Геометрическая прогрессия
Известно, что b1 = 2/3, q = -3. Найти b6
Решение. В этом случае решение основано на формуле n-го члена геометрической прогрессии.
Если в этой формуле заменить n = 6, получим:
b6 = b1 · q5 = 2/3 · (-3) 5 = -162
Ответ -162.
Пример 2.
Найти сумму бесконечно убывающей геометрической прогрессии: 12, 4, 4/3, …
решение
b1 = 12, b2 = 4,
q = 4/12 = 1/3
S = 12 / (1 — 1/3) = 12 / (2/3) = 12 · 3/2 = 18
Ответ 18.
Пример 3.
Сумма бесконечно убывающей геометрической прогрессии равна 150.
Найти b1, если q = 1/3
решение

150 = b1 / (1 / 1/3)
b1 = 150 · 2/3
b1 = 100
Ответ: 100.
Геометрическая прогрессия Является ли числовая последовательность b1, b2, …, bn, …, которая применяется к каждому натуральному n следующего уравнения:
где q — знаменатель геометрической прогрессии, q ≠ 0 и bn ≠ 0.
Пример: последовательность чисел 3, 12, 48, 192, 768, … представляет собой геометрическую прогрессию с imenomator q = 4.
Дизайнер определяет форму геометрическая прогрессия:
- Если q > 0, то все члены геометрической прогрессии имеют один и тот же характер, уравнение b1Primer: последовательность чисел 1, 2, 4, 8, 16, … с знаменателем q = 2.
- Если q < 0, затем меняются признаки геометрической прогрессии
Пример: последовательность чисел 2, -6, 18, -54, 162, …Онлайн калькуляторы для расчета прогрессии.
с знаменателем q = -3.
- Если -1 < Q < 1, геометрическая прогрессия бесконечно уменьшается
Пример: последовательность чисел 400, 200, 100, 50, 25, … с знаменателем q = 0,5.
Основные формулы геометрической прогрессии
Позиционер геометрической прогрессии
Геометрическая прогрессия может быть рассчитана с использованием текущего и следующих условий геометрической прогрессии:
Члены геометрической прогрессии
Общая формула для вычисления n-го члена геометрической прогрессии относительно первого слагаемого и знаменателя:
Следующее выражение геометрической прогрессии можно найти из предыдущего термина и знаменателя:
Предыдущее выражение геометрической прогрессии можно найти из следующего выражения и знаменателя:
Также можно найти элемент геометрической прогрессии, если известны следующие и предыдущие термины:
bn = √bn-1 ⋅ bn + 1, где n равно > 1
Сумма геометрической прогрессии
Сумма первых n членов геометрической прогрессии равна
Sn = b1 ⋅ (1 — qn) / (1 — q), где q ≠ 1
Он также может быть рассчитан с использованием другой формулы:
Sn = (b1 — bn ⋅ q) / (1 — q), где q ≠ 1
Решение проблем в геометрической прогрессии
Рассмотрим несколько типичных задач геометрической прогрессии.
Задача 1:
В зависимости от геометрической прогрессии 3, 6, 12, …. Найдите 8-й член геометрической прогрессии и сумму первых 10 членов.
решение:
b1 = 3
q = 6/3 = 2
b8 = b1 ⋅ q7 = 3 ⋅27 = 3 ⋅ 128 = 384
S10 = B1 ⋅ (1 — Q10) / (1 — q) = 3 ⋅ (1 — 210) / (1 — 2) = 3 ⋅ (1-1024) / (-1) = 3069
Ответ: 384 и 3069
Задача 2:
Номер 486 является членом геометрической прогрессии 2, 6, 18, …
. Найдите свой номер.
решение:
Если мы используем формулу для вычисления n-го члена геометрической прогрессии, мы можем получить n:
486 = 2 ⋅ 3n — 1
243 = 3n-1
35 = 3n-1
n-1 = 5
n = 6
Ответ: 6
Задача 3:
Сумма первых членов геометрической прогрессии равна -93.
b1 = -3, q = 2. Найдите n.
решение:
Чтобы вычислить число геометрических прогрессий, мы можем использовать формулу для ее суммы:
Sn = b1 ⋅ (1 — qn) / (1 — q)
-93 = -3 ⋅ (1 — 2n) / (1 — 2)
-93 = -3 ⋅ (1 — 2n) / (-1)
-31 = 1 — 2n
2n = 32
n = 5
Ответ: 5
Сумма членов геометрической прогрессии
Геометрическая прогрессия — последовательность чисел (обычно обозначаемая как — B1, B2, B3, …), причем каждый последующий член получается путем умножения предыдущего указанного числа, называемого прогрессией и обозначаемого буквой q. В этом случае первое выражение продвижения, равно как и знаменатель, должно быть ничем.
Найти выражение геометрической прогрессии по формуле:
{b_n = b_1 \ cdot q ^ {n-1}}
В этом случае выделяются три примера:
- если b1 и q больше нуля, то прогрессия возрастает;
- если q меньше нуля, но больше 1, то прогрессия уменьшается;
- если q<0, то такое продвижение называется альтернативным.
Характерная особенность геометрической прогрессии.
{| b_n | = \ sqrt {b_ {n-1} \ cdot b_ {n + 1}}}
Сумма членов геометрической прогрессии
находит одну из формул:
{S_n = \ frac {b_1-b_1 \ cdot q ^ n} {l-q}}
{S_n = \ frac {b_1 \ cdot {1-q ^ n}} {l-q}}
На нашем сайте вы можете найти количество участников в Интернете.
Произведение первых членов геометрической прогрессии
{P_n = (b_1 \ cdot b_n) ^ \ frac {n} {2}}
Продукт всех условий (от k-го до n-го)
{P_ {k, n} = \ frac {P_n} {P_ {k-1}}}
Примеры геометрической прогрессии
Одним из классических примеров геометрической прогрессии является серия, состоящая из двух возможных степеней:
2, 3, 4, 5, 6, 7, 8, 9 …
В этом случае первый член равен b1 = 2, знаменатель прогрессии q = 2
Ваш рейтинг
[Рейтинги: 24 В среднем: 3.3]
Что такое геометрическая прогрессия по среднему рейтингу mnogofof 3,3 / 5 — 24 пользовательских рейтинга
Количество просмотров на странице: 333
Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число.
Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают

Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя  прогрессия является монотонной последовательностью, причем если
прогрессия является монотонной последовательностью, причем если  это последовательность чисел является монотонно убывающей и при
это последовательность чисел является монотонно убывающей и при  монотонно возрастающей.
монотонно возрастающей.
Случай, когда знаменатель равен единице  на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса

Общий член геометрической прогрессии вычисляют по формуле

Сумма n первых членов геометрической прогрессии определяют по формуле

Рассмотрим решения классических задач на геометрическую прогрессию.
Начнем для понимания с простейших.
Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3.
Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде

Для вычислений используем формулу n-го члена геометрической прогрессии

На ее основе находим неизвестные члены прогрессии





Как можно убедиться, вычисления членов геометрической прогрессии несложные.
Сама прогрессия будет выглядеть следующим образом

Пример 2. Даны три первых члена геометрической прогрессии  : 6; -12; 24.
: 6; -12; 24.
Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения

Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле

На этом задача решена.
Пример 3.
Геометрическая прогрессия  задана двумя ее членами
задана двумя ее членами  . Найти десятый член прогрессии.
. Найти десятый член прогрессии.
Решение:
Запишем заданные значения через формулы

По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем

Такую же формулу можно получить на основе нехитрых манипуляций с входными данными.
Разделим шестой член ряда на другой, в результате получим

Если полученное значение умножить на шестой член, получим десятый

Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами

Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений

Выразим знаменатель разделив второе уравнение на первое

Найдем первый член прогрессии из первого уравнения


Вычислим следующие пять членов для нахождения суммы геометрической прогрессии





Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель

В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам.
Геометрическая прогрессия
Наконец найденные значения добавить.
Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:
Решение задач на бесконечно убывающую геометрическую прогрессию
Решение задач на бесконечно убывающую геометрическую прогрессию
Пример 1. Обратить периодическую дробь 0,454545…= 0,(45) в обыкновенную.
Решение. Представим исходную дробь в виде суммы: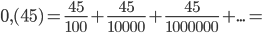
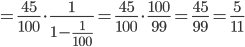
(так как у нас есть сумма бесконечно убывающей геометрической прогрессии со знаменателем 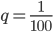 ).
).
Ответ: 
Пример 2. Сумма бесконечно убывающей геометрической прогрессии 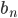
 , а сумма квадратов всех ее членов
, а сумма квадратов всех ее членов  . Найти четвертый член прогрессии.
. Найти четвертый член прогрессии.
Решение. Прогрессия, у которой каждый член есть квадрат 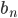 , то есть
, то есть  , имеет знаменатель
, имеет знаменатель  , который равен квадрату знаменателя заданной прогрессии
, который равен квадрату знаменателя заданной прогрессии 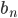 так как
так как

Отсюда имеем систему уравнении

Разделив второе уравнение системы на первое, возведенное в квадрат, получим


Тогда

Ответ:

Пример 3. В равносторонний треугольник со стороной вписан посредством соединения середин его сторон новый треугольник; в этот треугольник тем же способом вписан новый треугольник и так далее до бесконечности. Найти сумму периметров всех этих треугольников и сумму их площадей.
Решение.
Изобразим на рисунке несколько треугольников, удовлетворяющих условию задачи (рис.1).
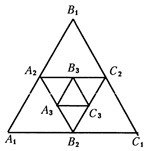
Рис.1
 . Так как
. Так как  — средние линии, то их длины равны
— средние линии, то их длины равны  . Аналогично
. Аналогично  Таким образом, последовательность длин сторон вписанных треугольников образует бесконечно убывающую геометрическую прогрессию
Таким образом, последовательность длин сторон вписанных треугольников образует бесконечно убывающую геометрическую прогрессию  . Последовательность периметров будет получаться путем утроения, т. е.
. Последовательность периметров будет получаться путем утроения, т. е.  . Знаменатель такой прогрессии
. Знаменатель такой прогрессии  а сумма периметров
а сумма периметров 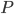 может быть вычислена по формуле для суммы бесконечно убывающей геометрической прогрессии:
может быть вычислена по формуле для суммы бесконечно убывающей геометрической прогрессии:  . Площади полученных правильных треугольников также образуют бесконечно убывающую геометрическую прогрессию
. Площади полученных правильных треугольников также образуют бесконечно убывающую геометрическую прогрессию  . поскольку
. поскольку

и т. д. Знаменатель такой прогрессии
 .
.Отсюда сумма площадей

Ответ:

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Определение 1. Числовую последовательность
b1 , b2 , … bk , …
все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства
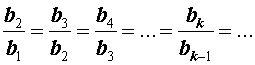
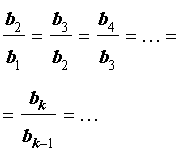
Определение 2. Если последовательность чисел
b1 , b2 , … bk , …
является геометрической прогрессией, то число q , определенное формулой
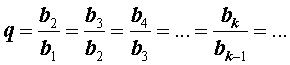

называют знаменателем этой геометрической прогрессии.
Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии b1 и знаменатель геометрической прогрессии q . Если числа b1 и q известны, то все остальные члены прогрессии можно найти по формулам:
| (1) |
По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел b1 и q.
Из формул (1) вытекает общая формула
| bk = b1qk – 1, k = 1, 2, 3, … | (2) |
позволяющая по любому номеру k вычислить член bk геометрической прогрессии, зная первый член и знаменатель прогрессии. Эта формула носит название формулы общего члена геометрической прогрессии.
Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: — «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при 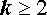 справедливо равенство
справедливо равенство
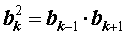 | (3) |
В случае, когда
b1 > 0 и q > 0
все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:
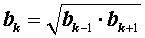 | (4) |
Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.
Если для суммы первых k членов геометрической прогрессии ввести обозначение
Sk = b1 + b2 + … + bk ,
k = 1, 2, 3, …
то, воспользовавшись равенствами (1), получаем
q Sk =
= b1q + b2q + … + bk q =
= b2 + b3 + … + bk +1 .
Следовательно,
Sk – q Sk = b1 – bk +1 .
Таким образом , при  будет справедливо равенство
будет справедливо равенство
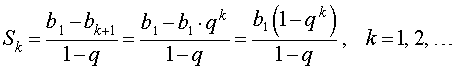

которое называется формулой для суммы первых k членов геометрической прогрессии.
В случае, когда q = 1, все члены геометрической прогрессии равны, что не представляет особого интереса.
Бесконечно убывающая геометрическая прогрессия
Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству
| q | < 1 .
В этом случае выполнено равенство
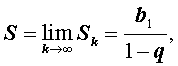
а величину S называют суммой бесконечно убывающей геометрической прогрессии.
Более подробно с понятием предела числовой последовательности можно ознакомиться в в разделе «Пределы числовых последовательностей» нашего справочника.
С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Урок математики в 9-м классе по теме «Бесконечно убывающая геометрическая прогрессия»
Урок математики в 9-м классе по теме «Бесконечно убывающая геометрическая прогрессия»
Цели урока:
ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией;
знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.
Ход урока
1. Проверка домашнего задания.
1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Учащиеся получают тест на печатной основе
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
__________________________
Имя, фамилия
Множество чисел, следующих одно за другим, образованное по какому-нибудь правилу (закономерности), называется ……………………………………………………………..
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа, называют
арифметической прогрессией
геометрической прогрессией
алгебраической прогрессией
последовательностью
Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же не равное нулю число, называют
арифметической прогрессией
геометрической прогрессией
алгебраической прогрессией
последовательностью
Последовательность задана формулой . Напишите первые пять членов данной последовательности.
4; 8; 16; 32; и т.д. ……………………………………………. прогрессия
Впишите пропущенные члены последовательности:
13; _____; 11; _____ ; 9; ____ ; 7;………
_____; ____ ; 10 ; 100 ; ______; 10000.
Напишите третий и четвёртый члены последовательности, а также определите разность/ знаменатель последовательности, если это последовательность является:
арифметической
геометрической
2 ; 12; … ….
3,2 ; 0,8 ; …….
-2 ; 8 ; …….
Затем обмениваются тестами, отмечают «+» и «- » верные и неверные ответы.
А как представить бесконечную десятичную дробь в виде обыкновенной 0, (03)? Возникла проблема : КАК и с помощью чего. Выход на новую тему
2. Изучение новой темы. (демонстрация презентации. Приложение 1)
1) Слайд №2.
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов 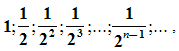 образующих геометрическую прогрессию со знаменателем
образующих геометрическую прогрессию со знаменателем  .
.
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
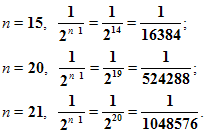
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность. Например, последовательность площадей квадратов:
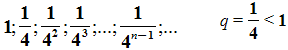 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
2) Слайд №3.
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
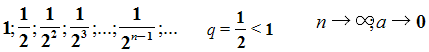
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
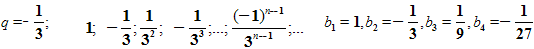
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Фронтальная работа.
Записать определение: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача №1.
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
а)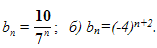
Решение:
а) (фронтальная работа, запись на доске)
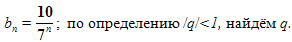
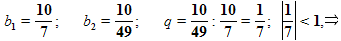 данная геометрическая прогрессия является бесконечно убывающей.
данная геометрическая прогрессия является бесконечно убывающей.
б) (самостоятельно)
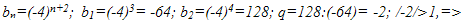 данная последовательность не является бесконечно убывающей геометрической прогрессией.
данная последовательность не является бесконечно убывающей геометрической прогрессией.
Продолжить работу с презентацией.
3) Слайд №4.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:
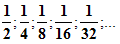
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
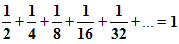
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.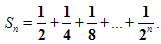
По формуле суммы n первых членов геометрической прогрессии, она равна 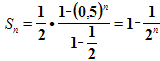 .
.
Если n неограниченно возрастает, то 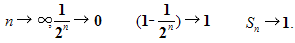
4) Слайд №5.
Записать определение. Суммой бесконечно убывающей геометрической прогрессии называют число, к которому стремится сумма её первых n членов при n → . Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии.
. Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии.
Рассмотрим формулу n первых членов геометрической прогрессии.
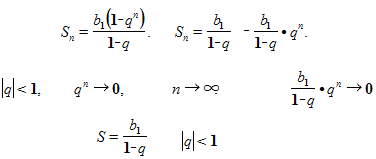
Тренировочные упражнения.
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.
Решение:
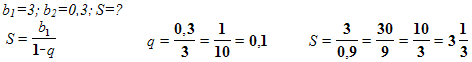
Задача №3стр 103 , № 237 (а)Найти сумму бесконечно убывающей геометрической прогрессии: 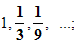
Решение:
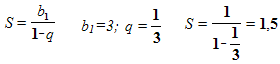
Задача №4. 236(а)
Найти сумму бесконечно убывающей геометрической прогрессии, если 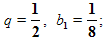
Решение:
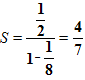
Пользуясь формулой суммы бесконечно убывающей геометрической прогрессии, можно записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Задача №4. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.
1-й способ. Пусть х=0,(5)= 0,555… /•10 2-й способ. 0,(5)=0,555…=
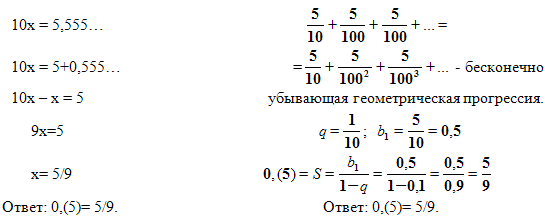
Задача №5. Стр 103 239
Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
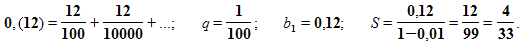
Ответ: 0,(12)= 4/33.
Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Самостоятельная работаЗадания (слайд №6):
Является ли геометрическая прогрессия бесконечно убывающей, если: b7= -30; b6= 15?
Найдите сумму бесконечно убывающей геометрической прогрессии: -25; -5; -1;…
Записать бесконечную десятичную периодическую дробь 0,(9) в виде обыкновенной дроби.
Самопроверка (слайд №7).
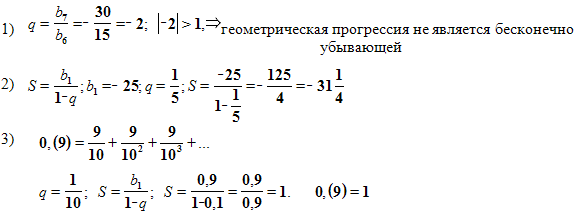
Домашнее задание. Стр104 , №426
Рефлексия, Уч-ся заполняют полученную ранее рефлексивную карточку. Учитель комментирует оценки.
Ученика(цы) «___»б класса _____________________________________
Сегодня я узнал… ______________________________________________________________________________________________________________________________________________
Было интересно… ______________________________________________________________________________________________________________________________________________
Было трудно… ______________________________________________________________________________________________________________________________________________
Полезным было… ______________________________________________________________________________________________________________________________________________
Я выполнял(а) задания… ________________________________________________________________________________________________________________________
Я понял(а), что… ______________
«Бесконечно убывающая геометрическая прогрессия. Число е.»
Дата урока: 14.11.2016
Алгебра и начала математического анализа, 10 класс.
Урок 28
Тема урока: «Бесконечно убывающая геометрическая прогрессия. Число е.»
Цели урока:
Введение понятия предела последовательности.
Формирование понятия бесконечно-убывающей геометрической прогрессии.
Познакомить со свойствами бесконечно-убывающей геометрической прогрессии.
Закрепить полученные знания на примерах решения задач.
Тип урока: Урок усвоения новых знаний.
Структура урока
1. Проверка домашнего задания, воспроизведение и коррекция опорных знаний учащихся (5 мин.).
2. Мотивация учебной деятельности учащихся. Сообщения темы, цели, задач урока и мотивация учебной деятельности школьников (3 мин.).
3. Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения (15 мин.).
4. Физкультминутка (2 мин.)
5. Первичная проверка понимания усвоенного, первичное закрепление усвоенного. (10 мин.).
6. Подведение итогов урока (рефлексия) и сообщение домашнего задания (5 мин.).
Ход урока.
Проверка домашнего задания.
Мотивация учебной деятельности учащихся
Приветствует учащихся, создаёт доброжелательную, рабочую атмосферу в классе, проверяет готовность рабочего места учителя и учащихся. Просит сформулировать цель урока, оформить работу в тетради.
Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения
П.4.5, стр.137. Бесконечно убывающая геометрическая прогрессия.


П.4.6, стр.140. Число е.




Решить упражнения письменно:

Физкультминутка
Закрыть глаза, сильно напрягая глазные мышцы, на счет 1-4, затем раскрыть глаза, расслабив мышцы глаз, посмотреть вдаль на счет 1-6. Повторить 4-5 раз.
Посмотреть на переносицу и задержать взор на счет 1-4. До усталости глаза не доводить. Затем открыть глаза, посмотреть вдаль на счет 1-6. Повторить 4-5 раз.
Не поворачивая головы, посмотреть направо и зафиксировать взгляд на счет 1-4, затем посмотреть вдаль прямо на счет 1-6. Аналогичным образом проводятся упражнения с фиксацией взгляда влево, вверх и вниз. Повторить 3-4 раза.
Перенести взгляд быстро по диагонали: направо вверх — налево вниз, потом прямо вдаль на счет 1-6; затем налево вверх — направо вниз и посмотреть вдаль на счет 1-6. Повторить 4-5 раз. Сомкнули ладошки в замок и покрутили 4 раза в одну и другую сторону. Расслабили руки.
Первичная проверка понимания усвоенного, первичное закрепление усвоенного.

Дополнительные задания:
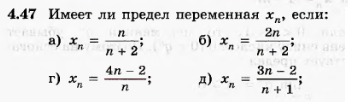
Подведение итогов урока (рефлексия) и сообщение домашнего задания
Самоанализ учащихся по вопросам:
Какая цель была у нас на уроке?
Как вы думаете, пригодятся ли вам знания, которые мы сегодня получили?
Появилось ли у вас желание больше узнать о задачах?
С каким настроение вы находились на уроке?
Отметки получают те ученики, кто отвечал у доски и активно работал с места. Учитель отвечает на вопросы, комментирует оценки за урок.
Домашнее задание: п.4.5, 4.6, выучить, №4.38(в), 4.39(в,г), 4.47 (в,е).
Урок «Бесконечо убывающая прогрессия»
ПЛАН-КОНСПЕКТ УРОКА
Урок математики в 9-м классе
Тема урока:»Бесконечно убывающая геометрическая прогрессия»
Цели урока:
1. Образовательная:
Повторить и обобщить знания учащихся по теме « Арифметическая и геометрическая прогрессии»
Познакомить учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией;
Формирование начального представления о пределе числовой последовательности;
Знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии.
Развивающая:
1.Развивать навыки коллективной работы, взаимопомощи, самоконтроля.
Воспитательная:
2. Воспитывать информационные компетенции, математическую зоркость, математическую речь
Ход урока
1. Организационный момент.
Приветствие. Отсутствующие. Запись темы урока. Сообщение целей и задач урока: обобщение изученного по теме «Прогрессии»; подготовка к контрольной работе; прослушаем сообщение об одном из учёных-математиков. Имя этого учёного узнаем, разгадав шифровку.
2. Устная работа.
На доске алфавит и зашифрованное имя учёного.
а
б
в
г
д
е
ё
ж
3
и
w
И
к
л
м
н
о
п
Р
с
т
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
У
Ф
X
ц
ч
ш
щ
ъ
ы
ь
э
ю
я
21
22
23
24
25
26
27
28
29
30
31
32
33
Выполнив задания, узнаем имя учёного, о котором затем прослушаем сообщение и решим задание, опираясь на доказанную им теорему.
l.a3=8, a5=26, а4=?
2. а1=5, d=5, S5=?
3. b6=144, b5=24, q=?
4. b1=2, b2=5, b3 =?
5. b4=4, b9=21, b8=?
6. b3= 16, b4=96, q=?
7. a3=9, a2=6, S3=?
8. a10=21, a11=35, d=?
9. (bn): 7; 7; 7;… q=?
Закодированное имя-Пьер Ферма.
2. Сообщение об учёном.
3. Проверка домашнего задания.
1) Проверка основных формул, связанных с арифметической и геометрической прогрессиями. Два ученика готовят записи формул у доски.
2) Остальные учащиеся выполняют математический диктант .
Математический диктант
1.
Задания:
№1. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен 6 (1-й вариант), -20 (2-й вариант), а пятый член -6 (1-й вариант), 20 (2-й вариант).
№2. Найдите сумму первых пяти членов арифметической прогрессии, если её первый член равен -20(1-й вариант), 6 (2-й вариант), а разность равна 10(1-й вариант), -3(2-й вариант).
№3. Найдите сумму первых пяти членов геометрической прогрессии, если её первый член равен 1(1-й вариант), -1 (2-й вариант), а знаменатель равен -2(1-й вариант), 2(2-й вариант).
По окончании диктанта, выборочно, у двоих учеников работы проверяются на оценку, остальные выполняют самопроверку по готовым решениям на экране.
Решения:
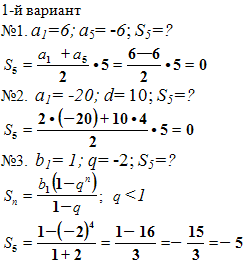
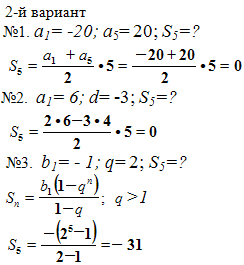
4. Изучение новой темы.
1) Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.
В результате, мы получили последовательность сторон квадратов 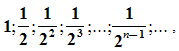 образующих геометрическую прогрессию со знаменателем
образующих геометрическую прогрессию со знаменателем 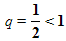 .
.
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
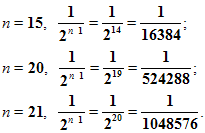
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
С помощью этого рисунка можно рассмотреть и ещё одну последовательность. Например, последовательность площадей квадратов:
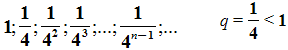 . И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
. И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.
2)
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.
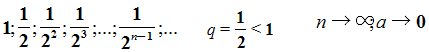
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
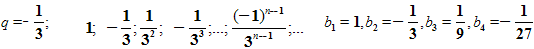
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Фронтальная работа.
Записать определение: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Задача №1.
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:
а)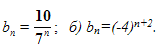
Решение:
а) (фронтальная работа, запись на доске)
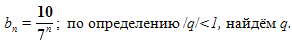
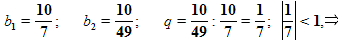 данная геометрическая прогрессия является бесконечно убывающей.
данная геометрическая прогрессия является бесконечно убывающей.
б) (самостоятельно)
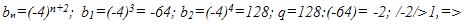 данная последовательность не является бесконечно убывающей геометрической прогрессией.
данная последовательность не является бесконечно убывающей геометрической прогрессией.
3)
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:
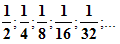
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
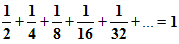
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.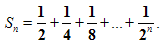
По формуле суммы n первых членов геометрической прогрессии, она равна 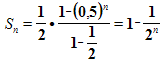 .
.
Если n неограниченно возрастает, то 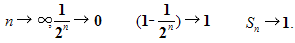
4) Записать определение. Суммой бесконечно убывающей геометрической прогрессии называют число, к которому стремится сумма её первых n членов при n →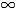 . Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии.
. Теперь получим формулу, с помощью которой будем вычислять сумму бесконечно убывающей геометрической прогрессии.
Рассмотрим формулу n первых членов геометрической прогрессии.
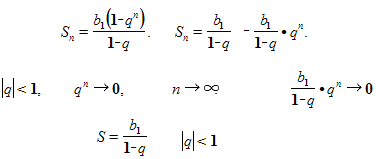
Закрепление.
Задача №2. Найти сумму бесконечно убывающей геометрической прогрессии с первым членом 3,вторым 0,3.
Решение:
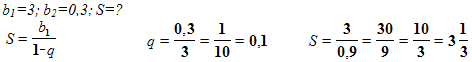
Задача №3.
Найти сумму бесконечно убывающей геометрической прогрессии: 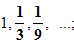
Решение:
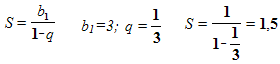
Задача №4. Найти сумму бесконечно убывающей геометрической прогрессии, если 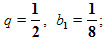
Решение:
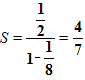
Пользуясь формулой суммы бесконечно убывающей геометрической прогрессии, можно записывать бесконечную периодическую десятичную дробь в виде обыкновенной дроби.
Задача №5. Записать бесконечную периодическую десятичную дробь 0,(5) в виде обыкновенной дроби.
1-й способ. Пусть х=0,(5)= 0,555… /•10 2-й способ. 0,(5)=0,555…=
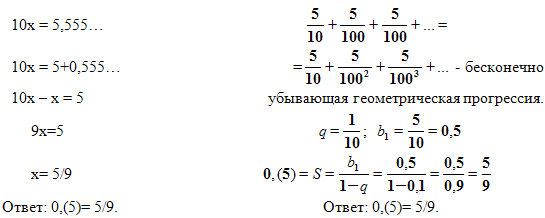
Задача №6. Записать бесконечную периодическую десятичную дробь 0,(12) в виде обыкновенной дроби.
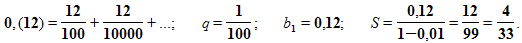
Ответ: 0,(12)= 4/33.
8. Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Самостоятельная работа.
(выполняется в рабочих тетрадях ,по окончании работы записи решений сдаются на проверку)
Задания
Является ли геометрическая прогрессия бесконечно убывающей, если: b7= -30; b6= 15?
Найдите сумму бесконечно убывающей геометрической прогрессии: -25; -5; -1;…
Записать бесконечную десятичную периодическую дробь 0,(9) в виде обыкновенной дроби.
Самопроверка 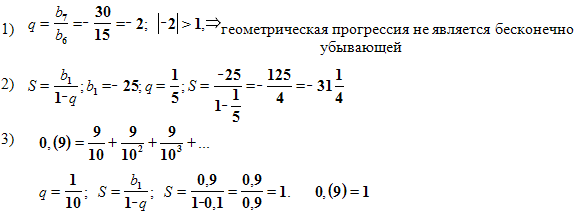
Домашнее задание.
№ 236,237,238.
Самоанализ урока
Кипчакбаевой Л.
Класс: 9«в»
Дата :11.01.2016
Тема: Формула суммы бесконечно убывающей геометрической прогрессии
Тип урока: усвоение нового материала;
Цели урока:
1. получить формулу для суммыбесконечно убывающей геометрической прогрессии;
2. повторить теорию о геометрической прогрессии ;
3. прочное закрепление знаний и умений по теме;
4. формировать наблюдательность учащихся.
Содержание урока:
1. Урок соответствует программе целям и задачам урока.
2. Проведена устная работа по актуализации тем, необходимых для продолжения и обобщения темы урока.
3. Урок способствует формированию знаний умений и навыков использование математических формул при нахождении суммы геометрической прогрессии
4. Урок способствовал развитию творческих сил и способностей каждого ученика.
5. Во время урока совершенствовались умения и навыки при решении с геометрической прогресией.
6. Урок способствовал развитию интереса к учению.
Структура урока
1. Организационный момент.
2. Актуализация знаний: устный опрос, проверка домашнего задания, математический диктант
3. Изучение нового материала
4. Решение различных примеров с применением формулы суммы геометрической прогрессии. .
5. Обобщение нового материла. Решение тренировочных заданий.
6. Самостоятельная работа с взаимопроверкой.
8. Домашнее задание.
9. Подведение итогов урока.
Таким образом, урок был проведен с комбинированной структурой, была построена логическая цепь последовательно соединенных этапов урока.
Методы обучения:
В начале урока проведен фронтальный по теории, далее письменный опрос по теме.
Во второй части урока был применен частичнопоисковый метод обучения, который заключался в организации активного поиска решения примеров с применением формулы суммы n первых членов геометрической прогрессии и суммы бесконечно убывающей, выдвинутых под руководством учителя .
По источникам знаний применились словесные и наглядные методы.
Организация учебной работы на уроке:
При проектировании урока были учтены индивидуальные особенности учащихся, темп работы, степень обученности и уровень обучаемости, что позволило добиться дифференцированного подхода к каждому конкретному учащемуся. В течение всего урока оценивалось интеллектуальное и эмоциональное состояние учащихся. Для этого использовались такие приёмы, как психо – эмоциональный настрой как в начале урока, так и в течение всего урока.
Проведение организационного момента обеспечило психологический настрой на деятельность, что позволило создать все условия для дальнейшей работы и учащиеся смогли самостоятельно сформулировать цели урока (Повторить, обобщить, закрепить знания, умения и навыки ).
После вывода формулы суммы n первых членов геометрической прогрессии были предложены учителем различные примеры с использованием суммы геометрической прогресии.
Применение методов проблемного обучения позволило активизировать мыслительную деятельность учащихся в процессе обучения, научить мыслить логически, научно, творчески, формировать такие чувства, как удовлетворённость от учебной работы, положительное отношение к математике.
Система работы учащихся:
1. Учащиеся были организованы и активны во время урока
2. Учащиеся очень хорошо относятся к предмету.
3. Усвоили основные понятия, умело и творчески использовали полученные знания.
При подведении итогов урока ученики определили те вопросы, над которыми им предстоит еще работать, каждый сделал вывод о том, на что требуется особо обратить внимания с их стороны.
Общие результаты урока:
1. План урока выполнен.
2. На уроке реализовывались общеобразовательные, воспитывающие развивающие задачи урока.
3. Урок был эффективный.
4. Атмосфера на уроке была дружеская, творческая;
5. Цель урока достигнута.
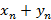 – новая последовательность, ее предел
– новая последовательность, ее предел 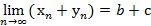 . Предел суммы последовательностей, равен сумме пределов этих последовательностей.
. Предел суммы последовательностей, равен сумме пределов этих последовательностей.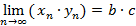 . Этот предел равен произведению
. Этот предел равен произведению 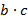
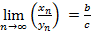 . Предел этой последовательности, то есть предел частного равен
. Предел этой последовательности, то есть предел частного равен  , где
, где 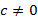 .
.