arccos 0 найти
Добрый вечер!
Спасибо за обращение. Ваш вопрос — не очень сложен и, скорее всего, Ваше непонимание появилось только из-за того, что Вы не совсем понимаете что значит arсcos, уже не говоря о более конкретном задании arсcos 0.
Давайте попробуем разобраться, что же это такое и с чем его едят.
Первым делом давайте уточним, что таких непонятных, на первый взгляд, обозначений существует несколько (это обратные тригонометрические функции): арксинус, арккосинус, арктангенс, арккотангенс. Это очень простые понятия. Которые могут облегчить человеку жизнь при решении тригонометрических уравнений!
Для понимания конкретно этих обозначений Вам нужно будет вспомнить, что такое синус, косинус, тангенс и котангенс. А также их табличные значения для некоторых углов. И тогда Вы полностью усвоите эту тему.
Итак: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Вы знаете угол 45 градусов. А бывает угол arcsin 0,4, или arctg(-1,3)
Давайте расшифруем Ваш пример:
— это угол
— косинус
— значение
То есть получаем, что:
— это угол, косинус которого равен 0
А теперь давайте подумаем, какой угол скрывается под таким обозначением, как
Для того, чтоб понять это не нужно придумывать велосипед. Достаточно просто вспомнить таблицу и мы с Вами получим следующее:
Другими словами, если расшифруем все возможные варианты, то получим такое:
То есть, ответ:
ru.solverbook.com
Таблица Брадиса: арккосинус
Замечание 1
Таблица Брадиса — это таблица, позволяющая высчитывать значения арктангенсов и других тригонометрических функций с высокой точностью.
Для того чтобы воспользоваться таблицей Брадиса, ищут угол в градусах в крайнем столбце слева для синуса (для косинуса в соответствующем столбце справа), а затем в верхней строке минуты. На пересечении строки со столбцом находится искомое значение.
При необходимости найти значения обратных тригонометрических функций — таблицу Брадиса используют наоборот. Например, ищут числовое значение в таблице арктангенсов и тангенсов и для него определяют, в какой строке градусов и столбце минут оно находится.
Таким образом, Таблицу Брадиса можно использовать не только для поиска обычных тригонометрических функций, но и как таблицу арккосинуса и арксинуса, арктангенсов и арккотангенсов.
Сверху в этой статье расположена таблица значений arcsin и arccos, ближе к концу — таблица значений arctg и arcctg.
Таблица Брадиса: таблица arcsin, arccos, cos и sin
Рисунок 1. Таблица Брадиса таблица значений arcsin и arccos. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Таблица. Автор24 — интернет-биржа студенческих работ
Таблица значений арктангенсов и арккотангенсов, тангенсов и котангенсов
Рисунок 4. Таблица Брадиса: таблица значений арктангенсов arctg и арккотангенсов arctg. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Таблица. Автор24 — интернет-биржа студенческих работ
Рисунок 7. Таблица. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите значение $\arccos (0,2504)$.
Найдём в строке число, находящееся максимально близко к $0,2504$. В нашем случае это число $0,2588$. Так как оно больше чем $0,2504$, дальше смотрим в строки, которые находятся справа сверху от этого значения. Наконец, значение $0,2504$ найдено, оно находится на пересечении строки 75 градусов и 30 минут, значит $\arccos (0,2504)=75°30’$.
Рисунок 8. Таблица. Автор24 — интернет-биржа студенческих работ
spravochnick.ru
arccos 1 найти
Добрый вечер!
Спасибо за обращение. Ваш вопрос — не очень сложен и, скорее всего, Ваше непонимание появилось только из-за того, что Вы не совсем понимаете что значит arсcos, уже не говоря о более конкретном задании arсcos 1.
Давайте попробуем разобраться, что же это такое и с чем его едят.
Первым делом давайте уточним, что таких непонятных, на первый взгляд, обозначений существует несколько (это обратные тригонометрические функции): арксинус, арккосинус, арктангенс, арккотангенс. Это очень простые понятия. Которые могут облегчить человеку жизнь при решении тригонометрических уравнений!
Для понимания конкретно этих обозначений Вам нужно будет вспомнить, что такое синус, косинус, тангенс и котангенс. А также их табличные значения для некоторых углов. И тогда Вы полностью усвоите эту тему.
Давайте расшифруем Ваш пример:
— это угол
— косинус
— значение
То есть получаем, что:
— это угол, косинус которого равен 1
А теперь давайте подумаем, какой угол скрывается под таким обозначением, как
Для того, чтоб понять это не нужно придумывать велосипед. Достаточно просто вспомнить таблицу и мы с Вами получим следующее:
или же
Другими словами, если расшифруем все возможные варианты, то получим такое:
либо
То есть, ответ: либо
ru.solverbook.com
Тригонометрия: арккосинус
Абитуриентам и старшеклассникам – для повторения и закрепления
Уравнение cos x = a, где -1 ≤ a ≤ 1, на отрезке [0; π] имеет решение и при том только одно. Действительно, функция y = cos x непрерывна и на концах отрезка [0; π] принимает значения -1 (в точке π) и 1 (в точке 0) – это обеспечивает существование корня, а единственность следует из монотонности функции (убывает) на указанном отрезке (рис.1).
Записывают этот корень (это число) в виде arccos a. Можно сказать и так: arccos a – это единственный корень системы
Итак, под записью arccos a мы понимаем число, которое удовлетворяет двум условиям:
1) 0 ≤ arccos a ≤ π и 2) cos(arccos a) = a.
Отметим, что запись «arccos a» будет числом, если -1 ≤ a ≤ 1. В противном случае эта запись теряет смысл. На практике удобно работать с числовой окружностью (рис.2).
Из точки a оси абсцисс проведем перпендикуляр к этой оси и точку его пересечения с верхней полуокружностью обозначим буквой М. На точке М имеем бесконечно много чисел. Среди них находится и число arccos a – число из отрезка [0 ; π]. Число arccos a , при девяти значениях числа a, можно (и нужно) записать в более простой форме (см.рис.3).
Задача 1.
Почему данные записи не имеют смысла (не являются числами) ?
Решение.
arccos a имеет смысл лишь при -1 ≤ a ≤ 1. Данные записи не являются числами, так как
Задача 2.
При каких значениях переменной x, выражение arccos(|x| — 3) имеет смысл (будет числом) . Решение.
arccosa имеет смысл лишь при -1 ≤ a ≤ 1. Следовательно:
Задача 3.
Найти значение числового выражения (вычислить).
Решение.
Воспользуемся таблицей значений арккосинуса (их нужно помнить!).
Задача 4.
Вычислить cos(arccos 0,7) + cos(arccos(-0,3)) .
Решение.
Воспользуемся равенством cos(arccosa) = a. cos(arccos 0,7) + cos(arccos(-0,3)) = 0,7 – 0,3 = 0,4
Задача 5.
Вычислить
Решение.
Задача 6.
Вычислить sin(arccos 0,8).
Решение.
Заметим, что 0 ≤ arccos 0,8 ≤ π , следовательно, sin(arccos0,8) ≥ 0. Воспользуемся основным тригонометрическим тождеством и заметим, что
Абитуриентам на заметку
Задача 7.
Вычислить cos(arccos0,6 +arccos0,8) .
Решение.
Воспользуемся тождеством cos (x + y) = cosx•cosy – sinx•siny и указанной выше формулой.
Уравнение cosx = a
Задача 8.
Решить уравнение cosx = π .
Решение.
Уравнение решений не имеет, т.к. π > 1.
Задача 9.
Решить уравнение cosx = 0,3 .
Решение. x = ± arccos0,3 + 2πn , n = 0; ±1; ±2; … .
Три свойства arccosa , которые должен знать абитуриент.
1. Сумма арккосинусов двух противоположных чисел равна π:
arccos(-a) + arccosa =π , или в виде arccos(-a) = π – arccosa . Действительно, числа arccos(-a) и arccosa равноудалены от точки π/2 (строгое доказательство мы опустим, но из рисунков 4 или 5 в этом легко убедиться). И так, π/2 – среднее арифметическое этих чисел, следовательно
Задача 10.
Вычислить.
.
Решение.
Так как ( a – b ) и (b – a) противоположные числа, то arccos(a –b) = π – arccos(b –a ).
2. Если b < a , то arccos b > arccos a и обратно, если arccos b > arccos a , то b < a.
Задача 11.
Расположить числа в порядке возрастания.
Решение.
Задача 12.
Принадлежит ли число arccos(-0,6) интервалу (2,08 ; 2,37) ?
Решение.
Ответить на данный в задаче вопрос нам поможет рисунок 3.
Ответ: да, принадлежит.
Задача 13 .
Решить неравенство: arccos(x – 2) > arccos( 2x –3).
3. Равенство arccos a = arccos b равносильно системе из двух условий: 1) a = b ; 2) -1 ≤ a ≤ 1 Разумеется, что в двойном неравенстве вместо числа a можно взять число b.
Задача 14.
Решить уравнение
arccos(x – 2) = arccos(3|x| – 7).
Решение.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Пособие по теме Арксинус, арккосинус, арктангенс числа
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА: алгебра и начало математического анализа; геометрия
Тема: «АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС ЧИСЛА»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2019
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2019 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: тригонометрических функций, радианной меры углов, таблицы значений тригонометрических функций, формулы перевода градусов в радианы и наоборот, определения арксинуса, арккосинуса, арктангенса числа и подготовится к занятию по теме «Арксинус, арккосинус, арктангенс числа».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Арксинус, арккосинус, арктангенс числа, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Арксинус, арккосинус, арктангенс числа
Арксинус
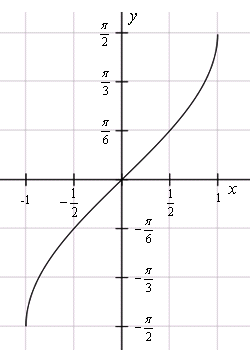
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:

Так как f(x) нечетная, то arcsin (- x) = — arcsin x.
Y = 0 при x = 0.
На всей своей протяженности график возрастает.
Если сопоставить графики sin и arcsin, у двух тригонометрических функций можно найти общие закономерности.

Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
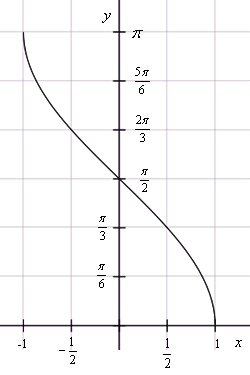
Рассмотрим функцию арккосинуса более подробно:
Функция определена на отрезке [-1; 1].
ОДЗ для arccos — [0, π].
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.

Задание 1. Укажите функции изображенные на рисунке.
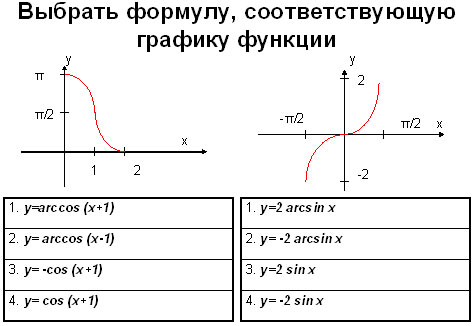
Ответ: рис. 1 – 4, рис.2 — 1.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
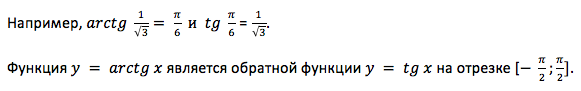
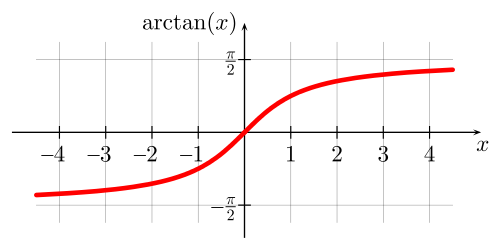
Если рассмотреть график арктангенса, можно выделить следующие свойства:
График бесконечен и определен на промежутке (- ∞; + ∞).
Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
Y = 0 при x = 0.
Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
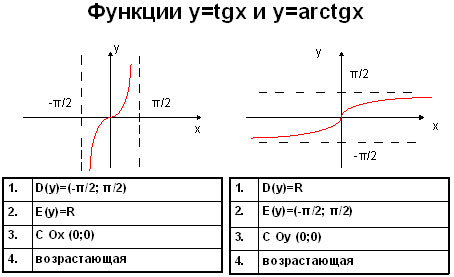
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
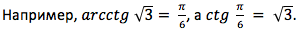

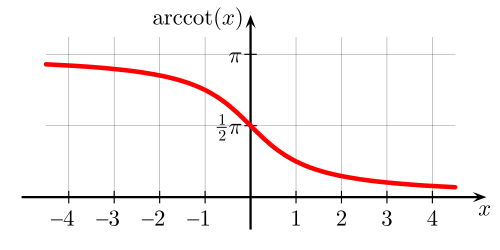
Свойства функции арккотангенса:
Интервал определения функции – бесконечность.
Область допустимых значений – промежуток (0; π).
F(x) не является ни четной, ни нечетной.
На всем своем протяжении график функции убывает.
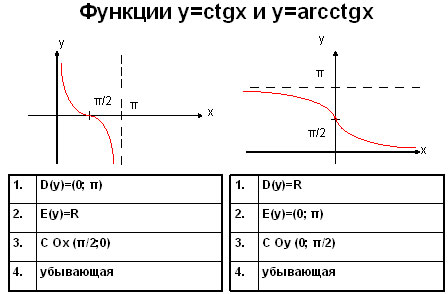
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
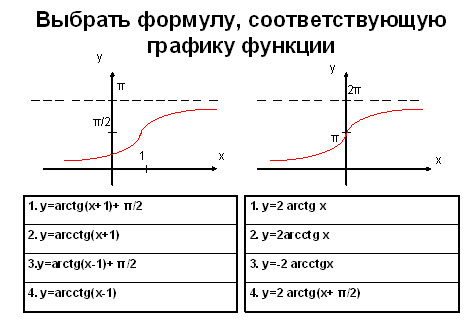
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
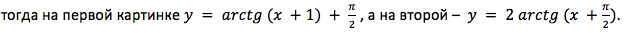
Ответ: рис. 1 – 1, рис. 2 – 4.
Пример 1. Вычислить значение 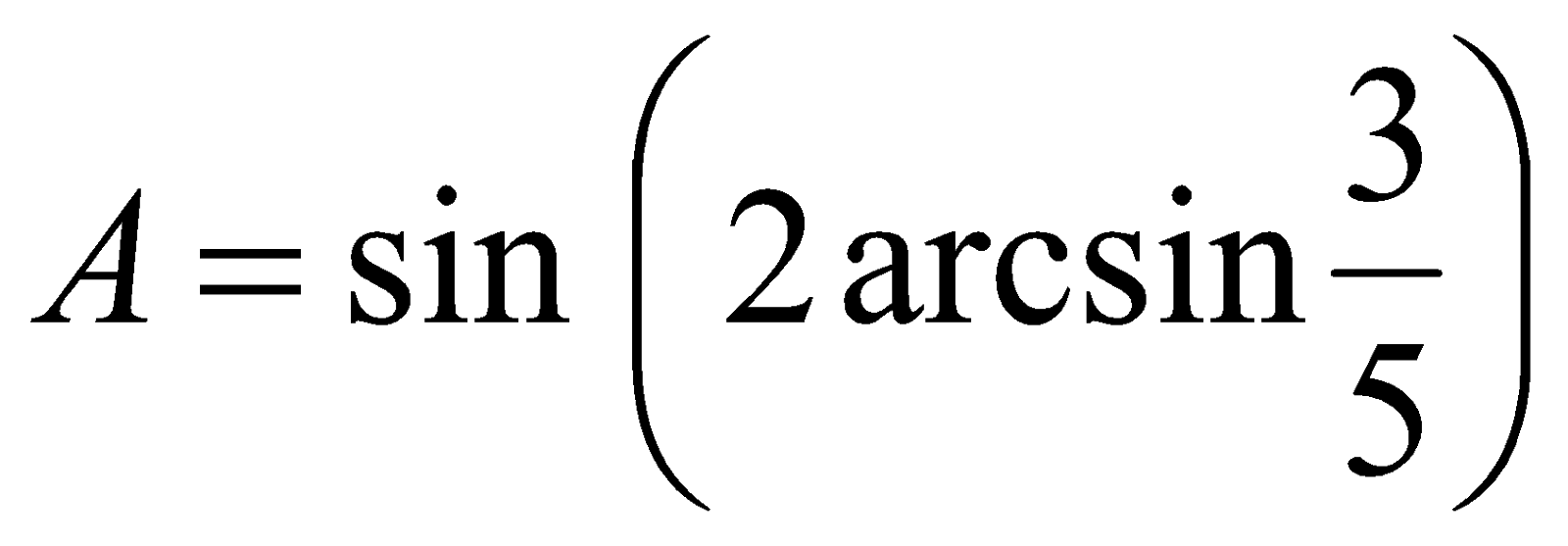 .
.
Решение. Если обозначить 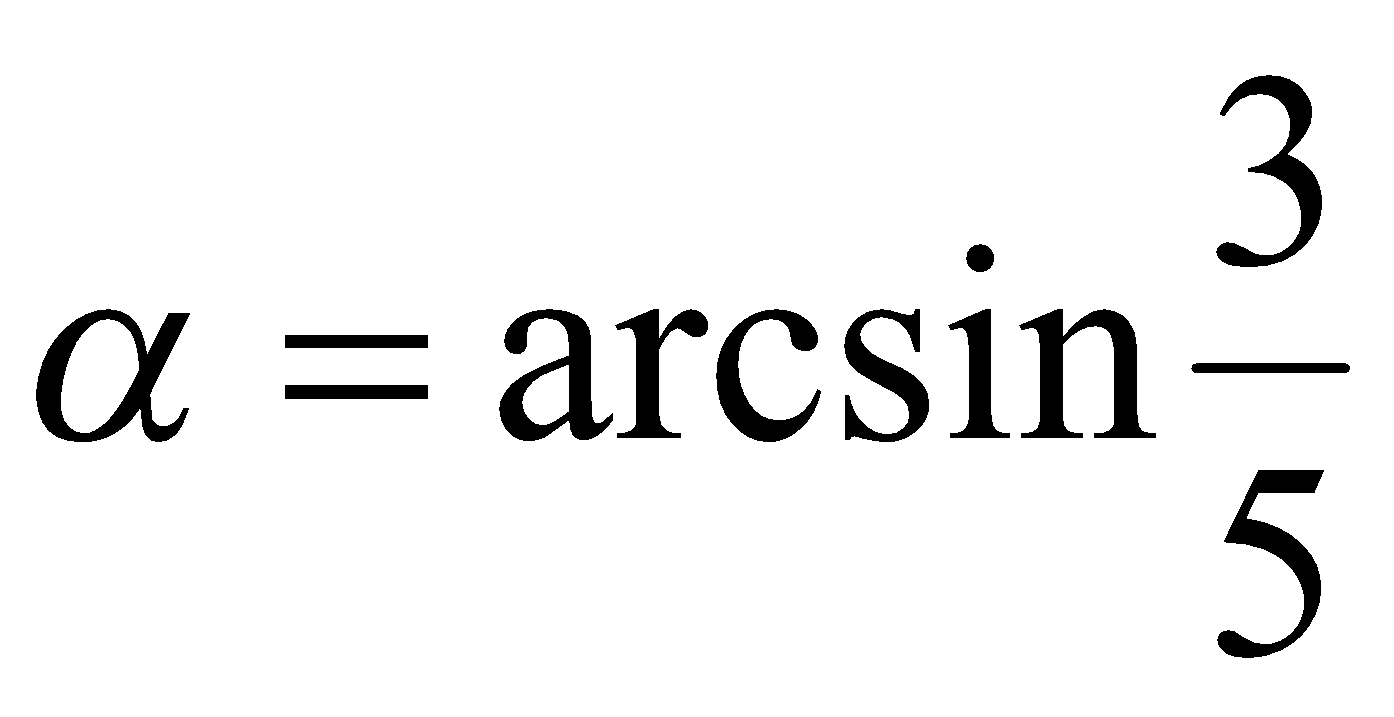 , то
, то 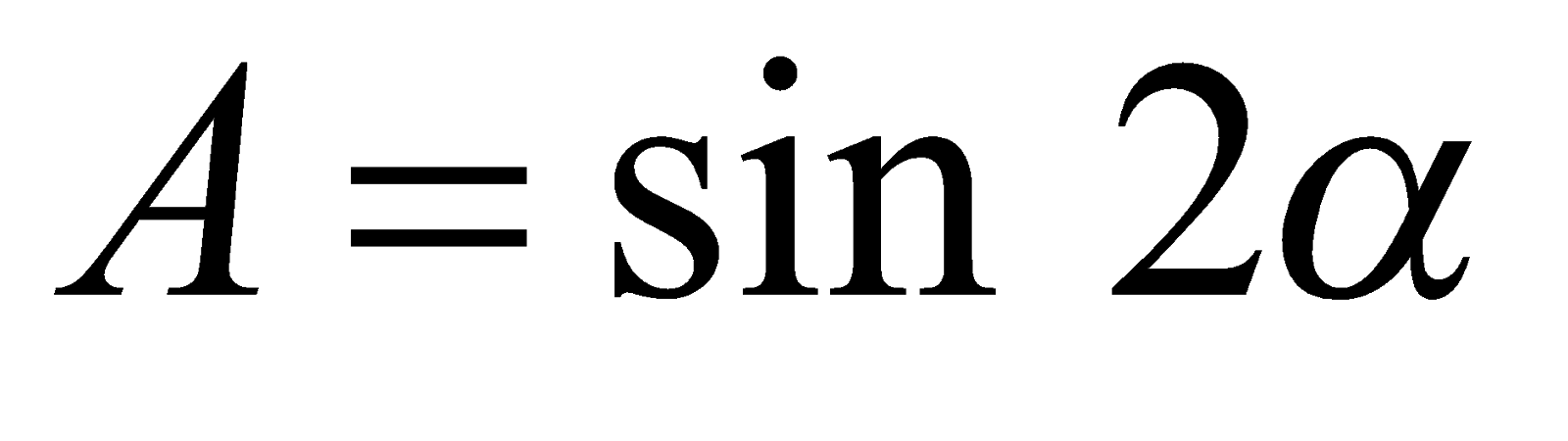 . Из определения функции
. Из определения функции 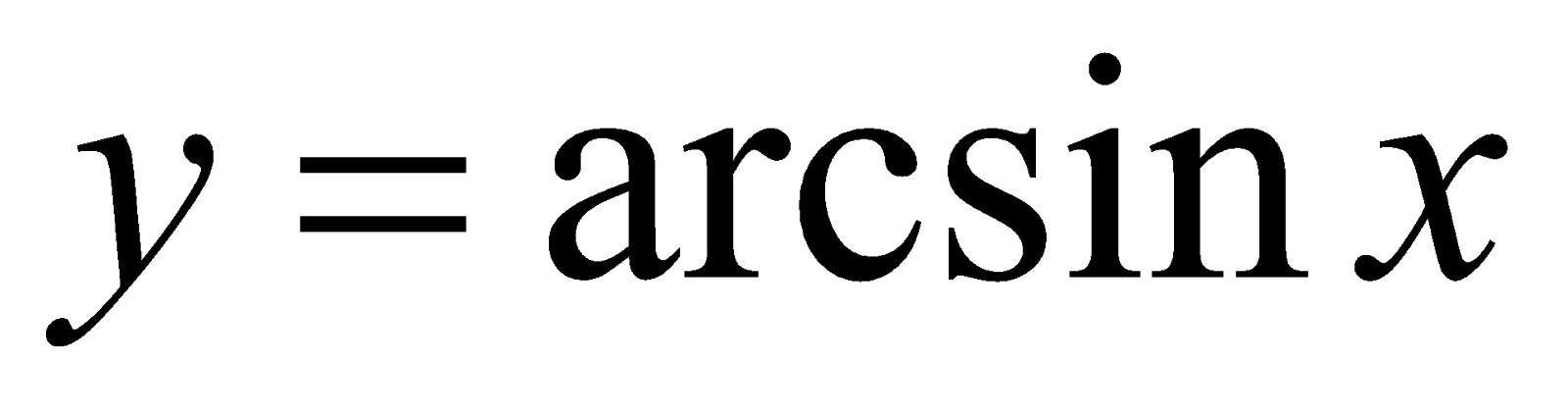 следует, что
следует, что 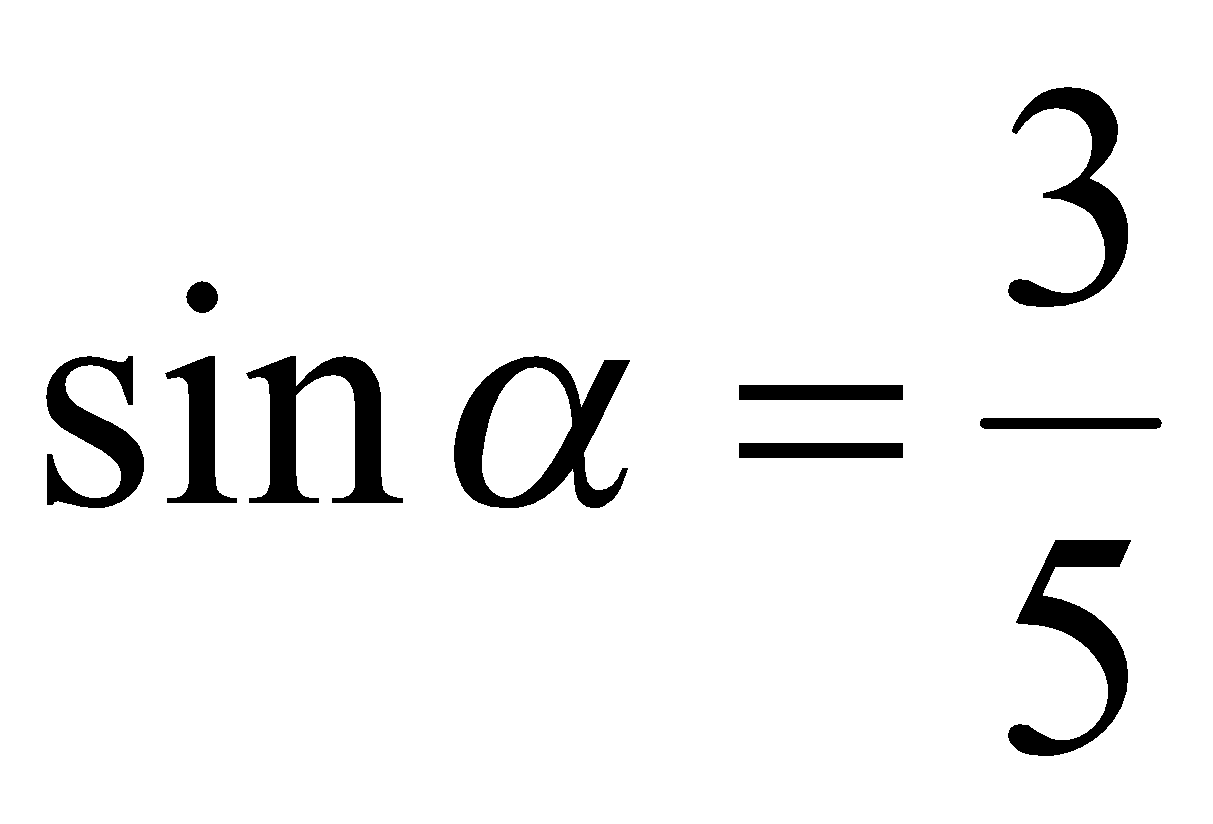 и
и 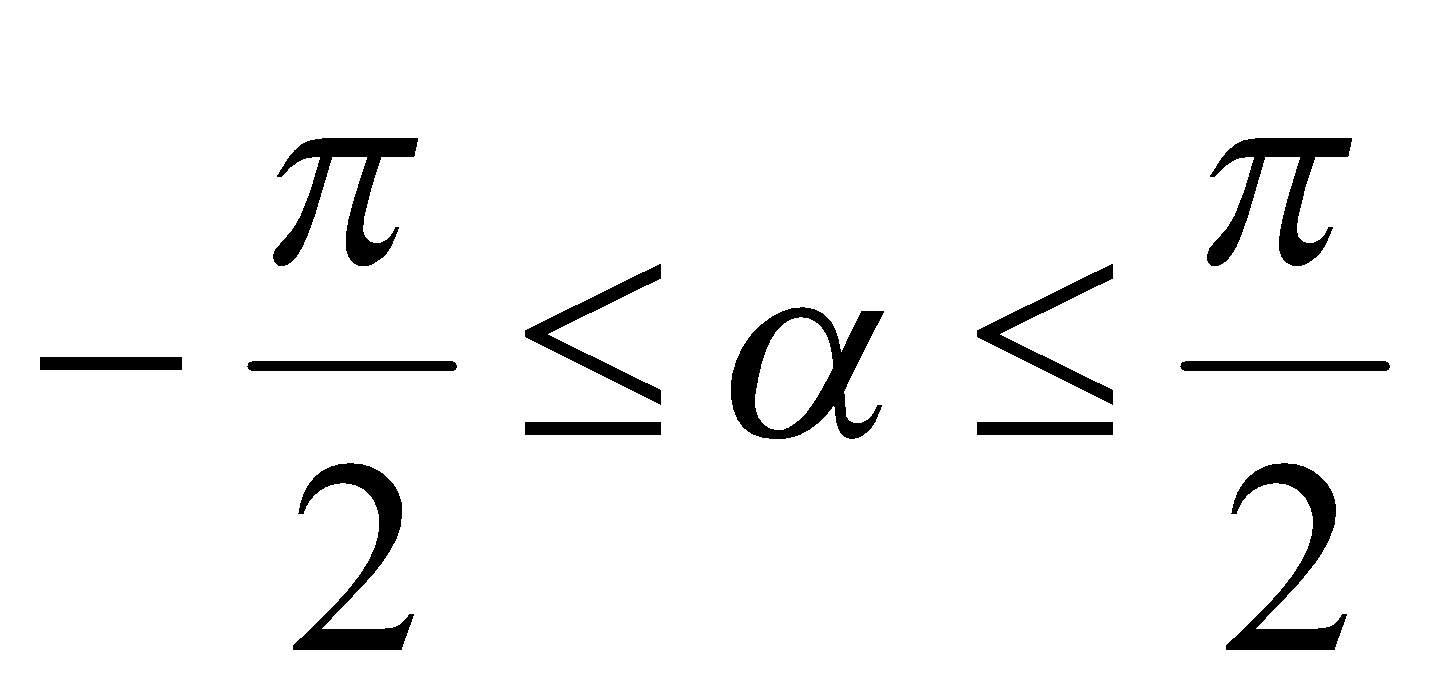 . Так как
. Так как 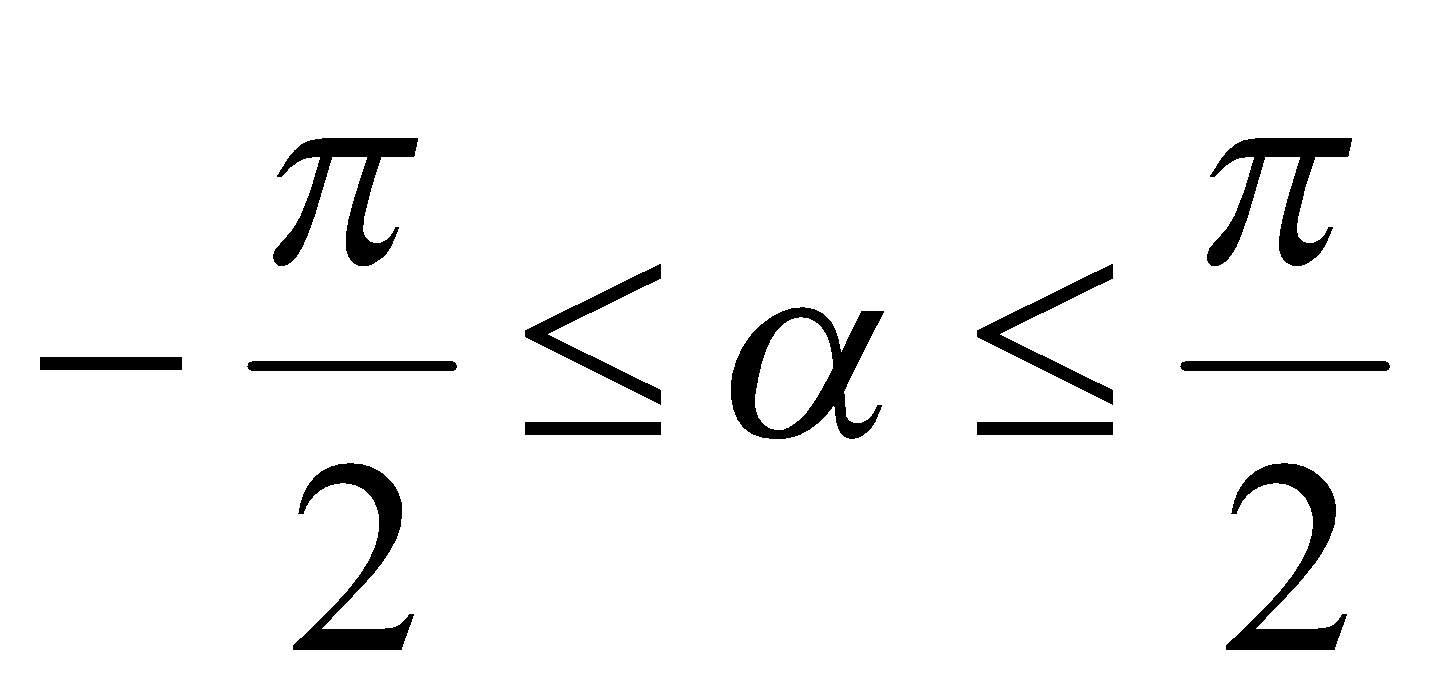 , то
, то 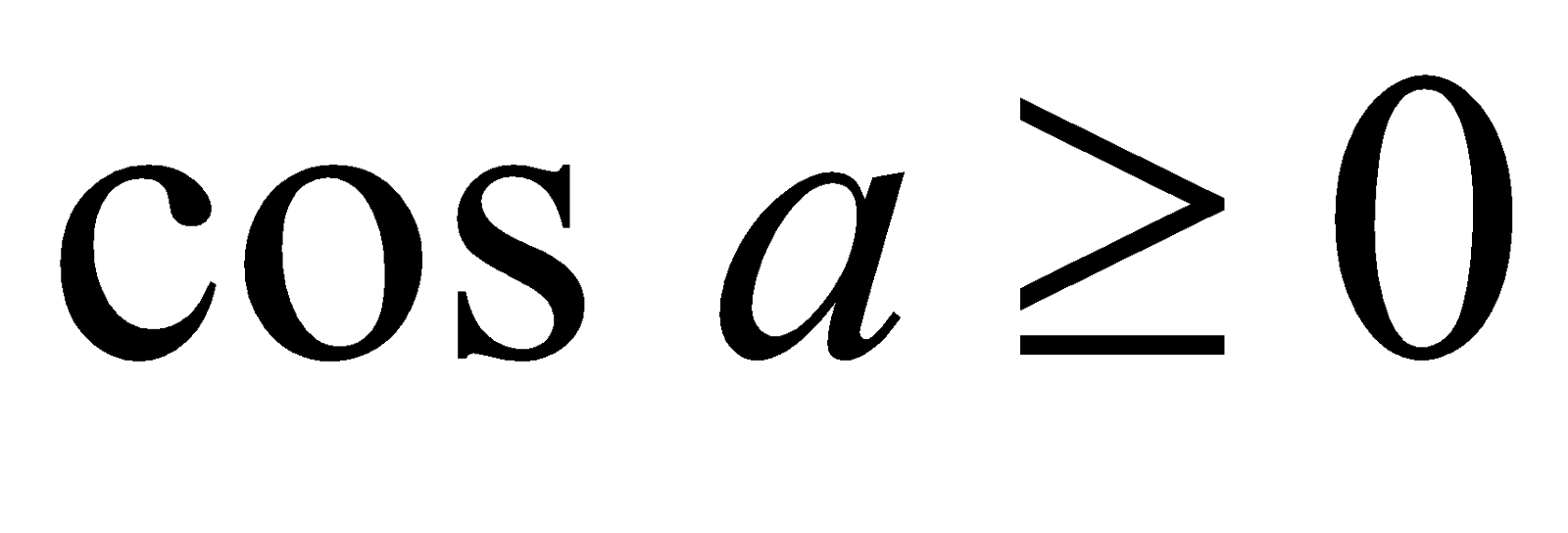 и
и 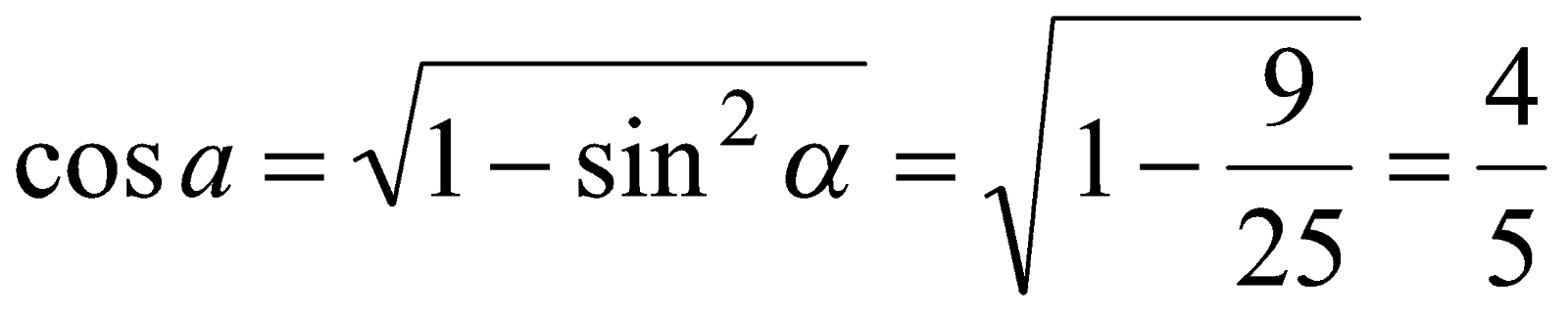 .
.
Однако 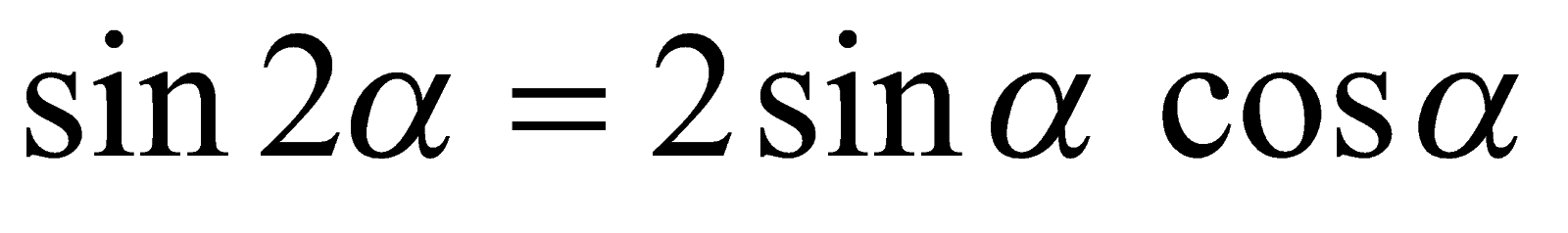 , поэтому
, поэтому 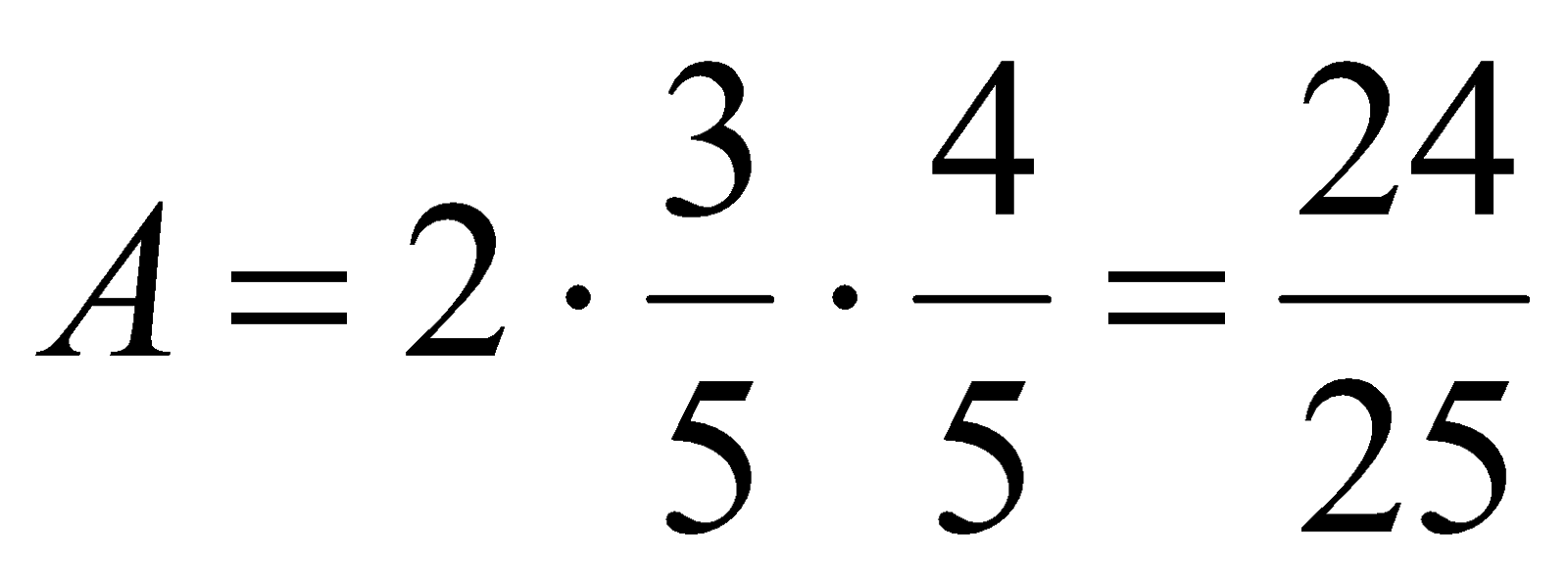 .
.
Ответ: 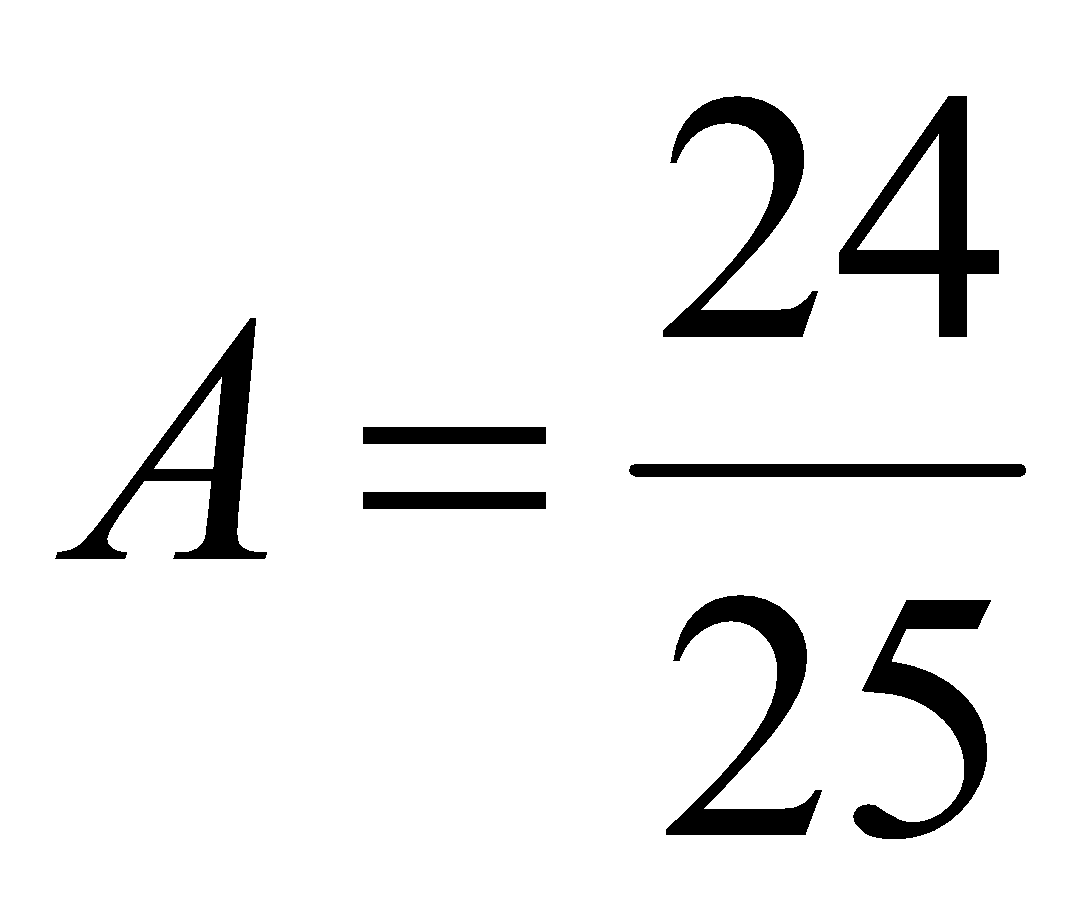 .
.
Пример 2. Вычислить значение 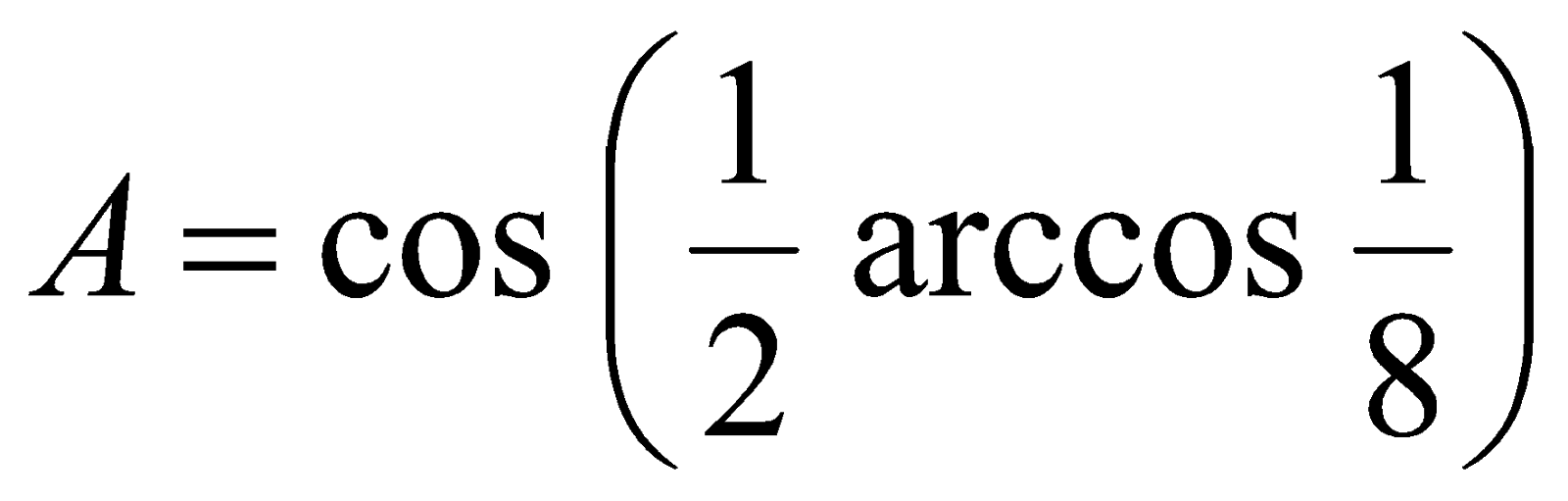 .
.
Решение. Если 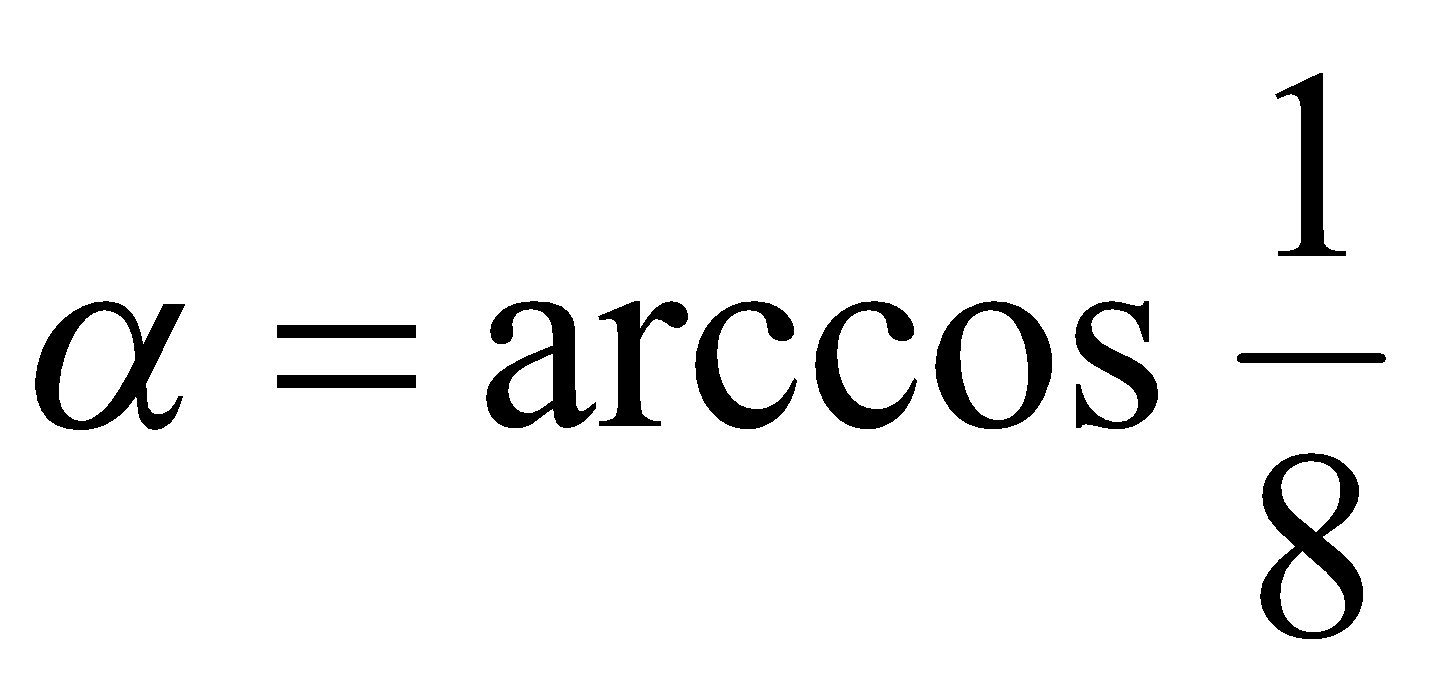 , то
, то 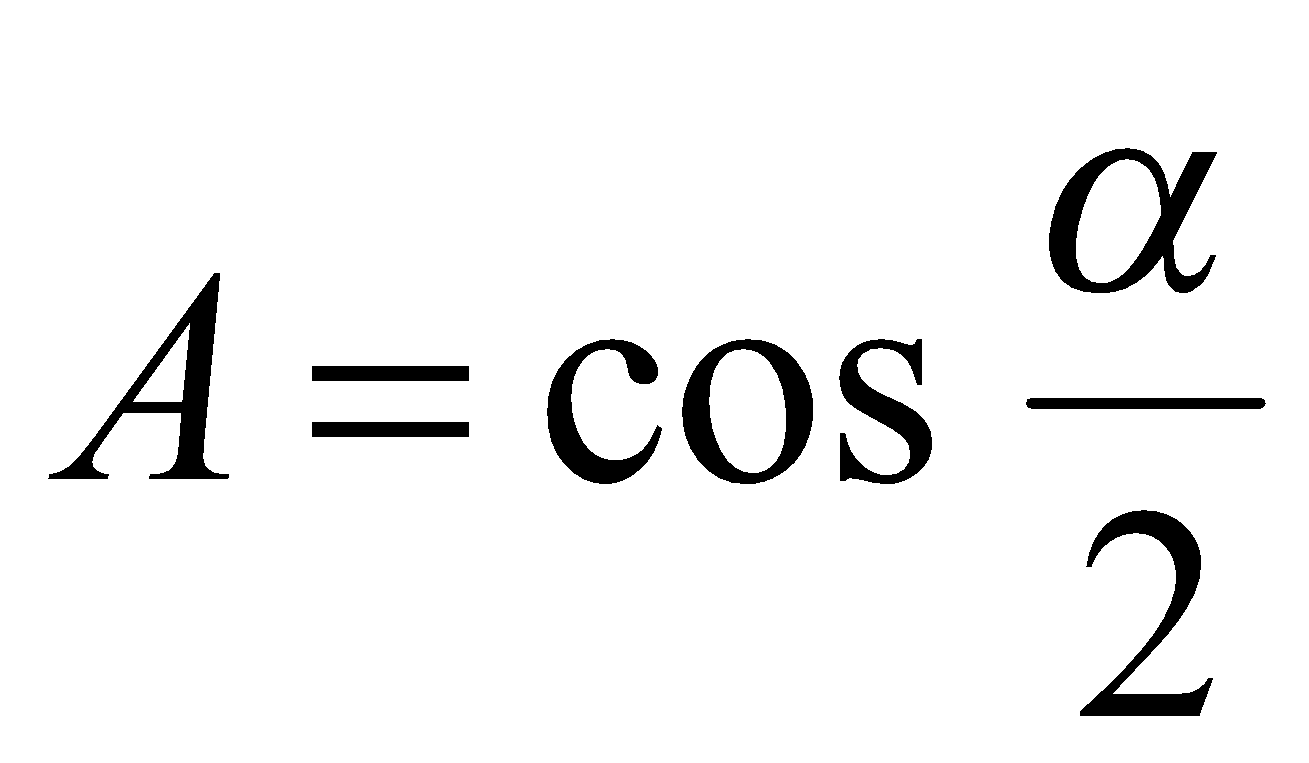 . Согласно определению функции
. Согласно определению функции 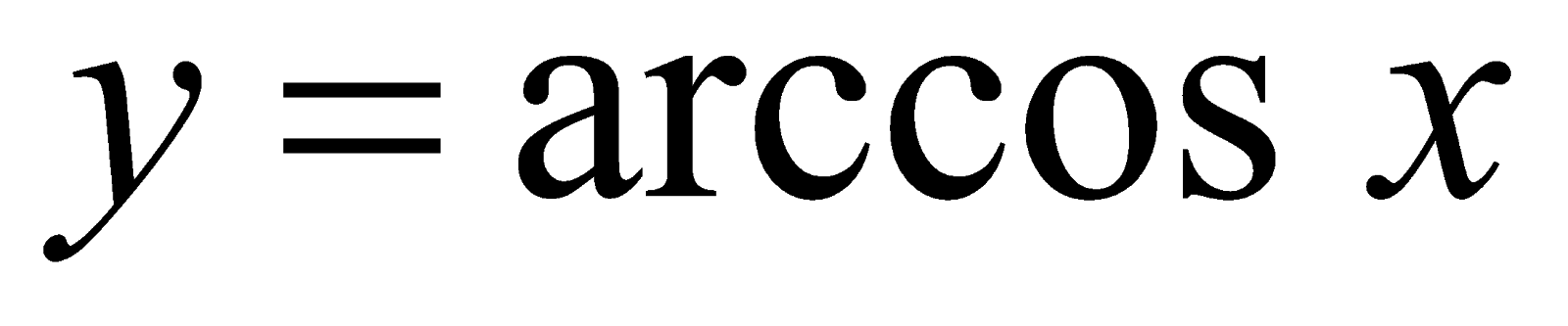 , имеем
, имеем 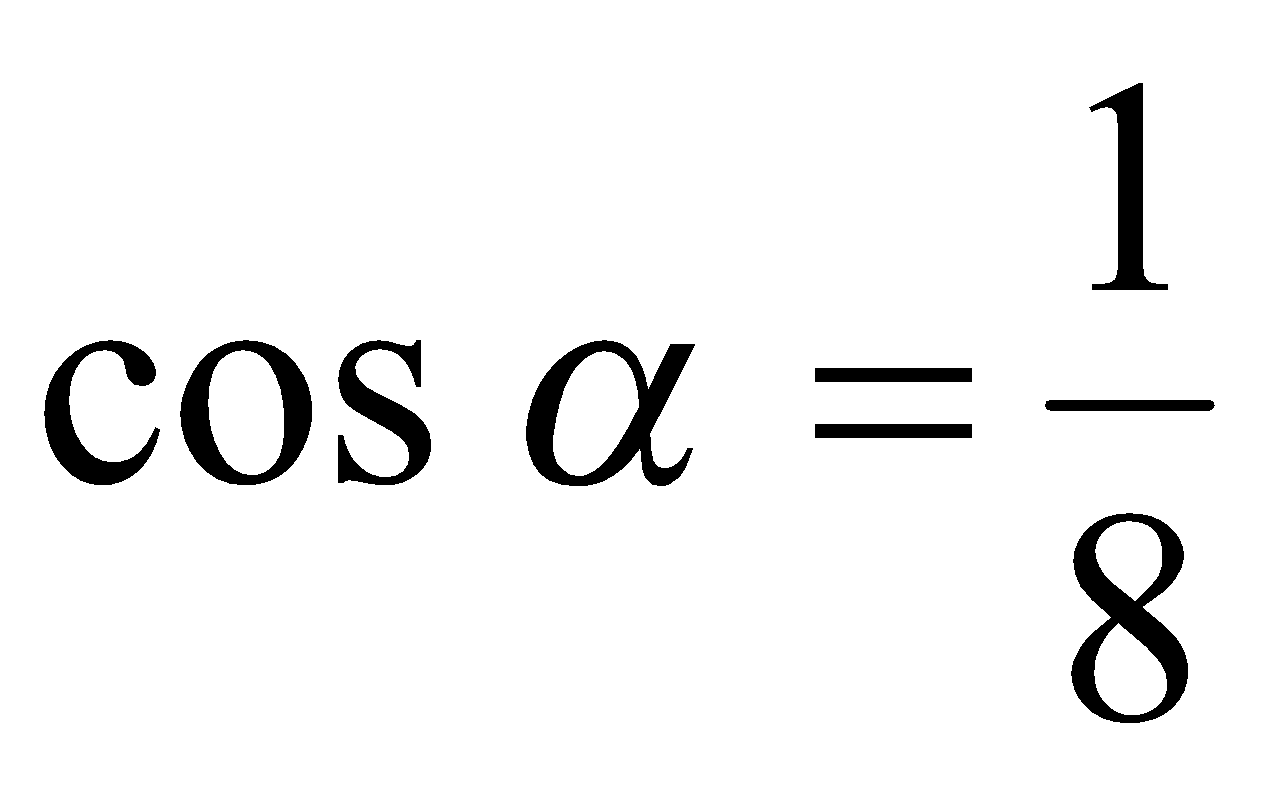 и
и 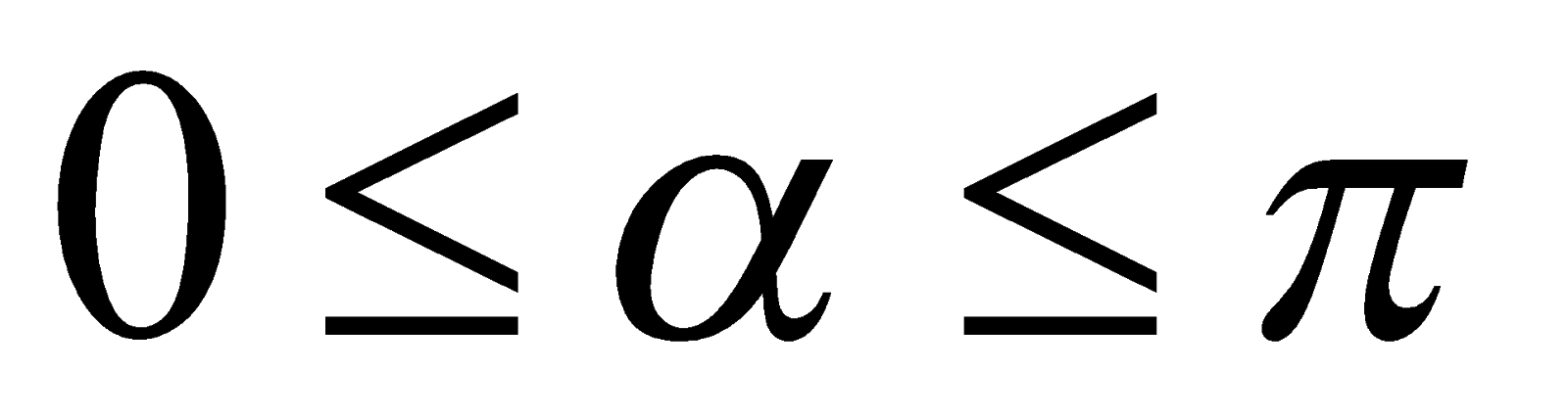 . Так как
. Так как 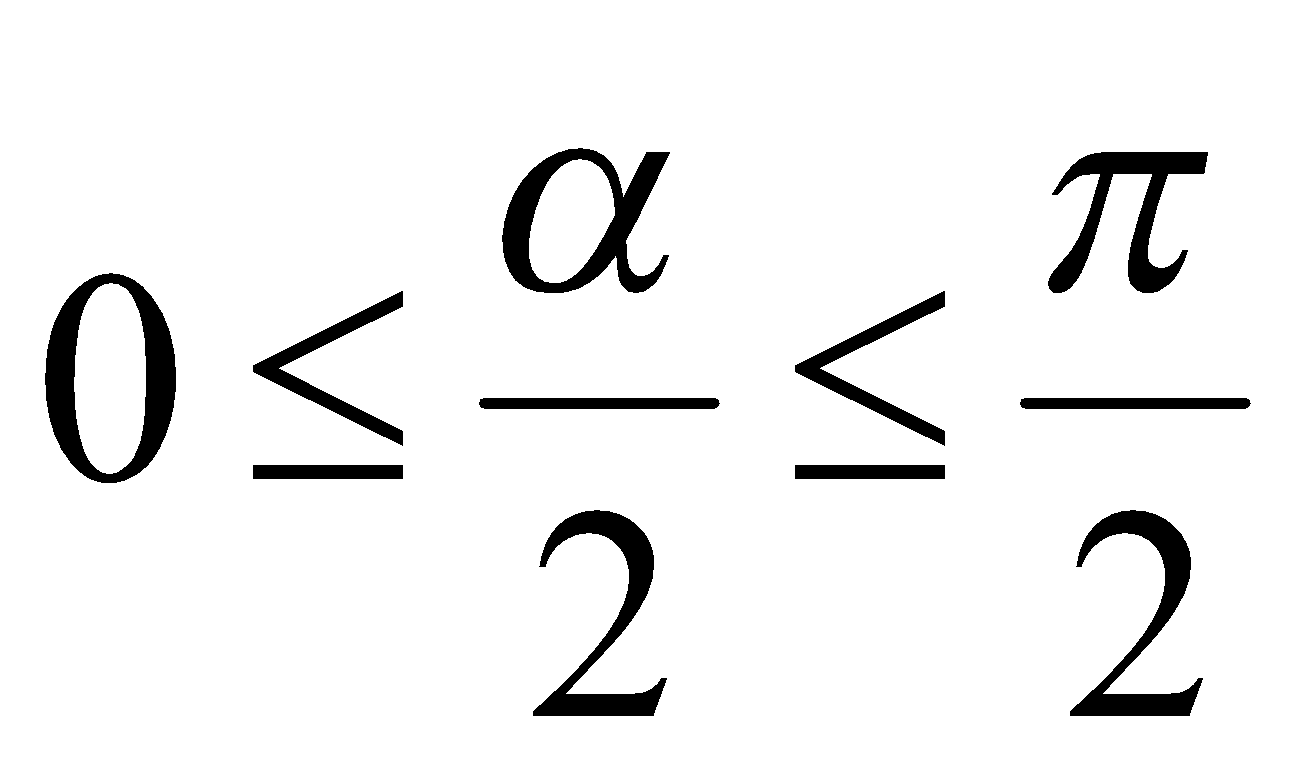 , то
, то 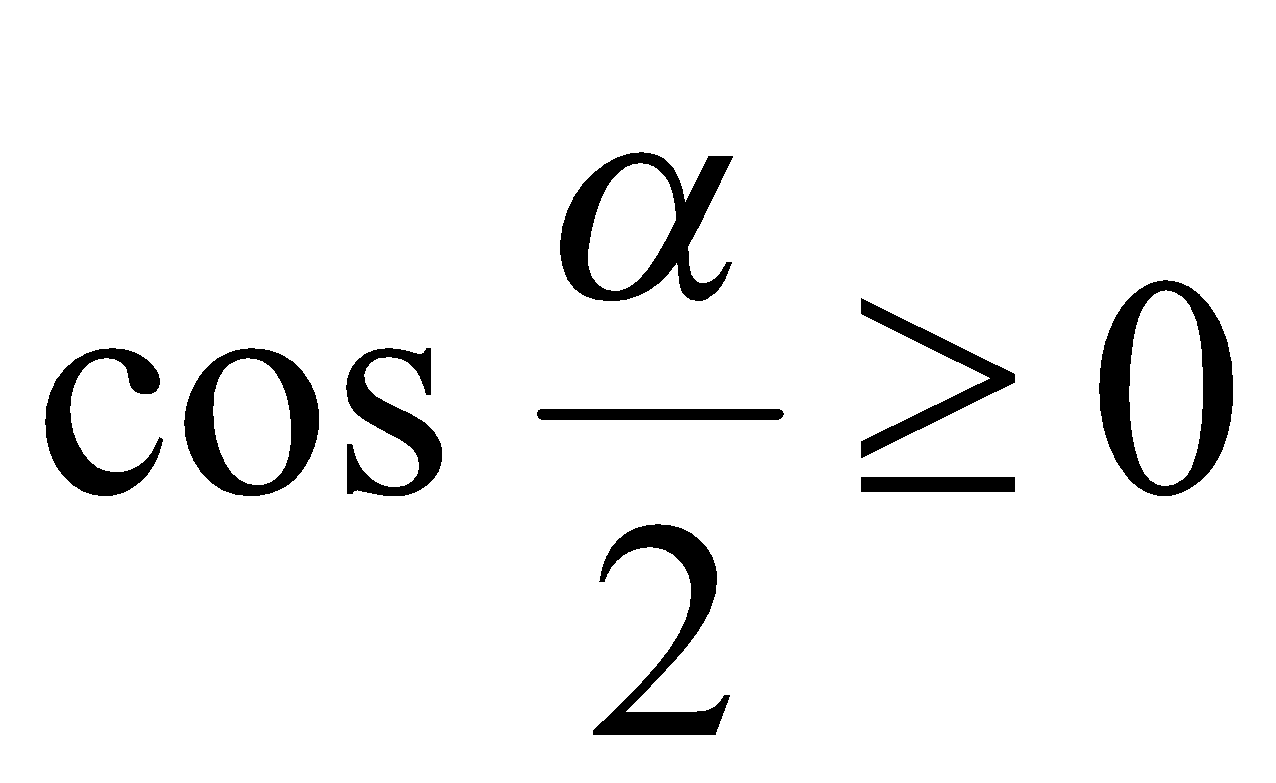 .
.
Поскольку 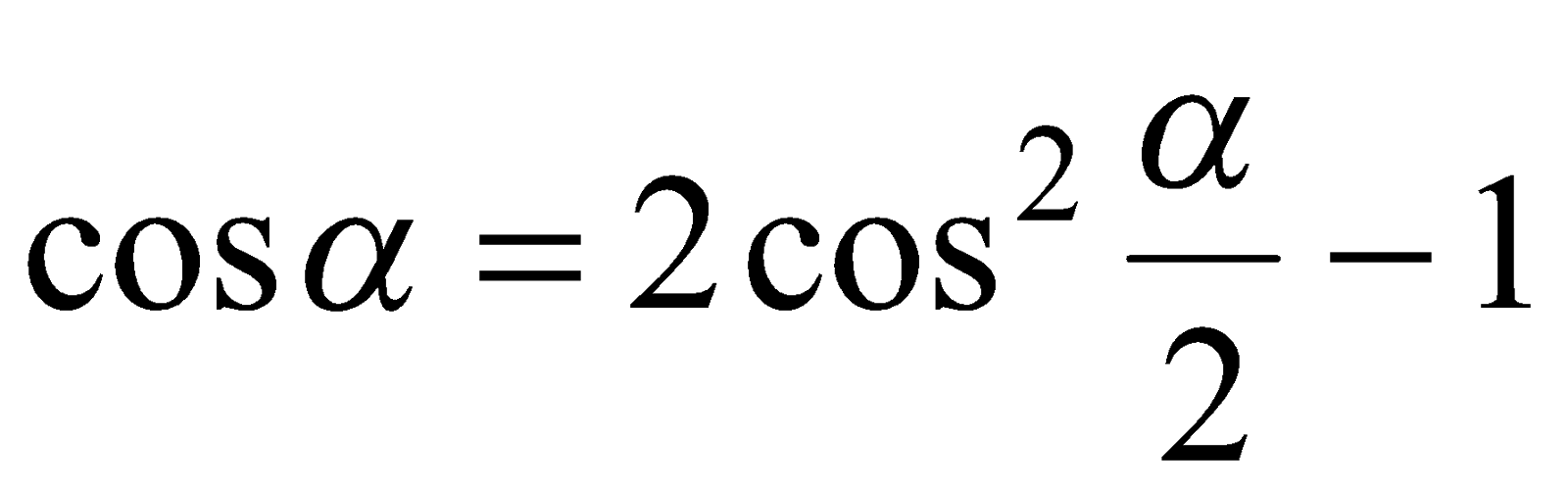 и
и 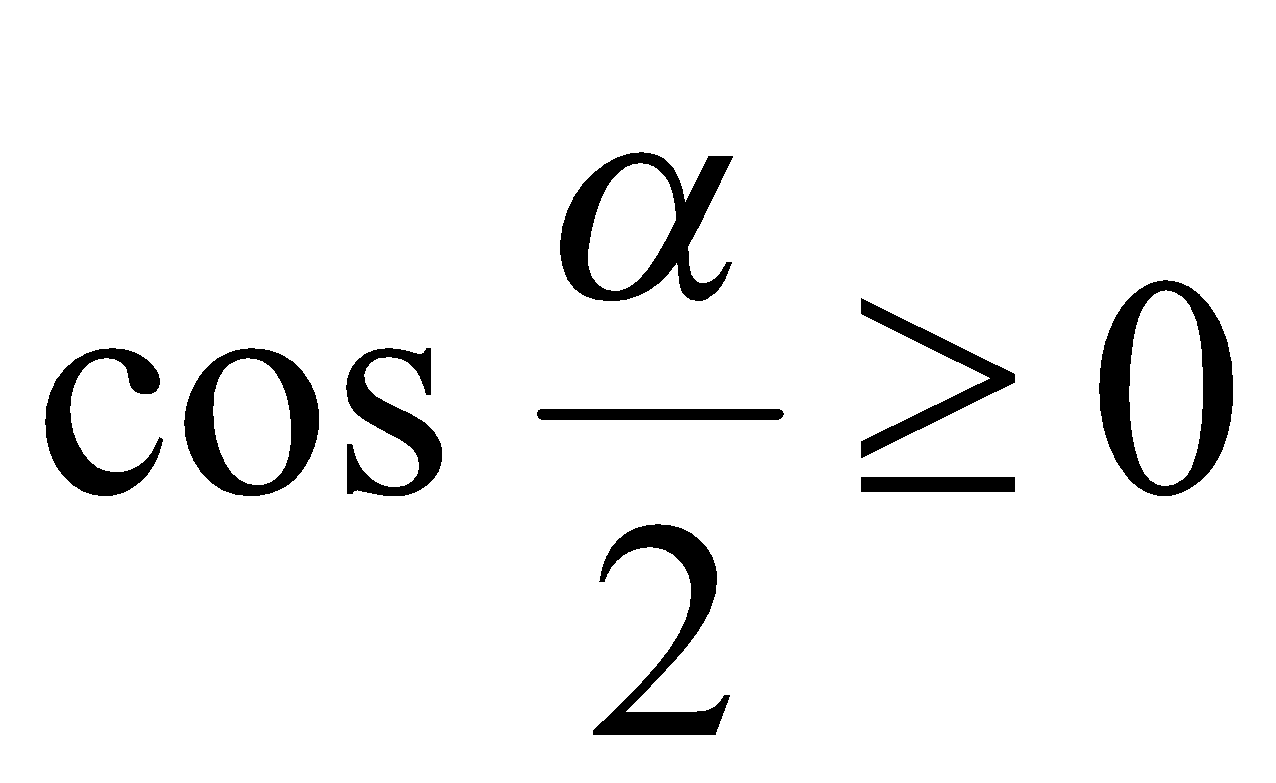 , то
, то 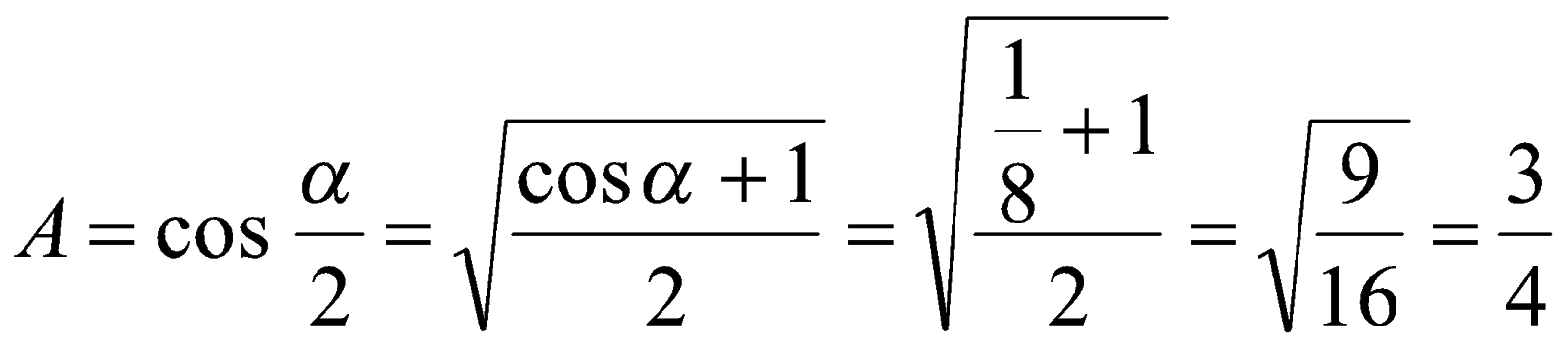 .
.
Ответ:  .
.
Пример 3. Вычислить значение 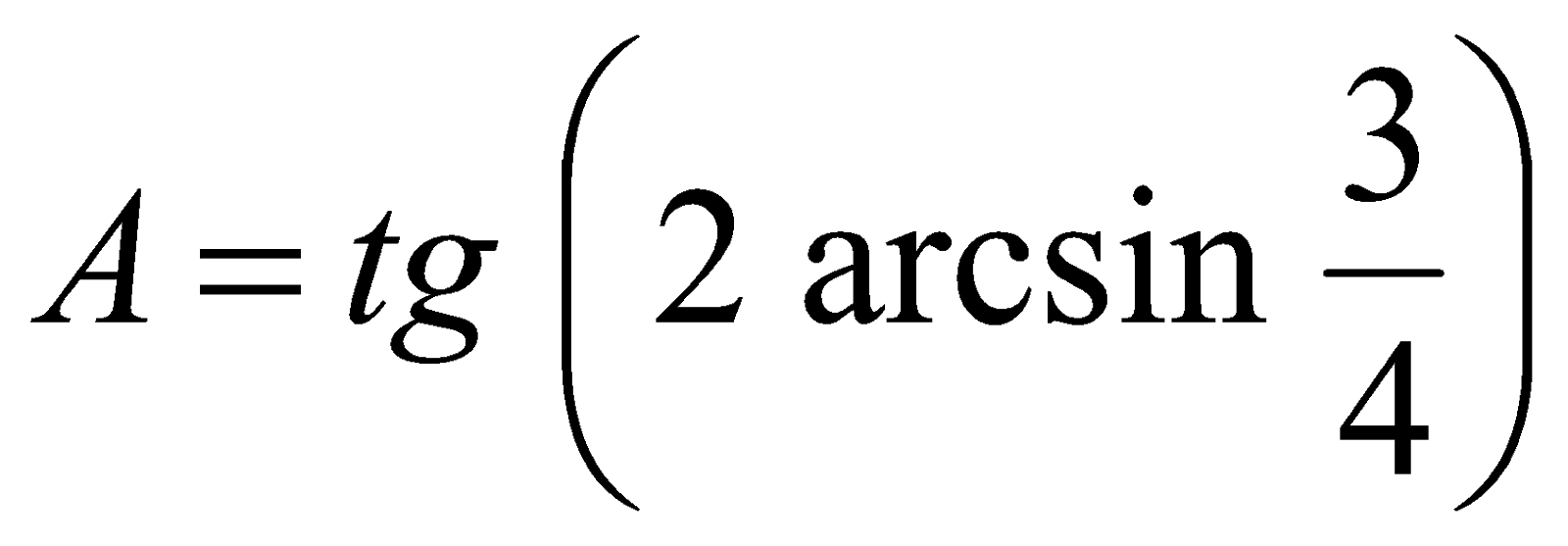 .
.
Решение. Пусть 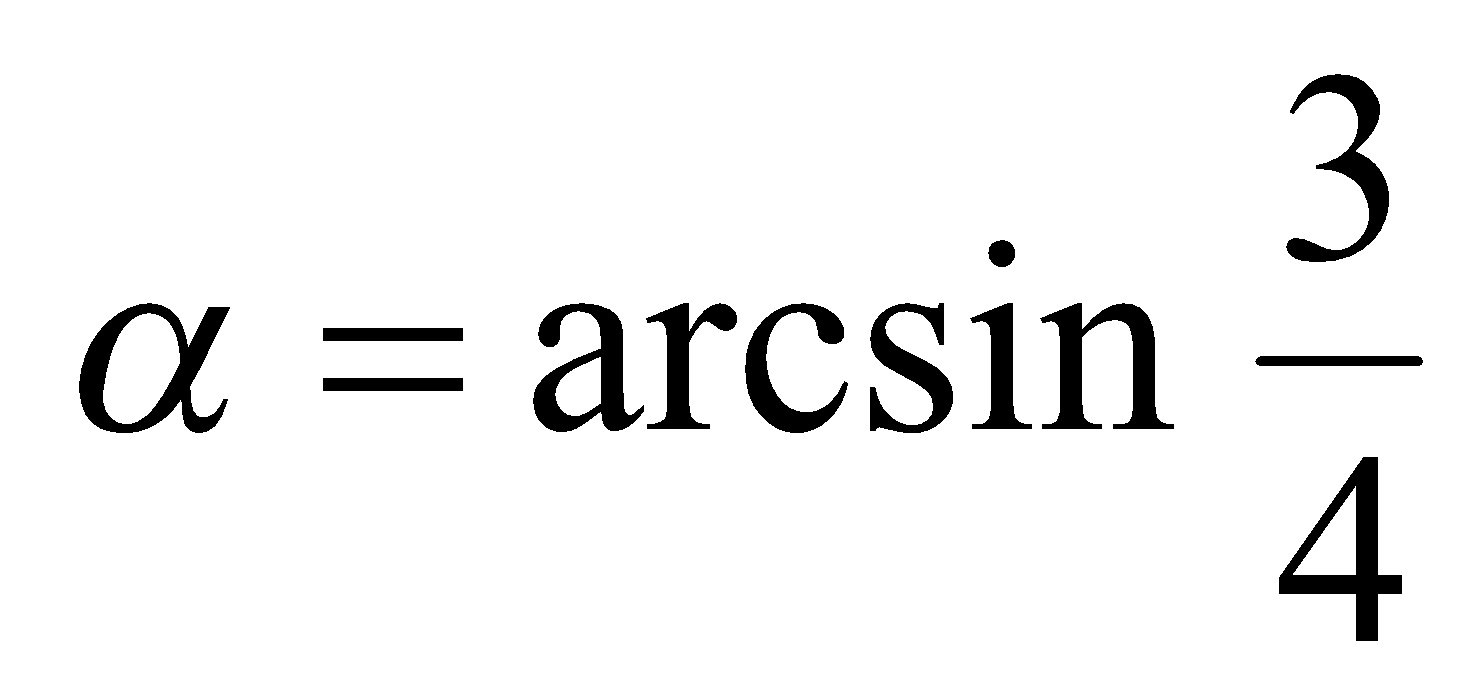 , тогда
, тогда 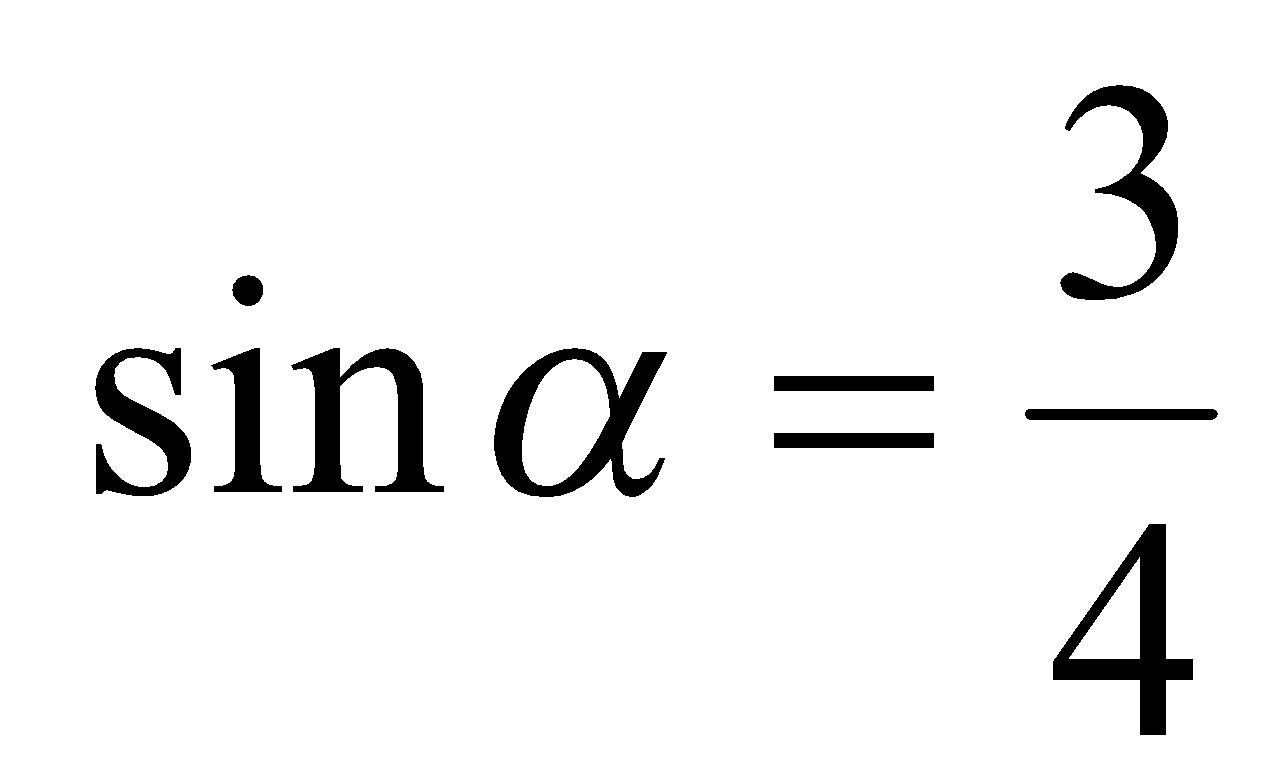 и
и  , где
, где 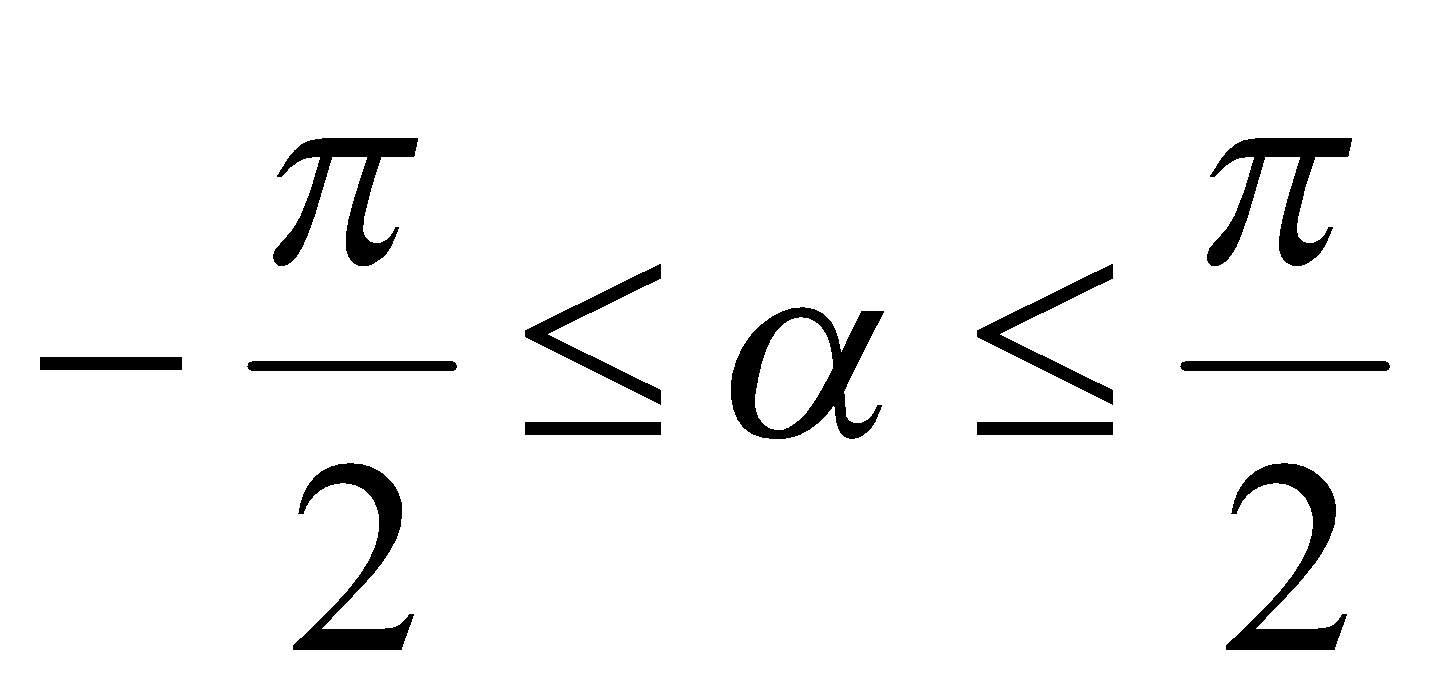 . В таком случае
. В таком случае 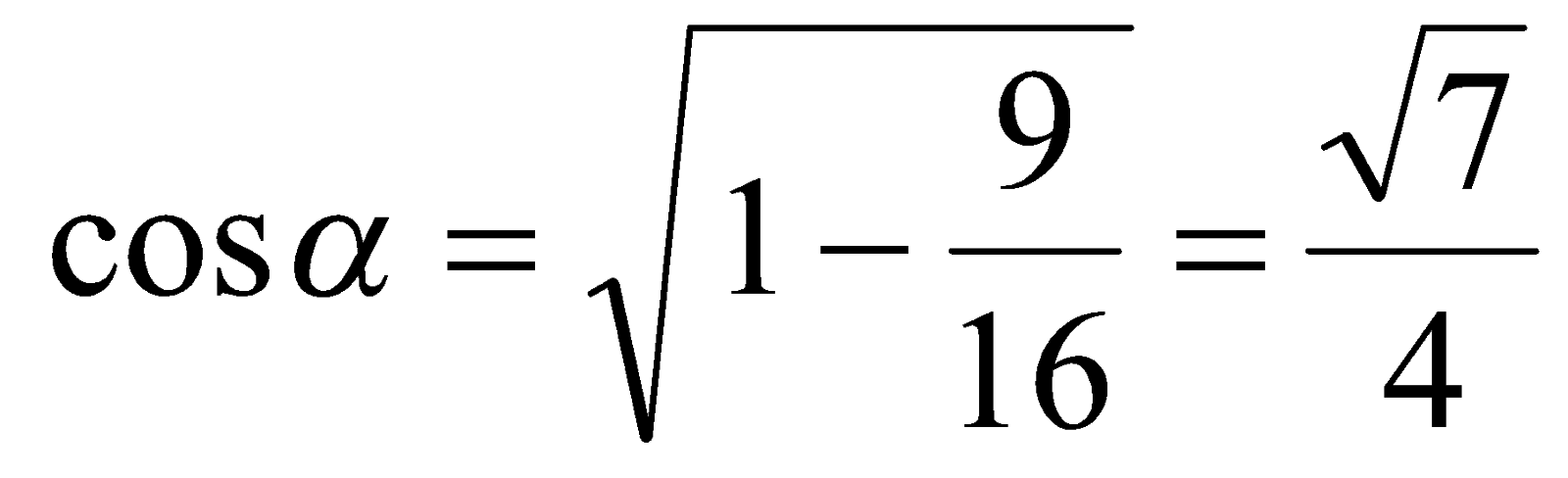 и
и 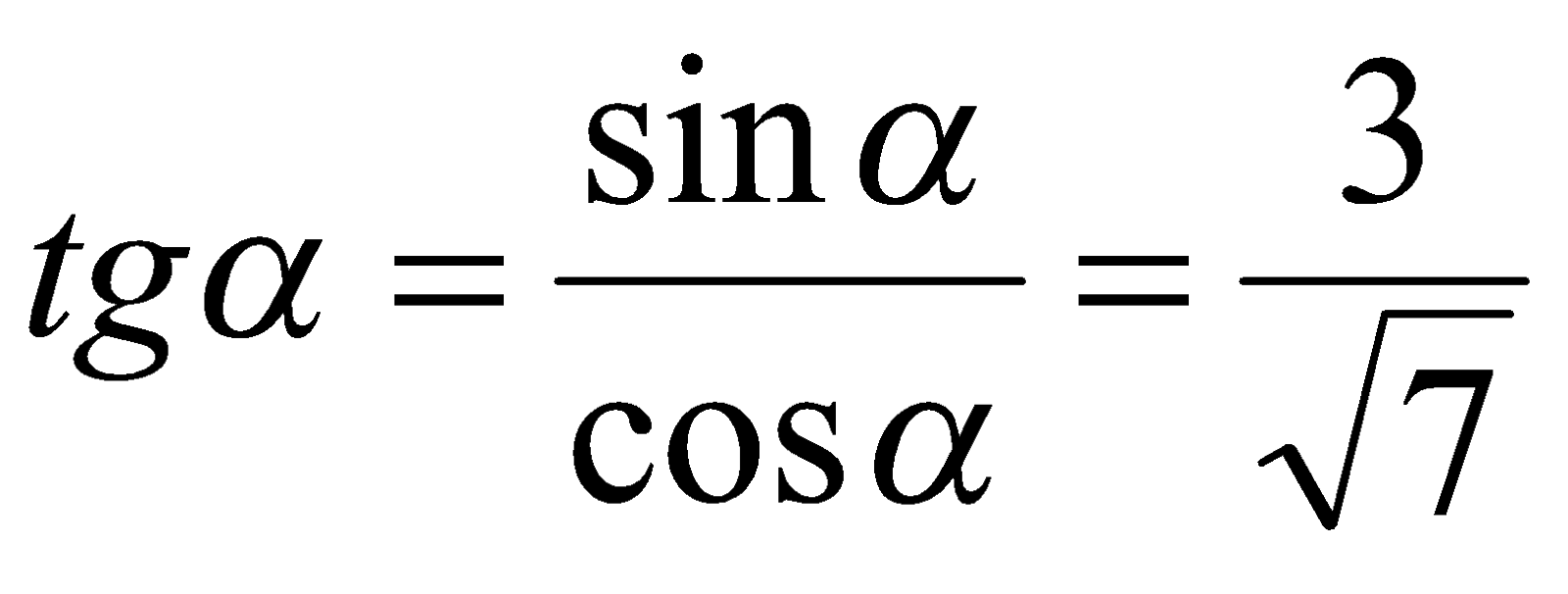 .
.
Поскольку 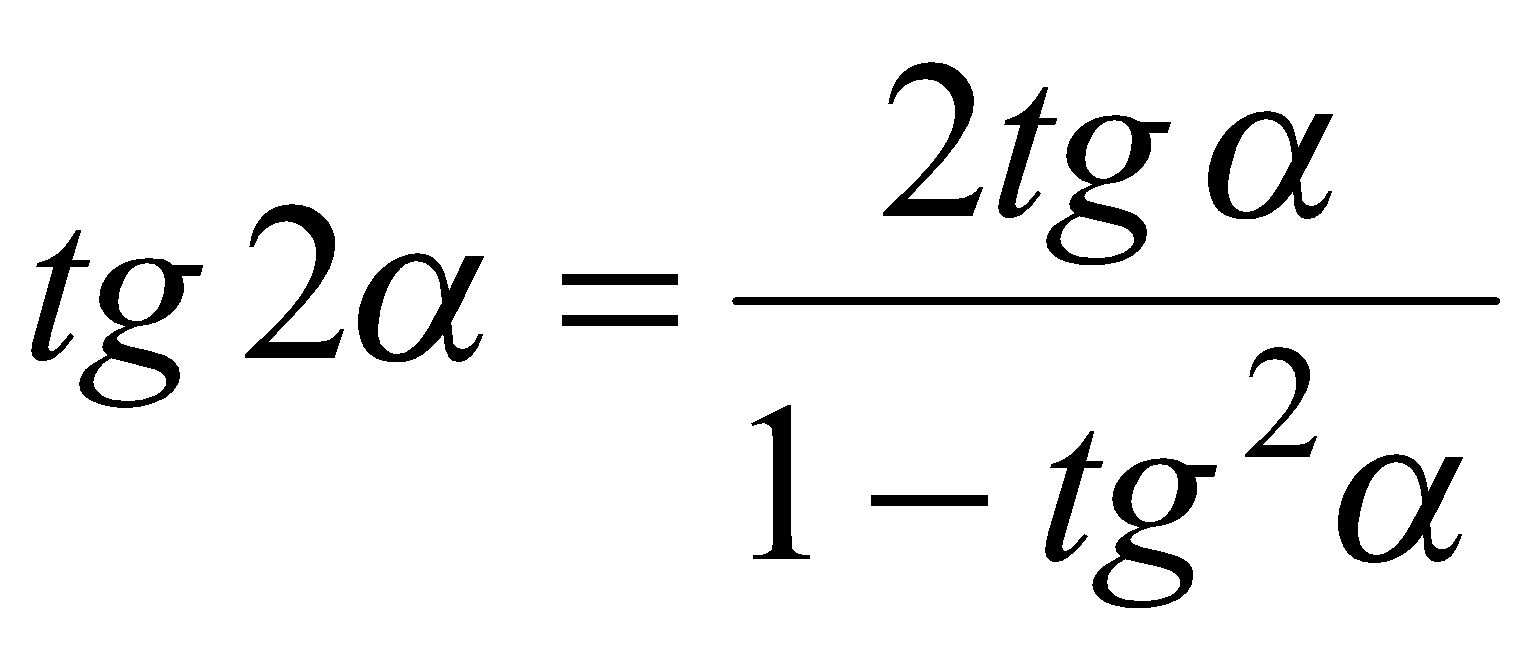 , то
, то 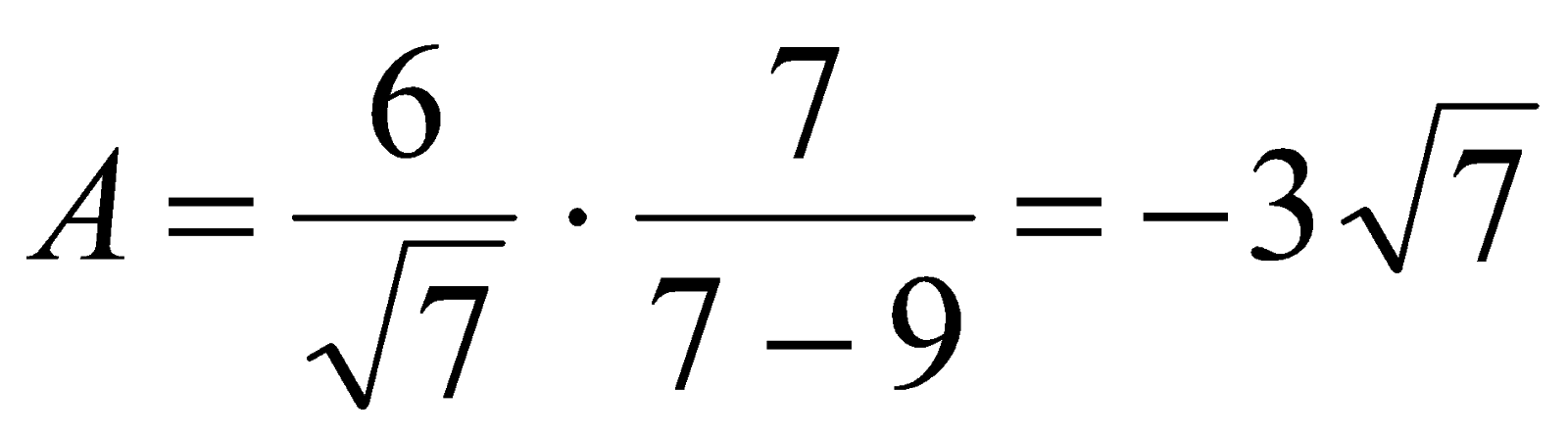 .
.
Ответ: 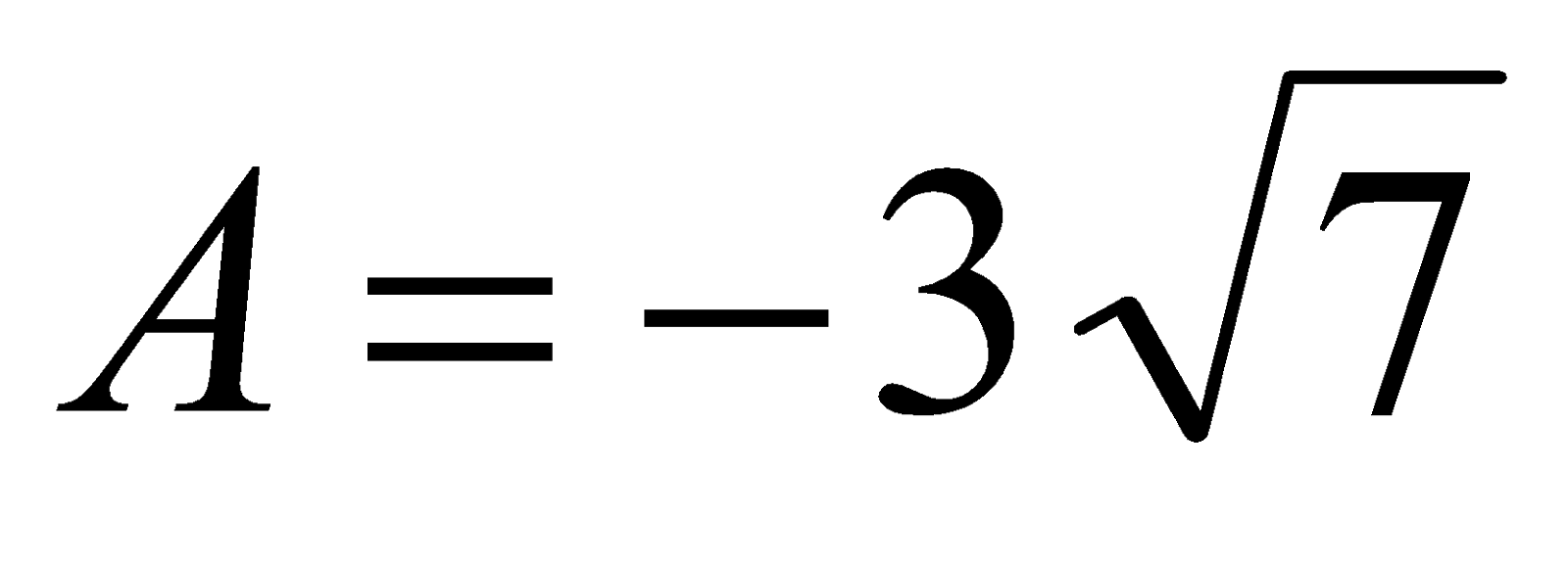 .
.
Пример 4. Вычислить значение 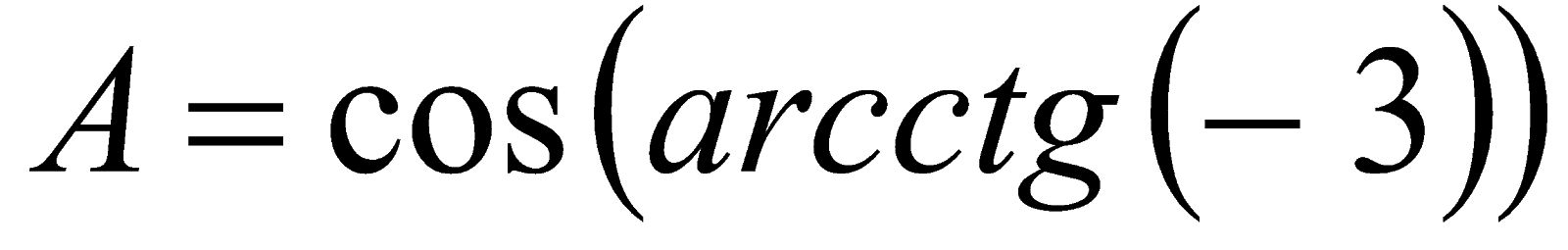 . Решение. Так как
. Решение. Так как 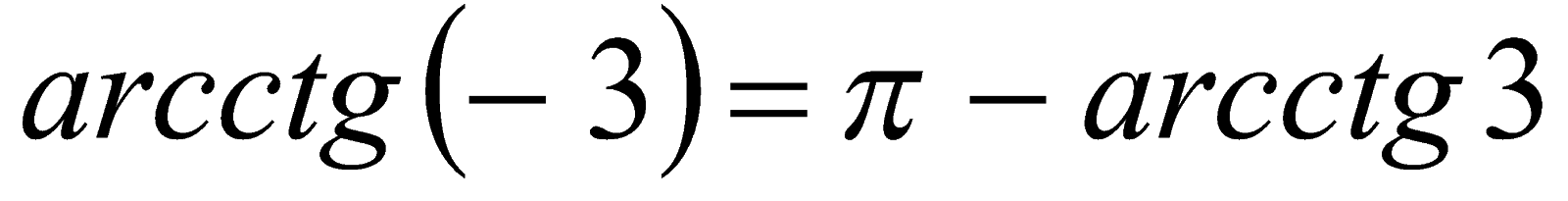 , то
, то 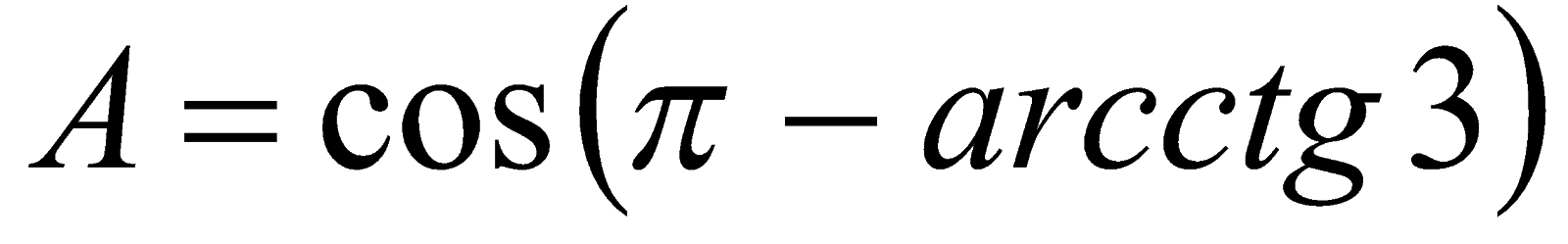 или
или 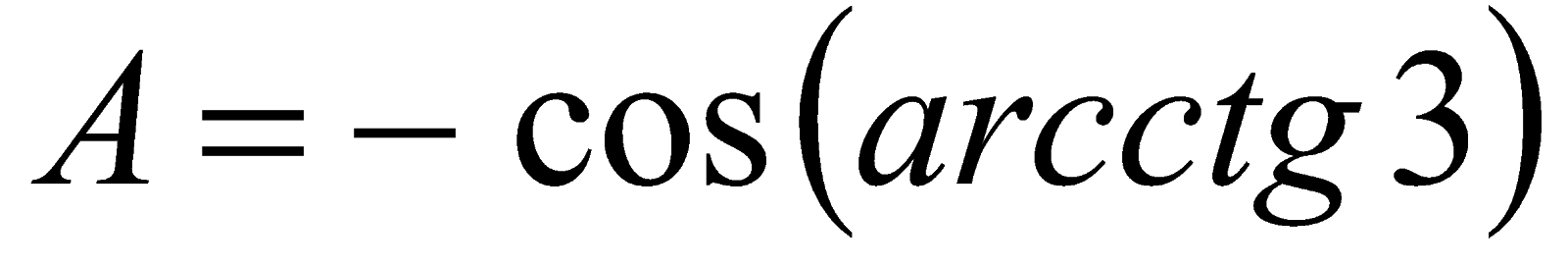 . Обозначим
. Обозначим 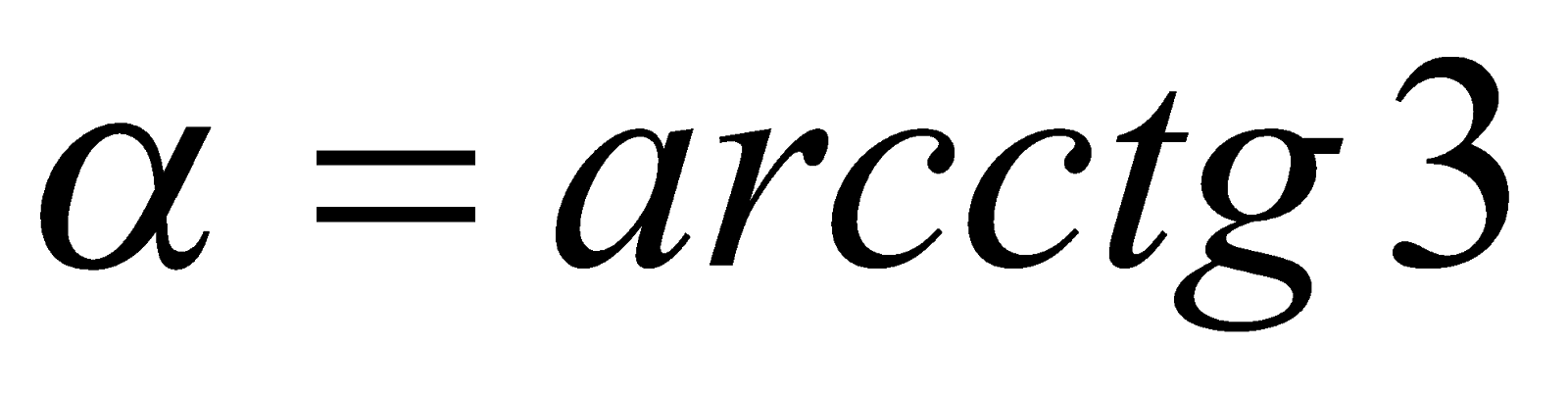 , тогда
, тогда 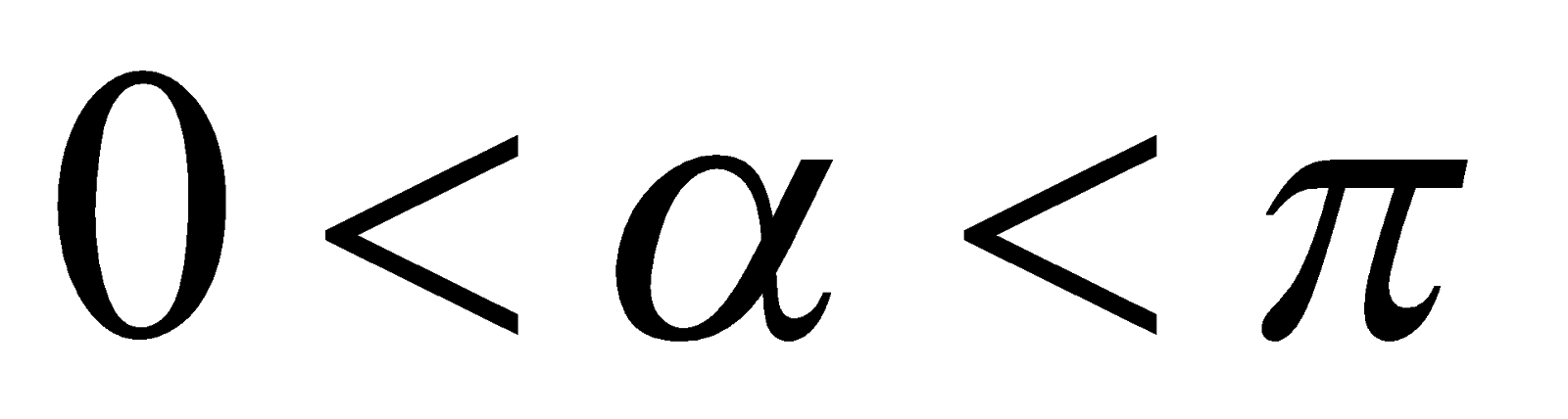 ,
, 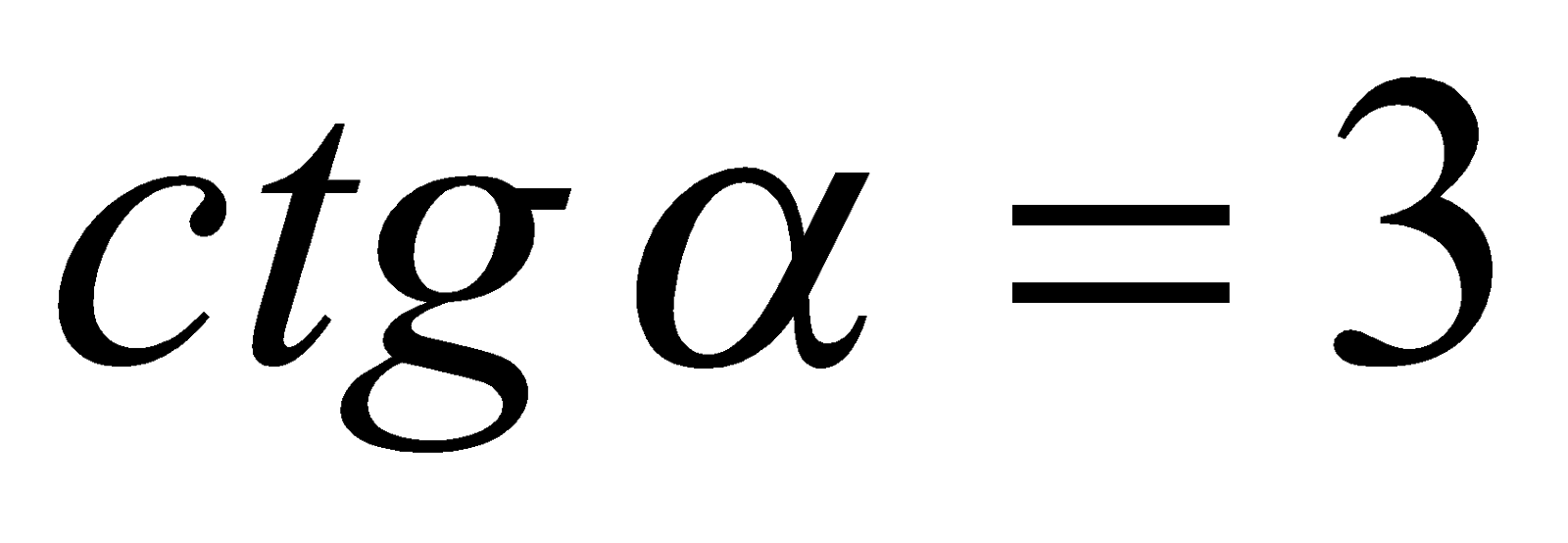
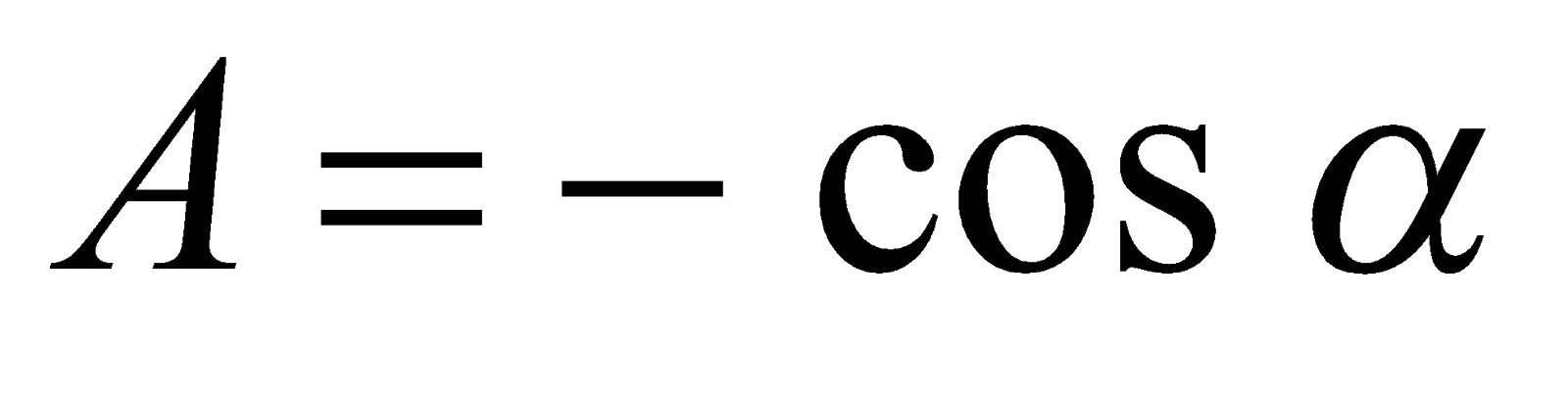 . Поскольку
. Поскольку 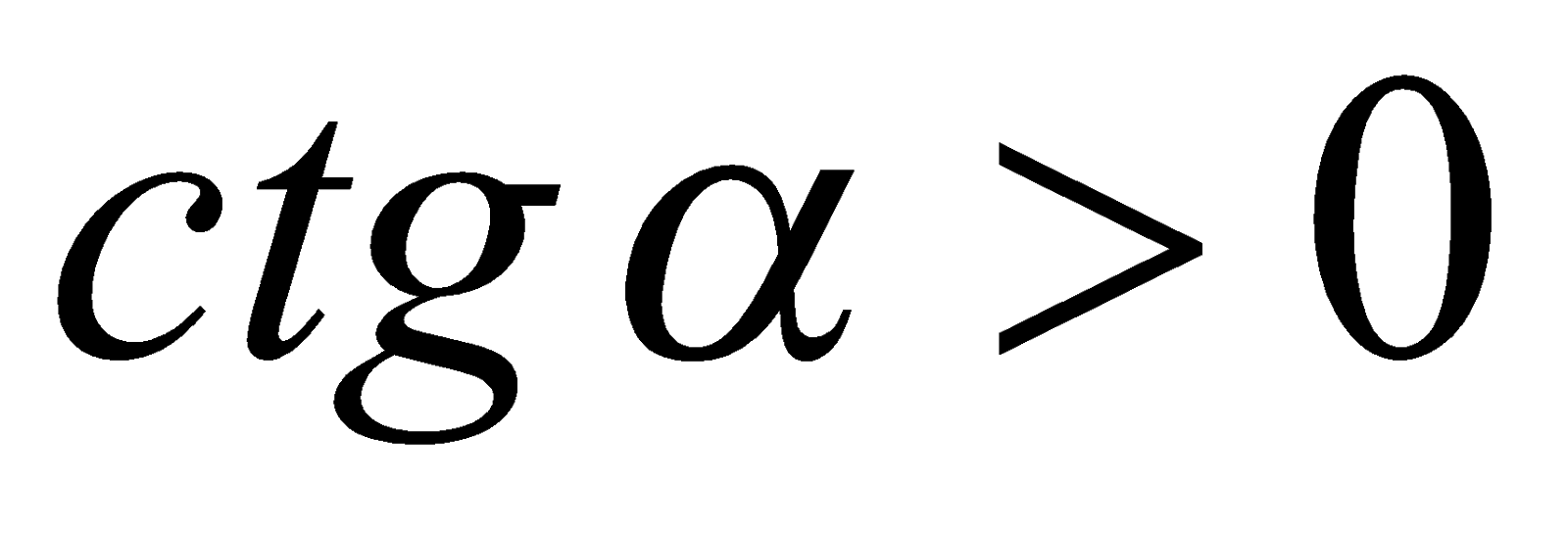 , то
, то 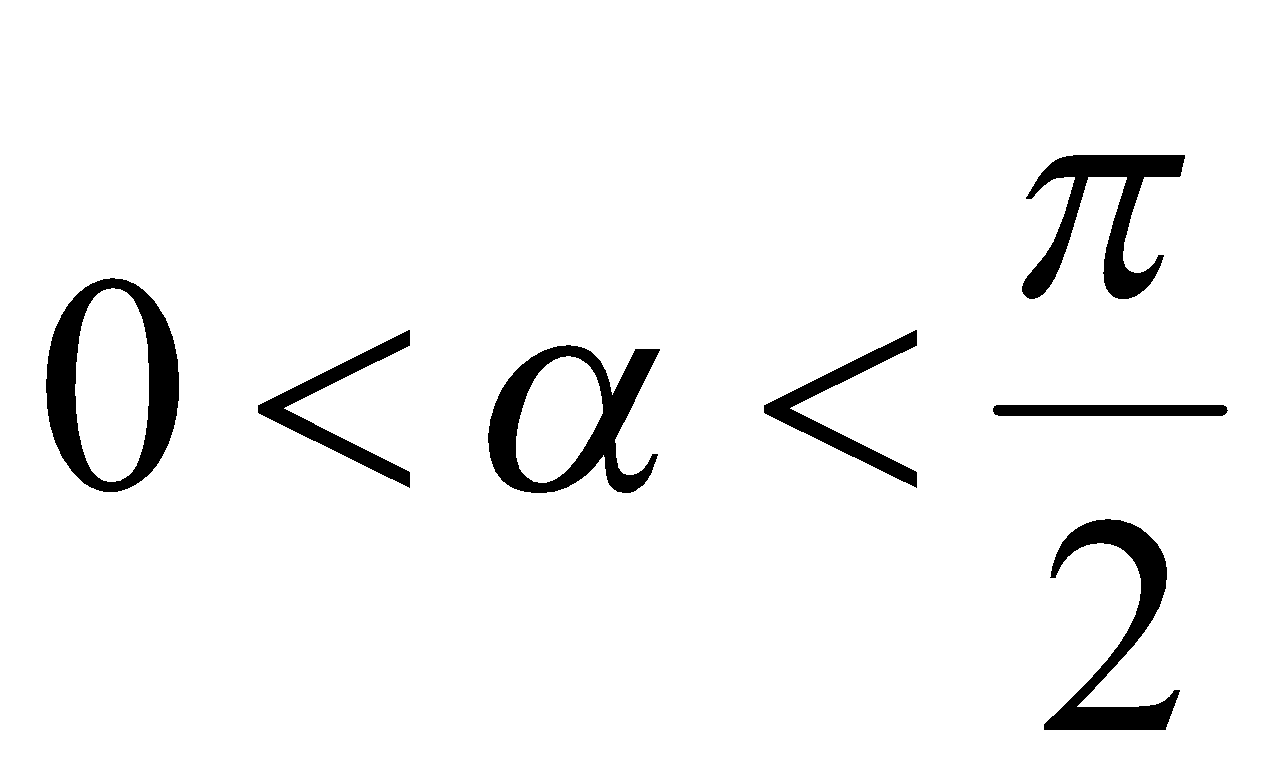 .
.
Если 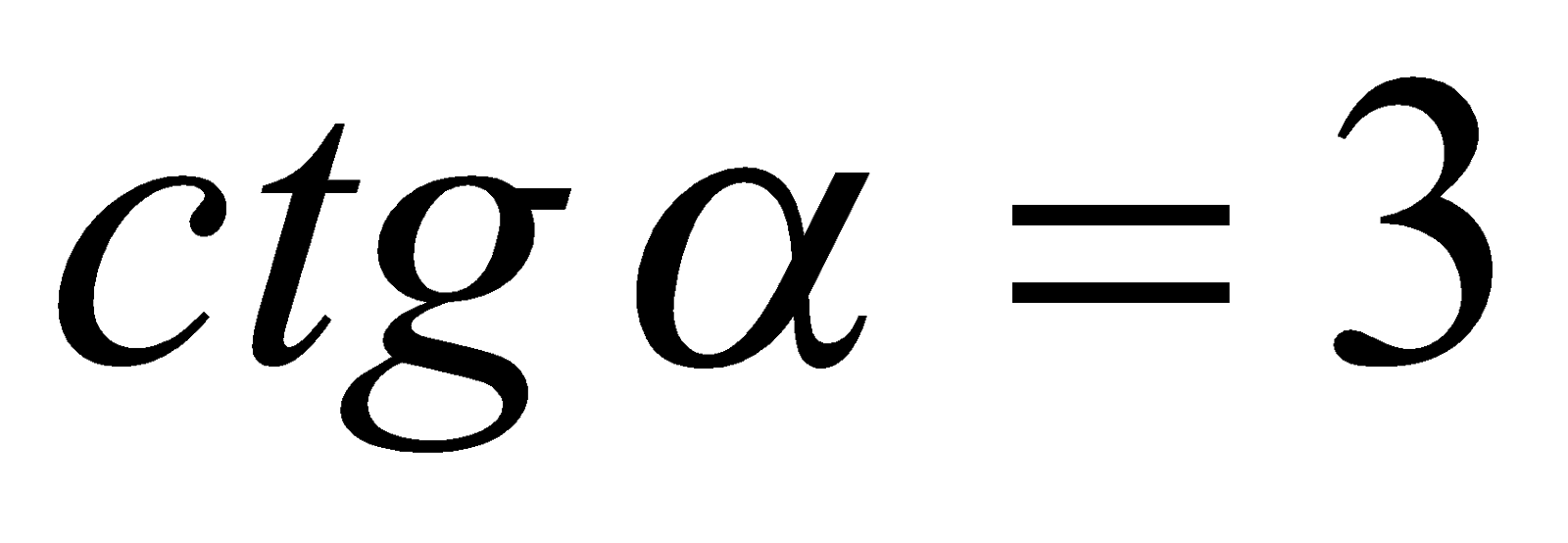 , то
, то  ,
, 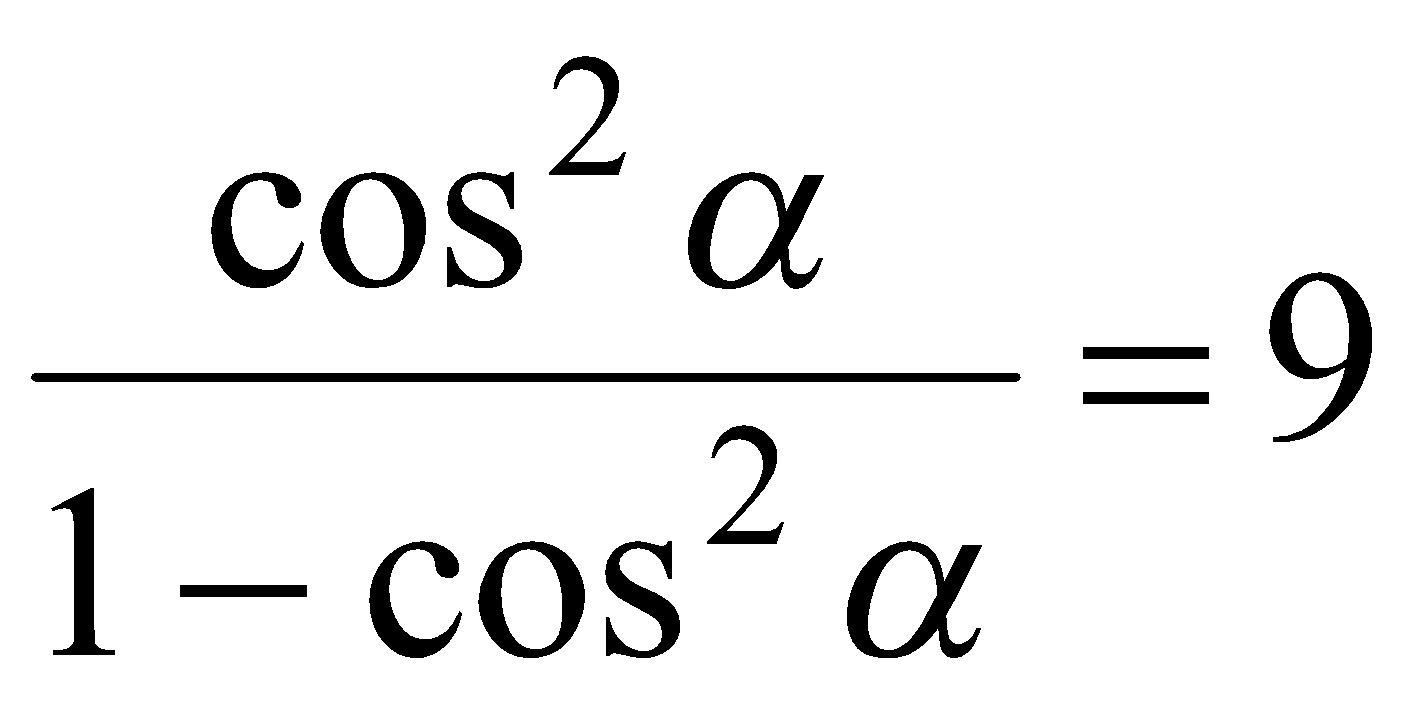 или
или 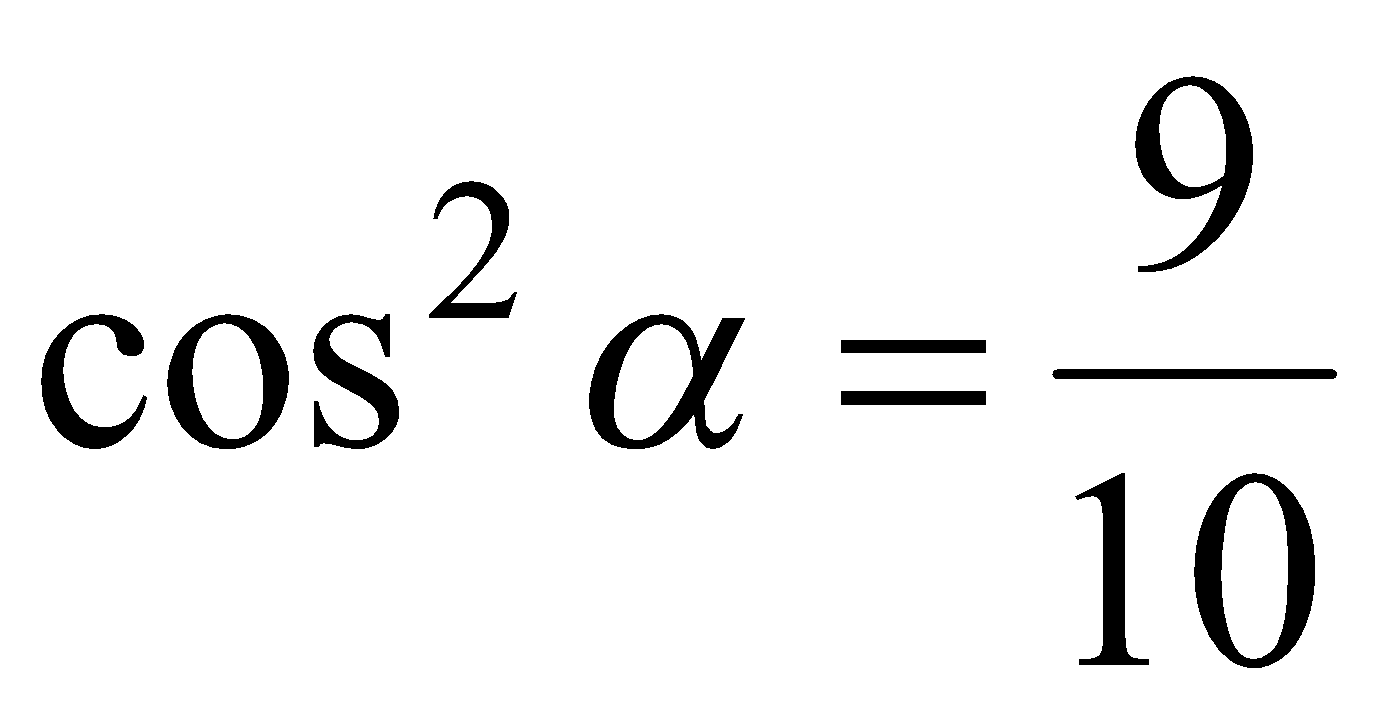 . Однако
. Однако 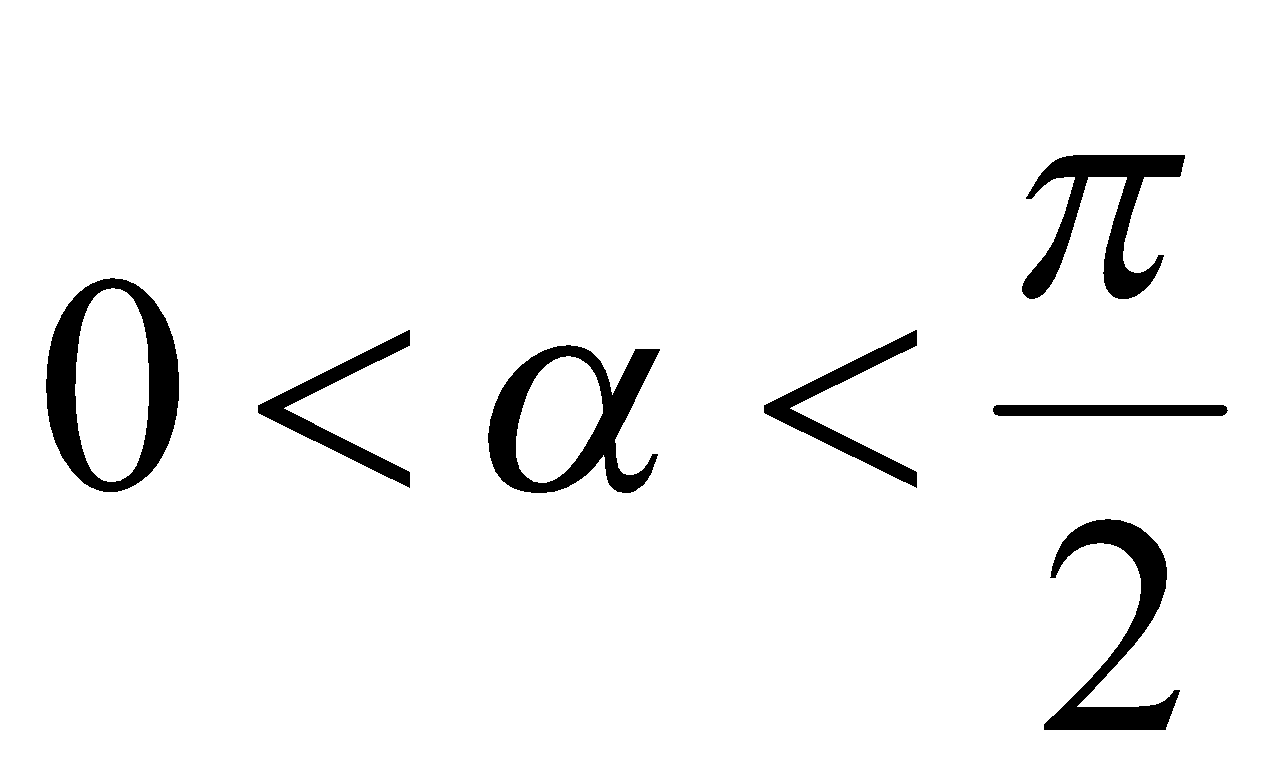 , поэтому
, поэтому 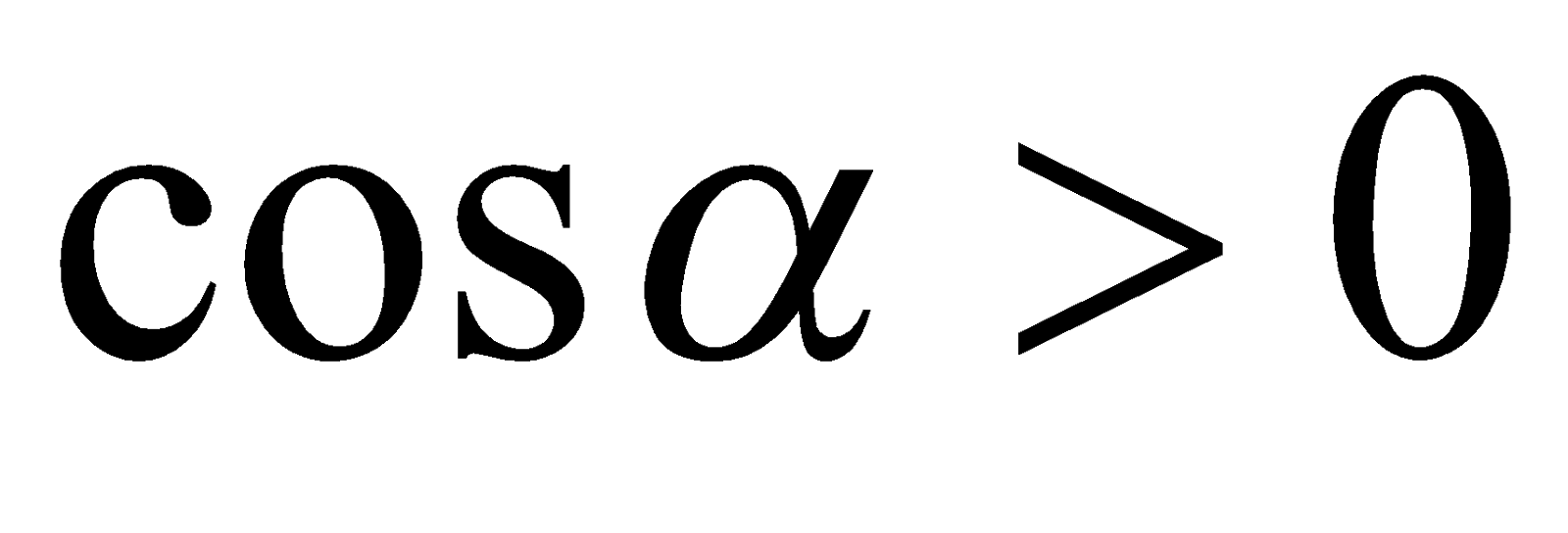 ,
, 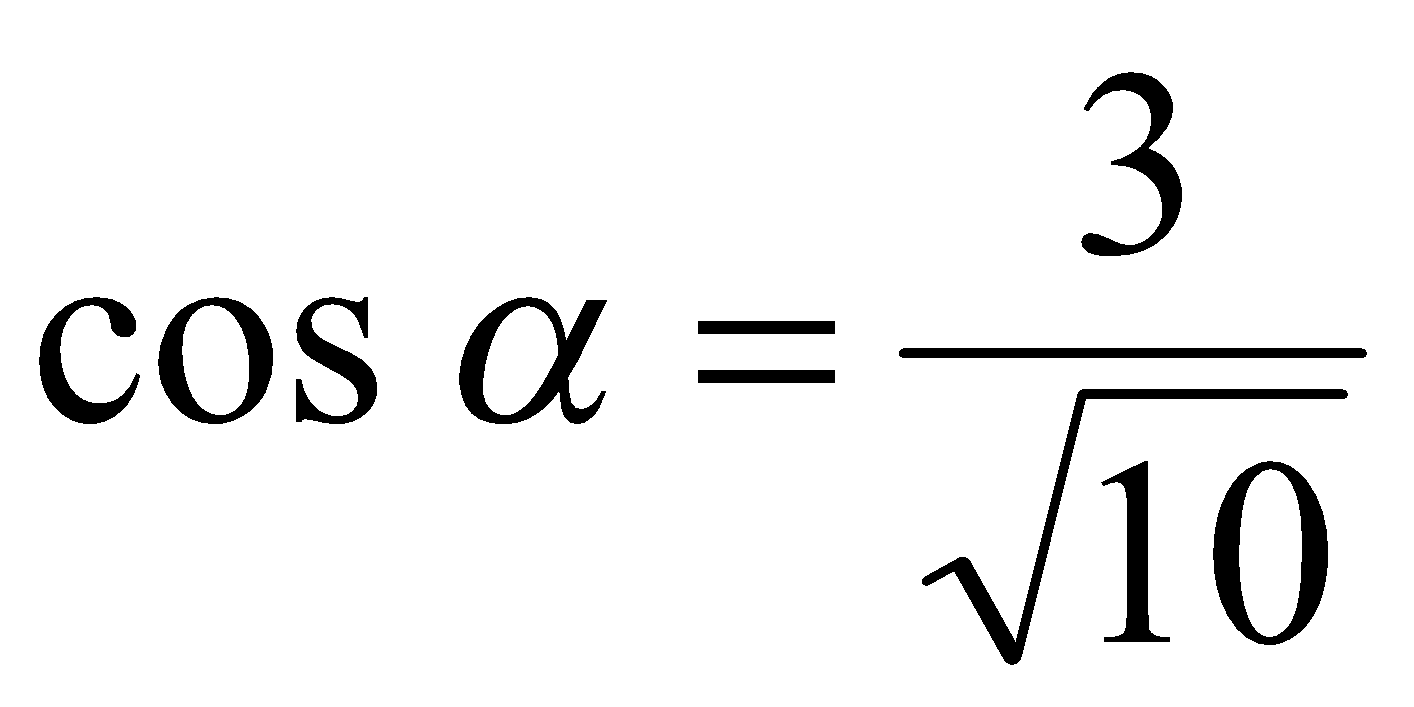 и
и 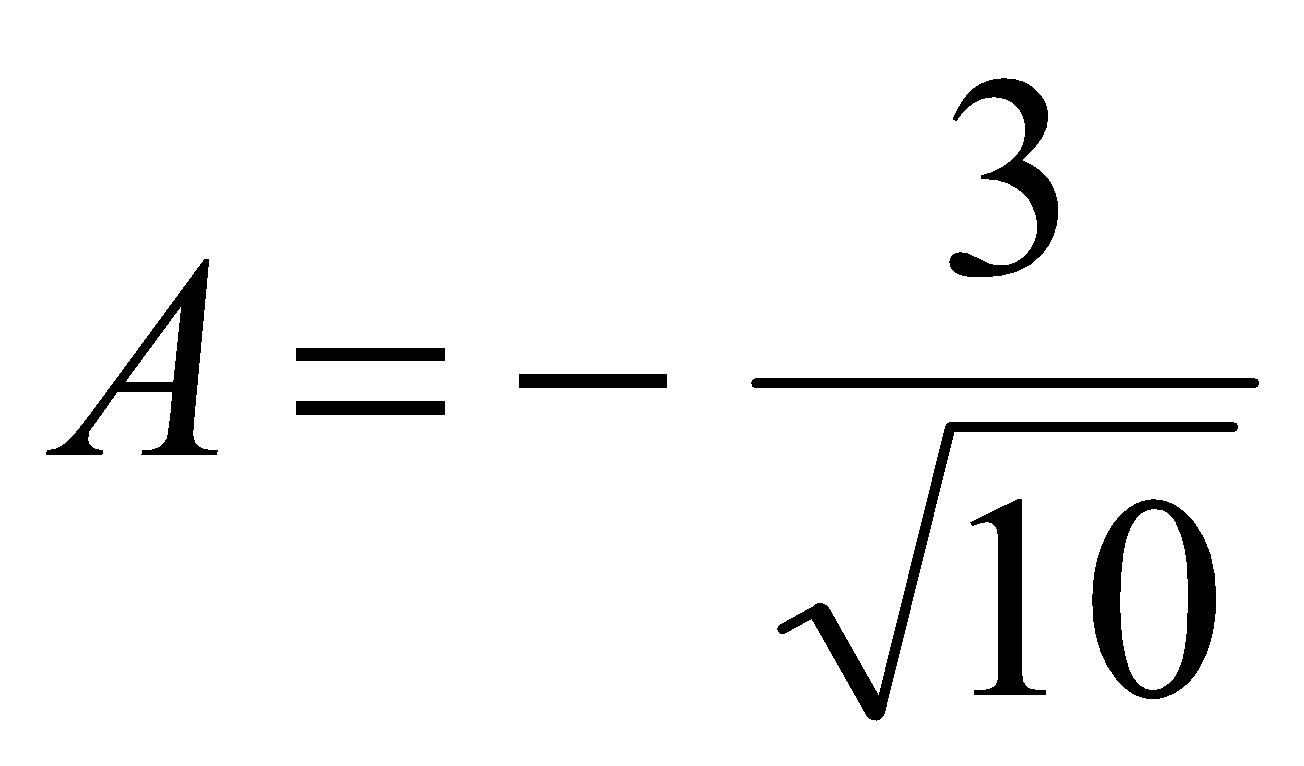 .
.
Ответ: 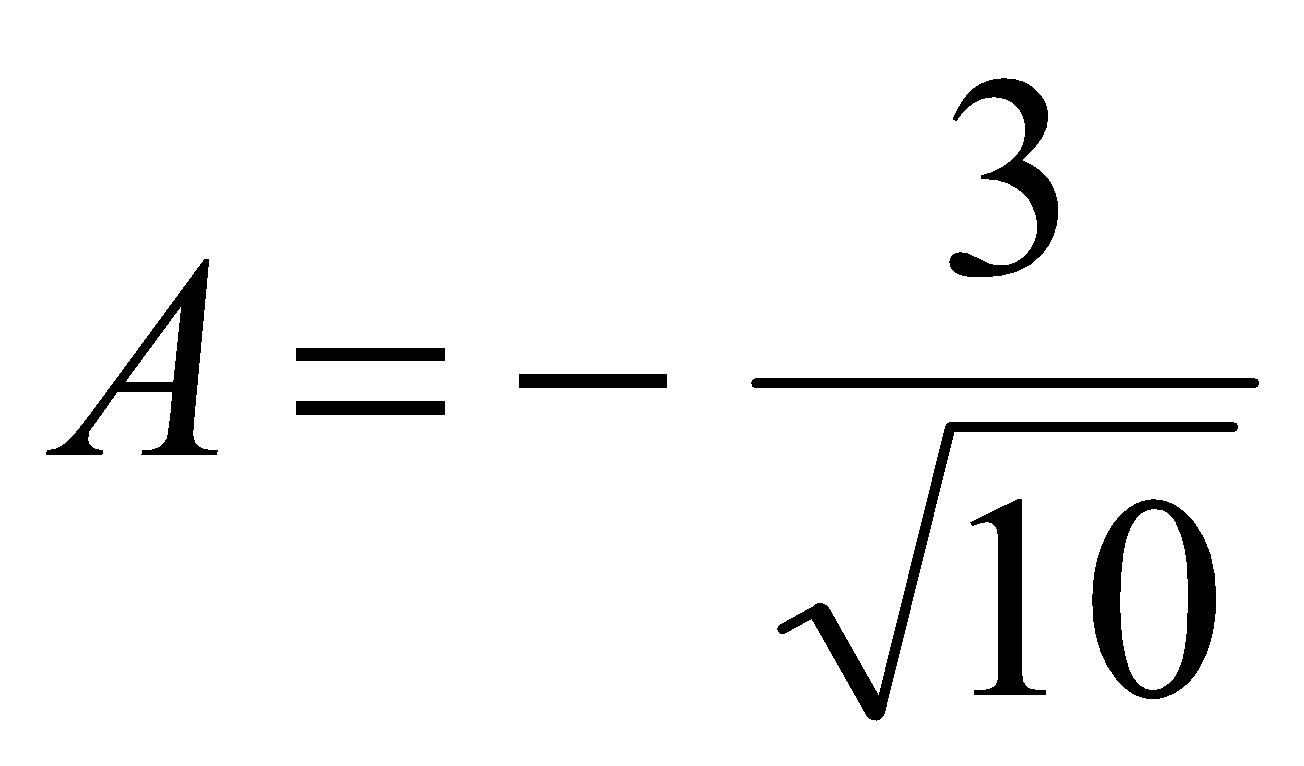 .
.
Пример 5. Вычислить значение 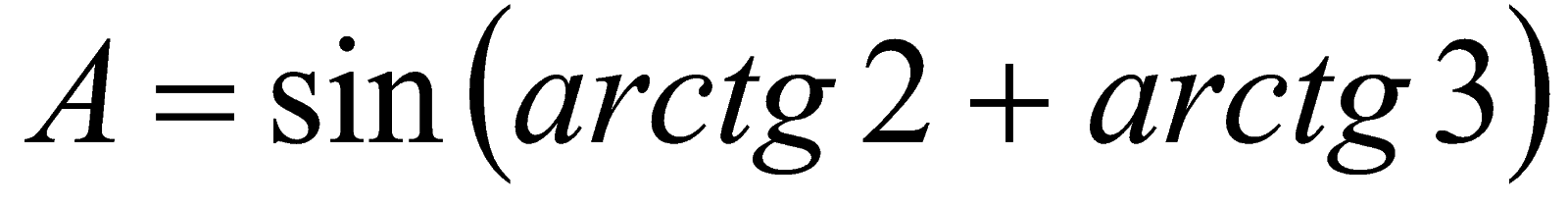 .
.
Решение. Если положить 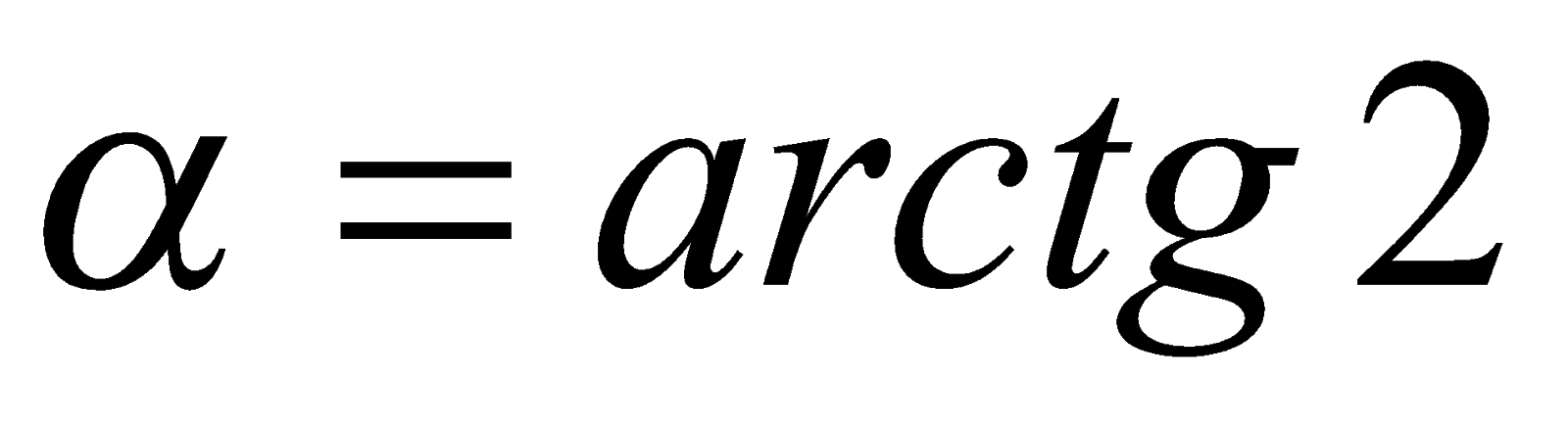 и
и 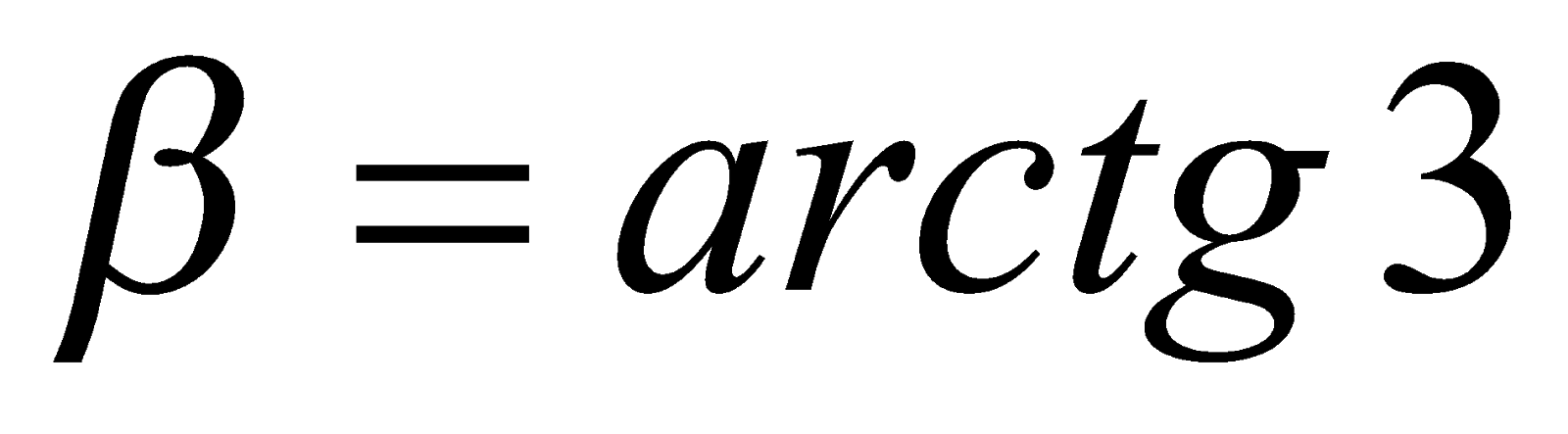 , то
, то 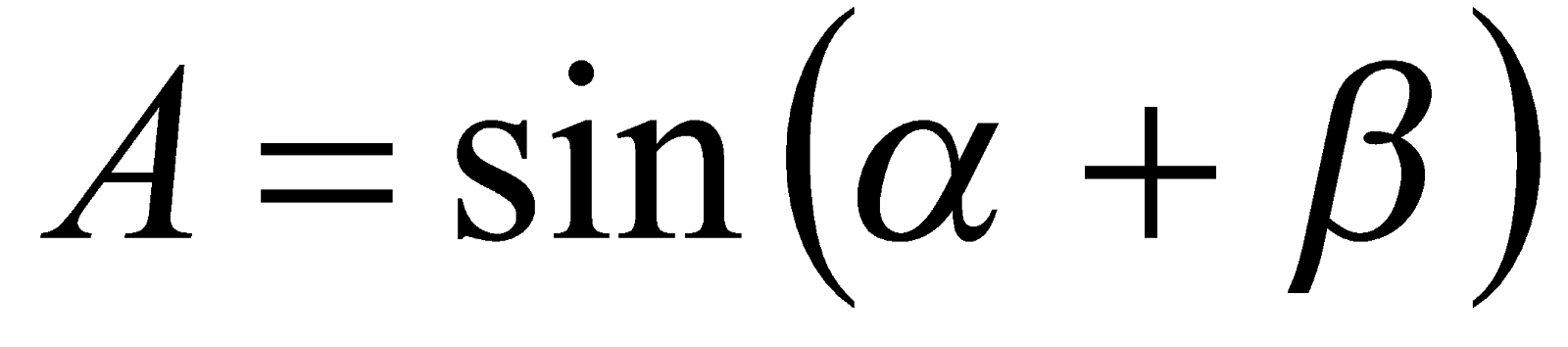 или
или
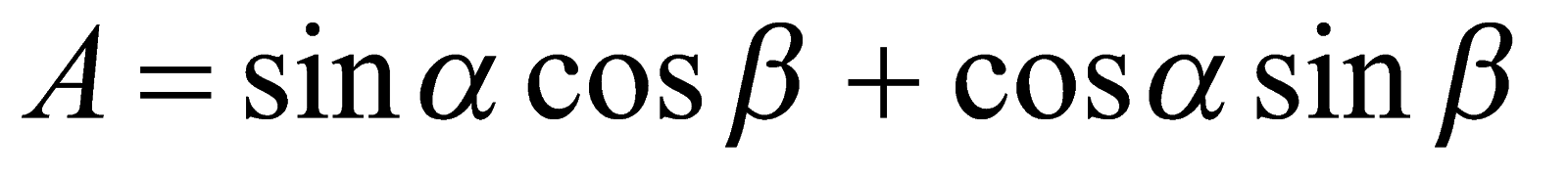 , (1)
, (1)
где из определения функции  имеем
имеем 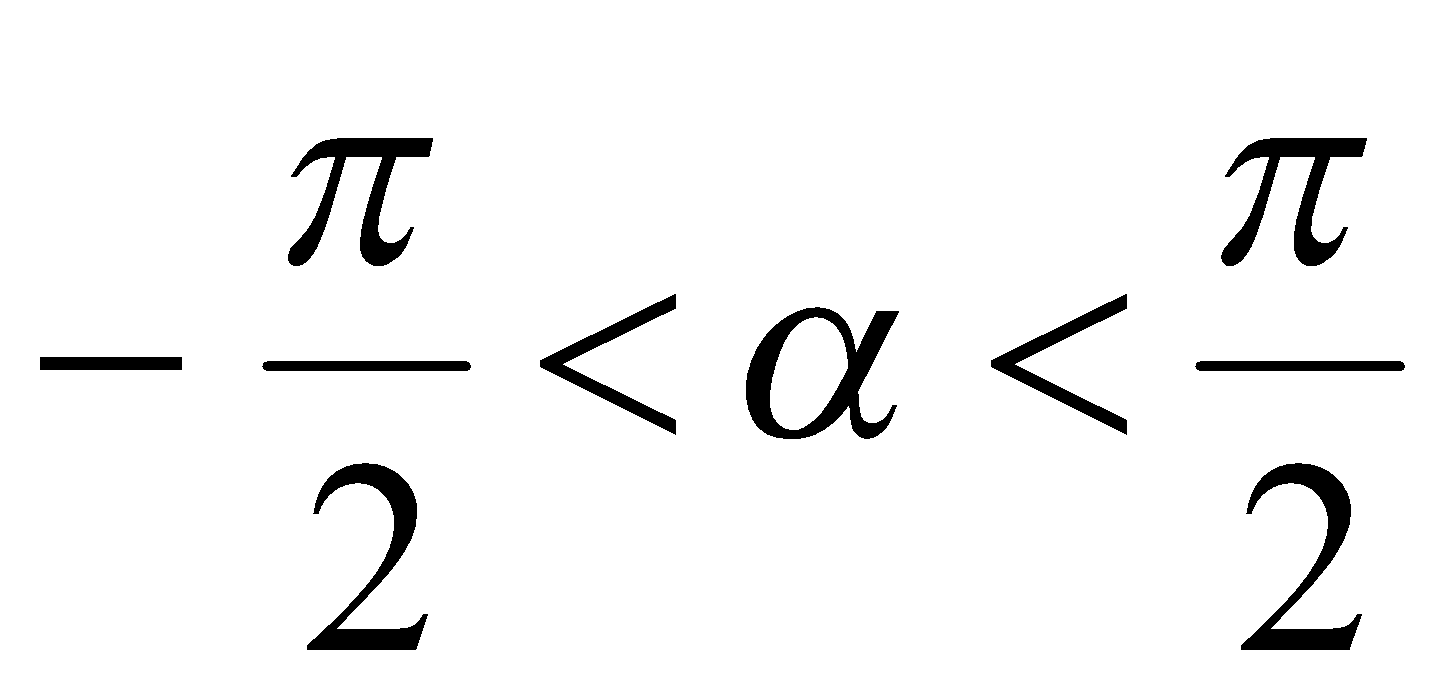 и
и 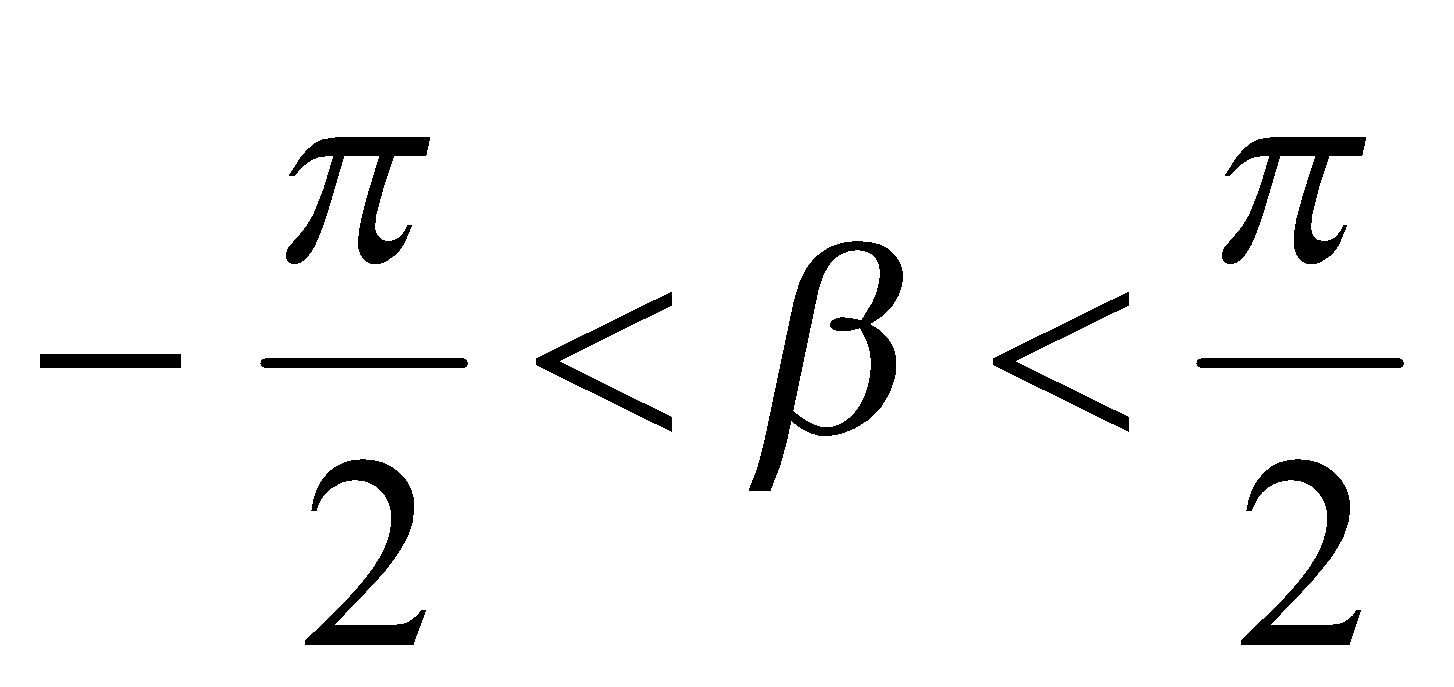 .
.
Однако 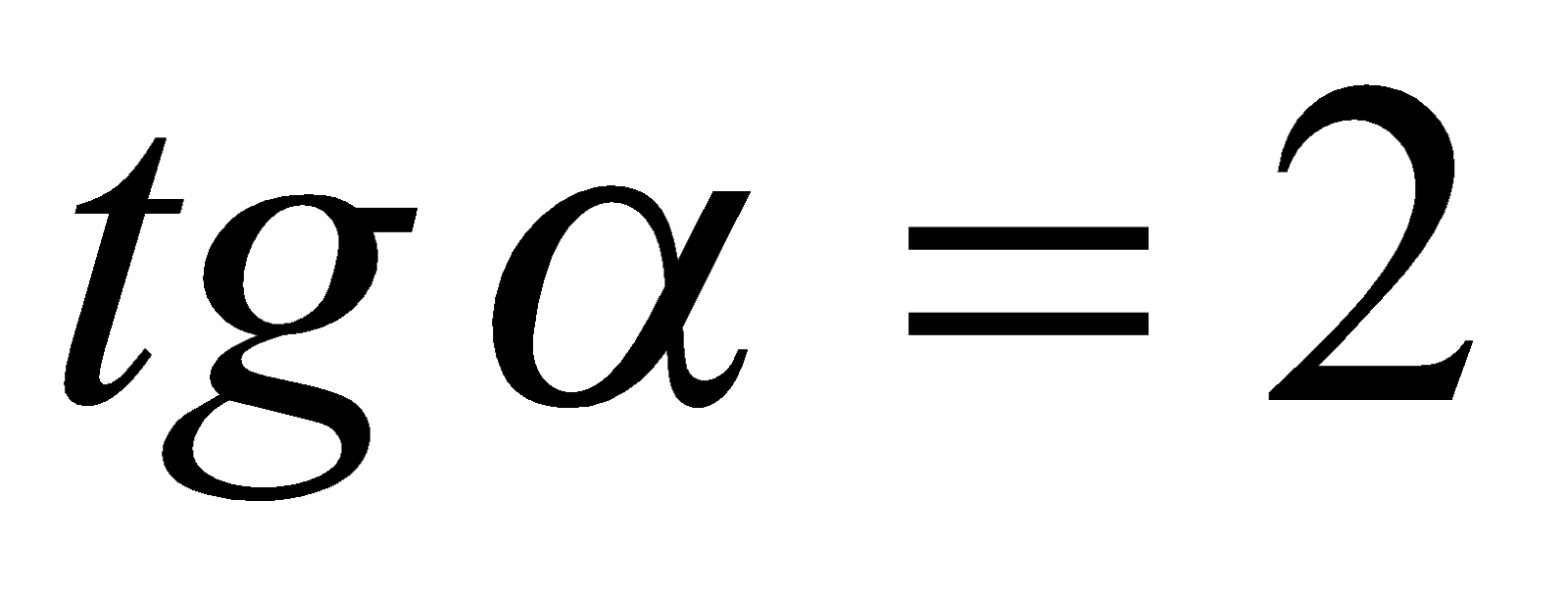 и
и 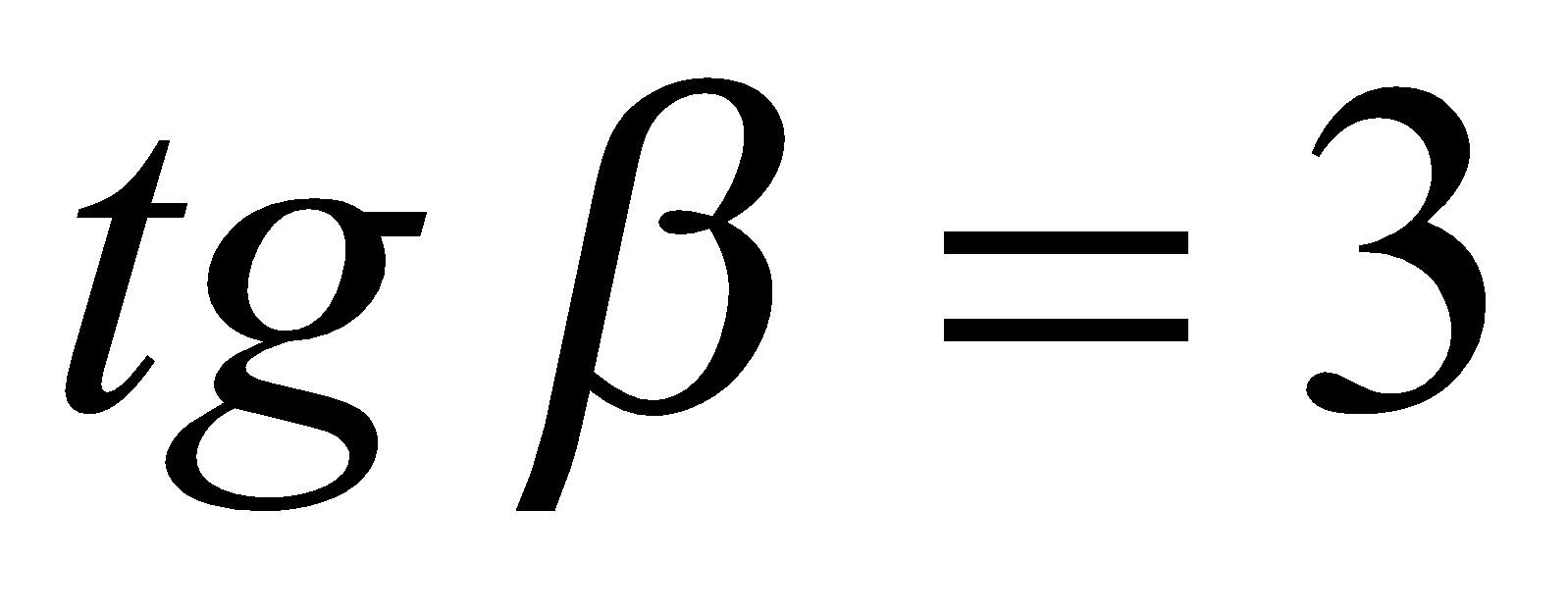 , поэтому
, поэтому 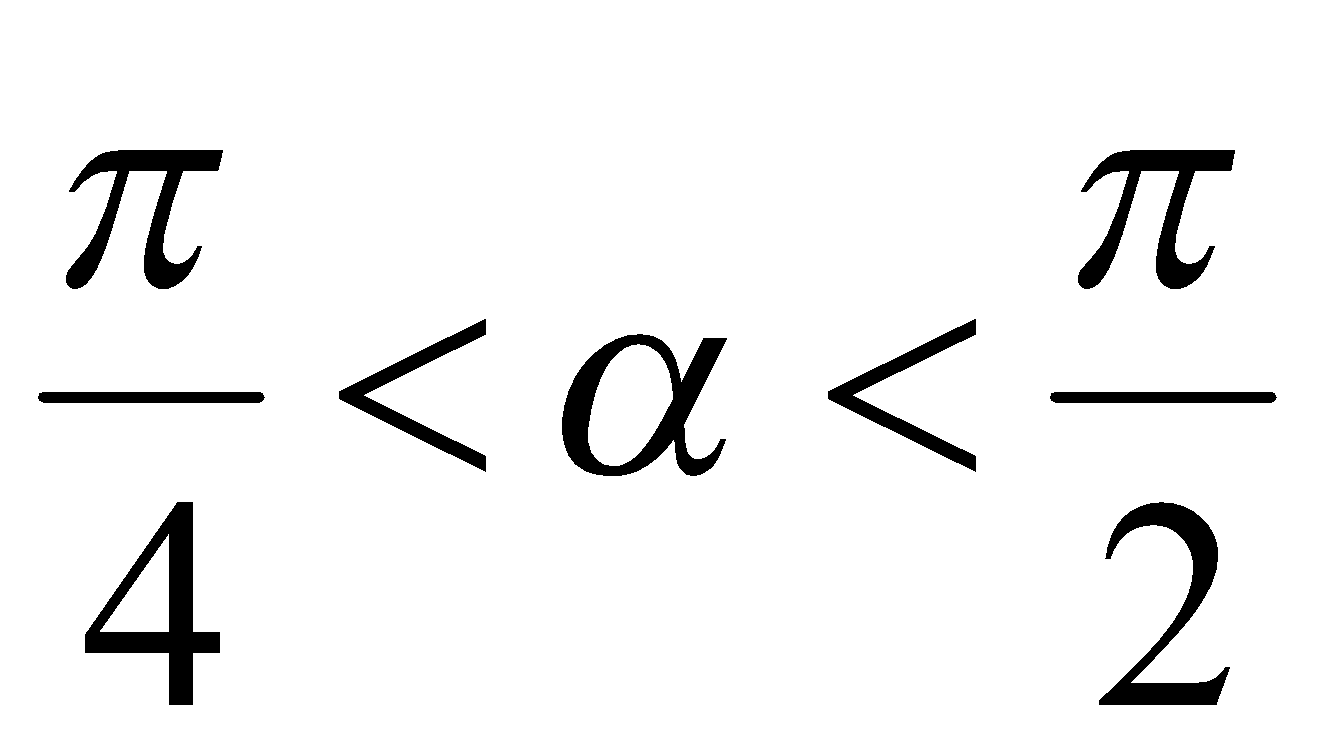 и
и 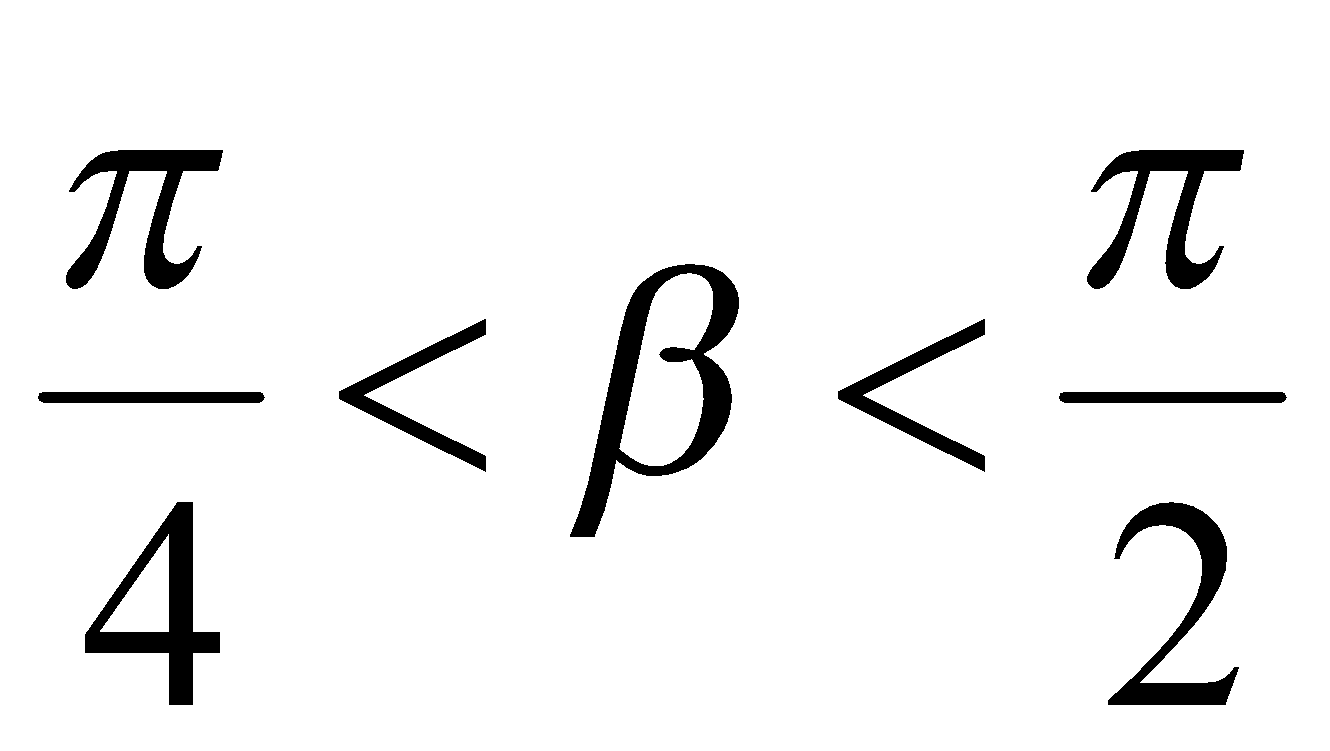 . В таком случае
. В таком случае 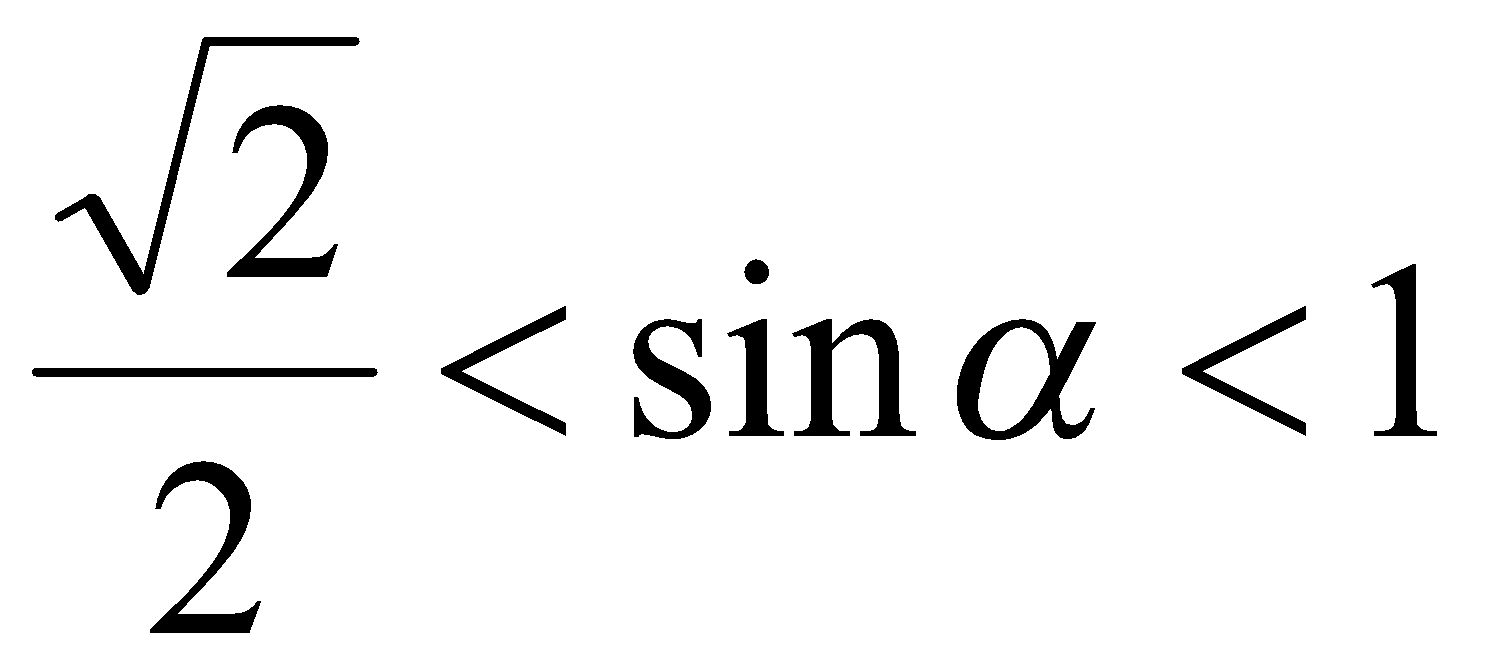 ,
, 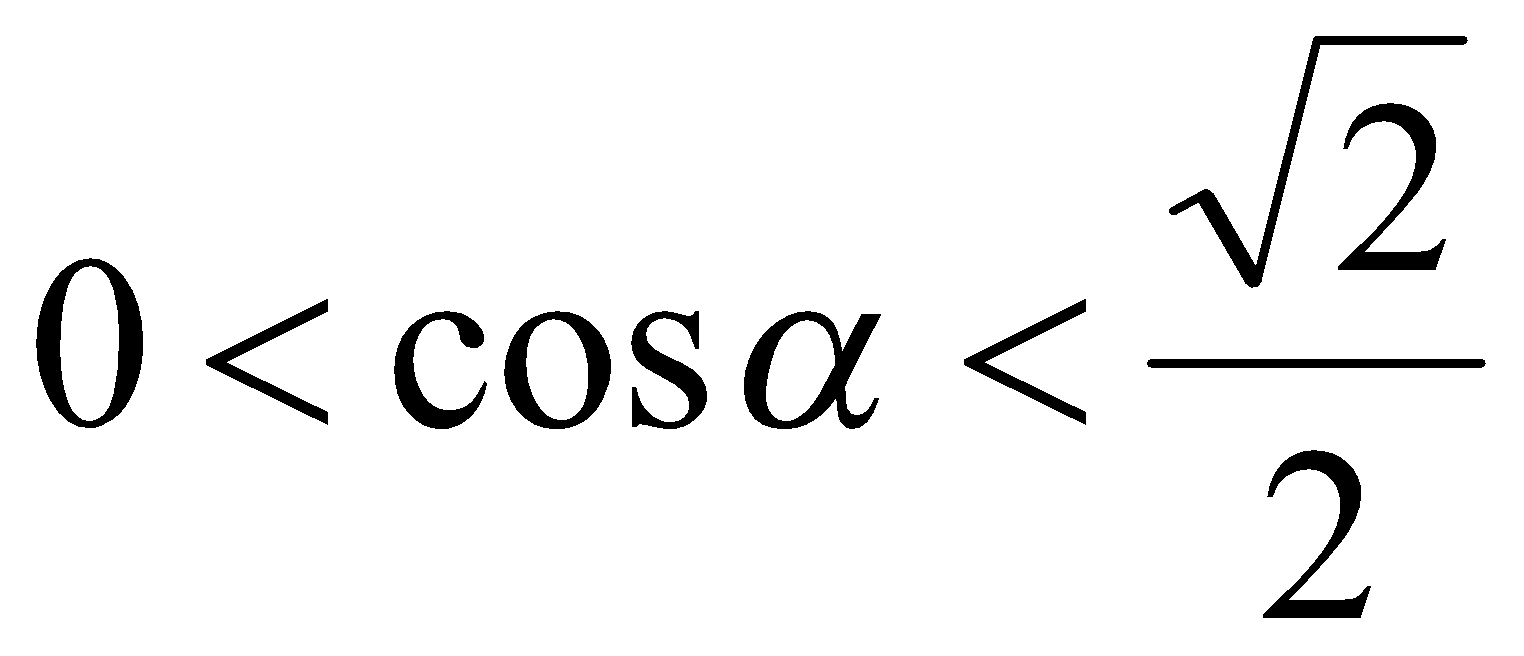 и
и 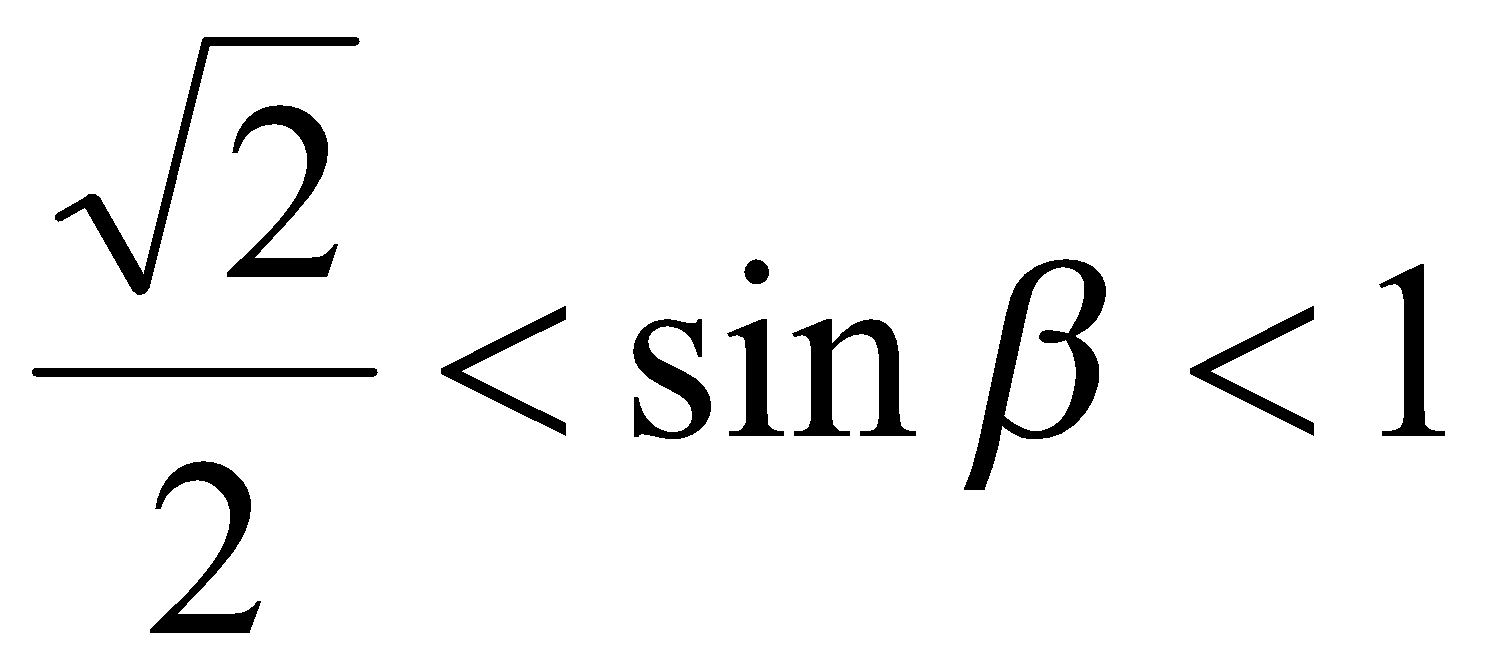 ,
, 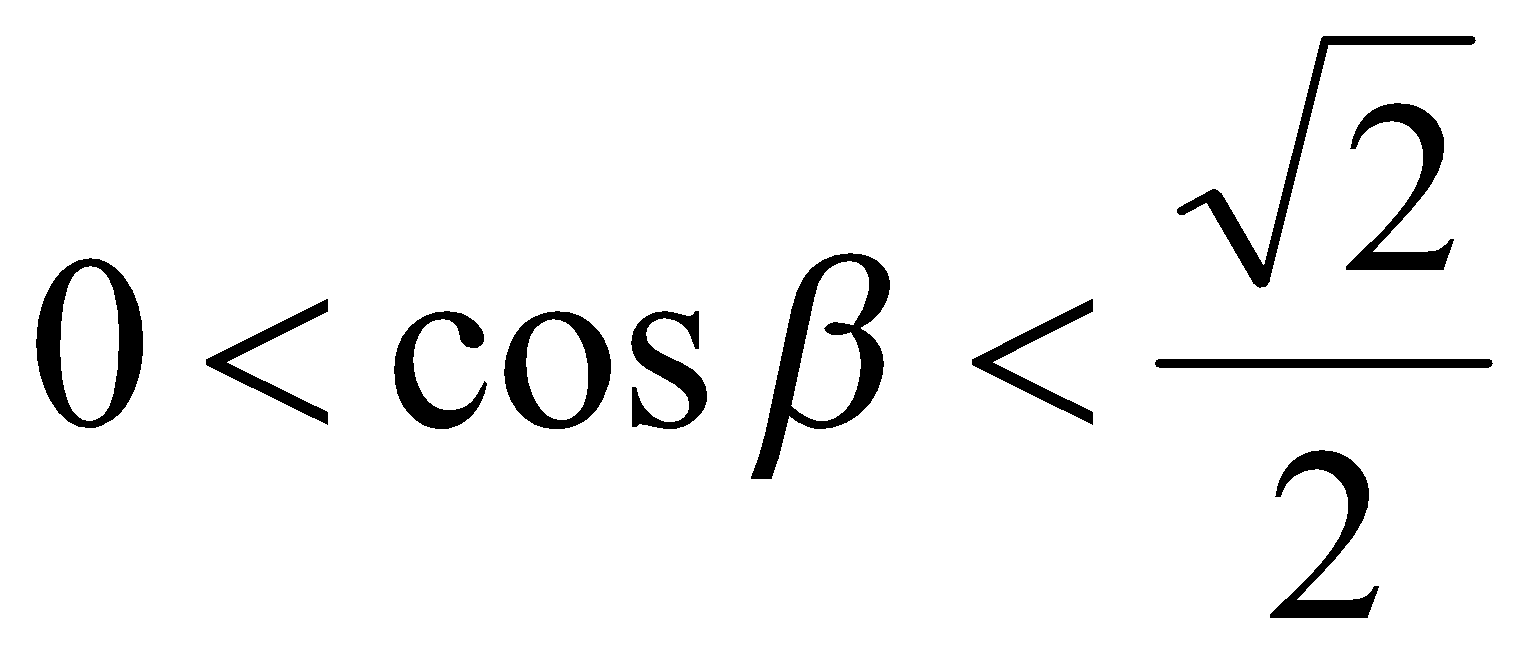 .
.
Если 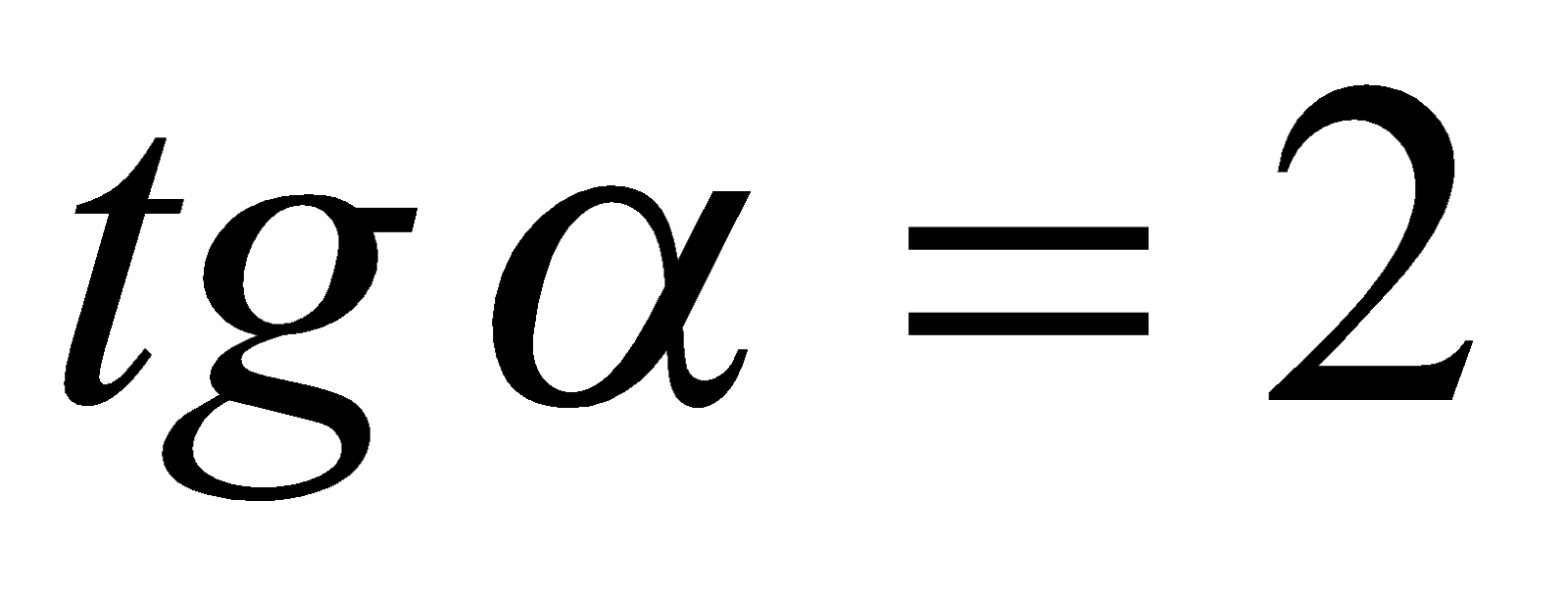 , то
, то 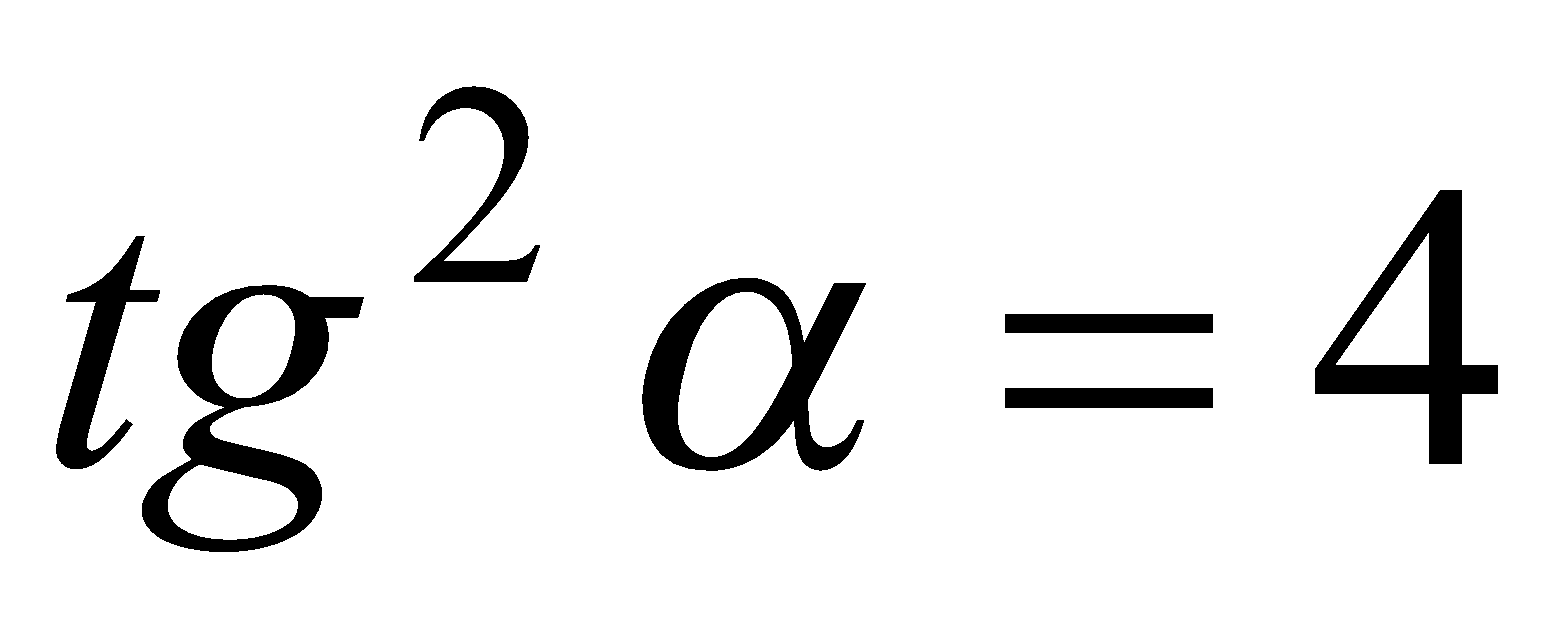 ,
, 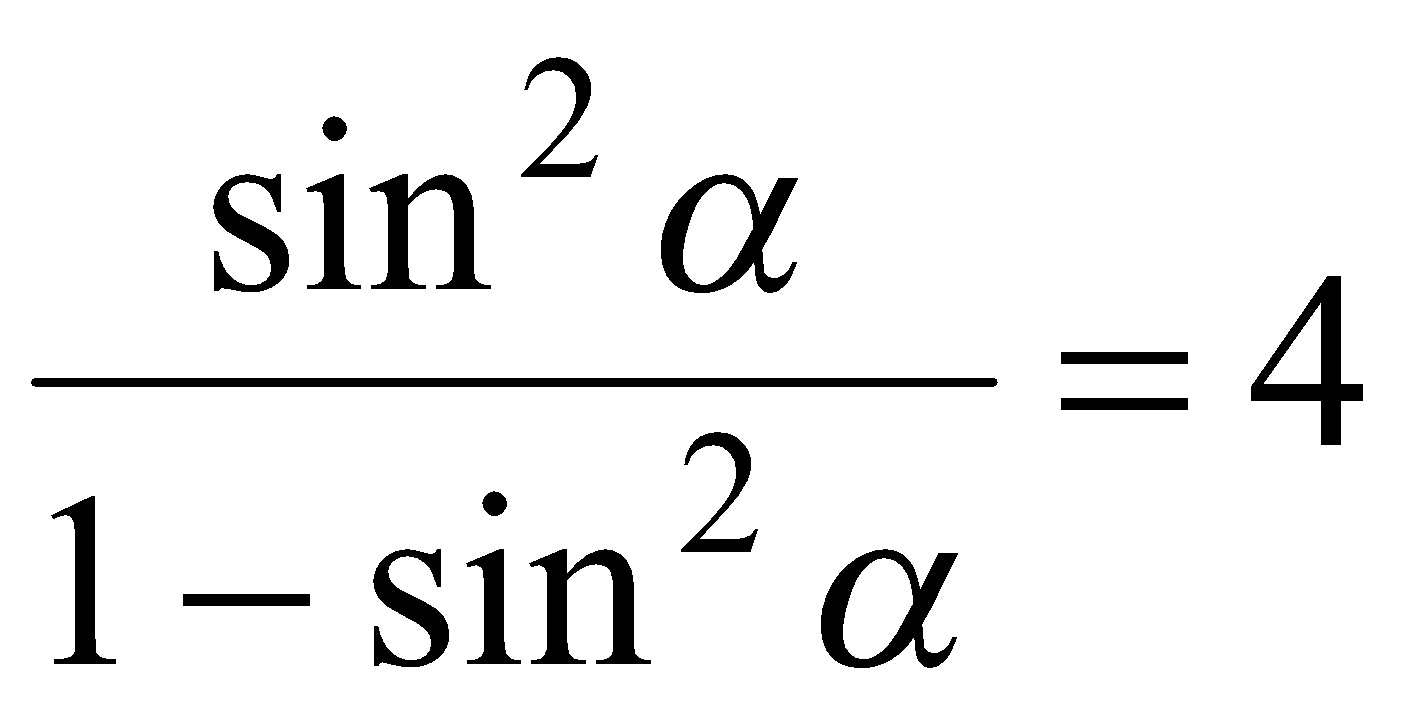 или
или 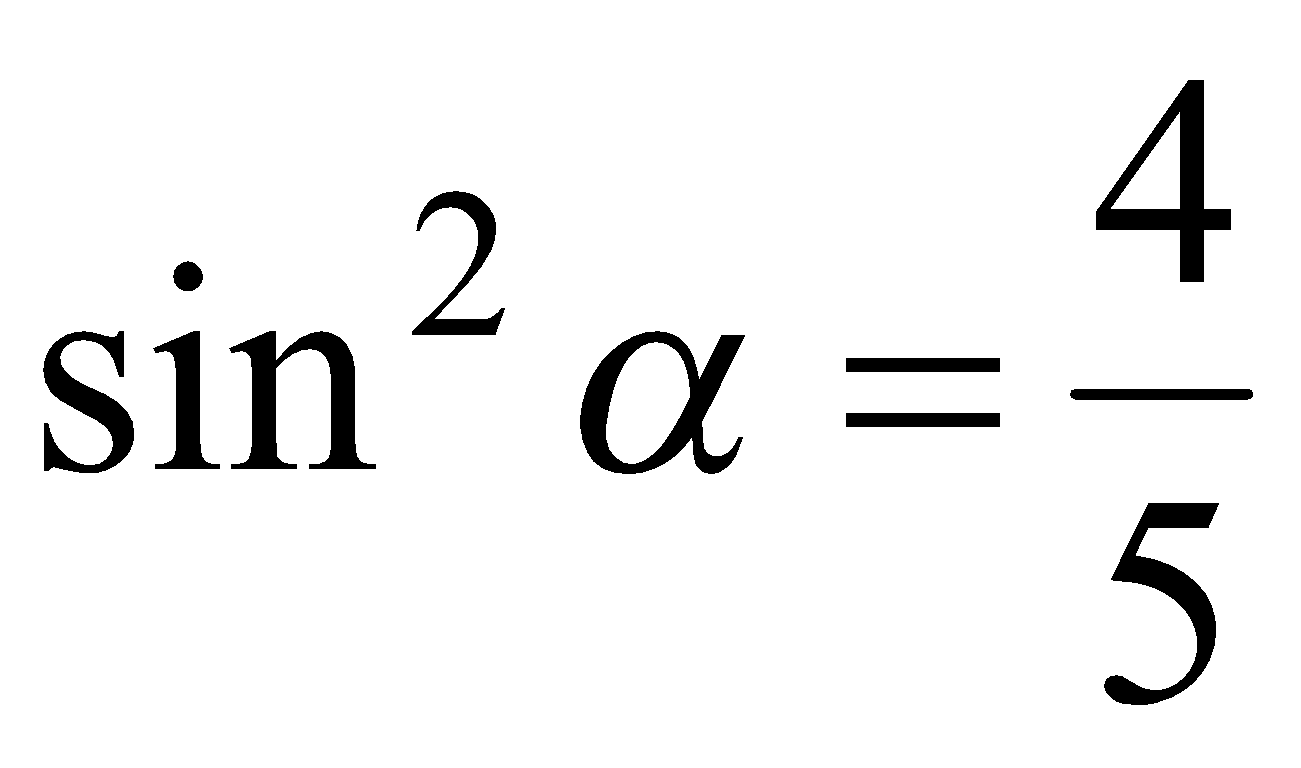 . Поскольку
. Поскольку 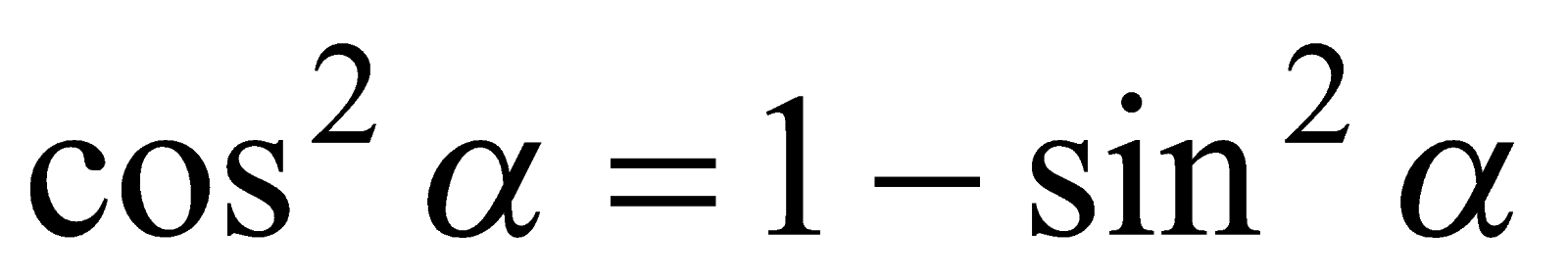 , то
, то 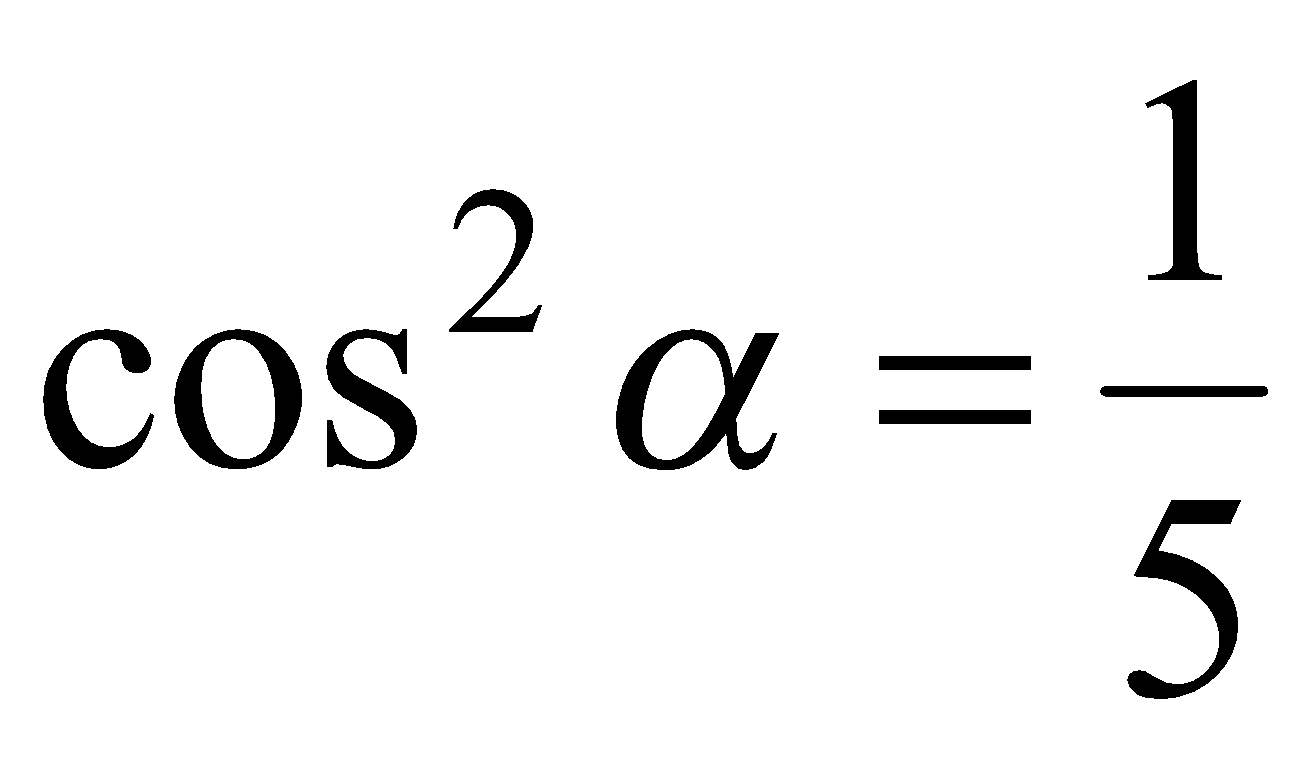 .
.
С учетом того, что 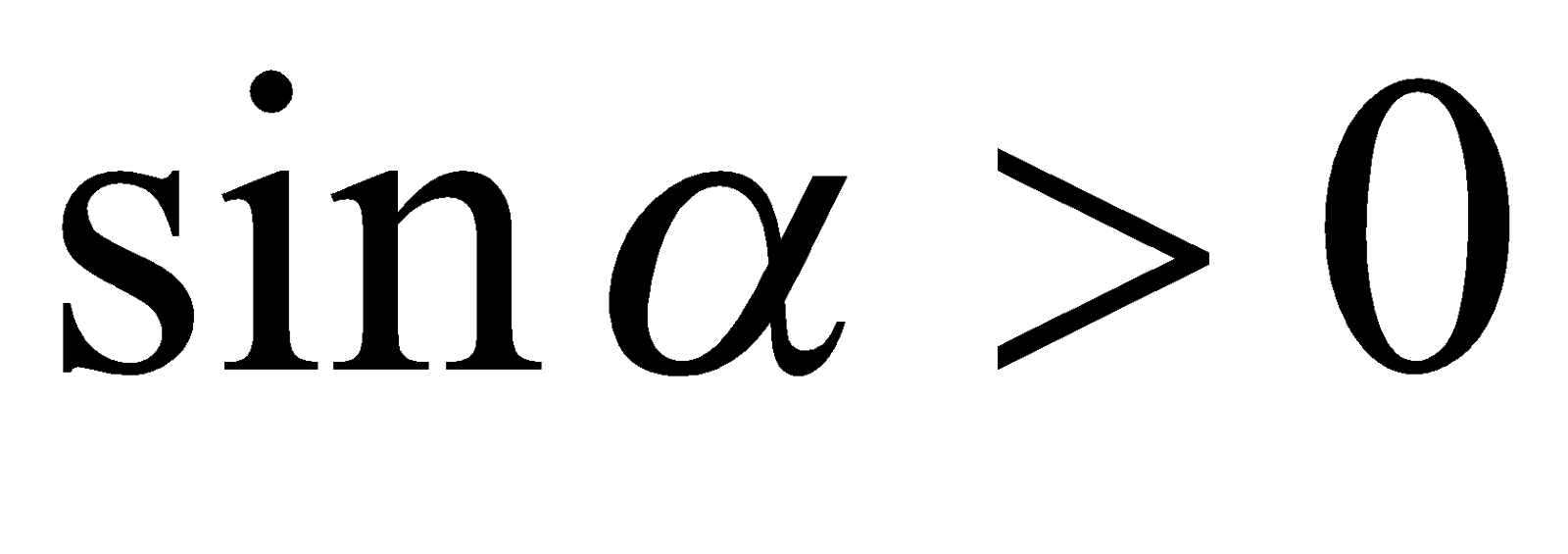 и
и 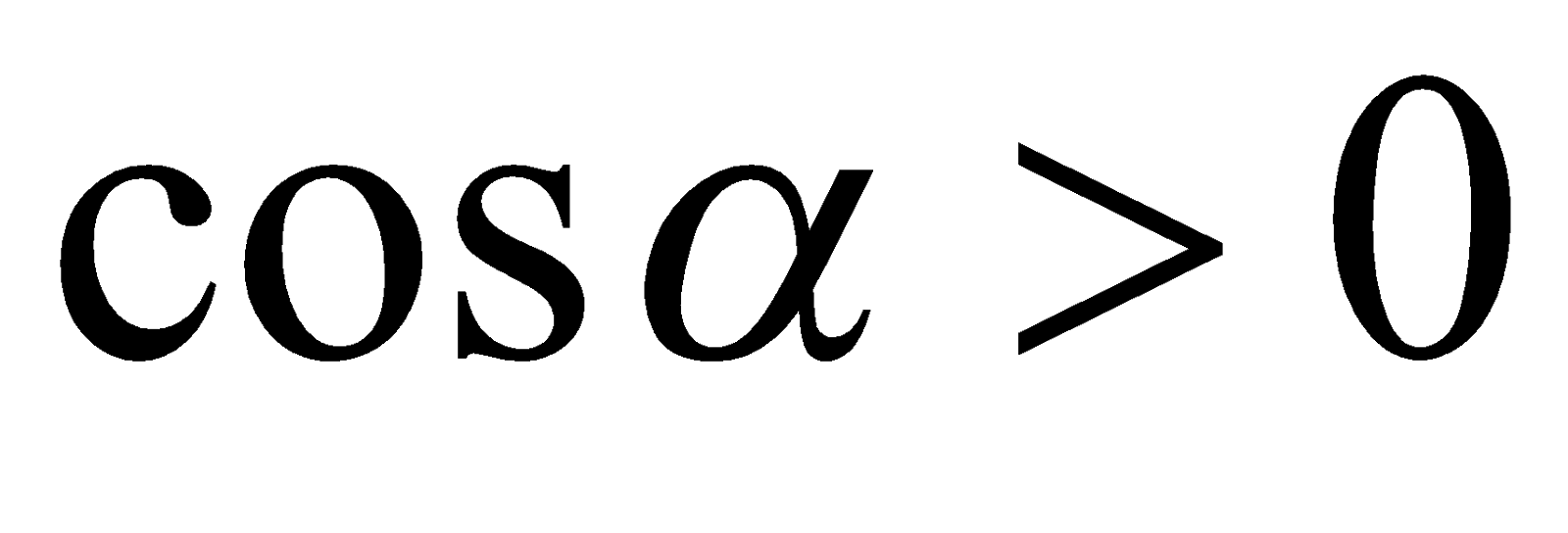 , имеем
, имеем 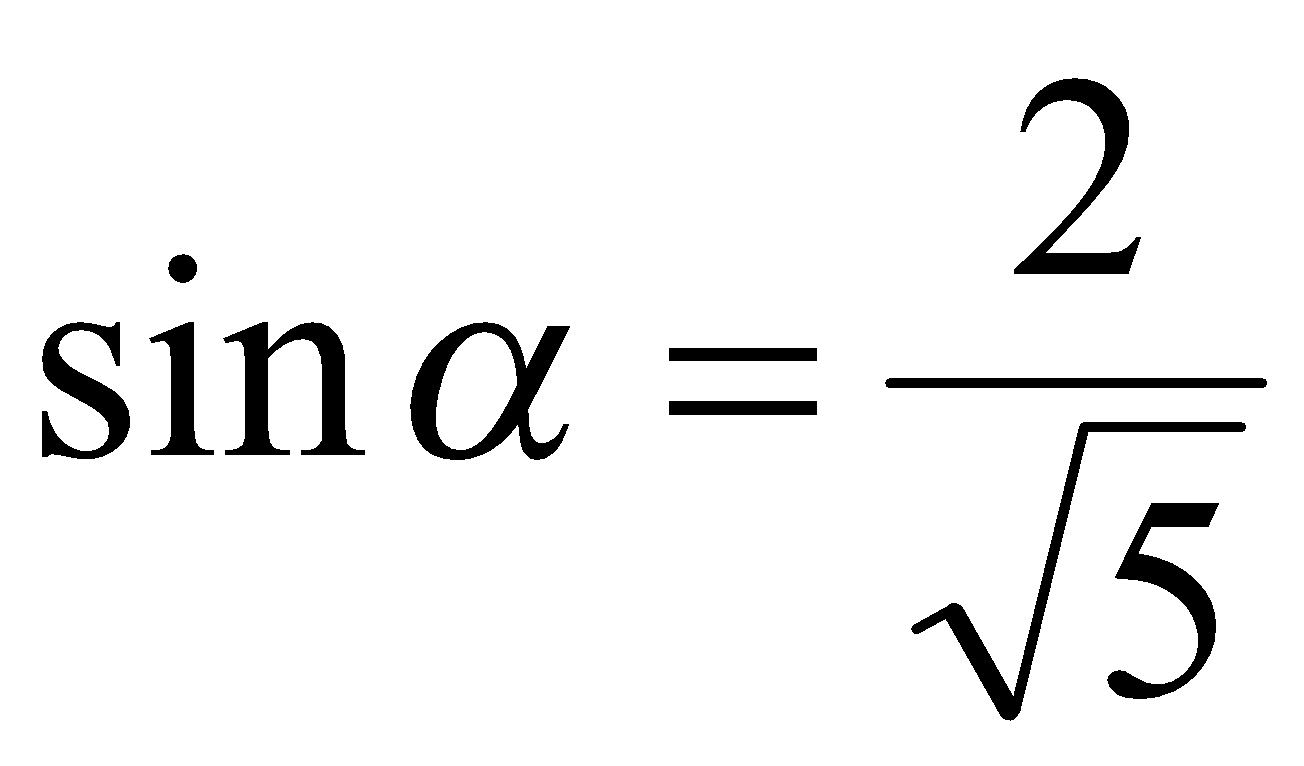 и
и 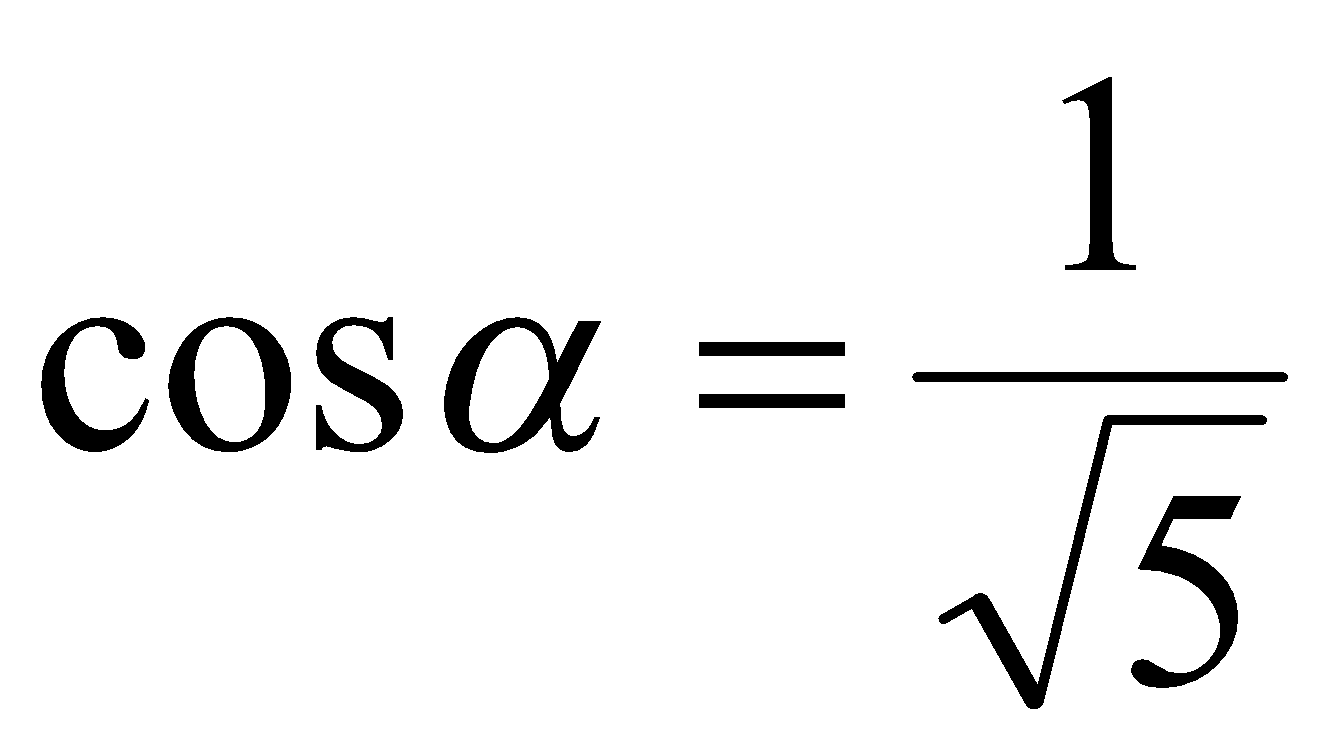 .
.
Если 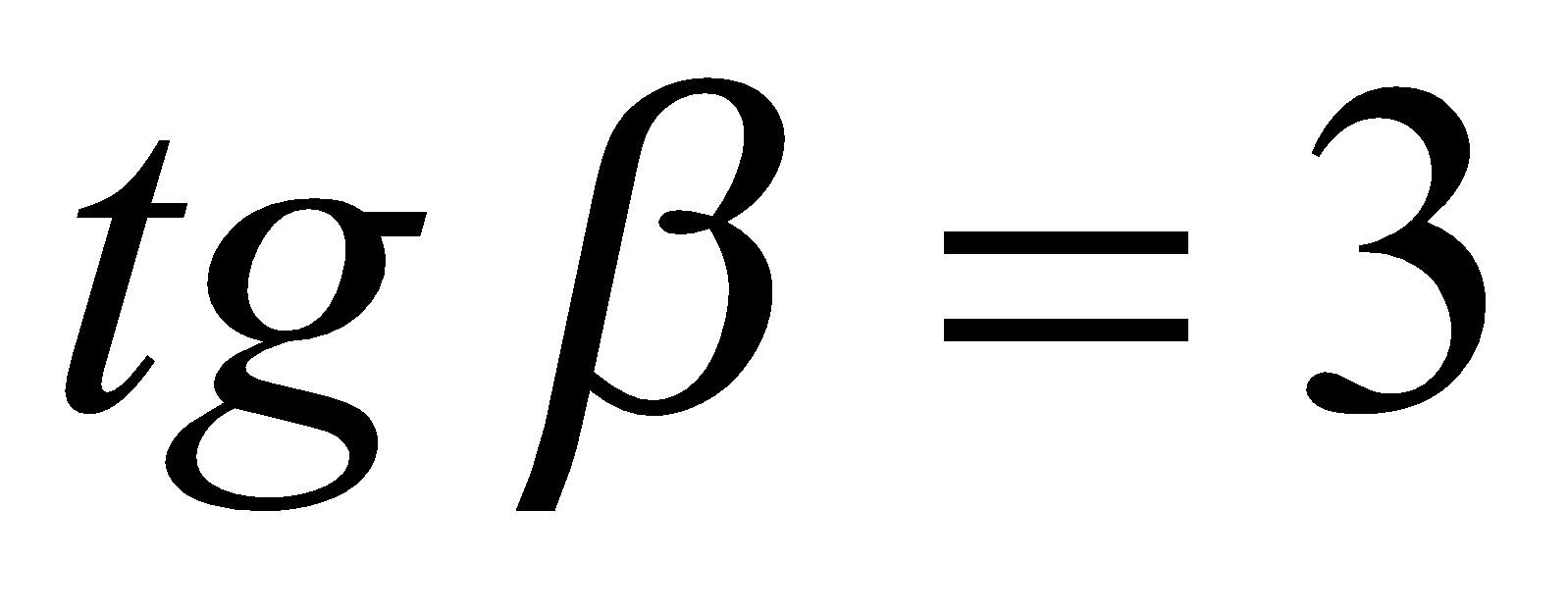 , то повторяя рассуждения, приведенные выше, получаем
, то повторяя рассуждения, приведенные выше, получаем 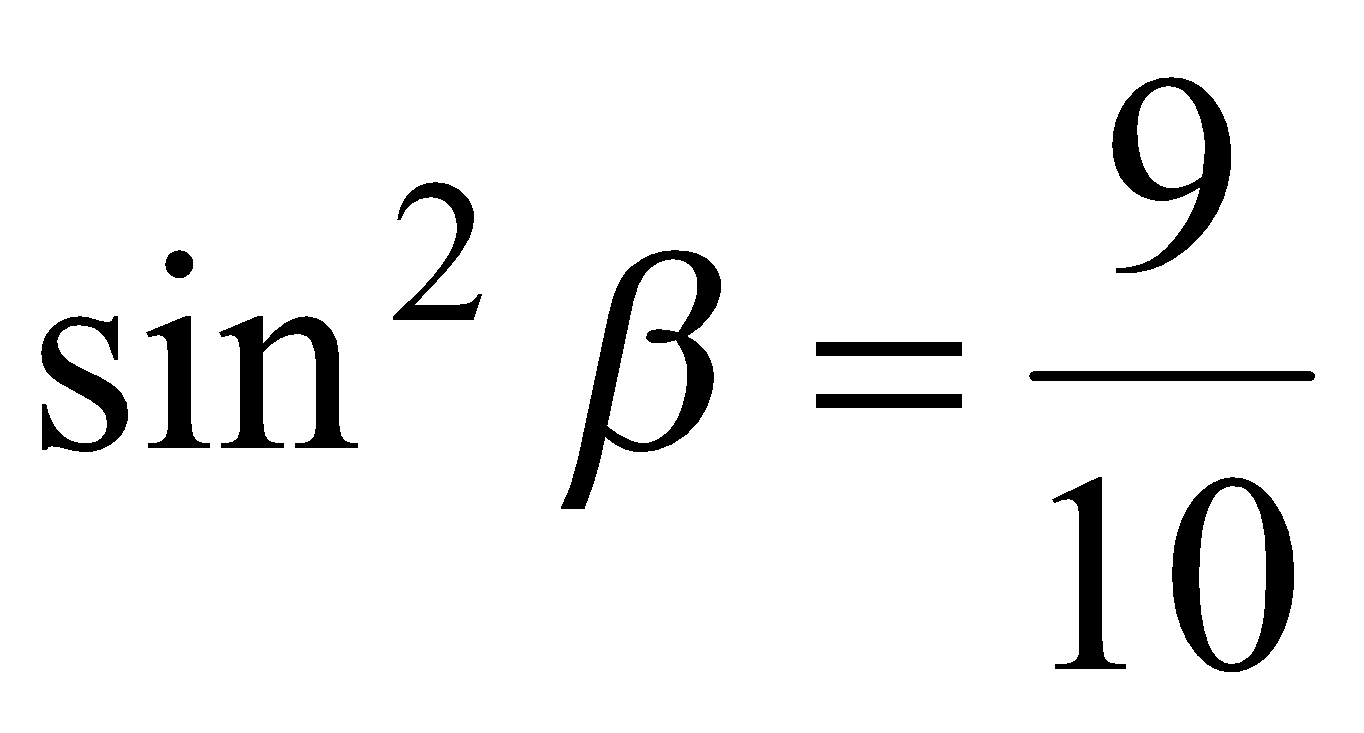 ,
, 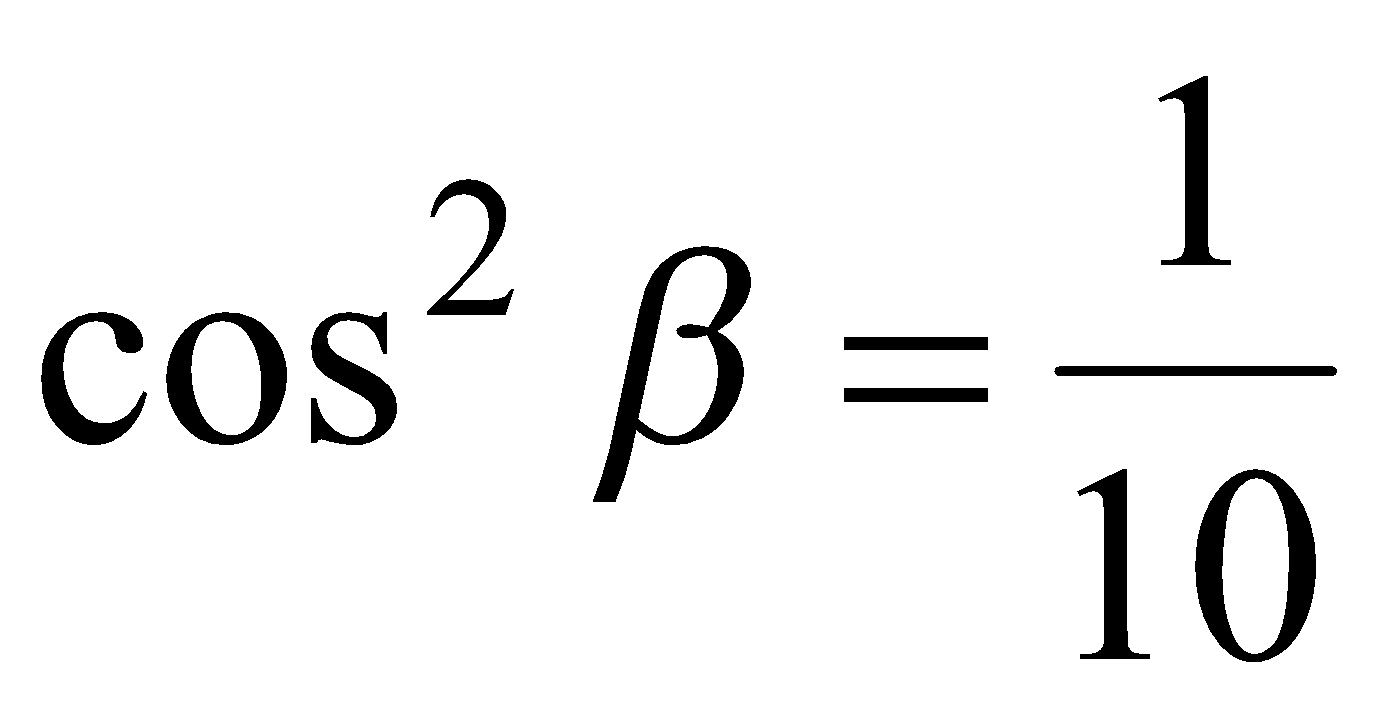 и
и 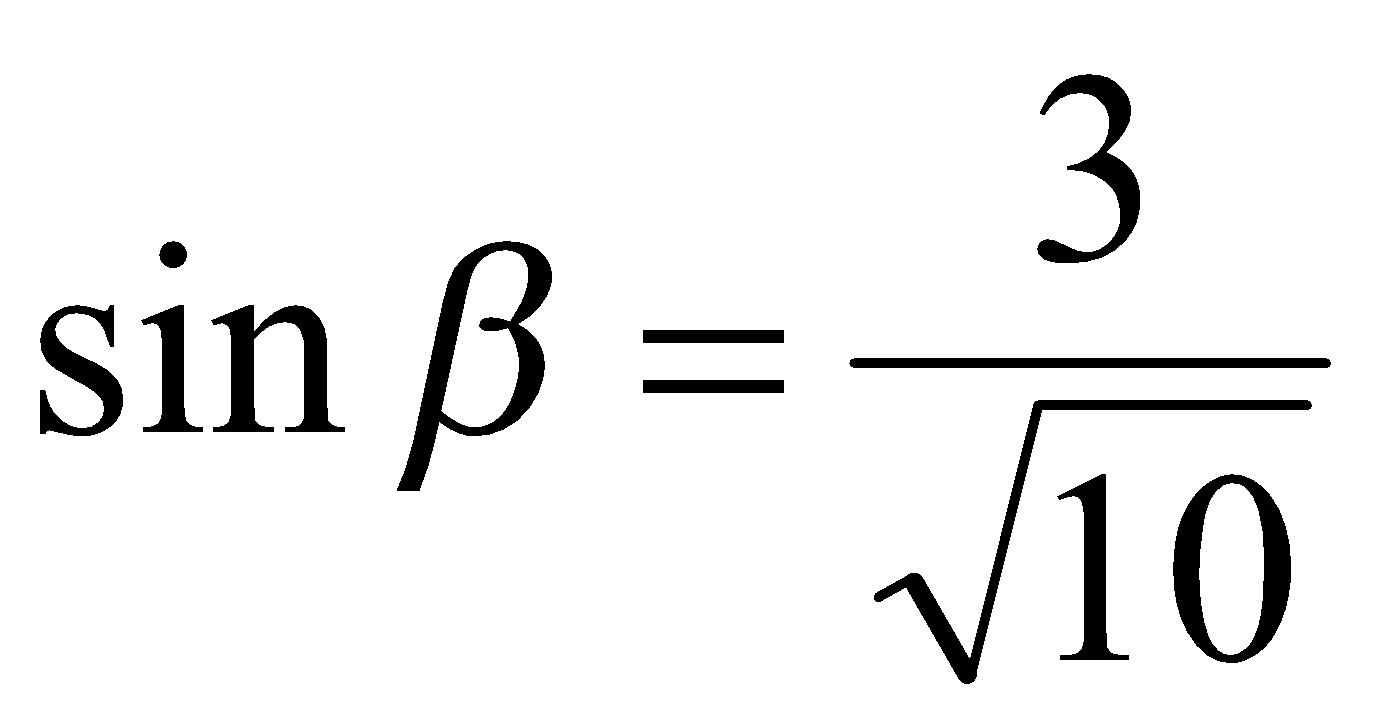 ,
, 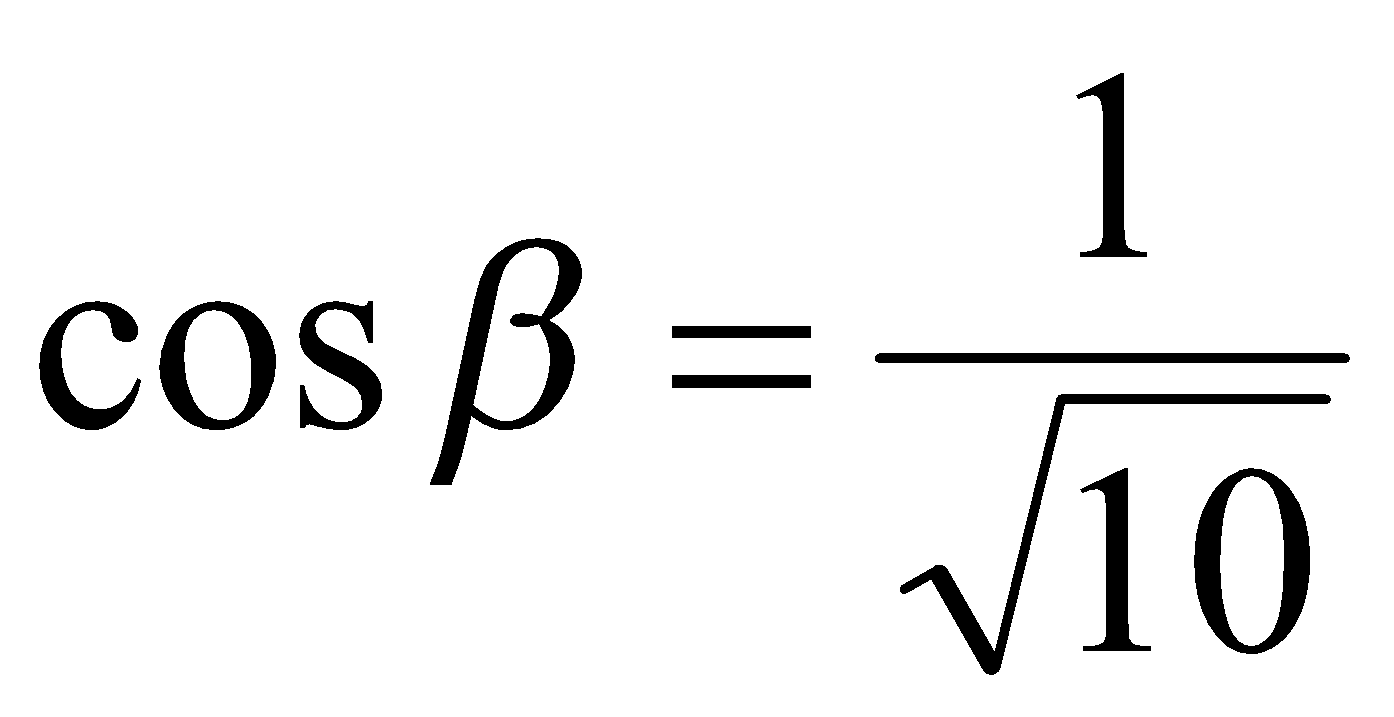 .
.
Подставляя значения 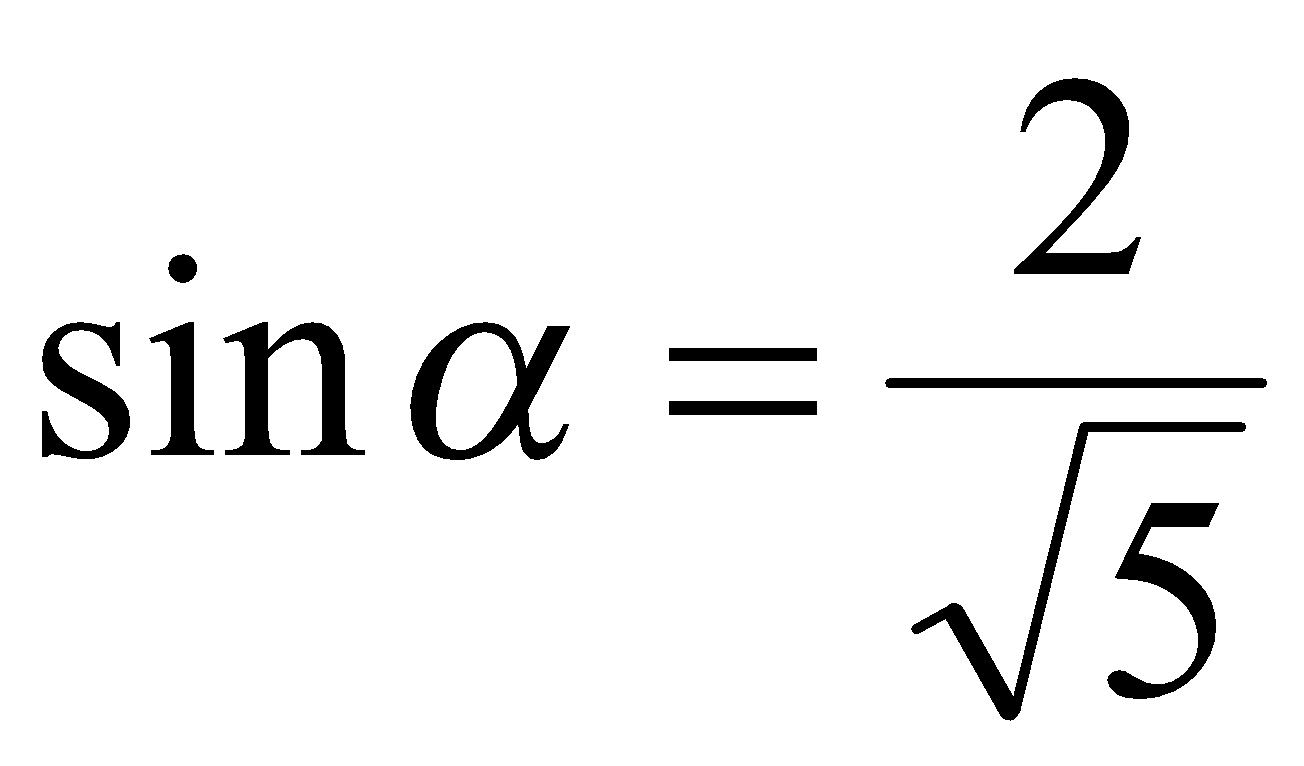 ,
, 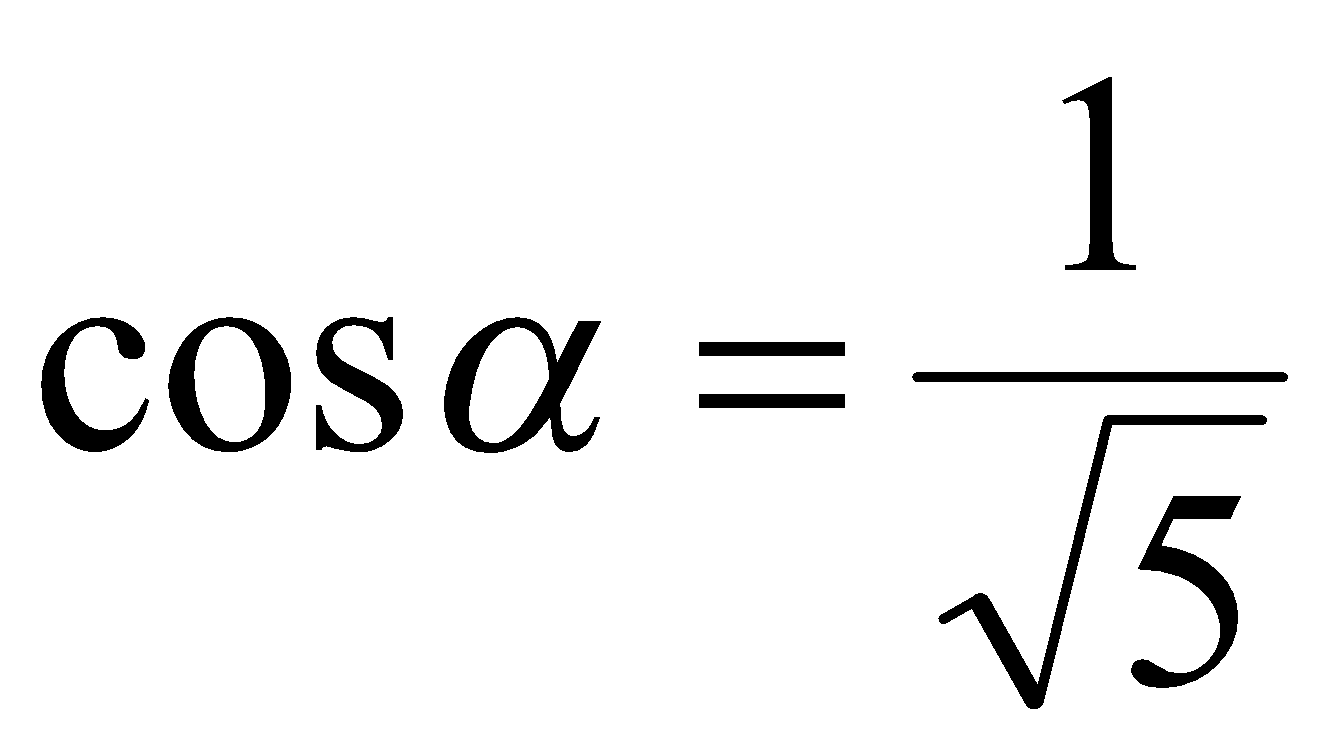 ,
, 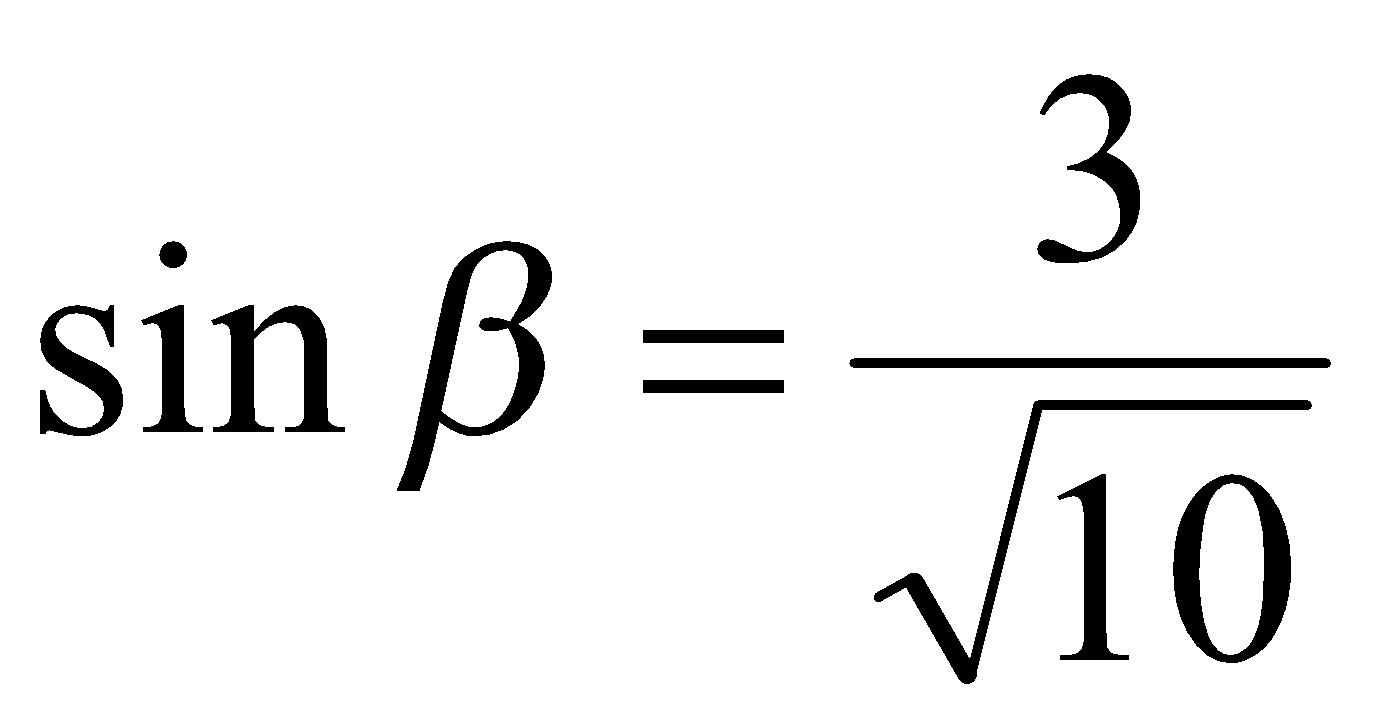 ,
, 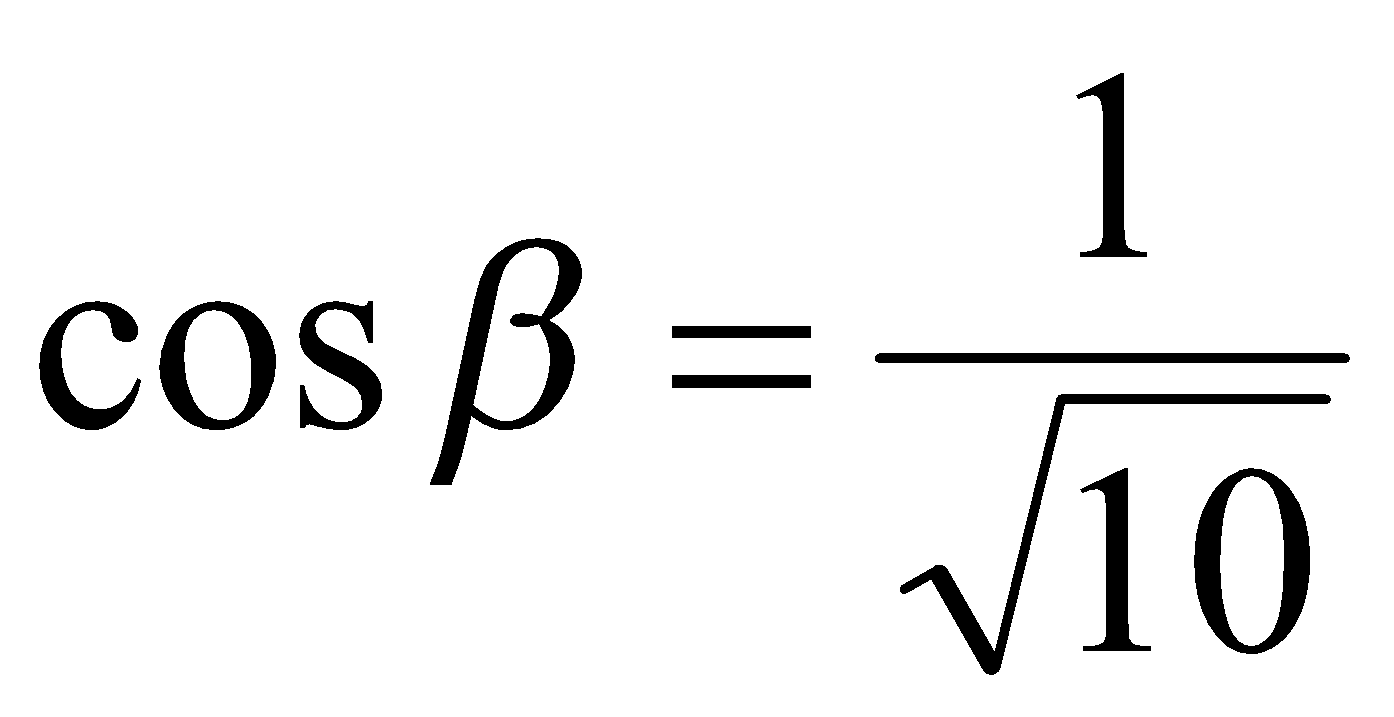 в выражение (1) получаем
в выражение (1) получаем 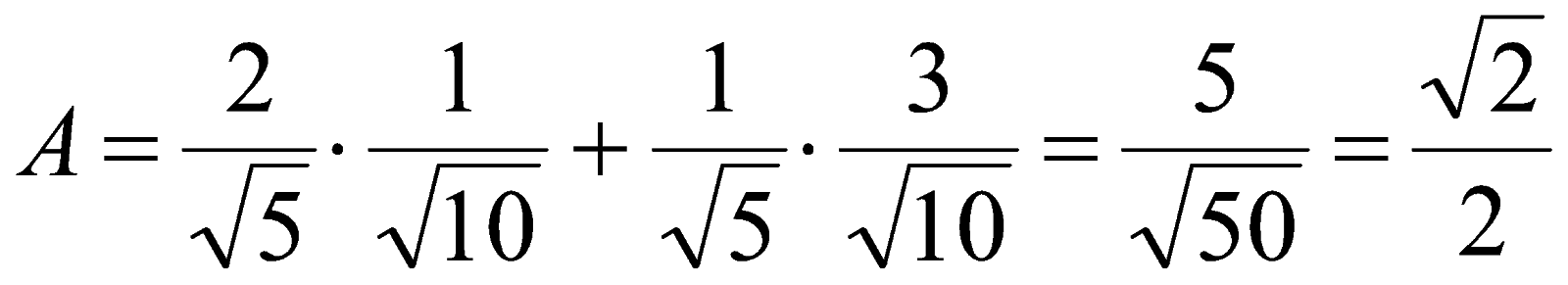 .
.
Ответ: 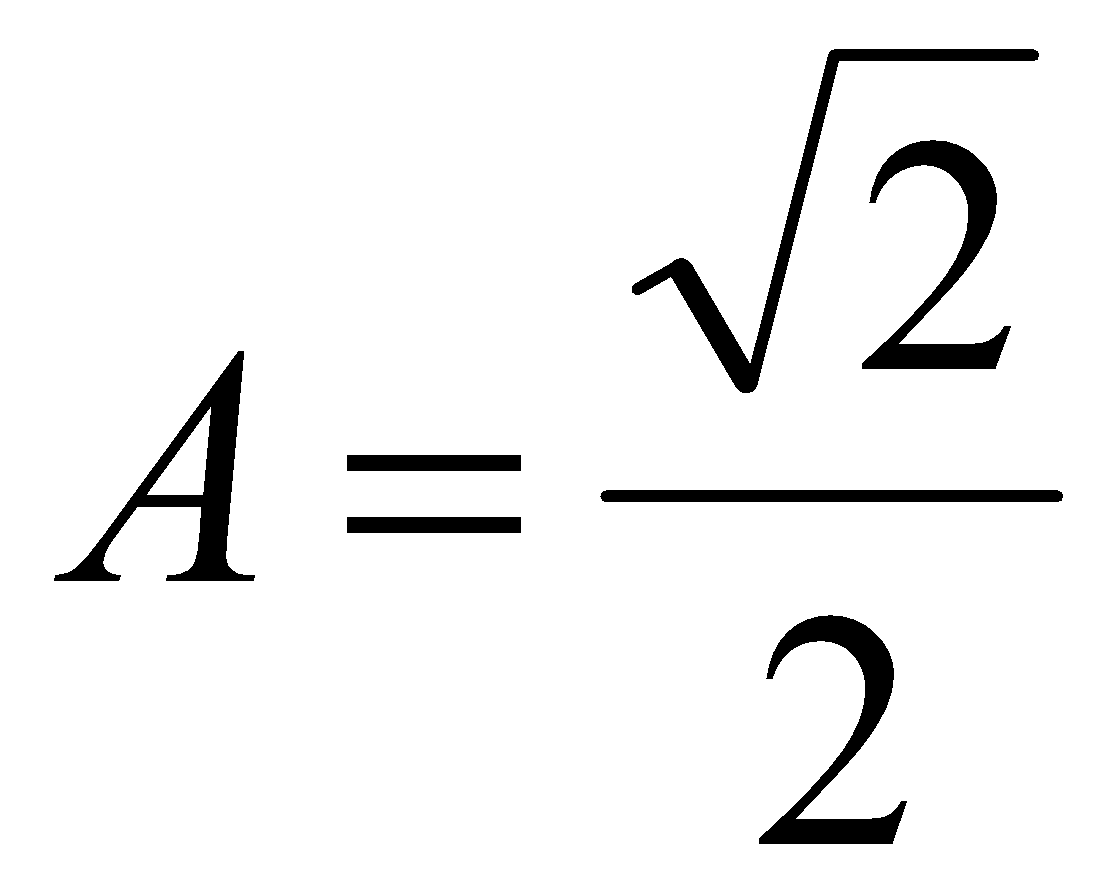 .
.
Примечание. Так как в примере 5 показано, что  , где
, где 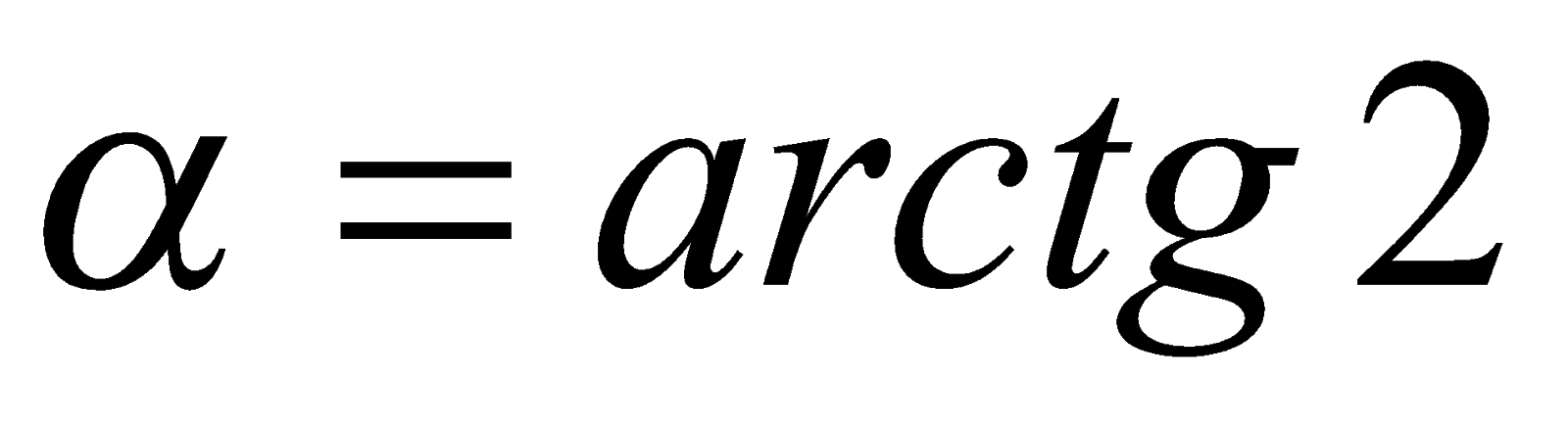 ,
, 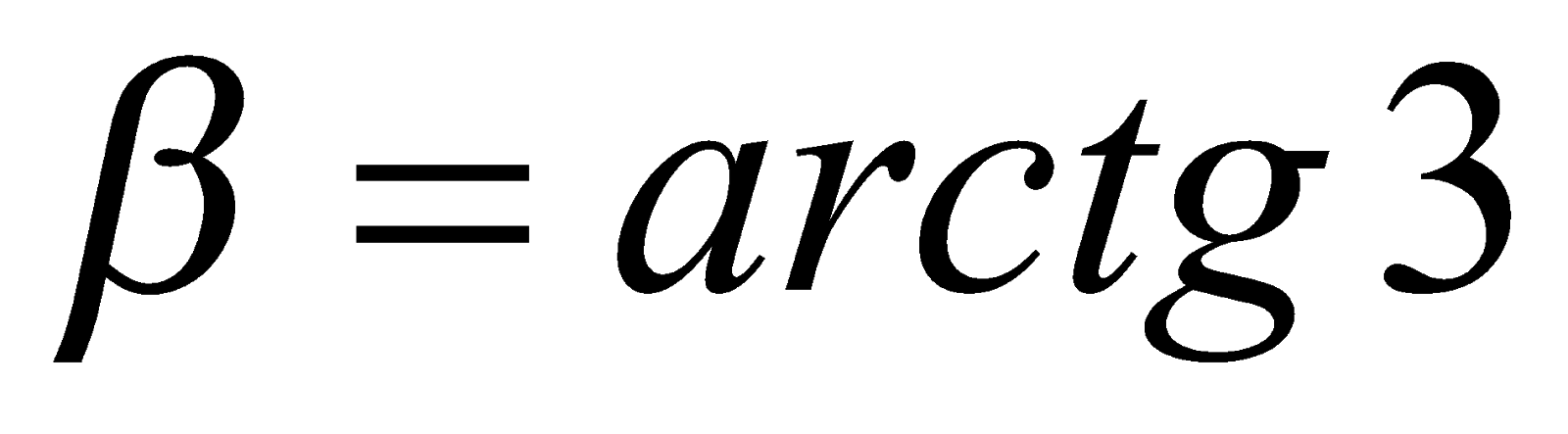 и
и 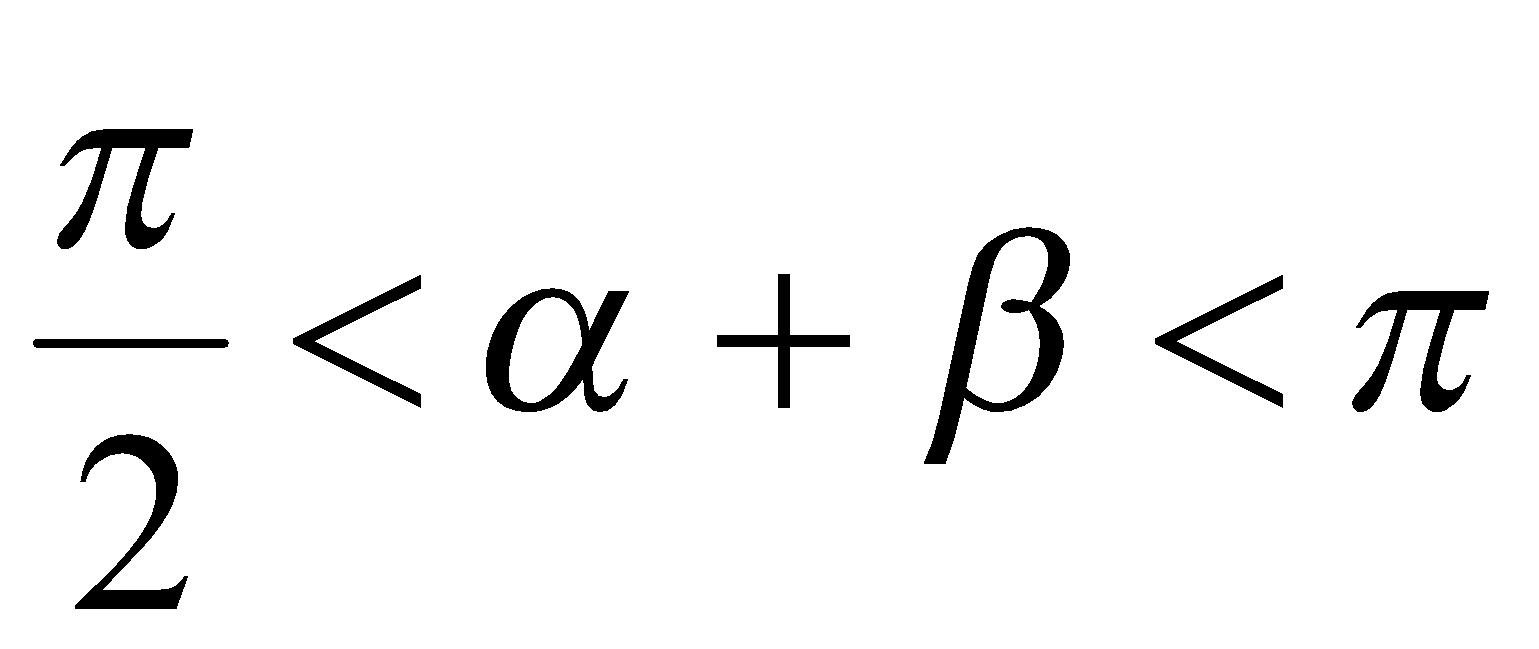 , то справедливо равенство
, то справедливо равенство
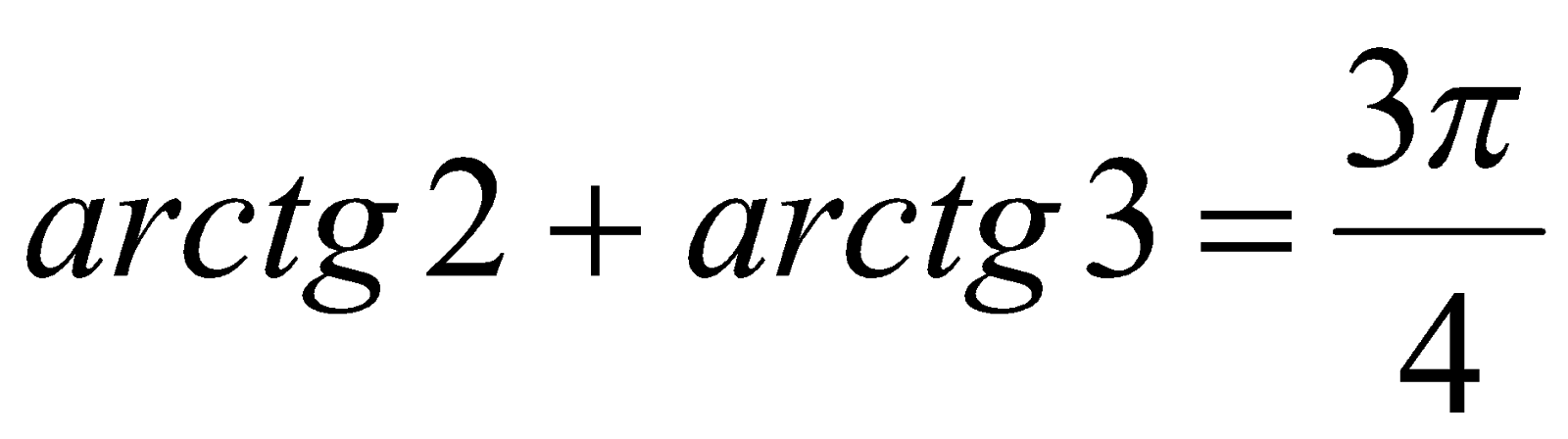 .
.
Отсюда также следует, что 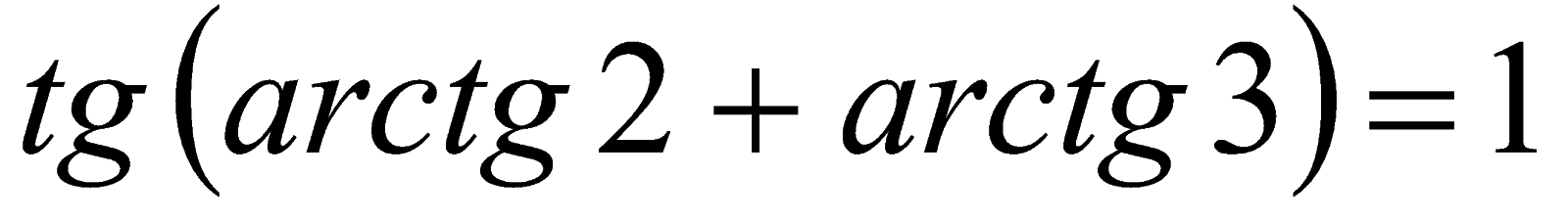 .
.
Пример 6. Вычислить значение 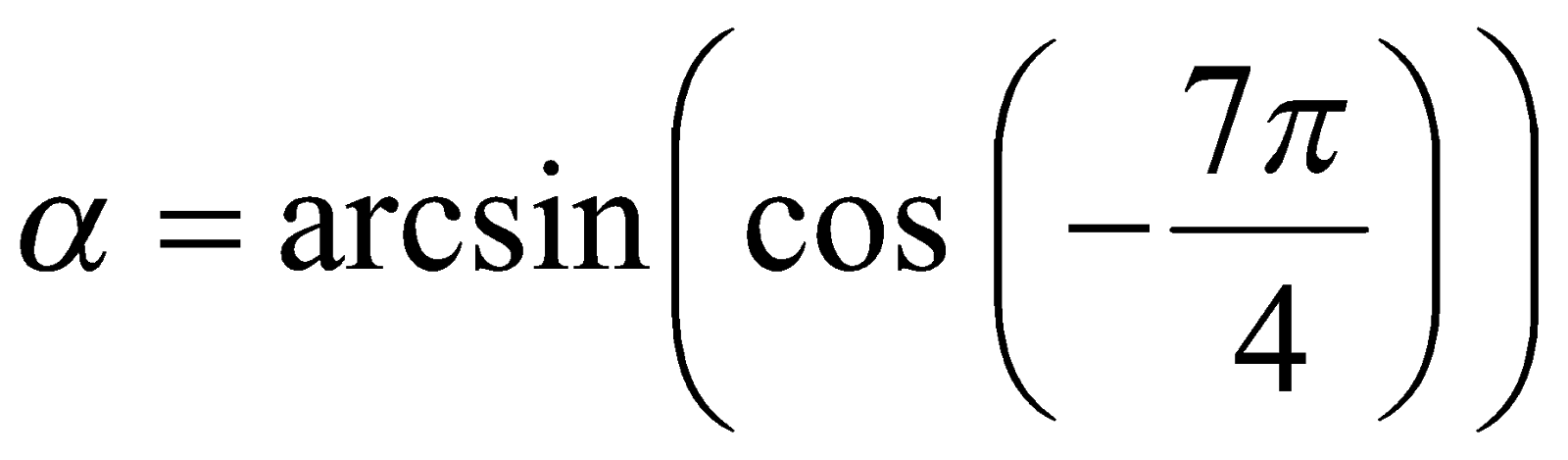 .
.
Решение. Из определения функции 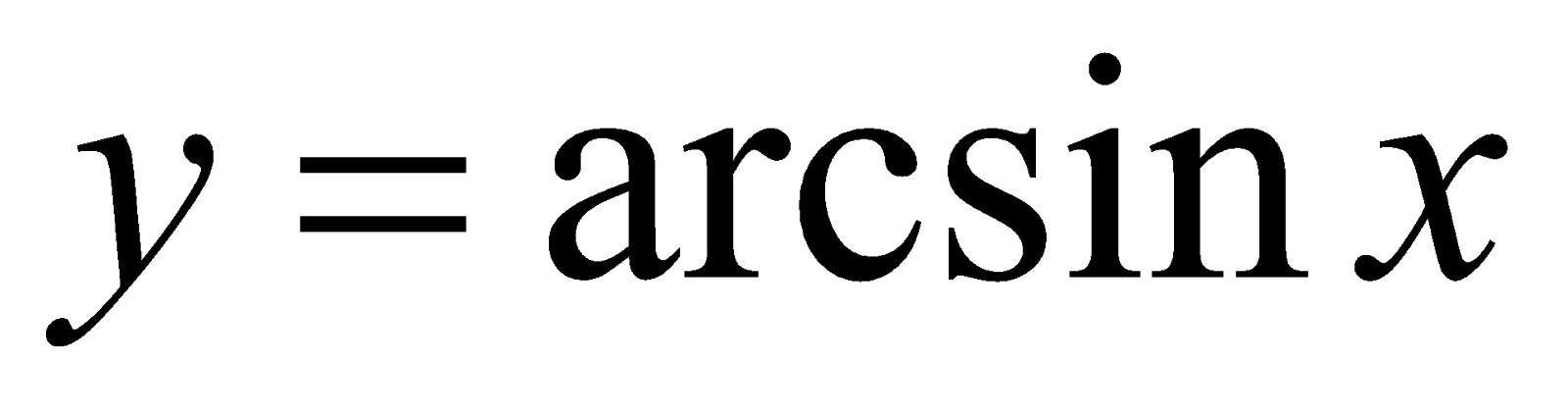 следует, что
следует, что 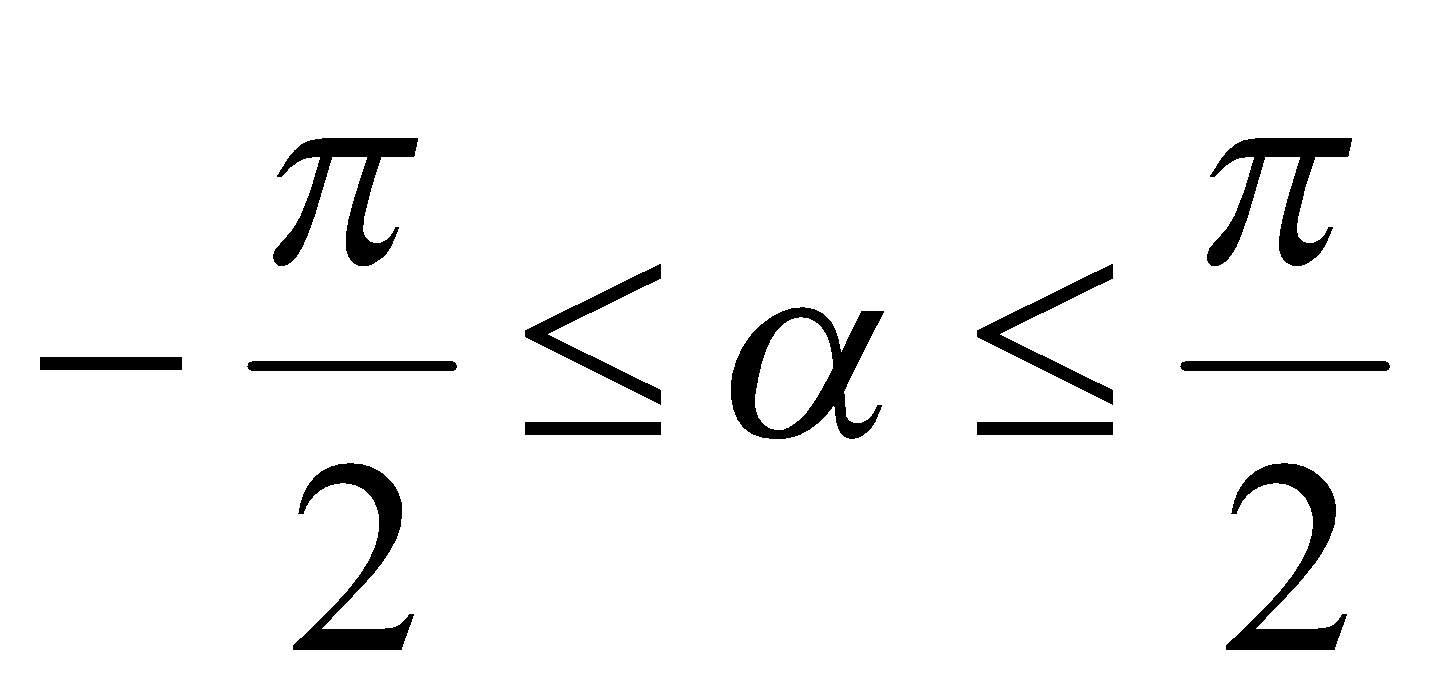 . Из условия примера получаем
. Из условия примера получаем 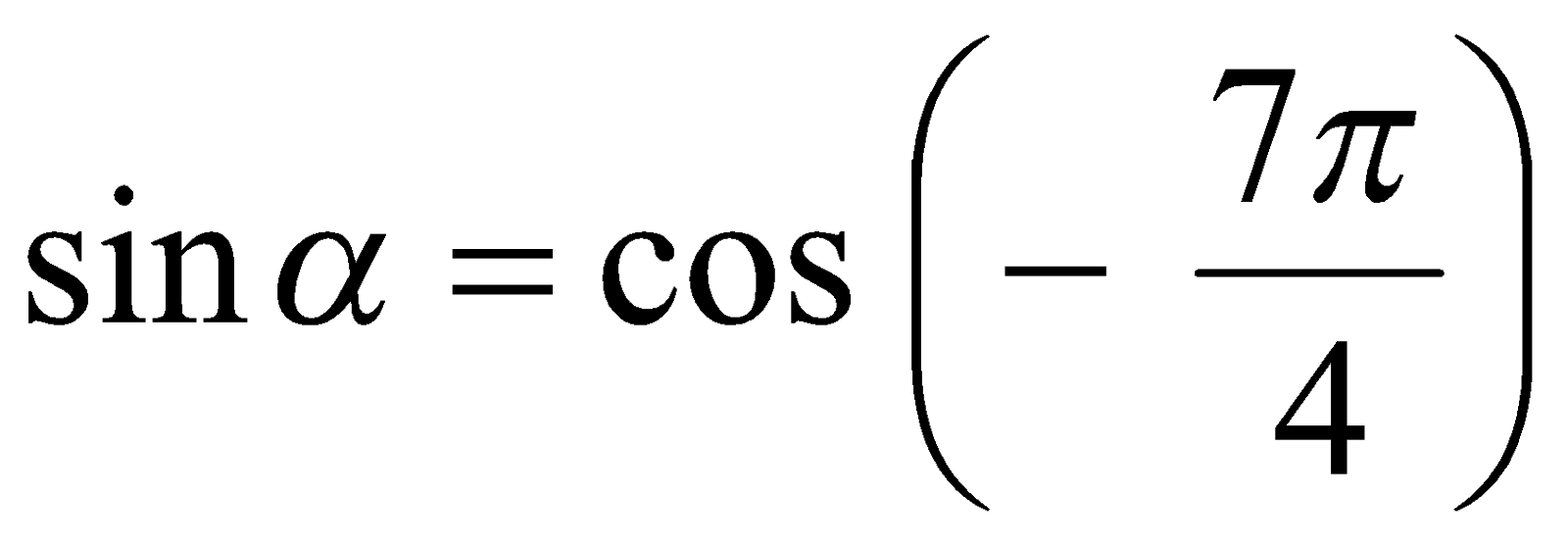 .
.
Так как 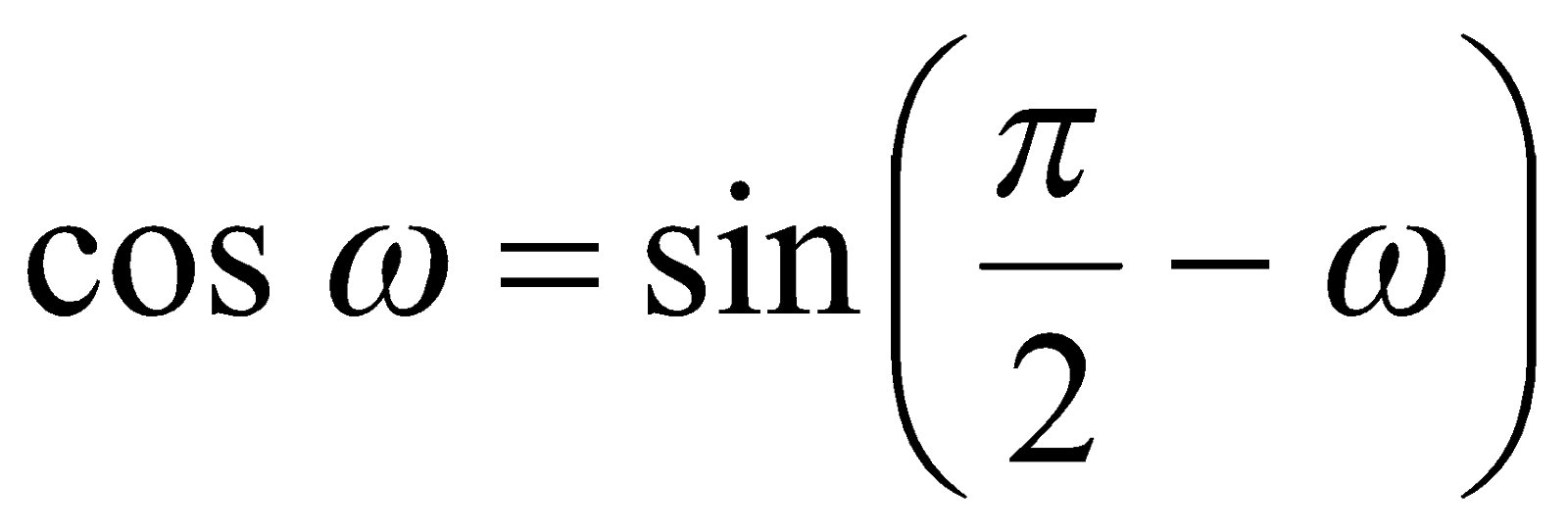 , то имеем уравнение
, то имеем уравнение 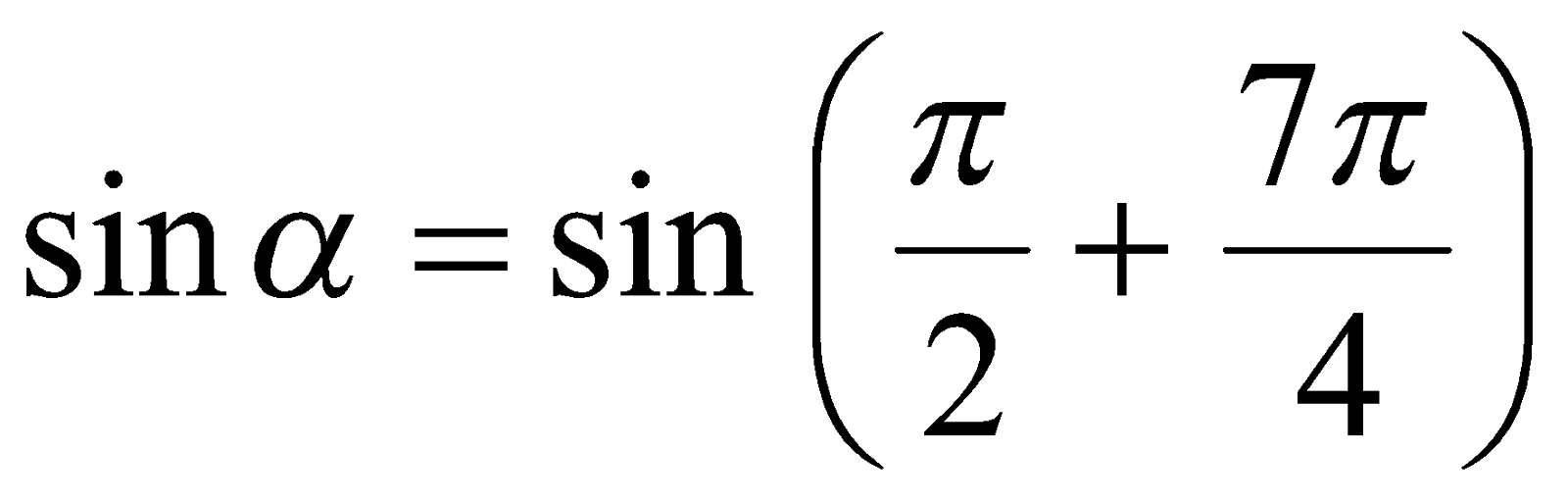 или
или 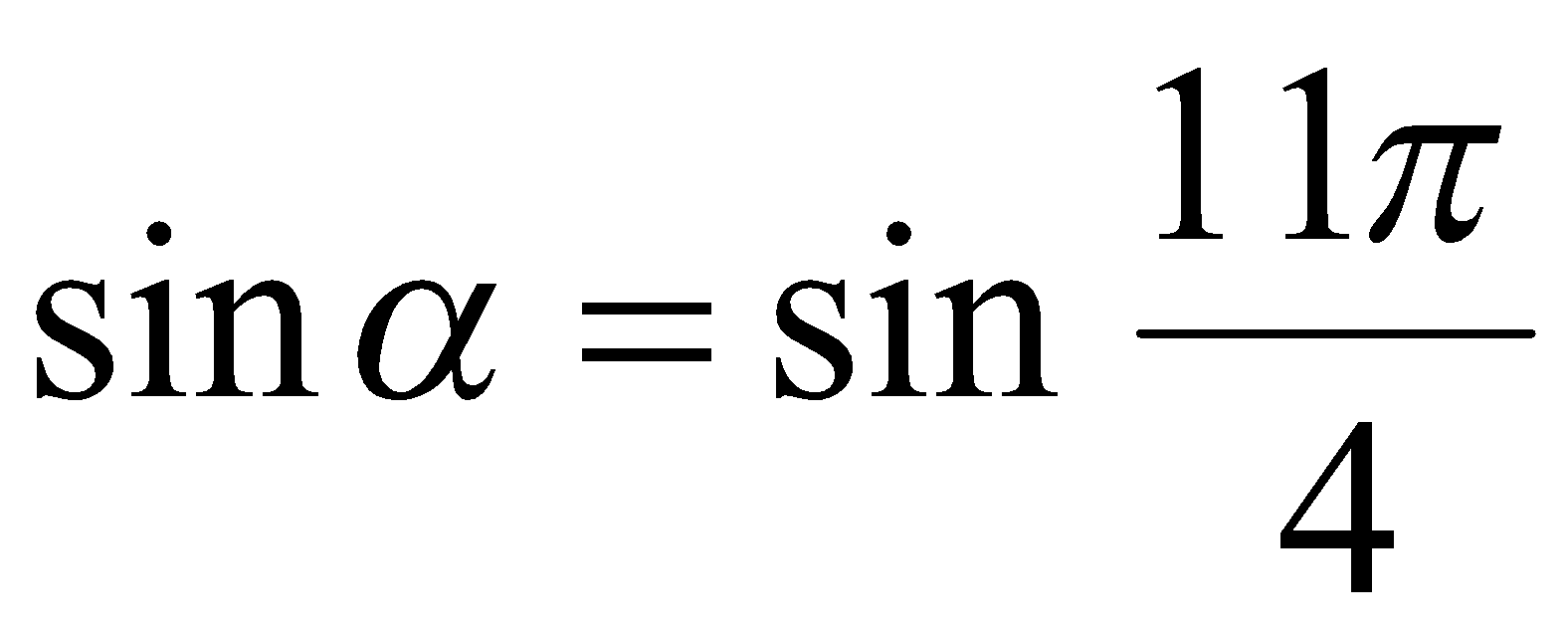 . Далее, принимая во внимание теорему 1, записываем две серии корней уравнения
. Далее, принимая во внимание теорему 1, записываем две серии корней уравнения 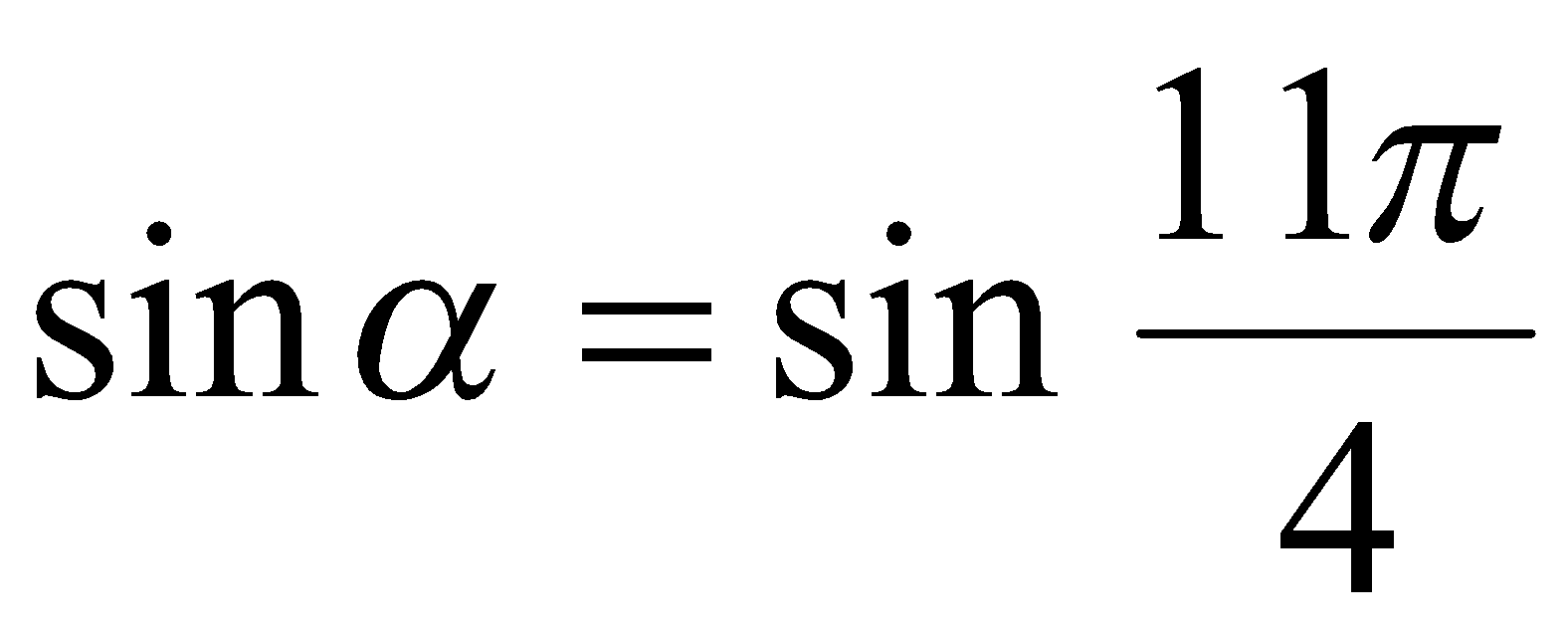 вида
вида
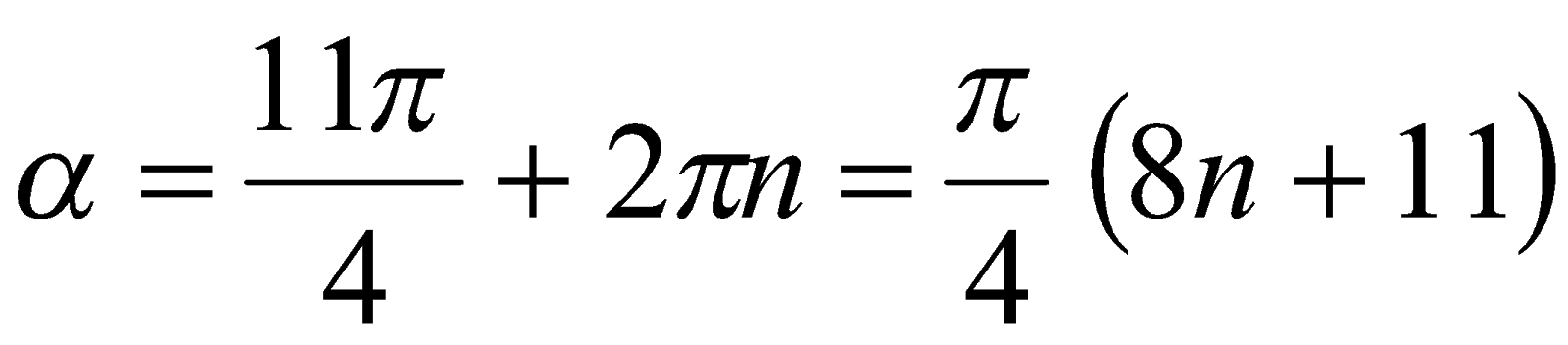 и
и 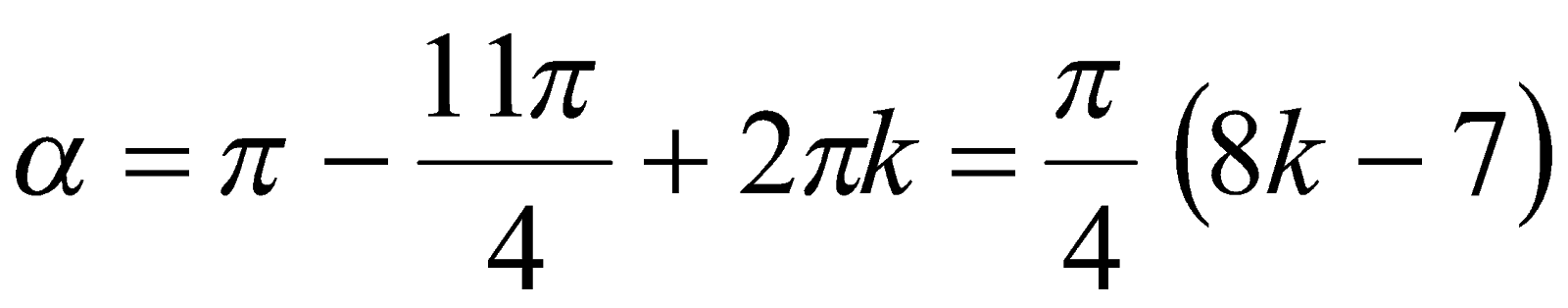 ,
,
где 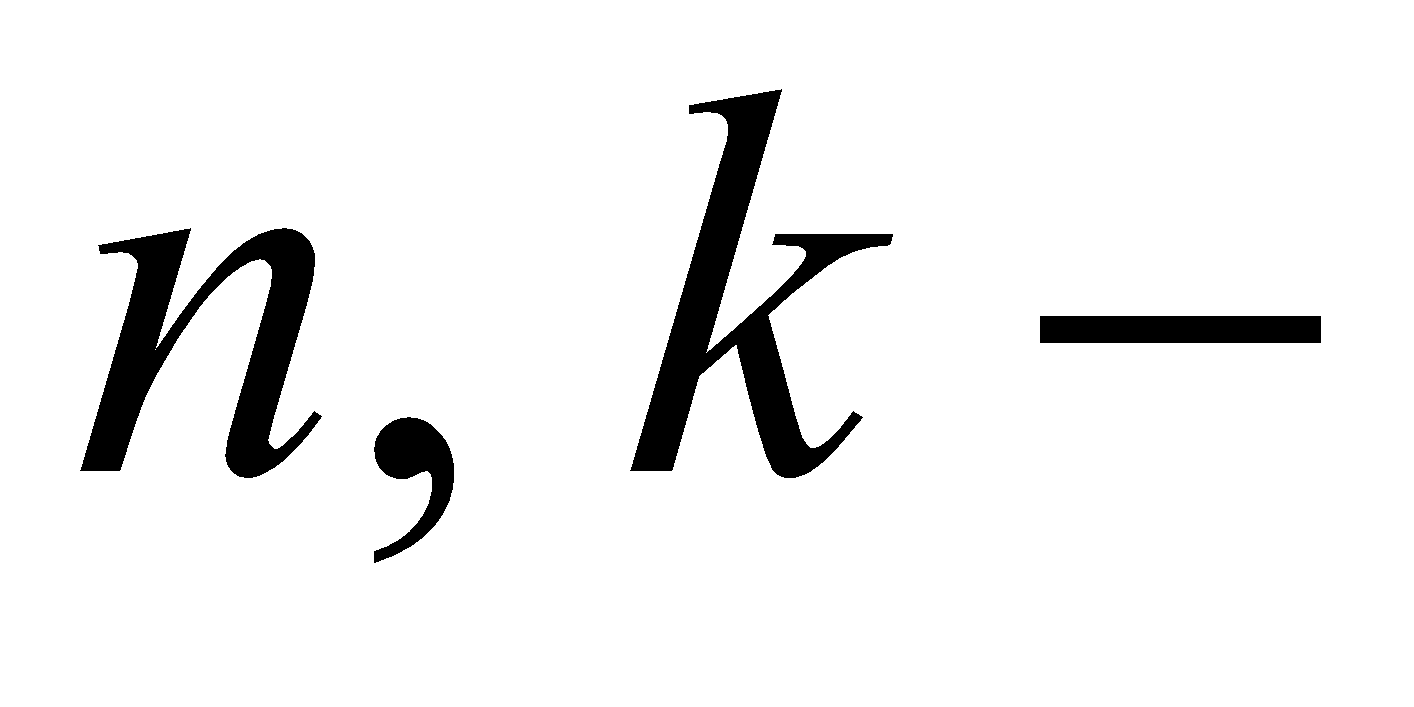 целые числа. Если положить
целые числа. Если положить 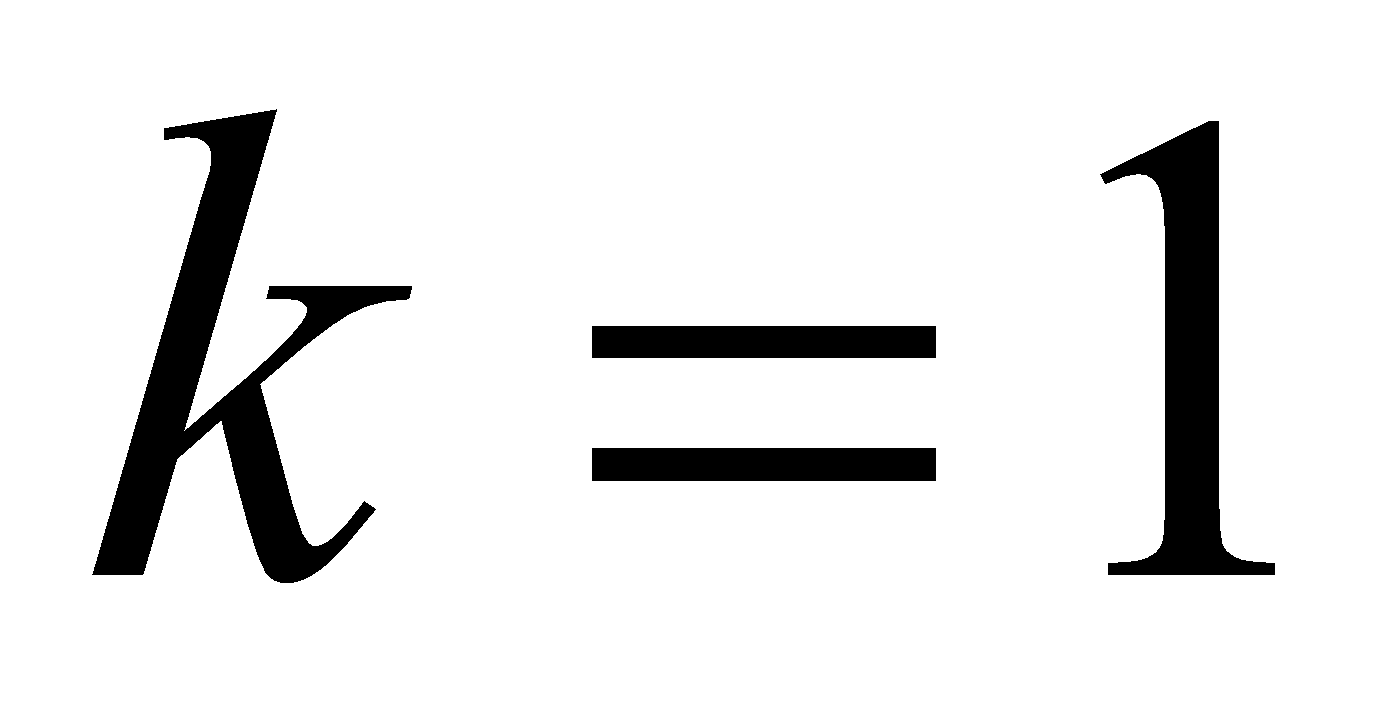 , то из второй серии корней вытекает единственное значение
, то из второй серии корней вытекает единственное значение  , которое удовлетворяет двойному неравенству
, которое удовлетворяет двойному неравенству 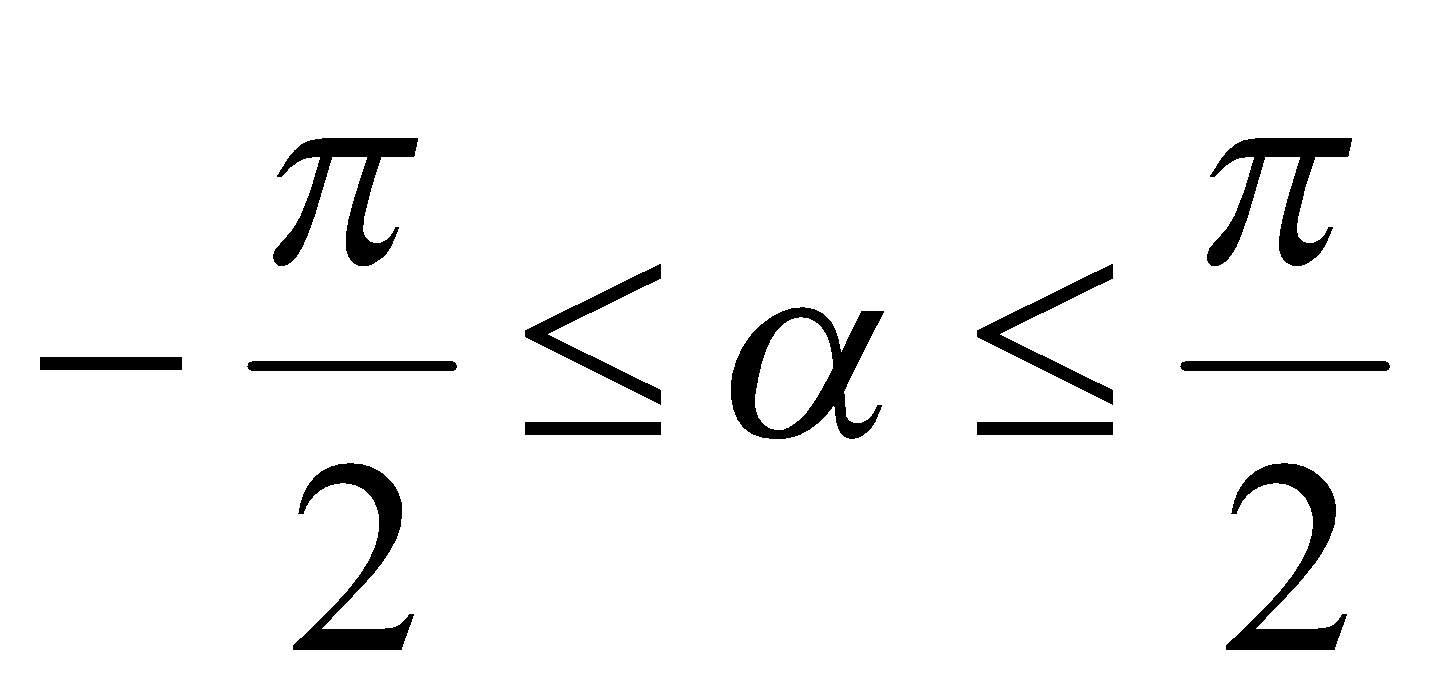 .
.
Ответ: 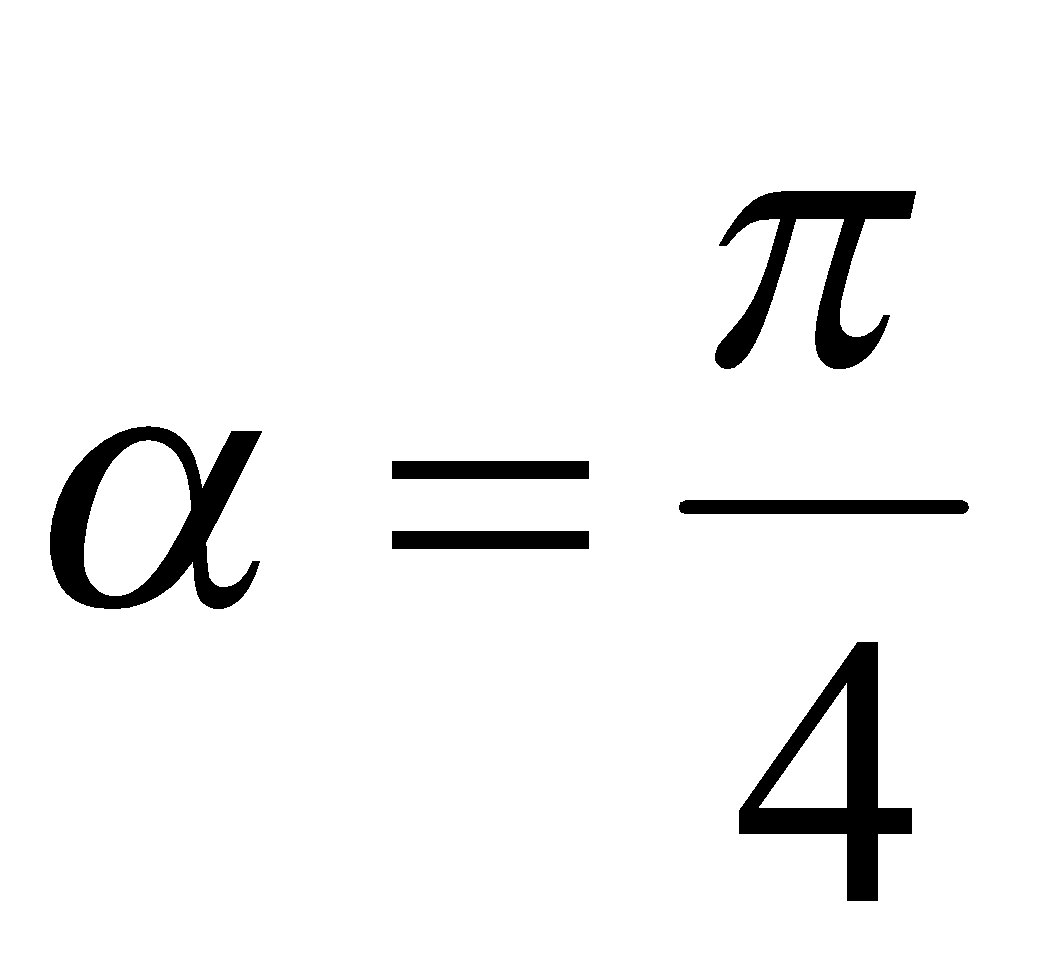 .
.
Пример 7. Вычислить значение 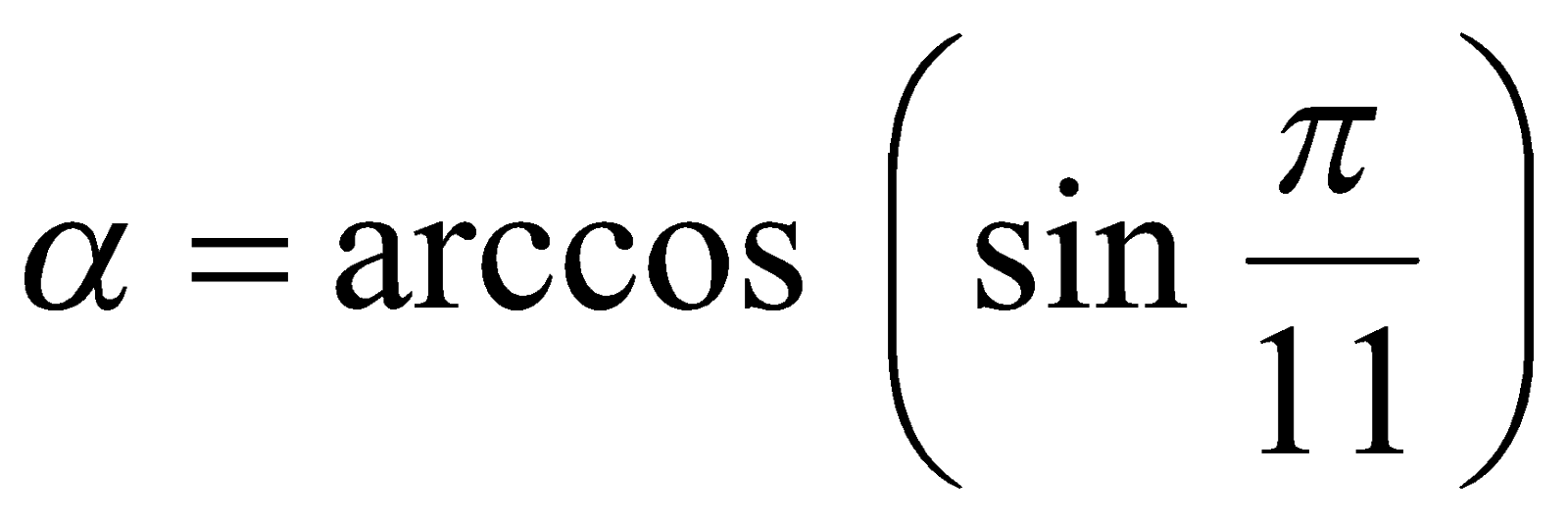 .
.
Решение. По определению функции 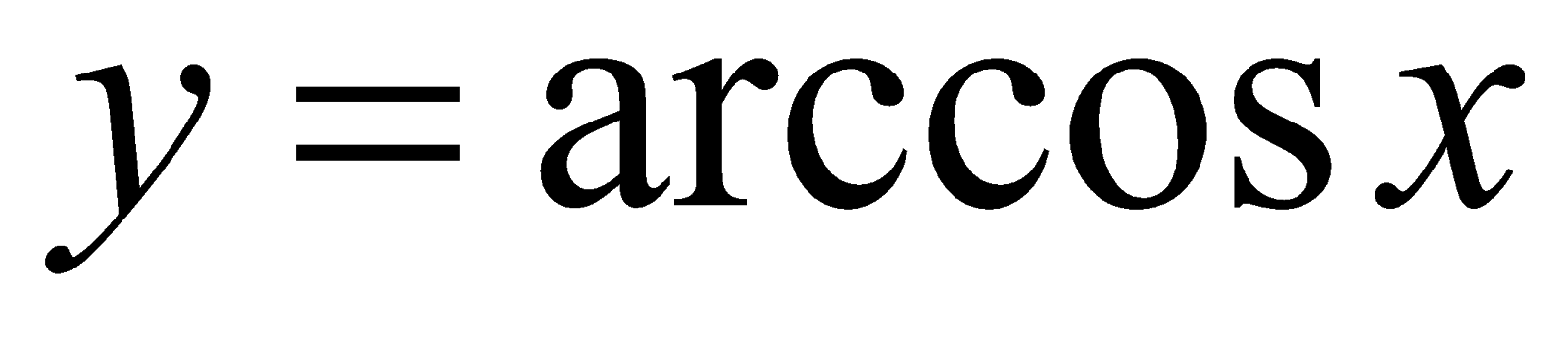 имеем
имеем 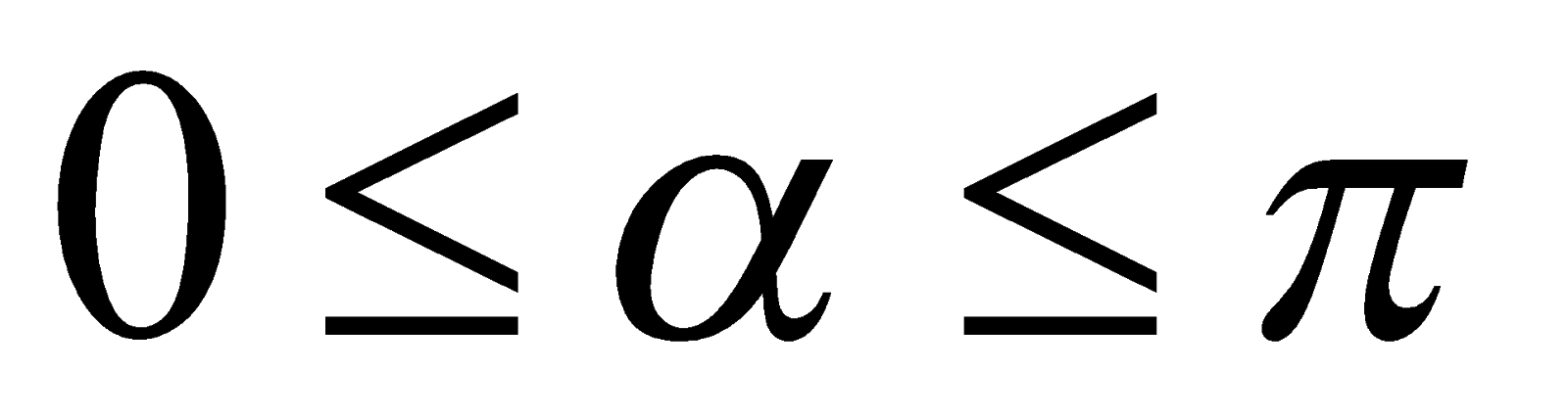 . Из условия следует, что
. Из условия следует, что  ,
, 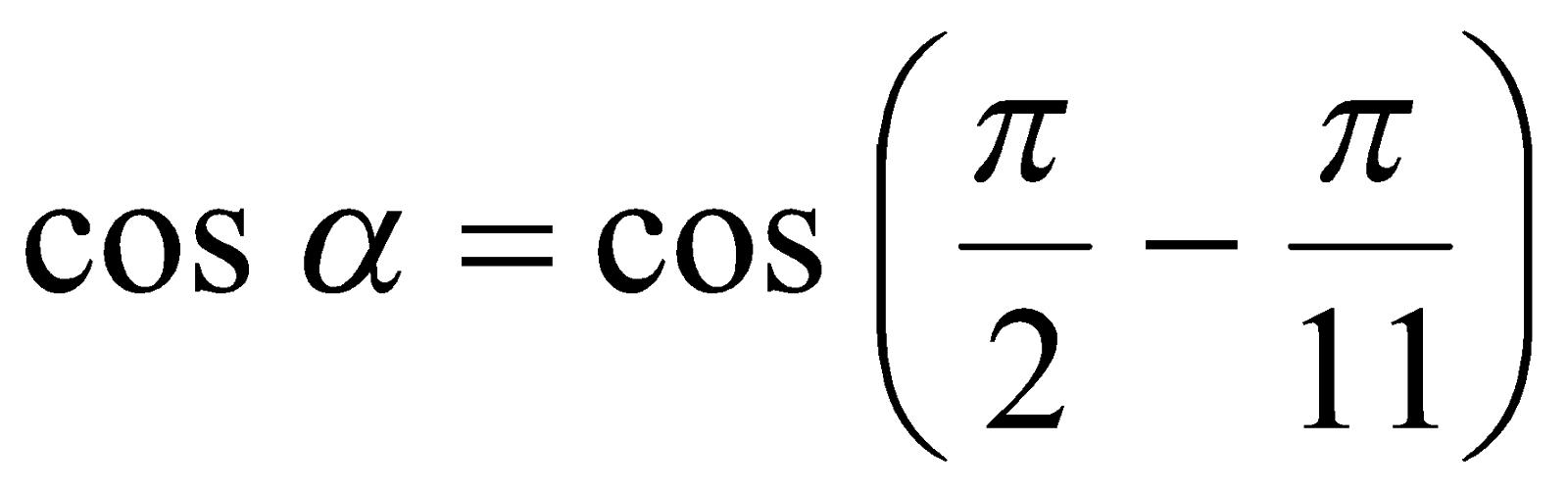 или
или
 . (2)
. (2)
Согласно теореме 2, здесь имеем две серии корней уравнения (2):
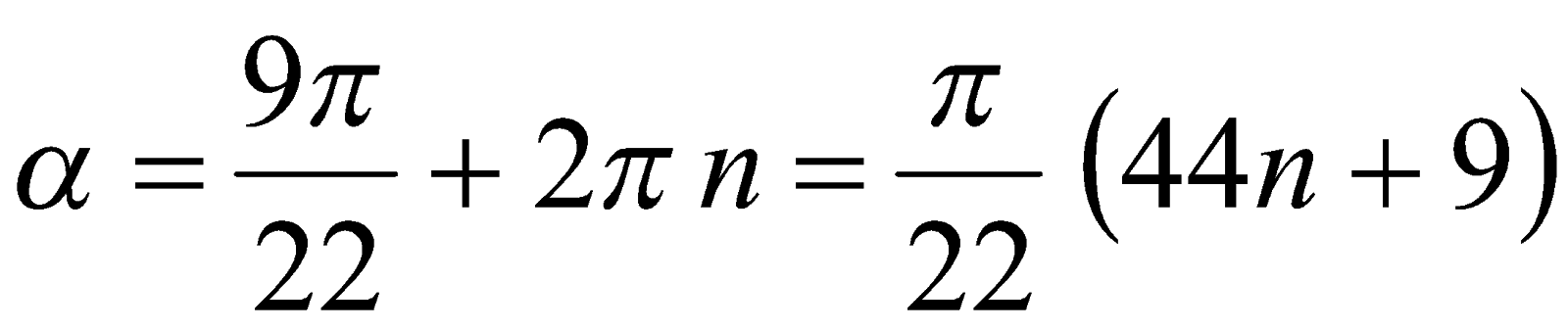 и
и 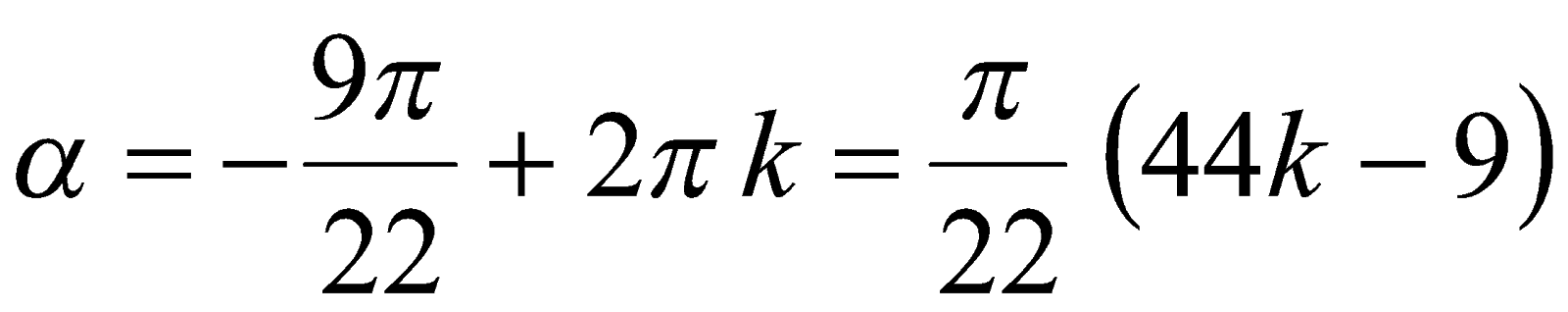 , где
, где 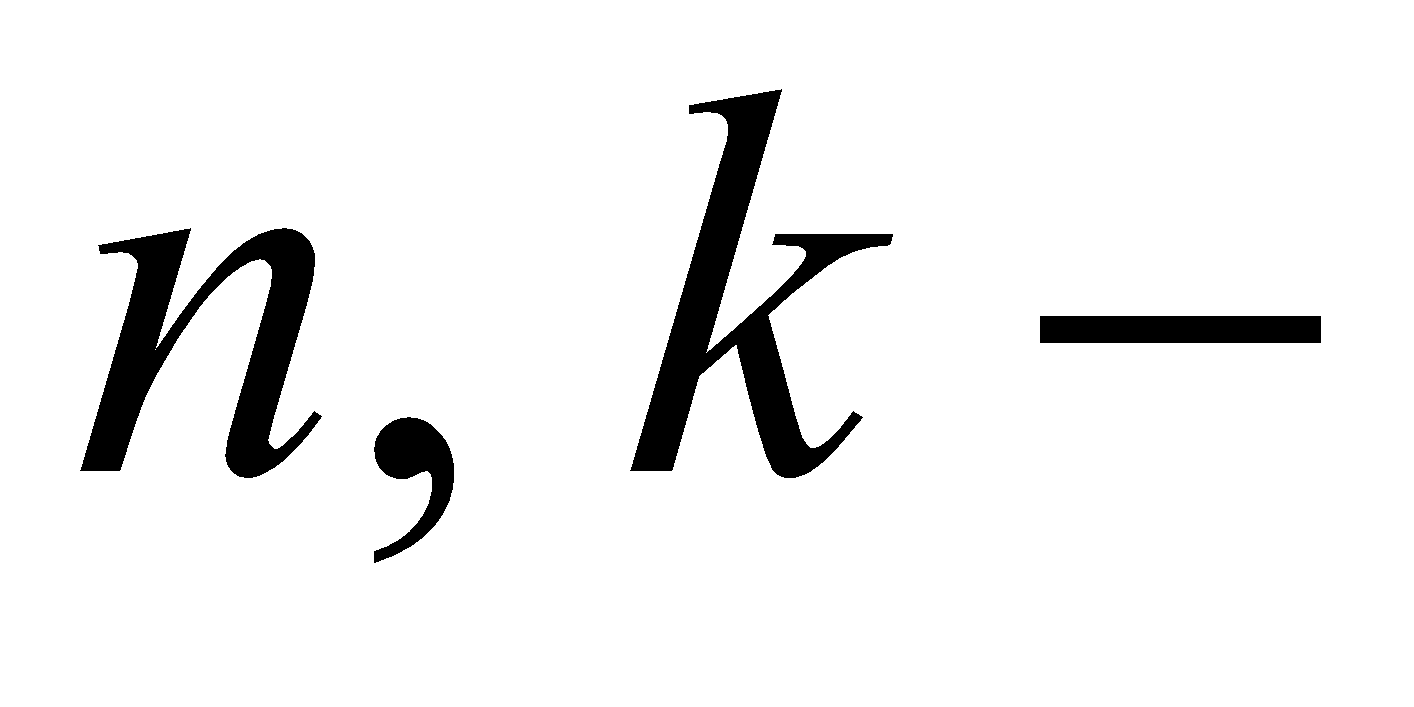 целые числа.
целые числа.
Так как 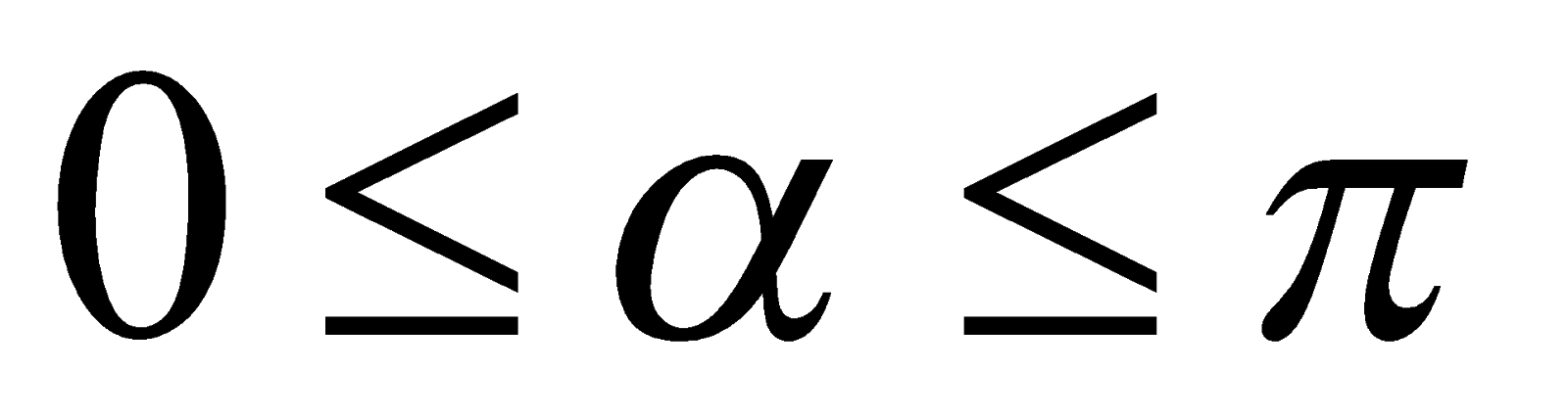 , то из первой серии корней при условии, что
, то из первой серии корней при условии, что 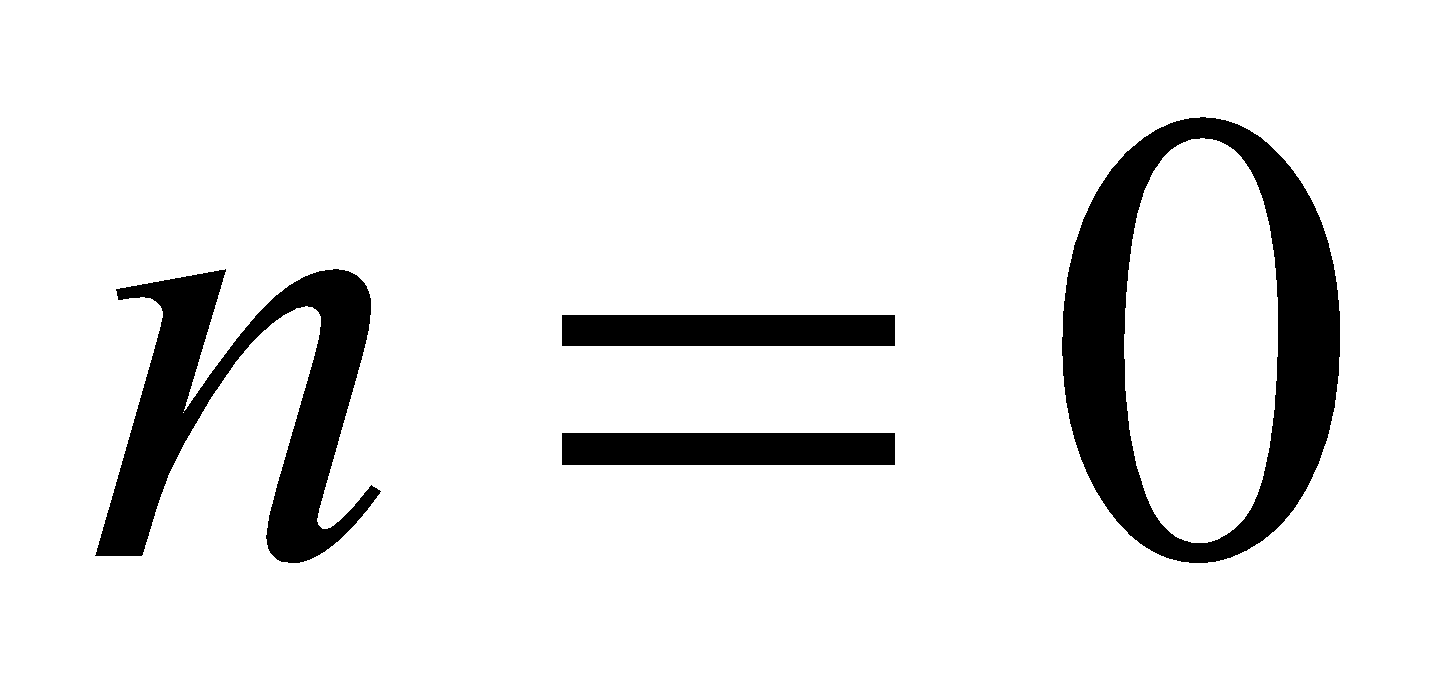 , получаем
, получаем  .
.
Ответ:  .
.
Тест по теме Арксинус, арккосинус, арктангенс числа
Найдите значение выражения:аrcsin (-

а)  ; б) —
; б) —  ; в)
; в) 
2. arcos (-1)
а) 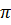 ; б) —
; б) — 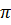 ; в) 0
; в) 0
arctg

а)  ; б) —
; б) —  ; в) 0
; в) 0
arctg (- 1) + arcsin 0
а) —  ; б)
; б)  ; в) 0
; в) 0
аrcsin (-
 ) + arcsin 0
) + arcsin 0
а)  ; б)
; б)  ; в)
; в)  г) нет верного ответа
г) нет верного ответа
sin (arcsin
 )
)
а)  ; б) —
; б) —  ; в) 0
; в) 0
sin (arcsin 0)
а) 0; б)  ; в) 1
; в) 1
Вариант 2
Найдите значение выражения:
аrcsin ( —
 )
)
а)  ; б)
; б)  ; в) —
; в) — 
arcos (-
 )
)
а) — ; б)
; б)  ; в)
; в) 
arctg

а)  ; б) —
; б) —  ; в) 1
; в) 1
arctg 1 + arcos 1
а)  ; б) 0; в)
; б) 0; в) 
аrcsin (-
 ) + arcos (-
) + arcos (- )
)
а)  ; б)
; б)  ; в) —
; в) — 
cos (arcos

а)  ; б) —
; б) —  ; в) 1
; в) 1
arcos (cos
 )
)
а)  ; б)
; б)  ; в) —
; в) — 
Ключ к тесту по теме Арксинус, арккосинус, арктангенс числа
п/пВариант
1
2
3
4
5
6
7
1
б
а
а
а
г
а
а
2
в
б
а
а
а
а
б
Критерии оценивания тестовых заданий
7 вопросов 5 (отлично) (7 ответов)
7 вопросов 4 (хорошо) (6 ответов)
7 вопросов 3 (удов) (5 ответов)
Литература
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
infourok.ru
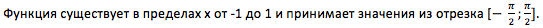


 )
)