Чему равно расстояние между 2 совпадающими точками: Attention Required! | Cloudflare

Posted on by alexxlab

Содержание

Чему равно расстояние между двумя совпадающими точками?

Углы при основаниях равны по 30 градусов.
треугольник ЕВС прямоугольный, угол С=30 и ВЕ=10, значит ВС=2ВЕ=20. 
АВ=ВС=20
АВД развёрнутый угол=180, значит угол ДВС=180-120=60, отсюда угол ДСВ=30.
треугольник ДСВ прямоугольный, угол С 30 и Вс 20, отсюда ВД=1/2 ВС = 10
АД=АВ+ВД= 30

Ответ:

D=130; B=130; C=50, A=50

Объяснение:

1)т.к АВСD- параллелограмм, то АВ||DC и BC||AD

2) противолежащие углы параллелограмма равны, следовательно D=B=130 С=А

3) сумма внутренних углов четырехугольника равна 360, то 2С=360-260

2С=100

С=100/2

С=50

С=А=50

Ну блин, ладно
пусть будет
угол 3, 6 и 7
🙂

210                                                                                                                        Продолжим ВС до пересечения с АР1 в т.К 

Продолжим АС до пересечения с ВР2 в т.М

АР1||ВР2⇒ при их пересечении секущими АМ и КВ накрестлежащие ∠КАМ=∠ВМА и ∠КВМ=∠ВКА

Рассмотрим ∆ КАС. Угол АСВвнешний и  и равен сумме  внутренних углов этого треугольника , не смежных с ним. 

∠АСВ=∠САК+∠АКС

Но угол АКС=МВС, следовательно, ∠АСВ=∠КАМ+∠МВС, что равно сумме углов САР1+СВР2. Доказано. 

211

                   

Расстояние между прямыми на плоскости онлайн

С помощю этого онлайн калькулятора можно найти расстояние между прямыми на плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми, задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Расстояние между прямыми на плоскости − теория, примеры и решения

1. Расстояние между прямыми в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:

где M1(x1, y1) и M2(x2, y2) − точки, лежащие на прямых L1 и L2, соответственно, а q1={m1, p1} и q2={m2, p2} − направляющие векторы прямых L1 и L2, соответственно.

Прямые (1) и (2) могут совпадать, быть паралленьными или пересекаться. Если прямые пересекаются, то понятие расстояния между ними не имеет смысла (не определено). Если прямые совпадают, то расстояние между ними равно нулю. Если же они параллельны, то расстояние между ними можно вычислить следующими методами:

Метод 1. От точки M1 прямой L1 проводим прямую L3, перпендикулярно прямой L2. Находим точку M3(x3, y3) пересечения прямых L3 и L2. Далее вычисляем расстояние между точками M1(x1, y1) и M3(x3, y3), которое и является расстоянием между прямыми L1 и L2 (Рис.1).

Рассмотрим этот метод подробнее. Каноническое уравнение прямой L3, проходящей через точку M1(x

1, y1) имеет следующий вид:

где q3={m3, p3} − направляющий вектор прямой L3.

Для того, чтобы прямая L3 была перпендикулярна прямой L2, направляющие векторы этих прямых должны быть ортогональны, т.е. скалярное произведение этих векторов должен быть равным нулю:

Так как направляющий вектор прямой не может быть равным нулю, то предположим, что координата m2 вектора q2 отлична от нуля. Тогда в качестве вектора q3 можно взять вектор q3={m3, p3}={p2, −m2}. Следовательно, уравнение прямой L3 получит следующий вид:

Для вычисления координат точки пересечения прямых L2 и L3, решим систему линейных уравнений (2) и (5). Преобразуем эти уравнения сделав перекрестное умножение:

Откроем скобки и перенесем налево переменную y:

Запишем (6) и (7) в матричном виде:

где

Решим (8):

Для построения обратной матрицы воспользуемся методом алгебраических дополнений. Сначала вычислим определитель матрицы:

Тогда обратная матрица примет следующий вид:

Подставляя значение обратной матрицы (12) в (11), получим:

Получили координаты точки M3(x3, y3) пересечения прямых L2 и L3:

Расстояние между точками M1 и M3 равно:

Полученное расстояние d также является расстоянием между прямыми L1 и L2.

Пример 1. Найти расстояние между прямыми L1 и L2:

Решение. Прямая L1 проходит через точку M1(x

1, y1)=M1(1, 2) и имеет направляющий вектор

Прямая L2 проходит через точку M2(x2, y2)=M2(5, −1) и имеет направляющий вектор

Пользуясь формулой (5), построим уравнение прямой L3, проходящей через точку M1 и перпендикулярной прямой L2:

Для вычисления координат точки пересечения прямых L2 и L3, решим систему линейных уравнений (16) и (17). Преобразуем эти уравнения сделав перекрестное умножение:

Сделаем эквивалентные преобразования:

Запишем систему линейных уравнений (18)-(19) в матричном виде:

Вычислим вектор (x, y)T:

Получили точку M3(x3, y3)=(3, −2), которая является точкой пересечения прямых L2 и L

3. Расстояние между прямыми L1 и L2 равно расстоянию между точками M1 и M3. Вычислим это расстояние:

Ответ: Расстояние между прямыми L1 и L2 равно d=4.47213595.

Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Уравнение прямой L3 в общем виде, проходящей через точку M1 и перпендикулярной прямой L2 имеет следующий вид:

Для того, чтобы прямая L3 была перпендикулярна прямой L2, нормальный вектор n3={A3, B3} прямой L3 должен быть коллинеарным направляющему вектору q2 прямой L2. Поэтому в качестве нормального вектора прямой L3 можно взять вектор q2={

m2, p2}. Подставим координаты вектора q2 в (20):

Сделаем преобразования:

Приведем уравнение прямой (2) к параметрическому виду:

Подставим (22) в (21) и решим относительно t:

Мы получили такое значение t, при котором соответствующая точка на прямой L2 удовлетворяет уравнению прямой L3, т.е. находится на этой прямой (является точкой пересечения прямых L2 и L3). Подставляя значение t в (22), получим координаты точки M3(x3, y3). Далее вычисляем расстояние между точками M1 и M3:

Пример 2. Найти расстояние между прямыми

и

Прямая L1 проходит через точку M1(x1, y1)=M1(1, 1) и имеет направляющий вектор

Прямая

L2 проходит через точку M2(x2, y2)=M2(3, −1) и имеет направляющий вектор

Уравнение прямой L3, проходящей через точку M1 и имеющий нормальный вектор n3={A3, B3} представляется формулой:

Для того, чтобы прямая L3 была перпендикулярна прямой L2, нормальный вектор n3={A3, B3} прямой L3 должен быть коллинеарным направляющему вектору q2 прямой L2. Поэтому в качестве нормального вектора прямой L3 можно взять вектор q2={m2, p2}={6, 9}. Подставим координаты вектора q2 и координаты точкиM1 в (27):

После упрощения получим уравнение прямой L

3, проходящей через точку M1 и перпендикулярной прямой L2:

Для нахождения точки пересечения прямых L2 и L3 проще всего пользоваться параметрическим уравнением прямой L2. Составим параметрическое уравнение прямой L2:

Выразим переменные x, y через параметр t :

Подставим значения x, y из выражения (29) в (28) и решим относительно t:

Подставляя значение t в выражения (29), получим координаты точки M3:

Вычислим расстояние между точками M1 и M3

Ответ. Расстояние между прямыми L1 и L2 равно:

2. Расстояние между прямыми в общем виде.

Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы параллельные прямые L1 и L2:

где n1={A1, B1} и n2={A2, B2} − направляющие векторы прямых L1 и L2, соответственно. Так как прямые параллельны, то можно один из них умножить на какое-то число так, чтобы нормальные векторы этих прямых совпадали. Пусть A2≠0. Умножим (31′) на A1/A’2. Тогда уравнение (2′) примет следующий вид:

где n2={A1, B1} − направляющий вектор прямой L2, а

Покажем, что расстояние между прямыми L1 и L2 равно:

Метод 1. Пусть A1≠0. Тогда точка M1(x1, y1)=M1(−C1/A1, 0) принадлежит прямой L1. Это легко проверить, подставив координаты точки M1 в (30). Построим уравнение прямой, проходящей через точку M1 и перпендикулярной прямой L2:

Поскольку прямая L3 перпендикулярна прямой L2, то нормальные векторы этих прямых ортогональны. Тогда вместо нормального вектора n3={A3, B3} прямой L3 можно взять вектор, ортогональный нормальному вектору n2, т.е. вектор n3={B1, −A1} (так как скалярное произведение этих векторов равно нулю). Тогда имеем:

Подставим координаты точки M1(x1, y1)=M1(−C1/A1, 0) в (33) и откроем скобки:

Найдем точку пересечения прямых L2 и L3. Для этого решим систему линейных уравнений (31),(34), представляя в матричном виде:

Решим (34):

Получили точку пересечения M3(x3, y3) прямых L2 и L3:

Вычислим расстояние между мочками M1(x1, y1) и M3(x3, y3):

Наконец, расстояние между точками M1 и M3, и следовательно, расстояние между прямыми L1 и L2 равно:

Метод 2. Воспользуемся понятием отклонения точки от прямой. Пусть M1(x1, y1) точка, принадлежащая прямой (30), Тогда выполняется равенство

Запишем уравнение (31) прямой L2 в нормальном виде:

При С2≥0

При С2<0

Запишем формулу отклонения точки M1(x1, y1) от прямой L2:

Учитывая равенство (35), получим:

Расстояние от точки M1(x1, y1) до прямой L2 равно модулю отклонения M1 от прямой L2:

Мы получили расстояние от точки M1 до прямой L2. Это же расстояние также является расстоянием между прямыми L1 и L2

Пример 3. Найти расстояние между прямыми

Нормальный вектор прямой L1 равен n1={A1, B1}={1, 2}. Нормальный вектор прямой L2 равен n2={A2, B2}={A1, B1}={1, 2}. Поскольку нормальные векторы этих плоскостей совпадают, то расстояние между прямыми L1 и L2 можно вычислить формулой (38):

Ответ. Расстояние между прямыми L1 и L2 равно:

Чему равно растояние между двумя совпадающими точками?

AH = 5
Рассмотрим треугольник ABH — он является прямоугольным (угол АНВ =90°, так как ВН — высота)
Раз этот треугольник прямогульный, мы можем применить теорему Пифагора АВ — гипотенуза, значит АВ²=ВН²+АН²
13²=12²+АН²
АН²=169-144
АН²=25
АН=5

Дано  АВСД — ромб
ВН перпендикулярно АД
АН=НД
ВД=12
Найти  углы А,В,С.Д и   Р авсд
Решение
Рассмотрим  треугольник АВД. Так как  высота ВН делит его основание пополам — треугольник равнобедренный ( боковые стороны равны) АД=ВД=12. У ромба все стороны равны АВ=ВС=СД=АД=12 см Периметр равен сумме всех сторон  т.е. 48 см.
Рассмотрим треугольник АВН — прямоугольный АН= 1/2 гипотенузы АВ. следовательно угол АВН = 30 градусов.   угол А= 180-30-90=60 Сумма углов при основании параллелограмма равна 180 угол Д=120. Противоположные углы равны. угол А=углу С=60  угол Д=углу В=120

Ответ:

Угол 2 равен. угол1+40

Допустим, что треугольник прямоугольный.

Обозначим острые углы в прямоугольном треугольнике 1 и 2. Сумма этих углов равна 90гр.

Внешние углы для углов 1 и 2 в сумме равны 360гр — (уг. 1 + уг. 2). Тогда

360-90 = 270гр.

Да, треугольник является прямоугольным.

Ответ:

Да, верно.

Объяснение:

Проще всего понять это, просто изобразив этот треугольник графически. АС больше АБ, следовательно и расстояние из точки С к середине отрезка АБ будет больше, чем расстояние от точки Б к отрезку АС

Всегда ли прямая линия — самое короткое расстояние между двумя точками?

Нет, прямая линия не всегда является самым коротким расстоянием между двумя точками. Наименьшее расстояние между двумя точками зависит от геометрии объекта/поверхности. Для плоских поверхностей линия действительно является кратчайшим расстоянием, но для сферических поверхностей, таких как Земля, расстояния по большому кругу на самом деле представляют собой самое короткое расстояние.

В раннем возрасте всех нас учили, что «линия — это наикратчайшее расстояние между двумя точками». Однако, что если бы кто-то сказал вам, что эта почтенная во времени поговорка не совсем верна.

Как оказалось, это утверждение лишь отчасти правдиво. Самое короткое расстояние между двумя точками на самом деле зависит от геометрии рассматриваемого объекта.

Если бы мы жили на плоской земле (чего у нас нет), то да, прямая линия была бы наименьшим расстоянием между точками A и B. Однако, Земля — это приблизительная сфера, а наименьшее расстояние между двумя точками на поверхности сферы — это дуга, известная как «расстояние по большой окружности».

Большое расстояние круга

Большое расстояние круга не новая концепция; на самом деле, многие из вас уже видели это в действии.

Люди, которые путешествовали по воздуху или только проверяли маршруты полета, вероятно, заметили, что рейсы не следуют прямым путем, а вместо этого берут изогнутый маршрут к месту назначения. Изогнутые маршруты не используются для того, чтобы выкопать более глубокую яму в карманах пассажиров, а используются потому, что на самом деле они являются самым коротким расстоянием между любыми двумя заданными точками на нашей планете.

Эти изогнутые маршруты часто сбивают с толку, так как маршруты очерчены на плоской двухмерной карте, где прямая линия может показаться наименьшим расстоянием. Однако ни одна двумерная карта Земли не является точной.

Чтобы дать вам понять суть, наша любимая Земля является трехмерным пространством и лучше всего представлена с помощью модели глобуса. Однако, когда пытаешься сравнять сферу с прямоугольной формой, как это делают большинство карт, на первый план выходит вековая дилемма искажений. Большинство прямоугольных карт торгуют формами страны, размерами, промежуточными расстояниями и даже легитимной информацией для удобства понимания.

Представьте, что вы хотите улететь из кишащих крысами глубин Нью-Йорка в город любви, Париж. На глобусе кратчайшее расстояние между двумя городами было бы дугой примерно 3630 миль, но та же самая дуга, когда она проецируется на 2D-карту, превращается в прямую линию, измеряющую приблизительно 3750 миль.

Чтобы убедиться в этом самим, откройте Google Maps на соседней вкладке и найдите Нью-Йорк. Найдя его, щелкните правой кнопкой мыши на именном теге и выберите «измерить расстояние». Затем уменьшите масштаб или прокрутите немного вправо, чтобы найти Париж, и нажмите на него. Следующее расстояние будет представлять собой кривую, представляющую собой кратчайшее расстояние между двумя городами. Нажмите в любом месте на этой кривой, чтобы сделать ключевую фигуру, и перетащите её немного на юг, чтобы преобразовать кривую в прямую линию. Вы можете использовать несколько ключевых кадров, чтобы составить прямую линию между двумя точками. После этого сравните размеры кривой и прямой линии (и приготовьтесь к тому, что ваша реальность будет разрушена!).

Разница между двумя числами (3,750 – 3,630 = 120 миль) может показаться несущественной, но, учитывая тот факт, что Boeing 747 потребляет в среднем 5 галлонов топлива на милю полета, самолет потребует дополнительных (5 галлонов/км × 120 миль =) 600 галлонов (2250 литров), чтобы пройти дополнительное расстояние, что является большим делом и добавит к стоимости билетов на самолет.

Расстояние большого круга в математических терминах

Говоря чисто математическим языком, большой круг (также известный как геодезические сферы) — это любой круг, нарисованный на сфере, центр которой совпадает с центром сферы, и таким образом делит сферу на две равные половины. Проще говоря, большой круг — это самый большой круг, который можно вырезать из сферы. Малый круг, с другой стороны, это когда центр круга и сферы не совпадают.

Представьте себе (или просто посмотрите на рисунок ниже), разрезая землю вдоль экватора или полюсов. Результирующие полушария в обоих случаях будут равны, и грани этих полушарий будут иметь тот же диаметр и центр, что и сама сфера (Земля).

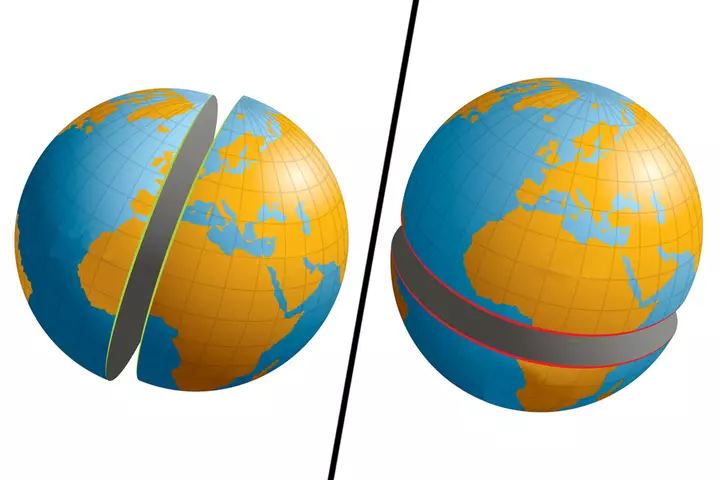
Для любых двух не диаметральных точек (положений) на сфере (Земле) существует только один уникальный большой круг, тогда как для диаметральных точек на сфере можно нарисовать бесконечное число больших кругов. Эти точки делят окружность на две дуги; меньшая дуга представляет собой истинное кратчайшее расстояние между двумя точками и называется расстоянием большого круга.

На приведенном ниже изображении точки P и Q являются двумя не диаметральными точками, а дуга PQ представляет собой кратчайшее расстояние между ними (расстояние большого круга). Точки u и v, с другой стороны, известны как противоположные или диаметрально противоположные точки и разделяют большой круг на две идентичные дуги.

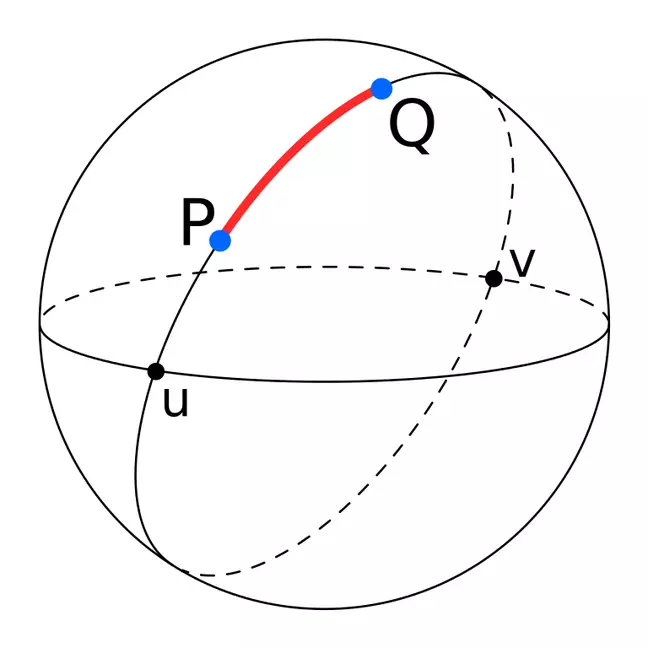
Вычисление расстояния большого круга между любыми двумя точками на поверхности сферы требует использования сферической тригонометрии, и хотя мы, возможно, не были знакомы с существованием больших расстояний круга еще в наши школьные годы, всеобщая ненависть к синусам и косинусам хорошо известна.

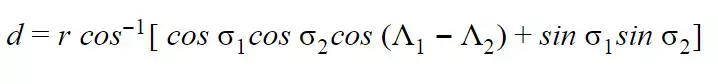
Здесь d-расстояние большого круга, r-радиус сферы (Земли) и термин cos -1 (cos σ 1 .cos σ 2 .cos (λ1 – λ2) + sin σ 1 .sin σ 2) — центральный угол , под которым расположены две точки с координатами σ 1 , λ 1 и σ 2, λ 2 соответственно.

Как уже говорилось ранее, большие круги находят свое основное применение в дальних путешествиях, в частности в воздушной и морской навигации. Искривленный характер больших окружных расстояний, дополненный вращением нашей планеты, заставляет пилотов и моряков постоянно корректировать свой курс. Поэтому большое расстояние по окружности разбивается на «линии Румба», которые представляют собой постоянное направление.

Сказав все это, даже большие расстояния по кругу не представляют собой истинное кратчайшее расстояние между двумя заданными местоположениями. Расстояния большого круга рассчитываются исходя из предположения, что Земля является идеальной сферой, но планета представляет собой более плоскую сферу с различными значениями радиуса в направлении экватора и полюсов. Значения большого круга, таким образом, имеют допуск около ± 5%.

Тем не менее, большие расстояния по окружности сыграли огромную роль в дальних поездках за последние несколько лет и будут продолжать делать это, экономя топливо авиакомпаний и экономя деньги путешественников!

Расстояние между прямыми в пространстве онлайн

С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Расстояние между прямыми в пространстве − теория, примеры и решения

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:

где M1(x1, y1, z1) и M2(x2, y2, z2) − точки, лежащие на прямых L1 и L2, а q1={m1, p1, l1} и q2={m2, p2, l2} − направляющие векторы прямых L1 и L2, соответственно.

Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.

1. Расстояние между параллельными прямыми в пространстве

Рассмотрим два метода вычисления расстояния между прямыми.

Метод 1. От точки M1 прямой L1 проводим плоскость α, перпендикулярно прямой L2. Находим точку M3(x3, y3, y3) пересечения плоскости α и прямой L3. По сути мы находим проекцию точки M1 на прямую L2. Как найти проекцию точки на прямую посмотрите здесь. Далее вычисляем расстояние между точками M1(x1, y1, z1) и M3(x3, y3, z3):

которое и является расстоянием между прямыми L1 и L2 (Рис.1).

Пример 1. Найти расстояние между прямыми L1 и L2:

Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор

Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор

Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.

Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:

Подставляя значения m2, p2, l2, x1, y1, z1 в (5) получим :

После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:

Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.

Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:

Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):

Решив уравнение получим:

Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:

Остается найти расстояние между точками M1 и M3:

Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.

Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.

Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов и q1 дает площадь параллелограмма, образованного этими векторами (Рис.2). Узнав площадь параллелограмма, можно найти вершину параллелограмма d, разделив площадь на основание q1 параллелограмма.

Вычислим координаты вектора :

Вычислим векторное произведение векторов и q1:

Вычисляя определители второго порядка находим координаты вектора c:

Далее находим площадь параллелограмма:

Расстояние между прямыми L1 и L2 равно:

где

Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми

и

Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор

Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор

Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.

Построим вектор ={x2−x1, y2−y1, z2−z1}={7, 2, 0}.

Вычислим векторное произведение векторов и q1. Для этого составим 3×3 матрицу, первая строка которой базисные векторы i, j, k, а остальные строки заполнены элементами векторов и q1:

Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов и q1:

Таким образом, результатом векторного произведения векторов и q1 будет вектор:

Поскольку векторное произведение векторов и q1 дает плошадь параллелограмма образованным этими векторами, то расстояние между прямыми L1 и L2 равно :

Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.

2. Расстояние между скрещивающимися прямыми в пространстве

Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).

Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).

Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:

где n1={A1, B1, C1} − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:

Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:

Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение

получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).

Аналогичным образом находим уравнение плоскости α2:

Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1={A1, B1, C1} и n2={A2, B2, C2} этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).

Тогда расстояние между параллельными плоскостями вычисляется формулой:

Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.

Пример 3. Найти расстояние между прямыми

и

Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(2, 1, 4) и имеет направляющий вектор q1={m1, p1, l1}={1, 3, −2}.

Прямая L2 проходит через точку M2(x2, y2, z2)=M2(6, −1, 2) и имеет направляющий вектор q2={m2, p2, l2}={2, −3, 7}.

Шаг 1.

Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.

Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1={m1, p1, l1} плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:

а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:

Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:

Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (34)−(36). Подставим значения x1, y1, z1, m1, p1, l1, m2, p2, l2 в (27)−(29):

Представим эти уравнения в матричном виде:

Решим систему линейных уравнений (40) отностительно A1, B1, C1, D1:

Искомая плоскость может быть представлена формулой:

Подставляя значения A1, B1, C1, D1 в (42), получим:

Упростим уравнение, умножив на число 17.

Шаг 2.

Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.

Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2={m2, p2, l2} плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:

а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:

Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:

Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (37)−(39). Подставим значения x2, y2, z2, m2, p2, l2, m1, p1, l1 в (37)−(39):

Представим эти уравнения в матричном виде:

Решим систему линейных уравнений (50) отностительно A2, B2, C2, D2:

Искомая плоскость может быть представлена формулой:

Подставляя значения A2, B2, C2, D2 в (52), получим:

Упростим уравнение, умножив на число −83.

Шаг 3.

Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).

Запишем формулы уравнений плоскостей α1 и α2 :

где n1={A1, B1, C1}={15, −11, −9} и n2={A2, B2, C2}={15, −11, −9} − нормальные векторы плоскостей α1 и α2, соответственно, а свободные члены равны D1=17, D2=−83, соответственно.

Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:

Подставим значения A1, B1, C1, D1, D2 в (54):

Упростим и решим:

Расстояние между прямыми равно: d=4.839339

Расстояние между 2 точками

Краткое объяснение

Когда мы знаем расстояния по горизонтали и по вертикали между двумя точками, мы можем вычислить расстояние по прямой следующим образом:

расстояние = √ a 2 + b 2

Представьте, что вы знаете расположение двух точек (A и B), как здесь.

Какое расстояние между ними?

Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник.

И с небольшой помощью Пифагора мы знаем, что:

a 2 + b 2 = c 2

Теперь отметьте координаты точек A и B.

x A означает координату x точки A
y A означает координату y точки A

Горизонтальное расстояние a равно (x A — x B )

Расстояние по вертикали b равно (y A — y B )

Теперь мы можем найти c (расстояние между точками):

Начнем с: c 2 = a 2 + b 2

Введите вычисления для a и b: c 2 = (x A — x B ) 2 + (y A — y B ) 2

Корень квадратный из обеих сторон: Готово!

Примеры

Пример 1

Введите значения:

Пример 2

Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет любые негативы:

Введите значения:

Пример 3

А вот еще пример с некоторыми отрицательными координатами… все еще работает:

Введите значения:

(Примечание √136 можно дополнительно упростить до 2√34, если хотите)

Попробуйте сами

Перетащите точки:

Три или более измерения

Отлично работает в 3 (и более!) Измерениях.

Возвести в квадрат разность для каждой оси, затем сложить их и извлечь квадратный корень:

Расстояние = √ [(x A — x B ) 2 + (y A — y B ) 2 + (z A — z B ) 2 ]

Пример: расстояние между двумя точками (8,2,6) и (3,5,7) составляет:

= √ [(8−3) 2 + (2−5) 2 + (6−7) 2 ]
= √ [5 2 + (−3) 2 + (−1) 2 ]
= √ (25 + 9 + 1)
= √35
Что около 5.9

.

python — Как найти расстояние между двумя точками?

Переполнение стека
  1. Около
  2. Товары
  3. Для команд
  1. Переполнение стека Общественные вопросы и ответы
  2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
  3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
  4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
  5. Реклама Обратитесь к разработчикам и технологам со всего мира
  6. О компании
.

c # — Расчет расстояния между 2 точками

Переполнение стека
  1. Около
  2. Товары
  3. Для команд
  1. Переполнение стека Общественные вопросы и ответы
  2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
  3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
  4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
  5. Реклама Обратитесь к разработчикам и технологам со всего мира
.

Программа на Java для расчета расстояния между двумя точками

Программа на Java для расчета расстояния между двумя точками. Код был написан в пяти различных форматах с использованием стандартных значений, ввод данных через класс сканера, аргументы командной строки, цикл while и цикл do while, создание отдельного класса. Если у вас нет сомнений в отношении информации, которой мы поделились, оставьте комментарий здесь, в конце сообщения.

Как рассчитать расстояние между двумя точками?

Формула расстояния между двумя точками, полученная из теоремы Пифагора.

По какой формуле найти расстояние между двумя точками?

A: Вот формула , чтобы найти расстояние между двумя точками:

Чтобы найти расстояние между двумя точками (x 1 , y 1 ) и (x 2 , y 2 ), все, что вам нужно сделать, это использовать координаты этих упорядоченных пар и применить формулу на фото ниже.

источник

1.Программа на Java с использованием стандартных значений

[wp_ad_camp_3]

Вот и программа на основе формул с образцом вывода.

импорт java.lang.Math. *;

class DistanceBwPoint

{

public static void main (String arg [])

{

int x1, x2, y1, y2;

двойной диск;

x1 = 1; y1 = 1; x2 = 4; y2 = 4;

дис = Мат.sqrt ((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));

System.out.println («distancebetween» + «(» + x1 + «,» + y1 + «),» + «(» + x2 + «,» + y2 + «) ===>» + dis);

}

}

вывод:

расстояние между (1,1), (4,4) ===> 4,242640687119285

2.Прием входных данных через сканер класса

Пример кода № 2: Получение входных данных через класс сканера.

1

2

3

4

5

6

7

8

9

10

11

12

13

140002

14000

18

19

20

21

22

23

24

25

26

27

28

29

30

000

34

35

36

импорт java.util.Scanner;

class DistanceBwPoint

{

public static void main (String arg [])

{

int x1, x2, y1, y2;

двойной диск;

Scanner sc = новый сканер (System.in);

System.out.println («введите точку x1»);

x1 = sc.nextInt ();

System.out.println («введите точку y1»);

y1 = сбн.nextInt ();

System.out.println («введите x2point»);

x2 = sc.nextInt ();

System.out.println («введите точку y2»);

y2 = sc.nextInt ();

dis = Math.sqrt ((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1));

System.out.println («distancebetween» + «(» + x1 + «,» + y1 + «),» + «(» + x2 + «,» + y2 + «) ===>» + dis);

}

}

вывод:

1

2

3

4

5

6

7

8

9

10

11

12

13

140002

14000

18

19

20

21

22

23

24

25

26

27

28

29

30

000

34

35

36

37

Вывод: 1

C: \ Users \ goutham \ Desktop \ E> java DistanceBwPoint

введите точку x1

1

введите точку y1

2

введите точку x2point

1

введите

точку

2

расстояние между (1,2), (1,2) ===> 0.0

Вывод: 2

C: \ Users \ goutham \ Desktop \ E> java DistanceBwPoint

введите точку x1

4

введите точку y1

4

введите точку x2point

введите точку y2

1

расстояние между (4,4), (1,1) ===> 4,242640687119285

Вывод: 3

C: \ Users \ goutham \ Desktop \ E> java DistanceBwPoint

введите точку x1

5

введите точку y1

3

введите точку x2

2

введите точку y2

3

расстояние между (5,3), (2,3) ===> 3.0

3. Использование аргументов командной строки

[wp_ad_camp_3]

Получение входных данных через аргументы командной строки. Ознакомьтесь с полным руководством по аргументам командной строки здесь .

1

2

3

4

5

6

7

8

9

10

11

12

13

140002

14

18

19

20

21

22

23

импорт java.util.Scanner;

класс DistanceBwPoint

{

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *