Как найти диагональ трапеции. Формулы для нахождения диагоналей трапеции

Знакомство с трапецией впервые происходит при изучении курса планиметрии. Хотя и до этого вы наверняка встречали предметы, форма которых совпадает с данной геометрической фигурой. Четырехугольник отличается тем, что только 2 из его четырех сторон параллельны. Если соединить противолежащие вершины фигуры отрезками, то получим ее диагонали. Как определить их длину? Величина этих отрезков связана с углами фигуры, длиной ее сторон и высоты.

1

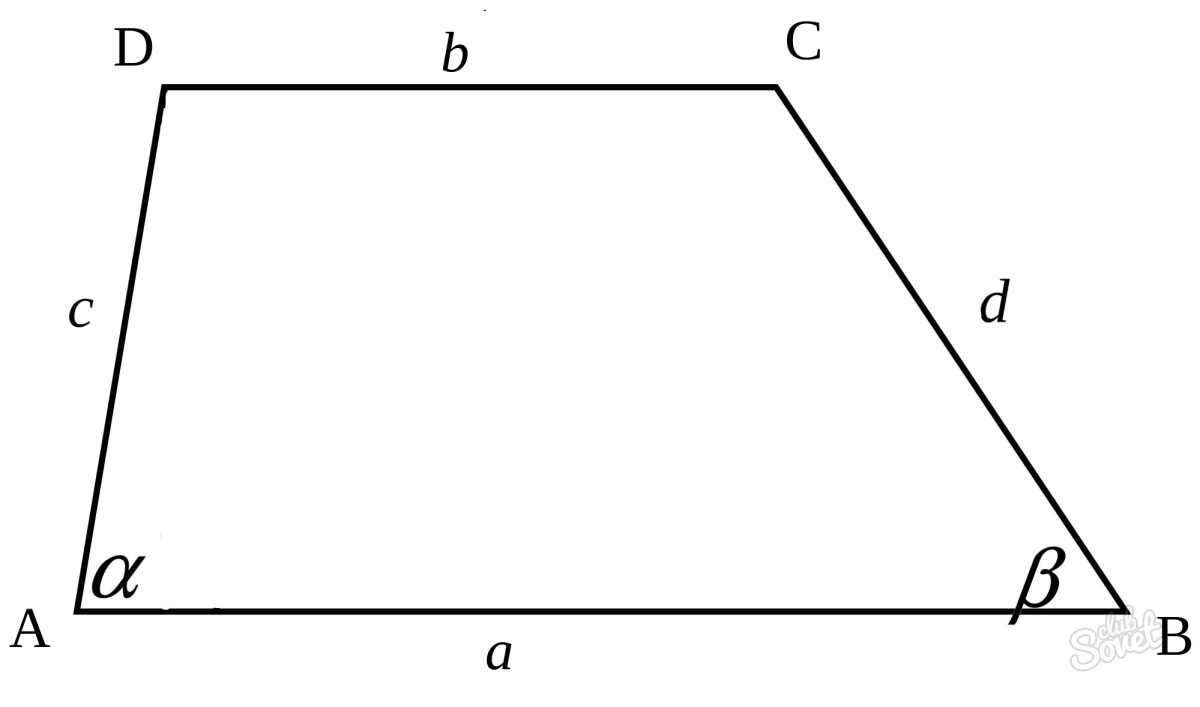
Диагонали и углы трапеции

Если перед вами произвольная трапеция с известными углами в основании, а также боковыми сторонами и основанием, то в определении величины диагоналей поможет следующее соотношение:

d1 = √a² + d² – 2ad*cosβ,
d2 = √a² + c² – 2ac*cosα,

d1, d2 – искомые диагонали,
a – основание,
c, d – боковые стороны,
β, α – углы, лежащие в основании.

В его основе лежит теорема косинусов, позволяющая в треугольнике определить длину стороны, используя известные величины двух других сторон, а также угла, лежащего против искомой стороны.

2

Диагонали и стороны трапеции

• При наличии известных всех четырех сторон фигуры для нахождения ее диагоналей можно использовать выражения:

d1 = √ d² + ab – (a(d² – c²)/(a-b)),
d2 = √ c² + ab – (a(c² – d²)/(a-b)).

• Взаимосвязь между диагоналями:

d1² + d2² = c² + d² + 2ab,
d1 = √c² + d² + 2ab – d2²

,
d2 = √c² + d² + 2ab – d1²,

Как в первом, так и во втором случаях:
d1, d2 – искомые диагонали,
a, b – основания,
c, d – боковые стороны.

3

Диагонали и высота трапеции

При известном значении одного из оснований фигуры или боковой стороны, угла при нижнем основании, а также высоты четырехугольника, с определением длин диагоналей также не возникнет сложностей.

d1 = √h² + (a – h*ctgβ)²,
d1 = √h² + (b + h*ctgα)²,
d1 = √a² + d² – 2a √d² – h²,

d1 = √h² + (a – h*ctgα)

2,
d1 = √h² + (b + h*ctgβ)²,
d1 = √a² + c² – 2a √c² – h²,

d1, d2 – искомые диагонали,
a, b – основания,
β, α – углы, лежащие в основании.
c, d – боковые стороны,
h – высота фигуры.

4

Диагонали и средняя линия трапеции

Если в числе заданных величин присутствует средняя линия, то с ее помощью также можно вычислить длину диагоналей фигуры. Соотношение верно лишь в случаях, когда sinφ = sin γ.

Т.к. l = d1*d2*sinφ/2h = d1*d2*sin γ/2h,

d1 = 2hl/ d2*sinφ = 2hl/ d2*sin γ,
d2 = 2hl/ d1*sinφ = 2hl/ d1*sin γ,

d1, d2 – искомые диагонали,
φ, γ – углы между ними,
h – высота фигуры,
l – ее средняя линия.

5

Фигура равнобокая

Если по условиям задания трапеция имеет равные боковые стороны, то выражения для нахождения диагоналей фигуры преобразуются с учетом того, что c=d:

d1 = d2 = √c² + ab,
d1 = d2 = √a² + c² – 2ac*cosα,
d1 = d2 = √a² + c² + 2ac*cosβ,
d1 = d2 = √b² + c² – 2bc*cosβ,
d1 = d2 = √b² + c² + 2bc*cosα,
d1 = d2 = √h² + l²,
d1 = d2 = √h² + (a+b)²/4,
d1 = d2 = √h*(a+b)/sinφ = √2S/ sinφ = √2lh/sinφ (sinφ = sin γ),

d1, d2 – искомые диагонали,
φ, γ – углы между ними,

h – высота фигуры,
S – площадь,
a, b – основания (a < b),
c – боковая сторона,
l – средняя линия.

sovetclub.ru

Как найти диагональ трапеции

Добрый вечер!
Как я вижу, то снова трапеция интересует. По видимому — это не такая лёгкая тема. Но на этот раз нас будет интересовать, как найти диагональ трапеции.
Первое что нам надо вспомнить, так как про саму трапецию и что это такое сказано много, это определение диагонали трапеции. Диагональ — это отрезок, который соединяет вершины, которые не принадлежат одной стороне многоугольника, в нашем случае — четырёхугольника.
Давайте попробуем решить задачку. Например нам дана трапеция ABCD, AC — диагональ, которую нам следует найти. Но при этом нам известны все стороны трапеции: AB = 6 см, BC = 4 см, CD = 12 см, AD = 20 см.

А теперь приступим к решению:  

   

 

   

 

   

 

   

 

   

 

   

 

   

 

   

Ответ: см

ru.solverbook.com

Если диагонали трапеции делятся точкой пересечения в отношении 1 : 3

Решение:
Сначала вспомним теорию.

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.

Трапеция

Трапеция называется равнобедренной трапецией, если ее боковые стороны равны.

Равнобедренная трапеция

Трапеция, один из углов которой прямой, называется прямоугольной трапецией.

Прямоугольная трапеция

Также будет полезно вспомнить следующую теорему:

Трапеция разбивается диагоналями на два равновеликих треугольник (примыкающих к боковым сторонам) и два подобных треугольника (примыкающих к основаниям).

А также будет полезно вспомнить свойство трапеции:

Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении:

Свойство трапеции

Это справедливо, в том числе , для самых диагоналей и высоты.

Снова обратимся к рисунку.

Так как треугольники AOD и BOC подобны, то справедливы следующие соотношения:

По условию диагонали трапеции делятся точкой пересечения в отношении 1 : 3, значит

Далее вспомним еще одно определение.

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме. На приведенном ниже рисунке это отрезок MN.

MN — средняя линия трапеции

 

Из соотношения: следует, что 3BC = AD, значит:

MN = (AD + BC) : 2 = (3BC + BC): 2 = 4BC: 2 = 2BC

Таким образом, средняя линия трапеции в два раза больше меньшего основания. Утверждение верное.

Ответ: утверждение верно.

shkolnaiapora.ru

Диагональ равнобедренной трапеции

Как известно, диагонали у равнобедренной трапеции одинаковые, поэтому в дальнейшем будем говорить о диагоналях в единственном числе.
Итак, диагональ равнобедренной трапеции можно найти несколькими способами, в зависимости от того, значения каких параметров даны в задаче.
Рассмотрим несколько вариантов.

1-й вариант. Известны стороны трапеции.

   

2-й вариант. Известны основание, боковая сторона и угол между ними.
В этом случае применяется теорема косинусов, согласно которой получается следующая формула:

   

   

   

   

где
, — нижнее и верхнее основание соответственно;
— боковая сторона;
— острый угол;
— тупой угол.

3-й вариант. Высота и средняя линия.

   

4-й вариант. Высота и основания.

   

5-й вариант. Площадь и острый угол между диагоналями.

   

Здесь представлены основные формулы для вычисления длины диагонали равнобокой трапеции. На самом деле можно вывести также формулу через среднюю линию, высоту и угол между диагоналями, через стороны трапеции и высоту, через высоту, основание и угол при нем и т.д.

ru.solverbook.com

Как найти диагональ трапеции?

Прежде, чем разбираться, как найти диагональ трапеции, вспомним, что такое трапеция. В планиметрии трапецией называют четырехугольник, у которого две противоположные стороны параллельны друг другу. Эти параллельные стороны называют основаниями трапеции, а остальные — боковыми сторонами. Боковые стороны могут быть одинаковыми, тогда мы имеем дело с равнобедренной трапецией.

Далее подробно разберем порядок нахождения длины диагоналей для общего случая — неравнобедренной трапеции. При этом будем исходить из того, что исходными данными являются длины всех четырех сторон трапеции, углы у основания неизвестны.

Расчет диагонали трапеции

В изображенной на рисунке трапеции ABCD имеются две диагонали AC и BD. Порядок нахождения их длины одинаков, поэтому рассмотрим все на примере нахождения диагонали BD, противолежащей ˂BAD.

Диагональ BD одновременно является стороной треугольника ABD и может быть рассчитана по теореме косинусов с помощью формулы:

BD = √(AB²+AD²-2AB^.AD^.cos ˂BAD)

В этой формуле нам известны все величины, кроме косинуса ˂BAD. Чтобы вычислить его, нам необходимо будет выполнить небольшое преобразование рисунка. «Вырежем» из исходной трапеции прямоугольник BNMC. В результате получим треугольник ABD’, в котором сторона BD’ будет равна стороне трапеции CD.

˂BAD’ в треугольнике равен ˂BAD в трапеции, так как никаких преобразований с треугольником ABN мы не выполняли. Итак, в этом треугольнике ABD’ сторона AB нам известна, сторона BD’ = CD, а сторона AD’ = AD – NM = AD – BC.

Получается, что по теореме косинусов cos ˂BAD = cos ˂BAD’ = (AB² + AD’² – BD’²)/2AB^.AD’ = (AB² +(AD – BC)² – CD²)/2AB^.(AD – BC)

Подставив теперь полученное выражение в найденную ранее формулу, получим:

BD = √(AB²+AD²-2AB^.AD^.cos ˂BAD) = √(AB²+AD²-2AB^.AD^.(AB² +(AD – BC)² – CD²)/2AB^.(AD – BC)) = √(AB² + AD² – AD^.(AB² +(AD – BC)² – CD²)/(AD – BC)) = √(AB² + AD² – AD^.(AD – BC)²/(AD – BC) – AD^.(AB² – CD²)/(AD – BC)) = √(AB² + AD² – AD² + AD^.BC – AD^.(AB² – CD²)/(AD – BC)) = √(AB² + AD^.BC – AD^.(AB² – CD²)/(AD – BC))

BD = √(AB² + AD^.BC – AD^.(AB² – CD²)/(AD – BC))

Полученная формула диагонали трапеции справедлива для любых значений длин сторон исходного четырехугольника.

Для второй диагонали формула соответственно примет вид:

AC = √(CD² + AD^.BC – AD^.(CD² – AB²)/(AD – BC))

Диагональ равнобедренной трапеции

Если вас интересует, как найти диагональ равнобедренной трапеции, получившуюся формулу можно значительно упростить. Ведь в равнобедренной трапеции AB = CD, следовательно AB² – CD² = 0 и формула длины диагонали приводится к виду:

BD = √(AB² + AD^.BC)

Диагонали равнобедренной трапеции равны друг другу, поэтому вторая диагональ находится по той же формуле.

В том случае, если исходными данными являются длины оснований трапеции, одна из боковых сторон и углы при основании, то задача нахождения диагонали трапеции сводится к расчету стороны треугольника по теореме косинусов.

elhow.ru