Теория по геометрии — Математика
Признаки равенства треугольников
1 признак (по двум сторонам и углу между ними): Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2 признак (по стороне и двум прилежащим к ней углам ): Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3 признак (по трём сторонам): Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Признаки параллельности двух прямых
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
Если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны;
Если две параллельные прямые пересечены секущей, то соответственные углы равны;
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180
Треугольник
Сумма углов треугольника равна 180
В треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона
Каждая сторона треугольника меньше суммы двух других его сторон
Сумма двух острых углов прямоугольного треугольника равна 90
Катет прямоугольного треугольника, лежащий против угла в 30, равен половине гипотенузы
Признаки равенства прямоугольных треугольников
1 признак (по двум катетам): Если катеты одного прямоугольного треугольника соответственно равны катетам другого , то такие треугольники равны.
2 признак (по катету и прилежащему к нему острому углу): Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
3 признак (по гипотенузе и острому углу): Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
4 признак (по гипотенузе и катету): Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Параллелограмм
Определение: Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
Свойства: 1) В параллелограмме противоположные стороны равны и противоположные углы равны,
2) Диагонали параллелограмма точкой пересечения делятся пополам
Признаки: 1)Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник-параллелограмм,
2) Если в четырёхугольнике противоположные стороны попарно равны , то этот четырёхугольник-параллелограмм
3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм
Трапеция
Определение: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Свойство средней линии трапеции: Средняя линия трапеции параллельна основаниям и равна их полусумме
Свойство отрезка, соединяющего середины диагоналей трапеции: Отрезок, соединяющий середины диагоналей трапеции параллелен основаниям трапеции и равен их полуразности.
Площадь
Площадь квадрата равна квадрату его стороны
Площадь прямоугольника равна произведению двух его смежных сторон
Площадь параллелограмма равна произведению его основания на высоту, проведённую к этому основанию
Площадь треугольника равна половине произведения его основания на высоту
Площадь прямоугольного треугольника равна половине произведения его катетов
Если высоты двух треугольников равны, то их площади относятся как основания
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
Площадь трапеции равна произведению полусуммы её оснований на высоту, проведённую к одному из оснований
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Теорема, обратная теореме Пифагора: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
Подобные треугольники
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одног о треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон подобных треугольников называется коэффициентом подобия
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Отношение периметров двух подобных треугольников равно коэффициенту подобия
Отношение сходственных сторон подобных треугольников равно отношению высот, проведённых к этим сторонам
Теорема о биссектрисе треугольника: Биссектрисса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Признаки подобия треугольников
1 признак (по двум углам): Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2 признак (по двум пропорциональным сторонам и углу между ними): Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
3 признак (по трём пропорциональным сторонам ): Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника , то такие треугольники подобны.
Средняя линия треугольника
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон
Свойство: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы
Медиана треугольника делит его на два равновеликих треугольника ( т.е имеющих равные площади)
Пропорциональные отрезки в прямоугольном треугольнике
Высота прямоугольного треугольника, проведённая из вершины прямого угла к гипотенузе, есть среднее геометрическое для отрезков, на которые делится гипотенуза этой высотой
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла
Окружность
Свойства касательных к окружности
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Центральные и вписанные углы
Угол с вершиной в центре окружности называется её центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Свойства:
Вписанный угол измеряется половиной дуги, на которую он опирается. Центральный угол равен дуге, на которую он опираетя
Если вписанный и центральный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального
Вписанные углы, опирающиеся на одну и ту же дугу, равны
Вписанный угол, опирающийся на полуокружность, прямой.
Теорема о произведении отрезков пересекающихся хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Своиства четырёхугольника вписанного в окружность и описанного около окружности
В любом вписанном четырёхугольнике сумма противоположных углов равна 180
В любом описанном четырёхугольнике суммы противоположных сторон равны
Подготовка к ОГЭ по геометрии
Вопросы к зачету №1 по геометрии.
1)Свойство смежных углов.
2) Свойство вертикальных углов.
3)Сумма углов в треугольнике.
4)Сумма острых углов прямоугольного треугольника.
5)Признаки равенства треугольников ( три )
6) Признаки подобия треугольников ( три )
7)Определение равнобедренного треугольника.
8)Свойство углов при основании равнобедренного треугольника.
9) Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
10) Понятие медианы, высоты и биссектрисы треугольника.
Вопросы к зачету № 2 по геометрии.
1)Теорема Пифагора.
2)Свойство диагоналей прямоугольника.
3)Свойство диагоналей равнобедренной трапеции.
4)Свойство диагоналей ромба.
5)Определение и свойство средней линии треугольника.
6)Определение и свойство средней линии трапеции.
7)Понятие центрального и вписанного углов. Чему равен вписанный угол?
8) Внешний угол треугольника( определение, свойство)
9)Признаки параллельности прямых (три)
10) Периметр многоугольника(определение и умение находить периметр фигуры)
Вопросы к зачету №3 по геометрии ( формулы).
1)Площадь треугольника, если известна сторона и проведенная к ней высота.
2) Площадь треугольника, если известны две стороны и угол между ними.
3)Площадь равностороннего треугольника.
4)Площадь треугольника, если известны все стороны.
5) Площадь прямоугольника.
6) Площадь параллелограмма, если известна сторона и проведенная к ней высота.
7) Площадь параллелограмма, если известны две стороны и угол между ними.
8) Площадь ромба
9) Площадь трапеции.
10)Площадь квадрата.
11)Площадь круга.
12) Длина окружности
13)Отношение площадей подобных треугольников
Вопросы к зачету № 4 по геометрии
1) Понятие радиуса, диаметра, хорды окружности.
2) Свойство хорд окружности.
3) Определение и свойство касательной к окружности.
3) Где находится: а) центр вписанной в треугольник окружности
б) центр описанной около треугольника окружности
в) центр описанной около прямоугольного треугольника окружности
4) При каком условии около четырехугольника можно описать окружность?
5) При каком условии в четырехугольник можно вписать окружность?
6) Свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла.
7) Свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла.
8) Свойство биссектрисы треугольника.
9) Свойство медиан треугольника.
10) Теорема синусов.
11) Теорема косинусов.
Пособие для подготовки к ОГЭ по геометрии.
Слайд 1
Пособие для подготовки к ОГЭ по геометрии. Подготовила: ученица 9Б класса Лустина Анастасия. Научный руководитель: Дубеева Галина Геннадьевна.Слайд 2
Помочь учащимся в подготовке к сдаче ОГЭ в соответствии с требованиями, предъявляемыми новыми образовательными стандартами. Цели:
Слайд 3
Оказать помощь в подготовке учащихся к итоговой аттестации; повторить материал, изученный ранее; углубить имеющиеся знания; Задачи:
Слайд 4
Благодаря этому пособию ученикам будет легче подготовиться к экзамену по математике. Гипотеза:
Слайд 5
7 класс 8 класс 9 класс Содержание.
Слайд 6
7 класс Основные свойства простейших геометрических фигур. Смежные и вертикальные углы. Признаки равенства треугольников. Сумма углов треугольника. Геометрические построения.
Слайд 7
Основные свойства простейших геометрических фигур.
Слайд 8
Основные геометрические фигуры- точка и прямая. Точки обозначают буквами A,B,C,D,E,F,M,K,P,…, прямые обозначают a,b,c,d,m,l,k ,… . A a Через любые две точки можно провести прямую, и только одну. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. c M N m D C B A E Из трёх точек прямой одна и только одна лежит между двумя другими. B C D Каждый отрезок имеет определённую длину. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой. M P K MK = MP + PK Прямая разбивает плоскость на две полуплоскости. a a₁ a₂ Полупрямая (луч)- часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. А В
Слайд 9
Каждый угол имеет определенную градусную меру, большую нуля. Градусная мера развёрнутого угла равна 180°. М Р К Градусная мера угла равна сумме мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. О М Р К На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один. М К а МК = а единиц длины. Угол МОК = m° М О К Угол- это фигура, которая состоит из точки (вершины угла) и двух различных полупрямых, исходящих из этой точки (сторон угла). А В С Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной. М b║a a b
Слайд 10
Два отрезка равны, если они имеют одинаковую длину. Два угла равны, если они имеют одинаковую градусную меру. Треугольники равны, если у них соответствующие стороны равны и соответствующие углы равны. а А В а М К АВ=МК А В С А₂ В₂ С₂ 2 2 2 В равных треугольниках против равных углов лежат равные стороны, а против равных сторон лежат равные углы. Треугольник- это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки ( точки называют вершинами, отрезки- сторонами треугольника). Периметр треугольника — сумма длин всех его сторон. А В С ∆АВС K P M B A C
Слайд 11
Смежные и вертикальные углы.
Слайд 12
Смежные углы — это углы, одна сторона которых общая, а две другие являются дополнительными полупрямыми. Сумма смежных углов равна 180 ° . Прямой угол — это угол, равный 90 ° . Острый угол- это угол, меньший 90 ° . Тупой угол- это угол, больший 90 ° и меньший 180 ° . Вертикальные углы — это углы, у которых стороны одного угла являются дополнительными полупрямыми сторон другого. Вертикальные углы равны. Перпендикулярные прямые – это прямые, которые пересекаются под прямым углом. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну. Биссектриса угла – это луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам. D A B C Прямой угол Острый угол Тупой угол 1 2 90° а b В М А С
Слайд 13
Признаки равенства треугольников.
Слайд 14
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны. Равнобедренный треугольник – это треугольник, у которого две стороны (боковые стороны) равны . Равносторонний треугольник – это треугольник, у которого все стороны равны. А В С А ’ В ’ С ’ A A’ B’ B С ’ A A’ С ’ B B’ A A B B C C
Слайд 15
Высота треугольника, опущенная из данной вершины, — это перпендикуляр, проведенный из этой вершины к прямой, которая содержит противолежащую сторону треугольника. Биссектриса треугольника, проведенная из данной вершины, — это отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. Медиана треугольника, проведенная из данной вершины, — это отрезок, соединяющий эту вершину с серединой противолежащей стороны. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой. А В С А В С А В С В А С
Слайд 16
Сумма углов треугольника.
Слайд 17
Две прямые, параллельные третьей прямой, параллельны. а с b Углы 1 и 2 или 3 и 4 – внутренние односторонние углы. Углы 5 и 6 или 7 и 8 – внутренние накрест лежащие углы. 3 4 1 2 5 8 7 6 Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 ° , то прямые параллельны. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 °. 1 3 2 Сумма углов треугольника равна 180 ° . Внешний угол треугольника при данной вершине – это угол, смежный с углом треугольника при этой вершине. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним. А В С А В С D
Слайд 18
Прямоугольный треугольник- это треугольник, у которого есть прямой угол. Гипотенуза прямоугольного треугольника – это его сторона, противолежащая прямому углу. Катеты прямоугольного треугольника – это его стороны, прилежащие к прямому углу. гипотенуза катет катет А В С Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны. А В С А ’ В ’ С ’ Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один. Расстояние от точки до прямой – это длина перпендикуляра, опущенного из данной точки на прямую. В прямоугольном треугольнике с углом 30 ° катет, противолежащий этому углу, равен половине гипотенузы. K m a b M a P 30° A B C
Слайд 19
Геометрические построения.
Слайд 20
В А С Окружность – это фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка – это центр окружности. Радиус окружности ( R) – это расстояние от центра окружности до её точки или любой отрезок, соединяющий точку окружности с её центром. Хорда – это отрезок, соединяющий две точки окружности. Диаметр – это хорда, проходящая через центр окружности. Радиус, перпендикулярный хорде, делит ее пополам. Окружность, описанная около треугольника, — это окружность, которая проходит через все его вершины. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон. Серединный перпендикуляр к отрезку – это прямая, проходящая через середину отрезка перпендикулярно к нему. Чтобы найти центр окружности, описанной около треугольника, нужно построить точку пересечения серединных перпендикуляров к его сторонам (достаточно двух). хорда диаметр радиус B O C A О С В А ОС= R (радиус)
Слайд 21
Касательная к окружности – это прямая, проходящая через точку окружности перпендикулярно к радиусу, проведённому в эту точку (её называют точкой касания). Касательная к окружности не имеет с ней других общих точек, кроме точки касания. а O A касательная Окружность, вписанная в треугольник, — это окружность, которая касается всех его сторон. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис. Чтобы найти центр окружности, вписанной в данный треугольник, нужно построить точку пересечения его биссектрис (достаточно двух). O А В С r Геометрическое место точек – это фигура, которая состоит из всех точек плоскости, обладающих определённым свойством. Окружность – это геометрическое место точек, равноудалённых от данной точки. Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудалённых от его концов. Биссектриса угла – это геометрическое место точек, равноудалённых от его сторон.
Слайд 22
8 класс Четырёхугольники. Теорема Пифагора. Декартовы координаты на плоскости. Движение . Векторы.
Слайд 23
Четырёхугольники.
Слайд 24
Четырёхугольник – это фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. (Никакие три из этих точек не должны лежать на одной прямой, а отрезки не должны пересекаться). Диагональ четырёхугольника – это отрезок, соединяющий его противоположные вершины. Периметр четырёхугольника – это сумма длин всех его сторон. Параллелограмм – это четырёхугольник, противолежащие стороны которого параллельны. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. У параллелограмма противолежащие стороны равны, противолежащие углы равны. A B C D A B C D AB+CD+BC+AD=P ABCD A B C D C A B D A B C D
Слайд 25
Прямоугольник – это параллелограмм, у которого все углы прямые. Диагонали прямоугольника равны. Ромб – это параллелограмм, у которого все стороны равны. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Квадрат – это прямоугольник, у которого все стороны равны. У квадрата все углы прямые, диагонали равны, диагонали пересекаются под прямым углом и являются биссектрисами его углов. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. ( th Фалеса) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна противолежащей стороне и равна ее половине. A B C D A B C D A B C D m 1 m 2 m3 a1 a2 b1 b2 Если m1║m2║m3 …, и a1=a2 …, то b1=b2 … А В С М К
Слайд 26
Трапеция – это четырёхугольник, у которого только две противолежащие стороны параллельны. Равнобокая трапеция – это трапеция, у которой боковые стороны равны. Средняя линия трапеции – это отрезок, соединяющий середины боковых её сторон. Средняя линия трапеции параллельна основаниям и равна их полусумме. Прямоугольная трапеция – это трапеция, одна из боковых сторон которой перпендикулярна основаниям. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки( th о пропорциональных отрезках). Если даны отрезки a , b и c , то четвертый пропорциональный отрезок – это отрезок, удовлетворяющий условию a : b = c : x , тогда x =( b * c ): a A B C D A B C D A B C D A B C D m k B1 B2 A1 A2 m║k CB1:CB2=CA1:CA2 C
Слайд 27
Теорема Пифагора.
Слайд 28
Косинус острого угла прямоугольного треугольника – это отношение прилежащего(к этому углу) катета к гипотенузе. Косинус угла зависит только от градусной меры этого угла. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Следствия: 1.Квадрат катета равен разности между квадратом гипотенузы и квадратом другого катета. (В прямоугольном треугольнике любой из катетов гипотенузы.) 2.Косинус любого острого угла меньше 1. Если для сторон треугольника выполняется равенство a ²+ b ²= c ²( a , b и c – длины его сторон), то больший его угол равен 90°(т.е. треугольник прямоугольный). Если к прямой (a) из одной точки (M) проведены перпендикуляр (MA) и наклонные (MB,MC,MD,ME) , то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции (MB=MC,BA=AC) , из двух наклонных больше та, у которой проекция больше. A B C a Cos a = AC/AB A B C c a b A B C 5 3 4 ∆ ABC- египетский M B A C D E a
Слайд 29
Каковы бы ни были три точки, расстояние между любыми двумя из них не больше суммы расстояний от них до третьей точки. В любом треугольнике каждая сторона меньше суммы двух других сторон. Синус острого угла прямоугольного треугольника – это отношение катета, противолежащего этому углу, к гипотенузе. Тангенс острого угла – это отношение катета, противолежащего углу, к катету, прилежащему к этому углу. Катет, противолежащий углу a , равен произведению гипотенузы на sin a . ( a=c*sin a) Катет, прилежащий к углу a , равен произведению гипотенузы на cos a . (b=c* cos a) Катет, противолежащий углу a , равен произведению второго катета на tg a . (a=b* tg a) Катет, прилежащий к углу a , равен второму катету, деленному на tg a . (b=a/ tg a) Гипотенуза равна катету, противолежащему углу a , деленному на sin a . (c=a/sin a) Гипотенуза равна катету, прилежащему к углу a , деленному на cos a . (c=b/ cos a) AC≤AB+BC A B C A B C AC=AB+BC AC
Слайд 30
Для любого острого угла а справедливы равенства Для любого острого угла справедливы равенства При возрастании острого угла sin a и tg a возрастают, а cos a убывает. Если a 1 >a 2 , то sin a 1 >sin a 2 , tg a 1 > tg a 2 , cos a 1
Слайд 31
Декартовы координаты на плоскости.
Слайд 32
Абсцисса точки А – это число x , абсолютная величина которого равна расстоянию от точки О(начала координат) до точки А х (пересечения прямой, параллельной оси ординат, с осью абсцисс). Число x >0, если точка А х принадлежит положительной полуоси, и х 0, если точка А y принадлежит положительной полуоси, и y
Слайд 33
Уравнение фигуры – это уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки этой фигуры. И любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры. Уравнение окружности с центром в точке А( a ; b ) и радиусом R : Уравнение окружности с центром в начале координат О(0;0) и радиусом R : Любая прямая m ( в декартовых координатах x , y ) имеет уравнение вида ax + by + c =0, где a , b , c — некоторые числа, причем хотя бы одно из чисел a , b не равно нулю. Координаты ( x , y ) точки пересечения прямых, заданных уравнениями a 1 x + b 1 y + c 1=0, a 2 x + b 2 y + c 2=0, являются решениями системы уравнений R A( a;b ) R O m
Слайд 34
Если в уравнении прямой ax + by + c =0: 1) a =0, b ≠ 0, c ≠ 0, то прямая параллельна оси абсцисс; 2) b =0, a ≠ 0, c ≠ 0, то прямая параллельна оси ординат; 3) c =0, то прямая проходит через начало координат( При a =0 прямая совпадает с осью абсцисс; при b =0 прямая совпадает с осью ординат.) Уравнение прямой с угловым коэффициентом k — это уравнение прямой, записанное в виде y = kx + l . Если прямая проходит через точки А( x 1 ; y 1 ) и В( x 2 ; y 2 ), то │ k │ равен тангенсу острого угла, образованного прямой с осью абсцисс; l — ордината точки пересечения прямой с осью ординат. Если точка А( х;у ) лежит на окружности радиуса R с центром в начале координат и угол a отложен от положительной полуоси Ох в верхнюю плоскость, то Для любого угла a , 0 °
Слайд 35
Движение.
Слайд 36
Движение- это преобразование одной фигуры в другую, если оно сохраняет расстояние между точками, т.е. переводит любые две точки Х, Y одной фигуры в точки Х1, Y 1 другой фигуры так, что Х Y = Х1 Y 1. Точка Х1, симметричная точке Х относительно точки О,- это конец Х1 отрезка ОХ1, отложенного на продолжении отрезка ОХ на точку О, причем ОХ1=ОХ. Преобразование симметрии относительно точки О- это преобразование фигуры F в фигуру F 1, при котором каждая ее точка Х переходит в точку Х1, симметричную относительно данной точки О. Преобразование симметрии относительно точки является движением. При симметрии относительно начала координат О(0;0) любая точка М( х;у ) переходит в точку М1(- х;-у ). Точка Х1 симметричная точке Х относительно прямой с- это конец Х1 отрезка АХ1, отложенного на продолжении перпендикуляра ХА к прямой с за точку А, причем АХ1=АХ. Если точка Х лежит на прямой с, то симметричная ей точка есть сама точка Х. Преобразование симметрии относительно прямой с- это преобразование фигуры F в фигуру F 1, при котором каждая ее точка Х переходит в точку Х1, симметричную относительно данной прямой с. Преобразование симметрии относительно прямой является движением. X Y F X’ Y’ F’ O X X’ O Y Y’ X X’ F F’ M( x;y ) M(-x;-y) O X X’ F F’
Слайд 37
При симметрии относительно оси абсцисс любая точка М( х;у ) фигуры F переходит в точку М 1 ( х;-у ). При симметрии относительно оси ординат любая точка М( х;у ) фигуры F переходит в точку М2(- х;у ). Поворот плоскости около данной точки — это движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении(угол поворота). Поворот фигуры — это преобразование фигуры при повороте плоскости. Параллельный перенос – это преобразование фигуры, при котором произвольная ее точка М(Х;У) переходит в точку М 1 ( х+а;у+ b ). Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. При параллельном переносе прямая переходит в параллельную прямую (или в себя). М( х;у ) М 1 ( х;-у ) М 2 (- х;у ) Х Х ’ а О М М ’
Слайд 38
Две одинаково направленные (сонаправленные) полупрямые – это полупрямые, которые совмещаются параллельным переносом (т.е. существует параллельный перенос, который переводит одну полупрямую в другую). Если прямые a и b одинаково направлены и полупрямые b и c одинаково направлены, то полупрямые a и c тоже одинаково направлены. Две противоположно направленные полупрямые- это полупрямые, каждая из которых одинаково направлена с полупрямой, дополнительной к другой. Равные фигуры – это фигуры, одна из которых движением переводится в другую. a b c
Слайд 39
Векторы.
Слайд 40
Вектор- это направленный отрезок. Его обозначают буквами Абсолютная величина( модуль) вектора – это длина отрезка, изображающего этот вектор. Его обозначают Одинаково направленные векторы – это векторы, соответствующие полупрямые которых одинаково направлены. Противоположно направленные векторы – это векторы, соответствующие полупрямые которых противоположно направлены. Нулевой вектор – это вектор, начало и конец которого совпадают. Равные векторы – это векторы, которые могут быть совмещены параллельным переносом. Равные векторы одинаково направлены и равны по абсолютной величине. Координаты вектора , где А(х1;у1), В(х2;у2),- это числа (х2-х1), (у2-у1), т.е. Равные векторы имеют равные координаты. A B C A D B М К Р F C A D B А(х1;у1) В(х2;у2)
Слайд 41
Абсолютная величина вектора Абсолютная величина(модуль) вектора вычисляется по формуле , где А(х1;у1), В(х2;у2) вычисляются по формуле Абсолютная величина нулевого вектора равна 0. Сумма двух векторов и – это вектор , координаты которого равны: и . Каковы бы ни были точки А,В и С, имеет место векторное равенство Правило треугольника для построения суммы произвольных векторов : и От произвольной точки М откладываем вектор , равный вектору О т точки К откладываем вектор , равный вектору . Вектор равен сумме векторов Правило параллелограмма для построения суммы произвольных векторов : и Откладываем от точки М( общее начало) векторы и , равные соответственно векторам и . Достраиваем полученную фигуру до параллелограмма М N РК. Вектор (диагональ параллелограмма) равен сумме данных векторов и А(х1;у1) В(х2;у2) А В С М К Р N
Слайд 42
Разность векторов и — это вектор , который в сумме с вектором дает вектор : Откладываем от одной точки М векторы Правило треугольника для построения разности произвольных векторов : и и , соответственно равные векторам и . Вектор (указываем первый вектор) равен разности векторов . и Произведением вектора на число m называется вектор . Абсолютная величина вектора равна Направление вектора при совпадает с направлением вектора , если m >0, и противоположно направлению вектора , если m
Слайд 43
(разложение вектора Если и – отличные от нуля неколлинеарные векторы, то любой вектор можно представить в виде по векторам и ). Скалярное произведение векторов и — это число Скалярный квадрат вектора – скалярное произведение вектора на себя: Свойства скалярного произведения векторов: 1) 2)для любых векторов верно равенство Угол между ненулевыми векторами — это угол ВАС. Угол между любыми двумя ненулевыми векторами – это угол a между равными им векторами с общим началом. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними: ( а – это угол между векторами ). 2) Свойства скалярного произведения векторов: 1) (для любых векторов). A C B
Слайд 44
Если , то Если , то Скалярное произведение ненулевых векторов равно нулю, если эти векторы перпендикулярны. Два ненулевых вектора перпендикулярны, если их скалярное произведение равно 0. (если а =90 °, то cos a =0). Единичный вектор- это вектор, абсолютная величина которого равна 1. Координатные векторы (орты) – это единичные векторы, имеющие направления положительных координатных полуосей. Любой вектор допускает разложение по координатным векторам:
Слайд 45
9 класс Подобие фигур Решение треугольников Многоугольники Площади фигур
Слайд 46
Подобие фигур.
Слайд 47
Преобразование подобия- это преобразование фигуры F 1 , при котором расстояния между точками изменяются в одно и тоже число раз. Если любые точки Х и Y переходят в точки Х 1 и Y 1 фигуры F 1 , то Х 1 Y 1 = k* Х Y(k — коэффициент подобия). F X Y F X Y Гомотетия с центром О — это преобразование фигуры F в фигуру F 1 , при котором каждая точка Х фигуры F переходит в точку Х 1 , такую, что Х 1 лежит на луче ОХ и ОХ 1 = k* ОХ( k>0 ). Гомотетия есть преобразование подобия. У подобных фигур соответственные углы равны, а соответственные стороны пропорциональны. Отношение периметров подобных треугольников равно отношению соответствующих сторон этих треугольников. А В С А ’ В ’ С ’
Слайд 48
Признаки подобия треугольников. Признак подобия по двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны. Признак подобия по двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники равны. Признак подобия по трем сторонам. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. А В С А ’ В ’ С ’ А В С А ’ В ’ С ’ А В С А ’ В ’ С ’
Слайд 49
Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по одному равному острому углу. Для подобия двух прямоугольных треугольников достаточно, чтобы их катеты были пропорциональны. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. C A B C’ A’ B’ A B C c a b h b²= c·b ’, a²= c·a ’, h²= b’·a ’ b’ a’ A B C K Если ВК — биссектриса, то АК /KC=AB/BC или AK/AB = KC/BC
Слайд 50
Плоский угол – это одна из частей плоскости, на которые разбивает её угол. Дополнительные плоские углы – это плоские углы с общими сторонами. Градусная мера плоского угла, содержащего полуплоскость а1 , равна 360°- а , где а – градусная мера дополнительного плоского угла. Центральный угол- это плоский угол с вершиной в центре окружности. Дуга окружности, соответствующая центральному углу,- это часть окружности, расположенная внутри центрального угла. Градусная мера дуги окружности – это градусная мера соответствующего центрального угла. Угол, вписанный в окружность, — это угол, вершина которого лежит в окружности, а стороны пересекают её. Угол, вписанный в окружность, равен половине соответствующего центрального угла. a- плоский угол а и а 1- дополнительные плоские углы О В А a АВ- дуга окружности, соответствующая центральному углу а О В А С Если хорды AB и CD окружности пересекаются в точке М, то произведение отрезков одной хорды (АМ и МВ) равно произведению отрезков другой хорды ( СМ и MD ). М С В А D АМ·МВ=СМ·М D
Слайд 51
М С В А D Если из точки Р к окружности проведены две секущие, пересекающие окружность в точках А, В, С и D соответственно, то РВ · РА = Р D · РС Р С А D В Угол, вершина которого лежит внутри окружности, равен половине суммы двух центральных углов, которым соответствуют дуги окружности, заключённые между их сторонами и их продолжениями. ( Градусная мера этого угла равна половине суммы градусных мер дуг, заключённых между его сторонами и их продолжениями.) Угол, вершина которого лежит вне окружности, а стороны пересекают её, равен половине разности центральных углов, которым соответствуют дуги окружности, заключённые между его сторонами. ( Градусная мера этого угла равна половине разности градусных мер дуг, заключённых между его сторонами.) М С А D В Если из точки В к окружности с центром О проведены касательная АВ и хорда ВС, то ( Градусная мера этого угла равна половине градусной меры дуги, заключённой между его сторонами.) О В А С
Слайд 52
Решение треугольников.
Слайд 53
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. С А В а b с Если в треугольнике, стороны которого равны a , b , c , выполнено условие: 1) a ²+ b ²> c ² , то угол, лежащий просив стороны с, острый; 2) a ²+ b ²
Слайд 54
Многоугольники.
Слайд 55
Ломаная — это фигура, которая состоит из точек А 1 , А 2 , А 3 …, А n — 1 , А n и соединяющих их отрезков А 1 А 2 , А 2 А 3 , А 3 А 4 ,…, А n -1 А n . Простая ломаная – это ломаная, которая не имеет самопересечений. Замкнутая ломаная – это ломаная, концы которой совпадают. Длина ломаной не меньше длины отрезка, соединяющего её концы. (А 1 А 2 +А 2 А 3 +А 3 А 4 +А 4 А 5 + А 5 А 6 ≥ А 1 А 6 ) А 1 А 2 А 3 А 4 А 5 А 6 Многоугольник- это простая замкнутая ломаная, соседние стороны которой не лежат на одной прямой. Плоский многоугольник ( многоугольная область) – это конечная часть плоскости, ограниченная многоугольником. Выпуклый многоугольник – это многоугольник, который лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. А 1 А 2 А 3 А 4 А 5 А 6 А 1 А 2 А 3 А 4 А 5 А 6 Сумма всех углов выпуклого n -угольника равна 180 ° ( n -2). Сумма внешних углов выпуклого n -угольника, взятых по одному при каждой вершине, равна 360 ° .
Слайд 56
Правильный многоугольник- это выпуклый многоугольник, у которого все стороны равны и все углы равны. Многоугольник, вписанный в окружность,- это многоугольник, все вершины которого лежат на некоторой окружности. Многоугольник, описанный около окружности, — это многоугольник, все стороны которого касаются некоторой окружности. n 3 4 6 R r Правильный многоугольник ( выпуклый) является вписанным в окружность и описанным около окружности. ( Эти окружности имеют один и тот же центр- центр правильного многоугольника.) r R a n a n
Слайд 57
У четырёхугольника, вписанного в окружность, сумма противолежащих углов равна 180°. Если у четырёхугольника сумма противолежащих углов равна 180°, то около него можно описать окружность. В описанном четырёхугольнике суммы противолежащих сторон равны. АВ+С D =А D +ВС Если в выпуклом четырёхугольнике суммы противолежащих сторон равны, то в него можно вписать окружность. D C B A A B C D Правильные выпуклые n -угольники подобны. У правильных n -угольников отношения периметров, радиусов вписанных и радиусов описанных окружностей равны. F 1 a 1 r 1 R 1 F 2 a 2 r 2 R 2 C R C 1 R 1 O O 1 Отношение длины окружности к её диаметру не зависит от окружности ( оно одно и то же для любых окружностей). С- длина окружности π (пи) 3,14- иррациональное число.
Слайд 58
Длина дуги окружности радиуса R , отвечающей центральному углу в n° равна n° R R O B A Радианная мера угла — это отношение длины соответствующей дуги к радиусу окружности. Радиан- это единица радианной меры угла. Угол в один радиан- это угол, длина соответствующей дуги которого равна длине радиуса. Радианная мера угла получается из градусной умножением на O A B
Слайд 59
Площади фигур.
Слайд 60
Простая фигура- это фигура, которую можно разбить на конечное число треугольников. Площадь простой фигуры- это положительная величина, численное значение которой обладает следующими свойствами: 1)Равные фигуры имеют равные площади. 2)Площадь фигуры, разбитой на простые фигуры, равна сумме площадей её частей. 3)Площадь квадрата со стороной, равной единице измерения, равна единице. Равновеликие фигуры – это фигуры, площади которых равны. Равносоставленные фигуры – это фигуры, которые можно разбить на конечное число попарно равных фигур. Равносоставленные фигуры являются равновеликими. Площади подобных фигур относятся как квадраты их линейных размеров.
Слайд 62
Вывод: Работая над составлением данного пособия, я ставила перед собой цель помочь выпускникам 9 классов в изучении и усвоении ими основных теоретических фактов в области геометрии. А насколько результативным является составленное мною пособие покажет предстоящий экзамен.
Слайд 63
Использованная литература: А.В. Погорелов геометрия 7-9 класс учебник для общеобразовательных организаций. Ю.П. Дудницын геометрия рабочая тетрадь 7 класс учебное пособие для общеобразовательных организаций Ю.П. Дудницын геометрия рабочая тетрадь 8 класс учебное пособие для общеобразовательных организаций Ю.П. Дудницын геометрия рабочая тетрадь 9 класс учебное пособие для общеобразовательных организаций
Ключевые понятия по геометрии для подготовки к ОГЭ
Ключевые понятия по геометрии при подготовке к ОГЭ
Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
У равных дуг равны и хорды.
Дуги, заключённые между параллельными хордами, равны.
Свойства касательной к окружности
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
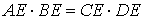
Если из точки, взятой вне окружности, проведены к окружности секущая и касательная, то произведение секущей на её внешнюю часть равно квадрату касательной.
Если из точки, взятой вне окружности, проведены к окружности секущие, то произведение каждой секущей на её внешнюю часть есть число постоянное для всех этих секущих
Угол между хордой и касательной
Угол, образованный хордой и касательной, имеющими общую точку на окружности, равен половине дуги, заключенной между его сторонами.

Свойства вписанного угла окружности.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность (диаметр) – прямой.
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от хорды.
Вписанные углы, опирающиеся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от хорды.
Свойства биссектрисы угла треугольника
Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
Свойства биссектрисы параллелограмма
Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны
Свойства прямоугольного треугольника
В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
Если в треугольнике медиана равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.
В прямоугольном треугольнике радиус вписанной окружности вычисляется по формуле
 , где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.
, где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.
Свойства медианы треугольника
В треугольнике медианы пересекаются в одной точки и делятся этой точкой в отношении 2:1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника, а три медианы – на шесть равновеликих треугольников.
Если О – точка пересечения медиан треугольника АВС, то S(ABC)=3S(AOB)=3S(AOC)=3S(BOC).
Свойства элементов трапеции
Во всякой трапеции:
Середины боковых сторон и середины диагоналей лежат на одной прямой
Средняя линия трапеции равна полусумме оснований; отрезок, соединяющий середины диагоналей, равен полуразности оснований
Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой
Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении OX:OY=BC:AD
Биссектриса угла трапеции отсекает от нее равнобедренный треугольник
Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны и точка их пересечения лежит на средней линии трапеции
В описанной около окружности трапеции:
Сумма оснований равна сумме боковых сторон
Полусумма боковых сторон равна средней линии
Если трапеция равнобедренная, то ее боковая сторона равна средней линии, высота трапеции равна среднему геометрическому ее оснований
Отрезки, соединяющие центр окружности, вписанной в трапецию, с вершинами трапеции, попарно перпендикулярны
Диаметр вписанной в трапецию окружности является высотой трапеции
Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой – их полусумме, т.е. равен средней линии трапеции.
S(ABC)=S(DBC)
S(ABD)=S(ACD)
S(ABO)=S(COD)
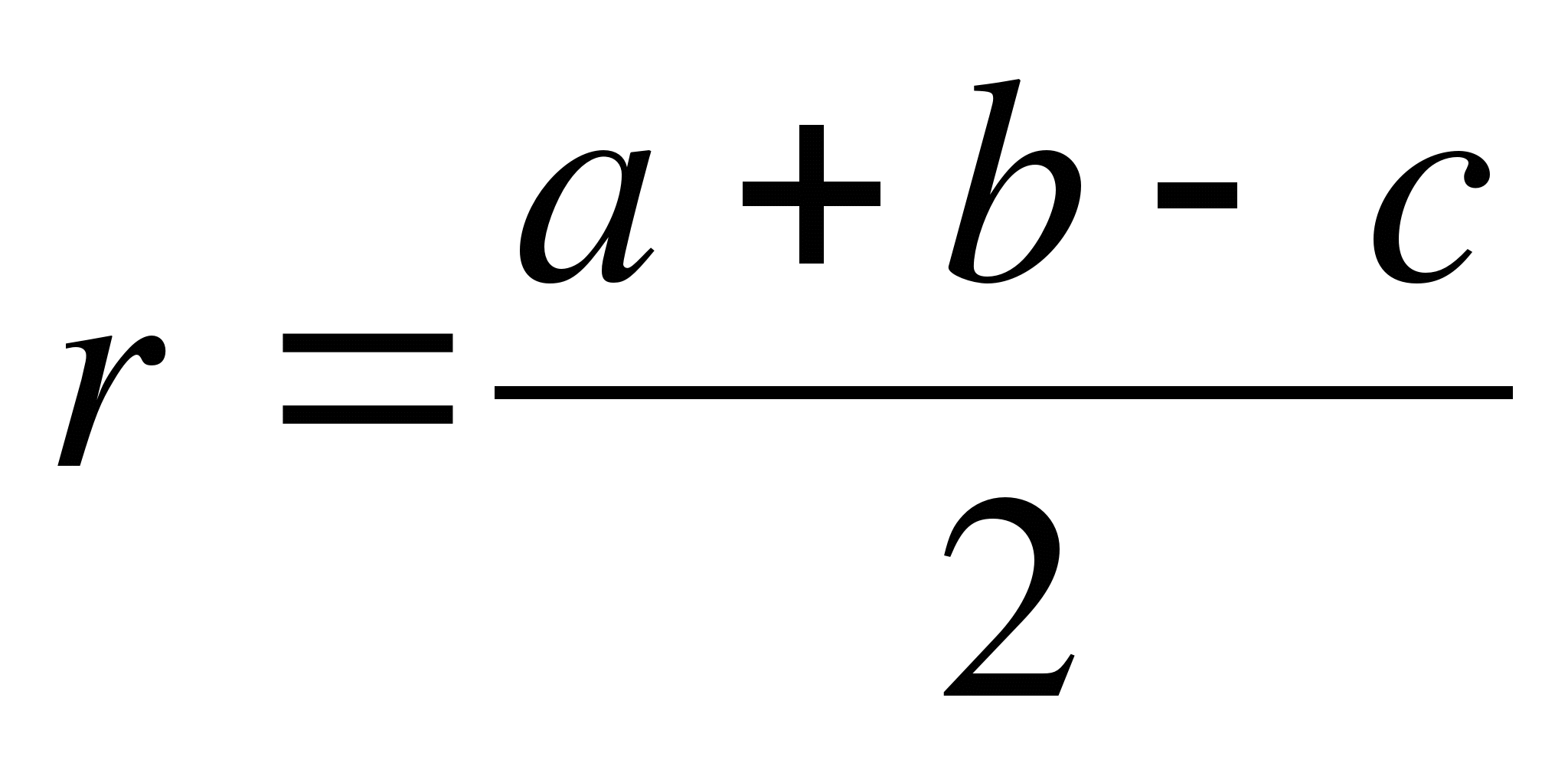 , где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.
, где a, b – катеты, c –гипотенуза прямоугольного треугольника АВС.