Онлайн-подготовка к ЕГЭ по математике
Приближается пора экзаменов, и самое время начать активную подготовку. На этой странице вы найдете подборки материалов и видеоуроки от ведущих педагогов.
Для успешных результатов очень важно заниматься систематически, но при этом соблюдать баланс. Не тратьте много времени на прорешивание вариантов, потому что занятия должны быть тематическими. И не стоит забывать про задачи, которые даются вам легко – их решение позволит избежать случайных ошибок и придаст вам уверенности на экзамене.
Эксперты советуют уделять 15 минут в день простым заданиям, а остальное время потратить на выполнение домашних заданий к урокам.
Используйте для подготовки проверенные материалы ФИПИ, привычные учебники, рекомендации учителей и другие авторитетные источники. И помните, что даже 15 минут тренировки в день в итоге окажутся полезными на экзаменах.
Каждый урок включает: видеозапись, теоретические материалы и задачи.
ЕГЭ по математике. Базовый уровень.
Арифметика. Задание 1.
Видео Текстовый урок Тест
Преобразование показательных выражений. Задание 2.
Видео Текстовый урок Тест
Задачи на доли, проценты, отношения. Задание 3.
Видео Текстовый урок Тест
Вычисления по формуле. Задание 4.
Видео Текстовый урок Тест
Преобразование выражений. Задание 5.
Видео Текстовый урок Тест
Арифметические задачи. Задание 6.
Видео Текстовый урок Тест
Уравнения. Задание 7.
Видео Текстовый урок Тест
Наглядная планиметрия. Задание 8.
Видео Текстовый урок Тест
Сравнение величин. Задание 9.
Видео Текстовый урок Тест
Теория вероятностей. Задание 10.
Видео Текстовый урок Тест
Графики, диаграммы и таблицы. Задание 11.
Видео Текстовый урок Тест
Наилучший выбор. Задание 12.
Задание 12.
Видео Текстовый урок Тест
Наглядная стереометрия. Задание 13.
Видео Текстовый урок Тест
Функции и их графики. Задание 14.
Видео Текстовый урок Тест
Планиметрия. Задание 15.
Видео Текстовый урок Тест
Стереометрия. Задание 16.
Видео Текстовый урок Тест
Числовая ось и неравенства. Задание 17.
Видео Текстовый урок Тест
Логика. Задание 18.
Видео Текстовый урок Тест
Свойства чисел. Задание 19.
Видео Текстовый урок Тест
Алгебра и арифметика. Задание 20.
Видео Текстовый урок Тест
ЕГЭ по математике. Профильный уровень.
Арифметические задачи. Задание 1
Графики и диаграммы. Задание 2
Видео Текстовый урок Тест
Задачи на клетчатой бумаге. Задание 3
Видео Текстовый урок Тест
Теория вероятностей. Задание 4
Задание 4
Видео Текстовый урок Тест
Простейшие уравнения. Задание 5
Видео Текстовый урок Тест
Планиметрия. Задание 6
Видео Текстовый урок Тест
Планиметрия. Задание 16. Урок 1
Видео Текстовый урок Тест
Планиметрия. Задание 16. Урок 2
Видео Текстовый урок Тест
Задачи прикладного содержания. Задание 10
Видео Текстовый урок Тест
Тригонометрические уравнения. Задание 13. Урок 1
Видео Текстовый урок Тест
Тригонометрические уравнения. Задание 13. Урок 2
Видео Текстовый урок Тест
Преобразование выражений. Задание 9
Видео Текстовый урок Тест
Неравенства. Задание 15. Урок 1
Видео Текстовый урок Тест
Неравенства. Задание 15. Урок 2
Видео Текстовый урок Тест
Текстовые задачи. Задание 11
Видео Текстовый урок Тест
Задачи с экономическим содержанием. Задание 17. Урок 1
Задание 17. Урок 1
Видео Текстовый урок Тест
Задачи с экономическим содержанием. Задание 17. Урок 2
Видео Текстовый урок Тест
Стереометрия. Задание 8
Видео Текстовый урок Тест
Стереометрия. Задание 14. Урок 1
Видео Текстовый урок Тест
Стереометрия. Задание 14. Урок 2
Видео Текстовый урок Тест
Функции, заданные графиками, и их производные. Задание 7
Задачи с параметром. Задание 18. Урок 1
Видео Текстовый урок Тест
Задачи с параметром. Задание 18. Урок 2
Видео Текстовый урок Тест
Исследование функций. Задание 12
Видео Текстовый урок Тест
Авторы и методисты
Иван Валериевич Ященко, научный руководитель ЦПМ, руководитель федеральной группы разработчиков ЕГЭ по математике.
Андрей Викторович Семенов, член федеральной группы разработчиков ЕГЭ по математике, ведущий методист ЦПМ.
Иван Ростиславович Высоцкий, член федеральной группы разработчиков ЕГЭ по математике, начальник отдела ЦПМ.
Андрей Сергеевич Трепалин, член федеральной группы разработчиков ЕГЭ по математике, научный сотрудник Математического института им. В.А.Стеклова.
Екатерина Александровна Кукса
, член федеральной группы разработчиков ЕГЭ по математике, разработчик контента образовательных продуктов МЦНМО и Яндекса.Павел Иванович Самсонов, президент ассоциации учителей математики Москвы, член федеральной группы разработчиков ЕГЭ по математике.
Максим Яковлевич Пратусевич, член федеральной группы разработчиков ЕГЭ по математике, директор Президентского лицея 239.
Математические функции — Visual Basic
- Статья
- Чтение занимает 2 мин
Были ли сведения на этой странице полезными?
Хотите оставить дополнительный отзыв?
Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Отправить
Спасибо!
В этой статье
Методы System.Math класса предоставляют тригонометрические, Логарифмические и другие общие математические функции.
Комментарии
В следующей таблице перечислены методы System.Math класса. их можно использовать в программе Visual Basic:
| Метод .NET | Описание |
|---|---|
| Abs | Возвращает абсолютное значение числа. |
| Acos | Возвращает угол, косинус которого равен указанному числу. |
| Asin | Возвращает угол, синус которого равен указанному числу. |
| Atan | Возвращает угол, тангенс которого равен указанному числу. |
| Atan2 | Возвращает угол, тангенс которого равен отношению двух указанных чисел. |
| BigMul | Возвращает полное произведение 2 32-разрядных чисел. |
| Ceiling | Возвращает наименьшее целочисленное значение, которое больше или равно указанному Double . |
| Cos | Возвращает косинус указанного угла. |
| Cosh | Возвращает гиперболический косинус указанного угла. |
| DivRem | Возвращает частное от 2 32-битных или 64-битовых целых чисел со знаком, а также возвращает остаток в выходном параметре. |
| Exp | Возвращает значение e (основание натуральных логарифмов), возведенное в указанную степень. |
| Floor | Возвращает максимальное целое число, которое меньше или равно указанному Decimal Double значению или. |
| IEEERemainder | Возвращает остаток, полученный от деления указанного числа на другое заданное число. |
| Log | Возвращает натуральный (базовый e) логарифм указанного числа или логарифм указанного числа в заданном базовом массиве. |
| Log10 | Возвращает логарифм с основанием 10 указанного числа. |
| Max | Возвращает большее из двух чисел. |
| Min | Возвращает меньшее из двух чисел. |
| Pow | Возвращает указанное число, возведенное в указанную степень. |
| Round | Возвращает Decimal значение или, Double округленное до ближайшего целого значения или до указанного числа цифр дробной части. |
| Sign | Возвращает Integer значение, указывающее знак числа. |
| Sin | Возвращает синус указанного угла. |
| Sinh | Возвращает гиперболический синус указанного угла. |
| Sqrt | Возвращает квадратный корень из указанного числа. |
| Tan | Возвращает тангенс указанного угла. |
| Tanh | Возвращает гиперболический тангенс указанного угла. |
| Truncate | Вычисляет целую часть указанного Decimal Double числа или. |
в следующей таблице перечислены методы System.Math класса, которые не существуют в платформа .NET Framework но добавляются в .NET Standard или .net Core:
| Метод .NET | Описание | Доступно в |
|---|---|---|
| Acosh | Возвращает угол, гиперболический косинус которого равен указанному числу. | Начиная с .NET Core 2,1 и .NET Standard 2,1 |
| Asinh | Возвращает угол, гиперболический синус которого равен указанному числу. | Начиная с .NET Core 2,1 и .NET Standard 2,1 |
| Atanh | Возвращает угол, гиперболический тангенс которого равен указанному числу. | Начиная с .NET Core 2,1 и .NET Standard 2,1 |
| BitDecrement | Возвращает ближайшее самое маленькое значение, которое меньше, чем x. | Начиная с .NET Core 3,0 |
| BitIncrement | Возвращает ближайшее самое большое значение, превышающее x. | Начиная с .NET Core 3,0 |
| Cbrt | Возвращает кубический корень из указанного числа. | Начиная с .NET Core 2,1 и .NET Standard 2,1 |
| Clamp | Возвращает value, ограниченное диапазоном от min до max включительно. | Начиная с .NET Core 2,0 и .NET Standard 2,1 |
| CopySign | Возвращает значение с величиной x и знаком y. | Начиная с .NET Core 3,0 |
| FusedMultiplyAdd | Возвращает (x * y) + z, округленное как одна операция ternary. | Начиная с .NET Core 3,0 |
| ILogB | Возвращает целочисленный логарифм с основанием 2 указанного числа. | Начиная с .NET Core 3,0 |
| Log2 | Возвращает логарифм с основанием 2 указанного числа. n, вычисленное эффективно. n, вычисленное эффективно. | Начиная с .NET Core 3,0 |
Чтобы использовать эти функции без уточнения, импортируйте System.Math пространство имен в проект, добавив следующий код в начало исходного файла:
Imports System.Math
Пример-ABS
В этом примере используется Abs метод Math класса для расчета абсолютного значения числа.
Dim x As Double = Math.Abs(50.3)
Dim y As Double = Math.Abs(-50.3)
Console.WriteLine(x)
Console.WriteLine(y)
' This example produces the following output:
' 50.3
' 50.3
Пример — Atan
В этом примере используется Atan метод Math класса для вычисления значения PI.
Public Function GetPi() As Double
' Calculate the value of pi.
Return 4.0 * Math.Atan(1.0)
End Function
Примечание
System.MathКласс содержит Math.PI постоянное поле. Его можно использовать вместо вычисления.
Пример — COS
В этом примере используется Cos метод Math класса для возврата косинуса угла.
Public Function Sec(angle As Double) As Double
' Calculate the secant of angle, in radians.
Return 1.0 / Math.Cos(angle)
End Function
Пример — exp
В этом примере используется Exp метод класса, Math возвращающий значение e, возведенное в степень.
Public Function Sinh(angle As Double) As Double
' Calculate hyperbolic sine of an angle, in radians.
Return (Math.Exp(angle) - Math.Exp(-angle)) / 2.0
End Function
Пример журнала
В этом примере используется Log метод Math класса для возврата натурального логарифма числа.
Public Function Asinh(value As Double) As Double
' Calculate inverse hyperbolic sine, in radians.
Return Math.Log(value + Math.Sqrt(value * value + 1.0))
End Function
Пример-Round
В этом примере Round метод Math класса используется для округления числа до ближайшего целого числа.
Dim myVar2 As Double = Math.Round(2.8)
Console. WriteLine(myVar2)
' The code produces the following output:
' 3
WriteLine(myVar2)
' The code produces the following output:
' 3
Пример — подпись
В этом примере используется Sign метод Math класса для определения знака числа.
Dim mySign1 As Integer = Math.Sign(12)
Dim mySign2 As Integer = Math.Sign(-2.4)
Dim mySign3 As Integer = Math.Sign(0)
Console.WriteLine(mySign1)
Console.WriteLine(mySign2)
Console.WriteLine(mySign3)
' The code produces the following output:
' 1
' -1
' 0
Пример — Sin
В этом примере используется Sin метод Math класса для возврата синуса угла.
Public Function Csc(angle As Double) As Double
' Calculate cosecant of an angle, in radians.
Return 1.0 / Math.Sin(angle)
End Function
Пример. Sqrt
В этом примере используется Sqrt метод Math класса для вычисления квадратного корня числа.
Dim mySqrt1 As Double = Math.Sqrt(4)
Dim mySqrt2 As Double = Math.Sqrt(23)
Dim mySqrt3 As Double = Math.Sqrt(0)
Dim mySqrt4 As Double = Math. Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN
Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN
Пример — Tan
В этом примере используется Tan метод Math класса для возврата тангенса угла.
Public Function Ctan(angle As Double) As Double
' Calculate cotangent of an angle, in radians.
Return 1.0 / Math.Tan(angle)
End Function
См. также
Страницы — Заданные вопросы
|
↓ Наиболее популярные вопросы ↓ | |
|
Давно закончили Омский филиал или отчислились, но не забрали документы? |
Образец заявления находится здесь. Отправьте подписанное и отсканированное заявление на адрес [email protected] |
|
Вы отчислились и вам нужна справка об обучении? |
Образец заявления находится здесь. Отправьте подписанное и отсканированное заявление на адрес [email protected] |
|
Как перевестись в Омский филиал? Или восстановиться после отчисления? |
Подробная информация о восстановлениях и переводах, образец заявления, расположены на странице |
|
Какие документы необходимо предоставить для оформления государственной социальной стипендии? |
Подробная информация расположена на странице |
|
Как подать документы для поступления в Финансовый университет? |
Подача документов в дистанционной форме через личный кабинет |
|
Для поступления требуется медицинская справка? |
Для поступления справка 086у не нужна. |
|
Для поступления в ваш ВУЗ нужно сдавать какие-то внутренние экзамены или достаточно результатов ЕГЭ? |
ЕГЭ — это тоже вступительные испытания. После 11 класса вы поступаете по результатам ЕГЭ, Дополнительные вступительные испытания для выпускников школ Финансовый университет не проводит. |
|
ЕГЭ по математике нужно сдавать базового или профильного уровня? |
В том случае, если в перечне вступительных испытаний на образовательную программу указан ЕГЭ по математике, абитуриенту необходимо представить результаты ЕГЭ профильного уровня. |
|
Есть ли возможность поступления на базе среднего специального образования (без ЕГЭ, по внутреннему экзамену) |
На базе среднего специального образования вы
можете поступать на первый курс на общих основаниях по результатам внутренних испытаний университета. |
|
Какой проходной балл в университет? |
Проходные баллы на бюджет и на места с оплатой стоимости обучения ежегодно формируют сами абитуриенты в рамках приёмной кампании текущего года. С началом новой приёмной кампании статистика приёма прошлого года теряет свою актуальность, так как проходные баллы каждого года уникальны и не имеют тенденции повторяться. Статистика приема прошлых лет. |
Приемная
комиссия Омского филиала Финуниверситета!
Адрес: ул. Партизанская, д. 6
Телефон +7-983-524-16-94 (WhatsApp, Viber, Telegram)
+7 (3812) 23-15-06, 23-32-37
Группа VK: @club194580181
График работы:
понедельник – четверг: с 10:00 — 17:00
пятница: с 10:00 — 16:30
суббота: с 10:00 — 13:00
воскресенье: выходной
Способы задания последовательностей | Математика, которая мне нравится
Определение. Последовательностью (бесконечной) называется функция, область определения которой — множество натуральных чисел.
Последовательностью (бесконечной) называется функция, область определения которой — множество натуральных чисел.
Обозначения. .
Способы задания последовательностей
I. Задается формула или правило вычисления n-го члена последовательности по значению .
Пример.
II. Рекуррентный способ задания последовательности. В этом случае задается формула или правило, позволяющая вычислить каждый член последовательности, если известно определенное число предыдущих членов. Если каждый член, начиная с -го, выражен через предыдущих, то нужно, кроме того, задать первых членов последовательности.
Пример. Арифметическая прогрессия задается рекуррентным соотношением вида Задан первый член арифметической прогрессии . Число называется разностью прогрессии.
Пример. Геометрическая прогрессия задается рекуррентным соотношением вида Задан первый член геометрической прогрессии . Число называется знаменателем прогрессии.
Число называется знаменателем прогрессии.
Пример. Последовательность Фибоначчи.
Леонардо Пизанский (1180–1240) имел прозвище Фибоначчи, т.е. “сын Боначчо” (Боначчо — добродушный). Основные достижения Леонардо Пизанского изложены в его сочинениях “Книга абака” и “Практика геометрии”.
К последовательности чисел Фибоначчи привела следующая задача:
Некто поместил пару кроликов в некоем месте, огороженном со всех строн стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года. Причем природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождаются кролики со второго месяца.
Пример. Возвратные последовательности — последовательности, определенные рекуррентными соотношениями вида при заданных и .
Н.Н. Петров, А.Я. Нарманов. Многократная поимка заданного числа убегающих в задаче с дробными производными и простой матрицей .
 {(\alpha)}f$ — производная по Капуто порядка $\alpha $ функции $f.$ Множество допустимых управлений $V$ — строго выпуклый компакт, $a$ — вещественное число. Целью группы преследователей является поимка не менее $q$ убегающих, причем каждого убегающего должны поймать не менее чем $r$ различных преследователей, при этом моменты поимки могут не совпадать. Терминальные множества — начало координат. В предположении, что убегающие используют программные стратегии, а каждый преследователь ловит не более одного убегающего, в терминах начальных позиций получены достаточные условия разрешимости задачи преследования. При исследовании в качестве базового используется метод разрешающих функций, позволяющий получить достаточные условия разрешимости задачи сближения c одним убегающим за некоторое гарантированное время. Для доказательства основного результата используется теорема Холла о системе различных представителей.
{(\alpha)}f$ — производная по Капуто порядка $\alpha $ функции $f.$ Множество допустимых управлений $V$ — строго выпуклый компакт, $a$ — вещественное число. Целью группы преследователей является поимка не менее $q$ убегающих, причем каждого убегающего должны поймать не менее чем $r$ различных преследователей, при этом моменты поимки могут не совпадать. Терминальные множества — начало координат. В предположении, что убегающие используют программные стратегии, а каждый преследователь ловит не более одного убегающего, в терминах начальных позиций получены достаточные условия разрешимости задачи преследования. При исследовании в качестве базового используется метод разрешающих функций, позволяющий получить достаточные условия разрешимости задачи сближения c одним убегающим за некоторое гарантированное время. Для доказательства основного результата используется теорема Холла о системе различных представителей.Ключевые слова: дифференциальная игра, групповое преследование, многократная поимка, преследователь, убегающий, дробная производная
СПИСОК ЛИТЕРАТУРЫ
1. Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.
Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.
2. Чикрий A.A. Конфликтно управлямые процессы. Киев: Наук. думка, 1992. 384 с.
3. Григоренко Н.Л. Математические методы управления несколькими динамическими процессами. М.: Изд-во МГУ, 1990. 197 c.
4. Благодатских А.И., Петров Н.Н. Конфликтное взаимодействие групп управляемых объектов. Ижевск: Изд-во Удмурт. ун-та, 2009. 266 с.
5. Эйдельман С.Д., Чикрий А.А. Динамические задачи сближения для уравнений дробного порядка// Укр. мат. журн. 2000. Т. 52. № 11. С. 1566–1583.
6. Чикрий А.А., Матичин И.И. Игровые задачи для линейных систем дробного порядка// Тр. Ин-та математики и механики УрО РАН. 2009. Т. 15. № 3. С. 262–278.
7. Пшеничный Б.Н. Простое преследование несколькими объектами // Кибернетика. 1976. № 3. C. 145–146.
8. Григоренко Н.Л. Игра простого преследования-убегания группы преследователей и одного убегающего // Вестн. МГУ. Сер. вычислит. математика и кибернетика. 1983. № 1. C. 41–47.
Сер. вычислит. математика и кибернетика. 1983. № 1. C. 41–47.
9. Петров Н.Н., Прокопенко В.А. Об одной задаче преследования группы убегающих //Дифференц. уравнения. 1987. Т. 23, № 4. С. 724–726.
10. Сахаров Д.В. О двух дифференциальных играх простого группового преследования // Вестн. Удмурт. ун-та. Математика. Механика. Компьютерные науки. 2012. № 1. С. 50–59.
11. Благодатских А.И. Одновременная многократная поимка в задаче простого преследования // Прикл. математика и механика. 2009. Т. 73, вып. 1. C. 54–59.
12. Петров Н.Н. Многократная поимка в примере Л. С. Понтрягина с фазовыми ограничениями // Прикл. математика и механика. 1997. Т. 61, вып. 5. C. 747–754.
13. Петров Н.Н., Соловьева Н.А. Многократная поимка в рекуррентном примере Л. С. Понтрягина // Автоматика и телемеханика. 2016. № 5. С. 128–135.
14. Благодатских А.И. Одновременная многократная поимка в конфликтно управляемом процессе // Прикл. математика и механика. 2013. Т. 77, вып. 3. C. 433–440.
Т. 77, вып. 3. C. 433–440.
15. Петров Н.Н. Многократная поимка в одной задаче группового преследования с дробными производными // Тр. Ин-та математики и механики УрО РАН. 2018. Т. 24, № 1. С. 156–164.
16. Петров Н.Н., Соловьева Н.А. К задаче группового преследования в линейных рекуррентных дифференциальных играх // Современная математика и ее приложения. Тематические обзоры. 2016. Т. 132. С. 81–85.
17. Петров Н.Н. Об одной задаче преследования группы убегающих // Автоматика и телемеханика. 1996. №. 6. С. 48–54.
18. Петров Н.Н., Нарманов А.Я. Многократная поимка заданного числа убегающих в задаче простого преследования// Вестн. Удмурт. ун-та. Математика. Механика. Компьютерные науки. 2018. Т. 28, вып. 2. С. 193–198.
19. Caputo M. Linear model of dissipation whose q is almost frequency independent-II // Geophys. R. Astr. Soc. 1967. No. 13. P. 529–539.
20. Чикрий А.А., Матичин И.И. Об аналоге формулы Коши для линейных систем произвольного дробного порядка// Доповiдi Нацiональноi академii наук Украiни. 2007. № 1. C. 50–55.
2007. № 1. C. 50–55.
21. Джрбашян М.М. Интегральные преобразования и представления функций в комплексной области. М.: Наука, 1966.
22. Попов А.Ю., Седлецкий А.М. Распределение корней функции Миттаг — Леффлера // Современная математика. Фундаментальные направления. 2011. Т. 40. С. 3–171.
23. Холл М. Комбинаторика. М.: Мир. 1970. 424 с.
Поступила 6.05.2019
После доработки 19.06.2019
Принята к публикации 24.06.2019
Петров Николай Никандрович
д-р физ.-мат. наук, профессор
директор
Институт математики, информационных технологий и физики,
Удмуртский государственный университет, г. Ижевск
e-mail: [email protected]
Нарманов Абдигаппар Якубович
д-р физ.-мат. наук, профессор
профеcсор кафедры геометрии
Национальный университет Узбекистана им. Мирзо Улугбека, г. Ташкент
e-mail: [email protected]
Ссылка на статью: Н.Н. Петров, А.Я. Нарманов. Многократная поимка заданного числа убегающих в задаче с дробными производными и простой матрицей // Тр. {(\alpha)}f$ is the Caputo fractional derivative of order $\alpha$ of the function $f$, the set of admissible controls $V$ is strictly convex and compact, and $a$ is a real number. The aim of the group of pursuers is to capture at least $q$ evaders; each evader must be captured by at least $r$ different pursuers, and the capture moments may be different. The terminal sets are the origin. Assuming that the evaders use program strategies and each pursuer captures at most one evader, we obtain sufficient conditions for the solvability of the pursuit problem in terms of the initial positions. Using the method of resolving functions as a basic research tool, we derive sufficient conditions for the solvability of the approach problem with one evader in some guaranteed time. Hall’s theorem on a system of distinct representatives is used in the proof of the main theorem.
{(\alpha)}f$ is the Caputo fractional derivative of order $\alpha$ of the function $f$, the set of admissible controls $V$ is strictly convex and compact, and $a$ is a real number. The aim of the group of pursuers is to capture at least $q$ evaders; each evader must be captured by at least $r$ different pursuers, and the capture moments may be different. The terminal sets are the origin. Assuming that the evaders use program strategies and each pursuer captures at most one evader, we obtain sufficient conditions for the solvability of the pursuit problem in terms of the initial positions. Using the method of resolving functions as a basic research tool, we derive sufficient conditions for the solvability of the approach problem with one evader in some guaranteed time. Hall’s theorem on a system of distinct representatives is used in the proof of the main theorem.
Keywords: differential game, group pursuit, multiple capture, pursuer, evader, fractional derivative
Received May 6, 2019
Revised June 19, 2019
Accepted June 24, 2019
Funding Agency: The research of the first and second authors was supported by the Russian Federation for Basic Research (project no. 18-51-41005) and by Grant MRU-10-17 (Uzbekistan), respectively.
18-51-41005) and by Grant MRU-10-17 (Uzbekistan), respectively.
Nikolai Nikandrovich Petrov, Dr. Phys.-Math. Sci., Prof., Udmurt State University, Izhevsk, 426034 Russia, e-mail: [email protected]
Abdigappar Yakubovich Narmanov, Dr. Phys.-Math. Sci., Prof., National University of Uzbekistan, Tashkent, 100174 Uzbekistan, e-mail: [email protected]
Cite this article as: N.N. Petrov, A.Ya. Narmanov. Multiple capture of a given number of evaders in a problem with fractional derivatives and a simple matrix, Trudy Instituta Matematiki i Mekhaniki URO RAN, 2019, vol. 25, no. 3, pp. 188–199.
Отцу девятилетней студентки МГУ задали «самый главный вопрос»
У отца девятилетней студентки факультета психологии МГУ им. М. В. Ломоносова Евгения Теплякова спросили, как организовано обучение девочки в однокомнатной квартире, где также обитают ее много численные братья и сестры. Данным фактом поинтересовался основатель проекта «Альтернативное образование в России», психолог, специалист по домашнему обучению Алексей Семенычев. Это один из главных вопросов к родителям девочки, заявил он изданию Lenta.ru.
Это один из главных вопросов к родителям девочки, заявил он изданию Lenta.ru.
По его словам, вопросом о том, как Тепляковы учат пятерых детей в одной комнате, задаются многие родители, чьи дети также обучаются в домашних условиях и которым известно, насколько непросто организовать обучение даже двух детей.
«Я бы очень хотел спросить родителей: как вы решали проблемы с опытами по химии, какими электронными сервисами пользовались, какой учебник по математике был у вас, наконец, где у вас были учебные места для ваших детей? Тепляков почему-то не отвечает на эти простые вопросы», — сказал Семенычев.
Эксперт полагает, что девочку можно было отдать в школу для одаренных детей, где педагоги работают с юными гениями еще со времен СССР. Также ребенок с хорошей памятью мог бы учиться в математической школе, допустил Семенычев. Он согласился с мнением директора московской школы № 109 Евгения Ямбурга, усомнившегося в верности решения Тепляковых отправить дочь в МГУ. Педагог сравнил таких детей с фигуристами, которые показывают свои лучшие результаты в 14-15 лет, а затем их уровень снижается.
В 2021 году восьмилетняя московская школьница сдала ЕГЭ и поступила на коммерческое отделение факультета психологии МГУ. Во время сдачи зимней сессии у семьи девочки возник конфликт с представителями факультета. Отец ребенка сообщил, что преподаватели специально «завалили» его дочь не экзамене. В результате инцидента Евгений Тепляков напал на заведующего кафедрой факультета.
Ранее в МГУ заявили о беспрецедентном давлении на факультет психологии со стороны семьи девятилетней студентки вуза. Родственники девочки, подчеркнули в университете, продолжают публиковать порочащую честь учебного учреждения информацию.
Поделиться статьей
«Учитель не должен обращать внимание на зарплату». Рассказываем, что известно о новом министре образования
Сегодня Александр Лукашенко назначил нового министра образования. Им стал Андрей Иванец. (Напомним, предыдущий глава ведомства Игорь Карпенко в середине декабря стал председателем Центризбиркома). Zerkalo.io собрало интересные факты из его биографии.
Успешный ученый и самый молодой доктор наук
Андрей Иванцу 37 лет. Он родился в Минске.
В 2006 году окончил БГУ. В том же году начал работать в Институте общей и неорганической химии НАН Беларуси. С 2011 года стал заведующим лабораторией.
С 2013 года Иванец является председателем Совета молодых ученых НАН Беларуси. Кроме того, известно, что новый министр образования в 33 года стал самым молодым доктором наук в Беларуси.
В 2016 году Иванец стал заместителем директора по научной работе в своем Институте. Через три года — главным ученым секретарем НАН Беларуси. Одновременно с 2018 года он является профессором Института подготовки научных кадров Национальной академии наук.
Иванец — автор более 180 научных работ, четырех патентов и одной монографии. Новый министр был лауреатом президентской стипендии аспирантам и талантливым молодым ученым, стипендиатом Всемирной федерации ученых.
Фото: портал «Белнефтехимия»Представитель Лукашенко во время президентской кампании
Андрей Иванец уже долгое время является членом Республиканского Совета РОО «Белая Русь».
Он был доверенным лицом Александра Лукашенко во время президентской кампании 2020 года. На одной из встреч с белорусами ученый отмечал, что «перемены гражданам предлагают лица с уголовным прошлым». Им же была озвучена информация о 20 несовершеннолетних задержанных одной из акций в Минске. Тогда Иванец упрекнул альтернативных кандидатов в том, что именно эта цифра показывает «зрелость гражданского общества».
Кроме того, он убеждал присутствующих, что задержания после 14 и 15 июля были полностью правомерными, поскольку преследовали целью восстановление «законности» и «общественного порядка». Он отмечал, что «обстановку внутри страны пытаются расшатать не только из-за рубежа, но и внутри страны».
По информации правозащитников, Иванец заявлял, что Парк высоких технологий является исключительно заслугой Лукашенко, а Валерий Цепкало должен быть благодарен за представленную ему честь возглавлять ПВТ на протяжении нескольких лет.
Кроме этого, Иванец отмечал, что «Беларусь не идеальная страна, есть сложности, есть вопросы, но только мы вместе сможем их решить». Он также рассказывал, что правоохранители применяют силу по отношению к протестующим не на пустом месте — «вам просто никто не показывает провокаций, с которых это все начинается».
Он также рассказывал, что правоохранители применяют силу по отношению к протестующим не на пустом месте — «вам просто никто не показывает провокаций, с которых это все начинается».
При этом, когда доверенному лицу Лукашенко задали вопрос о зарплатах педагогов, Андрей Иванец сказал: «Учитель не должен обращать внимание на свою зарплату, поскольку профессия учителя является призванием».
Андрей Иванец (слева). Фото: «Белая Русь»Критик протестов 2020 годаПосле начала протестов в Беларуси в сентябре около полусотни российских ученых поддержали политические акции в нашей стране. Тогда им ответил Президиум Национальной академии наук Беларуси. Напомним, в это время Иванец был его главным ученым секретарем.
— К большому сожалению, нам стало известно о так называемом заявлении группы российских ученых «О Беларуси». Информируем вас, что заявление полностью построено на недостоверных фактах, полученных из электронных СМИ, которые, как известно, часто показывают сведения исходя из своих интересов — преподнести все односторонне и «раздуть из мухи слона».
— В заявлении говорится об имевших место издевательствах. Но не является ли издевательством агрессивное навязывание воли малой части огромному большинству. Не является ли насилием к своему народу так называемая уличная демократия, когда толпа, действующая по методичкам цветных революций, чинит беззаконие, провоцирует деятелей правопорядка и открыто призывает к другим действиям, направленным на свержение законной власти, уничтожение экономики страны и взывает к западным странам о помощи, — говорилось в ответе Президиума НАН.
Кроме того, в ноябре 2020 года со старшим научным сотрудником Института общей и неорганической химии НАН Беларуси Сергеем Бесарабом, известным как автор «Блога белорусского химика», не продлили контракт. Тогда он рассказывал TUT.BY, что пришел в кабинет Андрея Иванца после упомянутого выше ответа НАН российским ученым.
— Спросил: «Андрей Иванович, вы подписали это письмо?» На что он мне с улыбкой ответил: мол, да, подписал и готов подписаться под каждым словом. После чего я сказал, что в таком случае с ним за один стол не сяду, — рассказывал изданию химик.
После чего я сказал, что в таком случае с ним за один стол не сяду, — рассказывал изданию химик.
Семьянин и спортсмен
Кроме этого, об Андрее Иванце известно, что он — многодетный отец. Об этом он рассказывал во время агитационной встречи с избирателями в июле 2020 года.
Кроме успехов в профессиональной сфере, новый министр успел отличиться и в спорте. Он — чемпион Европы и рекордсмен мира по пауэрлифтингу. По поводу своих спортивных успехов он говорил следующее:
— Человеку нужно и важно быть разносторонним, чтобы иметь несколько точек опоры в жизни. Нужно любить то, чем занимаешься, тогда и получается легко совмещать такие, на первый взгляд, несовместимые грани в жизни.
Что такое математика? | Наука
Ученик пытается решить математическую задачу. AlpamayoФото Все началось с безобидного видео в TikTok, опубликованного ученицей старшей школы по имени Грейси Каннингем. Нанося макияж и говоря в камеру, подросток задался вопросом, реальна ли математика. Она добавила: «Я знаю, что это реально, потому что мы все учимся этому в школе… но кто придумал эту концепцию?» У Пифагора, размышляет она, «не было даже водопровода — и он такой: «Позволь мне побеспокоиться о y = mx + b» — имея в виду уравнение, описывающее прямую линию на двумерной плоскости.Она задавалась вопросом, откуда все это взялось. «Я понимаю дополнение, — сказала она, — но как бы вы придумали концепцию алгебры? Для чего он вам нужен?»
Нанося макияж и говоря в камеру, подросток задался вопросом, реальна ли математика. Она добавила: «Я знаю, что это реально, потому что мы все учимся этому в школе… но кто придумал эту концепцию?» У Пифагора, размышляет она, «не было даже водопровода — и он такой: «Позволь мне побеспокоиться о y = mx + b» — имея в виду уравнение, описывающее прямую линию на двумерной плоскости.Она задавалась вопросом, откуда все это взялось. «Я понимаю дополнение, — сказала она, — но как бы вы придумали концепцию алгебры? Для чего он вам нужен?»
Кто-то повторно разместил видео в Твиттере, где оно вскоре стало вирусным. Многие комментарии были недобрыми: один человек сказал, что это «самое тупое видео», которое они когда-либо видели; другие предположили, что это свидетельствует о неудачной системе образования. Другие тем временем встали на защиту Каннингем, заявив, что ее вопросы на самом деле были довольно глубокими.
@Грейси.ham
это видео имеет смысл в моей голове, но типа ПОЧЕМУ МЫ СОЗДАЛИ ЭТОТ МАТЕРИАЛ
♬ оригинальный звук — Грейси
Математики из Корнелла и Висконсинского университета, а также философ Филип Гофф из Даремского университета в Великобритании Математик Евгения Ченг, в настоящее время научный сотрудник Чикагского института искусств, написал двухстраничный ответ и сказал, что Каннингем поднял глубокие вопросы о природе математики «очень глубоко и глубоко.
Каннингем невольно вновь разжег очень древний и неразрешенный спор в философии науки. Что именно есть математика? Это изобретено или обнаружено? И реальны ли вещи, с которыми работают математики — числа, алгебраические уравнения, геометрия, теоремы и т. д.?
Некоторые ученые очень твердо убеждены в том, что математические истины находятся «где-то там» и ждут, чтобы их открыли, — позиция, известная как платонизм. Он получил свое название от древнегреческого мыслителя Платона, который вообразил, что математические истины обитают в собственном мире — не в физическом мире, а в нефизическом царстве неизменного совершенства; мир, существующий вне пространства и времени. Роджер Пенроуз, известный британский физик-математик, убежденный платоник. В «Новый разум императора» он писал, что, по-видимому, «в этих математических концепциях есть какая-то глубокая реальность, выходящая далеко за рамки мысленных размышлений любого конкретного математика. Как будто вместо этого человеческая мысль направляется к какой-то внешней истине — истине, имеющей собственную реальность…»
Роджер Пенроуз, известный британский физик-математик, убежденный платоник. В «Новый разум императора» он писал, что, по-видимому, «в этих математических концепциях есть какая-то глубокая реальность, выходящая далеко за рамки мысленных размышлений любого конкретного математика. Как будто вместо этого человеческая мысль направляется к какой-то внешней истине — истине, имеющей собственную реальность…»
Похоже, многие математики поддерживают эту точку зрения. Вещи, которые они открыли на протяжении столетий: что не существует самого большого простого числа; что квадратный корень из двух — иррациональное число; что число пи, выраженное в виде десятичной дроби, длится вечно, — кажутся вечными истинами, не зависящими от открывших их умов.Если бы мы однажды столкнулись с разумными инопланетянами из другой галактики, они бы не разделяли наш язык или культуру, но платоники утверждали бы, что вполне могли бы сделать такие же математические открытия.
«Я считаю, что единственный способ понять математику — это поверить, что существуют объективные математические факты и что они открыты математиками», — говорит Джеймс Роберт Браун, философ науки, недавно вышедший на пенсию из Университета Торонто. «Работающие математики в подавляющем большинстве являются платониками.Они не всегда называют себя платониками, но если вы зададите им соответствующие вопросы, они всегда дадут вам платонистский ответ».
«Работающие математики в подавляющем большинстве являются платониками.Они не всегда называют себя платониками, но если вы зададите им соответствующие вопросы, они всегда дадут вам платонистский ответ».
Другие ученые, особенно работающие в других областях науки, относятся к платонизму скептически. Ученые склонны быть эмпириками; они воображают, что вселенная состоит из вещей, которые мы можем потрогать, попробовать на вкус и так далее; вещи, о которых мы можем узнать посредством наблюдения и эксперимента. Идея чего-то существующего «вне пространства и времени» заставляет эмпириков нервничать: это звучит смущающе похоже на то, как религиозные верующие говорят о Боге, а Бог давным-давно был изгнан из респектабельного научного дискурса.
Платонизм, как выразился математик Брайан Дэвис, «имеет больше общего с мистическими религиями, чем с современной наукой». Опасение состоит в том, что если математики дадут Платону дюйм, он получит милю. Если истинность математических утверждений можно подтвердить, просто подумав о них, то почему не решить этические или даже религиозные вопросы? Зачем вообще заниматься эмпиризмом?
Массимо Пильюччи, философ из Городского университета Нью-Йорка, изначально увлекался платонизмом, но с тех пор стал считать его проблематичным. Если что-то не имеет физического существования, спрашивает он, то какое существование оно могло бы иметь? «Если в математике «стать платоническим», — пишет Пиглиуччи, — эмпиризм «вылетает в окно». (Если доказательство теоремы Пифагора существует вне пространства и времени, то почему не «золотое правило» или даже божественность Иисуса Христа?)
Если что-то не имеет физического существования, спрашивает он, то какое существование оно могло бы иметь? «Если в математике «стать платоническим», — пишет Пиглиуччи, — эмпиризм «вылетает в окно». (Если доказательство теоремы Пифагора существует вне пространства и времени, то почему не «золотое правило» или даже божественность Иисуса Христа?)
Платоник должен ответить на новые вызовы: если математические объекты существуют вне пространства и времени, как мы можем что-либо знать о них? У Брауна нет ответа, но он предполагает, что мы постигаем истинность математических утверждений «мысленным взором» — возможно, подобно тому, как такие ученые, как Галилей и Эйнштейн, интуитивно постигали физические истины с помощью «мысленных экспериментов, ” до фактических экспериментов могли решить этот вопрос.Рассмотрим знаменитый мысленный эксперимент, придуманный Галилеем, чтобы определить, падает ли тяжелый предмет быстрее, чем более легкий. Просто подумав об этом, Галилей смог сделать вывод, что тяжелые и легкие объекты должны падать с одинаковой скоростью. Хитрость заключалась в том, чтобы представить два объекта, связанных вместе: тянет ли более тяжелый объект за более легкий, чтобы тот падал быстрее? Или более легкий действует как «тормоз», замедляя более тяжелый? Единственное разумное решение, рассуждал Галилей, состоит в том, что объекты падают с одинаковой скоростью независимо от их веса.Подобным образом математики могут доказать, что сумма углов треугольника равна 180 градусам, или что не существует наибольшего простого числа, и им не нужны физические треугольники или камешки для счета, чтобы доказать это, достаточно ловкого мозга. .
Хитрость заключалась в том, чтобы представить два объекта, связанных вместе: тянет ли более тяжелый объект за более легкий, чтобы тот падал быстрее? Или более легкий действует как «тормоз», замедляя более тяжелый? Единственное разумное решение, рассуждал Галилей, состоит в том, что объекты падают с одинаковой скоростью независимо от их веса.Подобным образом математики могут доказать, что сумма углов треугольника равна 180 градусам, или что не существует наибольшего простого числа, и им не нужны физические треугольники или камешки для счета, чтобы доказать это, достаточно ловкого мозга. .
Между тем, отмечает Браун, нас не должна слишком шокировать идея абстракций, потому что мы привыкли использовать их в других областях исследования. «Я совершенно убежден, что существуют абстрактные сущности, и они просто не являются физическими», — говорит Браун. «И я думаю, что вам нужны абстрактные сущности, чтобы понять массу вещей — не только математику, но и лингвистику, этику — возможно, все виды вещей.
Платонизм имеет различные альтернативы. Одна из популярных точек зрения состоит в том, что математика — это просто набор правил, составленный из набора исходных предположений, которые математики называют аксиомами. Как только аксиомы установлены, следует огромное количество логических выводов, хотя найти многие из них может быть чертовски сложно. С этой точки зрения математика больше похожа на изобретение, чем на открытие; по крайней мере, это кажется гораздо более ориентированным на человека усилием. Крайняя версия этой точки зрения сводила бы математику к чему-то вроде игры в шахматы: мы записываем правила игры в шахматы, и из этих правил следуют различные стратегии и последствия, но мы не ожидаем, что андромедианцы найдут шахматы особенно значимыми.
Но у этого представления есть свои проблемы. Если математика — это всего лишь нечто, что мы придумываем в собственных головах, почему она должна так хорошо «соответствовать» тому, что мы наблюдаем в природе? Почему цепная реакция в ядерной физике или рост населения в биологии должны следовать экспоненциальной кривой? Почему орбиты планет имеют форму эллипсов? Почему последовательность Фибоначчи проявляется в фигурах подсолнухов, улиток, ураганов и спиральных галактик? Короче говоря, почему математика оказалась столь ошеломляюще полезной в описании физического мира? Физик-теоретик Юджин Вигнер подчеркнул эту проблему в известном эссе 1960 года под названием «Необоснованная эффективность математики в естественных науках». Вигнер пришел к выводу, что полезность математики в решении проблем физики «является прекрасным даром, который мы не понимаем и не заслуживаем».
Вигнер пришел к выводу, что полезность математики в решении проблем физики «является прекрасным даром, который мы не понимаем и не заслуживаем».
Однако ряд современных мыслителей считают, что у них есть ответ на дилемму Вигнера. Хотя математику можно рассматривать как серию выводов, вытекающих из небольшого набора аксиом, они утверждают, что эти аксиомы не были выбраны по прихоти. Скорее, они были выбраны именно по той причине, что они, кажется, имеют какое-то отношение к физическому миру.Как говорит Пиглиуччи: «Лучший ответ, который я могу дать [на вопрос Вигнера], заключается в том, что эта «необоснованная эффективность» на самом деле очень разумна, потому что математика на самом деле привязана к реальному миру и была привязана с самого начала».
Карло Ровелли, физик-теоретик из Экс-Марсельского университета во Франции, приводит пример евклидовой геометрии — геометрии плоского пространства, которую многие из нас изучали в средней школе. (Студенты, которые узнают, что равносторонний треугольник имеет три угла по 60 градусов каждый или что сумма квадратов двух меньших сторон прямоугольного треугольника равна квадрату гипотенузы, т. е. теоремы Пифагора — занимаются евклидовой геометрией.) Платоник может возразить, что открытия евклидовой геометрии «кажутся» универсальными, — но это не так, говорит Ровелли. «Только потому, что нам довелось жить в месте, которое оказалось странно плоским, мы пришли к этой идее евклидовой геометрии как «естественной вещи», которую должен делать каждый», — говорит он. «Если бы Земля была немного меньше, чтобы мы могли видеть ее кривизну, мы бы никогда не разработали евклидову геометрию.Помните, что «геометрия» означает «измерение земли», а земля круглая. Вместо этого мы разработали бы сферическую геометрию».
е. теоремы Пифагора — занимаются евклидовой геометрией.) Платоник может возразить, что открытия евклидовой геометрии «кажутся» универсальными, — но это не так, говорит Ровелли. «Только потому, что нам довелось жить в месте, которое оказалось странно плоским, мы пришли к этой идее евклидовой геометрии как «естественной вещи», которую должен делать каждый», — говорит он. «Если бы Земля была немного меньше, чтобы мы могли видеть ее кривизну, мы бы никогда не разработали евклидову геометрию.Помните, что «геометрия» означает «измерение земли», а земля круглая. Вместо этого мы разработали бы сферическую геометрию».
Ровелли идет дальше, ставя под сомнение универсальность натуральных чисел: 1, 2, 3, 4… Большинству из нас, и уж тем более платонику, натуральные числа кажутся, скажем так, естественными. Если бы мы встретились с этими разумными инопланетянами, они бы точно знали, что мы имели в виду, когда говорили, что 2 + 2 = 4 (после того, как это утверждение было переведено на их язык). Не так быстро, говорит Ровелли.Счет «существует только там, где есть камни, деревья, люди — отдельные исчисляемые вещи», — говорит он. «Почему это должно быть более фундаментальным, чем, скажем, математика жидкостей?» Если бы были найдены разумные существа, живущие, скажем, в облаках атмосферы Юпитера, у них вообще не было бы интуиции для счета или натуральных чисел, говорит Ровелли. Предположительно, мы могли бы научить их натуральным числам — точно так же, как мы могли бы научить их правилам игры в шахматы, — но если Ровелли прав, это предполагает, что эта область математики не так универсальна, как воображают платоники.
Не так быстро, говорит Ровелли.Счет «существует только там, где есть камни, деревья, люди — отдельные исчисляемые вещи», — говорит он. «Почему это должно быть более фундаментальным, чем, скажем, математика жидкостей?» Если бы были найдены разумные существа, живущие, скажем, в облаках атмосферы Юпитера, у них вообще не было бы интуиции для счета или натуральных чисел, говорит Ровелли. Предположительно, мы могли бы научить их натуральным числам — точно так же, как мы могли бы научить их правилам игры в шахматы, — но если Ровелли прав, это предполагает, что эта область математики не так универсальна, как воображают платоники.
Как и Пиглиуччи, Ровелли считает, что математика «работает», потому что мы создали ее для ее полезности. «Это все равно что спросить, почему молоток так хорошо забивает гвозди, — говорит он. «Это потому, что мы сделали это для этой цели».
На самом деле, говорит Ровелли, заявление Вигнера о том, что математика чрезвычайно полезна для занятий наукой, не выдерживает критики. Он утверждает, что многие открытия, сделанные математиками, вряд ли имеют какое-либо отношение к ученым. «Существует огромное количество математики, которая чрезвычайно красива для математиков, но совершенно бесполезна для науки», — говорит он.«И есть много научных проблем, таких как турбулентность, например, для решения которых каждый хотел бы найти полезную математику, но мы ее не нашли».
Он утверждает, что многие открытия, сделанные математиками, вряд ли имеют какое-либо отношение к ученым. «Существует огромное количество математики, которая чрезвычайно красива для математиков, но совершенно бесполезна для науки», — говорит он.«И есть много научных проблем, таких как турбулентность, например, для решения которых каждый хотел бы найти полезную математику, но мы ее не нашли».
Мэри Ленг, философ из Йоркского университета в Великобритании, придерживается похожей точки зрения. Она называет себя «беллетристом» — она рассматривает математические объекты как полезные вымыслы, сродни персонажам рассказа или романа. «В каком-то смысле они наши создания, как Шерлок Холмс».
Но есть ключевое различие между работой математика и работой романиста: математика уходит своими корнями в такие понятия, как геометрия и измерения, которые очень тесно связаны с физическим миром.Правда, некоторые вещи, которые открывают сегодняшние математики, являются в высшей степени эзотерическими, но, в конце концов, математика и естественные науки — тесно связанные занятия, говорит Ленг. «Поскольку [математика] была изобретена как инструмент, помогающий в науках, неудивительно, что она на самом деле полезна в науках».
«Поскольку [математика] была изобретена как инструмент, помогающий в науках, неудивительно, что она на самом деле полезна в науках».
Учитывая, что эти вопросы о природе математики были предметом горячих споров в течение примерно 2300 лет, маловероятно, что они исчезнут в ближайшее время. Поэтому неудивительно, что старшеклассники, такие как Каннингем, могут остановиться и подумать о них, размышляя над теоремой Пифагора, геометрией треугольников и уравнениями, описывающими прямые и кривые.Вопросы, которые она задавала в своем видео, были вовсе не глупыми, а весьма проницательными: математики и философы задают одни и те же невесомые вещи на протяжении тысячелетий.
Математика Социальные медиаРекомендуемые видео
Математика — Что такое математика
Зачем изучать математику?
Потому что это весело и может подготовить вас к множеству отличных профессий! Если хочешь
разгадывать головоломки и разбираться во всем, то вас может заинтересовать специальность по математике. Кроме того, приложения математики повсюду, и прочная основа в
математика может помочь вам во многих различных профессиях.
Кроме того, приложения математики повсюду, и прочная основа в
математика может помочь вам во многих различных профессиях.
В разделах ниже представлена информация о карьере в области математики и возможностях доступны для наших математических специальностей.
Вакансии
Следующие ссылки ведут на страницы с информацией о доступных вакансиях
студентам математики.
Американское математическое общество
Американская статистическая ассоциация
Это статистика
Математическая ассоциация Америки
Общество промышленной и прикладной математики (SIAM)
Общество актуариев
Исследования бакалавриата
Если вы планируете поступить в аспирантуру по математике, вам следует подумать об участии
в некоторых исследованиях в качестве бакалавра. Есть возможность сделать это с профессорами
в нашем отделе или в других учреждениях летом в REU (Research Experience for
Магистранты). REU обычно длятся от четырех до восьми недель и обычно оплачивают
стипендия.
Есть возможность сделать это с профессорами
в нашем отделе или в других учреждениях летом в REU (Research Experience for
Магистранты). REU обычно длятся от четырех до восьми недель и обычно оплачивают
стипендия.
Что такое математика? | The New Yorker
Недавно я заинтересовался математикой, главным образом потому, что плохо учился по ней в школе.Я скромничаю. у меня не плохо получилось; Я почти потерпел неудачу. Я прошел только обманом. Как бы то ни было, я купил экземпляр «Алгебры для чайников», чтобы посмотреть, смогу ли я улучшить свои знания, но оказалось, что во взрослом возрасте мне алгебра нравилась не больше, чем в детстве. Тем не менее, я был полон решимости увидеть, смогу ли я понять, почему я не смог его выучить. Однако заниматься математикой в подростковом возрасте в более старшем возрасте оказалось труднее, чем я ожидал, и я не знаю, как долго я мог бы продолжать заниматься, если бы не узнал, в основном из книг по математике и разговаривая с математиками, я понял, что за пределами моего перегретого номера в отеле «Алгебра» математика обладает таким величием и размахом, о которых я даже не подозревал. Затем я потратил больше времени, пытаясь узнать все, что мог, о его качествах.
Затем я потратил больше времени, пытаясь узнать все, что мог, о его качествах.
Математики знают, что такое математика, но с трудом говорят об этом. Я слышал: математика — это ремесло создания новых знаний из старых с использованием дедуктивной логики и абстракции. Теория формальных закономерностей. Математика изучает количество. Дисциплина, которая включает в себя натуральные числа, плоскостную и объемную геометрию. Наука, которая делает необходимые выводы. Символическая логика. Изучение структур.Отчет, который мы даем о вневременной архитектуре космоса. Поэзия логических идей. Высказывания связаны очень строгими правилами дедукции. Средство поиска дедуктивного пути от набора аксиом к набору утверждений или их опровержений. Наука о вещах, которые вы не можете видеть, чье присутствие ограничивается воображением. Прототекст, существование которого только постулируется. Точный понятийный аппарат. Изучение идей, с которыми можно обращаться так, как если бы они были реальными вещами. Манипулирование бессмысленными символами языка первого порядка в соответствии с явными синтаксическими правилами.Область, в которой исследуются свойства и взаимодействия идеализированных объектов. Наука искусных операций с понятиями и правилами, придуманными для этой цели. Предположения, вопросы, разумные догадки и эвристические аргументы о том, что, вероятно, является правдой. Самая длинная непрерывная человеческая мысль. Тщательно построенная интуиция. То, чем становятся научные идеи по мере их совершенствования. Идеальная реальность. История, которая писалась тысячи лет, постоянно дополняется и, возможно, никогда не будет закончена.Крупнейший целостный артефакт, созданный цивилизацией. Только формальная игра. Что делают математики, так музыканты делают музыку.
Манипулирование бессмысленными символами языка первого порядка в соответствии с явными синтаксическими правилами.Область, в которой исследуются свойства и взаимодействия идеализированных объектов. Наука искусных операций с понятиями и правилами, придуманными для этой цели. Предположения, вопросы, разумные догадки и эвристические аргументы о том, что, вероятно, является правдой. Самая длинная непрерывная человеческая мысль. Тщательно построенная интуиция. То, чем становятся научные идеи по мере их совершенствования. Идеальная реальность. История, которая писалась тысячи лет, постоянно дополняется и, возможно, никогда не будет закончена.Крупнейший целостный артефакт, созданный цивилизацией. Только формальная игра. Что делают математики, так музыканты делают музыку.
Бертран Рассел сказал, что математика, по своей природе исследовательского искусства, является «предметом, в котором мы никогда не знаем, о чем мы говорим и истинно ли то, что мы говорим». Дарвин пытался изучать математику с репетитором, когда ему было девятнадцать, и ненавидел ее, в основном из-за «неспособности увидеть какой-либо смысл в первых шагах алгебры». Предполагается, что он пришел к выводу, что «математик — это слепой в темной комнате, ищущий черную кошку, которой там нет.В «Приключениях Алисы в Стране Чудес» Льюис Кэрролл заставляет Мнимую Черепаху сказать, что четыре операции арифметики (сложение, вычитание, умножение и деление) — это честолюбие, отвлечение внимания, уродство и насмешка. Усложняющим обстоятельством является то, что математику, особенно в ее более высоких диапазонах, — это , трудно понять. Он начинается с простой общей речи (все могут считать) и становится специализированным диалектом, настолько загадочным, что на некоторых из них говорит всего несколько сотен человек в мире.Другие месторождения еще даже не открыты.
Предполагается, что он пришел к выводу, что «математик — это слепой в темной комнате, ищущий черную кошку, которой там нет.В «Приключениях Алисы в Стране Чудес» Льюис Кэрролл заставляет Мнимую Черепаху сказать, что четыре операции арифметики (сложение, вычитание, умножение и деление) — это честолюбие, отвлечение внимания, уродство и насмешка. Усложняющим обстоятельством является то, что математику, особенно в ее более высоких диапазонах, — это , трудно понять. Он начинается с простой общей речи (все могут считать) и становится специализированным диалектом, настолько загадочным, что на некоторых из них говорит всего несколько сотен человек в мире.Другие месторождения еще даже не открыты.
Ни одна книга не старее математики. Все остальные науки моложе, большинство на тысячи лет. Математика — это не только история, но и летопись, которую человечество ведет о себе. История может быть пересмотрена или изменена, стерта или потеряна. Математика неизменна. A² + B² = C² было истинным до того, как Пифагор присоединил к нему свое имя, и будет истинным, когда солнце погаснет и никто не останется, чтобы думать об этом. Это верно для любой инопланетной жизни, которая может подумать об этом, и верно независимо от того, думают они об этом или нет.Его нельзя изменить. Пока существует мир с горизонтальной и вертикальной осью, небом и горизонтом, он неприкосновенен и так же верен, как и все, что можно помыслить.
Это верно для любой инопланетной жизни, которая может подумать об этом, и верно независимо от того, думают они об этом или нет.Его нельзя изменить. Пока существует мир с горизонтальной и вертикальной осью, небом и горизонтом, он неприкосновенен и так же верен, как и все, что можно помыслить.
Математики живут в мире, который по существу определен. Остальные из нас, даже другие ученые, живут внутри одного, где то, что представляет уверенность, — это то, что, насколько мы можем сказать, этот результат происходит почти все время. Из-за того, что математика настаивает на доказательстве, она может рассказать нам, в пределах того, что она знает, что происходит раз за разом.
Какой бы точной ни была математика, это также самый подробный язык, который у нас есть для описания тайн. Будучи языком физики, он описывает настоящие тайны — вещи, которые мы не можем ясно видеть в естественном мире, но подозреваем, что они истинны, а позже подтверждаем — и воображаемые тайны, вещи, которые существуют только в умах математиков. Вопрос в том, где существуют эти абстрактные загадки, каков их ареал. Некоторые люди сказали бы, что они находятся в человеческом разуме, что только человеческий разум способен постичь то, что называется математическими объектами, имея в виду числа, уравнения, формулы и т. они возникают, и что такие вещи появляются именно так, как они появляются, из-за того, как устроен наш разум.Нас побуждают исследовать мир таким образом, который согласуется с инструментами, которые у нас есть для его исследования. (Например, мы видим цвета такими, какими мы их видим, из-за того, как устроен наш мозг, чтобы воспринимать отражение света от поверхностей.) Это точка зрения меньшинства, которой придерживаются в основном нейробиологи и определенное количество математиков, не склонных к спекуляциям. Более широко распространено мнение, что никто не знает, где находится математика. Нет ни одного математика/натуралиста, который мог бы указать куда-то и сказать: «Вот откуда берется математика» или «Математика живет там», скажем, при этом, может быть, указывая на магнитный север и Арктику, что, я думаю, уместно для такой противоположности и холодно указывая на дисциплину.
Вопрос в том, где существуют эти абстрактные загадки, каков их ареал. Некоторые люди сказали бы, что они находятся в человеческом разуме, что только человеческий разум способен постичь то, что называется математическими объектами, имея в виду числа, уравнения, формулы и т. они возникают, и что такие вещи появляются именно так, как они появляются, из-за того, как устроен наш разум.Нас побуждают исследовать мир таким образом, который согласуется с инструментами, которые у нас есть для его исследования. (Например, мы видим цвета такими, какими мы их видим, из-за того, как устроен наш мозг, чтобы воспринимать отражение света от поверхностей.) Это точка зрения меньшинства, которой придерживаются в основном нейробиологи и определенное количество математиков, не склонных к спекуляциям. Более широко распространено мнение, что никто не знает, где находится математика. Нет ни одного математика/натуралиста, который мог бы указать куда-то и сказать: «Вот откуда берется математика» или «Математика живет там», скажем, при этом, может быть, указывая на магнитный север и Арктику, что, я думаю, уместно для такой противоположности и холодно указывая на дисциплину.
Вера в то, что математика существует где-то еще, а не внутри нас, что она открывается, а не создается, называется платонизмом, в честь платоновской веры в внепространственно-временную область, которая является областью совершенных форм, в которых объекты на земле несовершенны. репродукции. По определению внепространственно-временная сфера находится вне времени и пространства. Это не творение какого-либо божества; это просто есть. Сказать, что оно вечно или всегда существовало, значит сделать временное замечание, которое не применимо.Это вневременное нигде, которое никогда нигде не существовало и нигде не будет, но тем не менее есть. Физический мир временен и приходит в упадок; непространственно-временная идеальна и не идеальна.
Третья точка зрения, историческая и современная, для небольшого, но немаловажного числа математиков, заключается в том, что дом математики находится в разуме высшего существа и что математики каким-то образом заняты Их мыслями. Георг Кантор, создатель теории множеств, которую в моем детстве преподавали как часть «новой математики», сказал: «Высшее совершенство Бога заключается в способности создавать бесконечное множество, и его безграничная доброта ведет Его к создать это. А дико изобретательный и математик-самоучка Шриниваса Рамануджан, о котором снят фильм «Человек, познавший бесконечность», в 2015 году сказал: «Уравнение для меня не имеет смысла, если оно не выражает мысль Бога».
А дико изобретательный и математик-самоучка Шриниваса Рамануджан, о котором снят фильм «Человек, познавший бесконечность», в 2015 году сказал: «Уравнение для меня не имеет смысла, если оно не выражает мысль Бога».
В 7-й книге «Государства» Платона Сократ говорит, что математики — это люди, которым снится, что они бодрствуют. Я отчасти это понимаю, отчасти нет.
Что такое математика? | Матназиум
Математики не согласны с определением математики.Математики раздвигали границы математики на протяжении тысячелетий. Слово «математика» происходит от древнегреческого и означает «то, чему учат».
Различные математические определения
Dictionary.com определяет математику как «систематическое рассмотрение величин, отношений между фигурами и формами, а также отношений между величинами, выраженными символически».
Merriam-Webster определяет математику как «науку о числах и их операциях, взаимосвязях, комбинациях, обобщениях и абстракциях, а также о пространственных конфигурациях и их структурах, измерениях, преобразованиях и обобщениях»
Аристотель определял математику как «науку о количестве».
Бертран Рассел сказал: «Вся математика — это символическая логика».
Некоторые говорят, что математика — это «наука, занимающаяся логикой формы, количества и расположения». Многие математики говорят, что их не волнует определение математики, и говорят просто: «Математика — это то, чем занимаются математики».
Прикладная и чистая математика
Чистая математика больше похожа на искусство, чем на науку, а прикладная математика больше похожа на науку, чем на искусство.
Прикладная математика помогает решать проблемы в науке, технике, финансах, физике, криптологии, технике, астрономии, криминалистике и других областях.Ньютон изобрел исчисление для описания движущихся объектов.
Чистая математика исследует математические закономерности, головоломки и абстрактные идеи. Чистые математики не ограничены рамками реального мира. Как композиторы не ожидают, что их музыка решит проблему, так и чистый математик не ожидает, что их идеи решат проблему. Альберт Эйнштейн сказал: «Чистая математика — это своего рода поэзия логических идей».
Альберт Эйнштейн сказал: «Чистая математика — это своего рода поэзия логических идей».
Абстрактные идеи из чистой математики иногда приводят к практическим приложениям.Компьютерное программирование началось из-за идей «Машины Тьюринга» в чистой математике. Алан Тьюринг представил машину Тьюринга с бесконечными лентами. Машину Тьюринга построить невозможно, но логика машины Тьюринга проложила путь для программируемых машин, таких как ваш мобильный телефон.
Как Mathnasium of Littleton определяет математику?
Нам нравится определение Бертрана Рассела: «Вся математика — это символическая логика. « Мы фокусируемся на математике, изучаемой в начальной, средней и старшей школе.Вся математика на этом уровне является прикладной математикой. Школы классифицируют математику по нескольким дисциплинам, в том числе:
· Арифметика (вся начальная школа и часть средней школы)
· Предварительная алгебра (обычно проводится в седьмом или восьмом классе)
· Алгебра (обычно проводится в восьмом, девятом и/или одиннадцатом классе)
· Геометрия (сдается после сдачи алгебры)
· Тригонометрия (часто в сочетании с геометрией, второй год обучения алгебре или предварительному исчислению)
· Предварительное исчисление (сдается после двух лет изучения алгебры и геометрии)
· Исчисление (сдается после прохождения предварительного исчисления)
· Статистика, информатика и многомерное исчисление (эти курсы менее распространены на уровне средней школы. Некоторые средние школы предлагают их вместо или после математического анализа.)
Некоторые средние школы предлагают их вместо или после математического анализа.)
Возможно, мы не сможем помочь математикам определить математику, но мы можем помочь вашему ребенку добиться успеха в математике. Нажмите кнопку внизу страницы, чтобы узнать больше о нашей программе.
Для получения дополнительной информации об определении математики и чистой математики читайте:
https://www.etymonline.com/word/mathematic
https://www.computerworld.com/article/2504774/data-center/how-alan-turing-set-the-rules-for-computing.html
https://scholarworks.umt.edu/cgi/viewcontent.cgi?referer=https://www.google.com/&httpsredir=1&article=1242&context=tme.
https://theconversation.com/explainer-the-point-of-pure-mathematics-2385
Вам также могут понравиться эти другие статьи Mathnasium.
· Математическая идея настолько нелепа, что вы не поверите, что она верна!
· Великая традиция арифметики
· Подготовьте ребенка к алгебре
· Мы облегчаем изучение алгебры
· Резко упали оценки вашего ребенка по алгебре или геометрии? Почему это происходит и как это исправить
· Я никогда не буду заниматься математическим анализом после школы!
· 5 лучших математических курсов, которые нужно пройти, чтобы добиться успеха в 21 веке
Эта статья защищена авторским правом. Mathnasium of Littleton имеет разрешение на его использование. Другие места Mathnasium должны приобрести его на http://hdwrite.com, прежде чем использовать.
Mathnasium of Littleton имеет разрешение на его использование. Другие места Mathnasium должны приобрести его на http://hdwrite.com, прежде чем использовать.
Кто боится математики? Что такое математическая тревога? И что вы можете с этим поделать? · Границы для молодых умов
Аннотация
Математика — это необходимый навык, который люди используют на протяжении всей своей жизни, например, когда они путешествуют, используют деньги или отслеживают время. Таким образом, математика является важным навыком для изучения в школе.К сожалению, многие дети и взрослые испытывают стресс и тревогу, когда им приходится заниматься математикой. Люди, испытывающие стресс при столкновении с математическими ситуациями, могут испытывать так называемую «математическую тревогу». Математическая тревожность затрагивает многих людей и связана с плохими математическими способностями в школе, а затем во взрослой жизни. Исследователи изучили, как впервые появляется математическая тревожность, что происходит в мозгу, когда люди испытывают математическую тревожность, и как лучше всего помочь людям, страдающим от математической тревожности.
Испытывали ли вы когда-нибудь стресс и тревогу, когда учитель математики задавал вам вопрос? Или когда вы делаете домашнее задание по математике? Если это так, вы, возможно, испытали то, что называется математической тревогой . Если вы испытали математическую тревогу, вы не одиноки. Многие люди очень нервничают, когда сталкиваются с ситуацией, требующей от них базовых математических знаний. Тревога по поводу математики — это больше, чем просто нервозность из-за того, что вы занимаетесь математикой. Нервозность – это разумная реакция на ситуацию, которая на самом деле пугает.Напротив, беспокойство может не иметь смысла. Это означает, что человек может чувствовать беспокойство, даже если он или она знает, что на самом деле нет причин для беспокойства. Кроме того, беспокойство может вызывать физические симптомы, такие как учащенное сердцебиение или потливость. Обычно люди, которые боятся математики, считают, что у них плохо с математикой, и из-за этого они не любят математику. Эти чувства заставляют их избегать ситуаций, в которых им приходится заниматься математикой. Дети с математической тревожностью часто имеют плохие математические навыки [1]. У взрослых с математической тревожностью часто возникают проблемы с математикой в карьере и повседневной жизни [2].Взрослые с математической тревожностью с меньшей вероятностью проявят интерес, поступят и преуспеют в карьере, связанной с наукой, технологиями, инженерией и математикой.
Эти чувства заставляют их избегать ситуаций, в которых им приходится заниматься математикой. Дети с математической тревожностью часто имеют плохие математические навыки [1]. У взрослых с математической тревожностью часто возникают проблемы с математикой в карьере и повседневной жизни [2].Взрослые с математической тревожностью с меньшей вероятностью проявят интерес, поступят и преуспеют в карьере, связанной с наукой, технологиями, инженерией и математикой.
Поскольку тревожность по поводу математики затрагивает многих людей и связана с плохими математическими навыками, важно понимать, когда и как впервые появляется тревожность по математике, что происходит в мозгу, когда люди испытывают тревогу по поводу математики, и как лучше всего помочь людям с математикой. беспокойство.
Когда и как впервые появляется математическая тревога?
До недавнего времени ученые и педагоги считали, что страх перед математикой впервые появляется, когда дети начинают изучать сложную математику (например, алгебру). Это означало бы, что маленькие дети (которые еще не умеют выполнять сложные математические действия) не испытывают математической тревожности. Тем не менее, недавние исследования показали, что некоторые дети в возрасте 6 лет говорят, что испытывают беспокойство по поводу математики. Группа исследователей задала 154 ученикам 1-го и 2-го классов такие вопросы, как «Как вы себя чувствуете, когда сдаете большой контрольный по математике?» [3] Дети должны были указать, насколько они нервничают, указывая на положение на шкале, от очень нервного лица слева до спокойного лица справа.(См. изображение шкалы на Рисунке 1.) Ответив на эти вопросы, дети прошли тест по математике, который измерял их математические способности. Эти исследователи обнаружили, что почти половина детей, участвовавших в исследовании, сказали, что они, по крайней мере, немного нервничают по поводу занятий математикой [3]. Кроме того, дети с более высокой математической тревожностью получили худшие результаты на тесте по математике.
Это означало бы, что маленькие дети (которые еще не умеют выполнять сложные математические действия) не испытывают математической тревожности. Тем не менее, недавние исследования показали, что некоторые дети в возрасте 6 лет говорят, что испытывают беспокойство по поводу математики. Группа исследователей задала 154 ученикам 1-го и 2-го классов такие вопросы, как «Как вы себя чувствуете, когда сдаете большой контрольный по математике?» [3] Дети должны были указать, насколько они нервничают, указывая на положение на шкале, от очень нервного лица слева до спокойного лица справа.(См. изображение шкалы на Рисунке 1.) Ответив на эти вопросы, дети прошли тест по математике, который измерял их математические способности. Эти исследователи обнаружили, что почти половина детей, участвовавших в исследовании, сказали, что они, по крайней мере, немного нервничают по поводу занятий математикой [3]. Кроме того, дети с более высокой математической тревожностью получили худшие результаты на тесте по математике. Это исследование говорит нам, что математическая тревожность и взаимосвязь между математической тревожностью и математическими способностями развиваются, когда дети очень маленькие.
Это исследование говорит нам, что математическая тревожность и взаимосвязь между математической тревожностью и математическими способностями развиваются, когда дети очень маленькие.
Исследователи также интересуются тем, как развивается математическая тревожность. Хотя исследования показали, что математическая тревожность и математические способности связаны [1], ни одно исследование до сих пор не смогло сказать нам, что на первом месте. Другими словами, мы не знаем, вызывает ли математическая тревожность плохая математика или математическая тревожность делает людей плохими в математике.
У исследователей есть две идеи о том, как может развиться математическая тревожность. Одна идея состоит в том, что дети, которые борются с изучением чисел, когда они очень маленькие, с большей вероятностью разовьют математическую тревожность, когда они начнут ходить в школу.Эта идея еще не была проверена на детях. Другая идея заключается в том, что математическая тревожность развивается у детей, которые сталкиваются с определенными социальными ситуациями, влияющими на мысли или чувства ребенка. Это означает, что на эмоции, мнения или поведение ребенка влияют вещи, которые говорят или делают другие люди. Одно исследование, в котором приводится пример этого, показало, что учителя с высокой математической тревожностью с большей вероятностью имели учеников с более низкими математическими достижениями в конце учебного года [4]. Это исследование предполагает, что поведение учителя каким-то образом повлияло на математические способности учеников.Хотя исследователи еще не ответили на вопрос, что первично, математические способности или математическая тревожность, было сделано много важных открытий, которые дали нам подсказки о том, когда и как появляется математическая тревожность.
Это означает, что на эмоции, мнения или поведение ребенка влияют вещи, которые говорят или делают другие люди. Одно исследование, в котором приводится пример этого, показало, что учителя с высокой математической тревожностью с большей вероятностью имели учеников с более низкими математическими достижениями в конце учебного года [4]. Это исследование предполагает, что поведение учителя каким-то образом повлияло на математические способности учеников.Хотя исследователи еще не ответили на вопрос, что первично, математические способности или математическая тревожность, было сделано много важных открытий, которые дали нам подсказки о том, когда и как появляется математическая тревожность.
Что происходит в мозгу, когда человек испытывает математическую тревогу?
Чтобы лучше понять, как развивается математическая тревожность и как помочь людям, страдающим от нее, нам нужно понять, что происходит в мозгу, когда человек с математической тревожностью занимается математикой.Одна из идей состоит в том, что человеческий мозг может обрабатывать только определенное количество информации за раз. Система в мозгу, которая позволяет нам обрабатывать информацию, называется рабочей памятью . Рабочая память — это часть системы памяти человека, которая позволяет нам помнить и думать о нескольких вещах одновременно. Этот навык очень важен для занятий математикой. Например, если учитель зачитывает математическую задачу, ученик должен удерживать в уме все числа, обдумывать шаги, необходимые для решения задачи, и одновременно записывать ответ.Исследователи считают, что, возможно, когда люди испытывают тревогу, математическая тревога, которую они испытывают, использует часть их рабочей памяти, поэтому у них не остается достаточно рабочей памяти для решения математической задачи. Возможно, рабочая память, которая используется для беспокойства, использовалась бы для решения математической задачи, если бы эти люди не чувствовали себя так беспокойно [3]. Другими словами, математическая тревожность заставляет учащихся думать и беспокоиться о том, насколько они боятся математики, которая занимает ресурсы рабочей памяти, которые в противном случае они использовали бы для решения математических задач.
Система в мозгу, которая позволяет нам обрабатывать информацию, называется рабочей памятью . Рабочая память — это часть системы памяти человека, которая позволяет нам помнить и думать о нескольких вещах одновременно. Этот навык очень важен для занятий математикой. Например, если учитель зачитывает математическую задачу, ученик должен удерживать в уме все числа, обдумывать шаги, необходимые для решения задачи, и одновременно записывать ответ.Исследователи считают, что, возможно, когда люди испытывают тревогу, математическая тревога, которую они испытывают, использует часть их рабочей памяти, поэтому у них не остается достаточно рабочей памяти для решения математической задачи. Возможно, рабочая память, которая используется для беспокойства, использовалась бы для решения математической задачи, если бы эти люди не чувствовали себя так беспокойно [3]. Другими словами, математическая тревожность заставляет учащихся думать и беспокоиться о том, насколько они боятся математики, которая занимает ресурсы рабочей памяти, которые в противном случае они использовали бы для решения математических задач. Идея о том, что математическая тревожность использует рабочую память, была подтверждена исследованиями. Важно отметить, что исследователи сообщают, что дети с высоким уровнем рабочей памяти лучше справляются с математическими тестами, чем дети с низким уровнем рабочей памяти.
Идея о том, что математическая тревожность использует рабочую память, была подтверждена исследованиями. Важно отметить, что исследователи сообщают, что дети с высоким уровнем рабочей памяти лучше справляются с математическими тестами, чем дети с низким уровнем рабочей памяти.
Исследователи также изучили, насколько интенсивно работают различные части мозга, когда дети с высокой или низкой математической тревожностью решают сложные математические задачи [5]. Эти исследователи попросили группу детей в возрасте от 7 до 9 лет с математическим беспокойством и без него решить некоторые математические задачи, пока они находились в устройстве под названием магнитно-резонансный томограф (МРТ) [5].МРТ-сканер — это устройство, которое можно использовать для измерения интенсивности работы каждой области мозга при выполнении определенной задачи с помощью инструмента под названием функциональной магнитно-резонансной томографии (фМРТ) . (См. изображение МРТ-сканера на рис. 2.) Это измерение называется « активация мозга ». Если область мозга усердно работает, активация мозга будет больше. Эти исследователи обнаружили, что часть мозга, называемая миндалевидным телом, более активна (работает усерднее) у детей с высокой математической тревожностью, чем у детей с низкой математической тревожностью.Кроме того, у детей с высокой математической тревожностью области мозга, отвечающие за оперативную память и математическую обработку (называемые дорсолатеральной префронтальной корой и внутритеменной бороздой), менее активны (работают менее усердно) по сравнению с теми областями мозга у детей, у которых имеется повышенная тревожность. низкая математическая тревожность [5]. Миндалевидное тело — это небольшая миндалевидная структура в нижней средней части мозга, которая важна для переживания и обработки эмоций, включая страх и тревогу. Дорсолатеральная префронтальная кора — это большая часть мозга, расположенная в самой передней части мозга, и она участвует во многих сложных поведенческих процессах, таких как планирование и принятие решений.
2.) Это измерение называется « активация мозга ». Если область мозга усердно работает, активация мозга будет больше. Эти исследователи обнаружили, что часть мозга, называемая миндалевидным телом, более активна (работает усерднее) у детей с высокой математической тревожностью, чем у детей с низкой математической тревожностью.Кроме того, у детей с высокой математической тревожностью области мозга, отвечающие за оперативную память и математическую обработку (называемые дорсолатеральной префронтальной корой и внутритеменной бороздой), менее активны (работают менее усердно) по сравнению с теми областями мозга у детей, у которых имеется повышенная тревожность. низкая математическая тревожность [5]. Миндалевидное тело — это небольшая миндалевидная структура в нижней средней части мозга, которая важна для переживания и обработки эмоций, включая страх и тревогу. Дорсолатеральная префронтальная кора — это большая часть мозга, расположенная в самой передней части мозга, и она участвует во многих сложных поведенческих процессах, таких как планирование и принятие решений. Внутритеменная борозда — это область мозга в верхней части мозга, которая важна для математики и концентрации внимания. (На рисунке 3 показано, где расположены эти области мозга.) Таким образом, в целом это исследование показывает, что, когда дети решают математические задачи, дети с высокой математической тревожностью активируют области мозга, связанные с тревожностью, в то время как дети с низкой математической тревожностью активировать области мозга, отвечающие за решение математических задач.
Внутритеменная борозда — это область мозга в верхней части мозга, которая важна для математики и концентрации внимания. (На рисунке 3 показано, где расположены эти области мозга.) Таким образом, в целом это исследование показывает, что, когда дети решают математические задачи, дети с высокой математической тревожностью активируют области мозга, связанные с тревожностью, в то время как дети с низкой математической тревожностью активировать области мозга, отвечающие за решение математических задач.
- Рис. 2. Это изображение МРТ-сканера.
- МРТ-сканер представляет собой большой магнит в форме пончика, который часто имеет туннель в центре. Исследуемого помещают на удобный стол, который выдвигается в туннель. Затем человек остается неподвижным, пока МРТ-сканер работает с компьютером, создавая четкие черно-белые изображения мозга. Эти изображения можно делать, когда люди выполняют какие-либо действия, чтобы показать, какие области мозга активированы.
- Рисунок 3
- На этом рисунке показаны области мозга, которые более активны (работают усерднее) и области мозга, которые менее активны (работают менее усердно) у людей с высокой математической тревожностью, когда они решают математические задачи.

Как мы можем помочь людям с математической тревогой?
Одна из главных целей понимания того, что вызывает математическую тревогу и как математическая тревога влияет на мозг, состоит в том, чтобы найти способы помочь людям с математической тревогой и, в конечном счете, предотвратить ее возникновение. Некоторые исследователи создали инструменты, помогающие людям с математической тревожностью. Эти инструменты называются вмешательствами . Например, исследователи вмешались, основываясь на исследованиях, показывающих, что предварительное запись мыслей и чувств может помочь людям меньше нервничать при сдаче тестов.Исследователи считали, что если дети будут записывать свои мысли и чувства, эти чувства не будут занимать рабочую память, пока дети выполнят тест по математике. Итак, исследователи провели интервенцию, в которой попросили детей с математическим страхом написать о своих опасениях, связанных с математикой. Эти исследователи обнаружили, что, когда учащиеся писали о своих опасениях, связанных с математикой, их результаты тестов по математике улучшались [6]. Другая группа исследователей показала, что если студенты колледжа с математической тревожностью выполняли дыхательные упражнения, чтобы успокоиться перед контрольной по математике, они чувствовали себя спокойнее, и их результаты на тесте улучшались [7].Вместе эти интервенционные исследования предоставляют научные доказательства того, как мы можем помочь людям с математической тревожностью. Это исследование очень многообещающе, потому что оно говорит нам, что людям с математической тревогой можно помочь — они не застряли с математической тревогой на всю жизнь.
Другая группа исследователей показала, что если студенты колледжа с математической тревожностью выполняли дыхательные упражнения, чтобы успокоиться перед контрольной по математике, они чувствовали себя спокойнее, и их результаты на тесте улучшались [7].Вместе эти интервенционные исследования предоставляют научные доказательства того, как мы можем помочь людям с математической тревожностью. Это исследование очень многообещающе, потому что оно говорит нам, что людям с математической тревогой можно помочь — они не застряли с математической тревогой на всю жизнь.
Заключение
Поскольку мы знаем, что люди с математической тревожностью сталкиваются с проблемами на уроках математики, в карьере и в повседневной жизни, многие исследователи работали над тем, чтобы узнать больше о математической тревожности. Исследователи продолжают добиваться успехов в этой области.Исследования математической тревожности показали, что она развивается рано и связана как с социальными ситуациями, так и с такими мозговыми процессами, как рабочая память. Кроме того, люди с математической тревожностью демонстрируют большую активацию мозга в областях, связанных с негативными эмоциями, и меньшую активацию в областях мозга, связанных с математическим мышлением. Исследователи также начали тестировать возможные вмешательства, которые, по-видимому, помогают людям, страдающим математической тревожностью. Тем не менее, предстоит еще много работы, чтобы выяснить, как впервые появляется математическая тревожность, что вызывает ее только у некоторых людей и как мы можем помочь людям, страдающим математической тревожностью.А пока, независимо от того, испытываете ли вы математическую тревогу или нет, поговорите со своими однокурсниками и учителями о математической тревоге. Важно обсуждать свои эмоциональные реакции на математику, потому что это первый шаг к уменьшению потенциально вредных последствий математической тревожности.
Кроме того, люди с математической тревожностью демонстрируют большую активацию мозга в областях, связанных с негативными эмоциями, и меньшую активацию в областях мозга, связанных с математическим мышлением. Исследователи также начали тестировать возможные вмешательства, которые, по-видимому, помогают людям, страдающим математической тревожностью. Тем не менее, предстоит еще много работы, чтобы выяснить, как впервые появляется математическая тревожность, что вызывает ее только у некоторых людей и как мы можем помочь людям, страдающим математической тревожностью.А пока, независимо от того, испытываете ли вы математическую тревогу или нет, поговорите со своими однокурсниками и учителями о математической тревоге. Важно обсуждать свои эмоциональные реакции на математику, потому что это первый шаг к уменьшению потенциально вредных последствий математической тревожности.
Глоссарий
Математическая тревога : ↑ Чувство чрезвычайной нервозности при выполнении элементарной математики.
Рабочая память : ↑ Часть системы памяти, которая используется для запоминания и удержания информации в уме, чтобы вы могли использовать ее при выполнении действий.
Магнитно-резонансная томография (МРТ) : ↑ МРТ — это аппарат, который использует сильный магнит для создания изображений вашего мозга.
Функциональная магнитно-резонансная томография (фМРТ) : ↑ Инструмент, который измеряет, какие области мозга активируются, когда вы выполняете различные действия в МРТ-сканере, такие как сложение и вычитание.
Активация мозга : ↑ Мера того, насколько интенсивно работает область мозга во время выполнения конкретной задачи.Если область мозга усердно работает, активация мозга будет больше.
Вмешательство : ↑ Инструмент или программа, которая дается людям с целью помочь им улучшить или улучшить свои навыки.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Ссылки
[1] ↑ Ву, С.С., Барт М., Амин Х., Малкарн В. и Менон В. 2012. Математическая тревога у второ- и третьеклассников и ее связь с успеваемостью по математике. Фронт. Психол. 3:1–11. doi:10.3389/fpsyg.2012.00162
[2] ↑ Ma, X. 1999. Метаанализ взаимосвязи между тревогой по отношению к математике и достижениями в математике. Дж. Рез. Мат. Образовательный 30: 520–40. дои: 10.2307/749772
[3] ↑ Рамирес Г., Гундерсон Э. А., Левин С. К. и Бейлок С.Л. 2013. Математическая тревожность, рабочая память и математические достижения в начальной школе. Дж. Когн. Дев. 14:187–202. дои: 10.1080/15248372.2012.664593
[4] ↑ Бейлок, С. Л. , Гундерсон, Э. А., Рамирес, Г., и Левин, С. К. 2010. Беспокойство женщин-учителей по математике влияет на успеваемость девочек по математике. проц. Натл. акад. науч. США 107:1860–3. doi:10.1073/pnas.0910967107
, Гундерсон, Э. А., Рамирес, Г., и Левин, С. К. 2010. Беспокойство женщин-учителей по математике влияет на успеваемость девочек по математике. проц. Натл. акад. науч. США 107:1860–3. doi:10.1073/pnas.0910967107
[5] ↑ Янг, К. Б., Ву, С. С., и Менон, В. 2012. Неврологическая основа математической тревожности.Психол. науч. 23:492–501. дои: 10.1177/0956797611429134
[6] ↑ Парк, Д., Рамирес, Г., и Бейлок, С.Л. 2014. Роль выразительного письма в математической тревожности. Дж. Эксп. Психол. заявл. 20:103–11. дои: 10.1037/xap0000013
[7] ↑ Брунье, Т. Т., Махони, Ч. Р., Джайлз, Г. Э., Рапп, Д. Н., Тейлор, Х. А., и Канарек, Р. Б. 2013. Учимся расслабляться: оценка четырех кратких вмешательств для преодоления негативных эмоций, сопровождающих математическую тревогу.Учиться. Индивид. Отличаться. 27:1–7. doi:10.1016/j.lindif.2013.06.008
Что такое математика? Чем занимаются математики?
32 ОБНОВЛЕНИЕ – ВЕСНА/ЛЕТО 2020 Г. – В начале пандемии я записал видео для семей под названием «Что такое математика?». Слишком много взрослых и студентов, которых я встречаю, говорят: «Я не умею заниматься математикой» или «Я плохо разбираюсь в математике». заблуждение, основанное на запоминании и скорости. Если вы предпочитаете получить представление об этом посте из видео, а не из чтения, нажмите ниже. В противном случае — продолжайте читать для получения более подробной информации для класса.
– В начале пандемии я записал видео для семей под названием «Что такое математика?». Слишком много взрослых и студентов, которых я встречаю, говорят: «Я не умею заниматься математикой» или «Я плохо разбираюсь в математике». заблуждение, основанное на запоминании и скорости. Если вы предпочитаете получить представление об этом посте из видео, а не из чтения, нажмите ниже. В противном случае — продолжайте читать для получения более подробной информации для класса.
Я начал преподавать в 1991 году, когда во многих школах по всей стране были введены реформы, финансируемые NSF. Мой район начал использовать IMP (когда-нибудь я напишу в блоге «Любовное письмо IMP»), и в течение 13 лет я преподавал математику по этим текстам. Много раз в первые годы преподавания я думал: «О, вот почему математика работает».Здесь я был учителем математики и в каком-то смысле впервые открывал для себя математику и то, что значит быть математиком. Честно говоря, я был немного зол из-за того, как меня учили математике на протяжении всего моего образования. Я получал пятерки на каждом уроке математики, который когда-либо посещал, но в глубине души я знал, что это только потому, что я хорошо разбирался в школьной системе. Я был в порядке, не зная, почему, и просто делая то, что они сказали мне делать. Когда моя подруга расстраивалась из-за неудовлетворительного ответа на ее вопросы «Почему это работает», я тихо думала: «ей нужно отпустить это и просто делать то, что они говорят».Мой бедный друг. Тогда для нее не были созданы математические классы. Печально то, что спустя 30 с лишним лет многие до сих пор не работают на таких, как мой друг. Мне повезло, мои первые годы преподавания были полны лучших практик PD, которые, как я с любовью говорю, промыли мне мозги и заставили меня думать о математике и о том, что математики делают до конца моей карьеры.
Много раз в первые годы преподавания я думал: «О, вот почему математика работает».Здесь я был учителем математики и в каком-то смысле впервые открывал для себя математику и то, что значит быть математиком. Честно говоря, я был немного зол из-за того, как меня учили математике на протяжении всего моего образования. Я получал пятерки на каждом уроке математики, который когда-либо посещал, но в глубине души я знал, что это только потому, что я хорошо разбирался в школьной системе. Я был в порядке, не зная, почему, и просто делая то, что они сказали мне делать. Когда моя подруга расстраивалась из-за неудовлетворительного ответа на ее вопросы «Почему это работает», я тихо думала: «ей нужно отпустить это и просто делать то, что они говорят».Мой бедный друг. Тогда для нее не были созданы математические классы. Печально то, что спустя 30 с лишним лет многие до сих пор не работают на таких, как мой друг. Мне повезло, мои первые годы преподавания были полны лучших практик PD, которые, как я с любовью говорю, промыли мне мозги и заставили меня думать о математике и о том, что математики делают до конца моей карьеры.
Последние 20 лет моей учительской карьеры я задавал одно и то же домашнее задание в первую неделю учебы. Одна из моих целей на первой неделе учебы — убедить учеников, что все они, да, ВСЕ, математики. Многие ученики входят в мою комнату, не веря этому. В последние годы много людей говорили об этом, и было создано множество ресурсов, чтобы помочь учащимся поверить в то, что они могут стать умнее в математике. Джо Боалер, Стэнфорд и команда YouCubed создали одни из лучших ресурсов для своей недели вдохновляющей математики. Нам повезло жить в эпоху легкого доступа к недавно созданным ресурсам, которые мы можем сразу использовать в нашем классе.
Несмотря на все ресурсы, созданные в последнее время, я думаю, что есть кое-что, чего не хватает большинству учителей математики в своих первых сообщениях ученикам о математике.По моему опыту, многие студенты — даже студенты высших учебных заведений — имеют неправильное представление о том, что такое математика и чем занимаются математики. Как только я проясню это заблуждение и дам последовательную информацию о нашей работе на уроке математики, я обнаружу, что все больше учеников вовлекаются в работу, чтобы стать математиками. Это послание ученикам в конечном итоге изменило меня как учителя и то, что я решаю предложить им, когда они изучают математику.
Как только я проясню это заблуждение и дам последовательную информацию о нашей работе на уроке математики, я обнаружу, что все больше учеников вовлекаются в работу, чтобы стать математиками. Это послание ученикам в конечном итоге изменило меня как учителя и то, что я решаю предложить им, когда они изучают математику.
Что такое математика? Вам нужно сделать на этой неделе 1!
У меня есть пара постов первой недели с кучей просмотров за последний год.Многим из вас нравится мое групповое задание 100# за первую неделю, и вы использовали палатки с моим именем для налаживания отношений со студентами. То, что следует дальше, может быть, более важно для меня на первой неделе. Это послание продолжается в течение всего учебного года. Именно так я задаю тон тому, как будет выглядеть работа вашего класса в течение всего учебного года. Вот как это происходит в течение первой недели в школе. Я дам вам своего рода сценарий.
- В первый или второй день я даю это домашнее задание (HW #1 Что такое математика я называю их ежедневными практическими заданиями, а не домашней работой) своим ученикам.
 « Сегодня вечером я хочу, чтобы ты выполнил это домашнее задание. Есть 2 правила. Вы не можете использовать свои телефоны или компьютеры для поиска ответов. Я просто хочу знать твои настоящие мысли. Также вам необходимо задать и записать вопрос как минимум 2 людям, которые не находятся в South HS. Спросите свою младшую сестру, позвоните бабушке или дяде, перейдите улицу и спросите своего любопытного соседа. Завтра я попрошу вас сообщить, что вы услышали ».
« Сегодня вечером я хочу, чтобы ты выполнил это домашнее задание. Есть 2 правила. Вы не можете использовать свои телефоны или компьютеры для поиска ответов. Я просто хочу знать твои настоящие мысли. Также вам необходимо задать и записать вопрос как минимум 2 людям, которые не находятся в South HS. Спросите свою младшую сестру, позвоните бабушке или дяде, перейдите улицу и спросите своего любопытного соседа. Завтра я попрошу вас сообщить, что вы услышали ». - На следующий день я начинаю урок с этих гифок, где дети впервые едят лимоны.(кстати, таких гифок полно — просто погуглите «дети едят лимон». Кто знал, что это такое.)
— проведите пальцем влево/вправо, чтобы увидеть больше
После размещения этих GIF-файлов я говорю: «Что общего между этими тремя GIF-файлами? Как вы думаете, какое отношение они имеют к математике?» Я просто выслушиваю их идеи и говорю, что отвечу через несколько минут.
- После показа этих GIF-файлов я предлагаю учащимся встать и сравнить ответы с партнером по комнате (я ОБОЖАЮ стоять и говорить — скоро опубликую об этом).
 Затем я прошу класс выкрикнуть 20 вещей по математике — это , пока я записываю то, что они говорят, на смарт-доске. Я делал это на 5 занятиях в год в течение 15+ лет, и каждый год ответы были одинаковыми. Я записываю все, даже когда говорят: «Математика — это сложно». Большая часть того, что говорят учащиеся, относится к навыкам или понятиям (дроби, формы, сложение…) в математике или названиям математических занятий (геометрия, исчисление). Когда я нарисовал массу вещей, я сказал: » Да, математика — это все эти вещи.Сегодня я собираюсь дать вам общее определение, которое мы все будем использовать для математики в течение всего учебного года. Пожалуйста, запишите это в свой блокнот. Математика это…»
Затем я прошу класс выкрикнуть 20 вещей по математике — это , пока я записываю то, что они говорят, на смарт-доске. Я делал это на 5 занятиях в год в течение 15+ лет, и каждый год ответы были одинаковыми. Я записываю все, даже когда говорят: «Математика — это сложно». Большая часть того, что говорят учащиеся, относится к навыкам или понятиям (дроби, формы, сложение…) в математике или названиям математических занятий (геометрия, исчисление). Когда я нарисовал массу вещей, я сказал: » Да, математика — это все эти вещи.Сегодня я собираюсь дать вам общее определение, которое мы все будем использовать для математики в течение всего учебного года. Пожалуйста, запишите это в свой блокнот. Математика это…» - Затем я говорю: «У меня в классе есть одно правило. Все 50 минут каждый день мы будем заниматься математикой. Мы выступим в роли математиков. Все, что мешает нам всем быть математиками, меня будет раздражать. Итак, нам также нужно знать, чем занимаются математики.
 Есть 3 вещи, которыми занимаются математики.Как вы думаете, что они собой представляют?
Есть 3 вещи, которыми занимаются математики.Как вы думаете, что они собой представляют? - Затем я раскрываю каждую из трех вещей, которые делают математики, и говорю что-то вроде…. «Первое, что делают математики, — замечают закономерности. У вас была способность замечать закономерности с рождения. Вы уже математик. Замечать закономерности — врожденная способность. Также как младенцы, которые едят лимоны, всегда корчат одинаковые лица. Этому лицу их никто не учит, они просто делают это. Точно так же вы всегда были математиком.У каждого есть способность замечать закономерности. Все. Я ожидаю, что вы будете вести себя как математик каждый день и работать, чтобы замечать. Второе, чем занимаются математики, — это описание закономерностей. Каждый день на этом занятии вы будете описывать то, что вы заметили. Вы можете описать его любым удобным для вас способом. Не беспокойтесь об использовании правильных слов. Это может помочь вам сказать, что вы заметили, используя правильный математический язык.
 Большинство из вас пришли на урок математики уже очень хорошо в этих первых двух аспектах математики.Я ожидаю, что вы будете делать это каждый день в этом классе. Третье, что делают математики – это обобщают закономерности. Это та часть, с которой многие из нас борются. Не волнуйтесь, к концу этого учебного года вы будете действительно хороши в этом. Я в порядке. Обещаю, это будет легко, если ты пообещаешь продолжать замечать и описывать».
Большинство из вас пришли на урок математики уже очень хорошо в этих первых двух аспектах математики.Я ожидаю, что вы будете делать это каждый день в этом классе. Третье, что делают математики – это обобщают закономерности. Это та часть, с которой многие из нас борются. Не волнуйтесь, к концу этого учебного года вы будете действительно хороши в этом. Я в порядке. Обещаю, это будет легко, если ты пообещаешь продолжать замечать и описывать».
Затем я говорю: «Каждый день на уроке математики от вас ожидают, что вы будете действовать как математик. Я ожидаю, что вы заметите и опишете модели и отношения.Я помогу вам с академическим языком, который вам нужен, а также обобщить. Как ваш учитель, если я не ставлю перед вами что-то, чтобы вы замечали каждый день, вам нужно связаться с мистером Апонте (нашим директором) и сказать ему, что я плохой учитель математики и не учу вас математике. Математики замечают, описывают и обобщают». - Затем я вывешиваю плакаты с этим в холле за моей дверью и в паре мест в моей комнате.
 Этот замечательный блоггер по математике из Миннесоты, Грета Бергман, пришла на один из моих тренингов и услышала мое сообщение в начале года об определении математики, и она превратила его в отличный постер в формате pdf.Вы можете увидеть ее запись в блоге об этом ЗДЕСЬ или скачать ее прекрасный постер прямо ЗДЕСЬ: Плакат «Математика — это узоры»
Этот замечательный блоггер по математике из Миннесоты, Грета Бергман, пришла на один из моих тренингов и услышала мое сообщение в начале года об определении математики, и она превратила его в отличный постер в формате pdf.Вы можете увидеть ее запись в блоге об этом ЗДЕСЬ или скачать ее прекрасный постер прямо ЗДЕСЬ: Плакат «Математика — это узоры» - После определения математики и того, чем занимаются математики, я говорю «Сегодня мы снова начнем практиковать математику после длинное лето. Начнем с этой числовой последовательности. ЧТО ДАЛЬШЕ? Что ты заметил?» Некоторое время я молча жду и часто говорю: «Руки не поднимайте». Моя цель состоит в том, чтобы удалить скорость как ценность в моем классе. Немного погодя я говорю: «Какое число будет следующим?» Наиболее распространенный ответ – «8 и 10».Я говорю: «Опишите, почему». Ученики делают то, что я комментирую их мысли. Затем я говорю: «Кто видел этот шаблон?» Большинство людей поднимают руки, и я говорю: «Отлично, видите ли, вы математики, вы заметили и описали закономерность.
 Как мы можем это обобщить?» Затем я продолжаю обобщать то, что они говорят словами, а также как «2n», если «n» — это число терминов. Мы также добавляем к этому академическое слово «четные числа». Затем я говорю: «Кто-нибудь получил что-то отличное от 8 и 10, чтобы заполнить пробелы?».У меня всегда поднимается несколько рук. Самый нормальный альтернативный ответ — «10 и 16». Затем я прошу учащихся описать, откуда они взялись, и сказать: «Много раз в этом классе будет несколько правильных ответов. Если вы можете описать закономерность, которую вы заметили, вы математик. Иногда я выбираю один конкретный ответ, чтобы мы сосредоточились на нем, чтобы мы могли изучить математику в углубленном курсе алгебры. Если я не использую шаблон, который вы заметили первым, не волнуйтесь, вы не ошиблись, мы просто сосредоточимся на чем-то другом в течение дня.
Как мы можем это обобщить?» Затем я продолжаю обобщать то, что они говорят словами, а также как «2n», если «n» — это число терминов. Мы также добавляем к этому академическое слово «четные числа». Затем я говорю: «Кто-нибудь получил что-то отличное от 8 и 10, чтобы заполнить пробелы?».У меня всегда поднимается несколько рук. Самый нормальный альтернативный ответ — «10 и 16». Затем я прошу учащихся описать, откуда они взялись, и сказать: «Много раз в этом классе будет несколько правильных ответов. Если вы можете описать закономерность, которую вы заметили, вы математик. Иногда я выбираю один конкретный ответ, чтобы мы сосредоточились на нем, чтобы мы могли изучить математику в углубленном курсе алгебры. Если я не использую шаблон, который вы заметили первым, не волнуйтесь, вы не ошиблись, мы просто сосредоточимся на чем-то другом в течение дня. - После того, как в течение многих лет я давал версию этого сообщения, я посмотрел выступление Энни Феттер Ignite под названием «Когда-нибудь замечали, чему они удивляются».
 Я не могу поверить, что есть еще люди, которые этого не видели, но если вы этого не сделали, остановитесь и посмотрите прямо сейчас. Это всего 5 минут. Видео Энни дало название сообщению, которое я делал много лет назад. Мой любимый вопрос в классе уже был «Что вы замечаете?». С тех пор я добавил другие любимые вопросы «Что вас интересует?» и мой новый фаворит «Что еще?»
Я не могу поверить, что есть еще люди, которые этого не видели, но если вы этого не сделали, остановитесь и посмотрите прямо сейчас. Это всего 5 минут. Видео Энни дало название сообщению, которое я делал много лет назад. Мой любимый вопрос в классе уже был «Что вы замечаете?». С тех пор я добавил другие любимые вопросы «Что вас интересует?» и мой новый фаворит «Что еще?»
- В течение следующих 10 дней в школе я кладу кое-что перед учениками, чтобы они их заметили.Каждый день я повторяю определение математики и три вещи, которые делают математики. Каждый день я спрашиваю: «Что ты замечаешь?» и дайте учащимся пространство для заметок. Я хожу по комнате, ловлю на себе внимание студентов и говорю: «Вы математик! Вы описали то, что заметили…».
 Моя цель — поймать каждого ученика, действующего как математик, и назвать его, когда я его увижу. Я хочу изменить то, как они считают себя математиками.
Моя цель — поймать каждого ученика, действующего как математик, и назвать его, когда я его увижу. Я хочу изменить то, как они считают себя математиками. - Это сообщение также в значительной степени является итогом моего плана управления поведением в классе.Все, что мешает всем нам действовать как математики в течение полных 50 минут, меня раздражает. Поэтому опоздания раздражают. Нахождение в социальных сетях раздражает. Спать раздражает. Любая отстраненность раздражает. Я говорю студентам, что все, кроме того, чтобы быть математиком в течение 50 минут, для меня неприемлемо.
- Мои сообщения об определении математики также меняют мое планирование как учителя. У меня должно быть несколько возможностей на каждом уроке, чтобы ученики могли заметить и удивиться.Я часто работаю с директорами и другими людьми, которые наблюдают за учителями, и я говорю им: каждый раз, когда вы наблюдаете за уроком математики, если учитель не спрашивает какую-то форму «Что вы заметили?» учеников, то урок математики не так хорош, как мог бы быть.
 Они не дают учащимся возможности стать математиками и владеть собственным изучением математики. Когда вы планируете урок в этом учебном году, я рекомендую вам начать с такого вопроса: «Какую математику я попрошу учащихся обратить внимание сегодня?» и/или «Как мне настроить эту математическую концепцию, чтобы мои ученики что-то знали?» замечать?’.
Они не дают учащимся возможности стать математиками и владеть собственным изучением математики. Когда вы планируете урок в этом учебном году, я рекомендую вам начать с такого вопроса: «Какую математику я попрошу учащихся обратить внимание сегодня?» и/или «Как мне настроить эту математическую концепцию, чтобы мои ученики что-то знали?» замечать?’. - Предостережение. Легко попросить студентов всегда практиковать то, о чем я говорю, используя числовые последовательности. Будьте осторожны с этим. Если вы сделаете это, то мощная способность учащихся замечать закономерности скажет им, что математика — это только числовые последовательности. По этой причине я смешиваю вещи первые несколько недель. Я использую все виды вещей. Некоторые из них связаны с контентом, который мы изучаем, а некоторые — глупые вещи, которые я нахожу в твиттере или фейсбуке. Вот несколько примеров.Большинство используют максимум 5-10 минут занятий. Моя цель — убедить студентов, что они математики и способны замечать и удивляться.

- Первое изображение, которое я получил от Кристофера Дэниелсона. Что ты заметил? Сколько авокадо? Как вы увидели такое количество авокадо?
- Я нашел этот знак в каком-то твите. Я спрашиваю: «Что вы заметили? Затем я редактирую фотографию и спрашиваю: «Сколько будет стоить «Привет, один маленький кофе»?» «Обоснуйте эту стоимость».
— Листайте влево/вправо, чтобы увидеть больше
- Я разместил первое изображение зеленой рубашки, которое Кристен Фусс написала в Твиттере, и спросила: «Что вы заметили?» Я продолжаю вопрос Джима Пардуна: «Если схема сохранится, сколько билетов вы могли бы получить за 40 долларов?» и попросите партнеров обосновать свою сумму на доске.
— Проведите влево/вправо, чтобы увидеть больше
- Я даю партнерам-учащимся следующие 3 графика и уравнения в факторизованной форме и спрашиваю: «Что вы заметили?» Я спрашиваю студентов: «Как мы можем найти координаты вершины, если все, что у нас есть, — это уравнение в факторизованной форме?» Студентам не требуется много времени, чтобы заметить, что вершина находится посередине двух х-пересечений/корней.
 В ходе 10-минутного обсуждения учащиеся открывают визуальный метод нахождения вершины без необходимости преобразования формы уравнения.
В ходе 10-минутного обсуждения учащиеся открывают визуальный метод нахождения вершины без необходимости преобразования формы уравнения. - В этом изображении много шаблонов. Я сделал это из снимков экрана с этого крутого анимированного сайта факторизации. Вы видите закономерности в строках и столбцах? Я использую это в начале своего раздела по экспоненциальным и степенным функциям. Многое, что можно заметить и описать… и обобщить. Много шансов попрактиковаться в математике.
- Если вы не следите за хэштегами #cthenc (обдумать, а затем вычислить) и #connecingreps (соединить представления) — 2 учебные программы из бесплатного онлайн-курса по математике New Visions — в Твиттере, то вы многое упускаете. чтобы учащиеся смотрели, чтобы замечать, удивляться, а затем вычислять.
- Любой вопрос «Какой из них не принадлежит?» отлично подходит для практики в математике.
- Я нашел эту фотографию, опубликованную родственником, любящим домашних животных, на Facebook.
 Я скрыл часть информации. Попросите учащихся замечать и удивляться. Вы не можете не попытаться придать этому какой-то смысл. Затем я добавляю дополнительную информацию, используя одну из этих фотографий за раз.
Я скрыл часть информации. Попросите учащихся замечать и удивляться. Вы не можете не попытаться придать этому какой-то смысл. Затем я добавляю дополнительную информацию, используя одну из этих фотографий за раз.— проведите влево/вправо, чтобы увидеть больше
Когда я открываю вторую фотографию (2 фрагмента данных), ученики хотят сделать это линейным и найти скорость изменения — даже без моего ведома их тоже.Третья фотография раскрывается позже, и студенты раздражены (что мне нравится)… но они действуют как математики (и я называю это в их честь) и критически думают о том, чтобы понять смысл данных.
- Одна важная вещь, которой я научился у Энни Феттер, Макса Рэя и всех других замечательных людей на The Math Forum, заключается в том, чтобы превращать задачи в сценарии (удалить все вопросы и некоторые детали) и спросить, что вы замечаете и что вы делаете. удивляться. Вот исходная задача. По моему опыту, за 5 минут наблюдения и размышлений ученики решают все эти вопросы без моего предварительного ответа.
 Они также видят больше вещей, чем это. Они спрашивают/говорят: «Это прямоугольные треугольники?», «Интересно, можем ли мы использовать теорему Пифагора». Я даю информацию типа «эти треугольники похожи», когда учащиеся замечают детали. Я даю вопрос для решения после того, как они сказали его первым. Попробуйте сами. Создавайте «сценарии» вместо вопросов. Посмотрите, как это изменит способность ваших учеников считать себя математиками.
Они также видят больше вещей, чем это. Они спрашивают/говорят: «Это прямоугольные треугольники?», «Интересно, можем ли мы использовать теорему Пифагора». Я даю информацию типа «эти треугольники похожи», когда учащиеся замечают детали. Я даю вопрос для решения после того, как они сказали его первым. Попробуйте сами. Создавайте «сценарии» вместо вопросов. Посмотрите, как это изменит способность ваших учеников считать себя математиками. - Любой шаблон от Visual Patterns был бы потрясающим.
Замечать, что закономерности идут не так, как надо
Один из моих основных посылов в первый день, первую неделю, первый месяц: «Мы все математики. У всех нас есть способность замечать, описывать и обобщать закономерности. Вы все обладали этой способностью с рождения». Один из способов убедиться в этом основан на том, насколько сильны ошибочные представления учащихся о математике. Я бы сказал, что большинство, если не все неверные представления возникают из-за того, что они действуют как математики и замечают закономерности, данные им их учителями. Вот пример того, что я имею в виду.
Вот пример того, что я имею в виду.
За последние 20 лет было написано множество статей об улучшении понимания учащимися концепции равенства, но я считаю, что многие учителя не знают о нашей роли в создании этого заблуждения. Студенты часто создавали неправильное представление о знаке равенства, замечая закономерности в работе, которую мы им давали. Если большая часть наших работ для студентов выглядит так…
— Листайте влево/вправо, чтобы увидеть больше
. .неудивительно, что студенты создали неправильное представление о знаке равенства.Они просто заметили, что для решения математических задач я просто делаю то, что слева.
.неудивительно, что студенты создали неправильное представление о знаке равенства.Они просто заметили, что для решения математических задач я просто делаю то, что слева.
Хорошей новостью об ошибках наших учеников является то, что они умеют замечать закономерности. Нам нужно видеть активы наших студентов, а не их недостатки. Таким образом, задача для нас, учителей математики, состоит в том, чтобы представить нашим ученикам вещи, чтобы они заметили, что не создает неправильных представлений, когда наши ученики замечают закономерности. С тех пор, как я понял это много лет назад, я всегда пишу уравнения разными способами. Например, y=2x + 3 vs.3 + 2x = y, чтобы линейные уравнения не начинались с y=.
Вот еще несколько классических способов, которыми мы, учителя, создаем математические заблуждения.
Загуглите «область рабочего листа треугольника» и посмотрите на подавляющее большинство задач, заданных учащимся. Неудивительно, что студенты думают, что «основание» означает «дно» треугольника.
Будьте осторожны, чтобы не привести примеры, которые могут дать правильные ответы при неправильном выполнении задачи. Вот 2 классики….
Ответственность учителей.
Если вы согласны с идеей, что «математика — это изучение закономерностей» и что «математики замечают, описывают и обобщают закономерности», то это изменит ваш подход к обучению. Если мы верим в это, то каждый день мы должны планировать уроки, которые позволяют ученикам действовать как математики. Мы должны поставить что-то перед нашими учениками, чтобы они их заметили. Мы должны что-то ставить перед нашими учениками, чтобы описать, обобщить. Как мы можем ожидать, что наши ученики станут математиками, если мы будем замечать и описывать за них.Мой опыт показывает, что учащиеся чувствуют себя увереннее в своих способностях к математике, когда мы позволяем им действовать как математики каждый божий день в наших классах. Этот процесс замечать, описывать и обобщать становится для них все легче и легче.
Задача на новый учебный год.
В этом учебном году я призываю вас начать учебный год с определения математики и роли математика. Дайте своим ученикам общую картину и не начинайте с деталей. Мы, учителя математики, склонны относиться к определению математики как к набору деталей и не дорожим нашими учениками, которым необходимо видеть общую картину того, что такое математика, чтобы добиться успеха.Дополнительные ресурсы:
- Этим летом я читал книгу Трейси Джонстон Загер « Как стать учителем математики, которого вы хотели бы иметь» , и она потрясающая. Вам нужно заказать его и прочитать сегодня. Первая глава книги касается определения математики, начиная с определения ее собственной матери. В этой книге есть и другие замечательные материалы, подтверждающие то, о чем я говорил выше, более подробно.
— проведите влево/вправо, чтобы увидеть больше
- Математика как наука о закономерностях от Математической ассоциации Америки (MAA)«Математики теперь рассматривают свою работу как изучение паттернов — реальных или воображаемых, визуальных или мысленных, возникающих из мира природы или из человеческого разума».
 Используя это основное определение в качестве своей центральной темы, Девлин исследует модели счета, измерения, рассуждения, движения, формы, положения и предсказания, раскрывая мощное влияние математики на наше восприятие реальности. Переплетая исторические события и современные разработки и используя минимум формул, Девлин прославляет точность, чистоту и элегантность математики.
Используя это основное определение в качестве своей центральной темы, Девлин исследует модели счета, измерения, рассуждения, движения, формы, положения и предсказания, раскрывая мощное влияние математики на наше восприятие реальности. Переплетая исторические события и современные разработки и используя минимум формул, Девлин прославляет точность, чистоту и элегантность математики.
Дополнение: Сегодня моя подруга Лора Вагенман разместила на Facebook это замечательное видео «Математика есть». Люблю, когда другие находят ресурсы, связанные с моими увлечениями. Дайте ему представление.
Что такое математическое моделирование? | Общество промышленной и прикладной математики
Сокращенное описание процесса для новичков
Математическое моделирование относится к процессу создания математического представления сценария реального мира для прогнозирования или получения информации. Существует различие между применением формулы и фактическим созданием математической зависимости. Некоторые графические иллюстрации процесса моделирования можно увидеть на этой странице.
Существует различие между применением формулы и фактическим созданием математической зависимости. Некоторые графические иллюстрации процесса моделирования можно увидеть на этой странице.
Реальные запутанные проблемы можно решать с помощью математики, что приводит к ряду возможных решений, помогающих принимать решения. И учащимся, и учителям иногда не нравится понятие математического моделирования, потому что оно настолько открыто. Такое количество неизвестной информации кажется запредельным.И какие факторы наиболее важны? Но именно этот открытый характер реальных проблем приводит к развитию и применению навыков решения проблем, творчества, инноваций и математики.
Математическое моделирование можно рассматривать как повторяющийся процесс, состоящий из следующих компонентов. (Обратите внимание, что слово «этапы» намеренно опущено, чтобы подчеркнуть отсутствие предписанного порядка этих компонентов, поскольку некоторые из них могут выполняться одновременно, а некоторые могут повторяться. )
)
- Идентификация проблемы Поскольку проблемы моделирования открыты, разработчик модели должен быть конкретным в определении того, что он хотел бы выяснить.
- Делайте предположения и идентифицируйте переменные Поскольку невозможно учесть все важные факторы в данной ситуации, разработчик модели должен сделать выбор, что включить в свое представление реального мира. Создание предположений помогает выявить переменные, которые будут учитываться, а также уменьшить их количество, решив не включать все. В рамках этого процесса отношения между переменными будут возникать на основе наблюдений, физических законов или упрощений.
- Займитесь математикой В конце концов связь между вводом и выводом позволит найти решение.
- Анализ и оценка решения При рассмотрении результатов и выводов, полученных с помощью модели, возникает вопрос, имеет ли ответ смысл.
- Итерация Обычно модель можно уточнить и повторить процесс для улучшения производительности модели.

- Реализация модели и отчет о результатах Четкий отчет о модели и ее реализации делает модель понятной для других.
Одной из самых больших ловушек при разработке разумной модели является тайм-менеджмент. Когда моделирование является новым для студентов, они легко могут быть перегружены. Они могут проводить слишком много времени «в сорняках». Чтобы определить краткую постановку проблемы, учащиеся должны провести мозговой штурм, и их следует поощрять не выбрасывать какие-либо идеи. Однако бывают случаи, когда учащиеся могут увязнуть в попытке включить переменные или отношения в свою модель, которые не поддаются обработке или данные по которым просто недоступны.На этом этапе учащиеся должны сделать предположение и двигаться дальше. Они должны размышлять над этими предположениями после прохождения всего процесса моделирования. При этом иногда учащиеся включают в свою документацию ненужные допущения, которые никогда явно не используются в процессе моделирования. Это также может отнять драгоценное время и отвлечь внимание от представления решения. Учащиеся могут сбиться с пути при создании моделей, в частности делая выбор или делая предположения, которые подрывают качество решения.
Это также может отнять драгоценное время и отвлечь внимание от представления решения. Учащиеся могут сбиться с пути при создании моделей, в частности делая выбор или делая предположения, которые подрывают качество решения.
Когда учащиеся испытывают нехватку времени, опасения могут привести к математическим отношениям, далеким от реальности. Нередко можно увидеть бессмысленной математики . Например, учащиеся могут сформировать аддитивную связь между ключевыми переменными, которые они определили, но единицы измерения не имеют смысла (например, добавление долларов к времени для получения модели ресурсов). Коэффициенты часто используются в моделях, которые также неправильно отражают единицы измерения или не имеют обоснования того, почему они были выбраны.В других случаях учащиеся могут иметь здравую идею математических отношений, но затем чрезмерно усложняют ее, чтобы математика выглядела более сложной (например, вводя тройной интеграл, когда на самом деле уместно сложение). Это еще одна причина, по которой так важно оставлять время для размышлений, чтобы учащийся мог прочитать свое решение целиком и спросить себя: «Имеет ли это смысл?»
Это еще одна причина, по которой так важно оставлять время для размышлений, чтобы учащийся мог прочитать свое решение целиком и спросить себя: «Имеет ли это смысл?»
Работа с данными также может быть сложной. У студентов может быть блестящая идея для модели, но они не могут найти данные, необходимые для ее продвижения вперед (опять же, на этом этапе они должны сделать предположение и перестать тратить время на поиски).В других случаях наборы данных могут быть непомерно большими, а учащиеся не оснащены инструментами для интерпретации ключевых тенденций. Линейная регрессия или полиномы высокой степени часто используются для подбора данных без какой-либо веской причины, а затем используются в качестве предикторов. Связь с лежащей в основе физической проблемой может быть потеряна, или качество подгонки может быть полностью проигнорировано.
Все вышеперечисленные подводные камни (это далеко не исчерпывающий список) могут быть исправлены, если команда отразит качество своей работы. Если предположение кажется несостоятельным, учащиеся могут честно сообщить о выявленных недостатках своего подхода и указать путь к улучшениям, даже если у них нет для этого средств или доступа к информации. Более того, анализ чувствительности может помочь учащемуся оценить надежность своей модели и прокомментировать ее применимость. Многое из этого относится к тайм-менеджменту.
Если предположение кажется несостоятельным, учащиеся могут честно сообщить о выявленных недостатках своего подхода и указать путь к улучшениям, даже если у них нет для этого средств или доступа к информации. Более того, анализ чувствительности может помочь учащемуся оценить надежность своей модели и прокомментировать ее применимость. Многое из этого относится к тайм-менеджменту.
Имея больше опыта моделирования, учащиеся, естественно, приобретут навыки и уверенность, которые могут решить эти проблемы.
* Написано для краткого изложения семинара, 2021 г., Кэти Кавана и Беном Галлуццо, Университет Кларксона, и основано на идеях, представленных в GAIMME : Руководство по оценке и обучению математическому моделированию, издание 4 90

 WriteLine(myVar2)
' The code produces the following output:
' 3
WriteLine(myVar2)
' The code produces the following output:
' 3
 Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN
Sqrt(-4)
Console.WriteLine(mySqrt1)
Console.WriteLine(mySqrt2)
Console.WriteLine(mySqrt3)
Console.WriteLine(mySqrt4)
' The code produces the following output:
' 2
' 4.79583152331272
' 0
' NaN

 Она
потребуется первокурснику в сентябре для прохождения диспансеризации, а также
необходима при заселении в общежитие.
Она
потребуется первокурснику в сентябре для прохождения диспансеризации, а также
необходима при заселении в общежитие.
 ham
ham
 « Сегодня вечером я хочу, чтобы ты выполнил это домашнее задание. Есть 2 правила. Вы не можете использовать свои телефоны или компьютеры для поиска ответов. Я просто хочу знать твои настоящие мысли. Также вам необходимо задать и записать вопрос как минимум 2 людям, которые не находятся в South HS. Спросите свою младшую сестру, позвоните бабушке или дяде, перейдите улицу и спросите своего любопытного соседа. Завтра я попрошу вас сообщить, что вы услышали ».
« Сегодня вечером я хочу, чтобы ты выполнил это домашнее задание. Есть 2 правила. Вы не можете использовать свои телефоны или компьютеры для поиска ответов. Я просто хочу знать твои настоящие мысли. Также вам необходимо задать и записать вопрос как минимум 2 людям, которые не находятся в South HS. Спросите свою младшую сестру, позвоните бабушке или дяде, перейдите улицу и спросите своего любопытного соседа. Завтра я попрошу вас сообщить, что вы услышали ». Затем я прошу класс выкрикнуть 20 вещей по математике — это , пока я записываю то, что они говорят, на смарт-доске. Я делал это на 5 занятиях в год в течение 15+ лет, и каждый год ответы были одинаковыми. Я записываю все, даже когда говорят: «Математика — это сложно». Большая часть того, что говорят учащиеся, относится к навыкам или понятиям (дроби, формы, сложение…) в математике или названиям математических занятий (геометрия, исчисление). Когда я нарисовал массу вещей, я сказал: » Да, математика — это все эти вещи.Сегодня я собираюсь дать вам общее определение, которое мы все будем использовать для математики в течение всего учебного года. Пожалуйста, запишите это в свой блокнот. Математика это…»
Затем я прошу класс выкрикнуть 20 вещей по математике — это , пока я записываю то, что они говорят, на смарт-доске. Я делал это на 5 занятиях в год в течение 15+ лет, и каждый год ответы были одинаковыми. Я записываю все, даже когда говорят: «Математика — это сложно». Большая часть того, что говорят учащиеся, относится к навыкам или понятиям (дроби, формы, сложение…) в математике или названиям математических занятий (геометрия, исчисление). Когда я нарисовал массу вещей, я сказал: » Да, математика — это все эти вещи.Сегодня я собираюсь дать вам общее определение, которое мы все будем использовать для математики в течение всего учебного года. Пожалуйста, запишите это в свой блокнот. Математика это…»  Есть 3 вещи, которыми занимаются математики.Как вы думаете, что они собой представляют?
Есть 3 вещи, которыми занимаются математики.Как вы думаете, что они собой представляют?  Большинство из вас пришли на урок математики уже очень хорошо в этих первых двух аспектах математики.Я ожидаю, что вы будете делать это каждый день в этом классе. Третье, что делают математики – это обобщают закономерности. Это та часть, с которой многие из нас борются. Не волнуйтесь, к концу этого учебного года вы будете действительно хороши в этом. Я в порядке. Обещаю, это будет легко, если ты пообещаешь продолжать замечать и описывать».
Большинство из вас пришли на урок математики уже очень хорошо в этих первых двух аспектах математики.Я ожидаю, что вы будете делать это каждый день в этом классе. Третье, что делают математики – это обобщают закономерности. Это та часть, с которой многие из нас борются. Не волнуйтесь, к концу этого учебного года вы будете действительно хороши в этом. Я в порядке. Обещаю, это будет легко, если ты пообещаешь продолжать замечать и описывать».  Этот замечательный блоггер по математике из Миннесоты, Грета Бергман, пришла на один из моих тренингов и услышала мое сообщение в начале года об определении математики, и она превратила его в отличный постер в формате pdf.Вы можете увидеть ее запись в блоге об этом ЗДЕСЬ или скачать ее прекрасный постер прямо ЗДЕСЬ: Плакат «Математика — это узоры»
Этот замечательный блоггер по математике из Миннесоты, Грета Бергман, пришла на один из моих тренингов и услышала мое сообщение в начале года об определении математики, и она превратила его в отличный постер в формате pdf.Вы можете увидеть ее запись в блоге об этом ЗДЕСЬ или скачать ее прекрасный постер прямо ЗДЕСЬ: Плакат «Математика — это узоры» Как мы можем это обобщить?» Затем я продолжаю обобщать то, что они говорят словами, а также как «2n», если «n» — это число терминов. Мы также добавляем к этому академическое слово «четные числа». Затем я говорю: «Кто-нибудь получил что-то отличное от 8 и 10, чтобы заполнить пробелы?».У меня всегда поднимается несколько рук. Самый нормальный альтернативный ответ — «10 и 16». Затем я прошу учащихся описать, откуда они взялись, и сказать: «Много раз в этом классе будет несколько правильных ответов. Если вы можете описать закономерность, которую вы заметили, вы математик. Иногда я выбираю один конкретный ответ, чтобы мы сосредоточились на нем, чтобы мы могли изучить математику в углубленном курсе алгебры. Если я не использую шаблон, который вы заметили первым, не волнуйтесь, вы не ошиблись, мы просто сосредоточимся на чем-то другом в течение дня.
Как мы можем это обобщить?» Затем я продолжаю обобщать то, что они говорят словами, а также как «2n», если «n» — это число терминов. Мы также добавляем к этому академическое слово «четные числа». Затем я говорю: «Кто-нибудь получил что-то отличное от 8 и 10, чтобы заполнить пробелы?».У меня всегда поднимается несколько рук. Самый нормальный альтернативный ответ — «10 и 16». Затем я прошу учащихся описать, откуда они взялись, и сказать: «Много раз в этом классе будет несколько правильных ответов. Если вы можете описать закономерность, которую вы заметили, вы математик. Иногда я выбираю один конкретный ответ, чтобы мы сосредоточились на нем, чтобы мы могли изучить математику в углубленном курсе алгебры. Если я не использую шаблон, который вы заметили первым, не волнуйтесь, вы не ошиблись, мы просто сосредоточимся на чем-то другом в течение дня.  Я не могу поверить, что есть еще люди, которые этого не видели, но если вы этого не сделали, остановитесь и посмотрите прямо сейчас. Это всего 5 минут. Видео Энни дало название сообщению, которое я делал много лет назад. Мой любимый вопрос в классе уже был «Что вы замечаете?». С тех пор я добавил другие любимые вопросы «Что вас интересует?» и мой новый фаворит «Что еще?»
Я не могу поверить, что есть еще люди, которые этого не видели, но если вы этого не сделали, остановитесь и посмотрите прямо сейчас. Это всего 5 минут. Видео Энни дало название сообщению, которое я делал много лет назад. Мой любимый вопрос в классе уже был «Что вы замечаете?». С тех пор я добавил другие любимые вопросы «Что вас интересует?» и мой новый фаворит «Что еще?» Моя цель — поймать каждого ученика, действующего как математик, и назвать его, когда я его увижу. Я хочу изменить то, как они считают себя математиками.
Моя цель — поймать каждого ученика, действующего как математик, и назвать его, когда я его увижу. Я хочу изменить то, как они считают себя математиками. Они не дают учащимся возможности стать математиками и владеть собственным изучением математики. Когда вы планируете урок в этом учебном году, я рекомендую вам начать с такого вопроса: «Какую математику я попрошу учащихся обратить внимание сегодня?» и/или «Как мне настроить эту математическую концепцию, чтобы мои ученики что-то знали?» замечать?’.
Они не дают учащимся возможности стать математиками и владеть собственным изучением математики. Когда вы планируете урок в этом учебном году, я рекомендую вам начать с такого вопроса: «Какую математику я попрошу учащихся обратить внимание сегодня?» и/или «Как мне настроить эту математическую концепцию, чтобы мои ученики что-то знали?» замечать?’.
 В ходе 10-минутного обсуждения учащиеся открывают визуальный метод нахождения вершины без необходимости преобразования формы уравнения.
В ходе 10-минутного обсуждения учащиеся открывают визуальный метод нахождения вершины без необходимости преобразования формы уравнения. Я скрыл часть информации. Попросите учащихся замечать и удивляться. Вы не можете не попытаться придать этому какой-то смысл. Затем я добавляю дополнительную информацию, используя одну из этих фотографий за раз.
Я скрыл часть информации. Попросите учащихся замечать и удивляться. Вы не можете не попытаться придать этому какой-то смысл. Затем я добавляю дополнительную информацию, используя одну из этих фотографий за раз. Они также видят больше вещей, чем это. Они спрашивают/говорят: «Это прямоугольные треугольники?», «Интересно, можем ли мы использовать теорему Пифагора». Я даю информацию типа «эти треугольники похожи», когда учащиеся замечают детали. Я даю вопрос для решения после того, как они сказали его первым. Попробуйте сами. Создавайте «сценарии» вместо вопросов. Посмотрите, как это изменит способность ваших учеников считать себя математиками.
Они также видят больше вещей, чем это. Они спрашивают/говорят: «Это прямоугольные треугольники?», «Интересно, можем ли мы использовать теорему Пифагора». Я даю информацию типа «эти треугольники похожи», когда учащиеся замечают детали. Я даю вопрос для решения после того, как они сказали его первым. Попробуйте сами. Создавайте «сценарии» вместо вопросов. Посмотрите, как это изменит способность ваших учеников считать себя математиками.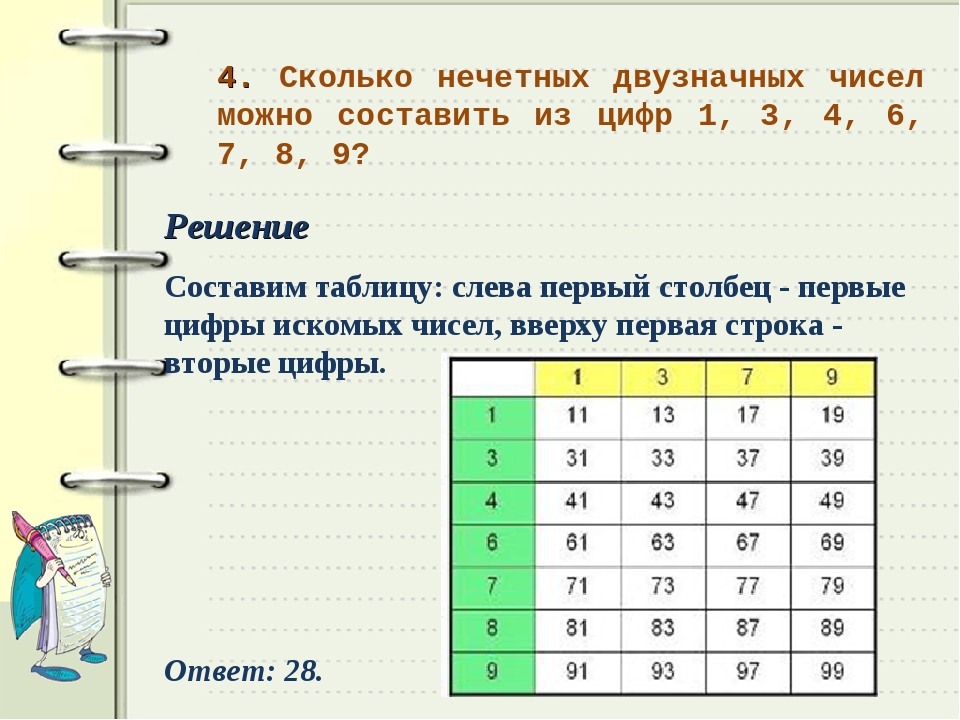 Используя это основное определение в качестве своей центральной темы, Девлин исследует модели счета, измерения, рассуждения, движения, формы, положения и предсказания, раскрывая мощное влияние математики на наше восприятие реальности. Переплетая исторические события и современные разработки и используя минимум формул, Девлин прославляет точность, чистоту и элегантность математики.
Используя это основное определение в качестве своей центральной темы, Девлин исследует модели счета, измерения, рассуждения, движения, формы, положения и предсказания, раскрывая мощное влияние математики на наше восприятие реальности. Переплетая исторические события и современные разработки и используя минимум формул, Девлин прославляет точность, чистоту и элегантность математики.