Умножение степеней с одинаковыми основаниями . Видеоурок. Алгебра 7 Класс
На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства 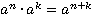 . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
. Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула 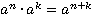 )
)
Основные определения:
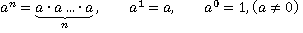
Здесь a — основание степени,
n — показатель степени,
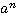 — n-ая степень числа.
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:

По-иному: если а – любое число; n и k натуральные числа, то:

Отсюда правило 1:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Разъясняющие примеры:
1) 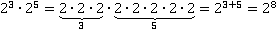
2) 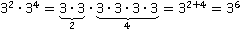
Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
Дано число а – любое; числа n и k – натуральные. Доказать:
Доказательство основано на определении степени.
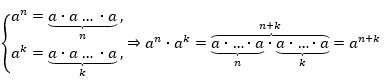
То есть
Пример 1: Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
а) 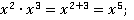
б) 
в)
г) 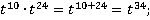
д) 
е) 
ж)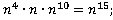
Здесь использовано обобщение:
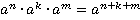
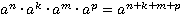
з)
и) 
к)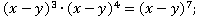
л) 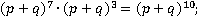
м)
Пример 2: Вычислите (можно использовать таблицу основных степеней).
а)  (по таблице)
(по таблице)
б) 
Пример 3: Запишите в виде степени с основанием 2.
а) 
б) 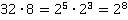
в)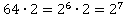
г)
Пример 4: Определите знак числа:
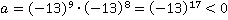 , а – отрицательное, так как показатель степени при -13 нечетный.
, а – отрицательное, так как показатель степени при -13 нечетный.
По-иному:
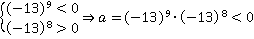
Пример 5: Замените (·) степенью числа с основанием r:

Имеем 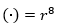 , то есть
, то есть  .
.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Школьный помощник (Источник).
2. Testent.ru (Источник).
3. Математика-повторение (Источник).
Рекомендованное домашнее задание
1. Представьте в виде степени:
а)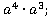 б)
б) 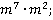 в)
в) 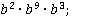 г)
г) д)
д) 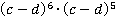
2. Вычислите:
а) 

3. Запишите в виде степени с основанием 2:
а)  б)
б) 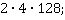
4. Определите знак числа:
а) 
5. Замените (·) степенью числа с основанием r:
а) r4 · (·) = r15; б) (·) · r5 = r6
Умножение и деление степеней с одинаковыми основаниями
Умножение степеней с одинаковыми основаниями
При умножении степеней с одинаковыми основаниями их показатели складываются.
Рассмотрим, почему показатели складываются. Во-первых, возведение в степень — это сокращённая запись умножения:
23 = 2 · 2 · 2
Во-вторых, умножение числа самого на себя, имеющего при этом разные степени, означает, что это число берётся сомножителем столько раз, сколько указывают показатели степеней:
| 23 · 22 = | (2 · 2 · 2) | · | (2 · 2) | = | 2 · 2 · 2 · 2 · 2 | = 25 |
| 3 множ. | 2 множ. | 5 множ. |
Из примера становится понятно, что при сложении показателей степеней мы получаем общую сумму сомножителей, поэтому для любого выражения будет верна формула:
ax · ay = ax+y
Примеры умножения степеней
Пример 1. Запишите в виде степени:
n3n5
Решение:
n3n5 = n3 + 5 = n8
Пример 2. Упростите:
xy2z3x4y5z6
Решение: чтобы легче было провести умножение степеней с одинаковыми основаниями, можно сначала сгруппировать степени по основаниям:
(xx4)(y2y5)(z3z6)
Теперь выполним умножение степеней:
(xx4)(y2y5
Следовательно:
xy2z3x4y5z6 = x5y7z9
Пример 3. Выполните умножение:
а) nxn5; б) xxn; в) amam
Решение:
а) nxn5 = nx + 5
б) xxn = xn + 1
в) amam = am + m = a2m
Пример 4. Упростите выражение:
а) —a2 · (-a)2 · a; б) -(-a)2 · (-a) · a
Решение:
а) —a2 · (-a)2 · a = —a2 · a2 · a = -(a2a2a) = -(a2 + 2 + 1) = —a5
б) -(-a)2 · (-a) · a = —a2 · (-a) · a = a3 · a = a4
Деление степеней с одинаковыми основаниями
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Рассмотрим частное двух степеней с одинаковыми основаниями:
n12 : n5
где n – это число, не равное нулю, так как на 0 делить нельзя. Запишем частное в виде дроби:
Представим n12 в виде произведения n7 · n5. Тогда числитель и знаменатель дроби можно будет сократить на общий множитель n5:
| n12 | = | n7 · n5 | = n7 |
| n5 | n5 |
Верность совершённого действия легко проверить с помощью умножения:
n7 · n5 = n7+5 = n12
Следовательно, общая формула для деления степеней с одинаковым основанием будет выглядеть так:
ax : ay = ax-y
Примеры деления степеней
Пример 1. Частное степеней замените степенью с тем же основанием:
| а) | a5 | ; б) | m18 |
| a | m10 |
Решение:
| а) | a5 | = | a4 · a | = a4 |
| a | a |
| б) | m18 | = | m8 · m10 | = m8 |
| m10 | m10 |
Пример 2. Выполните деление:
а) x7 : x2; б) n10 : n5; в) a30 : a10
Решение:
а) x7 : x2 = x7 — 2 = x5
б) n10 : n5 = n10 — 5 = n5
в) a30 : a10 = a30 — 10 = a20
Пример 3. Чему равно значение выражения:
| а) | an | ; б) | mx | ; в) | b5 · b8 |
| a2 | m | b3 |
Решение:
| в) | b5 · b8 | = | b2 · b3 · b8 | = b2 · b8 = b10 |
| b3 | b3 |
naobumium.info
Степень — свойства, правила, действия и формулы

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом:
an = a * a * a * …an.
Причем, левая часть уравнения будет читаться, как a в степ. n.
Например:
- 23 = 2 в третьей степ. = 2 * 2 * 2 = 8;
- 42 = 4 в степ. два = 4 * 4 = 16;
- 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
- 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- an * am = (a)(n+m);
- an : am = (a)(n-m);
- (ab ) m=(a)(b*m).
Проверим на примерах:
23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
(23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 33 + 24 = 27 + 16 = 43;
- 52 – 32 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3)2 = 22 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.
Как производить вычисления в более сложных случаях? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.
Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: am/n.
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается:
A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.
И наоборот:
1 / A(-n) = An, 1 / 2(-3) = 23 = 8.
А если дробь?
(A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A0 = 1, 10 = 1; 20 = 1; 3.150 = 1; (-4)0 = 1…и т. д.
A1 = A, 11 = 1; 21 = 2; 31 = 3…и т. д.
Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: Am/n. Читается как: корень n-ой степени из числа A в степени m.

С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
- А˃1.
Аr1 ˂ Аα ˂ Аr2, r1 ˂ r2 – рациональные числа;
В этом случае наоборот: Аr2 ˂ Аα ˂ Аr1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r1 – в этом случае равно 3;
r2 – будет равно 4.
Тогда, при А = 1, 1π = 1.
А = 2, то 23 ˂ 2π ˂ 24, 8 ˂ 2π ˂ 16.
А = 1/2, то (½)4 ˂ (½)π ˂ (½)3, 1/16 ˂ (½)π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
1001student.ru
Умножение и деление чисел со степенями
Если вам нужно возвести какое-то конкретное число в степень, можете воспользоваться таблицей степеней натуральных чисел от 2 до 25 по алгебре. А сейчас мы более подробно остановимся на свойствах степеней.
Экспоненциальные числа открывают большие возможности, они позволяют нам преобразовать умножение в сложение, а складывать гораздо легче, чем умножать.
Например, нам надо умножить 16 на 64. Произведение от умножения этих двух чисел равно 1024. Но 16 – это 4×4, а 64 – это 4х4х4. То есть 16 на 64=4x4x4x4x4, что также равно 1024.
Число 16 можно представить также в виде 2х2х2х2, а 64 как 2х2х2х2х2х2, и если произвести умножение, мы опять получим 1024.
А теперь используем правило возведения числа в степень. 16=42, или 24, 64=43, или 26, в то же время 1024=64=45, или 210.
Следовательно, нашу задачу можно записать по-другому: 42х43=45 или 24х26=210, и каждый раз мы получаем 1024.
Мы можем решить ряд аналогичных примеров и увидим, что умножение чисел со степенями сводится к сложению показателей степени, или экспонент, разумеется, при том условии, что основания сомножителей равны.
Таким образом, мы можем, не производя умножения, сразу сказать, что 24х22х214=220.
Это правило справедливо также и при делении чисел со степенями, но в этом случае экспонента делителя вычитается из экспоненты делимого. Таким образом, 25:23=22, что в обычных числах равно 32:8=4, то есть 22. Подведем итоги:
amх an=am+n, am: an=am-n, где m и n — целые числа.
С первого взгляда может показаться, что такое умножение и деление чисел со степенями не очень удобно, ведь сначала надо представить число в экспоненциальной форме. Нетрудно представить в такой форме числа 8 и 16, то есть 23 и 24, но как это сделать с числами 7 и 17? Или как поступать в тех случаях, когда число можно представить в экспоненциальной форме, но основания экспоненциальных выражений чисел сильно различаются. Например, 8×9 – это 23х32, и в этом случае мы не можем суммировать экспоненты. Ни 25 и ни 35 не являются ответом, ответ также не лежит в интервале между этими двумя числами.
Тогда стоит ли вообще возиться с этим методом? Безусловно стоит. Он дает огромные преимущества, особенно при сложных и трудоемких вычислениях.
Для того чтобы легче было двигаться дальше, давайте подробнее рассмотрим понятие экспоненты и попробуем дать ей более обобщенное толкование.
До сих пор мы считали, что экспонента – это количество одинаковых сомножителей. В этом случае минимальная величина экспоненты – это 2. Однако если мы производим операцию деления чисел, или вычитания экспонент, то можем получить также число меньше 2, значит, старое определение нас больше не может устроить. Подробнее читайте в следующей статье.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…matemonline.com
Умножение и деление степеней
Вопросы занятия:
· познакомиться с правилами умножения и деления степеней с одинаковыми основаниями.
Материал урока
На прошлом уроке мы с вами ввели понятие степени с натуральным показателем.

Например,

Определение.

Также вспомним, что:

Например,

Сейчас мы выясним, как умножать и делить степени с натуральным показателем.
Преобразуем выражение:

Вообще, для любого числа а и натуральных чисел m и n верно равенство:

Таким образом, можно сформулировать правило.
При умножении степеней с одинаковыми основаниями основание остаётся прежним, а показатели степеней складываются.
Например,

Теперь давайте рассмотрим выражение:

То есть, мы получили, что частное двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.
Вообще,

Сформулируем правило деления степеней.
При делении степеней с одинаковыми основаниями основание остаётся прежним, а из показателя степени делимого вычитается показатель степени делителя.
Например,

Также, следует знать, что

Для закрепления нового материала выполним несколько упражнений.
Пример.

Пример.

videouroki.net
Как умножать степени | Алгебра
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
www.algebraclass.ru