Уравнение касательной к графику функции. Видеоурок. Алгебра 10 Класс
Тема: Производная
Урок: Уравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую  (см. рис.1).
(см. рис.1).
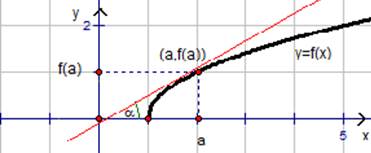
Рис. 1. График функции  .
.
Зафиксируем точку  . Если
. Если 
 . Значит, имеем точку с координатами (
. Значит, имеем точку с координатами (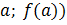 .
.Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции  в точке с абсциссой
в точке с абсциссой  , в которой
, в которой 
Уравнение касательной – это прямая, которая задается формулой 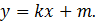
Любая прямая, в том числе и касательная, определяется двумя числами: и
и 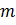 . Исходя из геометрического смысла производной
. Исходя из геометрического смысла производной  (тангенс угла наклона касательной) – это есть угловой коэффициент
(тангенс угла наклона касательной) – это есть угловой коэффициент  .
.
Параметр 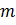
 , то есть
, то есть 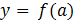 .
.  .
.
Стало быть 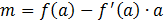 .
.
Запишем уравнение касательной
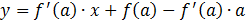 .
.
Или, 
Получили уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
– точка касания касательной и графика функции.
2)  — угловой коэффициент касательной к графику функции.
— угловой коэффициент касательной к графику функции.
3) 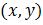 – произвольная точка на касательной.
– произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что 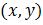
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Задача.
К кривой  в точке с абсциссой
в точке с абсциссой  провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
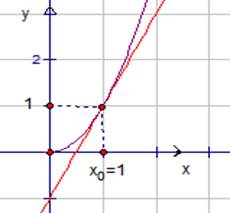
Рис. 2. Касательная к графику функции  .
.
Зафиксируем точку  . Значение функции в этой точке равно 1.
. Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти  и точку касания.
и точку касания.
 — дано.Точка касания: (
— дано.Точка касания: ( ;
;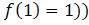
2) Найти производную в любой точке 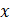 .
.
 .
.
3) Найти значение производной в точке с абсциссой  .
.
 .
.
4) Выписать и проанализировать уравнение касательной.
 .
.
Упрощаем и получаем: 
Ответ:  .
.
Задача 1.
Пусть дано уравнение касательной  .
.
Найдите точки пересечения касательной с осями координат.
Если  , то
, то  .
. 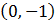 – это первая точка.
– это первая точка.
Если 
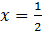 .
. 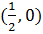 — вторая точка.
— вторая точка.Итак, первая точка – это точка 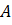 с координатами
с координатами 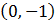 . Вторая точка – точка пересечения с осью
. Вторая точка – точка пересечения с осью 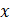 , точка
, точка  с координатами
с координатами 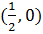

Рис.3. Точки пересечения касательной к графику функции  с осями координат. Задача 2.
с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка  .
.
Рассмотрим прямоугольный треугольник  (Рис. 3). Длина катета
(Рис. 3). Длина катета 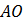
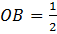 . Длину отрезка
. Длину отрезка  из прямоугольного треугольника найдем по теореме Пифагора:
из прямоугольного треугольника найдем по теореме Пифагора: 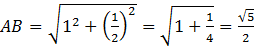
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника  (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
(Рис. 3) — площадь треугольника, образованного касательной и осями координат.
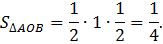
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник  . Радиус окружности, описанной около треугольника
. Радиус окружности, описанной около треугольника  .
.
Рассмотрим пример.
Дана функция  . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
. Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).

Рис. 4. Касательная к графику функции  .
.
Нахождение точки касания.
1.  Точка касания имеет координаты
Точка касания имеет координаты 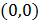 .
.
2. Найти 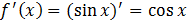 .
.
3. Найти 
И, последнее действие, – написать уравнение касательной.
4. 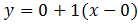 .
.
Упростим и получим 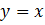 .
.
Заметим в точке 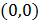 синусоида и касательная соприкасаются. В районе точки
синусоида и касательная соприкасаются. В районе точки  синусоида и прямая почти не различаются.
синусоида и прямая почти не различаются.
Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал Exponenta.ru (Источник).
Сделай дома
№ 43.22, 43.25 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
interneturok.ru
Касательная. Задачи на касательную | Статья в журнале «Молодой ученый»
Чтобы правильно и рационально решать задачи, связанные с уравнением касательной, нужно четко понимать, что такое касательная, владеть техникой составления уравнения касательной к графику функции и представлять себе, для решения каких задач (в том числе и задач с параметрами) можно использовать метод касательной.
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при

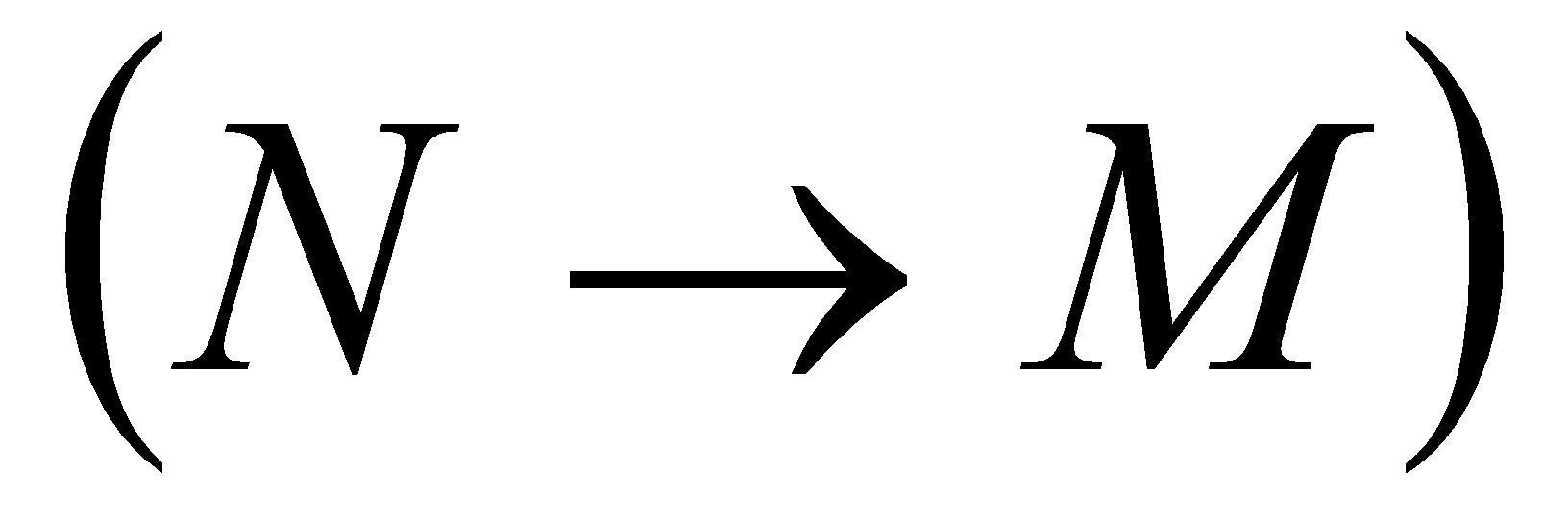 (рис. 1).
(рис. 1).

Рис. 1
Касательная к кривой может иметь с ней несколько общих точек или пересекать ее. Можно дать и другое определение касательной к кривой.
Опр. 2. Касательной к графику функции у = f(x) в точке A0(x0; f(x0)) называется прямая, проходящая через точку A0, угловой коэффициент которой равен значению производной функции у =f(x) в точке с абсциссой x0.
Уравнение
касательной
к кривой у =
f(x)
в точке с
абсциссой х0имеет вид:
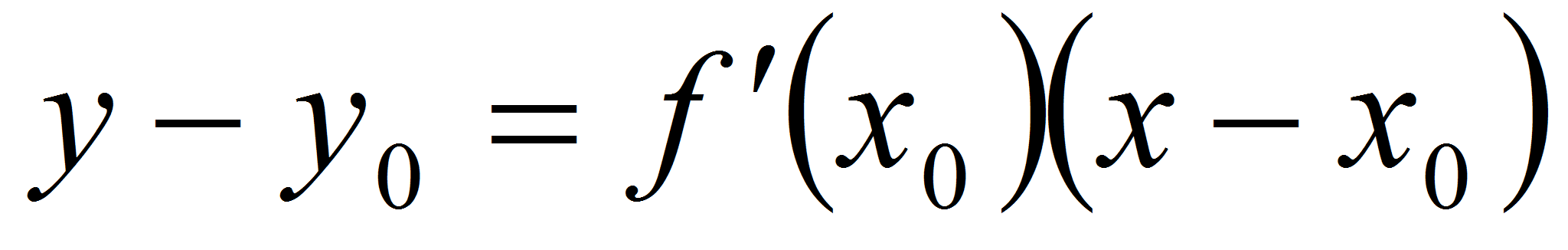 .
.
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
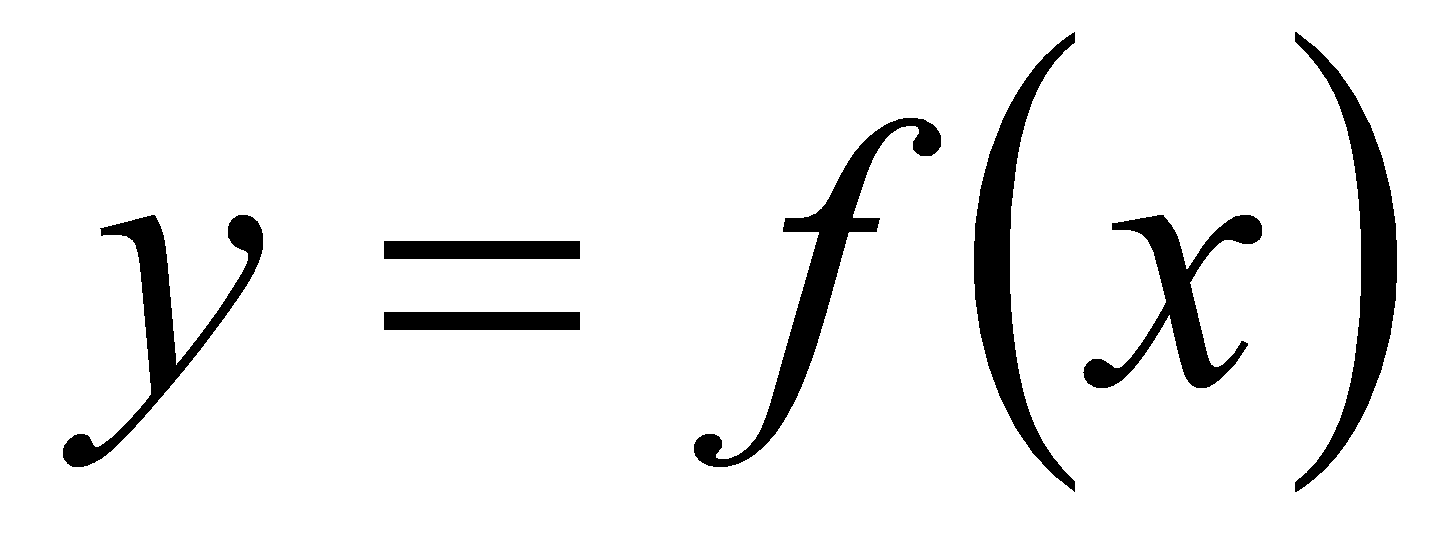 ,
причем ее
угловой коэффициент
равен
,
причем ее
угловой коэффициент
равен
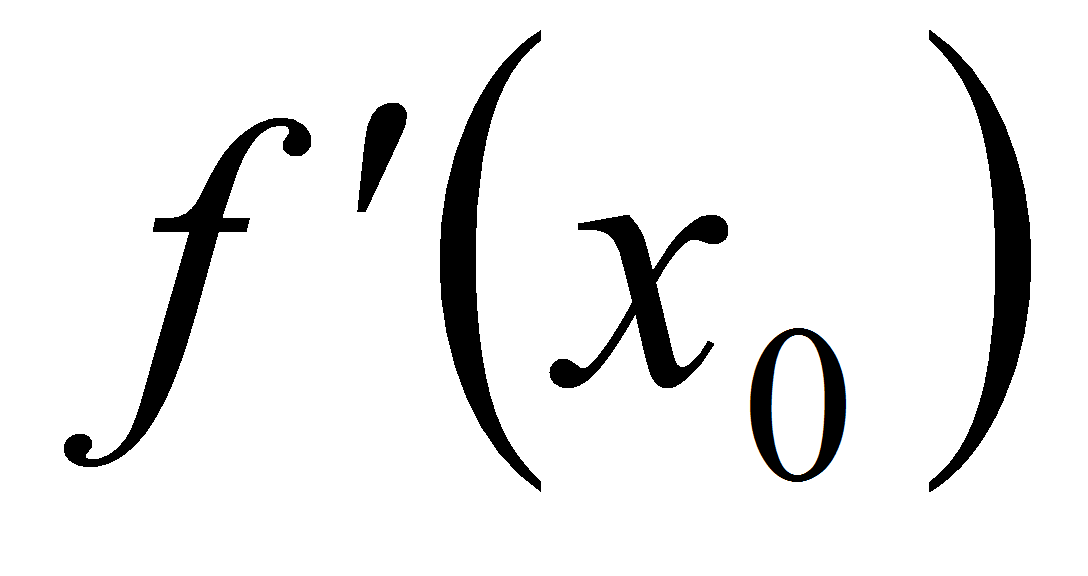 .
Вывод: если в точке х0
есть производная
функции
.
Вывод: если в точке х0
есть производная
функции
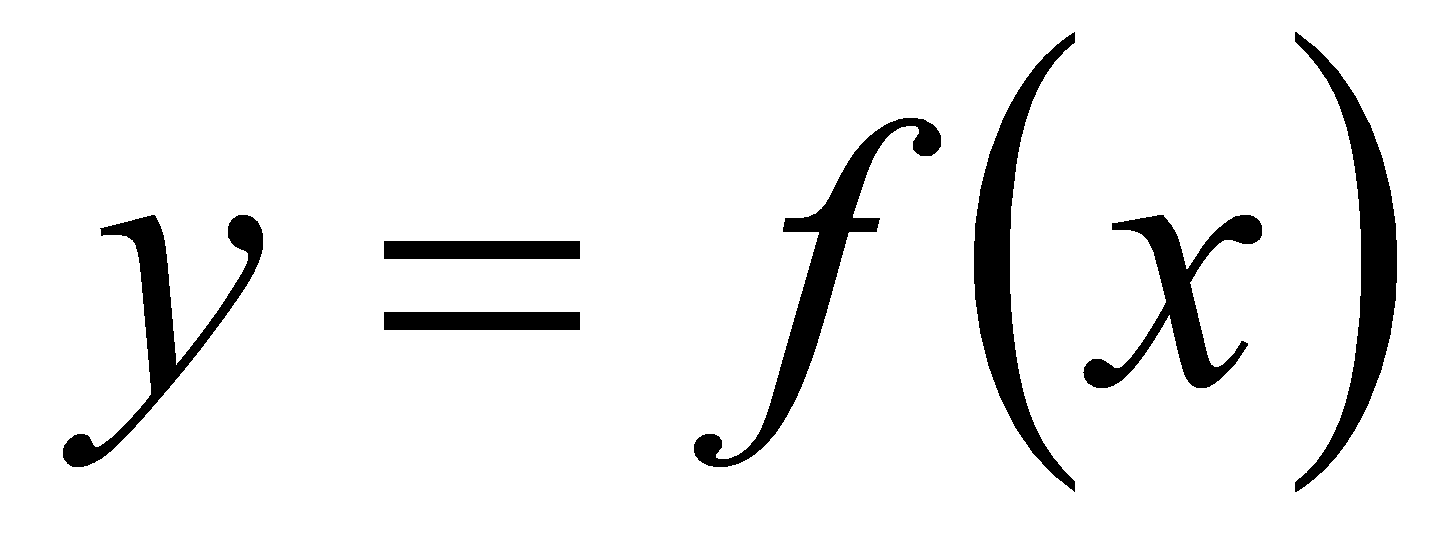 ,
то в точке с
этой абсциссой есть касательная к графику
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
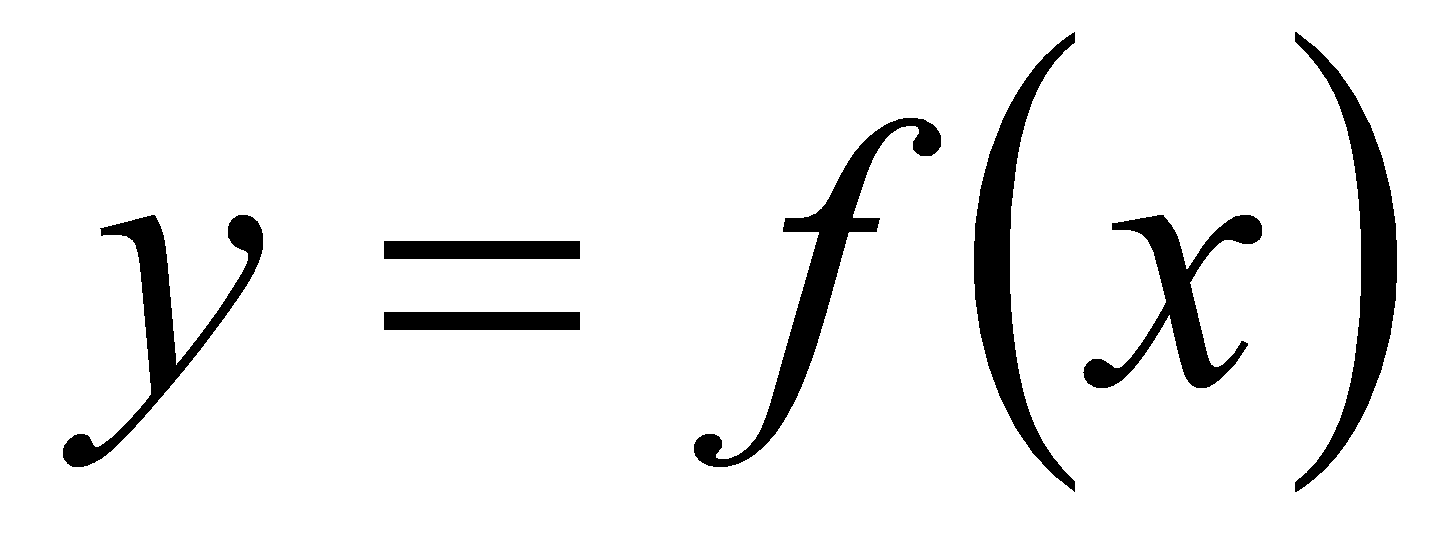 и наоборот; если
в точке х0
нет производной
функции
и наоборот; если
в точке х0
нет производной
функции
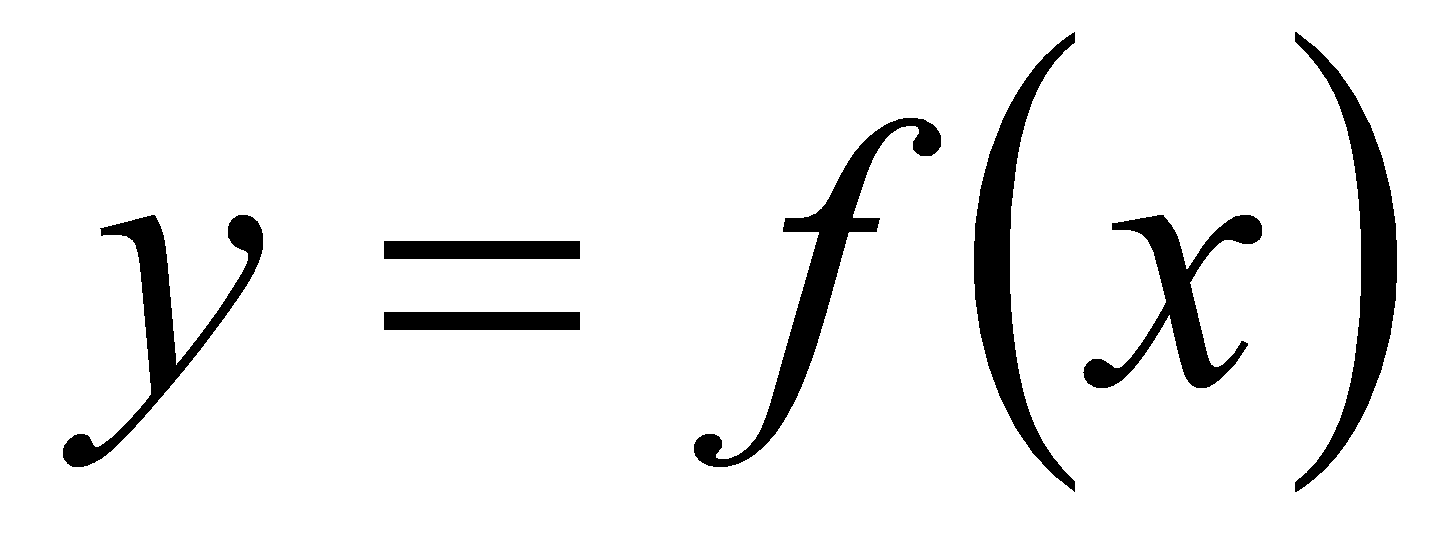 ,
то в точке с
этой абсциссой нет касательной к графику функции
,
то в точке с
этой абсциссой нет касательной к графику функции
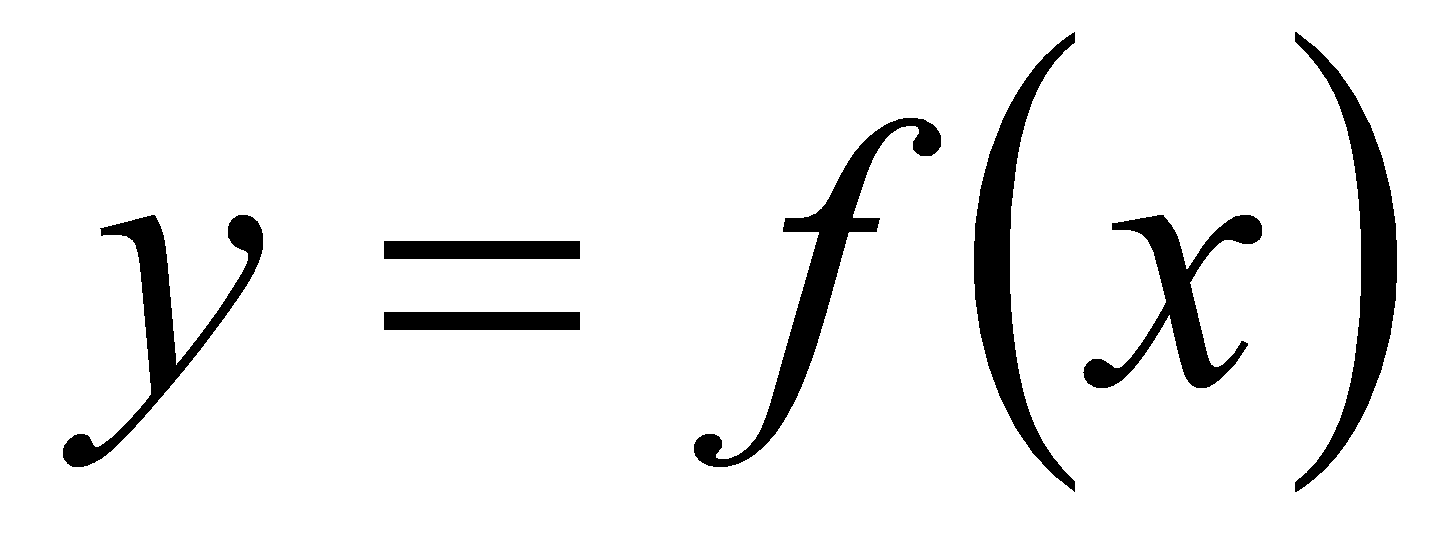 и наоборот.
и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).
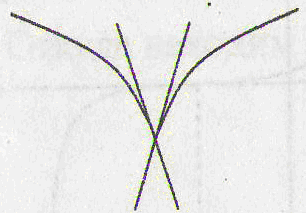

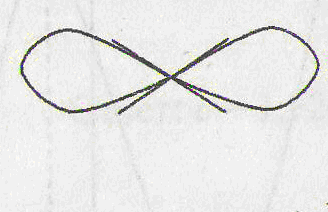
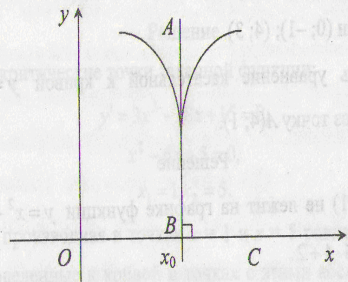
угловая точка
точка возврата узловая
точка

а) б) в) г)
Рис. 2
Рассмотрим решение некоторых задач.
Задачи, связанные с определением того, является ли прямая у = kx + b касательной к графику функции у = f(x). Можно указать два способа решения таких задач.
Находим общие точки графиков, т. е. решаем уравнение f(x) = kx + b, а затем для каждого из его решений вычисляем
 .
В тех случаях, когда
.
В тех случаях, когда
 = k,
имеет место касание, в других —
пересечение.
= k,
имеет место касание, в других —
пересечение.Находим корни уравнения
 = k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
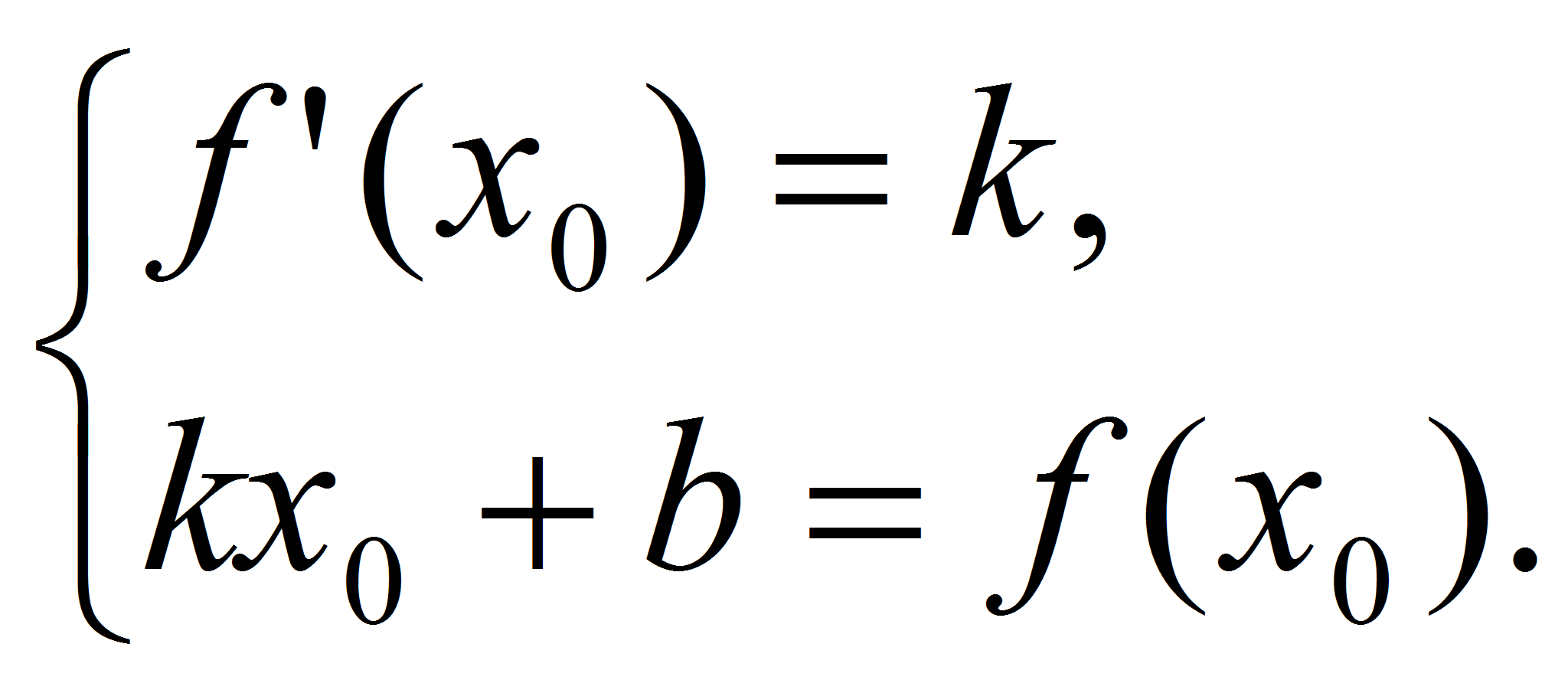
При каких значениях b прямая у = 3х +b является касательной к графику функции у =
 ?
?
Решение.
Записав условие касания
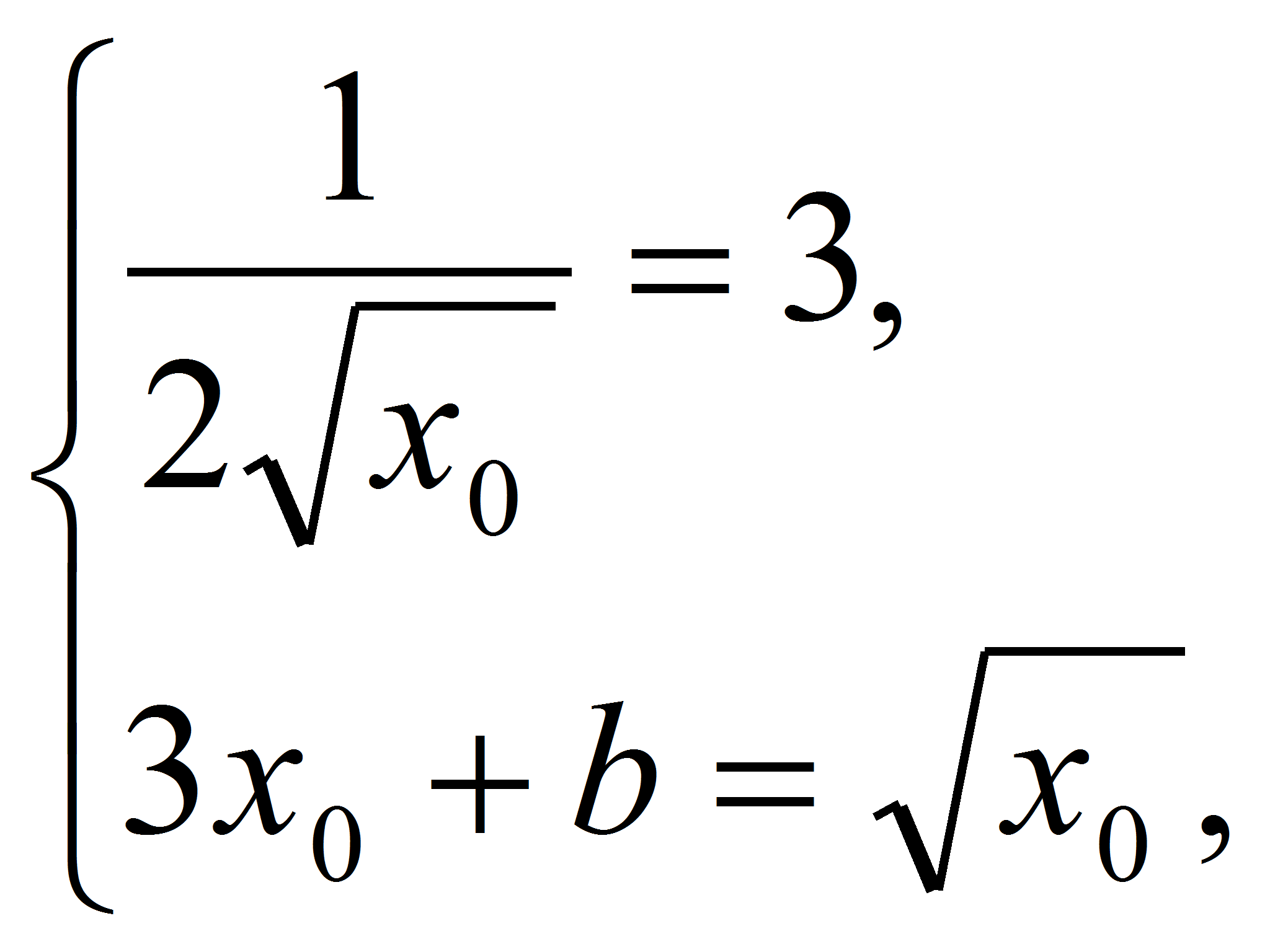 получим
получим
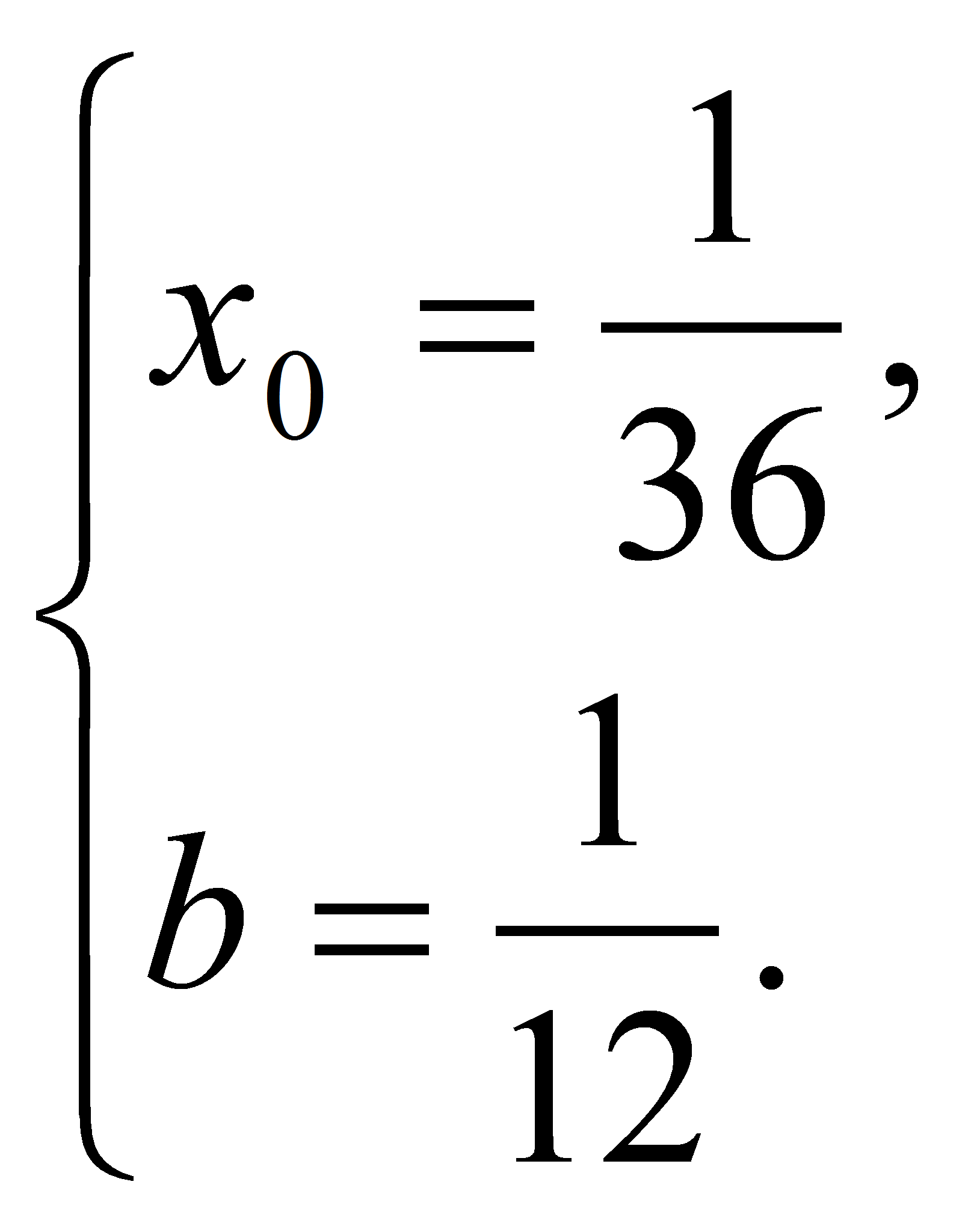
Ответ:
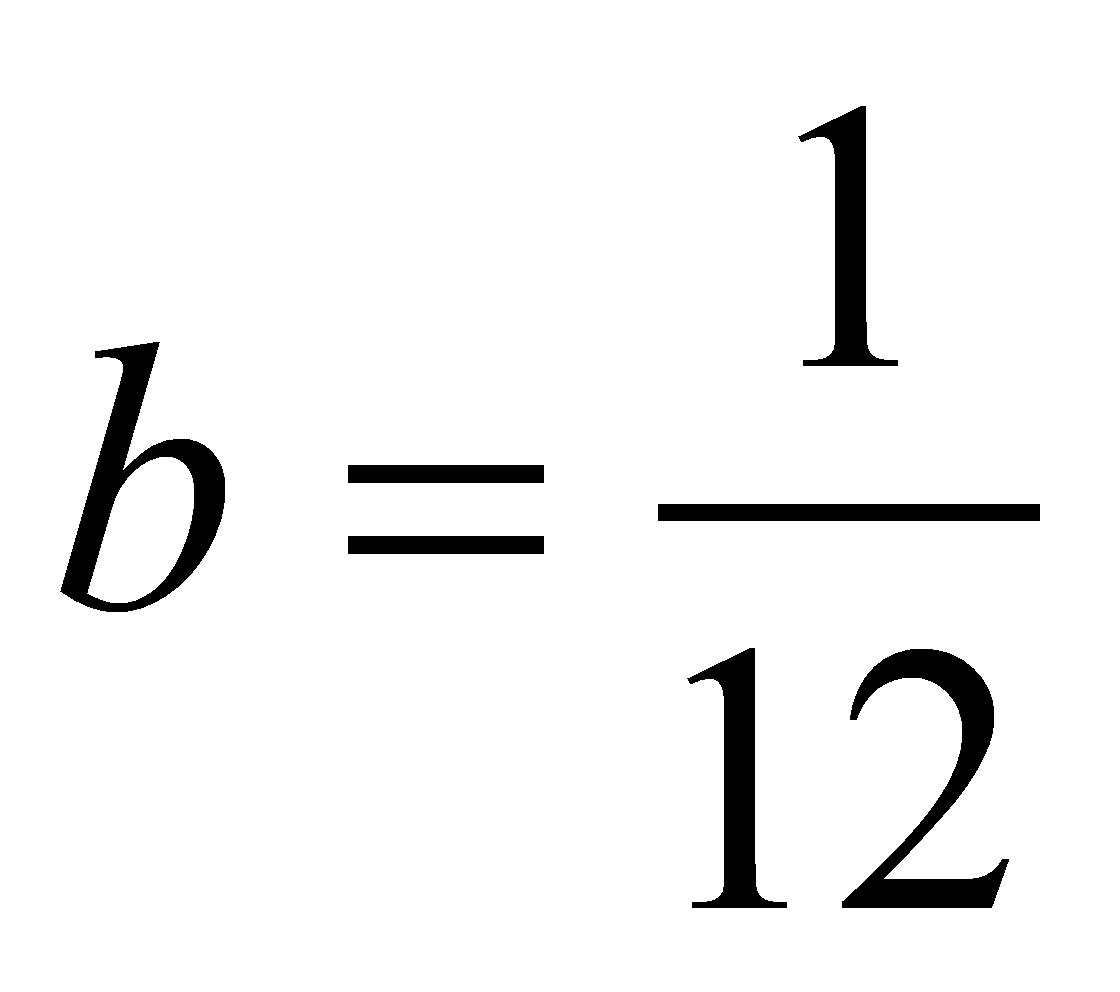 .
.
При каких значениях а прямая у=ах+2 является касательной к графику функции

Указание.
Ответ: а = e-3
При каких значениях а прямая
 является касательной к графику функции
является касательной к графику функции

Указание.
Ответ: а = 7 или а = -1.
Является ли прямая
 касательной к графику функции
касательной к графику функции
 ?
Если является, то найти координаты точки касания.
?
Если является, то найти координаты точки касания.
Решение.
Пусть
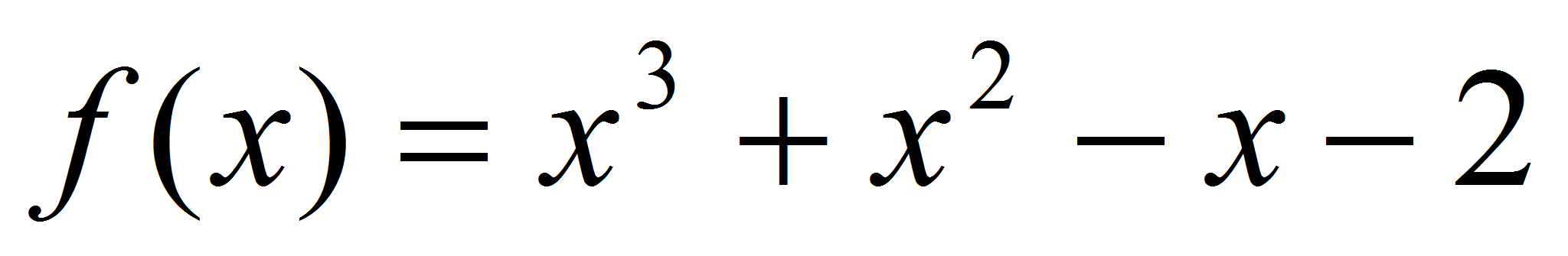 .
Из условия следует, что должны выполняться равенство
.
Из условия следует, что должны выполняться равенство
 ,
где
,
где
 -
возможная абсцисса точки касания. Имеем:
-
возможная абсцисса точки касания. Имеем:
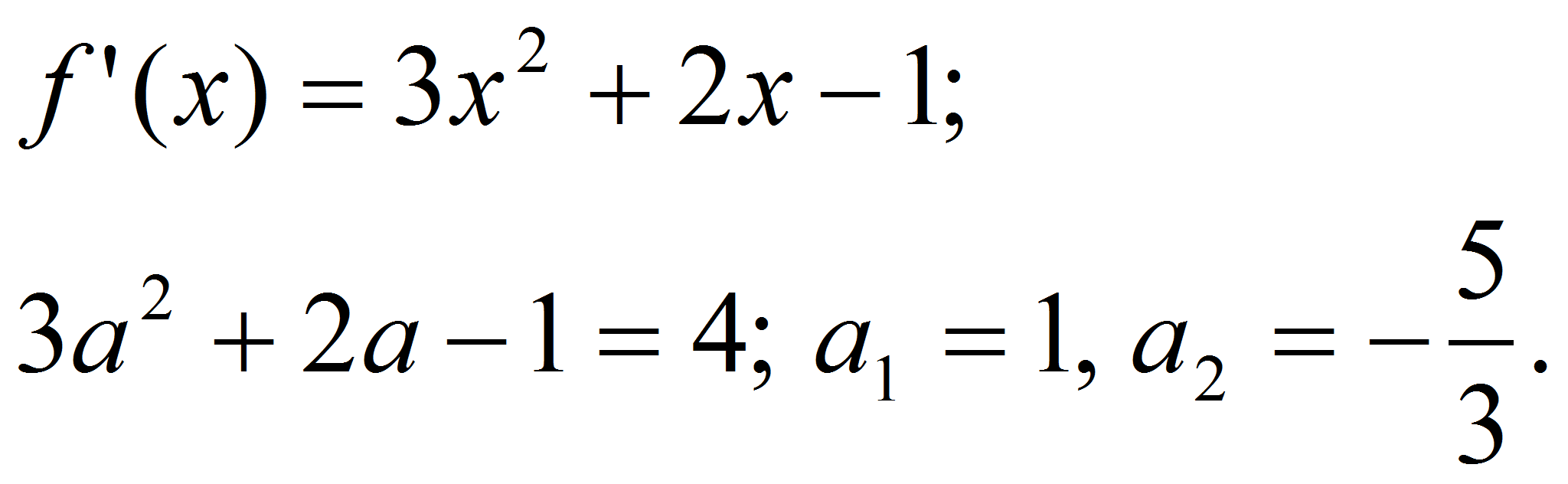
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
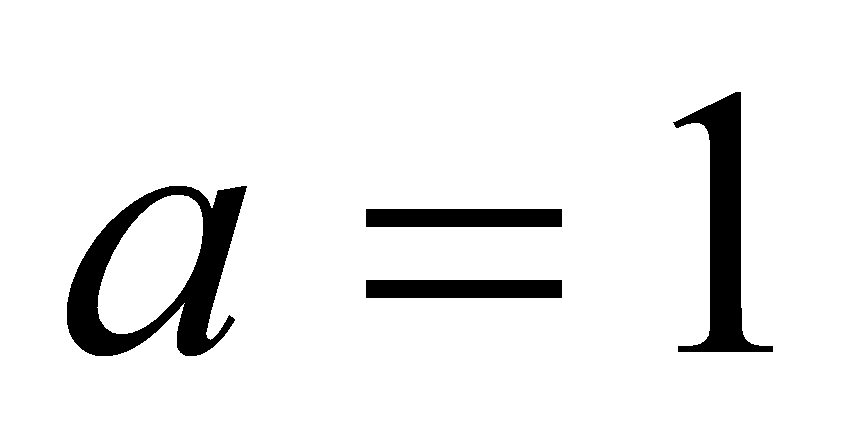 как раз и получится
как раз и получится
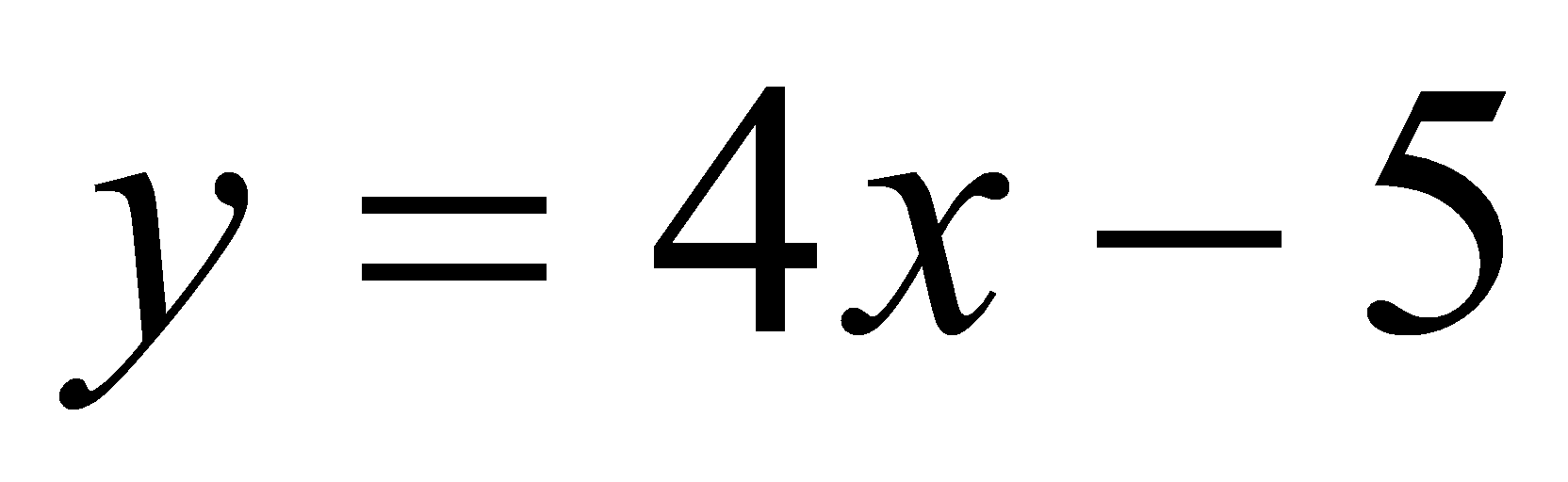 .
Значит, точка касания имеет координаты (1;-1).
.
Значит, точка касания имеет координаты (1;-1).
К графику функции
 проведена
касательная, параллельная прямой
проведена
касательная, параллельная прямой
 .
Найти ординату точки касания.
.
Найти ординату точки касания.
Решение.
 .
Абсцисса интересующей нас точки касания удовлетворяет уравнению
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
 .
Имеем:
.
Имеем:
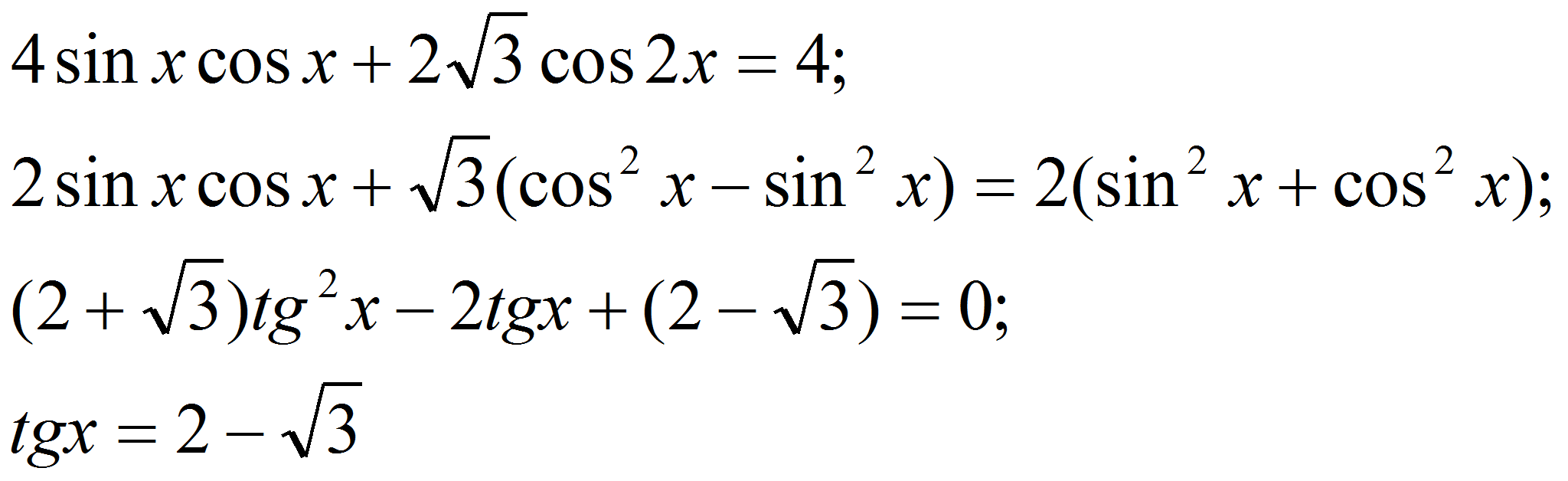
Таким образом,
 .
Значит,
.
Значит,
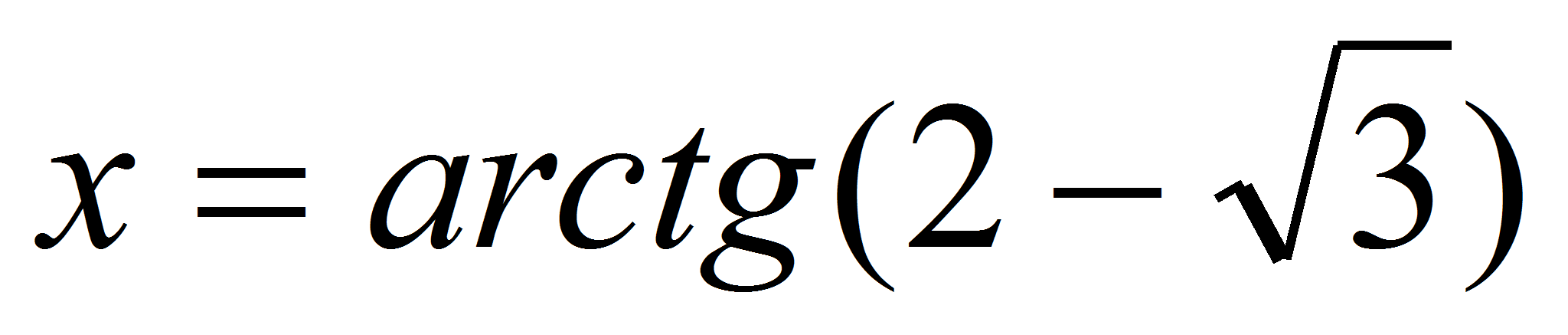 -
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
-
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
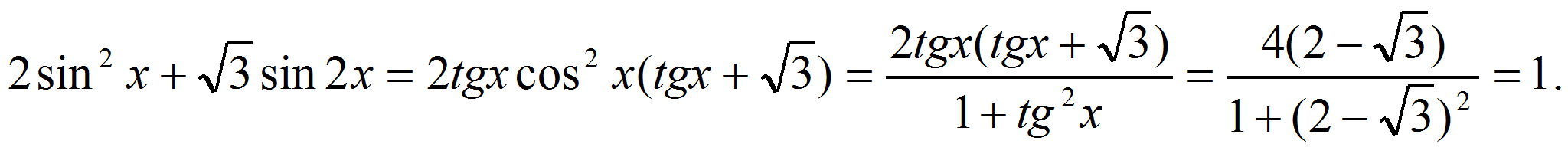
Ответ: 1.
Написать уравнение всех касательных к графику функции
 ,
параллельных прямой
,
параллельных прямой
 .
.
Решение.
Так как касательная должна быть параллельна прямой
 ,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
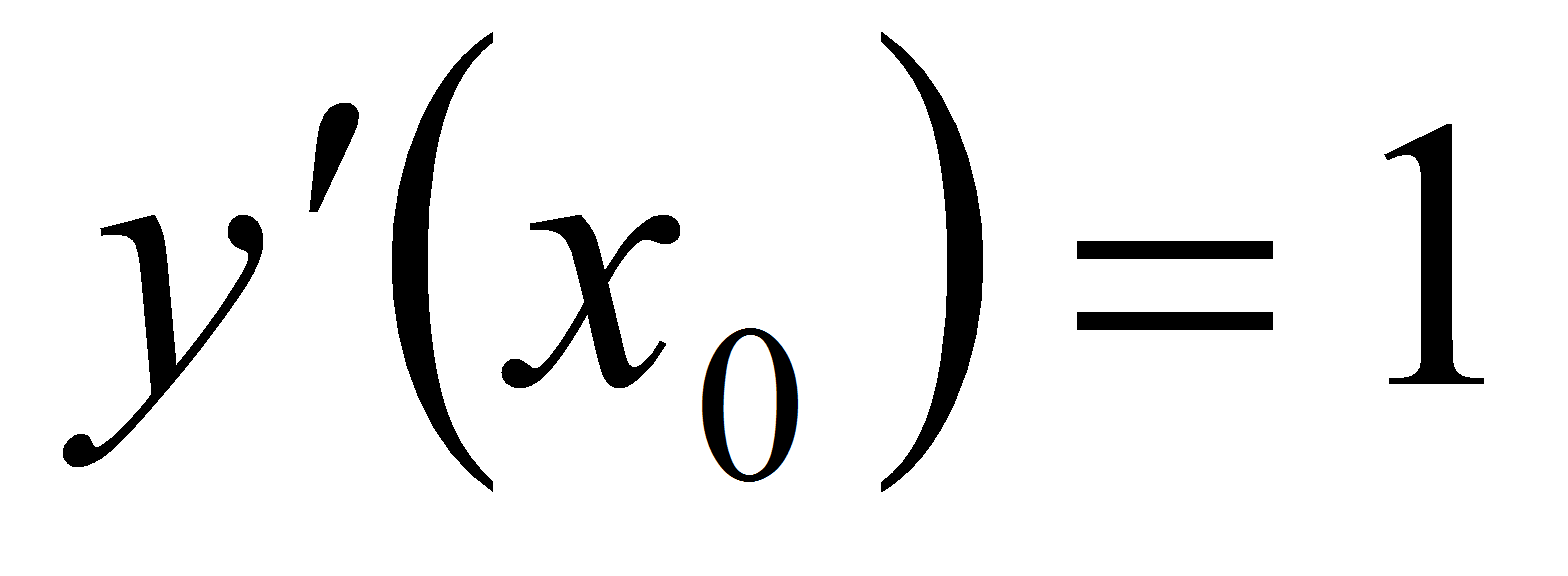 .
Отсюда
.
Отсюда
 или
или

 .
Далее составляем уравнение касательной для каждой точки.
.
Далее составляем уравнение касательной для каждой точки.
Ответ:

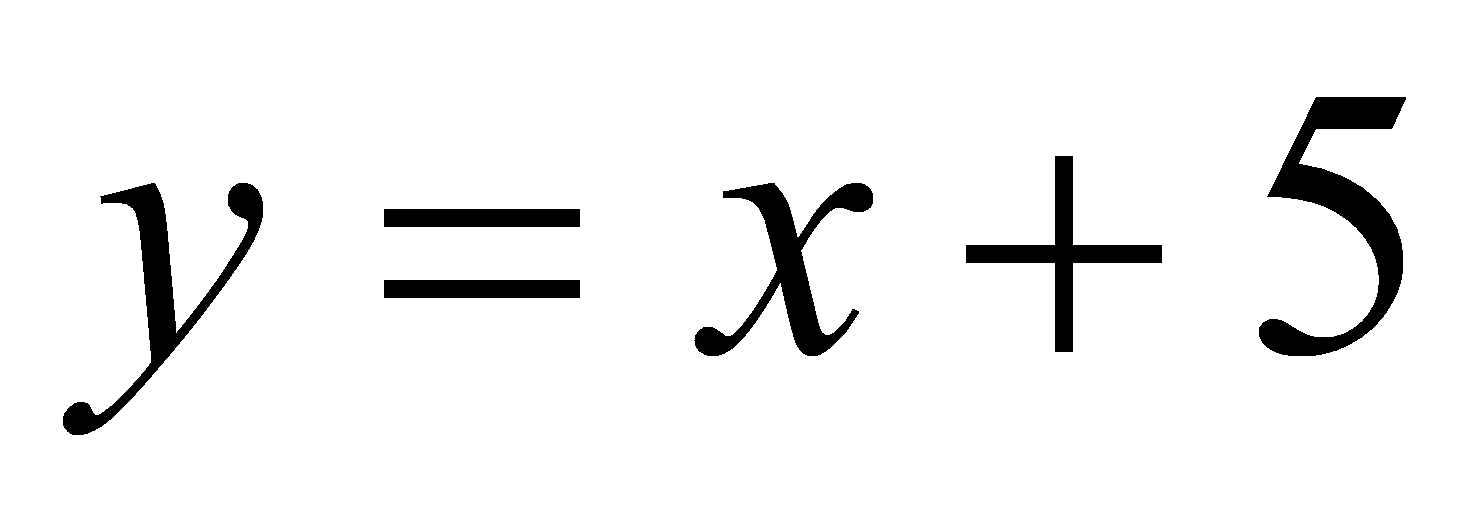 ,
,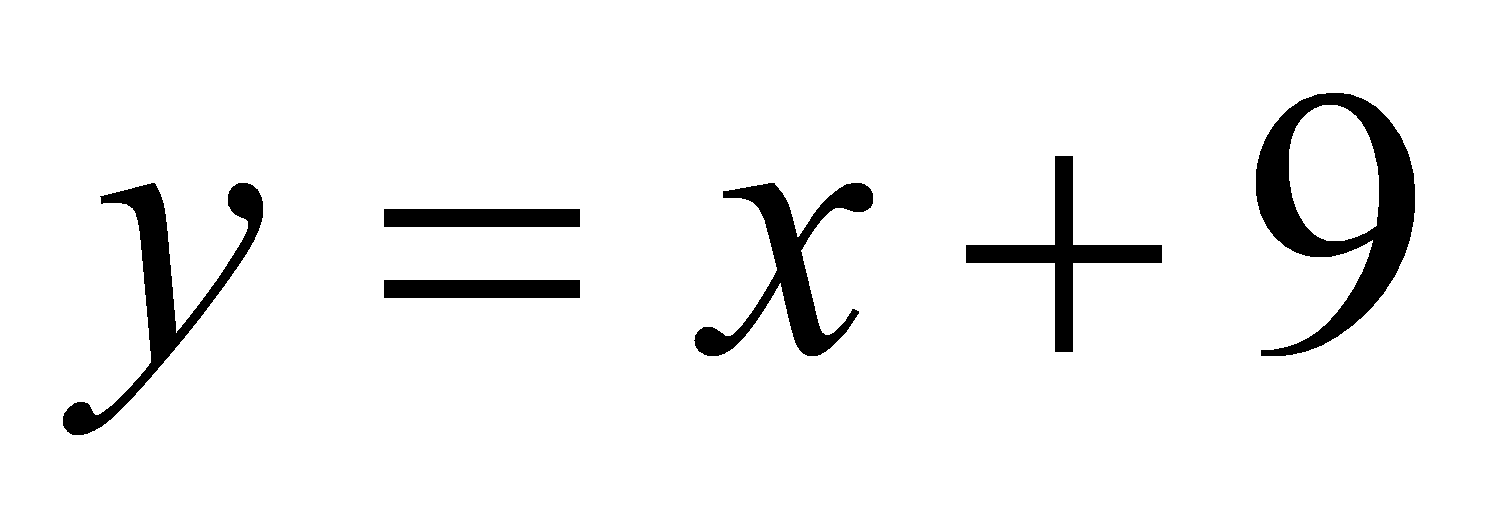 .
.
Найти все значения
 ,
при каждом из которых касательная к графикам функций
,
при каждом из которых касательная к графикам функций
 и
и
 в
точках с абсциссой
в
точках с абсциссой
 параллельны.
параллельны.
Решение.
Известно, что тангенс угла наклона касательной к графику функций
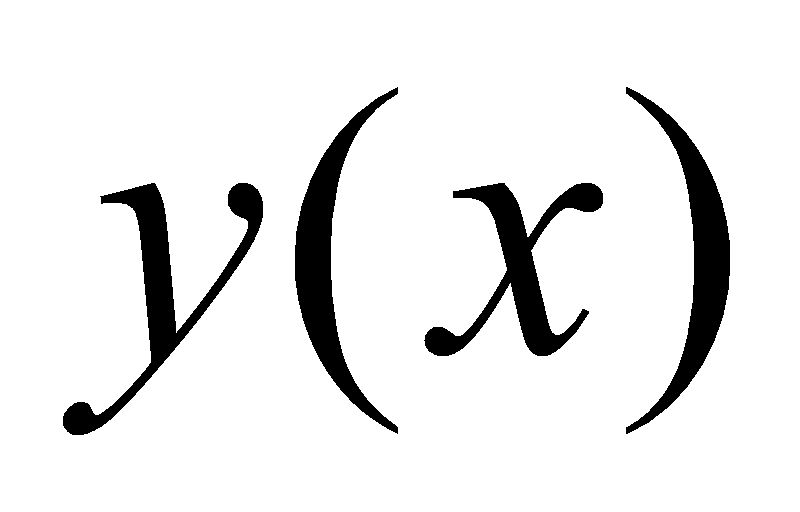 в точке с абсциссой
в точке с абсциссой
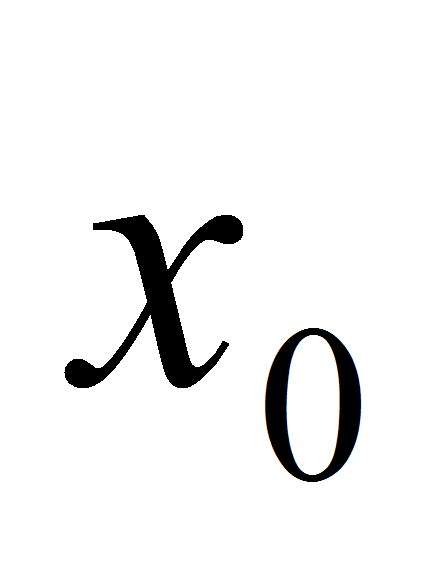 равен
равен
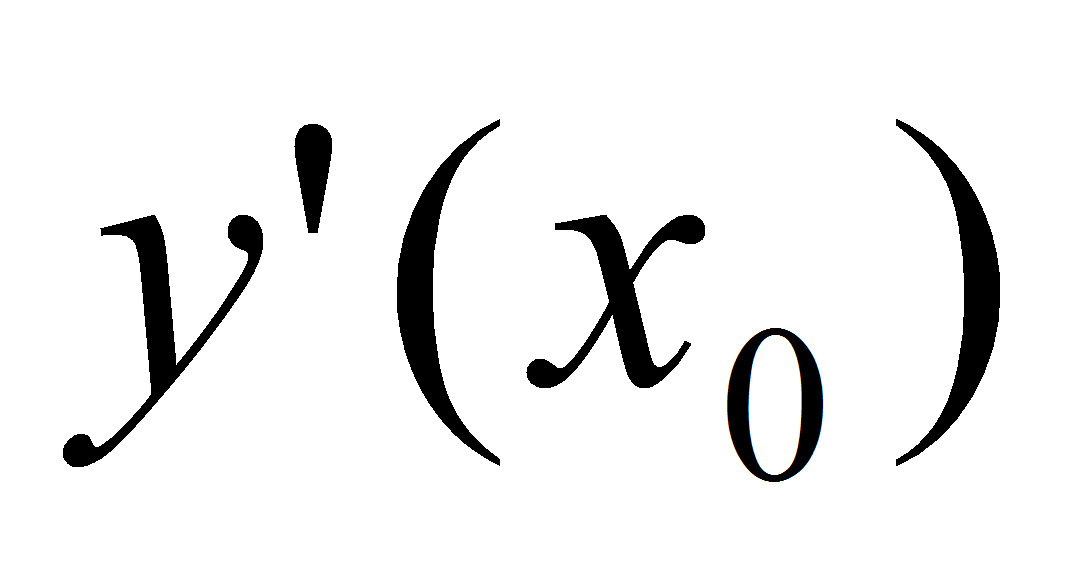 .
Следовательно, все искомые значения
.
Следовательно, все искомые значения
 будут корнями уравнения
будут корнями уравнения
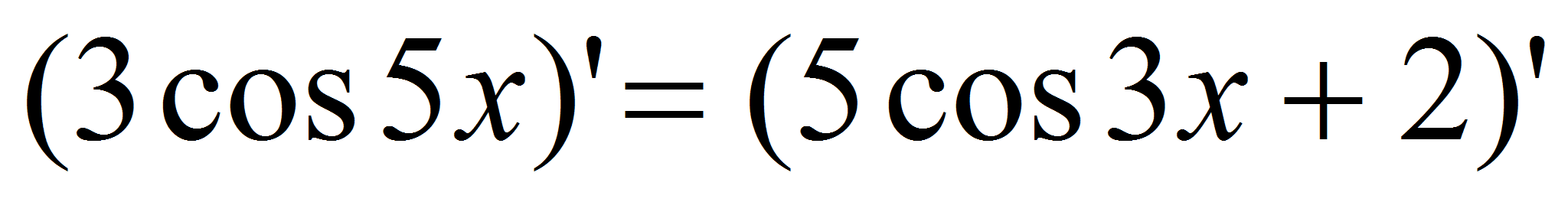 ,
откуда
,
откуда
 .
Используя формулу разности синусов углов, будем иметь
.
Используя формулу разности синусов углов, будем иметь
 .
Решая полученное уравнение, получаем
.
Решая полученное уравнение, получаем
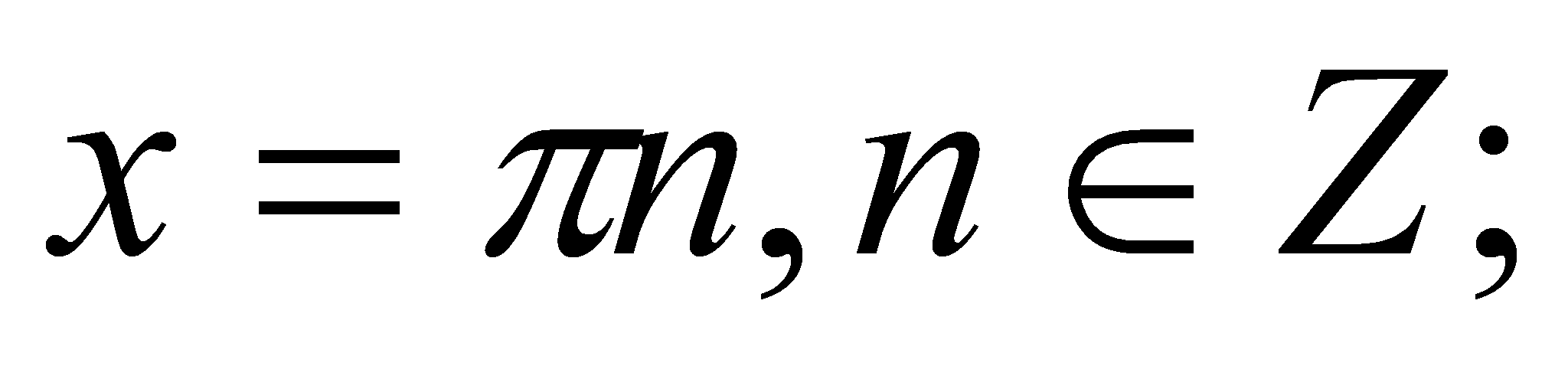
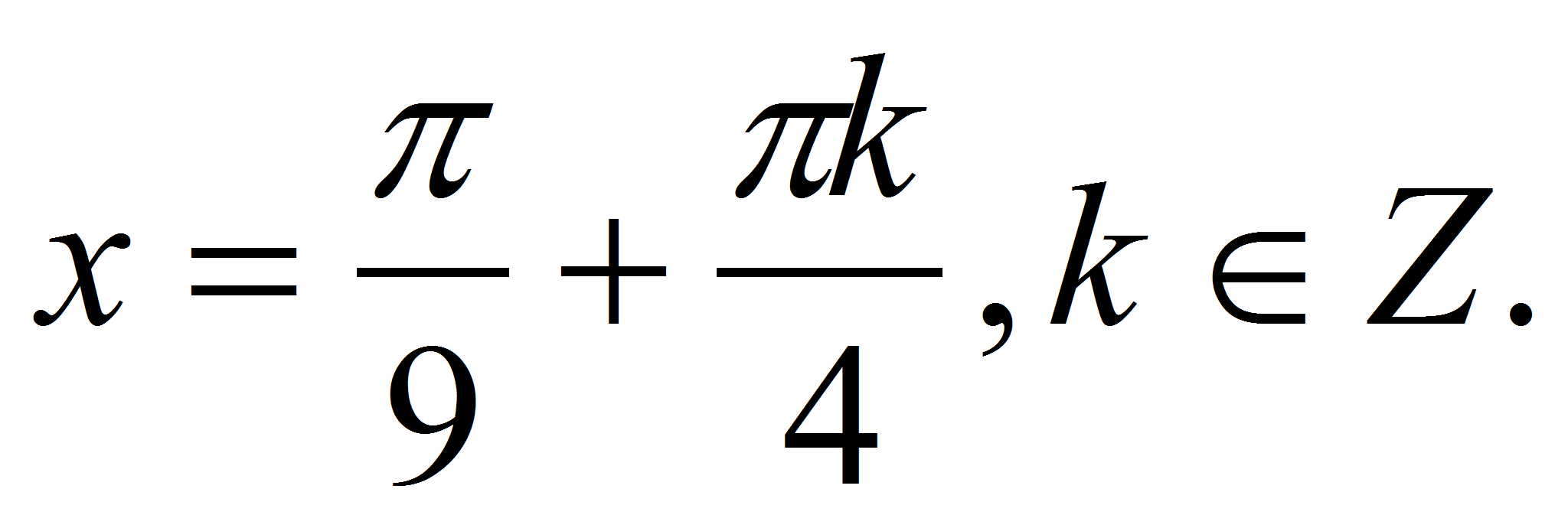
Найти расстояние между касательными к графику функции
 ,
расположенными параллельно оси
,
расположенными параллельно оси
 .
.
Решение. Найдем критические точки заданной функции:
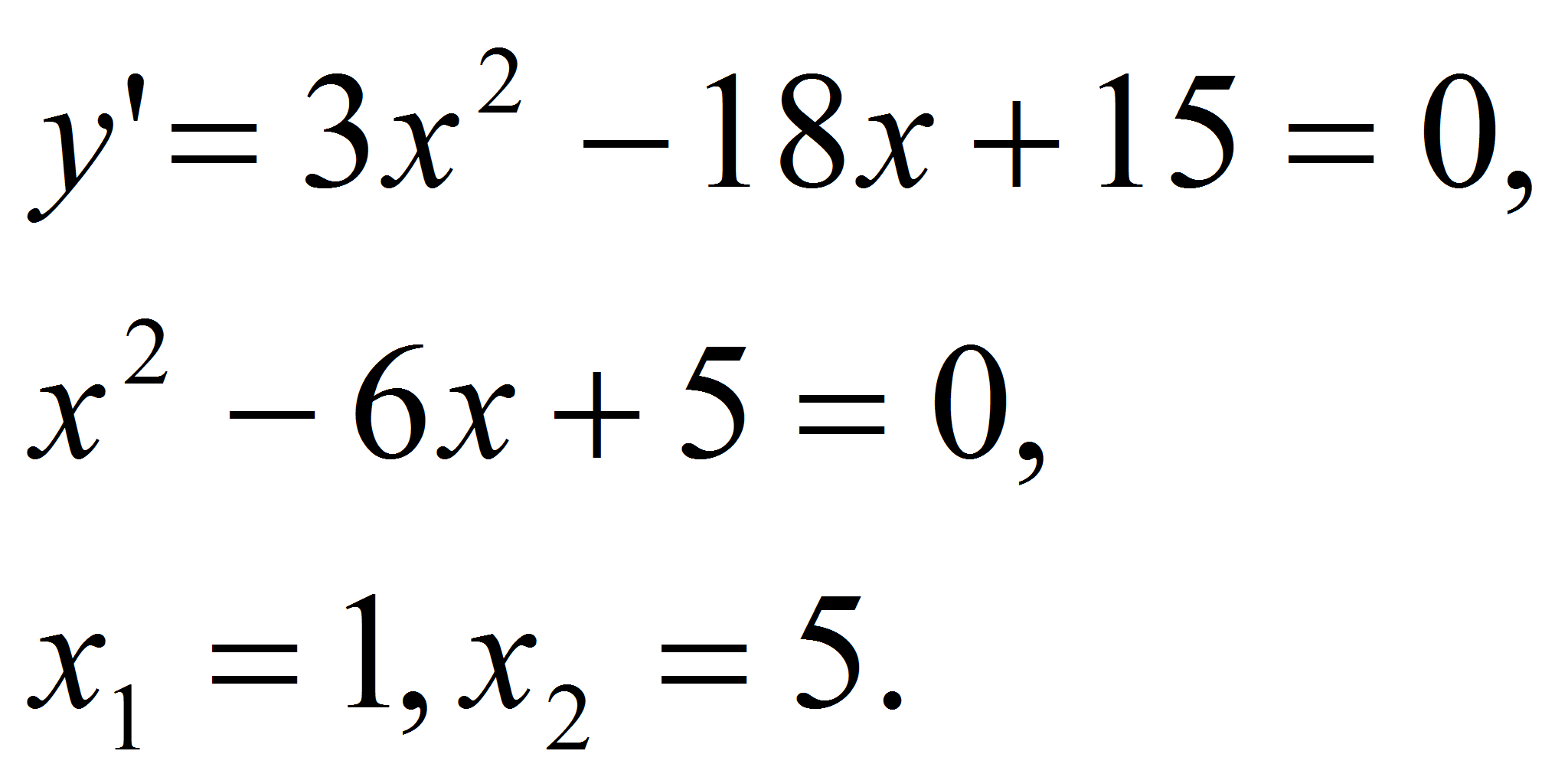
Так как,
производная в точках
 и
и
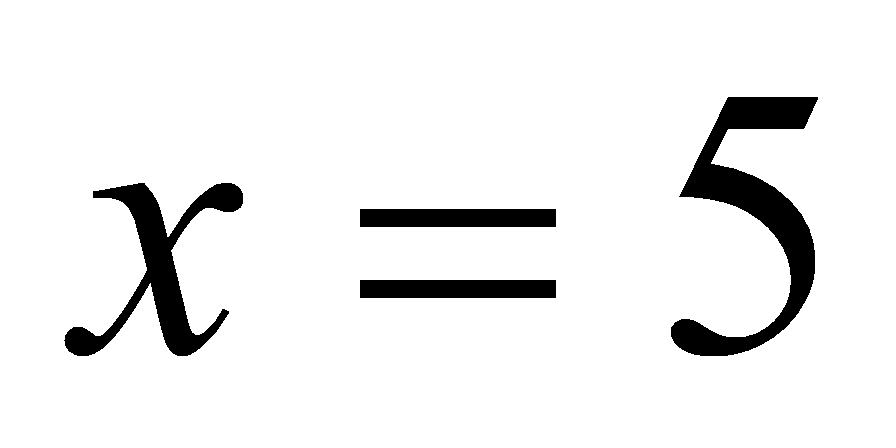 равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
 .
Найдем значения функций в этих точках.
.
Найдем значения функций в этих точках.

Итак,
расстояние d
между касательными, параллельными оси
 ,
равно
,
равно
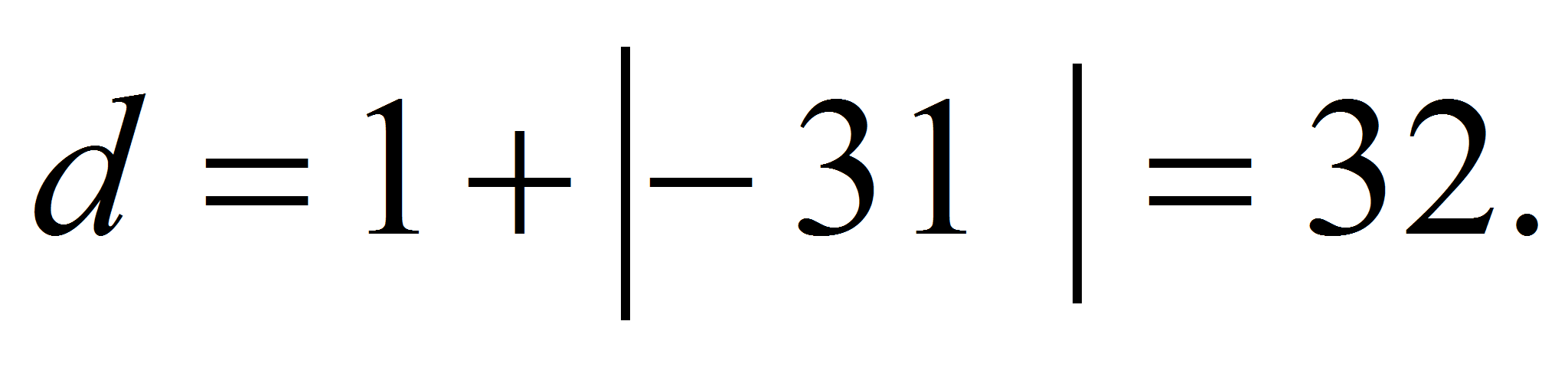
С составлением
уравнения касательной, параллельной данной прямой, связана задача о
нахождении кратчайшего расстояния между графиком
некоторой функции f(x)
и прямой
 .
.
Во многих
случаях удается найти касательную к графику
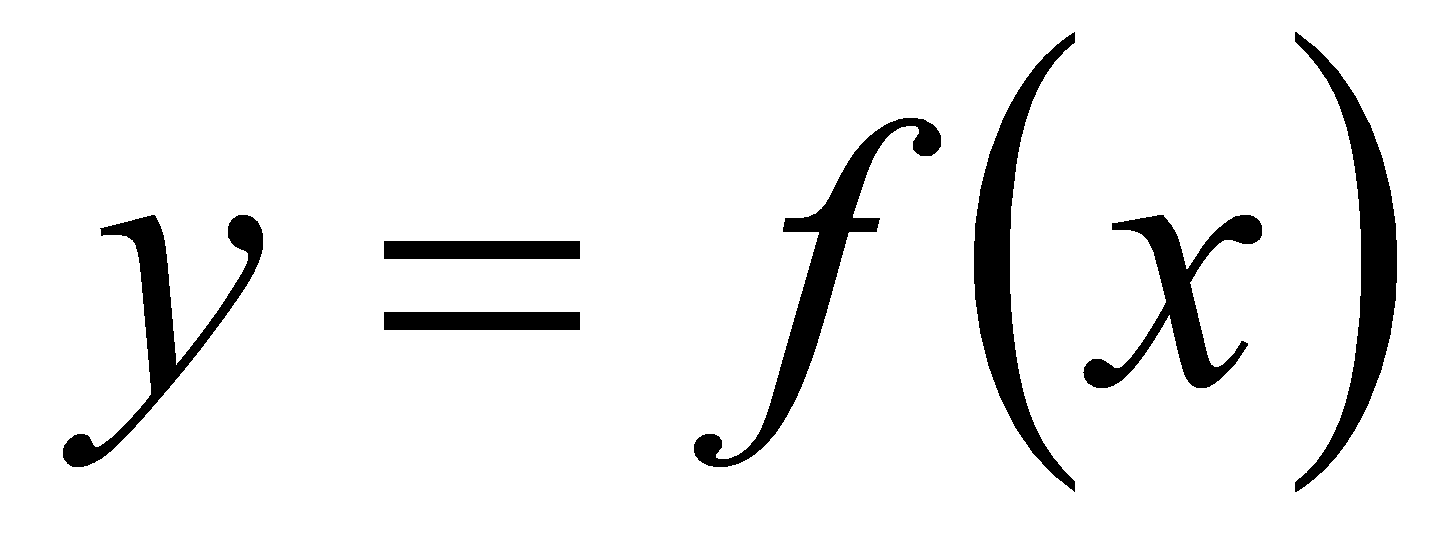 ,
параллельную данной прямой
,
параллельную данной прямой
 и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
 является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
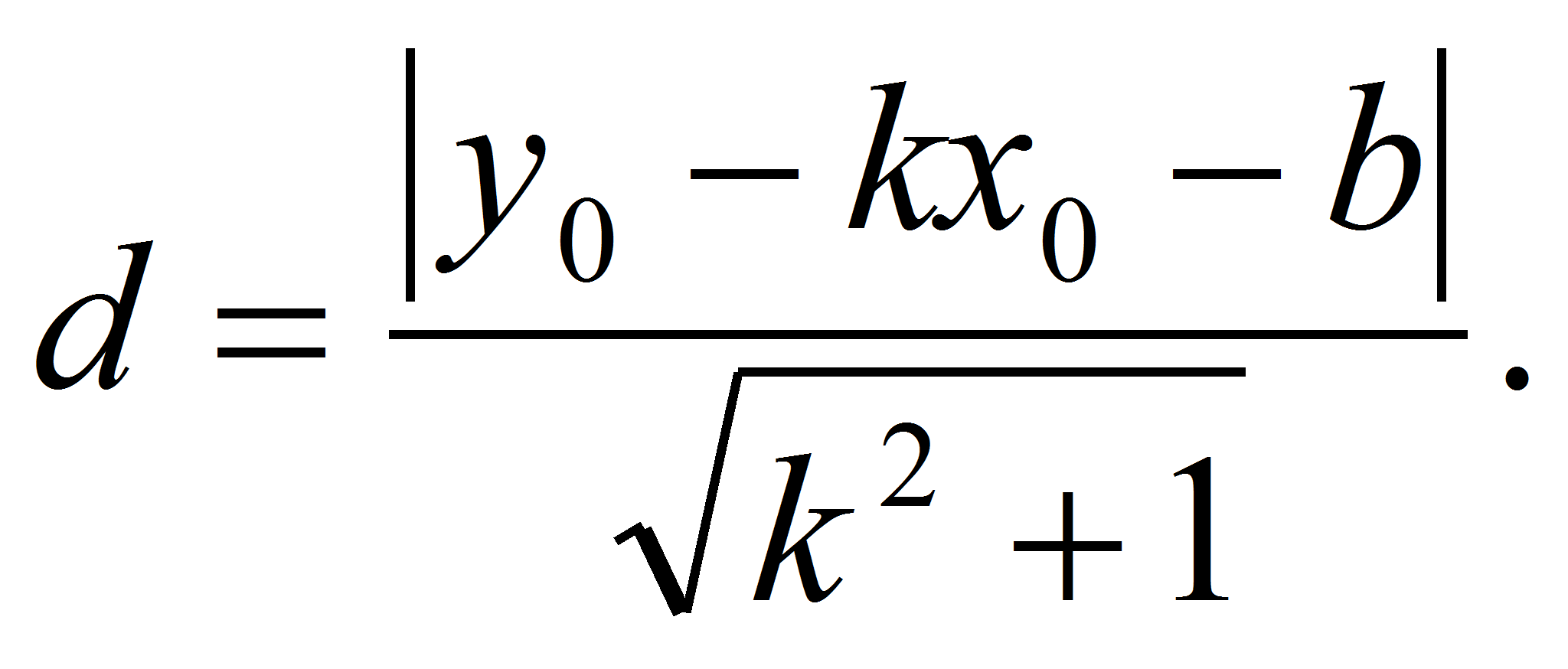
Найти кратчайшее расстояние между параболой
 и прямой
и прямой

Решение.
Убедившись, что графики не имеют общих
точек (уравнение
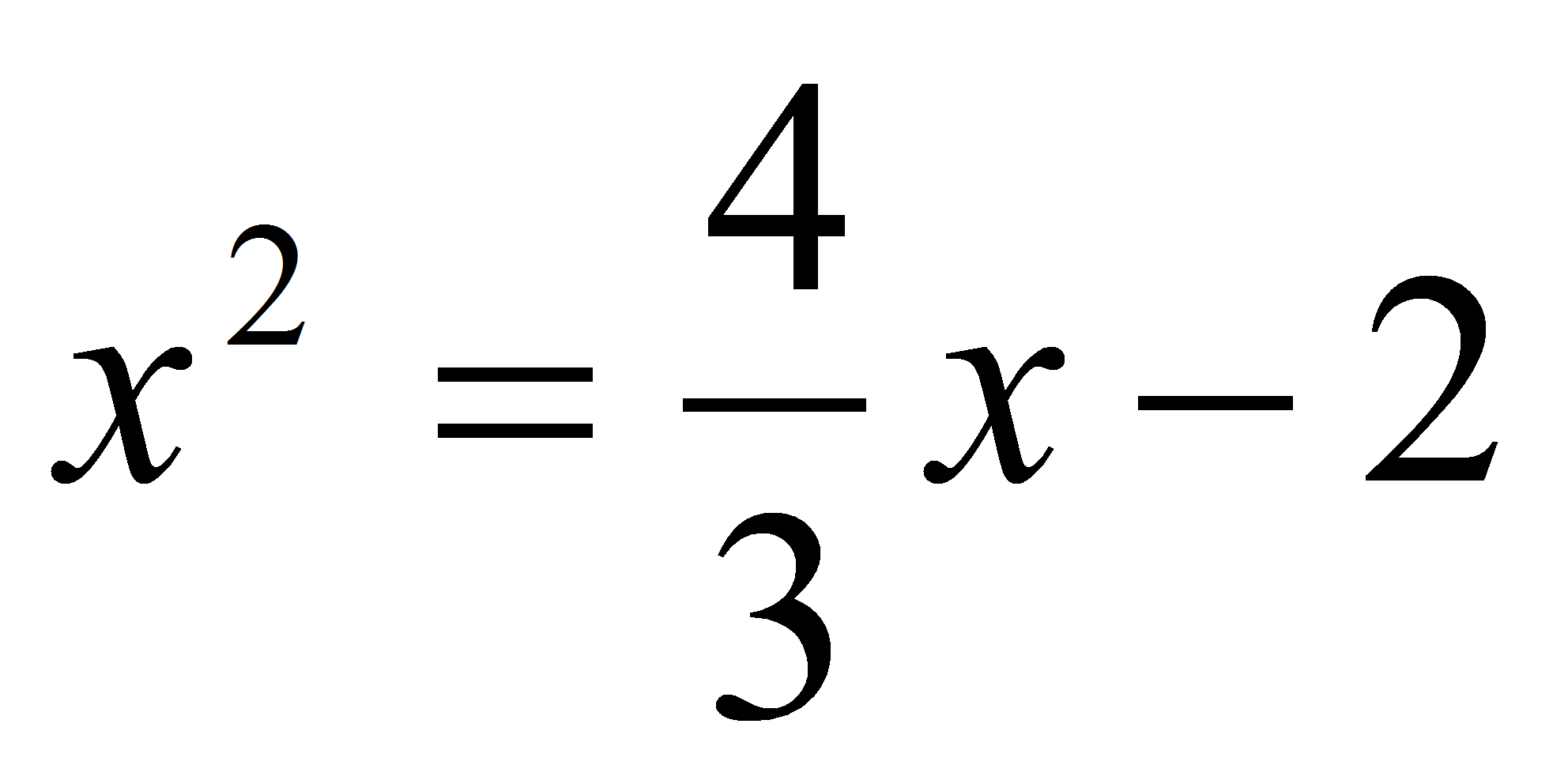 не имеет решений), запишем
уравнение такой касательной к графику функции
не имеет решений), запишем
уравнение такой касательной к графику функции
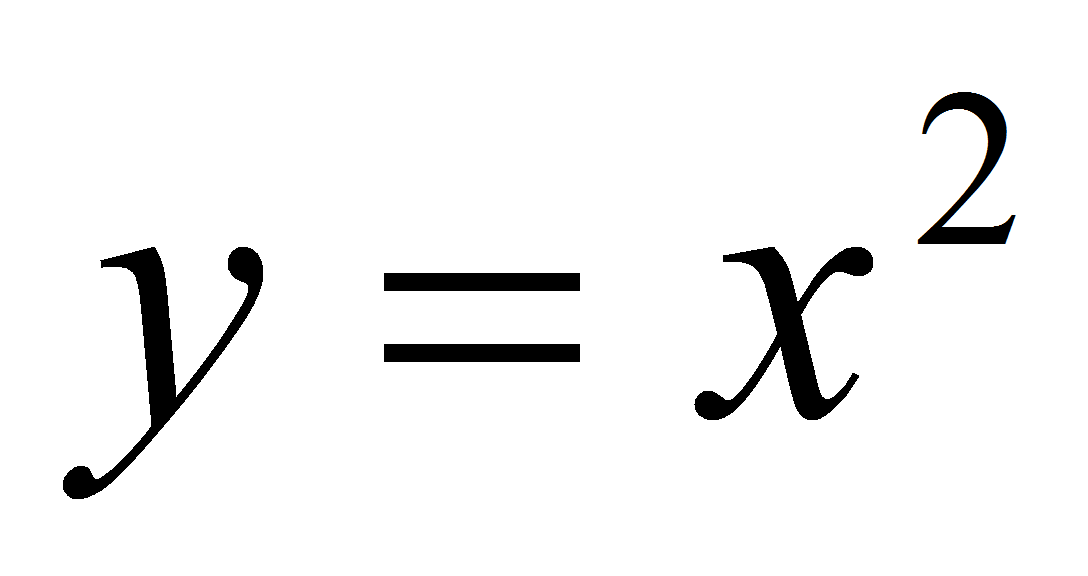 ,
которая параллельна прямой
,
которая параллельна прямой
 Уравнение касательной имеет
вид
Уравнение касательной имеет
вид
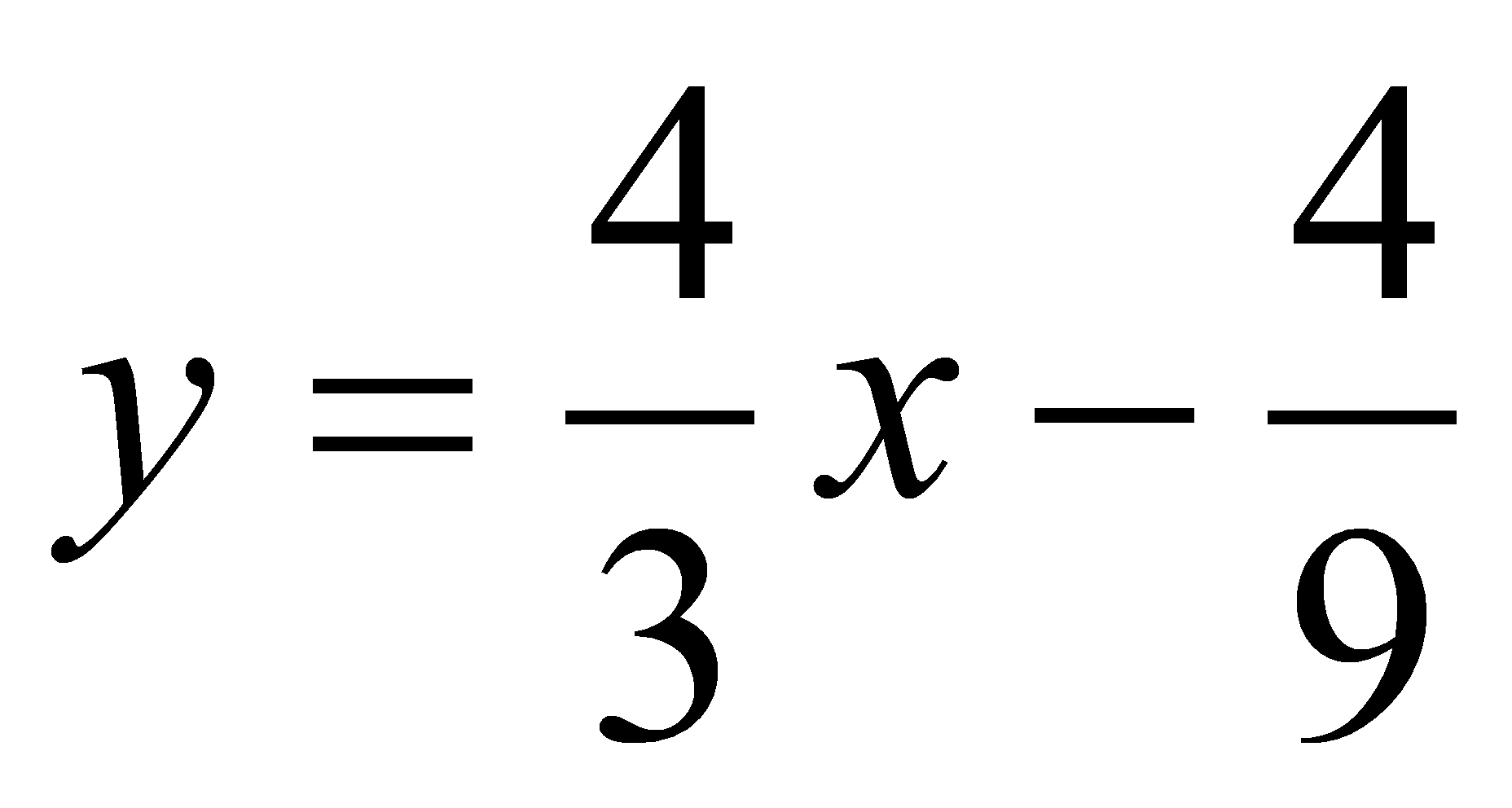 касание происходит в точке
касание происходит в точке
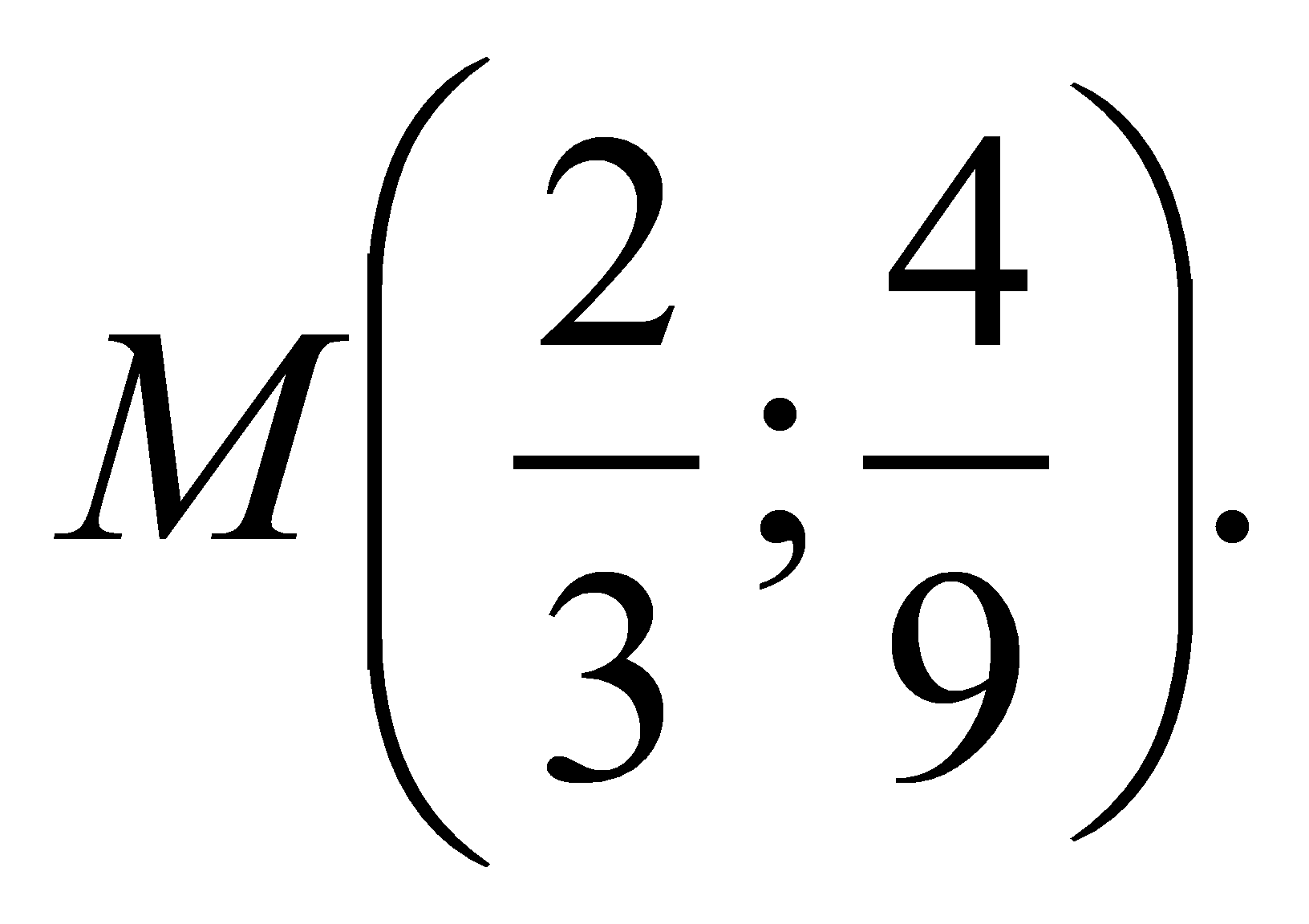 Прямая у =
Прямая у =
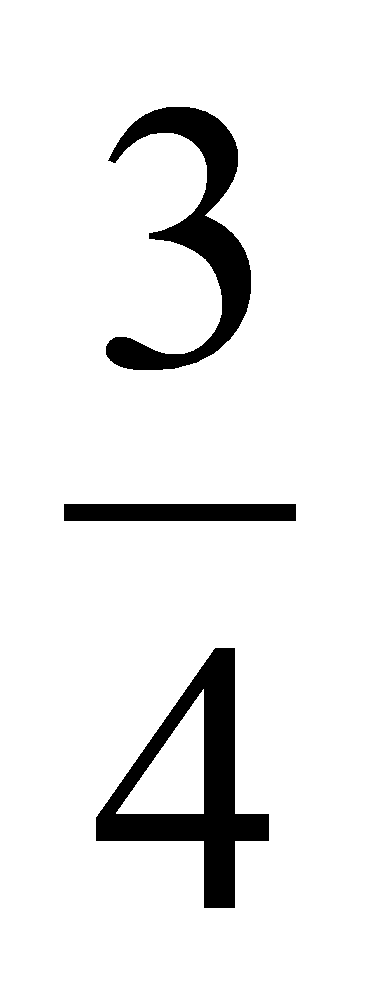 х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
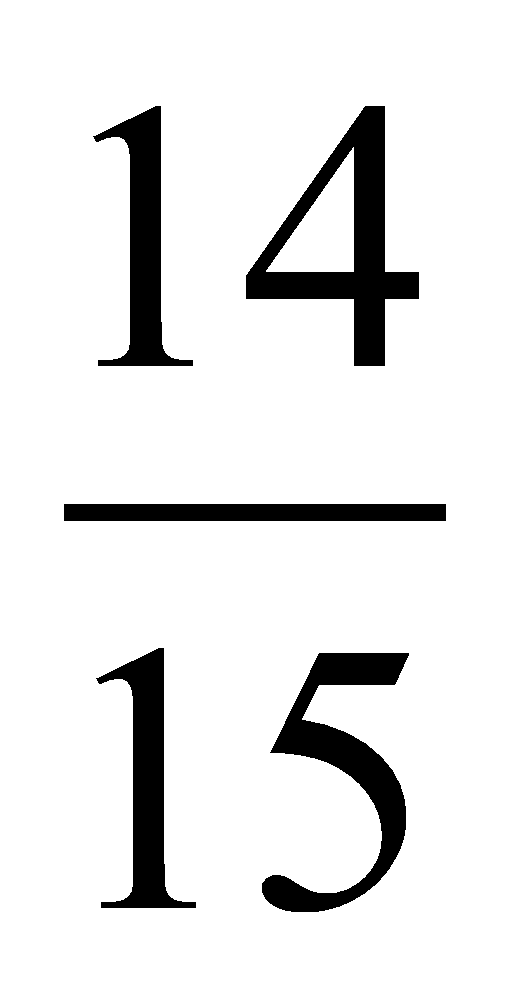 .
.
Ответ:
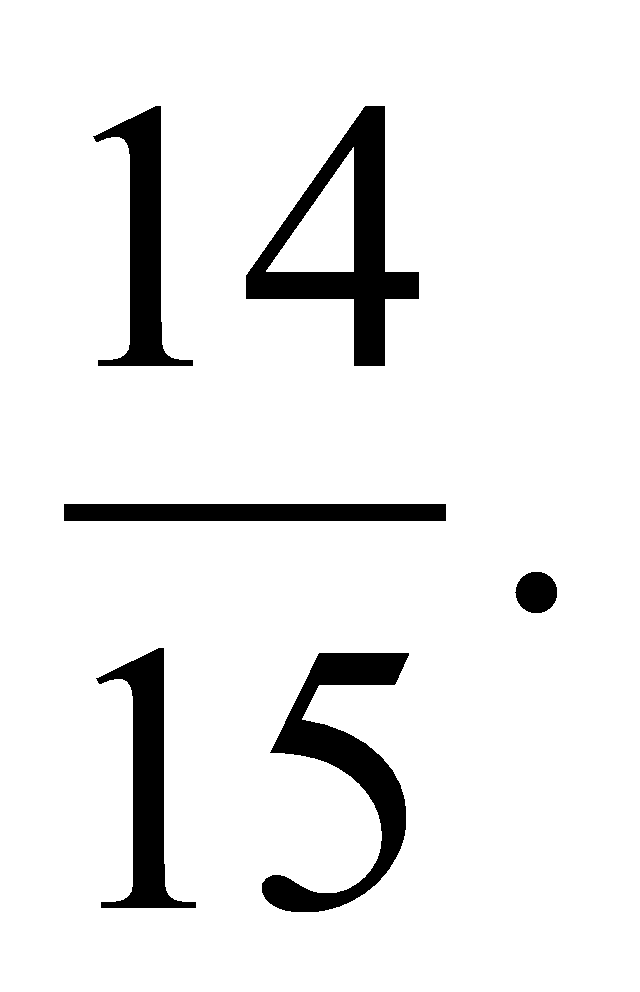
Довольно сложной является задача составления уравнения всех касательных к графику функции у = f(x), проходящих через заданную точку М(х0; у0), вообще говоря, не лежащую на графике. Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:
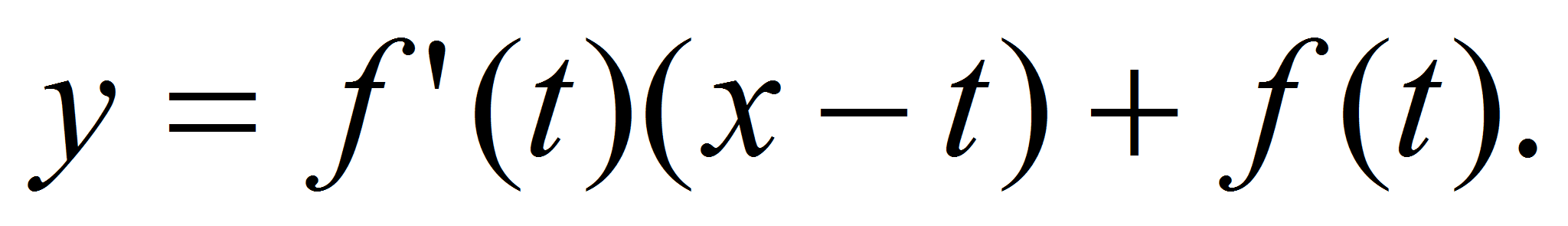

2. Решаем
относительно t
уравнение
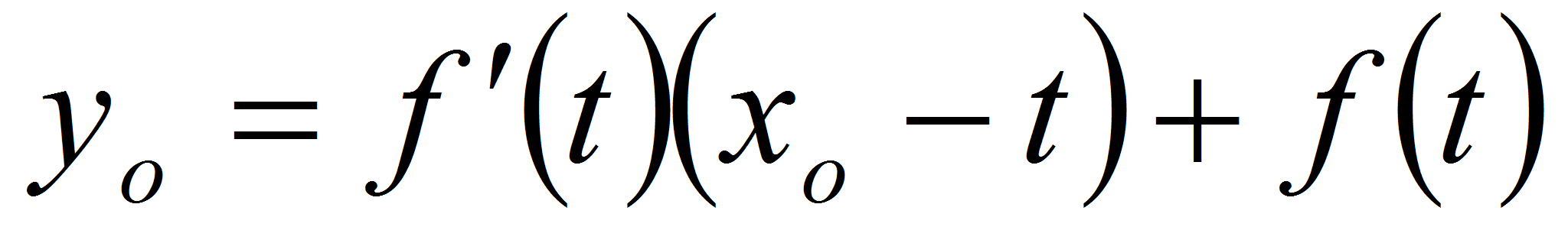 и для каждого его
решения t
записываем
соответствующую
касательную в виде
и для каждого его
решения t
записываем
соответствующую
касательную в виде
 .
.
Написать уравнение всех касательных к графику функции
 ,
проходящих через точку
М(2; -2).
,
проходящих через точку
М(2; -2).
Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
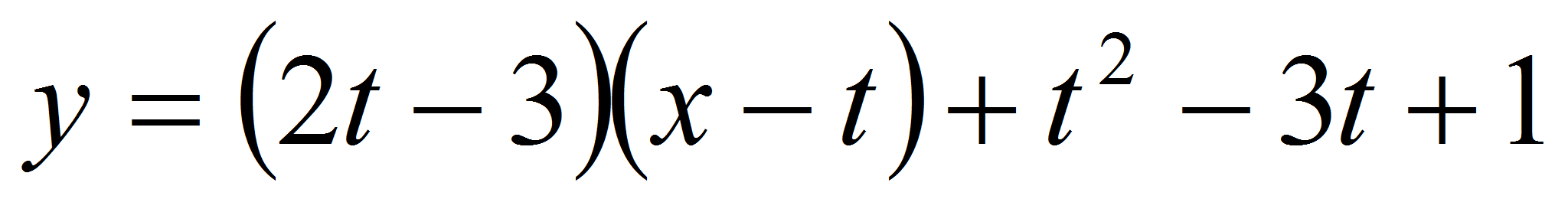 .
Так как эта
касательная проходит через точку
(2; -2), то
.
Так как эта
касательная проходит через точку
(2; -2), то 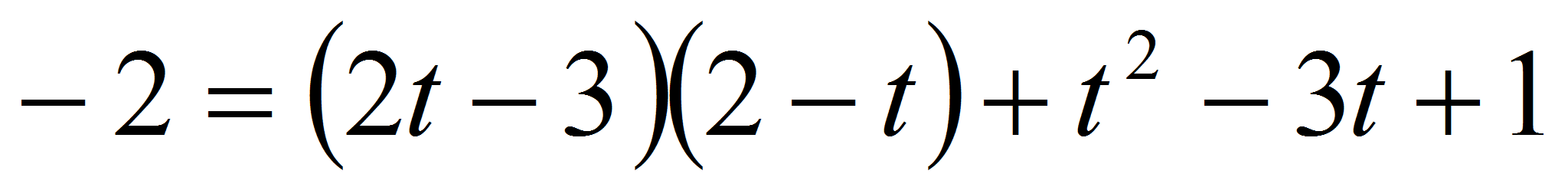 ,
откуда
,
откуда
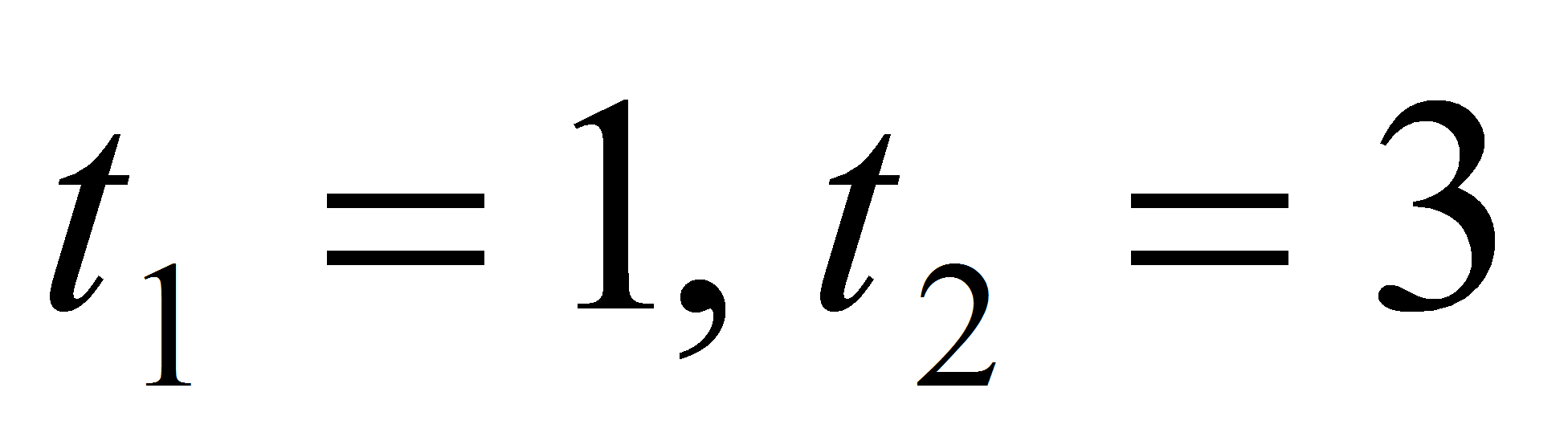 .
.
Ответ:
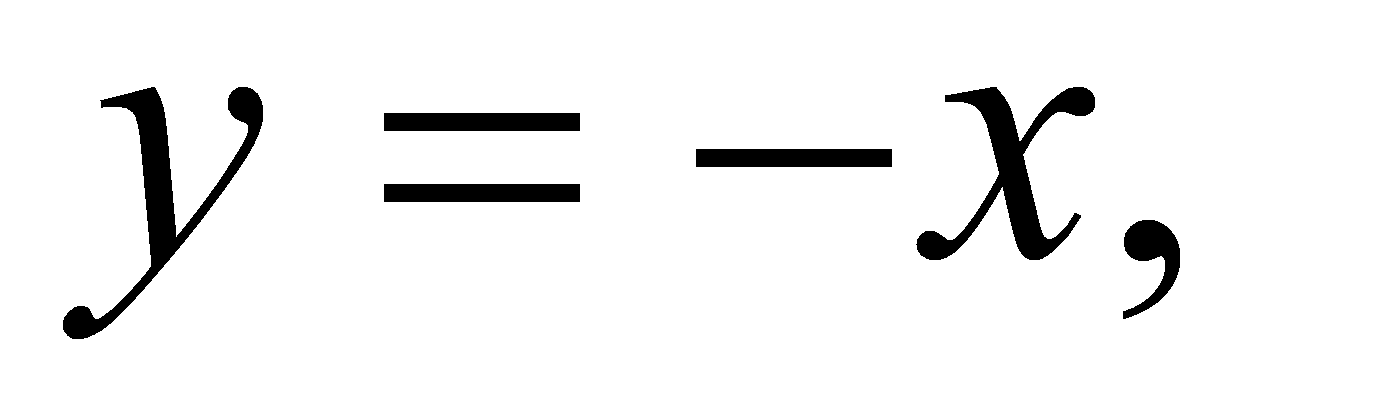
 .
.
Найти площадь треугольника, образованного касательными, проведенными к графику функции
 через точку
через точку
 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания.
Указание.
Уравнение
 дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
Ответ: 0,25.
Говорят, что
прямая
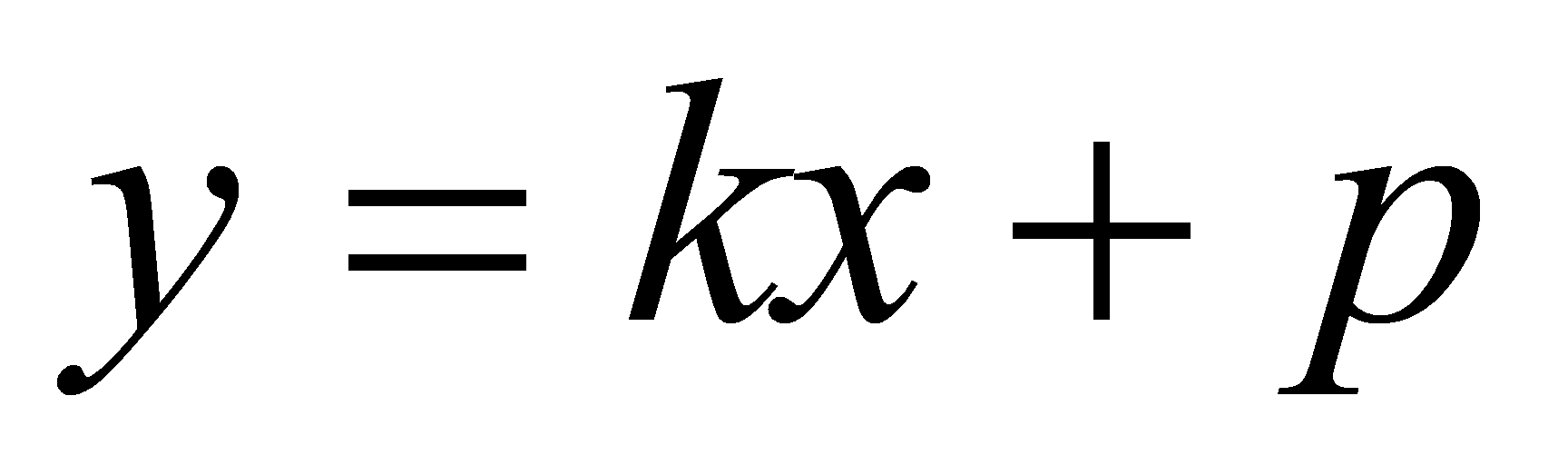 является общей касательной графиков функции
является общей касательной графиков функции
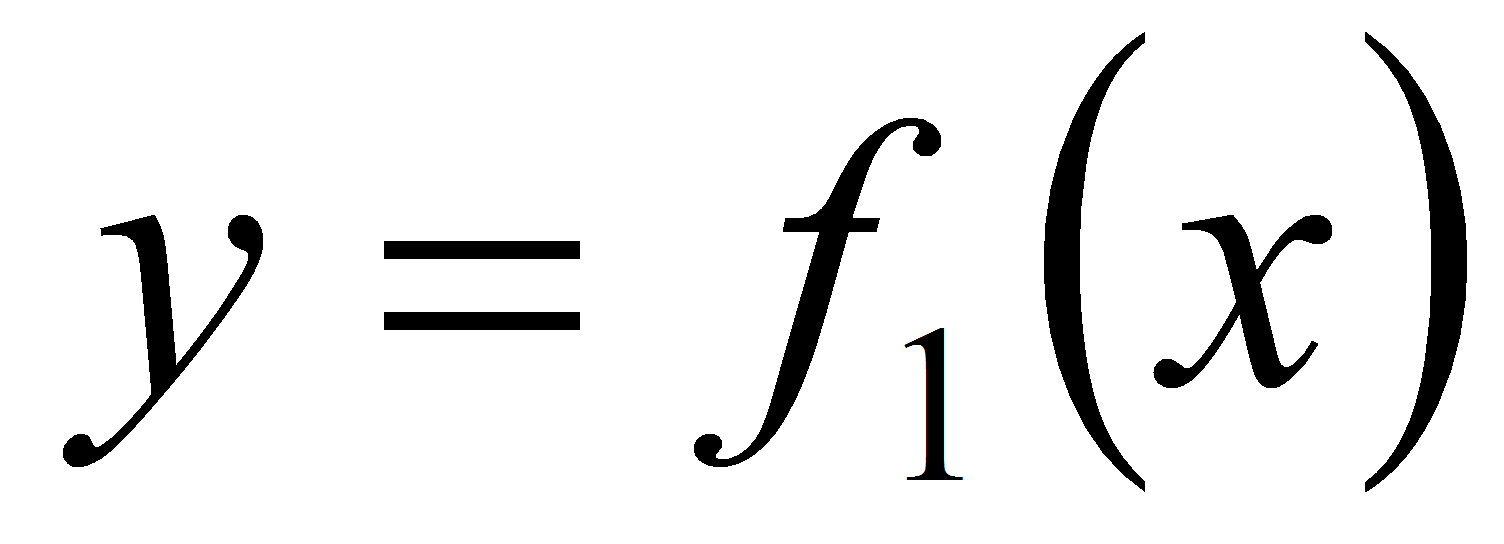 и
и
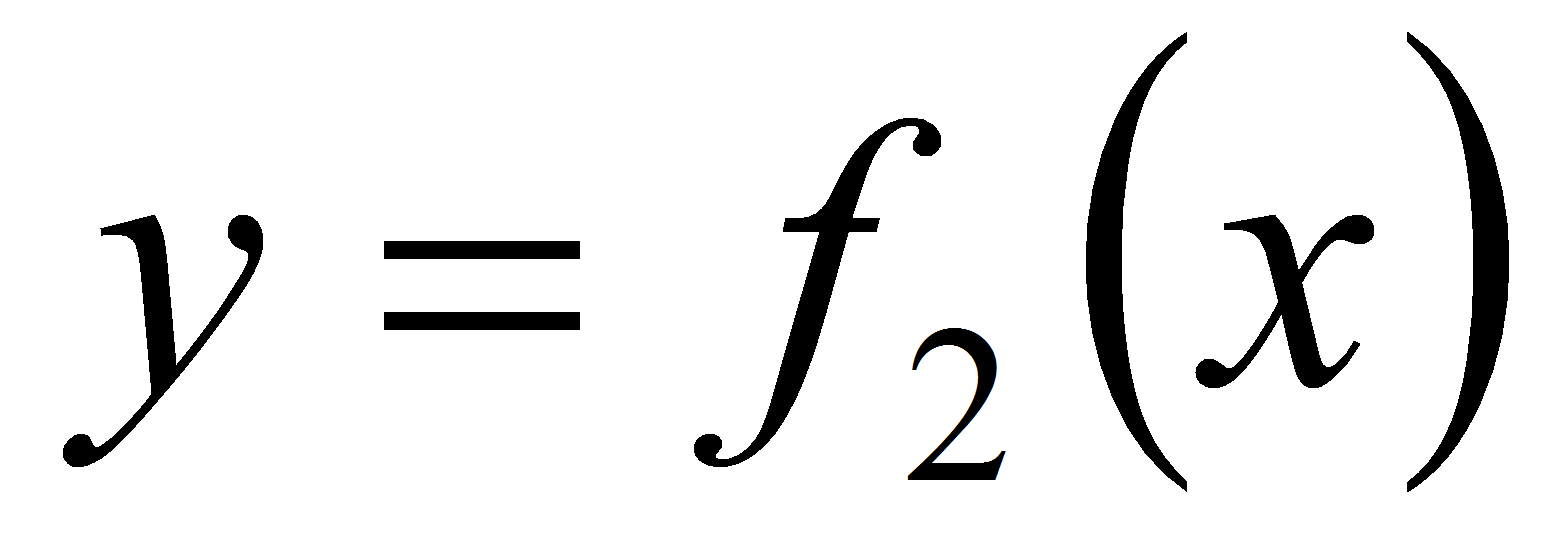 ,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
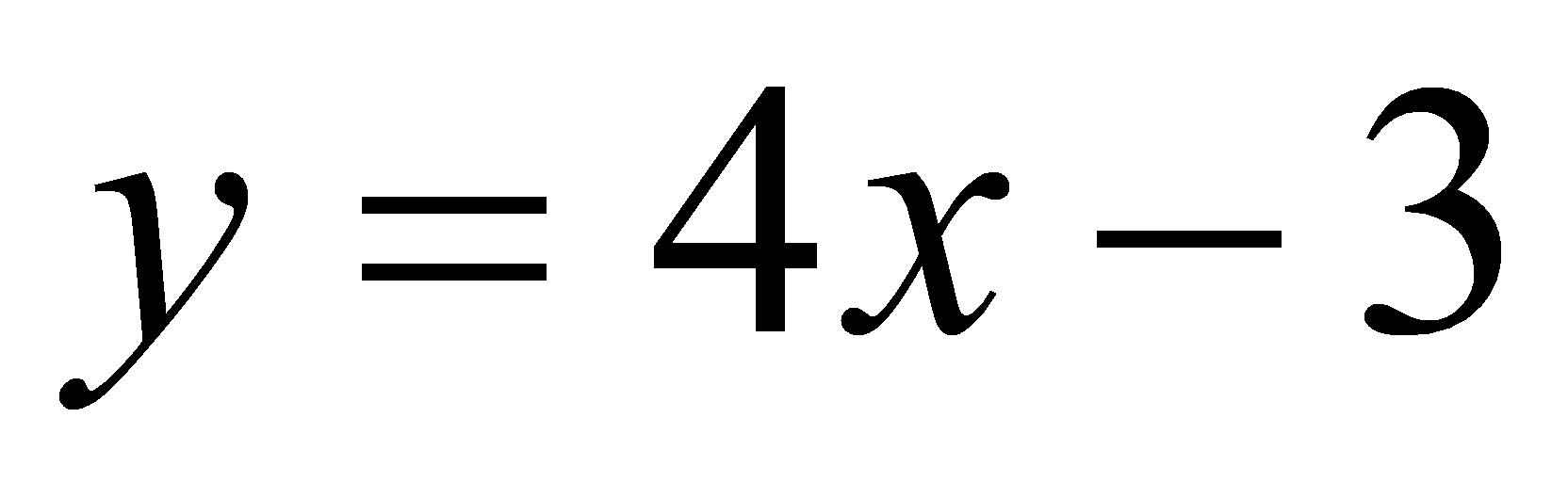 является общей касательной графиков функций
является общей касательной графиков функций
 (в точке М(2; 5) и
(в точке М(2; 5) и
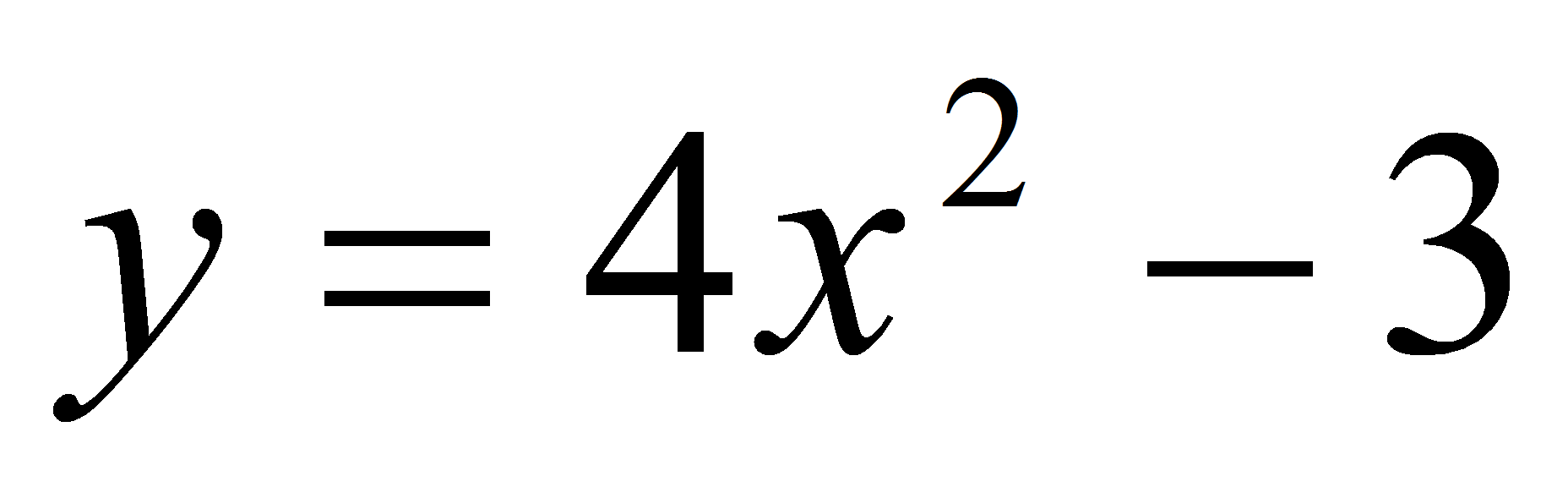 (в точке K(0,5;
-1)). Заметим, что графики функций
(в точке K(0,5;
-1)). Заметим, что графики функций
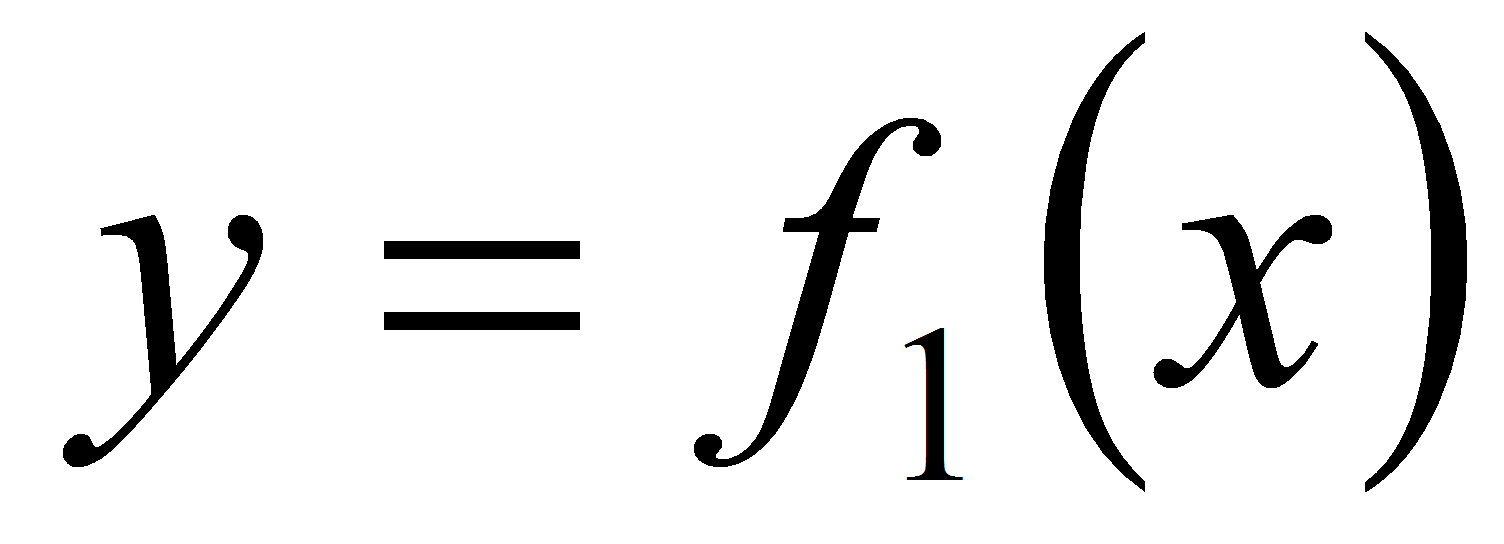 и
и
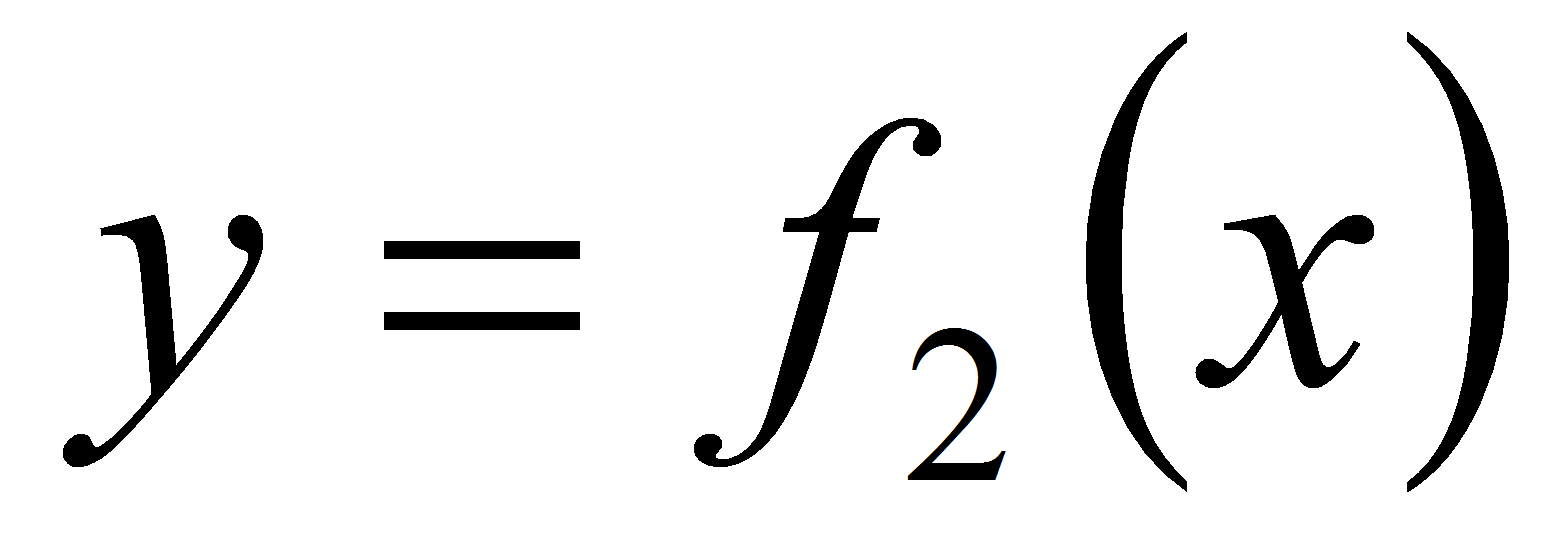 имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
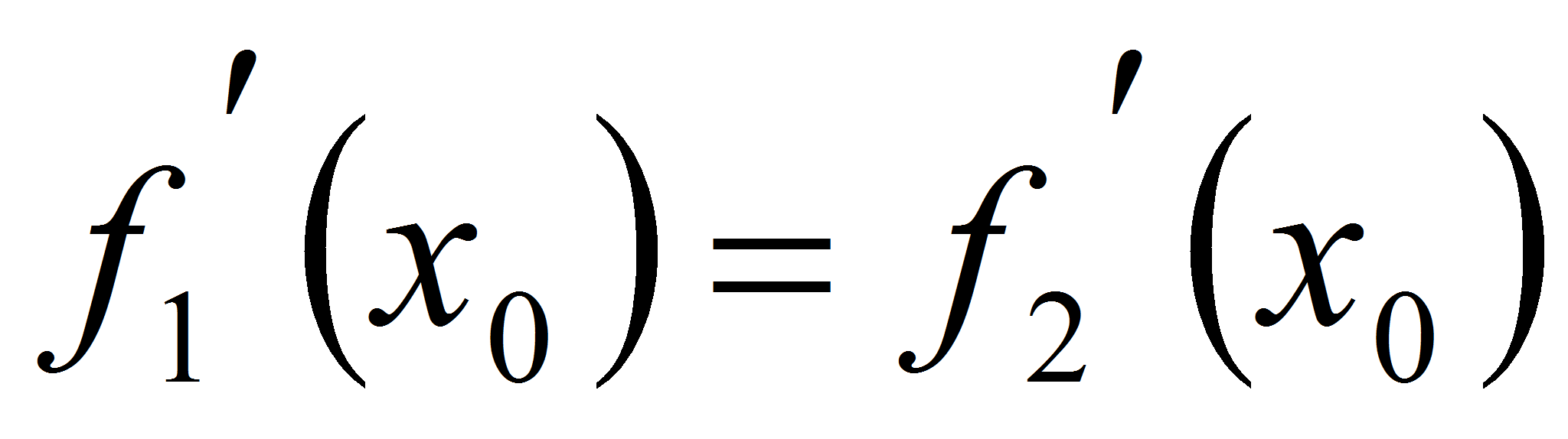 .
.
Доказать, что параболы
 и
и
 имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
 имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
 и
и
 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной.
Ответ: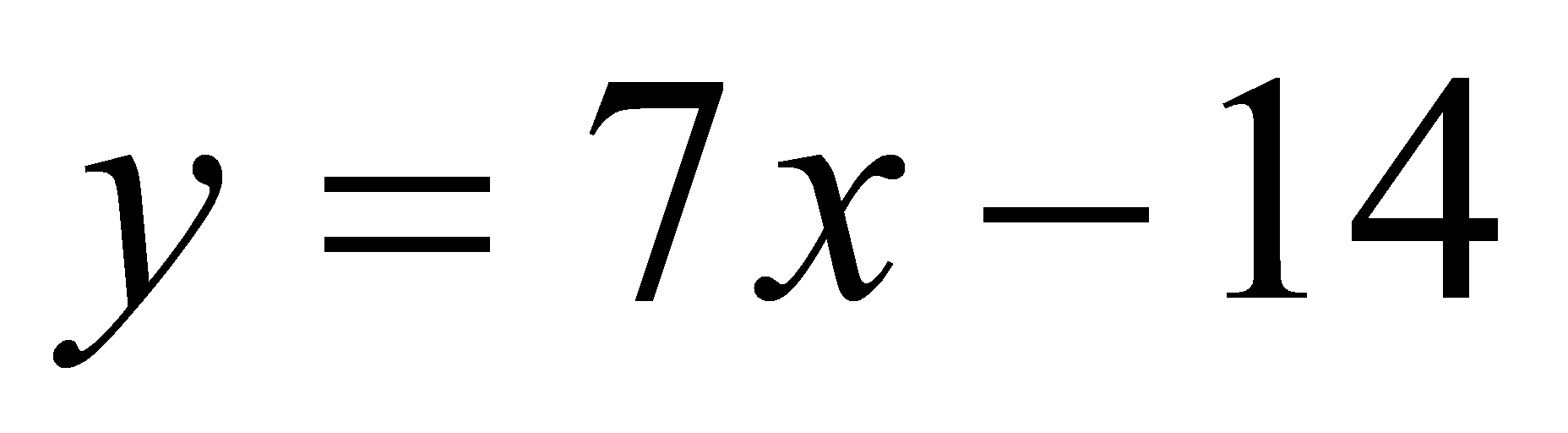 .
.
В завершении рассмотрим решение еще нескольких задач на касательную с параметром.
При каких значениях параметра
 касательная
к графику функции
касательная
к графику функции
 в точке
в точке
 проходит через точку (2;3)?
проходит через точку (2;3)?
Решение.
Составим уравнение касательной к графику заданной функции в точке
 :
:
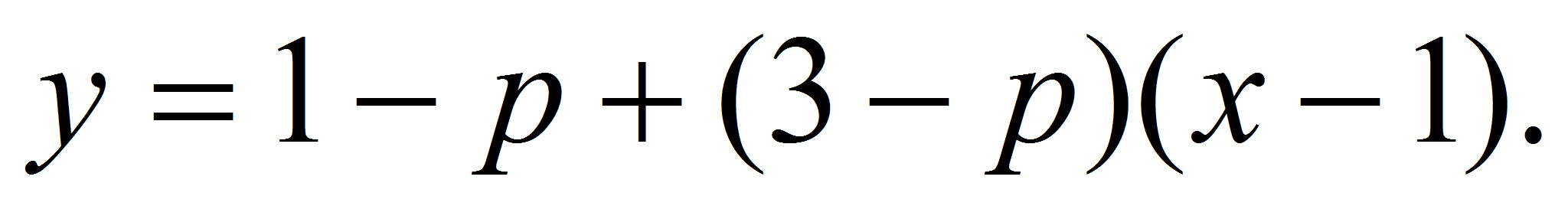 Так как эта прямая проходит через точку (2;3), то имеет место
равенство
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
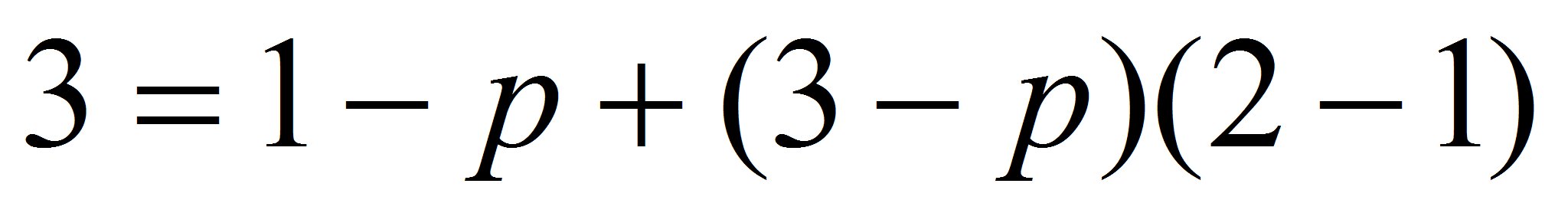 ,
откуда находим:
,
откуда находим:
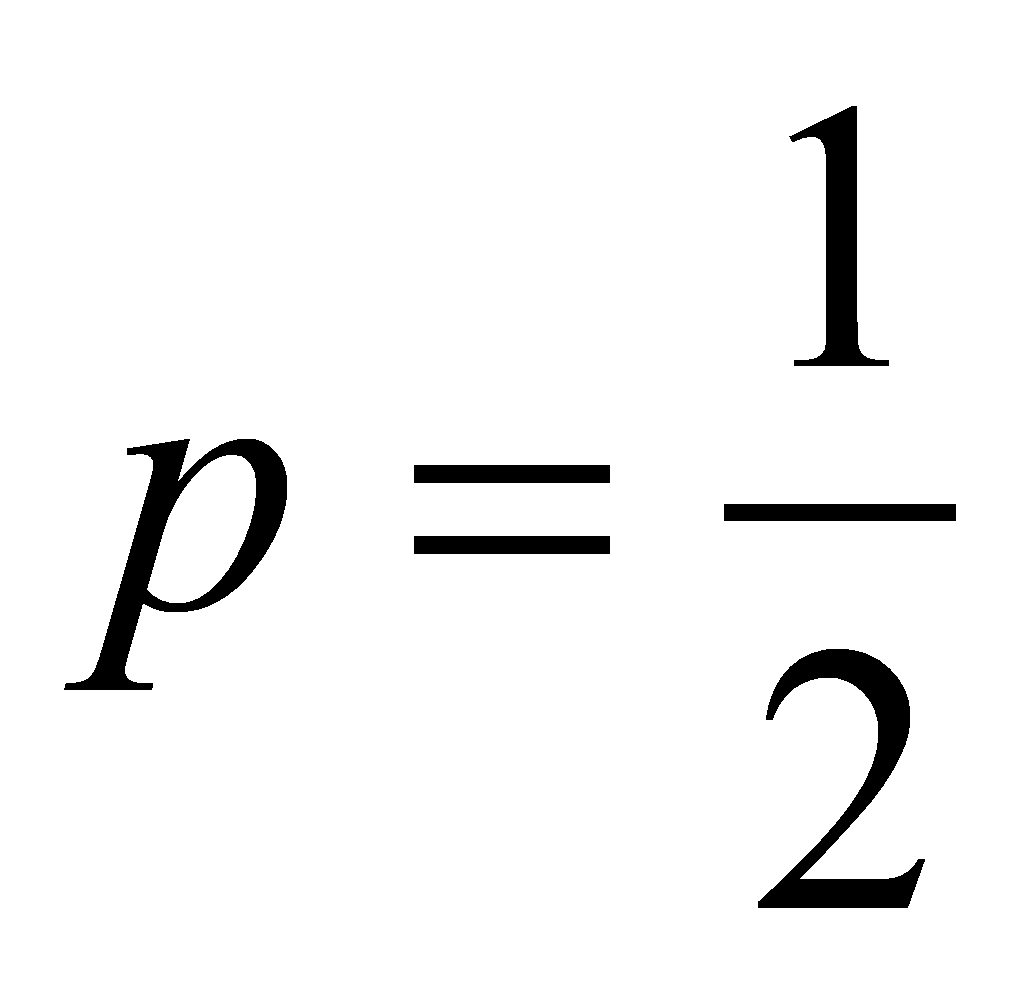 .
.
Может ли касательная к кривой
 в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
 ?
?
Решение.
Найдем производную функции
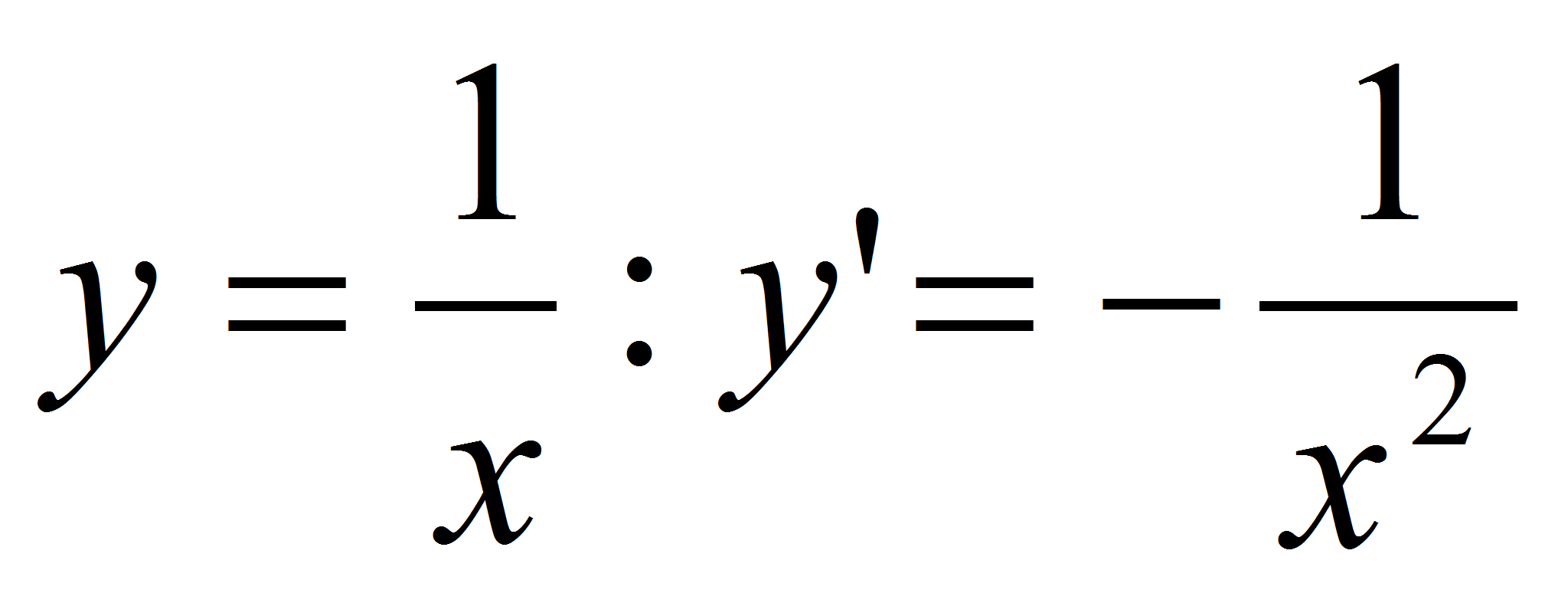 .
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не может.
Найти значение параметра
 ,
при котором касательная к графику функции
,
при котором касательная к графику функции
 в точке
в точке
 проходит через точку М(1;7).
проходит через точку М(1;7).
Решение.
Пусть
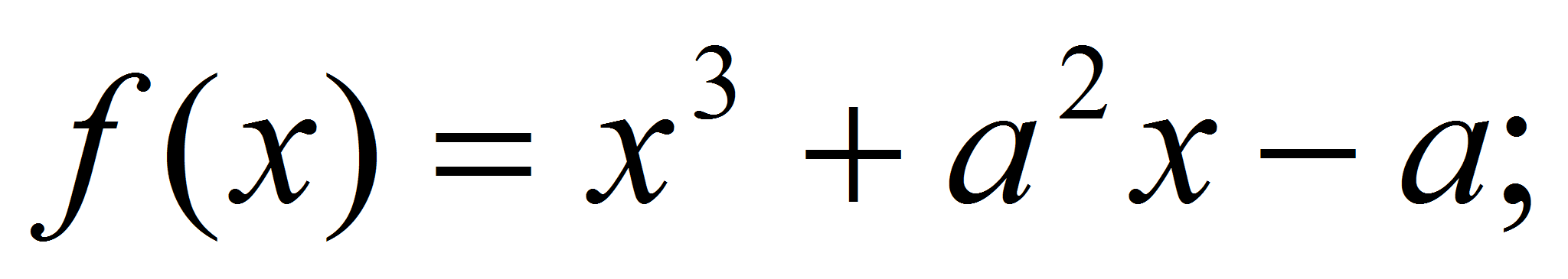 тогда
тогда
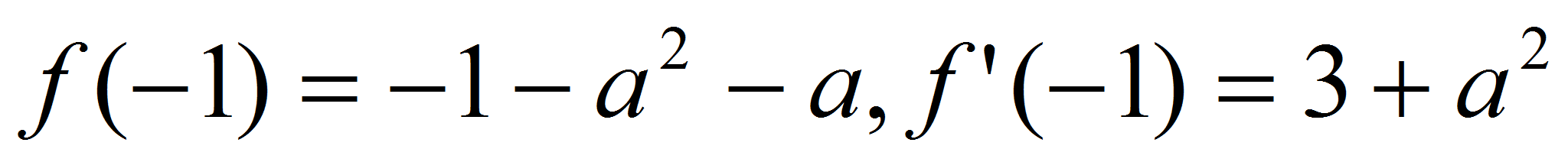 .
Составим уравнение касательной:
.
Составим уравнение касательной:
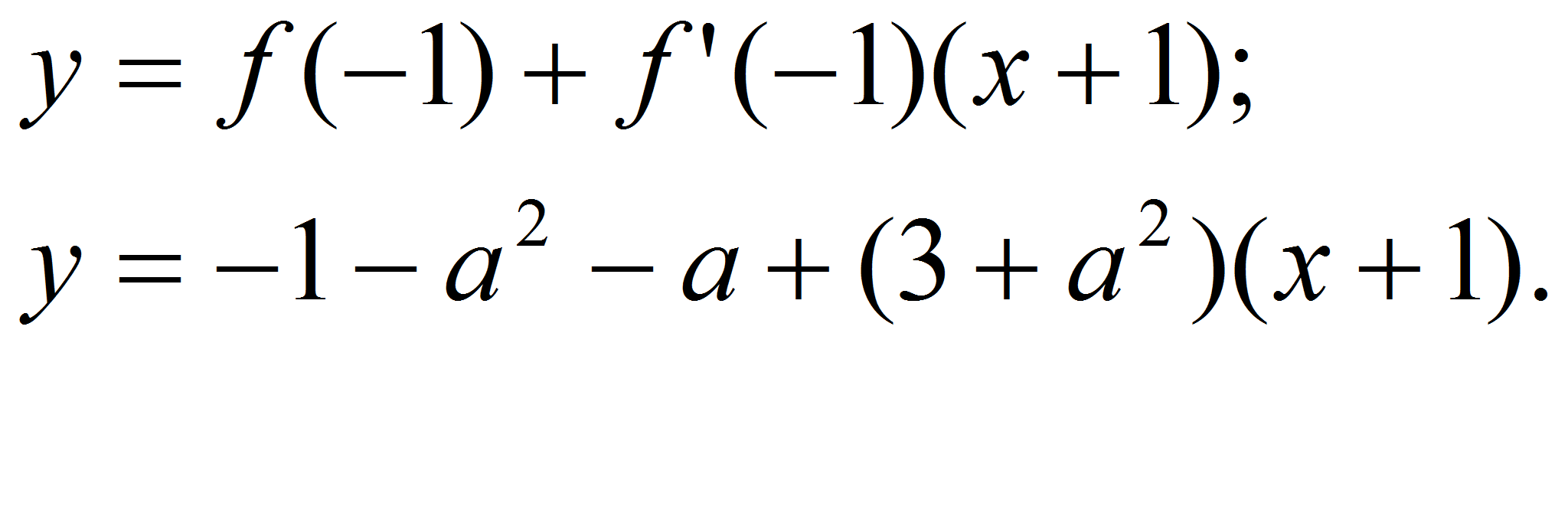
По условию эта
касательная проходит через точку М(1;7), значит,
 ,
откуда получаем:
,
откуда получаем:

При каких значениях параметра
 прямая
прямая
 является касательной к графику функции
является касательной к графику функции
 ?
?
Решение.
Из условия следует, что должно выполнятся равенство
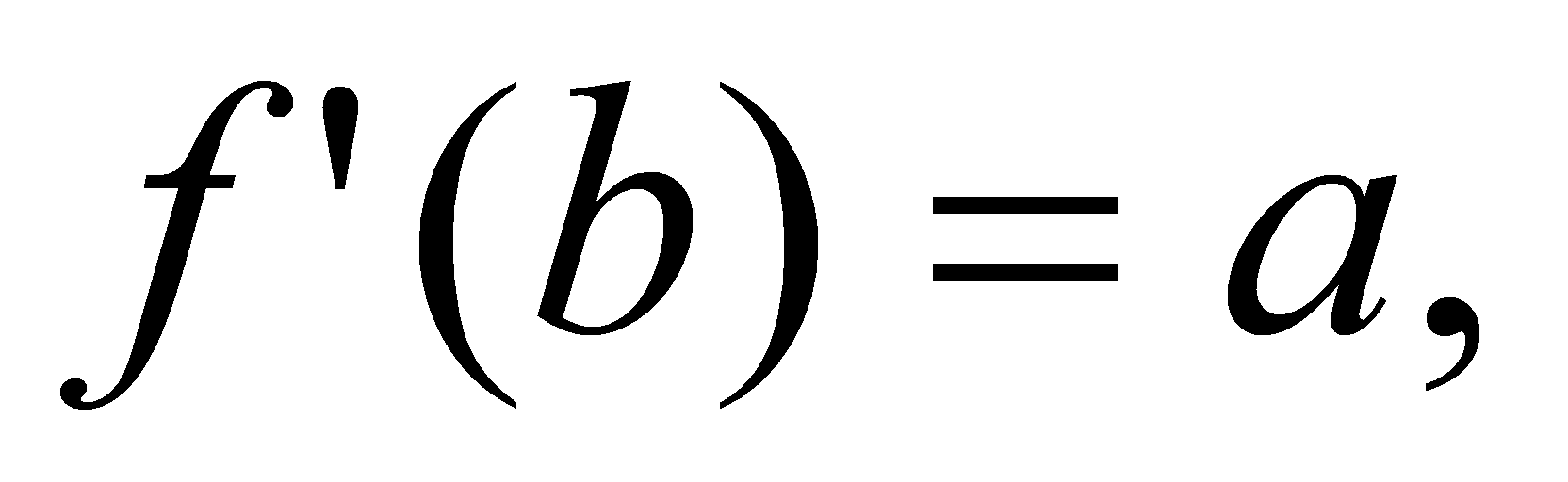 где
где

 абсцисса
точки касания. Значит,
абсцисса
точки касания. Значит,
 и
и
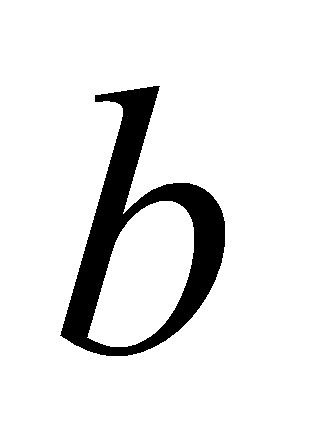 связаны между собой равенством
связаны между собой равенством
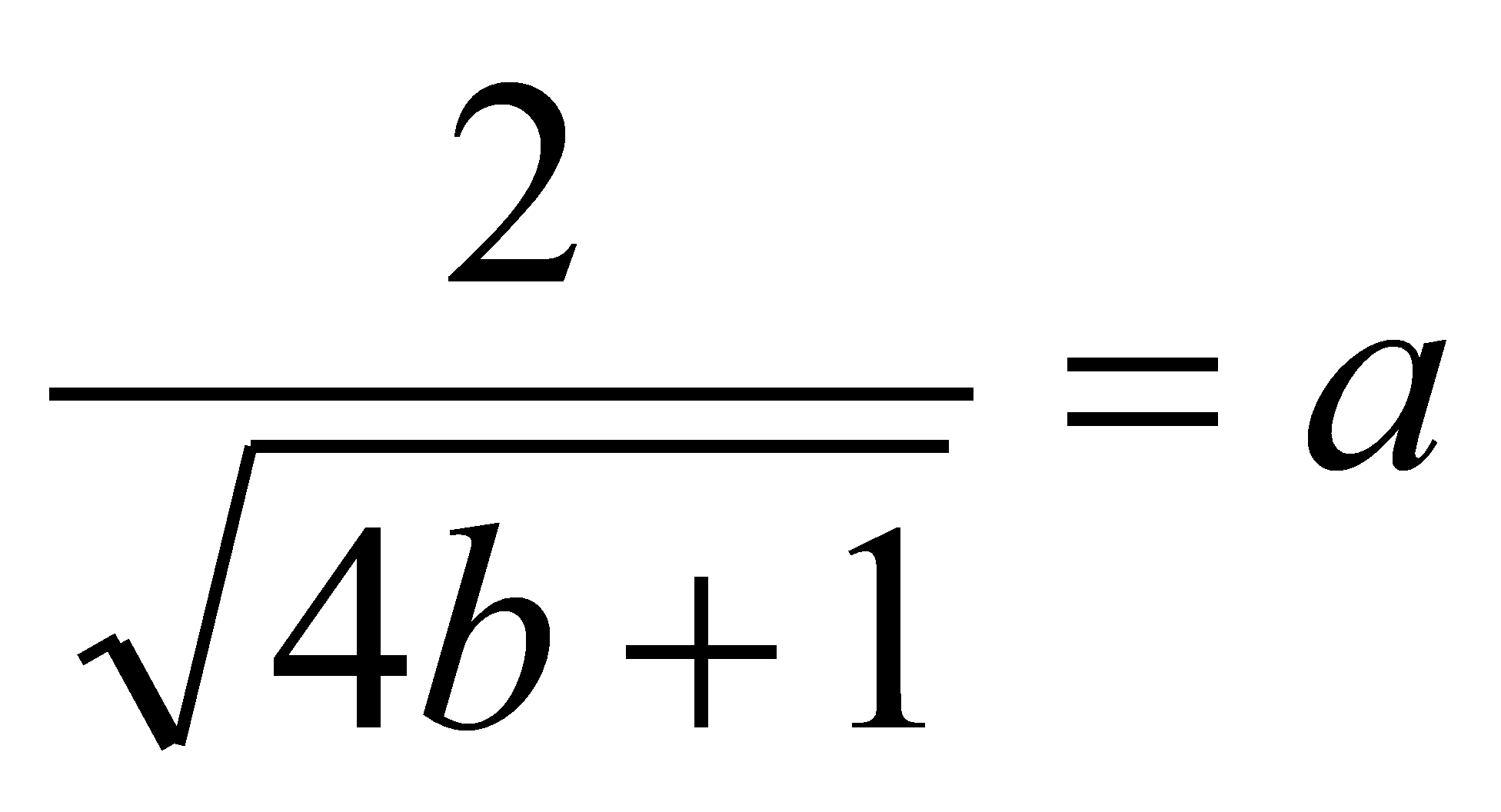 (1). Составим уравнение касательной к графику заданной функции в
точке
(1). Составим уравнение касательной к графику заданной функции в
точке
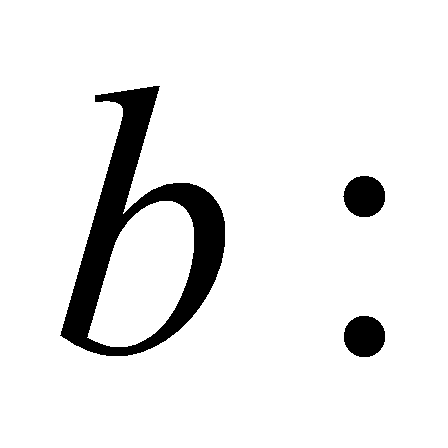
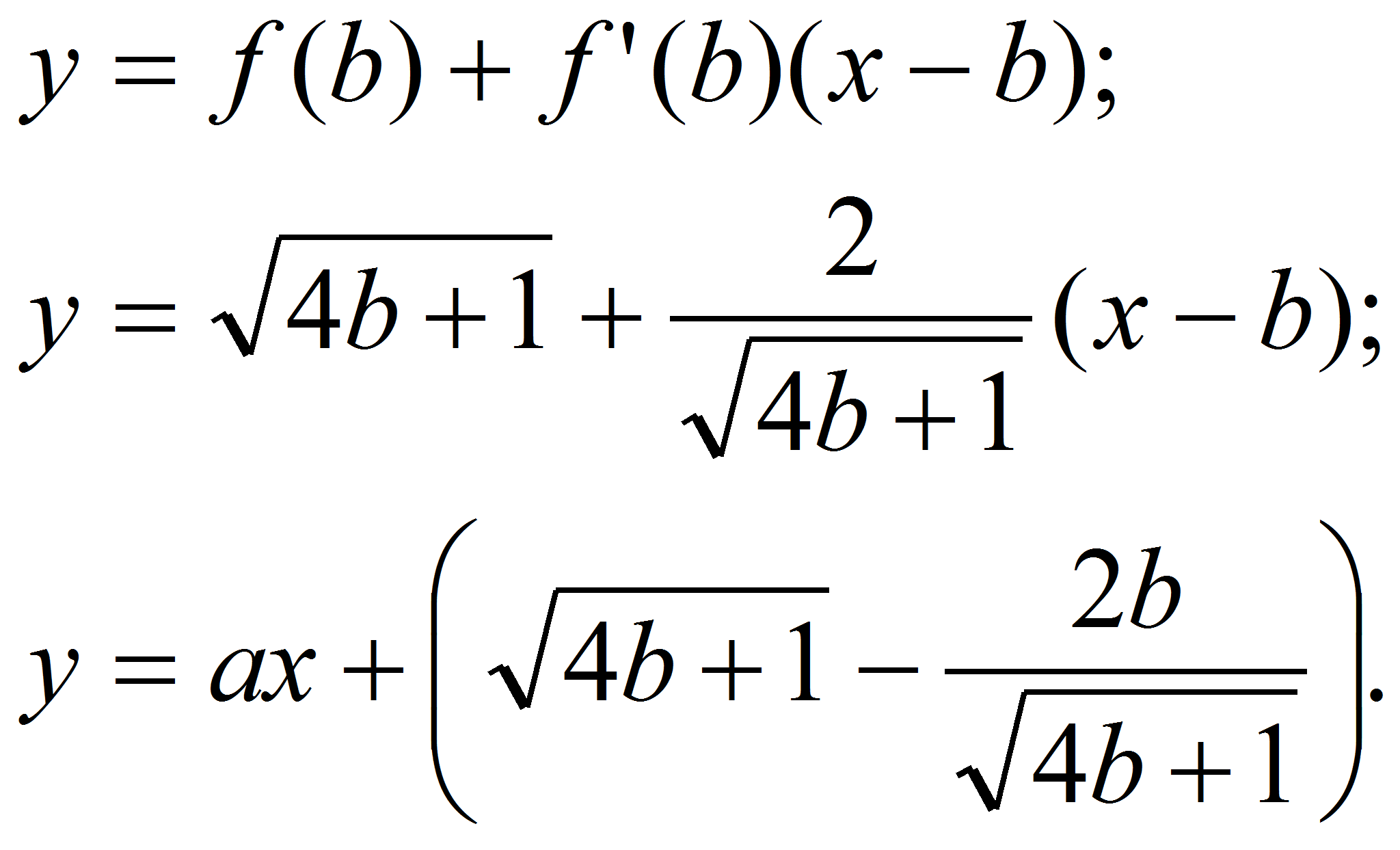
Из условия
следует, что должно выполняться равенство
 .
Решив это уравнение, получим
.
Решив это уравнение, получим
 .
Тогда из (1) получаем, что
.
Тогда из (1) получаем, что
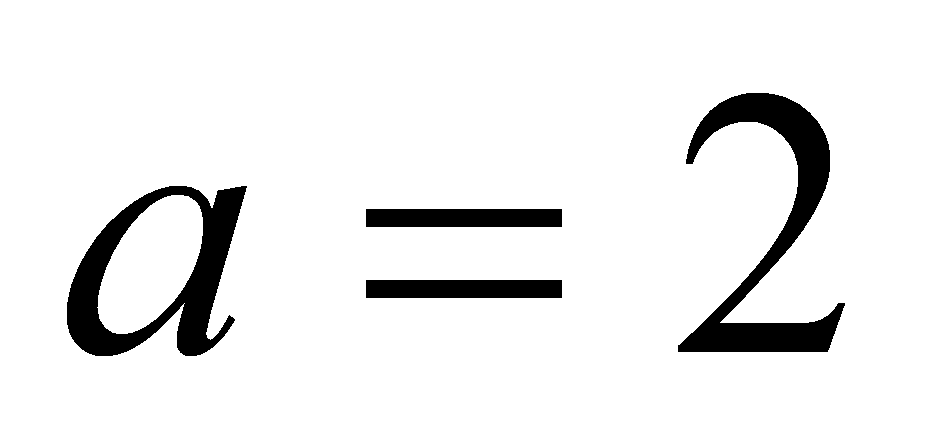 .
.
При каком значении
 прямая
прямая
 является касательной у графику
является касательной у графику
 ?
?
Решение.
Так как прямая
 является касательной к графику функции
является касательной к графику функции
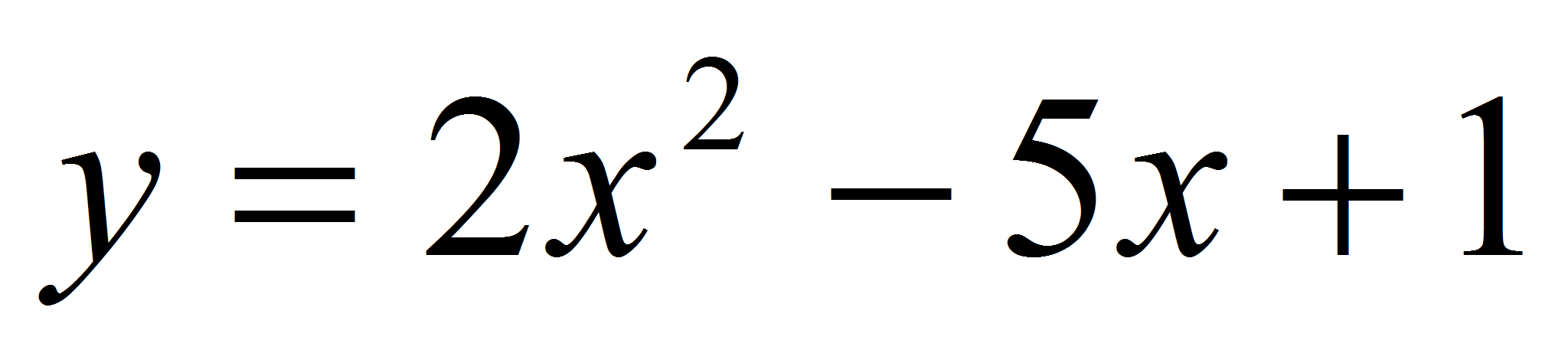 ,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
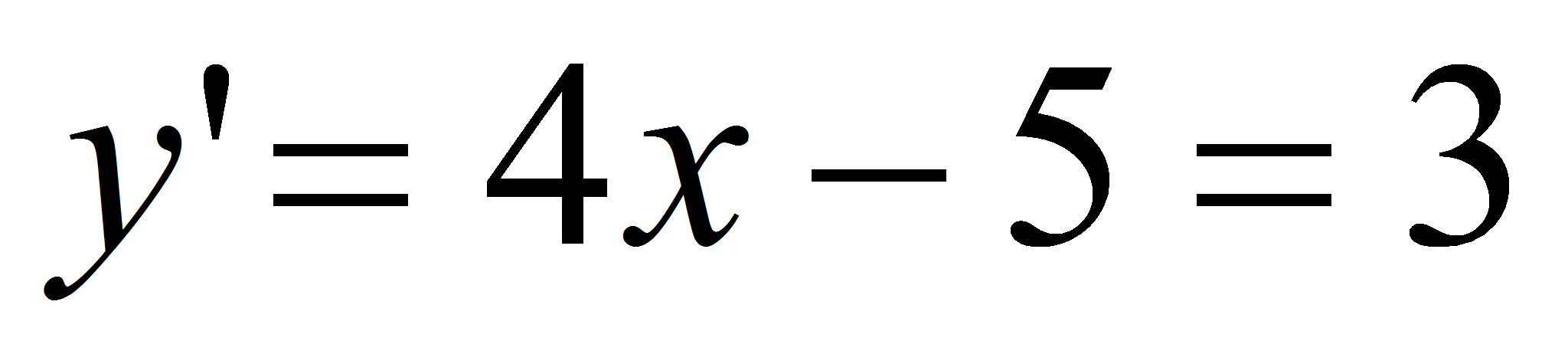 ,
откуда
,
откуда
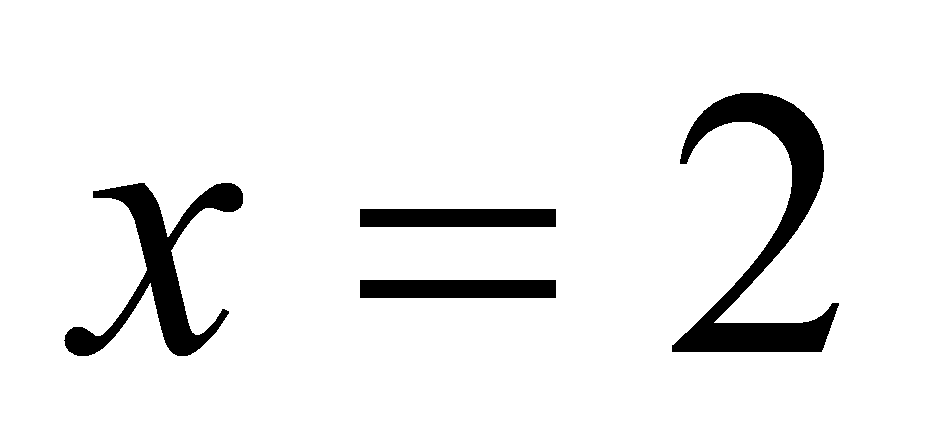 ,
следовательно,
,
следовательно,
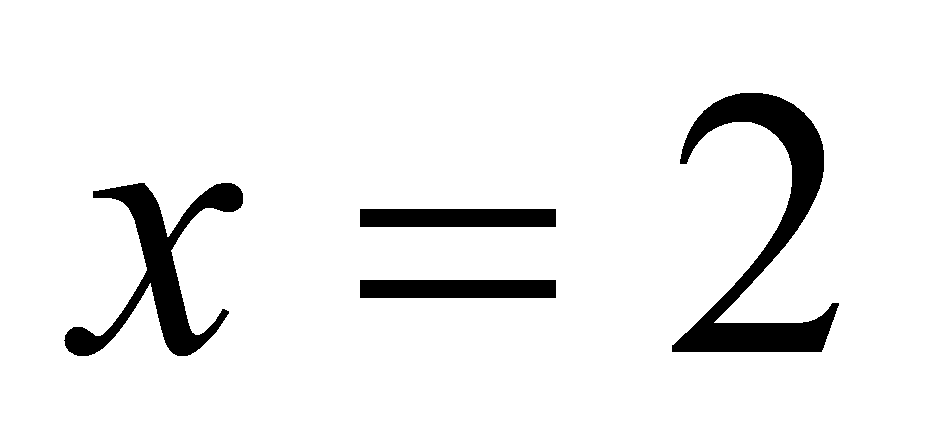 -
абсцисса точки касания. Найдем теперь
-
абсцисса точки касания. Найдем теперь
 из
условия равенства значений функций
из
условия равенства значений функций
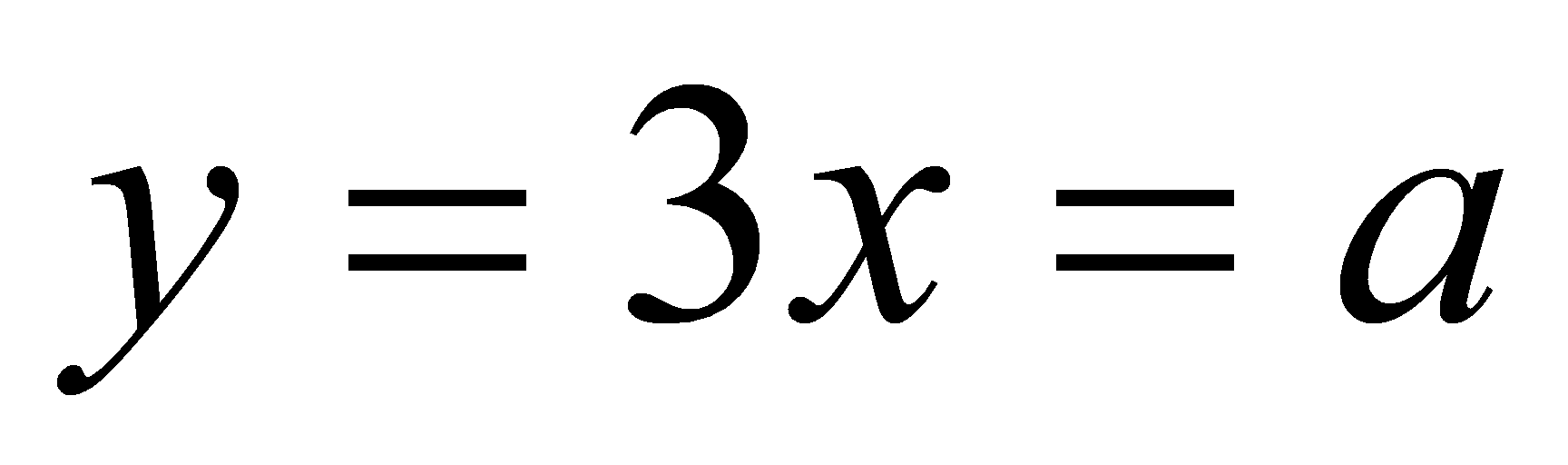 и
и
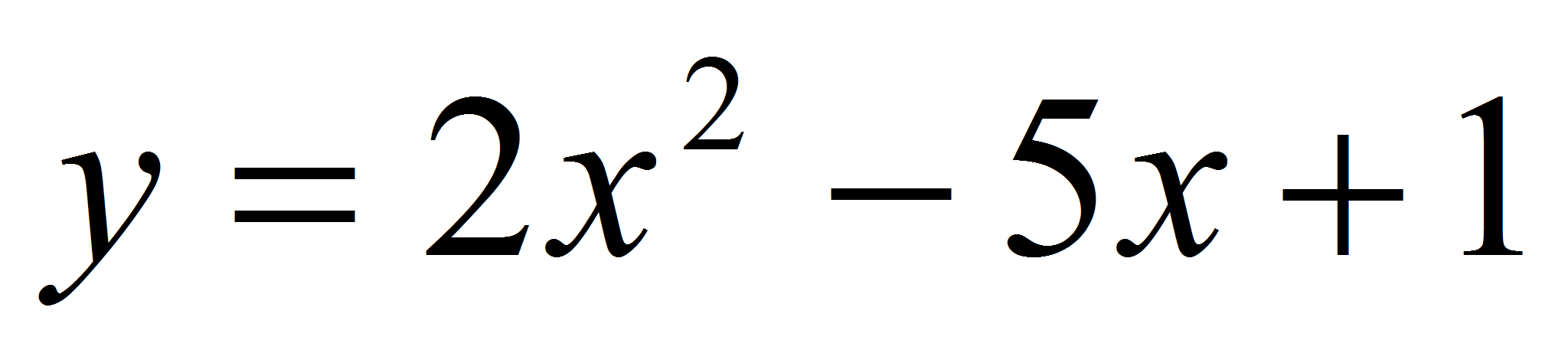 при
при
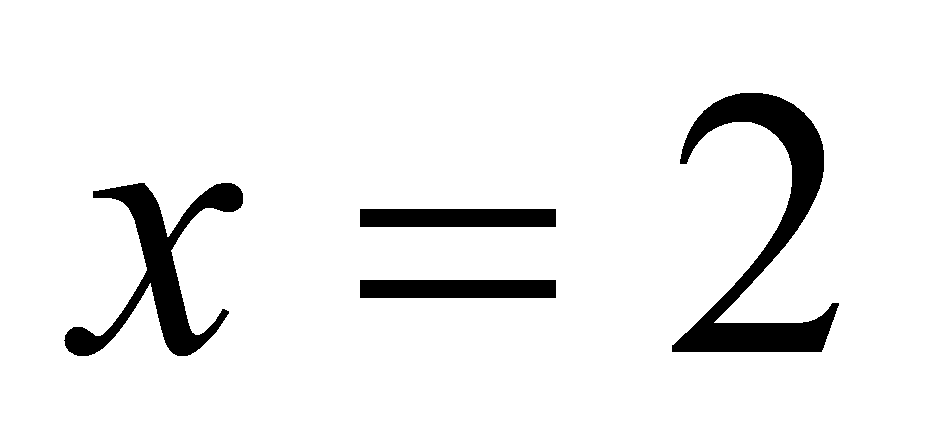 .
Имеем
.
Имеем
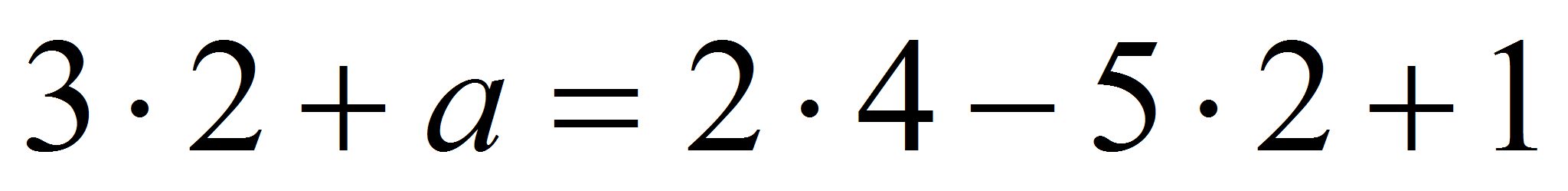 ,
откуда
,
откуда
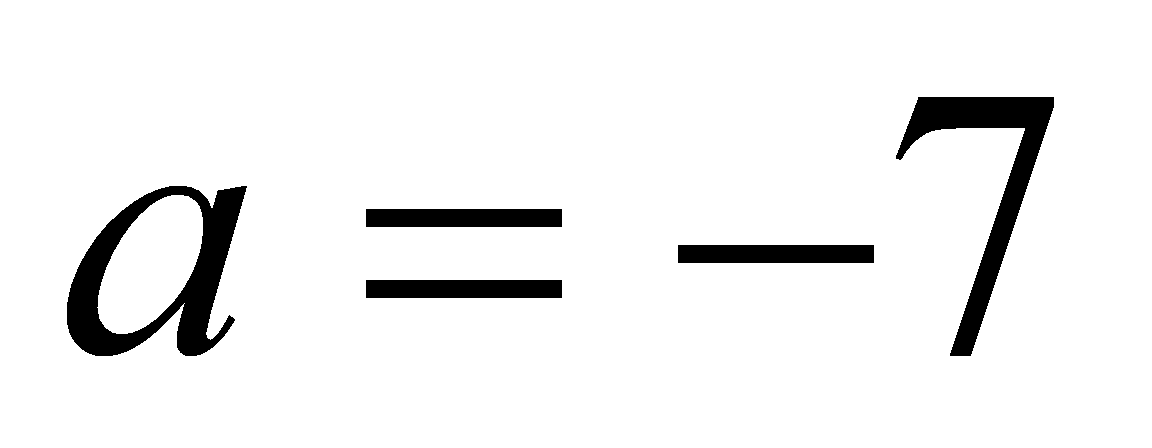 .
.
При каких значениях параметра а касательные к графику функции
 ,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
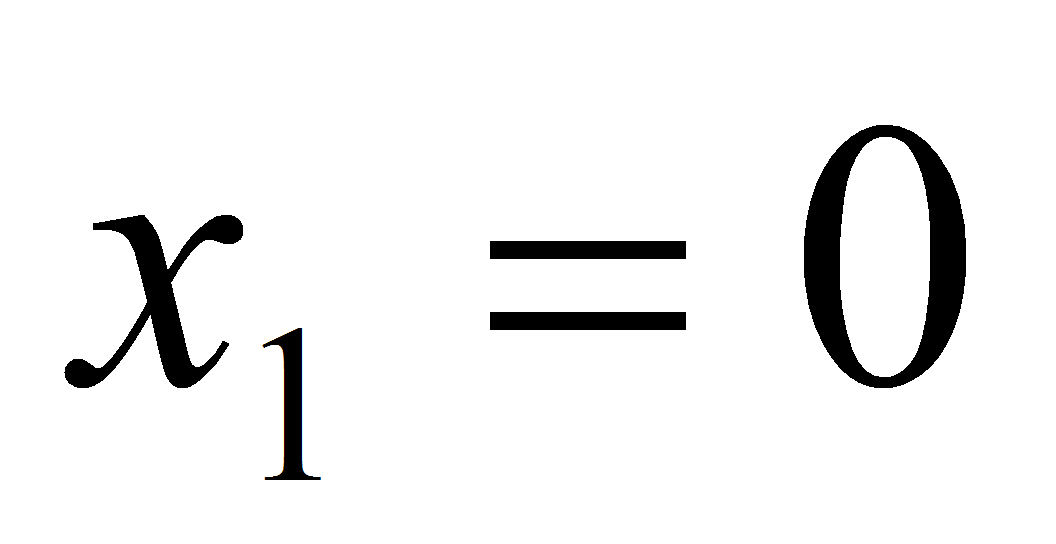 и
и
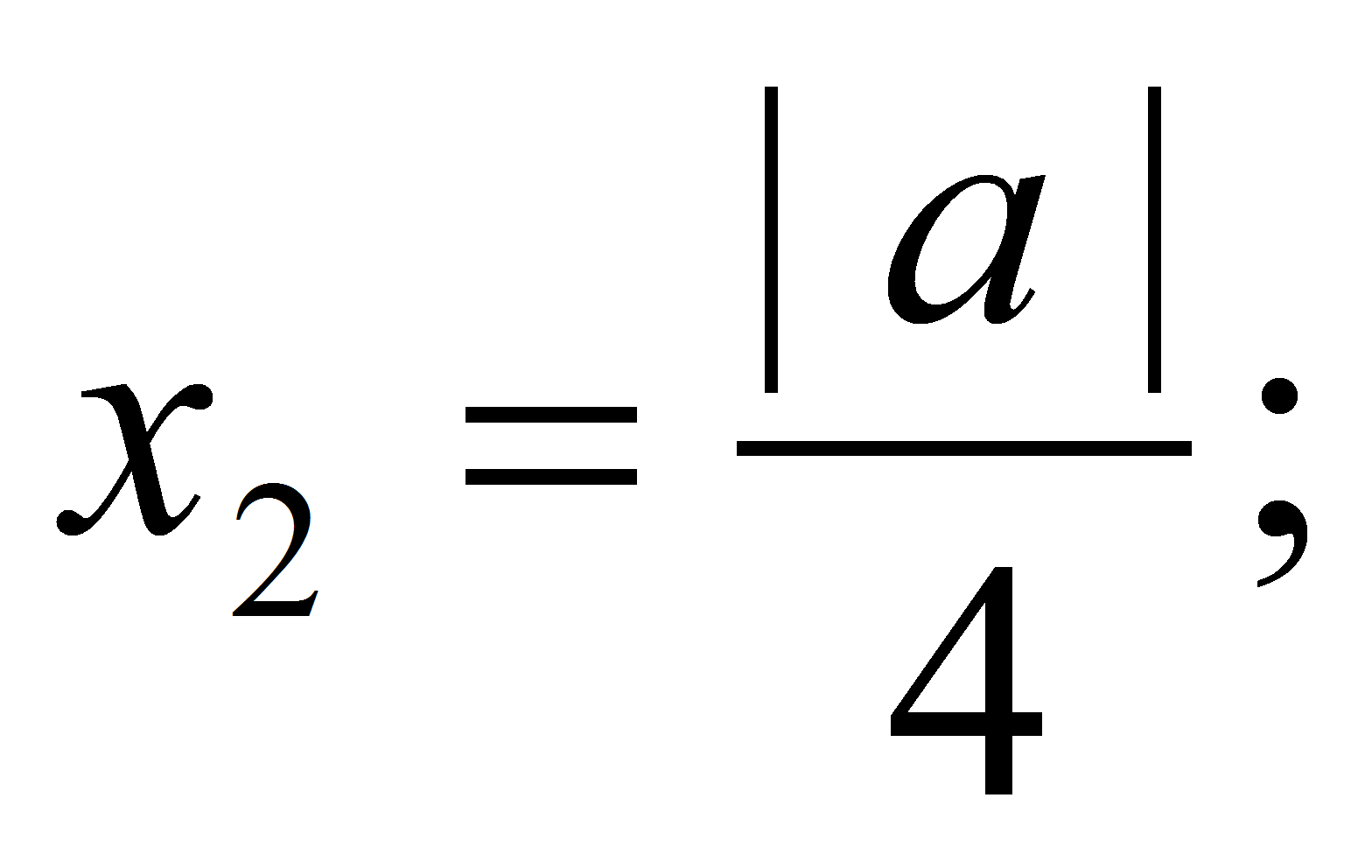 учитываем,
что х2>0
(рис. 3)
учитываем,
что х2>0
(рис. 3)

Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
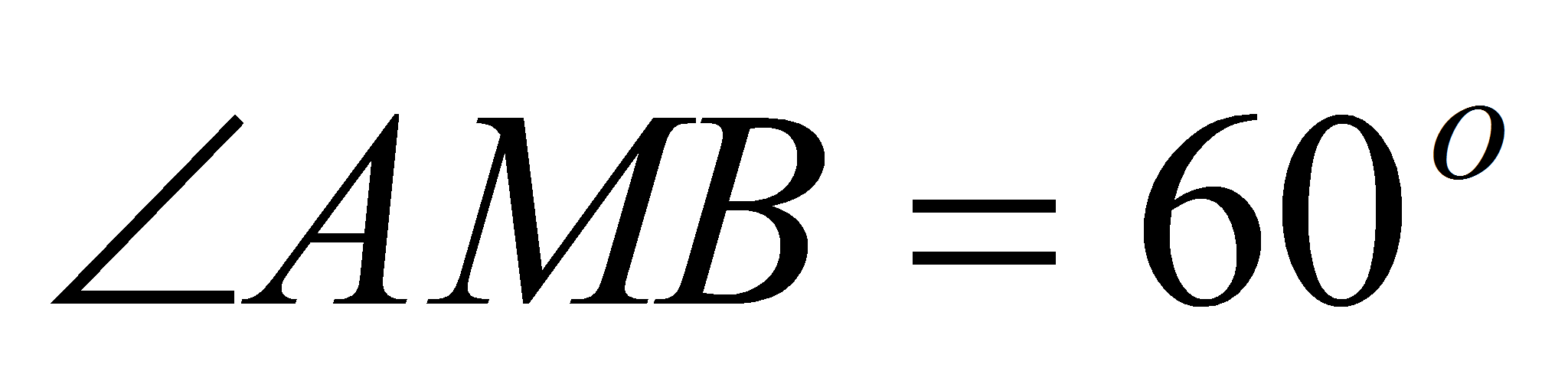 ,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
 Далее имеем:
Далее имеем:
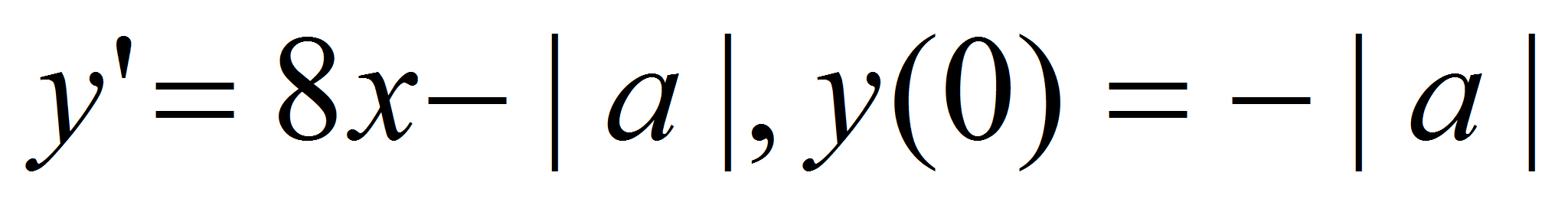 .
Таким образом, получаем, что
.
Таким образом, получаем, что
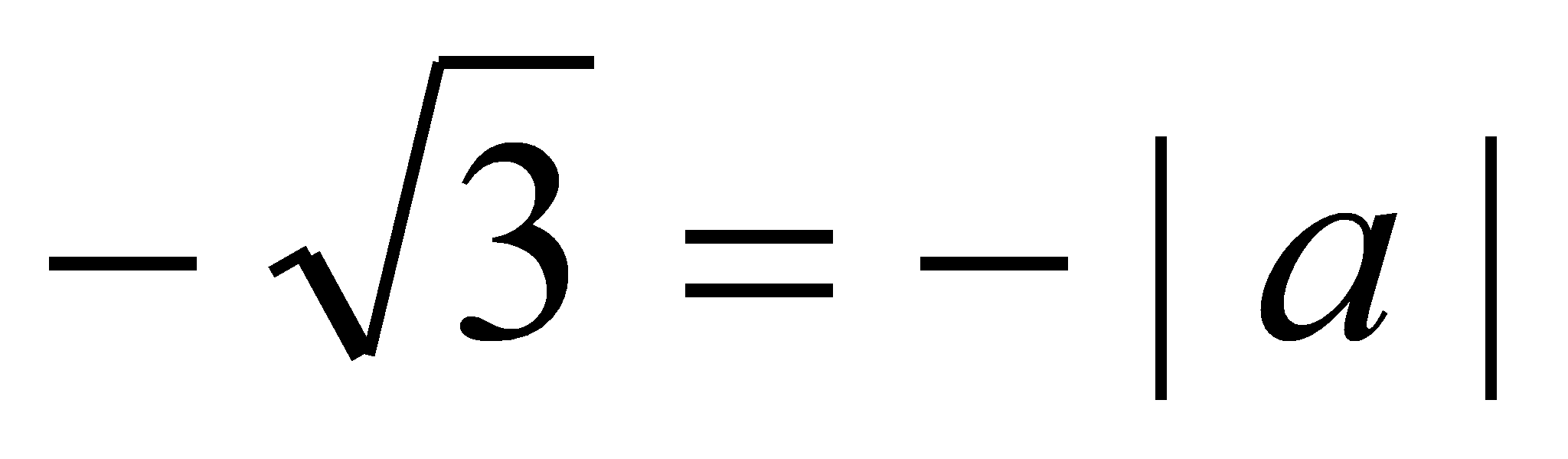 ,
то
,
то
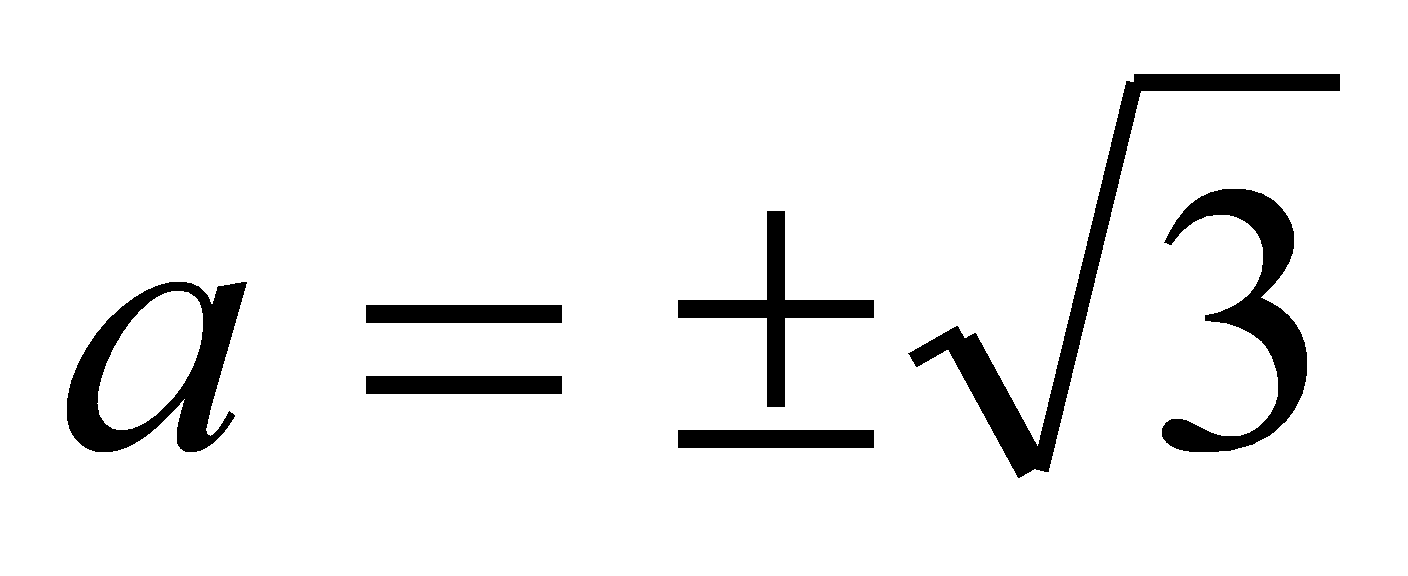 .
Во втором случае
.
Во втором случае
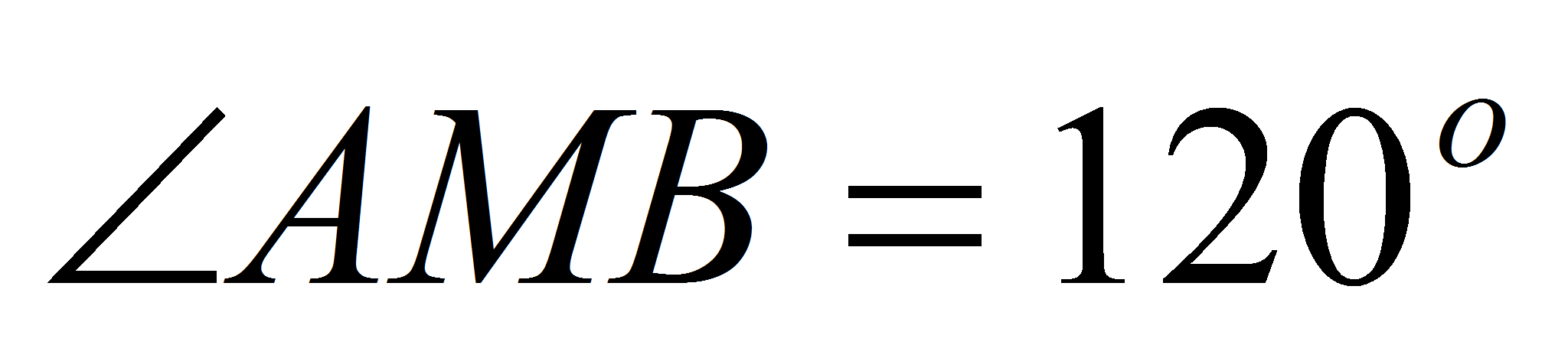 ,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
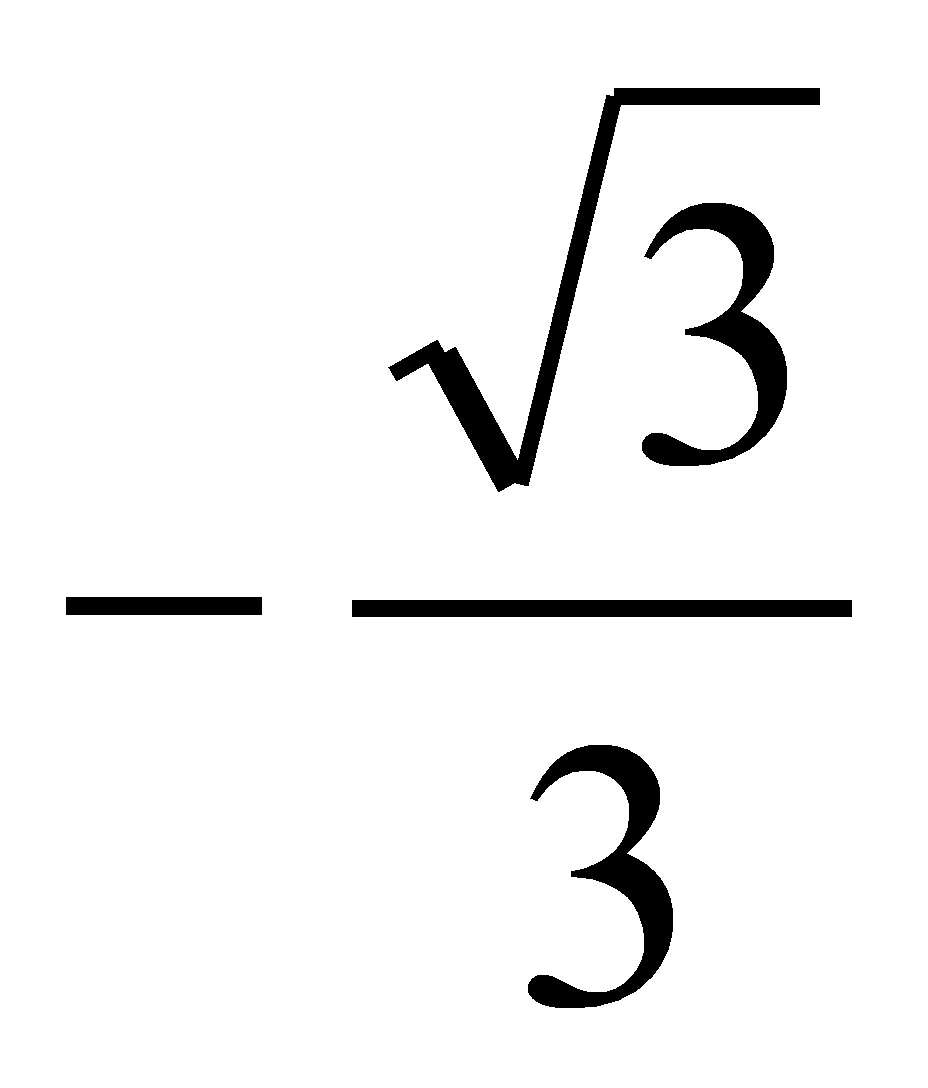 .
Таким образом, получаем, что
.
Таким образом, получаем, что
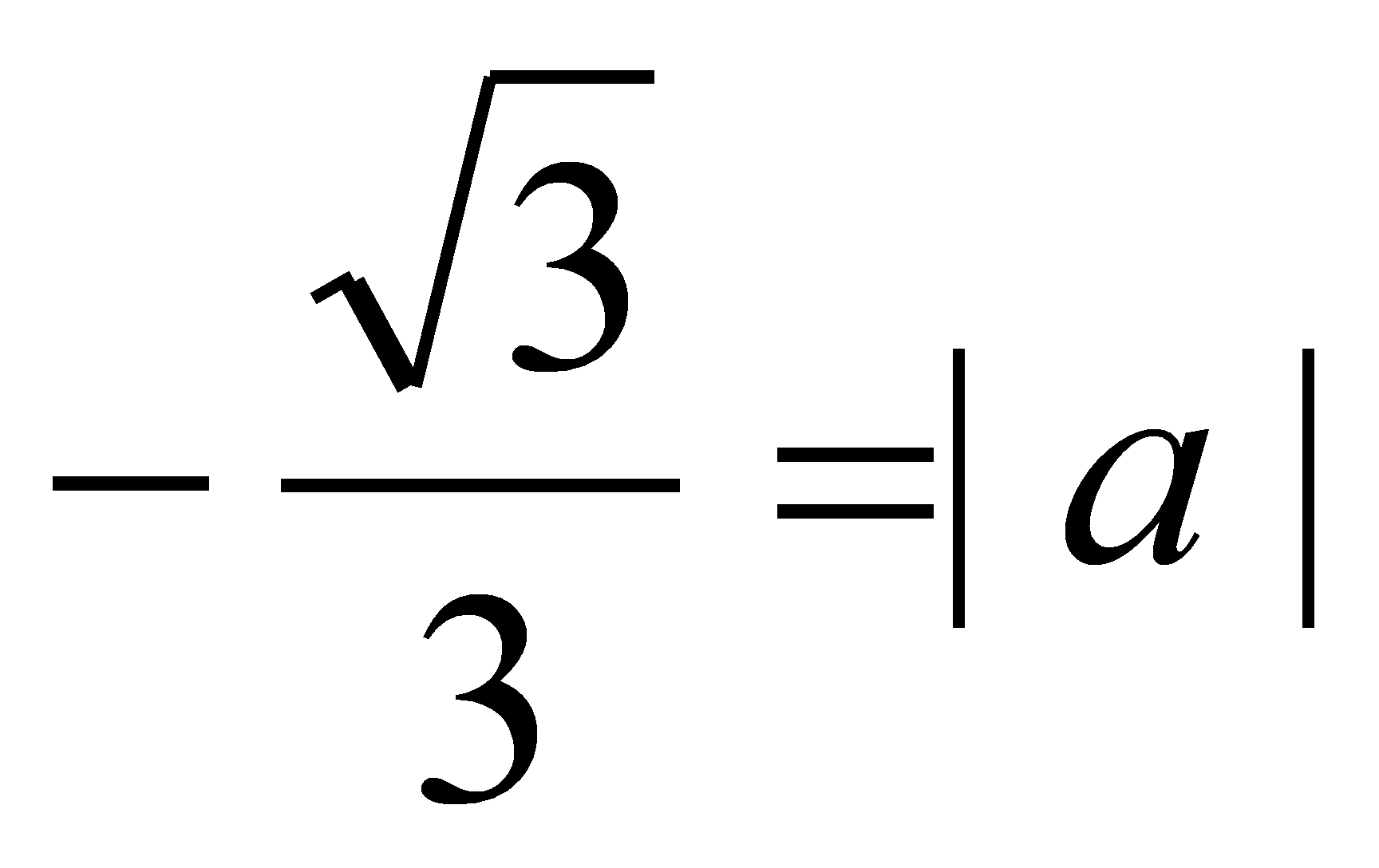 ,
то есть
,
то есть
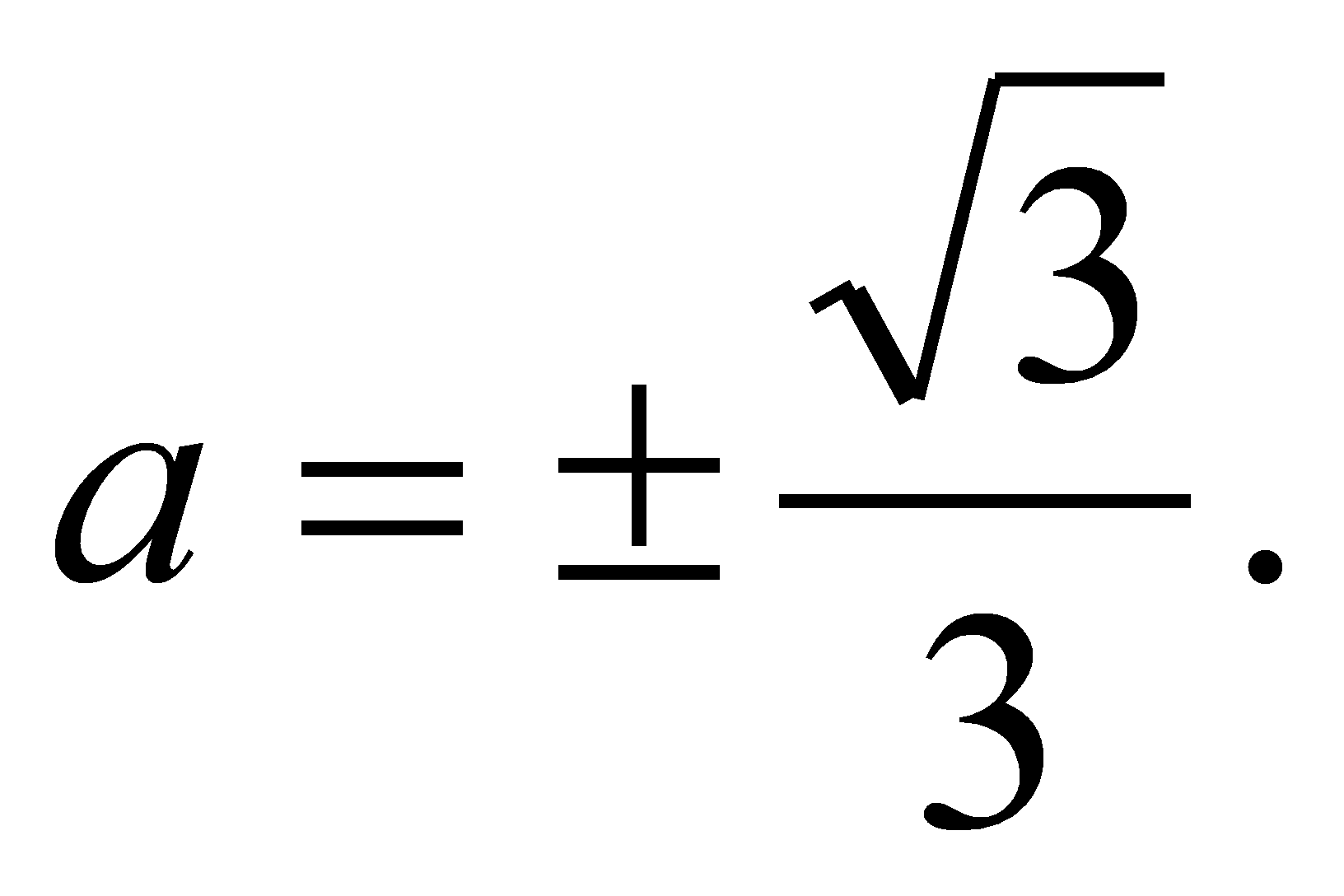
Ответ:
 .
.
Литература:
Далингер, В.А. Начала математического анализа в задачах [Текст]: учебное пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. – 312 с.
Звавич, Л.И. Алгебра и начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.– М.: Дрофа, 1999. – 352 с.
moluch.ru
Касательная к графику ункции: уравнение касательной
Рассмотрим следующий рисунок:
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной. Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
y = k*x + b.
Так как у нас угловой коэффициент равен производной f’(x0), то уравнение примет следующий вид: y = f’(x0)*x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) – f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) – f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).
y = f(x0) + f’(x0)*(x — x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.
1. х0 = 2.
2. f(x0) = f(2) = 22 — 2*22 + 1 = 1.
3. f’(x) = 3*x2 – 4*x.
4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Ответ: y = 4*x — 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
4. Вычислить f’(x0)
5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x — x0).
Нужна помощь в учебе?
Предыдущая тема: Применения непрерывности: метод интервалов и примеры
Следующая тема:   Критические точки функции: максимумы и минимумы
Все неприличные комментарии будут удаляться.
www.nado5.ru
Касательная к графику функции — урок обобщения и систематизации знаний
Цель занятия. Повторить владение техникой составления уравнения касательной к графику функции, систематизировать основные типы задач, при решении которых используется метод касательной.
Оборудование: компьютер; мультимедийный проектор.
Ход занятия
Повторение.
Учащиеся отвечают на вопросы (тексты на экране):
Какие из ниже приведенных определений касательной верные, а какие неверные?
1) Касательная есть предельное положение секущей при
2) Касательная к графику дифференцируемой в точке х0 функции f – это прямая, проходящая через точку (х0;f(x0)) и имеющая угловой коэффициент f \(х0).
3)Касательной к графику функции называется прямая, имеющая с данной кривой единственную общую точку.
Если функция непрерывна в точке, но не имеет в этой точке производной, то какой вывод можно сделать относительно касательной к графику функции в этой точке?
Учащиеся отвечают, что, вообще говоря, неверным является третье определение. В этом случае достаточно привести один пример.
Прямая х=2 имеет с параболой у=(х-1)2 одну общую точку (2;1), но касательной не является. Прямая у=2х-3, проходящая через эту точку, является касательной к графику данной функции.
Покажем это. Мы знаем, что если существует производная функции у=f(x) в точке х0, то существует и касательная к графику этой функции. Уравнение касательной имеет вид:
у= f(x0)+f \(x0)(х-х0)
у \(х)=2х-2, у \(х0)=у \(2)=2, у(х0)=у(2)=1. Уравнение касательной
у=1+2(х-2)=2х-3, у=2х-3.
Ответ на второй вопрос дан в п.19,с.129.Алгебра и начала математического анализа.10-А45 11 классы: учебник для общеобразовательных учреждений с приложением на электронном носителе / [ А.Н.Колмогоров, А.М.Абрамов, Ю.Н.Дудницын и др.]; под редакцией А.Н. Колмогорова-18-е изд.-М.: Просвещение, 2009 , а именно, если же f \(x0) не существует( как у функции , в точке (0;0), либо вертикальна ( как у графика функции в точке (0;0))
Учитель. На сегодняшнем занятии мы с вами рассмотрим четыре основных типа задач на касательную:
- составить уравнение касательной к графику функции в точке на этом графике;
- составить уравнение касательной к графику функции, параллельной данной прямой;
- составить уравнения касательных к графику данной функции, проходящих через заданную точку;
- составить уравнения общих касательных для графиков двух функций.
Первые два типа задач вам хорошо известны; решения этих задач рассмотрим на экране.
Задача 1. Составить уравнение касательной к графику функции у=х3-2х+3 в точке А(-1;4), лежащей на графике.
Решение. Уравнение касательной к графику функции f в точке А(х0;f(х0)) имеет вид:
y=f(x0)+f \(x0)(x-x0)
В нашей задаче х0= -1,f(x0)=f(-1)=4, f \(x0)=f \(-1)=.
Подставляя эти числа в уравнение касательной, получим уравнение у=4+(х+1), т.е. у=х+5
Ответ: у=х+5
Задача 2. Написать уравнение всех касательных к графику функции
у=х3-2х+7, параллельных прямой у=х.
Решение. Параллельные прямые имеют равные угловые коэффициенты, поэтому у \(x0)=1, где у \(х0) – значение производной функции у=х3-2х+7,х0— абсцисса точки касания.
Находим у\(х)= 3х2-2, , х0=1 или х0= -1
Для каждой из этих точек составляем уравнение касательной.
y=f(x0)+f \(x0)(x-x0)
x0 =1,f(x0)=f(1)=6;f \(x0)=f \(1)=1; y=6+(x-1)=x+5; y=x+5
x0= -1, f(x0)=f(-1)=8;f \(x0)=f \(-1)=1;у=8+(х+1)=х+9; у=х+9
Ответ: у=х+5,у=х+9
Следующие задачи решаются у доски с записью решений в тетрадях.
Задача 3. Написать уравнение всех касательных к графику функции у=х2—4х+3, проходящих через точку А(3;-2).
Учитель. При решении таких задач составляется уравнение касательной, а затем это уравнение решается относительно х0и для каждого х0 находится соответствующее уравнение касательной.
Решение. Убедимся, что точка А(4;-1) не лежит на графике данной функции.
Действительно, 42-4+3.
Находим f(x0)=-4
Уравнение касательной у=(х-х0)
Так как касательная проходит через точку А(4;-1), то ее координаты удовлетворяют уравнению касательной.
Составим уравнение касательной для каждого значения х0.
При х0=6 имеем f(x0)=15, , у=15+8(х-6)=8х-33, у=8х-33- уравнение первой касательной.
При х0=2 имеем f(x0)=-1, f(х0)=-1,f\(х0)=0, у= -1— уравнение второй касательной. Это уравнение касательной можно составить, учитывая, что вторая координата вершины параболы имеет значение -1.
Ответ: у=8х-33,у= -1
Задача 4. Найдите уравнение всех общих касательных к графикам функций у=3х2-5х-2 и у=2х2-х-6.
Решение. Пусть х=t – абсцисса точки касания всех касательных к графику функции у=3х2-5х-2 .
Уравнение всех касательных к графику этой функции имеет вид:
у=3t2-5t-2+(6t-5)(x-t)
Пусть и – абсцисса всех касательных к графику функции у=2х2-х-6.
Получим уравнение всех касательных:
у=2и2-и-6+(4и-1)(х-и)
Полученные два уравнения задают одну и туже прямую. Следовательно, надо решить систему
Учитывая равенство 6t-5=4u-1, второе уравнение системы запишем в виде
3t2-5t-2-(6t-5)t=2u2-u-6-(4u-1)u
или после упрощения 3t2-2u2-u=0
Из первого уравнения системы .
Подставляя в последнее уравнение, получим (t-2)2=0, t=2, тогда u=2.
Получили уравнение единственной касательной у=7х-14
Ответ: у=7х-14
Учитель. Рассмотрим еще две задачи на касательную. Прежде всего, представляют интерес задачи, где требуется определить является ли прямая у= кх+b касательной к графику функции у=f(x) и как уравнение касательной используется при нахождении площадей фигур.
Задача 5. При каких значениях параметра а прямая у= ах+ касается графика функции .
Решение. Если существует хотя бы одно значение х0, для которого имеет решение система , где х0 — абсциссы общих точек графиков функций у=кх+b и у=f(x), то прямая у=кх+b является касательной к графику у=f(x).
Находим .
Решим систему
Из первого уравнения системы
Подставляя во второе уравнение системы, получим
Откуда
Ответ: а=
Задача 6. Найти площадь треугольника, образованного касательными, проведенными к графику функции f(x)=3x-x2, проходящими через точки А(1;3) и В(1;2).
Решение. Запишем уравнение касательной к графику функции f(x) в точке с абсциссой х0
y=f(x0)+f \(x0)(x-x0)
Точка А(1;3) находится вне параболы, так .
Находим f \(x0)=3-2x, f \(x0)=3-2x0, f(x0)=3x0 – x02.
Тогда уравнение касательной примет вид
или у =
Касательная проходит через точку А(1;3), поэтому
Получили, что через точку А(1;3) проходит две касательные к параболе f(x)=3x-x2, а именно у=3х и у = — х+4.
Точка В(1;2)лежит на параболе, так как 2=, и уравнение касательной имеет вид у=2+(х-1)=х+1
На рис.1 изображена парабола с вершиной ,точками пересечения с осью абсцисс О(0;0),Е(3;0) и касательными, которые образуют треугольник АСD, площадь которого требуется найти.
Рис.1
Найдем координаты точек пересечения касательной у=х+1 с касательными у=3х и у = -х+4. Для этого решим совокупность двух систем
Получили
Теперь найдем длины сторон треугольника ACD по формуле расстояния между двумя точками
,
Для нахождения площади треугольника воспользуемся формулой Герона
Вычислим отдельно:
Далее имеем:
Ответ: 0,5
Задание на дом.
1. Составьте уравнение касательной к графику функции у=х3-2х+3 в точке А(-1;4).
2. Составить уравнения касательных, проведенных к графику функции у = -2х2-х-3 в точках пересечения графика с прямой у = -х-11. Сделать чертеж.
3. Составьте уравнения всех общих касательных к графикам функций
у = х2-х+1 и у=2х2-х+0,5
Для более подготовленных учащихся вместо задачи №1 можно предложить задачу: Вычислить площадь треугольника, образованного тремя касательными, проведенными к графикам функции в точках с абсциссами х1= -2, х2 =2, х3=6
Литература
1. Звавич Л.И. и др.Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы \ .И.Звавич, Л.Я.Шляпочник,М.В. Чинкина, Дрофа, 1999.\
2.Звавич Л.И. и др. Алгебра и начала анализа. Решение задач письменного экзамена.11кл\Л.И.Звавич, Л.Я.Шляпочник, И.Кулагина.-М.: Дрофа,2000\
3.Кравцев СВ. и др Методы решения задач по алгебре: от простых до самых сложных \С.В. Крацев и др..-М.:Издательство: “Экзамен”, 2005/
4.Нараленков М.И. Вступительные экзамены по математике. Алгебра: как решать задачи: Учебно- практическое пособие \М.И. Нараленков.-М.: Издательство “Экзамен”,2003\
5.Математика. Подготовка к ЕГЭ-2009. Вступительные испытания. Под редакцией Ф.Ф.Лысенко.- Ростов – на – Дону: Легион,2008 (“Готовимся к ЕГЭ”)
6.СадовничийЮ.В. Алгебра. Конкурсные задачи с решениями: учебное пособие \Ю.В.Садовничий.-М.:Издательство “Экзамен”,2007\
urok.1sept.ru
КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ — Студопедия.Нет
I. Таблица производных
1. , где С – const;
2.
3. 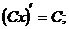
4. 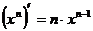 ;
;
5.
6.  7.
7.  ;
;
8.  ; 9.
; 9.  ;
;
10. 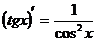 ; 11.
; 11. 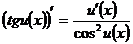 ;
;
12. 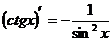 ; 13.
; 13. 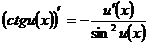 ;
;
14.  ; 15.
; 15.  ;
;
16.  ; 17.
; 17. 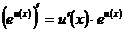 ;
;
18.  ; 19.
; 19.  ;
;
20. 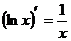 ; 21.
; 21. 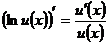 .
.
Правила дифференцирования
I. 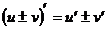 , где
, где 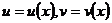 ;
;
II.  , где
, где 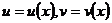 ;
;
III. 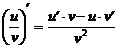 , где
, где 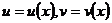 ;
;
IV. 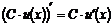 ;
;
V.  ;
;
II. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ
(§4, п15-17)
Рассмотрим применение основных правил дифференцирования и применение таблицы производных при решении задач.
Пример . Вычислить производную:
а) 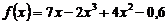 ; б)
; б) 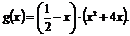 ;
;
в) 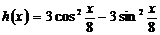 ; г)
; г)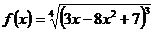 ;
;
д) 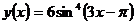 ; е)
; е) 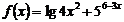 ;
;
ж) 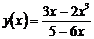 .
.
РЕШЕНИЯ
а) Вычислить производную: 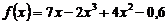 ;
;
Решение:
Так как производная суммы нескольких слагаемых равна сумме производных от этих слагаемых (см.правило I), то получим:

Постоянный множитель можно выносить за знак производной (см.правило №4):
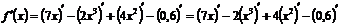
Применяя последовательно формулы под номерами 3, 4 и 1 в таблице производных, получим:
 =
= 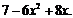
Ответ: 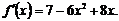
б) Вычислить производную: 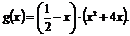
Решение:
Так как функция g(x) представляет собой произведение, то необходимо применить правило дифференцирования произведения (формула №II).
В данном примере 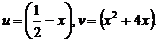
Подставляя данные значения в правую часть формулы №II, получим:
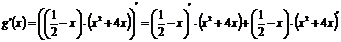 ;
;
Теперь необходимо вычислить значения производной первого и последнего сомножителей. Применяя к ним последовательно правило дифференцирования I и формулы № 1, 2, 4, 3 из таблицы производных, имеем:

Раскроем скобки и приведем подобные члены:
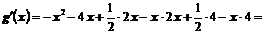
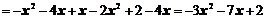
Ответ:  .
.
в) Вычислить производную 
Решение:
Прежде чем дифференцировать данную функцию, упростим ее, для этого вынесем общий множитель за скобку, а выражение, стоящее в скобке свернем по формуле косинуса двойного угла, то есть, применим формулу  , получим:
, получим:
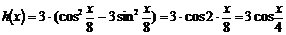
Применяя последовательно формулы 9, 14, 3, имеем:
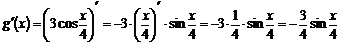 .
.
Ответ:  .
.
г). Вычислить производную: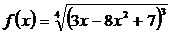
Решение:
Применяя формулу  преобразуем данное выражение:
преобразуем данное выражение:
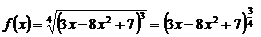 .
.
Применяя правило дифференцирования сложной функции (правило V), получим:
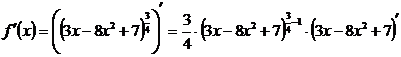 Учитывая, что
Учитывая, что 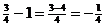 и применяя к последней скобке правило дифференцирования I, а затем последовательно формулы №3, 4 и 1, имеем:
и применяя к последней скобке правило дифференцирования I, а затем последовательно формулы №3, 4 и 1, имеем:

Преобразовывая степенное выражение по формуле 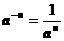 , и учитывая, что
, и учитывая, что 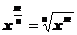 получим:
получим:
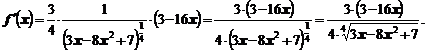
Ответ: 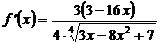 .
.
д) Вычислить производную: 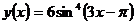
Решение:
Для нахождения производной данной функции необходимо вынести постоянный множитель (т.е.число 6) вынести за знак производной (правило дифференцирования IV) и применить правило дифференцирования сложной функции (формула V):

Производная выражения, стоящего в скобке, находится по формуле №7 (см. таблицу производных):
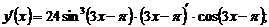
Раскрывая последнюю производную по правилу дифференцирования I, применяя формулы №,3 и 1 из таблицы производных и перемножая коэффициенты, получим:

Ответ: 
е) Вычислить производную: 
Решение:
Данная функция представляет собой сумму двух функций, зависящих от х, поэтому производная функции равна сумме производных от каждого слагаемого (применяется правило дифференцирования I).

Каждое слагаемое представляет собой сложную функцию, поэтому для нахождения производной последовательно применяем формулы 19 и 15, имеем:

Раскрывая производную числителя по формуле 4, а производную скобки по правилу дифференцирования I и формулам 1 и 3 (см таблицу производных), после сокращения дроби на выражение 4х, получим:

Ответ: 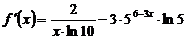
ж) Вычислить производную: 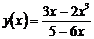
Решение:
Так как исходная функция представляет собой дробное выражение, то для нахождения ее производной необходимо применить правило дифференцирования дроби, т.е. правило III. Учитывая, что в данном примере
 ,
,
а  ,
,
получим:
 ;
;
Для вычисления производной первой и последней скобок, стоящих в числителе, необходимо сначала применить правило дифференцирования I, а затем последовательно формулы 3, 4 1 и 3.
В результате получим:

Раскрывая скобки и приводя подобные члены, получим значение производной исходной функции:
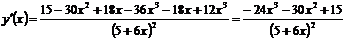
Ответ: 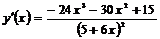
III. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ
КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
(§5, п.19)
Если функция задана уравнением y=f(x), то тангенс угла наклона касательной, проведенной к графику функции в точке 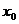 , с осью абсцисс равен производной от этой функции в точке
, с осью абсцисс равен производной от этой функции в точке 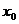 , то есть:
, то есть:
 у
у 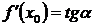 ,
,
где a — угол наклона касательной
Уравнение касательной к
y=f(x) графику функции f(x) в точке 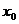 имеет вид:
имеет вид:

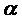
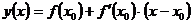 (*)
(*)
О  х Угол наклона касательной вычисляется по формуле:
х Угол наклона касательной вычисляется по формуле:
 (**)
(**)
 |
Пример 1. Написать уравнение касательной к графику функции 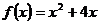 в точке
в точке 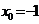 и найти тангенс угла наклона касательной к оси Ох.
и найти тангенс угла наклона касательной к оси Ох.
Решение:
Для решения данной задачи необходимо использовать формулу (*):
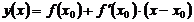 ,
,
Поэтому необходимо вычислить значение функции в точке 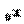 и значение производной в данной точке.
и значение производной в данной точке.
Вычислим значение функции в точке 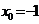 :
:

Применяя формулы дифференцирования, найдем производную исходной функции:
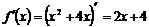 ;
;
Определим значение производной в точке 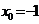 :
:
 . (***)
. (***)
Подставляя найденные значения в формулу (*), получим:

Раскрывая скобки и приводя подобные члены, получим уравнение касательной к графику заданной функции в точке 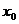 :
:
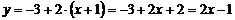 .
.
Для нахождения тангенса угла наклона касательной, воспользуемся формулой (**) и значением производной в точке 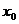 (***):
(***):
 ;
; 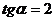 .
.
Ответ: 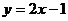 —уравнение касательной,
—уравнение касательной,
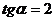 — тангенс угла наклона.
— тангенс угла наклона.
Пример 2. Написать уравнение касательной к графику функции 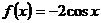 в точке
в точке 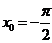
Решение:
Уравнение касательной к графику функции будем находить при помощи формулы(*). Найдем значение функции в точке  :
:

Определим производную заданной функции:

Вычислим значение производной в точке 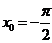 :
:
 .
.
Для вывода уравнения касательной подставим полученные значения в формулу (*):

Ответ: 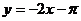 .
.
Пример 3. Составить уравнения касательных к кривой
 ,
,
проходящих через точку  .
.
Решение:
Проверим, принадлежит ли заданная точка А параболе  ? Для этого подставим координаты точки А в уравнение параболы:
? Для этого подставим координаты точки А в уравнение параболы:

Так как координаты заданной точки Ане удовлетворяют условию  , то это значит, что точка А не лежит на графике заданной функции. Поэтому, прежде всего надо найти точки на параболе, через которые пройдут искомые касательные. Обозначим координаты этих точек через
, то это значит, что точка А не лежит на графике заданной функции. Поэтому, прежде всего надо найти точки на параболе, через которые пройдут искомые касательные. Обозначим координаты этих точек через 
Найдем уравнения касательных, проходящих через эти точки, пользуясь формулой (*). Для этого:
1. Вычислим значение функции в точке 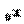 :
:
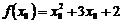 ;
;
2. Найдем производную исходной функции:
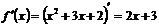
3. Вычислим значение производной в точке 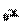 :
:
 .
.
4. Подставим найденные значения функции и ее производной, вычисленные в точке 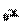 , в формулу (*):
, в формулу (*):
 ; (****)
; (****)
Полученное уравнение – это уравнение касательной, проведенной к заданной параболе в точке  . Найдем координаты точки касания
. Найдем координаты точки касания  . Так как по условию задачи эта касательная должна проходить через точку А, следовательно, ее координаты удовлетворяют полученному уравнению. Заменяя координаты
. Так как по условию задачи эта касательная должна проходить через точку А, следовательно, ее координаты удовлетворяют полученному уравнению. Заменяя координаты  на координаты точки А(2;8) в уравнении (****), получим:
на координаты точки А(2;8) в уравнении (****), получим:
 .
.
После раскрытия скобок и приведения подобных членов получаем неполное квадратное уравнение:
 или
или 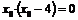
Это уравнение равносильно совокупности уравнений:
 , следовательно,
, следовательно, 
 .
.
Определим ординаты полученных точек:
при 
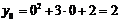 ,
,
при 

Таким образом, через точку А(2;8) проходят две касательные к заданной параболе. Точки касания имеют координаты 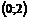 и
и  .
.

у
 |
Пример 4. Найти координаты точки А, в которой касательная к параболе 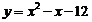 образует с осью Ох угол 45°.
образует с осью Ох угол 45°.
Решение:
Найдем тангенс угла наклона касательной, проведенной в искомой точке, к оси Ох, применяя формулу (**):

Угол a по условию задачи равен 45°, следовательно,

Так как 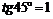 , то получим
, то получим
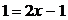 ,
,
откуда
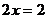 или
или 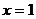
Определим ординату полученной точки. Для этого подставим значение 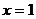 в уравнение параболы
в уравнение параболы 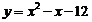 , получим:
, получим:
 .
.
Таким образом, искомая точка имеет координаты А(1;-12).
Ответ: А(1;-12).
ПРОИЗВОДНАЯ В ФИЗИКЕ
(§5, п.21)
Механический смысл производной 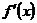 функции
функции 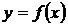 — это скорость изменения функции в точке х. Поэтому при решении прикладных задач следует помнить, что какой бы процесс ни описывался рассматриваемой функцией
— это скорость изменения функции в точке х. Поэтому при решении прикладных задач следует помнить, что какой бы процесс ни описывался рассматриваемой функцией 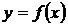 , производную, с физической точки зрения, можно представить как скорость, с которой протекает процесс.
, производную, с физической точки зрения, можно представить как скорость, с которой протекает процесс.
В частности, если S– это путь, пройденный точкой за время t, то функция S=S(t)задает закон движения точки, а производная 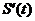 — определяет скорость v(t), с которой движется точка в момент времени t, т.е.
— определяет скорость v(t), с которой движется точка в момент времени t, т.е.
Скоростью тела в произвольный момент времени t называется производная по времени от закона движения тела:
а) прямолинейное движение:
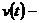 скорость тела,
скорость тела, 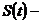 закон движения тела;
закон движения тела;
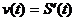 (*)
(*)
б) круговое движение
 угловая скорость тела,
угловая скорость тела, 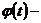 закон движения тела;
закон движения тела;
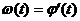
Ускорением тела в произвольный момент времени t называется производная по времени от скорости тела:
а) прямолинейное движение
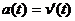 (**)
(**)
б) круговое движение
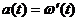
 |
Пример 1. Маховик вращается по закону
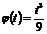 рад.).
рад.).
Через сколько времени от начала движения угловая скорость маховика будет равна 3 рад/сек? Чему равно ускорение в этот момент времени?
Решение:
Определим угловую скорость маховика в произвольный момент времени t.Так как скорость тела – это производная от закона движения, то
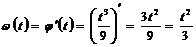 (рад/сек).
(рад/сек).
Для того, чтобы найти время, при котором скорость тела равна 3 (рад/сек), необходимо решить уравнение:
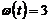 или
или  ,
,
откуда 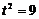 ,
, 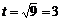 (cек).
(cек).
Таким образом, через 3 секунды от начала движения скорость маховика будет равна 3 рад/сек.
Чтобы вычислить ускорение в данный момент времени, нужно определить ускорение тела в произвольный момент времени t, для чего применим формулу (**):
 , получим:
, получим:
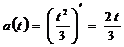
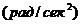 .
.
Для нахождения ускорения в момент времени 3 сек., необходимо в полученное выражение вместо параметра t подставить 3, получим:

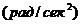 .
.
Ответ: t = 3 (сек.) ; а(3)= 2 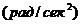
Пример 2. Тело, выпущенное вертикально вверх, движется по закону:
 (м)
(м)
Найти скорость тела в момент соприкосновения с землей.
Решение:
Найдем момент времени, при котором тело соприкоснется с землей. В это время расстояние от тела до земли будет равно нулю, т.е. 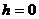 , значит, для нахождения этого времени необходимо решить уравнение
, значит, для нахождения этого времени необходимо решить уравнение
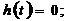 или
или 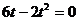 .
.
Вынесем общий множитель за скобку, после чего каждый сомножитель приравняем к нулю:
 ,
,
 ,
, 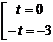 ,
, 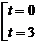 .
.
Таким образом, тело соприкоснется с землей через 3 сек.
Найдем скорость тела в произвольный момент времени t, используя формулу (*):
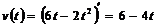 .
.
Определим скорость тела в момент времени 3 сек:
 (м/сек).
(м/сек).
Ответ:  (м/сек).
(м/сек).
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
(§6, п.22-24)
Исследование функции и построение ее графика удобно проводить по следующей схеме:
1. Область определения функции.
2. Производная.
3. Критические точки.
4. Промежутки возрастания и убывания функции.
5. Значения функции в критических точках.
6. Точки пересечения с осями координат.
7. Экстремумы функции.
8. Построение графика функции.
Результаты исследования функции целесообразно свести в таблицу, а построение графика начать с нанесения точек максимума и минимума, а также точек пересечения с осями координат.
Для исследования функции необходимо знать следующие определения:
— Внутренние точки области определения функции, в которых ее производная не существует или равна нулю, называются критическими.
— Точки, в которых производная меняет свой знак с плюса на минус, называются точками максимума функции.
— Точки, в которых производная меняет свой знак с минуса на плюс, называются точками минимума функции.
— Функция называется возрастающей на промежутке [a;b], если ее производная положительна на этом отрезке.
— Функция называется убывающей на промежутке [a;b], если ее производная отрицательна на этом отрезке.
— Точки минимума и максимума называются экстремумами функции.
Для того, чтобы найти точки пересечения графика функции 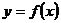 с осью Ох, надо решить уравнение
с осью Ох, надо решить уравнение  , в частных случаях в этих точках возможно лишь касание графика оси Ох.
, в частных случаях в этих точках возможно лишь касание графика оси Ох.
Для того, чтобы найти точки пересечения графика функции 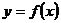 с осью Оу, нужно вычислить значение функции в точке х = 0, если эта точка входит в область определения функции.
с осью Оу, нужно вычислить значение функции в точке х = 0, если эта точка входит в область определения функции.
Рассмотрим применение схемы исследования функции при решении задач.

Пример1. Исследовать функцию 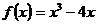 и построить ее график.
и построить ее график.
Решение:
Исследование проведем по приведенной выше схеме:
1. Область определения функции – вся числовая прямая, так как  — многочлен, то есть
— многочлен, то есть
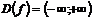
2. Вычислим производную функцию:
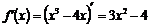
3. Производная функции определена на всей числовой прямой, поэтому критических точек, в которых производная не существует, нет. Найдем точки, в которых производная равна нулю.


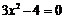 , откуда
, откуда 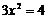 ,
,
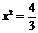 ,
, 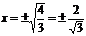 .
.
Следовательно, рассматриваемая функция имеет две критические точки.
4. Для нахождения промежутков возрастания и убывания функции определим знак производной слева и справа от критических точек:
 |
+ — +

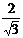 х
х
Таким образом, в промежутках
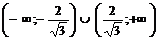 — функция возрастает,
— функция возрастает,
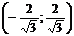 — функция убывает.
— функция убывает.
5. Вычислим значения функции в критических точках.

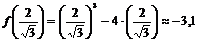
6. Найдем точки пересечения с осями координат.
Точки пересечения с осью Ох:
 ;
; 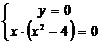
Последнее уравнение системы равносильно совокупности двух уравнений, решая которые, получим:
 ,
, 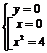 ,
,  ,
, 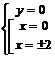 ,
, 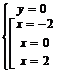 .
.
Найденные значения – это абсциссы точек пересечения графика заданной функции с осью Ох.
Точки пересечения с осью Оу:
Для нахождения этих точек необходимо вычислить значение функции в точке х = 0.
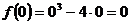 .
.
Таким образом, график пересекает ось Оу в начале координат.
7. Результаты исследования функции занесем в таблицу:
studopedia.net
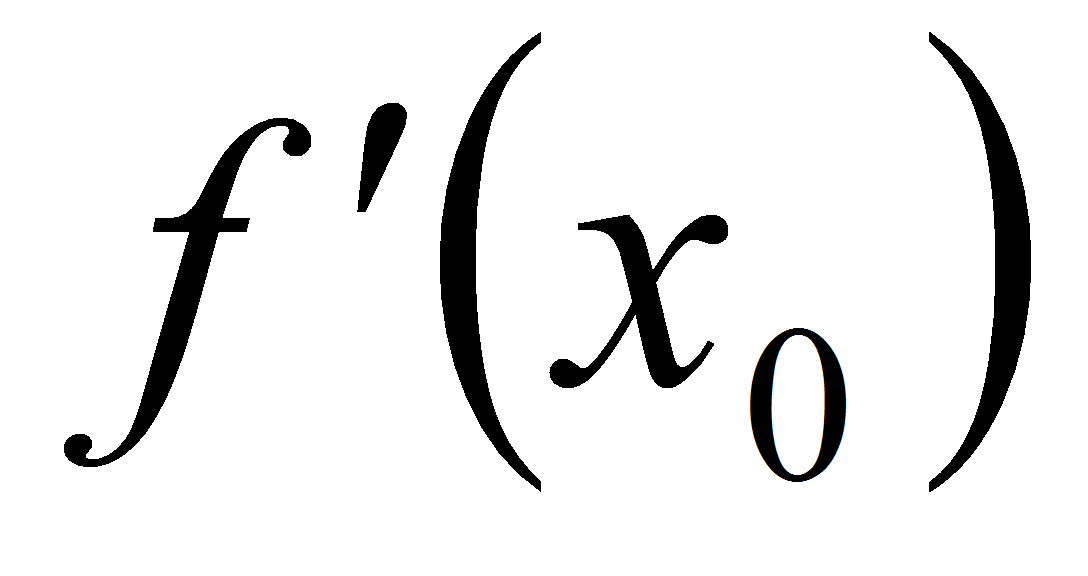 .
В тех случаях, когда
.
В тех случаях, когда
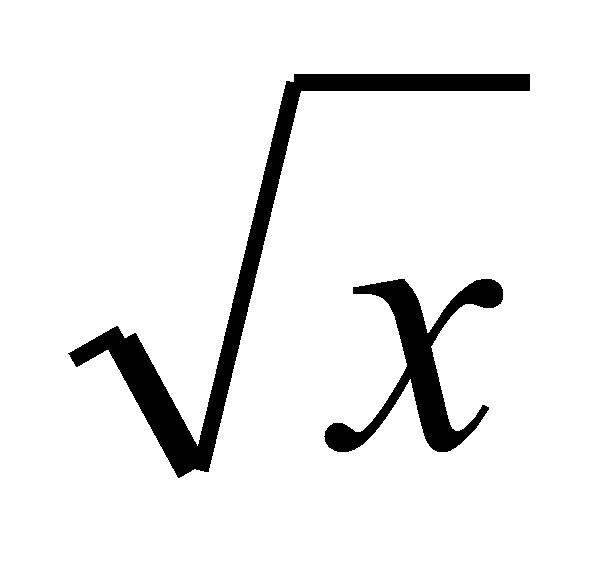 ?
?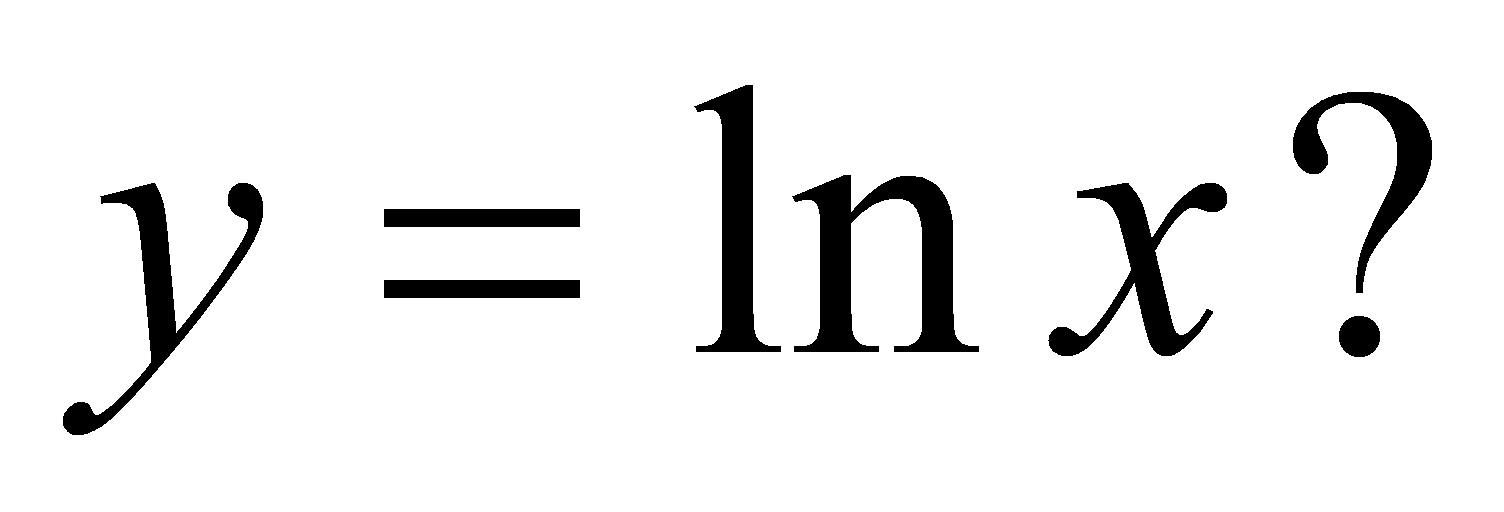
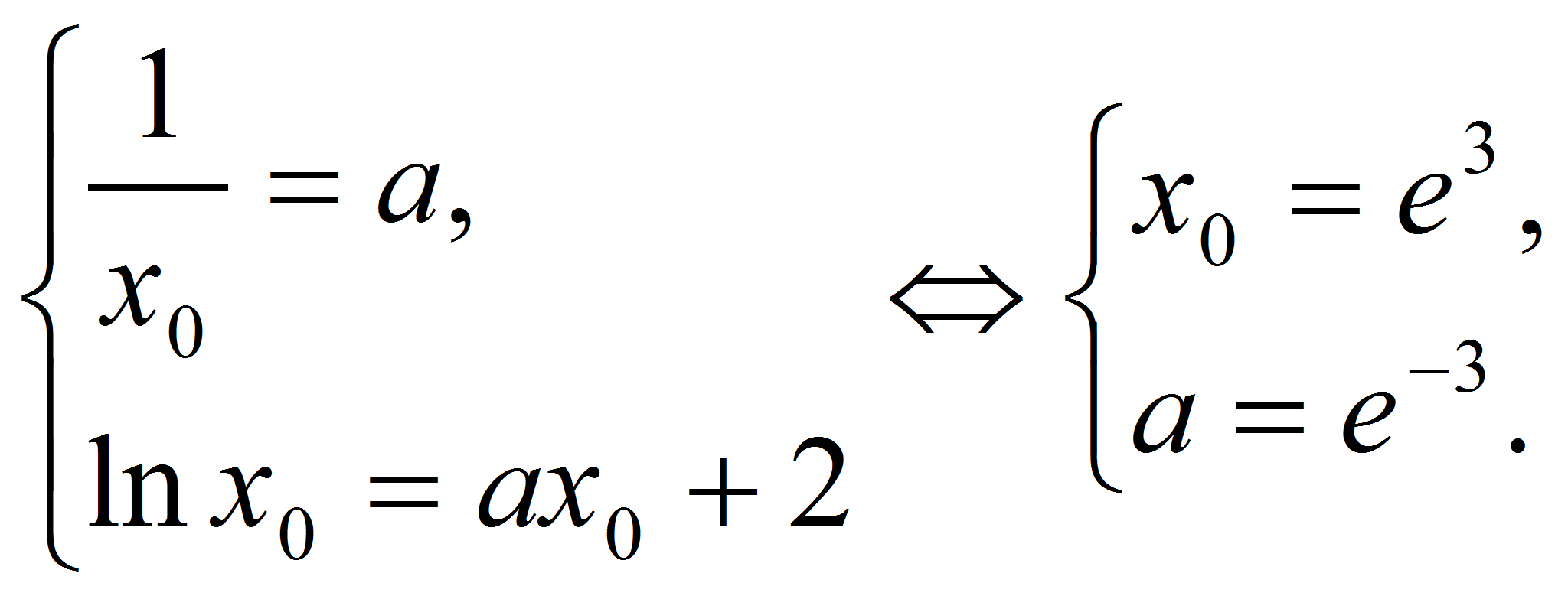
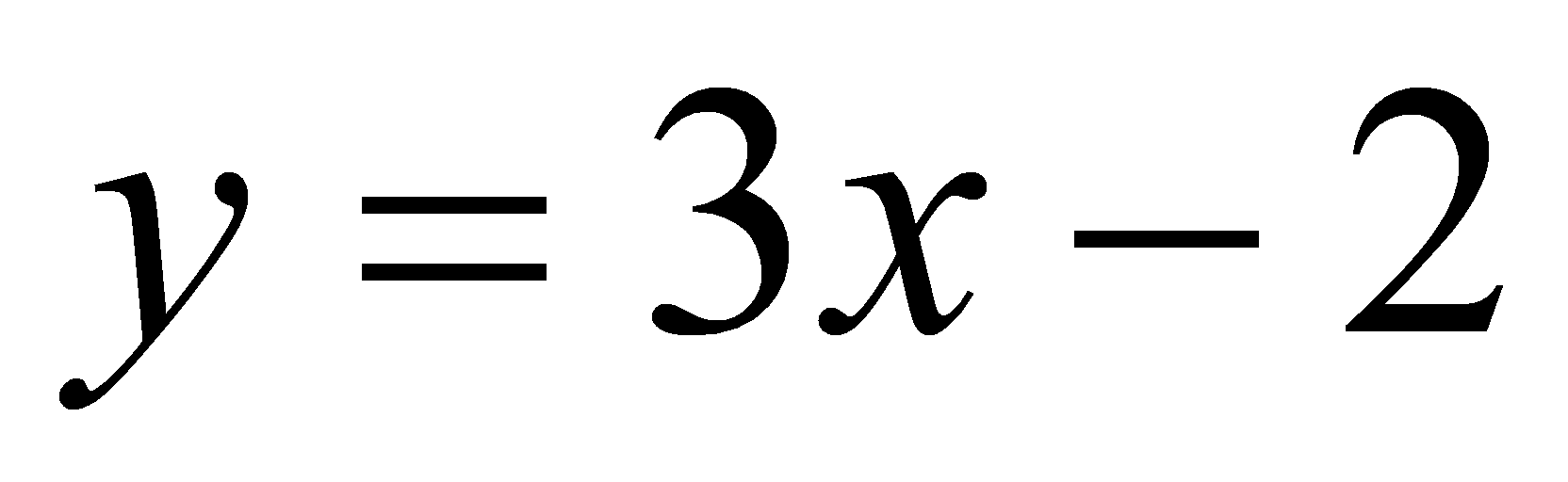 является касательной к графику функции
является касательной к графику функции

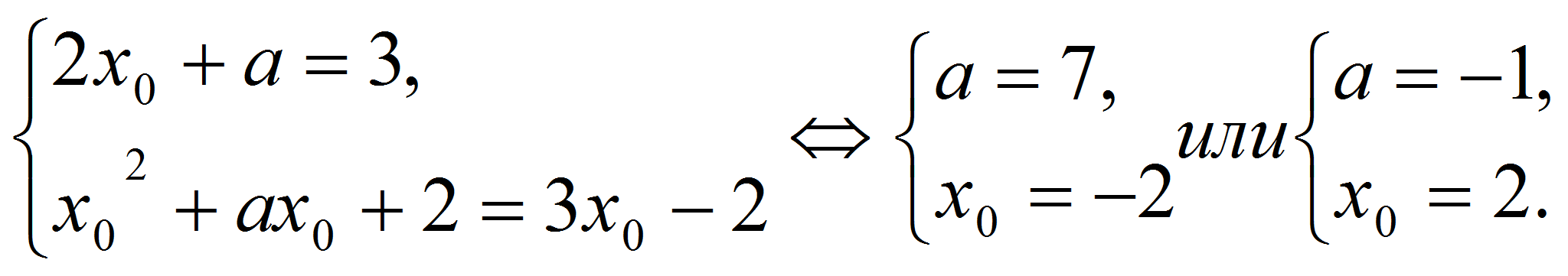
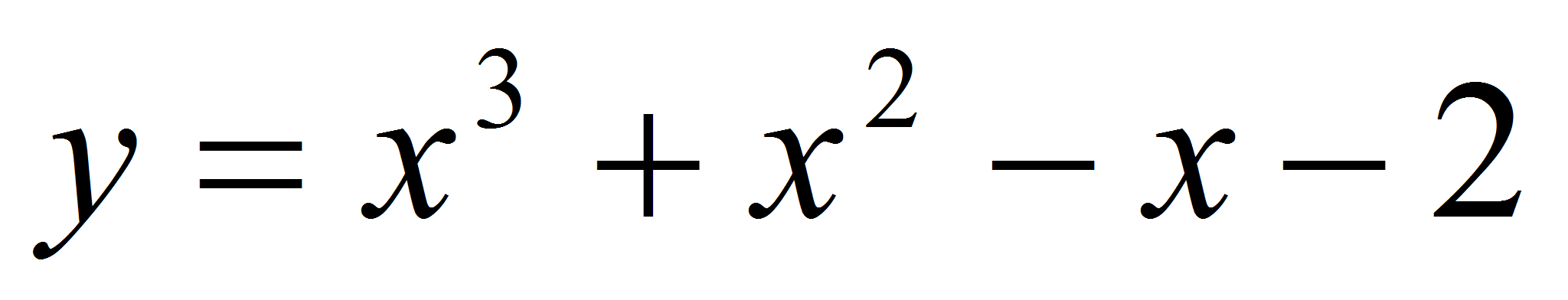 ?
Если является, то найти координаты точки касания.
?
Если является, то найти координаты точки касания.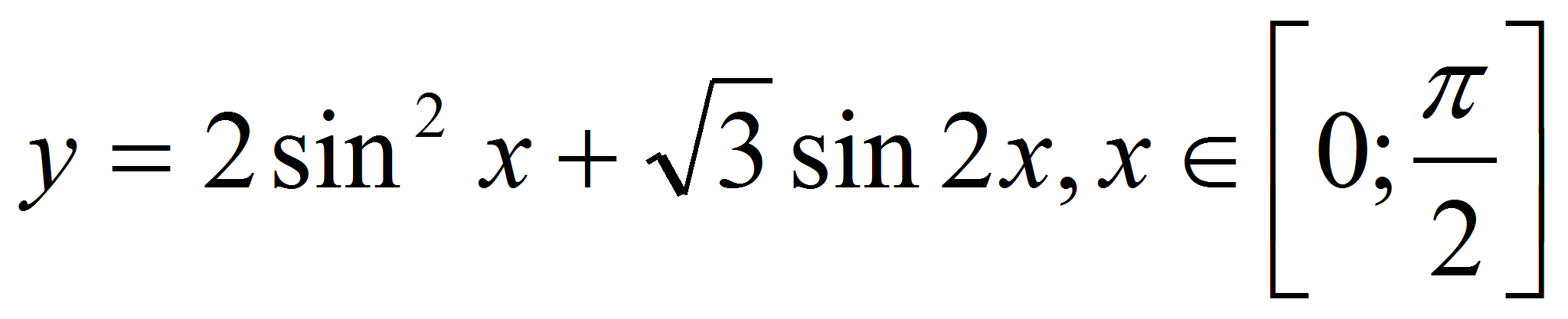 проведена
касательная, параллельная прямой
проведена
касательная, параллельная прямой
 .
Найти ординату точки касания.
.
Найти ординату точки касания.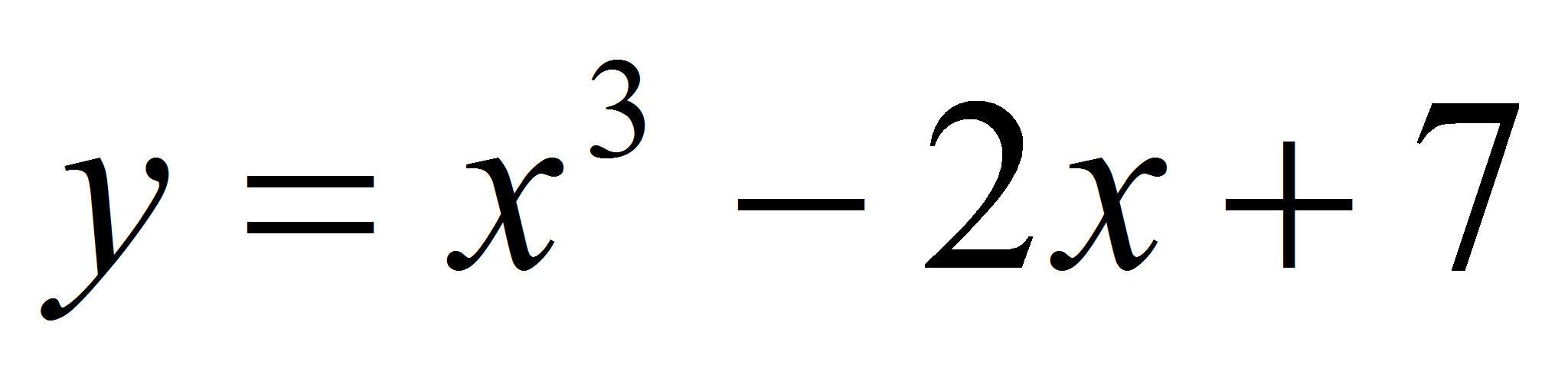 ,
параллельных прямой
,
параллельных прямой
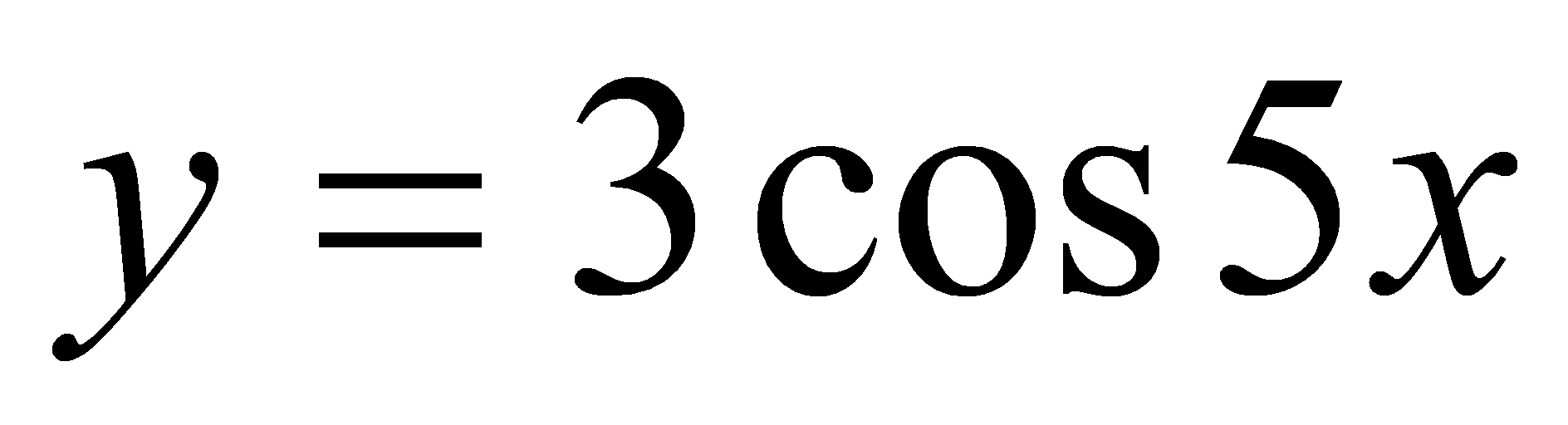 и
и
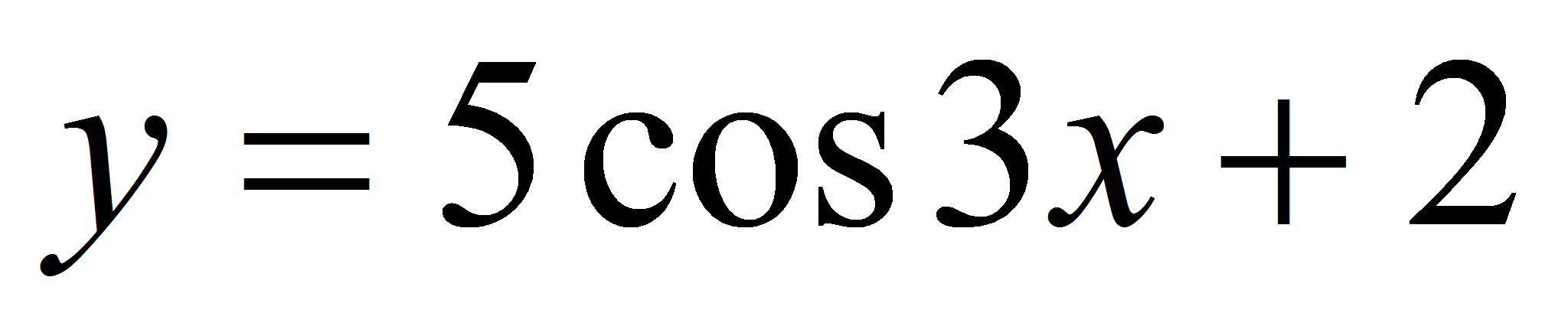 в
точках с абсциссой
в
точках с абсциссой
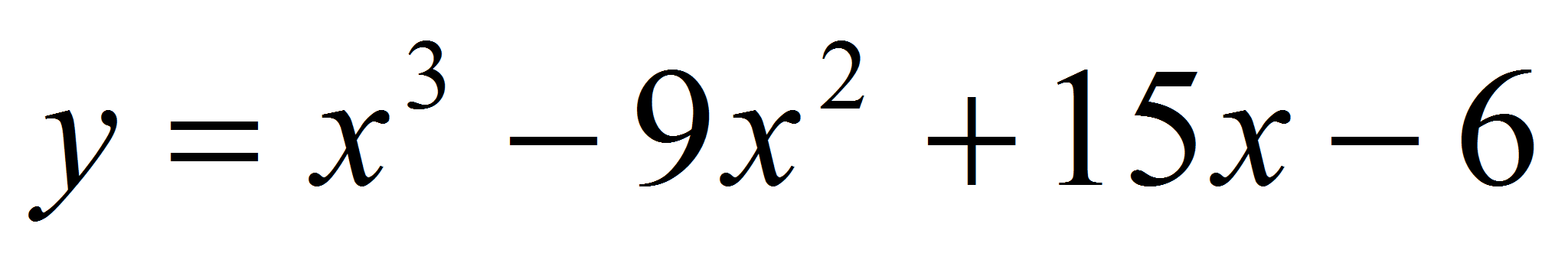 ,
расположенными параллельно оси
,
расположенными параллельно оси
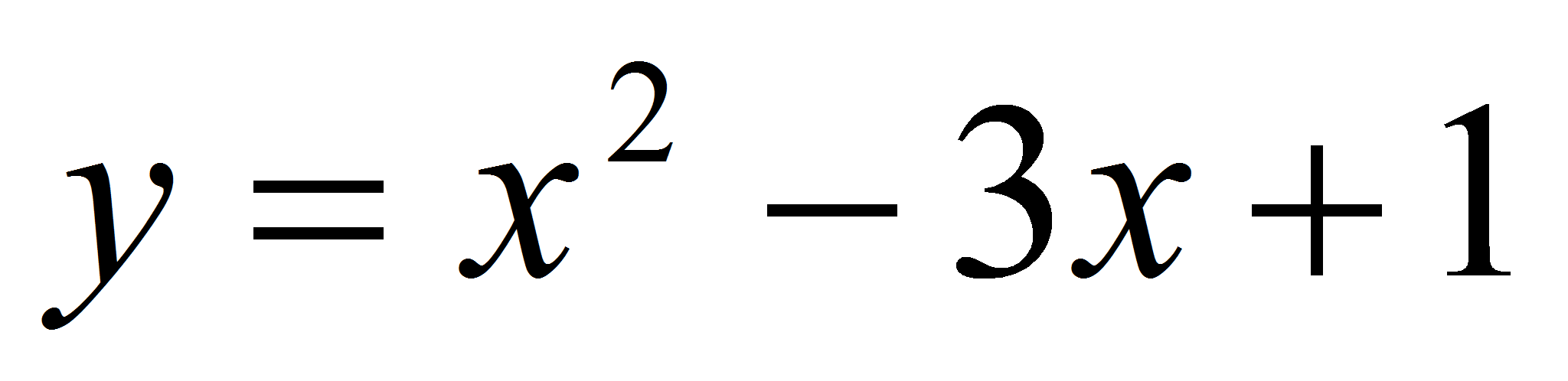 ,
проходящих через точку
М(2; -2).
,
проходящих через точку
М(2; -2). через точку
через точку
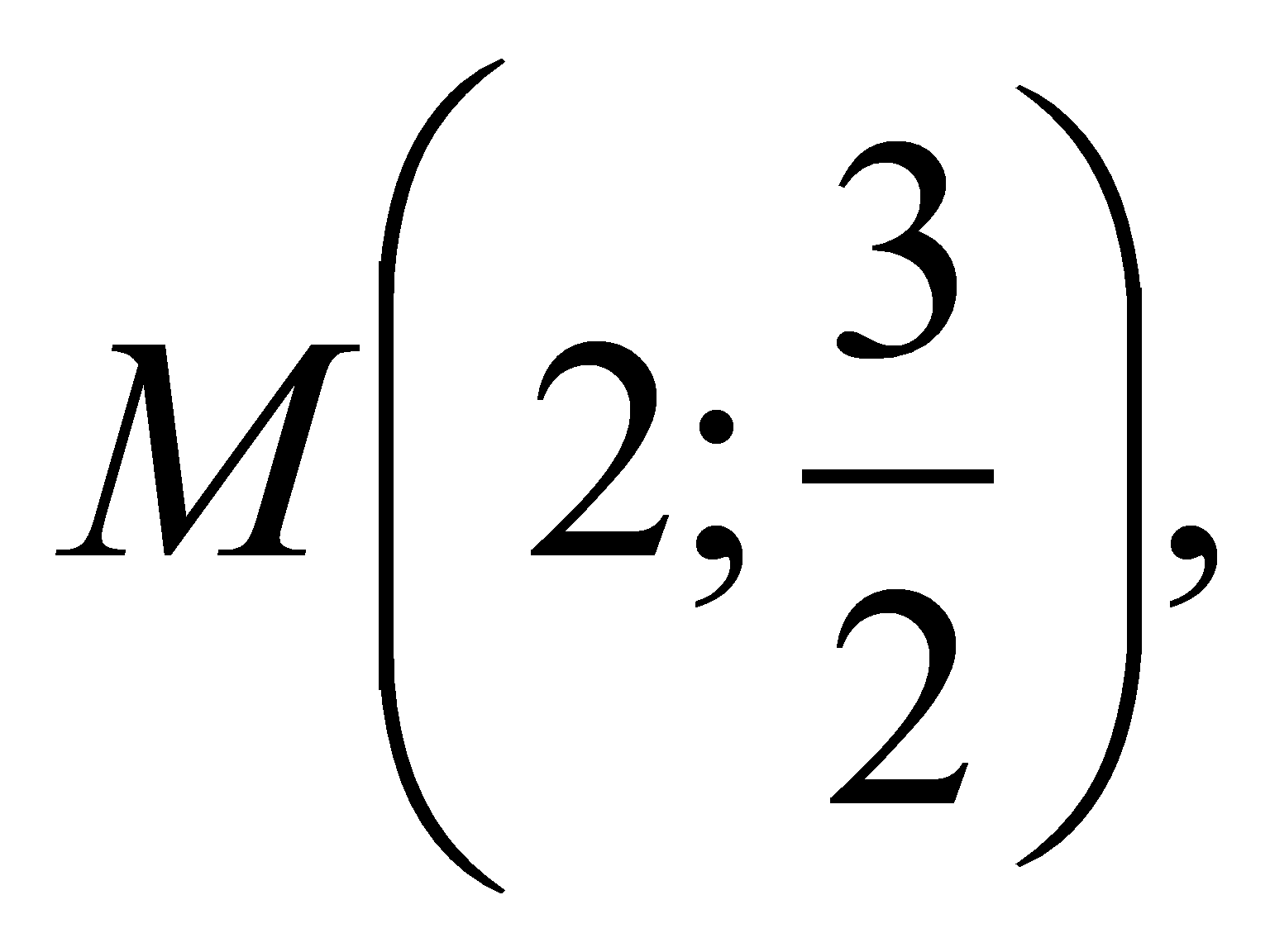 и секущей,
проходящей через точки касания.
и секущей,
проходящей через точки касания.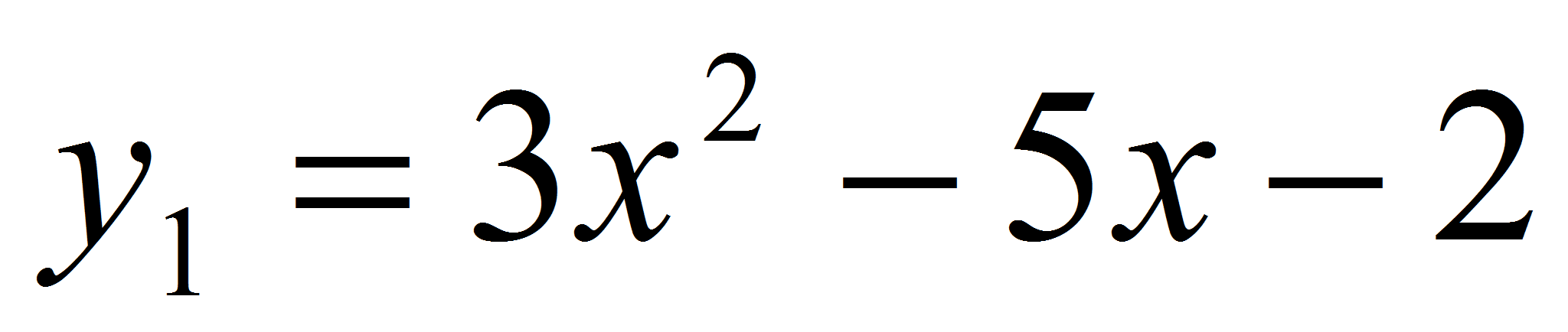 и
и
 имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
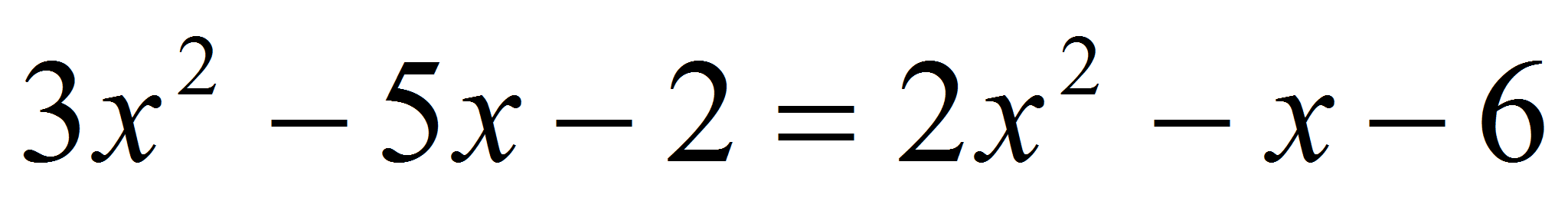 имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
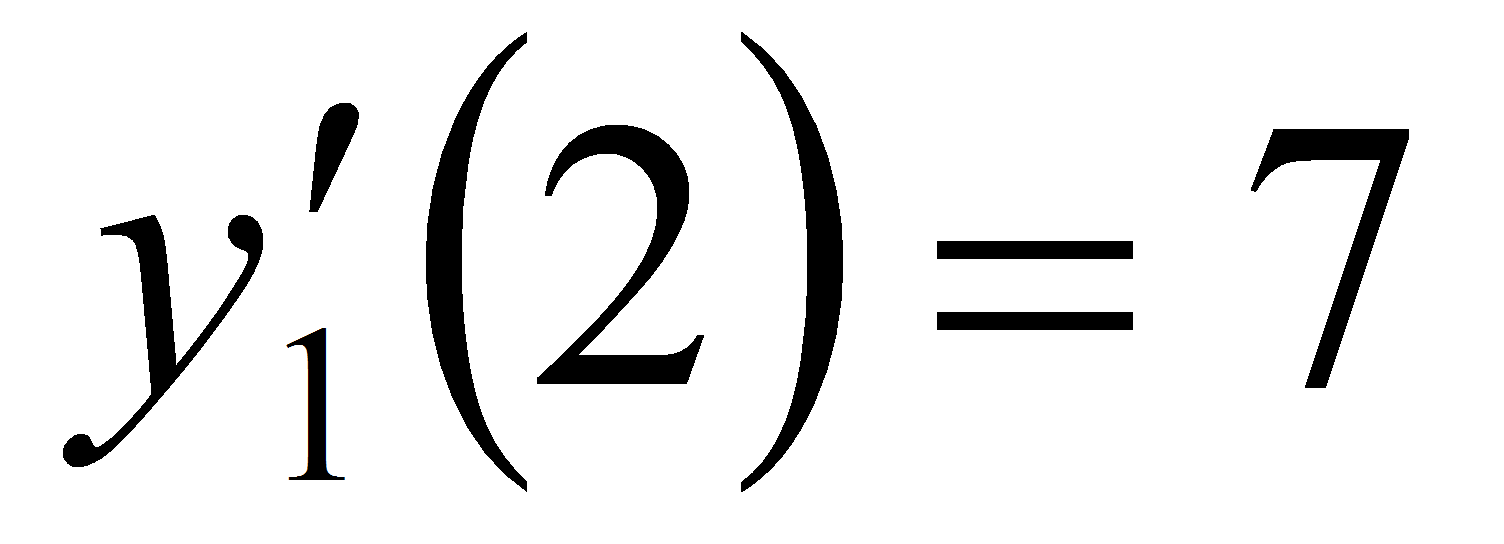 и
и
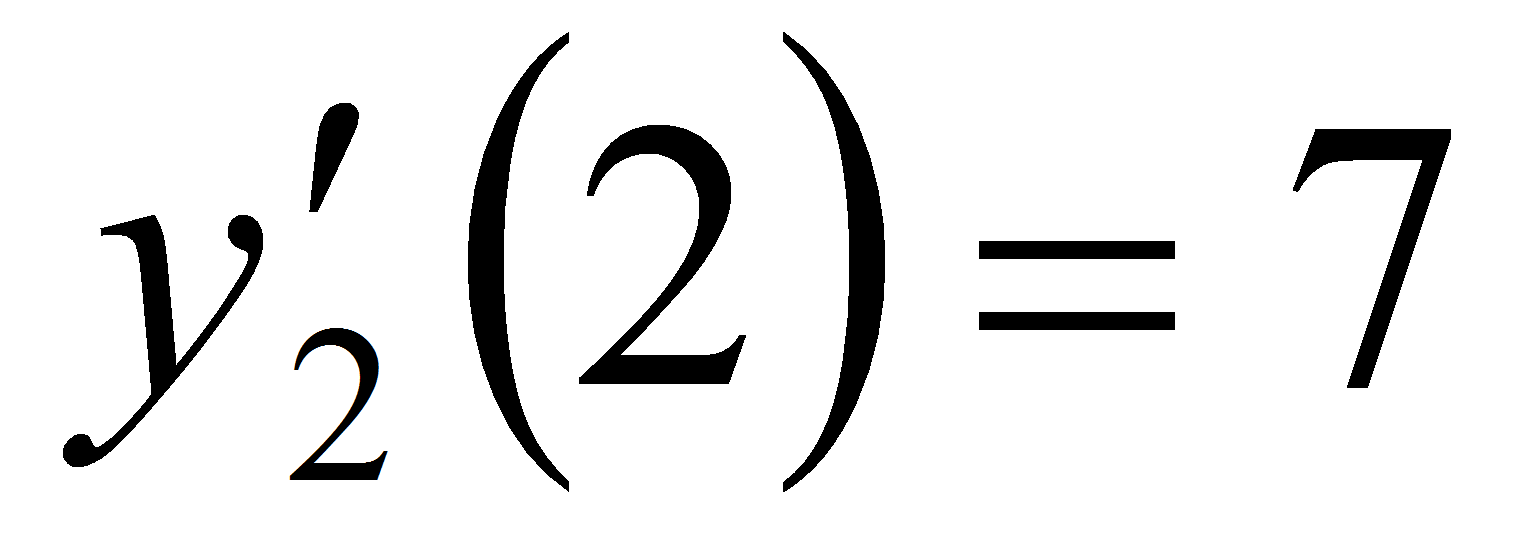 .
Далее составляем уравнение касательной.
.
Далее составляем уравнение касательной.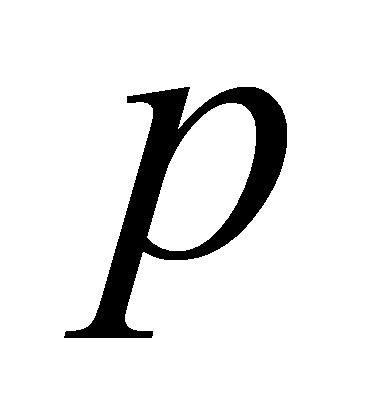 касательная
к графику функции
касательная
к графику функции
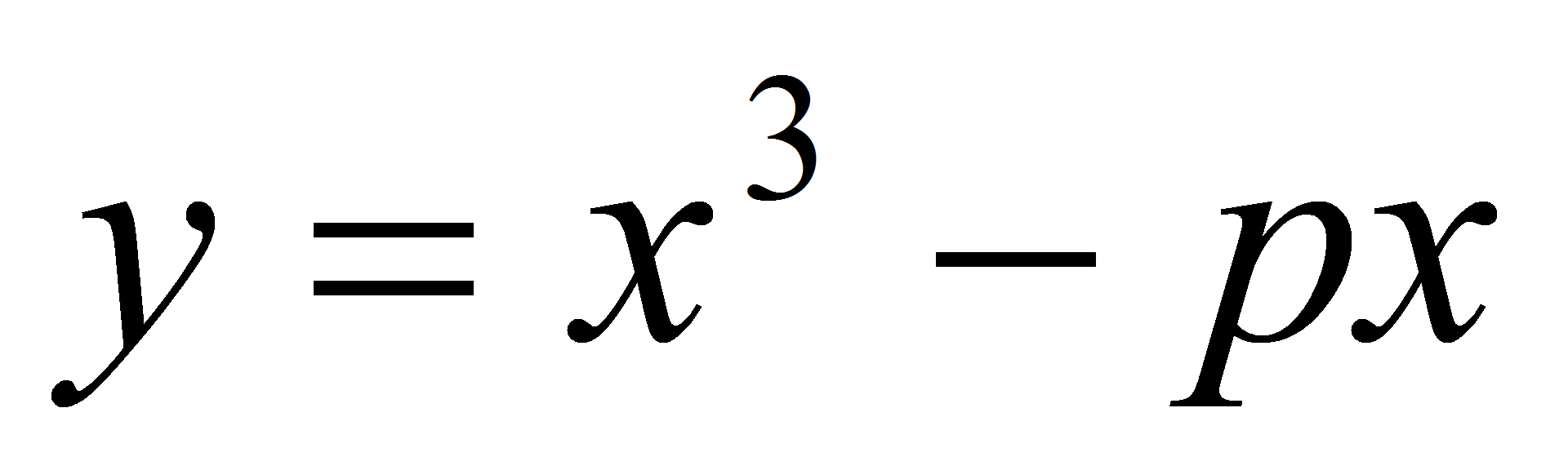 в точке
в точке
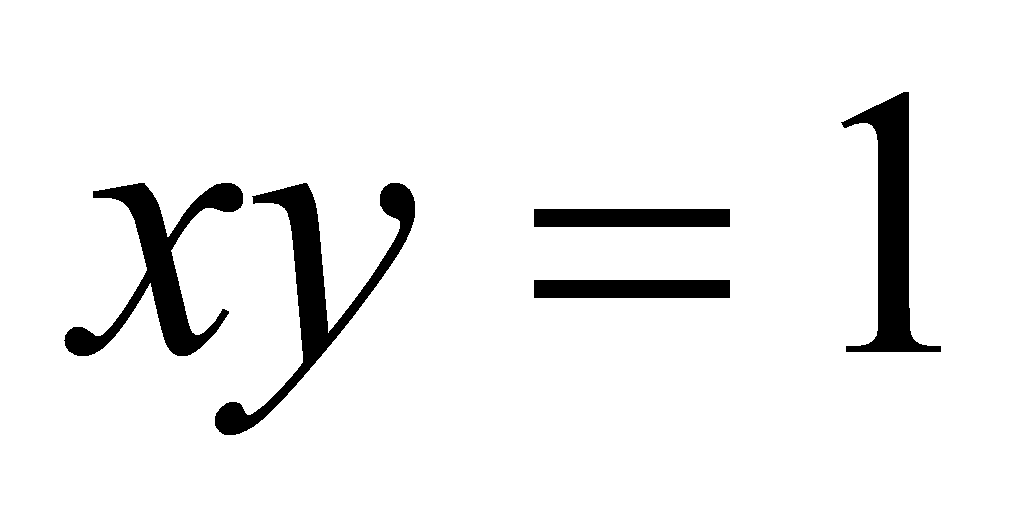 в какой-либо ее точке составлять острый угол с положительным
направлением оси
в какой-либо ее точке составлять острый угол с положительным
направлением оси
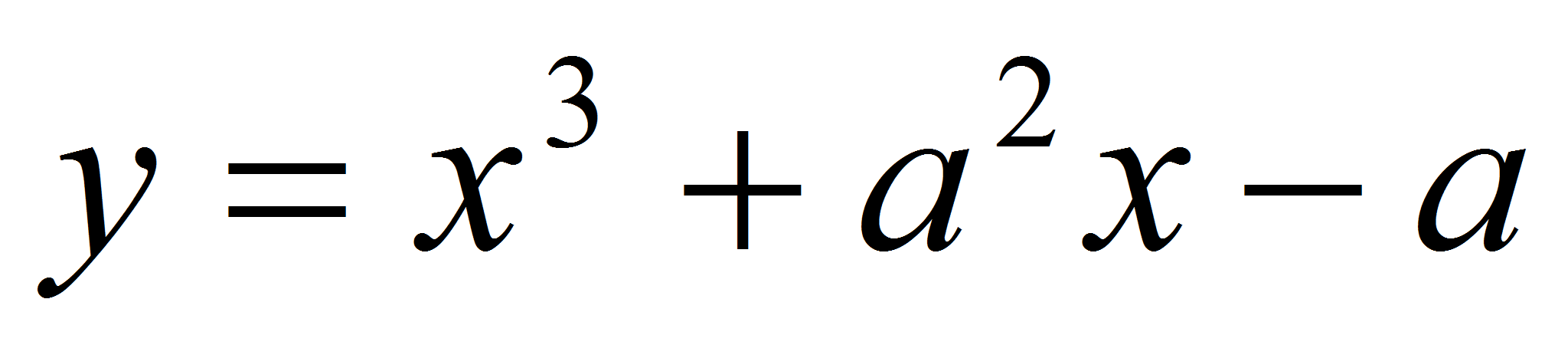 в точке
в точке
 проходит через точку М(1;7).
проходит через точку М(1;7).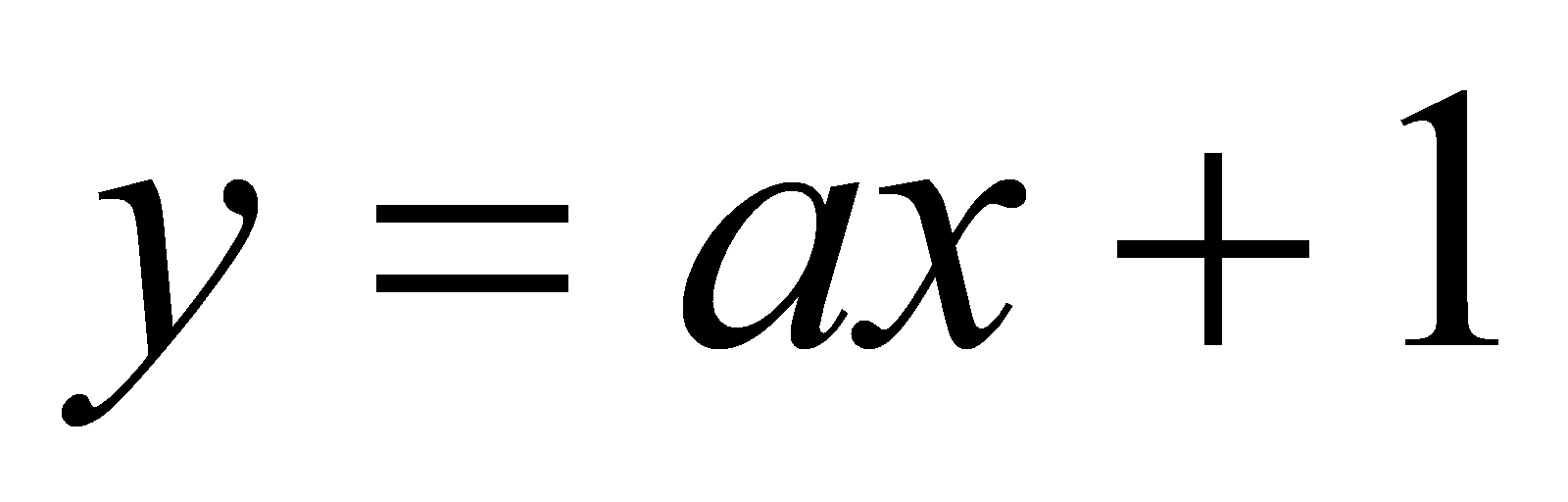 является касательной к графику функции
является касательной к графику функции
 ?
?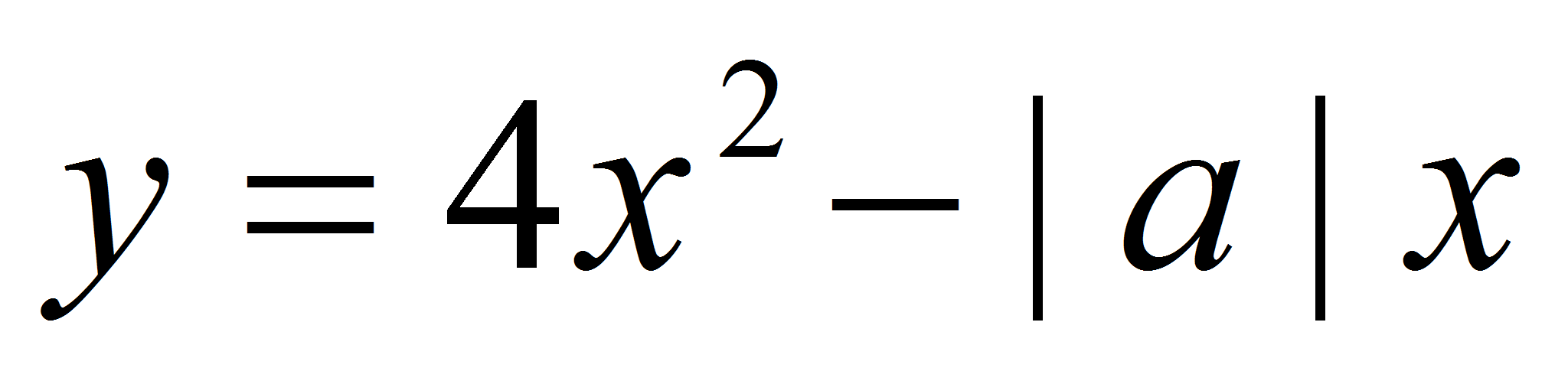 ,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
,
проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?