ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — это… Что такое ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ?
геодезиче-ская,- геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный элемент, линейная связность) лежит в основе геометрии рассматриваемого пространства. В геометрии тех пространств, где метрика считается заданной априори, Г. л. определяют как локально кратчайшие. В пространствах со связностью Г. л. определяют как кривые, у к-рых касательный вектор остается касательным при параллельном перенесении вдоль кривой. В римановой и финслеровой геометриях, где первоначально задается линейный элемент (иначе говоря,- метрика в касательном пространстве в каждой точке рассматриваемого многообразия), а длины кривых получаются последующим интегрированием, Г. л. определяют как экстремали функционала длины кривой.
Впервые Г. л. изучались И. Бернулли (J. Bernoulli) и Л. Эйлером (L. Euler) при отыскании кратчайших на регулярных поверхностях в евклидовом пространстве. На таких линиях обращается в нуль
В римановых пространствах Г. л. изучены наиболее полно.
Пусть Mn есть n-мерное риманово пространство с метрич. тензором  класса
класса  .
Определение Г. л. как экстремали позволяет написать ее дифференциальные уравнения в произвольных локальных координатах
.
Определение Г. л. как экстремали позволяет написать ее дифференциальные уравнения в произвольных локальных координатах  ,
, 
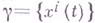 :
: 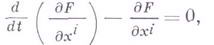
где

Другая эквивалентная форма уравнений Г. л. выводится из требования параллельности переноса вдоль  касательного вектора
касательного вектора  Если t есть длина s дуги вдоль Г. л. или линейная функция от s, то
Если t есть длина s дуги вдоль Г. л. или линейная функция от s, то

Определение Г. л. уравнением (1) включает и канонич. выбор параметра. При таком определении через каждую точку 
 с начальным касательным вектором
с начальным касательным вектором  Отображение
Отображение  касательного пространства в точке
касательного пространства в точке  в изучаемое пространство есть экспоненциальное отображение с полюсом
в изучаемое пространство есть экспоненциальное отображение с полюсом  . Вблизи начальной точки х 0 — диффеоморфизм, вводящий в изучаемом пространстве римановы координаты.
. Вблизи начальной точки х 0 — диффеоморфизм, вводящий в изучаемом пространстве римановы координаты. Ряд свойств Г. л. сохраняется у кривых, определяемых уравнениями 2-го порядка  если, подобно (1), функция F — однородная 2-й степени по
если, подобно (1), функция F — однородная 2-й степени по 
Поведение Г. л. в малом похоже на поведение прямых в евклидовом пространстве. Достаточно малая дуга Г. л. является кратчайшей среди всех спрямляемых кривых с теми же концами. Через любую точку в любом направлении проходит единственная Г. л. У каждой точки есть окрестность U, в к-рой любые две точки соединимы единственной Г. д., не выходящей из U(см. [3]).
Вопрос о том, как далеко можно продолжить из точки х 0 дугу Г. л., чтобы она оставалась кратчайшей по сравнению с близкими к ней кривыми, составляет одну из задач вариационного исчисления. Сравнение Г. л. с близкими кривыми основано на изучении второй вариации длины, к-рая исследуется путем рассмотрения поля скоростей ( Якоба поле).в точках Г. л.
 . При любом фиксированном tкривая
. При любом фиксированном tкривая  остается геодезической, а параметр s на ней — каноническим. Если в начале кривой
остается геодезической, а параметр s на ней — каноническим. Если в начале кривой  скорость равна нулю, то те точки кривой
скорость равна нулю, то те точки кривой  , где эта скорость при каком-либо ненулевом поле Якоби оказывается нулем, наз. сопряженными точками. Г. л. остается кратчайшей по сравнению с близкими кривыми до первой сопряженной точки. Для дуги Г. л., продолженной за сопряженную точку, существует сколь угодно близкая более короткая кривая с теми же концами. Поле Якоби
, где эта скорость при каком-либо ненулевом поле Якоби оказывается нулем, наз. сопряженными точками. Г. л. остается кратчайшей по сравнению с близкими кривыми до первой сопряженной точки. Для дуги Г. л., продолженной за сопряженную точку, существует сколь угодно близкая более короткая кривая с теми же концами. Поле Якоби  удовлетворяет уравнению
удовлетворяет уравнению 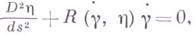
где  — касательный вектор геодезической
— касательный вектор геодезической 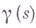 , а
, а  — кривизны преобразование, или, в координатах Ферми
— кривизны преобразование, или, в координатах Ферми 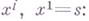
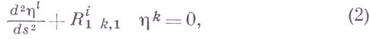
где 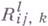 — тензор кривизны. Связь поля Якоби с кривизной обусловливает зависимость свойств геодезических от кривизны пространства. Напр., в пространствах отрицательной кривизны сопряженных точек нет; если пространство еще и односвязно, то любая дуга Г. л.- кратчайшая, а выходящие из точки Г. л. экспоненциально расходятся. Эти свойства играют роль в теории динамич. систем (см.
— тензор кривизны. Связь поля Якоби с кривизной обусловливает зависимость свойств геодезических от кривизны пространства. Напр., в пространствах отрицательной кривизны сопряженных точек нет; если пространство еще и односвязно, то любая дуга Г. л.- кратчайшая, а выходящие из точки Г. л. экспоненциально расходятся. Эти свойства играют роль в теории динамич. систем (см.
 ) убывают с ростом кривизны пространства. Здесь подразумевается сравнение двух Г. л., в соответствующих по длине точках к-рых все кривизны второго пространства мажорируют любую из кривизн первого пространства [4].
) убывают с ростом кривизны пространства. Здесь подразумевается сравнение двух Г. л., в соответствующих по длине точках к-рых все кривизны второго пространства мажорируют любую из кривизн первого пространства [4]. В общей теории относительности уравнение (2) служит источником физического истолкования кривизны пространства-времени через поведение Г. л. (см. [5]).
При отказе от сравнения только с близкими кривыми дуга Г. л. может перестать быть кратчайшей раньше, чем пройдет сопряженную точку. Это возможно даже в односвязном пространстве, т. е. причины этого могут быть топологическими и метрическими.
Вопрос о том, как влияет кривизна на протяженность дуги, на к-рой Г. л. остается кратчайшей, играет существенную роль в изучении связей кривизны с то-пологич. строением пространства. Зависимость количества замкнутых Г. л. или количества разных Г. л., соединяющих две точки, от топологич. строения пространства составляет предмет вариационного исчисления в целом (СМ. [6], [4], [7]).
Семейства Г. л., рассматриваемые как возможные траектории движения, являются предметом теории динамич. систем и эргодич. теории.
В пространствах аффинной связности Г. л. определяются уравнением (1). Для них сохраняются локальные теоремы существования и единственности Г. л., соединяющих две точки, и существования выпуклой окрестности.
Г. л. с аналогичными свойствами определяются и в пространствах проективной связности, а также в случае более общих связностей на многообразиях.
Геометризацня задач вариационного исчисления для функционалов, отличных от длины кривой, привела к понятию финслерова пространства и Г. л. в нем. Выделение основных геометрических свойств подобных пространств привело к понятию геодезических геометрии, которое определяется наличием и продолжаемостью Г. л.
Из метрич. пространств с нерегулярной метрикой наиболее изучены Г. л. на выпуклых поверхностях и в двумерных многообразиях ограниченной кривизны. Здесь Г. л. не обязательно гладкая кривая; Г. л. может не иметь продолжения, а в двумерном многообразии ограниченной кривизны может также иметь неединственное продолжение. Г. л. на выпуклой поверхности всегда имеют полукасательную; если продолжается, то только единственным образом; из точки Г. л. исходят почти во всех направлениях. В таких пространствах более естественным, чем Г. л., оказался класс квазигеодезических линий, к-рые служат замыканием класса геодезических (см. [8]).
Лит.:[1] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [2] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [3] Хелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [4] Громол Д., Клингенберг В., Мейер В..Риманова геометрия в целом, пер. с нем., М., 1971; [5] Синг Дж. Л., Общая теория относительности, пер. с англ., М., 1963; [6] Люстерник Л. А., Шнирельман Л. Г., Топологические методы в вариационных задачах, М., 1930; [7] Милкор Дж., Теория Морса, пер. с англ., М., 1963; [8] Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948. Ю.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Тема: Общие сведения по геодезии. Предмет геодезии
Лекция 11. Что такое геодезия
_______ Геодезия – это наука об измерениях на земной поверхности, выполняемых для изучения общей фигуры Земли, для составления планов и карт, для решения инженерных задач при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений.
_______В процессе своего развития геодезия разделилась на ряд самостоятельных научных дисциплин: высшую геодезию, топографию, инженерную геодезию, аэрофотогеодезию, картографию и космическую геодезию.
_______Высшая геодезия занимается определением фигуры и размеров всей Земли и значительных ее частей.
_______Топография занимается измерением и изображением на планах и картах земной поверхности.
_______Инженерная геодезия занимается вопросами геодезических работ при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений, при монтаже оборудования, при наблюдениях за вертикальными и горизонтальными смещениями инженерных сооружений и технологического оборудования.
_______Аэрофотогеодезия занимается изучением методов и средств создания топографических карт и планов по материалам фотографирования Земли.
_______Картография занимается изучением методов составления, издания и использования карт.
_______Космическая геодезия занимается обработкой измерений, полученных при помощи искусственных спутников Земли, орбитальных станций и межпланетных кораблей.
_______Геодезия имеет тесную связь с другими научными дисциплинами: математикой, астрономией, физикой, механикой, автоматикой, электроникой, географией, фотографией и черчением.2. Предмет геодезии. Понятие о форме и размерах Земли
_______Предметом геодезии является планета Земля. Общая площадь Земли – 510 млн. км2; 71% поверхности Земли – это моря и океаны, 29% – суша. При определении положения точек земной поверхности обычно относят их к общей фигуре Земли, которую называют геоидом.
_______Геоид – это геометрическое тело, ограниченное уровенной поверхностью.
_______Уровенная поверхность – поверхность, совпадающая с поверхностью воды в морях и океанах, которые находятся в спокойном состоянии, продолженная под материками.
_______Уровенная поверхность в каждой своей точке перпендикулярна к отвесной линии, проведенной через эту точку.
_______Фигура геоида в геометрическом отношении является весьма сложной, однако она очень близка к эллипсоиду вращения. Такой эллипсоид получается в результате вращения вокруг малой полуоси эллипса РQP1Q1 (рис. 1).
_______Эти величины определяют форму и размеры Земли. В 1946 году были приняты размеры земного эллипсоида, вычисленные группой российских ученых под руководством профессора Ф.Н. Красовского. Эти размеры: а = 6378245 м и b = 6356863 м.
3. Способы изображения земной поверхности. Метод проекций в геодезии
_______На местности точки, линии, углы и контуры расположены в силу неровностей земной поверхности на возвышениях или впадинах. Так как возвышения и впадины являются пространственными формами, изобразить их на бумаге в виде плоской карты или плана достаточно непросто. Способы изображения земной поверхности на плоскости основываются на методе проекций.
_______При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.
_______В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость (рис. 2).
4. Системы координат, принятые в геодезии
_______В геодезии применяются следующие системы координат:
• Географическая система координат,
• Зональная система плоских прямоугольных координат Гаусса–Крюгера,
• Полярная система координат.
_______С помощью географических координат, то есть широт (φ) и долгот (λ), определяют положение точки относительно экватора и начального меридиана.
_______Широтой (φ) точки называется угол, составленный отвесной линией в данной точке и плоскостью экватора.
_______Долготой (λ) точки называется двугранный угол между плоскостью меридиана данной точки и плоскостью начального меридиана.
_______Широта отсчитывается по дуге меридиана к северу и к югу от экватора от 0° до 90°. К северу от экватора широта называется северной, к югу – южной.
_______Долгота отсчитывается от меридиана, проходящего через Гринвич на окраине Лондона. Долгота отсчитывается по дуге экватора или параллели от начального меридиана в сторону востока и запада от 0° до 180°. Долгота к востоку от Гринвичского меридиана называется восточной долготой, к западу – западной. Широты и долготы определяют положение любой точки на земной поверхности и выражаются в угловой мере. Географические координаты определяются из астрономических наблюдений и, а также с помощью геодезических измерений.
4.2. Зональная система плоских прямоугольных координат Гаусса–Крюгера
_______При геодезических работах на больших территориях применяется зональная система плоских прямоугольных координат Гаусса–Крюгера (рис. 4). Для этого земной шар делится меридианами на шестиградусные или трехградусные зоны (рис. 3). Счет зон ведется к востоку от Гринвичского меридиана. Каждая зона проецируется на плоскость таким образом, чтобы средний меридиан зоны был изображен прямой линией. Средний меридиан зоны называется осевым меридианом.
_______Изображение осевого меридиана принимается за ось абсцисс (x), изображение экватора – за ось ординат (y). За начало координат принимают точку пересечения осевого меридиана с экватором.
_______Чтобы не иметь отрицательных ординат, ординату осевого меридиана принимают равной 500 км. Перед ординатой точки указывается номер зоны, в которой точка расположена.
Зональная система плоских прямоугольных координат Гаусса–Крюгера
_______Зная географические координаты точки земной поверхности, можно вычислить зональные прямоугольные координаты, и, наоборот.
4.3. Полярная система координат
_______В полярной системе координат используются полярные углы и расстояния. Подробнее эта система будет рассмотрена в последующих лекциях.
5. Системы высот, принятые в геодезии
_______Для полного определения положения точек земной поверхности необходимо знать высоты точек над принятой уровенной поверхностью. Высоты точек, которые определяются относительно поверхности эллипсоида (по отвесной линии), называются абсолютными высотами.
_______Абсолютная высота – длина перпендикуляра, опущенного из точки на уровенную поверхность, принятую за начало отсчета (поверхность эллипсоида).
_______За начало счета абсолютных высот принимается нуль Кронштадтского футштока (средний уровень воды в Балтийском море). Такая система высот называется Балтийской.
_______Уровень Балтийского моря установленный по данным многолетних наблюдений и отмеченный награвированной чертой на металлической пластине, вмурованной в гранитный устой одного из мостов через обводной канал в Кронштадте, является началом счета высот уже третий век. Если счет высот ведется от другой уровенной поверхности, такая высота называется относительной высотой. _______Числовые значения абсолютных высот точек земной поверхности называют отметками. Разность абсолютных высот двух любых точек называют превышением (h).
_______В строительстве для отдельных зданий счет высот ведется от чистого пола первого этажа.
6. Ориентирование линий
_______Ориентировать линию – значит определить ее направление относительно исходного меридиана.
_______В качестве исходного направления служит меридиан начальной точки линии, или осевой меридиан зоны. Для ориентирования линий служат углы, называемые азимутами, дирекционными углами и румбами.
_______Азимутом — горизонтальный угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до направления данной линии.
_______Азимуты изменяются от 0º до 360º.
_______Азимутом называется истинным, если он отсчитывается от истинного меридиана, и магнитным, если отсчитывается от магнитного меридиана. Направление истинного меридиана в данной точке определяется из астрономических наблюдений, а направление магнитного меридиана – при помощи магнитной стрелки.
_______Азимут одной и той же линии в разных ее точках различен. Меридианы разных точек не параллельны между собой, так как они сходятся в точках полюсов. Отсюда азимут линии в разных ее точках имеет разное значение. Угол между направлениями двух меридианов называется сближением меридианов и обозначается γ. _______Для определения положения магнитного меридиана в геодезии применяют буссоль. Буссоль применяется в комплекте геодезических приборов (теодолитов, тахеометров и т.д.)_______Дирекционным углом называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной по часовой стрелке до направления данной линии. Обозначается буквой α.
_______Дирекционные углы бывают прямыми и обратными (рис.10).
_______Обратный дирекционный угол вычисляется по формуле:
_______Румбом называется острый угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии (r).
Румб всегда сопровождается названием четверти, в которой расположена линия (рис. 11).
7. Съемки
_______Для составления планов и карт необходимо на местности производить геодезические измерения. Комплекс таких измерений называется съемкой.
В зависимости от приборов и методов работы съемка бывает теодолитной, тахеометрической, фототопографической и т.д.Геодезические измерения, выполняемые на местности, называют полевыми работами. Обработка результатов измерений, вычислений и графические работы по составлению карт и планов называют камеральной обработкой полевых измерений. Тест
Инструкция по прохождению теста
- Выберите один из вариантов в каждом из 10 вопросов;
- Нажмите на кнопку «Показать результат»;
- Скрипт не покажет результат, пока Вы не ответите на все вопросы;
- Загляните в окно рядом с номером задания. Если ответ правильный, то там (+). Если Вы ошиблись, там (-).
- За каждый правильный ответ начисляется 1 балл;
- Оценки: менее 5 баллов — НЕУДОВЛЕТВОРИТЕЛЬНО, от 5 но менее 7.5 — УДОВЛЕТВОРИТЕЛЬНО, 7.5 и менее 10 — ХОРОШО, 10 — ОТЛИЧНО;
- Чтобы сбросить результат тестирования, нажать кнопку «Сбросить ответы»;
- Геодезия это-
Наука, которая изучает мир и все, что его окружает.
Наука о изучение минеральных веществ, полезных ископаемых и частиц.
Наука об измерениях на земной поверхности, выполняемых для изучения общей фигуры Земли, для составления планов и карт, для решения инженерных задач при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений. - Какая наука занимается изучением методов составления, издания и использования карт?
Высшая геодезия
Картография
Аэрография - В геодезии НЕ применяются системы координат:
Географическая система координат
Зональная система плоских прямоугольных координат Гаусса– Крюгера
Математическая система координат
Полярная система координат - Географической координатой называется?
Широта и долгота
Высота и долгота
Широта и высота - Что такое Абсолютная высота?
Расстояние от точки до указанной прямой
Расстояние от точки до уровня земли
Длина перпендикуляра, опущенного из точки на уровенную поверхность, принятую за начало отсчета - Что принимается за начало отчета абсолютных высот?
Нуль Кронштадтского футштока
Любая точка на поверхности Земли
Начало измерямой линии - Что означает «ориентировать линию» ?
Нарисовать ее
Определить направление относительно исходного
Найти угол между линей и поверхностью - Горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной по часовой стрелке до направления данной линии — это …
Дирекционный угол
Угол наклона
Румб - Острый угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии — это …
Дирекционный угол
Угол наклона
Румб - Какой вид сьемки не используется в геодезии?
Теодолитная съемка
Видео съемка
Тахеометрическая съемка
Линия определение
Кривая
У этого термина существуют и другие значения, см. Кривая (значения).Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Элементарная геометрия
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».
По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.
Определение в топологии
Отображение отрезка
Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:
γ : [ a , b ] → X {\displaystyle \gamma :[a,b]\to X}При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [ a , b ] = [ 0 , 1 ] {\displaystyle [a,b]=[0,1]} , путями.
Отношение эквивалентности
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
γ 1 : [ a 1 , b 1 ] → X {\displaystyle \gamma _{1}:[a_{1},b_{1}]\to X} и γ 2 : [ a 2 , b 2 ] → X {\displaystyle \gamma _{2}:[a_{2},b_{2}]\to X}эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h {\displaystyle h} из отрезка [ a 1 , b 1 ] {\displaystyle [a_{1},b_{1}]} на отрезок [ a 2 , b 2 ] {\displaystyle [a_{2},b_{2}]} , такая что
γ 1 ≡ γ 2 ∘ h . {\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Комментарий
Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.
Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Кривая Жордана
Кривая Жордана на плоскости с положительной мерой Лебега.Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.
Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.
Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом[1]. .
Определение в анализе
В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R 2 {\displaystyle R^{2}} ). Пусть x ( t ) {\displaystyle x(t)} и y ( t ) {\displaystyle y(t)} — функции на отрезке [ a , b ] {\displaystyle [a,b]} , непрерывно дифференцируемые на этом отрезке, и такие, что ( x ′ ( t ) ) 2 + ( y ′ ( t ) ) 2 {\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ : [ a , b ] → R 2 , t ↦ ( x ( t ) , y ( t ) ) {\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую парамет
Простая линия — это… Что такое Простая линия?
- Простая линия
Простая дуга (простая линия или жорданова дуга) — множество точек плоскости или пространства, находящихся во взаимно однозначном и взаимно непрерывном соответствии с отрезками прямой.
Связанные определения
- Точки, соответствующие конечным точкам отрезка, называются конечными точками простой дуги.
- Две дуги называются примыкающими, если одна пара концов этих дуг или обе пары этих концов совпадают между собой.
См. также
Wikimedia Foundation. 2010.
- Простая кровь
- Прост, Ален Мария Паскаль
Смотреть что такое «Простая линия» в других словарях:
Простая дуга — (простая линия или жорданова дуга) множество точек плоскости или пространства, находящихся во взаимно однозначном и взаимно непрерывном соответствии с отрезками прямой. Связанные определения Точки, соответствующие конечным точкам отрезка,… … Википедия
Линия — Участок двух , трех или четырехпроводной электрической сети Источник: ФЕРп 2001: Приложения (редакция 2009 г.). Приложения. Федеральные единичные расценки на пусконаладочные работы … Словарь-справочник терминов нормативно-технической документации
Линия задержки акустоэлектронная простая — 12 Источник: ГОСТ 28170 89: Изделия акустоэлектронные. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
ЛИНИЯ — кривая, геометрическое понятие, точное и в то же время достаточно общее определение к рого представляет значитю трудности и осуществляется в разных разделах геометрии различно. В рамках элементарной геометрии понятие Л. не получает отчетливой… … Математическая энциклопедия
Линия (кривая) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
ПРОСТАЯ ДУГА — гомеоморфный образ отрезка. Внутренняя характеристика: П … Математическая энциклопедия
прямая линия — ▲ линия ↑ прямая (линия) прямая линия линия нулевой кривизны; самая простая линия; линия, имеющая одно направление на всем своем протяжении; изображение линейной функции; линия 1 го порядка: две прямые линии могут пересечься между собой не более… … Идеографический словарь русского языка
одноотводная акустоэлектронная линия задержки — Ндп. простая акустоэлектронная линия задержки обычная акустоэлектронная линия задержки Акустоэлектронная линия задержки, осуществляющая задержку электрического сигнала на заданный интервал времени. [ГОСТ 28170 89] Недопустимые, нерекомендуемые… … Справочник технического переводчика
Кредитная линия — – это юридически оформленное обязательство банка выдавать клиенту кредит в определенном объеме в течение оговоренного времени. Кредитная линия отличается от единовременного кредитования тем, что клиент может получать ссуду не один раз в какой то… … Банковская энциклопедия
Одноотводная акустоэлектронная линия задержки — 12. Одноотводная акустоэлектронная линия задержки Ндп. Простая акустоэлектронная линия задержки Обычная акустоэлектронная линия задержки Акустоэлектронная линия задержки, осуществляющая задержку электрического сигнала на заданный интервал времени … Словарь-справочник терминов нормативно-технической документации
Книги
- Визуальный инвестор. Как определять тренды, Джон Дж. Мэрфи. Визуальный анализ позволяет инвестору исследовать поведение акции или отраслевой группы фондового рынка, не прибегая к сложным математическим формулам и техническим понятиям. Напротив, с его… Подробнее Купить за 896 грн (только Украина)
- Современное искусство в деталях Почему пятилетнему ребенку не под силу сделать подобное, Ходж С.. В прошлом особо большое значение предавалось способности автора отражать сходство его произведения на холсте, в дереве или камне с окружающим миром. Официальный портрет должен был передавать… Подробнее Купить за 726 руб
- Выходит продюсер, Роднянский Александр Ефимович. Это дополненное издание книги о тонкостях профессии, о том, каково быть теле- и кинопродюсером в России и в мире. В книгу вошли новые главы о том, как создавались `Сталинград`, `Левиафан` и… Подробнее Купить за 523 грн (только Украина)
Линия построения — это… Что такое Линия построения?
Линия построения – вспомогательная линия, используемая для графического построения характерных точек, фигур, проекций и т. п., не входящая в состав окончательного изображения.
[Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)]
Рубрика термина: Проектирование
Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги, Автотехника, Автотранспорт, Акустические материалы, Акустические свойства, Арки, Арматура, Арматурное оборудование, Архитектура, Асбест, Аспирация, Асфальт, Балки, Без рубрики, Бетон, Бетонные и железобетонные, Блоки, Блоки оконные и дверные, Бревно, Брус, Ванты, Вентиляция, Весовое оборудование, Виброзащита, Вибротехника, Виды арматуры, Виды бетона, Виды вибрации, Виды испарений, Виды испытаний, Виды камней, Виды кирпича, Виды кладки, Виды контроля, Виды коррозии, Виды нагрузок на материалы, Виды полов, Виды стекла, Виды цемента, Водонапорное оборудование, Водоснабжение, вода, Вяжущие вещества, Герметики, Гидроизоляционное оборудование, Гидроизоляционные материалы, Гипс, Горное оборудование, Горные породы, Горючесть материалов, Гравий, Грузоподъемные механизмы, Грунтовки, ДВП, Деревообрабатывающее оборудование, Деревообработка, ДЕФЕКТЫ, Дефекты керамики, Дефекты краски, Дефекты стекла, Дефекты структуры бетона, Дефекты, деревообработка, Деформации материалов, Добавки, Добавки в бетон, Добавки к цементу, Дозаторы, Древесина, ДСП, ЖД транспорт, Заводы, Заводы, производства, цеха, Замазки, Заполнители для бетона, Защита бетона, Защита древесины, Защита от коррозии, Звукопоглащающий материал, Золы, Известь, Изделия деревянные, Изделия из стекла, Инструменты, Инструменты геодезия, Испытания бетона, Испытательное оборудование, Качество цемента, Качество, контроль, Керамика, Керамика и огнеупоры, Клеи, Клинкер, Колодцы, Колонны, Компрессорное оборудование, Конвеера, Конструкции ЖБИ, Конструкции металлические, Конструкции прочие, Коррозия материалов, Крановое оборудование, Краски, Лаки, Легкие бетоны, Легкие наполнители для бетона, Лестницы, Лотки, Мастики, Мельницы, Минералы, Монтажное оборудование, Мосты, Напыления, Обжиговое оборудование, Обои, Оборудование, Оборудование для производства бетона, Оборудование для производства вяжущие, Оборудование для производства керамики, Оборудование для производства стекла, Оборудование для производства цемента, Общие, Общие термины, Общие термины, бетон, Общие термины, деревообработка, Общие термины, оборудование, Общие, заводы, Общие, заполнители, Общие, качество, Общие, коррозия, Общие, краски, Общие, стекло, Огнезащита материалов, Огнеупоры, Опалубка, Освещение, Отделочные материалы, Отклонения при испытаниях, Отходы, Отходы производства, Панели, Паркет, Перемычки, Песок, Пигменты, Пиломатериал, Питатели, Пластификаторы для бетона, Пластифицирующие добавки, Плиты, Покрытия, Полимерное оборудование, Полимеры, Половое покрытие, Полы, Прессовое оборудование, Приборы, Приспособления, Прогоны, Проектирование, Производства, Противоморозные добавки, Противопожарное оборудование, Прочие, Прочие, бетон, Прочие, замазки, Прочие, краски, Прочие, оборудование, Разновидности древесины, Разрушения материалов, Раствор, Ригеля, Сваи, Сваизабивное оборудование, Сварка, Сварочное оборудование, Свойства, Свойства бетона, Свойства вяжущих веществ, Свойства горной породы, Свойства камней, Свойства материалов, Свойства цемента, Сейсмика, Склады, Скобяные изделия, Смеси сухие, Смолы, Стекло, Строительная химия, Строительные материалы, Суперпластификаторы, Сушильное оборудование, Сушка, Сушка, деревообработка, Сырье, Теория и расчет конструкций, Тепловое оборудование, Тепловые свойства материалов, Теплоизоляционные материалы, Теплоизоляционные свойства материалов, Термовлажносная обработка бетона, Техника безопасности, Технологии, Технологии бетонирования, Технологии керамики, Трубы, Фанера, Фермы, Фибра, Фундаменты, Фурнитура, Цемент, Цеха, Шлаки, Шлифовальное оборудование, Шпаклевки, Шпон, Штукатурное оборудование, Шум, Щебень, Экономика, Эмали, Эмульсии, Энергетическое оборудование
Источник: Энциклопедия терминов, определений и пояснений строительных материалов
Энциклопедия терминов, определений и пояснений строительных материалов. — Калининград. Под редакцией Ложкина В.П.. 2015-2016.
Сразу предупрежу — мое изложение может сильно расходиться с официальной версией, но я, не являясь лицензированным преподавателем, могу себе такое позволить. Честно говоря — пишу цикл статей по геометрии для своих детей, им вскоре предстоит погрузиться в этот загадочный и непонятный мир параллельных линий и я не хочу, чтобы их постигла такая же судьба, как Я. Боуи. Янош Боуи параллельно с Лобачевским и Гауссом разрабатывал начала неевклидовой геометрии, в которой параллельные прямые пересекаются, однако труд его не был оценен по достоинству современниками. После неудачного участия в конкурсе на премию Лейпцигского ученого общества «по вопросу об усовершенствовании геометрической теории мнимых чисел» Я. Боуи впал в тяжелую депрессию и пребывал в ней до конца жизни. Так что отец его оказался достаточно качественным ясновидцем. Впрочем, приведенное в эпиграфе письмо только подтверждает, что сила эмоционального удовольствия от логического мышления для некоторых людей во много раз сильнее обычных житейских радостей. Если подобные последствия на пути постижения мира вас не пугают, то можно и продолжить изучение геометрии. Основные определенияРазличные варианты определений для большинства геометрических фигур существовали задолго до Евклида. Среди них следует выделить генетические определения, представляющие метод создания геометрической фигуры (например, если повернуть циркуль на 360о, то получится окружность), к ним примыкают форономические (кинематические) определения, в которых элемент геометрии или геометрическая фигура рассматривается как результат движения (например, линию можно представить как траекторию движения материальной точки, а поверхность, как траекторию движения линии). Но Евклид первый классифицировал признаки, общие для любых геометрических фигур и таким образом выделил составные элементы любой геометрической фигуры. Из этих элементов и строится геометрия Евклида. Такие понятия как длина, ширина и высота, Евклидом вообще не рассматриваются. Предполагается, что это интуитивно постигаемые понятия. Почти все определения Евклида являются описательными, или как говорили раньше, номинальными, т.е. ничего не доказывающими. Всего три определения в книге XI — для шара, конуса и цилиндра, у Евклида являются генетическими. Евклид четко разделяет элементы геометрии и геометрические фигуры. Давая определения геометрическим элементам и фигурам, Евклид придерживался четкого логического ряда: от простого к сложному, от общего к частному. Так сначала Евклид дает определение элементов геометрии, сначала точки, затем общее определение линии. После общего определения линии следует определение прямой линии — частного случая для всех возможных линий. Затем следует общее определение поверхности, после чего дается определение плоской поверхности — частного случая для всех возможных поверхностей. Затем дается определение плоского угла — частного случая для всех возможных углов, затем определение прямолинейного угла — частного случая для плоских углов. Затем дается определение перпендикулярных линий — частного случая пересечения прямых линий. Таким образом Евклид как бы дает понять, где именно будут происходить дальнейшие геометрические действия. А теперь рассмотрим определения и возможные толкования определений Евклида более подробно. Первая книга «Начал» Евклида (как тут не вспомнить латинское название — «Элементы») начинается с определения точки: 1. Точка есть то, что не имеет частей.Примечание 1: здесь и далее определения, постулаты и аксиомы Евклида даются согласно перевода Д.Д. Мордухай-Болтовского (ОГИЗ, 1948 г) с греческого текста издания Гейзенберга. Сам я, не смотря на корни, греческим не владею, да и аутентичного текста начал все равно не сохранилось, а потому доверяюсь указанному переводу. Даже такое простое определение в течение многих веков понималось по-разному различными комментаторами и исследователями труда Евклида. Более поздние комментаторы, отягощенные современной теорией строения материи, на основании этого определения относят Евклида к приверженцам атомистической теории строения материи и понимают точку, как аналог неделимого атома. Ранние комментаторы, не поняв сути, пытались на основании определений других геометрических фигур дать иное, по их мнению более точное определение точки. Например, определение Герона (одного из величайших древнегреческих инженеров, сформулировавшего золотое правило механики), которое звучит так: точка есть то, что не имеет величины, основанное на определениях линии и плоскости, рассматриваемых далее, может показаться достаточно логичным, однако вступает в явное противоречие со свойствами объектов, наблюдаемых в реальном мире. Даже элементарные частицы имеют размеры, не говоря уже об атомах и потому определение Герона не может считаться правильным. А если дать определение лучу (у Евклида подобное определение отсутствует вовсе) как линии, выходящей из некоторой точки (соответствующий этому определению образ реального мира — Солнце, испускающее лучи света, которые можно явственно видеть при облачной погоде), то точка — Солнце, объемом в миллион раз превышающее Землю, никак не вписывается в определение Герона. А вот определение Евклида подходит и для Солнца и вообще для всех звезд и планет галактики, если рассматривать эти объекты относительно друг друга, т.е. при таком взаимном расположении, когда размеры объектов пренебрежимо малы по сравнению с расстоянием между рассматриваемыми объектами. Некоторые комментаторы (Боссю, Безу) для большей наглядности рассматривали определения Евклида применительно к решению задач кинематики, ассоциируя понятия линии, окружности и др. с траекторией движения материальной точки. Это очень хороший прием, но мы форономические методы использовать не будем. А вот удержаться от аналогий с декартовой системой прямоугольных координат я не могу. Это логично, весь окружающий мир человек воспринимает, поставив себя в центр, и только так. Всякие там расчеты, вычисления нужны большинству людей не для гимнастики ума, а для удовлетворения своих утилитарных потребностей. Потому центром мироздания является человек и пусть мир вращается вокруг человека, а всяким там Коперникам, утверждающим, что это не так, место на костре. Но в целом нельзя забывать, что мир геометрии — некий абстрактный мир, который может не иметь ничего общего с реальным миром. Впрочем, мир геометрии создан с единственной целью — помочь человеку в решении конкретных задач, а потому реальные свойства предметов могут вовсе не учитываться и искать геометрическим понятиям аналогии в реальном мире порой бессмысленно. Хотя подобные аналогии очень нужны и полезны, так как помогают лучше понять суть предмета геометрии. 1.1. Таким образом у Евклида точка — это простейший элемент, который действительно можно рассматривать как атом геометрии, не имеющий никакого отношения к реальным атомам. При этом размеры точки не то чтобы равны нулю, но считаются настолько малыми, что для упрощения решения задач размерами этими можно пренебречьА еще это означает, что в зависимости от вида решаемой задачи один и тот же физический объект окружающего нас мира (например, Солнце) может рассматриваться и как точка, и как двухмерный круг и как трехмерный шар. И если Евклид вкладывал в свое определение точки именно этот смысл, то тем самым дал первый толчок к формированию теории относительности. Можно предположить, что из точек складываются или формируются все остальные геометрические фигуры. Однако сам Евклид нигде прямо об этом не говорит. В геометрии Евклида точка может рассматриваться как отдельный элемент, как элемент формообразования и как нечто общее для различных элементов и геометрических фигур. Далее различные трактовки определений Евклида подробно рассматриваться не будут, а только необходимые на мой взгляд пояснения. 2. Линия — длина без ширины.2.1. Это определение можно понимать так: Линия — это элемент геометрии, ширина и высота которого пренебрежимо мала по сравнению с длинойНапример, в строительной механике часто рассматриваются стержни — геометрические модели балок, при этом высота и ширина реальных балок на первом этапе расчета не учитываются, т.е. балки рассматриваются как некие геометрические линии, а точнее оси, проходящие через центры тяжести поперечных сечений. Из этого определения можно заключить, что Евклид не рассматривал линию, как геометрическую фигуру состоящую из точек, однако анализ следующих определений покажет, что это может быть не совсем так. Линия в геометрии Евклида, как и точка, может рассматриваться отдельный элемент, как элемент формообразования и как нечто общее для различных элементов и геометрических фигур. 3. Концы же линии — точки.Практически все комментаторы Евклида обходят это определение стороной. На первый взгляд в данном определении все достаточно просто и в дополнительных комментариях не нуждается, да и выглядит это определение, как продолжение определения №2, потому по большому счету и определением вовсе не является. Между тем — это одно из важнейших определений, без правильного понимания которого дальнейшее изучение геометрии Евклида просто бессмысленно. Во-первых, совместное рассмотрение определений №2 и №3 не позволяет сделать вывод, что линия состоит из точек и тогда линия — это качественно новый элемент геометрии, прямого отношения к точкам не имеющий, однако линия как и геометрические фигуры, рассматриваемые далее, имеет свои границы — точки. Во-вторых, определение №3 Евклида не допускает использования понятия бесконечности. Я думаю, это одна из причин, почему у Евклида нет отдельных определений для отрезка и для луча, да их и невозможно дать без использования понятия бесконечности. Примечание 2: Понятие бесконечности появилось относительно недавно, в результате развития математической науки (возможно и под влиянием христианской идеи о вечной жизни). На мой взгляд понятие бесконечности является попыткой определить то, что по умолчанию определить нельзя, тем не менее введение понятия «бесконечность» помогает решать определенные математические задачи. Мудрые греки не использовали понятия «бесконечность» в нашем понимании этого слова и далее при определении параллельных прямых Евклид (или один из его учеников) использует понятие «неопределенность». Это может показаться малозначимой мелочью, но на самом деле это один из краеугольных камней познания окружающего мира. В свое время я тоже попался на удочку «бесконечности». Когда мне было 6 лет я любил листать учебники старшей сестры и рассматривать картинки. На одной из страниц учебника был показан принцип относительности размеров: на первой иллюстрации было нарисовано яблоко и Земля, конечно же не в правильных пропорциях, а в таких, чтобы наглядно показать разницу размеров яблока и Земли. На следующей иллюстрации была нарисована Земля размером с яблоко предыдущей картинки и Солнце размером в Землю предыдущей картинки. Затем следовали иллюстрации, дающие представление о размерах солнечной системы и нашей галактики. Впрочем основную суть относительности размеров я понял после просмотра первых двух иллюстраций и задал сестре вопрос: «А где кончается Вселенная?». Сестра сказала, что Вселенная нигде не заканчивается, так как она — бесконечная. Несколько дней мы спорили по этому вопросу, но так и не пришли к единому мнению. Границы Вселенной остались для меня загадкой на всю жизнь, и, думаю, не только для меня. Но вот теперь, рассматривая основные понятия Евклида я пришел к выводу, что если бы сестра использовала вместо понятия «бесконечность» понятие «неопределенность», то никакого спора вообще не было бы. Спорить о том, что неизвестно или неопределенно, не имеет смысла. 4. Прямая линия есть та, которая равно расположена по отношению к точкам на ней. Другой вариант перевода: прямая есть линия, равномерно данная своими точками.Это одно из самых важных и самых сложных определений Евклида. Как видим, ни один из вариантов перевода не приближает нас к пониманию того, что есть прямая линия. Евклид, стремясь максимально упростить изложение материала, явно перестарался, а уж комментаторы перебрали не только все возможные значения древнегреческих слов, использованных в этом определении, но и своих определений прямой линии оставили на несколько томов. Все это безусловно интересно, но подробному рассмотрению всевозможных определений прямой линии следовало бы посвятить отдельную статью, а пока, если придерживаться принятой ранее логики, то можно сделать следующие выводы: Линии состоят из точек. При этом расстояния между соседними точками всегда одинаковы, а все точки кроме крайних являются общими для составляющих линию отрезков. Однако не все точки одинаково важны при определении характеристик геометрических элементов или фигур. Именно поэтому Евклид при определении линии не упомянул о том, что линия состоит из точек, но указал, что концы линии — точки. В связи с этим я бы ввел дополнительное понятие — характерные точки. Например, у любой линии есть как минимум две характерные точки: начальная точка и конечная точка. У ломаной линии, например, состоящей из двух прямолинейных отрезков будет как минимум 3 характерных точки, так как добавится точка, в которой свойства линии изменяются. В связи с этим определение Евклида можно понимать так: 4.1. Прямая линия — это линия, у которой есть только две характерные точки: начальная и конечная. Или, прямая линия — это линия, свойства которой ни в одной из точек не изменяются, за исключением точек начала и конца.Впрочем для прямой линии можно дать и другие определения. 4.2. Прямая линия — это линия, которая состоит из множества отрезков, при этом расстояния между соседними точками (общими точками для отрезков) равны, а расстояния между не соседними точками пропорциональны расстоянию между соседними точками. Более понятным в данном случае было бы следующее определение: длина прямой линии равна сумме расстояний между точками, ее составляющими. А из этого определения можно вывести и определение кривой линии: длина кривой линии, представляющая собой сумму расстояний между соседними точками, всегда меньше расстояния между крайними точками. Но такие определения будут не совсем верными, точнее верными, но только для прямолинейных и криволинейных линий с конечной длиной. Дело в том, что прямая линия с точки зрения современной геометрии может иметь неограниченную длину, т.е. неопределенную или, как сейчас говорят, бесконечную длину и потому использовать неопределенность для определения чего-либо некорректно (см. примечание 2). 4.3. Для прямой линии всегда можно подобрать такую систему координат, при которой значения высоты и ширины для всех точек прямой линии будут постоянными, а изменяться будут только координаты длины, причем для каждой следующей точки это изменение будет составлять постоянную величину. Таким образом прямая линия — это одномерная линияИ еще, если вспомнить о человеке, а если нет человека, то и геометрия никому не нужна, то, исходя из выше данного определения, можно сказать, что прямую линию всегда можно расположить так, что наблюдателю будет видна только одна точкаИ все. При таком определении невозможны геометрия Римана, Лобачевского и любые другие неевклидовы геометрии, точнее сказать — такое определение прямых линий не вписывается в указанные геометрии, но нам-то что? ведь мы рассматриваем именно евклидову геометрию, которая хотя и является частным случаем, тем не менее наиболее характерным частным случаем. 4.4. А между тем Евклид предельно краток и последователен в своих определениях и если допустить, что линия — это отдельный от точек элемент геометрии, ограниченный однако точками, то его определение скорее всего следует трактовать так: прямая линия — это расстояние между точками или длина прямой линии равна расстоянию между точками, прямую линию ограничивающими.Не смотря на то, что все эти определения допустимы, наиболее точно соответствующим духу Евклида я считаю определение 4.1, так как нельзя забывать о том, что понятия о функциях и уравнениях функций появились много позже (приблизительно в XVII в.), кроме того евклидова геометрия имеет дело только с фигурами и элементами, для которых есть прообразы в реальном мире, чисто математический анализ не входил в задачи геометрии. Тем не менее определение Евклида можно считать попыткой охарактеризовать прямую, как функцию длины от расстояния. Примечание 3: Прямую линию наши предки знали и использовали с древнейших времен. Пример тому — лук, тетива которого — прямая линия, да и стрелы считались хорошими, если они прямые. А целясь, человек смотрел на стрелу так, чтобы она становилась по возможности точкой да еще и совпадала с мишенью. Далее вполне логичным с современной точки зрения было бы определение луча — прямой линии, ограниченной с одной стороны точкой. Однако не смотря на кажущуюся простоту подобного определения и вполне наглядный прообраз луча в окружающем нас мире с геометрической точки зрения луч выглядит как половина неопределенности, или говоря современным языком, как половина бесконечности. Чем полубесконечность точнее бесконечности, я не знаю. Возможно и Евклид не нашел подходящего определения для луча, а потому оставил эту тему открытой. Но скорее всего с точки зрения Евклида луч не является формообразующим элементом геометрии, или существование луча в евклидовой геометрии по указанным выше причинам (отсутствие понятия бесконечности) — невозможно и луч, как элемент геометрии, древними геометрами не рассматривался. Отдельного определения кривой или ломанной линии Евклид не дает. Т.е. все линии, не являющиеся прямыми, являются кривыми или ломанными. 5. Поверхность есть то, что имеет только длину и ширину.6. Концы же поверхности — линии.Из этих определений, следуя логике, использованной при рассмотрении точки, линии и концов линии, можно заключить, что: 5.1. Поверхность — это элемент геометрии, высота которого пренебрежимо мала по сравнению с длиной и ширинойСейчас можно было бы сказать, что поверхность — это то, что имеет площадь. Поверхность в геометрии Евклида, как точка и линия, может рассматриваться отдельный элемент, как элемент формообразования и как нечто общее для различных элементов и геометрических фигур. 7. Плоская поверхность есть та, которая равно расположена к прямым на ней.Определение плоскости Евклида еще более сложно для осмысления, чем определение прямой. На сегодняшний день существуют сотни определений плоскости, но ни одно из них, на мой взгляд, не передает кратко и точно суть плоскости. Между тем люди с древнейших времен окружены плоскостями и постоянно стремятся плоскости создавать. Сейчас мы живем в домах, которые представляют собой набор плоскостей, пользуемся мебелью, в которой плоские поверхности преобладают, а многие читают этот текст с плоского монитора. Я вижу в определении Евклида тот смысл, что: 7.1. Плоская — это такая поверхность, свойства которой не изменяются по длине и ширине.7.2. Плоская поверхность (плоскость) — это двухмерный элемент геометрии. Это означает, что для плоскости всегда можно подобрать такую систему координат, при которой значения высоты для всех точек будут постоянными, а изменяться будут только координаты длины и ширины. Или плоскость всегда можно расположить так, что наблюдателю будет видна только одна прямая линия.На этом описание элементов геометрии, которые могут являться формообразующими элементами Евклид заканчивает. Далее следуют определения элементов геометрии, которые следует рассматривать, не как формообразующие, а как вспомогательные, т.е. дополнительно характеризующие любую геометрическую фигуру. 8. Плоский же угол, есть наклон друг к другу двух линий в плоскости касающихся, но не расположенных по одной прямой.Следует пояснить, что изначально угол мыслился, как часть целого. Например с древнейших времен зодиакальный круг был разбит на 360 частей, сейчас именуемых градусами. Но когда-то каждому градусу соответствовал день земного календаря. Такое разделение на градусы-дни появилось задолго до того, как Евклид сформулировал свою геометрию, тем не менее таким делением мы пользуемся и по сей день. Сейчас угол — это еще и одна из характеристик, которую можно использовать для определения линий, поверхностей и соотношений между ними. 8.1. Плоский угол — это важная характеристика любой двухмерной линии или линий, имеющих общую точкуЕще можно сказать, что плоский угол всегда находится в одной плоскости. 9. Когда же линии, содержащие угол, прямые, то угол называется прямолинейным.9.1. Прямолинейный угол — это линия, у которой есть 3 характерные точкиНапример, прямую линию можно рассматривать как множество отрезков, при этом угол между всеми соседними отрезками всегда постоянный. Для прямой линии угол между соседними отрезками равен половине целого. Угол, как и размеры, может измеряться в разных единицах. На сегодняшний день самыми распространенными являются упоминавшиеся выше градусы и радианы. За целое принимаются 360о и 2П, таким образом угол между соседними отрезками прямой линии всегда равен 180о или П. Такой угол называется развернутым углом. Так как этот угол постоянен для всех соседних отрезков прямой, то для упрощения решения задач геометрии углы в 180о как правило не рассматриваются, ведь изменений свойств геометрической фигуры в таких точках не происходит, кроме того развернутый угол — это одномерная геометрическая фигура. Между тем для задач геометрии важны точки и отрезки между которыми происходит изменение свойств. 10. Когда же прямая, восстановленная (поставленная) на другой прямой, образует рядом углы, равные между собой, то каждый из равных углов есть прямой, а восстановленная (поставленная) прямая называется отвесной (перпендикуляром) к той, на которой она восстановлена (поставлена).По сути это определение является довольно точным описанием древнейшего человеческого оберега — креста, а заодно и основанием для формирования прямоугольной системы координат. Сейчас это определение можно сформулировать так: 10.1. Если две прямые при пересечении образуют 4 равных угла, то такие углы называются прямыми, а линии являются перпендикулярами одна к другой.Этой отвесной (перпендикулярной) линией до сих пор пользуются строители при возведении стен и используют для этого древнейший инструмент — отвес. 11. Тупой угол — больший прямого.12. Острый угол — меньший прямого.Без комментариев. Проще и понятнее не скажешь. 13. Граница есть то, что является оконечностью чего-либо.14. Фигура (форма) есть то, что находится внутри какой-нибудь или каких-нибудь границ.По сути эти определения можно было бы и не давать, а отнести их к интуитивно понятным, подобно понятиям размеров. Тем не менее эти определения все-таки нужны. Этим как бы подчеркивается, что ранее перечисленные элементы геометрии по большому счету геометрическими фигурами не являются, а являются частью исследуемых геометрических фигур — формообразующими элементами, или одной из дополнительных характеристик геометрических фигур. Для завершения этого логического ряда следует привести определения для трехмерных геометрических фигур, данные Евклидом в книге XI: XI.1. Тело есть, то, что имеет длину ширину и высоту, (выражаясь современным языком — имеет объем). XI.2. Граница же тела — поверхность. А теперь посмотрим, что же это в итоге дает. Большинство объектов окружающего нас мира представляют собой трехмерные тела. Например, детский кубик, с помощью которого мы начинали в детстве изучение геометрии, если описать его с помощью данных выше определений, ограничен поверхностями, при этом каждая плоскость кубика ограничена линиями, при этом каждая линия ограничена точками. Геометрия же позволяет рассматривать свойства не всего кубика в целом, а свойства каждой отдельной поверхности и даже каждой отдельной линии или точки. Например, на одной из плоскостей кубика может быть изображен круг и с точки зрения геометрии допустимо рассматривать свойства круга только по отношению к плоскости, на которой круг находится, а на остальные плоскости кубика не обращать внимания, если условия задачи того не требуют. Ну и еще, определениями №13 и №14 косвенно подтверждается, что евклидова геометрия не работает с бесконечными, т.е. не имеющими границ геометрическими фигурами. А определение №14 прямо указывает на то, что ломаная линия из трех отрезков, соединяющих три точки и треугольник, ограниченный тремя прямыми линиями — принципиально разные вещи. Далее Евклид переходит к определениям плоских геометрических фигур, составляющих основной предмет изучения школьниками и по ныне, и сначала дает определение круга, одного из древнейших и важнейших обереговых символов. 15. Круг есть плоская фигура, содержащаяся внутри одной линии (окружности), на которую все из одной точки внутри фигуры падающие прямые равны между собой.16. Центром же круга называется эта точка.Сейчас такие определения кажутся довольно неуклюжими. К тому же у Евклида отсутствует прямое определение окружности, которое по логике должно идти до определения круга. В чем же дело, ведь окружность — один из важнейших элементов современной геометрии? Возможно, причиной стала мистическая противоречивость окружности. Ведь окружность по умолчанию не может быть прямой линией, у окружности нет ни начала ни конца, в то же время окружность не могла быть ломанной линией в представлении древних греков и потому была выделена в особый вид линии. А с другой стороны окружность приближается к прямой линии, если радиус ее достаточно велик и выходит, что угол между соседними отрезками приближается к развернутому. По сути эти противоречивые свойства окружности имеют место и сейчас. Более того, любую прямую можно рассматривать, как часть окружности с бесконечно большим радиусом, т.е. прямая это частный случай окружности. А из этого следует, что и плоскость, описанная Евклидом, не более чем частный случай сферы или любой другой объемной геометрической фигуры. Это впоследствии и позволило создать разного рода неевклидовы геометрии. Однако Евклид всегда оставался в четко очерченных пределах, когда плоскость — это плоскость, прямая — это прямая, а круг — это круг. К тому же в определении №15 присутствует косвенное определение окружности: падающие из одной точки на окружность прямые, равные между собой — это радиус окружности. Такое определение косвенно подтверждает, что Евклид мыслил окружность как линию, но не как некое множество точек. 17. Диаметр же круга есть какая угодно прямая, проведенная через центр и ограничиваемая с обеих сторон обводом (окружностью) круга, она и рассекает круг пополам.18. Полукруг же есть фигура, содержащаяся между диаметром и отсекаемой им частью обвода (окружности). Центр же полукруга — то же самое, что и у круга.Далее следуют определения прямолинейных фигур, т.е. таких фигур, границы которых прямые линии. Суть этих определений хорошо понятна и сейчас без дополнительных пояснений, хотя и не все названия фигур совпадают с нынешними, например, определение трапеции Евклида не соответствует нынешнему, сейчас трапеция, это фигура, имеющая две параллельные стороны. 19. Прямолинейные фигуры суть те, которые содержатся между прямыми, трехсторонние — между тремя, четырехсторонние — между четырьмя, многосторонние же — те, которые содержатся между более чем четырьмя прямыми.20. Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны, равнобедренный же — имеющая только две равные стороны, разносторонний же — имеющая три разных стороны.21. Кроме того из трехсторонних фигур прямоугольный треугольник есть имеющий прямой угол, тупоугольный же — имеющий тупой угол, а остроугольный — имеющий три острых угла.22. Из четырехсторонних фигур квадрат есть та, которая и равносторонняя и прямоугольная, разносторонник (прямоугольник) же — прямоугольная, но не равносторонняя, ромб — равносторонняя, но не прямоугольная, ромбоид (параллелограмм) — имеющая противоположные стороны и углы равные между собой, но не являющаяся ни равносторонней ни прямоугольной. Остальные же четырехугольники будем называть трапециями.Следующее определение, являющееся последним в книге I Евклида, нарушает выстроенный ранее логический ряд: 23. Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в неопределенность (см. примечание 2), ни с той ни с другой стороны между собой не встречаются.Если продолжать логический ряд Евклида, то этому определению место за определением №10, так как параллельность — одна из возможных характеристик взаиморасположения прямых линий, подобная перпендикулярности, другими словами параллельность — еще один частный случай взаиморасположения прямых, очень важный для геометрии. Кроме того, только в этом определении встречается упоминание о неопределенности длины, противоречащее всем остальным определениям Евклида. На этом основании я допускаю, что определение №23 Евклиду не принадлежит, а является позднейшей вставкой. Но даже если допустить, что это определение принадлежит Евклиду, то все равно этим определением не допускается не то что пересечение параллельных прямых, но даже и касание. За этим следуют первые постулаты (в частности знаменитый 5 постулат) и аксиомы, рассматриваемые впрочем отдельно. |
линий и углов — определения и свойства (руководство по геометрии)
Древние математики ввели понятие линий для обозначения прямых объектов, имеющих незначительную ширину и глубину. Считанные Евклидом шириной меньше длины, линии составляют основу евклидовой геометрии.
Когда два луча (часть прямой) пересекаются в одной плоскости, они образуют угол. Точка пересечения называется вершиной.
В этой статье мы рассмотрим основные свойства линий и углов, связанные с геометрией.
Ниже приводится краткое описание тем, которые мы рассмотрим в этой статье.
Определение строки
Линия не имеет конечных точек. Имеет бесконечную длину.
Определение линейного сегмента
Сегмент линии — это сегмент линии, или, другими словами, мы можем сказать, что сегмент линии — это линия с двумя конечными точками.
Например: На схеме показана линия L, один из сегментов которой — AB.
На плоскости может быть много отрезков или отрезков.
И эти линии можно разделить на несколько типов на основании взаимного расположения одной линии с другой.
Виды линий
Пересекающиеся линии
Две прямые являются пересекающимися, если они встречаются в общей точке.
Например: L 1 и L 2 являются пересекающимися линиями на диаграмме ниже
Параллельные линии
Пара прямых параллельна, если они никогда не пересекаются.
Например: L 1 , L 2 и L 3 — это параллельные линии на диаграмме ниже.
Поперечная линия
Поперечная линия разрезает две или более линий в разных точках.
Например: Линия L 3 — это поперечная линия на диаграмме ниже.
Далее мы рассмотрим углы и их свойства.
Угол образуется при пересечении двух прямых. Обозначим угол символом.
Угол состоит из двух сторон и одной общей вершины, в которой пересекаются две прямые.
Например: ∠AOD образуется при пересечении линий AB и CD.
Кроме того, ODAOD образуется между ветвью AO и OD, поэтому мы включаем A, O и D, называя угол.
Знаете ли вы, что положение точек ног не имеет значения, если общей вершиной является средняя буква в названии угла
Измерение угла
Угол измеряется в градусах.
Угол может составлять от нуля (0) градусов до 360 градусов.
Причем, по измерению угла они делятся на четыре типа.
1. Острый угол
При измерении угла от 0 до 90 градусов.
2. Прямоугольный
При измерении угла точно 90 градусов.
- Если между двумя линиями есть прямой угол, то говорят, что эти две линии перпендикулярны друг другу .
3. Тупой угол
При измерении угла от 90 до 180 градусов.
Прямая линия имеет угол 180 градусов.
4. Угол отражения
При измерении угла от 180 до 360 градусов.
Мы обсудили основной тип углов.
Давайте теперь обсудим углы, образующиеся при пересечении двух прямых.
1.1) Вертикально противоположные углы
Когда две прямые пересекаются друг с другом, образуются 4 угла.
- И, углы , , противоположные друг другу в точке пересечения , известны как вертикально противоположные углы .
- Вертикально противоположные углы всегда равны.
Давайте теперь обсудим углы, образованные, когда две прямые пересекаются третьей линией i.е. поперечная линия.
2) Углы, образованные поперечной линией
Когда поперечная линия пересекает две прямые, образуются восемь углов, как показано.
Итак, есть несколько специальных пар углов, которые получаются из этой диаграммы.
Например: Если вы заметили, что (∠1, ∠3), (∠2, ∠4), (∠5, ∠7) и (∠6, ∠8) все углы противоположны по вертикали.
Аналогичным образом получаем несколько других типов углов. Давайте обсудим их.
2.1) Внутренние и внешние углы
Внутренние углы — это углы, которые присутствуют внутри области между двумя линиями.
- И внешние углы — это углы , а не , присутствующие внутри этой области.
Например:
- 2, ∠3, ∠5 и ∠8 — внутренние углы.
- А, ∠1, ∠4, ∠6 и ∠7 — внешние углы.
2.2) Соответствующие углы
Два угла называются соответствующими углами, если они лежат на одной стороне от поперечной линии, так что:
- Один угол — это внутренний угол, а
- Другой внешний угол
Например:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5) и (∠2, ∠6) — 4 пары соответствующих углов
2.3) Альтернативные внутренние углы
Два внутренних угла, расположенных на противоположной стороне поперечной линии, называются альтернативными внутренними углами.
Например:
- (∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.
2.4) Альтернативные внешние углы
Два внешних угла, которые находятся на противоположной стороне поперечной линии, называются альтернативными внешними углами.
Например:
- (∠1, ∠7) и (∠4, ∠6) — альтернативные внешние углы.
Примечание: Если поперечная линия пересекает две параллельные прямые, то соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы равны.
Итак, мы обсудили все виды углов.
Давайте теперь узнаем о некоторых свойствах углов.
Свойства углов
1. Сумма углов на одной стороне прямой
Сумма всех углов на одной стороне прямой всегда составляет 180 градусов.
Например: сумма ∠1, ∠2 и ∠3 составляет 180 градусов.
2. Сумма углов вокруг точки
Сумма всех углов вокруг точки всегда составляет 360 градусов.
Например: сумма углов (∠1, ∠2 и ∠3) вокруг точки O составляет 360 градусов.
Если вам понравилась эта статья, вот еще несколько статей, которые могут вам понравиться:
Применение свойств линий и углов в вопросах
Линии и углы — Вопрос 1
На приведенной выше схеме линия CD параллельна линии EF.Если ∠AHD и ∠JIE равны 118 ° и 30 ° соответственно, то какова мера угла GIB?
- 30
- 32
- 34
- 40
- 62
Решение
Шаг 1: Дано
- линия CD параллельна линии EF.
- ∠AHD = 118 °
- ∠JIE = 30 °
Шаг 2: найти
Шаг 3: подход и разработка
Нам нужно найти меру угла GIB.
- Итак, имея данную информацию, мы знаем, что прямая CD параллельна прямой EF, а прямая AB трансверсальна им.
- Следовательно, ∠DHI = ∠FIB, поскольку оба являются соответствующими углами.
- Мы можем найти ∠DHI или ∠FIB как
- ∠AHD + ∠DHI = 180 °
- 118 ° + ∠FIB = 180 °
- ∠FIB = 62 °
- Теперь ∠FIB = ∠FIG + ∠GIB
- Наблюдая за диаграммой, ∠FIG = ∠JIE, поскольку это вертикально противоположные углы между EF и JG.
- ∠FIB = ∠FIG + ∠GIB
- 62 ° = ∠JIE + ∠GIB
- 62 ° = 30 ° + ∠GIB
- ∠GIB = 32 °
- Мы можем найти ∠DHI или ∠FIB как
- Следовательно, ∠DHI = ∠FIB, поскольку оба являются соответствующими углами.
Следовательно, правильный ответ — вариант Б.
Линии и углы — Вопрос 2
На приведенной выше диаграмме угол DFE и угол BFC представлены как X и Y соответственно. Если ∠AFC = 100 ° и ∠BFE = 45 ° , то каково значение Y-X?
- 20
- 25
- 30
- 35
- 40
Решение
Шаг 1: Дано
- ∠DFE = X
- ∠BFC = Y
- ∠AFC = 100 °
- ∠BFE = 45 °
Шаг 2: найти
Шаг 3: подход и разработка
Чтобы найти Y-X, нам нужно сначала найти Y и X.
Угол Y:
- Дано ∠AFC = 100 ° и,
- ∠AFC + ∠BFC = 180 °, так как сумма углов на одной боковой прямой равна 180 °
- 100 ° + ∠BFC = 180 °
Измерение угла X:
- Нам дано ∠BFE = 45 ° и,
- ∠DFE + ∠BFE + ∠BFC = 180 °, так как сумма углов на одной боковой прямой равна 180 °.
- X + 45 ° + 80 ° = 180 °
Следовательно, Y — X = 80 ° — 55 ° = 25 °.
Таким образом, правильный ответ — вариант Б.
,Что такое линейный сегмент? (Определение, формула расстояния, пример)
Что такое линии, сегменты линий и лучи?
Линии, отрезки и лучи встречаются в геометрии везде. Используя эти простые инструменты, вы можете создавать параллельные линии, серединные перпендикулярные линии, многоугольники и многое другое. В этом уроке вы узнаете определения линий, сегментов линий и лучей, как их называть и несколько способов измерения сегментов линий.
Содержание
- Что такое линии, отрезки линий и лучи?
- Линейный сегмент
- Что такое линия?
- лучей
- Сегменты измерительной линии
- Как найти длину диагонального сегмента на координатной плоскости
- Формула расстояния
- Примеры линейных сегментов в реальной жизни
Линейный сегмент
Сегмент линии — это часть или часть линии, которая позволяет строить многоугольники, определять уклоны и производить вычисления.Его длина конечна и определяется двумя его конечными точками.
Отрезок линии — это фрагмент линии. Независимо от длины отрезка, он конечен.
Обозначение сегмента линии
Вы называете отрезок линии по его двум конечным точкам. Сокращение для сегмента линии состоит в том, чтобы записать сегменты линии двумя конечными точками и нарисовать черту над ними, как CX¯:

Вы изображаете сегмент линии на бумаге для рисования, используя линейку для создания линии и помещая две точки на ее концах, обозначенные заглавными буквами; это конечные точки отрезка:
Что такое линия?
Определение линии — это набор точек между двумя точками и за ними.Линия бесконечна по длине. Все точки на линии коллинеарны.
Символ прямой линии
В геометрии символ прямой линии представляет собой отрезок с двумя наконечниками стрелок на концах, как CX↔. Вы идентифицируете его с помощью двух названных точек, обозначенных заглавными буквами. Выберите точку на линии и дайте ей букву, затем выберите вторую; теперь у вас есть название вашей линии:

Лучи
Луч — это часть линии, которая имеет одну конечную точку и продолжается бесконечно только в одном направлении.Вы не можете измерить длину луча.

Луч получает имя сначала по его конечной точке, а затем по любой другой точке луча. В этом примере у нас есть точка B и точка A (BA →).
Сегменты измерительной линии
Линейный сегмент называется по его конечным точкам, но могут быть названы и другие точки по его длине. Каждая часть линейного сегмента может быть помечена по длине, поэтому вы можете сложить их, чтобы определить общую длину линейного сегмента.
Пример сегмента строки
Здесь у нас есть отрезок CX¯, но мы добавили две точки по пути, точку G и точку R:

Чтобы определить общую длину линейного сегмента, вы добавляете каждый сегмент линейного сегмента.Формула для линейного сегмента CX будет: CG + GR + RX = CX
.7 единиц линейного сегмента CG
5 шт. Линейный сегмент GR
3 линейных сегмента RX
7 + 5 + 3 = 15 единиц длины для CX ¯
Координатная плоскость
Координатная плоскость , также называемая декартовой плоскостью (спасибо, Рене Декарт!), Представляет собой сетку, построенную из оси x и оси y. Вы можете думать об этом как о двух перпендикулярных числовых линиях или как о карте территории, занятой отрезками линий.
Чтобы определить длину горизонтальных или вертикальных отрезков линии на плоскости, подсчитайте отдельные единицы от конечной точки до конечной точки:

Чтобы определить длину линейного сегмента LM¯, мы начинаем с точки L и отсчитываем пять правых единиц, заканчиваясь в точке
.Определение сегмента строки — Math Open Reference
Определение сегмента линии — Открытая справка по математике Определение: прямая линия, соединяющая два точек, не выходя за их пределы.Попробуй это Отрегулируйте сегмент линии ниже, перетащив оранжевую точку на конечную точку, и посмотрите, как ведет себя сегмент PQ.
См. Рисунок выше. Отрезок PQ соединяет точки P и Q. Точки P и Q называются «конечными точками» отрезка.Слово «сегмент» обычно означает «кусок» чего-либо, а здесь оно означает «кусок». полный линия, которая обычно простирается до бесконечности в обоих направлениях.
Отрезок линии одномерный. Он имеет измеримую длину, но нулевую ширину. Если вы нарисуете линейный сегмент карандашом, осмотр под микроскопом покажет, что карандашный след имеет измеримую ширину. Карандашная линия — это просто способ проиллюстрировать идею на бумаге. Однако в геометрии отрезок линии не имеет ширины.
Наименование отрезков
Сегменты линии обычно называют двумя способами:- По конечным точкам.
На рисунке выше сегмент линии будет называться PQ, потому что он соединяет две точки P и Q. Напомним, что точки обычно обозначаются одними заглавными (заглавными) буквами. Сокращенный способ записи: Это читается как «отрезок линии PQ». Полоса над двумя буквами указывает на то, что это отрезок линии, а не линия, которая продолжается в обоих направлениях.
Это читается как «отрезок линии PQ». Полоса над двумя буквами указывает на то, что это отрезок линии, а не линия, которая продолжается в обоих направлениях. - Одной буквой.
Сегмент выше будет называться просто «y». По соглашению, это обычно одна строчная (строчная) буква. Этот метод часто используется для обозначения сторон треугольники и прочее многоугольники.
Строений
В главе о конструкциях есть анимированные демонстрации того, как выполнять различные конструкции относящиеся к линейным сегментам, используя только циркуль и линейку. Видеть:Координатная геометрия
В другом разделе математики, называемом координатной геометрией, точки, определяющие линию, расположены на плоскости, используя их
координаты — два числа, которые показывают, где находится точка.
Подробнее см. В разделе «Определение отрезка линии (координатная геометрия)».
Если мы знаем координаты двух конечных точек отрезка линии, мы можем вычислить расстояние между ними и таким образом найти длину отрезка. См. Раздел Расстояние между двумя точками (координатная геометрия)
Другие темы строки
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
косых линий | Геометрия (определение, примеры и видео) // Tutors.com
Косые линии в геометрии (определение, примеры и видео)
видео Определение Примеры Диагонали тестирование
В отличие от множества геометрических фигур, в нашем мире живут косые линии. Они являются частью геометрии трех измерений, так же как вы и все ваши друзья — трехмерные существа. Наклонные линии могут существовать только в трех измерениях; они не могут быть частью двумерного мира многоугольников и кругов.
Что вы узнаете:
Проработав этот урок и видео, вы сможете:
- Распознавать и определять перекосы
- Определить наклонные линии
- Сравните и сопоставьте наклонные линии с параллельными линиями в двух измерениях
- Тест на перекос
Что такое наклонные линии?
Косые линии — это линии, которые находятся в разных плоскостях , они никогда не параллельны , а они никогда не пересекаются с .С другой стороны, параллельные линии — это линии, которые находятся в одной плоскости , и никогда не пересекаются с .
Другими словами, Параллельные линии должны существовать в двух измерениях; они параллельны в одной плоскости. Наклонные линии не могут существовать в двух измерениях и всегда находятся в разных, непересекающихся плоскостях.
Помните, что в математике линии всегда идут в обоих направлениях.
Предположим, вы хотите построить большую деревянную коробку для отрезков линий.Вы бы нашли самый длинный отрезок линии и сделали бы прямоугольник немного больше, не так ли? Но что, если вы захотите провести лучи или линии? Не существует коробки, которая могла бы удерживать ее, потому что лучи всегда идут в одном направлении, а линии — в двух направлениях навсегда.
Перекос линий — это то, что было бы, если бы вы попытались сохранить строки в большом ящике. Как связка бесконечных двусторонних стрел, они не хотели сотрудничать.
Наклонные линии имеют несколько отличительных свойств, которые делают большой деревянный ящик непрактичным:
- Они продолжаются в двух направлениях навсегда
- Они в разных плоскостях
- Они никогда не параллельны
- Они никогда не пересекаются
Примеры наклонных линий
Пожалуйста, войдите в лифт с воображаемой геометрией.Подъемник — это прямоугольная призма (шесть граней, восемь вершин, 12 ребер и т. Д.).
Внутренние стены покрыты досками сухого стирания (как задумчиво!). У вас в руках есть маркер для сухого стирания и линейка (конечно, есть!), Поэтому вы проводите линию на боковой стене лифта, идущую от верха кабины лифта до пола, вместе с наконечниками стрел. :
[вставьте рисунок, аналогичный оригиналу, но сделайте его похожим на лифт]
Это выглядит красиво, поэтому вы проводите еще одну линию на противоположной боковой стене, идущую от передней части автомобиля к задней:
[вставьте рисунок, аналогичный оригиналу, но сделайте его похожим на лифт]
Не беспокойтесь, это не граффити; это сухое стирание! Обратите внимание, что две линии находятся в двух отдельных плоскостях, разделенных всем пространством, которое вы занимает.Более того, одна линия идет вверх и вниз, а другая идет вперед-назад.
Это косые линии. Они не параллельны и никогда не пересекутся (находятся в двух разных плоскостях).
Внутри лифта вы понимаете, что смотрите на 12 граней (где пересекаются плоскости):
- Четыре края потолка
- Четыре края стенки
- Четыре края пола
Выберите любую кромку. Затем выберите другое ребро:
- Не параллельно вашему первому краю и
- Не разделяет ни одну из плоскостей, создавших первую кромку
Сделайте эти две вещи, и вы обнаружите перекосы! Например, верхняя горизонтальная линия лифта наклонена к задней вертикальной линии.Эти линии никогда не пересекаются, и они не параллельны.
Диагонали
Поскольку наклонные линии должны существовать в трехмерном пространстве, вы можете включать диагонали в поиск наклонных линий. Линия, проходящая по диагонали от одного угла потолка лифта к другому углу того же потолка, скошена к четырем краям пола.
Сделайте еще более драматичным: линия от верхнего угла лифта к противоположному, нижнему углу — разрезая прямо через центральное пространство лифта (где вы стоите) — наклонена к двум вертикальным углам стены, не тронутая линия.
Тестирование перекосов
Линии, сегменты линий и лучи могут быть наклонными. Вы можете выполнить быструю проверку предполагаемых линий перекоса только с помощью линейки. Выровняйте его по одной линии и физически переместите на другую линию. Если вам нужно повернуть, повернуть, повернуть или иным образом изменить ориентацию линейки, чтобы выровнять ее со второй линией, то две линии будут наклонены.
Другой способ проверить это — это повесить мокрое постельное белье с одной линии на другую. Если вы можете представить, как повесить простыню между двумя линиями так, чтобы простыня висела совершенно плоско (как самолет), две линии имеют наклон , а не .Если простыня должна скручиваться, две линии имеют перекос на .
Краткое содержание урока
Теперь, когда вы закончили этот урок, вы можете распознавать и идентифицировать наклонные линии, определять наклонные линии, сравнивать и сравнивать наклонные линии с параллельными линиями в двух измерениях, а также проверять наличие наклонных линий.
Следующий урок:
Что такое горизонтальные линии?
, Это читается как «отрезок линии PQ». Полоса над двумя буквами указывает на то, что это отрезок линии, а не линия, которая продолжается в обоих направлениях.
Это читается как «отрезок линии PQ». Полоса над двумя буквами указывает на то, что это отрезок линии, а не линия, которая продолжается в обоих направлениях.