Несобственный интеграл — Википедия
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
- Область интегрирования является бесконечной. Например, является бесконечным промежутком [a,+∞){\displaystyle [a,+\infty )}.
- Функция f(x){\displaystyle f(x)} является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал [a,b]{\displaystyle [a,b]} конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.
![[a,b]](/800/600/https/upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Improperintegral2.png/200px-Improperintegral2.png) Несобственный интеграл первого рода
Несобственный интеграл первого родаПусть f(x){\displaystyle f(x)} определена и непрерывна на интервале [a,+∞){\displaystyle [a,+\infty )} и ∀A>a ∃∫aAf(x)dx{\displaystyle \forall A>a\ \exists \int \limits _{a}^{A}f(x)dx}. Тогда:
- Если ∃limA→+∞∫aAf(x)dx=I∈R{\displaystyle \exists \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} называется сходящимся.
- Если не существует конечного limA→+∞∫aAf(x)dx{\displaystyle \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫a+∞f(x)dx{\displaystyle \int \limits _{a}^{+\infty }f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена и непрерывна на множестве от (−∞,b]{\displaystyle (-\infty ,b]} и ∀B<b⇒∃∫Bbf(x)dx{\displaystyle \forall B<b\Rightarrow \exists \int \limits _{B}^{b}f(x)dx}. Тогда:
- Если ∃limB→−∞∫Bbf(x)dx=I∈R{\displaystyle \exists \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} называется сходящимся.
- Если не существует конечного limB→−∞∫Bbf(x)dx{\displaystyle \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫−∞bf(x)dx{\displaystyle \int \limits _{-\infty }^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
∫−∞+∞f(x)dx=∫−∞cf(x)dx+∫c+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{c}f(x)dx+\int \limits _{c}^{+\infty }f(x)dx}, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода[править | править код]
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры[править | править код]
∫−∞−11x2dx=lima→−∞∫a−11x2dx=lima→−∞−1x|a−1=1+lima→−∞1a=1+0=1{\displaystyle \int \limits _{-\infty }^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }\int \limits _{a}^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }{\Bigl .}-{\frac {1}{x}}{\Bigr |}_{a}^{-1}=1+\lim _{a\to -\infty }{\frac {1}{a}}=1+0=1}
 Несобственный интеграл Римана второго рода
Несобственный интеграл Римана второго родаПусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]}, терпит бесконечный разрыв в точке x = a и ∀δ>0⇒∃∫a+δbf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена на [a,b){\displaystyle [a,b)} , терпит бесконечный разрыв при x = b и ∀δ>0⇒∃∫ab−δf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a}^{b-\delta }f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} терпит разрыв во внутренней точке c{\displaystyle c} отрезка [a;b]{\displaystyle [a;b]}, то несобственный интеграл второго рода определяется формулой:
∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx.{\displaystyle \int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx.}
Геометрический смысл несобственных интегралов II рода[править | править код]
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.
Пример[править | править код]
∫01dxx=limδ→0+0ln|x||0+δ1=0−limδ→0+0lnδ=+∞{\displaystyle \int \limits _{0}^{1}{dx \over x}=\lim _{\delta \to 0+0}{\Bigl .}\ln |x|{\Bigr |}_{0+\delta }^{1}=0-\lim _{\delta \to 0+0}\ln \delta =+\infty }
Пусть функция f(x){\displaystyle f(x)} определена на всей числовой оси и имеет разрыв в точках x1,x2,…,xk{\displaystyle x_{1},x_{2},\dots ,x_{k}}.
Тогда можно найти несобственный интеграл ∫−∞+∞f(x)dx=∫−∞x1f(x)dx+∑j=1k−1∫xjxj+1f(x)dx+∫xk+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{x_{1}}f(x)dx+\sum _{j=1}^{k-1}{\int \limits _{x_{j}}^{x_{j+1}}f(x)dx}+\int \limits _{x_{k}}^{+\infty }f(x)dx}
1. Пусть f(x){\displaystyle f(x)} определена на множестве от [a,+∞){\displaystyle [a,+\infty )} и ∀A>a⇒∃∫aAf(x)dx=I{\displaystyle \forall A>a\Rightarrow \exists \int \limits _{a}^{A}f(x)dx={\mathcal {I}}}.
- Тогда I=∫a+∞f(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{+\infty }f(x)dx} сходится ⇔∀ε>0⇒∃A(ε)>a:∀(A2>A1>A)⇒|∫A1A2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists A(\varepsilon )>a:\forall (A_{2}>A_{1}>A)\Rightarrow \left|\,\int \limits _{A_{1}}^{A_{2}}f(x)dx\right|<\varepsilon }
2. Пусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]} и ∀δ>0⇒∃∫a+δbf(x)dx=I{\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}}.
- Тогда I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} сходится ⇔∀ε>0⇒∃δ(ε)>0:∀(0<δ1<δ2<δ)⇒|∫a+δ1a+δ2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists \delta (\varepsilon )>0:\forall (0<\delta _{1}<\delta _{2}<\delta )\Rightarrow \left|\,\int \limits _{a+\delta _{1}}^{a+\delta _{2}}f(x)dx\right|<\varepsilon }
Интеграл ∫a+∞f(x)dx (∫abf(x)dx){\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ \left(\int \limits _{a}^{b}f(x)dx\right)} называется абсолютно сходящимся, если ∫a+∞|f(x)|dx (∫ab|f(x)|dx){\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ \left(\int \limits _{a}^{b}|f(x)|dx\right)}сходится.
Если интеграл сходится абсолютно, то он сходится.
Интеграл ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } называется условно сходящимся, если ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } сходится, а ∫a+∞|f(x)|dx {\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ } расходится.
Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
Несобственные интегралы от неограниченных функций
Пусть функция  непрерывна на конечном промежутке
непрерывна на конечном промежутке  ,
но не ограничена на этом промежутке.
,
но не ограничена на этом промежутке.
Определение
2. Несобственным интегралом  от
функции у = f(x) на
промежутке [а, b) называется предел
от
функции у = f(x) на
промежутке [а, b) называется предел  ,
т.е.
,
т.е.
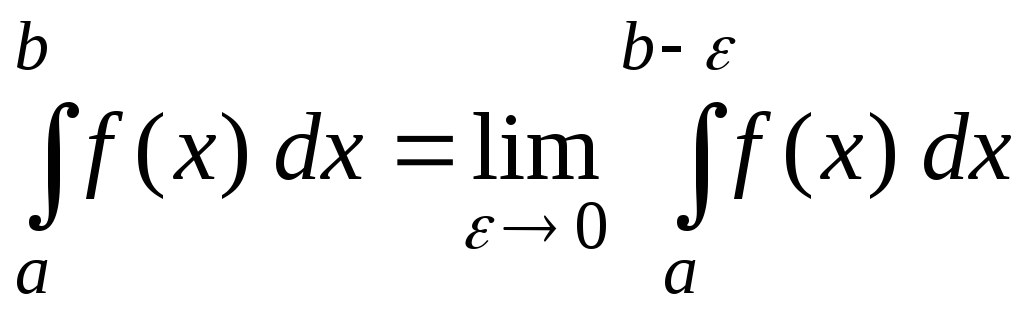 .
.
Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Несобственные интегралы от неограниченных функций иногда называют несобственными интегралами второго рода.
Аналогично вводится
понятие несобственного интеграла от
функции  непрерывной, но не ограниченной на
промежутке
непрерывной, но не ограниченной на
промежутке  :
:
 .
.
Если функция 
 ,
где
,
где  ,
и непрерывна при
,
и непрерывна при 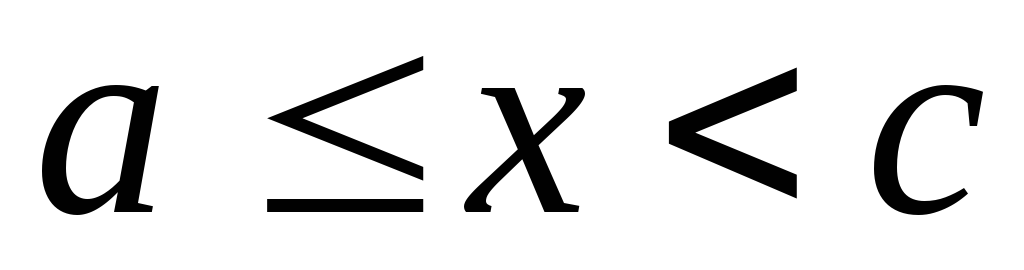 и
и  ,
то несобственный интеграл от функции у = f(x) на отрезке
,
то несобственный интеграл от функции у = f(x) на отрезке  обозначается
обозначается 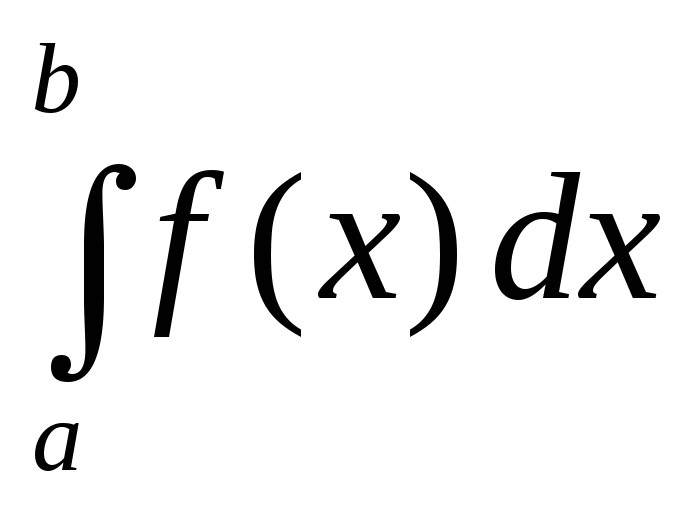 и определяется равенством
и определяется равенством  .
.
Несобственный интеграл называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства. В противном случае данный интеграл называется расходящимся.
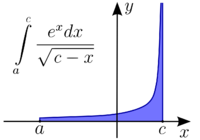
Пример 3. Исследовать на сходимость несобственный интеграл
 .
.
Решение. Данный интеграл является интегралом
от неограниченной функции (подынтегральная
функция  не определена в точке
не определена в точке  ,
при
,
при  эта функция неограниченно возрастает).
эта функция неограниченно возрастает).
По определению имеем
 [замена:
[замена: 
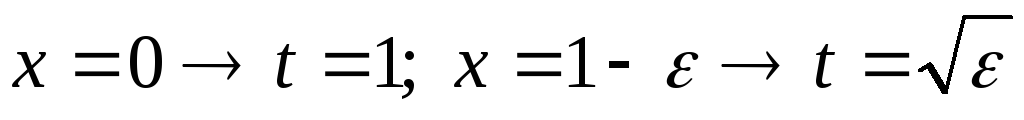 ]
=
]
= 
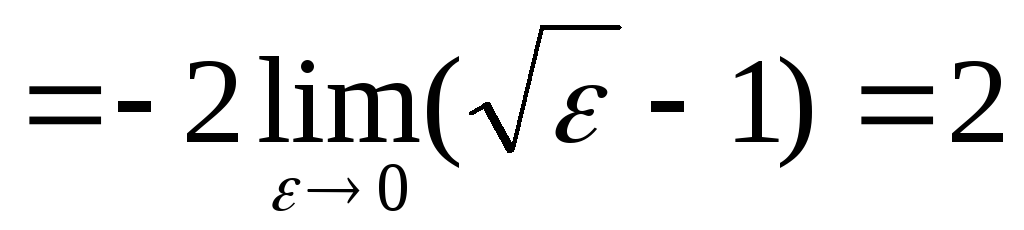 ,
,следовательно, данный интеграл сходится.
Задачи для самостоятельного решения
10. Применение определенных интегралов. Несобственные интегралы
1. Найти площадь фигуры, ограниченной линиями:
a)  и осью Ox;
б)
и осью Ox;
б)  ;
;
в)  и
и 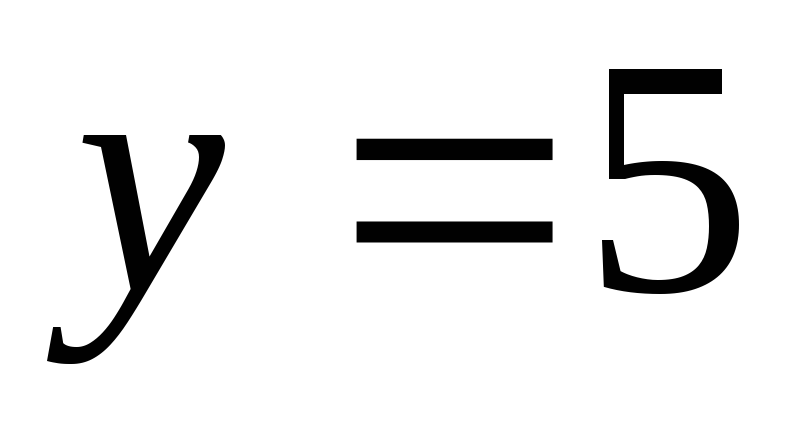 ;
г)
;
г) 
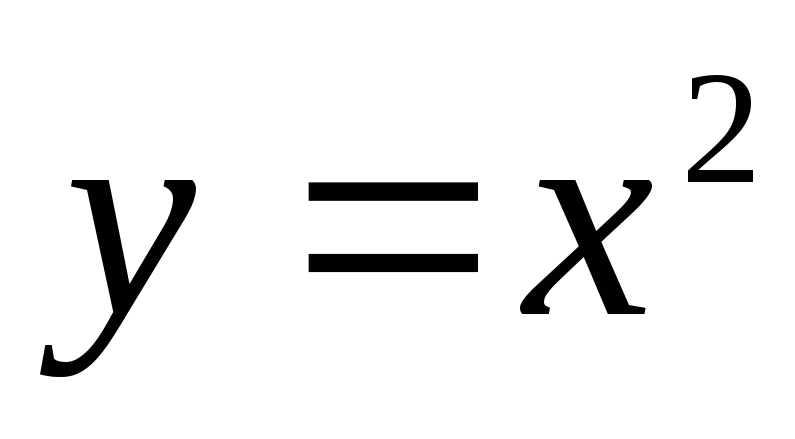 ;
; д)  и
и  ;
е)
;
е) 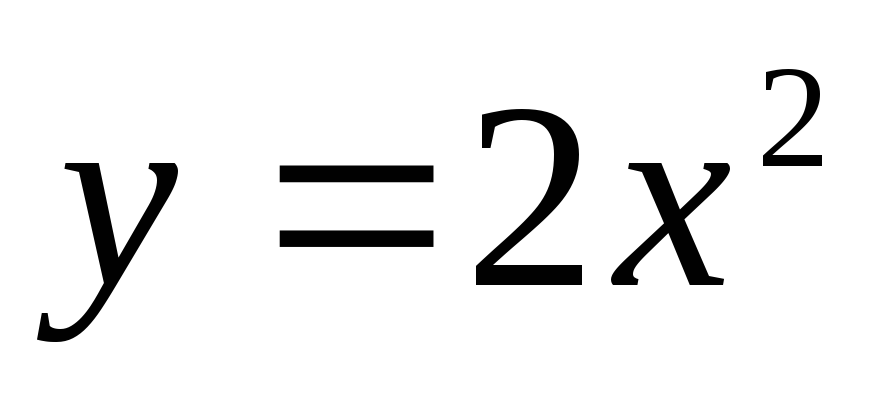 и
и  .
.
2. Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной линиями:
а)  где
где  ;
б)
;
б) 
в)  ;
г)
;
г)  .
.
3. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями:
а)  ;
б)
;
б)  ;
;
в)  ;
г)
;
г)  .
.
4. а) вычислить
длину дуги кривой 
 .
. б) вычислить длину
дуги кривой 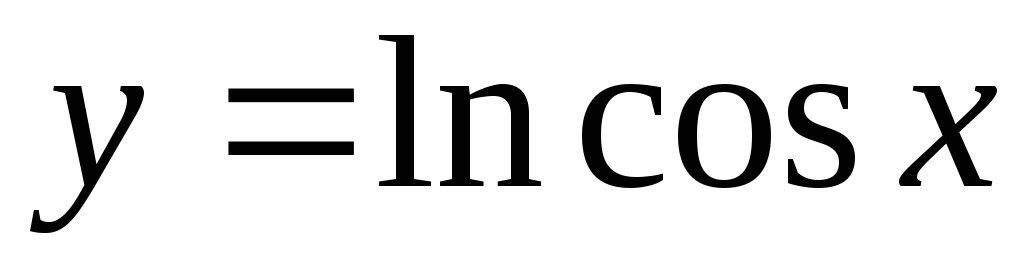 ,
заключенной между точками, для которых
,
заключенной между точками, для которых  .
.
5. Исследовать на сходимость несобственные интегралы:
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
;
д) 
 ;
ж)
;
ж)  ;
з)
;
з)  ;
; и)  ;
к)
;
к)  ;
л)
;
л)  ;
м)
;
м)  .
.
11. Дифференциальные уравнения
Пусть F:  – непрерывная функция. Соотношение
– непрерывная функция. Соотношение
| (1) |
связывающее
независимую переменную х,
неизвестную функцию  и ее производные
и ее производные  (наличие хотя бы одной производной
обязательно), называется дифференциальным
уравнением.
(наличие хотя бы одной производной
обязательно), называется дифференциальным
уравнением.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
График решения дифференциального уравнения называется интегральной кривой.
Процесс нахождения решения дифференциального уравнения называется
интегрированием этого уравнения. Решение может быть
задано в неявном виде  .
В этом случае его называют интегралом
дифференциального уравнения.
.
В этом случае его называют интегралом
дифференциального уравнения.
Общим решением дифференциального уравнения (1) называется функция
| (2) |
зависящая от х и n произвольных независимых постоянных  ,
обращающая это уравнение в тождество.
Заметим, что число произвольных постоянных
равно порядку дифференциального
уравнения.
,
обращающая это уравнение в тождество.
Заметим, что число произвольных постоянных
равно порядку дифференциального
уравнения.
Общее решение, заданное в неявном виде
 ,
,
называется общим интегралом.
Частным решением дифференциального уравнения (1) называется решение, которое получается из (2), если придать конкретные значения произвольным постоянным, т. е.
 ,
,
где  – фиксированные числа.
– фиксированные числа.
Частным интегралом называется интеграл, полученный из общего путем фиксирования произвольных постоянных
 ,
,
где 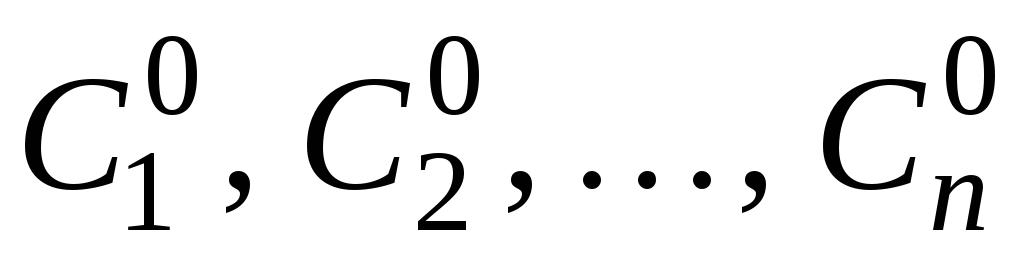 – фиксированные числа.
– фиксированные числа.
Несобственные интегралы
Интегралы с бесконечными пределами интегрирования
Обычно определенный интеграл (ОИ) $I=\int \limits _{a}^{b}f\left(x\right)\cdot dx $ от функции $y=f\left(x\right)$ рассматривается при условии, что отрезок интегрирования $\left[a,\; b\right]$ является конечным. Однако, существует множество задач, в которых возникает необходимость рассмотреть ОИ на каком-то из бесконечных промежутков $\left[\left. a,\; +\infty \right)\right. $, $\left(\left. -\infty ,\; b\right]\right. $ или $\left(-\infty ,\; +\infty \right)$. Такие интегралы называют несобственными.
Понятно, что традиционное определение ОИ на эти случаи распространять нельзя, поскольку построение интегральных сумм Римана на бесконечных промежутках невозможно. Именно поэтому для таких несобственных интегралов вводят дополнительные определения.
Рассмотрим несобственный интеграл $\int \limits _{a}^{+\infty }f\left(x\right)\cdot dx $, в котором является бесконечным верхний предел интегрирования. Пусть функция $f\left(x\right)$ непрерывна на промежутке $\left[\left. a,\; +\infty \right)\right. $. Сначала ограничим этот промежуток до $\left[a,\; B\right]$ и рассмотрим интеграл $F\left(B\right)=\int \limits _{a}^{B}f\left(x\right)\cdot dx $, который является функцией своего верхнего предела. Теперь предположим, что $B\to +\infty $. При таких условиях принимают, что $\int \limits _{a}^{+\infty }f\left(x\right)\cdot dx =\mathop{\lim }\limits_{B\to +\infty } \; \int \limits _{a}^{B}f\left(x\right)\cdot dx $.
Определение
Если указанный предел имеет конечное значение, то несобственный интеграл $\int \limits _{a}^{+\infty }f\left(x\right)\cdot dx $ называют сходящимся. Если же этот предел бесконечен или не существует совсем, то такой несобственный интеграл называють расходящимся.
Геометрический смысл сходящегося несобственного интеграла $\int \limits _{a}^{+\infty }f\left(x\right)\cdot dx $ состоит в том, что он представляет собой конечное значение площади неограниченной криволинейной трапеции.
Задача 1
Найти несобственный интеграл $\int \limits _{1}^{+\infty }\frac{1}{x^{2} } \cdot dx $.
Имеем: $\int \limits _{1}^{+\infty }\frac{1}{x^{2} } \cdot dx =\mathop{\lim }\limits_{B\to +\infty } \; \int \limits _{1}^{B}x^{-2} \cdot dx =\mathop{\lim }\limits_{B\to +\infty } \; \left[-\frac{1}{x} \right]_{1}^{B} =\mathop{\lim }\limits_{B\to +\infty } \; \left[-\frac{1}{B} +\frac{1}{1} \right]=1$.
Данный несобственный интеграл является сходящимся.
Задача 2
Найти несобственный интеграл $\int \limits _{1}^{+\infty }\frac{1}{x} \cdot dx $.
Имеем: $\int \limits _{1}^{+\infty }\frac{1}{x} \cdot dx =\mathop{\lim }\limits_{B\to +\infty } \; \int \limits _{1}^{B}\frac{1}{x} \cdot dx =\mathop{\lim }\limits_{B\to +\infty } \; \left[\ln \left|x\right|\right]_{1}^{B} =\mathop{\lim }\limits_{B\to +\infty } \; \left[\ln B-\ln 1\right]=+\infty $.
Данный несобственный интеграл является расходящимся.

Графики обеих подынтегральных функций приведены на рисунках. Обе функции сходны по поведению (убывающие и имеют асимптотой ось $Ox$). Но бесконечная криволинейная трапеция, которая соответствует подынтегральной функции $\frac{1}{x^{2} } $ (фигура слева), все же имеет конечную площадь. В то же время площадь бесконечной криволинейной трапеции, которая соответствует подынтегральной функции $\frac{1}{x} $ (фигура справа), является неограниченной. Это объясняется тем, что функция $\frac{1}{x^{2} } $ убывает до нуля значительно быстрее, нежели функция $\frac{1}{x} $.
Аналогично определяются также следующие несобственные интегралы:
- $\int \limits _{-\infty }^{b}f\left(x\right)\cdot dx =\mathop{\lim }\limits_{A\to -\infty } \; \int \limits _{A}^{b}f\left(x\right)\cdot dx $ — интеграл на бесконечном промежутке $\left(\left. -\infty ,\; b\right]\right. $;
- $\int \limits _{-\infty }^{+\infty }f\left(x\right)\cdot dx =\int \limits _{-\infty }^{c}f\left(x\right)\cdot dx +\int \limits _{c}^{+\infty }f\left(x\right)\cdot dx =\mathop{\lim }\limits_{A\to -\infty } \; \int \limits _{A}^{c}f\left(x\right)\cdot dx +\mathop{\lim }\limits_{B\to +\infty } \; \int \limits _{c}^{B}f\left(x\right)\cdot dx $ — интеграл на бесконечном промежутке $\left(-\infty ,\; +\infty \right)$, где $c$ — произвольное действительное число.
Задача 3
Пусть на точку $m$ действует сила, направленная к некоторой фиксированной точке $M$ и по величине обратно пропорциональная квадрату расстояния $r$ между точками. Так ведет себя, в частности, гравитационная сила для материальных точек и электростатическая сила для точечных противоположных зарядов. Нужно найти работу, затраченную на перемещение точки $m$ из некоторого положения $r_{0} $ на бесконечность.
Величина силы выражается формулою $F=\frac{k}{r^{2} } $, где $k$ — некоторый коэффициент пропорциональности. Затраченная работа называется потенциалом и может быть вычислена с помощью следующего интеграла:
\[A=\int \limits _{r_{0} }^{+\infty }\frac{k}{r^{2} } \cdot dr =\mathop{\lim }\limits_{R\to +\infty } \; \int \limits _{r_{0} }^{R}\frac{k}{r^{2} } \cdot dr =k\cdot \mathop{\lim }\limits_{R\to +\infty } \; \left[-\frac{1}{r} \right]_{r_{0} }^{R} =k\cdot \mathop{\lim }\limits_{R\to +\infty } \; \left(-\frac{1}{R} +\frac{1}{r_{0} } \right)=\frac{k}{r_{0} } .\]Из полученной формулы видно, что при перемещении на бесконечное расстояние получаем конечную работу.
Интегралы от неограниченных функций
Известно, что необходимым условием интегрируемости функции $y=f\left(x\right)$ на некотором отрезке $\left[a,\; b\right]$ является её ограниченность на нём. Однако существует немало задач, в которых подынтегральная функция $f\left(x\right)$ стремится к бесконечности при приближении $x$ к какому-то одному или сразу к обоим пределам интегрирования. Целесообразно расширить понятие ОИ и на такие функции посредством введения дополнительных определений. Интегралы от неограниченных функций также называют несобственными.
Рассмотрим несобственный интеграл $\int \limits _{a}^{b}f\left(x\right)\cdot dx $, в котором функция $f\left(x\right)$ определена на промежутке $\left[a,\; b\right)$. Предположим, что $f\left(x\right)\to \infty $ при $x\to b-0$, то есть функция неограниченно возрастает, если $x$ неограниченно приближается к точке $x=b$ слева. При этом точка $x=b$ называется особой. Чтобы придать такому интегралу смысл, сначала ограничим этот промежуток до $\left[a,\; b-\varepsilon \right]$, где число $\varepsilon >0$ такое, что $b-\varepsilon >a$. Теперь рассмотрим интеграл $F\left(\varepsilon \right)=\int \limits _{a}^{b-\varepsilon }f\left(x\right)\cdot dx $, который является функцией $\varepsilon $ и предположим, что $\varepsilon \to 0$. При таких условиях принимают $\int \limits _{a}^{b}f\left(x\right)\cdot dx =\mathop{\lim }\limits_{\varepsilon \to 0} \; \int \limits _{a}^{b-\varepsilon }f\left(x\right)\cdot dx $. Если указанная граница имеет конечное значение, то несобственный интеграл $\int \limits _{a}^{b}f\left(x\right)\cdot dx $ называют сходящимся. Если же этот предел бесконечен или не существует совсем, то такой несобственный интеграл называют расходящимся.
Геометрический смысл сходящегося несобственного интеграла $\int \limits _{a}^{b}f\left(x\right)\cdot dx $ состоит в том, что он представляет собой конечное значение площади криволинейной трапеции, высота которой бесконечна.
Аналогично определяются также следующие несобственные интегралы:
- $\int \limits _{a}^{b}f\left(x\right)\cdot dx =\mathop{\lim }\limits_{\varepsilon \to 0} \; \int \limits _{a+\varepsilon }^{b}f\left(x\right)\cdot dx $ — интеграл с особой точкой $x=a$;
- $\int \limits _{a}^{b}f\left(x\right)\cdot dx =\mathop{\lim }\limits_{\varepsilon \to 0} \; \int \limits _{a}^{c-\varepsilon }f\left(x\right)\cdot dx +\mathop{\lim }\limits_{\delta \to 0} \; \int \limits _{c+\delta }^{b}f\left(x\right)\cdot dx $ — интеграл с особой точкой $x=c$ такой, что $a
- $\int \limits _{a}^{b}f\left(x\right)\cdot dx =\mathop{\lim }\limits_{\varepsilon \to 0} \; \int \limits _{a+\varepsilon }^{c}f\left(x\right)\cdot dx +\mathop{\lim }\limits_{\delta \to 0} \; \int \limits _{c}^{b-\delta }f\left(x\right)\cdot dx $ — интеграл с особыми точками $x=a$ и $x=b$; $c$ — произвольная точка из интервала $\left(a,\; b\right)$.
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — что такое в Математической энциклопедии
— интеграл от неограниченной функции или от функции по неограниченному множеству. Пусть функция f определена на конечном или бесконечном полуинтервале , и для любого функция f интегрируема но Риману (по Лебегу) на отрезке Тогда предел
(в случае условие понимается как ) наз. несобственным интегралом
Если предел (1) существует, то говорят, что Н. и. сходится, если не существует — расходится. Напр., Н. и.при сходится, а при расходится. Если же , то
сходится при и расходится при .
Если и функция f интегрируема по Риману (по Лебегу) на отрезке [ а, b], то Н. и.(1) совпадает с определенным интегралом.
Аналогично при соответствующих предположениях определяют Н. и. по промежутку
Если функция/ интегрируема по Риману (по Лебегу) на каждом отрезке и существуют то Н. и.
определяется как сумма
и не зависит от выбора точки с.
Если на интервале ( а, b )имеется конечное число точек
: таких, что функция f интегрируема по Риману (по Лебегу) на каждом отрезке , не содержащем ни одной точки , и для каждого существуют Н. и.
то Н. и.
Это определение не зависит от выбора точек .
На Н. и. переносятся общие свойства интегралов: линейность, аддитивность относительно промежутков, по к-рым производится интегрирование, правило интегрирования неравенств, теоремы о среднем, интегрирование по частям и замены переменного, формула Ньютона — Лейбница. Напр., если функция f почти всюду на [ а, b )совпадает с производной функции F, к-рая абсолютно непрерывна на каждом отрезке то
Для выяснения сходимости Н. и. от знакопостоянных функций применяется признак сравнения: напр., для Н. и. вида (1) при выполнении условия
из сходимости Н. и.
следует сходимость Н. и.
функция наз. в этом случае функцией сравнения. В качестве функции сравнения для интегралов (1) в случае конечного предела интегрирования bчасто используются функции ; для интегралов вида (2) в случае конечности предела интегрирования а- функции , при наличии одного или двух бесконечных пределов интегрирования — функции . Из признака сравнения следует, напр., если для неотрицательной функции f, определенной при , существует предел
то при Н. и.
вида (1) сходится, а при Н. и. расходится.
Необходимое и достаточное условие сходимости Н. и. дает критерий Коши. Так, Н. и. вида (1) сходится тогда и только тогда, когда для любого существует такое что для всех выполняется неравенство
—
Н.
наз. абсолютно сходящимся, если сходится Н. и.
Если Н. и, абсолютно сходится, то он сходится и совпадает с интегралом Лебега. Существуют Н.
а для бесконечного:
Существуют различные признаки для установления сходимости Н. и. Так, если функции f и gопределены для , функция f имеет на полуоси ограниченную первообразную, a g- монотонная функция, стремящаяся к нулю при то Н. и.
сходится. Другой признак: если Н. и.
сходится, а функция gмонотонна и ограничена при , то Н. и.
сходится.
Сходимость Н. и. можно выразить в терминах сходящихся рядов: напр., для того чтобы Н. и. (1) сходился, необходимо и достаточно, чтобы для любой последовательности сходился ряд
причем в случае его сходимости сумма ряда совпадает с Н. и. (1).
Понятие Н. и. обобщается для функций многих переменных. Пусть функция f определена на открытом (ограниченном или неограниченном) множестве G n -мерного евклидова пространства и интегрируема по Риману на любом измеримом по Жордану множестве Функцию f наз. интегрируемой в несобственном смысле по множеству G, если для любой последовательности измеримых по Жордану множеств таких, что существует предел
не зависящий от выбора указанной последовательности . Этот предел, если он существует, наз. Н. и.
и, как в одномерном случае, говорят, что этот интеграл сходится. Он существует тогда и только тогда, когда существует интеграл
В этом случае Н. и.
совпадает с интегралом Лебега. Это обстоятельство связано с тем, что при n=1 и данном выше определении Н. и. переход к пределу осуществлялся по весьма специальному классу измеримых по Жордану множеств, а именно по отрезкам. В качестве же были взяты произвольные измеримые по Жордану множества. Впрочем, при сделанное утверждение остается в силе и в том случае, когда в качестве множеств взяты только измеримые по Жордану области. Таким образом, в этом случае понятие Н. и. не приводит к новому понятию по сравнению с интегралом Лебега.
Для Н. и. от функции многих переменных справедлив признак сравнения, аналогичный одномерному случаю. В качестве интегралов сравнения берут
где
Первый сходится при и расходится при , второй сходится при и расходится при .
К Н. и. относятся интегралы в смысле главного значения. Пусть функция f определена на открытом множестве , кроме, быть может, точки , и пусть для любого функция f интегрируема (по Риману или по Лебегу) на множестве есть -окрестность точки х. Тогда если существует предел
то его наз. интегралом в смысле главного значения и обозначают
Если интеграл
существует как Н. и., то он существует и в смысле главного значения. Обратное, вообще говоря, неверно. Напр., Н. и. расходится, а
Аналогично определяют интегралы в смысле главного значения в бесконечно удаленной точке.
Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, т. 2, М., 1973; [2] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975.
Л. Д. Кудрявцев.
 ,
, ,
,