Урок 6. прямоугольник. ромб. квадрат — Геометрия — 8 класс
Понятие прямоугольника всем знакомо с начальной школы. Прямоугольник – это параллелограмм, у которого все углы прямые. Прямоугольник обладает всеми свойствами параллелограмма:
— противоположные стороны равны и параллельны;
— противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180°;
— особо можно выделить, что все углы равны;
— диагонали пересекаются и точкой пересечения делятся пополам.
У прямоугольника есть особое свойство: диагонали прямоугольника равны.
| Элементы | Свойства от параллелограмма | Особое свойство |
|---|---|---|
| Стороны | Противоположные стороны равны и параллельны | |
| Углы | Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° | Все углы равны |
| Диагонали | Диагонали пересекаются и точкой пересечения делятся пополам | Диагонали равны |
Для доказательства рассмотрим прямоугольник ABCD с диагоналями AC и BD.

Прямоугольные треугольники ABD и DCA равны по двум катетам, т.к. AD – общий катет, AB = CD. Следовательно, AC = BD.
Для того, чтобы определить, является ли данный параллелограмм прямоугольником нужен признак прямоугольника. Он вытекает из особого свойства прямоугольника: если в паралеллограмме диагонали равны, то этот паралеллограмм – прямоугольник.
Рассмотрим параллелограмм ABCD с равными диагоналями AC и BD.
ABD и DCA равны по трем сторонам: AC = BD (по условию), AB = CD (свойство параллелограмма). AD – общая сторона. Следовательно, ∠BAD = ∠CDA, но ∠BAD + ∠CDA = 180° и ∠BAD = ∠ BCD, ∠CDA = ∠CDA, поэтому ∠BAD = ∠BCD = ∠CDA = ∠CDA = 90° значит, ABCD – прямоугольник.
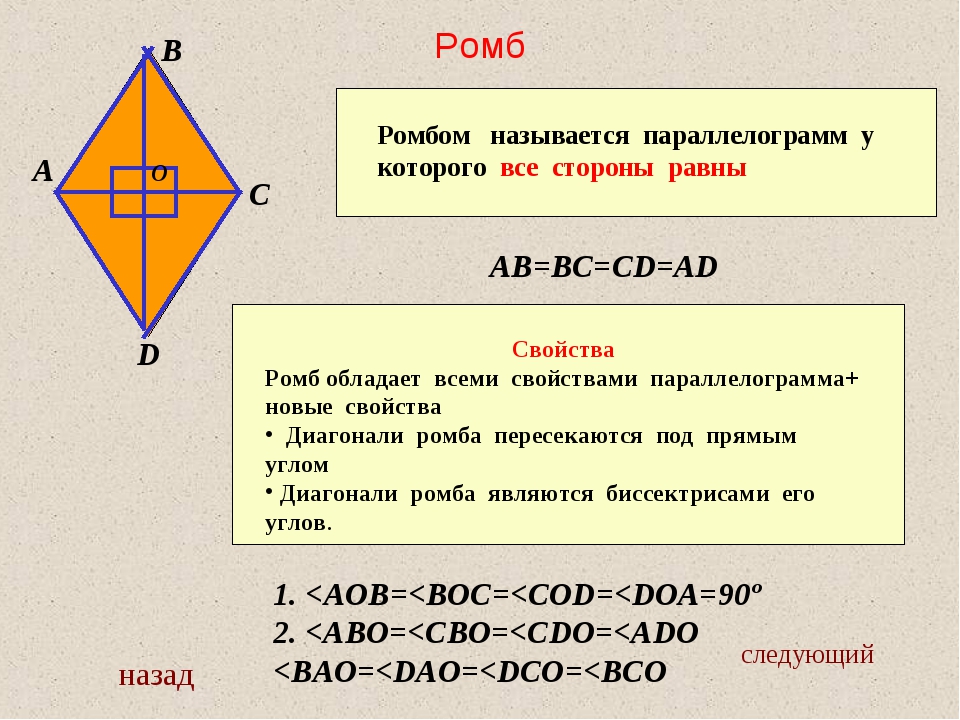
Параллелограмм, у которого все стороны равны, называется ромбом, он обладает всеми его свойствами, а из определения ромба следует, что все стороны равны.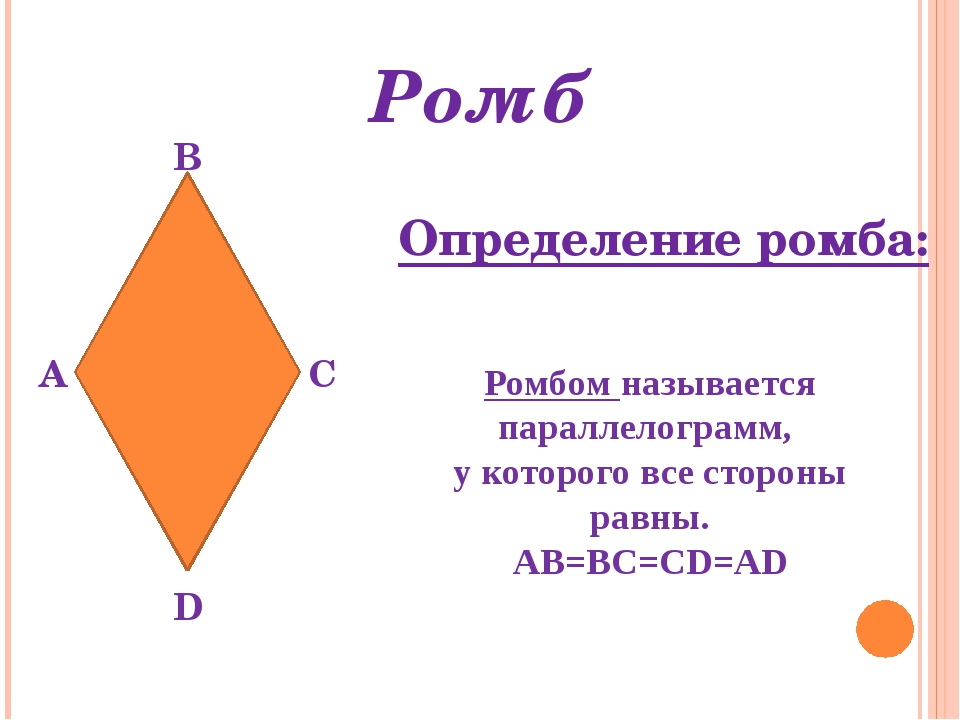
Ромб обладает и особым свойством: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
| Элементы | Свойства от параллелограмма | Особое свойство |
|---|---|---|
| Стороны | Противоположные стороны равны и параллельны | Все стороны равны |
| Углы | Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° | |
| Диагонали | Диагонали пересекаются и точкой пересечения делятся пополам | Диагонали взаимно перпендикулярны и делят углы пополам |
Для доказательства особого свойства рассмотрим ромб ABCD с диагоналями AC и BD.
AB = AD (ромб). Треугольник ABD – равнобедренный, AO – медиана, а значит высота и биссектриса этого треугольника. Следовательно, AC ⊥ BD, AC – биссектриса ∠BAD.
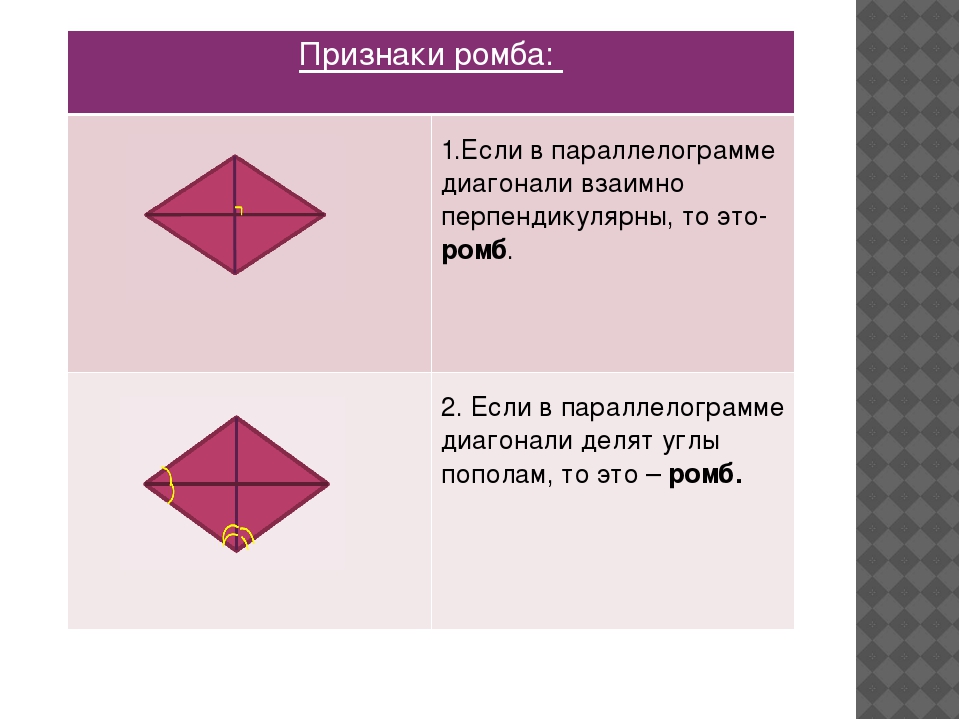
Признаки ромба получаются из особого свойства ромба:
— если диагонали параллелограмма взаимно перпендикулярны, то он является ромбом
— если диагональ параллелограмма является биссектрисой его угла, то он является ромбом.
Еще один знакомый с начальной школы четырёхугольник – это квадрат. Квадрат – это прямоугольник с равными сторонами или ромб с прямыми углами.
Ромб — что это такое, его свойства и признаки
Главная / ЧАстые ВОпросы15 января 2021
- Ромб — это…
- Признаки
- Свойства ромба
- Периметр
- Площадь ромба
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.
Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.
Ромб — это…
А вот как звучит официальное определение ромба:
Ромб – это геометрическая фигура, которая представляет собой особый вид параллелограмма (это как ?). И у него все стороны равны.
История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
И переводятся оба слова как «бубен».
Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.
И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.
Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.
Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.
Выглядит классический параллелограмм вот так:
Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.
В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.
Признаки ромба
Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:
- Все четыре стороны параллелограмма равны;
- Диагонали параллелограмма пересекаются под углом 90 градусов;
- Диагонали параллелограмма являются еще и биссектрисами.
И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.
Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:
На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.
Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.
Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).
Свойства ромба
А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:
- Диагонали ромба пересекаются между собой под прямым углом.
- Диагонали ромба также представляют собой и биссектрисы его углов.

И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:
Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.
Периметр ромба
Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.
В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:
Как несложно догадаться, буква «а» здесь – это длина стороны ромба.
Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.
Площадь ромба
Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.
Классическая формула для расчета площади ромба – через длины стороны и высоты.
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.
Она обозначается буквой «h» или «H» и выглядит вот так:
И наконец, формула для расчета площади ромба через сторону и высоту:
Есть и другие формулы для расчета площади ромба:
- Если известны диагонали:
- Если известны сторона и угол:
- Если известны угол и радиус вписанной окружности:
- Если известны сторона и радиус вписанной окружности:
Вот и все, что мы хотели рассказать о ромбе.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Ромб и его свойства — доказательство
- Главная
- Геометрия
- Свойства выпуклых многоугольников.
 Параллелограмм, прямоугольник, квадрат, ромб, трапеция
Параллелограмм, прямоугольник, квадрат, ромб, трапеция - Ромб и его свойства — доказательство

Ромб, проект по геометрии | Образовательная социальная сеть
Слайд 1
Ромб Работу сделала:Ересова Светлана Ученица 8 класса Рководитель : Ивашкевич Наталья МихайловнаСлайд 2
Ромб-это параллелограмм, у которого все стороны равны Определение
Слайд 3
Свойства ромба : 1)Противоположные стороны равны.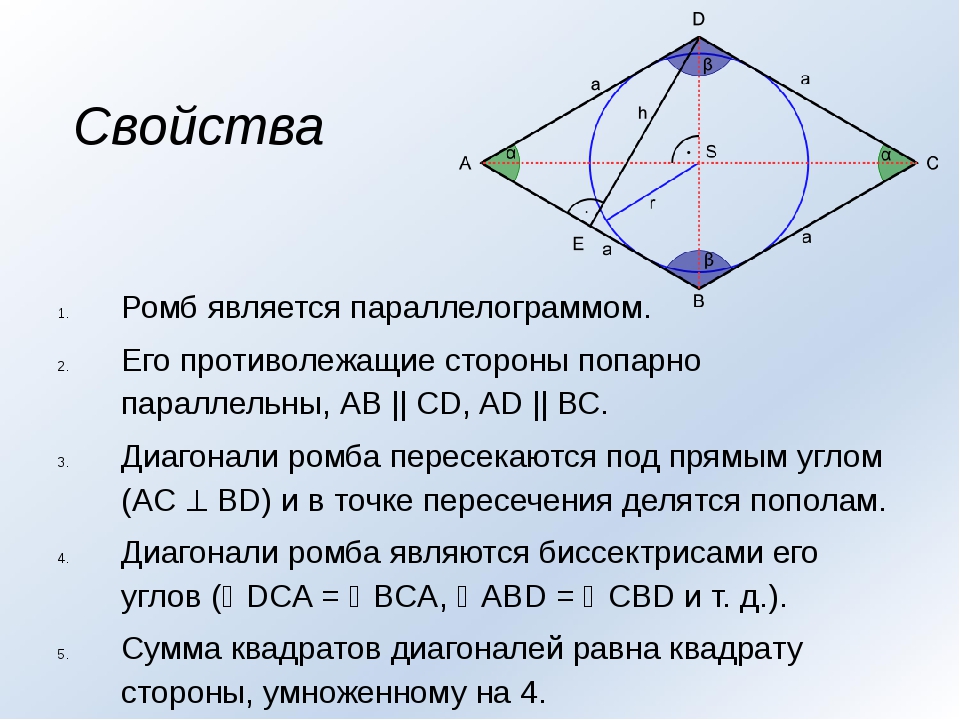 2)Противоположные углы равны. 3)Диагонали делятся пополам. 4)Диагонали перпендикулярны. 5)Диагонали делят углы пополам.
2)Противоположные углы равны. 3)Диагонали делятся пополам. 4)Диагонали перпендикулярны. 5)Диагонали делят углы пополам.
Слайд 4
Шуточные названия:
Слайд 5
Загадки: Если встали все квадраты На вершины под углом бы, То бы видели ребята Не квадраты мы, а.. Чуть приплюснутый квадрат. Приглашает опознать: Острый угол и тупой Вечно связаны судьбой. Догадались дело в чем? Как фигуру назовем? (Ромб)
Слайд 6
Другой вариант: Превращать его умеем — Две вершины отведем, И трапецию имеем! Не трапецию, так ромб Встал квадрат на уголок – Ткнулся носом в потолок. Вверх он рос еще дней пять. Как теперь его назвать? ( ромб ) Загадки:
Слайд 7
Стих: Ромб Квадрат обмяк, Устал. Дал за углы себя схватить И ромбом стал. И загрустил: А вдруг он промахнулся, А вдруг бы жизнь другим путем пошла, Подставь он Два других угла?..
Слайд 8
Квадрат, круг, ромб и треугольник вырезаны из белой, синей, красной и зеленой бумаги. Известно, что: круг не белый и не зеленый; синяя фигура лежит между ромбом и красной фигурой; треугольник не синий и не зеленый; квадрат лежит между треугольником и белой фигурой. Из зеленой бумаги вырезан: 1) круг; 2) квадрат; 3) ромб 4) треугольник; 5) круг или ромб. Задача Ответы: 1–2
Из зеленой бумаги вырезан: 1) круг; 2) квадрат; 3) ромб 4) треугольник; 5) круг или ромб. Задача Ответы: 1–2
Слайд 9
Задача У ромба ABCD диагональ BD равна 14 см, длина диагонали AC равна 48 см. Найти длину стороны АВ Решение . Поскольку диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам, то DO = OB = BD / 2 DO = OB = 24 см AO = OC = AC /2 AO = OC = 7 см Исходя из того, что диагонали ромба пересекаются под прямім углом, треугольники AOD и AOB — прямоугольные. Откуда AO 2 + OB 2 = AB 2 откуда 7 2 + 24 2 = AB 2 49 + 576 = 625 = AB 2 AB =25 см Ответ : 25 см
Слайд 10
Ромб является родоначальником множества символов характерных для геометрического орнамента. Ромбо-меандровый орнамент широко применялся при орнаментировании глиняной посуды, например для ритуальной посуды и пластики он являлся почти обязательным, сосуществуя с другими ритуальными символами.
Слайд 11
Символ «ромб». Считается установленным, что знак в виде ромба в народной и древней орнаментике происходит от условного изображения земельного участка и является символом земли. Соответствующий скифо-сарматский знак обозначает Солнце, Мировое Древо. В разные исторические эпохи ромб символизировал Великую богиню, родительницу всего сущего. В христианской иконографии ромб сочетался с изображением Богоматери. Исторические сведения
Соответствующий скифо-сарматский знак обозначает Солнце, Мировое Древо. В разные исторические эпохи ромб символизировал Великую богиню, родительницу всего сущего. В христианской иконографии ромб сочетался с изображением Богоматери. Исторические сведения
Слайд 12
В архитектурном декоре форма ромба встречается в оформлении наличников окон Ромб, как и меандр, один из древнейших орнаментальных мотивов. Изначально ромб использовался лишь для ограничения декрируемой поверхности, и в таком виде особо широко применялся в гончарных изделиях доисторического периода. Однако, с течением времени, в архитектуре, ромб стал играть самостоятельную декоративную роль. Главный «эмоциональный заряд», который можно обнаружить в ромбе,- это впечатление постоянно повторяющегося, замкнутого, движения. В отличие от квадрата, ромб не имеет статичной составляющей, и поэтому стал излюбленным в таких стилях, как Ренессанс, Неоклассицизм и, конечно, Барокко. В Средние века ромб успел стать ещё одним из геральдических символов Ромб в архитектуре
Слайд 13
Спасибо за внимание!!!
Место фотографии | |
Краткая характеристика: _________________________________________________________________________________________________________________________________________________________________________ _________________________________________________________ _________________________________________________________ _________________________________________________________ | |
Особые приметы: _______________________________________________________ _______________________________________________________ _________________________________________________________ ________________________________________________________ _________________________________________________________ _______________________________________________________ | Место печати |
Кем и когда выдан: ________________________________________________________ ________________________________________________________ _________________________________________________________ ________________________________________________________ ________________________________________________________ |
Типы четырехугольников. Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.
Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.
Различные типы четырехугольников имеют разные свойства, которые определяются различным соотношением сторон и углов четырехугольника. Вполне возможно иметь четырехугольник, в котором никакие две стороны и никакие два угла не совпадают. С другой стороны, любые две или более сторон могут быть равны по длине, а любые два или более углов могут быть одинаковой величины. Кроме того, одна или обе пары противоположных сторон могут быть параллельны. Многие конфигурации приводят к фигурам с определенными именами, и, по крайней мере, некоторые из этих имен, вероятно, вам знакомы. Примеры различных конфигураций показаны ниже, вместе с именем, котор дали к каждой форме и кратко описанием своих характеристик.
Квадрат- самый простой тип четырехугольника. Квадрат называется равносторонним, потому что все четыре стороны имеют одинаковую длину то есть квадрат является правильным многоугольником, и все четыре внутренних угла равны девяносто градусов. Диагонали в квадрате имеют одинаковую длину, пересекают друг друга перпендикулярно, то есть пересекаются под прямым углом. По определению квадрат- это тоже прямоугольник, параллелограмм и ромб .
Диагонали в квадрате имеют одинаковую длину, пересекают друг друга перпендикулярно, то есть пересекаются под прямым углом. По определению квадрат- это тоже прямоугольник, параллелограмм и ромб .
- Квадрат имеет четыре равные стороны и четыре прямых угла.
Прямоугольник — четырехугольник, где все четыре внутренних угла имеют прямые углы (т. е. девяносто градусов), только противоположные стороны имеют равную длину. Смежные стороны могут быть разной длины. По определению прямоугольник является и параллелограммом.
- Только противоположные стороны прямоугольника должны быть равны
Параллелограмм — обе пары противоположных сторон параллельны (отсюда и название), противоположные стороны равны, и противоположные углы равны по величине. Диагонали, хотя и одинаковой длины, когда параллелограмм представляет собой квадрат или прямоугольник, всегда разделяют друг друга.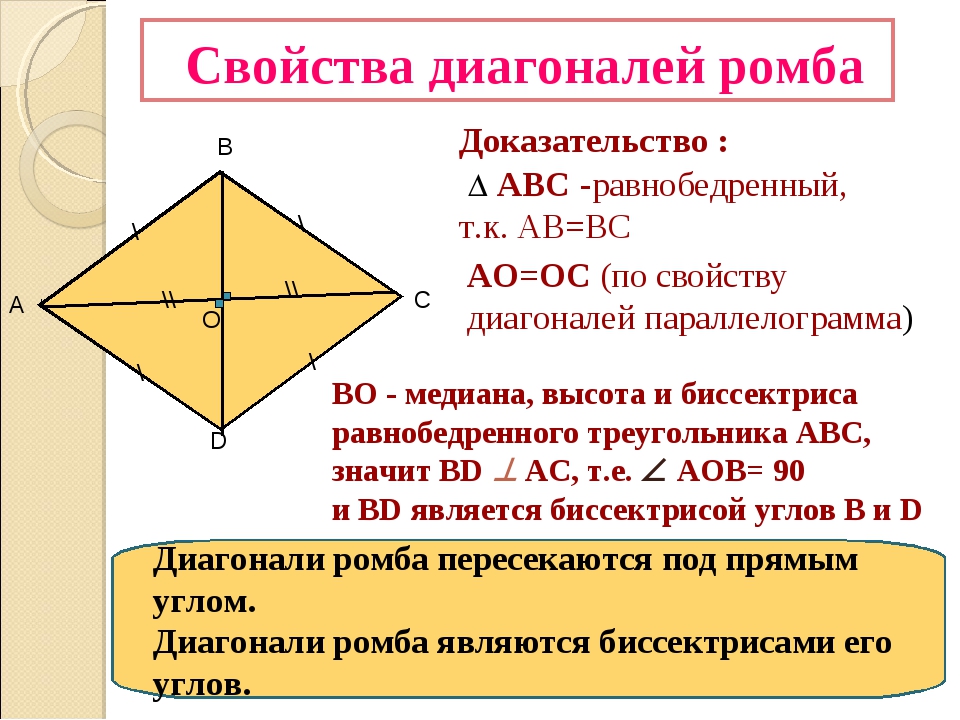 Диагональ разбивает параллелограмм на два равных треугольников. Последовательные углы являются дополнительными (т. е. они всегда составляют сто восемьдесят градусов). Обратите внимание, что параллелограмм, в котором смежные стороны имеют разную длину и в котором все внутренние углы наклонены, иногда называют ромбом (в отличие от ромба, который является параллелограммом, в котором все четыре стороны имеют одинаковую длину ).
Диагональ разбивает параллелограмм на два равных треугольников. Последовательные углы являются дополнительными (т. е. они всегда составляют сто восемьдесят градусов). Обратите внимание, что параллелограмм, в котором смежные стороны имеют разную длину и в котором все внутренние углы наклонены, иногда называют ромбом (в отличие от ромба, который является параллелограммом, в котором все четыре стороны имеют одинаковую длину ).
- Параллелограмм, показанный здесь, является ромбом
Ромб-ромб представляет собой равносторонний параллелограмм, т. е. имеет четыре стороны равной длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют равную величину, последовательные углы являются дополнительными (т. е. они составляют сто восемьдесят градусов), а диагонали разделяют друг друга. Диагонали ромба также рассекают внутренние углы и ортодиагональны (т. е. пересекаются под прямым углом).
- Ромб-равносторонний параллелограмм
Трапеция-это выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.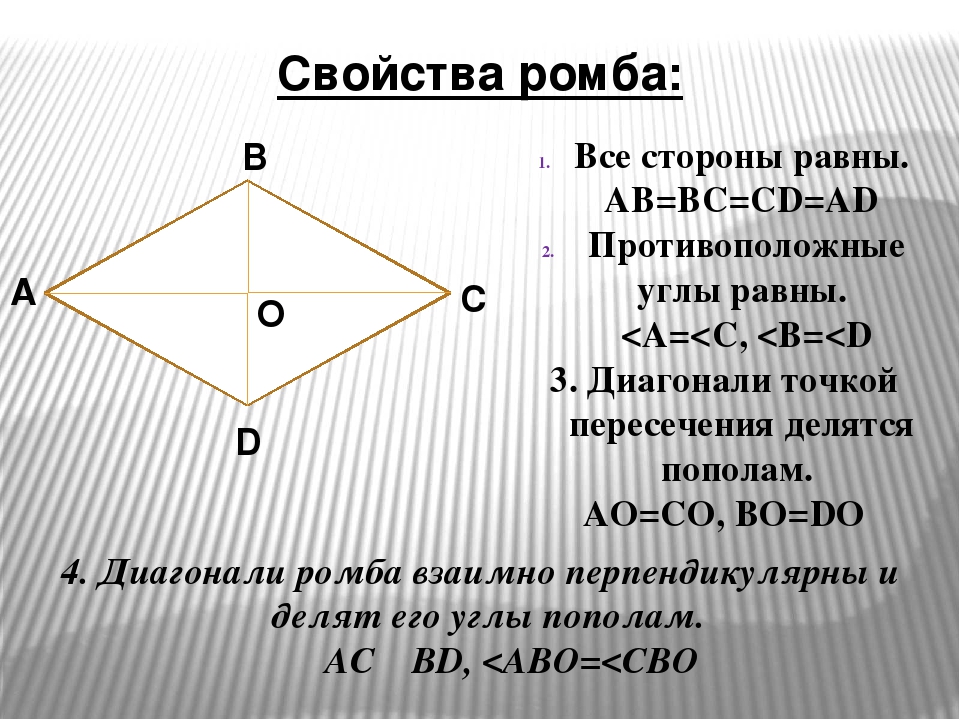 На рисунке ниже показаны три возможных варианта трапеции. На рисунке слева изображена равнобедренная трапеция, в которой углы, прилегающие к каждой из параллельных сторон равны. Центральная фигура имеет одну сторону, перпендикулярную обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. Последняя, самая правая, фигура имеет стороны разной длины, и все внутренние углы разные.
На рисунке ниже показаны три возможных варианта трапеции. На рисунке слева изображена равнобедренная трапеция, в которой углы, прилегающие к каждой из параллельных сторон равны. Центральная фигура имеет одну сторону, перпендикулярную обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. Последняя, самая правая, фигура имеет стороны разной длины, и все внутренние углы разные.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Ромб [wiki.eduVdom.com]
Ромбом называется параллелограмм, все стороны которого равны (рис.1).
Рис.1
Ромб обладает всеми свойствами параллелограмма.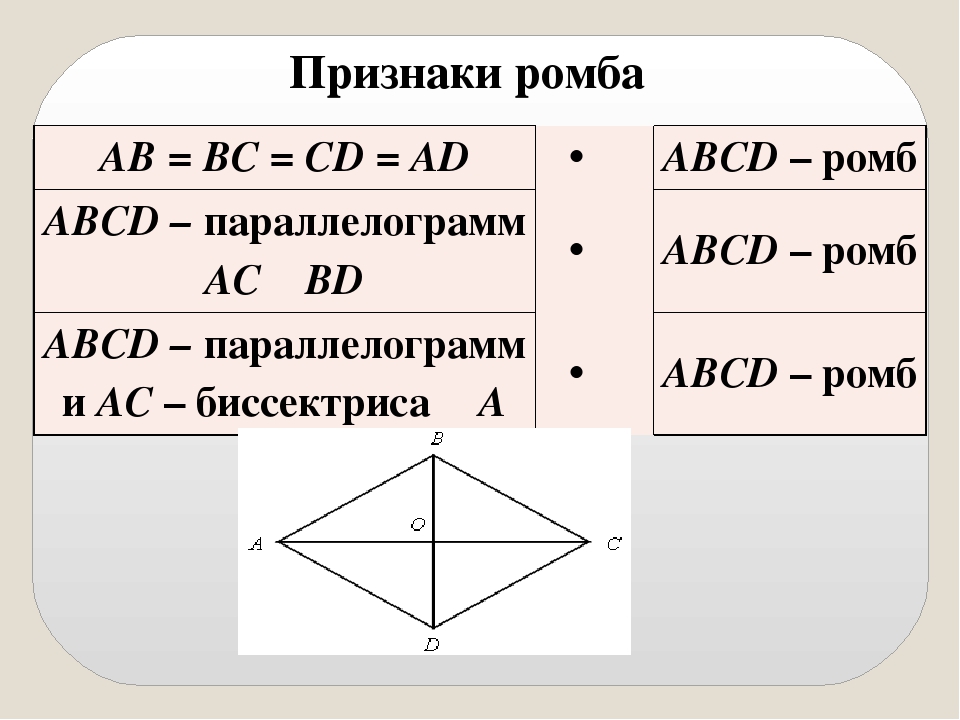
Рассмотрим особое свойство ромба.
Теорема 1. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Доказательство. Рассмотрим ромб ABCD (рис.2).
Рис.2
Требуется доказать, что АС ⊥ BD и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ∠ ВАС = ∠ DAC.
По определению ромба АВ = AD, поэтому треугольник BAD равнобедренный. Так как ромб — параллелограмм, то его диагонали точкой О делятся пополам. Следовательно, АО — медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому АС ⊥ BD и ∠ ВАС = ∠ DAC, что и требовалось доказать.
Пример 1. Определить углы ромба ABCD (рис.3) при условии, что его меньшая диагональ АС равна стороне ромба.
Рис.3
Решение. Так как по условию диагональ АС равна стороне ромба (а в ромбе все стороны равны), то треугольник ABC — равносторонний и, значит, ∠ ABC = 60°.
Тогда (теорема 1) ∠ BAD = 120°.
Наконец, по той же теореме ∠ D = ∠ B = 60° и ∠ BCD = ∠ BAD = 120°.
Так как по условию диагональ АС равна стороне ромба (а в ромбе все стороны равны), то треугольник ABC — равносторонний и, значит, ∠ ABC = 60°.
Тогда (теорема 1) ∠ BAD = 120°.
Наконец, по той же теореме ∠ D = ∠ B = 60° и ∠ BCD = ∠ BAD = 120°.
Пример 2. Сторона ромба составляет с его диагоналями два угла, из которых один больше другого на 50%. Вычислить углы ромба.
Решение. Пусть условию задачи удовлетворяет рисунок 2.
Рис.2
Обозначим градусную меру угла АВО через х, тогда ∠ ВАО = x + O,5 x = 1,5 x. В силу теоремы 1 треугольник АОВ — прямоугольный и, значит, откуда х = 36. Теперь согласно той же теореме имеем:
∠ ABC = 36° • 2 = 72° , следовательно, ∠ BAD = 180° — 72° = 108°.
Наконец, ∠ ADC = ∠ ABC = 72° и ∠ BCD = ∠ BAD = 108°.
Пример 3. Укажите номера верных утверждений.
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Треугольник со сторонами 1, 2, 4 существует.
Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
Видео-решение.
Ромб
(Перейти к области ромба или периметру ромба)
Ромб — это плоская форма с 4 равными прямыми сторонами.
Ромб похож на ромб
| Все стороны имеют одинаковую длину | |
| Противоположные стороны параллельны, а противоположные углы равны (это параллелограмм). | |
| Высота — это расстояние под прямым углом к двум сторонам | |
| И диагонали «p» и «q» ромба. разделите друг друга пополам под прямым углом. |
Играть ромбом:
Площадь ромба
Площадь можно рассчитать по:
- высота, умноженная на длину стороны:
Площадь = высота × с
- квадрат длины стороны (s 2 ), умноженный на синус угла A (или угла B):
Площадь = с 2 sin (A)
Площадь = с 2 sin (B)
- путем умножения длин диагоналей и последующего деления на 2:
Площадь = (p × q) / 2
Пример: ромб имеет диагонали 6 м и 8 м. Какова его площадь?
Какова его площадь?
Площадь = (6 м × 8 м) / 2 = 24 м 2
Если вы можете нарисовать свой ромб, попробуйте инструмент «Площадь многоугольника путем рисования».
Периметр ромба
Периметр — это расстояние по краям.
Периметр равен , в 4 раза умноженным на s (длина стороны) Периметр = 4s |
Пример: длина стороны ромба 12 см. Каков его периметр?
Периметр = 4 × 12 см = 48 см
Квадрат — это ромб?
Да, потому что квадрат — это просто ромб, в котором все углы прямые.
Другие названия
Эту форму чаще называют ромбом , но некоторые люди называют ее ромбом или даже ромбом .
Множественное число — ромбов или ромбов , и, реже, ромбов или ромбов (с двойной буквой b).
Название «ромб» происходит от греческого слова rhombos : кусок дерева крутился на веревке и издавал рев!
Что такое ромб? (Определение, Форма, Свойства) // Репетиторы.com
Содержание
- Ромб Определение
- Как построить ромб
- Как выглядит ромб?
- Различные названия для ромба
- Квадрат — это ромб?
- Форма ромба
- Свойства ромба
- Уголки ромбические
- Диагонали ромба
Определение ромба
Ромб представляет собой четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу.Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы квадраты. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда пересекают друг друга под прямым углом.
Как построить ромб
Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта. Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка.
Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка.
Положите четыре прямых предмета на плоскую поверхность так, чтобы их восемь концов соприкасались только в четырех местах. Вы не можете потерпеть неудачу в этом! Положите два предмета параллельно друг другу, но на небольшом расстоянии друг от друга. Если вы используете два других объекта для соединения конечных точек, у вас есть ромб!
Как выглядит ромб?
Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными). Ваш четырехугольник по определению должен быть ромбом!
Это означает, что каждый ромб равен:
- Фигурка плоская (двухмерная)
- Закрытая форма (имеет внутреннюю и внешнюю)
- Четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами)
Различные названия ромба
У ромба может быть три дополнительных имени:
- Ромб
- Пастилки
- Бриллиант
Ромб — это частный случай параллелограмма, потому что он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон. У него есть четыре стороны равной длины, но это все еще разновидность параллелограмма.
У него есть четыре стороны равной длины, но это все еще разновидность параллелограмма.
Каждый увиденный вами ромб также будет параллелограммом, но не каждый встречный параллелограмм будет ромбом.
Квадрат — это ромб?
Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат . Квадрат — это особый случай ромба, потому что у него четыре стороны равной длины, и он выходит за пределы и имеет четыре прямых угла.
Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом.
Форма ромба
В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, а нижняя сторона будет служить основанием фигуры.
Но будьте осторожны, потому что ромб может появиться в любой ориентации. Когда он «встает» и выглядит симметричным (его диагонали горизонтальны и вертикальны), его обычно называют ромбом.
Если вам сложно вспомнить его название, представьте себе квадрат, в который наехал автобус, так что он перевернулся (, наезд на на автобус … ромб).
Свойства ромба
Одной из двух характеристик, которые делают ромб уникальным, является то, что его четыре стороны равны по длине или совпадают. Другое отличительное свойство — параллельность противоположных сторон.
Если у вас есть четырехугольник только с одной парой параллельных сторон, у вас определенно нет ромба (потому что две его стороны не могут быть одинаковой длины).У вас трапеция .
Если у вас есть четырехугольник с двумя парами параллельных сторон, у вас не обязательно есть ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.
Уголки ромбические
В дополнение к этим четырем сторонам ромб имеет четыре внутренних угла. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).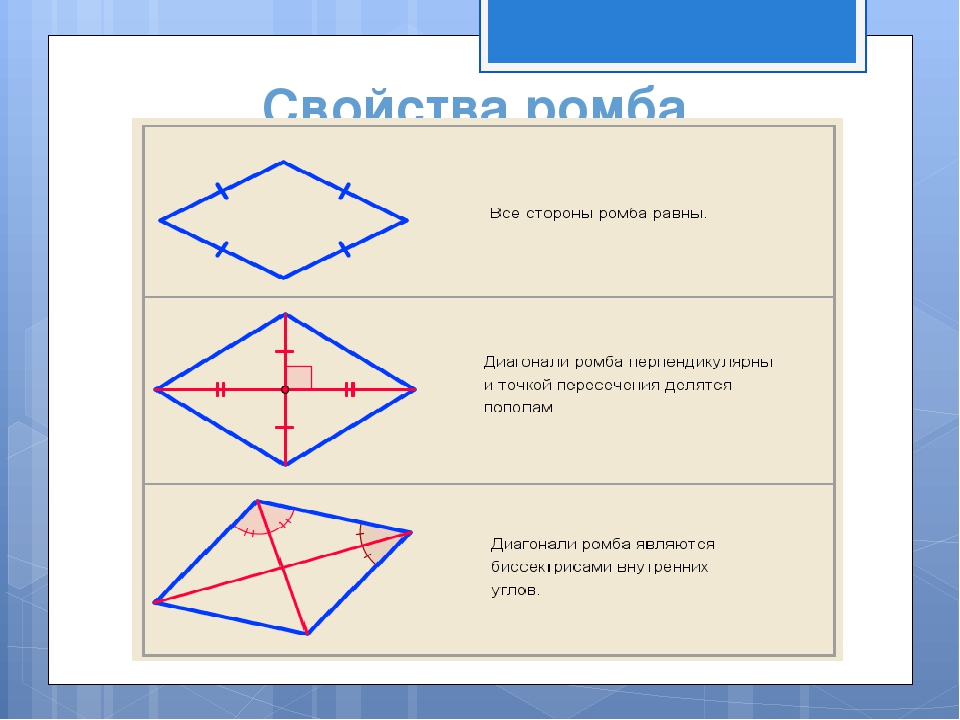
Неважно, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов.Начните сначала с двух ваших предметов, и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый (менее 90 °) угол. Используйте два других объекта, чтобы соединить два исходных объекта, вверх и вправо, чтобы сделать вашу четырехстороннюю (четырехугольную) плоскую фигуру — ромб.
Посмотрите на нижний левый угол и верхний правый угол. Они одинаковые. Они совпадают. Посмотрите на нижний правый угол и верхний левый угол: они совпадают. Противоположные внутренние углы ромба совпадают.
Четыре внутренних угла ромба в сумме всегда составляют 360 °.
Диагонали ромба
Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. Вы можете убедиться в этом сами, если сложите четыре прямых предмета так, чтобы получился ромб, а затем начертите диагонали. Независимо от того, под каким углом у вас четыре вершины ромба, диагонали ромба всегда расположены под прямым углом друг к другу.
Независимо от того, под каким углом у вас четыре вершины ромба, диагонали ромба всегда расположены под прямым углом друг к другу.
Эти диагонали тоже разрезают друг друга ровно пополам. Геометристы говорят, что они делят пополам друг друга.Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника.
Краткое содержание урока
Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы квадраты. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда пересекают друг друга под прямым углом.
Что вы узнали:
Посмотрев этот урок и прочитав о ромбе, вы узнаете, как эта плоская фигура вписывается в семейство плоских фигур, какие свойства делают ромб уникальным и как распознать ромб по двум его особым идентифицирующим свойствам.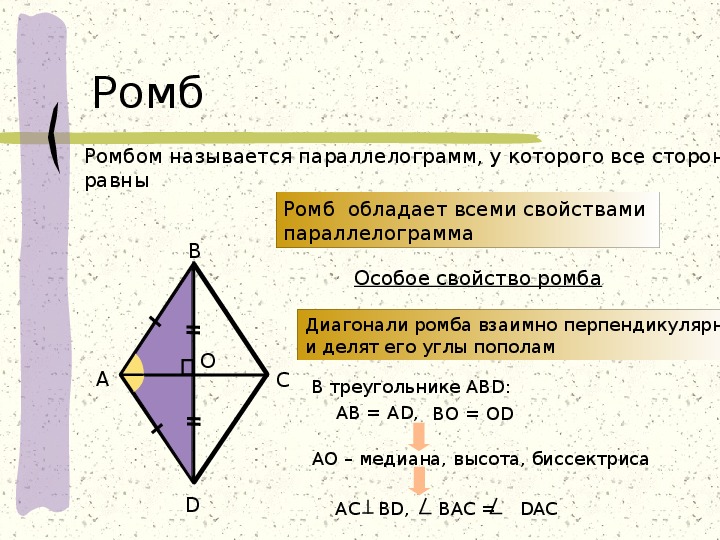
Следующий урок:
Как найти площадь ромба
Что такое ромб? — Определение и свойства — Класс геометрии (видео)
Посмотрите этот видеоурок, чтобы узнать, почему ромбы являются особым типом четырехугольника.Также узнайте, почему ромб — это еще и параллелограмм. Посмотрите, как мы исследуем стороны и углы ромба.
Что такое ромб?
Что такое ромб ? Это просто четырехсторонняя плоская форма, все стороны которой имеют одинаковую длину, а противоположные стороны параллельны. Попробуйте представить это в своей голове или, еще лучше, возьмите четыре зубочистки. Поставьте видео на паузу, если вам нужно время, чтобы достать зубочистки. Положите четыре зубочистки на ровную поверхность. Начните с перемещения двух зубочисток так, чтобы они были параллельны друг другу.Затем соедините две другие зубочистки так, чтобы она закрывала вашу форму. Возможно, вам придется переместить первую поставленную вами зубочистку, чтобы оставить место для боковых зубочисток.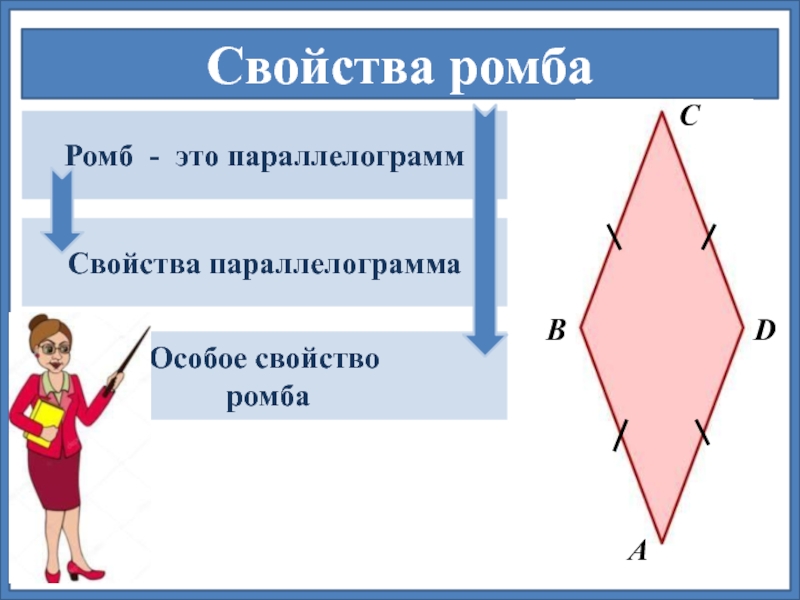 Только имейте в виду, что вы хотите, чтобы ваши стороны были параллельны друг другу.
Только имейте в виду, что вы хотите, чтобы ваши стороны были параллельны друг другу.
Поздравляем! Вы только что создали ромб! Вы видите, что все стороны одинаковой длины? Кроме того, вы видите, как противоположные стороны ромба параллельны друг другу? Попробуйте перемещать зубочистки, но держите стороны параллельно друг другу, а все концы касаются друг друга.Все остальные формы, которые вы придумываете, по-прежнему остаются ромбами.
A Четырехугольник
Все ромбы подпадают под категорию четырехугольников , плоскую форму с четырьмя сторонами. Особенность ромбов заключается в том, что все четыре стороны имеют одинаковую длину. Если вам дана длина только одной стороны ромба, то благодаря этому свойству вы также знаете размеры всех других сторон. Это отличительное свойство ромба.
Параллелограмм
Еще одним отличительным свойством ромба является то, что противоположные стороны параллельны друг другу.Из-за этих двух идентифицирующих свойств ромб также попадает в категорию параллелограмма , четырехгранной плоской формы, противоположные стороны которой параллельны и равной длины. Да, все ромбы — параллелограммы, но не все параллелограммы — ромбы. Это связано с тем, что определение параллелограмма более мягкое, чем определение ромба, поэтому вы можете иметь параллелограммы, у которых не все четыре стороны равны друг другу по длине.
Да, все ромбы — параллелограммы, но не все параллелограммы — ромбы. Это связано с тем, что определение параллелограмма более мягкое, чем определение ромба, поэтому вы можете иметь параллелограммы, у которых не все четыре стороны равны друг другу по длине.
Разблокировать содержимое
Более 83000 уроков по всем основным предметам Получите доступ без риска на 30 дней,
просто создайте аккаунт.
Нет обязательств, отменить в любой момент.
Хотите узнать больше?Выберите предмет для предварительного просмотра связанных курсов:
Angle Properties
Теперь давайте посмотрим на углы ромба. Как и все четырехгранные формы, у нашего ромба четыре угла. Видите ли вы что-нибудь уникальное в углах, когда вы перемещаете зубочистки в различные формы ромба? Вы могли заметить, что у вас всегда есть две пары противоположных углов, которые равны друг другу.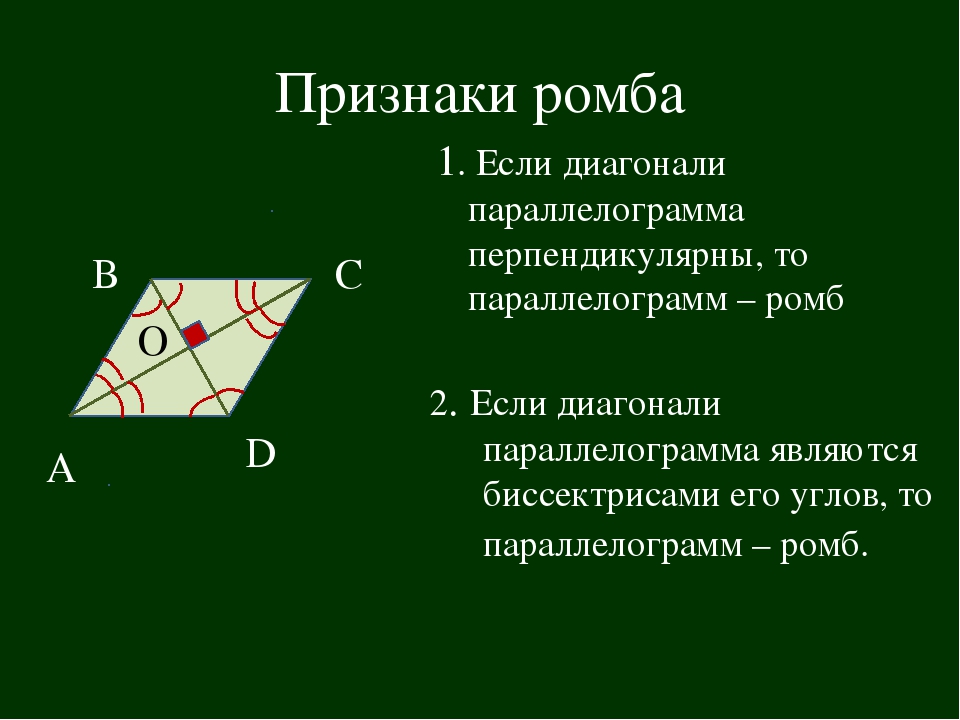 Если бы вы стояли спиной под одним углом и смотрели в сторону середины фигуры, противоположный угол — это угол прямо перед вами и тот, на который вы бы смотрели прямо. Глядя на различные формы ромбов ниже, можете ли вы заметить эти противоположные пары равных углов? Все ромбы обладают тем свойством, что противоположные углы равны друг другу.
Если бы вы стояли спиной под одним углом и смотрели в сторону середины фигуры, противоположный угол — это угол прямо перед вами и тот, на который вы бы смотрели прямо. Глядя на различные формы ромбов ниже, можете ли вы заметить эти противоположные пары равных углов? Все ромбы обладают тем свойством, что противоположные углы равны друг другу.
Еще одно свойство всех ромбов состоит в том, что если вы нарисуете диагонали, линии, соединяющие противоположные углы друг с другом, то точка пересечения диагоналей даст прямые углы.Кроме того, точка пересечения — это деление диагоналей пополам, а это означает, что точка пересечения оказывается средней точкой каждой диагонали.
Краткое содержание урока
Что мы узнали? Мы узнали, что ромбов — это четырехсторонние формы, все стороны которых равны друг другу, а противоположные стороны параллельны. Мы узнали, что эти формы также подпадают под категории четырехугольников , четырехсторонних плоских форм и параллелограммов , четырехсторонних плоских форм, противоположные стороны которых параллельны и равной длины.Тот факт, что ромб является четырехугольником и параллелограммом, не означает, что четырехугольник или параллелограмм является ромбом.
Мы узнали, что эти формы также подпадают под категории четырехугольников , четырехсторонних плоских форм и параллелограммов , четырехсторонних плоских форм, противоположные стороны которых параллельны и равной длины.Тот факт, что ромб является четырехугольником и параллелограммом, не означает, что четырехугольник или параллелограмм является ромбом.
Ромб имеет четыре равные стороны и две пары противоположных сторон, параллельных друг другу. Также есть две пары противоположных углов, которые равны друг другу. Когда вы рисуете две диагонали ромба, эти две диагонали делят друг друга пополам и образуют прямые углы в точке пересечения.
Результаты обучения
После этого урока вы должны уметь:
- Определить ромб
- Опишите свойства ромба
- Укажите, какое свойство является идентифицирующим свойством
Что такое ромб — определение, свойства и периметр
- Смежные углы в ромбе в сумме составляют 180 °.

- Диагонали пересекают друг друга под прямым углом.
- Все квадраты — ромбы, но не все ромбы — квадраты.
Решенные примеры на ромбе
Раджив нарисовал ромб, в котором длины двух диагоналей \ (d_1 \) и \ (d_2 \) ромба составляют 5 см и 10 см соответственно. Он просит свою сестру Лолу помочь ему найти этот район. Вы можете помочь Лоле найти ответ?
Решение
Дано:
Диагональ \ (d_1 = 5 \ text {см} \)
Диагональ \ (d_2 = 10 \ text {см} \)
| \ (A = \ dfrac {{d_1 d_2}} {2} \) |
\ (\ begin {align} A & = \ frac {{5 \ times 10}} {2} \\ A & = 25 \ text {sq.2 \ text {и} d_1 = 20 \ text {см} \)
\ (\ begin {align} A & = \ dfrac {{d_1 \ times d_2}} {2} \\ 100 & = \ dfrac {20 \ times {d_2}} {2} \\ d_2 & = 10 \ text {см} \ end {align} \)
| \ (\ следовательно \) \ (d_2 = 10 \ text {cm} \) |
Соня и Аман играли в классики, когда заметили на детской площадке плитку в форме ромба. Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки?
Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки?
Решение
Дано:
Длина стороны \ (= 15 \ text {см} \)
Поскольку все стороны ромба равны, все четыре стороны равны 15 см.
\ (Периметр = 4 \ times \ text {Side} = 4 \ times 15 = 60 \)
| \ (\ следовательно \) \ (\ text {Perimeter} = 60 \ text {cm} \) |
Размер острого угла ромба составляет половину его тупого угла.Найдите значение двух углов.
Решение
Дано:
Мы знаем, что тупой угол вдвое больше острого.
Из свойств ромба мы также знаем, что сумма двух смежных углов равна 180 °.
Итак, пусть острый угол будет \ (x \), а тупой угол будет \ (2x \)
\ (\ begin {align} x + 2x & = 180 \\ 3x & = 180 \\ x & = 180 \ div3 \\ x & = 60 \\ \ следовательно 2x & = 120 \ end {align} \)
| \ (\ следовательно \) 1 st угол \ (= 60 ^ \ circ \) и 2 nd угол \ (= 120 ^ \ circ \) |
В доме Аарава была крохотная кладовая в форме ромба с периметром 120 м. 2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
\ (\ begin {align} OB + OD & = BD \\ OB & = OD \\ \ поэтому 2OB & = BD \\ BD & = 2 \ times 10 \ sqrt {5} \\ BD & = 20 \ sqrt { 5} \\ \ end {align} \)
Часть 3
Теперь давайте вычислим площадь ромба, получив длину обеих диагоналей.
\ (\ begin {align} A & = \ dfrac {{d1 \ times d2}} {2} \\ A & = 20 \ sqrt {5} \ times {40} \ div {2} \\ A & = 400 \ sqrt {5} \ text {sq. M} \ end {align} \)
| \ (\ следовательно \) \ (A = 400 \ sqrt5 \ text {sq. M} \) |
Интерактивные вопросы о ромбе
Вот несколько упражнений для практики.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
- Параллелограмм называется ромбом, если его диагонали перпендикулярны друг другу.

- Две диагонали не равны по длине. Если они есть, то ромб — это квадрат.
Подведем итоги
Надеемся, вам понравилось изучать ромб с решенными примерами и интерактивными вопросами.Теперь вы легко сможете решать вопросы, связанные с ромбом.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению, обучению и обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Все ли квадраты ромбами?
Да, все квадраты ромбы. Фактически, вы даже можете назвать это очень частным случаем ромба. Как и у всех ромбов, все четыре стороны квадрата равны.
Как и у всех ромбов, все четыре стороны квадрата равны.
2. Какой формы ромб?
Ромб — это четырехугольник геометрической формы ромб. Люди говорят, что если вы посмотрите на колоду карт и вытащите 13 карточек с ромбами, геометрическая форма ромба будет иметь форму ромба.
3. Все ли ромбы прямоугольные?
Вы можете возразить, что все квадраты являются ромбами, и все квадраты также являются прямоугольниками, но означает ли это, что все ромбы являются прямоугольниками? Если вы сказали «да», тогда вам нужно будет рассмотреть некоторые действительно особые условия. Во-первых, помните, что все четыре стороны ромба равны. В случае прямоугольника дело обстоит иначе. Ромб станет прямоугольником только в том случае, если его свойства идентичны квадрату. Это потому, что все квадраты — ромбы.
4. Какова площадь ромба?
Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как:
\ (A = \ frac {{d_1 d_2}} {2} \)
Где d = — длина каждой диагонали
Что такое ромб — определение, свойства и периметр
- Смежные углы в ромбе в сумме составляют 180 °.

- Диагонали пересекают друг друга под прямым углом.
- Все квадраты — ромбы, но не все ромбы — квадраты.
Решенные примеры на ромбе
Раджив нарисовал ромб, в котором длины двух диагоналей \ (d_1 \) и \ (d_2 \) ромба составляют 5 см и 10 см соответственно. Он просит свою сестру Лолу помочь ему найти этот район. Вы можете помочь Лоле найти ответ?
Решение
Дано:
Диагональ \ (d_1 = 5 \ text {см} \)
Диагональ \ (d_2 = 10 \ text {см} \)
| \ (A = \ dfrac {{d_1 d_2}} {2} \) |
\ (\ begin {align} A & = \ frac {{5 \ times 10}} {2} \\ A & = 25 \ text {sq.2 \ text {и} d_1 = 20 \ text {см} \)
\ (\ begin {align} A & = \ dfrac {{d_1 \ times d_2}} {2} \\ 100 & = \ dfrac {20 \ times {d_2}} {2} \\ d_2 & = 10 \ text {см} \ end {align} \)
| \ (\ следовательно \) \ (d_2 = 10 \ text {cm} \) |
Соня и Аман играли в классики, когда заметили на детской площадке плитку в форме ромба. Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки?
Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки?
Решение
Дано:
Длина стороны \ (= 15 \ text {см} \)
Поскольку все стороны ромба равны, все четыре стороны равны 15 см.
\ (Периметр = 4 \ times \ text {Side} = 4 \ times 15 = 60 \)
| \ (\ следовательно \) \ (\ text {Perimeter} = 60 \ text {cm} \) |
Размер острого угла ромба составляет половину его тупого угла.Найдите значение двух углов.
Решение
Дано:
Мы знаем, что тупой угол вдвое больше острого.
Из свойств ромба мы также знаем, что сумма двух смежных углов равна 180 °.
Итак, пусть острый угол будет \ (x \), а тупой угол будет \ (2x \)
\ (\ begin {align} x + 2x & = 180 \\ 3x & = 180 \\ x & = 180 \ div3 \\ x & = 60 \\ \ следовательно 2x & = 120 \ end {align} \)
| \ (\ следовательно \) 1 st угол \ (= 60 ^ \ circ \) и 2 nd угол \ (= 120 ^ \ circ \) |
В доме Аарава была крохотная кладовая в форме ромба с периметром 120 м. 2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
\ (\ begin {align} OB + OD & = BD \\ OB & = OD \\ \ поэтому 2OB & = BD \\ BD & = 2 \ times 10 \ sqrt {5} \\ BD & = 20 \ sqrt { 5} \\ \ end {align} \)
Часть 3
Теперь давайте вычислим площадь ромба, получив длину обеих диагоналей.
\ (\ begin {align} A & = \ dfrac {{d1 \ times d2}} {2} \\ A & = 20 \ sqrt {5} \ times {40} \ div {2} \\ A & = 400 \ sqrt {5} \ text {sq. M} \ end {align} \)
| \ (\ следовательно \) \ (A = 400 \ sqrt5 \ text {sq. M} \) |
Интерактивные вопросы о ромбе
Вот несколько упражнений для практики.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
- Параллелограмм называется ромбом, если его диагонали перпендикулярны друг другу.

- Две диагонали не равны по длине. Если они есть, то ромб — это квадрат.
Подведем итоги
Надеемся, вам понравилось изучать ромб с решенными примерами и интерактивными вопросами.Теперь вы легко сможете решать вопросы, связанные с ромбом.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению, обучению и обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Все ли квадраты ромбами?
Да, все квадраты ромбы. Фактически, вы даже можете назвать это очень частным случаем ромба. Как и у всех ромбов, все четыре стороны квадрата равны.
Как и у всех ромбов, все четыре стороны квадрата равны.
2. Какой формы ромб?
Ромб — это четырехугольник геометрической формы ромб. Люди говорят, что если вы посмотрите на колоду карт и вытащите 13 карточек с ромбами, геометрическая форма ромба будет иметь форму ромба.
3. Все ли ромбы прямоугольные?
Вы можете возразить, что все квадраты являются ромбами, и все квадраты также являются прямоугольниками, но означает ли это, что все ромбы являются прямоугольниками? Если вы сказали «да», тогда вам нужно будет рассмотреть некоторые действительно особые условия. Во-первых, помните, что все четыре стороны ромба равны. В случае прямоугольника дело обстоит иначе. Ромб станет прямоугольником только в том случае, если его свойства идентичны квадрату. Это потому, что все квадраты — ромбы.
4. Какова площадь ромба?
Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как:
\ (A = \ frac {{d_1 d_2}} {2} \)
Где d = — длина каждой диагонали
Определение, формула, свойства и примеры
Практически каждый из нас знает, что Ромб — четырехугольник, и поэтому, как и другие четырехугольники, такие как квадрат, прямоугольник и т. Д., имеет четыре вершины и четыре ребра, охватывающие четыре угла. Тем не менее, это еще не все. Об этой удивительной двумерной фигуре, которая играет важную роль в математике, одном из основных предметов, которые сопровождают нас от школы до высшего образования, можно узнать гораздо больше. Итак, давайте познакомимся со всеми ключевыми аспектами Rhombus.
Д., имеет четыре вершины и четыре ребра, охватывающие четыре угла. Тем не менее, это еще не все. Об этой удивительной двумерной фигуре, которая играет важную роль в математике, одном из основных предметов, которые сопровождают нас от школы до высшего образования, можно узнать гораздо больше. Итак, давайте познакомимся со всеми ключевыми аспектами Rhombus.
Определение ромба
В евклидовой геометрии ромб — это особый тип четырехугольника, который выглядит как параллелограмм, диагонали которого пересекаются друг с другом под прямым углом, т.е.е., 90 градусов. Поскольку форма ромба такая же, как у алмаза, он также известен как алмаз. Ромбовидная фигура в игральных картах — один из лучших образцов ромба. Более того, возможно, все ромбы являются воздушными змеями и параллелограммами, но если все углы ромба равны 90 °, то это квадрат.
Другими словами, ромб — это особый тип параллелограмма, в котором противоположные стороны параллельны, а противоположные углы равны.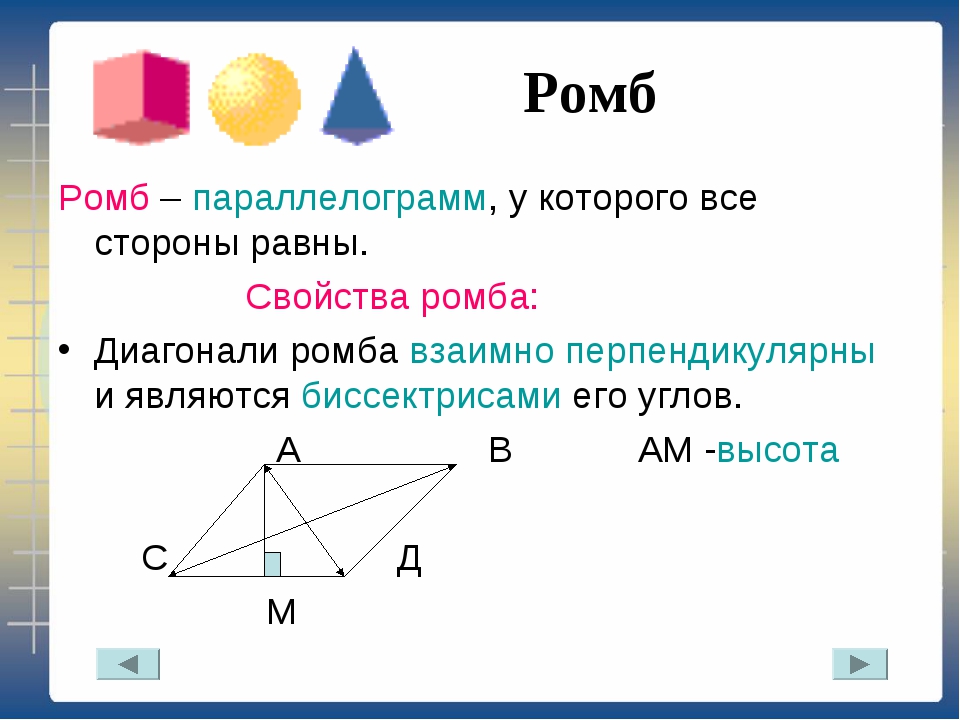 Помимо четырех сторон равной длины, у ромба есть диагонали, которые делят друг друга пополам под углом 90 градусов, т.е.е., прямые углы.
Помимо четырех сторон равной длины, у ромба есть диагонали, которые делят друг друга пополам под углом 90 градусов, т.е.е., прямые углы.
На рисунке ниже показан ромб ABCD с четырьмя равными сторонами — AB, BC, CD и AD, а также две диагонали AC и BD, пересекающиеся друг с другом под прямым углом.
Теперь, посмотрев на приведенный выше рисунок и прочитав информацию, упомянутую выше, вы можете немного запутаться в том, является ли ромб квадратным и наоборот или нет. Если да, не волнуйтесь, вот подходящее решение для вас.
Квадрат — это ромб?
Квадрат — это четырехугольник, у которого все стороны равны по длине, как и ромб.Кроме того, две диагонали квадрата перпендикулярны друг другу и делят пополам противоположные углы, как и ромб. Отсюда ясно, что квадрат — это ромб. С другой стороны, поскольку основное свойство квадрата гласит, что все его внутренние углы являются прямыми углами, ромб не считается квадратом, если все внутренние углы не равны 90 °.
Углы ромба
В любом ромбе есть четыре угла, из которых противоположные равны друг другу. Причем ромб состоит из диагоналей, которые пересекают друг друга под прямым углом.Другими словами, мы можем сказать, что каждая диагональ ромба разрезает другую на две равные части, а угол, образованный в точках их пересечения, составляет 90 °. Диагонали также делят пополам противоположные углы ромба.
Формулы ромба
Формулы для любого ромба определены с учетом двух основных атрибутов, таких как площадь и периметр.
Площадь ромба
Площадь ромба относится к области, покрытой им в 2D-плоскости. Основываясь на этом определении, формула для площади ромба равна произведению его диагоналей, разделенных на 2, и может быть представлена как:
Площадь ромба (A) = (d1 x d2) / 2 квадратных единицы, где d1 и d2 — диагонали ромба
Периметр ромба
Периметр ромба определяется как общая длина его границ или сумма всех четырех его сторон. Следовательно, формула для периметра ромба может быть представлена как:
Следовательно, формула для периметра ромба может быть представлена как:
Периметр ромба (P) = 4 единицы, где «а» — сторона ромба.
Свойства ромба
А теперь взглянем на некоторые важные свойства ромба.
Все четыре стороны равны по длине
Противоположные стороны параллельны
Противоположные углы равны
Диагонали делят друг друга пополам под прямым углом, т.е.е., 90 градусов
Диагонали ромба делят пополам его противоположные углы
Сумма двух соседних углов является дополнительной, т.е. 180 °
В ромбе две диагонали образуют четыре прямоугольных треугольника, которые конгруэнтны друг другу
Соединяя середины сторон ромба, вы получите прямоугольник
Если соедините середины половин диагоналей, вы получите еще один ромб
не должно быть окружности, описывающей ромб
Внутри ромба не может быть вписывающего круга
Если более короткая диагональ ромба равна одной из его сторон, вы получите два равносторонних треугольника
Когда ромб вращается вокруг линии, соединяющей середины противоположных сторон в качестве осей вращения, получается цилиндрическая поверхность с вогнутыми конусами на оба конца сформированы.

Когда ромб вращается вокруг любой из его сторон в качестве осей вращения, образуется цилиндрическая поверхность с вогнутым конусом на одном конце и выпуклым конусом на другом конце.
Если ромб вращается вокруг своей длинной диагонали как оси вращения, то образуется твердое тело, к основанию которого прикреплены два конуса. В этом случае максимальный диаметр фигуры (сплошного) будет равен меньшей диагонали ромба.
Когда ромб вращается вокруг своей более короткой диагонали в качестве оси вращения, вы получите твердую форму с двумя конусами, прикрепленными к его основаниям.Максимальный диаметр полученного твердого тела в этом случае будет равен большей диагонали ромба.
Когда середины всех четырех сторон ромба соединятся друг с другом, вы получите прямоугольник, длина и ширина которого будут равны половине значения простой диагонали.
 Причем площадь образующегося в этом случае прямоугольника составит половину ромба.
Причем площадь образующегося в этом случае прямоугольника составит половину ромба.
Определение, формулы, относящиеся к ромбу с решенными примерами
Свойства ромба? : Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину.Это особый вид параллелограмма, диагоналей которого пересекаются друг с другом под углом °. Это одно из особых свойств ромба, которое очень помогает во многих математических вычислениях.
Ромб также называют ромбом из-за его ромбовидной формы. Некоторые примеры ромбов в нашей повседневной жизни включают воздушный змей, окна автомобиля, серьги в форме ромба , структуру здания, зеркала, ромбовидные карты в колоде карт и т. Д. В этой статье мы предоставили все важные свойства ромба вместе с формулами, относящимися к ромбу.Читай дальше что бы узнать!
Определение ромба: Характеристики ромба
Прежде чем обсуждать ромб, давайте разберемся, что такое четырехугольник . В геометрии четырехугольник определяется как замкнутая двумерная форма, имеющая четыре прямые стороны.
В геометрии четырехугольник определяется как замкнутая двумерная форма, имеющая четыре прямые стороны.
Сумма внутренних углов четырехугольника равна 360 °. В основном существует 6 типов четырехугольника:
- Параллелограмм
- Трапеция
- Квадрат
- Прямоугольник
- Воздушный змей
- Ромб
Ромб — это особый тип параллелограмма, все четыре стороны которого равны.Таким образом, его еще называют равносторонним параллелограммом .
В ромбе ABCD выше AB, BC, CD и AD — это стороны ромба, а AC и BD — диагонали. Длина AC и BD равна d1 и d2 соответственно. Две диагонали ромба пересекаются под прямым углом, как вы можете видеть на рисунке.
Некоторые характеристики ромба:
- У ромба противоположные стороны параллельны, а противоположные углы равны.
- Все стороны ромба равны по длине.
- Диагонали ромба пересекают друг друга под прямым углом.

- Форма множественного числа ромба — ромбы или ромбы.
Другие важные статьи по математике:
Свойства ромба
Свойства ромба для класса 9 — одна из самых важных тем для студентов CBSE Class 9 , поскольку их часто спрашивают на выпускном экзамене. Кроме того, мы включили свойства ромба для класса 8, чтобы все учащиеся 8 класса могли воспользоваться ими.Вы можете прочитать свойства здесь или загрузить их в формате PDF для автономного доступа.
Мы перечислили все важные свойства ромба в пунктах ниже:
- Все стороны ромба равны.
- Противоположные стороны ромба параллельны.
- Противоположные углы ромба равны.
- В ромбе диагонали пересекают друг друга под прямым углом.
- Диагонали делят пополам углы ромба. Это одно из важнейших свойств диагоналей ромба.
- Сумма двух смежных углов равна 180 °.
- Две диагонали ромба образуют 4 прямоугольных треугольника, совпадающих друг с другом.

- Линии симметрии ромба : В ромбе только две линии симметрии.
- Вращательная симметрия ромба : Ромб имеет вращательную симметрию 180 ° (порядок 2).
- Когда вы соединяете середину всех 4 сторон ромба, он образует прямоугольник. Длина и ширина прямоугольника будут составлять половину значения главной диагонали, так что площадь прямоугольника будет равна половине ромба.
- Вы получите еще один ромб, если соедините середины половины диагонали.
- У ромба нет описывающего круга.
- Кроме того, не может быть вписывающего круга внутри ромба.
- Когда более короткая диагональ равна одной из сторон ромба, образуются два равносторонних треугольника.
- Вы получите цилиндрическую поверхность с выпуклым конусом на одном конце и вогнутым конусом на другом конце, когда ромб вращается вокруг любой стороны в качестве оси вращения.
- У вас получится цилиндрическая поверхность с вогнутыми конусами на обоих концах, когда ромб вращается вокруг линии, соединяющей середины противоположных сторон в качестве оси вращения.

- Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб будет вращаться вокруг большей диагонали в качестве оси вращения. В этом случае максимальный диаметр твердого тела равен меньшей диагонали ромба.
- Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб будет вращаться вокруг более короткой диагонали в качестве оси вращения.В этом случае максимальный диаметр твердого тела равен большей диагонали ромба.
Получите формулы алгебры снизу:
Формулы ромба
Мы представили вам список всех формул ромба. Формулы доступны для площади, периметра, диагонали и стороны. Возьмите ромб ABCD:
. Стороны: AB, BC, CD и AD
Длина каждой стороны: a
Диагонали: AC, BD
Длина диагоналей : d1, d2
У нас есть следующие формулы:
| Площадь ромба | Площадь, A = (d1. d2) / 2 d2) / 2 |
| Периметр ромба | Периметр, P = 4a |
| Сторона ромба | Сторона, a = P / 4 |
| Диагональ ромба | Диагональ , d1 = 2 (A / d2) Диагональ, d2 = 2 (A / d1) |
Решенные задачи на ромбе
Здесь мы предоставили ответы на некоторые вопросы, связанные со свойствами ромба:
Q1: Каков периметр ромба, все стороны которого равны 8 см?
Решение : Сторона ромба = 8 см (Дано)
Так как все стороны ромба равны, следовательно,
Периметр = 4 x сторона
P = 4 x 8 см
= 32 см
Следовательно, периметр ромба ромб 32 см.
Q2: Найдите диагональ ромба, если его площадь составляет 121 см 2 , а длина большей диагонали равна 22 см.
Решение : Площадь ромба = 121 см 2 (дано)
d 1 = 22 см.
Площадь ромба, A = (d 1 xd 2 ) / 2, получаем
121 = (22 xd 2 ) / 2
121 = 11 xd 2
или 11 = d 2
Итак, длина другой диагонали составляет 11 см.
Q3: Найдите периметр следующего ромба:
Решение : Все стороны ромба совпадают, поэтому HO = ( x + 2). А поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. С помощью теоремы Пифагора получаем,
( HB ) 2 + ( BO ) 2 = ( HO ) 2
x 2 + (x +1) 2 = ( x + 2) 2
x 2 + x 2 + 2x + 1 = x 2 + 4x + 4
x 2 — 2x -3 = 0
Решая относительно x с использованием формулы квадратичного уравнения, получаем:
x = 3 или x = –1. Мы можем отклонить x = –1, поскольку сторона ромба не может быть отрицательной.
Мы можем отклонить x = –1, поскольку сторона ромба не может быть отрицательной.
∴ Сторона ромба = x + 2
= 5
Следовательно, периметр ромба HRMO составляет 5 x 4 единицы = 20 единиц.
Q4: длина двух диагоналей ромба d 1 и d 2 составляет 5 см и 14 см соответственно. Найдите его область.
Решение : Дано:
Диагональ d 1 = 5 см
Диагональ d 2 = 14 см
Площадь ромба, A = (d 1 xd 2 ) / 2 квадратных единицы
A = ( 5 x 14) / 2
A = 70/2
A = 35 см 2
Следовательно, площадь ромба = 35 квадратных единиц.
Практические вопросы о свойствах ромба
Здесь мы предоставили вам несколько практических вопросов, связанных с ромбом.
Q1: Если площадь ромба 48 см, 2 и одна из его диагоналей равна 5 см. Найдите его высоту. Найдите его высоту.Q2: ABCD представляет собой ромб, в котором высота от D до стороны AB делит AB пополам. Найдите значение угла A и угла B. Q3: Покажите, что площадь ромба равна половине произведения его диагоналей. Q4: Диагональ AC параллелограмма ABCD делит пополам угол A. Q5: Если длина каждой стороны ромба составляет 8 см, а один из его углов равен 60 °, то найдите длину диагоналей ромба. Q6: Ромбовидный лист с периметром 32 м и длиной одной диагонали 10 м окрашен с обеих сторон из расчета 5 за квадратный метр. Узнать общую стоимость покраски? Q7: Длина диагнозов ромба находится в соотношении 5: 4.Площадь ромба 2250 кв. См. Найдите сторону ромба. Q8: ABCD представляет собой ромб с точкой пересечения диагонали O и углом DAO = 45 °. Найдите угол DCO. Q9: Докажите, что диагональ ромба пересекает друг друга под прямым углом. Q10: Если ABCD представляет собой ромб и начинается от D, высота проводится до AB и пересекает AB пополам. Найдите углы ромба. |
Часто задаваемые вопросы о свойствах ромба
Вот некоторые из часто задаваемых вопросов:
Q1: Каковы основные свойства ромба? A: Основные свойства ромба следующие:
(i) Противоположные углы совпадают.
(ii) Диагонали пересекают друг друга под углом 90 градусов.
(iii) Диагонали делят пополам противоположные внутренние углы.
(iv) Соседние углы являются дополнительными.
A: Площадь ромба = (d1.d2) / 2, где d1 и d2 — длины диагоналей ромба
Периметр ромба = 4 x Сторона ромба
A: Да, геометрически квадрат также является ромбом, все внутренние углы которого равны 90 градусам.Однако обратное неверно. Ромб может быть квадратом, а может и не быть.
A: Противоположные углы ромба равны друг другу. Также диагонали ромба делят пополам внутренние углы.
Q5: Каковы свойства симметрии ромба?A: Ромб имеет 2 линии симметрии, которые разрезают его на две идентичные части. Линии симметрии ромба являются его диагоналями. Также ромб имеет вращательную симметрию.Ромб имеет вращательную симметрию 180 ° (порядок 2).
Q6: Сколько линий симметрии у ромба?A: Ромб имеет 2 линии симметрии. Диагонали ромба — это линии его симметрии.
Теперь вам предоставлена вся необходимая информация о ромбе и его свойствах. Практикуйте больше вопросов и овладевайте этой концепцией.
Студенты могут использовать NCERT Solutions для математики, предоставляемые Embibe для подготовки к экзаменам.
Надеемся, эта подробная статья вам поможет. Если у вас есть какие-либо вопросы по этой статье, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.

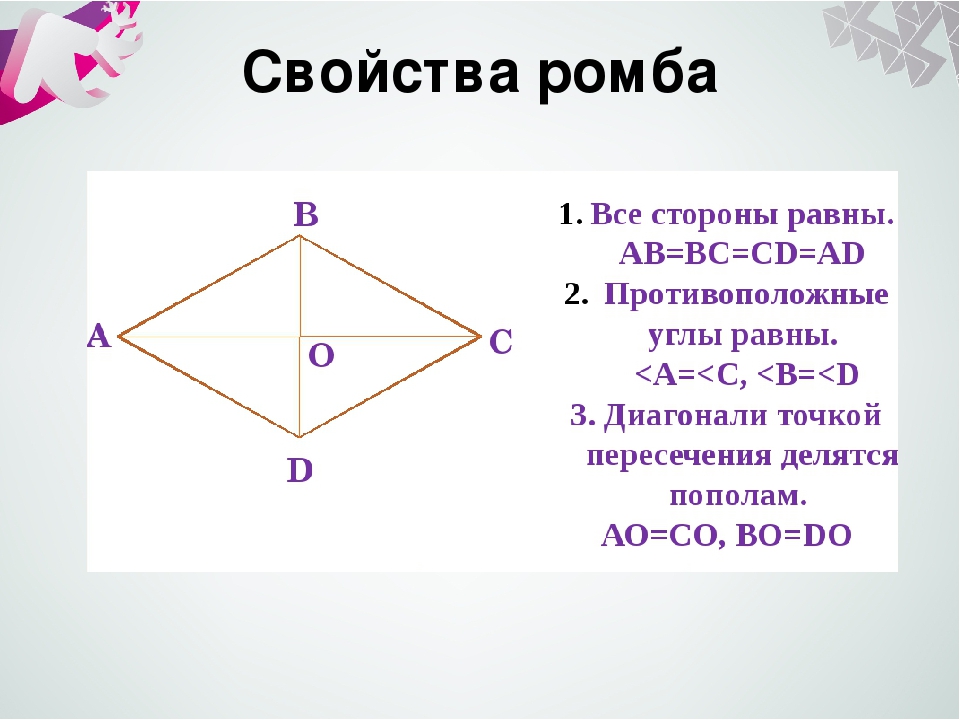 Параллелограмм, прямоугольник, квадрат, ромб, трапеция
Параллелограмм, прямоугольник, квадрат, ромб, трапеция

 Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.
Геометрия квадрат. Прямоугольник геометрии. Геометрия параллелограмм.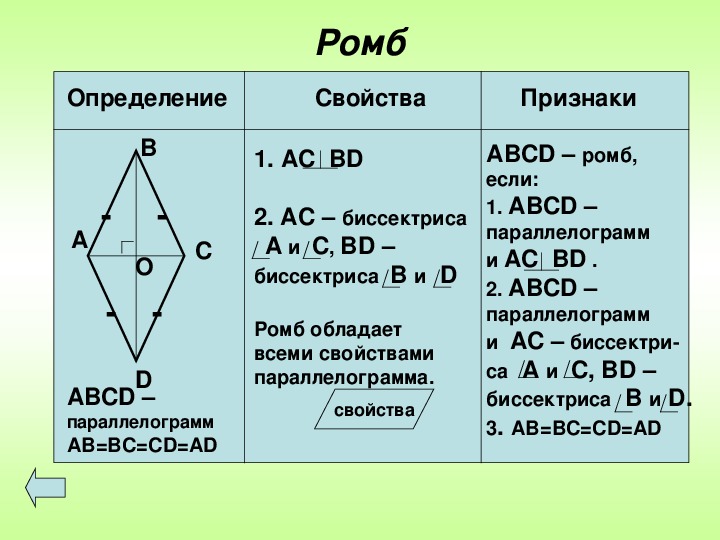
 Какова его площадь?
Какова его площадь? 




 Причем площадь образующегося в этом случае прямоугольника составит половину ромба.
Причем площадь образующегося в этом случае прямоугольника составит половину ромба.