Глава 2. Что такое тепло? – FIZI4KA

Ой, ребята, в свое время ученые головы себе сломали, раздумывая над этим вопросом!

Таких вопросов в истории науки было множество. Например, что такое время? Ну, в самом деле? Что такое вещество, мы понимаем, его можно потрогать, об него можно набить шишку. Ясно, что такое пространство. Это место, где вещество помещается. А вот что такое время? Что это за неуловимая субстанция такая?.. В этой книге мы ответим и на этот вопрос. А сейчас вернемся к теплу.

Вот лежит холодное тело. Мертвый мужик. Нет, лучше кирпич. Да, холодный кирпич. А рядом другой такой же кирпич, но теплый. Или даже горячий. Чем они отличаются?

Температурой, говорите вы?

А что это такое?

Состав вещества у кирпичей один. Свойства одинаковые – цвет, хрупкость, пористость, плотность, шершавость и т. д. Но один кирпич теплый, а другой холодный. Что такого есть в теплом кирпиче, что отличает его от холодного?

По простоте душевной ученые прежних времен предположили, будто теплота – это такая невидимая и невесомая жидкость, которая притекает в физическое тело. И чем ее больше притекло, тем горячее стало тело. Этой жидкости даже название дали – теплород, то есть рождающий тепло.

Вот какие фантазеры!

Но вы-то уже знаете, что такое тепло. Точнее, того, что вы уже знаете, вполне достаточно для ответа. Нужно только сделать одно маленькое усилие, чтобы догадаться.

Я вам помогу. Подтолкну, так сказать, на скользкую дорожку знаний.

Смотрите, мы нагреваем тело, то есть накачиваем в него тепло, и что же с ним происходит? Сначала тело расширяется. Почему? А все тела при нагревании расширяются, так как амплитуда, то есть размах колебаний, молекул этого тела увеличивается.

Потом тело постепенно нагревается до температуры плавления, тает, становится жидкостью, а затем, достигнув температуры кипения, и вовсе быстренько испаряется, превращаясь в газ. При этом мы уже знаем, что происходит с молекулами этого тела.

С повышением температуры они начинают двигаться все быстрее и быстрее и быстрее.

Если раньше в твердом теле они чуть шевелились, шлепая синими губами от холода, то потом ускорились настолько, что разломали всю кристаллическую структуру, в которой состояли. Как солдаты, отпущенные из строя, ломают строй, разбредаясь в разные стороны.

Вот почему тело при нагревании расширяется

Затем, по мере дальнейшего нагрева, молекулы становятся еще более активными и быстрыми. Им тесно в сумасшедшей толчее! Расстояние между молекулами растет. И в конце концов их скорости становятся такими большими, что пересиливают взаимное притяжение, самые шустрые улетают прочь, испаряясь. И в конце концов вся жидкость превращается в газ – ее молекулы разлетаются в разные стороны к чертовой матери.

Отсюда, кстати, понятно, почему летают воздушные шары, наполненные горячим воздухом. Потому что теплый воздух легче холодного! Что это значит? Это значит, что один объем теплого воздуха весит меньше, чем тот же объем воздуха холодного. Почему? А потому что в теплом воздухе скорости молекул и расстояния между молекулами больше, чем в холодном. При нагревании предметы расширяются, и газ – не исключение. Значит, в одном и том же объеме теплого воздуха помещается меньше молекул. Оттого и вес меньше.

Вот почему горячий воздух легче холодного – там вещества меньше! Или, иначе говоря, теплый воздух разряженнее.

А что происходит, когда мы даем телу тепло?

Что мы делаем? Мы разгоняем его молекулы, сообщая им все большую и большую скорость.

То есть что такое тепло? Тепло – это и есть скорость молекул, составляющих тело!

Еще раз: тепло – это средняя скорость движения частичек тела. Чем выше температура, тем выше скорость молекул.

В холодном кирпиче молекулы еле шевелятся. В горячем уже энергично пихаются и активно толкаются локтями. Вот именно эти толчки мы, приложив руку к кирпичу, ощущаем, как тепло. Поняли? Молекулы активно барабанят по нашей ладони, а мы думает, что это «тепло». Никакого отдельного от физического тела «тепла» нет. Оно всего лишь – наши ощущения от скорости движения его молекул.

Чем больше скорость колебания молекул, тем горячее нам кажется. А чем меньше – тем холоднее. Но тогда получается, что должна быть предельно низкая температура, ниже которой уже и быть не может – когда молекулы тела уже практически не дрожат, а замерли в оцепенении.

Именно так! Это для высокой температуры пределов практически нет – внутри Солнца, например, температура достигает 20 миллионов градусов – вот как быстро там носятся частицы. А для низкой температуры предел есть, он называется Абсолютным нулем температуры. Существует даже температурная шкала, названная по имени британского ученого шкалой Кельвина, которая начинает свой отсчет от абсолютного нуля. Абсолютный нуль Кельвина по привычной нам шкале Цельсия составляет минус 273 градуса. Ниже температур не бывает.

Ладно. А как передается тепло?

Ну, как мы нагреваем тело, то есть разгоняем его молекулы? Как мы сообщаем им дополнительную скорость? С помощью чего? С помощью другого нагретого тела, а как же иначе! То есть с помощью других энергичных молекул! Например, мы можем нагреть сковородку, поставив ее на горячую печку или раскаленную плиту. Мы можем нагреть холодный камень, положив его в горячую воду. Вода нагреет камень, а сама остынет. Их температуры сравняются. Это значит, что очень энергичные, то есть быстрые молекулы воды начинают барабанить по лежащему в воде камню. Точнее, по его еле шевелящимся холодным молекулам. И расталкивают их! При этом молекулы камня начинают двигаться быстрее (то есть камень нагревается), а молекулы воды «стынут», то есть начинают двигаться медленнее, поделившись с молекулами камня своим движением.

Другими словами, вода поделится с камнем своей энергией. И вскоре, как уже было сказано, температуры воды и камня выравняются. Это просто.

Но вы заметили, что я постепенно и незаметно ввел в оборот новое слово – «энергия»?

Это что еще такое?

Это весьма смутная категория в физике. И вместе с тем очень простая для понимания.

Думаю, интуитивно, что такое энергия, ясно каждому ребенку и в особых объяснениях не нуждается.

Мальчик бежит быстро, он весь красный и взъерошенный. Это очень энергичный мальчик! А вялый мальчик, который лежит на диване бледный, обладает низкой энергией. Ему нужно побольше каши есть, то есть подзарядиться слегка.

Если батарейка села, мы говорим, что энергия в ней кончилась.

Если мы разогнали тело до большой скорости – например, пулю, – то она стала высокоэнергичной и может пробить толстую доску. А пуля низкой энергии, то есть брошенная рукой, доску не пробьет. И газету может не пробить, если скорость низкая. Видите, энергия может быть связана со скоростью. Такая энергия называется кинетической (от греческого слова kinetikos – движение).

Автомобиль накапливает энергию для движения путем заполнения бака горючим. А почему оно называется «горючим»? Да потому что горит (окисляется, то есть химически реагирует с кислородом) и при этом выделяется много энергии. В бензине уйма энергии – если бензин сжечь, она высвободится в виде тепла и света. Это внутренняя, химическая энергия, запасенная внутри самого вещества. Вещество нужно разрушить, чтобы она высвободилась.

А еще энергия может быть связана с положением тела в пространстве. Часы с кукушкой видели? Они работают от гири с цепочкой. У вас есть такие часы? Если нет, это совершенно недопустимо, нужно непременно приобрести! Велите маме. Потому что это очень хорошие часы. Гирю поднимаешь, и она начинает постепенно опускаться. А цепочка, на которой висит гиря, медленно крутит шестерни часов. И они идут себе. Настоящее механическое чудо. Кукушка кукует. Плохо ли?

Когда гиря коснулась пола и опускаться ей больше некуда, часы, естественно, останавливаются. Но горевать не надо. Нужно просто потянуть за цепочку и поднять гирю снова. Что мы таким образом сделали с точки зрения энергетики? Запасли в гире энергию, изменив ее высоту. Если тело на высоте, оно в принципе может падать к земле. Значит обладает энергией. Какой? Такая энергия называется потенциальной, то есть возможной. Отпустим тело с высоты, чтобы оно падало, и этот потенциал реализуется – тело начнет набирать скорость и его потенциальная энергия будет переходить в кинетическую, то есть в скорость.

Выводы? Они прекрасны! И их два.

Первый. Энергия одних видов может переходить в другие, например, потенциальная в кинетическую, химическая в тепловую.

Второй. Энергию можно запасать. Поднял гирю – запас энергию.

Сжал пружину – запас энергию.

Зарядил аккумулятор – запас энергию.

Покушал – запас энергию в виде жира на боках.

Разогнал тело – придал ему энергию.

Значит, что такое энергия? Это некое свойство, способность тела совершить полезное действие, какую-то работу. Запустить ход часов, если это гиря. Вытолкнуть присоску на палочке из ствола детского пистолета, если это сжатая пружина. Зажечь лампочку, если это батарея или аккумулятор. Разогнать машину, если речь о бензине. Насытить хилого мальчика, придав ему скорость, если речь о пище.

Вот что такое энергия.

Ну, а если нужно что-то сделать, а энергии нету?

Идите ищите! Не будет энергии – не будет работы. Чудес не бывает. Сходите в магазин, купите аккумулятор. Постройте электростанцию. Разверните солнечную батарею. Поднимите гирю. Покушайте.

Но помните – за все за это придется заплатить. И за батарейку, и за еду из магазина. И за электричество в розетке. Даже на поднятие гири часов вы потратите свою личную энергию, которую получили из пищи. Совсем немножечко, но потратите.

Так уж устроен этот мир, что за все хорошее в нем приходится платить – за любое строительство, за любое созидание. Только за разрушение платить ничего не нужно: если опустить ручки и ничего не делать, все рано или поздно разрушится или испортится. Отчего это так, мы поймем позже. А пока нам нужно запомнить то, что все и так знают: энергия из ниоткуда не берется. Сколько позаимствовал, столько и потратишь, и ни капелькой больше.

А где позаимствовать? Где взять энергию? Откуда она вообще в природе берется?

Ну, за всю природу говорить пока рано, а вот откуда энергия на нашей планете, я скажу вам по секрету. В конечном счете от Солнца! Почти вся энергия, которой мы пользуемся – солнечная. Исключение – энергия земных недр, которую мы выковыриваем в виде полезных ископаемых. Например, топливо для атомных электростанций – ископаемый дар планеты. А вот энергия гидроэлектростанций имеет солнечную природу. Если б не было Солнца, все на планете вымерзло бы, не текли бы реки, а, значит, их течение не вращало бы турбины электростанций.

Энергия ветра, который крутит лопасти ветряков, – тоже солнечная в конечном итоге. Ведь Солнце нагревает атмосферу, отчего и случаются ветры, дожди, ураганы…

И пища, которую мы едим, – тоже дар звезды по имени Солнце. Потому как без света не могут расти растения, которые мы кушаем. Растениями питаются также животные, которых мы едим. Кушать было бы нечего без Солнца!

В Солнце энергии много, ее хватит еще на сотни миллионов лет, а там что-нибудь придумаем…

Про энергию мы еще поговорим. А сейчас я озвучу один хитрый вопрос, который должен был прийти вам в голову еще в прошлой главке.

Вот мы говорили о делимости вещества. Узнали, что все сложные вещества состоят из простых (элементарных). Простых веществ, которые еще называют химическими элементами, около сотни, и все они занесены в табличку Менделеева.

Самая маленькая частичка сложного (то есть сложенного из простых) вещества называется молекулой. И если молекулу разделить, получатся атомы уже совсем других веществ – те самые детальки мирового конструктора. У них уже совсем другие свойства: поваренная соль белая и полезная, а натрий и хлор, из которых сделана соль, очень даже агрессивные и ведут себя совершенно по-другому. Это понятно.

Но что будет, если попробовать разделить атом химического элемента, то есть детальку конструктора? Атом вообще делим?

Вот какой вопрос должен был прийти вам в голову. Приходил?

Глава 2. Что такое тепло?

5 (100%) 8 votes

fizi4ka.ru

ТЕПЛОТА — это… Что такое ТЕПЛОТА?

теплота́ — теплота, ы …   Русское словесное ударение

ТЕПЛОТА — ТЕПЛОТА, теплоты, мн. нет, жен. 1. отвлеч. сущ. к теплый в 1 знач. Теплота тела. Теплота воздуха. || Исходящее от чего нибудь тепло (см. тепло1 во 2 знач.). «Оно (солнце) своею теплотой огромные дубы и недра согревает.» Крылов. 2. перен. Доброе,… …   Толковый словарь Ушакова

теплота — ы; ж. 1. к Тёплый. Т. солнца, воды, воздуха. Т. дня. Т. рук. Т. шубы. Т. дома. Т. встречи. Т. души, взгляда, сердца. Любить теплоту. 2. = Тепло (1 2, 5 зн.). Лучистая т. Присутствие, наличие теплоты. Единицы измерения теплоты. Превращение… …   Энциклопедический словарь

Теплота — один из двух, известных современному естествознанию, способов передачи энергии мера передачи неупорядоченного движения. Количество переданной энергии называют количеством теплоты. В узком смысле о теплоте можно говорить как об энергии,… …   Википедия

ТЕПЛОТА — (количество теплоты) энергетическая характеристика процесса теплообмена, определяется количеством энергии, которое получает (отдает) тело (физическая система) в процессе теплообмена. Теплота функция процесса: количество сообщенной телу теплоты… …   Большой Энциклопедический словарь

Теплота — ж. 1. Форма движения материи, представляющая собою беспорядочное движение образующих тело микрочастиц (молекул, атомов, электронов и т.п.). отт. Энергия, создаваемая таким движением; теплота 1.. 2. Нагретое состояние кого либо или чего либо;… …   Современный толковый словарь русского языка Ефремовой

ТЕПЛОТА — ТЕПЛОТА, ы, жен. 1. см. теплый. 2. Форма движения материи беспорядочное движение частиц тела; энергетическая характеристика теплообмена, определяющаяся количеством энергии, к рое получает нагреваемое тело (отдает охлаждаемое тело) (спец.). Т.… …   Толковый словарь Ожегова

теплота — приветливость, мягкость, жар, тепло, нежность, ласковость, ласка Словарь русских синонимов. теплота сущ., кол во синонимов: 9 • жар (39) • ласка …   Словарь синонимов

ТЕПЛОТА — ТЕПЛОТА. Непосредственное ощущение позволяет различать холодные тела от теплых. Более точно можно определить состояние тела, используя изменения, которые испытывают вещества при действии теплоты: можно использовать расширение тел в зависимости от …   Большая медицинская энциклопедия

теплота — процесса; теплота Энергия, передаваемая одним телом другому при их взаимодействии, зависящая только от температуры этих тел и не связанная с переносом вещества от одного тела к другому. Энергия, передаваемая более нагретым телом менее нагретому,… …   Политехнический терминологический толковый словарь

polytechnic_dictionary.academic.ru

Теплота — Википедия. Что такое Теплота

Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой^[1]. Теплота — это одна из основных термодинамических величин в классической феноменологической термодинамике. Количество теплоты входит в стандартные математические формулировки первого и второго начал термодинамики.

Для изменения внутренней энергии системы посредством теплообмена также необходимо совершить работу. Однако это не механическая работа, которая связана с перемещением границы макроскопической системы. На микроскопическом уровне эта работа осуществляется силами, действующими между молекулами на границе контакта более нагретого тела с менее нагретым. Фактически при теплообмене энергия передаётся посредством электромагнитного взаимодействия при столкновениях молекул. Поэтому с точки зрения молекулярно-кинетической теории различие между работой и теплотой проявляется только в том, что совершение механической работы требует упорядоченного движения молекул на макроскопических масштабах, а передача энергии от более нагретого тела менее нагретому этого не требует.

Энергия может также передаваться излучением от одного тела к другому и без их непосредственного контакта.

Количество теплоты не является функцией состояния, и количество теплоты, полученное системой в каком-либо процессе, зависит от способа, которым она была переведена из начального состояния в конечное.

Единица измерения в Международной системе единиц (СИ) — джоуль. Как единица измерения теплоты используется также калория. В Российской Федерации калория допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность»

[2].

Определение

Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=A+ΔU{\displaystyle Q=A+\Delta U}. Здесь ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы, Q{\displaystyle Q} — количество теплоты, переданное системе, а A{\displaystyle A} — работа, совершённая системой. Однако определение теплоты должно указывать способ её измерения безотносительно к первому началу. Так как теплота — это энергия переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты.

Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y}, тело Y{\displaystyle Y} (пробное) заключено в жёсткую адиабатическую оболочку. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} также почти полностью заключено в адиабатическую, но не жёсткую оболочку, так что оно может совершать механическую работу, но обмениваться теплотой может лишь с Y{\displaystyle Y}.

Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в форме первого начала термодинамики:Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.

Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо^[3].

Неравенство Клаузиуса. Энтропия

Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N{\displaystyle N} бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный

круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале. Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре Ti{\displaystyle T_{i}}, количество теплоты Qi{\displaystyle Q_{i}}. Тогда верно следующее неравенство Клаузиуса:

∘∑i=1NQiTi⩽0.{\displaystyle \circ \sum _{i=1}^{N}{\frac {Q_{i}}{T_{i}}}\leqslant 0.}

Здесь ∘{\displaystyle \circ } обозначает круговой процесс. В общем случае теплообмена со средой переменной температуры неравенство принимает вид

∮⁡δQ(T)T⩽0.{\displaystyle \oint {\frac {\delta Q(T)}{T}}\leqslant 0.}

Здесь δQ(T){\displaystyle \delta Q(T)} — количество теплоты, переданное участком среды с (постоянной) температурой T{\displaystyle T}. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой

S=∫δQ(T)T,{\displaystyle S=\int {\frac {\delta Q(T)}{T}},}

dS=δQT.{\displaystyle dS={\frac {\delta Q}{T}}.}

Здесь T{\displaystyle T} — это абсолютная температура внешнего теплового резервуара. В этом смысле 1T{\displaystyle {\frac {1}{T}}} является интегрирующим множителем для количества теплоты, умножением на который получается полный дифференциал функции состояния.

Для неквазистатических процессов такое определение энтропии не работает. Например, при адиабатическом расширении газа в пустоту

∫δQ(T)T=0,{\displaystyle \int {\frac {\delta Q(T)}{T}}=0,}

однако энтропия при этом возрастает, в чём легко убедиться, переведя систему в начальное состояние квазистатически и воспользовавшись неравенством Клаузиуса. Кроме того, энтропия (в указанном смысле) не определена для неравновесных состояний системы, хотя во многих случаях систему можно считать локально равновесной и обладающей некоторым распределением энтропии.

Скрытая и ощущаемая теплота

Внутренняя энергия системы, в которой возможны фазовые переходы или химические реакции, может изменяться и без изменения температуры. Например, энергия, передаваемая в систему, где жидкая вода находится в равновесии со льдом при нуле градусов Цельсия, расходуется на плавление льда, но температура при этом остаётся постоянной, пока весь лёд не превратится в воду. Такой способ передачи энергии традиционно называется «скрытой» или изотермической теплотой^[4] (англ. latent heat), в отличие от «явной», «ощущаемой» или неизотермической теплоты (англ. sensible heat), под которой подразумевается процесс передачи энергии в систему, в результате которого изменяется лишь температура системы, но не её состав.

Теплота фазового превращения

Энергия, необходимая для фазового перехода единицы массы вещества, называется удельной теплотой фазового превращения^[5]. В соответствии с физическим процессом, имеющим место при фазовом превращении, могут выделять теплоту плавления, теплоту испарения, теплоту сублимации (возгонки), теплоту перекристаллизации и т. д. Фазовые превращения идут со скачкообразным изменением энтропии, что сопровождается выделением или поглощением тепла, несмотря на постоянство температуры.

О терминах «теплота», «количество теплоты», «тепловая энергия»

Многие понятия термодинамики возникли в связи с устаревшей теорией теплорода, которая сошла со сцены после выяснения молекулярно-кинетических основ термодинамики. С тех пор они используются и в научном, и в повседневном языке. Хотя в строгом смысле теплота представляет собой один из способов передачи энергии, и физический смысл имеет лишь количество энергии, переданное системе, слово «тепло-» входит в такие устоявшиеся научные понятия, как поток тепла, теплоёмкость, теплота фазового перехода, теплота химической реакции, теплопроводность и пр. Поэтому там, где такое словоупотребление не вводит в заблуждение, понятия «теплота» и «количество теплоты» синонимичны^[6]. Однако этими терминами можно пользоваться только при условии, что им дано точное определение, не связанное с представлениями теории теплорода, и ни в коем случае «количество теплоты» нельзя относить к числу первоначальных понятий, не требующих определения^[7]. Поэтому некоторые авторы уточняют, что во избежание ошибок теории теплорода под понятием «теплота» следует понимать именно способ передачи энергии, а количество переданной этим способом энергии обозначают понятием «количество теплоты»^[8]. Рекомендуется избегать такого термина, как «тепловая энергия», который по смыслу совпадает с внутренней энергией^[9].

Примечания

1. ↑ Сивухин, 2005, с. 57.
2. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Утверждено Постановлением Правительства РФ от 31 октября 2009 г. № 879.. Проверено 16 февраля 2014.
3. ↑ Сивухин, 2005, с. 58.
4. ↑ Путилов, 1971, с. 49.
5. ↑ Сивухин, 2005, с. 442.
6. ↑ Теплота / Мякишев Г. Я. // Струнино — Тихорецк. — М. : Советская энциклопедия, 1976. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 25).
7. ↑ Сивухин, 2005, с. 13.
8. ↑ Базаров, 1991, с. 25.
9. ↑ Сивухин, 2005, с. 61.

Литература

• Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с.
• Путилов К. А. Термодинамика. — М.: Наука, 1971. — 375 с.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: Физматлит, 2005. — 544 с. — ISBN 5-9221-0601-5.

wiki.sc

физическая теплота — это… Что такое физическая теплота?



Смотреть что такое «физическая теплота» в других словарях:

• физическая теплота — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN sensible heat …   Справочник технического переводчика

• физическая теплота — Syn: физическое тепло …   Металлургический словарь терминов

• теплота сгорания — [heat value] теплота горения, теплотворная способность, теплотворность, теплопроизводительность, калорийность количество теплоты, выделенное при полном cгании топлива; измеряется в Дж. Теплота сгорания единицы массы или объема топлива называют… …   Энциклопедический словарь по металлургии

• теплота образования — [formation heat] тепловой эффект реакции образования вещества из каких либо исходных веществ. Различают теплоту образования: из свободных атомов, теплоту образования из простых веществ, отвечающих наиболее устойчивым состоянием элементов при… …   Энциклопедический словарь по металлургии

• Теплота — [heat] количество теплоты энергия, получаемая или отдаваемая физической системой при теплообмене (при неизменных внешних параметрах системы: объеме, давлении и др.). Наряду с работой количество теплоты является мерой изменения внутренней энергии… …   Энциклопедический словарь по металлургии

• теплота фазового перехода — [phase transition heat] количество теплоты, которое необходимо сообщить веществу (или отвести от него) при равновесном изобарно изотермическом процессе его перехода из одной фазы в другую (фазовом переходе 1 го рода кипения, плавления,… …   Энциклопедический словарь по металлургии

• теплота плавления — [fusion heat] количество теплоты, необходимое веществу в равновесном изобарно изотермическом процессе для перехода из твердого (кристаллического) состояния в жидкое (то же количество теплоты выделяется при кристаллизации вещества). Теплота… …   Энциклопедический словарь по металлургии

• теплота испарения (парообразования) — [evaporation heat] количество теплоты, которое необходимо сообщить веществу в равновесном изобарно изотермическом процессе, чтобы перевести его из жидкого состояния в газообразное (то же количество теплоты выделяется при конденсации пара в… …   Энциклопедический словарь по металлургии

• ФИЗИЧЕСКАЯ ХИМИЯ — ФИЗИЧЕСКАЯ ХИМИЯ, «наука, объясняющая на основании положений и опытов физическую причину того, что происходит через хим. операции в сложных телах». Это определение, к рое ей дал первый физико химик М. В. Ломоносов в курсе, прочитанном …   Большая медицинская энциклопедия

• теплота — ы; ж. 1. к Тёплый. Т. солнца, воды, воздуха. Т. дня. Т. рук. Т. шубы. Т. дома. Т. встречи. Т. души, взгляда, сердца. Любить теплоту. 2. = Тепло (1 2, 5 зн.). Лучистая т. Присутствие, наличие теплоты. Единицы измерения теплоты. Превращение… …   Энциклопедический словарь

metallurgicheskiy.academic.ru

Глава 15. Тепловая энергия и работа: начала термодинамики – FIZI4KA

В этой главе…

• Достигаем теплового равновесия
• Сохраняем тепловую энергию при различных условиях
• Повышаем эффективность тепловых двигателей
• Падаем почти до абсолютного нуля

Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике.

Стремимся к тепловому равновесию: нулевое начало термодинамики

Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)

Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)

Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.

Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.

Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.

Сохраняем энергию: первое начало термодинамики

Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ​\( Q \)​, а сама система выполняет над окружающими телами работу ​\( W \)​ (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ​\( U_н \)​, становится равной \( U_к \) следующим образом:

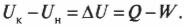
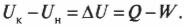
В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.

На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное \( Q \), то при отсутствии работы ее количество внутренней энергии, обозначаемое как \( U \), изменится на \( Q \). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия \( U \) изменится на \( W \). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.

Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.

Применяем закон сохранения энергии

Величина передаваемой тепловой энергии \( Q \) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы \( W \) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.

Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.

Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:

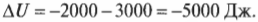
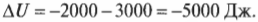
Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:

В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:

а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ​\( W \)​ считается отрицательным. Таким образом, получаем:

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.

В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).

Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.

Постоянное давление: изобарический процесс

Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.

Какую работу выполняет система при расширении газа? Работа равна произведению ​\( F \)​ на ​\( s \)​, означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ​\( P \)​ на ​\( A \)​, означающих, соответственно, давление и площадь. Это значит, что:

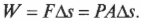
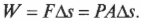
Но произведение площади \( A \) и перемещения \( s \) равно изменению объема ​\( \Delta\!V \)​. Таким образом:

Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ​\( W=P\Delta\!V \)​, то работа — это площадь, ограниченная графиком.

Допустим, имеется 60 м³ идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м³ (​\( PV= nRT \)​, где ​\( n \)​, ​\( R \)​ и ​\( Т \)​ означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:

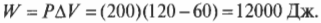
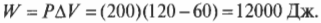
Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.

Постоянный объем: изохорический процесс

А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).

Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ​\( Fs \)​ (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.

Постоянная температура: изотермический процесс

В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как \( PV= nRT \) (см. главу 14), то температура также остается постоянной.

Какая работа выполняется при изменении объема? Поскольку \( PV= nRT \), то получается такое отношение между ​\( P \)​ и ​\( V \)​:

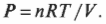
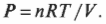
Эту формулу иллюстрирует график, показанный на рис. 15.6.

Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ​\( ln \)​ — натуральный логарифм, ​\( R \)​ — газовая постоянная (8,31), ​\( V_1 \)​ и ​\( V_0 \)​ означают, соответственно, конечный и начальный объем:

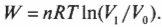
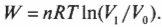
Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ​\( (3/2)nRT \)​ (см. главу 14), то эта энергия не меняется. Таким образом:

другими словами:

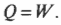
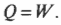
Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ​\( Q \)​, а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ​\( V_0 \)​ = 0,010 м³ до \( V_1 \)​ = 0,020 м³. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:

Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ​\( Q=W \)​, то добавляемая к газу тепловая энергия также равна 1690 Дж.

Постоянная энергия: адиабатический процесс

При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.

Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ​\( Q \)​ = 0, таким образом:

Так как внутренняя энергия ​\( U \)​ идеального газа равна ​\( (3/2)nRT \)​ (см. главу 14), то выполняется работа:

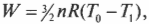
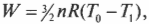
где ​\( T_0 \)​ и \( T_1 \) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).

Вычисляем удельную теплоемкость

Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:

Что такое ​\( \gamma \)​? Это отношение ​\( C_p/C_v \)​ двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ​\( C_p \)​, а в знаменателе — теплоемкость при постоянном объеме \( C_v \). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ​\( Q \)​, необходимой для изменения температуры тела единичной массы на величину ​\( \Delta T \)​, т.е. ​\( c=Q/m\Delta T \)​, где ​\( c \)​, ​\( m \)​ и \( \Delta T \) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ​\( C \)​ и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ​\( n \)​, а не массой ​\( m \)​:

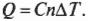
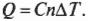
Как найти ​\( C \)​? Надо вычислить две разные величины: ​\( C_\mathrm{p} \)​ (при постоянном давлении) и \( C_\mathrm{v} \) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ​\( Q=\Delta U+W \)​. Поэтому достаточно только выразить ​\( \Delta U \)​ через ​\( T \)​. Выполняемая работа ​\( W \)​ равна ​\( P\Delta\!V \)​, тогда при постоянном объеме ​\( W \)​ = 0. А изменение внутренней энергии идеального газа равно ​\( (3/2)nR\Delta T \)​ (см. главу 14), поэтому ​\( Q \)​ при постоянном объеме выражается следующей формулой:

При постоянном давлении работа ​\( W \)​ равна \( P\Delta\!V \). А поскольку ​\( PV= nRT \)​, то ​\( W=P(V_1-V_0)=nR(T_1-T_0) \)​. Поэтому ​\( Q \)​ при постоянном давлении выражается следующей формулой:

Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ​\( Q=Cn\Delta T \)​, поэтому \( C=Q/n\Delta T \). Деля предыдущие две формулы на \( n\Delta T \), получаем:

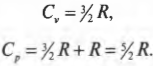
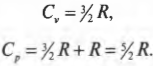
Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение ​\( \gamma \)​ равно отношению этих двух формул:

Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом:

Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление ​\( P_1 \)​? Путем простой алгебраической операции деления на ​\( V_1^{5/3} \)​ оставляем в левой части равенства только \( P_1 \)​ и получаем:

Подставив в эту формулу численные значения, получим:

Итак, новое давление должно быть равно 0,314 атмосферы.

Передаем тепловую энергию: второе начало термодинамики

Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.

Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.

Заставим тепловую энергию работать: тепловые двигатели

Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.

Оцениваем эффективность работы: КПД теплового двигателя

Тепловая энергия, подаваемая нагревателем, обозначается как ​\( Q_{нг} \)​, а отправляемая в холодильник (см. предыдущий раздел) — как ​\( Q_{\mathrm{x}} \)​. Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ​\( W \)​, выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:

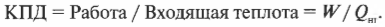
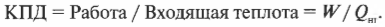
Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:

Это значит, что для записи КПД достаточно использовать \( Q_{нг} \) и \( Q_{\mathrm{x}} \):

Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·10⁷ Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ​\( W \)​ = 2,55·10⁷ Дж и

Это значит, что:

Количество входящей тепловой энергии равно 3,27·10⁷ Дж. А сколько тепловой энергии \( Q_{\mathrm{x}} \) остается неизрасходованной и отправляется в холодильник? Как известно:

поэтому:

Подставив в эту формулу численные значения, получим:

Количество тепловой энергии, отправляемое в холодильник, равно 0,72·10⁷ Дж.

Как сказал Карно: нельзя все тепло превратить в работу

Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.

А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.

Построение двигателя Карно

Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ​\( T_{нг} \)​. А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру \( T_{х} \). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):

А так как КПД теплового двигателя вычисляется по следующей формуле:

то получается такая формула для вычисления КПД двигателя Карно:

где температура выражается в кельвинах.

В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. \( T_{х} \) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.

Используем формулу Карно

Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:

Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:

Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.

Странные явления вблизи абсолютного нуля

Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!

(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)

Глава 15. Тепловая энергия и работа: начала термодинамики

Оценка

fizi4ka.ru