Урок 57. разные способы вычислений. проверка вычислений — Математика — 3 класс
Математика, 3 класс
Урок № 57. Разные способы вычислений.
Проверка вычислений
Перечень вопросов, рассматриваемых в теме:
Как выполнять устно вычисления в случаях, сводимых к действиям в пределах 1000, используя различные приёмы устных вычислений?
Как выбирать удобный способ?
Как выполнять проверку вычислений?
Глоссарий по теме:
Круглым называется число, которое делится на 10, 100, 1000 и так далее, без остатка.
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
единицы называют единицами 1-го разряда
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.
Сложение – арифметическое действие в математике, в результате которого два или более чисел объединяется в единое целое, оно обозначается знаком «+». Слагаемое, слагаемое, сумма – главные составляющие математического действия сложения.
Вычитание – арифметическое действие, обратное сложению и обозначается оно знаком «-». Уменьшаемое, вычитаемое, разность- главные составляющие математического действия вычитания.
Основная и дополнительная литература по теме урока:
Моро М.И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 68-69
Волкова С.И. математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018.С. 72-73
Рудницкая В.Н. Математика. Дидактические материалы. Ч.1. 3 кл. – М. «Вентана- Граф», 2016, с. 9-12
Теоретический материал для самостоятельного изучения
Вам уже знакомы приёмы устных вычислений в пределах 1000.
Но наша цель не просто узнать о них, а уверенно ими пользоваться.
Часто ученики допускают ошибки при решении примеров.
Сегодня мы более подробно остановимся на таких случаях и разберемся, как их избежать
Надеюсь, что после урока вы даже сможете посоревноваться с друзьями в устном счёте.
Вспомним приёмы устных вычислений, с которыми познакомились на прошлом уроке.
1 способ:
работаем с разрядными слагаемыми
2 способ:
работаем с общим количеством десятков.
Чтобы быстро и правильно решать такие примеры надо уметь выбирать более удобный способ.
А как выбрать удобный способ?
Решите примеры:
Выберем из этих примеров те, которые удобнее решать, работая с разрядными слагаемыми.
Согласитесь, что эти примеры будет легко решить, представив одно из слагаемых в виде суммы разрядных слагаемых.
Например: 420 + 50, десятки сложим с десятками и прибавим сотни, а при решении примера 320 + 500 сложим сотни и прибавим десятки.
Что же не так с остальными примерами?
Внимательно посмотри на числа. При выполнении действий с десятками происходит переход через разряд. Это вызывает затруднения.
Именно поэтому здесь удобнее воспользоваться вторым способом – работать с общим количеством десятков.
Рассмотрим первый пример: 150 — 90
Пользуясь первым способом, нам пришлось бы из 50 вычитать 90, а это невозможно.
Приходит на помощь второй способ:
15 дес. — 9 дес. это 6 дес. или 60. Никаких проблем.
Тоже самое с остальными примерами.
Но есть ещё одна опасность при решении подобных примеров на вычитание.
Рассмотрим два примера:
560 — 300 и 600 — 240.
Обрати внимание, в первом примере десятки в уменьшаемом, а во втором — в вычитаемом.
560 — 300
600 — 240
На это очень важно обращать внимание!
Понаблюдаем за решением.
560 — 300 = (500 — 300) + 60 = 260
600 — 240
= (600 — 200) — 40 = 360Заметили разницу?
В первом случае десятки прибавляем, а во втором вычитаем. Так как в первом случае вычитаем только сотни – 300, а во втором – сотни и десятки — 240
Так как в первом случае вычитаем только сотни – 300, а во втором – сотни и десятки — 240
Если же ты сомневаешься в результате или просто хочешь убедиться в правильности, можно выполнить проверку.
Проверка выполняется обратным действием. Сложение проверяем вычитанием и наоборот.
560 — 300 = 260
Проверка: 260 + 300 = 560
600 — 240 = 360
Проверка: 360 + 240 = 600
Сегодня мы раскрыли вам секреты приёмов устного сложения и вычитания.
Пользуйтесь ими и удачи!
Задания тренировочного модуля:
- Распределите карточки с примерами на две группы по более удобному способу решения.
Варианты ответов:
Правильные ответы:
Правильный вариант:
- Ученик решил примеры. Выберите отметку, которую он получил за работу.
420 + 500 = 920
830 — 200 = 630
240 + 60 = 300
650 + 50 = 700
560 — 100 = 340
Критерии оценивания:
без ошибок «5»
1 ошибка – «4»
2 ошибки – «3»
3 и более ошибок – не справился
Правильные ответы
без ошибок «5»
1 ошибка – «4»
2 ошибки – «3»
3 и более ошибок – не справился
Алгебра. Урок 1. Числа и вычисления
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Действия с дробями
Действия со степенями
Примеры решений заданий из ОГЭ
Понятие обыкновенной, десятичной, смешанной дроби.
Обыкновенная дробь – дробь вида
ab
где число a – числитель дроби, число b – знаменатель.
Примеры:

Обыкновенная дробь может быть правильной или неправильной, сократимой или несократимой:
Дробь называется правильной, если числитель (a) меньше знаменателя (b).
Примеры:
Дробь называется неправильной, если числитель (a) больше знаменателя (b).
Примеры:
Основное свойство обыкновенной дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число (натуральные числа – числа, которые используются при счете: 1, 2, 3, …), то получится дробь, равная данной.
Дробь называется сократимой, если числитель и знаменатель имеют общие множители (числитель и знаменатель можно поделить на одно и то же число).
Примеры сократимых дробей:
1216=3?44?4=34
2114=3?72?7=32
Дробь называется несократимой, если числитель и знаменатель дроби не имеют общих множителей.
Примеры несократимых дробей:
25;911;125126.
Дробь называется смешанной, если у нее есть целая часть. То есть саму дробь можно представить в виде суммы целого числа и обыкновенной дроби.
Примеры смешанных дробей:
312;278;901277.
Смешанную дробь всегда можно перевести в неправильную обыкновенную дробь.
312=3⋅2+12=72
278=2⋅8+78=238
901277=90⋅77+1277=694277
Дробь называется десятичной, если она представлена в десятичной записи.
Примеры десятичных дробей:
56,002; 4,125; 12,3; 0,01.
Десятичную дробь всегда можно перевести в смешанную дробь или в обыкновенную дробь с числителем и знаменателем. Так поступают, когда необходимо совершить действие между обыкновенной дробью и десятичной.
Перевод в смешанные дроби:
56,002=5621000=561500
56,002=5621000=561500
Перевод в обыкновенные дроби:
12,3=12310=12⋅10+310=123100,01=1100
Сложение и вычитание дробей.
Для того, чтобы складывать и вычитать смешанные дроби между собой, необходимо действовать следующим образом:
- превратить дроби из смешанных в неправильные, если такие дроби есть,
например: \[2\frac{7}{8} = \frac{{2 \cdot 8 + 7}}{8} = \frac{{23}}{8}\] - найти наименьший общий знаменатель у полученных дробей и домножить числители на недостающие множители;
- произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.
Примеры:
(1)216+178=2⋅6+16+1⋅8+78=136+158=13⋅46⋅4+15⋅38⋅3=52+4524=9724=4124(2)3712−2316=3⋅12+712−2⋅16+316=4312−3516=43⋅412⋅4−35⋅316⋅3=172−10548=6748=11948
(3)2314−0,6=2⋅14+314−610=3114−35=31⋅514⋅5−3⋅145⋅14=155−4270=11370=14370
Умножение и деление дробей.
При умножении двух дробей числитель первой дроби умножается на числитель второй дроби, знаменатель первой дроби умножается на знаменатель второй:
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{{a \cdot c}}{{b \cdot d}}\]
Чтобы умножить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:
\[\frac{a}{b} \cdot c = \frac{a}{b} \cdot \frac{c}{1} = \frac{{a \cdot c}}{{b \cdot 1}} = \frac{{a \cdot c}}{b}\]
При делении двух дробей необходимо первую дробь умножить на «перевёрнутую» предыдущую, то есть у дроби-делителя поменять местами числитель и знаменатель и поставить операцию умножения вместо операции деления между этими дробями:
\[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{{a \cdot d}}{{b \cdot c}}\]Чтобы разделить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:
\[\frac{a}{b} \div c = \frac{a}{b} \div \frac{c}{1} = \frac{a}{b} \cdot \frac{1}{c} = \frac{{a \cdot 1}}{{b \cdot c}} = \frac{a}{{b \cdot c}}\]Примеры:
(1)234⋅811÷0,5=11141⋅82111÷51102=2÷12=2⋅21=4(2)6÷2,25⋅1,5=61÷214⋅151102=61÷94⋅32=631⋅493⋅3121=4
Сравнение дробей. 6} = 1000000.\]
6} = 1000000.\]
Скачать домашнее задание к уроку 1.
Порядок действий в Математике
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
- Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
- Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
- Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо
- сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем. |
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
Как решаем:
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
- Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Какое действие в полученном выражении делается первым, умножение или деление? Выполняем слева направо: умножение, деление, затем — вычитание. Получилось:
10 + 2 * 8 : 2 = 10 + 18 : 2 = 10 + 6 = 16.
На этом все действия выполнены.
Ответ: 10 + (7 — 2 * 3) * (12 — 4) : 2 = 16.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Как решаем:
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
2 + 3 = 5.
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 24, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 4 + (3 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Как решаем:
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
(4 + 1) * 3 + 36 : 3 — 7.
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.
Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.
У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!
Еще больше практики — в детской школе Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с поддержкой внимательных учителей.
Чтобы ребенок занимался математикой в удовольствие и чувствовал себя увереннее в школе, запишите его на бесплатный вводный урок. Познакомим с форматом и вдохновим на учебу!
«Приёмы вычислений для случаев вида»
Цели урока:
- Образовательные:
- познакомить детей с приёмами вычислений для случаев вида: 27 + 2, 27 + 20, 60 + 18.
- совершенствовать вычислительные навыки;
- совершенствовать умение решать задачи;
- выполнять задания геометрического характера;
- закреплять умение заменять двузначные числа суммой разрядных слагаемых,
- закреплять навык применения свойства сложения (переместительного свойства).
- Развивающие:
- развивать умение решать задачи логического характера;
- развивать наблюдательность;
- развивать мыслительные операции: обобщение, сравнение;
- развивать внимание, интерес к предмету.

- Воспитательные : воспитывать аккуратность.
Оборудование:
- Картинка с изображением Знайки-Математика.
- Счётные палочки.
- Полоска с рисунками.
- Таблички с рисунками для выполнения заданий на развитие внимания и логического мышления.
ХОД УРОКА
I. Организационный момент
II. Постановка учебной задачи
– Ребята, посмотрите, кто у нас сегодня в гостях? (Знайка-Математик.)
– Знайка-Математик снова у нас на уроке.
Прозвенел долгожданный звонок.
Знайка с нетерпением встречи с вами ждёт.
Принёс он сегодня палочки и пучки палочек. Интересно, чему он нас хочет научить? Попробуем догадаться. Раскладывать числа на разряды? (Это уже мы умеем делать.)
– А вот чему же ещё хочет научить вас Знайка-Математик? Думаю, что мы непременно узнаем, расшифровав эту запись.
| 6 | 5 | 10 | 30 | 16 | 7 | 1 | 30 | 11 | 20 |
| С 13 – * = 7 Л * + 5 = 15 К 20 + * = 25 Д * – 6 = 10 |
А * + 60 = 90 Ь 50 – * = 30 Ы 7 + * = 14 В 40 – * = 39 |
Т * – 3 = 8 |
|
(Ответ: Складывать.)
– Молодцы! С приёмами сложения вас Знайка
познакомит чуть позже.
– Сегодня мы познакомимся с приёмами вычитания для – случаев вида: 36 + 2 , 36 + 20, 60 + 18.
III. Актуализация знаний и создание проблемы
1. Устный счёт.
Ну-ка в сторону карандаши!
Ни счётных палочек, ни ручек, ни мела.
Устный счёт.
Мы творим это дело
Только силой ума и души.
– А сначала как всегда “Гимнастика для ума.”
2. Задание на развитие внимания.
Учитель в течение 3–5 секунд показывает полоску с рисунками, учащиеся должны запомнить фигурки и нарисовать как можно точнее.
3. Геометрическая задача.
– Сколько на чертеже треугольников? (Ответ: 9.)
4. Логическая задача.
Лестница состоит из 9 ступенек. На какую ступеньку надо встать, чтобы быть как раз на середине лестницы? (На 9.)
Игра” Называй – не зевай.”(Замена двузначного числа однозначным.)
Один ученик называет сколько в числе десятков, другой сколько единиц. Учитель называет числа, а дети выполняют задание.
37, 68, 87, 43, 55.
IV. Открытие детьми нового знания через проблему.
На столах у детей пучки палочек (по 10) и палочки россыпью.
– Отложим на палочках число 36.
Дети откладывают 3 десятка 6 единиц.
– А сейчас прибавьте к вашему числу 36 число 2.
Добавляют две палочки.
– Куда вы положили 2 палочки, к пучкам или палочкам россыпью? (К палочкам россыпью.)
– Пучки палочек – это… (Десятки.)
– Палочки россыпью – это… (Единицы.)
– Что вы сделали, если говорить на языке терминов? (К единицам прибавили единицы.)
– Давайте, выполним эту операцию на числах:
– Какой можно сделать вывод? (Единицы
складываем с единицами. )
)
– Отложите на палочках число 36. Прибавьте к нему число 20.
– 20 – это … (Два десятка 2 пучка палочек.)
– Куда будете класть к пучкам или к палочкам россыпью? (К пучкам.)
– Или говоря математическими терминами… (Два десятка прибавляем к двум десяткам.)
– Выполним эту операцию на числах.
– Какой можно сделать вывод? (Десятки складывают с десятками.)
– Интересно, правы ли мы? Знайка Математик загадочно улыбается и предлагает отрыть учебник на стр. 48 и внимательно прочитать параграф.
Работа по учебнику. Стр.48.
– Какое правило вывел Знайка Математик?
Чтение правила из учебника.
– А какой вывод сделали мы? (Такой же.)
– Так вот почему улыбается Знайка, он радуется успехам. Подумайте, как сложить числа 60 и 18? Предлагаю порассуждать. Что значит 60? (6 дес.)
– Что значит 18? (1 дес. и 8 ед.)
– Как будем вычислять? (Сначала сложим 6 дес. и 1 дес., получим 7 дес. или 70. Затем к 70 прибавим 8 и получим 78.)
– Запишем так:
– Какое правило вы использовали? (Десятки складываются с десятками.)
V. Физминутка
Мы решали, мы решали.
Что-то очень мы устали.
Мы сейчас потопаем,
Ручками похлопаем.
Раз присядем,
Быстро встанем,
Улыбнёмся,
Тихо сядем.
VI. Первичное закрепление во внешней речи.
№ 1, стр. 48 – устно. Два первых выражения вычисляются с хоровых проговариванием. Два следующих выражения комментируют два ученика, класс проговаривает шёпотом. № 2. Стр. 48 ( 1 ст.) Один столбик выполнятся с комментированием. Самостоятельная работа. № 2, № 48 (3-4 ст.)
VII. Задание на повторение.
Задание на повторение.
1. Работа над текстовыми задачами. № 4 , стр. 48.
– Прочитайте задачу. О ком говориться в задаче? -Что о них говориться? Запишите условие кратко.
Краткая запись делается под руководством ученика на доске.
– Что надо узнать в задаче?
– Что значит старше?
– Дополните краткую запись.
– Как узнать на сколько одно число больше или меньше другого?
Самостоятельное решение задачи.
– На сколько дедушка старше бабушки?
2. Геометрическая задача. № 7. Стр. 48.
– Прочитайте задачу.
– Что предлагают сделать? (Начертить отрезки.)
– Их длина известна? (Длина 1-го – 3см, а длина 2-го – нет.)
– Что сказано о длине второго отрезка? (На 3см меньше.)
– Единицы измерения одинаковы? (Нет.)
– Что надо сделать? (Перевести 3мм в см.)
– Можем найти длину второго отрезка? Как? Запишите решение и начертите отрезки.
3. Отработка вычислительных навыков. С.р. № 5., стр. 48.
– Что значит “вычислить удобным способом?”
– Какое правило нам в этом поможет?
Один ученик работает у доски. Проверка. Самопроверка с записью на доске.
VIII. Итог урока.
– Что нового и интересного узнали на уроке?
IX. Домашнее задание.
– № 6 с. 48.
Урок математики «Числа и вычисления» (11 класс)
Тема урока: «Числа и вычисления»
Обучающая цель урока: предполагается, что в ход урока
учащиеся:
Обобщат понятие числовых множеств
Повторят понятие логарифма числа по данному основанию
Усовершенствуют свои умения по выполнению заданий с логарифмами
Задачи личностного развития:
Способствовать развитию умения анализировать, делать выводы.

Создать условия для развития самостоятельности учащихся
Создать условия для развития творческих способностей учащихся
Тип урока: урок повторения
Учебно-методическое обеспечение:
учебное пособие 11 класс §19, рабочая тетрадь, проектор, презентация, компьютеры, электронный тест для проведения промежуточного контроля, карточки для ответов на вопросы теста
Ход урока
Организационный момент
Мы с вами приступили к повторению курса математики, изученного в школе. И начали мы с темы «Числа и вычисления». Назовите по одной ассоциации со словом «число».
Целемотивационный этап
Давайте еще раз вспомним, с какими числами мы познакомились на уроках математики
Сообщение «Множества чисел» (Приложение 1, Презентация слайды 2-5)
Как было только что сказано, логарифмы, за редким исключением, являются иррациональными числами. И на сегодняшнем уроке мы повторим с вами понятие логарифма и основные свойства логарифмирования.
Актуализация знаний и умений учащихся
Фронтальная работа: (Учащиеся отвечают на вопросы, которые заранее были предложены в качестве домашнего задания для повторения. Формулы отображаются в презентации — слайд 7, приложение 3)
Какое число называется логарифмом данного числа по данному основанию?
Каким может быть основание логарифма?
Каким может быть подлогарифмическое выражение?
В чем заключается основное логарифмическое тождество?
Чему равен логарифм 1?
Чему равен логарифм основания?
Чему равен логарифм произведения?
Чему равен логарифм частного?
Чему равен логарифм степени?
Какой логарифм называется десятичным?
Какой логарифм называется натуральным?
Как перейти к логарифму с новым основанием?
Устный счет № 981 (1 и 3 столбики) № 982 (б, е)
(№№ на слайде)
Выполнение практических заданий (№№ на слайде)
№ 984 а
№ 985 а (б* дополнительно)
Тестовое задание (Приложение 2, 4)
Выполнение тестов, созданных в Гугл-форме. Результат выполнения каждого учащегося отображается в сводной электронной таблице.
Результат выполнения каждого учащегося отображается в сводной электронной таблице.
Учащиеся заполняют формы приложения 4.
Анализ выполненных тестов
Информация о домашнем задании
№ 984 (б, г), 984 (в-e)
Подведение итогов
Как вы оцениваете свою работу?
Определение темы следующего урока. (Приложение 5)
Составить из букв соответствующих правильным вариантам ответов на тестовые задания слово (ВЫРАЖЕНИЕ). Тема следующего урока «Выражения и их преобразование»
Рефлексия
Продолжите фразы:
Приложение 1
Натуральные числа — это числа, которые используют при счете предметов.
Наименьшее натуральное число — единица. Нуль не является натуральным числом.
Все натуральные числа образуют множество натуральных чисел(N).
Наибольшего натурального числа не существует. Множество натуральных чисел бесконечно.
Во множестве натуральных чисел всегда выполнимы действия сложения и умножения, а действие вычитания выполнимо не всегда.
Для натуральных чисел можно сформулировать признаки делимости:
Натуральное число, имеющее точно два различных натуральных делителя, называется простым числом, а число, имеющее более двух различных натуральных делителей, называется составным числом. Число 1 не является простым и не является составным.Любое натуральное число можно представить в виде произведения простых множителей. На этом основываются алгоритмы нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) чисел.
Если к натуральным числам присоединить противоположные им числа −1, −2, −3, … и число 0, то образуется множество целых чисел.
Во множестве целых чисел всегда выполнимы действия сложения, вычитания и умножения, а действие деления, во множестве целых чисел остается не всегда выполнимым.
Множество, состоящее из всех целых и дробных чисел, называется множеством рациональных чисел (Q). Во множестве рациональных чисел всегда выполнимы действия сложения, вычитания, умножения и деления (кроме деления на 0).
Каждое рациональное число можно единственным образом представить обыкновенной несократимой дробью , где m целое число, n натуральное. Рациональные числа можно представлять и десятичными дробями, конечными или бесконечными периодическими.
Некоторые часто используемые дроби имеют специальные названия. Сотая доля называется процентом, а тысячная — промилле.
Число, не являющееся рациональным, называется иррациональным. Иррациональными числами являются числа и е. Результаты действий извлечения корня, нахождения значений тригонометрических функций, логарифмирования, за редким исключением, являются иррациональными числами.
Рациональные и иррациональные числа вместе составляют множество действительных чисел, которое обозначают R.
Приложение 2
Тестовое задание
Найдите логарифм по основанию 3 числа 81
1) 2
2) 4
3) 3
4) 1
5) 9
Найдите логарифм по основанию 2 числа
1)
2)
3) -3
4) 3
5) 4
Найдите значение выражения
1) 10
2) 25
3) 3
4) 9
5) 5
Укажите выражение, значение которого равно 0,5
1)
2)
3)
4) 12
5)
Найдите значение выражения
1)
2)
3)
4)
5)
Найдите значение выражения
1)
2)
3)
4)
5) 9,5
7. Вычислите )
Вычислите )
8. Найдите значение выражения
https://docs.google.com/forms/d/e/1FAIpQLSch5k-BUMKS_VuWSYuA0wymLkw0Kb_gobGIg08uG-AsEotkYQ/viewform?usp=sf_link
Приложение 3
Приложение 4
Приложение 5
А
Б
В
Г
Д
Е
2
Ж
З
И
Й
К
Л
3
М
Н
О
П
Р
С
4
Т
У
Ф
Х
Ц
Ч
5
Ш
Щ
Ь
Ы
Ю
Я
БУКВА, КОТОРАЯ В АЛФАВИТЕ СТОИТ ПОД НОМЕРОМ, РАВНЫМ ПОЛУЧЕННОМУ ЧИСЛУ
8
БУКВА В
Тренажёр по математике для 2 класса «Устные и письменные вычисления » | Тренажёр по математике (2 класс) на тему:
8 + 1 = 18 – 1 = 9 + 1= 14 + 1 = 19 + 1 = 3 + 1=
10 +1 = 26 – 1 = 16 – 1 = 27 –1 = 40 –1 = 60 –1=
12+1 = 17 –1 = 27 – 1= 40 –1 = 29 + 1= 59 + 1=
34 +1 = 30 –1 = 34 +1= 71 –1 = 80 – 1 = 80 +1 =
18+1= 10 –1= 40 +1 = 100+1= 39 +1= 100 — 1=
39 +1= 30 – 1 = 80 – 1 = 97 – 1 = 50 – 1= 93 – 1=
60 – 1 = 43 + 1= 71 – 1 = 60 + 1 = 101 –1 = 76 +1=
54 +1 = 86 – 1 = 65 – 1 = 17 –1 = 81 –1 = 90 +1=
87 +1= 43 + 1= 89 + 1 = 99 +1= 75 +1= 64 –1=
100 +1= 101 –1= 100 — 1= 83 +1= 99 – 1= 100-1=
0 + 7 = 4 + 90 = 87 – 80 = 57 –7 = 45 – 5 =
20 + 8 = 5 + 10 = 56 – 50 = 62 – 2 = 18 –10 =
30 + 2 = 6 + 70 = 63 – 60 = 63 –3 = 43 – 40 =
40 + 4 = 2 + 90 = 45 – 40 = 83 – 3 = 50 + 5 =
50 + 6 = 3 + 20 = 33 – 30 = 48 – 8 = 33 – 3 =
60 + 3 = 1 + 30 = 27 – 20 = 39 – 9 = 99 – 9 =
70 + 4 = 8 + 40 = 17 – 10 = 16 – 6 = 62 – 60 =
80 + 5 = 3 + 50 = 92 – 90 = 86 – 6 = 73 – 3 =
90 +1 = 7 + 70 = 88 – 80 = 44 – 4 = 5 + 70 =
30 + 4 = 9 + 20 = 77 – 70 = 53 – 3 = 80 + 9 =
60 + 7 = 3 + 40 = 59 – 50 = 12 – 2 = 1 + 90 =
50 + 4 = 7 + 30 = 69 – 60 = 8 3 – 3 = 77 – 7=
5 + 20 = 89 – 80 = 36 – 30 = 34 – 4 = 53 – 3 = 32 – 2 =
30 + 6 = 32 – 30 = 24 – 20 = 20 + 8 = 42 – 40 = 60 + 6 =
46 – 6 = 27 –7 = 76 – 6 = 14 – 10 = 15 – 10 = 22 – 20=
40 + 2 = 39 – 9 = 80 + 2 = 45 – 5 = 10 + 7 = 15 – 10=
27 — 20 = 40 + 5 = 93 – 3 = 29 – 20 = 40 + 6 = 77 – 7 =
32 – 30 = 42 – 2 = 90 + 7 = 22 – 2 = 52 – 50 = 55 – 5 =
74 – 4 = 33 – 3 = 82 – 80 = 38 – 8 = 37 – 30 = 99 – 90=
28 – 8 = 90 + 7 = 30 + 8 = 29 – 9 = 46 – 6 = 30 + 7 =
80 + 5 = 78 – 70 = 59 – 9 = 50 + 6 = 78 – 70 = 70 + 8=
91 – 1 = 33 – 3 = 44 – 40 = 59 – 50 = 96 –6 = 83 – 3 =
47 – 40 = 70 +6 = 54 – 4 = 60 + 5 = 93 – 90 = 57 –7 =
3 + 70 = 80 + 6 = 55 – 50 = 20 + 9 = 13 – 3 = 47 – 40=
40 + 6 = 64 – 4 = 69 – 60 = 8 + 70 = 93 – 3 = 85 – 80 =
98 – 8 = 40 + 9 = 79 – 9 = 57 – 50 = 8 + 60 = 70 + 6 =
57 – 7 = 90 + 4 = 75 – 5 = 41 – 1 = 2 + 20 = 69 – 9 =
40 +4 = 53 – 3 = 60 + 4 = 72 – 70 = 63 – 3 = 55 – 5=
40 + 3 = 67 – 7 = 60 + 9 = 58 – 50 = 85 –5 = 48 –8=
78 – 8 = 89 – 80 = 47 – 40 = 30 + 5 = 66 – 6 = 2 + 60 =
67 – 60 = 7 + 40 = 69 –60 = 55 – 50 = 28 – 8 = 19 – 10=
23 – 20 = 60 + 9 = 43 – 3 = 92 – 90 = 76 – 6 = 7 + 60 =
40 + 8 = 50 + 3 = 80 + 4 = 40 + 3 = 60 + 7 = 50 + 4=
65 – 5 = 87 – 7 = 95 –5 = 78 – 8 = 34 – 4 = 62 –2 =
45 – 40 = 67 – 60 = 32 – 30 = 67 – 60 = 56 – 50 = 87 – 80=
5 + 90 = 7 + 60 = 3 + 40 = 6 + 50 = 7 + 60 = 6 + 40 =
50 + 6 = 40 + 4 = 30 + 3 = 20 + 2 = 10 + 1 = 70 + 7 =
36 – 30 = 33 – 30 = 22 –20 = 11 – 10 = 44 – 40 = 99 – 90=
5 + 50 = 2 + 20 = 3 + 30 = 4 + 40 = 7 + 70 = 9 + 90 =
11 – 1 = 22 – 2 = 33 – 3 = 44 – 4 = 55 – 5 = 66 – 6=
40 + 7 = 60 + 7 = 50 + 7 = 20 + 7 = 30 + 7 = 40 + 8=
30 + 6 = 50 + 4 = 30 + 9 = 60 + 3 = 40 + 6 = 30 + 8=
35 – 5 = 61 – 1 = 56 – 6 = 73 – 3 = 86 – 6 = 62 – 2=
6 + 70 = 7 + 60 = 3 + 50 = 4 + 60 = 8 + 50 = 1 + 50=
46 – 40= 49 – 40= 57 – 50= 72 – 70= 56 – 50= 99 – 90=
40 + 7 = 50 + 2 = 60 + 4 = 40 + 5 = 20 + 6 = 30 + 4=
82 – 2 = 47 – 7 = 23 –3 = 76 – 6 = 27 – 7 = 37 – 7 =
4 + 70 = 2 + 60 = 3 + 50 = 4 + 70 = 5 + 70 = 4 + 70=
78 – 70= 32 – 30= 43 – 40= 52 – 50= 64 – 60= 87 –80=
60 + 1 = 90 + 2 = 80 + 3 = 70 + 4 = 80 + 6 = 50 + 6=
45 – 5 = 34 – 4 = 23 – 3 = 43 – 3 = 56 –6 = 79 – 9=
1 + 90 = 2 + 80 = 3 + 70 = 4 + 60 = 5 + 50 = 6 + 40=
12 – 4 = 12 – 5 = 17 – 9 = 3 + 9 = 12 – 7 = 5 + 6 =
6 + 5 = 7 + 5 = 11 — 5 = 9 + 6 = 11 – 2 = 17 –9 =
5 + 9 = 8 + 4 = 14 – 9 = 7 + 7 = 6 + 5 = 12 – 5 =
11 — 8 = 13 – 7 = 8 + 8 = 7 + 8 = 6 + 6 = 12 – 7 =
14 – 5 = 15 – 6 = 16 – 7 = 6 + 5 = 7 + 5 = 12 – 3 =
4 + 7 = 8 + 8 = 8 + 7 = 15 – 7 = 13 – 8 = 13 – 4 =
5 + 7 = 6 + 8 = 7 + 9 = 8 + 7 = 3 + 8 = 7 + 5 =
12 – 5 = 11 – 3 = 11 – 5 = 15 – 8 = 2 + 9 = 16 – 9 =
15 — 8 = 18 – 9 = 9 + 3 = 18 – 9 = 14 – 9 = 12 – 3 =
5 + 8 = 9 + 5 = 6 + 6 = 5 + 6 = 17 – 8 = 17 – 9 =
3 + 9 = 8 + 9 = 15 – 7 = 2 + 9 = 8 + 8 = 11- 5 =
14 – 6 = 6 + 7 = 14 – 9 = 11 – 3 = 7 + 5 = 12 – 5=
11 – 3 = 15 – 6 = 7 + 6 = 11 – 9 = 16 – 7 = 8 + 8=
7 + 6 = 16 – 8 = 17 – 9 = 18 – 9 = 11 – 2 = 11- 3 =
11 – 4 = 11 – 5 = 11 – 6 = 11 – 7 = 11 – 8 = 11 – 9=
2 + 9 = 3 + 8 = 4 + 7 = 5 + 8= 6 + 9 = 7 + 4=
12 – 3 = 12 – 4 = 12 – 5 = 12 – 6= 12 – 7 = 12 – 8 =
12 – 9 = 2 + 9 = 3 + 9 = 4 + 9 = 5 + 9 = 6 + 9 =
9 + 7 = 9 + 8 = 8 + 9 = 13 – 4 = 13 – 5 = 14 – 6 =
13 – 6 = 13 – 7 = 13 – 8 = 13 – 9 = 8 + 3 = 8 + 4 =
8 + 5 = 8 + 6 = 8 + 7 = 8 + 8 = 8 + 9 = 14 — 7=
14 – 5 = 14 – 8 = 14 – 9 = 15 – 6 = 15 – 7 = 15 – 8 =
15 – 9 = 5 + 6 = 5 + 7 = 5 + 8 = 5 + 9 = 16 – 7 =
16 – 8 = 16 – 9 = 17 – 8 = 9 + 2 = 12 – 7 = 13 – 5=
12 – 7 = 12 – 6 = 12 – 5 = 12 – 4 = 12 – 3 = 5 + 6 =
12 – 3 = 15 – 7 = 14 –8 = 15 – 8 = 11 – 8 = 12 – 6 =
8 + 8 = 9 + 8 = 7 + 7 = 6 + 6 = 16 – 9 = 6 + 9=
3 + 8 = 7 + 8 = 6 + 9 = 4 + 7 = 5 + 8 = 5 + 6=
7 + 7 = 9 + 2 = 4 + 7 = 8 + 5 = 7 + 4 = 16 – 9= 3 + 8 = 8 + 3 = 5 + 9 = 7 + 5 = 13 – 5= 13 – 7=
8 + 7 = 12 – 4 = 8 + 4 = 2 + 9 = 7 + 6 = 13 – 5=
14 – 8 = 17- 8 = 11 – 3 = 11 – 9 = 15 – 8 = 2 + 9=
16 – 8 = 9 + 4 = 13 – 4 = 12 – 4 = 16 – 8 = 11 – 9=
7 + 9 = 13 – 7 = 8 + 7 = 8 + 8 = 6 + 8 = 11 – 4=
5 + 6 = 9 + 4 = 4 + 9 = 17 – 8 = 13 – 6 = 12 – 8=
12 – 5 = 15 – 9 = 14 – 5 = 12 – 6 = 5 + 7 = 12 – 7=
13 – 4 = 13 – 5 = 13 – 6 = 13 – 7 = 13 –8 = 13 – 9 =
2 + 9 = 3 + 9 = 4 + 9 = 5 + 9 = 6 + 9 = 7 + 9 =
8 + 9 = 9 + 9 = 14 – 5 = 14 – 6 = 14 – 7 = 14 – 8=
14 – 9 = 3 + 8 = 4 + 8 = 5 + 8 = 6 + 8 = 7 + 8 =
60 + 10 = 40 + 10 = 30 + 20 = 70 – 40 = 80 – 30 =
50 + 30 = 30 + 60 = 40 + 50 = 70 – 20 = 90 – 50 =
80 – 20 = 50 + 20 = 20 – 10 = 20 + 60 = 90 – 30 =
60 – 10 = 70 – 40 = 70 – 30 = 30 + 50 = 40 + 50 =
40 – 10 = 50 + 40 = 30 + 50 = 70 – 50 = 90 – 60 =
30 – 20 = 80 + 10 = 60 – 50 = 80 – 70 = 40 – 30 =
40 + 50 = 70 – 20 = 80 – 30 = 70 + 20 = 80 – 60 =
30 + 50 = 40 – 20 = 80 – 40 = 20 + 70 = 60 – 50 =
70 – 10 = 70 – 30 = 70 – 50 = 70 – 60 = 10 + 80 =
10 + 70 = 10 + 60 = 10 + 50 = 10 + 40 = 10 + 30=
10 + 20 = 80 – 10 = 80 – 20 = 80 – 30 = 80 – 40 =
20 + 20 = 30 + 30 = 40 + 40 = 70 – 20 = 70 – 30 =
90 + 10 = 40 + 60 = 100 – 10 = 100 – 90 = 100 – 40 =
80 + 20 = 20 + 80 = 100 – 50 = 100 –70 = 50 + 50 =
30 + 70 = 10 + 90 = 100 – 20 = 100 – 80 = 100 – 30 =
50 + 50 = 70 + 30 = 100 – 40 = 100 – 60 = 60 + 40 =
20 + 80 = 30 + 70 = 100 – 80 = 100 – 50 = 100 – 70 =
60 + 40 = 80 + 20 = 100 – 30 = 100 – 10 = 20 + 80 =
17 + 2 = 20 + 15 = 10 + 88 = 28 + 70 =
/ \ / \ / \ / \
60 + 18 = 70 + 19 = 22 + 7 = 43 +6 =
/ \ / \ / \ / \
56 + 3 = 61 + 4 = 91 + 7 = 25 + 4 =
/ \ / \ / \ / \
70 + 24 = 50 + 34 = 35 + 60 = 4 + 32 =
/ \ / \ / \ / \
31 + 7= 76 + 3 = 34 + 4 = 56 + 3 = 36 + 20 =
80 + 14 = 30 + 12 = 30 + 62 = 70 + 24 = 25 + 3 =
62 + 10 = 22 + 60 = 33 + 6 = 62 + 20 = 81 + 8 =
82 + 4 = 30 + 25 = 20 + 71 = 53 + 40 = 60 + 27 =
73 + 5 = 15 + 80 = 82 + 10 = 20 + 78 = 32 + 60 =
24 + 3 = 41 + 50 = 23 + 60 = 50 + 14 = 37 + 2 = 42 + 30 =
72 + 20 = 20 + 69 = 56 + 40 = 57 + 30 = 41 + 20 = 23 + 50 =
18 + 30 = 4 + 34 = 4 + 72 = 17 + 80 = 54 + 30 = 3 + 65 =
20 + 36 = 54 + 20 = 26 + 3 = 8 + 31 = 3 + 62 = 57 + 2=
44 + 5 = 3 + 71 = 17 + 40 = 24 + 70 = 57 + 1 = 45 + 50 =
36 + 40 = 81 + 7 = 36 + 50 = 56 + 30 = 63 + 5 = 36 + 3 =
35 + 20 = 54 + 30 = 76 + 20 = 56 + 20 = 37 + 60 = 21 + 50 =
4 + 42 = 56 + 3 = 5 + 43 = 4 + 63 = 2 + 56 = 5 + 42 =
50 + 35 = 40 + 37 = 20 + 76 = 10 + 56 = 40 + 29 = 30 + 34 =
45 + 3 = 57 + 2 = 56 + 3 = 32 + 7 = 42 + 5 = 75 + 4 =
12 + 8 = 53 + 7 = 36 + 4 = 93 + 7=
/ \ / \ / \ / \
43 + 7 = 68 + 2 = 91 + 9 = 27 + 3 =
/ \ / \ / \ / \
81 + 9 = 3 + 47 = 27 + 3 = 2 + 98 =
/ \ / \ / \ / \
65 + 5 = 3 + 67 = 4 + 96 = 5 + 45 =
/ \ / \ / \ / \
78 + 2 = 83 + 7 = 1 + 29 = 3 + 47 = 5 + 35 =
64 + 6 = 4 + 76 = 33 + 7 = 77+ 3 = 4 + 56 =
41 + 9 = 85 + 5 = 17 + 3 = 4 + 76 = 62 + 8 =
97 + 3 = 15 + 5 = 4 + 96 = 37 + 3 = 42 + 8 =
73 + 7 = 5 + 85 = 56 + 4 = 6 + 44 = 51 + 9 =
56 + 4 = 1 + 99 = 2 + 68 = 67 + 3 = 5 + 65 =
64 + 6 = 86 + 4 = 15 + 5 = 6 + 44 = 8 + 82 = 7 + 53=
33 + 7 = 91 + 9 = 47 + 3 = 6 + 94 = 54 + 6 = 27 + 3 =
18 + 2 = 3 + 77 = 4 + 66 = 1 + 69 = 2 + 58 = 7 + 43 =
5 + 95 = 6 + 74 = 53 + 7 = 62 + 8 = 22 + 8 = 88 + 2 =
64 + 6 = 99 + 1 = 17 + 3 = 98 + 2 = 84 + 6 = 36 + 4 =
7 + 53 = 6 + 54 = 2 + 98 = 64 + 6 = 4 + 46 = 3 + 57 =
93 + 7 = 74 + 6 = 32 + 8 = 75 + 5 = 64 + 6 = 57 + 3 =
56 + 4 = 77 + 3 = 33 + 7 = 22 + 8 = 11 + 9 = 13 + 7 =
55 + 5 = 66 + 4 = 99 + 1 = 7 + 53 = 2 + 58 = 3 + 47 =
1 + 69 = 2 + 28 = 3 + 37 = 4 + 46 = 5 + 55 = 6 + 64 =
7 + 73 = 8 + 82 = 9 + 91 = 1 + 99 = 2 + 48 = 24 + 6 =
35 + 5 = 56 + 4 = 67 + 3 = 78 + 2 = 89 + 1 = 91 + 9 =
86 – 5 = 86 – 50 = 77- 6 = 77 — 60 =
/ \ / \ / \ / \
78 – 6 = 78 – 60 = 44 – 3 = 44 – 30 =
/ \ / \ / \ / \
56 – 4 = 56 –40 = 89 – 7 = 89 –70 =
/ \ / \ / \ / \
65 – 4 = 65 –40 = 96 – 5 = 96 – 50 =
/ \ / \ / \ / \
47 – 2 = 54 – 3 = 78 – 6 = 54 – 2 = 16 – 4 =
64 – 20 = 54 – 30 = 78 – 60 = 54 – 20 = 26 – 10 =
34 – 3 = 63 –2 = 76 – 5 = 53 – 1 = 19 – 7 =
16 – 5 = 27 – 10 = 56 – 30 = 64 – 30 = 96 – 90 =
37 – 7 = 36 – 3 = 79 – 6 = 57 – 6 = 46 – 6 =
58 – 30 = 47 – 20 = 87 – 60 = 47 – 10 = 54 – 50 =
88 – 2 = 94 – 2 = 54 – 3 = 56 – 5 = 17 – 3 = 84 – 6 =
67 – 30 = 86 – 70 = 78 – 50 = 72 – 60 = 92 – 40 = 56 – 50=
82 – 50 = 76 – 50 = 59 – 8 = 46 – 3 = 46 –30 = 86 –30 =
73 –50 = 77 – 5= 36 – 10 = 62 – 40 = 67 – 10 = 72 – 30 =
68 – 4 = 65 – 2 = 99 – 8 = 88 – 5 = 13 – 2 = 26 – 4 =
68 – 40 = 65 – 20 = 99 – 80 = 88 – 50 = 27 – 20 = 76 – 40=
29 – 5 = 38 – 6 = 47 – 5 = 56 – 4 = 32 – 1 = 43 – 2 =
45 – 30 = 43 – 20 = 78 – 60 = 83 – 40 = 74 – 50 = 74 – 20 =
50 – 6= 30 – 5 = 100 – 4 = 60 – 8 =
/ \ / \ / \ / \
70 – 4 = 40 – 5 = 100 – 9 = 100 – 2 =
/ \ / \ / \ / \
80 – 3 = 20 – 4 = 30 – 5 = 40 – 6 =
/ \ / \ / \ / \
90 – 4 = 50 – 6 = 60 – 3 = 20 – 5 =
/ \ / \ / \ / \
70 – 8 = 80 – 4 = 90 – 3 = 100 – 4 = 20 – 3 =
20 – 7 = 30 – 6 = 40 – 8 = 50 –3 = 60 – 2 =
70 – 9 = 80 – 1= 90 – 6 = 20 – 3 = 100 – 9 =
40 – 7= 40 – 9 = 30 – 4 = 50 – 5 = 60 – 4 =
70 – 7 = 80 – 8 = 90 – 9 = 100 – 4 = 20 – 2=
20 – 1 = 30 – 2 = 40 – 3 = 50 –4 = 60 – 5= 70 – 6 =
80 – 7 = 90 – 8 = 100 – 9 = 20 – 9 = 30 – 8 = 40 – 7 =
50 – 6 = 60 – 5 = 70 – 4 = 80 – 3 = 90 – 2 = 100 – 1 =
20 – 2 = 30 — 4 = 40 – 5 = 50 – 6 = 60 – 7 = 70 – 8=
80 – 9 = 100 – 1 = 20 – 1 = 30 –2 = 40 – 3 = 50 – 4 =
60 – 5= 70 – 6 = 80 – 7 = 90 – 8 = 100 – 9 = 20 – 4 =
30 – 5 = 40 – 6 = 50 – 7 = 60 – 8 = 70 – 9 = 90 – 2 =
100 – 4 = 20 – 9 = 30 – 1 = 40 – 2 = 50 – 3 = 60 –4 =
70 – 5 = 80 – 6 = 70 – 4 = 90 – 7 = 20 – 7 = 30 – 8 =
40 – 9 = 50 – 7 = 70 – 1 = 80 – 2 = 90 – 3 = 100 – 4 =
70 – 28 = 90 – 39 40 – 28 = 80 – 67 =
/ \ / \ / \ / \
30 – 23 = 40 – 36 = 50 – 21 = 80 – 76 =
/ \ / \ / \ / \
40 –14 = 100 – 44 = 70 – 29 = 100 – 21 =
/ \ / \ / \ / \
50 – 36 = 70 –23 = 80 – 77 = 40 – 34 =
/ \ / \ / \ / \
40 –15 = 70 – 18 = 100 – 18 = 50 – 46 = 30 –22 =
50 – 46 = 80 – 73 = 80 – 19 = 30 – 23 = 50 – 36 =
60 –57 = 40 – 33 = 40 – 36 = 40 – 16 = 100 – 34 =
80 – 57 = 30 –18 = 30 – 12 = 70 – 16 = 100 – 78 =
50 — 47 = 30 – 29 = 50 – 38 = 40 – 27 = 50 – 36 =
50 – 32 = 30 – 21 = 50 – 43 = 60 – 56 = 30 – 26 = 60 – 44 =
80 – 75 = 90 – 56 = 100 – 98= 40 – 17 = 70 – 48 = 90 – 81 =
90 – 72 = 60 – 31 = 70 – 48 = 90 – 66 = 90 – 24 = 90 – 75 =
100 – 87 = 60 – 43 = 70 – 67 = 100 – 17 = 80 – 57 = 80 – 16 =
60 – 12 = 70 – 34 = 60 – 57 = 90 – 12 = 60 – 28 = 50 – 23 =
40 – 23 = 40 – 14 = 70 – 29 = 80 – 76 = 40 – 24 = 50 – 25 =
70 – 51 = 70 – 31 = 70 – 54 = 50 – 43 = 70 – 32 = 100 – 99 =
100 – 56 = 80 – 37 = 90 – 51 = 60 – 43 = 80 – 54 = 60 – 51 =
80 = 31 = 80 – 44 = 50 – 32 = 60 – 45 = 70 – 53 = 80 – 54 =
90 – 73 = 80 – 56 = 70 – 43 = 60 – 43 = 90 – 72 = 80 – 65 =
40 – 23 = 50 – 32 = 60 – 45 = 70 – 53 = 80 – 54 = 80 — 53 =
60 – 45 = 70 – 32 = 80 – 34 = 80 – 65 = 90 – 64 = 40 – 32 =
50 – 34 = 60 – 23 = 30 – 13 = 30 – 23 = 90 – 72 = 70 – 45 =
63 + 9 = 54 + 8 = 73+ 9 = 43 + 9 =
/ \ / \ / \ / \
76 + 6 = 63 + 9 = 86 + 8 = 56 + 8 =
/ \ / \ / \ / \
62 + 9 = 75 + 6 = 32 + 9 = 39 + 7 =
/ \ / \ / \ / \
46 + 8 = 46 + 8 = 27 + 8 = 48 + 5 =
/ \ / \ / \ / \
57 + 8 = 72 + 9 = 44 + 9 = 78 + 8 = 76 + 6 =
37 + 8 = 36 + 7 = 45 + 7 = 56 + 7 = 88 + 7 =
24 + 7 = 25 + 6 = 74 + 9 = 57 + 7 = 92 + 9 =
77 + 8 = 44 + 8 = 66 + 5 = 54 + 8 = 55 + 7 =
56 + 8 = 45 +6 = 39 + 9 = 65 + 7 = 87 + 4 = 23 + 8 =
34 + 8 = 47 + 7 = 26 + 9 = 74 + 8 = 48 + 9 = 43 + 9 =
22 + 9 = 53 + 8 = 29 + 4 = 67 + 8 = 58 + 7 = 56 + 8 =
54 + 7 = 58 + 3 = 84 + 8 = 63 + 8 = 78 + 8 = 44 + 7 =
47 + 7 = 53 + 8 = 26 + 7 = 26 + 9 = 73 + 8 = 13 + 9 =
14 + 8 = 23 + 7 = 34 + 7 = 34 + 8 = 36 + 7 = 35 + 6 =
46 + 7 = 56 + 5 = 67 + 5 = 78 + 8 = 89 + 7 = 23 + 9 =
34 + 7 = 34 + 9 = 54 + 7 = 65 + 8 = 65 + 7 = 76 + 5 =
85 + 7 = 67 + 5 = 27 + 8 = 17 + 5 = 26 + 9 = 27 + 8 =
35 + 9 = 42 + 9 = 54 + 8 = 65 + 8 = 45 + 8 = 83 + 8 =
26 – 8 = 65 – 8 = 44 – 8 = 36 – 8 =
/ \ / \ / \ / \
32 – 6 = 43 – 6 = 74 – 6 = 2 5 – 6 =
/ \ / \ / \ / \
27 – 8 = 36 – 9 = 45 – 9 = 23 – 9 =
/ \ / \ / \ / \
75 – 7 = 23 – 7 = 34 – 7 = 46 – 7 =
/ \ / \ / \ / \
72 – 5 = 25 – 7 = 27 – 9 = 23 – 4 = 97 – 9 =
56 – 7 = 76 – 8 = 63 – 8 = 76 – 7 = 83 – 4 =
37 – 9 = 53 – 9 = 56 – 9 = 76 – 8 = 45 – 7 =
26 – 7 = 46 – 8 = 78 – 9 = 46 – 9 = 37 – 8 =
73 – 4 = 57 – 9 = 92 – 7 = 55 – 7 = 26 – 9 = 34 – 6 =
96 – 7 = 63 – 6 = 85 – 6 = 72 – 3 = 52 – 3 = 84 – 8 =
82 – 4 = 44 – 5 = 44 – 6= 81 – 4 = 61 – 2 = 64 – 5 =
27 – 9 = 83 – 6 = 26 – 8 = 71 – 5 = 33 – 4 = 34 – 6 =
64 – 9 = 73 – 5= 63 – 6 = 51 – 5 = 91 – 9 = 75 – 8 =
81 – 7 = 56 – 7 = 51 – 6 = 48 – 9 = 36 – 9 = 66 – 8 =
34 – 8 = 76 – 7 = 72 – 6 = 43 – 7 = 38 – 8 = 45 – 8 =
82 – 3 = 85 – 8 = 54 – 9 = 57 – 8 = 67 – 8 = 93 – 6 =
61 – 7 = 62 – 8 = 43 – 9 = 56 – 7 = 82 – 6 = 72 – 5 =
34 – 7 = 45 – 6 = 24 – 6 = 23 – 6 = 43 – 8 = 25 – 6 =
Maxima — Руководства
Материал был опубликован в «Компьютерра» №16 (636)
в апреле 2006 г.
В давние, давние времена компьютеры занимались только своими прямыми обязанностями: они считали. Складывали и вычитали, решали системы уравнений, интегрировали и дифференцировали. Рассчитывали траектории баллистических ракет и аэродинамические характеристики самолетов, предсказывали погоду и моделировали атомные реакторы. С тех пор отношение к технике, которая когда-то называлась вычислительной, сильно изменилось — и сейчас во многих домашних и офисных компьютерах самой сложной «математической» программой является стандартный «Калькулятор». Неужели математика сдала свои позиции в эпоху персональных компьютеров?
Компьютеры и математика
Разумеется, это не так. Просто компьютеры в полной мере демонстрируют свое главное свойство: быть универсальным устройством — каждый получает от них то, что ему нужно. Так что если вы являетесь студентом, инженером или научным сотрудником и вам требуется решать на ПК именно математические задачи, то современные компьютеры открывают перед вами самые широкие возможности.
Существует множество программ, предназначенных для узкоспециализированных математических расчетов. Больше всего известны и широко распространены универсальные пакеты-комбайны, пригодные для занятий самой разной математической деятельностью. По функциональности они делятся в целом на две категории: пакеты, предназначенные в основном для численных расчетов (например, MatLab) и системы компьютерной алгебры (Computer Algebra System), к которым относятся Mathematica, Maple и (отчасти) MathCAD — они также называются системами символьных или аналитических вычислений (Symbolic Manipulation Program). Это наиболее универсальные математические программы, способные решать самые разные задачи, причем как численно, так и точно — аналитически.
Возможностей у подобного софта — множество, и есть только
одна проблема: все эти программы довольно дороги. А как же свободное
программное обеспечение, спросите вы? Оказывается, и здесь дело
обстоит неплохо. Существуют альтернативы как для MatLab (системы
Octave и Scilab), так и свободные системы аналитических вычислений —
Maxima и Axiom. О последних и поведем речь.
А как же свободное
программное обеспечение, спросите вы? Оказывается, и здесь дело
обстоит неплохо. Существуют альтернативы как для MatLab (системы
Octave и Scilab), так и свободные системы аналитических вычислений —
Maxima и Axiom. О последних и поведем речь.
Системы аналитических вычислений
Но сначала чуть подробнее о том, что же умеют делать универсальные системы компьютерной алгебры, к которым относятся Maxima и Axiom. Если кратко, то подобные программы обладают «знаниями» алгебры и математического анализа в объеме первых курсов любого технического университета. Системы аналитических вычислений (САВ) умеют преобразовывать выражения: упрощать, приводить подобные, раскрывать скобки или, наоборот, группировать подобные члены. Они умеют вычислять производные, пределы и интегралы, решать системы алгебраических и дифференциальных уравнений, производить вычисления с матрицами. Могут упрощать и преобразовывать тригонометрические выражения. Все это делается точно, аналитически.
Рис. 1
Впрочем, не всякая задача имеет точное решение, и поэтому численные вычисления тоже не забыты, причем с рядом очень приятных особенностей. Так, величина целых чисел неограничена, а вычисления с плавающей точкой могут выполняться с любой заранее заданной точностью. Хотите увидеть факториал 1000 — пожалуйста! А ведь это число с 2568 цифрами. Хотите число π с сотней знаков после запятой — никаких проблем! Главное, чтобы хватило вычислительных ресурсов компьютера. Ну и наконец, построение красивых графиков — неотъемлемая часть любой системы аналитических вычислений. Математика — наука абстрактная, а человеческое мышление образно. Хорошо известно — подавляющая часть информации поступает к человеку через зрение, поэтому без визуализации математических данных не обойтись.
Рис. 2
Помимо основных математических возможностей, каждая система
аналитических вычислений имеет встроенный язык программирования. С
помощью этого языка возможности системы можно расширять, и каждая САВ
имеет большую библиотеку пакетов для решения специальных
математических задач.
С
помощью этого языка возможности системы можно расширять, и каждая САВ
имеет большую библиотеку пакетов для решения специальных
математических задач.
Рис. 3
Посмотрим, как работает САВ не практике. На рис. 1 и 2 показано, как Maxima справляется с тремя задачками из курса школьной алгебры: упрощение тригонометрического выражения, решение системы линейных уравнений и построение графика функции y=x/[(x–1)(x2–2)]. Трехмерные графики выглядят еще интереснее. Axiom обладает своей собственной графической подсистемой, способной создавать двух- и трехмерные графики очень высокого качества. На рис. 3 изображена поверхность, известная как тригонометрический винт и построенная с помощью Axiom. А Maxima для построения графиков использует внешнюю программу gnuplot. Результат работы такой «связки» можно видеть на рис. 4. Давайте устроим маленькую математическую викторину — что за функция изображена на этом рисунке? Ответ найдете в конце статьи.
Рис. 4
Как видите, все довольно просто. Правда, и задачи тоже простые — они выбраны такими для иллюстрации. Но главная сила САВ в том, что они способны решать чрезвычайно громоздкие задачи. Например, Axiom может взять любой интеграл, если только он «берется» в элементарных функциях. Более того: в отличие от численных расчетов, являющихся по своей природе приближенными и потому не имеющих «доказательной силы» с точки зрения чистой математики, аналитические результаты, полученные с помощью САВ, вполне можно использовать для строгих математических доказательств. Но даже если вы не профессионал в математике и подобные возможности вам ни к чему, все равно использование САВ в виде интеллектуального калькулятора может быть весьма полезным.
Математика и свобода
Из далеко не полного перечисления общих возможностей САВ
ясно, что подобные программы весьма сложны и требуют для своего
создания больших усилий. Трудозатраты на такую систему оцениваются в
несколько десятков человеко-лет и требуют от программиста солидной
математической подготовки. Откуда тогда могли появиться свободные
системы аналитических вычислений Maxima и Axiom? На самом деле оба
пакета имеют весьма длительную историю.
Трудозатраты на такую систему оцениваются в
несколько десятков человеко-лет и требуют от программиста солидной
математической подготовки. Откуда тогда могли появиться свободные
системы аналитических вычислений Maxima и Axiom? На самом деле оба
пакета имеют весьма длительную историю.
Особенно любопытна «биография» Maxima. Все началось в 1967 году в Массачусетском технологическом институте. В рамках проекта создания искусственного интеллекта была инициирована разработка первой системы компьютерной алгебры Macsyma. Далее программа в течение многих лет использовалась и развивалась в университетах Северной Америки, где появилось множество вариантов системы. Maxima является одним из таких вариантов, созданным профессором Вильямом Шелтером (William Schelter) в 1982 году. В 1998 году он получил официальное разрешение Министерства энергетики США на выпуск Maxima под лицензией GPL. А начиная с 2001 года Maxima развивается как свободный международный проект, базирующийся на SourceForge.
История Axiom почти столь же долгая. Система аналитических вычислений Scratchpad развивалась с 1971 года как научный проект исследовательского центра имени Томаса Ватсона фирмы IBM. В начале 1990-х годов Scratchpad был продан фирме NAG (Numerical Algorithms Group) и переименован в Axiom. А в 2002 году NAG выпустила Axiom под свободной лицензией типа лицензии BSD (здесь можно попробовать Axiom в действии через веб-интерфейс).
Многообразие и свобода
Maxima и Axiom — полнофункциональные системы аналитических вычислений и по возможностям сравнимы с Mathematica и Maple. Тем не менее каждая из них имеет свои особенности. И в этом тоже есть элемент свободы — пользователи самого разного уровня подготовки и потребностей смогут найти себе подходящее орудие для работы.
Будучи самой первой системой аналитических вычислений, Maxima
развивалась прагматически. В результате получилась программа, довольно
простая в освоении и использовании людьми даже без специальной
подготовки. Ну а продвинутые пользователи, несомненно, оценят тесную
интеграцию Maxima с языком Lisp, на котором система реализована.
В результате получилась программа, довольно
простая в освоении и использовании людьми даже без специальной
подготовки. Ну а продвинутые пользователи, несомненно, оценят тесную
интеграцию Maxima с языком Lisp, на котором система реализована.
Maxima отлично документирована — объемное справочное руководство описывает практически все встроенные функции системы. Это руководство интегрировано в программу в виде онлайнового справочника, оснащенного средствами поиска. Не прерывая работы с Maxima, можно легко найти необходимый справочный материал. Руководство уже переведено на несколько языков, и в настоящее время переводится на русский.
Математика — наука точная. Все свойства и взаимосвязи математических объектов четко определены или доказываются при помощи строгих логических рассуждений. Axiom является единственной САВ, которая последовательно реализует данный подход на уровне компьютерной программы. Для этого язык Axiom сделан строго типизированным. Концепция строгой типизации в языках программирования хорошо известна, но в Axiom это выливается в нечто необычное — типы языка представляют собой типы математических объектов (числа, полиномы, ряды и т. д.). Axiom «знает» около тысячи иерархически организованных математических категорий и типов. Строгая математическая типизация Axiom уникальна, ничего подобного нет ни в одной другой системе аналитических вычислений.
С документацией у Axiom тоже все обстоит отлично. Имеется интерактивная гипертекстовая справка и книга, детально описывающая все аспекты работы с Axiom. Эта книга была даже издана, а новая, существенно расширенная версия свободно доступна на сайте проекта в формате PDF. К сожалению, вся документация только на английском языке.
Компьютеры и свобода
Есть еще один элемент свободы — свобода выбора
платформы. Особенно в этом отношении хороша Maxima. Она успешно
работает на всех современных операционных системах: Windows (готовые
сборки доступны на сайте проекта), Linux и UNIX, Mac OS и даже на КПК
под управлением Windows CE/Mobile. Переносимость Axiom чуть хуже:
система работает под Linux, UNIX, а под Windows пока не работает
построение графиков.
Особенно в этом отношении хороша Maxima. Она успешно
работает на всех современных операционных системах: Windows (готовые
сборки доступны на сайте проекта), Linux и UNIX, Mac OS и даже на КПК
под управлением Windows CE/Mobile. Переносимость Axiom чуть хуже:
система работает под Linux, UNIX, а под Windows пока не работает
построение графиков.
Главную роль в переносимости Maxima и Axiom играет язык Lisp, на котором они написаны. Исторически Lisp имеет очень большое количество несовместимых друг с другом диалектов, но сейчас эпоха разнообразия закончилась, поскольку появился официальный стандарт ANSI Common Lisp. Maxima была модифицирована в соответствии с этим стандартом, и в результате она может работать под управлением разных реализаций Common Lisp, как свободных, так и проприетарных. Axiom пока работает только с GCL (GNU Common Lisp), но принципиальных сложностей с переносом на другие Common Lisp системы не существует.
Компьютеры и человек
До сих пор мы говорили о математических возможностях Axiom и Maxima.Но есть еще один важный аспект — взаимодействие с программой. Традиционно все системы аналитических вычислений, включая Axiom, Maxima, а также Maple и Mathematica, имеют простой текстовый интерфейс. И это создает определенные проблемы — как отобразить в удобочитаемом виде математические выражения со всеми их радикалами, скобками и знаками интегралов? Приходится прибегать к своеобразному ASCII Art. Пример того, что получается, представлен на рис. 5, где изображен результат вычисления интеграла и произведения в системе Axiom. Довольно неплохо, но вряд ли вполне соответствует современным потребностям. Поэтому все системы аналитических вычислений имеют графические пользовательские оболочки, способные представить данные красиво и облегчающие взаимодействие с пользователем.
Рис.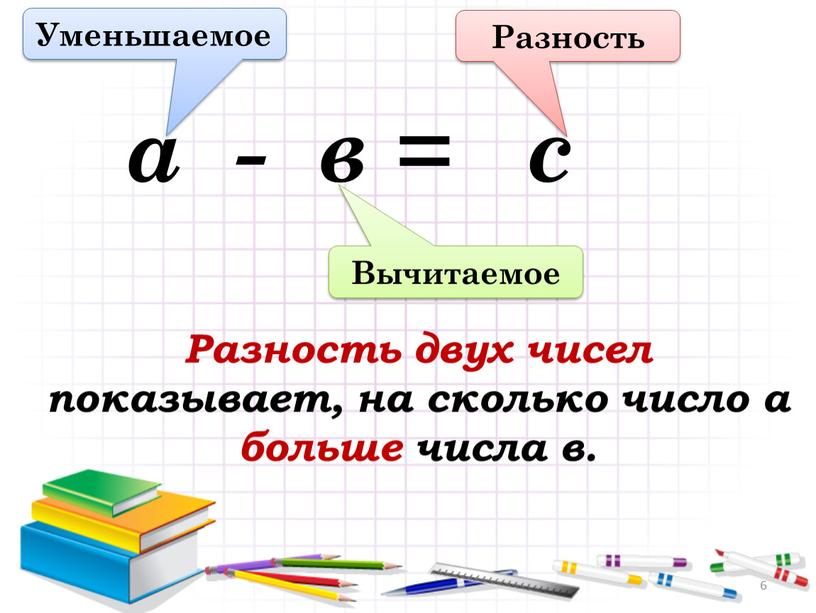 5
5
Одной из таких оболочек для Axiom и Maxima является TeXmacs. TeXmacs — это вполне самостоятельная программа, научный WYSIWYG-редактор. Помимо своего основного назначения, он может использоваться как графическая оболочка для ряда программ с текстовым интерфейсом. На рис. 6 изображена работа Axiom под управлением TeXmacs: те же самые интеграл и произведение, что и на рис. 5.
У Maxima есть несколько других оболочек, лучшей из которых является wxMaxima. На рис. 1 — работа Maxima под управлением wxMaxima. Тем не менее нужно признать, что по функциональности графические оболочки свободных систем аналитических вычислений пока уступают коммерческим аналогам.
И это не конец
Axiom и Maxima — результат коллективного труда сотен людей. Несмотря на свой солидный возраст, системы продолжают активно развиваться. Новые релизы Axiom выпускаются каждые несколько месяцев, ежегодно проводится семинар, целиком посвященный Axiom.
Рис. 6
Последний релиз Maxima 5.9.3 выпущен 19 марта текущего года, спустя пять месяцев после предыдущего. Интерес к обеим системам со стороны как пользователей, так и разработчиков весьма отраден: уже сейчас в руках исследователей-математиков есть очень мощные свободные инструменты, которые со временем будут становиться только лучше.
И наконец, ответ на вопрос мини-викторины: на рис. 4 изображен график модуля гамма-функции на комплексной плоскости в районе 0.
Что такое навыки математических вычислений?
Навыки математических вычислений включают то, что многие люди называют базовой арифметикой: сложение, вычитание, умножение и деление. Вообще говоря, вычисления влекут за собой поиск ответа на проблему с помощью математики или логики. Их могут выполнять не только люди, но и калькуляторы или компьютеры.
Важность математических вычислений
Однако даже при наличии современных технологий навыки математических вычислений остаются неотъемлемой частью математического образования учащихся, поскольку они закладывают основу для успеха в будущем обучении математике, такой как алгебра, геометрия, тригонометрия и исчисление. .Они также важны, потому что они позволяют учащимся — как взрослым — легко ориентироваться в повседневных жизненных задачах, таких как определение цены уцененных товаров, выяснение того, какой размер товара обеспечивает наилучшее соотношение цены и качества, и точное удвоение или сокращение вдвое рецептов приготовления пищи, и это лишь некоторые из них.
.Они также важны, потому что они позволяют учащимся — как взрослым — легко ориентироваться в повседневных жизненных задачах, таких как определение цены уцененных товаров, выяснение того, какой размер товара обеспечивает наилучшее соотношение цены и качества, и точное удвоение или сокращение вдвое рецептов приготовления пищи, и это лишь некоторые из них.
Развитие вычислительных навыков
Навыки математических вычислений обычно вводятся в начальных классах начальной школы в следующем порядке: сложение, вычитание, умножение и затем деление.Учителя часто укрепляют навыки математических вычислений с помощью игр, тестов на время и упражнений. Новое обучение основывается на предшествующих знаниях и постоянно зависит, пока учащиеся не овладеют всеми четырьмя навыками. Например, задачи могут быть достаточно простыми, чтобы их можно было решить мысленно, например 5–2, или многоэтапные задачи, требующие карандаша и бумаги, например 3–4 * 17–8.
Не только целые числа
Требуются вычислительные навыки. не только для целых чисел, но и для десятичных, дробных, смешанных чисел, процентов, соотношений и пропорций.Они включают в себя арифметические операции с этими типами чисел, а также преобразования между ними: например, изменение дроби на процент. Математические вычисления также включают округление и оценку.
образование — Что означает «математика вычислений»?
Мне кажется, что этот журнал посвящен вычислительной математике и численным методам. Мы говорим о прикладной математике в области вычислений . Вычисление в этом смысле означает, что вычисляет что-то .Это не обязательно означает, что мы используем современный ПК на базе транзисторов, но это часто связано.
Математика — довольно точный предмет, но когда дело доходит до фактического вычисления числовых значений, мы сталкиваемся с проблемами. Как люди, наше решение — разработать инструменты: каменные таблички, счеты, карандаш и бумагу, логарифмическую линейку, карманный калькулятор, компьютер. У этих инструментов есть достоинства и недостатки.
У этих инструментов есть достоинства и недостатки.
Современные ПК — невероятно быстрые компьютеры, но есть ограничения.Возьмем, к примеру, скорость. Мы всегда стремимся к более мощным технологиям, но часть этих исследований заключается в оптимизации уже существующих алгоритмов. Например, вы можете знать, что матрицы и компьютерная графика тесно связаны. Обработка изображений и рендеринг графики, насколько мне известно, сводятся к линейной алгебре. Даже простая операция, такая как умножение матриц, может превратиться в обременительную задачу для компьютера, когда размеры матрицы становятся все больше. Чтобы преодолеть эти ограничения, мы разрабатываем более эффективные алгоритмы.
Еще одно ограничение заключается в конечном характере вычислительных вычислений. Как мы выполняем, скажем, интегрирование, когда речь идет о неточных значениях и проблемах с незамкнутой формой? Или забудьте об этом, как мы обрабатываем непрерывных вещественных переменных? Мы могли бы, например, использовать методы конечных разностей. Большинство нелинейных систем дифференциальных уравнений основано на таких методах.
Чаще всего приходится жертвовать числовой точностью ради практичности. Любой, кто использовал $ \ pi \ приблизительно 3.В этом виноват 14 $! Используя численные методы, мы часто вынуждены признать, что точные значения — несбыточная мечта. Я говорю это, даже не затрагивая тему ошибки с плавающей запятой …
… который приведет нас к информатике. Во всяком случае, вычислительная математика также может справиться с устранением этих недостатков.
Это те виды математики, которые, вероятно, исследуются в журнале как в теоретическом, так и в прикладном смысле.
Что такое вычисления? — Глава книги
Эта книга о вычислениях в контексте научных исследований.Ученые всегда должны стараться быть точными в том, что они говорят, поэтому я начну с объяснения того, что на самом деле означает этот термин. Оказывается, это не так тривиально, как может показаться. Более того, есть также прагматические причины для обсуждения природы вычислений, потому что хорошее понимание того, что на самом деле вычисление есть , значительно упрощает понимание того, для чего оно может и не может использоваться в научных исследованиях.
Оказывается, это не так тривиально, как может показаться. Более того, есть также прагматические причины для обсуждения природы вычислений, потому что хорошее понимание того, что на самом деле вычисление есть , значительно упрощает понимание того, для чего оно может и не может использоваться в научных исследованиях.
Определения вычислений в общем словаре чрезвычайно неточны.Оксфорд предлагает «действие математических вычислений» или «использование компьютеров, особенно в качестве объекта исследования или изучения». У Merriam-Webster есть «действие или действие вычислений: вычисление» или «использование или работа компьютера», но также и «система расчетов». Оба словаря относятся к «вычислению», но также не дают полезных определений для этого слова. Расплывчатость этих словарных определений может быть прослежена до давней путаницы в отношении того, что такое вычисления и как они соотносятся с математикой.Только развитие формальной логики и математического формализма в начале 20 века привело к точному определению вычислений, что помогло проложить путь к развитию автоматических вычислительных машин. Это определение является темой раздела 1.1.
Помимо изучения того, что определяет вычисления, я также рассмотрю, что такое вычисления для ученых, т.е. , почему вычисления так важны в научных исследованиях. Большинство ученых, вероятно, думают о компьютерах и вычислениях как об инструментах, которые они используют для обработки экспериментальных данных или математических уравнений.Однако есть и другие роли, которые вычисления играют в науке, о которых я кратко расскажу в разделе 1.2.
1.1.1. Числовые вычисления
Наиболее знакомые вычисления — это числовые вычисления, которые мы все делаем в повседневной жизни: складывание цен, умножение длины и ширины комнаты для вычисления ее площади, деление количества на равные части и т. Д. Большинство людей сегодня имеют еще больше поводов для численных расчетов в своей профессиональной жизни. Базовая арифметика для всего, что можно выразить количественно, настолько фундаментальна, что занимает значительную часть обучения в первые годы обучения в школе.Механические вспомогательные средства для числовых операций, такие как счеты, использовались не менее 2000 лет, а, возможно, даже намного дольше.
Базовая арифметика для всего, что можно выразить количественно, настолько фундаментальна, что занимает значительную часть обучения в первые годы обучения в школе.Механические вспомогательные средства для числовых операций, такие как счеты, использовались не менее 2000 лет, а, возможно, даже намного дольше.
Мы не особо задумываемся о том, как мы выполняем простые арифметические операции с небольшими числами, и на самом деле мы часто просто вспоминаем результат, который мы усвоили из-за частого использования. Но как только мы работаем с большими числами, мысленный расчет становится механической деятельностью, основанной на правилах, которые мы усвоили. Пример такого правила: умножить число на 9, умножить на 10, а затем вычесть исходное число.
Когда операции становятся слишком сложными для обработки в голове, мы обращаемся к ручке и бумаге для более надежной записи промежуточных результатов в наших расчетах. На протяжении веков было разработано большое количество вычислительных техник с ручкой и бумагой, начиная от сложения через длинное деление и заканчивая вычислением кубических корней.
В качестве простого примера рассмотрим сложение чисел 173 и 51. Один из способов сделать это систематически начинается с написания одного под другим, добавления нулей слева от меньшего числа, чтобы количество цифр было равным:
Затем мы обрабатывать цифры справа налево, начиная с добавления 3 и 1.Мы «знаем», что результат 4, потому что мы так часто делали. Но что касается чуть более сложной операции умножения, большинство читателей, вероятно, помнят, как они запоминали таблицы умножения в школе — таблицы, которые фактически были напечатаны в книгах. Чтобы быть точным в нашем описании сложения, мы будем использовать столь же явную таблицу сложения для однозначных целых чисел:
Нам действительно нужны две таких таблицы, вторая — для цифры переноса, которая равна 1, когда сумма двух цифр равна 10 или больше, в противном случае — 0.Мы отмечаем однозначную сумму и цифру переноса и переходим влево для обработки следующей цифры:
Этот метод и все другие арифметические операции, которые мы используем, основываются на позиционной записи чисел, которая используется повсюду. мир сегодня. Любое натуральное число может быть записано как последовательность цифр от 0 до 9. Другой символ, знак минус, учитывает отрицательные целые числа, а еще один символ, десятичная точка или косая черта деления, позволяет выражать дроби.Затем правила арифметики можно сформулировать как правила для управления последовательностями символов, как показано выше для сложения, которые можно применять механически.
мир сегодня. Любое натуральное число может быть записано как последовательность цифр от 0 до 9. Другой символ, знак минус, учитывает отрицательные целые числа, а еще один символ, десятичная точка или косая черта деления, позволяет выражать дроби.Затем правила арифметики можно сформулировать как правила для управления последовательностями символов, как показано выше для сложения, которые можно применять механически.
1.1.2. От чисел к символам
Действительно важно понимать, что описанный выше метод работает не с числами , а с конкретным представлением чисел. Числа — это абстрактное понятие, которым нельзя управлять с помощью механических правил. Различные представления приводят к различным методам выполнения арифметических операций.Несмотря на то, что строка десятичных символов «42», строка римско-цифровых символов «XLII» и строка символов английского языка «сорок два» относятся к одному и тому же числу, ими нельзя управлять одинаковым образом. Фактически, наш рецепт сложения никогда не относится к числам. Он принимает две последовательности цифр на входе и производит одну последовательность цифр на выходе. Применение рецепта не требует знания чисел, только умение работать с конечным набором символов и применять к ним правила.
Рецепт решения конкретной проблемы путем манипулирования символами называется алгоритмом . Слово происходит от имени персидского математика аль-Хваризма, жившего в 9 веке. Его книга, описывающая «индийские числа», которые сегодня мы называем арабскими цифрами, ввела нашу современную десятичную систему счисления и ее правила для арифметики в Европу [1]. Использование этой системы в позднем средневековье называлось «алгоритмом», а позже орфография и значение трансформировались в сегодняшний «алгоритм».Позиционная запись чисел превратила арифметику из сложного ремесла, выполняемого подготовленными специалистами, в рутинную задачу, с которой мог справиться почти каждый.
Сегодня десятичное представление чисел кажется нам настолько очевидным, что мы часто не делаем различия между числом и его десятичным представлением. Это явление не ограничивается числами. Мы также редко проводим четкое различие между словом и его значением, и в квантовой физике, если привести пример из науки, путаница между квантовым состоянием и одним из его множества возможных представлений очень распространена.Размышляя о вычислениях, часто важно вспомнить, что вселенная символов и вселенная значений разделены. В информатике это известно как различие между синтаксисом и семантикой . Синтаксис определяет, с какими последовательностями символов работает конкретный алгоритм, например «последовательность из любого числа цифр от 0 до 9». Семантика определяет, как интерпретируются такие последовательности символов, например, «натуральное число». Чтобы применить наш алгоритм сложения двух натуральных чисел, не требуется никаких знаний семантики, но важно понимать, что алгоритм делает, и в частности, какие проблемы он может помочь решить.
Признаком путаницы между числами и их представлениями является популярная поговорка, что «компьютеры работают только с числами». Это явно неверно: то, над чем работают современные цифровые компьютеры, — это последовательности битов, бит представляет собой символ из алфавита, состоящего из двух символов. Мы часто выбираем цифры 0 и 1 для представления этого алфавита, предлагая интерпретацию как двоичные числа, то есть числа, представленные в позиционной системе счисления с основанием 2. Идея о том, что компьютеры работают с числами, ошибочна, поскольку биты могут одинаково хорошо представлять информацию, отличную от чисел. .Это также вводит в заблуждение еще одним способом, потому что предполагает, что любую проблему, связанную с числами, можно решить с помощью компьютера. Однако большинство чисел не могут быть представлены последовательностями битов и, следовательно, не могут входить в какие-либо вычисления.
Легко видеть, что биты могут представлять любую информацию, которая вообще может быть записана как последовательности символов. Предположим, у нас есть алфавит с N символами, например N = 26 букв английского алфавита. Затем мы можем составить таблицу перевода, которая присваивает уникальный набор значений для пяти битов каждому символу в нашем алфавите.С пятью битами у нас есть разные значения, поэтому шесть значений останутся неиспользованными. Наша таблица перевода позволяет кодировать любое английское слово в виде битовых последовательностей.
Менее очевидно и, возможно, даже удивительно для многих читателей, что большинство чисел не могут быть представлены в виде битовых последовательностей. Для натуральных чисел проблем нет: любую последовательность битов можно интерпретировать как натуральное число в системе счисления с основанием 2. И наоборот, каждое натуральное число может быть записано в системе счисления с основанием 2 и, следовательно, как последовательность битов.Таким образом, можно определить взаимно однозначное соответствие между натуральными числами и битовыми последовательностями. В математической терминологии набор натуральных чисел изоморфен набору битовых последовательностей. Поскольку мы можем выполнять вычисления с последовательностями битов, мы можем выполнять вычисления с натуральными числами. Фактически, любой набор значений, над которым мы хотим произвести вычисления, должен быть изоморфен набору битовых последовательностей или, что эквивалентно, набору натуральных чисел или подмножеству такого набора. Такие наборы называются счетными .Все конечные множества являются счетными: просто запишите элементы в определенном порядке, а затем напишите число ниже для каждого элемента, начиная с 1. Бесконечные счетные множества называются счетно бесконечными наборами.
Нетрудно убедиться, что целые числа по-прежнему можно считать: используйте один бит для знака, а затем последовательность битов натурального числа для абсолютного значения. Требуется немного больше усилий, чтобы показать, что рациональные числа, то есть множество всех частных целых чисел, являются счетными.По определению счетности, это требует присвоения уникального натурального числа каждому рациональному числу. Стандартная процедура основана на двумерном матричном расположении рациональных чисел:
Требуется немного больше усилий, чтобы показать, что рациональные числа, то есть множество всех частных целых чисел, являются счетными.По определению счетности, это требует присвоения уникального натурального числа каждому рациональному числу. Стандартная процедура основана на двумерном матричном расположении рациональных чисел:
Элементы этой бесконечной матрицы теперь могут быть пронумерованы по диагоналям:
Более сложная схема перечисления пропускала бы каждое число, равное тот, который уже получил индекс ранее. Например, будет пропущено, потому что оно равно.
Доказательство того, что набор действительных чисел — это , а не , является более сложным, и я не буду воспроизводить его здесь. Как и многие другие доказательства, касающиеся бесконечных множеств, оно восходит к Георгу Кантору, немецкому математику, который заложил основы теории множеств в конце 19 века и фактически дал первое строгое определение действительных чисел. Комплексные числа, являющиеся надмножеством действительных чисел, также неисчислимы. Однако есть счетные числа, превышающие рациональные числа.В математике хорошо известен набор из алгебраических чисел , определенных как корни многочленов с целыми коэффициентами. В контексте вычислений наибольшее полезное счетное подмножество действительных чисел — это набор из вычислимых чисел , который был введен Аланом Тьюрингом в той же публикации 1936 года, что и машина Тьюринга. Я вернусь к этому вопросу в главах 2 и 3, потому что он имеет центральное значение для использования вычислений в науке.
Теперь мы можем записать первое определение вычисления, которое будет уточнено в главе 3:
Вычисление — это преобразование последовательностей символов в соответствии с точными правилами.
Что потребует уточнения, так это «точные правила», которые должны быть выражены так точно, чтобы машина могла их применять однозначно.
1.
 1.3. Нечисловые вычисления
1.3. Нечисловые вычисленияКак только мы избавимся от идеи, что вычисления связаны с числами, мы можем легко идентифицировать другие операции, которые квалифицируются как вычисления. Один из примеров — решение уравнений с помощью алгебраических манипуляций. Шаги от
до
полностью механические и могут быть сформулированы в виде алгоритма.Практическое доказательство того, что компьютеры могут выполнять эту работу. Программные пакеты, реализующие такие операции, называются системами компьютерной алгебры , делая упор на алгебраические манипуляции. Однако системы компьютерной алгебры также выполняют другие нечисловые алгоритмы, например, поиск производной или интеграла элементарной функции. Алгоритм вычисления производных прост и преподается в каждом курсе исчисления. Напротив, алгоритм вычисления неопределенных интегралов очень сложен [2] и был реализован в виде компьютерной программы только в 1987 году [3].
Возможно, более удивительное использование вычислений в математике — это проверка доказательств. Доказательство — это последовательность шагов дедукции, каждый из которых устанавливает истинность утверждения на основе других утверждений, уже известных как истинные, и конечного набора правил логической дедукции. В учебниках и математических публикациях доказательства написаны кратко для читателей-людей, у которых есть предварительные знания математики. Но когда все детали изложены, доказательства состоят только из применения конечного набора правил дедукции.Эти правила применяются к утверждениям, которые должны соответствовать правилам формального языка. Использование компьютеров для проверки таких подробных доказательств становится все более и более распространенным, как в математических исследованиях, так и в промышленных приложениях. Это включает в себя запись доказательства на каком-то формальном языке в виде последовательности символов. Вычисление «проверка доказательства» преобразует эту последовательность символов в «истинное» или «ложное» утверждение о действительности доказательства.
Оставляя узкую область математики, мы обнаруживаем огромное количество областей, в которых вычисления применяются к текстовым данным.Поиск слова в тексте — это вычисление: оно преобразует входные данные (текст и слово для поиска) в выходные данные (положение в тексте, где встречается слово), оба из которых могут быть закодированы как последовательности символов. . Точно так же выравнивание двух последовательностей ДНК, перевод предложения с английского на французский или компиляция программы на языке Fortran — это вычисления, в которых обрабатываемые данные являются текстом. Фактически, числа и текст — это два типа элементарных данных, из которых почти все остальное состоит из композиции: изображения представлены в виде двумерных массивов чисел, словари — в виде наборов пар слов и т. Д.Однако эта фундаментальная роль чисел и текста обусловлена их важностью для людей, а не компьютеров.
Другой вид данных, которые становятся все более важными для научных вычислений, — это графики, в частности, когда они используются для описания сетей. Транспортный поток, взаимодействия белков в клетке и молекулярные структуры — все это примеры того, что можно описать с помощью графиков. Пример вычисления на графах — проверка на циклы. Это преобразует входные данные (график) в выходные данные (список всех циклов на графике).Кодирование графиков, циклов и списков как последовательностей символов не так очевидно, как кодирование чисел и текста. Люди уже представляли числа и текст последовательностями символов задолго до того, как задумывались о компьютерах и вычислениях. С другой стороны, человеческое представление графиков принимает форму двухмерных рисунков. Точные методы представления графов в виде последовательностей символов выходят за рамки этой книги, но я вернусь к общему вопросу о представлении информации в компьютерах в разделе 5.3.2.
Вычисления как инструмент
Наиболее заметная роль вычислений в научных исследованиях — это их использование в качестве инструмента. Экспериментаторы обрабатывают свои необработанные данные, например, чтобы исправить артефакты своего оборудования. Затем они подгоняют теоретическую модель к своим данным, корректируя параметры. Теоретики вычисляют численные прогнозы на основе модели, чтобы сравнить их с экспериментальными результатами. И экспериментаторы, и теоретики активно используют вычисления для понимания своих данных, в частности, используя методы визуализации.
Экспериментаторы обрабатывают свои необработанные данные, например, чтобы исправить артефакты своего оборудования. Затем они подгоняют теоретическую модель к своим данным, корректируя параметры. Теоретики вычисляют численные прогнозы на основе модели, чтобы сравнить их с экспериментальными результатами. И экспериментаторы, и теоретики активно используют вычисления для понимания своих данных, в частности, используя методы визуализации.
Стоит проводить различие между вычислением как инструментом и компьютером как инструментом. Компьютеры выполняют вычисления, но они также решают другие задачи. Ученые используют компьютеры для общения со своими коллегами, поиска информации в Википедии и для управления лабораторным оборудованием. Ни одна из этих задач не требует видимых вычислений, хотя вычисления выполняются под капотом. Сегодняшние компьютеры — это такие же коммуникационные устройства, как и вычислительные устройства.
Вычисления для понимания
Ричард Фейнман написал на своей доске: «То, что я не могу создать, я не понимаю». Мы не сможем понять теорию, модель или приближение, если не сделаем с ними что-то. Один из способов получить опыт работы с математическими моделями — применить их к конкретным ситуациям. Другой, даже более мощный, — реализовать их в виде компьютерных программ. Дональд Кнут очень лаконично выразился [4]:
Часто говорят, что человек действительно чего-то не понимает, пока не научит этому кого-то другого.На самом деле человек действительно чего-то не понимает, пока не научит этому компьютер, то есть выразит это в виде алгоритма. Попытка формализовать вещи как алгоритмы ведет к гораздо более глубокому пониманию, чем если бы мы просто пытались понять вещи традиционным способом.
Полезность написания программ для понимания научных концепций и математических моделей проистекает из крайней строгости и точности, необходимых при программировании. Общение между людьми основывается на общих знаниях, начиная с определения слов повседневного языка.Типичная научная статья предполагает, что читатель обладает значительными специальными знаниями в области естественных наук и математики. Даже математическое доказательство, вероятно, самый точный вид утверждения в научной литературе, предполагает, что читателю известно множество определений и теорем, даже без их списка. У компьютера нет таких предварительных знаний. Мы должны общаться с компьютером на формальном языке, который точно определен. Каждый аспект нашей науки, который так или иначе влияет на результат вычислений, должен быть выражен на этом формальном языке, чтобы получить работающую компьютерную программу.
Общение между людьми основывается на общих знаниях, начиная с определения слов повседневного языка.Типичная научная статья предполагает, что читатель обладает значительными специальными знаниями в области естественных наук и математики. Даже математическое доказательство, вероятно, самый точный вид утверждения в научной литературе, предполагает, что читателю известно множество определений и теорем, даже без их списка. У компьютера нет таких предварительных знаний. Мы должны общаться с компьютером на формальном языке, который точно определен. Каждый аспект нашей науки, который так или иначе влияет на результат вычислений, должен быть выражен на этом формальном языке, чтобы получить работающую компьютерную программу.
Другая причина, по которой написание программы часто бывает полезным для понимания математической модели, заключается в том, что алгоритм обязательно конструктивен. В физических науках большинство теорий принимает форму дифференциальных уравнений. Эти уравнения полностью определяют свои решения, а также полезны для рассуждений об их общих свойствах, но не предоставляют очевидного способа найти решение . Написание компьютерной программы требует, прежде всего, думать о том, что эта программа делает , а затем о , как она должна это делать.
Реализация научной модели в виде компьютерной программы также имеет то преимущество, что в качестве бонуса вы получаете инструмент для изучения последствий модели для простых приложений. Компьютерное исследование — еще один хороший способ лучше понять научную модель (некоторые выдающиеся примеры см. В [5, 6]). При изучении сложных систем с моделями, которые непосредственно формулируются в виде алгоритмов, вычислительные исследования часто являются единственным способом получения научного понимания [7].
Вычисления как форма научного знания
Компьютерная программа, реализующая теоретическую модель, например программа, написанная с целью понимания этой модели, является своеобразным письменным представлением этой модели. Следовательно, это выражение научных знаний, во многом как учебник или журнальная статья. В следующих главах мы увидим, что многие научные знания могут быть выражены в форме компьютерных программ, и что большая часть сегодняшних научных знаний существует на самом деле только в форме компьютерных программ, потому что традиционные представления научных знаний не могут справиться со сложными структурированная информация.Это поднимает важные вопросы для будущего вычислительной науки, к которым я вернусь в главе 6.
Следовательно, это выражение научных знаний, во многом как учебник или журнальная статья. В следующих главах мы увидим, что многие научные знания могут быть выражены в форме компьютерных программ, и что большая часть сегодняшних научных знаний существует на самом деле только в форме компьютерных программ, потому что традиционные представления научных знаний не могут справиться со сложными структурированная информация.Это поднимает важные вопросы для будущего вычислительной науки, к которым я вернусь в главе 6.
Вычисление как модель обработки информации в природе
Компьютеры — это физические устройства, разработанные инженерами для выполнения вычислений. Многие другие спроектированные устройства также выполняют вычисления, хотя обычно с гораздо более ограниченными возможностями. Классическим примером из учебников по информатике является торговый автомат, который преобразует действия оператора (нажатие кнопок, вставка монет) в действия (доставка товаров) — задача, требующая вычислений.Конечно, торговый автомат делает больше, чем просто вычисления, и мы, как пользователи, больше всего заинтересованы в этом дополнительном поведении. Тем не менее обработка информации и, следовательно, вычисления — важный аспект работы машины.
То же самое можно сказать и о многих системах, встречающихся в природе. Хорошо известным примером является процесс деления клеток, общий для всех биологических организмов, который включает копирование и обработку информации, хранящейся в форме ДНК [8]. Другой пример биологического процесса, основанного на обработке информации, — рост растений [9].У большинства животных есть нервная система, часть тела, которая почти полностью посвящена обработке информации. Неврология, изучающая нервную систему, тесно связана как с биологией, так и с информатикой. Это также верно в отношении когнитивной науки, которая занимается процессами человеческого разума, которые все чаще моделируются с помощью вычислений.
Конечно, живые организмы — это не , а компьютера. Обработка информации в организмах неразрывно связана с другими процессами.Фактически, идентификация вычислений как изолированного явления и их реализация с помощью сконструированных устройств, которые выполняют точные вычисления любое количество раз, с минимальной зависимостью от окружающей среды, насколько это технически возможно, является отличительной чертой человеческой инженерии, не имеющей аналогов. в природе. Тем не менее, сосредоточение внимания на вычислительных аспектах жизни и написание компьютерных программ для моделирования обработки информации в живых организмах внесло значительный вклад в лучшее понимание их функций.
В гораздо более широком масштабе можно рассматривать все физические законы как правила обработки информации и заключить, что вся Вселенная — это гигантский компьютер. Эта идея была впервые предложена в 1967 году немецким пионером компьютеров Конрадом Цузе [10] и дала начало области исследований под названием цифровая физика , расположенная на пересечении физики, философии и информатики [11].
Вычисления уходят корнями в числа и арифметику, историю, рассказанную Жоржем Ифра в «Всеобщей истории чисел » [12].
Использование вычислений для понимания было подчеркнуто в контексте физики Сассманом и Уиздом [13]. Они разработали оригинальный подход к обучению классической механике с помощью вычислений [14]. Компьютерное программирование также начинает интегрироваться в учебные программы по естествознанию из-за его полезности для понимания. См., Например, учебник Лангтангена [15].
Вычисления и стратегии решения проблем | Американская федерация учителей
Одна из самых сложных областей, которую определили для внешкольного персонала, — это помощь ученикам с математикой.Мы включаем несколько советов, как помочь студентам, которых обучают вычислениям, с некоторыми новыми и более традиционными стратегиями. Мы также предлагаем модель, помогающую учащимся осмыслить словесные проблемы, возникшие в странах Восточной Азии с высокими успеваемостями.
A. Стратегии, основанные на использовании и построении чувства числа
Сложение и вычитание: работа с десятками
Помогите учащимся использовать числа, с которыми легко работать. Заставьте самых молодых работать с 10. Легко складывать в уме числа, оканчивающиеся на ноль.Студенты должны хорошо освоиться со всеми комбинациями, составляющими 10!
| Задача | Математическое мышление |
| Чтобы превратить 9 в 10, вам нужно еще 1, поэтому думайте о 6 как о 1 и 5. | |
| Чтобы превратить 27 в 30 вам нужно 3. Разделите 18 на 3 и 15. | |
| Чтобы вычесть из 10, сначала уберите 4 единицы. См. 6 как 4 и 2. | |
Легко вычесть числа, оканчивающиеся на ноль.Вычтем 40. Но мы вычли 2 слишком много. Мы должны вернуть их сейчас. |
B. Умножение и деление
Дети должны понимать, что умножение — это подсчет по группам вещей, причем каждая группа имеет одинаковое количество. Помогите им увидеть, как строятся таблицы, по одной группе за раз. Вот некоторые стратегии решения, которые помогают учащимся понять алгоритм умножения:
1. Постройте массив, чтобы показать значение умножения.
(4 ряда по 12)
4 x 12 | Математическое мышление |
| OOOOOOOOOOOO OOOOOOOOOO 902OOOO19 ОООOOOOOOO 902OOOOOO19 рядов OOOOOOOOOO 902OOOOOO19 ООООООО 902OOOO19 24 3 строки содержат 36 4 строки содержат 48 |
2. Т-образные столы. Эти числа могут быть записаны в t-таблицу, которая придает смысл таблицам умножения.
Позже студенты могут начать рассуждать с такими таблицами, и им не нужно будет записывать все числа.
12 коробок по 18 штук в коробке | ||
| Кол-во уп. | № Артикулы | Рассуждения |
| 1 | 18 | Дано |
| 2 | 36 | Добавить еще 18 |
| 4 2 коробки | ||
| 6 | 108 | Добавьте суммы в 2 и 4 коробки |
3.Модели с областями
Эти модели более абстрактны и могут позволить учащимся видеть частичные продукты и в конечном итоге могут быть связаны с традиционным алгоритмом.
Начните с построения модели массива с блоками base-10. Для этого учащиеся должны знать, как разбивать числа по разрядам. Вот иллюстрация для 24 x 45. (Вы бы начали с чего-нибудь попроще, например, 8 x 12.)
24 разделено на 20 и 4. 45 разделено на 40 и 5.
9027 9027 9027 9027 9027 9027 9027 100 8 10 9027| Х | 40 | 5 | |||||||||||||
| 20 | 100 | 100 | 100 | 100 | 10 | 10 | 10 | 100 | 100 | 100 | 10 | 10 | 10 | 10 | 10 |
| 4 | 10 | 10 | 1 | 1 | 1 | 1 | |||||||||
| 10 | 10 | 10 | 10 | 1 | 1 | 1 | 1 | 1 | |||||||
| 10 | 10 | 10 | 1 | 1 | 1 | 1 | 1 | ||||||||
| 10 | 10 | 10 | 1 | 1 | 1 | 1 | |||||||||
Всего восемь 100 блоков или 8 x 100 = 800. Есть 26 блоков по 10 или 26 x 10 = 260. Есть 20 блоков по 1 или 20 x 1 = 20.
Есть 26 блоков по 10 или 26 x 10 = 260. Есть 20 блоков по 1 или 20 x 1 = 20.
800
260
+ 20
1080
В конце концов ученики разбивают числа и рисуют четыре больших блока. Это отражает фундаментальное свойство распределения.
| 40 + 5 | ||
20 + 4 | 20×40 9 80022800207 | |
4×40 160 | 4×5 20 | |
800 + 160 = 960 100 + 20 = 120
9602 + 120 может связать числа из модели площади с задачей умножения.Сначала держите полные количества на виду. Это 20 умножить на 40, а не на 2 умножить на 4. Когда этот уровень станет чистым, сделайте то же самое, но покажите, как вы можете начать вычисление с одного места. Продолжайте записывать полные количества. Наконец, когда эта процедура станет удобной, покажите, что традиционный алгоритм — это еще один способ сделать то же самое. На этот раз записываются не все частичные продукты. В голове какое-то воспоминание, что у тебя десятки больше. Что очень сложно, так это то, что они не могут быть добавлены к разряду десятков, пока это умножение не будет выполнено.Учащимся, которые испытывают трудности с «перемещением» или с запоминанием, когда добавлять перегруппированные числа, следует разрешить записывать полные числа как частичные произведения.
4. Division
Язык, используемый для разделения, может быть препятствием для понимания учащимися, что такое разделение. Например, сказать «9 переходит в 81, 9 раз» сложно представить. Что это обозначает? Почему он «входит» так много раз? Вместо этого спросите, сколько групп из 9 человек в 81?
Прежде чем учащихся заставят думать абстрактно, помогите им понять, что означают эти числа. Поскольку деление — это обратное умножение, мы по-прежнему имеем дело с группами. В задаче 3528, разделенной на 24, они находят, сколько групп из 24 есть в 3528 или сколько групп размером 24 может быть создано. Может быть 100? Безусловно. 100 x 24 — это 2400. Остается 1 128. Тогда некоторые студенты могут узнать, что их еще как минимум 20. Другие могут продолжать думать еще по 10 штук за раз.
Поскольку деление — это обратное умножение, мы по-прежнему имеем дело с группами. В задаче 3528, разделенной на 24, они находят, сколько групп из 24 есть в 3528 или сколько групп размером 24 может быть создано. Может быть 100? Безусловно. 100 x 24 — это 2400. Остается 1 128. Тогда некоторые студенты могут узнать, что их еще как минимум 20. Другие могут продолжать думать еще по 10 штук за раз.
По мере того, как они решают проблему, помогите им понять, что уже было учтено и сколько еще осталось для объединения в группы.
Вычислительная математика | Карьерное образование и развитие
Вы всегда были очарованы компьютерами и сложными математическими алгоритмами, управляющими их процессами? Вы хотите превратить свою страсть к математике в карьеру, создавая реальные приложения и осязаемые технологии? Получение специализации по программе Specialized Honors BSc по вычислительной математике познакомит вас с основными принципами использования компьютеров для решения и выполнения повседневных задач, таких как Интернет, различных распространенных технологий и применения научной теории на практике.Кроме того, вы сможете сосредоточить свое обучение и выбрать между специализацией в прикладной и промышленной математике или финансовой математике.
Варианты карьеры в области вычислительной математики
Ниже приведен примерный список некоторых будущих вариантов для изучения следующих исследований по вычислительной математике. Этот список не является исчерпывающим, но он дает твердое представление о том, чем поступили другие выпускники и какую потенциальную карьеру может предложить степень по вычислительной математике. Некоторые варианты более напрямую связаны с конкретными областями вычислительной математики, чем другие.
- Инженер по банковскому программному обеспечению
- Брокер
- Бизнес-консультант
- Бизнес-аналитик
- Инженер по вычислительной технике
- Программист
- Специалист по компьютерному моделированию
- Товарный трейдер
- Корпоративный стратег
- Предприниматель
- Инженер
- Финансовый аналитик
- Следователь по расследованию финансовых преступлений
- Финансовый юрист
- Советник по финансовой политике
- Генетик
- Конструктор оборудования
- Управляющий хедж-фондом
- Разработчик страховых продуктов
- Аналитик по международной безопасности
- Инвестиционный банкир
- Математик
- Маркетолог
- Корреспондент СМИ
- Медицинский исследователь
- Операционный менеджер
- Менеджер по заработной плате
- Управляющий пенсионным фондом
- Профессор
- Руководитель проекта
- Исследователь
- Риск-аналитик
- Разработчик программного обеспечения
- Статистик
- Исследователь системных операций
- Разработчик веб-сайтов
Важно помнить, что для некоторых из этих вариантов карьеры может потребоваться дополнительное образование или подготовка в форме аспирантуры, экспериментального обучения или профессиональных формирующих курсов и экзаменов. Для более подробного описания некоторых из упомянутых выше профессий посетите Career Cruising (информацию для входа можно найти на домашней странице онлайн-системы Центра карьеры) или на веб-сайте Национальной классификации профессий.
Для более подробного описания некоторых из упомянутых выше профессий посетите Career Cruising (информацию для входа можно найти на домашней странице онлайн-системы Центра карьеры) или на веб-сайте Национальной классификации профессий.
Mathematics and Computing — Ideas
Здесь публикуются три слегка отредактированных отрывка из «Mathematics and Computing», новой книги Ави Вигдерсона, Герберта Х.Маасс, профессор математической школы, который вскоре будет опубликован издательством Princeton University Press (онлайн-проект доступен здесь). Эти отрывки выбраны, чтобы кратко познакомить читателя с теорией вычислений, теорией вычислительной сложности и новым поколением алгоритмов машинного обучения, обсуждаемых в соответствующей статье о программе теоретического машинного обучения в IAS.
Теория вычислений (ToC) — это исследование формальных основ информатики и технологий.Эта динамичная и быстро развивающаяся область объединяет математику и информатику. Обе стороны естественно возникли из основополагающей статьи Тьюринга 1936 года «О вычислимых числах в приложении к проблеме Entscheidungsproblem». В этой статье формально определен алгоритм в форме того, что мы сегодня называем «машиной Тьюринга». С одной стороны, машина Тьюринга — это формальная математическая модель вычислений, позволяющая строго определять вычислительные задачи, алгоритмы их решения и ресурсы, которые для этого требуются.С другой стороны, определение машины Тьюринга позволило легко реализовать ее простую и логичную конструкцию в аппаратном и программном обеспечении. Эти теоретические и практические аспекты повлияли на двойственную природу области. С математической стороны абстрактное понятие вычислений оказалось чрезвычайно глубоким и загадочным математическим понятием, и в его изучении ToC прогрессирует, как и любая другая математическая область. Его исследователи доказывают теоремы, и они следуют стандартной математической культуре, чтобы обобщать, упрощать и следовать своим носам, основываясь на эстетике и красоте. С практической точки зрения универсальная применимость автоматизированных вычислений способствовала быстрому развитию компьютерных технологий, которые сейчас доминируют в нашей жизни. Этот быстро развивающийся мир компьютерных наук и промышленности постоянно создает новые модели, режимы и свойства вычислений, которые требуют теоретического понимания и напрямую влияют на математическую эволюцию ToC, в то время как идеи и методы, созданные в нем, возвращаются в практический мир.
С практической точки зрения универсальная применимость автоматизированных вычислений способствовала быстрому развитию компьютерных технологий, которые сейчас доминируют в нашей жизни. Этот быстро развивающийся мир компьютерных наук и промышленности постоянно создает новые модели, режимы и свойства вычислений, которые требуют теоретического понимания и напрямую влияют на математическую эволюцию ToC, в то время как идеи и методы, созданные в нем, возвращаются в практический мир.
Теория вычислений — обширная область.Многие из его подполей напрямую связаны с приложениями. Они разрабатывают формальные, математические основы и теории языков программирования, операционных систем, оборудования, сетей, баз данных, безопасности, робототехники, и искусственного интеллекта , а также многочисленные эффективные алгоритмы и алгоритмические методы для решения основных проблем, возникающих в этих поля. Эти модели и алгоритмы вносят непосредственный вклад в удивительное разнообразие способов, которыми компьютеры влияют на нашу жизнь.Во многих других подразделах ToC разрабатываются вычислительные модели и теории различных природных и искусственных процессов, взаимодействующие с научными дисциплинами, включая биологию, физику, экономику, и социальные науки . Действительно, если рассматривать такие процессы как информационные процессы , вычислительная линза проливает новый мощный свет, который во всех этих дисциплинах возрождает и пересматривает основные вопросы, убеждения и теории. Эти растущие взаимодействия приводят к лучшему пониманию мира природы.
Центральным ядром ToC является теория вычислительной сложности , которая часто мотивируется, но обычно наиболее удалена от приложений и наиболее тесно связана с математикой. Первоначальным зарядом теории сложности было понимание эффективных вычислений в самом общем смысле: какие минимальные количества природных ресурсов, таких как время, память и другие, необходимы для решения естественных вычислительных задач с помощью естественных вычислительных моделей . В ответ он разработал мощный инструментарий алгоритмических методов и способов их анализа, а также систему классификации вычислительных задач на классы сложности . Он также сформулировал естественные долгосрочные цели для этой области.
В ответ он разработал мощный инструментарий алгоритмических методов и способов их анализа, а также систему классификации вычислительных задач на классы сложности . Он также сформулировал естественные долгосрочные цели для этой области.
Со временем, а также благодаря внутренним и внешним мотивам, теория вычислительной сложности значительно расширила свои цели. Это потребовало компьютерного моделирования и понимания множества центральных понятий, некоторые из которых веками изучались великими умами, включая секрет , доказательство, обучение, знание, случайность, взаимодействие, эволюцию, игру, стратегию, координацию, синхронность и другие. .Эта вычислительная линза часто приводила к совершенно новому пониманию этих старых концепций. Более того, в некоторых из этих случаев возникшие теории предшествовали значительному технологическому прогрессу и действительно способствовали его достижению. Кроме того, некоторые из этих теорий составляют основу взаимодействия с другими науками.
Таким образом, начиная с цели понимания того, что можно эффективно вычислить , возникло множество естественных долгосрочных целей глубокого концептуального значения. Что можно эффективно изучить? Что можно эффективно доказать? Намного легче проверить доказательство, чем его найти? Что знает машина? В чем сила случайности в алгоритмах? Можем ли мы подключиться к естественным источникам случайности и использовать эту силу? Какова мощность квантово-механических компьютеров? Можем ли мы использовать квантовые явления в алгоритмах? Что можно достичь совместно в условиях, когда разные вычислительные объекты имеют разные (возможно, конфликтующие) стимулы? В частном порядке? Могут ли компьютеры эффективно моделировать природу или мозг?
Итак, вполне очевидно, что алгоритмы будут управлять Землей, но какие алгоритмы? На протяжении десятилетий компьютерные ученые разрабатывали и анализировали алгоритмы, лежащие в основе компьютерной революции, затрагивающей все аспекты нашей жизни. Это жемчужины человеческого изобретения. Но недавно сочетание выдающейся вычислительной мощности, важных методов оптимизации и массивных данных позволило создать новое поколение алгоритмов, которое возникает в машинном обучении. Одним словом, алгоритмы как технологические продукты. Технологические и медицинские компании, а также правительства вкладывают огромные средства и усилия в эти новые алгоритмы.
Это жемчужины человеческого изобретения. Но недавно сочетание выдающейся вычислительной мощности, важных методов оптимизации и массивных данных позволило создать новое поколение алгоритмов, которое возникает в машинном обучении. Одним словом, алгоритмы как технологические продукты. Технологические и медицинские компании, а также правительства вкладывают огромные средства и усилия в эти новые алгоритмы.
В отличие от элегантных и лаконичных алгоритмических жемчужин, созданных руками человека, многие новые алгоритмы просто «создают себя» при относительно небольшом вмешательстве людей, в основном посредством взаимодействия с массивными данными.Этот контраст с «классическим» дизайном алгоритмов усиливается, поскольку эти новые алгоритмы обычно (и, возможно, обязательно) гигантские и очень плохо понимаются людьми. Я, конечно же, имею в виду «глубокие сети» — общее название эвристики, смоделированной на основе нейронных сетей.
Эти алгоритмы-самоучки пытаются решить множество проблем, которые часто трудно определить формально, например, поиск «значимых сигналов» в огромных наборах данных, которые часто чрезвычайно зашумлены — будь то финансовые, астрофизические, биологические или Интернет.Структура, которую можно извлечь / раскрыть, может быть кластерами, корреляциями, геометрическими или числовыми шаблонами и т. Д. Или совершенно неожиданными. Они могут представлять, например, знакомые лица или объекты на фотографиях, группы друзей и интересы в социальных сетях, рыночные показатели компаний при покупке и продаже акций, эффекты лечения или генетические дефекты в биологических данных, а также освещающие взаимодействия материи и энергия в физических наблюдениях.
Здесь не место для полноценного описания глубоководных сетей и их тренировочного процесса.Достаточно сказать, что сегодня их размер может доходить до миллионов ворот и проводов между воротами. Каждое соединение имеет параметр силы, который пытается оптимизировать тренировочный процесс. Короче говоря, обучение — это огромная проблема оптимизации с плохо определенной целью и многочисленными степенями свободы эвристики, управляющей попыткой оптимизации. Эта «черная магия» пока работает исключительно хорошо только в относительно немногих случаях. Но во все большем числе случаев он значительно превосходит любой алгоритм, созданный человеком.Чрезвычайно интересно, когда такая программа-самоучка может обозначать по имени основное содержание произвольных снимков, сделанных людьми, почти так же хорошо, как люди. Очень впечатляет, что еще одна такая программа, сыграв против себя миллиард игр в го, теперь может победить лучших игроков мира. Такие программы достигли значительного прогресса в понимании и переводе человеческого языка, и, возможно, их самый быстрый рост наблюдается в «науке о данных», где эти программы играют все более важную роль в реальных научных открытиях.Действительно, интересно, в какой момент они смогут лучше сформулировать новые открытые научные законы и преследовать их последствия, такие как медицинские препараты и лечение, питание и энергоснабжение и т. Д., Также без помощи человека.
Эта «черная магия» пока работает исключительно хорошо только в относительно немногих случаях. Но во все большем числе случаев он значительно превосходит любой алгоритм, созданный человеком.Чрезвычайно интересно, когда такая программа-самоучка может обозначать по имени основное содержание произвольных снимков, сделанных людьми, почти так же хорошо, как люди. Очень впечатляет, что еще одна такая программа, сыграв против себя миллиард игр в го, теперь может победить лучших игроков мира. Такие программы достигли значительного прогресса в понимании и переводе человеческого языка, и, возможно, их самый быстрый рост наблюдается в «науке о данных», где эти программы играют все более важную роль в реальных научных открытиях.Действительно, интересно, в какой момент они смогут лучше сформулировать новые открытые научные законы и преследовать их последствия, такие как медицинские препараты и лечение, питание и энергоснабжение и т. Д., Также без помощи человека.
Главный вопрос, который я считаю захватывающим и сложным на этом фронте, и в который теория вычислений может и должна внести свой вклад, — это теоретическое понимание таких алгоритмов. Это понимание должно включать способы сделать их обучение более принципиальным и эффективным, а также разработать модели и инструменты для оценки их производительности и качества результатов.Основная задача — понять, почему и для каких задач глубокие сети успешны и каковы их ограничения. Кроме того, крайне важно, учитывая их растущее преобладание в системах, от которых в решающей степени зависят люди, изучить, как сделать их справедливыми (и что это означает), насколько они восприимчивы к злоумышленникам и как от них защититься. Конечно, размер и сложность глубоких сетей могут ограничивать их теоретическое понимание (во многом как массивные творения природы, такие как мозг и другие биологические системы).В самом деле, вполне вероятно, что теоретическое изучение глубоководных сетей (на которых, в отличие от животных, экспериментирование не оговорено в рекомендациях Хельсинкской декларации) поможет лучше понять биологические системы и наоборот.
Учитывая наше текущее невежество (а именно, пробелы между верхними и нижними границами) в отношении многих хорошо поставленных важных проблем, я не сомневаюсь, что есть гораздо больше возможностей для открытия алгоритмических жемчужин, которые мы можем легко понять, оценить и использовать.Чтобы понять это, позвольте мне в заключение отметить, что ни одна глубокая сеть не существовала бы без нескольких замечательных алгоритмических жемчужин, встроенных практически во все из них, в том числе чрезвычайно эффективного обратного распространения и градиентного спуска .
Математика и вычислительные науки | Колледж наук
Изучение математики и вычислительных наук включает информатику, математику, прикладную математику, статистику и информационные технологии. Преподаватели и студенты этой программы открывают для себя новые знания, которые можно использовать для решения математических, научных, инженерных и технологических задач.Этот междисциплинарный подход готовит профессионалов к карьере в области науки, медицины, инженерии и образования. Определяя общие цели в исследованиях и образовании, преподаватели сотрудничают по вопросам, важным для науки и общества.
Кафедра компьютерных наук готовит профессионалов для деловой и научной карьеры в области разработки и проектирования аппаратных и программных систем. Студенты и преподаватели используют свое понимание и исследования алгоритмов, языков программирования, операционных систем, баз данных, сетей, распределенных вычислений и теории вычислений для создания систем, преобразующих информацию.
Кафедра математики создает фундамент математических и статистических знаний для студентов, ищущих карьеру в области математики, естественных наук и технологий. Программа включает обширные предложения курсов по чистой и прикладной математике. Факультет разрабатывает и поддерживает многочисленные информационные программы для обучения студентов, родителей и учителей.
Школа информации: наука, технологии и искусство (SISTA) готовит студентов к удовлетворению потребностей информационного века посредством сбора, хранения, обработки и анализа данных.

