Подобие треугольников — это… Что такое Подобие треугольников?

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Признаки подобия треугольников

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

То есть

Дано: и

Доказать:

Доказательство

1)По условию по теореме о сумме углов треугольника.

Согласно условию, по теореме об отношении площадей треугольников, имеющих по равному углу; но по той же причине, так как ; следовательно, . Аналогично используя равенства и , получаем, что .

Итак, в рассматриваемых треугольниках все их углы соответственно равны, и сходственные стороны пропорциональны, то есть эти треугольники являются подобными по определению, ч.т.д.

Второй признак

Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.

Дано: и Доказать:

Доказательство

Третий признак

Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Признаки подобия прямоугольных треугольников

1. По острому углу — см. первый признак;
2. По двум катетам — см. второй признак;
3. По катету и гипотенузе — см. третий признак.

Свойства подобных треугольников

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:

Связанные определения

• Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 26 декабря 2012.

Литература

• Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.

См. также

Ссылки

3dic.academic.ru

Признаки подобия треугольников — это… Что такое Признаки подобия треугольников?



Признаки подобия треугольников

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.

Признаки подобия треугольников

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, ∠B=∠B₁.

Доказать: ∆ABC ∆A₁B₁C₁

.

Доказательство

Второй признак

Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Третий признак

Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Дано

: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Признаки подобия прямоугольных треугольников

1. По острому углу — см. первый признак;
2. По двум катетам — см. второй признак;
3. По катету и гипотенузе — см. второй признак.

Свойства подобных треугольников

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:

Связанные определения

• Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

Литература

• Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.

См. также

Ссылки

Wikimedia Foundation. 2010.

• Признак Абеля
• Признание: Два лица зла (фильм)

Смотреть что такое «Признаки подобия треугольников» в других словарях:

• Признаки равенства треугольников — Стандартные обозначения Треугольник  простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника …   Википедия

• Подобие треугольников

  — Признаки подобия треугольников геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Преобразование подобия — Подобие  преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k  положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны …   Википедия

• Подобные треугольники — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве)  это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… …   Википедия

• Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие  преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где   положительное число, называемое… …   Википедия

• Подобные фигуры — Подобие  преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k  положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны …   Википедия

• подобие — я; ср. 1. Пренебр. Нечто похожее, сходное с чем л. Жалкое п. старинного полонеза. П. человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на себя). 2. Матем …   Энциклопедический словарь

• Площадь треугольника — Стандартные обозначения Треугольник  простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника …   Википедия

• подобие — я; ср. 1) пренебр. Нечто похожее, сходное с чем л. Жалкое подо/бие старинного полонеза. Подо/бие человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на… …   Словарь многих выражений

partners.academic.ru

Подобные треугольники | Математика

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

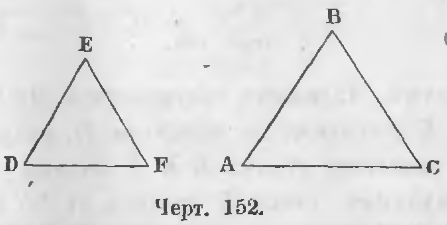
Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.)

Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

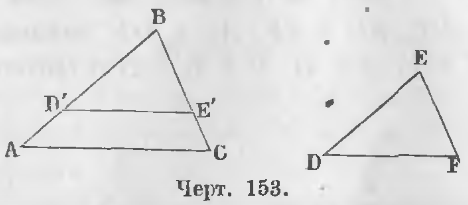
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

∠D’ = ∠D, ∠D = ∠A

откуда

∠D’ = ∠A.

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,

∠D’ = ∠D, ∠E’ = ∠F.

Так как имеет место пропорция

AB/BD’ = BC/BE’

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

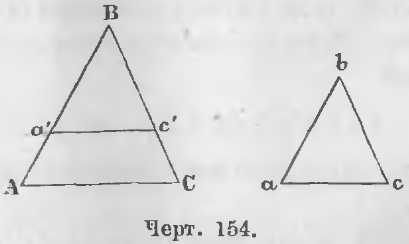
Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc’ = bc, a’c’ = ac,

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

а так как

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

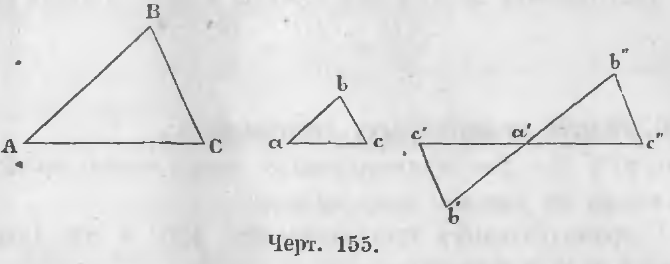
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a’b»c», следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

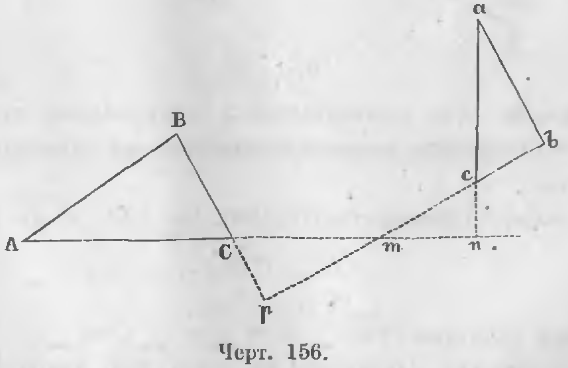
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

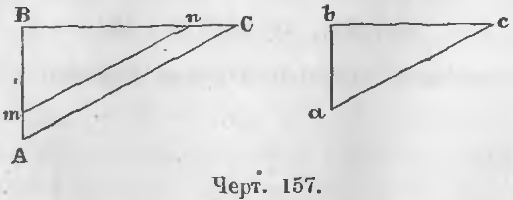
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

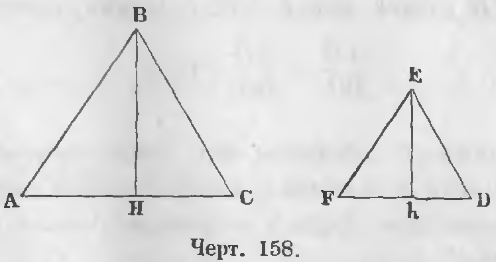
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

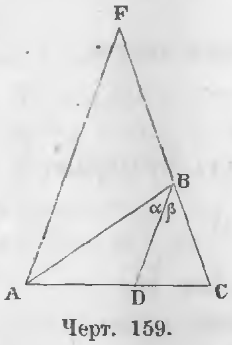
Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

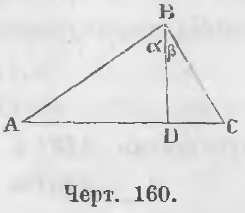
Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

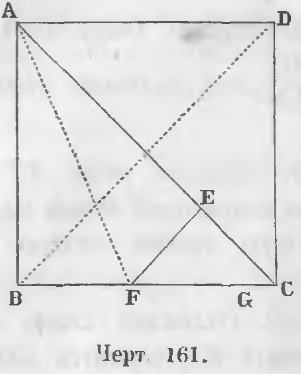
Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз. Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т. д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² — 2AC · DC.

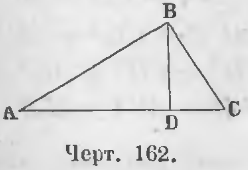
Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC — DC, AD² = (AC — DC)² = AC² + DC² — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² — DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² — DC² + AC² + DC² — 2AC · DC, откуда
AB² = BC² + AC² — 2AC · DC (ЧТД).

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

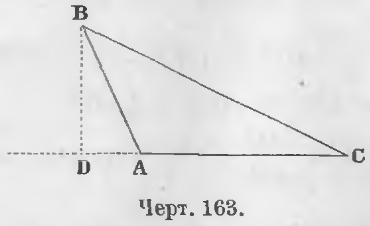
Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² — CD²

следовательно,

AB² = BC² — CD² + DA².

Так как

DA = CD — AC
DA² = (CD — AC)² = CD² + AC² — 2CD · AC, то
AB² = BC² — CD² + CD² + AC² — 2CD · AC, откуда
AB² = BC² + AC² — 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

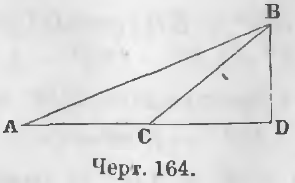
Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² — CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² — CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

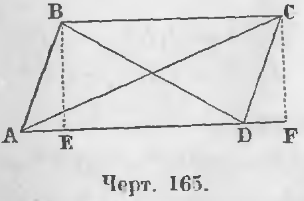
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD — DE)² = CD² + DE² — 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².

Из прямоугольного треугольника BDE видно, что

BE² = BD² — DE²

следовательно

AB² + BC² = 2BD² — 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).

 

maths-public.ru

подобные треугольники — это… Что такое подобные треугольники?



подобные треугольники

мат. similar triangles

Большой англо-русский и русско-английский словарь. 2001.

• подобные тела
• подобные фигуры

Смотреть что такое «подобные треугольники» в других словарях:

• Подобные треугольники — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Признаки подобия треугольников — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Теорема Пифагора — Теорема Пифагора  одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 …   Википедия

• Пифагора теорема — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства …   Википедия

• ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… …   Энциклопедия Кольера

• ПОДОБНЫЙ — ПОДОБНЫЙ, подобная, подобное; подобен, подобна, подобно. 1. кому чему. Сходный, совершенно похожий. Происшествие, подобное этому, было в прошлом году. 2. Такой, этот (о котором говорится). «Где еще мыслимы подобные вещи?» Маяковский. Перечислить… …   Толковый словарь Ушакова

• Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника  перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав …   Википедия

• Теорема Наполеона — Теорема Наполеона  утверждение евклидовой планиметрии о равносторонних треугольниках …   Википедия

• подо́бный — ая, ое; бен, бна, бно. 1. кому чему. Сходный с кем , чем л., похожий на кого , что л. [Белесова:] Если бы вы или кто нибудь из подобных вам людей навещали меня хоть изредка, мне было бы лучше, теплее на душе. А. Островский, Богатые невесты. Он… …   Малый академический словарь

• ПОДОБИЕ — ср. (доба, время, пора, срок, год, година: добрый, удобный, сдобный и пр.) сходство, согласие, одновидность, схожесть. И подобия нет подлинника. | Вещь сделанная по образцу или в подражанье; изображенье чего; образ чего либо. Иссеченное из камня… …   Толковый словарь Даля

• Мгновенный центр скоростей — Мгновенный центр скоростей  при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Содержание 1 Положение… …   Википедия

dic.academic.ru

Подобные треугольники | Треугольники

Два треугольника подобны, если об этом сказано в условии либо если это можно доказать по одному из признаков подобия треугольников.

Определение

Подобные треугольники — это треугольники, у которых углы равны, а стороны пропорциональны.

(или:

Два треугольника подобны, если между их точками можно установить взаимно-однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек равно одной и той же постоянной k, k — коэффициент подобия).

Как и в случае равных треугольников, важно правильно называть подобные треугольники: равные углы должны находиться на соответствующих позициях.

   

   

Определение подобных треугольников предполагает выполнение шести пар равенств (равенство трёх пар углов и пропорциональность трёх пар сторон). Признаки подобия позволяют сократить число равенств до 2-3 (для прямоугольных треугольников — до 1-2).

Свойства подобных треугольников

1) Периметры подобных треугольников относятся как их соответствующие стороны:

   

2) Соответствующие линейные элементы подобных треугольников (медианы, высоты, биссектрисы и т.д.) относятся как их соответствующие стороны.

3) Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

   

www.treugolniki.ru

подобные треугольники — с английского на русский

Подобные треугольники — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

Признаки подобия треугольников — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

Теорема Пифагора — Теорема Пифагора  одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 …   Википедия

Пифагора теорема — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства …   Википедия

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… …   Энциклопедия Кольера

ПОДОБНЫЙ — ПОДОБНЫЙ, подобная, подобное; подобен, подобна, подобно. 1. кому чему. Сходный, совершенно похожий. Происшествие, подобное этому, было в прошлом году. 2. Такой, этот (о котором говорится). «Где еще мыслимы подобные вещи?» Маяковский. Перечислить… …   Толковый словарь Ушакова

Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника  перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав …   Википедия

Теорема Наполеона — Теорема Наполеона  утверждение евклидовой планиметрии о равносторонних треугольниках …   Википедия

подо́бный — ая, ое; бен, бна, бно. 1. кому чему. Сходный с кем , чем л., похожий на кого , что л. [Белесова:] Если бы вы или кто нибудь из подобных вам людей навещали меня хоть изредка, мне было бы лучше, теплее на душе. А. Островский, Богатые невесты. Он… …   Малый академический словарь

ПОДОБИЕ — ср. (доба, время, пора, срок, год, година: добрый, удобный, сдобный и пр.) сходство, согласие, одновидность, схожесть. И подобия нет подлинника. | Вещь сделанная по образцу или в подражанье; изображенье чего; образ чего либо. Иссеченное из камня… …   Толковый словарь Даля

Мгновенный центр скоростей — Мгновенный центр скоростей  при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Содержание 1 Положение… …   Википедия

translate.academic.ru

Подобные треугольники, формулы и примеры

Определение и формулы подобных треугольников

ОПРЕДЕЛЕНИЕ Треугольники называются подобными, если у них равные углы и соответствующие стороны пропорциональны.

Рис.1

Например, на рисунке 1 изображены треугольники и , у которых

   

По определению, эти треугольники подобные. Пишут: .

Число 2, которое равняется отношению соответствующих сторон, называют коэффициентом подобия.

Если и , то .

ЛЕММА

Лемма (Про подобные треугольники). Прямая параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от данного треугольника ему подобный.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com