ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
Круглов Н.П. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Холинова О.А. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Математику называют «царицей всех наук». Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет для нас сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы (ок. 1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
В исследовательской работе рассматриваются числа последовательности Фибоначчи, их свойства, а также, тесно связанный с этой темой, феномен золотого сечения, в котором большинство ученых видят одно из наиболее ярких, давно уже замеченных человеком проявлений гармонии природы. Феномен золотого сечения рассмотрен в работе в общей картине исторического становления архитектуры, на формах живой природы и за пределами предметного мира, в области гармонии и математических абстракций. Он рассмотрен и как объективная характеристика объектов искусства, экономики и т. д.
Общеизвестно, что золотое сечение – это закон пропорциональной связи целого и составляющих это целое частей. Классический пример золотого сечения – деление отрезка в среднепропорциональном отношении, когда целое так относится к большей своей части, как большая часть – к меньшей: (a+b)/b = b/a. Такая задача имеет решение в виде корней уравнения x2 – x – 1 = 0.За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения пропорции золотого сечения.
Золотое сечение, как и загадочные свойства чисел Фибоначчи, владели мыслью и чувствами многих выдающихся мыслителей прошлого и продолжает волновать умы современников наших не ради самих математических свойств, а потому, что неотделимо от ценности объектов искусства и в то же время обнаруживает себя как признак структурного единства объектов природы. Скульптура, архитектура, музыка, астрономия, биология, психология, техника – вот те сферы, где так или иначе обнаруживает свою жизнь золотое сечение. Современные исследователи находят его при описании строения растений, пропорций тел животных, птиц, человека, в статистике популяций, в строении глаза и строении космоса и т. д.
Сегодня невозможно с абсолютной достоверностью определить, когда и как понятие золотого сечения было выделено в человеческом знании из интуитивной и опытной категорий. Но судить обоснованно, кто прав: те ли, кто относит открытие золотого сечения к цивилизациям древнего Востока (Египет. Индия), или те, кто, подобно Кеплеру, связывает открытие золотого сечения с именем Пифагора, можно, но для этого необходимо владеть базовыми историческими и математическими познаниями.
В эпоху Ренессанса среднепропорциональное отношение именовали Sectio divina – божественной пропорцией. Леонардо да Винчи дает ему имя Sectio aurea (золотое сечение), живое поныне, а много раньше, в 1202 г., открытием ряда Фибоначчи было обнажено фундаментальное свойство золотого сечения – единство аддитивности и мультипликативности.
Сегодня сущность гармонии невозможно выявить ни в биологии, ни в искусстве, ни в абстрактно-математических построениях, если рассматривать их раздельно, – здесь можно лишь наблюдать и осмысливать ее проявления. «Философия, – говорил Галилео Галилей, – написана в той величественной книге, которая постоянно открыта у нас перед глазами (я имею в виду Вселенную), но которую невозможно понять, если не научиться предварительно ее языку и не узнать те письмена, которыми она начертана». «Божественная пропорция – бесценное сокровище, одно из двух сокровищ геометрии», – развивает эту же мысль Кеплер. Действительно, гармония может быть расшифрована лишь на ее собственном языке, отображенном фундаментальными принципами естествознания.
Существуют любопытные закономерности, которые могут быть описаны с помощью математики. Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Актуальность данной работы заключается в необходимости исследования чисел Фибоначчи, так как они встречаются нам в различных творениях природы. Знания о них будут полезны во многих науках.
Цель: изучить практическую значимость чисел Фибоначчи
Задачи:
1.Познакомиться с числами Фибоначчи и историей их создания.
2. Рассмотреть рекурентную формулу ряда Фибоначчи.
3. Познакомиться с биографией итальянского математика Леонардо Пизанского (Фибоначчи).4. Изучить свойства числового ряда Фибоначчи
5. Проверить на практике проявление чисел Фибоначчи в неживой природе, в строении человека и растений.
Предмет исследования — числа Фибоначчи.
Объект исследования — область применения чисел Фибоначчи; свойства чисел Фибоначчи.
Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.
Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.
Методы исследования в работе:
теоретический (логическая ступень познания).
эмпирический (наблюдение, эксперимент, измерение).
сравнение.
классификация.
математическое моделирование
практический (расчеты числа фи)
Структура работы: исследовательская работа состоит из введения, двух глав, заключения, списка используемой литературы. Во введении определена актуальность темы, связанная с понятием последовательности ряда Фибоначчи и проявление чисел Фибоначчи в неживой природе, в строении человека и растений, цели, задачи, объекты и методы исследования. В первой главе описана историческая справка о Леонарде Пизанском, итальянском математике средневековья; последовательность ряда Фибоначчи и его свойства. Во второй главе рассмотрены проявления последовательности Фибоначчи в окружающем мире. Далее следует заключение. В нем определены выводы по проделанной работе. В списке используемых источников перечислена основная литература, которая использовалась в процессе работы.
В теоретической части исследования была изучена литература по данной теме, узнали, как образуется этот ряд, историю его возникновения, какими свойствами он обладает. Рассмотрели разные объекты природы где, обнаруживает себя ряд Фибоначчи. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах, в строении человеческого тела и в строении раковин моллюсков, в океане, в космосе и т.д. В проверке этих фактов заключается практическая часть нашего исследования.
1 Числа Фибоначчи.
1.1.Биография Леонардо Пизанского
Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты.
Его отец был купцом и государственным вельможей, представителем нового класса бизнесменов. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование.
Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков.
Все эти знания он впитывал в себя как губка. А потом принес их в Европу, он «открыл» арабские цифры вместо римских и десятичную систему счисления для европейцев. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Libег аЬасi, 1202; до наших дней сохранилась только дополненная рукопись 1228 г.). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной и одно из величайших открытий всех времён и народов – десятичную систему счисления.
Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.
Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II.
1.2. Числа Фибоначчи и их свойства.
Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку.
Иначе обстоит дело с математикой средневековья. Кроме Виета, жившего в шестнадцатом столетии, и математиков более близких нам времен школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci – сокращенное filius Bonacci, т. е. сын Боиаччи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г.
«Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата. Рассмотрим одну такую задачу, помещенную на стр. 123-124 рукописи 1228 г.
«Сколько пар кроликов в один год от одной пары рождается?»
«Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар, рожденных в этом месяце, не дают в том же месяце потомства, а остальные 8 пар рождают, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в девятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары; сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар; столько пар произвела первая пара в данном месте к концу одного года.
Действительно, на этих полях ты можешь увидеть, как мы это делаем; именно, мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с. четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев».
Построим алгебраическую модель задачи о кроликах и рассмотрим следующую числовую последовательность: , в которой u1 = u2 = 1, а каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов, то есть при всяком n > 2 выполняется равенство: .
Такие последовательности, в которых каждый член определяется как некоторая функция предыдущих, часто встречаются в математике и называются рекуррентными или, по-русски, возвратными последовательностями. Сам процесс последовательного определения элементов таких последовательностей называется рекуррентным процессом, а равенство (2) – возвратным (рекуррентным) уравнением [2].
Возвратная последовательность, задаваемая условием u1 = u2 = 1 и формулой (2) называется последовательностью Фибоначчи, а её члены –
числами Фибоначчи.
Перечислим основные свойства последовательности Фибоначчи.
1) Каждое следующее число, начиная с третьего равно сумме двух предыдущих.
2) Отношение каждого числа к последующему при увеличении порядкого номера все более и более стремится к 0,618.
3) Отношение каждого числа ряда к предыдущему стремится к 1,618.
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стремится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду, как арифметическому выражению закона золотого деления.
Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.
1.3 Спираль Фибоначчи
Спираль Фибоначчи – это некоторая кривая, которая огибает точку своего центра, приближаясь или удаляясь от неё, все зависит от направления, избранного вами. Эти фигуры могут быть как двухмерными, так и трехмерными, однако, если мы говорим о Фибоначчи, как о рыночной модели, то рассматривать можно только один вариант – двухмерный.
Когда строятся такие фигуры, то используется стартовая точка, построенная на плоскости, радиус выступает в роли непрерывной монотонной функции от угла.
Спираль Фибоначчи, отличается от Золотой пропорции и имеет точку начала. Беря начало в некоторой точке, такая фигура обычно разворачивается бесконечно долго.
У последовательности Леонардо есть интересные свойства. Ряд Фибоначчи отличается от Золотого Сечения, так как начинается с единицы или нуля и при этом стремится к Золотой пропорции.
Также он постоянно увеличивает точность. В некоторой точке (когда почти достигнута фи =1,618) уже невозможно найти разницу, которая прослеживалась между двумя спиралями. Понимание этого свойства Спирали Фибоначчи и определяет её удивительность.
Это поразительно, однако, строение спирали Фибоначчи можно наблюдать в большом количестве предметов и явлений.
2 Числа Фибоначчи в нашей жизни
2.1 Числа Фибоначчи в природе
С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи. Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис — листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи.
Чёткая, симметричная форма цветов также подчинена строгому закону.
У многих цветов количество лепесточков является числами из ряда Фибоначчи.
Встретить числовые закономерности в живой природе можно в различных спиральных формах, которыми так богат мир растений. Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число «правых «и «левых» спиралей часто оказываются соседними числами Фибоначчи
Можно привести множество примеров.
Первый и очень яркий пример – это подсолнухи. Их семена расположены так, чтобы максимально использовать всю площадь соцветия, не теряя ни миллиметра. А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.
Нечто подобное происходит и с ячейками ананаса: у него 8 правосторонних спиралей, 13 левосторонних и 21 вертикальная. И снова последовательность Фибоначчи.
В сосновой шишке, если хорошо присмотреться, можно увидеть две спирали, закручены одна по часовой стрелкой, а другая против. Число этих спиралей 8 и 13.
Количество лепестков во многих соцветиях совпадает с числами из этой последовательности, например, ирис имеет 3 лепестка, у примулы их 5, у амброзии полыннолистной — 13, у астр бывает 55 или 89 лепестков.
Листья на деревьях и других растениях распределены в последовательности, основанной на золотом числе, таким способом, чтобы получать максимум света и не мешать друг другу.
У многих бабочек отношения размеров грудной и брюшной части тела очень близки к золотому числу.
Раковины моллюсков закручены по спирали, и если измерить ее завитки, то их отношение постоянно и равно 1.618.
Спиралеобразно паук плетет паутину. По спирали закручивается ураган. Стадо северных оленей по тревоге разбегается по спирали. По спирали закручиваются волны, которые разбиваются об берега океана. Молекулы ДНK живых организмов закручены двойной спиралью. Гете называл эту спираль «кривой жизни».
2.2. Числа Фибоначчи в строении животных
Кроме растений, числа Фибоначчи проявляются в строении различных живых организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13.
У хорошо знакомого комара – три пары ног, брюшко делится на 8 сегментов на голове 5 усиков – антенн. И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.
2.3. Числа Фибоначчи в строении человека
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно проявляются и в строении человеческого тела. Рассмотрим это поподробнее.
У человека одно туловище, одна голова, одно сердце и т. д. Многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. Можно рассмотреть части тела и с другой стороны. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи. (Приложение 1, 2).
Позвоночник человека состоит из 34 позвонков. Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Числа Фибоначчи можно обнаружить и в «крови» у человека. Так распределение людей по трём группам крови отвечает отношениям чисел 8/ 21 /3.
Сердечная мышца сокращается до 0,618 от своей изначальной длины и нарушение этого числа при сокращении ведет к болезням сердца. А это число отражает одно из свойств чисел Фибоначчи. В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34. В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи. (Приложение 1, 2).
Этот ряд получается, если провести измерения длин фаланг пальцев и расстояний между различными частями лица.
2.4. Числа Фибоначчи и золотой прямоугольник
Было отмечено, что числа Фибоначчи тесно связаны со спиралевидным строением многих представителей живой и неживой природы. Чтобы рассмотреть еще несколько таких примеров, необходимо познакомиться с так называемым «золотым прямоугольником». Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров.
Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по спирали, которая называется спираль Фибоначчи.
Эту спираль можно обнаружить в самых различных и неожиданных предметах и явлениях.
У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Раковины улиток подчиняются последовательности и спирали Фибоначчи.
Паук плетет паутину спиралеобразно. Интересно, что спиралью закручиваются ураган, облака циклона и это хорошо видно из космоса.
Числа Фибоначчи оказались и в спирали, описывающей изгиб гребня набегающей волны в океане, и в спирали, убегающей воды в раковине умывальника. Да и живём мы тоже в спирали, ведь галактика – это спираль, соответствующая спирали Фибоначчи.
На рисунке показаны относительные размеры Земли и Луны в масштабе.
Нарисуем радиус Земли. Проведем отрезок от центральной точки Земли до центральной точки Луны. Нарисуем отрезок для соединения двух данных отрезков, чтобы сформировать треугольник. Получаем золотой треугольник.
Сатурн показывает золотую пропорцию в нескольких ее измерениях
Диаметр Сатурна очень близко находится в отношении золотой пропорции с диаметром колец, как показано зелеными линиями. Радиус внутренней части колец находится в отношении, очень близком к с внешним диаметром колец, как показано синей линией.
Расстояние планет от Солнца также подчиняется золотой пропорции.
2.5 Числа Фибоначчи в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
2.6.Числа Фибоначчи в искусстве
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики применение закона золотого сечения распространилось на конструирование машин, мебели и пр.
Пропорция, выражаемая числом Ф, по мнению многих исследований, является наиболее приятной для человеческого глаза.
Леонардо де Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф. Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье.
Прямоугольник с таким отношением сторон стали называть «золотым прямоугольником».
Форму «золотого сечения» придавали книгам, столам почтовым открыткам. В дальнейшем книгам и другим бумажным изделиям стали чаще придавать форму прямоугольника с отношением сторон корень из двух. Это связано с тем, что при перегибании такого прямоугольника по средней линии образуются два прямоугольника с тем же соотношением сторон.
Число золотого сечения Ф обладает какой-то странной неуловимостью. Оно появляется в различных проекциях, так и не давая ответа на вопрос, как это число связано с тем или иным явлением. Интерес к мистическому числу Ф достаточно периодичен. Он возникает с обнаружением нового проявления этого числа в каком-либо явлении природы.
Проходит время, и интерес к нему спадает. Но ненадолго. Числу Ф находят всё новое и новое применение, но оно так и остается недоступным для ясного и полного понимания его свойств и степени его влияния на окружающий мир.
2.7. Числа Фибоначчи и фотография
Применительно к фотографическому искусству правило золотого сечения делит кадр двумя горизонтальными и двумя вертикальными линиями на 9 неравных прямоугольников. Чтобы облегчить себе задачу съемки сбалансированных изображений, фотографы немного упростили задачу и стали делить кадр на 9 равных прямоугольников в соответствии с числами Фибоначчи. Так правило золотого сечения трансформировалось в правило третей, которое относится к одному из принципов построения композиции.
В видоискателях современных цифровых камер точки фокусировки расположены на позициях 2/8 или на воображаемых линиях, делящих кадр по правилу золотого сечения.
Наиболее удачным примером для демонстрации является пейзаж. Принцип композиции заключается в том, что небо и суша (либо водная гладь) должны иметь соотношение 1:2. Одну треть кадра следует отвести под небо, а две трети под сушу или наоборот.
Практическое исследование
Вторая часть нашего практического исследования заключается в конкретных подсчетах и измерениях.
Числа Фибоначчи в строении подсолнуха
Первым для изучения мы взяли подсолнух и сосчитали количество спиралей, идущих в одну сторону и количество спиралей в другую сторону. Правых спиралей, они закрашены красным, получилось 34, левых, они закрашены синим – 55. Эти числа 34 и 55 являются соседними в последовательности Фибоначчи.
Числа Фибоначчи в строении еловой и сосновой шишек
Продолжая исследование, числа, входящие в ряд Фибоначчи мы увидели в сосновых и еловых шишках. Подсчет спиралей выявил следующие результаты. Замечаем две серии спиралей Фибоначчи: одна — по часовой стрелки, другая — против, их число 8 и 13.
Числа Фибоначчи в строении ананаса
На фотографиях показано как мы проводили подсчеты чешуек на кожуре ананаса. Нами получены числа: 8 и 13. Как мы снова можем убедиться, эти числа являются членами последовательности Фибоначчи.
Числа Фибоначчи в ветке дерева
Последовательность ответвлений, идущих по стволу растений, мы подсчитывали, рассматривая ветку дерева. Положив её на ватман, мы провели горизонтальные линии, соответствующие пазам выхода веток, и посчитали их количество. Получили следующие данные: 1,2,3,5,8… Полученный ряд является частью ряда Фибоначчи.
ЗАКЛЮЧЕНИЕ
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве и архитектуре, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.
В своей работе, мы, конечно же, не можем до мельчайших подробностей изложить суть этого вопроса, но мы постарались отразить наиболее интересные и весомые аспекты. Мы рассказали о Леонардо Пизанском и дали понятное определение последовательности Фибоначчи; затем, на ярких примерах показали присутствие чисел Фибоначчи и Золотого сечения в разных сферах нашей жизни; выяснили что такое «Закон сохранения света», «Платоновы тела» и как они связаны с последовательностью.
Золотое сечение и последовательность чисел Фибоначчи помогают учёным описывать строение галактик и планетарных систем, а некоторые социологи начинают их использовать для прогнозирования различных катаклизмов, обусловленных массовой истерией (войн, беспорядков, революций и т.д).
Одна и та же закономерность используется в совершенно разных областях, практически не связанных между собой, а это значит, что она является универсальной.
Экономика, как и другие общественные сферы жизни человека поддаются определенным законам, несмотря на свою определенную непредсказуемость и зависимость от многих факторов современные экономические системы (в теории волнового анализа) поддаются законам «уровней Фибоначчи» построенных на основе одноименной последовательности.
С появлением финансовых рынков математики и статисты попробовали при помощи золотых чисел Фибоначчи строить уровни поддержки и сопротивления. Логично, ведь если поведение социума подчиняется божественной пропорции, разумно предположить, что и в действиях участников рынка также будет прослеживаться данная закономерность.
Как известно, эксперимент оказался удачным, и сегодня золотые числа Фибоначчи на Форекс используются для построения сеток, расширений, вееров, каналов и временных зон. В частности, при помощи первого инструмента можно найти сильные уровни, на которых следует ждать завершения коррекции, сформированной по отношению к последнему импульсу.
Мы убеждены, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние суммационной последовательности Фибоначчи на нашу жизнь.
Список литературы
1. Маркушевич, А. И. Возвратные последовательности. / А. И. Маркушевич.М.: Наука, 1975.
2. Воробьёв, Н. Н. Числа Фибоначчи. / Н. Н. Воробьёв. М.: Наука, 1978.
3. Савин, А. П. Энциклопедический словарь юного математика. / А. П. Савин. М.: Педагогика, 1989.
4. Мохнаткина, К. В. Последовательности в школьном курсе. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 3. Саратов: Научная книга, 2005. С. 63-67.
5. Мохнаткина, К. В. Изучение последовательностей в старших классах. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 4. Саратов: Научная книга, 2005. С. 59-63.
1.http://fb.ru/article/323642/chisla-fibonachchi-i-zolotoe-sechenie-vzaimosvyaz
2.https://studwood.ru/1851811/matematika_himiya_fizika/biografiya_fibonachchi
3.https://multiurok.ru/files/issliedovatiel-skaia-rabota-po-matiematikie-chisla-fibonachchi.html
4.http://fibonachi.gimnaziayanaul.edusite.ru/p11aa1.html
Приложение 1.
Золотые пропорции в частях тела человека.
Приложение 2
Просмотров работы: 500
school-science.ru
Число Фибоначчи — это… Что такое Число Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 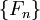 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 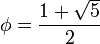 — золотое сечение. При этом
— золотое сечение. При этом 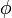 и
и 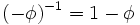 являются корнями квадратного уравнения
являются корнями квадратного уравнения 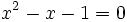 .
.
Из формулы Бине следует, что для всех 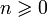 , Fn есть ближайшее к
, Fn есть ближайшее к 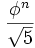 целое число, то есть
целое число, то есть 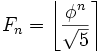 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 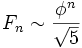 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
dal.academic.ru
Числа фибоначчи — это… Что такое Числа фибоначчи?
Числа Фибоначчи — Числа Фибоначчи элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух… … Википедия
Числа Фибоначчи — последовательность целых чисел, заданная с помощью рекуррентного соотношения: каждое последующее равно сумме двух предыдущих. Последовательность чисел Фибоначчи начинается так: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Леонардо Фибоначчи… … Судьба эпонимов. Словарь-справочник
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
Фибоначчи числа — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Числа Фиббоначчи — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Числа Фибоначи — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Фибоначчи — Леонардо Пизанский Leonardo Pisano Дата рождения: ок. 1170 года … Википедия
Фибоначчи числа — элементы числовой возвратной последовательности (См. Возвратная последовательность) 1, 1, 2, 3, 5, 8,… (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо … Большая советская энциклопедия
Числа трибоначчи — Числа трибоначчи последовательность целых чисел , заданная с помощью линейного рекуррентного соотношения: . Название является вариацией «чисел Фибоначчи» с добавкой «три» (лат. tri ), обозначающей количество суммируемых чисел.… … Википедия
Числа Люка — Не следует путать с последовательностями Люка. Числа Люка задаются рекуррентной формулой с начальными значениями и . Последовательность чисел Люка начинается так: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, … (последовательность A000032 в… … Википедия
dic.academic.ru
Код Фибоначчи — это… Что такое Код Фибоначчи?
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
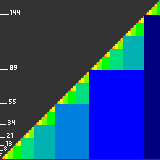 | ||
| Число | Запись в ФСС | Код Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | 1011 |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn-1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn+1 | 10……01 | 10……011 |
Представление натуральных чисел
Любому неотрицательному целому числу 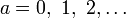 можно единственным образом представить через последовательность битов …εk…ε4ε3ε2:
можно единственным образом представить через последовательность битов …εk…ε4ε3ε2: 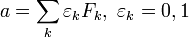 , причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц:
, причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: 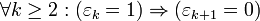 . За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование
В основе лежит теорема Цеккендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно.
Доказательство существования легко провести по индукции. Любое целое число 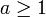 попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого
попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого 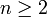 верно неравенство:
верно неравенство: 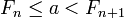 . Таким образом, a = Fn + a‘, где
. Таким образом, a = Fn + a‘, где 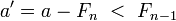 , так что разложение числа a‘ уже не будет содержать слагаемого Fn − 1.
, так что разложение числа a‘ уже не будет содержать слагаемого Fn − 1.
Использование в теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
- ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика
При сложении чисел в позиционных системах счисления приходится выполнять перенос, то есть устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что F1=1=F2 и F0=0. Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: 0200 = 0100 + 0011 = 0111 = 1001.
Обобщение на действительные числа
Похожее устройство имеет позиционная система счисления для действительных чисел, основанием которой служит золотое сечение 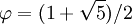 — иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
— иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
где {εk} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с 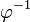 — золотым сечением отрезка [0,1], вычитанием
— золотым сечением отрезка [0,1], вычитанием 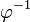 (если εk=1) и умножением на
(если εk=1) и умножением на 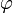 . Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
. Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
где N таково, что 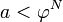 . Разумеется, следует считать что
. Разумеется, следует считать что 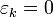 для всех
для всех 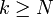 .
.
| Число | Представление через степени 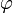 |
|---|---|
| 1 | 1, |
| 2 | 10,01 |
| 3 | 100,01 |
| 4 | 101,01 |
| 5 | 1000,1001 |
| 6 | 1010,0001 |
| 7 | 10000,0001 |
| 8 | 10001,0001 |
| 9 | 10010,0101 |
| 10 | 10100,0101 |
| 11 | 10101,0101 |
| 12 | 100000,101001 |
| 13 | 100010,001001 |
| 14 | 100100,001001 |
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент кольца 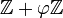 ) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств:
позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.
Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение.
Фибоначчиево «произведение»
Для целых чисел 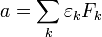 и
и 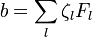 можно определить «произведение»[2]
можно определить «произведение»[2]
 ,
,
формула для которого аналогична формуле умножения двоичных чисел.
Разумеется, данная операция не является настоящим умножением чисел, и выражается[3] формулой:
![a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) где […] — целая часть.
где […] — целая часть.
Эта операция обладает ассоциативностью. Впервые на ассоциативность этой операции обратил внимание Дональд Кнут[4]. Следует отметить, что другое «произведение» 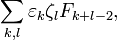 отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно.
отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно.
Источники
Wikimedia Foundation. 2010.
dic.academic.ru
Числа Фибоначчи — это… Что такое Числа Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что .
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц будет равна . В это время только те кролики, которые жили в месяце , являются способными к размножению и производят потомков, тогда пар прибавится к текущей популяции . Таким образом общее количество пар будет равно:
Формула Бине
Формула Бине выражает в явном виде значение как функцию от n:
- ,
где — золотое сечение. При этом и являются корнями характеристического уравнения .
Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .
Формула Бине может быть аналитически продолжена следующим образом:
При этом соотношение выполняется для любого комплексного числа z.
Тождества
Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи[2].И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть
- , а также ,
- где матрицы имеют размер , i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
- Отношения являются подходящими дробями золотого сечения и, в частности,
- Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
- .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:
- , , , .
- Производящей функцией последовательности чисел Фибоначчи является:
- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена
- на множестве неотрицательных целых чисел x и y.[4]
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:
- 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.[5]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[6]
- Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.
Вариации и обобщения
В других областях
Следует отметить, что существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который почти всегда оказывается неточной подгонкой под желаемый результат[7][8].
В природе
В культуре
- Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[14] и главном вокзале Цюриха[15].
- В фильме «Двадцать одно» (англ. 21) последовательность Фибоначчи представлена в виде надписи на торте.
- «Ряд Фибоначчи» — дополнительное название песни 2012 года «Новый сигнал из космоса» российской рок-группы «Сплин».
- В java-игре Doom RPG для мобильных телефонов в «Проходе» после прохождения 7 сектора есть секретная дверь, кодом которой являются числа Фибоначчи
- Числам Фибоначчи посвящён один их шуточных лимериков Джеймса Линдона[16]:
Плотная пища жён Фибоначчи
Только на пользу им шла, не иначе.
Весили жёны, согласно молве,
Каждая — как предыдущие две.
См. также
Примечания
Литература
Ссылки
biograf.academic.ru
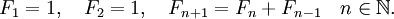
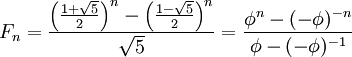 ,
,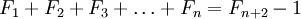
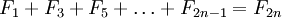
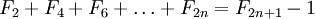
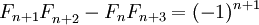

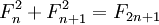
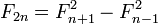
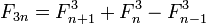
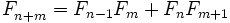
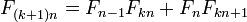
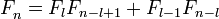
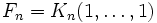 , то есть
, то есть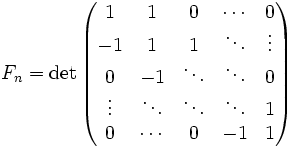 , а также
, а также 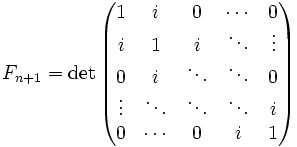 ,
,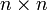 , i — мнимая единица.
, i — мнимая единица.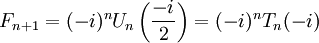
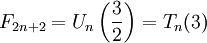
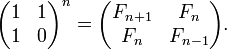
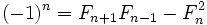
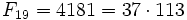 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.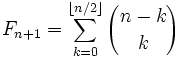 .
.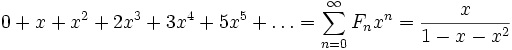
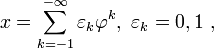
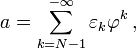
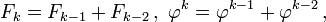
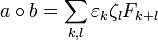 ,
,![a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,](/800/600/https/dic.academic.ru/pictures/wiki/files/48/08c1b4cbe18e534a0bfa7f377219722d.png) где […] — целая часть.
где […] — целая часть.