Памятка «Правила действий с дробями»

Правила действий с дробями 5 класс	Правила действий с дробями 5 класс
Чтобы сложить ( вычесть) дроби с одинаковыми знаменателями, надо сложить (вычесть) их числители, а знаменатель оставить тот же.	Чтобы сложить ( вычесть) дроби с одинаковыми знаменателями, надо сложить (вычесть) их числители, а знаменатель оставить тот же.
Чтобы сложить или вычесть дроби с разными знаменателями, надо сначала привести их к общему знаменателю, а потом применить правило сложения дробей с одинаковыми знаменателями.	Чтобы сложить или вычесть дроби с разными знаменателями, надо сначала привести их к общему знаменателю, а потом применить правило сложения дробей с одинаковыми знаменателями.
Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели	3. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.	4.Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Чтобы сложить смешанные числа, надо сложить отдельно целые части и отдельно дробные части и полученные результаты сложить. Если в результате сложения дробная часть станет неправильной дробью, то из нее надо выделить целую часть и прибавить к целой части результата.	5. Чтобы сложить смешанные числа, надо сложить отдельно целые части и отдельно дробные части и полученные результаты сложить. Если в результате сложения дробная часть станет неправильной дробью, то из нее надо выделить целую часть и прибавить к целой части результата.
Если дробные части смешанных чисел имеют разные знаменатели, то их сначала надо привести к общему знаменателю, а потом применить правило сложения смешанных чисел.	6.Если дробные части смешанных чисел имеют разные знаменатели, то их сначала надо привести к общему знаменателю, а потом применить правило сложения смешанных чисел.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то у целой части уменьшаемого надо занять единицу, представить ее в виде дроби с тем же знаменателем и добавить ее к дробной части уменьшаемого. Затем применить правило вычитания дробей.	7. Если дробная часть уменьшаемого меньше дробной части вычитаемого, то у целой части уменьшаемого надо занять единицу, представить ее в виде дроби с тем же знаменателем и добавить ее к дробной части уменьшаемого. Затем применить правило вычитания дробей.
Чтобы умножить или разделить смешанные числа, можно представить их в виде неправильных дробей, а затем применить правило умножения или деления обыкновенных дробей.	8. Чтобы умножить или разделить смешанные числа, можно представить их в виде неправильных дробей, а затем применить правило умножения или деления обыкновенных дробей.

План конспект урока по математике на тему «Решение упражнений на все действия со смешанными дробями»

Дата: 27.04.2018 г.

Урок № 150

Класс: 5-Б (учитель Бушманова А. Н.)

Тема урока «Решение упражнений на все действия со смешанными дробями»

Цель урока: обобщить знания по теме «Все действия со смешанными дробями».

Образовательная:

— повторить сложение, вычитание, умножение, деление смешанных дробей; рассмотреть их применение при решении задач на вычисления; создать условия для мотивации учащихся к изучению новой темы.

Развивающая:

— продолжить работу по развитию вычислительных  навыков, развивать логическое мышление, память, познавательный интерес; продолжить формирование математической речи; вырабатывать умение анализировать и сравнивать, делать выводы, проводить аналогии.
Воспитательная:

  

-воспитывать соблюдение норм поведения в коллективе, навыков совместной деятельности при работе в парах, умения аргументировать свои действия; содействовать воспитанию интереса к математике.

Формирование УУД:

-Личностные: способность к самооценке на основе критерия успешной учебной деятельности. Формировать умения ясно, точно и грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры.

-Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения; высказывать свое предположение.

-Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других.

-Познавательные УУД: умение ориентироваться в своей системе знаний; отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Тип урока: повторительно-обобщающий, урок – игра «Математический аукцион»

Форма организация учебной деятельности: групповая, фронтальная, парная, индивидуальная.

Оборудование: карточки-задания, компьютерные презентации, листы А-4, цветные карандаши, жетоны за правильные ответы.

План урока.

1. Организационный момент. Девиз урока (Чем больше я знаю, тем больше я умею.) 3 мин.

2. Актуализация опорных знаний. (определение целей урока.)5 мин

Решите устно и определите тему урока (на карточках) индивидуальная работа:

1. 12 * 12 = 144 14. 200 – 21 = 179

2. 25 * 3 = 75 15. 5 * 5 * 5 = 75

3. 100 : 4 = 25 16. 10 * 10 = 100

4. 100 — 44 =56 17. 283 * 2 =566

5. 72 * 2 = 144 18. 4 * 8 =32

6. 600 — 525 =75 19. 200 – 88 =111

7. 155 — 130 = 25 20. 7 * 7 = 49

8. 1111 — 1000 = 111 21. 100 * 10 =1000

9. 1000 — 242 =756

10. 7 * 8 =56

11. 6 * 11 = 66

12. 600 – 34 =566

13. 1110 : 10 =111

МАТЕМАТИЧЕСКИЙ АУКЦИОН (тема урока) – Значение слова (историческая справка) –

Сегодня мы проводим урок- аукцион. Что такое аукцион? «Аукцион — публичная распродажа, при которой покупателем становится тот, кто предложит высокую цену. 
Аукционер- участник аукциона. 
Аукционист- человек, ведущий аукцион. На аукционе будут продаваться различные задания на смекалку, внимание, задания логического характера, требующие нестандартных приемов решения, сообразительности это лоты. Ценой каждого лота будут не деньги, а знания. Кто приведет более глубокое и полное решение, тот становится покупателем.» 
-Сегодня мы продаём знания по математике. Побеждает тот, кто на аукционе наберёт наибольшее количество баллов. За каждый правильный ответ- жетон- 5 баллов. 

По удару молотка начинаем игру. 2 мин

3. Игра

Лот № 1. Решение примеров: Математический диктант (групповая работа на 4 группы) :

1. Запишите дроби: , , , , .

2. Найдите сумму двух первых дробей. (

    + ).

3. Найдите разность четвертого числа и пятой дроби.( — ) 5 мин

Лот № 2. Сравнение дробей (запись на доске) .3 мин

Пример1.

Сравните смешанные числа  и 

.

Решение.

Целая часть смешанного числа  меньше целой части смешанного числа  , поэтому .

Ответ:

Пример 2.

Какое из смешанных чисел  и 

 больше?

Решение.

Целые части сравниваемых смешанных чисел равны, поэтому сравнение сводится к сравнению дробных частей  и . Так как , то . Таким образом, смешанное число  больше, чем смешанное число 

.

Ответ:

.

Лот № 3. Решить уравнение (запись на доске): 10 мин.

1)  ;

2) х :.

4. Физминутка.2 мин.

5. Решение задачи (парная):

Лот № 4. (задания на карточках) 5 мин.

Задача 1. В одном ящике 

 кг слив, а во втором ящике на  кг больше. Сколько килограммов слив в двух ящиках?

Задача 2. Периметр треугольника MNK равен 30 см. Найдите длину стороны MK, если длина MN равна  см, а NK на   см длиннее MN.

6. Закрепление изученного материала:

Лот № 5.

Геометрический материал:5 мин.

7. Дополнительное задание:

Лот № 6. Логика.

Поле для крестиков-ноликов

Условие. Необходимо переложить 3 спички так, чтобы получить ровно 3 квадрата.

Ответ. Чтобы получить ровно три квадрата в этой задаче необходимо переместить 2 нижних вертикальных спички вправо и влево соответственно, чтобы они замыкали боковые квадраты. А нижней центральной горизонтальной спичкой нужно замкнуть верхний квадрат.

Соприкасающиеся друг с другом спички

Задание. Необходимо разместить 6 спичек так, чтобы каждая спичка соприкасалась с остальными пятью.

Ответ. Это задание требует подключения ваших творческих способностей, и выход за рамки плоскости – ведь спички можно класть друг на друга. Верное решение выглядит следующим образом. На схеме все спички действительно соприкасаются друг с другом. Хочу отметить, онлайн нарисовать такую фигуры гораздо проще, чем выложить так настоящие спички.

8. Рефлексия. 2мин.

9. Самооценивание (лист самооценивания) 2 мин.

10. Домашнее задание.1 мин.

Урок 47. смешанные дроби произвольного знака — Математика — 6 класс

Математика

6 класс

Урок № 47

Смешанные дроби произвольного знака

Перечень рассматриваемых вопросов:

• сложение и вычитание смешанных дробей произвольного знака.
• умножение и деление смешанных дробей произвольного знака.

Тезаурус

Натуральные числа – это числа, которые используются при подсчёте предметов.

Правильная дробь – это дробь, у которой числитель меньше знаменателя.

Положительная смешанная дробь есть сумма натурального числа и правильной дроби.

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Повторение – мать учения. Именно с этой поговорки начнём мы наше занятие. Т.к. на этом уроке мы повторим все рассмотренные ранее арифметические действия со смешанными дробями с различными знаками.

Сложение (вычитание) смешанных дробей.

Чтобы сложить (вычесть) два числа (две смешанные дроби) одинаковых знаков, надо сложить их модули и поставить перед суммой (разностью) знак слагаемых.

Необходимо помнить, что дроби складываются, если они имеют одинаковые знаки, и вычитаются, если они имеют разные знаки.

При сложении дробей знак сохраняется, а при вычитании дробей ставится знак большего по модулю числа.

Найдём разность

Умножение смешанных дробей произвольного знака.

Чтобы найти произведение смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила умножения дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби.

При выборе знака произведения используем следующее правило:

если количество отрицательных множителей чётное, то произведение будет положительным, если количество отрицательных множителей нечётное, то знак произведения будет отрицательным.

Найдём произведение

Количество отрицательных множителей нечётное, значит, произведение будет отрицательным.

Переведём каждую дробь в неправильную.

Перемножим отдельно числители и отдельно знаменатели.

Выделим целую часть и сократим дробную часть на 4.

Ответ

Деление смешанных дробей произвольного знака.

Чтобы найти частное смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила деления дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби).

Если отрицательных дробей в исходном выражении чётное количество, то частное будет положительным.

Если отрицательных дробей в исходном выражении нечётное количество, то частное будет отрицательным.

Решим задачу.

Фокус с числом.

Разбор заданий тренировочного модуля

№ 1. Сравните значение выражения с нулём.

Решение

Для решения данного выражения достаточно посмотреть на знак числа, возведённого в третью степень. Данная степень показывает, что число умножается само на себя три раза.

Знак «минус» повторяется 3 раза, т.е. нечётное число раз. Поэтому знак результата будет «минус». А мы знаем, что любое отрицательное число меньше нуля, следовательно, данное выражение меньше нуля.

№ 2. Решение задач

Решение

Чтобы определить пройденный путь S, нужно воспользоваться формулой

Где v – скорость движения, t – время движения. Подставив в формулу значения, получим результат.

Тест «Действия со смешанными числами»

Действия со смешанными числами 1 вариант Запишите смешанное число в виде неправильной дроби. а) б) в) г) Вычислите: а) б) в) г) Вычислите: а) б) в) г) Решите уравнение: а) б) в) г) Решите уравнение: а) б) в) г) Чтобы получить сплав для майки металлов, сплавили олова, свинца и висмута. Определите вес полученного сплава. а) б) в) г) Скорость слабого ветра умеренного – в 2 раза больше, скорость сильного ветра в раза больше скорости слабого и умеренного ветров вместе. Определите скорость сильного ветра. а) б) 6 м/с в) г)

Действия со смешанными числами 2 вариант Запишите смешанное число в виде неправильной дроби. а) б) в) г) Вычислите: а) б) в) г) Вычислите: а) б) в) г) Решите уравнение: а) б) в) г) Решите уравнение: а) б) в) г) На токарном станке деталь обрабатывали , на фрезерном — и на строгальном станке. Сколько часов обрабатывали деталь? а) б) в) г) С цветов белой акации, растущей в саду, пчёлы собирают мёда, с цветов жёлтой акации этого количества, с цветов яблони — веса мёда, собираемого с цветов жёлтой акации. Сколько килограммов мёда собирают пчёлы с цветов яблони? а) 50 кг б) 200 кг в) г) 20 кг

Контрольная работа»Действия со смешанными дробями» 5 класс

Контрольная работа 1 вариант №1 Выполнить действия 1) ; 2) ; 3) ; 4) ; 5) ; 6) . №2 Решить уравнение 1) ; 2) х : . №3 Задача Отрезок разделили на части длиной дм. Сколько получится частей, если длина отрезка 8дм; 13дм; 19дм. №4 Найти значение выражения

Контрольная работа 2 вариант №1 Выполнить действия 1) ; 2) ; 3) ; 4) ; 5) ; 6) . №2 Решить уравнение 1) ; 2) х : . №3 Задача Веревку разделили на части длиной м. Сколько получится частей, если длина веревки 7м; 11м; 18м. №4 Найти значение выражения

Сложение дробей | Онлайн калькулятор

Сложение дробей с одинаковыми знаменателями:

Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.

Формула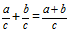
Сложим две дроби с одинаковым с одинаковыми знаменателями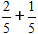
По формуле складываем числители, а знаменатель оставляем исходный

Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.

Пример: 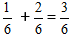При сокращении дроби у нас получится число 1/2

Сложение дробей с разными знаменателями:

Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:

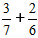
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК — наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение: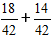

2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21

Сложение дроби и целого числа:

Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.

Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби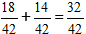
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример: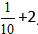
Решение: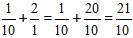
Вычисляем целую часть, и получаем ответ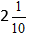

Сложение смешанных дробей:

Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
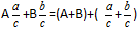
Пример:
Подставляем цифры в формулу:
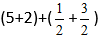
Получаем:

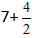
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.

Сложение дробей с помощью онлайн калькулятора:

Смотрите также