Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

 

Формулы корней квадратного уравнения. Дискриминант.

  

Формула №1:

         —b ± √D
x =  ————,  где D = b² – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12x² + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b² – 4ac = 7² – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         —b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x₁ = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x₂ = ——— = —— = — = – — .
           24           24       3          3

 

                        1                   1
Ответ: x₁ = – —,    x₂ = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D₁
x = ————,   где D₁ = k² – ac
             a

Пример. Решим уравнение 5x² – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8,  a = 5,  c = 3. Мы уже можем найти дискриминант D₁:

D₁ = k² – ac = (-8)² – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      —k ± √D₁       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x₁ = ——— =  — = 3
            5            5

 

         8 – 7         1
x₂ = ——— =  — = 0,2
             5           5 

 

Ответ: x₁ = 3; x₂ = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

 

Дискриминант уравнения — Справочник химика 21

    Вычислим дискриминанты уравнения (II.4) [c.29]

    В точке с уравнение (3.136) принимает вид (г — — 1) = О, что соответствует трем равным корням = г, = г, = —1 или Г1 = Гз = Гз = —Го- Область диаграммы, в которой все корни характеристического уравнения третьей степени действительные и отрицательные, находят приравниванием нулю дискриминанта уравнения (3.136)  [c.217]

    Формула (65) показывает, в частности, величину максимального диаметра, превышение которого уже не обеспечивает при заданной величине т необходимую фильтрующую поверхность ф. Из этой же формулы можно определить минимальную длину фильтра 1ф, при которой обеспечивается заданная поверхность Рф. Для этого дискриминант уравнения (65) должен быть больше нуля  [c.108]

    Поскольку дискриминант уравнения (10.127) 4AD—С =—Ка2 [c.245]

    Вычислим дискриминанты уравнения (111.12а) [c.45]

    Вычислим дискриминанты уравнения (IX.4) [c.103]

    Вычислим дискриминанты уравнения (Х.Ю) [c.115]

    Легко убедиться, что при выполнении условия (1.56) дискриминант уравнения 1 > О, г один из корней уравнения (1.47) является побочным и возникает вследствие возведения в квадрат выражения (1.41). Действительным корнем является наименьший (с учетом знака) при дН и наибольший — при дЬ > 1 . [c.39]

    Исследование корней производится с помощью дискриминанта уравнения А — р . Если Д > О, то один корень действительный, два — мнимые если Д [c. 523]

    Дискриминант квадратного уравнения (10.69) О = 1 — 4 со положителен, поскольку со 1. Поэтому корни характеристического уравнения 

[c.328]

    Форма решения полученного дифференциального уравнения 2-го порядка зависит от знака дискриминанта х характеристического уравнения, а границы устойчивости — от знаков постоянных коэффициентов. Результат анализа представлен на рис. 16.8. [c.211]

    При вычис.пении дискриминанта квадратного уравнения (9.6) следует вос- [c.535]

    Введем обозначения дискриминантов квадратных уравнений н составных частей корней  [c.155]

    Величина Л — дискриминант нормированного уравнения третьей степени. При Л > О имеем один действительный и два комплексных корня, при = О — два или три равных корня [c.218]

    Уравнения (6.2а) и (6.3а) для контуров / и II, как и в -пространстве, являются уравнениями эллипсов, так как дискриминанты соответствующих квадратичных форм удовлетворяют неравенствам [c. 80]

    Если дискриминант > 4Ло, то из уравнения (3.69) получаем [c.74]

    Если дискриминант характеристического уравнения [c.490]

    Уравнения типа руq = О имеют один вещественный и два комплексных корня, если дискриминант равен  [c.80]

    Считаем о Зм, и ярк, нормированными, тогда S = = Sk=1, и дискриминант системы уравнений (III.11) можно записать в виде [c.55]

    Корни уравнения ( 13 ) зависят от дискриминанта [c.16]

    Дискриминант общего уравнения будет [c.57]

    Вычислим дискриминант общего уравнения А и дискриминант старших членов б (см. Приложения 2 и 3)  [c.62]

    Вопрос о распадении кривой второго порядка решается величиной дискриминанта общего уравнения второго порядка  [c.479]

    Левая часть (3.7) представляет собой квадратное уравнение относительно а/Ь, не имеющее различных действительных корней.

Поэтому дискриминант этого уравнения не превосходит нуля, т. е. > [c.56]

    Уравнение (6.3.6) относится к линейным дискриминирующим функциям. Если имеется более чем два кластера, то требуется множественный линейный дискриминант. [Линейные дискриминанты редко отвечают требованиям диагностирования процессов, потому что кластеры обычно не являются однородно сферичными. Редко когда величины стандартных отклонений переменных не имеют различий между кластерами. Часто наблюдается пересечение кластеров, как на рис. 6.12. К тому же пики плотностей кластеров часто радикально различны. Наконец, даже в тех случаях, когда линейные дискриминанты могут быть рационально использованы, они дают меньше информации, чем квадратичные дискриминанты. Точка, лежащая далеко от ближайшего к ней кластера, и точка в его центре дают одну и ту же дискриминирующую величину. Такая ситуация не возникает при квадратичной дискриминации, когда значение дискриминанта само по себе указывает на положение точки внутри или вне соответствующего кластера.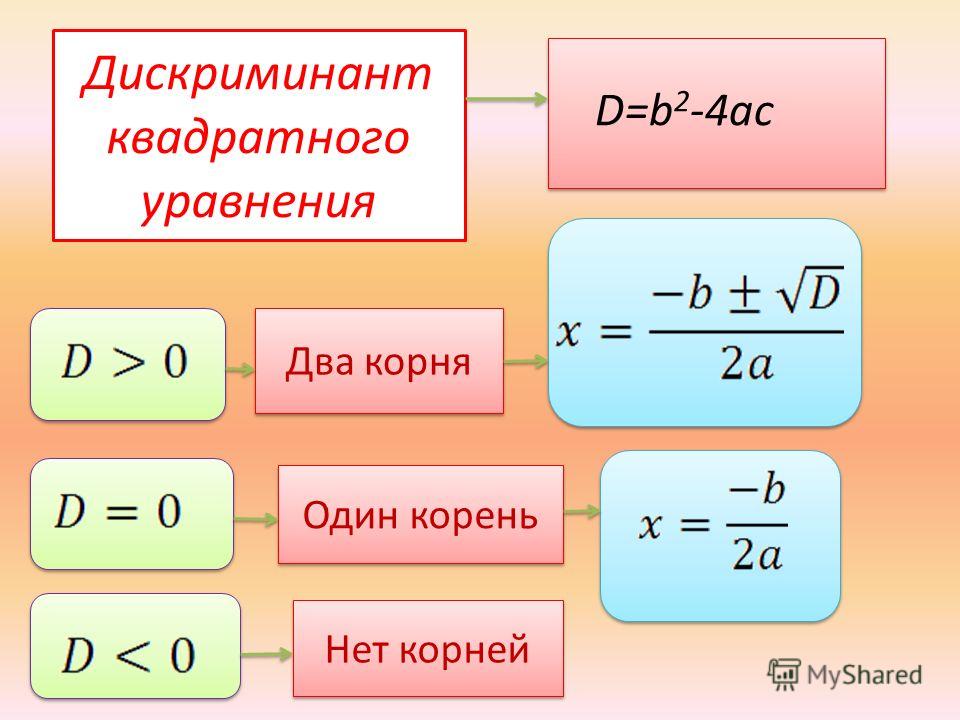

 [c.254]

    Для этого частного случая гауссовых распределений логарифмический дискриминант L [см. уравнение (6.3.7)], имеет вид [c.258]

    Решая уравнение (12.41), получаем соответствующие шесть значений т, положительных и отрицательных. Четыре корня, отвечающие выражению в квадратных скобках, являются действительными, так как дискриминант [Л 1 — 4 Жд О- [c.331]

    Дискриминант этого уравнения выражается в виде [c.69]

    Этот вопрос решается путем определения величины так называемого дискриминанта А общего уравнения кривой второго порядка. Этот дискриминант представляет собою определитель третьего порядка, составленный из коэффициентов уравнения (1.35) 

[c.20]

    В последнем случае следует дополнительно вычислить дискриминант старших членов о, который представляет собою определитель второго порядка, составленный из коэффициентов уравнения (1. 35) [c.21]

    Последнее уравнение есть уравнение второго порядка. Вычислим его дискриминанты [c.22]

    Так как дискриминант равен нулю, то уравнение второго порядка (И—139) является произведением двух уравнений первого поряд- [c.104]

    Число действительных корней уравнения (7.83) зависит от знака дискриминанта О = + р . Если О > О, то уравнение имеет один действительный корень и два мнимых. При решении его вводятся вспомогательные величины г = У р [c.408]

    Как известно, существование корней квадратного уравнения зависит от знака его дискриминанта [c.35]

    Дискриминант этого уравнения имеет вид  

[c.131]

    При проведении интегрирования, как видно, играет роль условие о существовании различных вещественных корней йь кг. Покажем, что, согласно термодинамической теории фазового равновесия, это условие можно считать выполненным. Для этого убедимся, что дискриминант уравнения (111,9) D = (S22 — В з) А В32В23 положителен. Воспользуемся полученным ранее выражением (11,21). В применении к тройной системе 2 — 3 — 4 оно будет иметь вид  [c.43]

    Полученныг нами уравнения (III.4), (III.5), (III.6), (111.6а представляют свойство как функцию N а- Вычислим дискриминанты уравнения (III.6) [c.41]

    В зависимости от )начсиий дискриминантов dj н будем иметь действительные или комплексные корни характеристических уравнений  [c.155]

    Данное уравнение третьей степени относительно [Н] может быть преобразовано к виду + Зрг/+ 2только один действительный, поскольку дискриминант О = 2 + рЗ всегда положителен). Однако соответствующая такому способу 

[c.50]

    Если дискриминант общего уравнения не равен нулю, то уравнение (Х.9) выражает собой параболу. Эта парабола отнесена к осям, параллельным ее директриссе и оси. Координаты вершины этой параболы будут [c.115]

    Обозначим коэффициенты при неизвестных ац= — 166 ), 0 2= —2са2, 22= 4, 23= О, 13= 8с Ь , адз= —АЬ с и проверил , не распадается ли наше уравнение на пару прямых. Для этого найдем дискриминант общего уравнения, равный определителю  [c.104]

    Второй случай наличия одного корня уравнения (1.41) будет при равенстве нулю дискриминанта (1.48). Соответствующие графики функщ1й изображены на рис. 1.9, д, е. Аналитические выражения, связьтающие скорость движения пены, высоту ее слоя и структурные параметры, могут быть получены из уравнения (1.48), но оказываются вьгсокой степени и весьма сложны для анализа. Отметим только, что в этом случае необходимым условием является вьшолнение следующих неравенств  

[c.39]

    Постоянные коэффициенты частотного уравнения (116) р=—2,68х ХЮ12 1/с q= —1,68- 1018 1/с H(u p = V U + 1 loe. Само частотное уравнение принимает вид —2,68-10 2 V—1,68-10 8=0. Нетрудно убедиться, что дискриминант этого уравнения отрицателен, следовательно, имеет три [c.112]

---

Бифуркационная диаграмма и дискриминант спектральной кривой интегрируемых систем на алгебрах Ли

БИФУРКАЦИОННАЯ ДИАГРАММА И ДИСКРИМИНАНТ СПЕКТРАЛЬНОЙ КРИВОЙ 59

где производная берется по λ. Заметим, что это в точности −1

2(p2−4q2)′. Таким

образом, D′

zзадается одним уравнением: p2−4q2= (p−2q)(p+ 2q)=0.

Заметим, что наличие кратного корня равносильно тому, что либо p±2q

имеют кратные корни, либо у них есть общий корень, что равносильно тому,

что общий корень есть у pиq, т.е. равен нулю их результант. Без ограни-

чения общности считаем, что c1̸= 0. Тогда уравнение спектральной кривой

с точностью до умножения на ненулевую константу имеет вид

0 = (z4−2z1)2−4(c2−2c1)(z3−2z2)

×(z4+ 2z1)2−4(c2+ 2c1)(z3+ 2z2)

×c1(c2z2−c1z3)2+z1(c2z2−c1z3)(c1z4−c2z1) + z2(c1z4−c2z1)2.(13)

Автор благодарит А. В. Болсинова и А. Т. Фоменко за плодотворные обсуж-

дения и постоянное внимание к работе.

Список литературы

[1] А. В. Болсинов, А.Т. Фоменко, Интегрируемые гамильтоновы системы.Гео-

метрия,топология,классификация, т.1, 2, РХД, Ижевск, 1999;англ. пер.:

A. V. Bolsinov, A.T. Fomenko, Integrable Hamiltonian systems. Geometry,topology,

classification, Chapman & Hall, CRC, Boca Raton, FL, 2004.

[2] M. Audin, Spinning tops.A course on integrable systems, Cambridge Stud. Adv.

Math., 51, Cambridge Univ. Press, Cambridge, 1999.

[3] В. В. Трофимов, А.Т. Фоменко, “Групповые неинвариантные симплектические

структуры и гамильтоновы потоки на симметрических пространствах”, Тр.

сем.по вект.и тенз.анализу,21 (1983), 23–83;англ. пер.: V. V. Trofimov,

A. T. Fomenko, “Non-invariant symplectic group structures and Hamiltonian flows

on symmetric spaces”, Selecta Math.Soviet., 7:4 (1988), 356–414.

[4] А. С. Мищенко, А.Т. Фоменко, “Уравнения Эйлера на конечномерных группах

Ли”, Изв.АН СССР.Сер.матем.,42:2 (1978), 396–415;англ. пер.: A. S. Miˇsˇcenko,

A. T. Fomenko, “Euler equations on finite-dimensional Lie groups”, Math.USSR-Izv.,

12:2 (1978), 371–389.

[5] А. С. Мищенко, А.Т. Фоменко, “Интегрируемость уравнений Эйлера на полупро-

стых алгебрах Ли”, Тр. сем.по вект.и тенз .анализу,19 (1979), 3–94;англ. пер.:

A. S. Mishchenko, A. T. Fomenko, “Integrability of Euler equations on semisimple Lie

algebras”, Selecta Math.Soviet., 2:4 (1982), 207–291.

[6] С. В. Манаков, “Замечание об интегрировании уравнений Эйлера динамики

n-мерного твердого тела”, Функц .анализ и его прил.,10:4 (1976), 93–94;англ.

пер.: S. V. Manakov, “Note on the integration of Euler’s equations of the dynamics

of an n-dimensional rigid body”, Funct.Anal.Appl., 10:4 (1976), 328–329.

[7] А. Т. Фоменко, Симплектическая геометрия.Методы и приложения, Изд-во

Моск. ун-та, М., 1988;англ. пер.: A. T. Fomenko, Symplectic geometry, Adv. Stud.

Contemp. Math., 5, Gordon and Breach, New York, 1988.

[8] Ю. А. Браилов, “Геометрия сдвигов инвариантов на полупростых алгебрах Ли”,

Матем.сб.,194:11 (2003), 3–16;англ. пер.: Yu. A. Brailov, “Geometry of

translations of invariants on semisimple Lie algebras”, Sb.Math., 194:11 (2003),

1585–1598.

[9] Yu. A. Brailov, A. T. Fomenko, “Lie groups and integrable Hamiltonian systems”,

Recent advances in Lie theory (Vigo, Spain, 2000), Res. Exp. Math., 25, Heldermann,

Lemgo, 2002, 45–76.

Формулы корней квадратных уравнений

здравствуйте тема этого урока формула корней квадратного уравнения мы уже с вами знаем что уравнение вида x квадрат плюс bx плюс c равна нулю называется полным квадратным уравнением а этот урок вам поможет узнать как решать такие уравнения что такое дискриминант и как с помощью значения дискриминанта определить количество корней как использовать формулы для решения квадрату полных квадратных уравнений начнем с первого понятия что такое дискриминант дискриминант квадратного уравнения называется выражение в квадрат минус 4 акция и реакция где b a и c это коэффициенты квадратного уравнения обозначается дискриминант большой латинской буквой д а вычисляется формулой d равна b квадрат минус 4 от c при решении дискриминанта возможны три случая дискриминант может быть больше 0 может оказаться значение равное нулю и может быть значение меньше 0 давайте рассмотрим случай если дискриминант больше нуля в этом случае уравнение имеет два действительных корни которые вычисляются по следующей формуле минус b плюс минус корень квадратный из дискриминанта разделить на 2а где b это коэффициент квадратного уравнения минус bms коэффициент минус b мы используем для ночь и счисления корней квадратного уравнения а значит коэффициент бы сюда мы должны поставлять противоположным знаком и коэффициент а мы используем для того чтобы вычислить корни квадратного уравнения если дискриминант меньше нуля то уравнение корней не имеет и действительно нам необходимо будет вычислять арифметический квадратный корень из дискриминанта а мы уже знаем по свой что по свойству что арифметический квадратный корень из отрицательного числа не существует поэтому атлетам такое уравнение всегда будет решений нет если дискриминант равен нулю в этом случае уравнение имеет один действительный корень и действительно проверим если мы формулу корней минус b плюс минус корень квадратный из 0 разделить на над на 2-ом проведем вычисления то получаем что корень квадратный корень данного квадратного уравнения можно вычислить минус b разделить на 2а это будет единственный корень уравнения рассмотрим пример решим такое вот простое уравнение 2x квадрат минус 5 x плюс 2 равна нулю решаются не очень просто и легко главное запомнить три главных шага первое определяем официанты вспоминаем что коэффициентами уравнения квадратного являются значение стоящие для коэффициента а это значение стоящая перед x квадрат знать о коэффициент б это значение стоящие перед x с его знаком и коэффициент ция это свободный член уравнения итак нашем уравнении коэффициента равны и равен двум b равно минус 5 и c равно 2 следующий шаг мы находим дискриминант для этого используем формулу квадратных корней формула дискриминанта d равно b квадрат минус 4 отце где b a и c это те значения которые мы определились этого уравнения коэффициенты этого уравнения подставляя коэффициенты полученные выше мы получаем результат в данной ситуации дискриминант равен 9 а мы уже говорили выше так как дискриминант больше нуля то уравнение имеет два действительных корни находим корни по формуле x равно минус b плюс-минус арифметический квадратный корень из дискриминанта разделить на два соответственно подставляем x 1 находим у нас коэффициент b равен был -5 формулу корней мы подставляем положительное число 5 корень квадратный из дискриминанта равен 3 помним что дискриминант у нас данной ситуации был равен 9 знаменателе 2 умножить на коэффициент а который был равен двум выполнив это вычисление мы получаем корень 1 2 же нахождение 2 корня единственно что изменяется это знак 5 плюс 3 и деленное на те же множитель едва-едва в результате вычислений мы получаем второй корень и тогда в ответ этого уравнения мы записываем x первое равное 2 и 2 равна целых пять десятых рассмотрим следующее уравнение 2x квадрат минус 3 x плюс пять равно нулю действую тем же самым способом первое находим коэффициенты в этом уравнении коэффициентами будет а равное 2 b равна -3 и c равная 5 находим дискриминант подставляем формула дискриминанта b квадрат минус 4 акция соответствующие коэффициенты то есть вместо b подставляем минус 3 и возводим в квадрат вместо а подставляем 2 вместо c подставляем множитель 5 в результате вычисления мы получаем минус 31 из вышесказанного мы знаем так как дискриминант меньше нуля то уравнения не имеют действительных корней а значит в ответ уравнения мы напишем решений нет есть уравнение решения не имеет решим еще одно уравнение x квадрат минус 2 x плюс 1 равная действием точно также первый шаг всегда находим коэффициенты определяем в этом уравнении а равную 1 b равно минус 2 и c равно единице следующий шаг находим дискриминант формула тоже самое b квадрат минус 4ac и подставляя формулу коэффициенты которые мы получили из этого уравнения мы получаем значение дискриминанта и в данном уравнении дискриминант равен нулю мы уже знаем что равенстве дискриминанта нулю уравнение имеет один корень а значит подставляя формулу x равна минус b разделить на 2 мы сможем найти этот корень уравнения подставляем в значение вместо b значения минус 2 вместо а значение 1 вычисление нам дает икс равное единице и в ответ мы записываем что решением уравнения является корень x равна 1 решение квадратных уравнений уравнений с использованием формул квадратных корней очень легкий способ главное запомнить и правильно определить первое во значит определить коэффициенты данного уравнения напоминаю что коэффициентами являются значения стоящей коэффициент а это значение перед x квадрат с его знаком значит коэффициент б это значение стоящие перед x с его знаком и коэффициент ция это свободный член уравнения с его знаком следующий шаг мы находим дискриминант подставляя формулу b квадрат минус 4 акции значение b и c соответственно выбор взятые в данном уравнении и уже по значению которое мы получаем дискриминанта мы можем дать ответ если дискриминант равен нулю соответственно мы выбираем форму x равно минус b разделить на 2а если дискриминант меньше нуля то уравнение решения и если дискриминант больше нуля то мы вычисляем корни данного уравнения по формуле минус b плюс минус корень квадратный из дискриминанта разделить на 2а если вы будете следовать этому алгоритму у вас все получится желаю успехов до новых уроков

Памятка по теме «Квадратное уравнение»

Квадратное уравнение

Квадратное уравнение – это уравнение вида ax2 + bx + c = 0, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.

 

Пример квадратного уравнения:

3×2 + 2x – 5 = 0.

Здесь а = 3, b = 2, c = –5.

 

Числа a, b и c – коэффициенты квадратного уравнения.

Число a называют первым коэффициентом, число b – вторым коэффициентом, а число c – свободным членом.

 

Приведенное квадратное уравнение.

Квадратное уравнение, в котором первый коэффициент равен 1, называют приведенным квадратным уравнением.

Примеры приведенного квадратного уравнения:

x2 + 10x – 11 = 0

x2 – x – 12 = 0

x2 – 6х + 5 = 0

здесь коэффициент при x2 равен 1 (просто единица во всех трех уравнениях опущена).

 

Неполное квадратное уравнение.

Если в квадратном уравнении ax2 + bx + c = 0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют неполным квадратным уравнением.

Примеры неполного квадратного уравнения:

-2×2 + 18 = 0

здесь есть коэффициент а, который равен -2, есть коэффициент c, равный 18, а коэффициента b нет – он равен нулю.

x2 – 5x = 0

здесь а = 1,  b = -5,  c = 0 (поэтому коэффициент c  в уравнении отсутствует).

Как решать квадратные уравнения.

Чтобы решить квадратное уравнение, надо совершить всего два действия:

1) Найти дискриминант D по формуле:

D = b2 – 4ac.

Если дискриминант – отрицательное число, то квадратное уравнение не имеет решения, вычисления прекращаются. Если D ≥ 0, то

2) Найти корни квадратного уравнения по формуле:

             –b ± √D
х1,2 = —————.
                  2а

Пример: Решить квадратное уравнение 3х2 – 5х – 2 = 0.

Решение:

Сначала определимся с коэффициентами нашего уравнения:

а = 3, b = –5, c = –2.

Вычисляем дискриминант:

D = b2 – 4ac = (–5)2 – 4 · 3 · (–2) = 25 + 24 = 49.

D > 0, значит, уравнение имеет смысл, а значит, можем продолжить.

Находим корни квадратного уравнения:

           –b + √D            5 + 7          12
х1 = ————— = ———— = —— = 2
               2а                    6              6

          –b – √D             5 – 7              2             1
х2 = ————— = ———— = – —— = – ——.
             2а                     6                  6             3

                                       1
Ответ: х1 = 2,  х2 = – ——.
                                       3

Формулы корней квадратного уравнения. Дискриминант.

Формула №1:

         —b ± √D
x =  ————,  где D = b2 – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12×2 + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b2 – 4ac = 72 – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         -b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x1 = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x2 = ——— = —— = — = – — .
           24           24       3          3

 

                        1                   1
Ответ: x1 = – —,    x2 = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D1
x = ————,   где D1 = k2 – ac
             a

Пример. Решим уравнение 5×2 – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8, a = 5,  c = 3. Мы уже можем найти дискриминант D1:

D1 = k2 – ac = (-8)2 – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      -k ± √D1       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x1 = ——— =  — = 3
            5            5

 

         8 – 7         1
x2 = ——— =  — = 0,2
             5           5 

 

Ответ: x1 = 3; x2 = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

Здесь будет файл: /data/edu/files/n1461134193.docx (Квадратное уравнение)

Квадратное уравнение где дискриминант равен нулю. Решение квадратных уравнений с помощью дискриминанта

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. 2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):

D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. .

Общая формула для нахождения корней квадратного уравнения :

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)

Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0) ,

или парабола ветвями вниз (a

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox .
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D

Неполные квадратные уравнения

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается. ) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно. ) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат.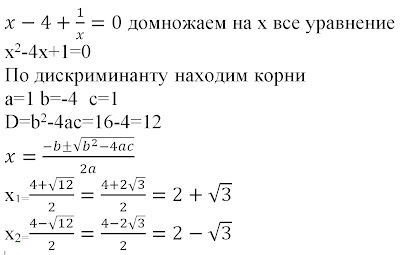 Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать. )

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В данной статье мы рассмотрим решение неполных квадратных уравнений.

Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах 2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным . Как мы видим коэффициент при х 2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.

Неполные квадратные уравнения бывают трех видов :

1) Если b = 0, с ≠ 0, то ах 2 + с = 0;

2) Если b ≠ 0, с = 0, то ах 2 + bх = 0;

3) Если b= 0, с = 0, то ах 2 = 0.

• Давайте разберемся как решаются уравнения вида ах 2 + с = 0.

Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим

ах 2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х 2 = ‒с/а.

Если ‒с/а > 0 , то уравнение имеет два корня

x = ±√(–c/a) .

Если же ‒c/a

Давайте попробуем разобраться на примерах, как решать такие уравнения.

Пример 1 . Решите уравнение 2х 2 ‒ 32 = 0.

Ответ: х 1 = ‒ 4, х 2 = 4.

Пример 2 . Решите уравнение 2х 2 + 8 = 0.

Ответ: уравнение решений не имеет.

• Разберемся как же решаются уравнения вида ах 2 + bх = 0.

Чтобы решить уравнение ах 2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах + b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах + b = 0. Решая уравнение ах + b = 0, получим ах = ‒ b, откуда х = ‒ b/a. Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a. Посмотрите как выглядит на схеме решение уравнений этого вида.

Закрепим наши знания на конкретном примере.

Пример 3 . Решить уравнение 3х 2 ‒ 12х = 0.

х(3х ‒ 12) = 0

х= 0 или 3х – 12 = 0

Ответ: х 1 = 0, х 2 = 4.

• Уравнения третьего вида ах 2 = 0 решаются очень просто.

Если ах 2 = 0, то х 2 = 0. Уравнение имеет два равных корня х 1 = 0, х 2 = 0.

Для наглядности рассмотрим схему.

Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.

Пример 4. Решить уравнение 7х 2 = 0.

Ответ: х 1, 2 = 0.

Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.

Пример 5. Решить уравнение

Умножим обе части уравнения на общий знаменатель, то есть на 30

Сократим

5(5х 2 + 9) – 6(4х 2 – 9) = 90.

Раскроем скобки

25х 2 + 45 – 24х 2 + 54 = 90.

Приведем подобные

Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный

Ответ: корней нет.

Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.

Если у вас появились вопросы по данной теме, записывайтесь на мои уроки , мы вместе решим возникшие проблемы.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Рассмотрим задачу. Основание прямоугольника больше высоты на 10 см., а его площадь равна 24 см². Найти высоту прямоугольника. Пусть х сантиметров — высота прямоугольника, тогда его основание равно (х +10) см. Площадь этого прямоугольника равна х (х + 10) см². По условию задачи х (х + 10) = 24. Раскрывая скобки и перенося число 24 с противоположным знаком в левую часть уравнения, получаем: х ² + 10х -24 = 0. При решении этой задачи было получено уравнение, которое называют квадратным.

Квадратным уравнением называется уравнение вида

ax ²+bx +c= 0

где a, b, c — заданные числа, причем а ≠ 0, а х — неизвестное.

Коэффициенты a, b, c квадратного уравнения обычно называют так: a — первым или старшим коэффициентом, b — вторым коэффициентом, c — свободным членом. Например в нашей задаче старший коэффициент равен 1, второй коэффициент 10, свободный член -24. Решение многих задач математики и физики сводится к решению квадратных уравнений.

Решение квадратных уравнений

Полные квадратные уравнения. Первым делом надо заданное уравнение привести к стандартному виду ax ²+ bx + c = 0. Вернемся к нашей задаче, в которой уравнение может быть записано как х (х + 10) = 24 приведем его к стандартному виду, раскроем скобки х ² + 10х — 24 = 0, решим это уравнение с помощью формулы корней квадратного уравнения общего вида.

Выражение под знаком корня в этой формуле называется дискриминант D = b ² — 4ac

Если D>0, то квадратное уравнение имеет два различных корня, которые можно найти по формуле корней квадратного уравнения.

Если D=0, то квадратное уравнение имеет один корень.

Если D

Подставим значения в нашу формулу а = 1, b = 10, c = -24.

получаем D>0, следовательно у нас получится два корня.

Рассмотрим пример где D=0, при этом условии должен получится один корень.

25x ² — 30x + 9 = 0

Рассмотрим пример где D

2x ² + 3x + 4 = 0

Число, стоящее под знаком корня (дискриминант) отрицательное, ответ запишем так: уравнение не имеет действительных корней.

Решение неполных квадратных уравнений

Квадратное уравнение ax ² + bx + c = 0 называют неполным, если хотя бы один из коэффициентов b или c равен нулю. Неполное квадратное уравнение, есть уравнение одного из следующих видов:

ax ² = 0,

ax ² + c = 0, c ≠ 0,

ax ² + bx = 0, b ≠ 0.

Рассмотрим несколько примеров, решим уравнение

Разделив обе части уравнения на 5, получим уравнение х ² = 0, в ответе будет один корень х = 0.

Рассмотрим уравнение вида

3х ² — 27 = 0

Разделив обе части на 3, получим уравнение х ² — 9 = 0, или его можно записать х ² = 9, в ответе будет два корня х = 3 и х = -3.

Рассмотрим уравнение вида

2х ² + 7 = 0

Разделив обе части на 2, получим уравнение х ² = -7/2. Это уравнение действительных корней не имеет, так как х ² ≥ 0 для любого действительного числа х .

Рассмотрим уравнение вида

3х ² + 5х = 0

Разложив левую часть уравнения на множители, получим х (3х + 5) = 0, в ответе будет два корня х = 0, х =-5/3.

Самое главное при решении квадратных уравнений, привести квадратное уравнение к стандартному виду, выучить наизусть формулу корней квадратного уравнения общего вида и не запутаться в знаках.

Библиографическое описание: Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Способы решения квадратных уравнений // Юный ученый. — 2016. — №6.1. — С. 17-20..03.2019).



Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.

Что же такое «квадратные уравнения»?

Квадратное уравнение — уравнение вида ax 2 + bx + c = 0 , где a , b , c — некоторые числа (a ≠ 0 ), x — неизвестное.

Числа a, b,c называются коэффициентами квадратного уравнения.

• a называется первым коэффициентом;
• b называется вторым коэффициентом;
• c — свободным членом.

А кто же первый «изобрёл» квадратные уравнения?

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Вавилонские математики примерно с IV века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).

Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax2 + bх = с, а>0

В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = bх.

2) «Квадраты равны числу», т. е. ах2 = с.

3) «Корни равны числу», т. е. ах2 = с.

4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах2.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в. , не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи . Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Рассмотрим несколько способов решения квадратных уравнений.

Стандартные способы решения квадратных уравнений из школьной программы:

1. Разложение левой части уравнения на множители.
2. Метод выделения полного квадрата.
3. Решение квадратных уравнений по формуле.
4. Графическое решение квадратного уравнения.
5. Решение уравнений с использованием теоремы Виета.

Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.

Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.

Пример. x 2 -5x+6=0

Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.

Ответ: x 1 =2, x 2 =3.

Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.

Пример. 3x 2 +2x-5=0

Берём первый коэффициент и умножаем его на свободный член: x 2 +2x-15=0

Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.

Ответ: x 1 =-5/3, x 2 =1

6. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а≠0.

Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0, равносильному данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 2 = у 2 /а.

При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример. 2х 2 — 11х + 15 = 0.

«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.

Согласно обратной теореме Виета

у 1 = 5, х 1 = 5/2, х 1 =2,5 ;у 2 = 6, x 2 = 6/2, x 2 = 3.

Ответ: х 1 =2,5; х 2 = 3.

7. Свойства коэффициентов квадратного уравнения.

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.

1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.

2. Если а — b + с = 0, или b = а + с, то х 1 = — 1.

Пример. 345х 2 — 137х — 208 = 0.

Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.

Ответ: х 1 =1; х 2 = -208/345 .

Пример. 132х 2 + 247х + 115 = 0

Т.к. a-b+с = 0 (132 — 247 +115=0), то х 1 = — 1, х 2 = — 115/132

Ответ: х 1 = — 1; х 2 =- 115/132

Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.

8. Решение квадратных уравнений с помощью номограммы.

Рис 1. Номограмма

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В. М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис. 1):

Полагая ОС = р, ED = q, ОЕ = а (все в см), из рис.1 подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

Рис. 2 Решение квадратных уравнения с помощью номограммы

Примеры.

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0

Ответ:8,0; 1,0.

2) Решим с помощью номограммы уравнение

2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 — 4,5z + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Ответ: 4; 0,5.

9. Геометрический способ решения квадратных уравнений.

Пример. х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».

Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25

Рис. 3 Графический способ решения уравнения х 2 + 10х = 39

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

10. Решение уравнений с использованием теоремы Безу.

Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т.е. значению P(x) при x = α).

Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.

Пример. х²-4х+3=0

Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3

х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0

х-1=0; х=1, или х-3=0, х=3; Ответ: х 1 =2, х 2 =3.

Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.

Литература:

1. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
2. Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
3. https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
4. Глейзер Г.И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодшего. — М.: Просвещение, 1964.

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида , где . 

— коэффициент при  , или старший коэффициент.

— коэффициент при х, или второй коэффициент.

— свободный член.

Например, в уравнении   , , .

B уравнении   , ,

Если в квадратном уравнении  или  , то такое квадратное уравнение называется НЕПОЛНЫМ.

Неполное квадратное уравнение решается с помощью разложения на множители.

1. Если , то нужно вынести за скобки общий множитель.

Например,

Приравняем каждый множитель к нулю:

или

Ответ: {0,  }

2. Если , то нужно разложить на множители по формуле разности квадратов:

Например:

Приравниваем каждый множитель  к нулю, получаем:

или 

Коротко это уравнение решается так:

В этом месте важно не забыть знак  перед корнем!

Ответ: {}

Если  в квадратном уравнении  и  , то такое квадратное уравнение называется ПОЛНЫМ.

Полное квадратное уравнение решается с помощью нахождения ДИСКРИМИНТА.

Дискриминант квадратного уравнения  вычисляется по формуле:

.

Формулы для вычисления корней квадратного уравнения выглядят так:

В этих формулах дискриминант присутствует под знаком квадратного корня, поэтому

Eсли , то квадратное уравнение не имеет действительных корней.

Если , то квадратное уравнение имеет два различных действительных корня, которые можно найти по приведенным выше формулам.

Если ,  то квадратное уравнение имеет два совпадающих корня:

.

Иногда  говорят, что в этом случае квадратное уравнение имеет один корень.

Итак, при решении квадратного уравнения удобно пользоваться таким алгоритмом:

1. Определяем, является ли квадратное уравнение полным, или неполным.

2. Если уравнение неполное, раскладываем левую часть на множители и приравниваем каждый множитель к нулю.

3. Если уравнение полное, то

• находим дискриминант квадратного уравнения по формуле
• если дискриминант меньше нуля, то записываем, что квадратное уравнение не имеет действительных корней
• если дискриминант равен нулю, то находим корни квадратного уравнения по формуле 
• если дискриминант больше нуля, то находим корни квадратого уравнения по формулам:, 

Если коэффициент   квадратного уравнения — четное число, то есть его можно записать как , или  то для нахождения корней квадратного уравнения удобно пользоваться формулами для четного второго коэффициента:

Два полезных замечания:

1. Если для коэффициентов квадратного уравнения  выполняется равенство , то , 

2. Если для коэффициентов квадратного уравнения  выполняется равенство , то , 

Эти свойства помогают устно решать некоторые громоздкие квадратные уравнения. Например, в квадратном уравнении  сумма коэффициентов равна 0, поэтому ,  .

В уравнении выполняется равенство , поэтому ,  

Рассмотрим несколько примеров.

Решим квадратные уравнения:

1.

а) найдем дискриминант этого уравнения:

Дискриминант больше нуля, значит уравнение имеет два различных корня.

б) Тогда: , 

Ответ:   {1; 1/2}

2.  

а) Найдем дискриминант этого уравнения:

. Очевидно, что  , и даже нет необходимости вычислять его точное значение.

Ответ: уравнение не имеет действительных корней.

3. 

а) Найдем дискриминант этого уравнения:

б) Так как , уравнение имеет два совпадающих корня,

Если внимательно посмотреть на квадратный трехчлен, стоящий в левой части уравнения, то становится очевидно, то что его можно преобразовать по формуле квадрата разности к выражению

, отсюда 

Ответ: 1/4.

А теперь я предлагаю вам посмотреть видеоурок с решением квадратного уравнения:

 

И.В. Фельдман, репетитор по математике.

Дискриминанты и определение числа действительных корней квадратного уравнения

Что такое дискриминант?

Дискриминант — это величина, вычисляемая по квадратному уравнению. Он использует его, чтобы «различать» корни (или решения) квадратного уравнения.

Квадратное уравнение имеет вид: ax ² + bx + c

Дискриминант, D = b ² — 4ac

Примечание. Это выражение внутри квадратного корня квадратной формулы

.

Дискриминант бывает в трех случаях;

Корпус 1:

b ² — 4ac> 0

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных (разных) корня .

Пример

х ² — 5х + 2 = 0

а = 1, б = -5, в = 2

Дискриминант, D = b ² — 4ac

= (-5) ² — 4 * (1) * (2)

= 17

Следовательно, квадратное уравнение

имеет два действительных различных корня.

х ² — 5х + 2.

Корпус 2:

b ² — 4ac <0

Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет действительных корней .

Пример

3x ² + 2x + 1 = 0

а = 3, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ^{2 —} 4 * (3) * (1)

= — 8

Следовательно, у квадратного уравнения 3x ² + 2x + 1 нет действительных корней.

Корпус 3:

b ² — 4ac = 0

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных идентичных корня .

Пример

х ² + 2х + 1 = 0

а = 1, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ² — 4 * (1) * (1)

= 0

Следовательно, есть два действительных идентичных корня квадратного уравнения x ² + 2x + 1.

Сводка

Квадратное уравнение: ax ² + bx + c

Определитель D = b ² — 4ac

D> 0 означает два реальных, различных корня.

D = 0 означает два настоящих одинаковых корня /

D <0 означает отсутствие реальных корней.

Теперь попробуйте эти (будьте осторожны со знаками минус)

вопросов

Q1.х ² — 7x + 2 = 0

Q2. — 3x ² + 2x — 1 = 0

Q3. 9x ² — 12x + 4 = 0

Q4. — х ² + х + 1 = 0

ответы

Q1. D = 41 означает два реальных, различных корня.

Q2. D = -16, означает отсутствие настоящих корней.

Q3. D = 0 означает два настоящих одинаковых корня.

Q4. D = 5 означает два реальных, различных корня.

Дискриминант — Концепция — Алгебра Видео от Brightstorm

Дискриминант — это член под квадратным корнем в квадратной формуле, который сообщает нам количество решений квадратного уравнения.Если дискриминант положительный, мы знаем, что у нас есть 2 решения. Если он отрицательный, решений нет, а если дискриминант равен нулю, у нас есть одно решение. Дискриминант вычисляется путем возведения в квадрат члена «b» и вычитания 4-кратного члена «а», умноженного на член «с».

Дискриминант — действительно удобный инструмент, когда вам кажется, что вы получаете странный ответ.Вот почему. Дискриминант сообщает вам, сколько существует решений квадратного уравнения или сколько пересечений по оси x существует для параболы. Он не говорит вам, каковы эти числа, каковы значения пересечения x, он просто говорит вам, сколько их должно быть. Звучит так, будто это бесполезно, но на самом деле это особенно важно, когда вы проверяете свою работу.
Вот как это выглядит. Дискриминант — это формула b в квадрате минус 4ac, помня, что a, b и c — это коэффициенты квадратичной функции в стандартной форме.Он сообщает вам количество решений квадратного уравнения. Если дискриминант больше нуля, есть два решения. Если дискриминант меньше нуля, решений нет, а если дискриминант равен нулю, есть одно решение.
Это то, что вам просто нужно запомнить. Это идет рука об руку с формулой корней квадратного уравнения. Так что, если вы, ребята, это усвоили, это будет иметь большой смысл. Если вы еще не выучили квадратную формулу, вы, вероятно, выучите ее завтра на уроке математики.Просто знайте, что вы смотрите на то, действительно ли b в квадрате минус 4ac больше нуля, меньше нуля или равно нулю. И это говорит мне, сколько ответов я должен получить. Он не говорит мне, каковы ответы, просто сколько из них мне нужно, чтобы решить проблему.

Все знаки указывают на дискриминант

Все знаки указывают на дискриминант

У вас когда-нибудь был один из этих Magic 8 Balls? Они выглядят как комично негабаритные шары для пула, но в них встроено плоское окно, так что вы можете видеть, что находится внутри 20-гранного кубика, плавающего в отвратительной непрозрачной синей слизи.Предположительно, бильярдный шар обладает прогностическими способностями; все, что вам нужно сделать, это задать ему вопрос, встряхнуть, и медленно, мистическим образом, как покрытый нефтью тюлень, выходящая из разлива нефти, игральная кость поднимется к маленькому окошку и откроет ответ на ваш вопрос.

Квадратное уравнение содержит своего рода Magic 8 Ball. Выражение b ² — 4 ac под знаком радикала называется дискриминантом , и оно может фактически определить для вас, сколько решений имеет данное квадратное уравнение, если вы не хотите на самом деле вычислять их.Учитывая, что квадратное уравнение, которое невозможно сформулировать, требует много работы для решения (квадратная формула изобилует тоннами арифметики, а для завершения квадратного метода требуется целая куча шагов), часто бывает полезно заглянуть в загадочную загадку, чтобы сделать убедитесь, что уравнение даже имеет любых вещественных числовых решений, прежде чем вы потратите какое-либо время на их поиски.

Talk the Talk

Дискриминант — это выражение b ² -4 ac , которое определено для любого квадратного уравнения ax ² + bx + c = 0. По знаку выражения можно определить, сколько действительных чисел имеет квадратное уравнение.

Вот как работает дискриминант. Дано квадратное уравнение ax ² + bx + c = 0, подставьте коэффициенты в выражение b ² -4 ac , чтобы увидеть, что в результате:

• Если вы получите положительное число, квадратичная функция будет иметь два уникальных решения.
• Если вы получите 0, у квадратичного будет ровно одно решение — двойной корень.
• Если вы получите отрицательное число, у квадратичного не будет реальных решений, только два мнимых. (Другими словами, решения будут содержать и , о которых вы узнали в «Борьбе с радикалами».)

Дискриминант не является магическим. Это просто показывает, насколько важен этот радикал в формуле корней квадратного уравнения. Если, например, его подкоренное выражение равно 0, то вы получите

единственное решение. Если, однако, b ² -4 ac отрицательно, то внутри квадратного корня в квадратной формуле будет отрицательное значение, что означает только мнимые решения.

Пример 4 : Не вычисляя их, определите, сколько реальных решений имеет уравнение 3 x ² — 2 x = -1.

Решение : Установите квадратное уравнение равным 0, добавив 1 к обеим сторонам.

У вас есть проблемы

Задача 4: Не вычисляя их, определите, сколько реальных решений имеет уравнение 25 x ² -40 x + 16 = 0.

Установите a = 3, b = -2 и c = 1 и оцените дискриминант.

• b ² — 4 ac
• = (- 2) ² — 4 (3) (1)
• = 4-12
• = -8

Поскольку дискриминант отрицательно, квадратное уравнение не имеет вещественных числовых решений, только два мнимых.

Выдержка из Полное руководство для идиотов по алгебре 2004 У. Майкла Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Эту книгу можно приобрести на Amazon.com и Barnes & Noble.

BestMaths

Корни из графиков

Графики трех квадратичных функций показаны ниже.

корней соответствующих квадратных уравнений задаются тем местом, где график пересекает ось x. то есть x- перехватывает.

Корни квадратного уравнения называются действительными корнями , если график пересекает или касается оси x. Эти корни являются действительными числами .

Если график НЕ пересекает ось x, то уравнение не имеет действительных корней. Уравнение этого типа можно решить с помощью комплексных или мнимых чисел, которые обычно изучаются в 12-м году обучения (13-й год Новой Зеландии).

Графики
Функция	у = (х + 3) 2	y = x 2 — 5x + 6 = (x — 3) (x — 2)	y = -x 2 + x — 2 = — (x — 0.5) 2 — 1,75
Количество и характер корней	Один настоящий корень	Два настоящих корня	Без настоящих корней

Существует более быстрый способ, чем рисование графиков или решение для определения количества корней квадратного уравнения, этот метод использует дискриминант .

Дискриминант

Дискриминант квадратного уравнения ax ² + bx + c = 0 определяется выражением b ² — 4ac.
Символ Δ иногда используется в качестве дискриминанта.

Обратите внимание, что дискриминант — это часть квадратной формулы , которая находится под знаком квадратного корня.

Изучая значение дискриминанта, мы можем определить количество и характер корней.

Если дискриминант равен нулю	b 2 — 4ac = 0	есть один (повторяющийся) рациональный корень
Если дискриминант положительный	b 2 — 4ac> 0	есть два настоящих корня
Если дискриминант отрицательный	b 2 — 4ac <0	настоящих корней нет

Если дискриминант является полным квадратом, например 49 или 100, то корнями будут рациональных (дробных) чисел.

Примеры:

	пример 1	пример 2	пример 3
Уравнение	y = (x + 3) 2 = x 2 + 6x + 9	y = x 2 — 5x + 6	y = -x 2 + x — 2
a, b и c	a = 1, b = 6, c = 9	a = 1, b = -5, c = 6	а = -1, б = 1, с = -2
Дискриминант	b 2 — 4ac = 6 2 — 4x1x9 = 0 Дискриминант = 0 (т. е. Ноль)	b 2 — 4ac = (-5) 2 — 4x1x6 = 1 Дискриминант = 1 (т.е. положительный)	b — 4ac = (1) 2 — 4x-1x-2 = -7 Дискриминант = -7 (т.е. отрицательный)
Количество и характер корней	Имеется один повторяющийся действительный корень	Есть два настоящих корня	Настоящих корней нет

Дискриминант

Дискриминант описывает характеристику корней многочленов.Он отличает разные многочлены одного типа друг от друга.

Существуют разные дискриминанты, используемые для разных степеней многочленов, но наиболее вероятно, что вы увидите, особенно в алгебре, b ² — 4ac, который используется для описания числа решений квадратичной. Хотя это только один дискриминант, термин «дискриминант» часто используется для обозначения этого конкретного дискриминанта. Этот дискриминант также используется как часть формулы корней квадратного уравнения в числителе.

Если дискриминант меньше 0, то квадратичная функция не имеет действительного решения. Вы можете вспомнить это, вспомнив, что вы не можете извлечь квадратный корень из отрицательного числа (без использования мнимых чисел). В квадратной формуле дискриминант заключен в радикал, поэтому, если дискриминант отрицательный, вы не сможете вычислить реальное решение.

Пример

f (x) = 3x ² — 2x + 2

а = 3; b = -2; с = 2

b ² — 4ac = (-2) ² — 4 (3) (2)

= 4–24 = -20

Если дискриминант отрицательный, настоящего решения нет.Как видно на рисунке ниже, на графике нет нулей:

Если дискриминант равен 0, то квадратичный имеет одно решение. Вы можете вспомнить это, вспомнив, что квадратный корень из 0 равен 0. Ниже приведен пример этого случая:

Пример

f (x) = 4x 2 — 4x + 1

a = 4; b = -4; с = 1

b 2 — 4ac = (-4) 2 — 4 (4) (1)

= 16-16 = 0

f (x) = 4x 2 — 4x + 1

Дискриминант равен 0, и есть одно решение при x = & frac12

Если дискриминант больше 0, то квадратичный имеет два решения. Вы можете вспомнить это, вспомнив, что квадратный корень из положительного числа имеет два решения, одно положительное и одно отрицательное, как показано ниже:

Пример

f (x) = x 2 — 2x — 3

a = 1; b = -2; с = -3

b 2 — 4ac = (-2) 2 — 4 (1) (- 3)

= 4 + 12 = 16

Поскольку дискриминант больше 0, существует два решения: x = -1 или x = 3.

См. Также формулу корней квадратного уравнения.

Равные или двойные корни

РАВНЫЕ ИЛИ ДВОЙНЫЕ КОРНИ

Если дискриминант b ² — 4ac равен нулю,

радикал в формуле корней квадратного уравнения обращается в нуль.

В этом случае корни равны; таких корней

иногда называют двойным корнем.

Рассмотрим уравнение

9x ² + 12x + 4 = 0

Сравнивая с общей квадратичной, замечаем, что

a = 9, b = 12 и c = 4

Дискриминант

Следовательно, корни равны.

ПРОВЕРКА: По формуле

Равенство корней проверено.

Корни могут быть равны, только если трехчлен это. идеальный квадрат. Его коэффициенты равны. Факторизация трехчлена в

9x ² + 12x + 4 = 0

видим, что

(3x + 2) ² = 0

Поскольку множитель 3x + 2 возведен в квадрат, фактически имеем

3x + 2 = 0

дважды, а у нас

дважды.

Дело в том, что надо считать один и тот же корень дважды объясняет использование термина «двойной» корень «. Двойной корень квадратного уравнения — это всегда рационально, потому что двойной корень может возникнуть только тогда, когда радикал обращается в нуль.

РЕАЛЬНЫЕ И НЕРАВНЫЕ КОРНИ Когда дискриминант положительный, корни должно быть настоящим. Также они должны быть неравными, поскольку равные корни возникают только тогда, когда дискриминант равно нулю.

Рациональные корни.

Если дискриминант — полный квадрат, корни рациональны. Например, рассмотрим уравнение

3x ² — x — 2 = 0

, в котором

a = 3, b = -1 и c = -2

Дискриминант

Мы видим, что дискриминант 25 представляет собой полный квадрат. Идеальный квадрат указывает на то, что радикал в квадратной формуле может быть удален, что корни уравнения рациональны, и что трехчлен можно факторизовать.Другими словами, когда мы оцениваем дискриминант и находим, что он представляет собой идеальный квадрат, мы знаем, что что трехчлен можно разложить на множители.

Таким образом,

, из которых

Мы видим, что информация, полученная из дискриминант правильный. Корни настоящие, неравный и рациональный.

Дискриминантные и сложные корни

Выражение $$ {b ^ 2} — 4ac $$, которое появляется под знаком радикала в формуле корней квадратного уравнения
\ [x = \ frac {{- b \ pm \ sqrt {{b ^ 2} — 4ac}} } {{2a}} \]

называется дискриминантом квадратного уравнения $$ a {x ^ 2} + bx + c = 0 $$.