Дискриминант на 4 | Алгебра

Дискриминант, делённый на 4 — D/4 — удобно использовать для упрощения вычислений при решении квадратных уравнений, если коэффициент b при x — чётное число.

Формула дискриминанта, деленного на 4 —

   

Как и для случая с обычным дискриминантом, количество корней  квадратного уравнения зависит от знака D/4.

• Если D/4>0, квадратное уравнение имеет два корня:

     

• Если D/4=0, квадратное уравнение имеет один корень

     

• Если D/4<0, квадратное уравнение не имеет действительных корней.

Рассмотрим примеры решения квадратных уравнений с помощью формулы четверти дискриминанта.

   

   

Так как b=16 — чётное число, вместо обычного дискриминанта вычислим дискриминант, делённый на 4 (иногда его еще обозначают через D1):

   

Так как D/4>0, уравнение имеет два корня:

   

   

   

Ответ: -0,2; -3.

   

   

   

   

Поскольку D/4>0, уравнение имеет два корня:

   

   

   

   

Ответ: 9; 1/3.

   

   

   

   

Так как D/4=0, данное квадратное уравнение имеет один корень

   

Ответ: -2 1/3.

   

   

   

   

Так как D/4<0, уравнение не имеет корней в действительных числах.

Ответ: нет корней.

Для решения квадратных уравнений вполне достаточно помнить обычную формулу дискриминанта и связанные с ним формулы корней. И все же, дополнительное знание формулы четверти дискриминанта не будет лишним.

Во-первых, с меньшими (по модулю) числами проще работать. Во-вторых, эта формула иногда ускоряет процесс нахождения корней уравнения.

   

   

   

   

Если находить корни через формулу обычного дискриминанта, придётся раскладывать его на множители, выносить множитель из-под корня, затем общий множитель — за скобки и сокращать дробь.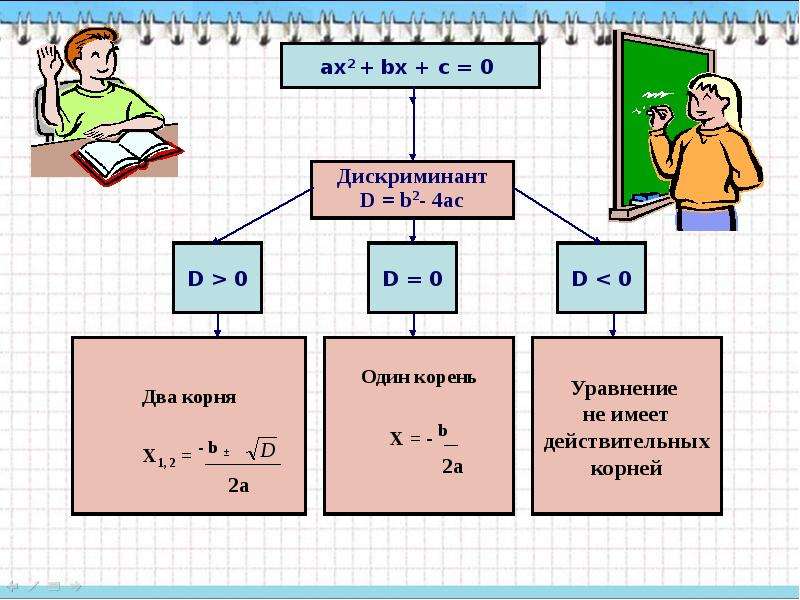

Ответ:

   

 

Что такое дискриминант 1. Как решить квадратное уравнение через дискриминант и четверть дискриминанта. Решение полных квадратных уравнений

Прежде чем мы узнаем, как найти дискриминант квадратного уравнения вида ax2+bx+c=0 и как найти корни данного уравнения, нам необходимо вспомнить определение квадратного уравнения. Уравнение, которое имеет вид ax 2 + bx + c = 0 (где a,b и c — любые числа, также надо помнить, что a ≠ 0) является квадратным. Все квадратные уравнения мы разделим на три разряда:

1. те, у которых нет корней;
2. имеется один корень в уравнении;
3. есть два корня.

Для того чтобы определить количество корней в уравнении нам необходим дискриминант.

Как найти дискриминант. Формула

Нам дано: ax 2 + bx + c = 0.

Формула дискриминанта: D = b 2 — 4ac .

Как найти корни дискриминанта

По знаку дискриминанта определяется количество корней:

1. D = 0, у уравнения один корень;
2. D > 0, у уравнения два корня.

Корни у квадратного уравнения находятся по следующей формуле:

X1= -b + √D/2а; X2= -b + √D/2a.

Если D = 0, то Вы можете смело использовать любую из представленных формул. У Вас получится одинаковый ответ в любом случае. А если получается так, что D > 0, то тогда Вам не придется ничего считать, так как корней уравнение не имеет.

Надо сказать, что находить дискриминант — это не так уж сложно, если знать формулы и внимательно осуществлять подсчеты. Иногда возникают ошибки при подстановке отрицательных чисел в формулу (нужно помнить, что минус на минус дает плюс). Будьте внимательны, и все получится!

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0

. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3.

Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:

a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности. … За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид Ax4+B=0.

Определение 1

Для решения этого типа уравнений применяются формулы сокращенного умножения:

Ax4+B=0x4+BA=0x4+2BAx2+BA-2BAx2=0x2+BA2-2BAx2=0x2-2BA4x+BAx2+2BA4x+BA=0

Остается лишь найти корни квадратных трехчленов.

Пример 1

Решить уравнение четвертой степени 4×4+1=0.

Решение

Для начала проведем разложение многочлена 4×4+1 на множители:

4×4+1=4×4+4×2+1=(2×2+1)2-4×2=2×2-2x+1(2×2+2x+1)

Теперь найдем корни квадратных трехчленов.

Первого:

2×2-2x+1=0D=(-2)2-4·2·1=-4×1=2+D2·2=12+ix2=2-D2·2=12-i

Второго:

2×2+2x+1=0D=22-4·2·1=-4×3=-2+D2·2=-12+ix4=-2-D2·2=-12-i

Мы получили четыре комплексных корня.

Ответ: x=12±i и x=-12±i.

Решение возвратного уравнения четвертой степени

Определение 2

Возвратные уравнения четвертого порядка имеют вид Ax4+Bx3+Cx2+Bx+A=0

х=0 не является корнем этого уравнения: A·04+B·03+C·02+B·0+A=A≠0. Поэтому на x2 можно смело разделить обе части этого уравнения:

Ax4+Bx3+Cx2+Bx+A=0Ax2+Bx+C+Bx+Ax2=0Ax2+Ax2+Bx+Bx+C=0Ax2+1×2+Bx+1x+C=0

Проведем замену переменных x+1x=y⇒x+1×2=y2⇒x2+1×2=y2-2:

Ax2+1×2+Bx+1x+C=0A(y2-2)+By+C=0Ay2+By+C-2A=0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Пример 2

Найти все комплексные корни уравнения 2×4+23+2×3+4+6×2+23+2x+2=0.

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x2:

2×2+23+2x+4+6+23+2x+2×2=0

Проведем группировку:

2×2+2×2+23+2x+23+2x+4+6+=02×2+1×2+23+2x+1x+4+6=0

Проведем замену переменной x+1x=y⇒x+1×2=y2⇒x2+1×2=y2-2

2×2+1×2+23+2x+1x+4+6=02y2-2+23+2y+4+6=02y2+23+2y+6=0

Решим полученное квадратное уравнение:

D=23+22-4·2·6=12+46+2-86==12-46+2=23-22y1=-23-2+D2·2=-23-2+23-24=-22y2=-23-2-D2·2=-23-2-23+24=-3

Вернемся к замене: x+1x=-22, x+1x=-3.

Решим первое уравнение:

x+1x=-22⇒2×2+2x+2=0D=22-4·2·2=-14×1=-2-D2·2=-24+i·144×2=-2-D2·2=-24-i·144

Решим второе уравнение:

x+1x=-3⇒x2+3x+1=0D=32-4·1·1=-1×3=-3+D2=-32+i·12×4=-3-D2=-32-i·12

Ответ: x=-24±i·144 и x=-32±i·12.

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид Ax4+Bx2+C=0. Мы можем свести такое уравнение к квадратному Ay2+By+C=0 путем замены y=x2. Это стандартный прием.

Пример 3

Решить биквадратное уравнение 2×4+5×2-3=0.

Решение

Выполним замену переменной y=x2, что позволит нам свести исходное уравнение к квадратному:

2y2+5y-3=0D=52-4·2·(-3)=49y1=-5+D2·2=-5+74=12y2=-5-D2·2=-5-74=-3

Следовательно, x2=12 или x2=-3.

Первое равенство позволяет нам получить корень x=±12. Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x=±i·3.

Ответ: x=±12 и x=±i·3.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 4

Найти все комплексные корни биквадратного уравнения 16×4+145×2+9=0.

Решение

Используем метод замены y=x2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16y2+145y+9=0D=1452-4·16·9=20449y1=-145+D2·16=-145+14332=-116y2=-145-D2·16=-145-14332=-9

Поэтому, в силу замены переменной, x2=-116 или x2=-9.

Ответ: x1, 2=±14·i, x3, 4=±3·i.

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x4+Ax3+Bx2+Cx+D=0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y0. Это любой из корней кубического уравнения y3-By2+AC-4Dy-A2D+4BD-C2=0. После этого необходимо решить два квадратных уравнения x2+A2x+y02+A24-B+y0x2+A2y0-Cx+y024-D=0, у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Пример 5

Найти корни уравнения x4+3×3+3×2-x-6=0.

Решение

Имеем А=3, В=3, С=-1, D=-6. Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y3-By2+AC-4Dy-A2D+4BD-C2=0y3-3y2+21y-19=0

Одним из корней кубического уравнения будет y0=1, так как 13-3·12+21·1-19=0.

Запишем два квадратных уравнения:
x2+A2x+y02±A24-B+y0x2+A2y0-Cx+y024-D=0x2+32x+12±14×2+52x+254=0x2+32x+12±12x+522=0

x2+32x+12+12x+52=0 или x2+32x+12-12x-52=0

x2+2x+3=0 или x2+x-2=0

Корнями первого уравнения будут x=-1±i·2, корнями второго х=1 и х=-2.

Ответ: x1,2=-1±i2, x3=1, x4=-2.

Урок 3. квадратные уравнения, неравенства и их системы — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №3. Квадратные уравнения, неравенства и их системы.

Перечень вопросов, рассматриваемых в теме:

• систематизация знаний учащихся о решении квадратных уравнений и неравенств;
• установление зависимости количества и расположения корней квадратного уравнения от его коэффициентов и значения дискриминанта;
• способы решения квадратных уравнений и неравенств с параметрами.

Глоссарий по теме:

Параметр — (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода.

Основная литература:

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М.: Просвещение, 2017.

Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.

Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.

Теоретический материал для самостоятельного изучения

В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.

Квадратные уравнения.

На уроке будем рассматривать различные способы решения квадратных уравнений.

Как определить, сколько корней имеет уравнение, подскажет дискриминант.

Дискриминант – это число, которое находим по формуле

Если D <0 корней нет, если D = 0 один корень, если D> 0 два корня.

Если дискриминант D> 0 , корни можно найти по формуле:

Если D = 0 , то

Рассмотрите пример. Решить уравнение

Шаг 1. Выпишем коэффициенты a, b, c. 

Шаг 2. Найдем дискриминант. D=16.

Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:

Заметим:

1.Перед решением квадратного уравнения привести его к стандартному виду.

2. Избавьтесь от минуса перед . Для этого надо умножить всё уравнение на -1.

3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.

4. Проверяйте корни по теореме Виета. Это просто, когда a=1.

Рассмотрите другие формулы:

, где второй коэффициент b=2k – четное число.

Приведенное квадратное уравнение , старший коэффициент равен a= 1, проще решать по теореме Виета.

Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.

Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.

Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.

Рассмотрим несколько примеров:

Пример 1.

Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.

Пример 2.

Применяем метод сложения. Выполнив сложение, получаем уравнение , далее x= ±5. Находим у= ±2. Составляем возможные пары чисел. 2+ bx + c больше или меньше нуля.  

Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».

Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.

Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.

Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.

Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:

если а>0 + — +, если а <0 — + -. Или путём подстановки произвольного значения квадратный трехчлен.

Рассмотрим несколько примеров:

D=0 все точки параболы выше оси и только одна х=2 на оси ОХ -нет решений.

D<0 коэффициент а=2>0 ветви вверх. Парабола выше оси, все значения положительны, значит х- любое число. Неравенство не имеет решений.

Далее рассмотрим схему решения системы неравенств.

Алгоритм решения системы неравенств.

1.Решить первое неравенство системы, изобразить его графически на оси x.

2.Решить второе неравенство системы, изобразить его графически на оси x.

3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Часть 3

Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Первый шаг в решении — найти особое значение параметра.

Второй шаг – определить допустимые значения.

Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.

Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.

Рассмотрите примеры решения неравенства с параметром.

Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.

Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.

Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.

Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.

Задания тренировочного модуля с разбором.

Пример 1.

При каких значениях параметра, а квадратное уравнение

имеет только один корень?

Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.

Пример 2.

Определите, на каком интервале значения квадратного трехчлена отрицательны?

Решаем неравенство: . Находим дискриминант квадратного трехчлена D= 1-4∙2∙ (-1) =1+8=9. Находим корни . Расставляем точки на числовой прямой.

Старший коэффициент а=2 ветви параболы вверх. Знаки чередуются + — +. Записываем ответ: — 0,5< х <1.

Чему равен дискриминант 1. Решение квадратных уравнений. Какой формулой нужно пользоваться

Во-первых, что же такое квадратное уравнение? Квадратным уравнением называется уравнение вида ax^2+bx+c=0, где х – переменная, a, b и с – некоторые числа, причем а не равно нулю. 2
D1>0, значит, уравнение имеет 2 корня
x1,2= k +/ квадратный корень из D1)/a
x1= (-(-12) +9)/3=21/3=7
x2= (-(-12) -9)/3=3/3=1

Оценили на сколько легче решение?;)
Спасибо за внимание, желаю Вам успехов в учебе =)

• В нашем случае в уравнениях D и D1 были >0 и мы получили по 2 корня. Если бы было D=0 и D1=0, то мы получили бы по одному корню, а если бы было D
• Через корень дискриминанта (D1) можно решать только те уравнения, в которых член b четный(!)

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Прежде чем мы узнаем, как найти дискриминант квадратного уравнения вида ax2+bx+c=0 и как найти корни данного уравнения, нам необходимо вспомнить определение квадратного уравнения. Уравнение, которое имеет вид ax 2 + bx + c = 0 (где a,b и c — любые числа, также надо помнить, что a ≠ 0) является квадратным. Все квадратные уравнения мы разделим на три разряда:

1. те, у которых нет корней;
2. имеется один корень в уравнении;
3. есть два корня.

Для того чтобы определить количество корней в уравнении нам необходим дискриминант.

Как найти дискриминант. Формула

Нам дано: ax 2 + bx + c = 0.

Формула дискриминанта: D = b 2 — 4ac .

Как найти корни дискриминанта

По знаку дискриминанта определяется количество корней:

1. D = 0, у уравнения один корень;
2. D > 0, у уравнения два корня.

Корни у квадратного уравнения находятся по следующей формуле:

X1= -b + √D/2а; X2= -b + √D/2a.

Если D = 0, то Вы можете смело использовать любую из представленных формул. У Вас получится одинаковый ответ в любом случае. А если получается так, что D > 0, то тогда Вам не придется ничего считать, так как корней уравнение не имеет.

Надо сказать, что находить дискриминант — это не так уж сложно, если знать формулы и внимательно осуществлять подсчеты. Иногда возникают ошибки при подстановке отрицательных чисел в формулу (нужно помнить, что минус на минус дает плюс). Будьте внимательны, и все получится!

Примеры решения квадратных и биквадратных уравнений

Пример 4. Решить квадратное уравнение x² + 12x + 36 = 0.

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 12, c = 36.

Так как b = 12 — четное число, то вычислим дискриминант D₁ :

D₁ = (b/2)² — ac = 6² — 1*36 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = (-6)/1 = -6.

Это уравнение можно решить и без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
x² + 12x + 36 = 0 (x+6)² = 0 x = -6.

Ответ: -6.

Пример 5. Решить квадратное уравнение 4x² -28x + 49 = 0.

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.

Так как b = -28 — четное число, то вычислим дискриминант D₁ :

D₁ = (b/2)² — ac = (-14)² — 4*49 = 196-196 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = 14/4 = 7/2.

Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:

4x² -28x + 49 = 0 (2x-7)² = 0 2x = 7 x = 7/2.

Ответ: 7/2.

Пример 6. Решить уравнение .

Решение.
Приведем к общему знаменателю левую часть уравнения:

Умножив обе части уравнения на -4, получим x² + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
x² + 3x = 0 x(x+3) = 0

x = 0, x = 0,
x — 3 = 0 x = 3.

Ответ: 0, 3.

Пример 7. Решить уравнение .

Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:

Получим 6x² + 3x = 20x-10 6x² + 3x — 20x + 10 = 0 6x² — 17x + 10 = 0.

Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10,
D = b² — 4ac = (-17)² — 4*6*10 = 289 — 240 = 49 > 0, следовательно, уравнение имеет два действительных корня.

Ответ: 5/6, 2.

Пример 8. Решить уравнение .

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.

Так как b = 2√2, то есть b делится на 2 (b/2 = √2), вычислим дискриминант D₁:

D₁ = (b/2)² — ac = (√2)² — 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.

Ответ: -√2-1, -√2+1.

Пример 9. Решить уравнение .

Решение.
Умножим левую и правую части уравнения на 6:

Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.

Так как b = -6, то есть b делится на 2 (b/2=3), вычислим дискриминант D₁:

D₁ = (b/2)² — ac = 3² — 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.

Ответ: (3-√3)/3, (3+√3)/3.

Пример 10. Решить уравнение x⁴ — 17x² + 16 = 0.

Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x² => x⁴ = t², перейдем к эквивалентному исходному квадратному уравнению:

x⁴ — 17x² + 16 = 0 => t² — 17t + 16 = 0.

Вычислим дискриминант квадратного трехчлена: a = 1, b = -17, c = 16,

D = b² — 4ac = (-17)² — 4*1*16 = 289-64 = 225 > 0, следовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Таким образом, исходное уравнение имеет 4 действительных корня.

Ответ: ±1, ±4.

Пример 11. Решить уравнение 9x⁴ + 32x² — 16 = 0.

Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x² => x⁴ = t², перейдем к эквивалентному исходному квадратному уравнению:

9x⁴ + 32x² — 16 = 0 => 9t² + 32t — 16 = 0

Вычислим дискриминант квадратного трехчлена. У нас a = 9, b = 32, c = -16.

Так как b = 32, то есть b делится на 2 (b/2=16), вычислим дискриминант D₁:

D₁ = (b/2)² — ac = 16² — 9*(-16) = 400 >0. Cледовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Первое уравнение x² = -4 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x= ±2/3.

Ответ: ±2/3.

Пример 12. Решить уравнение x⁴ + 3x² — 10 = 0.

Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x² => x⁴ = t², перейдем к эквивалентному исходному квадратному уравнению:

x⁴ + 3x² — 10 = 0 => t² + 3t — 10 = 0

Вычислим дискриминант полученного квадратного трехчлена: a = 1, b = 3, c = -10,

D = b² — 4ac = 3² — 4*1*(-10) = 9+40 = 49 > 0, следовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Первое уравнение x² = -5 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x = ±√2.

Ответ: ±√2.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

      Квадратным трёхчленом относительно переменной   x   называют многочлен

где a, b и c – произвольные вещественные числа, причем

      Квадратным уравнением относительно переменной   x   называют уравнение

где a, b и c – произвольные вещественные числа, причем

      Полным квадратным уравнением относительно переменной   x   называют уравнение

ax² + bx + c = 0,

где a, b и c – произвольные вещественные числа, отличные от нуля.

      Неполными квадратными уравнениями называют квадратные уравнения следующих типов:

Решение неполных квадратных уравнений

      Покажем, как решаются неполные квадратные уравнения на примерах.

      Пример 1. Решить уравнение

5x² = 0 .

      Решение.

      Ответ: 0 .

      Пример 2. Решить уравнение

      Решение. Вынося в левой части уравнения (3) переменную   x   за скобки, перепишем уравнение в виде

      Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:

      Ответ: .

      Пример 3. Решить уравнение

2x² – 5 = 0 .

      Решение.

      Ответ: .

      Пример 4. Решить уравнение

      Решение. Поскольку левая часть уравнения (5) положительна при всех значениях переменной   x, а правая часть равна 0, то уравнение  решений не имеет.

      Ответ: .

Выделение полного квадрата

      Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:

(6)

      Для того, чтобы получить формулу (6), совершим следующие преобразования:

      Формула (6) получена.

Дискриминант

      Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой   D   и вычисляется по формуле:

      Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.

      Используя дискриминант, формулу (6) можно переписать в виде

(8)

Разложение квадратного трёхчлена на множители

      Утверждение. В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда   D < 0, квадратный трехчлен нельзя разложить на линейные множители.

      Доказательство. В случае, когда   D = 0, формула (8) и является разложением квадратного трехчлена на линейные множители:

(9)

      В случае, когда   D > 0, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:

      Таким образом, в случае, когда   D > 0, разложение квадратного трехчлена (1) на линейные множители имеет вид

(10)

      В случае, когда  D < 0, выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.

      Замечание. В случае, когда  D < 0, квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.

Формула для корней квадратного уравнения

      Из формул (9) и (10) вытекает формула для корней квадратного уравнения .

      Действительно, в случае, когда   D = 0, из формулы (9) получаем:

      Следовательно, в случае, когда   D = 0, уравнение (1) обладает единственным корнем, который вычисляется по формуле

(11)

      В случае, когда   D > 0, из формулы (10) получаем:

      Таким образом, в случае, когда   D > 0, уравнение (1) имеет два различных корня, которые вычисляются по формулам

	(12)
	(13)

      Замечание 1. Формулы (12) и (13) часто объединяют в одну формулу и записывают так:

(14)

      Замечание 2. В случае, когда   D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда   D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:

(15)

      Замечание 3. В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.

      В случае, когда   D = 0, разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):

ax2 + bx + c = = a (x – x1)2.

(16)

      В случае, когда   D > 0, разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:

ax2 + bx + c = = a (x – x1) (x – x2) .

(17)

      Замечание 4. В случае, когда   D = 0, корни   x₁ и   x₂ совпадают, и формула (17) принимает вид (16).

Прямая и обратная теоремы Виета

      Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство

ax² + bx + c =
= a (x – x₁) (x – x₂) =
= a [x² – (x₁ + x₂) x + x₁x₂] =
= ax² – a(x₁ + x₂) x + ax₁x₂ .

      Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена

ax² + bx + c

равны соответствующим коэффициентам многочлена

ax² – a (x₁ + x₂) x + a x₁x₂ .

      Таким образом, справедливы равенства

следствием которых являются формулы

(18)

      Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).

      Словами прямая теорема Виета формулируется так: — «Если числа   x₁ и   x₂ являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».

      Обратная теорема Виета формулируется так: — «Если числа   x₁ и   x₂ являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».

      Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».

      Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

{2} -4x + 10 = 0 [/ latex] имеет два сложных решения.

В последнем примере мы проведем корреляцию между количеством и типом решений квадратного уравнения и графиком соответствующей функции.

Пример

Используйте следующие графики квадратичных функций, чтобы определить, сколько и какого типа решений будет соответствующее квадратное уравнение [latex] f (x) = 0 [/ latex]. Определите, будет ли дискриминант больше, меньше или равен нулю для каждого из них.{2}} — 4ac [/ латекс]. Он определяет количество и тип решений квадратного уравнения. Если дискриминант положительный, существуют [latex] 2 [/ latex] вещественные решения. Если это [latex] 0 [/ latex], существует [latex] 1 [/ latex] реальное повторяющееся решение. Если дискриминант отрицательный, существуют [latex] 2 [/ latex] комплексные решения (но нет реальных решений).

Дискриминант также может рассказать нам о поведении графика квадратичной функции.

Квадратичная формула: решения и дискриминант

Purplemath

Приведем еще несколько примеров.

• Решите

  x ( x — 2) = 4. Округлите ответ до двух десятичных знаков.

Я не только не могу применить квадратичную формулу на данном этапе, но и не могу использовать множители. Почему? Потому что это уравнение пока что в правильном виде.

И я, , конечно же, не могу с невозмутимым видом утверждать, что « x = 4, x — 2 = 4», потому что это , а не , как работает «решение с факторингом».

Независимо от того, какой метод решения я собираюсь использовать — факторизую ли я на множители или использую квадратичную формулу для поиска ответов — я должен сначала преобразовать уравнение в форму «(квадратичный) = 0».

MathHelp.com

Первое, что я сделаю здесь, это умножу на левую часть, а затем переместу 4 из правой части в левую:

x ( x — 2) = 4

x ² -2 x = 4

x ² -2 x -4 = 0

Поскольку нет множителей при (1) (- 4) = –4, которые в сумме дают –2, то эта квадратичная величина не множится.(Другими словами, невозможно, чтобы решение « x = 4, x — 2 = 4» могло быть хоть немного правильным.)

Значит, разложение на множители не сработает, но я могу использовать квадратичную формулу; в этом случае я вставлю значения a = 1, b = –2 и c = –4:

Тогда ответ:

x = –1.24, x = 3,24 с округлением до двух десятичных знаков.

---

Для справки, вот как выглядит график соответствующей квадратичной, y = x ² -2 x -4, выглядит так:

Как видите, решения квадратичной формулы совпадают с интерцепциями x . Точки пересечения графика с осью x дают значения, которые решают исходное уравнение.

Существует еще одна связь между решениями из квадратичной формулы и графиком параболы: вы можете определить, сколько x -перехватывание вы получите, исходя из значения внутри квадратного корня. Аргумент (то есть содержание) квадратного корня, являющийся выражением b ² — 4 ac , называется «дискриминантом», потому что, используя его значение, вы можете «различать» (что уметь различать) различные типы решений.

В данном случае значение дискриминанта b ² -4 ac было 20; в частности, значение было , а не нулевым, и было , а не отрицательным. Поскольку значение не было отрицательным, уравнение должно было иметь по крайней мере одно (действительное) решение; поскольку значение не было нулевым, два решения должны были быть разными (то есть они должны были отличаться друг от друга).

---

• Решить 9

  x ² + 12 x + 4 = 0.Оставьте свой ответ в точной форме.

Используя a = 9, b = 12 и c = 4, квадратичная формула дает мне:

Тогда ответ:

---

В первом примере на этой странице я получил два решения, потому что значение дискриминанта (то есть значение внутри квадратного корня) было ненулевым и положительным.В результате часть формулы «плюс-минус» дала мне два различных значения; один для «плюсовой» части числителя и другой для «минусовой» части. Однако в этом случае квадратный корень уменьшился до нуля, поэтому плюс-минус ни для чего не учитывался.

Такое решение, при котором вы получаете только одно значение, потому что «плюс-минус ноль» ничего не меняет, называется «повторяющимся» корнем, потому что x равно

^–2 / ₃ , но оно равно этому значению как бы вдвое: ^–2 / ₃ + 0 и ^–2 / ₃ — 0.

Вы можете лучше увидеть это повторение, если разложите квадратичный множитель (и, поскольку решения были хорошими аккуратными дробями, квадратичный должен множить ): 9 x ² + 12 x + 4 = (3 x + 2) (3 x + 2) = 0, поэтому первый множитель дает нам 3 x + 2 = 0, поэтому

x = ^–2 / ₃ , и (из второго, идентичный коэффициент) 3 x + 2 = 0, поэтому x = ^–2 / _{снова 3} .

Каждый раз, когда вы получаете ноль внутри квадратного корня квадратной формулы, вы получаете только одно решение уравнения в смысле получения одного числа, которое решает уравнение. Но вы получите два решения в том смысле, что одно значение будет подсчитано дважды. Другими словами, дискриминант (то есть выражение b ² — 4 ac ) с нулевым значением означает, что вы получите одно «повторяющееся» значение решения.

---

Ниже показан график связанной функции, y = 9 x ² + 12 x + 4, выглядит так:

Парабола только касается оси x в точке

x = ^–2 / ₃ ; это на самом деле не пересекает.Это соотношение всегда верно: если у вас есть корень, который встречается ровно дважды (или, что то же самое, если вы получаете ноль внутри квадратного корня), то график будет «целовать» ось в значении решения, но он не пройдет через ось.

---

Поскольку нет множителей при (3) (2) = 6, которые в сумме дают 4, эта квадратичная величина не множится. Но квадратичная формула работает всегда; в этом случае я вставлю значения a = 3, b = 4 и c = 2:

На данный момент у меня есть отрицательное число внутри квадратного корня.Если вы еще не узнали о комплексных числах, вам придется остановиться на этом, и ответ будет «нет решения»; если вы знаете комплексные числа, то можете продолжить вычисления:

Таким образом, в зависимости от вашего уровня обучения, ваш ответ будет одним из следующих:

Решения

с вещественными числами: нет решения

комплексно-числовых решений:

---

Филиал

---

Но знаете ли вы о комплексах или нет, вы знаете, что вы не можете изобразить свой ответ, потому что вы не можете изобразить квадратный корень из отрицательного числа на обычном декартовом месте.На оси x таких значений нет. Поскольку вы не можете найти графическое решение квадратичной функции, разумно не должно быть никаких перехватов x (потому что вы можете построить график перехвата x ).

---

Вот график связанной функции: y = 3 x ² + 4 x + 2:

Как видите, график не пересекает и даже не касается оси x .Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, тогда не будет решения действительное число и, следовательно, не будет перехватов x . Другими словами, если дискриминант (являющийся выражением b ² — 4 ac ) имеет отрицательное значение, то у вас не будет графически отображаемых нулей.

(взаимосвязь между дискриминантом (являющимся значением внутри квадратного корня), типом решения (два различных решения, одно повторяющееся решение или отсутствие графифицируемых решений) и количеством точек пересечения x на графике (два , один или нет) сведены в диаграмму на следующей странице.)

---

URL: https://www.purplemath.com/modules/quadform2.htm

Дискриминант

Дискриминант описывает характеристику корней многочленов. Он отличает разные многочлены одного типа друг от друга.

Существуют разные дискриминанты, используемые для разных степеней многочленов, но наиболее вероятно, что вы увидите, особенно в алгебре, b ² — 4ac, который используется для описания числа решений квадратичной.Хотя это только один дискриминант, термин «дискриминант» часто используется для обозначения этого конкретного дискриминанта. Этот дискриминант также используется как часть формулы корней квадратного уравнения в числителе.

Если дискриминант меньше 0, то квадратичная функция не имеет реального решения. Вы можете вспомнить это, вспомнив, что вы не можете извлечь квадратный корень из отрицательного числа (без использования мнимых чисел). В квадратной формуле дискриминант заключен в радикал, поэтому, если дискриминант отрицательный, вы не сможете вычислить реальное решение.

Пример

f (x) = 3x ² — 2x + 2

а = 3; b = -2; с = 2

b ² — 4ac = (-2) ² — 4 (3) (2)

= 4-24 = -20

Если дискриминант отрицательный, настоящего решения нет. Как видно на рисунке ниже, на графике нет нулей:

Если дискриминант равен 0, то квадратичный имеет одно решение. Вы можете вспомнить это, вспомнив, что квадратный корень из 0 равен 0.Ниже приведен пример этого случая:

Пример

f (x) = 4x 2 — 4x + 1

а = 4; b = -4; с = 1

b 2 — 4ac = (-4) 2 — 4 (4) (1)

= 16-16 = 0

f (x) = 4x 2 — 4x + 1

Дискриминант равен 0, и есть одно решение при x = & frac12

Если дискриминант больше 0, то квадратичный имеет два решения.Вы можете вспомнить это, вспомнив, что квадратный корень из положительного числа имеет два решения, одно положительное и одно отрицательное, как показано ниже:

Пример

f (x) = x 2 — 2x — 3

а = 1; b = -2; с = -3

b 2 — 4ac = (-2) 2 — 4 (1) (- 3)

= 4 + 12 = 16

Поскольку дискриминант больше 0, существует два решения: x = -1 или x = 3.

См. Также формулу корней квадратного уравнения.

Дискриминант — Концепция — Алгебра Видео от Brightstorm

Дискриминант — это член под квадратным корнем в квадратной формуле, который сообщает нам количество решений квадратного уравнения. Если дискриминант положительный, мы знаем, что у нас есть 2 решения. Если он отрицательный, решений нет, а если дискриминант равен нулю, у нас есть одно решение.Дискриминант вычисляется путем возведения в квадрат члена «b» и вычитания 4-кратного члена «а», умноженного на член «с».

Дискриминант — действительно удобный инструмент, когда вам кажется, что вы получаете странный ответ. Вот почему. Дискриминант говорит вам, сколько существует решений квадратного уравнения или сколько пересечений по оси x существует для параболы. Он не говорит вам, каковы эти числа, каковы значения пересечения x, он просто говорит вам, сколько их должно быть.Звучит так, будто это бесполезно, но на самом деле это особенно важно, когда вы проверяете свою работу.
Вот как это выглядит. Дискриминант — это формула b в квадрате минус 4ac, помня, что a, b и c — это коэффициенты квадратичной функции в стандартной форме. Он сообщает вам количество решений квадратного уравнения. Если дискриминант больше нуля, есть два решения. Если дискриминант меньше нуля, решений нет, а если дискриминант равен нулю, есть одно решение.
Это то, что вам просто нужно запомнить. Это идет рука об руку с формулой корней квадратного уравнения. Так что, если вы, ребята, это усвоили, в этом будет большой смысл. Если вы еще не выучили квадратную формулу, вы, вероятно, выучите ее завтра на уроке математики. Просто знайте, что вы смотрите на то, действительно ли b в квадрате минус 4ac больше нуля, меньше нуля или равно нулю. И это говорит мне, сколько ответов я должен получить. Он не говорит мне, каковы ответы, просто сколько из них мне нужно, чтобы решить проблему.

Дискриминант квадратного уравнения — Концепция

Дискриминант — это часть формулы корней квадратного уравнения. Дискриминант квадратного уравнения важен, потому что он сообщает нам количество и тип решений. Эта информация полезна, потому что она служит двойной проверкой при решении квадратных уравнений любым из четырех методов (факторизация, завершение квадрата, использование квадратных корней и использование формулы квадратного уравнения).

Дискриминант квадратного уравнения является частью формулы корней квадратного уравнения. На самом деле это та часть, которая лежит под квадратным корнем. Итак, различение, которое вы услышите, это b в квадрате минус 4ac, что, надеюсь, выглядит знакомо, потому что вы знаете формулу квадратичного уравнения. И действительно, что делает дискриминант, так это то, что он сообщает нам, какой тип решения и количество решений будут у наших квадратных уравнений.Он не говорит нам, что это такое. Он просто сообщает нам тип и номер. ХОРОШО?
Как это работает, есть четыре сценария. Я предпочитаю не запоминать их, но я собираюсь пройтись по каждому из них, а затем вы можете использовать логику или запомнить их, чтобы как бы понять их.
Хорошо. Итак, какой может быть дискриминант? Есть разные варианты. Во-первых, он будет больше нуля и будет точным квадратом. Под этим я подразумеваю 16, 25, любое число больше нуля и полный квадрат.
Итак, дискриминант — это то, что находится под квадратным корнем, поэтому, если это точный квадрат, вы сможете извлечь из него квадратный корень, а наш квадратный корень исчезнет из нашей формулы квадратичного уравнения. Это говорит нам о том, что у нас есть два рациональных решения. Идеальный квадрат. Вы можете извлечь квадратный корень. Квадратный корень уходит.
Хорошо, дискриминант больше нуля, а не точный квадрат. Итак, это будет примерно 10, 20 или что-то в этом роде, где мы не можем извлечь квадратный корень.Это говорит нам о том, что мы помещаем его под знаком квадратного корня. Наш квадратный корень никуда не денется.
У нас все еще есть квадратный корень из числа, из которого мы можем извлечь квадратный корень, поэтому в итоге мы получим два иррациональных числа. Итак, у нас есть квадратный корень, плюс квадратный корень минус квадратный корень. Итак, у нас есть два иррациональных решения.
Дискриманент равен нулю. Хорошо, с точки зрения нашей формулы квадратиков это приводит к исчезновению всего квадратного корня.Итак, у вас есть плюс или минус квадратный корень из нуля, исчезает, и мы просто остаемся с отрицательным b над 2a.
Итак, в этом случае у нас есть одно рациональное решение, одно дробное решение. И последний сценарий для нашего дискриминанта — меньше нуля. Хорошо, это означает отрицательное число. Дискриминант отрицательный, что означает, что квадратный корень отрицателен, что означает, что у нас есть два воображаемых решения.
Квадратный корень отрицательного числа — мнимое число. И поэтому у нас не будет никаких реальных решений; у нас просто будут воображаемые решения.ОК.
Итак, дискриминант — это то, что стоит под квадратным корнем в квадратной формуле, и он говорит нам о количестве и типе решений для этого квадратного уравнения.
Вы можете запомнить эти четыре разные вещи. В общем, я просто предпочитаю использовать логику, хорошо? Знайте, что такое дискриминант, знайте, что он находится под квадратным корнем, а затем вы знаете, как квадратный корень ведет себя достаточно, чтобы иметь возможность вывести их в любое время, когда вам нужно.

Найти корни квадратного уравнения с помощью дискриминанта

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Все знаки указывают на дискриминант

Все знаки указывают на дискриминант

У вас когда-нибудь был один из этих Magic 8 Balls? Они выглядят как комично негабаритные шары для пула, но в них встроено плоское окно, так что вы можете видеть, что находится внутри 20-гранного кубика, плавающего в отвратительной непрозрачной синей слизи.Предположительно, бильярдный шар обладает прогностическими способностями; все, что вам нужно сделать, это задать ему вопрос, встряхнуть, и медленно, мистическим образом, как покрытая нефтью печать, выходящая из разлива нефти, игральная кость поднимется к маленькому окошку и откроет ответ на ваш вопрос.

Квадратное уравнение содержит своего рода Magic 8 Ball. Выражение b ² — 4 ac под знаком радикала называется дискриминантом , и оно может фактически определить для вас, сколько решений имеет данное квадратное уравнение, если вы не хотите на самом деле вычислять их.Учитывая, что квадратное уравнение, которое невозможно сформулировать, требует много работы для решения (квадратная формула изобилует тоннами арифметики, а для завершения квадратного метода требуется целая куча шагов), часто бывает полезно заглянуть в загадочную мистику, чтобы сделать Убедитесь, что уравнение даже имеет любых вещественных числовых решений, прежде чем вы потратите время на их поиски.

Talk the Talk

Дискриминант — это выражение b ² — 4 ac , которое определено для любого квадратного уравнения ax ² + bx + c = 0.По знаку выражения можно определить, сколько действительных чисел имеет квадратное уравнение.

Вот как работает дискриминант. Дано квадратное уравнение ax ² + bx + c = 0, подставьте коэффициенты в выражение b ² -4 ac , чтобы увидеть, какие результаты:

• Если вы получите положительное число, у квадратичной будет два уникальных решения.
• Если вы получите 0, у квадратичного будет ровно одно решение — двойной корень.
• Если вы получите отрицательное число, у квадратичного не будет реальных решений, только два мнимых. (Другими словами, решения будут содержать i , о которых вы узнали в «Борьбе с радикалами».)

Дискриминант не является магическим. Это просто показывает, насколько важен этот радикал в формуле корней квадратного уравнения. Если, например, его подкоренное выражение равно 0, вы получите

единственное решение. Если, однако, b ² — 4 ac отрицательно, то внутри квадратного корня в квадратной формуле будет отрицательное значение, что означает только мнимые решения.

Пример 4 : Не вычисляя их, определите, сколько реальных решений имеет уравнение 3 x ² — 2 x = -1.

Решение : Установите квадратное уравнение равным 0, добавив 1 к обеим сторонам.

У вас есть проблемы

Задача 4: Не вычисляя их, определите, сколько реальных решений имеет уравнение 25 x ² -40 x + 16 = 0.

Установите a = 3, b = -2 и c = 1 и оцените дискриминант.