Калькулятор квадратных уравнений — решение квадратных уравнений онлайн
Этот калькулятор квадратных формул работает как решить квадратное уравнение решатель квадратных уравнений, который помогает решить квадратное уравнение заданное квадратное уравнение с помощью формулы квадратного уравнения.
Что ж, прежде чем узнать об этом калькулятор квадратных уравнений квадратных уравнений, давайте начнем с некоторых основ!
Что такое квадратичная формула?Квадратичная формула считается одним из самых эффективных инструментов математики. Эта формула является решение квадратного уравнения полиномиального уравнения второй степени. Стандартная форма квадратного уравнения упоминается ниже:
ax1 bx c = 0
Куда;
- ‘A’ – квадратичный коэффициент
- «X» – неизвестное
- ‘B’ – линейный коэффициент
- “C” – постоянная
Решение этого уравнения называется корнем уравнения.
Итак, решение квадратного уравнения квадратных уравнений онлайн имеет не более двух корней, поэтому решение квадратных уравнений в конечном итоге означает нахождение корней (квадратного уравнения).
Наш калькулятор квадратных формул также использует ту же формулу для [решения квадратного уравнения].
Есть три возможности получить корни (квадратного уравнения), но помните, что эти возможности зависят от значения Дискриминанта.
- Если b2 – 4ac = 0, то будет только один корень
- Если b2 – 4ac> 0, то будет только два действительных корня
- Если b2 – 4ac <0, то будет два комплексных корня
Коэффициенты квадратного уравнения:
Также важно отметить, что числа, то есть a, b и c, считаются коэффициентами уравнения и не могут быть «0». Все они действительные числа, не зависящие от x. Если A = 0, то уравнение называется не квадратичным, а линейным.
Если B² <4AC, то определитель Δ будет отрицательным, как решать квадратные уравнения уравнение это уравнение не имеет действительных корней.
Наш квадратичный калькулятор также может вам помочь, если вы можете записать уравнение в такой форме:
ax2 bx c = 0
Калькулятор квадратной формулы:Этот калькулятор квадратных уравнений квадратной формулы представляет собой инструмент, который помогает решить квадратное уравнение квадратное уравнение, используя квадратную формулу или завершив метод квадратов. Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Не волнуйтесь; этот решатель решение квадратного уравнения квадратных уравнений онлайн довольно прост в использовании и имеет продуманный и удобный интерфейс!
Входы:Форма уравнения:
Вы должны выбрать форму уравнения; это форма, в соответствии с которой вы должны ввести значения в обозначенные поля нашего калькулятора квадратичных функций.
В этом калькулятор квадратных уравнений используется следующая форма:
- Ax2 Bx C = 0 (стандартная форма)
- A (x – H) 2 K = 0 (форма вершины)
- A (x-x₁) (x-x₂) = 0 (Факторная форма)
Наш калькулятор квадратных уравнений квадратного уравнения позволяет вам решить квадратное уравнение квадратное уравнение, используя формулу корней квадратного уравнения и завершив метод квадратов.
Если вы выбрали форму Ax2 Bx C = 0, вам необходимо ввести значения A, B и C
Если вы выбрали форму A (x – H) 2 K = 0, то вам необходимо ввести значения A, H и K
Если вы выбрали форму A (x-x₁) (x-x₂) = 0, вам необходимо ввести значения A, x1 и x2
Вывод:После того, как решить квадратное уравнение указанные выше значения, наш решатель (квадратного уравнения) покажет следующее:
Показать корни:Этот калькулятор квадратного корня показывает корень или корни вашего данного уравнения.
Покажите упрощение:Калькулятор шаг за шагом упростит данное уравнение.
Показать дискриминант:Если вы решите решение квадратных уравнений онлайн с помощью формулы квадратичного, то наш калькулятор квадратичного дискриминанта покажет дискриминант
Покажите квадратичный график:Этот калькулятор квадратичных графиков показывает вам полный квадратичный график для данного уравнения!
Как решать квадратные уравнения?Когда дело доходит до решения квадратных уравнений, квадратная формула используется для выполнения вычислений. 2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
как решать квадратные уравнения следующего выражения x2 3x 1?
В этом случае a = 1 (это коэффициент умножения на квадратный член x2), b = 3b = 3 (коэффициент, умноженный на линейный член x) и c = 1 (константа).
Какие сейчас коэффициенты, если у вас есть следующее выражение: 5/4 3/4 x 1/2 x2
В этом случае a = 1/2 (это коэффициент умножения на квадратичный член x2), b = 3/4 (коэффициент, умноженный на линейный член x) и c = 5/4 (константа).
Пример №3:Какие коэффициенты, если у вас есть следующее выражение: -3 1/2
В этом случае a = 0, поскольку данное выражение не содержит квадратичного члена x2. Итак, это не считается квадратичным выражением.
Подставьте коэффициенты, которые вы нашли в формуле (шаг 2):
Формула:\ [x = \ dfrac {-b \ pm \ sqrt {b ^ 2 – 4ac}} {2a} \]
Теперь вам нужно заменить значения коэффициентов a, b и c. 2 – 4 (-3) (1)}} {2 (-3)} \]
2 – 4 (-3) (1)}} {2 (-3)} \]
После того, как вы подставили значения a, b и c, вы должны упростить значения в уравнении. Из предыдущего примера у вас есть:
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
Загляните внутрь квадратного корня (шаг 4):Если значение положительное, то уравнение имеет два действительных корня. Если значение равно 0, то существует только один действительный корень, а если значение внутри квадратного корня отрицательное, то будет два комплексных корня. В предыдущем примере у вас есть -8 внутри квадратного корня, что означает, что у вас есть два сложных решения (как показано ниже):
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8} \, i} {(- 6)} \]
К счастью, вы узнали, как решать квадратные уравнения (вручную). 2 – 4ac}} {2a} \]
2 – 4ac}} {2a} \]
Имейте в виду, поскольку b2 – 4ac <0, квадратный корень из определителя будет мнимым значением. Отсюда:
Re (x) = -B / 2A
Im (x) = ± (√Δ) / 2A
Решение квадратного уравнения методом построения графиков:Итак, из графика параболы узнайте вершину, ось симметрии, точку пересечения по оси y, точку пересечения с x.
Задача имеет два решения, и они демонстрируют точки пересечения уравнения, которые являются точкой пересечения с осью x (это точка, в которой ось x пересекается кривой. При этом составляется график данного уравнения x2 3x – 4 = 0, можно рассматривать как решить квадратное уравнение:
Вершина:Это демонстрация пика. Итак, вершина (квадратного уравнения) указывает точку пика параболы. Если парабола открывается вверх, то говорят, что вершина – это самая высокая точка, а если парабола открывается вниз, то вершина называется самой низкой точкой.
Ось симметрии:Ось симметрии делит параболу на две равные половины; он всегда проходит через вершину параболы.
Корни также называют пересечением по оси x. Он расположен ниже оси x или выше оси x на графике. Поэтому для определения корня квадратичной функции положим y = 0
Y-перехват:Каждая парабола имеет точку пересечения с осью y, и говорят, что это точка, в которой функция пересекает ось y. Это вычисляется путем установки переменной x в уравнении на 0.
Итак, давайте начнем решать графически,
Сначала возьмем уравнение f (x) = 2×2 – 4x-1 или Y = 2×2 – 4x-1.
Здесь a = 2, b = -4 и c = -1.
Если «a» имеет положительное значение, то помните, что парабола открывается вверх на графике. Сначала вам нужно найти вершину x:
х = (- Ь) / 2а
х = (- (- 4)) / 2 (2)
х = 1
Теперь вам нужно найти вершину Y:
Вы должны подставить значение x в уравнение 2×2 – 4x-1
у = 2 (1) 2-4 (1) -1
у = 2 – 4 – 1
у = 3
Итак, у вас есть ось симметрии: x = 1
Теперь вам нужно найти точку пересечения по оси x, используя формулу корней квадратного уравнения:
\ [x = \ dfrac {- (- 4) \ pm \ sqrt {(- 4) ^ 2 – 4 (2) (- 1)}} {2 (2)} \]
\ [x = \ dfrac {4 \ pm \ sqrt {16 8}} {4} \]
\ [x = \ dfrac {4 \ pm \ sqrt {24}} {4} \]
\ [x = \ dfrac {4 \ pm 4. 2 – 4 (-1) (1)}} {2 (-1)} \]
2 – 4 (-1) (1)}} {2 (-1)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8}} {-2} \]
х1 = – 0,414214
х2 = 2,414214
Теперь найдите y-точку пересечения:
х2 2х 1 = 0
(0) 2 2 (0) 1 = 0
y-intercept = 1, теперь вам нужно нанести значения на график!
Для чего используется квадратичная формула?Квадратичная формула – это хорошо известная формула, которая встречается повсюду в математике. Он часто учитывается при решении всевозможных геометрических задач, таких как:
- Увеличение площади
- Учитывая фиксированный периметр
- Многочисленные проблемы с Word
Есть много людей, которые задаются вопросом, есть ли какая-либо связь между этой формулой (квадратным уравнением) и методом завершения квадрата. Проще говоря, вы получите квадратную формулу, просто решив решение квадратных уравнений онлайн, заполнив квадрат. Это в точности та же идея, которая вытекает из известной всем нам формулы квадратичных уравнений!
Важность квадратного уравнения в реальной жизни:Будучи студентом, вас могут принимать во внимание по различным вопросам математики. Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
- Военные и правоохранительные органы – (для определения траектории ракет, выпущенных артиллерией)
- Инженеры – (относится к гражданскому строительству)
- Уравнение движения (как на игровой площадке, так и в игровых ситуациях, оно описывает траекторию полета мяча и определяет высоту брошенного мяча)
- Наука (Астрономы – описывают орбиту планет, солнечных систем и галактик)
- Сферы сельского хозяйства (оптимальное расположение границ для производства самого большого поля)
- Проще говоря, вам просто нужно заполнить квадрат ax2 bx c = 0, чтобы получить формулу корней
- квадратного уравнения
- Вам следует разделить обе части уравнения на «а», чтобы коэффициент при x2 был равен 1.
 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.Как узнать, имеет ли квадратное уравнение одно решить квадратное уравнение онлайн, два или нет?
Это помогает определить, сколько существует решений (квадратного уравнения). Если дискриминант положительный, говорят, что есть 2 корня. Если он равен нулю, значит есть только 1 корень. Если дискриминант отрицательный, то говорят, что корней 0.
Other Languages: Quadratic Formula Calculator, Løs Andengradsligning, Quadratische Gleichungen Lösen, Kinci Dereceden Denklem Çözücü, Rozwiązywanie Równań Kwadratowych, Kalkulator Persamaan Kuadrat, Risolvere Equazioni Di Secondo Grado, Résoudre Une Équation Du Second Degré, Equazioni Di Secondo Grado, Resolver Ecuaciones De Segundo Grado, Toisen Asteen Yhtälön Ratkaisu, Řešení Kvadratické Rovnice, 二次方程式の解, حل المعادلات التربيعية, 이차방정식 계산기
Квадратное уравнение. Онлайн калькулятор с примерами
Решение квадратных уравнений
Как бы кто ни говорил, но тема квадратных уравнений – это база всей школьной программы.
 Читая дальше, вы поймете почему.
Читая дальше, вы поймете почему.Решая линейные уравнения, требуется лишь навык применения арифметических операций. Даже решать систему линейных уравнений несложно, все сводится к сложению, вычитанию или раскрытию скобок, когда подставляем одно уравнение в другое. И так далее.
Иное дело, когда возрастает старшая степень неизвестной переменной, и первый вид таких уравнений как раз называется квадратным уравнением, когда неизвестная переменная представлена во второй степени.
Есть прямая связь квадратных уравнений с тем, что мы можем наблюдать вокруг нас. Тема квадратных уравнений легкая, но очень важная и требует полного изучения, однако, этим пренебрегают ученики, да и учителя тоже.
Например, полет снаряда, выпущенного из орудия, летит по траектории, описываемой квадратным уравнением, и называется параболой. Парабола имеет вершину и две ветви, расположенные зеркально, что напоминает подкову.
Где встречаются квадратные уравнения
На практике квадратные уравнения встречаются практически во всех сферах жизненной деятельности человека, от науки до искусства.
 В школьной программе обязательно в алгебре, геометрии со стереометрией, тригонометрии, при упрощении выражений и так далее. Разумеется, не только в математике. В химии, физике, экономике, биологии и других науках без квадратных уравнений никак не обойтись.
В школьной программе обязательно в алгебре, геометрии со стереометрией, тригонометрии, при упрощении выражений и так далее. Разумеется, не только в математике. В химии, физике, экономике, биологии и других науках без квадратных уравнений никак не обойтись.Более того, в некоторых задачах необходимо оперировать со значениями, являющимися корнями квадратного уравнения, и опять-таки требуется находить корни. Если нахождение корней квадратного уравнения является промежуточным действием, например, необходимо использовать только сумму корней или их произведение, то глядя на уравнение, это сразу видно. Но опять же это нужно знать!
График квадратного уравнения
Как вы уже знаете графиком квадратного уравнения является парабола. По виду уравнения можно легко определить расположение ее вершины и направление ветвей относительно системы координат.
Парабола может либо пересекать ось абсцисс (в одной или двух точках), либо не пересекать ее. Во втором случае говорят, что квадратное уравнение не имеет действительных решений (корней).
Если же график параболы пересекает ось абсцисс, то корней два или один как минимум.
Запомните! У квадратного уравнения всегда имеются либо два разных, либо один кратности два корень, потому что уравнение второй степени. В том случае, когда корни не принадлежат полю действительных чисел, они находятся в поле комплексных чисел. Если вы еще не слышали про комплексные числа, просто примите это к сведению.
Что такое дискриминант
Общий вид квадратного уравнения следующий:
a*x2 + b*x + c = 0
Умножим обе части уравнения на 4*a, прибавим b2 к обеим частям и применим формулу сокращенного умножения «квадрат суммы». Перенесем 4*a*c в правую часть уравнения. В результате получим:
(2*a*x + b)2 = b2 – 4*a*c
Отсюда очевидно, что при b2 – 4*a*c действительных корней нет, потому что нет такого числа, которое в квадрате давало бы отрицательное.
При b2 – 4*a*c = 0 только один кратный корень.

И третий случай, при b2 – 4*a*c > 0 уравнение имеет два разных корня.
Рассмотрим последний случай, когда уравнение имеет два разных корня x1 и x2. Соответственно график параболы пересекает ось X в двух разных точках.
Координата вершины параболы определяется значением x = –b/2a.
Так как график параболы симметричен, то оба корня равноудалены от линии, проходящей через ее вершину.
Отсюда очевидно, что чем больше значение дискриминанта, тем дальше друг от друга располагаются корни уравнения. В этом заключается геометрический смысл дискриминанта.
Другими словами, значение дискриминанта напрямую указывает на удаленность корней уравнения друг от друга на числовой оси.
Так вот, удаленность корней друг от друга и называются дискриминантом, а формула, которую дают в школе под соусом «дискриминант», всего лишь выражает этот факт.
Как найти корни квадратного уравнения
Самое интересное это поиск корней уравнения. Есть несколько методов их нахождения, перечислим более известные.
Есть несколько методов их нахождения, перечислим более известные.1. Первый из них, самый известный всем школьникам, описанный выше, – это поиск по формуле квадратного уравнения, используя значение дискриминанта.
2. Принято отдельно считать метод выделения полного квадрата. Но как мы видели из поиска дискриминанта, это вытекает из первого способа.
3. Другой популярный способ – это разложение уравнения на множители, когда его приводят к виду (x+A)*(x+B)=0. Частный случай такого уравнения x*(x+A)=0 с нулевым корнем.
4. Еще один не менее важный способ – графический. В этом методе исследуют график параболы и находят ее пересечение с осями координат.
5. Очень удобный способ определения корней квадратного уравнения и часто применяемый в практических задачах – применение теоремы Виета.
Рассмотрим пример определения корней по теореме Виета
Пусть дано уравнение x2 — 5 x + 6 = 0
Согласно этой теореме, сумма корней есть коэффициент перед x, но с противоположным знаком, а произведение корней – это значение свободного члена квадратного уравнения.

Очевидно, что x1=2, а x2=3, так как x1+x2=2+3=5, а x1*x2=2*3=6
Калькулятор решения квадратных уравнений
С нашим калькуляторе вы без проблем решите любое квадратное уравнение онлайн. Он полезен как для самопроверки, таки и для изучения этой темы, поскольку пошагово покажет весь ход решения до определения корней.
В калькуляторе предусмотрены различные варианты решения квадратного уравнения. Это по формуле через дискриминант, с помощью выделения полного квадрата и методом разложения на множители.
Каждый способ решения хорош по-своему, а главное помогает школьникам лучше усвоить столь важную тему как решение квадратных уравнений.
Желаем успехов!
Решение квадратных уравнений по формуле корней
Решение квадратных уравнений
по формуле корней онлайнКвадратные уравнения бывают следующих видов:
— неполное уравнение вида ax2 = 0;
— неполное уравнение вида ax2 + bx = 0;
— неполное уравнение вида ax2 + с = 0;
— полное квадратное уравнение ax2
Решать полные уравнения по готовой формуле корней – самый простой способ (нужно просто запомнить формулу).
Сначала можно выписать коэффициенты a, b, c квадратного уравнения (хотя впоследствии, если «набить руку», этого делать не обязательно).
Затем необходимо найти дискриминант уравнения (обозначается буквой D). Дискриминант находится по формуле D = b2 – 4ac.
Если дискриминант получается отрицательный, то решение уравнения на этом этапе окончено. Оно не будет иметь действительных корней.
Если дискриминант получается положительный, уравнение имеет два корня, которые вычисляются по формулам
Если дискриминант равен нулю, то уравнение имеет один корень х = Решение неполных квадратных уравнений
1) Уравнение вида ax2 = 0 всегда имеет единственный корень 0.

2) Чтобы решить уравнение вида ax2 + bx = 0, нужно вынести х за скобки. Получится уравнение
х(ax + b) = 0.
Оно будет иметь два корня:3) Чтобы решить уравнение вида ax2 + с = 0, необходимо перенести c в правую часть. Получится уравнение
ax2 = –с, откуда
Здесь число корней зависит от знака выражения –с/а: если оно отрицательное, то корней не существует. Если же оно положительное, то уравнение будет иметь два корня.
Онлайн калькулятор
для решения квадратных уравненийВы можете получить объяснение решения любого квадратного уравнения (полного либо неполного), просто введя его коэффициенты в форму вверху страницы (в качестве коэффициентов можно вводить целые числа и десятичные дроби).
Решить квадратное уравнение онлайн
Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.
Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн, вначале приведите уравнение к общему виду:
ax2 + bx + c = 0
Заполните соответственно поля формы:Как решить квадратное уравнение
Как решить квадратное уравнение: Виды корней: 1. Привести квадратное уравнение к общему виду:
Общий вид Аx2+Bx+C=0
Пример : 3х — 2х2+1=-1 Приводим к -2х2+3х+2=02. Находим дискриминант D.
D=B2-4*A*C .
Для нашего примера D= 9-(4*(-2)*2)=9+16=25.3. Находим корни уравнения.
x1=(-В+D1/2)/2А .
Для нашего случая x1=(-3+5)/(-4)=-0,5
x2=(-В-D1/2)/2А.
Для нашего примера x2=(-3-5)/(-4)=2
Если В — четное число, то дискриманант и корни удобнее считать по формулам:
D=К2-ac
x1=(-K+D1/2)/А
x2=(-K-D1/2)/А,
Где K=B/21.  Действительные корни. Причем. x1 не равно x2
Действительные корни. Причем. x1 не равно x2
Ситуация возникает, когда D>0 и A не равно 0.2. Действительные корни совпадают. x1 равно x2
Ситуация возникает, когда D=0. Однако при этом, ни А, ни В, ни С не должны быть равны 0.3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1)1/2
Ситуация возникает, когда D4. Уравнение имеет одно решение.
A=0, B и C нулю не равны. Уравнение становиться линейным.5. Уравнение имеет бесчисленное множество решений.
A=0, B=0, C=0.6. Уравнение решений не имеет.
A=0, B=0, C не равно 0.
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений.Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B2-4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число1/2!
x1=(-В+D1/2)/2А = (-3+7)/2 = 2
x2=(-В-D1/2)/2А = (-3-7)/2 = -5Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10Пример 2.
 Решение квадратного уравнения с совпадением действительных корней.
Решение квадратного уравнения с совпадением действительных корней.
х2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k2 – AC = 16 – 16 = 0
X = -k/A = 4Подставим
(x-4)*(x-4) = (x-4)2 = X2 – 8x + 16Пример 3. Решение квадратного уравнения с комплексными корнями.
13х2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.x1=(-В+D1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:Решение квадратных уравнений онлайн калькулятор.

Основные понятия и определения.
Квадратным уравнением называется уравнение следующего вида: ax2+bx+c=0, где a, b, с — любые действительные числа, но a не равно 0, x — неизвестная искомая переменная.
Коэффициенты a, b, c имеют соответственно названия: a— старший коэффициент (коэффициент при ), — второй коэффициент (коэффициент при ), — свободный член.
Если старший коэффициент , то квадратное уравнение является приведенным, если же , то неприведенным.
Квадратное уравнение называется полным, если оно содержит все три слагаемых (то есть коэффициенты и не равны нулю).
Квадратное уравнение называется неполным, если оно содержит не все три слагаемых ( то есть коэффициент или , или и ).

Корнем квадратного уравнения называется такое значение переменной , при подстановке которого квадратный трехчлен обращается в ноль.
Решить квадратное уравнение – это значит найти все его корни или установить, что корней нет.
Теория для школьников.
При решении квадратного уравнения школьникам необходимо придерживаться следующей схемы:
1) Найти так называемый дискриминант по формуле:
2) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:
— Если , то квадратное уравнение корней не имеет;
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Решение квадратного уравнения также можно получить, используя следующие формулы :
1) Найти значение :
2) Найти дискриминант по формуле:
3) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:
— Если , то квадратное уравнение корней не имеет;
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Теория для студентов.

При обучении в высшем учебном заведении нередко приходится сталкиваться с таким понятием, как комплексные корни уравнения.
Решение квадратных уравнений студентами – именно такой случай.
Напомним, что комплексное число имеет вид:
Где и — действительные числа, — так называемая мнимая единица. При этом носит название действительной части, а — мнимой части комплексного числа.
Мнимая единица обладает свойством:
Именно свойство мнимой единицы и будет использовано при решении квадратных уравнений.
При решении квадратного уравнения студентам необходимо придерживаться следующей схемы:
1) Найти так называемый дискриминант по формуле:
2) Найти корни квадратного уравнения, опираясь на следующие рассуждения:
— Если , то квадратное уравнение имеет два комплексных корня:
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Решение квадратного уравнения также можно получить, используя следующие формулы :
1) Найти значение :
2) Найти дискриминант по формуле:
3) Найти корни квадратного уравнения, опираясь на следующие рассуждения:
— Если , то квадратное уравнение имеет два комплексных корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Примеры решения квадратных уравнений для школьников.

Пример 1: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 2: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение не имеет корней.
Ответ: Корней нет.
Пример 3: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 4: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Решим заданное уравнение вторым способом, предложенным в теории:
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 5: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным.

Для удобства расчетов умножим обе части уравнения на 9 и получим:
Будем решать полученное уравнение. Оно имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 6: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Во всех примерах, рассмотренных выше, были заданы полные квадратные уравнения. Как же решать неполные уравнения? Рассмотрим решения на примерах.
Пример 7: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Поэтому либо , либо
Ответ:
Пример 8: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня. Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Ответ:
Пример 9: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение корней не имеет.
Ответ: Корней нет.
Пример 10: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение имеет один корень .
Ответ: .
Примеры решения квадратных уравнений для студентов.
Пример 1: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 2: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два комплексных корня:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 3: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 4: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Воспользуемся вторым способом решения квадратных уравнений студентами, описанный в теории:
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 5: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 6: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два комплексных корня:
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Во всех примерах, рассмотренных выше, были заданы полные квадратные уравнения. Как же решать неполные уравнения? Рассмотрим решения на примерах.
Пример 7: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Поэтому либо , либо
Ответ:
Пример 8: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня. Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Ответ:
Пример 9: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Ответ:
Пример 10: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение имеет один корень .
Ответ: .
Квадратные уравнения. дискриминант., калькулятор онлайн, конвертер
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax3 + bx2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ (1 вещественный и пару комплексно сопряженных корней)
- Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано решения кубических уравнений (нахождения корней).
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).
Канонической формой кубического уравнения называется уравнение вида
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q1, y2, y3 и подставьте их в (3).
Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем
- α = β, и
- y1=2α,
- y2= y3 = — α.
Аналогично подставляем в (3) и получаем ответ.
Тригонометрическая формула Виета решения кубических уравнений (нахождения корней).
Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
1. Вычисляем
2. Вычисляем
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
б) Если S
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q|1/2*ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- x2= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i
- x3= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i
Тренировочные упражнения по решению квадратных уравнений
Попрактикуйтесь! Попробуйте решить следующие уравнения. На каждое уравнение смотрите в следующей последовательности:
- если уравнение подходит под первый лайфхак (когда a + b + c = 0), то решаем с его помощью;
- если уравнение подходит под второй лайфхак (когда a + c = b), то решаем с его помощью;
- если уравнение подходит под третий лайфхак (теорему Виета), решаем с его помощью;
- и только в самом крайнем случае – если ничего не подошло и/или с помощью теоремы Виета решить не получилось – считаем дискриминант. Еще раз: дискриминант – в самую последнюю очередь!
- Решите уравнение x2 + 3x + 2 = 0
Просмотреть решение и ответ
См. лайфхак второйВ данном уравнении a = 1, b = 3, c = 2. Таким образом, a + c = b, откуда x_1=-1, x_2 = -\frac{c}{a} = -\frac{2}{1}=-2.Ответ: -1, -2.
- Решите уравнение x2 + 8x – 9 = 0
Просмотреть решение и ответ
См. лайфхак первыйВ данном уравнении a = 1, b = 8, c = -9. Таким образом, a + b + c = 0, откуда x_1=1, x_2 = \frac{c}{a} = \frac{-9}{1}=-9.2 – 4 \cdot 15 \cdot 2 = 121 – 120 = 1.x_1=\frac{11-1}{2 \cdot 15}=\frac{10}{30}=\frac{1}{3}x_2= \frac{11+1}{2 \cdot 15}=\frac{12}{30}=\frac{2}{5}Ответ: \frac{1}{3}, \frac{2}{5}.
- Решите уравнение x2 + 9x + 20 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = -9 \\ x_1 \cdot x_2 = 20 \end{cases} Подбором устанавливаем, что x_1 = -4, x_2 = -5.Ответ: -4, -5.
- Решите уравнение x2 – 7x – 30 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 7 \\ x_1 \cdot x_2 = -30 \end{cases} Подбором устанавливаем, что x_1 = 10, x_2 = -3.Ответ: 10, -3.
- Решите уравнение x2 – 19x + 18 = 0
Просмотреть решение и ответ
См. лайфхак первыйВ данном уравнении a = 1, b = -19, c = 18. Таким образом, a + b + c = 0, откуда x_1=1, x_2 = \frac{c}{a} = \frac{18}{1}=18.Ответ: 1, 18.
- Решите уравнение x2 + 7x + 6 = 0
Просмотреть решение и ответ
См. лайфхак второйВ данном уравнении a = 1, b = 7, c = 6. Таким образом, a + c = b, откуда x_1=-1, x_2 = -\frac{c}{a} = -\frac{6}{1}=-6.Ответ: -1, -6.
- Решите уравнение x2 – 8x + 12 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 8 \\ x_1 \cdot x_2 = 12 \end{cases} Подбором устанавливаем, что x_1 = 6, x_2 = 2.Ответ: 6, 2.
- Решите уравнение x2 – x – 6 = 0
Просмотреть решение и ответ
См. лайфхак третий (теорема Виета)В данном уравнении a = 1, поэтому можем записать, что \begin{cases} x_1+x_2 = 1 \\ x_1 \cdot x_2 = -6 \end{cases} Подбором устанавливаем, что x_1 = 3, x_2 = -2.Ответ: 3, -2.
- Решите уравнение x2 – 15x – 16 = 0
Просмотреть решение и ответ
См. лайфхак второйВ данном уравнении a = 1, b = -15, c = -16. Таким образом, a + c = b, откуда x_1=-1, x_2 = -\frac{c}{a} = -\frac{-16}{1}=16.Ответ: -1, 16.
- Решите уравнение x2 + 11x – 12 = 0
Просмотреть решение и ответ
См. лайфхак первыйВ данном уравнении a = 1, b = 11, c = -12. Таким образом, a + b + c = 0, откуда x_1=1, x_2 = \frac{c}{a} = \frac{-12}{1}=-12.Ответ: 1, -12.
Дискриминант
Эту формулу надо знать наизусть
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение
А именно:
- Если
- Если = 0, есть ровно один корень;
- Если > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:. Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: = 5; = 3; = 7; = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение: = 1; = −6; = 9; = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок
Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Общие сведения
Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.
Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.
Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий»
Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных
При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.
Примеры решения задач
Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м2. При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?
Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:
Обозначим ширину комнаты через x. А длину комнаты через 2x, потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:
Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:
2x × x
По условию задачи площадь должна быть 8 м2. Значит выражение 2x × x следует приравнять к 8
2x × x = 8
Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.
Первое что можно сделать это выполнить умножение в левой части уравнения:
2×2 = 8
В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.
Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2
Теперь воспользуемся квадратным корнем. Если x2 = 4, то . Отсюда x = 2 и x = −2.
Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2. Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.
А длина была обозначена через 2x. Значение x теперь известно, подставим его в выражение 2x и вычислим длину:
2x = 2 × 2 = 4
Значит длина равна 4 м, а ширина 2 м. Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м2
4 × 2 = 8 м2
Ответ: длина комнаты составляет 4 м, а ширина 2 м.
Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м2
Решение
Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м2. Умножим длину участка на его ширину и приравняем к 1200, получим уравнение:
x(x + 10) = 1200
Решим данное уравнение. Для начала раскроем скобки в левой части:
Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется
Решим получившееся уравнение с помощью формул:
Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30. Потому что ширина не может выражаться отрицательным числом.
Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10. Подставим в него найденное значение x и вычислим длину:
x + 10 = 30 + 10 = 40 м
Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30) получится 1200 м2
40 × 30 = 1200 м2
Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно участка.
Периметр прямоугольника это сумма всех его сторон. Тогда:
P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.
Ответ: длина изгороди огородного участка составляет 140 м.
Смысл дискриминанта
Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.
Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m2 + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.
Первые три члена представляют собой квадрат суммы, который можно свернуть по формуле сокращённого умножения до вида a2 +2ab + b2 = (a+b)2. Отсюда, применительно к рассматриваемому примеру, получится: (m + 1)2 — 1 — 8 = 0. После преобразований с переносом неизвестного в одну сторону (а известных — в другую) и раскрытием скобки получится равенство: (m + 1)2 = 9. То есть возможными решениями будут m = 2 для (m + 1) = 3 и m = -4 для (m + 1) = -3.
В общем виде все эти преобразования можно выполнить в следующей последовательности:
Уравнение am2 + bm + c = 0 нужно переписать в приведённом виде, то есть разделить каждый член на первый коэффициент: m2 + bm / a + c / a = 0.
Согласно формуле сокращённого умножения нужно добиться того, чтобы при неизвестном во втором члене стояло удвоенное произведение. Поэтому числитель и знаменатель нужно помножить на двойку: m2 + 2bm / 2a + c / a = 0.
Полученное выражение стоит переписать в более наглядном виде m 2 + 2 m * (b /2 a) + c / a = 0. Это равенство являлось бы приведённым к формуле сокращённого умножения, если бы в последнем члене был квадрат.
Ко второму члену следует прибавить и вычесть (b/2a)2. В итоге получится m2 + 2m * (b/2a) + (b/2a)2 — (b/2a)2 + c/a = 0.
Первые три слагаемые — это классическая формула квадрата суммы. Применив её, получится: (m + b/2a)2 = (b/2a)2 — c/a.
Затем нужно раскрыть скобки и привести к общему знаменателю. Получится конструкция вида (m + b/2a)2 = b 2 -4 ac /4 a 2.
Умножив на 4a2 обе части. Выражение примет вид (2 am + b)2 = b 2 — 4 ac.Вычисления на онлайн-калькуляторе
Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.
Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.
Из сервисов, предлагающих такие услуги, можно отметить:
- Math.semestr;
- Kontrolnaya-rabota;
- Onlinemschool;
- Wpcalc;
- Webmath.
Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.
Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.
Предыдущая
МатематикаТранспортир — как правильно пользоваться инструментом для построения и измерения углов?
Следующая
МатематикаКак решать пропорции — правила, методы и примеры вычисленийПример неравенства через дискриминант
Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.
В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4
Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а, b и c.
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант. Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Или так:
Узнали?) Да! Это неполные квадратные уравнения.
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с.
Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать:
х1 = 0, х2 = 4.Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х1 — то, что меньше, а х2 — то, что больше.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х1 = -3, х2 = 3.
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
Формулы корней выглядят так: \(x_{1}=\)\(\frac{-b+\sqrt{D}}{2a}\) и \(x_{2}=\)\(\frac{-b-\sqrt{D}}{2a}\). И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:
\(x_{1}=\)\(\frac{-b+\sqrt{D}}{2a}\)\(=\)\(\frac{-b+\sqrt{0}}{2a}\)\(=\)\(\frac{-b+0}{2a}\)\(=\)\(\frac{-b}{2a}\)
\(x_{2}=\)\(\frac{-b-\sqrt{D}}{2a}\)\(=\)\(\frac{-b-\sqrt{0}}{2a}\)\(=\)\(\frac{-b-0}{2a}\)\(=\)\(\frac{-b}{2a}\)
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.2-4x+4\) будет выглядеть вот так:
Типовые примеры
Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:
Дано равенство 6×2 — 13x +2 = 0. Нужно определить количество его корней, если они существуют, их числовые значения. В первую очередь нужно нарисовать таблицу, в которую выписаны все заданные коэффициенты. Так: a = 6; b = -13; c = 2. Эти значения нужно подставить в формулу дискриминанта и найти его: D = b2 — 4ac = (-13)2 — 4 * 6 *2 = 149 — 68 = 121. То есть D больше нуля. Значит, согласно правилу, уравнение будет иметь два корня. Теперь их нужно рассчитать: x1 = (13 + √126) / 2 * 6 = 2; x2 = (13 — √126) / 2 * 6 = 1/6. Задание решено.
Определить возможность решения уравнения 4m2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.
Решить уравнение: x /3 — x2 / 4 + 1 /6 = 3x / 2 — 4×2 / 3. Для упрощения равенства нужно правую и левую сторону умножить на двенадцать: 12x / 3 — 12 * x2 / 4 + 12 /6 = (3 * 12x) / 2 — (4 * 12×2) / 3. Получится 4 x — 3 x 2 + 2 = 18 x — 16 x 2. Члены нужно привести к стандарту: 4 x — 3 x 2 + 2 — 18 x + 16 x 2 = 13 x 2 — 14 x + 2 = 0. Считаем дискриминант: D = (-14)2 — 4 * 13 * 2 = 92. Он больше нуля, поэтому есть смысл искать корни: X = (14 ± √ 92) / 2 * 13 = (14 ± 2 √ 23) / 2 * 13 = 2 (7±√23) / 2 *13 = (7± √23) /13.
Лайфхак третий (теорема, обратная теореме Виета). Если a = 1, то \begin{cases} x_1+x_2 = -b \\ x_1 \cdot x_2 = c \end{cases}
Рассмотрим уравнение x2 – 12x + 35 = 0. В нём a = 1, b = -12, c = 35. Ни под первый, ни под второй лайфхак оно не подходит – условия не соблюдаются. Если бы оно подходило под первый или под второй, то мы бы обошлись без теоремы Виета.
Само использование теоремы Виета подразумевает понимание некоторых полезных приёмов.
Первый приём. Не стоит стесняться записывать саму систему вида \begin{cases} x_1+x_2 = -b \\ x_1 \cdot x_2 = c \end{cases} , которая получается при использовании теоремы Виета. Не нужно пытаться во что бы ты ни стало решить уравнение абсолютно устно, без письменных пометок, как это делают “продвинутые пользователи”.
Для нашего уравнения x2 – 12x + 35 = 0 эта система имеет вид
\begin{cases} x_1+x_2 = 12 \\ x_1 \cdot x_2 = 35 \end{cases}
Теперь нам нужно устно подобрать числа x_1 и x_2 , которые удовлетворяют нашей системе, т.е. в сумме дают 12, а при умножении 35.
Так вот, второй приём заключается в том, что начинать подбор нужно не с суммы, а с произведения. Посмотрим на второе уравнение системы и зададимся вопросом: какие числа при умножении дают 35? Если всё в порядке с таблицей умножения, то сразу приходит на ум ответ: 7 и 5. И только теперь подставим эти числа в первое уравнение: будем иметь 7 + 5 = 12, что является верным равенством. Итак, числа 7 и 5 удовлетворяют обоим уравнениям, поэтому мы сразу пишем:
x_1 = 7, x_2 = 5
Третий приём заключается в том, что если числа не удаётся подобрать быстро (в течение 15-20 секунд), то вне зависимости от причины нужно считать дискриминант и использовать формулу корней. Почему? Потому что корни могут не подбираться, если уравнение их вообще не имеет (дискриминант отрицательный), или же корни представляют собой числа, не являющиеся целыми.
Задача на определение дискриминанта
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.
Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- 2 + 9 = 0;
- 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: = = 0. В этом случае уравнение принимает вид a2 = 0. Очевидно, такое уравнение имеет единственный корень: = 0.
Рассмотрим остальные случаи. Пусть = 0, тогда получим неполное квадратное уравнение вида 2 + = 0. Немного преобразуем его:
Решение неполного квадратного уравнения
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−/) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида 2 + = 0 выполнено неравенство (−/) ≥ 0, корней будет два. Формула дана выше;
- Если же (−/)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−/) ≥ 0. Достаточно выразить величину 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида 2 + = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
2 − 7 = 0 ⇒ · ( − 7) = 0 ⇒ 1 = 0; 2 = −(−7)/1 = 7.
52 + 30 = 0 ⇒ 52 = −30 ⇒ 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
42 − 9 = 0 ⇒ 42 = 9 ⇒ 2 = 9/4 ⇒ 1 = 3/2 = 1,5; 2 = −1,5.
- Теорема Виета
- Следствия из теоремы Виета
- Тест на тему «Значащая часть числа»
- Правила комбинаторики в задаче B6
- Как представить обычную дробь в виде десятичной
- Задача B15: частный случай при работе с квадратичной функцией
Как решать квадратные уравнения? Формулы и Примеры
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный вводный урок в онлайн-школе Skysmart и попробуйте сами!
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1. Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Для самых любопытных объясняем откуда появились такие названия: - Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax
2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax
2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем c в правую часть: ax2 = — c,
- разделим обе части на a: x2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
В двух словах Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое:
- не имеет корней при — c/а < 0;
- имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.
Как решить уравнение ax
2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = 0,125,
х = 0,125/0,5 - Разделить:
х = 0,25
- Значит корни исходного уравнения — 0 и 0,25.
Ответ: х = 0 и х = 0,25.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
- Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Выводим формулу корней квадратного уравнения
Продолжим изучать формулу корней квадратного уравнения.
Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:
Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.
Отсюда выводы про корни уравнения :
И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.
По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.
Повторим:
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате.
Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.
Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле;
- если же D1> 0, значит можно найти два действительных корня по формуле
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Онлайн калькулятор: Дискриминант
В алгебре дискриминант многочлена — это полиномиальная функция его коэффициентов, что позволяет вывести некоторые свойства корней, не вычисляя их.
Вы, вероятно, знаете хорошо известную формулу дискриминанта квадратного многочлена, которая есть, и используете эту формулу для вычисления корней.
Однако дискриминант фактически позволяет нам вывести некоторые свойства корней, не вычисляя их.В случае квадратичного многочлена он равен нулю, если — и только если — многочлен имеет двойной корень. Он положительный, если у многочлена два действительных корня, и отрицательный, если корни комплексные.
Калькулятор ниже вычисляет дискриминант, и вы можете найти немного больше теории дискриминантов непосредственно под ним.
Дискриминант квадратичного многочлена
content_copy Ссылка сохранить Сохранить extension Widget
Дискриминант
Дискриминант полинома степени n : может быть определен либо в терминах частного результата, либо в терминах корней.
По корням дискриминант равен
Технически можно вывести формулу квадратного уравнения, ничего не зная о дискриминанте. Затем, если вы вставите производные выражения для корней в приведенное выше определение, вы получите расширение.
В терминах частного от полученного результата дискриминант равен
, где Res является результатом A и первой производной A ‘. Результирующая, короче говоря, является определителем матрицы Сильвестра A и A ‘.В случае квадратичного многочлена A есть, а A ‘равно. Если вы запишете матрицу Сильвестра для этих двух многочленов и получите определитель, вы снова получите.
Вычисление дискриминанта более высокой степени
Используя второе определение, вы можете вывести формулы для полинома более высоких степеней (в приведенной ниже ссылке есть формулы для степени 3 и степени 4), но они довольно сложны.
Последовательность OEIS A007878 перечисляет 5 членов для многочленов степени 3; 16 семестров для получения степени 4; 59 семестров по 5-й степени; и, наконец, 3 815 311 членов для многочленов степени 12.
Калькулятор ниже вычисляет дискриминант полинома более высокой степени из результата полинома и его производнойДискриминант
Коэффициенты дивидендного полинома, разделенные пробелами, в порядке от старшей степени члена к младшей
Цифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить расширение Виджет
Дискриминантный калькулятор
Что такое дискриминантный калькулятор
Калькулятор дискриминанта — это онлайн-калькулятор, который вычисляет дискриминант данного квадратного уравнения.
Для квадратного уравнения ax 2 + bx + c = 0, где a ≠ 0, формула дискриминанта b 2 — 4ac.
Дискриминант также обозначается символом Δ
∴ Δ = b 2 — 4ac
Значение дискриминанта помогает расшифровать
◾ Число корней — независимо от того, имеет ли квадратное уравнение два корня, один корень или ни одного.
◾ Тип корней — являются ли корни действительными или мнимыми.Природа корней квадратного уравнения
◾ Если Δ> 0, то & Sqrt; Δ вещественно; следовательно, мы получаем два реальных и различных корня.
◾ Если Δ = 0, то & Sqrt; Δ также равно нулю; следовательно, значения x 1 и x 2 будут одинаковыми, и, следовательно, мы получим действительные и равные корни.
◾ Если Δ <0, то & Sqrt; Δ - мнимое число; отсюда мы получаем мнимые корни.
◾ Если Δ — полный квадрат, то & Sqrt; Δ — рациональное число; следовательно, мы получаем рациональные корни, иначе мы получаем иррациональные корни.
Обобщить
Значение дискриминанта Количество корней Вид корней Δ> 0 2 Реальный Δ = 0 1 Реальный Δ <0 0 Воображаемое Как пользоваться дискриминантным калькулятором
Шаг 1 — Чтобы использовать дискриминантный калькулятор, первым делом необходимо преобразовать квадратное уравнение, в котором мы хотим использовать дискриминантный калькулятор, в стандартную форму квадратного уравнения.
Стандартная форма квадратного уравнения: ax 2 + bx + c = 0
Следовательно, первым шагом является изменение нашего квадратного уравнения в стандартной форме, которое представлено как ax 2 + bx + c = 0
Итак, предположим, что нам нужно решить квадратное уравнение, которое в настоящее время имеет вид
x 2 — 10x = -16
Итак, мы изменим это уравнение так, чтобы оно было представлено в стандартной форме ax 2 + bx + c = 0.Следовательно,
x 2 — 10x = -16 теперь равно x 2 — 10x + 16 = 0.
Теперь квадратное уравнение успешно преобразовано в стандартную форму
Шаг 2 — Теперь это самый важный шаг, где найти значение коэффициентов a, b и c, сравнивая его со стандартной формой квадратного уравнения ax 2 + bx + c = 0.
Например, сравнивая x 2 — 10x + 16 = 0. с ax 2 + bx + c = 0, получаем
a = 1,
b = -10,
c = 16Шаг 3 — Вставьте значения a, b и c в формулу калькулятора дискриминанта b2 — 4ac
Следовательно, Дискриминант, Δ = (-10) 2 — 4 (1) (16) = 36
Так как Δ> 0, уравнение имеет два действительных и различных корня
Калькулятор полиномиального дискриминанта— Онлайн-вычислитель дельты Δ
Поиск инструмента
Дискриминант многочлена
Инструмент для вычисления дискриминанта полинома. 2-4ac $$
Факт знания значения дискриминанта затем решает уравнение более легко с помощью формул (используя этот дискриминант ).2 = \ Delta $$
$$ x_1 = \ frac {-b + \ delta} {2a} \\ x_2 = \ frac {-b — \ delta} {2a} $$
Для уравнений более высоких степеней вычисления намного сложнее, но важно знать детерминанты.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Дискриминант многочлена». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Дискриминант полинома» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой другой Дискриминант полиномиальной функции (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанную на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Дискриминанта полинома» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
дискриминант, многочлен, дельта, корень, квадратичный, уравнение, калькулятор
Ссылки
Источник: https: // www.dcode.fr/polynomial-discriminant
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. Дискриминантный калькулятор— Дискриминантный калькулятор Oniine
Дискриминантное выражение b 2 — 4ac используется при вычислении квадратных уравнений. Дискриминантная формула также используется для определения природы корней уравнения.
Что такое дискриминантный калькулятор?
«Калькулятор дискриминанта Cuemath» — это онлайн-инструмент, помогающий вычислить значение дискриминанта полиномиального уравнения.Онлайн-калькулятор дискриминанта Cuemath поможет вам рассчитать значение дискриминанта за несколько секунд.
Как пользоваться калькулятором дискриминанта?
Чтобы найти значение дискриминанта, выполните следующие действия.
- Шаг 1: Введите значения a, b и c из уравнения (ax 2 + bx + c = 0) в указанные поля ввода.
- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти значение дискриминанта.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести другие значения.
Как найти дискриминантный калькулятор?
Дискриминат — это математическая величина, полученная из коэффициентов полиномиального уравнения, которая используется в дальнейшем для определения природы корней, независимо от того, являются ли корни уравнения действительными, равными или мнимыми. Дискриминант уравнения вида ax 2 + bx + c = 0 вычисляется по приведенной ниже формуле:
Здесь D — значение дискриминанта.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример:Каким должно быть значение дискриминанта (D) в уравнении 2x 2 — x + 8?
Раствор:D = b 2 — 4ac
(-1) 2 — 64 = 0
1–64
Следовательно, D = — 63
Таким образом, дискриминант равен -63 уравнения 2x 2 — x + 8
Аналогичным образом можно найти дикриминант
- 5x 2 + 2x + 5 = 0
- 2x 2 -7x + 3 = 0
Дискриминант в квадратных уравнениях — наглядное пособие с примерами, практическими задачами и бесплатным PDF-файлом для печати
Чтобы понять, что делает дискриминант, важно хорошо понимать:
Предварительное требование 2: Какое решение квадратное уравнение:
ОтвечатьРешение можно представить двумя разными способами.2 + \ blue bx + \ color {green} c $$.
- Графически, поскольку y = 0 — ось x, решение находится там, где парабола пересекает ось x. (работает только для реальных решений) .
- Если решение — действительное число или мнимое число.
- Если решение рациональное или иррациональное.2 + 2x + 1 $$.
Практика 1
Вычислите дискриминант, чтобы определить количество и характер решений следующего квадратного уравнения: $$ y = x² — 2x + 1 $$.2-4 \ cdot \ красный 1 \ cdot \ color {зеленый} 1 \\ & = \ в коробке {0} \ end {выровнен} $$
Поскольку дискриминант равен нулю, мы должны ожидать 1 реальное решение, которое вы можете увидеть на графике ниже.
Практика 2
Воспользуйтесь дискриминантом, чтобы узнать природу и количество решений: $$ y = x² — x — 2 $$.2-4 \ cdot \ red 1 \ cdot \ color {green} {-2} \\ & = 1 — -8 \\ & = 1 + 8 = \ 9 в штучной упаковке \ end {выровнен} $$
Поскольку дискриминант положительный и рациональный, у этого уравнения должно быть 2 реальных рациональных решения. Как вы можете видеть ниже, если вы используете квадратичную формулу для поиска фактических решений, вы действительно получите 2 реальных рациональных решения.
Практика 3
Вычислите дискриминант, чтобы определить характер и количество решений: y = x² — 1.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(- 1)} = 4 $$
Поскольку дискриминант положительный и представляет собой полный квадрат, у нас есть два вещественных решения, которые являются рациональными.
Опять же, если вы хотите увидеть реальные решения и график, просто посмотрите ниже:
Практика 4
Вычислите дискриминант, чтобы определить характер и количество решений: y = x² + 4x — 5.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(- 5)} \\ 16-4 (-5) = 16 +20 \\ = 36 $$
Поскольку дискриминант этого квадратного уравнения является положительным и представляет собой полный квадрат, существуют два рациональных решения.
Практика 5
Вычислите дискриминант, чтобы определить характер и количество решений: y = x² — 4x + 5.
Покажи ответВ этом квадратном уравнении y = x² — 4x + 5.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(5)} \\ = 16-20 = -4 $$
Поскольку дискриминант отрицательный, у этого квадратного уравнения нет реальных решений. Единственные решения мнимые.
Ниже приведено изображение этого квадратичного графика.
Практика 6
Найдите дискриминант, чтобы определить природу и количество решений: y = x² + 4. 2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(4)} = -16 $$
Поскольку дискриминант отрицательный, у этого квадратного уравнения есть два мнимых решения.
Решения: 2i и -2i.
Ниже приведено изображение этого графика уравнений.
Практика 7
Найдите дискриминант, чтобы определить природу и количество решений: y = x² + 25.2} — 4 \ color {Magenta} {(1)} \ color {Blue} {(25)} = -100 $$
Поскольку дискриминант отрицательный, у этого квадратного уравнения есть два мнимых решения.
Решения 5i и -5i.
Калькулятор квадратного уравнения — Хорошие калькуляторы
Воспользуйтесь нашим удобным калькулятором квадратного уравнения, чтобы решить все квадратные задачи.
- Сначала введите коэффициенты a , b , c (a ≠ 0) квадратного уравнения ax 2 + bx + c = 0.
- Затем нажмите «Рассчитать», и решение отобразится.
Квадратные уравнения всех видов с действительными или комплексными корнями можно решить с помощью калькулятора квадратных уравнений. Этот полезный инструмент определит дискриминант D = (b 2 -4ac) и, если он равен, больше или меньше нуля.
Когда дискриминант равен нулю, в уравнении один действительный корень; когда он больше нуля, есть два действительных корня; а когда он меньше нуля, в уравнении есть два комплексных корня.
Квадратичная формула
В калькуляторе используется следующая формула:
x = (-b ± √D) / 2a, где D = b 2 — 4ac
Эта формула вычисляет решение квадратных уравнений (ax 2 + bx + c = 0), где x неизвестно, a — квадратичный коэффициент (a ≠ 0), b — линейный коэффициент, а c — константа уравнения. Буквы a , b и c являются известными числами и являются коэффициентами квадратного уравнения.
Пример квадратного уравнения
Давайте возьмем пример 2x 2 -6x + 3 = 0, где a представляет 2, b представляет -6 и c представляет 3 и применим квадратную формулу к этому уравнению .
В этом случае коэффициенты квадратного уравнения следующие: a = 2, b = -6, c = 3
Определитель определяется следующим образом: D = b 2 — 4ac = (-6) 2 -4 · 2 · 3 = 36-24 = 12
Кроме того, поскольку дискриминант больше нуля, уравнение имеет два действительных корня.
Эти два корня находятся по квадратичной формуле, как показано ниже:
x (1,2) = (-b ± √D) / 2a
x 1 = (-b + √D) / 2a = (- (- 6) +3,46) / 2 · 2 = 9,46 / 4 = 2,37
x 2 = (-b — √D) / 2a = (- (- 6) -3,46) / 2 · 2 = 2,54 / 4 = 0,63
Решение: x 1 = 2,37, x 2 = 0,63
Использование и понимание дискриминанта — стало проще
”Привет! Настало время снова для вашей любимой викторины СТЕНА СЛАВЫ! » »Первая участница сегодняшнего шоу — Тереза! Надеюсь, вы готовы сыграть в СТЕНУ СЛАВЫ! » Прежде чем мы начнем сегодняшнюю игру, давайте быстро рассмотрим наши правила игры.Тереза, ты скоро увидишь сегодняшнюю стену. На стене 5 секретных дверей с одним уравнением , написанным над каждой дверью. Во время игры вы сможете открыть 3 из этих дверей. За каждую выбранную дверь вы получите приз, равный количеству решений уравнения. Если каждая дверь, которую вы выбираете, открывает приз, вы вернетесь на шоу завтра и получите шанс выиграть еще больший приз!
Понимание дискриминанта
Секрет этой игры в том, что понимает и использует дискриминант .Если Тереза придумает, как использовать этот инструмент, у нее будет шанс выиграть все призы и вернуться завтра! Давайте взглянем на сегодняшнюю СТЕНУ СЛАВЫ! Уравнения , , которые мы имеем сегодня:
Уравнение 1: квадрат x минус 10 плюс 34.
Уравнение 2: 3 квадрат x минус 4 плюс 10.
Уравнение 3: квадрат x минус 3x плюс 5.
Уравнение 4: x-квадрат плюс 2 корня 2x плюс 2.
Уравнение 5: x-квадрат плюс 6x минус 16.Сделав свой первый выбор, Тереза выбирает дверь номер 4.Помните, мы говорили, что можем использовать дискриминант , чтобы быстро определить, выиграла ли Тереза один из наших потрясающих призов. Дискриминант происходит от квадратной формулы , и ее формула представляет собой b-квадрат минус 4ac, где a, b и c относятся к коэффициентам и константе квадратного уравнения в стандартной форме .
Когда дискриминант положительный , наше уравнение будет иметь 2 решения ; когда дискриминант равен 0 , наше уравнение имеет 1 решение , а когда дискриминант отрицательный , наше уравнение не будет иметь решений .Давайте посмотрим на уравнение , которое только что выбрала Тереза . В уравнении, которое только что выбрала Тереза, «a» равно 1, «b» равно двукратному квадратному корню из 2, а «c» равно 2.
Рассчитаем дискриминант ! Величина, умноженная на квадратный корень из 2 в квадрате, будет равна 8. 8 минус 8 будет равно 0. Поскольку дискриминант равен 0, это уравнение будет иметь одно решение. Тереза, вы только что выиграли 1 новенького единорога! Разве она не выглядит счастливой ?! Это самое хорошее начало, о котором вы можете мечтать!
Второй пример
При втором выборе Тереза выбирает пятое уравнение.Давайте посмотрим внимательнее! В этом уравнении «a» равно 1, «b» равно 6, а «c» равно отрицательному 16. Давайте вычислим дискриминант! Подставляя наши значения, мы получаем 6 в квадрате минус 4 умножить на 1 отрицательное 16.
Используя PEMDAS , мы получаем 36 плюс 64, что равно 100. Вау! Посмотри на это! Тереза только что выиграла пару фигурок Позитрона и Негатрона! 2 приза за уравнение с 2 решениями! У Терезы пока все отлично! Если она выберет дверь с еще одним призом, ее снова пригласят на завтрашнее шоу и шанс выиграть главный приз!И, сделав последний выбор, Тереза выбирает уравнение двери номер 2! Давайте посмотрим на ее уравнение! В этом уравнении «a» равно 3, «b» равно отрицательному 4, а «c» равно 10.Рассчитаем дискриминант! Подставляя наши значения , мы получаем отрицательные 4 в квадрате минус 4 умножить на 3 умножить на 10. Вычислив по нашей математике , мы получим 16 минус 120, что равно отрицательному 104. Что вы думаете это означает? Не только в отношении того, сколько решений имеет наше уравнение, но и в отношении шансов Терезы вернуться завтра?
Сводка
Помните, когда наш дискриминант на больше 0 , это означает, что уравнение будет иметь 2 решения .Когда наш дискриминант равен 0 , наше уравнение будет иметь 1 решение . И когда наш дискриминант является отрицательным , наше уравнение не будет иметь реальных решений .
Ну, ребята! Это также означает, что приза нет! Хотя Тереза будет разочарована, по крайней мере, у нее есть фигурки и новый Единорог! Хотя тот Единорог выглядит немного подозрительно .
На рисунке ниже левая парабола имеет 2 реальных решения (красные точки), средняя парабола имеет 1 реальное решение (красная точка), а самая правая парабола не имеет реальных решений (да, у нее есть мнимые решения).
Как выглядит дискриминант?
ОтвечатьПохоже на … число.
5, 2, 0, -1 — каждое из этих чисел является дискриминантом для 4 различных квадратных уравнений.
Что вообще такое дискриминант?
ОтвечатьДискриминант — это число , которое можно вычислить из любого квадратного уравнения.2-4 \ cdot \ красный 3 \ cdot \ color {зеленый} 5 \\ \ text {Дискриминант} = \ в коробке {6} $
Что говорит нам эта формула?
ОтвечатьДискриминант сообщает нам следующую информацию о квадратном уравнении:
 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня. Читая дальше, вы поймете почему.
Читая дальше, вы поймете почему. В школьной программе обязательно в алгебре, геометрии со стереометрией, тригонометрии, при упрощении выражений и так далее. Разумеется, не только в математике. В химии, физике, экономике, биологии и других науках без квадратных уравнений никак не обойтись.
В школьной программе обязательно в алгебре, геометрии со стереометрией, тригонометрии, при упрощении выражений и так далее. Разумеется, не только в математике. В химии, физике, экономике, биологии и других науках без квадратных уравнений никак не обойтись.
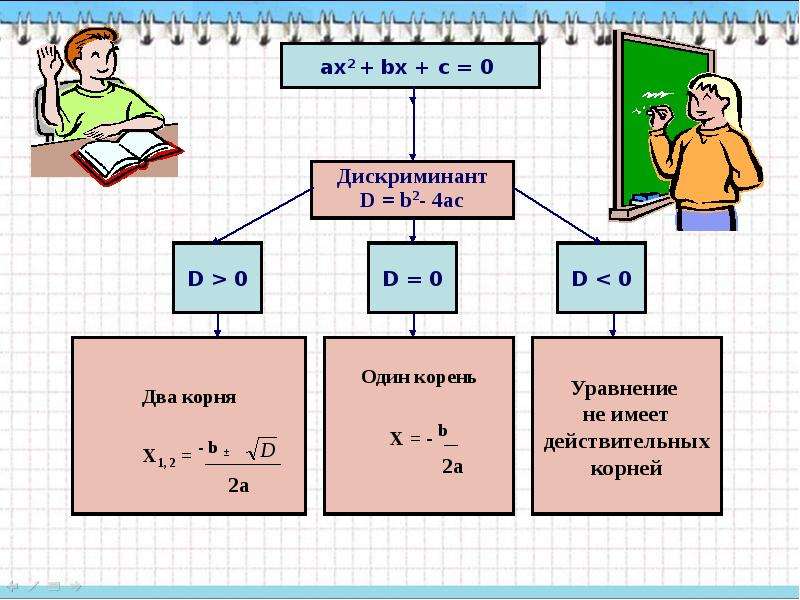
 Есть несколько методов их нахождения, перечислим более известные.
Есть несколько методов их нахождения, перечислим более известные.


 Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.
Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.  Действительные корни. Причем. x1 не равно x2
Действительные корни. Причем. x1 не равно x2 Решение квадратного уравнения с совпадением действительных корней.
Решение квадратного уравнения с совпадением действительных корней. 




