Тема проекта Различные способа доказательства теоремы Пифагора, практическое применение теоремы Пифагора.
Муниципальное бюджетное общеобразовательное учреждение «Средняя школа №15»
города Смоленска
Тема проекта: Различные способа доказательства теоремы Пифагора, практическое применение теоремы Пифагора.
Волченкова Надежда Николаевна
Руководитель:
Иванова Елена Анатольевна
2018 г.
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое деление отрезка в среднем и крайнем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень»
Иоганн Кеплер
Введение
Актуальность темы. На уроке геометрии мы познакомились с одной из важнейших теорем геометрии для прямоугольного треугольника, известной с древних времен – теоремой Пифагора. Кратко познакомились с историей этой теоремы, рассмотрели ее доказательство, но также узнали, что это одно из ее доказательств. Трудно найти человека, для которого имя Пифагора не ассоциировалось с его теоремой. Почти у каждого сохранились воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора очевидна: простота, красота и широкая значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Зная теорему Пифагора можно находить ее новые применения и способы доказательств. Это и то, что теорема Пифагора была известна задолго до его рождения меня и поразило. Я заинтересовалась и решила провести исследование.
Передо мной встала проблема: недостаточность школьного материала о доказательствах теоремы Пифагора и ее применение не позволяет показать практическую значимость теоремы в деятельности человека.
Цель исследования: выяснить различные способы доказательства теоремы Пифагора и изучить ее практическое применение.
Задачи:
Изучить биографию Пифагора
Изучить историю открытия теоремы Пифагора;
Исследовать различные способы доказательства данной теоремы, не рассматриваемые в школе;
Изучить практическое применение теоремы Пифагора.
Исследовать пифагоровы тройки.
Основной метод, который я использовала в своей работе – это метод исследования, систематизации и обработки данных
Гипотеза: Если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать ее в широком диапазоне.
Объект исследования: множество различных доказательств теоремы.
Предмет исследования: теорема Пифагора.
Глава I.
Биография Пифагора
Пифагор Самосский
О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью».)
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.
Перед Пифагором открылась неизвестная страна. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.
Когда Пифагор постиг науку египетских жрецов, то решил вернуться домой, чтобы там создать свою школу. Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне. Здесь и задумал Пифагор создать собственную философскую школу.
Довольно быстро он завоевывает большую популярность среди жителей. Пифагор умело использовал знания, полученные в странствиях по свету. Со временем ученый прекращает выступления в храмах и на улицах. Уже в своем доме Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Это был не только учитель, но и исследователь. Исследователями становились и его ученики. Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и проведя основополагающие эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер», впоследствии приведшие к революции в астрономии, впервые появились именно в Школе Пифагора.
Многое сделал ученый и в геометрии. Ему приписывают открытие и доказательство теоремы Пифагора, создание таблицы Пифагора. В школе Пифагора геометрия впервые оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически — как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию.
Важнейшей научной заслугой Пифагора считается систематическое введение доказательства в математику, и, прежде всего, в геометрию. Строго говоря, только с этого момента математика и начинает существовать как наука, а не как собрание древнеегипетских и древневавилонских практических рецептов. С рождением же математики зарождается и наука вообще, ибо «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» (Леонардо да Винчи).
Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд. Но учение Пифагора и его учеников продолжало жить.
Глава II. История открытия теоремы Пифагора.
В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что именно Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих “Начал”. С другой стороны, Прокл утверждает, что доказательство в “Началах” принадлежит самому Евклиду.
История математики почти не сохранила достоверных конкретных данных о математической деятельности Пифагора. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».
Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
«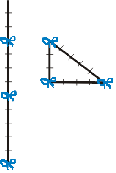
Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4″.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора, гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше было известно о теореме Пифагора вавилонянам. В одном тексте, относимом ко времени Хаммураби, т.е. к 2000 году до нашей эры, приводится приближенное вычисление гипотенузы прямоугольного треугольника; отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.
Геометрия у индусов была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 8 века до нашей эры. Наряду с чисто ритуальными предписаниями, существуют и сочинения геометрически теологического характера, называемые Сульвасутры. В этих сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.
В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена нередко употреблялся как символ математики.


В заключение приведу различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
У Евклида эта теорема гласит (дословный перевод):
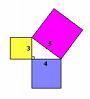
«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».
Латинский перевод арабского текста:
«Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол»
Перевод с немецкого (около 1400 года):
“Итак, площадь квадрата, измеренного по длиной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу”
В первом русском переводе евклидовых «Начал», теорема Пифагора изложена так:
«В прямоугольном треугольнике квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».
Как видим, в разных странах и разных языках существуют различные варианты формулировки знакомой нам теоремы. Созданные в разное время и в разных языках, они отражают суть одной математической закономерности, доказательство которой также имеет несколько вариантов.
Глава III. Различные способы доказательства теоремы Пифагора
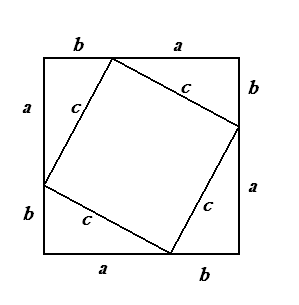
1. Древнекитайское доказательство
На древнекитайском чертеже четыре равных прямоугольных треугольника с
катетами a, b и гипотенузой с уложены так, что их внешний контур образует
квадрат со стороной a+b, а внутренний – квадрат со стороной с, построенный
на гипотенузе
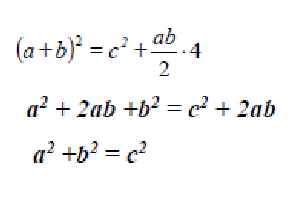
Доказательство Дж. Гардфилда (1882 г.)
Р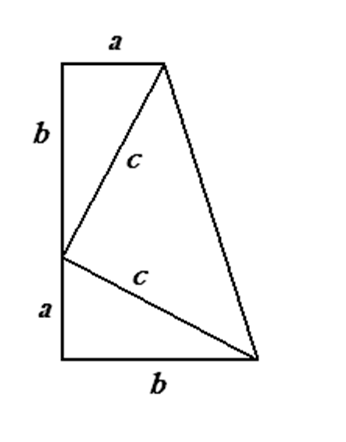
асположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту
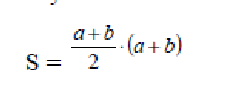
C другой стороны, площадь трапеции равна сумме площадей полученных
треугольников:
П
риравнивая данные выражения, получаем:
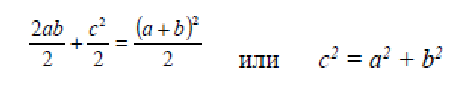
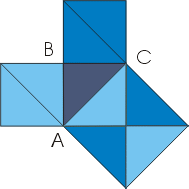
3. Доказательство простейшее
Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника.
Вероятно, с него и начиналась теорема.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.
Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два. Теорема доказана.
4. Доказательство древних индусов
Квадрат со стороной (a+b), можно разбить на части либо как на рисунке а), либо как на рисунке b). Ясно, что части 1,2,3,4 на обоих рисунках одинаковы. А если от равных (площадей) отнять равные, то и останутся равные, т.е.
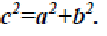

Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали лишь одним словом:
Смотри!
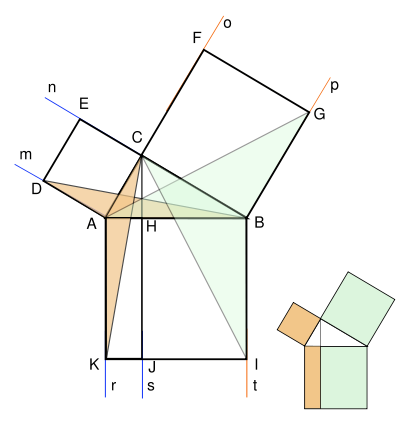
5. Доказательство Евклида
В течение двух тысячелетий наиболее распространенным было доказательство теоремы Пифагора, придуманное Евклидом. Оно помещено в его знаменитой книге «Начала».
Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.
Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.
Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост, или elefuga- бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.
Глава IV. Пифагоровы тройки
Теорема Пифагора продолжает оставаться живительным источником красоты, совершенства и творчества для новых поколений. Несмотря на то что, суть теоремы проста и изящна, но было бы ошибкой думать, что в плане её содержания не осталось места для каких-то новых исследований. Результатом одного из таких исследований являются Пифагоровы тройки -наборы из трёх натуральных чисел, из которых сумма квадратов двух чисел равна квадрату третьего числа.
Пифагоровы тройки – это тройки (x, y, z) натуральных чисел x, y, z, для которых выполняется равенство x2 + y2 = z2.
Например, (3, 4, 5) является пифагоровой тройкой. Геометрический смысл пифагоровых троек состоит в том, что они выражают стороны прямоугольного треугольника.
Прямоугольный треугольник, с катетами 3, 4 и гипотенузой 5 называется египетским треугольником. Площадь этого треугольника равна совершенному числу 6. Оно связано также со здоровьем и равновесием (поскольку состоит из двух троек). Периметр равен 12 – числу, которое считалось символом счастья и достатка.
Нахождением пифагоровых троек занимались Евклид, Пифагор, Диофант и многие другие.
Ясно, что если (x, y, z) – пифагорова тройка, то для любого натурального k тройка (kx, ky, kz) также будет пифагоровой тройкой. В частности, (6, 8, 10), (18, 24, 30) и т.д. являются пифагоровыми тройками.
По мере того, как числа возрастают, пифагоровы тройки встречаются всё реже и находить их становится все труднее и труднее. Пифагорейцы изобрели метод отыскания таких троек и, пользуясь им, доказали, что пифагоровых троек существует бесконечно много. Тройки, не имеющие общих делителей, больших 1, называются простейшими.
Рассмотрим некоторые свойства пифагоровых троек.
Свойство 1. Числа, входящие в простейшую пифагорову тройку, попарно взаимно просты.
Действительно, если два из них, например x и y имеют простой общий делитель p, то из равенстваx2 + y2 = z2 следует, что на p делится и третье число z. Это противоречит тому, что тройка – простейшая.
Следствие. В простейшей пифагоровой тройке только одно число может быть чётным.
Свойство 2. В простейшей пифагоровой тройке числа x и y не могут быть одновременно нечётными.
Пифагор нашёл формулы, которые в современной символике могут быть записаны так: a=2n+1, b=2n(n+1),c=2 n2 +2n+1, где n – целое число.
Эти числа – пифагоровы тройки.
Пифагоровы числа обладают рядом любопытных особенностей:
Один из катетов должен быть кратен трём.
Один из катетов должен быть кратен четырём.
Одно из пифагоровых чисел должно быть кратно пяти.
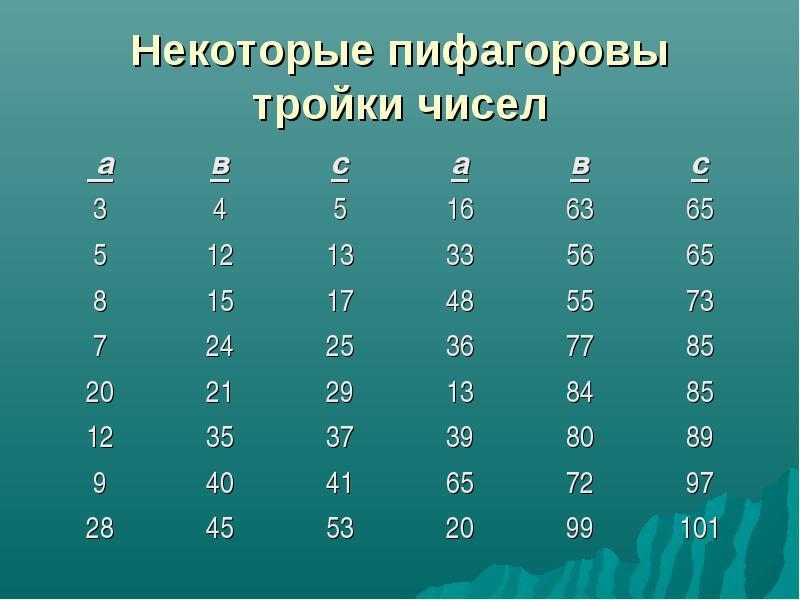
По-видимому, вавилоняне знали, как вычислить пифагоровы числа, но как они к этому пришли – неизвестно. Как позднее это делали древние греки – известно. По существу, их доказательство в модернизированном виде воспроизводится во многих книгах.
Некоторые пифагоровы тройки:
Глава V. Практическое применение теоремы Пифагора.
Теорема Пифагора по праву является одной из основных теорем математики. Ценность ее в современном мире также велика, поскольку теорема Пифагора применяется во многих отраслях деятельности человека. Например, ее используют при производстве окон некоторых архитектурных стилей, при строительстве домов и коттеджей и даже при вычислении высоты антенн операторов мобильной связи. И это далеко не весь перечень практического применения данной теоремы. Вот почему очень важно знать теорему Пифагора и понимать ее значение.
1. Строительство
Окно
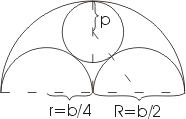

Крыша
Молниеотвод

Мобильная связь

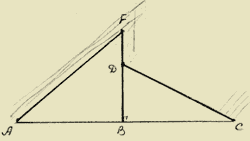
В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в радиусе 200 км, если известно, что радиус Земли равен 6380 км.
Решение:
Пусть АВ=х, BC=R=200 км, ОС=r=6380 км. ОВ=ОА+АВ, следовательно: ОВ=r+х.
Используя теорему Пифагора, получим ответ 2,3 км.
Заключение.
Работая по теме: «Различные способы доказательства теоремы Пифагора» я разрешила, поставленные перед собой задачи. Важность теоремы состоит, прежде всего, в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно привести все или даже самые красивые доказательства теоремы, однако приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней. Я в работе показала связь между теоремой Пифагора и другими дисциплинами; её практическую значимость. Попыталась собрать и обобщить информацию по данной теме. Мною было прочитано, изучено огромное количество литературы, посещено множество сайтов. Наука математика, через теорему Пифагора тесно связана с искусством, музыкой, философией, астрономией, даже обитателям Марса передавали сигнал в виде теоремы Пифагора.
Теорема Пифагора – это одно из двух имеющихся в геометрии сокровищ. И за эту ценность мы должны быть благодарны Пифагору – великому человеку, основоположнику современной математики. Именно он воспитал в человечестве веру в могущество разума, убеждённость в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика. Выяснила, что заслуга Пифагора состояла в том, что он дал полноценное научное доказательство теоремы. В процессе исследования способов доказательства этой знаменитой теоремы, я расширила знания в области геометрии и математики, узнала много ранее мне неизвестных имён учёных – математиков.
Считаю, что о результатах моей работы будет интересно послушать и моим одноклассникам, так как эта интересная информация расширяет кругозор, ещё раз демонстрирует красоту математики и логики.
По результатам проведённого мною исследования и полученного материала можно сделать следующиевыводы:
1. Теорема Пифагора является одним из самых великих открытий человечества;
2. Из теоремы Пифагора или с ее помощью можно вывести большинство теорем геометрии;
3. Способы доказательства теоремы Пифагора позволяют неочевидное сделать очевидным;
4. Пифагоровы тройки находят прямое применение в проектировании множества вещей, окружающих нас в повседневной жизни;
5. Теорема Пифагора имеет огромное применение в практике.
Литература:
Акимова С. Занимательная математика, серия «Нескучный учебник». – Санкт-Петербург. : «Тригон», 1997.
Волошников А.В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993.
Глейзер Г.И. История математики в школе. – М.: Просвещение, 1981.
Еленьский Ш. По следам Пифагора. М., 1961.
Литцман В. Теорема Пифагора. М., 1960.
Малыгин К.А. Элементы историзма в преподавании математики в средней школе. М., 1963.
Чистяков В.Д. Старинные задачи по элементарной математике. Минск, 1978.
Энциклопедический словарь юного математика / Сост. А.П. Савин. – 3-е изд., испр. и доп. – М.: Педагогика-Пресс, 1997.
500 доказательств теоремы пифагора. Несколько способов доказательства теоремы пифагора
Министерство образования РФ
МОУ Лицей № 1
Доклад на тему: «Пифагор и его теорема»
Ученицы группы 8 – 1, 2:
Миницкая Е. П.
Преподаватель:
Скворцова А. С.
Биография Пифагора
История теоремы
Пифагоровы числа
Доказательства теоремы (от простейших доказательств до самых сложных)
1. Биография Пифагора
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.
В 548 г. до н.э. Пифагор прибыл в Навкратис — самосскую колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно — этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас
Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.
2. История теоремы Пифагора
Теорема Пифагора гласит: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу — пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4» .
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство
3 ² + 4 ² = 5 ²
было известно уже египтянам еще около 2300 г. до н
Презентация учащегося по математике по теме «Некоторые способы доказательства теоремы Пифагора»
Описание слайда:Формулировки Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: Алгебраическая формулировка: То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a2 + b2 = c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника. Обратная теорема Пифагора: Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: Алгебраическая формулировка: Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a2 + b2 = c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника. Обратная теорема Пифагора: То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a2 + b2 = c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника. Обратная теорема Пифагора: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Проект-презентация «Теорема Пифагора и способы её доказательства»
Слайд 1
Теорема Пифагора и различные способы её доказательства Выполнил: Чернов Максим 8АСлайд 2
Цель проекта: Изложить теорему Пифагора, представить разные способы её доказательства.
Слайд 3
История В древнекитайской книге Чжоу би суань цзин говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары . Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н.э ., во времена царя Аменемхета I ( согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты , или « натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, — например, рисунки, изображающие столярную мастерскую. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 г. до н.э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников, Ван-дер- В арден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Вавилоне уже около XVIII века до н. э. Согласно комментарию Прокла к Евклиду, Пифагор (годами жизни которого принято считать 570—490 гг. до н. э.) использовал алгебраические методы, чтобы находить пифагоровы тройки. Однако Прокл писал между 410 и 485 гг. н. э. Томас Литтл Хит считал , что не существует явного упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы . Однако, когда авторы, такие как Плутарх и Цицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным .«Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики ».По преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков. Приблизительно в 400 г. до н. э., согласно Проклу , Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в « Началах» Евклида появилось старейшее аксиоматический доказательство теоремы Пифагора.
Слайд 4
Формулировки: Геометрическая формулировка: Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через , а длины катетов через a и b : a2+b2=c2 Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника .
Слайд 5
Доказательства На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).
Слайд 6
Через подобные треугольники Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры. Пусть ABC есть прямоугольный треугольник с прямым углом C . Проведём высоту из C и обозначим её основание через H . Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC . Введя обозначения получаем Что эквивалентно Сложив , получаем или , что и требовалось доказать
Слайд 7
Доказательства методом площадей Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора Доказательство через равнодополняемость Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной ( a+b ), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата. Что и требовалось доказать. .
Слайд 8
Доказательство Евклида Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно — AB=AK, AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше. Данное доказательство также получило название «Пифагоровы штаны».
Слайд 9
Доказательство Леонардо да Винчи Главные элементы доказательства — симметрия и движение. Рассмотрим чертёж, как видно из симметрии, отрезок рассекает квадрат на две одинаковые части (так как треугольники и равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки , мы усматриваем равенство заштрихованных фигур и . Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.
Слайд 10
Значение теоремы Пифагора Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение её состоит в том, что из неё или с помощью можно вывести большинство теорем геометрии.
Слайд 11
Спасибо за внимание !