Основное Тригонометрическое Тождество — Доказательство
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания.
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.

- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.

Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Если в голове вашего ребенка бурлит тригонометрическая каша, и все формулы смешались в один нераспутываемый клубок — записывайтесь на бесплатный вводный урок математики в онлайн-школу Skysmart.
Наши преподаватели помогут навести в голове порядок и разложить все знания по полочкам. На уроках вас ждут интересные задачки и располагающая атмосфера, в которой совсем не страшно задавать вопросы и получать от занятий — максимум.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = . - Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.

- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
1 | sin2α + cos2α = 1 |
2 | |
3 | |
4 | tgα * ctgα = 1 |
5 | tg2α + 1 = |
6 | 1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Алгебра любит практику — как можно больше практики. Чтобы натренироваться в решении задачек и накачать математический бицепс, записывайте вашего ребенка на бесплатный вводный урок математики в онлайн-школу Skysmart.
У нас есть все для эффективных и веселых занятий: опытные преподаватели, интересные задачки, интерактивный формат и внушительная порция вдохновения и поддержки!
Пояснение (доказательство) простейших тригонометрических тождеств
Пояснение, как получаются тригонометрические тождества
Поясним, как выводятся тригонометрические тождества на примере очень простых формул:На примере прямоугольного треугольника ABC выведем простейшие тригонометрические тождества и докажем их правильность.
Доказательство тождества sin α / cos α = tg α
Поясним, как частное от деления синуса на косинус альфа дает тангенс этого же угла (Формула номер 1)Из определения синуса следует, что
sin α = BC / AB
Из определения косинуса следует, что
cos α = AC / AB
Разделим одно выражение на второе
sin α / cos α
подставим вместо тригонометрических функций соотношение сторон, получим:
( BC / AB ) : (AC / AB)
При делении одной дроби на другую, подучим результат
sin α / cos α BC / AC
Из определения тангенса следует
tg α = BC / AC
Таким образом,
sin α / cos α = tg α
Тождество (1) доказано.
Краткое доказательство можно посмотреть на рисунке ниже:
Тождества 2 и 3 доказываются абсолютно аналогичным способом.
Доказательство тождества sin
2 α + cos2 α = 1 Теперь докажем тождество 4, что сумма квадрата синуса и косинуса одного и того же угла дает единицу.Из определения синуса следует, что
sin α = BC / AB
Из определения косинуса следует, что
cos α = AC / AB
Возведем каждое выражение в квадрат и вычислим их сумму.
sin2 α + cos2 α = ( BC / AB )2 + ( AC / AB )2
поскольку обе дроби имеют один и тот же знаменатель, то
BC2 / AB2 + AC2 / AB2 = ( BC2 + AC2 ) / AB2
Снова посмотрим на рисунок выше.
BC2 + AC2 — это сумма квадратов катетов прямоугольного треугольника. Согласно, теореме Пифагора
BC2 + AC2 = AB2
Заменим числитель (BC2 + AC2) на тождественное выражение AB2 и получим:
AB2 / AB2 = 1
Таким образом,
sin2 α + cos2 α = 1
Тождество (4) доказано
Краткое доказательство можно посмотреть на рисунке ниже
Доказательство тригонометрических тождеств
Существует много различных способов доказательства тригонометрических тождеств. На конкретных примерах мы рассмотрим некоторые из этих способов.
Пример 1. Доказать тождество
(1)
1-й способ. Выражение, стоящее в левой части этого тождества, преобразуем так, чтобы оно привелось к виду tg (α +π/4) Для этого запишем cos α как sin (π/2 + α). Тогда, используя формулы для суммы и разности синусов двух углов, получим:
cos α + sin α = sin (π/2 + α) + sin α = 2 sin (α +π/4)• cos π/4 = \/2 sin (α +π/4)
cos α — sin α = sin (π/2 + α) — sin α = 2 sin π/4• cos (α +π/4) = \/2 cos (α +π/4)
Поэтому
2-й способ. Выражение tg (α +π/4), стоящее в правой части данного тождества, преобразуем к виду для этого воспользуемся формулой для тангенса суммы двух углов:
Выражение tg (α +π/4), стоящее в правой части данного тождества, преобразуем к виду для этого воспользуемся формулой для тангенса суммы двух углов:
Однако здесь необходимо сделать одно принципиально важное замечание. Когда мы писали, что
, то фактически мы предполагали, что выражение tg α определено, то есть α =/= π/2 + nπ. На самом же деле это предположение может оказаться неверным. Поэтому случай, когда α = π/2 + nπ, нужно рассмотреть отдельно. В этом случае cos α = 0, и поэтому левая часть данного тождества принимает вид:
Правая же часть данного тождества при α = π/2 + nπ обращается в
tg (α +π/4) = tg (3π/4 + nπ). Но π есть период тангенса; следовательно,
Но π есть период тангенса; следовательно,
tg (α +π/4) = tg 3π/4 = — l.
Таким образом, и при α = π/2 + nπ равенство (1) справедливо.
Теперь можно считать, что данное тождество полностью доказано.
3-й способ. Выражения, стоящие в левой и правой частях данного тождества, преобразуем к одному и тому же виду. Для этого числитель и знаменатель дроби
разделим на cos α, предполагая сначала, что cos α =/= 0. В результате получим:
(1)
Правую часть данного тождества преобразуем, используя формулу для тангенса суммы двух углов:
(2)
Сравнивая (2) и (3), получаем:
Случай, когда cos α = 0, нужно рассмотреть отдельно, так же как мы это сделали при рассмотрении способа 2.
Пример 2. Доказать тождество
cos 3α • sin 5α — sin 2α = sin 3α • cos 5α.
Покажем, что разность между выражениями, стоящими в левой и правой частях данного тождества, равна 0. Действительно,
cos 3α • sin 5α — sin 2α — sin 3α • cos 5α =
= (cos 3α • sin 5α — sin 3α • cos 5α) — sin 2α =
= sin (5α — 3α) — sin 2α = sin 2α — sin 2α = 0.
Тем самым тождество доказано.
Упражнения
Доказать данные тождества:
Доказать основное тригонометрическое тождество
☰
Основным тригонометрическим тождеством является следующее равенство:
sin2 α + cos2 α = 1
Это значит, что в прямоугольном треугольнике сумма квадратов синуса и косинуса одного и того же острого угла равна единице.
Докажем это тригонометрическое тождество. Пусть дан прямоугольный треугольник ABC (∠C = 90º). Проведем в нем высоту CH к гипотенузе.
Выразим катеты треугольника ABC по косинусам углов. Так как cos A = AC/AB, то
AC = AB · cos A
Так как cos B = BC/AB, то
BC = AB · cos B
Теперь рассмотрим треугольник ACH. Он прямоугольный, т. к. CH ⊥ AB. АС в этом треугольнике является гипотенузой. Тогда cos A = AH/AC. Выразим отсюда отрезок AH:
AH = AC · cos A
Подставим вместо отрезка AC его значение, выраженное ранее через косинус угла A треугольника ABC. Получим:
AH = (AB · cos A) · cos A = AB · cos2 A
Теперь рассмотрим треугольник BCH. В нем cos B = BH/BC. Выразим BH и заменим BC его значением, найденным в треугольнике ABC:
BH = AB · cos2 B
Отрезок AB является суммой отрезков AH и BH:
AH + BH = AB
Заменим AH и BH на их выражения через косинусы углов:
AB · cos2 A + AB · cos2 B = AB
AB · (cos2 A + cos2 B) = AB
cos2 A + cos2 B = 1
Как известно, синус одного острого угла прямоугольного треугольника равен косинусу другого острого угла этого же треугольника. В данном случае:
В данном случае:
sin A = cos B
Следовательно, в тождестве cos2 A + cos2 B = 1 мы можем косинус угла B заменить на синус угла A. Таким образом получим:
cos2 A + cos2 B = 1
cos2 A + (cos B · cos B) = 1
cos2 A + (sin A · sin A) = 1
cos2 A + sin2 A = 1
Таким образом, сумма квадрата косинуса угла и квадрата синуса этого угла равна единицы, что и требовалось доказать.
их формулировки и вывод, связь косинуса и тангенса, как из синуса получить косинус
В статье подробно рассказывается об основных тригонометрических тождествах. Эти равенства устанавливают связь между sin, cos, tg, ctg заданного угла. При известной одной функции можно через нее найти другую.
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
sin2α+cos2α=1tg α=sin αcos α, ctg α=cos αsin αtg α·ctg α=1tg2α+1=1cos2α, 1+ctg2α=1sin2α
Связь между sin и cos одного угла
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin2α+cos2α=1
Заданные равенства tg2α+1=1cos2α, 1+ctg2α=1sin2α выводят из основного путем деления обеих частей на sin2α и cos2α. После чего получаем tg α=sin αcos α, ctg α=cos αsin α и tg α·ctg α=1 — это следствие определений синуса, косинуса, тангенса и котангенса.
Равенство sin2α+cos2α=1 является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .
Пусть даны координаты точки А(1,0), которая после поворота на угол αстановится в точку А1. По определению sin и cos точка А1 получит координаты (cos α, sin α). Так как А1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x2+y2=1 этой окружности. Выражение cos2α+sin2α=1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α.
Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α.
В тригонометрии выражение sin2α+cos2α=1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Используя единичную окружность, поворачиваем точку А с координатами (1,0) вокруг центральной точки О на угол α. После поворота точка меняет координаты и становится равной А1(х,у). Опускаем перпендикулярную прямую А1Н на Ох из точки А1.
На рисунке отлично видно, что образовался прямоугольный треугольник ОА1Н. По модулю катеты ОА1Н и ОН равные, запись примет такой вид: |А1H|=|у|,|ОН|=|х|. Гипотенуза ОА1 имеет значение равное радиусу единичной окружности, |ОА1|=1. Используя данное выражение, можем записать равенство по теореме Пифагора: |А1Н|2 +|ОН|2 =|ОА1|2. Это равенство запишем как |y|2+|x|2=12, что означает y2+x2=1.
Используя определение sin α=y и cosα=x, подставим данные угла вместо координат точек и перейдем к неравенству sin2α+cos2α=1.
Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin2α+cos2=1 относительно sin и cos, тогда получим выражения вида sin α=±1-cos2α и cos α=±1-sin2α соответственно. Величина угла αопределяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1. Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеТангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
tg α=sin αcos αctg α=cos αsin α
Из определения синус является ординатой у, а косинус – абсциссой x. Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:
tg α=yx=sin αcos α, а выражение котангенса имеет обратное значение, то есть
ctg α=xy=cos αsin α.
Отсюда следует, что полученные тождества tg α=sin αcos α и ctg α=cos αsin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Отметим, что tg α=sin αcos α и ctg α=cos αsin α верны для любого значение угла α, значения которого входят в диапазон. Из формулы tg α=sin αcos α значение угла α отлично от π2+π·z, а ctg α=cos αsin α принимает значение угла α, отличные от π·z, z принимает значение любого целого числа.
Связь между тангенсом и котангенсом
Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как tg α·ctg α=1. Оно имеет смысл при α с любым значением, кроме π2·z, иначе функции будут не определены.
Оно имеет смысл при α с любым значением, кроме π2·z, иначе функции будут не определены.
Формула tg α·ctg α=1 имеет свои особенности в доказательстве. Из определения мы имеем, что tg α=yx и ctg α=xy, отсюда получаем tg α·ctg α=yx·xy=1. Преобразовав выражение и подставив tg α=sin αcos α и ctg α=cos αsin α, получим tg α·ctg α=sin αcos α·cos αsin α=1.
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Тангенс и косинус, котангенс и синусПреобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам tg2α+1=1cos2α, 1+ctg2α=1sin2α.
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1, а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin2α+cos2α=1, можно разделить соответствующие стороны на cos2α и получить tg2α+1=1cos2α, где значение cos2α не должно равняться нулю. При делении на sin2α получим тождество 1+ctg2α=1sin2α, где значение sin2α не должно равняться нулю.
При делении на sin2α получим тождество 1+ctg2α=1sin2α, где значение sin2α не должно равняться нулю.
Из приведенных выражений получили, что тождество tg2α+1=1cos2α верно при всех значениях угла α, не принадлежащих π2+π·z, а 1+ctg2α=1sin2α при значениях α, не принадлежащих промежутку π·z.
Основные тригонометрические формулы
В самом начале этой статьи мы с Вами рассмотрели понятие тригонометрических функций. Основное назначение их назначение – это изучение основ тригонометрии и исследование периодических процессов. И тригонометрический круг мы не зря рисовали, потому что в большинстве случаев тригонометрические функции определяются, как отношение сторон треугольника или его определенных отрезков в единичной окружности. Так же я упоминал о неоспоримо огромном значении тригонометрии в современной жизни. Но наука не стоит на месте, в результате мы можем значительно расширить область применения тригонометрии и перенести ее положения на вещественные, а иногда и на комплексные числа.
Формулы тригонометрии бывают нескольких видов. Рассмотрим их по порядку.
Соотношения тригонометрических функций одного и того же угла
Выражения тригонометрических функций друг через друга
(выбор знака перед корнем определяется тем, в какой из четвертей круга расположен угол ?)
Далее следуют формулы сложения и вычитания углов:
Формулы двойных, тройных и половинных углов.
Замечу, что все они проистекают из предыдущих формул.

Формулы преобразования тригонометрических выражений:
Здесь мы подошли к рассмотрению такого понятия как основные тригонометрические тождества.
Тригонометрическое тождество — это равенство, которое состоит из тригонометрических соотношений и которое выполняется для всех значений величин углов, которые входят в него.
Рассмотрим наиболее важные тригонометрические тождества и их доказательства:
Первое тождество вытекает из самого определения тангенс.
Возьмем прямоугольный треугольник, в котором имеется острый угол х при вершине А.
Для доказательства тождеств необходимо воспользоваться теоремой Пифагора:
(ВС) 2 + (АС) 2 = (АВ) 2
Теперь разделим на (АВ) 2 обе части равенства и припомнив определения sin и cos угла, мы получаем второе тождество:
(ВС) 2/(AB) 2 + (AC) 2/(AB) 2 = 1
sin x = (BC)/(AB)
cos x = (AC)/(AB)
sin2 x + cos2 x = 1
Для доказательства третьего и четвертого тождеств воспользуемся предыдущим доказательством.
Для этого обе части второго тождества разделим на cos2 x:
sin2 x/ cos2 x + cos2 x/ cos2 x = 1/ cos2 x
sin2 x/ cos2 x + 1 = 1/ cos2 x
Исходя из первого тождества tg x = sin х /cos x получаем третье:
1 + tg2 x = 1/cos2 x
Теперь разделим второе тождество на sin2 x:
sin2 x/ sin2 x + cos2 x/ sin2 x = 1/ sin2 x
1+ cos2 x/ sin2 x = 1/ sin2 x
cos2 x/ sin2 x есть не что иное, как 1/tg2 x, поэтому получаем четвертое тождество:
1 + 1/tg2 x = 1/sin2 x
Пришла пора вспомнить теорему о сумме внутренних углов треугольника, которая гласит, что сумма углов треугольника = 1800. Получается, что при вершине В треугольника находится угол, величина которого 1800 – 900 – х = 900 – х.
Опять вспомним определения для sin и cos и получаем пятое и шестое тождества:
sin x = (BC)/(AB)
cos(900– x ) = (BC)/(AB)
cos(900– x ) = sin x
Теперь выполним следующее:
cos x = (AC)/(AB)
sin(900– x ) = (AC)/(AB)
sin(900– x ) = cos x
Как видите – здесь все элементарно.
Существуют и другие тождества, которые используются при решении математических тождеств, я приведу их просто в виде справочной информации, потому как все они проистекают из вышерассмотренных.
sin 2х =2sin х*cos х
cos 2х =cos2х -sin2х =1-2sin2х =2cos2х -1
tg 2x = 2tgx/(1 — tg2 x)
сtg 2x = (сtg2 x — 1) /2сtg x
sin3х =3sin х — 4sin3х
cos3х =4cos3х — 3cos х
tg 3x = (3tgx – tg3 x) /(1 — 3tg2 x)
сtg 3x = (сtg3x – 3сtg x) /(3сtg2 x — 1)
Когда-то, будучи школьником, я с удовольствием применял эти формулы для решения различного рода задач, как то упростить выражение или решить уравнение. Главное разглядеть — куда и какую формулу необходимо применить, и тогда многоярусная конструкция превращается в обычное числовое выражение. Очень полезная штука для развития логического мышления!
Очень полезная штука для развития логического мышления!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
|
| ||||||||||||||||
|
| ||||||||||||||||
| ]2 вариант
|
Подтверждение тригонометрических идентичностей | Блестящая вики по математике и науке
Подтвердите личность
tanθ + cotθ = 2sin2θ.
\ tan \ theta + \ cot \ theta = \ frac {2} {\ sin 2 \ theta}. tanθ + cotθ = sin2θ2.
(Рекомендация 2) Замена tanθ \ tan \ theta tanθ на sinθcosθ \ frac {\ sin \ theta} {\ cos \ theta} cosθsinθ и cotθ \ cot \ theta cotθ на cosθsin Θ \ frac {\ cos \ theta} {\ sin \ theta} sinθcosθ,
LHS = sinθcosθ + cosθsinθ = sin2θ + cos2θsinθcosθ = 1sinθcosθ.2 \ theta} {\ sin \ theta \ cos \ theta} = \ frac {1} {\ sin \ theta \ cos \ theta}. LHS = cosθsinθ + sinθcosθ = sinθcosθsin2θ + cos2θ = sinθcosθ1.
(Принцип 5) Мы сейчас застряли, потому что это очень просто. Посмотрим на RHS. Заменяя sin2θ \ sin 2 \ thetasin2θ на 2sinθcosθ 2 \ sin \ theta \ cos \ theta 2sinθcosθ, получаем
RHS = 2sin2θ = 22sinθcosθ = 1sinθcosθ. RHS = \ frac {2} {\ sin 2 \ theta} = \ frac {2} {2 \ sin \ theta \ cos \ theta} = \ frac {1} {\ sin \ theta \ cos \ theta}. Правая сторона = sin2θ2 = 2sinθcosθ2 = sinθcosθ1.
Таким образом, имеем
LHS = 1sinθcosθ = RHS.
□ LHS = \ frac {1} {\ sin \ theta \ cos \ theta} = RHS. \ _ \ Square LHS = sinθcosθ1 = RHS. □
Подтвердите личность
sinx − cosxsinx + cosx = −cos2×1 + sin2x. \ frac {\ sin x — \ cos x} {\ sin x + \ cos x} = — \ frac {\ cos 2x} {1 + \ sin 2 x}. sinx + cosxsinx − cosx = −1 + sin2xcos2x.
(Рекомендация 6) Эту личность трудно атаковать напрямую. Давайте подумаем, что это за цель, и сравним стороны друг с другом.2. 1 + sin2x = 1 + 2sinxcosx = sin2x + cos2x + 2sinxcosx = (sinx + cosx) 2.
Таким образом, получаем
RHS = — (cosx − sinx) (cosx + sinx) (sinx + cosx) (sinx + cosx) = sinx − cosxsinx + cosx = LHS. □ RHS = \ frac {- (\ cos x — \ sin x) (\ cos x + \ sin x)} {(\ sin x + \ cos x) (\ sin x + \ cos x)} = \ frac { \ sin x — \ cos x} {\ sin x + \ cos x} = LHS. \ _ \ square RHS = (sinx + cosx) (sinx + cosx) — (cosx − sinx) (cosx + sinx) = sinx + cosxsinx − cosx = LHS. □
Подтвердите личность
sin (A + B) + sin (A − B) sin (A + B) −sin (A − B) = tanAtanB.
\ frac {\ sin (A + B) + \ sin (A — B)} {\ sin (A + B) — \ sin (A — B)} = \ frac {\ tan A} {\ tan B}. sin (A + B) −sin (A − B) sin (A + B) + sin (A − B) = tanBtanA.
Используя формулы суммы и разности, получаем
LHS = (sinAcosB + cosAsinB) + (sinAcosB − cosAsinB) (sinAcosB + cosAsinB) — (sinAcosB −cosAsinB) = 2sinAcosB2cosAsinB = sinAcosBcosAsinB. \ Begin {выровнено} LHS & = \ frac {(\ sin A \ cos B + \ cos A \ sin B) + (\ sin A \ cos B — \ cos A \ sin B)} {(\ sin A \ cos B + \ cos A \ sin B) — (\ sin A \ cos B — \ cos A \ sin B)} \\\\ & = \ frac {2 \ sin A \ cos B} {2 \ cos A \ sin B} = \ frac {\ sin A \ cos B} {\ cos A \ sin B}.\ end {align} LHS = (sinAcosB + cosAsinB) — (sinAcosB − cosAsinB) (sinAcosB + cosAsinB) + (sinAcosB − cosAsinB) = 2cosAsinB2sinAcosB = cosAsinBsinAcosB.
Упрощая RHS с точки зрения sin и cos, получаем
RHS = sinAcosAsinBcosB = sinAcosBcosAsinB. RHS = \ frac {\ small {\ dfrac {\ sin A} {\ cos A}}} {\ small {\ hspace {3mm} \ dfrac {\ sin B} {\ cos B} \ hspace {3mm}}} = \ frac {\ sin A \ cos B} {\ cos A \ sin B}.
RHS = cosBsinB cosAsinA = cosAsinBsinAcosB.
Следовательно, LHS = RHS.3 \ theta + 3 \ sin \ theta = RHS. \ _ \ Квадрат \ end {align} 4sinθcos2θ − sinθ = 4sinθ (1 − sin2θ) −sinθ = −4sin3θ + 3sinθ = RHS. □
Подтвердите личность
кроваткаθ − cot2θ = 1sin2θ. \ Cot \ theta- \ cot2 \ theta = \ frac {1} {\ sin2 \ theta} .cotθ − cot2θ = sin2θ1.
Поскольку cotθ = cosθsinθ \ cot \ theta = \ frac {\ cos \ theta} {\ sin \ theta} cotθ = sinθcosθ, имеем
cotθ − cot2θ = cosθsinθ − cos2θsin2θ. \ Cot \ theta- \ cot2 \ theta = \ frac {\ cos \ theta} {\ sin \ theta} — \ frac {\ cos2 \ theta} {\ sin2 \ theta}.2 (А + В)} \\\\ & = \ frac {\ sin (A-B)} {\ sin (A + B)}. \ end {align} 2sin2 (A + B) cos2B − cos2A = 2sin2 (A + B) −2sin (B + A) sin (B − A) = sin2 (A + B) sin (A + B) sin (A − B) = sin (A + B) sin (A − B).
Следующий шаг — просто применить формулу суммы углов к числителю и знаменателю. Тогда у нас
sin (A − B) sin (A + B) = sinAcosB − cosAsinBsinAcosB + cosAsinB.
\ Frac {\ sin (AB)} {\ sin (A + B)} = \ frac {\ sin A \ cos B- \ cos A \ sin B} {\ sin A \ cos B + \ cos A \ sin B} .sin (A + B) sin (A − B ) = SinAcosB + cosAsinBsinAcosB − cosAsinB.
Теперь разделим числитель и знаменатель на cosAcosB \ cos A \ cos BcosAcosB, чтобы получить касательные следующим образом:
sinAcosB − cosAsinBsinAcosB + cosAsinB = sinAcosA − sinBcosBsinAcosA + sinBcosB = tanA − tan BtanA + tanB.□ \ frac {\ sin A \ cos B- \ cos A \ sin B} {\ sin A \ cos B + \ cos A \ sin B} = \ frac {\ hspace {3mm} \ frac {\ sin A} {\ cos A} — \ frac {\ sin B} {\ cos B} \ hspace {3mm}} {\ frac {\ sin A} {\ cos A} + \ frac {\ sin B} {\ cos B}} = \ frac {\ tan A- \ tan B} {\ tan A + \ tan B}. \ _ \ squaresinAcosB + cosAsinBsinAcosB − cosAsinB = cosAsinA + cosBsinB cosAsinA −cosBsinB = tanA + tanBtanA − tanB. □
[Другое решение]
Решение, приведенное выше, может быть довольно трудным. Если вы застряли, пытаясь организовать LHS, переключение и устранение RHS может сработать.
Просто попробуйте преобразовать касательные в синусы и косинусы, используя формулу tan = sinθcosθ \ tan = \ frac {\ sin \ theta} {\ cos \ theta} tan = cosθsinθ, и решите задачу наоборот. направление первого решения, как показано ниже:
tanA − tanBtanA + tanB = sinAcosA − sinBcosBsinAcosA + sinBcosB = sinAcosB − cosAsinBcosAcos BsinAcosB − cosAsinBcosAcosB = sin (A − B) sin (A + B) = sin (A − B) sin (A + B) sin2 ( A + B) = — 12⋅cos2A − cos2Bsin2 (A + B) = — 12⋅1−2sin2A− (1−2sin2B) sin2 (A + B) = sin 2A − sin2Bsin2 (A + B) = LHS.2 (А + В)} \\\\ & = LHS. \ _ \ Квадрат \ end {align} tanA + tanBtanA − tanB = cosAsinA + cosBsinB cosAsinA −cosBsinB = cosAcosBsinAcosB − cosAsinB cosAcosBsinAcosB − cosAsinB = sin (A + B) sin (A − B) = sin2 (A + B) sin (A − B) sin (A + B) = −21 ⋅sin2 (A + B) cos2A − cos2B = −21 ⋅sin2 (A + B) 1−2sin2A− (1 −2sin2B) = sin2 (A + B) sin2A − sin2B = LHS. □
Доказательство тригонометрических идентичностей
Расстойка
Тригонометрические тождества (стр. 1 из 3)
1 из 3)
Подтверждение личности очень отличается концепция от решения уравнения.Хотя вы будете использовать многие из тех же техник, они , а не , и различия в том, что может вызвать у вас проблемы.
«Идентичность» — это тавтология,
уравнение или утверждение, которое всегда верно, несмотря ни на что. Например, sin ( x ) = 1/ csc ( x )
это личность. Чтобы «подтвердить» личность, вы должны использовать логические
шаги, чтобы показать, что одна сторона уравнения может быть преобразована в
другая сторона уравнения.Вы делаете , а не , вставляете значения в идентичность
что-либо «доказать». Есть бесконечно много значений, которые вы можете
подключите. Вы действительно собираетесь что-то «доказать», перечислив
три или четыре значения, где две стороны уравнения равны? Из
конечно нет. Иногда вам будет предложено уравнение , а не .
личность. Если вы подставите значение там, где две стороны равны,
например π / 4
для (ложной) идентичности sin ( x )
= cos ( x ), вы могли бы
обмануть себя, думая, что простое уравнение — это тождество.Ты будешь
выстрелил себе в ногу. Так что не будем этого делать.
Иногда вам будет предложено уравнение , а не .
личность. Если вы подставите значение там, где две стороны равны,
например π / 4
для (ложной) идентичности sin ( x )
= cos ( x ), вы могли бы
обмануть себя, думая, что простое уравнение — это тождество.Ты будешь
выстрелил себе в ногу. Так что не будем этого делать.
Для подтверждения личности ваш инструктор может
сказал вам, что вы не можете работать с обеими сторонами уравнения в
в то же время. Это правильно. Вы можете работать с обеими сторонами вместе
регулярное уравнение, потому что вы пытаетесь найти, где уравнение
правда. Когда вы работаете с идентичностью, если вы работаете с обеих сторон
и работайте до тех пор, пока стороны не будут равны, вы только покажете, что , если исходное уравнение верно, то можно прийти к другому
истинное уравнение.Но логически вы не докажете, что оригинал
уравнение действительно было верным.
Так как вы будете работать с двух сторон уравнения, было бы полезно ввести некоторые обозначения, если вы не видел раньше. «Левая часть» уравнения обозначается LHS, а «правая часть» обозначается RHS.
- Подтвердите личность
Обычно это безопасная ставка, чтобы начать работать на той стороне, которая кажется более сложной.В этом случае это будет LHS. Еще один безопасный вариант — преобразовать вещи в синусы и косинусы, и посмотрите, к чему это приведет. Итак, моим первым шагом будет преобразование котангенс и косеканс в их альтернативные выражения:
Теперь переверну-n-умножу:
Теперь я вижу, что синусы отменяются, оставив меня с:
Тогда мое удостоверение личности — это все из этих шагов, вместе взятых:
Эта последняя строка уравнений — вот что
они ждут вашего ответа.
- Подтвердите личность
Я не уверен, с какой стороны сложнее, так что я начну слева. Мой первый шаг — преобразовать все на синусы и косинусы: Copyright © Элизабет Стапель 2010-2011 Все права защищены
Когда я получаю дроби, это почти всегда хорошая идея получить общий знаменатель, так что я сделаю это следующим образом:
Теперь, когда у меня есть общий знаменатель, Я могу объединить эти дроби в одну:
Теперь я замечаю пифагорейца идентичность в числителе, что позволяет упростить:
Оглядываясь на правую сторону оригинала идентичности, я заметил, что этот знаменатель может быть полезен.Я разделюсь произведение на две фракции:
А теперь я могу закончить преобразованием эти дроби к их обратным формам:
(я писал их в обратном порядке, чтобы
соответствует правому. ) Полный ответ — все шаги вместе, начиная с
с LHS и заканчивая RHS:
) Полный ответ — все шаги вместе, начиная с
с LHS и заканчивая RHS:
Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.«Провинивские тригонометрические идентичности». Purplemath .
Доступно по номеру |
4.1: Тригонометрические тождества — математика LibreTexts
Рассмотрим тригонометрическое уравнение \ (\ sin (2x) = \ cos (x) \). Исходя из наших текущих знаний, точно решить подобное уравнение может быть сложно, потому что периоды задействованных функций различны. {2} = 1 \) — это отношение между двумя выражениями, которое может быть истинным для некоторых значений переменной. Решить уравнение означает найти все значения переменных, которые делают два выражения равными друг другу. Идентификатор — это уравнение, которое истинно для всех допустимых значений переменной. Например, из предыдущих курсов алгебры мы видели, что
{2} = 1 \) — это отношение между двумя выражениями, которое может быть истинным для некоторых значений переменной. Решить уравнение означает найти все значения переменных, которые делают два выражения равными друг другу. Идентификатор — это уравнение, которое истинно для всех допустимых значений переменной. Например, из предыдущих курсов алгебры мы видели, что
для всех действительных чисел \ (x \). Это алгебраическое тождество, поскольку оно верно для всех значений действительных чисел \ (x \).{2} = 1 \), поскольку это верно для всех действительных числовых значений \ (x \).
Итак, пока мы решаем уравнения, чтобы определить, когда равенство действительно, нет причин решать тождество, поскольку равенство в тождестве всегда верно. Каждое тождество — это уравнение, но не каждое уравнение — это тождество. Чтобы знать, что уравнение является тождеством, необходимо предоставить убедительный аргумент, что два выражения в уравнении всегда равны друг другу. Такой убедительный аргумент называется доказательством , и мы используем доказательства для проверки тригонометрических тождеств. {2} = 1. \]
{2} = 1. \]
Тождества из определений
Определения функций тангенса, котангенса, секанса и косеканса были введены в разделе 1.6. Следующее верно для всех значений \ (t \), для которых определена правая часть каждого уравнения.
\ [\ tan (t) = \ dfrac {\ sin (t)} {\ cos (t)} \]
\ [\ cot (t) = \ dfrac {\ cos (t)} {\ sin (t)} \]
\ [\ sec (t) = \ dfrac {1} {\ cos (t)} \]
\ [\ csc (t) = \ dfrac {1} {\ sin (t)} \]
Отрицательные личности
Отрицательные были введены в главе 2, когда обсуждалась симметрия графов.{2} (х) \). Чтобы показать, что уравнение не является тождеством, достаточно продемонстрировать, что две стороны уравнения имеют разные значения на одном входе.
Пример \ (\ PageIndex {2} \): (Показывает, что уравнение не является идентификатором)
Рассмотрим уравнение с уравнением \ (\ cos (x — \ dfrac {\ pi} {2}) = \ sin (x + \ dfrac {\ pi} {2}) \), которое мы встретили в нашем Начальном упражнении. Хотя вы можете проверить, что \ (\ cos (x — \ dfrac {\ pi} {2}) \) и \ (\ sin (x + \ dfrac {\ pi} {2}) \) равны при некоторых значениях, \ (\ dfrac {\ pi} {4} \) например, они не равны при всех значениях — \ (\ cos (0 — \ dfrac {\ pi} {2}) = 0 \), но \ (\ sin (0 + \ dfrac {\ pi} {2}) = 1 \).Поскольку тождество должно обеспечивать равенство для всех допустимых значений переменной, если два выражения различаются на одном входе, то уравнение не является тождеством. Таким образом, уравнение \ (\ cos (x — \ dfrac {\ pi} {2}) = \ sin (x + \ dfrac {\ pi} {2}) \) не является тождеством.
Хотя вы можете проверить, что \ (\ cos (x — \ dfrac {\ pi} {2}) \) и \ (\ sin (x + \ dfrac {\ pi} {2}) \) равны при некоторых значениях, \ (\ dfrac {\ pi} {4} \) например, они не равны при всех значениях — \ (\ cos (0 — \ dfrac {\ pi} {2}) = 0 \), но \ (\ sin (0 + \ dfrac {\ pi} {2}) = 1 \).Поскольку тождество должно обеспечивать равенство для всех допустимых значений переменной, если два выражения различаются на одном входе, то уравнение не является тождеством. Таким образом, уравнение \ (\ cos (x — \ dfrac {\ pi} {2}) = \ sin (x + \ dfrac {\ pi} {2}) \) не является тождеством.
Пример 4.2 иллюстрирует важный момент. чтобы показать, что уравнение не является тождеством, достаточно найти один вход, при котором две стороны уравнения не равны. Мы резюмируем нашу работу с идентичностями следующим образом.
- Чтобы доказать, что уравнение является тождеством, нам нужно применить известные тождества, чтобы показать, что одна сторона уравнения может быть преобразована в другую.

- Чтобы доказать, что уравнение не является тождеством, нам нужно найти один вход, на котором две стороны уравнения имеют разные значения.
Важное примечание : При подтверждении идентичности может возникнуть соблазн начать работать с самим уравнением и манипулировать обеими сторонами, пока вы не придете к чему-то, что, как вы знаете, является истинным.НЕ ДЕЛАЙТЕ ЭТОГО! Работая с обеими сторонами уравнения, мы делаем предположение, что уравнение является тождеством, но это предполагает именно то, что нам нужно показать. Таким образом, надлежащий формат доказательства тригонометрического тождества состоит в том, чтобы выбрать одну сторону уравнения и применить существующие тождества, которые мы уже знаем, чтобы преобразовать выбранную сторону в оставшуюся. Обычно это облегчает жизнь, если начать с более сложной на вид стороны (если она есть).
Пример \ (\ PageIndex {3} \): проверка личности
Рассмотрим уравнение \ [2 \ cos ^ {2} (x) — 1 = \ cos ^ {2} (x) — \ sin ^ {2} (x). {2} (х) \). Любая надлежащая перестановка тождества также является тождеством, поэтому мы можем манипулировать известными тождествами, чтобы использовать их в наших доказательствах.
{2} (х) \). Любая надлежащая перестановка тождества также является тождеством, поэтому мы можем манипулировать известными тождествами, чтобы использовать их в наших доказательствах.
Повторюсь, правильный формат для доказательства тригонометрической идентичности — это выбрать одну сторону уравнения и применить существующие идентичности, которые мы уже знаем, чтобы преобразовать выбранную сторону в оставшуюся сторону. Не существует жестких и быстрых методов удостоверения личности — это своего рода искусство. Вы должны практиковаться, чтобы стать хорошим в этом.
Упражнение \ (\ PageIndex {1} \)
Для каждого из следующих случаев используйте графическую утилиту для построения графиков обеих сторон уравнения.{2} (х) \]
- Ответ
1. Графики обеих сторон уравнения показывают, что это отступ.
2. Графики обеих сторон уравнения показывают, что это не отступ.
 Например, если мы положим \ (x = \ dfrac {\ pi} {2} \), то
Например, если мы положим \ (x = \ dfrac {\ pi} {2} \), то\ [\ cos (\ dfrac {\ pi} {2}) \ sin (\ dfrac {\ pi} {2}) = 0 \ cdot 1 = 0 \] и \ [2 \ sin (\ dfrac {\ pi } {2}) = 2 \ cdot 1 = 2 \]
Сводка
В этом разделе мы изучили следующие важные концепции и идеи:
Идентификатор — это уравнение, которое справедливо для всех допустимых значений задействованных переменных.
- Чтобы доказать, что уравнение является тождеством, нам нужно применить известные тождества, чтобы показать, что одна сторона уравнения может быть преобразована в другую.
- Чтобы доказать, что уравнение не является тождеством, нам нужно найти один вход, на котором две стороны уравнения имеют разные значения.
1. Тригонометрические идентичности
М. Борна
Прежде чем мы начнем доказывать тригонометрические тождества, мы посмотрим, откуда берутся базовые тождества.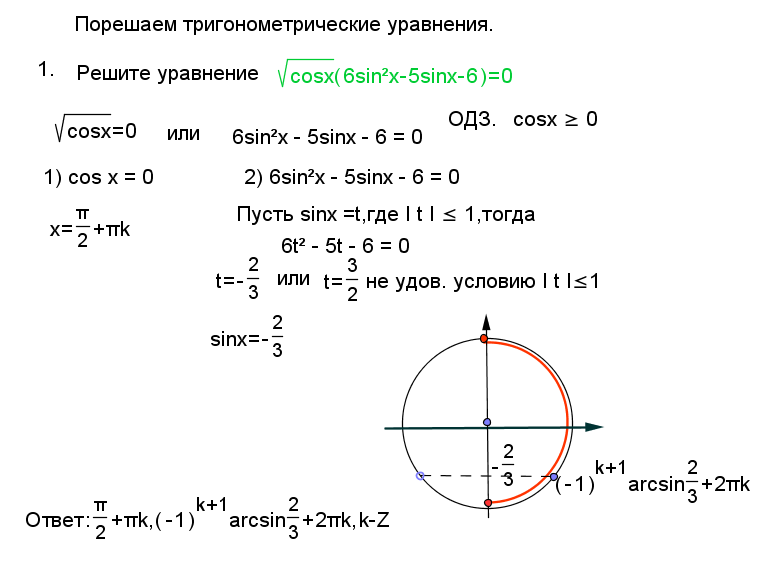
Вспомните определения взаимных тригонометрических функций, csc θ , sec θ и cot θ из главы о тригонометрических функциях:
`csc theta = 1 / (sin theta)`
`сек тета = 1 / (кос тета)`
`cot theta = 1 / (tan theta)`
Теперь рассмотрим следующую диаграмму, где точка ( x , y ) определяет угол θ в начале координат, а расстояние от начала координат до точки составляет r единиц:
Из диаграммы видно, что отношения sin θ и cos θ определяются как:
`sin theta = y / r`
и
`cos theta = x / r`
Теперь мы используем эти результаты, чтобы найти важное определение для tan θ :
`(sin theta) / (cos theta) = (y / r) / (x / r) = y / rxxr / x = y / x`
Теперь также `tan theta = y / x`, поэтому мы можем заключить:
`tan theta = (sin theta) / (cos theta)`
Соотношения, основанные на теореме Пифагора
Кроме того, для значений на приведенной выше диаграмме мы можем использовать теорему Пифагора и получить:
y 2 + x 2 = r 2
Деление на r 2 дает:
`y ^ 2 / r ^ 2 + x ^ 2 / r ^ 2 = 1`
, поэтому получаем важный результат:
`sin ^ 2 \ theta + cos ^ 2 \ theta = 1`
Родственные формулы
Теперь перейдем к выводу двух других связанных формул, которые можно использовать при доказательстве тригонометрических тождеств. 2 тета`
2 тета`
Доказательство тригонометрических тождеств
Предложения …
- Хорошо выучите приведенные выше формулы (или, по крайней мере, научитесь их быстро находить). Чем лучше вы знаете основные идентичности, тем легче вам будет распознать, что происходит в проблемах.
- Работайте со стороной самой сложной стороны и упростите ее так, чтобы она имела ту же форму, что и самая простая сторона.
- Не предполагать, что личность, а доказывать личность.Это означает, что не работайте по обе стороны от равной стороны и старайтесь встретиться посередине. Начните с одной стороны и сделайте так, чтобы она была похожа на другую.
- Многие из них получаются довольно легко, если вы выразите все на самой сложной стороне только в терминах синуса и косинуса .
- В большинстве примеров, где вы видите степень 2 (то есть 2 ), это будет включать использование тождества sin 2 θ + cos 2 θ = 1 (или одну из двух других формул, мы получили выше).
 2x = 1`)
2x = 1`)`=» RHS «`
Упражнения
1.2х) / (соз х \ грех х) `
`= 1 / (cos x \ sin x)`
`= 1 / (cos x) xx1 / (sin x)`
`= сек \ x \ csc \ x`
`=» RHS «`
2. Докажите, что
`(1 + cos x) / (sin x) = (sin x) / (1-cos x)`
Ответ
В этой задаче проще начать с RHS. Нам нужно выполнить трюк.
Умножаем числитель и знаменатель дроби на , сопряженное с знаменателя. (Мы видели эту идею в разделах «Рационализация знаменателя» (в сурдах) и при делении комплексных чисел.2 х) `
`= (1 + cos x) / (sin x)`
`=» LHS «`
Подтверждения тригонометрических тождеств
Подтверждение личности
Доказательство касательной и котангенса тождеств
Доказательство пифагорейской идентичности
Доказательство каждого из них следует из определений тригонометрических функций, Тема 15.
Доказательство взаимных отношений
По определению:
грех θ = y
r, csc θ = r
r. 
Следовательно, sin θ является обратной величиной csc θ:
грех θ = 1
csc θгде 1-над любым количеством является символом его обратного значения; Урок 5 алгебры. Аналогично для остальных функций.
Доказательство касательной и котангенса тождеств
Доказать:
тангенс угла θ = sin θ
cos θи детская кроватка θ = cos θ
sin θ. Доказательство . По определению
Следовательно, при делении числителя и знаменателя на r ,
тангенс угла θ = y / r
x / r= sin θ
cos θ. 
детская кроватка θ = 1
тангенс угла θ= cos θ
sin θ. Это две личности.
Доказательство пифагорейской идентичности
Доказать:
а) sin 2 θ + cos 2 θ = 1 б) 1 + загар 2 θ = сек 2 θ в) 1 + детская кроватка 2 θ = csc 2 θ Доказательство 1 .Согласно теореме Пифагора,
x 2 + y 2 = r 2 .
 . . . . . (1)
. . . . . (1)Следовательно, при разделении обеих сторон на r 2 ,
x 2
r 2+ y 2
r 2= r 2
r 2= 1. То есть по определениям
cos 2 θ + sin 2 θ = 1.. . . . (2)
Помимо порядка следования терминов, это первое пифагорейское тождество, а).
Чтобы получить b), разделите линию (1) на x 2 ; чтобы получить c), разделите на y 2 .
Или мы можем получить и b), и c) из a), разделив его сначала на cos 2 θ, а затем на sin 2 θ.На разделительной прямой 2) на cos 2 θ получаем
То есть
1 + tan 2 θ = сек 2 θ.

А если разделить а) на sin 2 θ, получим
То есть
1 + детская кроватка 2 θ = csc 2 θ.
Таким образом, три пифагорейских тождества эквивалентны друг другу.
Доказательство 2. sin 2 θ + cos 2 θ = y 2
r 2+ x 2
r 2= y 2 + x 2
r 2= r 2
r 2согласно теореме Пифагора, = 1. 
Тригонометрические идентификаторы
Темы | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
7.4 Доказательство тригонометрических тождеств | mhf4utrigonometry
Хотите верьте, хотите нет, но на самом деле большую часть этой главы вы имели дело с тригонометрическими тождествами.
Тригонометрическое тождество записывается как уравнение и просто утверждает, что обе части уравнения эквивалентны.
Однако тригонометрическое тождество не следует рассматривать так, как мы обычно относимся к уравнениям. Почему? Потому что мы на самом деле не пытаемся решить что-либо вроде того, как мы обычно решаем уравнения, поэтому мы на самом деле не пытаемся изолировать переменную (не изолировать переменные и т. Д.).
Кроме того, этот метод, при котором мы выполняем одни и те же операции с обеими сторонами уравнения (то есть умножение, деление, сложение и т.
 Д.) не обязательно используется. Это потому, что нам не обязательно это делать (ничего не решая). В конце концов, мы всего лишь пытаемся доказать, что обе части уравнения эквивалентны.
Д.) не обязательно используется. Это потому, что нам не обязательно это делать (ничего не решая). В конце концов, мы всего лишь пытаемся доказать, что обе части уравнения эквивалентны.При доказательстве мы рассматриваем обе части уравнения отдельно, как если бы каждая была отдельным выражением; упрощая левую сторону, упрощая правую сторону, а затем сравнивая их.
Так что мы делаем? Что ж, большая часть тригонометрических тождеств упрощается.На самом деле это все. Мы упрощаем обе стороны, пока они не будут выглядеть одинаково.
При доказательстве мы рассматриваем обе части уравнения отдельно, как если бы каждая была отдельным выражением; упрощая левую сторону, упрощая правую сторону, а затем сравнивая их.
В вашем распоряжении несколько инструментов для упрощения. Во-первых, все формулы двойного угла, формулы составного угла и взаимные тригонометрические отношения могут быть заменены (или исключены) при упрощении.Другие идентичности включают частные идентичности и пифагорейские идентичности. Все это изложено ниже.
Кроме того, вы всегда можете расширяться, что может привести вас к распознаванию других идентичностей или организации других стратегий.
11 советов по победе над тригонометрическим доказательством
Тригонометрическое доказательство идентичности — это распространенный тип вопросов, который включен в программу дополнительной математики O-Level. Упоминание о «триго-прувинге» часто заставляло даже старших школьников покрыться холодным потом.Это связано с тем, что, в отличие от большинства тем A-Math (O-level), вопросы по тригонометрии не имеют стандартного метода решения «подключи и работай». Каждый вопрос — это новая головоломка, для которой ученики должны найти маршрут от начала до конца. Очень часто учащиеся применяют подход 走 一步 看 一步 (прямой перевод как: «Ходить один шаг, смотреть один шаг») к решению этих вопросов.
Хотя каждый вопрос уникален, на самом деле существует несколько «практических правил», которым ученики могут следовать, чтобы не заблудиться.Здесь я приведу несколько ценных советов, которые помогут студентам справиться с испытанием Trigo.
Совет 1) Всегда начинайте с более сложной стороны
Чтобы доказать тригонометрическую идентичность, мы всегда начинаем либо с левой стороны (LHS), либо с правой стороны (RHS) и применяем идентификаторы шаг за шагом, пока мы достигаем другой стороны. Однако умные ученики всегда начинают с более сложной стороны. Это потому, что намного проще исключить термины, чтобы сделать сложную функцию простой, чем найти способы ввести термины, чтобы сделать простую функцию сложной.
Пример Q1) Докажите идентичность tan⁴x = sec²x (tan²x-1) +1
Подход: было бы разумно начать доказывать это с правой стороны (RHS), поскольку это более сложно.
Совет 2) Выразите все в виде синуса и косинуса
Для обеих сторон уравнения выразите все tan, cosec, sec и cot через sin и cos. Это сделано для стандартизации обеих сторон тригонометрического тождества, чтобы было легче сравнивать одну сторону с другой.
Совет 3) Объедините члены в одну дробь
Когда есть 2 члена на одной стороне и 1 член на другой стороне, объедините сторону с 2 членами в 1 дробь, сделав их знаменатели одинаковыми.
Совет 4) Используйте тождества Пифагора для преобразования между sin²x и cos²x
Обратите особое внимание на добавление элементов тригонометрии в квадрате. При необходимости примените тождества Пифагора. Особенно sin²x + cos²x = 1, поскольку все остальные тригонометрические члены были преобразованы в синус и косинус.Этот идентификатор можно использовать для преобразования в и наоборот. Его также можно использовать для удаления обоих, превратив его в 1.
Совет 5) Знайте, когда применять формулу двойного угла (DAF)
Обратите внимание на каждый тригонометрический термин в вопросе. Существуют ли термины с углами, которые в 2 раза больше другого? Если есть, будьте готовы использовать DAF, чтобы преобразовать их под таким же углом. Например, если вы видите sinθ и cot (θ / 2) в одном и том же вопросе, вы должны использовать DAF, поскольку θ в 2 раза больше (θ / 2).
Совет 6) Знайте, когда применять формулу сложения (AF)
Соблюдайте углы в тригонометрических функциях. Существуют ли суммирования двух разных членов в одном и том же тригонометрическом члене? Если да, примените формулу сложения (AF).
Совет 7) Старый добрый Expand / Factorize / Simplify / Cancel
Многие студенты придерживаются ложного убеждения, что каждый отдельный вопрос для доказательства тригонометрии требует использования тригонометрических тождеств из таблицы формул.Всякий раз, когда они застревают, они прибегают к тому, чтобы слепо смотреть на формулу и молиться, чтобы ответ волшебным образом «выпрыгнул» на них. Чаще всего чуда не бывает. Это связано с тем, что большинство подтверждающих вопросов в основном вращаются вокруг старого доброго расширения, факторизации, упрощения и отмены подобных терминов. Фактически, некоторые проверочные вопросы даже не требуют от ученика использования каких-либо правил тригонометрии.
Кроме того, всегда ищите возможности применить квадратичные тождества, которые вы освоили во Вторичной школе 2:
a²-b² = (a + b) (a-b) (a ± b) ² = a² + b² ± 2ab
Совет 8) Сделайте один шаг, следите за одним шагом.
Проверка функций тригонометрии — это искусство. Часто есть несколько способов найти ответ. Естественно, одни методы более элегантны и кратки, а другие грубы, массивны и уродливы. Однако важно отметить, что какой бы путь мы ни выбрали, пока мы можем добраться до конечного пункта назначения, мы получим оценки.
Некоторые студенты долго раздумывали над вопросом и пытались разработать все решение в своем мозговом процессоре Pentium 9999.Я аплодирую им за их героические попытки. К сожалению, у большинства из них заканчивается оперативная память, и они отключаются до того, как вопрос будет решен. С другой стороны, есть «пауки канчеонг», которые сразу же берут свои ручки и, не задумываясь, начинают записывать случайные шаги. Эти студенты в конечном итоге будут тратить время впустую, направляясь в никуда, и им придется перезапускать несколько раз.
Самые опытные студенты будут балансировать между обоими. Они потратили некоторое время на то, чтобы сориентироваться и отважно сделать свой первый шаг.После каждых одного или двух шагов они повторно анализировали свою близость к конечному пункту назначения, прежде чем принимать решение о следующем шаге.
Совет 9) В отчаянии… притворись!
Заявление об ограничении ответственности: используйте эту тактику только в том случае, если вы застряли на полпути во время процесса тригопроверки на экзамене (с тикающими часами), и вы не хотите подвергать риску остальную часть работы. Поскольку вы застряли на полпути, просто ответьте на вопрос, сделав вид, что вы подтвердили личность.С вашего текущего шага перейдите прямо к последнему шагу и затем напишите (= RHS (Проверено)). После экзамена не забудьте посетить ближайший храм / церковь / мечеть, чтобы усердно молиться, чтобы маркер был либо слепым, либо достаточно сострадательным, чтобы дать вам преимущество сомнения и присвоить вам оценки.
* Примечание: эта работа на самом деле неверна, потому что между вторым и последним шагом есть несколько пропущенных шагов. Тем не менее, эта работа показывает, что, когда вы застряли и отчаялись во время экзамена на уровень O, вам все равно следует «притвориться», чтобы доказать вопрос, записав последний шаг вниз.
Для полного решения этого вопроса прокрутите вниз.
Совет 10) Практика! Упражняться! Упражняться!
Доказательство тригонометрической функции становится простым делом после того, как вы ответили на огромное количество вопросов и столкнулись с множеством различных вопросов. Не существует жесткого и быстрого правила для обработки вопросов о тригонометрии уровня O, поскольку каждый вопрос подобен головоломке. Но как только вы уже решили головоломку, вам будет легче решить ту же головоломку снова.
Совет 11) Не пытайтесь доказывать вопрос с надписью «Решите»!
После отработки большого количества контрольных вопросов у некоторых студентов появляется роботизированная тенденция доказывать LHS = RHS всякий раз, когда они видят уравнение с тригонометрическими функциями.




 \ tan \ theta + \ cot \ theta = \ frac {2} {\ sin 2 \ theta}. tanθ + cotθ = sin2θ2.
\ tan \ theta + \ cot \ theta = \ frac {2} {\ sin 2 \ theta}. tanθ + cotθ = sin2θ2. □ LHS = \ frac {1} {\ sin \ theta \ cos \ theta} = RHS. \ _ \ Square LHS = sinθcosθ1 = RHS. □
□ LHS = \ frac {1} {\ sin \ theta \ cos \ theta} = RHS. \ _ \ Square LHS = sinθcosθ1 = RHS. □ \ frac {\ sin (A + B) + \ sin (A — B)} {\ sin (A + B) — \ sin (A — B)} = \ frac {\ tan A} {\ tan B}. sin (A + B) −sin (A − B) sin (A + B) + sin (A − B) = tanBtanA.
\ frac {\ sin (A + B) + \ sin (A — B)} {\ sin (A + B) — \ sin (A — B)} = \ frac {\ tan A} {\ tan B}. sin (A + B) −sin (A − B) sin (A + B) + sin (A − B) = tanBtanA. RHS = cosBsinB cosAsinA = cosAsinBsinAcosB.
RHS = cosBsinB cosAsinA = cosAsinBsinAcosB. \ Frac {\ sin (AB)} {\ sin (A + B)} = \ frac {\ sin A \ cos B- \ cos A \ sin B} {\ sin A \ cos B + \ cos A \ sin B} .sin (A + B) sin (A − B ) = SinAcosB + cosAsinBsinAcosB − cosAsinB.
\ Frac {\ sin (AB)} {\ sin (A + B)} = \ frac {\ sin A \ cos B- \ cos A \ sin B} {\ sin A \ cos B + \ cos A \ sin B} .sin (A + B) sin (A − B ) = SinAcosB + cosAsinBsinAcosB − cosAsinB. Просто попробуйте преобразовать касательные в синусы и косинусы, используя формулу tan = sinθcosθ \ tan = \ frac {\ sin \ theta} {\ cos \ theta} tan = cosθsinθ, и решите задачу наоборот. направление первого решения, как показано ниже:
Просто попробуйте преобразовать касательные в синусы и косинусы, используя формулу tan = sinθcosθ \ tan = \ frac {\ sin \ theta} {\ cos \ theta} tan = cosθsinθ, и решите задачу наоборот. направление первого решения, как показано ниже:
 Например, если мы положим \ (x = \ dfrac {\ pi} {2} \), то
Например, если мы положим \ (x = \ dfrac {\ pi} {2} \), то 2x = 1`)
2x = 1`)

 . . . . . (1)
. . . . . (1)
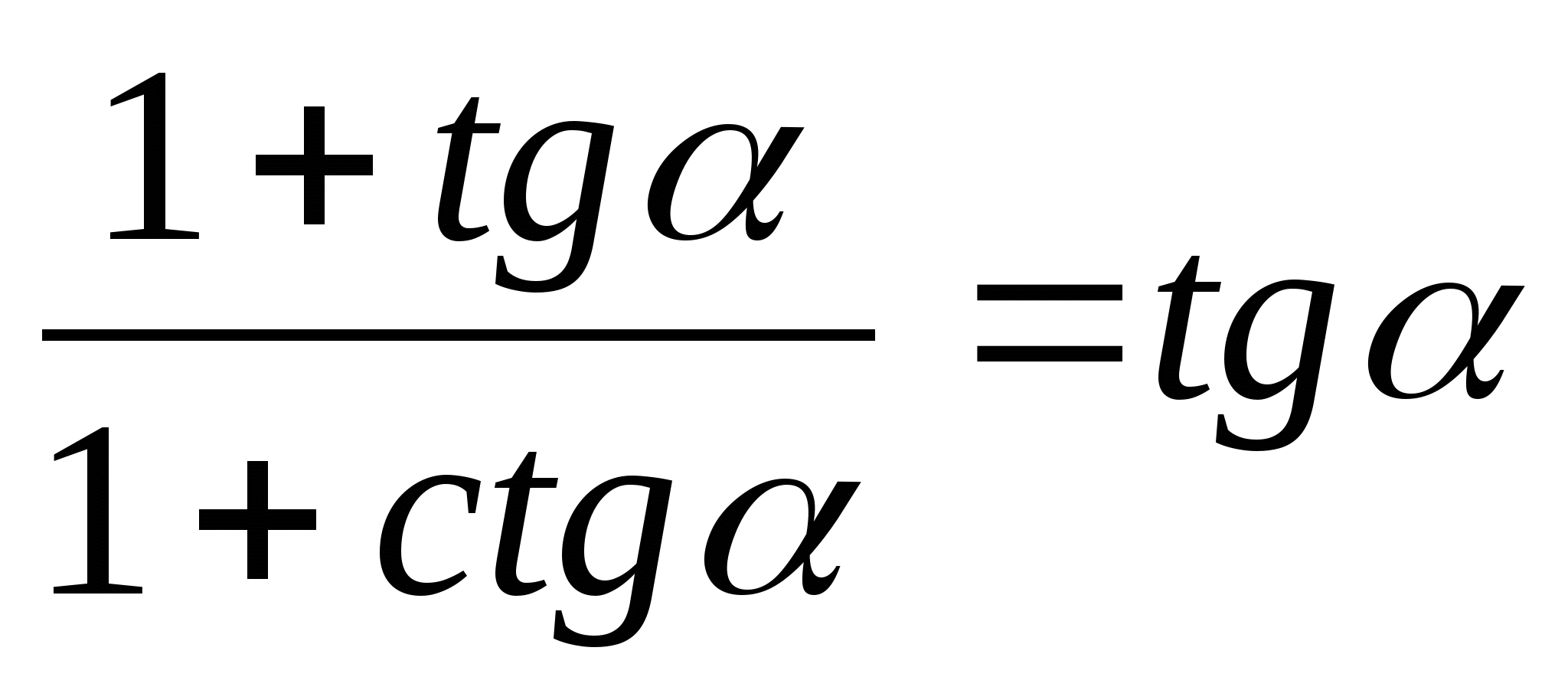
 Д.) не обязательно используется. Это потому, что нам не обязательно это делать (ничего не решая). В конце концов, мы всего лишь пытаемся доказать, что обе части уравнения эквивалентны.
Д.) не обязательно используется. Это потому, что нам не обязательно это делать (ничего не решая). В конце концов, мы всего лишь пытаемся доказать, что обе части уравнения эквивалентны.