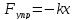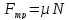Новости | Сила в Движении

Статья 35 Конституции РФ предусматривает, что: Право частной собственности охраняется законом. Каждый вправе иметь имущество в собственности, владеть, пользоваться и распоряжаться им как единолично, так и совместно с другими лицами. Никто не может быть лишен своего имущества иначе как по решению суда… 

Читать далее →

Рубрика: Мероприятия, Новости | Метки: акция протеста, екатеринбург, митинг, митинг на уралмаше, нет сносу домов, протест, строительство, частная собственность |

В связи с полным отсутствием строительства, имитации деятельности, постоянного срыва сроков сдачи готовых корпусов, нарушения всех обязательств — утром 16 ноября дольщики ЖК «Царицыно» пришли к недостроенным корпусам своих жилищных комплексов по адресу город Москва, улица 6-ая Радиальная, вл.7. Так началась акция обманутых дольщиков крупнейшей на сегодня проблемной площадки России — КРУГ-3 

Читать далее →

Рубрика: Новости, Фотогалерея | Метки: банкротство застройщика, голодовка, долевое строительство, ЖК «Царицыно», обманутые дольщики, сила в движении, царицинский круг | В очередной раз констатируем, что ВСЕ ПЛАНЫ ПО СТРОИТЕЛЬСТВУ И ВВОДУ В ЭКСПЛУАТАЦИЮ СОРВАНЫ. Сорваны при постоянных заявлениях о беспроблемном финансировании, достаточном количестве рабочих, бесперебойном снабжении стройматериалами 

Читать далее →

Рубрика: Новости, Фотогалерея | Метки: #ДольщикиЦарицыно #ОбманутыеДольщики #ЖкЦарицыно #ДостройтежкЦарицыно #МосОтделСтрой #Москомстройинвест #МКСИ #Мосгорстройнадзор #ПравительствоМосквы #Собянин, банкротство застройщика, долевое строительство, ЖК «Царицыно», квартира в новостройке, сила в движении, царицынские вторники |

Несколько сотен обманутых дольщиков ЖК Царицыно 12 октября 2019 г. вышли к мэрии предъявить свои требования по достройке, сдаче и передаче их законно купленного жилья. Выразили протест невыполненным обещаниям в стройке и сдаче их домов. Оставление людей без жилья — это национальная, социальная и экономическая угроза, а значит и порождающая политические настроения недоверия власти. Читать далее →

Рубрика: Мероприятия, Новости | Метки: #ДольщикиЦарицыно #ОбманутыеДольщики #ЖкЦарицыно #ДостройтежкЦарицыно #МосОтделСтрой #Москомстройинвест #МКСИ #Мосгорстройнадзор #ПравительствоМосквы #Собянин, домашний арест, ООН, Пинкевич, сила в движении |

Для того чтобы глупый  ослик шел вперед, у него перед носом вешают морковку. Ослик идет, а морковка все дальше. И вроде вот она, еще чуть-чуть и твоя! Старый хороший способ занять делом упрямое животное и получить попутно пользу… Читать далее →

Рубрика: Мероприятия, Новости | Метки: «За свободные выборы», долевое строительство, ЖК «Марьино град», ЖК «Царицыно», квартира в новостройке, митинг, новостройки Москвы, обманутые дольщики, протест |

xn--80aeahgfjecay5a6b.xn--p1ai

сила движения — это… Что такое сила движения?



сила движения

1) General subject: impetus

2) Patents: yang sign

Универсальный русско-английский словарь. Академик.ру. 2011.

• сила движений
• сила действия

Смотреть что такое «сила движения» в других словарях:

• Сила инерции — (также инерционная сила)  термин, широко применяемый в различных значениях в точных науках, а также, как метафора, в философии, истории, публицистике и художественной литературе. В точных науках сила инерции обычно представляет собой понятие …   Википедия

• ДВИЖЕНИЯ — ДВИЖЕНИЯ. Содержание: Геометрия Д………………..452 Кинематика Д……………….456 Динамика Д………………..461 Двигательные механизмы…………465 Методы изучения Д. человека………471 Патология Д. человека …………. 474… …   Большая медицинская энциклопедия

• СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

• СИЛА — в физическом смысле способность изменять форму материальных масс, вызывать их движение, менять направление и скорость движения или приводить тело в состояние покоя. «Живая» сила (редко употребляемое теперь выражение), или действующая сила, – сила …   Философская энциклопедия

• СИЛА — силы, ж. 1. Способность живых существ производить физические действие, энергия, порождаемая способностью управлять движениями мышц. «Какой то муравей был силы непомерной…» Крылов. «Пригожеством, ростом и силой ты ровни в селе не имел.» Некрасов.… …   Толковый словарь Ушакова

• Сила трения скольжения — Сила трения скольжения  силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение… …   Википедия

• Сила вечно непрерывного СЕЙЧАС — Сила вечно непрерывного СЕЙЧАС: Путь движения мысли к энергии сознания (The Power of NOW)  это книга, которую написал Экхарт Толле является своего рода духовным путеводителем и способствует ускорению процесса трансформации общечеловеческого… …   Википедия

• СИЛА ИНЕРЦИИ — векторная величина, численно равная произведению массы m материальной точки на её ускорение w и направленная противоположно ускорению. При криволинейном движении С. и. можно разложить на касательную, или тангенциальную составляющую Jt,… …   Физическая энциклопедия

• СИЛА КОРИОЛИСА — кориолисова сила [по имени французкого ученого Г. Кориолиса (1792 1843)], дополнительная сила инерции, действующая на относительное движение тела. Эффект, учитываемый силой кориолиса на Земле, обусловлен ее суточным вращением и заключается в том …   Экологический словарь

• Сила тяги локомотива — сила, реализуемая локомотивом и служащая для передвижения поезда. Собственно различают две силы тяги локомотива касательную и на сцепном устройстве (автосцепка или винтовая упряжь). Касательная сила тяги образуется в месте контакта движущих колёс …   Википедия

• СИЛА — в механике, мера механич. действия на данное материальное тело других тел. Это действие вызывает изменение скоростей точек тела или его деформацию и может иметь место как при непосредств. контакте (давление прижатых друг к другу тел, трение), так …   Физическая энциклопедия

Книги

• Параметрическое уравнение движения Ряполова. Вывод, решение и применение, Ряполов Лев Дмитриевич. Параметрическое уравнение Ряполова и уравнения, полученные при его решении, аналогично уравнениям равномерно-переменного движения, устанавливают связь между параметрами движения для случая,… Подробнее  Купить за 483 руб
• Сила и мистика пирамид, Евгения Востокова. Автор этой книги, за короткое время ставшей мировым бестселлером, основываясь на огромном количестве фактического материала, собранного в течение десятилетий и тщательно проанализированного,… Подробнее  Купить за 450 руб
• Сила мысли или магнетизм личности, Уильям Аткинсон. Удача и успех в жизни, карьера и любовь зависят от нашей способности привлекать к себе других людей, убеждать их, влиять на них и руководить ими. Такая способность называется магнетизмом… Подробнее  Купить за 189 руб аудиокнига

Другие книги по запросу «сила движения» >>

universal_ru_en.academic.ru

Лекция № 6. Биодинамика двигательных действий Силы в движениях человека

Сила — это мера механического воздействия одного тела на другое. Численно она определяется произведением массы тела на его ускорение, вызванное приложением этой силы.

F = m х а

Сила, действующая статически вызывает деформацию тела.

Сила, действующая динамически (действие), вызывает ускорение и деформацию, а также противодействие ускоряемого тела — силу инерции. Зная массу ускоряемого тела и его ускорение под действием динамической силы, определяют ее величину и направление.

Относительно направления скорости движущегося тела, различают:

—движущие силы, которые совпадают с направлением скорости (попутные) или образуют с ним острый угол и могут совершать положительную работу;

—тормозящие силы, которые направлены противоположно направлению скорости (встречные) или образуют с ним тупой угол и могут совершать отрицательную работу;

—отклоняющие силы, перпендикулярные к направлению скорости и увеличивающие кривизну траектории;

—возвращающие силы, также перпендикулярные к направлению движения, но уменьшающие .кривизну траектории.

От соотношения сил, приложенных к каждому звену тела, зависит и результат их действия.

От соотношения отклоняющих и возвращающих сил зависит действие поворачивающей силы, изменяющей кривизну траектории. С уменьшением поворачивающей силы траектория выпрямляется, приближаясь к прямолинейной.

Силы, приложенные к звену в месте контакта с соседним, — суставные силы. Силы, приложенные к звену тела на плече силы, создают относительно оси сустава суставные моменты. Действие их в основном такое же, как и самих сил: ускоряющее, замедляющее, поворачивающее

.

Именно действие суставных сил и суставных моментов сил и вызывает изменение положений тела и изменение движений.

Скорости звеньев изменяются в результате импульсов сил и моментов сил. Множество сил обусловливает для каждого звена в сочленении результирующий импульс момента сил. Каждое звено изменяет скорость вращения вокруг оси в суставе вследствие именно к нему приложенных сил. Причины движений для каждого звена в биокинематических цепях разные.

Для расчета действия сил тело человека рассматривается по редуцированной (сокращенной) схеме (14 или 16 звеньев вместо более 200) и др. Считается, что усилия передаются от одного звена к другому без потерь, в то время как полнота передачи определяется суставной жесткостью, зависящей от мышечных суставных моментов, от напряженности мышц.

Все силы, которые приложены к телу человека, делят на внешние и внутренние относительно него.

Внутренние силы возникают при взаимодействии частей тела человека друг с другом. Сами по себе они не могут изменить движения ЦМ, не могут привести все части системы в одинаковые движения. Но только внутренними силами тяги мышц человек управляет непосредственно, вызывая движения звеньев в суставах.

Внешние силы вызваны действием внешних для человека тел (опора, снаряды, другие люди, среда и т. п.). Только при их наличии возможно изменение траектории и скорости ЦМ; без них движение ЦМ не изменяется. Все силы, которые действуют извне на тело человека, возникая при контакте с соответствующими внешними телами (и средой в том числе), — это контактные силы. Лишь силы тяжести могут действовать на тело человека без контакта, на расстоянии (дистантные).

Внешние силы изменяют движения человека, вызывают ускорения — тогда-то и возникают силы инерции. Сила инерции внешнего тела — это мера действия на тело человека со стороны внешнего тела, ускоряемого человеком; она равна массе ускоряемого тела, умноженной на его ускорение:

Сила инерции внешнего тела при его ускорении человеком направлена в сторону, противоположную ускорению. Она приложена в месте контакта с ускоряемым телом, в рабочей точке тела человека.

Ускорение может быть положительным; человек увеличивает скорость, например, ядра, толкая его от себя. Тогда сила инерции ядра воспринимается как сопротивление.

Ускорение может быть отрицательным; человек уменьшает скорость, например, набивного мяча, когда ловит его движением «на себя». Тогда сила инерции мяча воспринимается как его напор.

Если же ускорение нормальное (центростремительное), человек удерживает, например, диск при его разгоне по криволинейной траектории, тогда центробежная сила инерции диска приложена к руке метателя и воспринимается как тяга — «стремление» диска вырваться из руки по радиусу.

По закону всемирного тяготения все тела на Земле испытывают силу ее притяжения.

Сила тяжести тела —_это мера его притяжения к Земле. F=mG

На каждое звено и на все тело человека действуют силы тяжести как внешние силы, вызванные притяжением и вращением Земли.

При воздействии головы на шейные позвонки взаимодействуют голова и позвоночный столб. Таким образом, вес головы относительно всего тела человека — сила внутренняя, относительно же позвоночного столба — внешняя. Вес, например, штанги, удерживаемой человеком, для него, конечно, внешняя сила.

При движении тела с ускорением, направленным по вертикали, возникает вертикальная сила инерции. Она направлена в сторону, противоположную ускорению. Если сила инерции направлена вниз, то она складывается со статическим весом; сила давления на опору при этом увеличивается. Если же сила инерции направлена вверх, то она вычитается из статического веса; сила давления на опору уменьшается. В обоих случаях измененный вес называют динамическим, он больше или меньше статического. Динамический вес штанги в руках спортсмена действует на него извне (внешняя сила). Динамический вес туловища при выпрыгивании вверх действует на ноги внутри тела (внутренняя сила относительно всего тела и внешняя — относительно ног).

Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору, направлена в противоположную сторону и приложена к этому телу.

Обычно человек, находясь на горизонтальной опоре, испытывает противодействие своему весу. В этом случае опорная реакция, как и вес тела, направлена перпендикулярно к опоре. Это нормальная (или идеальная) реакция опоры. Если поверхность не плоская, то опорная реакция перпендикулярна к плоскости, касательной к точке опоры.

Сила трения — это мера противодействия движущемуся телу, направленного по касательной к соприкасающимся поверхностям. Сила трения считается равной произведению нормального давления на коэффициент трения:

Предел, до которого может увеличиваться статическая сила трения, называется предельной силой трения скольжения покоя.

Механизм трения скольжения объясняют зацеплением неровностей поверхностей скользящих тел друг за друга (механическая теория), а также молекулярным сцеплением, когда гладкие поверхности обеспечивают плотный контакт тел (молекулярная теория). При смазке неровности поверхности «сглаживаются».

Второй вид трения, отличающийся от трения скольжения, проявляется при качении, когда точки соприкосновения тел все время сменяются (точки покрышки велосипеда и места его опоры на дорожке). Механизм трения качения объясняют деформацией соприкасающихся тел. Колесо как бы вдавливается в опору, образуя ямку, через край которой колесу все время приходится перекатываться.

Третий вид трения проявляется, когда между трущимися поверхностями имеется неподвижная точка. Это трение верчения — движение происходит вокруг этой точки. Так, стопа при отталкивании от опоры, если на подошве обуви нет шипов, вращается относительно грунта. У метателя молота на подошве обуви имеется один шип, верчение происходит при повороте вокруг шипа.

Силы трения, направленные навстречу движению, тормозят его. Они вызывают отрицательное ускорение, совершают отрицательную работу. Силы трения, направленные одинаково с движением, не создают положительного ускорения, не совершают положительной работы, а только не дают точке контакта движущегося тела «проскальзывать» назад.

Силы внутренние относительно тела человека возникают вследствие взаимодействия частей биомеханической системы тела. Они проявляются, в частности, как силы притягивания и отталкивания внутри тела. В абсолютно твердом теле такие силы взаимно уравновешены, деформации и напряжения не возникают. В теле человека внутренние силы могут действовать статически, вызывая только напряжения в деформированных тканях, и динамически, вызывая движение звеньев и изменяя позу.

Различают внутренние силы:

1.активного действия (мышечная работа). Силы мышечной тяги, приложенные к костям скелета, служат источниками энергии движения, сохраняют необходимые позы, управляют движениями, изменяют взаимодействие тела человека с окружающими физическими объектами (среда, опора, снаряды и другие люди).

2.пассивные механические силы (пассивного взаимодействия). Силы пассивного взаимодействия в отличие от сил мышечной тяги не вызваны непосредственно физиологической активностью, биологическими процессами, хотя в некоторой степени и зависят от них. При наличии опоры звенья тела человека всегда своим весом действуют на удерживающие их соседние звенья. При ускорениях звеньев к статическому весу прибавляются (или вычитаются из него) силы инерции звеньев. Как противодействие статическому и динамическому весу имеются соответствующие реакции опоры. Вследствие упругих деформаций возникают упругие силы, преимущественно в мягких тканях. Наконец, имеются и силы трения, обусловленные взаимным смещением органов и тканей в местах их контакта, в суставах, между мышцами, внутри мышц и т. п.

Силы веса, статических реакций опоры и трения невелики по сравнению с силами мышечной тяги, хотя статические моменты (например, в спортивной гимнастике, особенно на снарядах) и могут быть значительными. Зато силы инерции и упругой деформации могут быть очень большими.

Движения звеньев происходят с ускорениями центростремительными (неизбежны при суставных движениях) и тангенциальными (при разгоне звена — положительные, при торможении — отрицательные). Поэтому силы инерции имеются при движениях всегда. Это самая многочисленная группа сил внутреннего пассивного взаимодействия, ведущая среди реактивных сил.

Поскольку в любом движении, тормозя звено и останавливая его, растягиваются мышцы-антагонисты, то всегда возникают упругие силы (деформация соединительнотканных и мышечных элементов). При больших ускорениях инерционные и упругие силы особенно велики. При так называемой «упругой отдаче» роль этих двух групп сил становится ведущей в движениях.

Таким образом, внутренние силы пассивного (в биологическом смысле) взаимодействия играют роль не только связей, ограничивающих движения; в определенных условиях они используются как движущие силы, повышающие эффективность мышечной работы.

Роль сил в движениях человека

В механике изучаются законы действия механических сил независимо от их источников, их происхождения. В биомеханике же существенно, каковы источники сил и, следовательно, какова «цена» используемой силы для организма человека. Все силы, приложенные к его двигательному аппарату, составляют систему сил внешних и внутренних. Система внешних сил проявляется чаще как силы сопротивления. Для преодоления сопротивления затрачивается энергия движения и напряжения мышц человека. Различают рабочие и вредные сопротивления. Преодоление рабочих сопротивлений нередко составляет главную задачу движений человека (например, в преодолении веса штанги и заключается цель движений со штангой). Вредные сопротивления поглощают положительную работу; они, в принципе, неустранимы (например, силы трения лыж по снегу).

Внешние силы используются человеком в его движениях и как движущие. Для совершения необходимой работы, для преодоления человеком сил сопротивления могут использоваться вес, упругие силы, инерционные и др. Внешние силы являются в этом случае «даровыми» источниками энергии, поскольку человек расходует меньше внутренних запасов энергии мышц.

Человек преодолевает силы сопротивления мышечными силами и соответствующими внешними силами и совершает как бы две части работы: а) работу, направленную на преодоление всех сопротивлений (рабочих и вредных), и б) работу, направленную на сообщение ускорений своему телу и перемещаемым внешним объектам.

В биомеханике сила действия человека¹ — это сила воздействия на внешнее физическое окружение, передаваемого через рабочие точки тела. Рабочие точки, соприкасаясь с внешними телами, передают движение (количество движения, а также кинетический момент) и энергию (поступательного и вращательного движения) внешним телам.

Тормозящими силами, входящими в сопротивление, могут быть все внешние и внутренние силы, в том числе и мышечные. Какие из них будут играть роль вредных сопротивлений, зависит от условий конкретного упражнения. Только реактивные силы (силы реакции опоры и трения) не могут быть движущими силами; они всегда остаются сопротивлениями (как вредными, так и рабочими).

Все силы независимо от их источника действуют как механические силы, изменяя механическое движение. В этом смысле они находятся в единстве, как материальные силы: можно производить (при соблюдении соответствующих условий) их сложение, разложение, приведение и другие операции.

Движения человека представляют собой результат совместного действия внешних и внутренних сил. Внешние силы, выражающие воздействие внешней среды, обусловливают многие особенности движений. Внутренние силы, непосредственно управляемые человеком, обеспечивают правильное выполнение заданных движений.

studfile.net

Сила движения. Движение лучится повсюду

Сила движения

Я наступила на тонкий лед, он хрустнул и начал расползаться по ниточкам. Достаточно было мгновения, чтобы ощутить силу невероятного движения. Лед двигался, как и река, которая полна неуловимых ритмов, я скольжу по льду, словно парю в воздухе. Лед не может вечно сковывать реку, он лишь нерешительно хватается за ее волны. Лед это моя проверка, если могу идти по нему без страха, значит, я верю в силу движения. Идти по льду это значит не сомневаться. Что значит не сомневаться? Не надо усложнять, просто двигаться и не сомневаться.  Несомненно, всё находится в непрестанном движении.

Утренний свет плавно струится по комнате, не оставляя сомнений в новом дне. Рисунки на окне на первый взгляд застыли в своей морозной игривости. Проходит пару часов и Солнце стирает их, оставляя лишь ручейки и зигзаги. Хочу запечатлеть эти линии, но и они пропадают бесследно. Смотрю на горы, они потрясающе устойчивы, они прекрасны в своих неподвижных позах. Но, приблизившись к горе, понимаю, насколько она подвижна, ее камни неустойчивы, ее деревья рождаются, живут и умирают, ее звери и птицы снуют по горе непрестанно, верх, вниз, как кровь в новорожденном существе. В недрах горы живет огонь.

Фото: Жанна Иродова

Посмотрите, как движется человек. Он передвигает ногами, перемещает вес по всему телу, что бы идти или танцевать. Человек изменчивее горы. Это просто взрыв перемен. Кажется, что Природа создала человека, чтобы рассказать о непрестанном движении. В человеке движется абсолютно всё и вся, внутри и снаружи, это невероятный сгусток подвижности.

Движется само движение! Мы привыкли к этому, мы просто так живем. И никаких чудес. Движение это сила, невидимая сила, она настолько невидима, что заставляет даже поверить в застывшие формы, но ах, это визуальный обман. Так я говорю себе и тут же забываю при виде нового застывания. Движение лучится повсюду, уверенно убеждаю себя, и в теле постоянно движутся потоки, они подобны реке подо льдом. Порой смотрю на свою жизнь и расстраиваюсь, это означает,что попадаю в плен неподвижности.

Фото: Закир Умаров

Картины на стенах дают чувство устойчивости, наверное, поэтому мой дом полон картин и фотографий в рамах.  Я стараюсь окружить себя стабильностью, а поток жизни лишь смеется над этим, сметая очередные построения с легкостью виртуозного скрипача. Хватаюсь в панике за ускользающие образы, жду уверений в постоянстве, мечтаю о неразрушимом. Но всё, совершенно всё, что могу видеть, чувствовать, всё не имеет постоянной величины. Боюсь изменчивости и жажду ее.

Я не вижу тебя, движение, появись, напои меня своими просветами! Скучаю по тебе и опасаюсь тебя.
Движение подкрадывается как весна. Просыпаюсь утром и не могу понять, что изменилось, оглядываюсь по сторонам, хватаюсь за привычное, но его уже нет. Движение было здесь, но опять его не увидела.  Восхищаюсь игрой жизненных циклов, с придыханием говорю о силе времени, но не осознаю, не осознаю постоянного движения.

Фото: Алена Шевцова

Я думаю о нем, да, думаю. Я чувствую его, да, чувствую. Так чего же не хватает? Мне не хватает движения изнутри. Среди смены дня и ночи, среди ритмов и полос к которым привыкла, я не могу ощутить движение. Оно ускользает, но вижу его следы. Следы приводят к себе самой. Движение все время оставляет следы, таково его свойство.

Как, как это происходит, как растет трава, как наступает ночь, как меняется ракурс восприятия, в какой момент это происходит? Нет такого момента, это непрестанно происходит. В этом сила движения. Оно не останавливается,  оно не подвержено переменам, оно и есть перемены. Остановить его невозможно, но можно войти с ним в ритм.  Не надо усложнять, просто двигаться и не сомневаться.

Фото: Закир Умаров

О движение без сомнения еще здесь

На превью фото: Денис Соломахин 

Радости движения! 

Марианна Яцышина

altayazia.ru

6. Динамика материальной точки. Сила и движение. Инерциальные системы отсчета и первый закон Ньютона.

Динамика изучает движение тела в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения.

В основе классической (ньютоновской) механики лежат три закона динамики, сформулированные Ньютоном в 1687 г. Эти законы возникли как результат обобщения большого количества опытных фактов.

Инерциальные системы отсчета и первый закон Ньютона:

Формулировка первого закона Ньютона такова: всякое тело находится в состоянии покоя или равномерного и прямо­линейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба названных состояния отличаются тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело других тел не вызовет ее изменения.

Первый закон Ньютона выполняется не во всякой системе отсчета. Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением. Следовательно, первый закон Ньютона не может выполняться одновременно в обеих системах.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной, поэтому первый закон называют иногда законом инерции. Система отсчета, в которой первый закон Ньютона не выполняется, называется неинерциальной системой отсчета. Инерциальных систем существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

Опытным путем установлено, что система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, является инерциальной. Эта система называется гелиоцентрической (гелиос — по-гречески солнце). Любая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, будет инерциальной.

Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. По этим причинам система отсчета, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической системы отсчета и не является инерциальной. Однако ускорение такой системы настолько мало, что в большом числе случаев ее можно считать практически инерциальной. Но иногда неинерциальность системы отсчета, связанной с Землей, оказывает существенное влияние на характер рассматриваемых относительно нее механических явлений.

7. Фундаментальные взаимодействия. Силы различной природы (упругие, гравитационные, трения), второй закон Ньютона. Третий закон Ньютона.

Фундаментальные взаимодействия — различные, не сводящиеся друг к другу типы взаимодействия элементарных частиц и составленных из них тел. На сегодня достоверно известно существование четырех фундаментальных взаимодействий: гравитационного, электромагнитного, сильного и слабого взаимодействий.

Гравитация (всемирное тяготение, тяготение) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела.

Электромагнитное взаимодействие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядом.

Сильное взаимодействие (цветовое взаимодействие, ядерное взаимодействие) — одно из четырёх фундаментальных взаимодействий в физике. Сильное взаимодействие действует в масштабах атомных ядер и меньше, отвечая за притяжение между нуклонами в ядрах и между кварками в адронах.

Слабое взаимодействие, или слабое ядерное взаимодействие — одно из четырех фундаментальных взаимодействий в природе. Оно ответственно, в частности, за бета-распад ядра. Это взаимодействие называется слабым, поскольку два других взаимодействия, значимые для ядерной физики (сильное и электромагнитное), характеризуются значительно большей интенсивностью.

Название силы	Природа взаимодействия	Формула	Зависимость силы от расстояния или относительной скорости	Зависит ли сила от массы взаимодействующих тел	Как направлена сила
Сила тяготения	Гравитационная		Явл функцией расстояния м/у взаимод телами	Прямо пропорц массам взаимод тел	Вдоль прямой, соед взаимод тела
Сила упругости	Электромагнитная		Явл функцией расстояния (зав от деформации)	Не зависит	Противопол направл перемещ частиц при деформ
Сила трения: А) сухого Б) жидкого	электромагнитная		Явл функцией скорости относит-ого движения	Не зависит	Противопол направл вектора скорости

Второй закон Ньютона:

Второй закон Ньютона описывает движение частицы, вызванное влиянием окружающих тел, и устанавливает связь между ускорением частицы, ее массой и силой, с которой на нее действуют эти тела:

Если на частицу с массой т окружающие тела действуют с силой 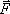, то эта частица приобретает такое ускорение, что произведение ее массы на ускорение будет равно действующей силе.

Математически второй закон Ньютона записывается в виде: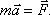

На основе этого закона устанавливается единица силы — 1 Н (ньютон). 1 Н — это сила, с которой нужно действовать на тело массой 1 кг, чтобы сообщить ему ускорение 1 м/с².

Если сила 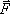, с которой тела действуют на данную частицу, известна, то записанное для этой частицы уравнение второго закона Ньютона называют ее уравнением движения.

Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на тело силе:

это уравнение называется уравнением движения тела.

Второй закон Ньютона часто называют основным законом динамики, так как именно в нем находит наиболее полное математическое выражение принцип причинности и именно он, наконец, позволяет решить основную задачу механики. Для этого нужно выяснить, какие из окружающих частицу тел оказывают на нее существенное действие, и, выразив каждое из этих действий в виде соответствующей силы, следует составить уравнение движения данной частицы. Из уравнения движения (при известной массе) находится ускорение частицы. Зная же ускорение можно определить ее скорость, а после скорости — и положение данной частицы в любой момент времени.

Практика показывает, что решение основной задачи механики с помощью второго закона Ньютона всегда приводит к правильным результатам. Это и является экспериментальным подтверждением справедливости второго закона Ньютона.

Масса в механике – это мера инертности тела; мера гравитационных свойств.

Третий закон Ньютона ( не вып-ся в электродинамике)

Третий закон Ньютона утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению, т.е.

Из третьего закона Ньютона вытекает, что силы возникают попарно: всякой силе, приложенной к какому-то телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу, взаимодействующему с данным.

studfile.net

Центральные силы и их поля

Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка на Рис.1). Тело при этом, как правило, рассматривается как материальная точка, а центр также считается точечным, обычно^[1] совпадая с физическим источником силы; в простейшем случае он фиксирован в пространстве.

Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.

Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой^[2]. Распределенные системы, в которых действуют центральные силы, в общем случае^[3] не могут быть представлены конечным количеством материальных точек. В случае распоеделенных систем общим подходом является разбиение их на очень большое (впределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый, которые и рассматриваются как материальные точки — между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией)) таких элементарных сил.

Kлассическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы. ^[4]

Рис.1 К определению центральной силы: частица в поле атомного ядра.(опыт Резерфорда)

• Для любой центральной силы выполняется соотношение

(где — радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы:

Силовые поля

Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения. Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.

При сохранении подобия в геометрических размерах тел и их взаимного расстояния, силы взаимного тяготения, равно как и силы электростатические (кулоновские) растут пропорционально 4-й степени абсолютных размеров рассматриваемой модели. В то же самое время в случае электрического взаимодействия, где между величиной заряда и размерами тел, несущих эти заряды, нет определённой связи, силы взаимодействия ослабляются пропорционально 2-й степени абсолютных размеров . Поэтому при сравнении этих сил в микромире доминируют Кулоновские силы, а в масштабах Вселенной — силы Всемирного тяготения.

Интенсивность силового поля

В ряде случаев в рассматриваемом силовом поле оказывается возможным определить пространственно локализованный его источник (нем. Quelle).

Одним из основных свойств рассматриваемых здесь полей является их экспериментально подтверждаемая аддитивность, иначе называемая принципом суперпозиции, заключающегося в том, что действие поля, создаваемого несколькими источниками на объект своего воздействия независимы друг от друга при любом значении их интенсивности. Это позволяет ввести в рассмотрение понятие о «точечном источнике» с чётко определённым его пространственным расположении и сформулировать понятие об суммарной интенсивности поля нескольких источников как сумму этих воздействий с учётом геометрии конкретной задачи.

Интенсивность определяется в заданной точке пространства силой, которая могла бы подействовать на единичный «пробный объект» с заданным свойством, который мог бы находиться в этой точке или же в действительности находящийся в ней. Выбор «пробного объекта» есть предмет договорённости. При необходимости источник поля и объект его воздействия могут поменяться местами.

Величина, характеризующая интенсивность центрального силового поля представляет собой вектор направленный по линии соединяющей точечный источник и заданную точку поля.

Потенциальные центральные поля

Работа центральной силы

Элементарная работа силы, в том числе и центральной силы, есть скалярная величина, исчисляемая изменением энергии при перемещении точки приложения силы (в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние  :

(5)

где есть угол между этими векторами. Поскольку , то направление отсчёта угла значения не имеет.

При перемещении на расстояние от до , весь пройденный путь можно разбить на элементарных участков. И тогда полная работа будет суммой этих элементарных работ с тем большей точностью, чем на большее количество участков будет разбита траектории, что выражается знаком интеграла, как предела этой суммы :

Рассматривая движение в Декартовой системе координат центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:

где , , суть единичные векторы (орты) для своих осей.

Потенциал поля

Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения . Иными словами, не зависит от формы пути.

Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция , в выражении полного дифференциала которой:

её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):

В этом случае функция будет называться потенциальной функцией, а поле силы -потенциальным полем. ^[5]

Но это станет возможным лишь при одновременном выполнении равенств:

Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.^[5]

Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией^[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).

Связь с потенциальной энергией естественно осуществляется через работу.

Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов ^[7] )Тогда, зафиксировав точку, находящуюся на расстоянии от центрального заряда и предоставив ему свободу, получим, что он под действием силы будет удаляться в бесконечность. При этом совершённая полем работа будет равна:

.

То же можно сказать и в случае, если поле продвинуло тело дальше и, следовательно, проделало больше работы и потому разница работ на пути между точками больше нуля.

И эти работы может быть названа с точностью до постоянной потенциалом точки : и , подразумевая под потенциалом возможность совершить работу, которая для более близкой точки выше, чем у более далёкой.

Тогда совершённая полем работа будет равна разности потенциалов , взятой со знаком «минус»

Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:

Поле как градиент потенциала

В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.

Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:

Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:

Знак минус, по обычному соглащению присутстсвующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чиcто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).

Кулоновское поле

Напряженность кулоновского поля определяется вектором , равным:

или, переходя, к скалярной форме записи:

Здесь ;  — заряд тела -источника силы; ,есть расстояние до точки, где определяется интенсивность, а константа зависит от диэлектрической постоянной среды , (для пустого пространства равная 1), в которой существует поле:

, где:

есть диэлектрическая постоянная вакуума. В таком случае для вакуума

= Vm/As в Международной системе единиц ^[8],

Кулоновские силы

Объектом действия кулоновского поля является материальное тело, несущее заряд

В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:

или, с учётом ():

или, в скалярном представлении:

Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряжённые материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.

Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)

Поле гравитации

В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» за рубежом иногда её называют напряжённостью гравитационного поля.

Или, переходя, к скалярной форме записи:

Здесь ;  — масса тела -источника гравитации; есть расстояние до точки, где определяется интенсивность, а константа есть гравитационная постоянная, равная по современным данным , ^[9]

Силы гравитации

Объектом действия поля гравитации является материальное тело,имеющее массу

В таком случае на него действует механическая сила, равная произведению массы тела на напряжённость поля. Существенно, что между массой, входящей во Второй закон Ньютона и массой того же тела, подверженного действию гравитации нет никакой разницы в величине. Тогда, с учётом ():

или, в скалярном представлении:

Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.^[10]

Потенциал поля гравитации

Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:

( 23)

Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:

^[11](24)

Движение под действием центральной силы

В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота C с различными значениями радиуса поворота на том же Рис 1.Применение представления о траектории реального трёхмерного тела смысла не имеет.

Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.

Замечание

Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (Если не принимать во внимание снос из-за сопротивления воздуха).Никаких сил, вызывающих искривление траектории здесь нет. Центростремительные силы возникают не потому, что траектория крива,но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.

Считается, что в центре силы находится источник силы которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка на Рис. Это совпадение имеет место лишь при повороте тела по дуге окружности. ^[4]

Как видно на Рис.1 единственная действующая между телами и сила может быть разложена на две составляющие: (2)

При этом есть тангенциальная сила, в зависимости от направления движения тела по своей траектории на рисунке либо тормозящая его движение, либо ускоряющая его.

есть сила, направленная по нормали к касательной к траектории в сторону мгновенного центра и потому являющаяся центростремительной силой.^[12]

Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса)следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела прямо пропорциональна величине приложенного к телу момента силы :

Однако в поле центральной силы её момент всегда равен нулю (Формула (1)).Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

. Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория, движения тела под действием центральной силы есть плоская кривая.

Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где гравитационное воздействия преоблаают и потому изучаемая система взаимодействующих сил может рассматриваться, как консервативная система , т.е. такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.^[4]

(25),где:

причём и соответствуют скоростям, создаваемым нормальной и тангенциальной составляющей действующей на тело силы на Рис.1

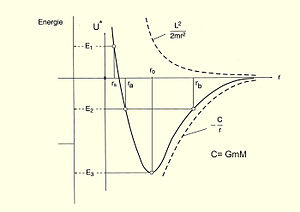Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты

Воспользовавшись определением кинетического момента: получаем для кинетической энергии тангенциального движения соотношение:

.

А для движения по нормали к траектории:

Тогда выражение для полной энергии тела будет иметь вид:

Введя в рассмотрение эффективный потенциал  :

Получаем возможость связать диапазон изменения длины радиуса -вектора траектории тела с запасённой им энергией, что представлено на рис.2 ^[13]

Так при минимальной энергии движущегося тела тело движется по круговой орбите с радиусом

Если энергия движения тела больше, скажем ,траектория тела будет представлять эллипс с малой полуосью и большой .

Наконец, при энергии тела разойдутся, сблизившись на минимальное расстояние

Примечания

1. ↑ Иногда бывает удобно — и удаётся — рассматривать как центр силы не её физический источник, а некоторую фиктивную точку. Так например при изучении движения двух точечных тел, между которыми действуют центральные силы, удобно рассматривать в качестве такого центра центр масс системы — потому что он неподвижен.
2. ↑ Имеются в виду сферически симметричные объекты (или объекты, досаточно мало отличающиеся от сферически симметричных, так чтобы можно было считать их сферически симметричными в рамках рабочего приближения).
3. ↑ По сути — почти в любом случае кроме описанных выше; даже в таком простом случае, как кулоновское взаимодействие абсолютно твердых тел несферической формы с фиксированными на них распределенными зарядами, обычно невозможно свести вычисление сил к силам между небольшим количеством материальных точек.
4. ↑ ^{1 2 3} Физический энциклопедический словарь/ Гл. ред. А.М.Прохоров. Ред.кол. Д.М.Алексеев, А.М. Бонч-Бруевич,А.С.Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
5. ↑ ^{1 2} Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
6. ↑ Поскольку сохраняться должна сумма потенциальной и кинетической энергий, в направлении действия силы (которая может разгонять в этом направлении частицу, увеличивая тем самым ее кинетическую энергию) потенциальная энергия убывает.
7. ↑ Тамм,И.Е. Основы теории электричества
8. ↑ ГОСТ 8.417-2002. Единицы величин
9. ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
10. ↑ Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука».Главная редакция физико-математической литературы.
11. ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
12. ↑ Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
13. ↑ ‘

biograf.academic.ru

Движение под действием нескольких сил: движение на плоскости | LAMPA

Шаг 5. В итоге мы имеем:

Fтяги−Fтр=maF_{тяги}-F_{тр}=maFтяги​−Fтр​=ma;

N−mg=0N-mg=0N−mg=0.

Вспомнив, что сила трения равна Fтр=μNF_{тр}=\mu NFтр​=μN, мы можем записать:

Fтяги−μN=maF_{тяги}-\mu N=maFтяги​−μN=ma;

N=mgN=mgN=mg.

Упрощая дальше, получаем:

Fтяги−μmg=maF_{тяги}-\mu mg=maFтяги​−μmg=ma;

N=mgN=mgN=mg.

Мы получили уравнение для силы тяги

Fтяги=μmg+maF_{тяги}=\mu mg+maFтяги​=μmg+ma.

Величины μ\muμ, mmm, aaa даны в условии задачи, ggg — константа. Видим, что мы уже можем спокойно найти силу тяги:

Fтяги=0,03⋅15⋅103⋅10+15⋅103⋅0,7=F_{тяги}=0,03\cdot 15\cdot 10^3\cdot 10+15\cdot 10^3\cdot 0,7=Fтяги​=0,03⋅15⋅103⋅10+15⋅103⋅0,7=

=300⋅15+15⋅700=15⋅(300+700)=15000=300\cdot 15+15\cdot 700=15\cdot(300+700)=15000=300⋅15+15⋅700=15⋅(300+700)=15000 (Н).

Ответ. Fтяги=15F_{тяги}=15Fтяги​=15 кН.

Разберем еще одну задачу.

Условие

Брусок массой 400400400 г под действием груза массой 100100100 г проходит из состояния покоя путь 808080 см за 222 с. Найти коэффициент трения.

(Источник: Рымкевич А.П. Сборник задач по физике)

Решение

Это задача на движение связанных тел. В таких задачах надо знать, что сила, с которой нитка тянет два связанных тела, — одинакова. Давайте разберемся, почему это так. Пусть у нас есть два бруска, связанных невесомой нитью (то есть нитью с массой, равной нулю). Пусть нить тянет первое тело с силой T⃗1\vec{T}_1T⃗1​, а второе тело — с силой T⃗2\vec{T}_2T⃗2​.

Тогда по 3-му закону Ньютона тело 1 и тело 2 также действуют на саму нить с силами T⃗1′\vec{T}_1’T⃗1′​ и T⃗2′\vec{T}_2’T⃗2′​. Причем по тому же 3-му закону Ньютона:

T⃗1=−T⃗1′\vec{T}_1=-\vec{T}_1’T⃗1​=−T⃗1′​

T⃗2=−T⃗2′\vec{T}_2=-\vec{T}_2’T⃗2​=−T⃗2′​.

Теперь посмотрим только на нить:

Получается, что на нить действуют две силы: T⃗1′\vec{T}_1’T⃗1′​ и T⃗2′\vec{T}_2’T⃗2′​. Значит, мы можем найти равнодействующую. Пусть суммарная (равнодействующая) сила равна TTT.

Тогда по 2-му закону Ньютона T=m⋅aT=m\cdot aT=m⋅a, где mmm — это масса нити, aaa — ускорение, с которым движется нить. Но масса нашей нити m=0m=0m=0. А это значит, что и равнодействующая сил, приложенных к нити, должна быть равна 000:

T=0T=0T=0.

А это, в свою очередь, значит, что T⃗1′+T⃗2′=0\vec{T}_1’+\vec{T}_2’=0T⃗1′​+T⃗2′​=0. Или: T1′=T2′T_1’=T_2’T1′​=T2′​.

То есть нить «передает» силу через себя от одного груза к другому без потери этой силы.

Блок, который присутствует в нашей задаче, лишь «поворачивает» силу, не изменяя ее по величине.

Вернемся к решению нашей задачи.

Шаг 1. Первое, что нужно сделать, — это рисунок.

Шаг 2. Записываем 2-й закон Ньютона.

В этой задаче у нас участвуют два тела. Поэтому 2-й закон Ньютона нужно записать для двух тел:

• для первого тела: T⃗1+F⃗тр+N⃗1+m1g⃗=m1a⃗1\vec{T}_1+\vec{F}_{тр}+\vec{N}_1+m_1\vec{g}=m_1\vec{a}_1T⃗1​+F⃗тр​+N⃗1​+m1​g⃗​=m1​a⃗1​
• для второго тела: T⃗2+m2g⃗=m2a⃗2\vec{T}_2+m_2\vec{g}=m_2\vec{a}_2T⃗2​+m2​g⃗​=m2​a⃗2​.

Шаг 3. Выберем оси и запишем 2-й закон Ньютона в проекции на каждую из осей.

а) Сначала для тела 1:

На ось OXOXOX: T1−Fтр+0+0=m1a1\,\,T_1-F_{тр}+0+0=m_1a_1T1​−Fтр​+0+0=m1​a1​.

На ось OYOYOY: 0+0+N1−m1g=m1⋅0\,\,0+0+N_1-m_1g=m_1\cdot 00+0+N1​−m1​g=m1​⋅0.

Итак: {T1−Fтр=m1a1N1−m1g=0.\begin{cases}T_1-F_{тр}=m_1a_1\\N_1-m_1g=0{.}\end{cases}{T1​−Fтр​=m1​a1​N1​−m1​g=0.​

б) Для тела 2:

Обратите внимание на то, что движение второго тела одномерное. Оно происходит вдоль одной оси. Поэтому достаточно ввести лишь одну ось.

Уравнение, полученное из 2-го закона Ньютона для второго тела, в проекции на ось OYOYOY:

−T2+m2g=m2a2-T_2+m_2g=m_2a_2−T2​+m2​g=m2​a2​.

Шаг 4. Собираем все, что было получено ранее:

{T1−Fтр=m1a1N1−m1g=0−T2+m2g=m2a2T1=T2.\begin{cases}T_1-F_{тр}=m_1a_1\\N_1-m_1g=0\\-T_2+m_2g=m_2a_2\\T_1=T_2{.}\end{cases}⎩⎪⎪⎪⎨⎪⎪⎪⎧​T1​−Fтр​=m1​a1​N1​−m1​g=0−T2​+m2​g=m2​a2​T1​=T2​.​

Дополнительно надо учесть, что нить (обычно) является не только невесомой, но еще и нерастяжимой.

lampa.io