Решение двойных неравенств — Алгебра
Просмотр содержимого документа
«Решение двойных неравенств»
Дата
Тема: РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
Задачи: научить решать двойные неравенства с одной переменной.
Ход урока
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Самостоятельная работа по вариантам.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Помним, что решением системы неравенств с одной переменной называется значение переменной, при котором выполняется каждое неравенство системы. Решить систему неравенств означает найти все ее решения или доказать, что решений нет.
Вспомним, какой вид имеет двойное неравенство 2
От двойного неравенства лучше переходить к системе. Например, имея двойное неравенство
Для его решения лучше перейти к равносильной системе неравенств
Как получается такой переход? Грубо говоря, двойное неравенство состоит из трех частей, которые разделены двумя знаками неравенства. Рассматриваем отдельно первую и вторую части двойного неравенства, а потом вторую и третью части неравенства, и записываем их в систему. Тогда
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем свои тетради и записываем сегодняшнее число и тему урока. Открываем учебник на странице 198 и выполним письменно №892 и №894(а, в).
№ 892. Решить двойное неравенство:
а) .
Для начала распишем его в виде системы (цветом я вам показываю, как двойное разбивается на линейные неравенства, это писать не обязательно):
А далее применяем стандартный алгоритм решения системы неравенств с одной переменной.
Изобразим решение системы на координатной прямой:
Видим, что две штриховки пересекаются на интервале ( -1; 2), это и будет ответом.
Ответ: .
б) .
Для начала распишем его в виде системы:
А далее применяем стандартный алгоритм решения системы неравенств с одной переменной.
Изобразим решение системы на координатной прямой:
Видим, что две штриховки пересекаются на интервале ( -12; 17), это и будет ответом.
Ответ: .
Самостоятельно выполните № 892 (в).
Все вместе выполним №894(а, в).
Изобразим решение на координатной прямой:
Ответ: .
Изобразим решение на координатной прямой:
Ответ: .
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Повторите алгоритм решения системы неравенств, подготовьтесь к самостоятельной работе.
Домашнее задание: № 891.
как решать двойные неравенства с дробями
Вы искали как решать двойные неравенства с дробями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как решить двойное неравенство с дробью, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как решать двойные неравенства с дробями».Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как решать двойные неравенства с дробями,как решить двойное неравенство с дробью. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как решать двойные неравенства с дробями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать двойные неравенства с дробями).
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как решать двойные неравенства с дробями,как решить двойное неравенство с дробью. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как решать двойные неравенства с дробями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать двойные неравенства с дробями).
Где можно решить любую задачу по математике, а так же как решать двойные неравенства с дробями Онлайн?
Решить задачу как решать двойные неравенства с дробями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Урок «Решение двойных неравенств»
Тема урока:Решение двойных неравенств.
Тип урока: урок изучения нового материала.
Цели урока:
Образовательная: Формировать умение учащихся применять алгоритм решения систем линейных неравенств и свойства числовых неравенств для решения двойных неравенств.
Развивающая:
способствовать формированию умений наблюдать, сравнивать, анализировать, строить гипотезы и делать выводы,
совершенствовать устную математическую речь.

Воспитательная: воспитывать чувство товарищества, чувство ответственности, побуждать учеников к само – взаимоконтролю.
Ожидаемые результаты:
знают алгоритм решения систем линейных неравенств с одной переменной;
понимают и применяют свойства числовых неравенств для решения систем неравенств и двойных неравенств.
Методы и приемы обучения (стратегии): психологический настрой, взаимопроверка, самопроверка,
Оборудование: презентация
План урока:
Организационный момент
Актуализация опорных знаний по теме: «Неравенства и системы неравенств»
Сообщение темы урока и совместное целеполагание
Сообщение темы урока и совместное целеполагание
Решение практических задач
Рефлексия учебной деятельности
Ход урока.
Организационный момент.
Здравствуйте. Открыли тетради, записали число, классная работа
Актуализация знаний.
Давайте вспомним «Неравенства и их свойства», Для этого выполним задания. Каждое задание теста предполагает ответ «Да» — фигура , «Нет» — фигура ____
В результате выполнения теста должна получиться какая-то фигура.
Верно ли утверждение: если х>2 и у>14, то х+у >16?
Верно ли утверждение: если х>2 и у>14, то х·у<28?
Является ли число 0 решением неравенства 3х-1<11?
Является ли неравенство 3х+ 12>2х – 2 строгим?
Существует ли целое число, принадлежащее промежутку ?
Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?
(ответ: ).
У кого нет ошибок ? Проверьте свои ответы.
Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.
2х+8>12
2х>12+8
2х>20
Х>10
Ответ [10;+ ]
Установить соответствие между неравенством и числовым промежутком
Х+4 ≥ 16 3
-1<х+3≤3 4
10,5 ≤5Х < 50 6
Х+0,7 < 0,4 1
Х-3>0 2
4х<48
1 (– ; – 0,3)
2. (3;+ )
3. [12; + )
4. (– 4; 0]
5. (-; 12]
6. [2,5; 10)
«Определение темы урока и целеполагание».
Какие вы встретили неравенства? Значит 2 вида неравенства простые и двойные
А как решить двойное неравенство? Как вы думаете какая тема нашего урока будет?
Мы научились на прошлых уроках решать линейные неравенства и системы линейных неравенств узнали их свойства. Сегодня мы разберем два способа решения двойных неравенств и свойства.
Сегодня мы разберем два способа решения двойных неравенств и свойства.
10 ≤5Х+20 <50
«Мозговой штурм», фронтальная работа.
Эффективные вопросы.
1.С помощью, каких свойств неравенств можно найти значения переменной? Учащиеся формулируют способ решения двойных неравенств.
1 способ мы можем воспользоваться свойствами
2 На какие Два неравенства можно разделить двойное неравенство? Для этого прочтите неравенство
3 Они должны выполнятся одновременно?
4 Что мы получили? 2 способ с помощью системы
Записывают в тетрадь способы решения двойных неравенств.
Решая двойные неравенства мы получили алгоритм.
Динамическая пауза.
Если верное неравенство – руки вверх. Выпадает неверное неравенство – руки в стороны: 7<9, -3>5, 0,5<0,75, -2,7>2,7, 987>986, 0,03 < 0,003.
Решение заданий по теме»
Номера из учебника 109 (1 столбик) 115 (2 столбик) 112б
Самостоятельная работа с самопроверкой
-2<0
Подведение итогов урока. Рефлексия (выберите одно из предложений).
«Сегодня на уроке я узнал …»
Трудным при решении двойных неравенств для меня было…»
«Больше всего мне понравилось решать двойные неравенства способом …»
«Завтра я буду более успешным, потому что…»
Домашнее задание.
109 2 столбик 115 1 столбик 112а
Приложение 2
Приложение 3
-2<0-2,5
Урок математики в 4 классе по теме «Двойные неравенства»
Очень строгая наука, Очень точная наука, Интересная наука – Это… II. Актуализация знаний. 1.Задания на развитие внимания и мыслительных операций. — Математика любит внимательных людей. Сейчас проверим, кто уже настроился на хорошую работу. А) Игра «Найди лишнее». На 1 секунду показываю табличку с наименованиями: КМ, ДМ, СМ, КГ, ММ. Б) А теперь – зарядка для ума. — Представь, что ты рыболов. Вчера ты поймал 5 штук мелких окуньков, возраст которых исчисляется тремя неделями. Сегодня была поймана щука, которая старше окуньков на 366 дней, но моложе рыболова на 10 лет. Сколько лет рыболову? — Что мы можем узнать в задаче? В) Знаете ли вы, какая из этих рыб лучше развивается в холодных водах, а в тёплых водоёмах её размеры уменьшаются в 2 раза: — карась – 5 — налим – 24 — ряпушка – 1? — Чтобы проверить свои предположения решите математическую цепочку: 25 х 40 – 904 : 48 х 12 = — Все эти рыбы водятся в наших реках. 2.В народе говорят: «Повторение – мать учения» А задание следующее… А) а+85 * 85+ а d х 16 * 21 х d в – 49 * в – 130 — Какое из выражений будет лишним? — Что такое неравенство? Б) – Посмотрите на числа, что вы о них можете сказать? 4 400 км, 400 кг, 150 кг, 2 273 км, 1 726 км, 440 кг? — Какую работу мы можем выполнить с этими числами? — На какие группы можно разделить числа? -1 вариант – запишет числа, обозначающие длину. 2 вариант – запишет числа, обозначающие массу, а работу с этими числами выберите самостоятельно. — Какую работу выполнял Витя? Хотите узнать, о чём могут рассказать эти числа? 1. р.Индигирка р.Алдан р.Лена (прикрепляю таблички с названиями) — Что вы можете сказать о длине реки Алдан? 150 кг – масса бурого медведя 400 кг – масса белого медведя 440 кг – масса лося. (прикрепляю рисунки) — Что можно сказать о массе белого медведя? — В жизни нам часто приходится прибегать к таким сравнениям. Используя «говорящие числа» составьте свои сравнения. (Раздаю карточки с числами). 1 гр. – рябина – до 1000 см берёза – до 30 м сосна – до 350 дм 2 гр. – ель – 350 лет берёза – 50 лет тополь – 1200мес. 3 гр. – росомаха – 16 кг волк – до 75 кг лиса – 10 000 г. 4 гр. волк – 130 см лиса – 90 см. 5 гр. – песец – 55см соболь – 50 см заяц-беляк – 70 см. III. Постановка проблемы и «открытие» детьми нового знания. — Говорят, что математика – это искусство называть разные вещи одним именем. Попробуем и мы. А) Слова – короче, легче, меньше в математике обозначают знаком … Слова – длиннее, тяжелее, дольше Обозначают знаком … Ставлю знаки в высказывания. 1.726 км ‹ 2.273 км ‹ 4.400км р.Индигирка р.Алдан р.Лена — Что же у нас получилось? — Чем эти записи отличаются от уже привычных нам неравенств? — Как бы вы назвали эти неравенства? — А в математике принято называть такие
неравенства двойные. — Кто может назвать тема нашего урока? Б) Представьте, что мы пошли с вами в магазин и покупаем арбуз. У продавца только 2 гири по 5кг. (работа с моделью весов). — Масса арбуза нам не известна, как её обозначим? При первом взвешивании получаем, что, Х › 5, при втором – Х ‹ 10. Но мы взвешиваем один и тот же арбуз. Как это можно записать по-другому? — Какова же масса арбуза? — Давайте проверим, всё ли правильно мы сделали? Работа с учебником, разбор правила. IV.ФИЗМИНУТКА. V. Первичное закрепление. А) с. 10 № 1. – чтение неравенства в парах, затем в слух. — Из неравенств выбери те, из которых составлено двойное неравенство: 18 ≤ С ‹ 75 с ≤ 18, с ≥ 18, с › 75, с ‹ 75. 274 ‹ n ≤ 360 n › 274, n ‹ 274, n ≤ 360, n ≥ 360. Б) с.10 № 2 — самостоятельно В) Показываю карточки с неравенствами, дети записывают двойное неравенство и множество решений. 2‹ y y‹ 6 z › 4 z ≤ 8 y › 2 z ≤ 8 VI. Самостоятельная работа с проверкой в классе. Работа проводится по учебнику. А) На с. 11 № 4, 5, 6, 7 – по заданию учебника. № 5 проверяем так: я показываю решение на числовом луче, ребята говорят к какому это неравенству и называют множество решений. VII. Задачи на повторение. А) У математики есть свой язык – язык формул. Давайте проверим, насколько мы владеем этим языком. Если высказывание верно, ставите +, если не верно, ставите -. ТЕСТ.
Показываю «ключ» к решению и проверяем с объяснением. Б) Дифференцированная самостоятельная работа. 1 вариант: 367 * 750 86040 * 8370 802000 : 5 2 вариант: с. 12 № 10 – примеры с окошечком. VIII. Итог урока. — Над чем работали на уроке? — Какой вид работы особенно вам понравился? — Домашнее задание: Составьте двойное неравенство и найдите множество его решений. — Спасибо за работу. | Математика. —
Лишнее КГ – это единица измерения
массы, а остальное – единицы измерения
длины. — Рыболову столько лет, сколько мне, т.к. я рыболов. Можно узнать возраст окуньков в днях: 3 недели – 21 день Возраст щуки – 366+21=387 дней. 25 х 40 – 904 : 48 х 12 = 24 (вычисления цепочкой по порядку) — Сравнить. -ставим знак =, т.к. от перестановки слагаемых сумма не изменяется. —ставим знак ‹, т. к. по одному из множителей. один., а другой ‹ в левой стороне. — ставим знак ›, т.к. уменьшаемые одинак., а вычитаемое в левой части ‹, значит разность будет больше в левой части. — Лишним будет равенство. — Это именованные числа. — Разделить на группы, перевести в новые единицы измерения, выполнить + и -, сравнить величины. 1-2
мин. самостоятельной работы, каждый
сам выбирает для себя задание. В это время один ученик записывает числа по группам на доске, начиная с маленького. 1726км 2273 км 4400км 150кг 400 кг 440кг (Задание шепчу ему на ушко) -Река Алдан длиннее Индигирки, но короче Лены. — Белый медведь тяжелее бурого медведя, но легче лося. Работа в группах. Каждой группе, прежде чем сравнить, необходимо привести к одинаковым единицам измерения. При ответе ребята говорят, какую величину сравнивали. Карточки прикрепляются к магнитной доске. ‹ › — Неравенства. — У них сразу два знака. Ребята предлагают свои варианты. «Двойное неравенство». Х х › 5 х ‹ 10. 5‹ х ‹ 10 х = {6, 7, 8, 9} Ребята
в полголоса читают друг другу. Устно называют неравенства с ≥ 18, с › 75 n › 274, n ≤ 360 1 ученик работает у доски для проверки. Первый, кто записал в тетради, записывает для проверки на доске. 2 ‹ y‹ 6 {3, 4, 5} 4 ‹ z ≤ 8 {5, 6, 7, 8 } составить нельзя, т. к. переменные разные. + — — + — Каждый работает индивидуально, выбирая задание по своему желанию. |
Отбор корней двойным неравенством в задаче 13 профильного ЕГЭ
В этой статье научимся отбирать корни в задании 13 ЕГЭ с помощью двойного неравенства. Решать сами уравнения здесь не будем, только подробно разберем отбор корней.
Задача 1. Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке . Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством:
Запишем это двойным неравенством:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б)
Задача 2. Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке . Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б)
Задача 3. Предположим, вы решили тригонометрическое уравнение и ваш ответ на пункт а) такой: . Отбор нужно произвести на отрезке . Таким образом, точки, которые мы отберем, больше или равны , и меньше или равны . Запишем это двойным неравенством для корня :
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Теперь берем второй корень из серии и проделываем для него то же самое: снова составляем двойное неравенство
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Очевидно, что подойдут значения , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Берем вторую серию корней и повторяем все действия:
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения, , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Теперь берем второй корень из серии и проделываем для него то же самое: снова составляем двойное неравенство
Перенесем дробь вправо и влево через знак неравенства:
Разделим все неравенство на :
Упростим:
Теперь подбором определим целые значения , оказавшиеся в промежутке . Очевидно, что подойдут значения , , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Очевидно, что подойдут значения , , . Осталось подставить найденные нами значения в решение пункта а), чтобы получить решения пункта б):
Ответ: б) .
Таким образом, отбор двойным неравенством наиболее рационален тогда, когда промежуток длинный (больше трех четвертей круга) и решений, полученных в пункте а) не более двух. Иначе, при отборе для 4-х решений, как в задаче 3, расчетов уже получается много. Тем не менее любители алгебраизировать отбор очень любят этот способ и предпочитают его отбору на окружности.
Неравенства, решение линейных неравенств, принцип решения неравенств
Неравенство это выражение с , ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно.
Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений. Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами.
Линейные неравенства
Принципы решения неравенств аналогичны принципам решения уравнений.Принципы решения неравенств
Для любых вещественных чисел a, b, и c:
Принцип прибавления неравенств: Если a Принцип умножения для неравенств: Если a 0 верно, тогда ac
Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами.
Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5
b) 13 — 7x ≥ 10x — 4
Решение
| 3x — 5 | Используя принцип прибавления для неравенств, прибавляем 2x |
| 5x — 5 | Используя принцип прибавления для неравенств, прибавляем 5 |
| 5x | Используя принцип умножения для неравенств, умножаем или делим на 5 |
| x |

Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y1 = 3x — 5 и y2 = 6 — 2x. Тогда отсюда видно, что для x 1 находится ниже графика y2, или y12.
| 13 — 7x ≥ 10x — 4 | вычитаем 10x |
| 13 — 17x ≥ -4 | вычитаем 13 |
| -17x ≥ -17 | Делим на 17 и меняем знак неравенства |
| x ≤ 1 |
Двойные неравенства
Когда два неравенства соединены словом и, или, тогда формируется двойное неравенство.
Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым, потому что в нём использовано и. Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2 Решите -3 Решение У нас есть
Двойное неравенство, как 2x — 5 ≤ -7 или называется разделённым, потому что оно содержит или. В отличие от некоторых соединённых неравенств, оно не может быть сокращено; поэтому, оно не может быть записано без или.
Пример 3 Решите 2x — 5 ≤ -7 или 2x — 5 > 1. Постройте график множества решений.
Решение У нас есть
| -3 | Вычитаем 5 |
| -8 | Делим на 2 |
| -4 |
| 2x — 5 ≤ -7 или 2x — 5 > 1. | Прибавляем 5 |
| 2x ≤ -2 или 2x > 6 | Делим на 2 |
x ≤ -1 или x > 3. |
Множество решений {x|x ≤ -1 или x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y1 = 2x — 5, y2 = -7, и y3 = 1. Заметьте, что для {x|x ≤ -1 или x > 3}, y1 ≤ y2или y1 > y3.
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x|
|x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x|
|y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2|
b) |5 — 2x| ≥ 1
Решение
a) |3x + 2|
b) |5 — 2x| ≥ 1
| |5 — 2x| ≤ -1 или 5 — 2x ≥ 1 | Вычитаем 5 |
| -2x ≤ -6 или -2x ≥ -4 | Делим на -2 и меняем знак неравенства |
| x ≥ 3 или x ≤ 2 |
Использование неравенств
Пример 5 Планы выплат. За выполнение малярных работ, Эрику может быть выплачена заработная плата одним из двух способов:
План A: \$250 плюс \$10 в час;
План B: $20 в час.
Предположим, что работа занимает n часов. Для каких значений n план B лучше для Эрика?
Решение
1. Понимание задачи. Предположим, что работа отнимет 20 часов. Тогда n = 20, и согласно плану A, Эрик заработает \$250 + \$10,20, или \$250 + \$200, или \$450. Его заработок согласно плану B составит \$20,20, или \$400. Это показывает, что план A лучше для Эрика, если он будет работать 20 часов. Подобным образом, если он будет работать 30 часов, тогда n = 30, и согласно плану A, Эрик заработает \$250 + \$10,30, или \$250 + \$300, или \$550. При плане B, он заработает \$20,30, или \$600, поэтому план B лучше в этом смысле. Чтобы определить все значения n, для которых план B является лучшим для Эрика, составим и решим неравенство.
2. Составление неравенства. Запишем это в виде неравенства.
Доход от плана B больше, чем доход от плана A.
20n > 250 + 10n
3. Решим неравенство:
| 20n > 250 + 10n | Вычитаем 10n из двух сторон |
| 10n > 250 | Делим на 10 обе стороны |
| n > 25 |
 Проверка. Для n = 25 выплаты согласно плану A составят: \$250 + \$10,25, или \$250 + \$250,
или \$500, и выплаты согласно плану B составят \$20,25, или \$500. То есть, для работы длительностью менее 25 часов,
доход одинаков для каждого плана. Согласно плану B выплаты больше для работы, которая занимает больше 30-и часов.
Так как 30 > 25, это обеспечивает частичную проверку результата, но мы не можем проверить все значения n.
Проверка. Для n = 25 выплаты согласно плану A составят: \$250 + \$10,25, или \$250 + \$250,
или \$500, и выплаты согласно плану B составят \$20,25, или \$500. То есть, для работы длительностью менее 25 часов,
доход одинаков для каждого плана. Согласно плану B выплаты больше для работы, которая занимает больше 30-и часов.
Так как 30 > 25, это обеспечивает частичную проверку результата, но мы не можем проверить все значения n.5. Вывод . Для значений, n больше, чем 25 часов, план B является лучшим.
Оценить число в неравенствах
☰
Для оценки чисел в неравенствах используются различные свойства числовых неравенств. Обычно в таких заданиях даются одно или несколько исходных неравенств, в которых присутствуют переменные. Требуется оценить результат арифметических действий над этими переменными (т. е. получаемые новые числа).
Например, даны два таких исходных двойных неравенства:
- –1 < p < 10;
- 2,5 < q < 3,2.

Требуется оценить числа, которые получаются в результате следующих действий над переменными:
- 0,1 × p,
- 1/q,
- p + q,
- q – p,
- p3.
При оценке числа 0,1p воспользуемся следующими свойством числовых неравенств:
- Если a < b и c > 0, то ac < bc. В данном случае c = 0,1.
- Если a < b и b < c, то a < c. В данном случае b = 0,1p, a = –1 × 0,1, c = 10 × 0,1.
На основе этих свойств мы можем умножить все части исходного двойного неравенства (не меняя знаки сравнения) на 0,1 и таким образом получить оценку для числа 0,1p:
–1 × 0,1 < 0,1p < 10 × 0,1
–0,1 < 0,1p < 1
То есть, число 0,1p лежит в пределах от –0,1 до 1.
При оценке числа 1/q следует воспользоваться свойством числовых неравенств, описывающим дроби:
- Если a < b и оба числа положительны, то 1/a > 1/b.

Отсюда можно заключить, что в исходном неравенстве следует поменять знаки сравнения на обратные:
1 / 2,5 > 1/q > 1/3,2
Запишем неравенство наоборот:
1/3,2 < 1/q < 1/2,5
Выполним действия:
0,3125 < 1/q < 0,4
Для оценки числа p + q используются такое свойство числовых неравенств:
- Если a < b, то a + c < b + c. Пусть в данном случае c = q.
Оба числовых неравенства складываются почленно:
–1 + 2,5 < p + q < 10 + 3,2
1,5 < p+q < 13,2
Число q – p можно представить в виде суммы: –p + q и решить также как выше. Однако по сравнению с предыдущим числом (p + q), здесь p сначала надо умножить на –1. Для выполнения этого действия воспользуемся таким свойством числовых неравенств:
- Если a < b и c < 0, то ac > bc. В данном случае c = –1.
Таким образом, из исходного неравенства получается неравенство противоположного смысла, т. е. меняются знаки на обратные:
е. меняются знаки на обратные:
–1 × –1 > –1p > –1 × 10
Перевернем неравенство и выполним действия:
–10 < –p < 1
Теперь можно сложить q и –p:
–10 + 2,5 < q – p < 1 + 3,2
–7,5 < q – p < 4,2
Для оценки числа p3 воспользуемся таким свойством:
- Если n — нечетное число, то для любых чисел a и b если a < b, то и an < bn.
(–1)3 < p3 < 103
–1 < p3 < 1000
Если бы p возводился в квадрат или в любую другую четную степень, то таким свойством мы бы воспользоваться без оглядки на абсолютные значения не могли. Так если бы вместо –1 было число –20, то (–20)2 > 102.
2.7: Решение сложных неравенств — математика LibreTexts
Решение сложных неравенств с помощью «и»
Теперь, когда мы знаем, как решать линейные неравенства, следующим шагом будет рассмотрение сложных неравенств. Сложное неравенство состоит из двух неравенств, связанных словом «и» или словом «или». Например, ниже представлены сложные неравенства.
Сложное неравенство состоит из двух неравенств, связанных словом «и» или словом «или». Например, ниже представлены сложные неравенства.
\ [\ begin {array} {lll} {x + 3> −4} & {\ text {and}} & {4x − 5 \ leq 3} \\ {2 (y + 1) <0} & { \ text {или}} & {y − 5 \ geq −2} \\ \ end {array} \ nonumber \]
НЕРАВЕНСТВО СОЕДИНЕНИЯ
Сложное неравенство состоит из двух неравенств, связанных словом «и» или словом «или».”
Решить составное неравенство означает найти все значения переменной, которые делают составное неравенство истинным. Мы решаем составные неравенства, используя те же методы, которые мы использовали для решения линейных неравенств. Мы решаем каждое неравенство отдельно, а затем рассматриваем два решения.
Чтобы решить сложное неравенство со словом «и», мы ищем все числа, которые делают и истинными. Чтобы решить сложное неравенство со словом «или», мы ищем все числа, которые делают неравенство либо истинным.
Начнем с сложных неравенств с «и». Нашим решением будут числа, которые являются решениями обоих неравенств , известных как пересечение двух неравенств. Рассмотрим пересечение двух улиц — часть пересечения улиц — принадлежит обеим улицам.
Чтобы найти решение составного неравенства, мы смотрим на графики каждого неравенства, а затем находим числа, которые принадлежат обоим графам, где графики перекрываются.
Для составного неравенства \ (x> −3 \) и \ (x \ leq 2 \) мы графически отображаем каждое неравенство. Затем мы ищем, где графики «перекрываются». Цифры, которые заштрихованы на обоих графиках, будут заштрихованы на графике решения составного неравенства. См. Рисунок \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \)Мы видим, что числа между \ (- 3 \) и \ (2 \) заштрихованы на обоих первых двух графиках. Затем они будут закрашены на графике решения.
Число \ (- 3 \) не заштриховано на первом графике, поэтому, поскольку оно не заштриховано на обоих графах, оно не включается в граф решения.
Число два затенено как на первом, так и на втором графике. Поэтому на графике решения он закрашен.
Вот как мы покажем наше решение на следующих примерах.
Пример \ (\ PageIndex {1} \)
Решите \ (6x − 3 <9 \) и \ (2x + 7 \ geq 3 \). Постройте график решения и запишите решение в интервальной записи.
- Ответ
- The final graph will show all the numbers that make both inequalities true—the numbers shaded on both of the first two graphs. The graph of x is less than 2 and x is greater than or equal to negative 3 has a left bracket at negative 3 and a right parenthesis at 2 and is shaded between the bracket and parenthesis. Each graph is marked at negative 3 and 2. Step 3 is to write the solution in interval notation. It is negative 3 to 2 within a bracket and a parenthesis. All the numbers that make both inequalities true are the solution to the compound inequality.»>
\ (6x − 3 <9 \) и \ (2x + 9 \ geq 3 \) Шаг 1. Решите каждое неравенство
.
\ (6x − 3 <9 \) \ (2x + 9 \ geq 3 \) \ (6x <12 \) \ (2x \ geq −6 \) \ (х <2 \) и \ (х \ geq −3 \) Шаг 2. Изобразите каждое решение. Затем нанесите на график числа, удовлетворяющие обоим неравенствам.  На последнем графике будут показаны все числа, которые делают оба неравенства истинными — числа, заштрихованные на на обоих первых двух графиков.
На последнем графике будут показаны все числа, которые делают оба неравенства истинными — числа, заштрихованные на на обоих первых двух графиков.Шаг 3. Запишите решение в интервальной записи. \ ([- 3,2) \) Все числа, которые делают оба неравенства верными, являются решением сложного неравенства.
Пример \ (\ PageIndex {2} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (4x − 7 <9 \) и \ (5x + 8 \ geq 3 \).
- Ответ
Пример \ (\ PageIndex {3} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (3x − 4 <5 \) и \ (4x + 9 \ geq 1 \).
Постройте график решения и запишите решение в интервальной записи: \ (3x − 4 <5 \) и \ (4x + 9 \ geq 1 \).
- Ответ
РЕШИТЬ СЛОЖНОЕ НЕРАВЕНСТВО с помощью «И.»
- Решите каждое неравенство.
- Изобразите каждое решение. Затем изобразите числа, которые делают и истинными.
На этом графике показано решение сложного неравенства. - Запишите решение в интервальной записи.
Пример \ (\ PageIndex {4} \)
Решите \ (3 (2x + 5) \ leq 18 \) и \ (2 (x − 7) <- 6 \).Постройте график решения и запишите решение в интервальной записи.
- Ответ
- 2 times the quantity x minus 7 is less than negative 6 simplifies to 2 x minus 14 is less than negative 6, which simplifies to 2 x is less than 8, which simplifies to x is less than 4. Graph each solution. The graph of x is less than or equal to one-half has a right bracket at one-half and is shaded to the left. The graph of x is less than 4 has a right parenthesis and is shaded to the left. Both graphs are marked at one-half. Graph the numbers that make both inequalities true. Graph the numbers that make both inequalities true. The graph has a right bracket at one-half and is shaded to the left. It is marked at one-half. Write the solution in interval notation. It is negative infinity and one-half within a parenthesis and a bracket.»>
\ (3 (2x + 5) \ leq 18 \) и \ (2 (x − 7) <- 6 \) Решите каждое неравенство
.
\ (6x + 15 \ leq 18 \) \ (2x − 14 <−6 \) \ (6x \ leq 3 \) \ (2x <8 \) \ (х \ leq \ frac {1} {2} \) и \ (х <4 \) Постройте график для каждого решения
.Изобразите на графике числа
, которые делают оба неравенства
истинными.
Запишите решение
в интервальной записи.\ ((- \ infty, \ frac {1} {2}] \)
Пример \ (\ PageIndex {5} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (2 (3x + 1) \ leq 20 \) и \ (4 (x − 1) <2 \).
- Ответ
Пример \ (\ PageIndex {6} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (5 (3x − 1) \ leq 10 \) и \ (4 (x + 3) <8 \).
- Ответ
Пример \ (\ PageIndex {7} \)
Решите \ (\ frac {1} {3} x − 4 \ geq −2 \) и \ (- 2 (x − 3) \ geq 4 \). Постройте график решения и запишите решение в интервальной записи.
Постройте график решения и запишите решение в интервальной записи.
- Ответ
Пример \ (\ PageIndex {8} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (\ frac {1} {4} x − 3 \ geq −1 \) и \ (- 3 (x − 2) \ geq 2 \).
- Ответ
Пример \ (\ PageIndex {9} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (\ frac {1} {5} x − 5 \ geq −3 \) и \ (- 4 (x − 1) \ geq −2 \).
- Ответ
Иногда встречается сложное неравенство, которое можно записать более кратко. Например, \ (a
ДВОЙНОЕ НЕРАВЕНСТВО
Двойное неравенство — это сложное неравенство, например \ (a
\ [\ text {Другие формы:} \ quad \ begin {array} {lllll} {a
Чтобы решить двойное неравенство, мы выполняем одну и ту же операцию со всеми тремя «частями» двойного неравенства с целью выделить переменную в центре.
Пример \ (\ PageIndex {10} \)
Решите \ (- 4 \ leq 3x − 7 <8 \). Постройте график решения и запишите решение в интервальной записи.
- Ответ
- Simplify. 3 is less than or equal to 3 x which is less than 15. Divided each part by 3. 3 divided by 3 is less than or equal to 3 x divided by 3 which is less than 15 divided by 3. Simplify. The result is 1 is less than or equal to x which is less than 5. Graph the solution. The solution on a number line is a left bracket at 1, a right parenthesis at 5, and shading between the bracket and parenthesis. Write the solution in interval notation. It is 1 to 5 within a bracket and a parenthesis.»>
\ (- 4 \ leq 3x — 7 <8 \) Добавьте 7 ко всем трем частям. \ (-4 \, {\ color {red} {+ \, 7}} \ leq 3x — 7 \, {\ color {red} {+ \, 7}} <8 \, {\ color {red} {+ \, 7}} \) Упростить. 
\ (3 \ le 3x <15 \) Разделите каждую часть на три. \ (\ dfrac {3} {\ color {red} {3}} \ leq \ dfrac {3x} {\ color {red} {3}} <\ dfrac {15} {\ color {red} {3} } \) Упростить. \ (1 \ leq x <5 \) Постройте график решения. Запишите решение в интервальной записи. \ ([1, 5) \)
Если записать двойное неравенство, \ (1 \ leq x <5 \), легко увидеть, что решения - это числа от одного до пяти, включая одно, но не пять. Затем мы можем сразу же построить график решения, как и выше.
Затем мы можем сразу же построить график решения, как и выше.
Другой способ построить график решения \ (1 \ leq x <5 \) - это построить график как решения \ (x \ geq 1 \), так и решения \ (x <5 \). Затем мы найдем числа, которые делают оба неравенства верными, как и в предыдущих примерах.
Пример \ (\ PageIndex {11} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (- 5 \ leq 4x − 1 <7 \).
- Ответ
Пример \ (\ PageIndex {12} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (- 3 <2x − 5 \ leq 1 \).
- Ответ
- Решите каждое неравенство.
- Изобразите каждое решение. Затем нанесите на график числа, удовлетворяющие любому неравенству.
- Запишите решение в интервальной записи.
- Ответ
- So, the interval notation of the solution is the union of negative infinity to negative three-halves within a parenthesis and a bracket and 2 to infinity within a bracket and a parenthesis.»>
\ (5−3x \ leq −1 \) или \ (8 + 2x \ leq 5 \) Решите каждое неравенство. \ (5−3x \ leq −1 \) \ (8 + 2x \ leq 5 \) \ (- 3x \ leq −6 \) \ (2x \ leq −3 \) \ (х \ geq 2 \) или \ (х \ leq — \ frac {3} {2} \) Изобразите каждое решение. 
Числа на графике, которые
делают любое неравенство
истинным.\ ((- \ infty, −32] \ чашка [2, \ infty) \) - Ответ
- Ответ
- Ответ
- Graph each solution. The graph of x is less than twenty-one halves has a right bracket at twenty-one halves and is shaded to the left. The graph of x is greater than or equal to negative 12 has a left bracket at negative 12 and is shaded to the right. Graph numbers that make either inequality true. All values are shaded on the number line. The solution is all real numbers. The interval notation is negative infinity to infinity within parentheses.»>
\ (\ frac {2} {3} x − 4 \ leq 3 \) или \ (\ frac {1} {4} (x + 8) \ geq −1 \) Решите каждое неравенство
.\ (3 (\ frac {2} {3} x − 4) \ leq 3 (3) \) \ (4⋅ \ frac {1} {4} (x + 8) \ geq 4⋅ (−1) \) \ (2x − 12 \ leq 9 \) \ (х + 8 \ geq -4 \) \ (2x \ leq 21 \) \ (х \ geq -12 \) \ (х \ leq \ frac {21} {2} \) \ (х \ leq \ frac {21} {2} \) или \ (х \ geq -12 \) Постройте график для каждого решения
.
Числа на графике
, которые делают неравенство
истинным.Решение охватывает все действительные числа. \ ((- \ infty, \ infty) \) - Ответ
- Ответ
- Ответ
- 72 plus 1.54 x. His bill will be between or equal to 57 dollars and 6 cents and 171 dollars and 2 cents. That is 57.06 is less than or equal to 24.72 plus 1.54 x which is less than 171.02. Solve the inequality. 57.06 minus 24.72 is less than or equal to 24.72 minus 24.72 plus 1.54 x which is less than 171.02 minus 24.72. 32.34 is less than or equal to 1.54 x which is less than or equal to 146.3. 32.34 divided by 1.54 is less than or equal to 1.54 x divided by 1.54 which is less than or equal to 146.3 divided by 1.54. The result is 21 is less than or equal to x which is less than or equal to 95. Answer the question. The property owner can use 21 to 95 h c f and still fall within the normal usage billing range.»>
Определите, что мы ищем. Количество hcf, которое он может использовать и оставаться в диапазоне выставления счетов «нормальное использование». Назовите то, что мы ищем. 
Пусть x = x = количество hcf, которое он может использовать. Переведем в неравенство. Билл стоит 24,72 доллара плюс 1,54 доллара на количество используемых им hcf или \ (24,72 + 1,54x \). \ (\ color {Cerulean} {\ underbrace {\ color {black} {\ text {Его счет будет между или равным} 57 долларов.06 \ text {and} 171,02 $.}}} \)
\ (57,06 \ leq 24,74 + 1,54x \ leq 171,02 \)
Решите неравенство. \ (57,06 \ leq 24,74 + 1,54x \ leq 171,02 \)
\ (57.
 06 \, {\ color {red} {- \, 24.72}} \ leq 24.74 \, {\ color {red} {- \, 24.72}} + 1.54x \ leq 171.02 \, {\ color {красный) } {- \, 24.72}} \)
06 \, {\ color {red} {- \, 24.72}} \ leq 24.74 \, {\ color {red} {- \, 24.72}} + 1.54x \ leq 171.02 \, {\ color {красный) } {- \, 24.72}} \)\ (32,34 \ leq 1,54x \ leq 146.3 \)
\ (\ dfrac {32.34} {\ color {red} {1.54}} \ leq \ dfrac {1.54x} {\ color {red} {1.54}} \ leq \ dfrac {146.3} {\ color {red} { 1.54}} \)
\ (21 \ leq x \ leq 95 \)
Ответьте на вопрос. Владелец собственности может использовать \ (21–95 \) hcf и по-прежнему находиться в пределах диапазона выставления счетов «нормальное использование». - Ответ
Домовладелец может использовать \ (5–20 \) hcf и по-прежнему попадать в диапазон выставления счетов за «экономичное использование».
- Ответ
Домовладелец может использовать \ (16–40 \) hcf и по-прежнему находиться в пределах диапазона выставления счетов «нормальное использование».
- Решить x 4 <0.
- найти «= 0» точки
- между точками «= 0» — это интервала, либо
- больше нуля (> 0) или
- меньше нуля (<0)
- , затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
- всегда больше нуля или
- всегда меньше нуля
- Уравнение равно нулю при −2 и 3
- Неравенство «<0" истинно между −2 и 3.
- всегда> 0 или
- всегда <0
- d = расстояние от земли (м) и
- t = время от прыжка (секунды)
- Из −1.1 до 1.3 и
- с 2,9 по
- Если \ (a
- Если \ (a 0 \), то \ (ac
- Если \ (a bc \) и \ (\ frac {a} {c}> \ frac {b} {c} \). В этом случае, в отличие от предыдущего факта, если \ (c \) отрицательно, нам нужно изменить направление неравенства, когда мы умножаем или делим обе части неравенства на \ (c \).
- \ (- 2 \ влево ({m — 3} \ right) <5 \ left ({m + 1} \ right) - 12 \)
- \ (2 \ left ({1 — x} \ right) + 5 \ le 3 \ left ({2x — 1} \ right) \)
- \ (- 6 \ le 2 \ left ({x — 5} \ right) <7 \)
- \ (- 3 <\ frac {3} {2} \ left ({2 - x} \ right) \ le 5 \)
- \ (- 14 <- 7 \ влево ({3x + 2} \ вправо) <1 \)
- Первый случай включает решение двух линейных неравенств, соединенных словом «и». Слово «и» также известно как союз. Решение составного неравенства «и» — это набор всех значений x, которые удовлетворяют обоим из двух неравенств. Другими словами, вам нужен набор решений, который работает с обоими неравенствами. Другой способ сказать, что множество решений составного неравенства «и» — это пересечение , представленное символом \ Large {\ color {red} \ cap} двух неравенств.

- Что касается второго случая , он включает в себя решение двух линейных неравенств, соединенных словом «или». Решение составного неравенства «или» — это совокупность всех x, которые удовлетворяют одному из двух неравенств или иногда удовлетворяют двум одновременно. Другими словами, вам нужно решение, которое работает хотя бы с одним неравенством. Другой способ сказать, что набор решений составного неравенства «или» — это объединение , представленное символом \ Large {\ color {red} \ cup} двух неравенств.
- Первое неравенство: x — 1> 1
- Второе неравенство: 27 \ ge 2x — 1
- Первое неравенство: 2 + 3x> — 10
- Второе неравенство: 2 \ left ({x — 1} \ right)
- Первое неравенство: 5 — 3 \ left ({x — 2} \ right) \ le x — \ left ({- 2x + 13} \ right)
- Второе неравенство: 5 — \ left ({x + 1} \ right) \ le 2 \ left ({7 — x} \ right) + 1
- Первое неравенство: 3x — 2 \ left ({1 — x} \ right)
- Второе неравенство: 10 — x
- Первое неравенство: 2x — 5> 3x + 2
- Второе неравенство: x — 1 <2x - 5
- Первое неравенство: 2 \ left ({x + 1} \ right) \ le x — 2
- Второе неравенство: 3 \ left ({x — 1} \ right) \ le 4x — 3
- Первое неравенство: 2 \ left ({x + 1} \ right) — 3 \ left ({x + 1} \ right) <0
- Второе неравенство: 4x + 3 \ ge 15 + 6x
- Первое неравенство: 0 <3 - \ left ({x + 4} \ right)
- Второе неравенство: 2 <1 - \ left ({x - 2} \ right)
- Первое неравенство: 10x — 8 <7x + 7
- Второе неравенство: 3x — 2 \ left ({2 — x} \ right) \ ge 1
Решите неравенство, как если бы это было уравнение.

Действительные решения уравнения становятся граничными точками для решения неравенства.
Обведите граничные точки сплошными кружками, если исходное неравенство включает равенство; в противном случае сделайте граничные точки открытыми кружками.
Выберите точки из каждой области, созданной граничными точками. Замените эти «контрольные точки» исходным неравенством.
Если контрольная точка удовлетворяет исходному неравенству, то область, содержащая эту контрольную точку, является частью решения.
Представьте решение в графической форме и в виде набора решений.
Решите сложные неравенства с помощью «или»
Чтобы решить составное неравенство с помощью «или», мы начинаем так же, как мы делали с составными неравенствами с «и» — решаем два неравенства. Затем мы находим все числа, которые делают неравенство или истинным.
Затем мы находим все числа, которые делают неравенство или истинным.
Так же, как Соединенные Штаты являются объединением всех 50 штатов, решением будет объединение всех чисел, которые делают любое неравенство истинным. Чтобы найти решение составного неравенства, мы смотрим на графики каждого неравенства, находим числа, принадлежащие любому графу, и складываем все эти числа вместе.
Чтобы записать решение в обозначении интервала , мы часто будем использовать символ объединения , \ (\ cup \), чтобы показать объединение решений, показанных на графиках.
РЕШИТЬ СЛОЖНОЕ НЕРАВЕНСТВО С «ИЛИ».
Пример \ (\ PageIndex {13} \)
Решите \ (5−3x \ leq −1 \) или \ (8 + 2x \ leq 5 \). Постройте график решения и запишите решение в интервальной записи.
Постройте график решения и запишите решение в интервальной записи.
Пример \ (\ PageIndex {14} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (1−2x \ leq −3 \) или \ (7 + 3x \ leq 4 \).
Пример \ (\ PageIndex {15} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (2−5x \ leq −3 \) или \ (5 + 2x \ leq 3 \).
Пример \ (\ PageIndex {16} \)
Решите \ (\ frac {2} {3} x − 4 \ leq 3 \) или \ (\ frac {1} {4} (x + 8) \ geq −1 \).Постройте график решения и запишите решение в интервальной записи.
Пример \ (\ PageIndex {17} \)
Решите составное неравенство.Постройте график решения и запишите решение в интервальной записи: \ (\ frac {3} {5} x − 7 \ leq −1 \) или \ (\ frac {1} {3} (x + 6) \ geq −2 \).
Пример \ (\ PageIndex {18} \)
Решите составное неравенство. Постройте график решения и запишите решение в интервальной записи: \ (\ frac {3} {4} x − 3 \ leq 3 \) или \ (\ frac {2} {5} (x + 10) \ geq 0 \) .
Постройте график решения и запишите решение в интервальной записи: \ (\ frac {3} {4} x − 3 \ leq 3 \) или \ (\ frac {2} {5} (x + 10) \ geq 0 \) .
Решение приложений со сложными неравенствами
Ситуации в реальном мире также связаны с комплексным неравенством.Мы будем использовать ту же стратегию решения проблем, которую мы использовали для решения линейных уравнений и приложений неравенства.
Напомним, что стратегии решения проблемы заключаются в том, чтобы сначала прочитать проблему и убедиться, что все слова понятны. Затем определите, что мы ищем, и назначьте переменную для его представления. Затем переформулируйте проблему одним предложением, чтобы упростить преобразование в составное неравенство . Наконец, мы решим составное неравенство.
Пример \ (\ PageIndex {19} \)
Из-за засухи в Калифорнии многие общины установили многоуровневый расход воды. Существуют разные ставки для использования с сохранением, нормального использования и чрезмерного использования. Использование измеряется количеством сотен кубических футов (hcf), которые использует собственник.
Существуют разные ставки для использования с сохранением, нормального использования и чрезмерного использования. Использование измеряется количеством сотен кубических футов (hcf), которые использует собственник.
Летом владелец недвижимости будет платить 24,72 доллара США плюс 1,54 доллара США за час на фут при нормальном использовании. Счет за нормальное использование будет составлять от 57,06 до 171,02 доллара или равняться ему. Сколько hcf может использовать владелец, если он хочет, чтобы его использование оставалось в пределах нормы?
Пример \ (\ PageIndex {20} \)
Из-за засухи в Калифорнии многие общины теперь установили многоуровневую оплату воды.Существуют разные ставки для использования с сохранением, нормального использования и чрезмерного использования. Использование измеряется количеством сотен кубических футов (hcf), которые использует собственник.
Использование измеряется количеством сотен кубических футов (hcf), которые использует собственник.
Летом владелец собственности будет платить 24,72 доллара плюс 1,32 доллара за гуц за охранное использование. Счет за использование консервации будет составлять от 31,32 до 52,12 доллара или равняться ему. Сколько hcf может использовать владелец, если она хочет, чтобы ее использование оставалось в пределах допустимого диапазона?
Пример \ (\ PageIndex {21} \)
Из-за засухи в Калифорнии многие общины установили многоуровневый расход воды. Существуют разные ставки для использования с сохранением, нормального использования и чрезмерного использования. Использование измеряется количеством сотен кубических футов (hcf), которые использует собственник.
Зимой владелец недвижимости будет платить 24,72 доллара США плюс 1,54 доллара США за гуф при нормальном использовании. Счет за нормальное использование будет составлять от 49,36 до 86 долларов или равняться им.32. Сколько hcf ему будет разрешено использовать, если он хочет, чтобы его использование оставалось в нормальном диапазоне?
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практических занятий по решению сложных неравенств.
Решение квадратичных неравенств: концепции
Решение Квадратные неравенства: концепции (стр. 1 из 3) Решение линейных неравенств,
например « x + 3> 0 «, было
довольно просто, если вы не забыли устранить неравенство
знак всякий раз, когда вы умножали или делили на отрицательное (как вы
при решении чего-то вроде «2 x <4 "). Но есть большой скачок, между линейными неравенствами и квадратичными неравенствами. Часть прыжка это тот факт, что концепции, которые были пропущены при обучении решать линейные неравенства полезны и даже необходимы при решении квадратичных неравенств. Итак, давайте сначала посмотрим на линейное неравенство и рассмотрим те концепции, которые пропускались ранее. Я это уже знаю, чтобы решить это неравенство, все, что мне нужно сделать, это добавить 4 на другую сторону, чтобы получить решение « x <4 ". Итак Я уже знаю ответ. Но сейчас подойду к этой проблеме под другим углом, рассмотрев соответствующий график с двумя переменными.
Неравенство « x 4 <0 "
спрашивает "когда линия y = x 4 ниже
линия y = 0? «Поскольку
линия y = 0 — это просто ось x ,
неравенство, следовательно, спрашивает, «когда линия y = x 4 ниже
ось x ? »
Первый шаг к ответу на этот вопрос — найти, где линия
пересекает ось x ;
то есть сначала мне нужно найти перехват x . Так строка у = x 4 крестика ось x при x = 4. Поскольку строка y = x 4 равно прямая линия, она будет выше оси x с одной стороны от перехвата и ниже оси x по ту сторону перехвата.Авторские права Элизабет Стапель 2002-2011 Все права защищены
Вспоминая графический метод представления решений линейных неравенство, на приведенном выше графике показано правильное решение « x <4 «. То есть, глядя на
график связанной линии и определение точки (на оси x )
графическая линия была ниже оси x ,
легко увидеть, что решение неравенства « x 4 <0 "это
неравенство " x <4 ". Давайте посмотрим на квадратичную неравенство: Сначала мне нужно посмотреть в соответствующем уравнении с двумя переменными, y = x 2 + 4, и рассмотрим, где его график находится ниже оси x . Для этого мне нужно знать, где график пересекает ось x .То есть сначала мне нужно найти где x 2 + 4 равно нулю: Это говорит о том, что квадратичная пересекает ось x при x = 2 и при x = 2. Теперь мне нужно вычислить
out где (то есть на каких интервалах) график находится под осью.
Тогда решение ясно: Я мог бы умножить
исходное неравенство через 1,
давая мне « x 2 4> 0 «. Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
| ||||||||||||||||||||||||||||
Решение квадратичных неравенств
… и более …
Квадратичный
Квадратное уравнение (в стандартной форме) выглядит так:
Квадратичное Уравнение в стандартной форме
( a , b и c могут иметь любое значение, за исключением того, что a не может быть 0.)
Выше приведено уравнение (=), но иногда нам нужно решить такие неравенства:
Символ | слов | Пример | ||
|---|---|---|---|---|
> | больше | x 2 + 3x> 2 | ||
< | менее | 7x 2 <28 | ||
≥ | больше или равно | 5 ≥ х 2 — х | ||
≤ | меньше или равно | 2 года 2 + 1 ≤ 7 лет | ||
Решение
Решение неравенств очень похоже на решение уравнений. .. мы делаем почти то же самое.
.. мы делаем почти то же самое.
| При решении уравнения мы пытаемся найти точки , , например, помеченные «= 0» |
| Но когда мы решаем неравенства мы пытаемся найти интервала (ов) , , например, помеченные «> 0» или «<0" |
Вот что мы делаем:
Вот пример:
Пример: x 2 — x — 6 <0
x 2 — x — 6 имеет эти простые коэффициенты (потому что я хотел упростить!):
(х + 2) (х − 3) <0
Сначала , давайте найдем, где это равно ноль:
(х + 2) (х − 3) = 0
Равно нулю, когда x = −2 или x = +3
, потому что, когда x = −2, тогда (x + 2) равен нулю
или
когда x = +3, то (x − 3) равно нулю
Итак, между −2 и +3, функция будет либо
Мы не знаем какой. .. еще!
.. еще!
Давайте выберем промежуточное значение и проверим его:
При x = 0: x 2 — x — 6
= 0–0–6
= −6
Таким образом, между -2 и +3 функция на меньше, чем на ноль.
И это тот регион, который нам нужен, так что …
x 2 — x — 6 <0 в интервале (−2, 3)
Примечание: x 2 — x — 6> 0 на интервале (−∞, −2) и (3, + ∞)
А вот график x 2 — x — 6: |
Также попробуйте Grapher неравенства.
Что делать, если он не проходит через ноль?
Вот график x 2 — x + 1 Нет баллов «= 0»! Но это упрощает задачу! | |
Поскольку линия не пересекает y = 0, это должно быть либо: Итак, все, что нам нужно сделать, это проверить одно значение (скажем, x = 0), чтобы увидеть, выше или ниже оно. | |
A «Реальный мир» Пример
Каскадер прыгнет с 20-метрового здания.
Высокоскоростная камера готова снять его на высоте от 15 до 10 метров над землей.
Когда его снимать на камеру?
Мы можем использовать эту формулу для расстояния и времени:
d = 20 — 5т 2
(Примечание: если вам интересна формула, она упрощена: d = d 0 + v 0 t + ½a 0 t 2 , где d 0 = 20 , v 0 = 0 и a 0 = −9.81 , то ускорение свободного падения.)
Хорошо, поехали.
Сначала , давайте набросаем вопрос:
Требуемое расстояние от 10 м до 15 м :
10
И мы знаем формулу для d:
10 <20 - 5 т 2 <15
Теперь решим!
Сначала вычтем 20 с обеих сторон:
−10 <−5t 2 <−5
Теперь умножьте обе стороны на — (1/5). Но поскольку мы умножаем на отрицательное число, неравенства изменят направление … прочтите «Решение неравенств», чтобы понять, почему.
Но поскольку мы умножаем на отрицательное число, неравенства изменят направление … прочтите «Решение неравенств», чтобы понять, почему.
2> т 2 > 1
Для аккуратности, меньшее число должно быть слева, а большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства по-прежнему указывают правильно):
1
Наконец, мы можем безопасно извлекать квадратные корни, поскольку все значения больше нуля:
√1
Съемочную группу можем сказать:
«Фильм из 1.От 0 до 1,4 секунды после прыжка »
Выше квадратичного
Те же идеи могут помочь нам решить более сложные неравенства:
Пример: x 3 + 4 ≥ 3x 2 + x
Во-первых, приведем его в стандартном виде:
x 3 — 3x 2 — x + 4 ≥ 0
Это кубическое уравнение (наивысший показатель — куб, т. е. x 3 ), и его трудно решить, поэтому давайте изобразим его вместо этого:
е. x 3 ), и его трудно решить, поэтому давайте изобразим его вместо этого:
Нулевые точки: приблизительно :
А на графике мы видим интервалы, где он больше (или равен) нулю:
В интервальной записи можно написать:
Приблизительно: [-1,1, 1,3] U [2,9, + ∞)
Решить сложные неравенства | Начальная алгебра
Поскольку это неравенство «больше чем», решение может быть переписано в соответствии с правилом «больше чем».
[латекс] \ Displaystyle х + 3 <-4 \, \, \, \, \, \, \, \ text {или} \, \, \, \, \, \, \, x + 3> 4 [/ латекс]
Решите каждое неравенство.
[латекс] \ begin {array} {r} x + 3 <-4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, x + 3> 4 \\\ подчеркивание {\, \, \, \, — 3 \, \, \, \, \, — 3} \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \ underline {\, \, \, \, \, \, — 3 \, \, — 3} \\ x \, \, \, \, \, \, \, \, \, <- 7 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , x \, \, \, \, \, \, \, \, \,> 1 \\\\ x <-7 \, \, \, \, \, \, \, \ text {или} \ , \, \, \, \, \, x> 1 \, \, \, \, \, \, \, \ end {array} [/ latex]
Проверьте решения в исходном уравнении, чтобы убедиться, что они работают. Проверьте конечную точку первого связанного уравнения [latex] −7 [/ latex] и конечную точку второго связанного уравнения 1.
Проверьте конечную точку первого связанного уравнения [latex] −7 [/ latex] и конечную точку второго связанного уравнения 1.
[латекс] \ Displaystyle \ begin {array} {r} \, \, \, \ left | x + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | х + 3 \ вправо |> 4 \\\ влево | -7 + 3 \ right | = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | 1 + 3 \ right | = 4 \\\, \, \, \, \, \, \, \ left | -4 \ right | = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \, \ влево | 4 \ право | = 4 \\\, \, \, \, \, \, \, \, \, \, \, \, 4 = 4 \, \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 4 = 4 \ конец {array} [/ latex]
Попробуйте [latex] -10 [/ latex], значение меньше [latex] -7 [/ latex], и 5, значение больше 1, чтобы проверить неравенство.
[латекс] \ Displaystyle \ begin {array} {r} \, \, \, \, \, \ left | x + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | х + 3 \ вправо |> 4 \\\ влево | -10 + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | 5 + 3 \ right |> 4 \\\, \, \, \, \, \, \, \, \, \, \ left | -7 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \ влево | 8 \ right |> 4 \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, 7> 4 \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 8> 4 \ end {array} [/ latex]
Оба решения проверяют!
Ответ
Неравенство: [латекс] \ displaystyle x <-7 \, \, \, \, \, \ text {or} \, \, \, \, \, x> 1 [/ latex]
Интервал: [латекс] \ left (- \ infty, -7 \ right) \ cup \ left (1, \ infty \ right) [/ latex]
График:
Алгебра — линейные неравенства
Показать мобильное уведомление Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-11: Линейные неравенства
До этого момента в этой главе мы сосредоточились на решении уравнений.Пришло время немного переключить передачи и начать думать о решении проблемы неравенства. Прежде чем мы перейдем к решению неравенств, мы должны сначала рассмотреть несколько основных моментов.
На данном этапе вашей математической карьеры предполагается, что вы знаете, что
\ [a означает, что \ (a \) — некоторое число, которое строго меньше \ (b \). Также предполагается, что вы знаете, что
Также предполагается, что вы знаете, что
означает, что \ (a \) — это некоторое число, которое либо строго больше, чем \ (b \), либо точно равно \ (b \).Точно так же предполагается, что вы знаете, что делать с двумя оставшимися неравенствами. > (больше) и \ (\ le \) (меньше или равно).
Мы хотим обсудить некоторые проблемы с обозначениями и некоторые тонкости, которые иногда возникают у студентов, когда они действительно начинают работать с неравенством.
Во-первых, помните, что когда мы говорим, что \ (a \) меньше \ (b \), мы имеем в виду, что \ (a \) находится слева от \ (b \) на числовой строке. Итак,
\ [- 1000— истинное неравенство.
Затем не забывайте, как правильно интерпретировать \ (\ le \) и \ (\ ge \). Оба следующих утверждения являются истинными неравенствами.
\ [4 \ le 4 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} — 6 \ le 4 \] В первом случае 4 равно 4 и, следовательно, «меньше или равно» 4. Во втором случае -6 строго меньше 4 и, следовательно, «меньше или равно» 4. Наиболее распространенный ошибка состоит в том, чтобы решить, что первое неравенство не является истинным неравенством. Также будьте осторожны, чтобы не принять эту интерпретацию и не перевести ее на <и / или>.Например,
Во втором случае -6 строго меньше 4 и, следовательно, «меньше или равно» 4. Наиболее распространенный ошибка состоит в том, чтобы решить, что первое неравенство не является истинным неравенством. Также будьте осторожны, чтобы не принять эту интерпретацию и не перевести ее на <и / или>.Например,
не является истинным неравенством, поскольку 4 равно 4, а не строго меньше 4.
Наконец, в этом и последующих разделах мы увидим много двойных неравенств , так что мы не можем забыть о них. Следующее — двойное неравенство.
\ [- 9В двойном неравенстве мы говорим, что оба неравенства должны выполняться одновременно. В этом случае 5 определенно больше -9 и в то же время меньше или равно 6.Следовательно, это двойное неравенство является истинным неравенством.
С другой стороны,
\ [10 \ le 5 не является истинным неравенством. Хотя верно, что 5 меньше 20 (так что второе неравенство верно), неверно, что 5 больше или равно 10 (поэтому первое неравенство неверно). Если хотя бы одно из неравенств в двойном неравенстве не верно, то все неравенство неверно. Этот момент более важен, чем вы можете себе представить.В следующем разделе мы столкнемся с ситуациями, когда многие ученики пытаются объединить два неравенства в двойное неравенство, которое просто невозможно объединить, так что будьте осторожны.
Если хотя бы одно из неравенств в двойном неравенстве не верно, то все неравенство неверно. Этот момент более важен, чем вы можете себе представить.В следующем разделе мы столкнемся с ситуациями, когда многие ученики пытаются объединить два неравенства в двойное неравенство, которое просто невозможно объединить, так что будьте осторожны.
Следующая тема, которую нам необходимо обсудить, — это идея обозначения интервала . Обозначение интервалов — это очень хорошее обозначение неравенств, которое будет широко использоваться в следующих нескольких разделах этой главы.
Наилучшим способом определения обозначения интервалов является следующая таблица.В таблице три столбца. Каждая строка содержит неравенство, график, представляющий неравенство, и, наконец, обозначение интервала для данного неравенства.
Помните, что квадратная скобка «[» или «]» означает, что мы включаем конечную точку, а скобка «(» или «)» означает, что мы не включаем конечную точку.
Итак, с первыми четырьмя неравенствами в таблице обозначение интервалов на самом деле представляет собой не что иное, как график без числовой линии на нем.С последними четырьмя неравенствами обозначение интервала — это почти график, за исключением того, что нам нужно добавить соответствующую бесконечность, чтобы убедиться, что мы получаем правильную часть числовой прямой. Также обратите внимание, что бесконечности НИКОГДА не получают скобки. У них есть только круглые скобки.
Прежде чем перейти к решению неравенств, необходимо сделать последнее замечание по поводу обозначения интервалов. Всегда помните, что когда мы записываем интервал для неравенства, число слева должно быть меньшим из двух.
Пришло время подумать о решении линейных неравенств. При решении неравенств мы будем использовать следующий набор фактов. Обратите внимание, что факты приведены для <. Однако мы можем записать эквивалентный набор фактов для оставшихся трех неравенств.
Это почти те же факты, которые мы использовали для решения линейных уравнений. Единственное реальное исключение — третий факт. Это важный факт, поскольку он часто используется неправильно и / или часто забывается при решении проблемы неравенства.
Если вы не уверены, что считаете, что знак \ (c \) имеет значение для второго и третьего фактов, рассмотрите следующий пример числа.
\ [- 3Я надеюсь, что мы все согласимся с тем, что это истинное неравенство.Теперь умножьте обе стороны на 2 и -2.
\ [\ begin {align *} — 3 и 5 \ left ({- 2} \ right) \\ — 6 & — 10 \ end {align *} \]Конечно, при умножении на положительное число направление неравенства остается неизменным, однако при умножении на отрицательное число направление неравенства меняется.
Хорошо, давайте устраним некоторые неравенства. Мы начнем с неравенств, в которых есть только одно неравенство.Другими словами, мы не будем решать двойные неравенства для следующего набора примеров.
Здесь мы должны помнить, что мы просим определить все значения переменной, которые мы можем подставить в неравенство и получить истинное неравенство. Это означает, что наши решения в большинстве случаев сами по себе будут неравенствами.
Решение отдельных линейных неравенств во многом повторяет процесс решения линейных уравнений. Мы упростим обе стороны, получим все члены с переменной с одной стороны и числа с другой стороны, а затем умножим / разделим обе стороны на коэффициент переменной, чтобы получить решение.Вы должны помнить одну вещь: если вы умножаете / делите на отрицательное число, то меняете направление неравенства.
a \ (- 2 \ left ({m — 3} \ right) Показать решение
Здесь действительно особо нечего делать, кроме как следовать описанному выше процессу.
Вы уловили тот факт, что направление неравенства здесь изменилось, не так ли? Мы разделились на «-7» и нам пришлось менять направление.Неравенство решения имеет вид \ (m> \ frac {{13}} {7} \). Обозначение интервала для этого решения: \ (\ left ({\ frac {{13}} {7}, \ infty} \ right) \).
b \ (2 \ left ({1 — x} \ right) + 5 \ le 3 \ left ({2x — 1} \ right) \) Показать решение
Опять же, здесь особо нечего делать.
\ [\ begin {align *} 2 \ left ({1 — x} \ right) + 5 & \ le 3 \ left ({2x — 1} \ right) \\ 2 — 2x + 5 & \ le 6x — 3 \\ 10 & \ le 8x \\ \ frac {{10}} {8} & \ le x \\ \ frac {5} {4} & \ le x \ end {align *} \] Теперь, с этим неравенством, мы закончили с переменной с правой стороны, когда это более традиционно с левой стороны.Итак, давайте поменяем местами так, чтобы переменная оказалась слева. Обратите внимание, однако, что нам нужно будет также изменить направление неравенства, чтобы убедиться, что мы не изменим ответ. Итак, вот обозначение неравенства для неравенства.
Обратите внимание, однако, что нам нужно будет также изменить направление неравенства, чтобы убедиться, что мы не изменим ответ. Итак, вот обозначение неравенства для неравенства.
Обозначение интервала для решения: \ (\ left [{\ frac {5} {4}, \ infty} \ right) \).
А теперь давайте решим несколько двойных неравенств.Здесь процесс в некотором смысле похож на решение отдельных неравенств, но в остальном сильно отличается. Поскольку существует два неравенства, невозможно получить переменные с «одной стороны» неравенства и числа с другой. Легче увидеть, как это работает, если мы рассмотрим пару примеров, так что давайте сделаем это.
Пример 2 Решите каждое из следующих неравенств. Приведите для решения формы неравенства и интервальных обозначений. Процесс здесь довольно похож на процесс для одиночных неравенств, но сначала нам нужно быть осторожными в нескольких местах. Нашим первым шагом в этом случае будет удаление скобок в среднем члене.
Нашим первым шагом в этом случае будет удаление скобок в среднем члене.
Теперь мы хотим, чтобы \ (x \) был сам по себе в среднем члене и только числа в двух внешних членах. Для этого мы будем добавлять / вычитать / умножать / делить по мере необходимости. Единственное, что нам нужно здесь помнить, это то, что если мы делаем что-то для среднего срока, нам нужно сделать то же самое для ОБЕИХ условий. Одна из наиболее распространенных ошибок на этом этапе — добавить что-то, например, в середину и добавить это только к одной из двух сторон.
Хорошо, мы добавим 10 ко всем трем частям, а затем разделим все три части на две.
\ [\ begin {array} {c} 4 \ le 2xЭто неравенство формы ответа. Ответ в виде интервальной записи \ (\ left [{2, \ frac {{17}} {2}} \ right) \).
b \ (- 3 Показать решение
В этом случае первое, что нам нужно сделать, это очистить дроби, умножив все три части на 2. Затем мы продолжим, как и в первой части.
Затем мы продолжим, как и в первой части.
На этом мы еще не закончили, но нам нужно быть очень осторожными со следующим шагом. На этом этапе нам нужно разделить все три части на -3. Однако напомним, что всякий раз, когда мы делим обе стороны неравенства на отрицательное число, нам нужно изменить направление неравенства. Для нас это означает, что оба неравенства должны изменить направление здесь.
\ [4> х \ ge — \ frac {4} {3} \]Итак, существует неравномерная форма решения.Нам нужно быть осторожными с обозначением интервалов для решения. Во-первых, обозначение интервала НЕ \ (\ left ({4, — \ frac {4} {3}} \ right] \). Помните, что в обозначении интервала меньшее число всегда должно располагаться слева! Следовательно, правильное обозначение интервала для решения: \ (\ left [{- \ frac {4} {3}, 4} \ right) \).
Также обратите внимание, что это также соответствует форме неравенства решения. Неравенство говорит нам, что \ (x \) — это любое число от 4 до \ (- \ frac {4} {3} \) или, возможно, само \ (- \ frac {4} {3} \), и это в точности что нам говорят обозначения интервалов.
Неравенство говорит нам, что \ (x \) — это любое число от 4 до \ (- \ frac {4} {3} \) или, возможно, само \ (- \ frac {4} {3} \), и это в точности что нам говорят обозначения интервалов.
Кроме того, неравенство можно перевернуть, чтобы получить меньшее число слева, если мы захотим. Вот та форма,
\ [- \ frac {4} {3} \ le xПри этом не забудьте также правильно обработать неравенства.
c \ (- 14 Показать решение
Не особо для этого. Мы продолжим так же, как и в предыдущих двух.
\ [\ begin {array} {c} — 14Не волнуйтесь, что одна из сторон теперь равна нулю.Это не проблема. Опять же, как и в предыдущей части, мы будем делить на отрицательное число, поэтому не забудьте изменить направление неравенств.
\ [\ begin {array} {c} \ displaystyle 0> x> — \ frac {{15}} {{21}} \\ \ displaystyle 0> x> — \ frac {5} {7} \ hspace {0,25 in} {\ mbox {OR}} \ hspace {0,25in} — \ frac {5} {7} Любое из неравенств во второй строке будет работать для решения. Интервальное обозначение решения — \ (\ left ({- \ frac {5} {7}, 0} \ right) \).
Интервальное обозначение решения — \ (\ left ({- \ frac {5} {7}, 0} \ right) \).
При решении двойных неравенств обязательно обратите внимание на неравенства, которые есть в исходной задаче. Одна из наиболее распространенных ошибок здесь — начать с задачи, в которой одно из неравенств имеет вид <или>, а другое — \ (\ le \) или \ (\ ge \), как мы делали в первых двух частях в предыдущем примере, а затем в окончательном ответе они оба являются <или> или оба являются \ (\ le \) или \ (\ ge \). Другими словами, легко сделать оба неравенства одинаковыми.Будьте осторожны с этим.
Есть еще один последний пример, над которым мы хотим работать.
Пример 3 Если \ (- 1 Показать решение Это проще, чем может показаться на первый взгляд. Все, что мы действительно собираемся сделать, это начать с данного неравенства, а затем изменить средний член, чтобы он выглядел как второе неравенство. Опять же, нам нужно помнить, что что бы мы ни делали со средним термином, нам также необходимо сделать с двумя внешними членами.
Итак, сначала умножим все на 2.
\ [- 2Теперь прибавьте 3 ко всему.
\ [1Теперь у нас есть средний член, идентичный второму неравенству в формулировке задачи, поэтому все, что нам нужно сделать, это выбрать \ (a \) и \ (b \). Из этого неравенства видно, что \ (a = 1 \) и \ (b = 11 \).
Решение сложных неравенств — ChiliMath
При решении сложных неравенств мы будем иметь дело с двумя общими случаями или типами.
Для обоих случаев решения сложных неравенств могут быть выражены в виде графиков на числовой прямой, а также в виде интервальных обозначений.
Я предлагаю вам сначала изобразить решения двух неравенств на числовой прямой, прежде чем записывать решение составного неравенства в интервальной записи. Имея наглядное представление о том, как два неравенства ведут себя на числовой прямой, гораздо проще написать соответствующее обозначение интервала.
Мы также рассмотрим некоторые примеры, в которых сложное неравенство не имеет решения или бесконечного решения.
Где-то в наших примерах мы обсудим случай составного неравенства «и», который можно сжать в одно неравенство, состоящее из трех частей: левой, средней и правой. Примером может быть — 1 \ le x \ le 3, которое является производным от -1 \ le x и x \ le 3. Записав его в такой форме, это может позволить нам решить составное неравенство намного быстрее.
Составные неравенства «И»
Решите составное неравенство «и», решая каждое из двух неравенств по отдельности, затем изучите или рассмотрите их решения вместе.Для случая «и» мы хотим найти все числа или значения, которые могут сделать и , и два неравенства истинными .
Пример 1: Решите составное неравенство x — 1> 1 и 27 \ ge 2x — 1. Изобразите решения на числовой прямой. Затем запишите свои решения в интервальной записи.
ШАГ 1. Решите каждое неравенство.
Добавьте 1 к обеим сторонам неравенства.
x — 1> 1
x — 1 + 1> 1 + 1
\ color {red} x> 2
Сложите обе части неравенства на 1, затем разделите на 2. Наконец, убедитесь, что переменная находится слева. В этом случае, когда вы меняете местами, переменная x будет перемещаться справа налево. Относительная ориентация символа неравенства должна оставаться неизменной, чтобы значение не изменилось. Можно подумать об этом, что «рот» символа неравенства открывается в сторону числа 14.Таким образом, когда вы меняете местами, «устье» неравенства должно по-прежнему указывать в сторону 14.
27 \ ge 2x — 1
27 + 1 \ ge 2x — 1 + 1
8 \ ge 2x
{\ Large {{{28} \ over 2}}} \ ge {\ Large {{{2x} \ over 2}}}
14 \ ge x
\ color {red} x \ le 14
Приведены решения by \ color {red} x> 2 и \ color {red} x \ le 14.
ШАГ 2. Изобразите решения на числовой прямой.
Для \ color {red} x> 2 точка 2 не входит в состав решений, так как x> 2 означает все числа больше 2.Кроме того, в нем нет условий равенства, поэтому мы должны исключить число 2. Итак, мы поставим пустой кружок над 2, чтобы указать, что это не решение. Все решения представляют собой числа больше 2, поэтому мы рисуем стрелку справа от 2.
Для \ color {red} x \ le 14 мы читаем это как «x меньше или равно 14». Обратите внимание, что существует условие равенства, поэтому число 14 является частью решения, поэтому мы поставим над ним замкнутый кружок. Все числа слева от 14 также являются решениями, поэтому мы нарисуем стрелку, указывающую слева от нее.
Окончательным решением будет пересечение или перекрытие двух неравенств: \ color {red} x> 2 и \ color {red} x \ le 14. Обратите внимание, что все числа от 2 до 14 пересекаются, поэтому они часть окончательных решений составного неравенства «и». Они также пересекаются под номером 14, поэтому мы добавляем его в набор решений. Однако они не пересекаются в точке 2, поэтому мы опускаем ее как часть решений. Мы только что выяснили полный набор решений данного составного неравенства.
Они также пересекаются под номером 14, поэтому мы добавляем его в набор решений. Однако они не пересекаются в точке 2, поэтому мы опускаем ее как часть решений. Мы только что выяснили полный набор решений данного составного неравенства.
ШАГ 3. Запишите решения в интервальной записи.
Обратите внимание, что все числа от 2 до 14 являются частью решений. Кроме того, число 2 исключено, потому что оно состоит из открытого круга , а число 14 включено, поскольку оно покрыто закрытым кругом . Теперь мы используем закругленную скобку или круглую скобку, если она исключена (2 исключено), и квадратную скобку, если она есть (14 включено).
\ Large {\ left ({2,14} \ right]}
Читается как «все числа больше 2, но меньше или равные 14».
Помните: Этот тип интервала также известен как полузакрытый или полуоткрытый интервал, потому что одна из двух конечных точек включена, а другая нет.
Пример 2: Решите составное неравенство 2 + 3x> — 10 и 2 \ left ({x — 1} \ right)
ШАГ 1. Решите каждое неравенство.
Вычтем обе части неравенства на 2.Затем разделите обе стороны на 3.
2 + 3x> — 10
2 — 2 + 3x> — 10 — 2
3x> — 12
{\ Large {{{3x} \ over 3}}}> {\ Large {{{- 12} \ over 3}}}
\ color {red} x> — \, 4
Распределите 2 на бином внутри скобок. Добавьте 2 с обеих сторон неравенства. Затем вычтите обе части на x.
2 \ влево ({x — 1} \ вправо)
2x — 2
2x — 2 + 2
2x
2x — x
\ color {red} x <6
Решения даются как \ color {red} x> — \, 4 и \ color {red} x <6.
ШАГ 2. Изобразите набор решений на числовой прямой.
Строгое неравенство — это тип неравенства, которое либо абсолютно больше, чем число, x> a, либо абсолютно меньше, чем число, x
С другой стороны, символ неравенства x \ ge a, который читается как «x больше или равен a», и символ неравенства x \ le a, который читается как «x меньше или равен a», являются оба нестрогих неравенств , потому что имеют условия равенства.
Неравенство \ color {red} x> — \, 4 является строгим неравенством, поэтому мы поместим пустой кружок над -4, так как он не является частью решений, и нарисуем стрелку вправо. Аналогично, \ color {red} x <6 - строгое неравенство, поэтому мы поместим пустой кружок над 6 и нарисуем стрелку влево.
Окончательный набор решений будет пересечением \ color {red} x> — \, 4 и \ color {red} x <6, которые являются числами от -4 до 6, но исключая конечные точки -4 и 6.
ШАГ 3. Запишите решения в интервальной записи.
Мы будем использовать закругленные скобки или круглые скобки с обеих сторон, чтобы обозначить, что обе конечные точки исключены из набора решений.
\ Large {\ left ({-4,6} \ right)}
Читается как «все числа больше -4, но меньше 6».
Помните: Этот тип интервала также известен как открытый интервал , потому что две конечные точки исключены из набора решений.То есть они НЕ являются частью решений.
Пример 3: Решите составное неравенство 5 — 3 \ left ({x — 2} \ right) \ le x — \ left ({- 2x + 13} \ right) и 5 - \ left ({x + 1} \ right) \ le 2 \ left ({7 — x} \ right) + 1. Изобразите множество решений, а затем запишите его решения в обозначениях интервалов.
ШАГ 1: Решите каждое неравенство.
Избавьтесь от скобок с каждой стороны неравенства используя распределительное свойство умножения над сложением. Складываем 5 и 6 слева. Вычтите обе стороны на 11. Вычтите обе стороны на 3x. Чтобы решить x, разделите обе части на -6. Поскольку мы делим каждую сторону на отрицательное число, мы изменим направление неравенства. То есть от «меньше или равно» до «больше или равно».
Складываем 5 и 6 слева. Вычтите обе стороны на 11. Вычтите обе стороны на 3x. Чтобы решить x, разделите обе части на -6. Поскольку мы делим каждую сторону на отрицательное число, мы изменим направление неравенства. То есть от «меньше или равно» до «больше или равно».
5 — 3 \ влево ({x — 2} \ right) \ le x — \ left ({- 2x + 13} \ right)
5 — 3x + 6 \ le x + 2x — 13
— 3x + 11 \ le 3x — 13
— 3x + 11-11 \ le 3x — 13 — 11
— 3x \ le 3x — 24
— 3x -3x \ le 3x — 3x + 24
— 6x \ le -24
{\ Large {{{- 6x} \ over {- 6}}}} \ le {\ Large {{{- 24} \ over {- 6}}}}
\ color {red} x \ ge 4
Удалите круглые скобки, используя распределительное свойство умножения сверх сложения.Вычтем 5 на 1 слева. Вычтем 4 из обеих частей неравенства. Затем прибавьте 2 раза к обеим сторонам, чтобы закончить.
5 — \ left ({x + 1} \ right) \ le 2 \ left ({7 — x} \ right) + 1
5 — x — 1 \ le 14 — 2x + 1
4 — x \ le 15 — 2x
4 — 4 — x \ le 15 — 4 — 2x
— x \ le 11 — 2x
— x + 2x \ le 11 — 2x + 2x
\ color {красный} x \ le 11
Решения задаются \ color {red} x \ ge 4 и \ color {red} x \ le 11.
ШАГ 2. Изобразите набор решений на числовой прямой.
Для \ color {red} x \ ge 4 закрасим кружок над 4, чтобы показать, что он включен в решения, потому что неравенство имеет условие равенства, то есть «больше или равно». Стрелка указывает вправо от 4, потому что у нее есть компонент «больше чем».
Для \ color {red} x \ le 11 мы также закрасим кружок над 11, чтобы указать, что он является частью набора решений, поскольку неравенство имеет условие равенства, то есть «меньше или равно ».Стрелка указывает слева от 11, потому что здесь меньше чем.
Что касается окончательного набора решений, мы находим все точки пересечения двух неравенств. Очевидно, они пересекаются между 4 и 11. Более того, они также перекрываются в конечных точках. Следовательно, окончательный набор решений содержит все точки между конечными точками 4 и 11, включая конечные точки.
ШАГ 3. Запишите набор решений в интервальной записи.
Мы будем использовать квадратные скобки с обеих сторон, чтобы обозначить, что обе конечные точки включены в набор решений.
\ Large {\ left [{4,11} \ right]}
Читается как «все числа больше или равные 4, но меньше или равные 11».
Помните: Этот тип интервала также известен как закрытый интервал , потому что две конечные точки включены в набор решений. То есть они являются частью решений.
Пример 4: Решите составное неравенство 3x — 2 \ left ({1 — x} \ right)
ШАГ 1. Решите каждое неравенство.
Распределите -2 на бином 1-x в левой части неравенства, чтобы убрать скобки. Добавьте также 3x и 2x с левой стороны. Добавьте 2 к обеим сторонам неравенства. Вычтите x с обеих сторон. Наконец, разделите обе части неравенства на 4.
3x — 2 \ left ({1 — x} \ right)
3x — 2 + 2x
5x — 2
5x — 2 + 2
5x
5x — x
4x <- 4
{\ Large {{{4x} \ over 4}}} <{\ Large {{{- 4} \ over 4}}}
\ color {red} x <- 1
Вычтем обе стороны неравенства на 10. Затем вычтите его с обеих сторон на x. Наконец, разделите каждую сторону на -2. Поскольку мы делим на отрицательное число, мы должны перевернуть или изменить направление символа неравенства. В этом случае от меньше чем до больше чем.
Затем вычтите его с обеих сторон на x. Наконец, разделите каждую сторону на -2. Поскольку мы делим на отрицательное число, мы должны перевернуть или изменить направление символа неравенства. В этом случае от меньше чем до больше чем.
10 — x
10 — 10 — x
— x
— x — x
— 2x <- 8
{\ Large {{{- 2x} \ over {- 2}}}}> {\ Large {{{- 8} \ over {- 2}}}}
\ color {red} x> 4
Обратите внимание, что решения двух неравенств \ color {red} x <- 1 и \ color {red} x> 4 не пересекаются, и, следовательно, составное неравенство не имеет решения .
Более очевидно, что они не пересекаются, если мы посмотрим на их графики на числовой прямой.
Пример 5: Решите составное неравенство — 5 <3x + 7 \ le 22. Изобразите набор решений, затем запишите его решения в обозначении интервала.
Это гибридно выглядящее неравенство, состоящее из двух символов неравенства и трех частей, на самом деле является комбинацией двух неравенств, соединенных соединением «И».
Мы можем разделить это составное неравенство на два неравенства с помощью соединителя «И», а затем решить их как обычно.Вот как это выглядит, если разложить составное неравенство на два более простых неравенства.
Однако нет необходимости разделять его на два неравенства. Мы можем решить сложное неравенство в его нынешнем виде. На самом деле мне нравится такой, как есть, потому что его намного проще решить.
Цель состоит в том, чтобы изолировать переменную средней части. Чтобы все было сбалансировано, что бы мы ни делали в средней части, мы должны делать то же самое и с левой, и с правой стороны. Когда все будет сделано правильно, ответ должен получиться красиво!
Поехали.Давайте разберемся!
ШАГ 1: Решите сложное неравенство.
Чтобы найти x, мы вычитаем среднее значение на 7, что означает, что мы должны проделать то же самое с левой и правой частью составного неравенства. Наконец, чтобы изолировать x, мы делим середину на 3, и делаем то же самое слева и справа.
— 5 <3x + 7 \ le 22
— 5 {\ color {red} — 7} <3x + 7 {\ color {red} - 7} \ le 22 {\ color {red} - 7}
— 12 <3x \ le 15
{\ Large {{{- 15} \ over {\ color {red} 3}}}} <{\ Large {{{3x} \ over {\ color {red} 3 }}}} \ le {\ Large {{{15} \ over {\ color {red} 3}}}}
— 4
Решения даются как — 4
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ Large {\ left ({-4,5} \ right]}
Читается как «все числа больше -4, но меньше или равные 5».
Неравенства соединения «ИЛИ»
Решите составное неравенство «или», решая каждое из двух неравенств по отдельности. Для случая «или» мы хотим найти все числа, которые могут сделать по крайней мере одно из двух неравенств истинным .
Пример 6: Решите составное неравенство 2x — 5> 3x + 2 или x — 1 <2x - 5. Изобразите решения на числовой прямой. Затем запишите свои решения в интервальной записи.
Изобразите решения на числовой прямой. Затем запишите свои решения в интервальной записи.
ШАГ 1. Решите каждое неравенство.
Добавьте 5 к обеим сторонам неравенства. Затем вычтите 3x с обеих сторон. Наконец, разделите -1 на обе стороны. Не забудьте перевернуть символ неравенства, потому что мы разделили число на отрицательное.
2x — 5> 3x + 2
2x — 5 + 5> 3x + 2 + 5
2x> 3x + 7
2x — 3x> 3x — 3x + 7
-x> 7
{\ Large {{{- x} \ over {- 1}}}} <{\ Large {{7 \ over {- 1}}}}
\ color {красный} x <- 7
Сложите обе стороны на 1.Затем вычтите 2x в обе стороны. Разделите обе части неравенства на -1, изменив направление символа неравенства.
x — 1 <2x - 5
x — 1 + 1 <2x - 5 + 1
x <2x - 4
x — 2x <2x - 2x - 4
— x <- 4
{ \ Large {{{- x} \ over {- 1}}}}> {\ Large {{4 \ over {- 1}}}}
\ color {red} x> 4
Решения даны по формуле \ color {red} x <- 7 или \ color {red} x> 4.
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ left ({- \ infty, 7} \ right) \ cup \ left ({4, \ infty} \ right)
Читается как «все числа меньше отрицательного 7 или все числа больше чем 4 “.
Пример 7: Решите составное неравенство 2 \ left ({x + 1} \ right) \ le x — 2 или 3 \ left ({x — 1} \ right) \ le 4x — 3. Постройте график решения на числовой прямой. Затем запишите свои решения в интервальной записи.
ШАГ 1. Решите каждое неравенство.
Разложите 2 на количество (x + 1). Вычтем 2 из обеих частей неравенства. Наконец, вычтите x с обеих сторон, чтобы получить окончательное решение.
Распределите 3 на количество (x-1). Затем прибавьте 3 к обеим сторонам неравенства. Затем вычтите стороны в 4 раза.Наконец, разделите обе стороны на -1. Не забудьте изменить направление неравенства с «меньше или равно» на «больше или равно».
Затем прибавьте 3 к обеим сторонам неравенства. Затем вычтите стороны в 4 раза.Наконец, разделите обе стороны на -1. Не забудьте изменить направление неравенства с «меньше или равно» на «больше или равно».
Решения представлены как \ color {red} x \ le — 4 или \ color {red} x \ ge 0.
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ left ({- \ infty, — 4} \ right) \ cup \ left ({0, \ infty} \ right)
Читается как «все числа, меньшие или равные -4 или все числа больше или равные 0 “.
Пример 8: Решите составное неравенство 2 \ left ({x + 1} \ right) — 3 \ left ({x + 1} \ right) <0 или 4x + 3 \ ge 15 + 6x. Изобразите набор решений на числовой прямой. Затем запишите набор решений в обозначении интервалов.
ШАГ 1. Решите каждое неравенство.
Дважды примените распределительное свойство умножения по сложению слева от неравенство. Объедините похожие термины. Добавьте по 1 с обеих сторон. Наконец, разделите обе части неравенства на -1. Не забудьте поменять направление открытия символа неравенства, так как мы разделили на отрицательное число.
Объедините похожие термины. Добавьте по 1 с обеих сторон. Наконец, разделите обе части неравенства на -1. Не забудьте поменять направление открытия символа неравенства, так как мы разделили на отрицательное число.
Вычтем 3 с обеих сторон с последующим вычитанием 6x. Разделите каждую сторону на -2 и переверните направление неравенства.
Решения даются как \ color {red} x> — 1 или \ color {red} x \ le — 6.
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ left ({- \ infty, — 6} \ right] \ cup \ left ({- 1, \ infty} \ right)
Читается как «все числа меньше или равные -6 или все числа больше или равны -1 «.
Пример 9: Решите составное неравенство 0 <3 - \ left ({x + 4} \ right) или 2 <1 - \ left ({x - 2 } \правильно).Изобразите набор решений на числовой прямой. Затем запишите набор решений в обозначении интервалов.
Затем запишите набор решений в обозначении интервалов.
ШАГ 1. Решите каждое неравенство.
Примените свойство распределения к правой части неравенства, затем добавьте x к обеим сторонам неравенства.
Примените свойство распределения с правой стороны, затем добавьте x к обеим сторонам неравенства.Наконец, вычтите 2 с обеих сторон, чтобы получить окончательный ответ.
Решения представлены как \ color {red} x <- 1 или \ color {red} x <1.
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ left ({- \ infty, 1} \ right)
Читается как «все числа меньше 1».
Пример 10: Решите составное неравенство 10x — 8 <7x + 7 или 3x - 2 \ left ({2 - x} \ right) \ ge 1. Изобразите набор решений на числовой прямой. Затем запишите набор решений в обозначении интервалов.
Изобразите набор решений на числовой прямой. Затем запишите набор решений в обозначении интервалов.
ШАГ 1. Решите каждое неравенство.
Добавьте 8 к обеим сторонам. Затем вычтите 7x с обеих сторон. Наконец, разделите обе части на положительное число 3.
Примените свойство распределения к левой части. Объедините похожие термины. Добавьте по 4 штуки с обеих сторон.Наконец, разделите положительное число 5 на обе стороны.
Решения представлены как \ color {red} x <5 или \ color {red} x \ ge 1.
ШАГ 2. Изобразите набор решений на числовой прямой.
ШАГ 3. Запишите решения в интервальной записи.
\ left ({- \ infty, \ infty} \ right)
Читается как «все действительные числа».
Возможно, вас также заинтересует:
Решение линейных неравенств
Решение квадратичных неравенств
Решение квадратичных неравенств
Чтобы решить квадратное неравенство, выполните следующие действия:
Пример 1
Решить ( x — 3) ( x + 2)> 0.
Решить ( x — 3) ( x + 2) = 0. По свойству нулевого произведения
Отметьте граничные точки. Здесь граничные точки — белые кружки, потому что исходное неравенство не включает равенство (см.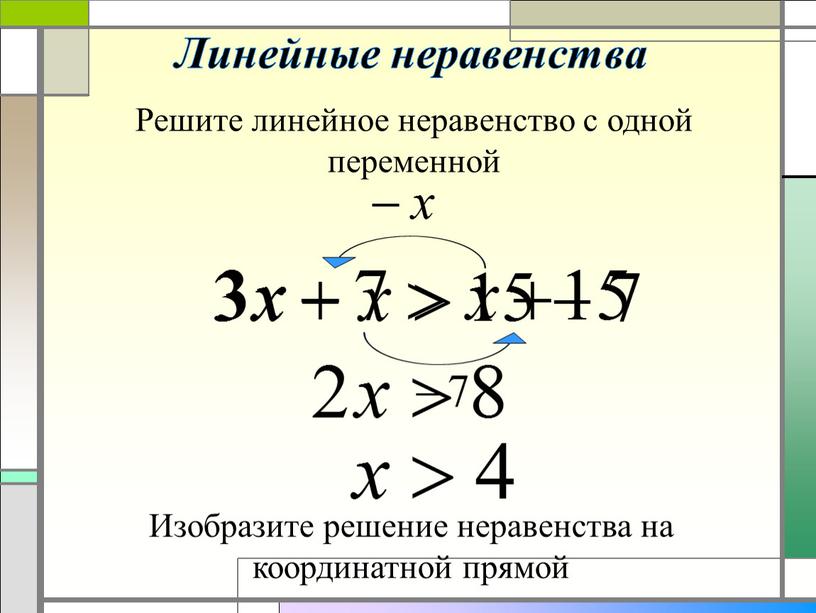 Рисунок 1).
Рисунок 1).
Выберите точки из разных созданных регионов (см. Рисунок 2).
Проверьте, удовлетворяют ли контрольные точки исходному неравенству.
Поскольку x = –3 удовлетворяет исходному неравенству, область x <–2 является частью решения. Поскольку x = 0 не удовлетворяет исходному неравенству, область –2 < x <3 не является частью решения. Поскольку x = 4 удовлетворяет исходному неравенству, область x > 3 является частью решения.
Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 3.
Форма набора решений: { x | x <–2 или x > 3}.
Рисунок 1. Граничные точки.
Рисунок 2. Созданы три региона.
Рисунок 3. Решение для примера
Пример 2
Решить 9 x 2 — 2 ≤ –3 x .
По факторингу,
Отметьте граничные точки сплошными кружками, как показано на рисунке 4, поскольку исходное неравенство включает равенство.
Выберите точки из созданных регионов (см. Рисунок 5).
Проверьте, удовлетворяют ли контрольные точки исходному неравенству.
Поскольку x = –1 не удовлетворяет исходному неравенству, эта область не является частью решения. Поскольку x = 0 действительно удовлетворяет исходному неравенству, область является частью решения.Поскольку x = 1 не удовлетворяет исходному неравенству, область составляет , а не часть решения.
Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 6.
Установленная форма
Рис. 4. Сплошные точки означают включение.
Рисунок 5. Области для тестирования в примере
Рисунок 6. Решение примера.
Пример 3
Решить 4 т 2 — 9 <–4 т .
Так как этот квадратичный коэффициент нелегко факторизовать, для его решения используется формула квадратичного уравнения.
Уменьшить, разделив общий множитель 4.
Начиная с примерно 3,2,
Отметьте граничные точки открытыми кружками, как показано на рис. 7, поскольку исходное неравенство не включает равенства.
Выберите точки из разных созданных регионов (см. Рисунок 8).
Проверьте, удовлетворяют ли контрольные точки исходному неравенству.
Поскольку t = 3 не удовлетворяет исходному неравенству, область не является частью решения. Поскольку t = 0 действительно удовлетворяет исходному неравенству, область является частью решения. Поскольку t = 2 не удовлетворяет исходному неравенству, область не является частью решения.
Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 9.
Форма набора решений
Рисунок 7.Открытые точки означают исключение.
Рисунок 8. Области для тестирования для примера.


 Налим (рис) – хищная рыба и в наших
холодных северных реках его масса
достигает 24 кг, а длина – свыше 1 метра.
В тёплых же водоёмах его масса снижается
даже до 1 кг. И размножается налим
зимой.
Налим (рис) – хищная рыба и в наших
холодных северных реках его масса
достигает 24 кг, а длина – свыше 1 метра.
В тёплых же водоёмах его масса снижается
даже до 1 кг. И размножается налим
зимой. 726 км 2.273 км 4.400км
726 км 2.273 км 4.400км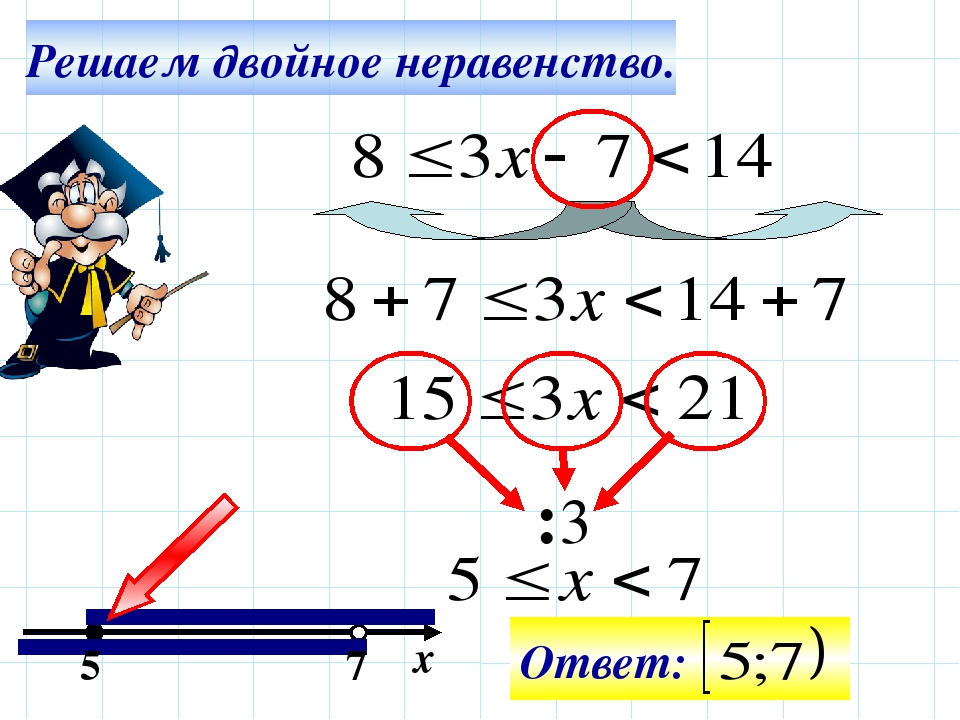 – росомаха – 1м
– росомаха – 1м


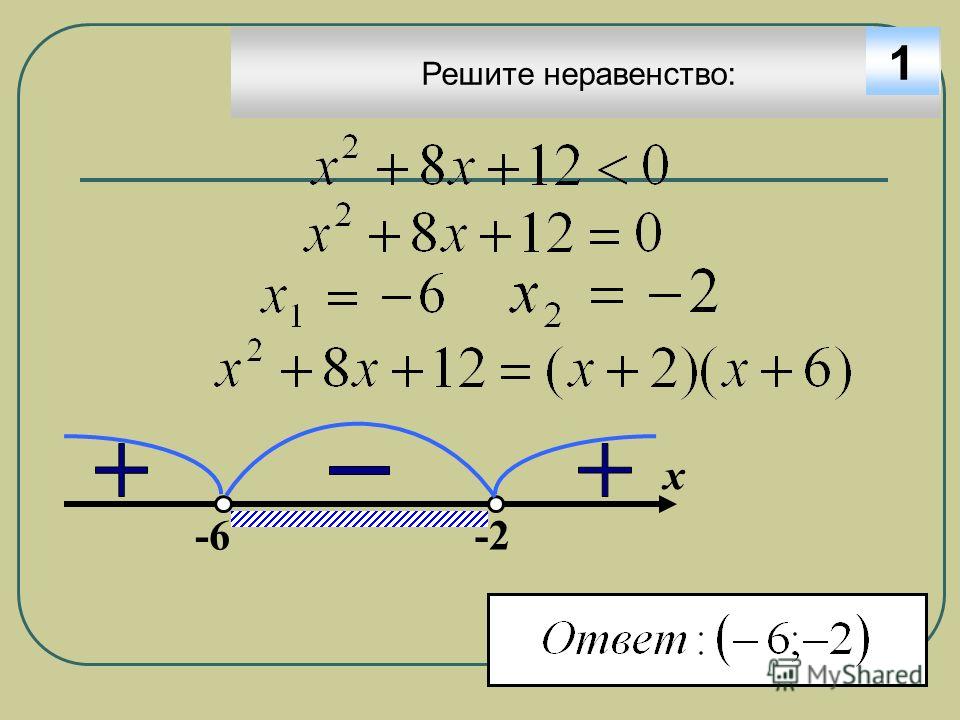
 Взаимопроверка в парах.
Взаимопроверка в парах.



 На последнем графике будут показаны все числа, которые делают оба неравенства истинными — числа, заштрихованные на на обоих первых двух графиков.
На последнем графике будут показаны все числа, которые делают оба неравенства истинными — числа, заштрихованные на на обоих первых двух графиков.





 06 \, {\ color {red} {- \, 24.72}} \ leq 24.74 \, {\ color {red} {- \, 24.72}} + 1.54x \ leq 171.02 \, {\ color {красный) } {- \, 24.72}} \)
06 \, {\ color {red} {- \, 24.72}} \ leq 24.74 \, {\ color {red} {- \, 24.72}} + 1.54x \ leq 171.02 \, {\ color {красный) } {- \, 24.72}} \)
 Итак, я установил y равным нулю и решаем:
Итак, я установил y равным нулю и решаем: Это происходит слева от точки перехвата:
Это происходит слева от точки перехвата: Вы можете
следуйте тому же методу поиска точек пересечения и использования графиков для решения
неравенства, содержащие квадратичные.
Вы можете
следуйте тому же методу поиска точек пересечения и использования графиков для решения
неравенства, содержащие квадратичные. Но это просто! Поскольку это «отрицательная» квадратичная функция, она
графики
как перевернутая парабола.
Но это просто! Поскольку это «отрицательная» квадратичная функция, она
графики
как перевернутая парабола. В
нули были бы одинаковы: x = 2 и x = 2. Но эта парабола
был бы правой стороной вверх, поскольку квадратичный был бы «положительным».
Это нормально, потому что, умножая на 1,
Я бы перевернул неравенство, поэтому искал бы где
квадратичная на больше, чем нуля (то есть там, где парабола выше оси).Поскольку парабола была бы направлена вверх,
график был бы выше осей на концах; так что решение
получилось бы таким же, как и раньше: x <2 или x > 2:
В
нули были бы одинаковы: x = 2 и x = 2. Но эта парабола
был бы правой стороной вверх, поскольку квадратичный был бы «положительным».
Это нормально, потому что, умножая на 1,
Я бы перевернул неравенство, поэтому искал бы где
квадратичная на больше, чем нуля (то есть там, где парабола выше оси).Поскольку парабола была бы направлена вверх,
график был бы выше осей на концах; так что решение
получилось бы таким же, как и раньше: x <2 или x > 2: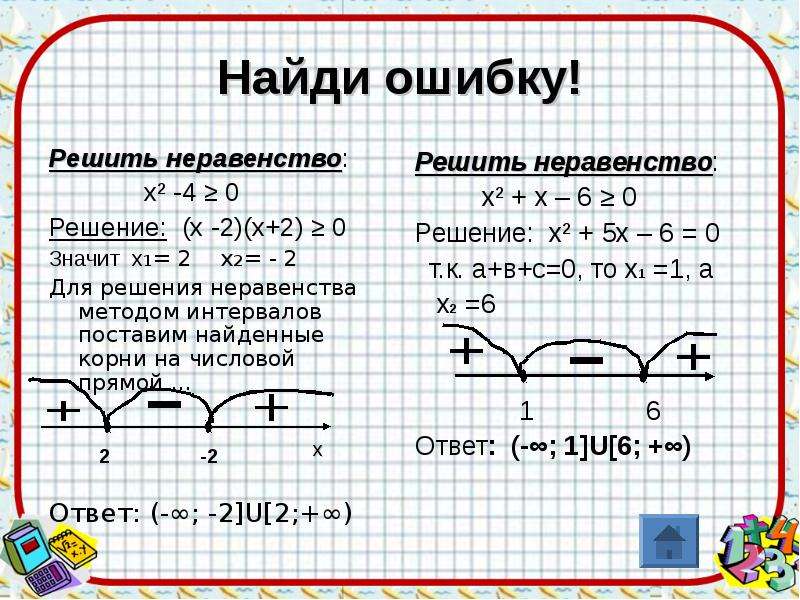 «Решение квадратичных неравенств: концепции». Purplemath .
Доступно по номеру
«Решение квадратичных неравенств: концепции». Purplemath .
Доступно по номеру 

