Круги Эйлера — это… Что такое Круги Эйлера?

Круги́ Э́йлера^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.

[2]

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

Множества А и B

См. также

Примечания

1. ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
2. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.

Логика
Формальная	Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление Изменение объёма понятия: сложение • умножение • вычитание Типы: Многозначная логика • Бинарная логика Законы: Закон обратного отношения между содержанием и объёмом понятия
Математическая (теоретическая, символическая)	Логические связки (операции) над высказываниями Высказывание — построение над множеством {B, , , , 0, 1} В — непустое множество, над элементами которого определены три операции: конъюнкция ( или &,бинарная) • дизъюнкция (,бинарная) • отрицание (,унарная) 2 константы: импликация () • Круги Эйлера/Диаграмма Венна • Теория множеств

biograf.academic.ru

круги Эйлера | Социальная сеть работников образования

Слайд 1

Круги Эйлера Работу выполнила учащаяся 8 «а»класса МОУ «СОШ № 56» Угрюмова Кристина Руководитель: Прохорова С.А

Слайд 2

Цель исследования : Знакомство с новым методом решения задач и изучение материала, применяемого на уроках математики и внеурочных занятиях, где можно использовать круги Эйлера как один из приемов решения задач.

Слайд 3

Актуальность работы состоит в том, что задачи имеют практический характер. Задачи развивают логическое мышление, заставляют задумываться, подходить к решению какой либо проблемы с разных сторон, выбирать из множества способов решения наиболее простой, легкий путь. Актуальность

Слайд 4

— Познакомиться с биографией одного из величайших ученых-математиков Леонарда Эйлера ; — Изучить теоретические основы понятия «Круги Эйлера»; — Решить ряд задач вышеназванным методом; Задачи исследования :

Слайд 5

Биография Леонард Эйлер родился 15 апреля 1707 года в семье пастора, жившеи ̆ в швейцарском городке Базеле. Начальное обучение Эйлер получил под руководством отца, который готовил его к духовной карьере. С детства увлекался математикой . В 13 лет Леонард Эйлер стал студентом факультета искусств Базельского университета . В 17 лет был удостоен учёнои ̆ степени магистра . В 19-лет Эйлер был включен в число кандидатов на должность профессора физики .

Слайд 6

Великии ̆ учёныи ̆ — Леонард Эйлер занимает одно из первых мест в истории мировой науки. Полное собрание его трудов составляет 72 тома, более 850 научных работ. Этот тихий и скромный человек, полностью ослепший, много работал, совершив великое множество научных открытий. С точки зрения математики, XVIII век — это век Эйлера. Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».

Слайд 7

Эйлер активно трудился до последних дней. 7 сентября после обеда, проведённого в кругу семьи, беседуя с астрономом А. И. Лекселем о недавно открытои ̆ планете Уран и её орбите, он внезапно почувствовал себя плохо и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг. Похоронен на Смоленском лютеранском кладбище в Петербурге. Умирая, он оставил много рукописей, которые Петербургская академия публиковала в течение последующих 47 лет.

Слайд 8

– геометрическая схема, с помощью которой можно изобразить отношения между множествами. Впервые он использовал их в письмах к немецкой принцессе. Эйлер писал тогда, что круги очень подходят для того, чтобы «облегчить наши размышления.» Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры. Круги Эйлера

Слайд 9

В математике множеством называют совокупность, набор каких-либо предметов (объектов). Предметы, составляющие множество, называются его элементами. Множества обычно обозначаются большими буквами латинского алфавита: А, В, С,… . Термин «множество» употребляется независимо от того, много или мало в этом множестве элементов, Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø

Слайд 10

Покажем, например, С помощью диаграммы Эйлера, что множество А является подмножеством множества В: С помощью такой диаграммы становиться наглядным, например, такое утверждение: если А принадлежит В, а В принадлежит С, то А принадлежит С.

Слайд 11

Пересечением двух множеств А и В называют множество, состоящее из всех общих элементов множеств А и В, т. е. Из всех элементов, которые принадлежат и множеству А, и множеству В. А В А ∩ В

Слайд 12

Объединением С двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих множеству А или множеству В. Обозначают это так: С = А U В. Иными словами, в объединение входят все элементы, принадлежащие хотя бы одному из множеств. А U В

Слайд 13

Разность множеств Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В. A B

Слайд 14

1. ВНИМАТЕЛЬНО ИЗУЧИ УСЛОВИЕ ЗАДАЧИ 2. ПОСТРОЙ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ 3. РАССТАВЬ ИСХОДНЫЕ ДАННЫЕ 4. НАЙДИ НЕДОСТАЮЩИЕ ДАННЫЕ 5. ПРОВЕРЬ РЕШЕНИЕ АЛГОРИТМ

Слайд 15

В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое? Решение: Так как 26 половина детей любит пирожные, а 20 — и пирожные, и мороженое, то исключительно пирожное любят ровно 6 человек. Всего ребят 52, из них 6 — любители только пирожных, значит, 52 – 6 = 46 человек, которые любят мороженое.

Слайд 16

Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг? Решение: : Изобразим два круга, так как у нас два вида цветовПоскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Слайд 17

Гарри Поттер, Рон и Гермиона На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон? Решение Учитывая условия задачи, чертеж будет таков: Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон. Ответ. 8 книг прочитал Рон. 5 8

Слайд 18

В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта? Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х ) человек, только автобусом и троллейбусом — (9 − х ) человек, только метро и автобусом — (12 − х ) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х ) − (10 − х ) − х = х − 2 Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение: Х + (12 − х ) + (9 − х ) + (10 − х ) + ( х + 4) + ( х − 2) + ( х − 6) = 30. отсюда х = 3

Слайд 19

Из 100 отдыхающих на турбазе « Графское » , 30 детей — отличники учебы, 28 — участники олимпиад, 42 — спортсмены. 8 учащихся одновременно участники олимпиад и спортсмены, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп? Решение: 20+13+30+3+5+7+2=80 (детей) 100-80=20 (детей не входят ни в одну из групп)

Слайд 20

Выводы Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.

Слайд 21

«Чем нагляднее метод, тем очевиднее решение»

Слайд 22

Спасибо за внимание !

nsportal.ru

Окружность Эйлера — это… Что такое Окружность Эйлера?



Окружность Эйлера

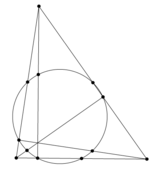
В геометрии треугольника окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек.

Окружность девяти точек получила такое название из-за следующей теоремы:

Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности.

Окружность девяти точек обладает ещё целым рядом свойств:

• Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.
• Радиус окружности девяти точек равен половине радиуса описанной окружности. Более того, описанная окружность есть образ окружности девяти точек относительно гомотетии с центром в ортоцентре и коэффициентом 2.
• (теорема Фейербаха) Окружность девяти точек произвольного треугольника касается вписанной и всех трёх вневписанных окружностей этого треугольника.

История

Эйлер в 1765 году доказал, что основания высот и середины сторон лежат на одной окружности (отсюда название «окружность шести точек»). Первое полное доказательство общего результата было, по-видимому, опубликовано в 1821 году, но есть указания на то, что оно было известно и ранее.

См. также

Ссылки

Литература

Wikimedia Foundation. 2010.

• Окружность Аполония
• Окружок

Смотреть что такое «Окружность Эйлера» в других словарях:

• Окружность девяти точек — 9 точек Окружность девяти точек  это окружность, проходящая через середины всех трёх сторон треугольника. Она также назы …   Википедия

• Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф …   Википедия

• ДЕВЯТИ ТОЧЕК ОКРУЖНОСТЬ — окружность Эйлера, окружность, на к роп расположены середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр треугольника с вершинами. Ее радиус равен половине радиуса окружности, описанной около треугольника.… …   Математическая энциклопедия

• Список объектов, названных в честь Леонарда Эйлера — Существует множество математических и физических объектов, названных в честь Леонарда Эйлера: Содержание 1 Теоремы 2 Лемма 3 Уравнения 4 …   Википедия

• Интеграл Эйлера — Существует множество математических и физических объектов, названных в честь Леонарда Эйлера: Содержание 1 Теоремы 2 Лемма 3 Уравнения 4 Тождества 5 …   Википедия

• Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри …   Википедия

• Теорема Эйлера (планиметрия) — В планиметрии, теорема Эйлера, названная в честь Леонарда Эйлера, утверждает, что расстояние d между центрами вписанной и описанной окружностей треугольника может быть определено по формуле где R и r  радиусы, соответственно, описанной и… …   Википедия

• Описанная окружность — многоугольника  окружность, содержащая все вершины многоугольника. Центром является точка (принят …   Википедия

• Вневписанная окружность — Вписанная (с центром I) и 3 вневписанные (с центрами в J) окружности в Вневписанная …   Википедия

• Характеристика Эйлера — В алгебраической топологии, эйлерова характеристика есть топологический инвариант (и даже гомотопический инвариант) определённый на большом классе топологических пространств. Обычно эйлерова характеристика пространства X обозначается χ(X).… …   Википедия

dic.academic.ru

Что такое круги Эйлера 🚩 задачи на круги эйлера 🚩 Математика

Если Вы считаете, что ничего не знаете о таком понятии, как круги Эйлера, то вы глубоко заблуждаетесь. Еще из младшей школы известны схематические изображения, или кружки, позволяющие наглядно осмыслить взаимоотношения между понятиями и элементами системы.

Метод, придуманный Леонардом Эйлером, использовался ученым для решения сложных математических задач. Кругами он изображал множества и сделал эту схему основой такого понятия, как символическая логика. Метод призван максимально упростить рассуждения, направленные на решении той или иной задачи, именно поэтому методика активно используется как в младшей школе, так и в академической среде. Интересно, что подобный подход был ранее использован немецким философом Лейбницем, а позже был подхвачен и применен в различных модификациях известными умами в области математики. Например, прямоугольные схемы чешского математика Больцано, Шредера, Венна, известного созданием популярной диаграммы, основанной на этом простом, но удивительно действенном методе.

Круги являются основой так называемых «наглядных интернет мемов», которые основаны на схожести признаков отдельных множеств. Забавно, наглядно, а главное понятно.

Круги мысли

Круги позволяют наглядно описать условия задачи и мгновенно принять верное решение, или выявить направление движение в сторону правильного ответа. Как правило, круги Эйлера используются для решения логико-математических задач, связанных с множествами, их объединениями или частичными наложениями. В пересечение кругов попадают объекты, обладающие свойствами каждого из изображенных кружком множеств. Объекты, не вошедшие в множество, находятся за пределами того или иного круга. Если понятия абсолютно равнозначны, они обозначаются одним кругом, представляющим собой объединение двух множеств, имеющих равные свойства и объемы.

Логика взаимосвязей

Используя круги Эйлера, вы можете решить ряд бытовых задач и даже определиться с выбором будущей профессии, стоит лишь проанализировать свои возможности и желания и выбрать их максимальное пересечение.

Теперь становится ясно, что круги Эйлера вовсе не абстрактное математическое и философское понятие из разряда теоретических знаний, они имеют весьма прикладное и практическое значение, позволяя разобраться не только с простейшими математическими проблемами, но и решить важные жизненные дилеммы наглядным и понятным каждому способом.

www.kakprosto.ru

Круги Эйлера в информатике

Сегодня разберём задачу на круги Эйлера в информатике.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

Рассмотрим метод Эйлера на примере:

Задача: В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (В тысячах)
(Информатика & ОГЭ) | (Информатика & ЕГЭ)	1100
Информатика & ЕГЭ	600
Информатика & ОГЭ & ЕГЭ	50

Какое количество страниц (в тыс.) будет найдено по запросу Информатика & ОГЭ ?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменился за время выполнения запросов.

Решение: Рассмотрим первый запрос: (Информатика & ОГЭ) | (Информатика & ЕГЭ). Нарисуем первую и вторую часть запроса отдельно в виде кругов Эйлера.

Чтобы применить операцию «И», необходимо закрасить только ту область, которая является общей для двух множеств, к которым применяется эта логическая операция. Чтобы применить операцию «ИЛИ» к двум или нескольким множествам, необходимо объединить эти области. У нас на рисунке изображено (Информатика & ОГЭ) и (Информатика & ЕГЭ) жёлтым цветом. Теперь необходимо применить к этим областям операцию «ИЛИ», т.е. объеднить эти области.

Второй запрос Информатика & ЕГЭ у нас уже нарисован на первой картинке справа. Теперь изобразим третий запрос Информатика & ОГЭ & ЕГЭ. Пересечение всех трёх окружностей.

Нас спрашивают, какое количество страниц (в тыс.) будет найдено по запросу Информатика & ОГЭ. Из рисунков видно, пересечение Информатика & ОГЭ состоит из двух частей: (Информатика & ОГЭ) | (Информатика & ЕГЭ) — (Информатика & ЕГЭ) и (Информатика & ОГЭ & ЕГЭ)

.

Тогда ответ будет (1100 — 600) + 50 = 550.

На этом всё. Не пропустите новые статьи!

Сортировка простым выбором C#

Привет! Сегодня рассмотрим cортировку методом простого выбора (простог…
Категория: Алгоритмы  Подкатегория: СортировкаДата: 15-01-2018 в 16:47:34 0

code-enjoy.ru