Способы… способы решения неполных квадратных уравнений:

Алгоритм решения неполных квадратных уравнений с дискриминантом и без него
Неполное квадратное уравнение – квадратное уравнение вида ах2+bх+с=0, где хотя бы один из коэффициентов b или с равен нулю.
Неполные квадратные уравнения бывают трёх видов:
1 тип – ах2+с=0, где с не равен нулю
2 тип – ах2+bх=0, где b не равен нулю
3 тип – ах2=0, где и b, и с равны нулю

Решение неполного квадратного уравнения 1 типа (ах2+с=0):
1) с дискриминантом
В уравнении ax2+bx+c=0 коэффициент b равен нулю
D=02- 4ac= — 4ac
Дискриминант отрицательный, значит, уравнение не имеет корней, если коэффициенты а или с однозначны (оба положительные или отрицательные) . Если или а, или с меньше нуля, уравнение будет иметь два корня (минус на минус даёт плюс) :

Например:
7х2 – 28 = 0
D = 02 – 4∙7∙(-28) = 784 > 0 (2 корня)

Ответ: — 2; 2

2) без дискриминанта
ах2+с=0
Чтобы решить уравнение без дискриминанта, надо перенести с на правую сторону:
ах2= — с
А дальше решать как обычное квадратное уравнение:

Если а и с – положительные числа, то уравнение не будет иметь корней. Если а или с – отрицательное число, то уравнение будет иметь два корня.

Например:
7х2 – 28 = 0
7х2 = 28
х2 = 28:7
х2 = 4
,
Ответ: 2; -2

Решение неполного квадратного уравнения 2 типа (ах2+bх=0):
1) с дискриминантом
ах2+bх+0=0
D=b2+4a∙0=b2

Например:
5х2 – 12х = 0
D = (-12)2 – 4∙5∙0 = 144 > 0 (2 корня)

Ответ: 0; 2,4

2) без дискриминанта
ах2+bх=0
Множитель х вынесем за скобки:
х (ах+b)=0
x1=0 или ах+b=0
ax= — b

Например:
5х2 – 12х = 0
х (5х – 12) = 0
5х – 12 = 0
5х = 12
х1 = 0 х2 = 12:5 = 2,4
Ответ: 0; 2,4
Решение неполного квадратного уравнения 3 типа (ах2=0):
1) с дискриминантом
ах2+0х+0=0
D=02+4∙0∙a=0

Например:
7х2 = 0
D = 02 – 4∙7∙0 = 0 – 0 = 0 (1 корень)

Ответ: 0
2) без дискриминанта
ах2=0
х2=0

Например:
7х2 = 0
х2 = 0:7 = 0
х = 0
Ответ: 0
Уравнение вида ах2=0 равносильно уравнению вида х2=0 и имеет только один корень 0

квадратное уравнение. зачем вообще надо находит когда квадратное уравнение равно нулю?

Тебе нужно найти при каких значениях икс уравнение равно нулю.

Если вас интересует практическое применение квадратичного уравнения, то как пример могу привести задачу о движения тела под действием силы тяжести. То есть применяется для баллистических расчетов в артиллерии. Поскольку выпущенный снаряд движется по параболической траектории, а парабола это кривая, выражающая квадратичное уравнение. Множество задач в жизни приводит к необходимости решения подобного уравнения.

То что квадратное уравнение = 0, не обозначает что у него нет решений! Вот ещё кое что: дискриминант>0 (два корня) дискриминант=0 (один корень или одинаковые повторяющиеся) дискриминант<0 (корней нет)

Согласен. Действительно зачем заниматься тем, что в результате дает ноль. Скажем, бизнес-план, предлагающий нулевую прибыль. Глупость!

Отлично рассказано тут: <a rel=»nofollow» href=»https://youtu.be/z5-EEkgnvAY?t=13m51s» target=»_blank»>https://youtu.be/z5-EEkgnvAY?t=13m51s</a> Краткая суть — вычислить длину стен двухкомнатной квартиры с известной площадью и длиной одной из стен. Не поверите, только вчера из этого видео узнал, для чего квадратные уравнения придумали изначально, и кто первый до этого додумался! )))

Какое уравнение не имеет корней? Примеры уравнений

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

1. Линейное уравнение

Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax² + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b² — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а < 0 ветви опущены вниз. Если дискриминант отрицателен, такое квадратное уравнение не имеет корней на множестве действительных чисел.

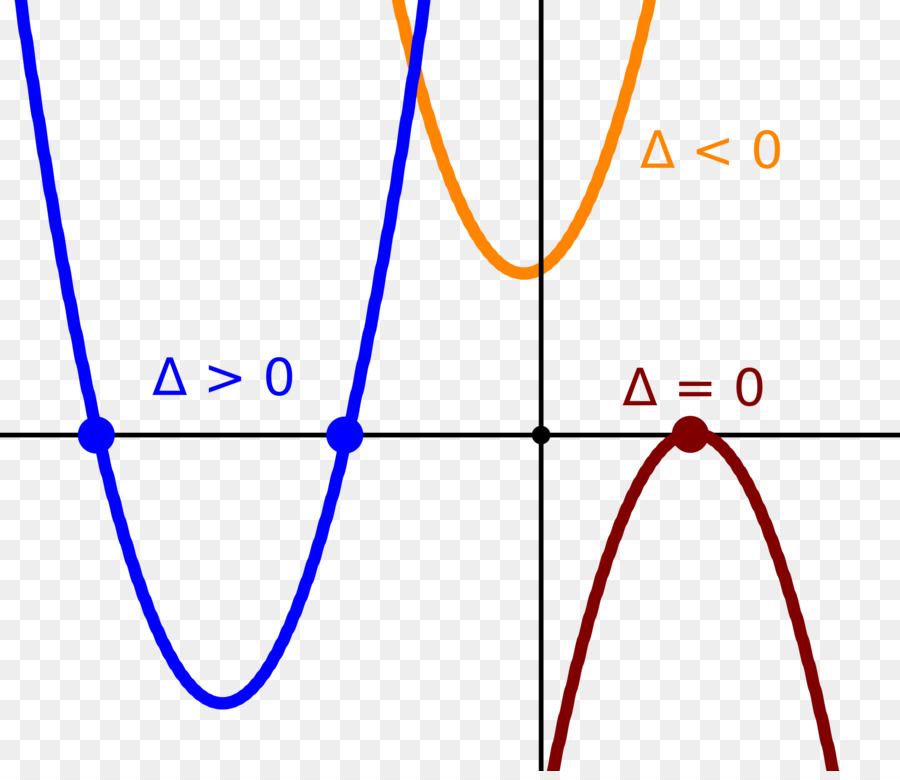
Также можно определить визуально количество корней, не вычисляя дискриминант. Для этого нужно найти вершину параболы и определить в какую сторону направлены ветви. Определить координату x вершины можно по формуле: х₀ = -b / 2a. В этом случае координата y вершины находится простой подстановкой значения х₀ в изначальное уравнение.

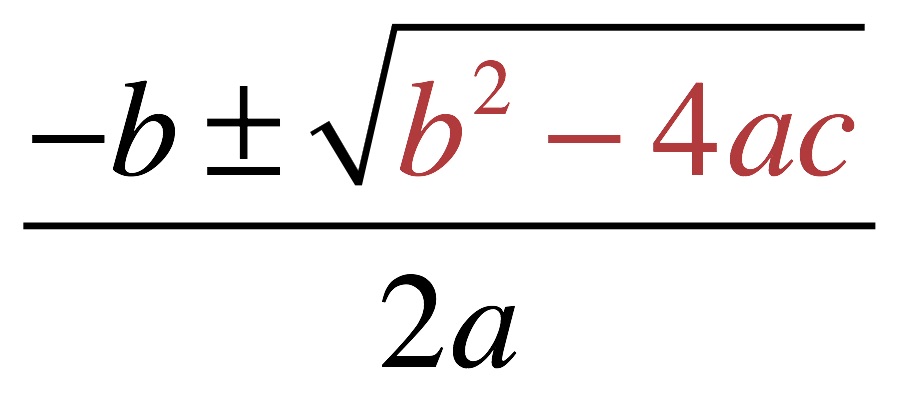
Квадратное уравнение x² – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8)² – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

3. Тригонометрические уравнения

Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

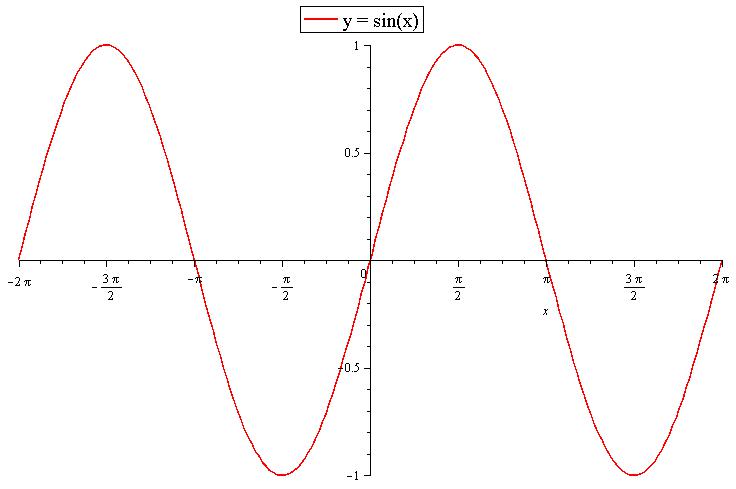
Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

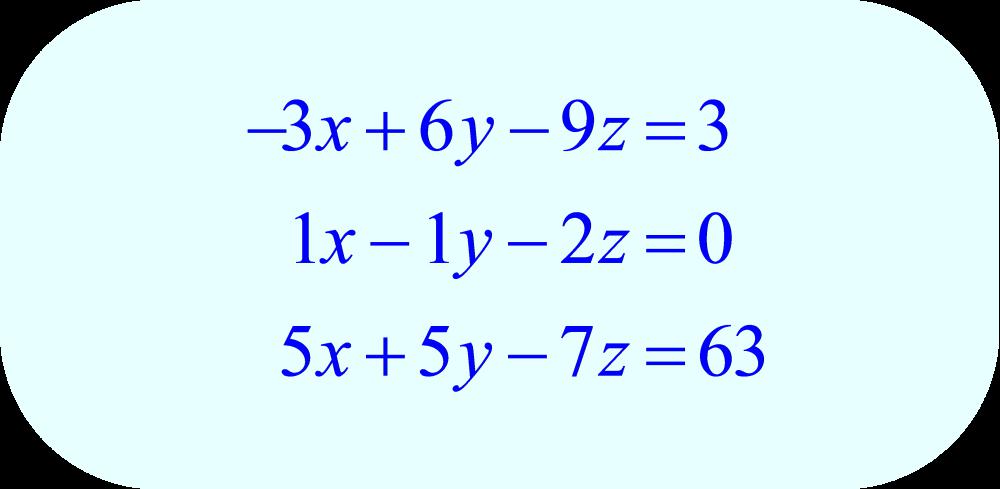
Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Обсуждение:Квадратное уравнение — Википедия

Материал из Википедии — свободной энциклопедии

Администратор, возможно-ли в содержание добавить ещё один раздел…»Нахождение корней по сумме коэффециентов» ??? Описание я дам, только раздел нужен! Итак если возможно, то нужно вставить после т. Виета.

GenHunt 22:48, 13 мая 2008 (UTC)Спасибо, Геннадий.

Добавил. — Obersachse 22:57, 13 мая 2008 (UTC)

Маловато, как-то… —OZH 11:59, 6 октября 2009 (UTC)

Ну так вперед — возьми, да и напиши что-нибудь, или попереводи из англовики :). Не жди пока это сделают другие. — X7q 14:00, 6 октября 2009 (UTC)

 :-/ Я попробую, конечно. А если это кому-то не понравится. Ведь, тут нельзя обойтись какой-то одной статьёй. А Вы хотите… —OZH 12:55, 7 октября 2009 (UTC)

Почитай ВП:ПС, и больше никогда не переживай, что твои правки кому-то могут не понравится. — X7q 17:45, 7 октября 2009 (UTC)

Мной была добавлена информация о теореме, обратной т. Виета в раздел «Т. Виета». —НиколайБаранов97 13:03, 17 июля 2012 (UTC)

Приведённое квадратное уравнение[править код]

Почему x2+px+q=0{\displaystyle x^{2}+px+q=0}? Если уравнение привести к виду x2+2px+q=0{\displaystyle x^{2}+2px+q=0}, то формула будет ещё проще: x1,2=−p±p2−q.{\displaystyle x_{1,2}=-p\pm {\sqrt {p^{2}-q}}.} — Monedula 14:04, 7 марта 2011 (UTC)

Видимо, по традиции и АИ… —Nashev 18:22, 7 апреля 2013 (UTC)

Необходимы существенные дополнения к этой статье[править код]

Здравствуйте, уважаемые участники проекта! Во-первых, мне бы хотелось узнать, почему внесённые мной в раздел «Нахождение формул для решения» изменения были удалены? Если Вы захотите их восстановить, у меня есть сохранённая копия этих правок, я могу их предоставить проекту. Может быть, стоит дополнить этими данными другой раздел, «Корни квадратного уравнения на множестве действительных чисел»? Во-вторых, помимо универсального способа нахождения корней квадратных уравнений через дискриминант, существует, насколько мне известно, ещё девять способов решения таких уравнений. Среди них обязательно следует указывать графический, а также методы решения неполных кв. уравнений. Где же в статье описаны эти методы? Буду очень благодарен за ответ. С уважением, —НиколайБаранов97 05:11, 17 июля 2012 (UTC)

Вверху страницы статьи есть кнопочка «История». Нажимаете, и видите историю изменений, в которой есть как личность изменившего, так и комментарии. Там же можно сравнивать версии между собой, чтобы увидеть сами изменения. • Евгений Мирошниченко • 06:52, 17 июля 2012 (UTC)

Девять способов? Описывайте. • Евгений Мирошниченко • 06:59, 17 июля 2012 (UTC)

Изменения, внесённые пользователем НиколайБаранов97 06:18, 17 июля 2012 (UTC) в раздел «Формулы корней квадратного уравнения при чётном b{\displaystyle b}».

Мне бы хотелось знать, что думают участники об этих изменениях. С уважением, —НиколайБаранов97 06:18, 17 июля 2012 (UTC).

Нормально, но вы пишете там о формуле (1), однако формула никак не занумерована, так что (1) непоннятно к чему относится. • Евгений Мирошниченко • 06:59, 17 июля 2012 (UTC)

Спасибо за отзыв! Я присвоил номер формуле корней, присутствующей в разделе «Корни квадратного уравнения на множестве действительных чисел».—НиколайБаранов97 07:35, 17 июля 2012 (UTC)

Новый раздел — «Исторические сведения о квадратных уравнениях»[править код]

Частные решения квадратного уравнения[править код]

Полагаю, что слишком много представлено частных решений в виде половинных коэффициентов и тп. Для энциклопедии может это и хорошо, а вот для структурного понятия этой темы — мешает. Может другим шрифтом или помельче как-то? Popugayka 10:56, 2 августа 2012 (UTC)

Извините, мне бы хотелось узнать, что Вы понимаете под структeрным понятием и каковой должна быть по Вашему мнению статья, чтобы удовлетворять этому критерию? НиколайБаранов97 12:46, 2 августа 2012 (UTC)

Структура должна содержать несколько главных позиций содержания. Здесь таковыми считаю:историю, понятие, геометрический смысл, получение решения, корни (в том числе и геометрический вариант решения), использование в нестандартных вычислениях. Все остальное с моей точки зрения должны рассматриваться как подпункты. Мое личное мнение. Ну чтоб усваивалось. Я обычно об этом думаю.Popugayka 14:45, 25 августа 2012 (UTC)