Случайная последовательность Фибоначчи — Википедия

Случайная последовательность Фибоначчи — это стохастический аналог последовательности Фибоначчи, который определяется рекуррентной формулой:

fn=fn−1±fn−2{\displaystyle f_{n}=f_{n-1}\pm f_{n-2}},

где знак «+» или «-» выбирается для каждого n случайно, с равной вероятностью 1/2. Согласно теореме Гарри Кестен и Гилель Фюрстенберга, случайные рекуррентные последовательности этого вида растут в определённой геометрической прогрессии, но трудно вычислить скорость их роста. В 1999 году Дивакар Висванат показал, что скорость роста случайной последовательности Фибоначчи равна 1,1319882487943…, математической константе, которая позже была названа константой Висваната^[1][2][3].

Случайная последовательность Фибоначчи — это случайная целочисленная последовательность {fn}{\displaystyle \left\{f_{n}\right\}}, где f1=f2=1{\displaystyle f_{1}=f_{2}=1} и последующие члены определяются случайной рекуррентной формулой:

fn={fn−1+fn−2,с вероятностью 1/2fn−1−fn−2,с вероятностью 1/2{\displaystyle f_{n}={\begin{cases}f_{n-1}+f_{n-2},&{\text{с вероятностью 1/2}}\\f_{n-1}-f_{n-2},&{\text{с вероятностью 1/2}}\end{cases}}}.

Таким образом, случайная последовательность Фибоначчи начинается с чисел 1, 1, и каждый последующий член последовательности является либо суммой двух предшествующих членов, либо их разностью, с вероятностью 1/2.

Если чередовать знаки: -, +, +, -, +, +, -, +, +, …, то в результате получится последовательность:

1, 1, 0, 1, 1, 0, 1, 1, 0, …

Однако, в этом случае пропадает влияние случайности. В типичном случае, члены последовательности не будут следовать по предсказуемой схеме. Пример случайной последовательности:

1, 1, 2, 3, 1, −2, −3, −5, −2, −3…

для последовательности знаков:

+, +, +, -, -, +, -, -, …

Случайная последовательность Фибоначчи может быть описана с помощью матриц:

(fn−1fn)=(01±11)(fn−2fn−1){\displaystyle {\begin{pmatrix}f_{n-1}\\f_{n}\end{pmatrix}}={\begin{pmatrix}0&1\\\pm 1&1\end{pmatrix}}{\begin{pmatrix}f_{n-2}\\f_{n-1}\end{pmatrix}}},

где знак «+» или «-» выбирается для каждого n случайно, с равной вероятностью 1/2. Тогда

(fn−1fn)=MnMn−1…M3(f1f2){\displaystyle {\begin{pmatrix}f_{n-1}\\f_{n}\end{pmatrix}}=M_{n}M_{n-1}…M_{3}{\begin{pmatrix}f_{1}\\f_{2}\end{pmatrix}}},

где {Mk}{\displaystyle \left\{M_{k}\right\}} — случайная последовательность матриц, принимающих значение A или B с вероятностью 1/2 матриц, принимающих значение A или B с вероятностью 1/2

A=(0111),B=(01−11){\displaystyle A={\begin{pmatrix}0&1\\1&1\end{pmatrix}},B={\begin{pmatrix}0&1\\-1&1\end{pmatrix}}}

1. ↑ D. Viswanath. Random Fibonacci sequences and the number 1.13198824… (англ.) // Mathematics of Computation. — 1999. — Vol. 69, no. 231. — P. 1131—1155.
2. ↑ J. O. B. Oliveira, L. H. De Figueiredo. Interval Computation of Viswanath’s Constant (англ.) // Reliable Computing. — 2002. — Vol. 8, no. 2. — P. 131.
3. ↑ E. Makover, J. McGowan. An elementary proof that random Fibonacci sequences grow exponentially (англ.) // Journal of Number Theory. — 2006. — Vol. 121. — P. 40.

Числа Леонардо — Википедия

Материал из Википедии — свободной энциклопедии

Числа Леонардо — последовательность чисел, задаваемая зависимостью:

L(n):={1если n=0;1если n=1;L(n−1)+L(n−2)+1если n>1.{\displaystyle L(n):={\begin{cases}1&{\text{если }}n=0;\\1&{\text{если }}n=1;\\L(n-1)+L(n-2)+1&{\text{если }}n>1.\\\end{cases}}}

Эдсгер Дейкстра^[1] использовал их как составную часть своего алгоритма плавной сортировки, и изучил их некоторые особенности.^[2]

Числа Леонардо связаны с числами Фибоначчи через формулуL(n)=2F(n+1)−1,n⩾0{\displaystyle L(n)=2F(n+1)-1,n\geqslant 0}.

Из этой формулы прямо следует выражение для чисел Леонардо, аналогичное формуле Бине для чисел Фибоначчи:

L(n)=2φn+1−(1−φ)n+1φ−(1−φ)−1=25(φn+1−(1−φ)n+1)−1{\displaystyle L(n)=2{\frac {\varphi ^{n+1}-(1-\varphi )^{n+1}}{\varphi -(1-\varphi )}}-1={\frac {2}{\sqrt {5}}}\left(\varphi ^{n+1}-(1-\varphi )^{n+1}\right)-1}

где φ=(1+5)/2{\displaystyle \varphi =(1+{\sqrt {5}})/2} является золотым сечением, и кроме того φ{\displaystyle \varphi } и 1−φ=(1−5)/2{\displaystyle 1-\varphi =(1-{\sqrt {5}})/2} являются корнями квадратного уравнения x2−x−1=0.{\displaystyle x^{2}-x-1=0.}

Первые двадцать членов последовательности чисел Леонардо таковы:

1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361, 13529 — последовательность A001595 в OEIS

Последовательность чисел Фибоначчи в трейдинге

Уровни фибоначчи – один из базовых инструментов анализа движений в контексте их размеров. На первый взгляд может показаться, что это значения, которые просто за уши притянуты к реальности, однако можно просто открыть любой график и посмотреть на соотношения между разными колебаниями. Тут даже самые упёртые скептики сдадутся. Этот необычный метод активно используется во многих стратегиях, а также играет важную роль при волновой разметке движений, Эллиотт уделял большое внимание пропорциям, что позволяет в значительной степени повысить точность таких прогнозов. На данный момент уровни фибоначчи входят в состав базовых графических инструментов практически любого терминала, и даже если он отсутствует, его легко можно найти в интернете или, на крайний случай, посчитать самому на калькуляторе.

В основе значений фибоначчи лежит числовая последовательность, которая имеет такое же название. Это достаточно простой алгоритм, последовательность строится по следующему принципу: каждый последующий член последовательности фибоначчи равен сумме двух предыдущих. Начинается она с нуля и двух единиц. Впрочем, ноль очень часто опускается.

 

По мере продолжения этой последовательности каждый предыдущий член будет всё больше приближаться к так называемому “Золотому сечению”. В процентном выражении это 61,8%. Взято это значение из простой формулы деления отрезка на две части так, чтобы меньшая часть относилась к большей так же, как большая часть относится ко всему отрезку. После несложных расчётов получается как раз 61,8%. Так мы получаем самое главное значение, от которого строятся все остальные. Второе важное значение – 38,2%. Оно получается путём вычета из 100% значения основного.  Рассмотрим, как это получается:

 

Интерес представляет правый столбик, показанный на картинке. Буквально десятый член последовательности уже показывает очень близкие к нашему золотому сечению значения. Далее, продолжая строить ряд, мы получаем ещё более точные. В целом, в трейдинге вполне достаточно использовать общепринятое значение 61,8%, дальнейшее уточнение уже ни к чему.

Важность последовательности фибоначчи

Теперь перейдём к более важному вопросу, а именно по какой причине всё это работает. Дело в том, что золотое сечение названо так совсем не случайно. Первые упоминания датируются аж четвёртым веком до нашей эры в работах известного математика Евклида, который упоминал золотое сечение в контексте построения пятиугольника.  Само же название связывают обычно с очень известным инженером, художником и изобретателем – да Винчи, хотя именно литературное распространение началось с математических пособий Германии, где другой известнейший учёный Ом ввёл его именно в этой формулировке. В целом, всё это не так важно, главное – это идея, которая лежит в самом соотношении. К которому приводит последовательность фибоначчи. Подобное соотношение можно встретить в следующих областях:

1. Архитектура. История знает огромное количество примеров, где было сознательно использовано правило разделения различных элементов исходя из их соотношений между собой определённым коэффициентом. Самый яркий пример – пирамиды в Египте, а также многие здания (храмы) в Древней Греции. Прямоугольник, разделённый таким образом получается очень гармоничным, поэтому он часто лоижлся в основу формы здания. То же самое относится и к элементам украшения, декора, везде можно проследить эту туенденцию. Конечно же, это не говорит о том, что прямо вот вся архитектура была заточена именно под такие пропорции, но тот факт, что они далеко нередко появлялись, свидетельствует о том, что золотое сечение было известно давно, и использовалось вполне сознательно. В целом, и последовательность фибоначчи появилась не просто так – числа, которые приближаются к золотому сечению позволяют определить само сечение через такую математическую операцию, как вычисление предела.

2. Геометрия молекул и химия. Очень сложные формы соединений на атомном уровне могут содержать как числа, входящие в последовательность фибоначчи, так и само золотое сечение. Как уже говорилось ранее, наш коэффициент присутствует в пятиугольнике, а сами атомы между собой образуют очень сложные геометрические фигуры. В основном, коэффициент прослеживается в додекаэдрах и икосаэдрах. Не вдаваясь в подробности, это многогранные фигуры, имеющие сложную симметрию. Также здесь присутствует число из поселдовательности фибоначчи –

21, которое получается одной молекулой, вокруг которой располагается ещё двадцать молекул. В итоге вся эта композиция из двадцати одной молекулы даёт додекаэдр.

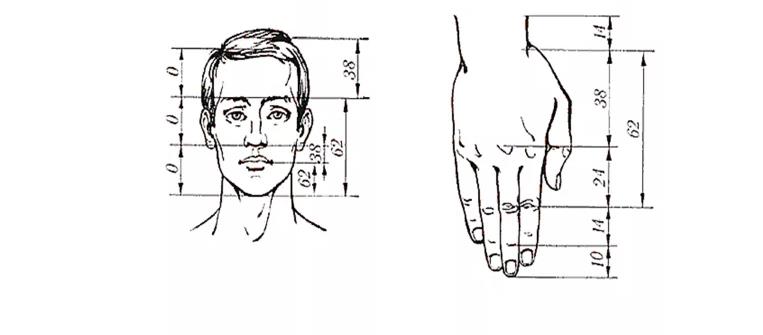
3. Биология. Пропорции тела очень приближены к главному коэффициенту.  Например, соотношение между расстояние от подбородка до бровей стремится к коэффициенту, входящему в последовательность чисел фибоначчи, по отношению оставшейся части головы, то есть лба. Аналогичная ситуация и с размером ладони, только в роли этого сечения выступает линия,

проходящая через сустав между третьей и второй фалангой. Также считается, что изначально на подобные части, как в последовательности фибоначчи, делил тело пупок. Однако, со временем начались отклонения от этих значений, что объясняется эволюцией и приспособлением под окружающие человека условия.

 

4. Музыка. Здесь речь идёт о количество нот разной длины. Например, золотое сечение использовал Иоганн Себастьян Бах, один из величайших композиторов в истории.

5. Природа. Золотое сечение прослеживается в цветах, листьях, расположении сучков на более крупном суке дерева. Наибольший интерес представляет раковина улитки, которая “раскручивается” по строгой спирали, шаг которой определяется нашим коэффициентом. Вообще, если взглянуть на все примеры, становится очевидным, что каким-то необъяснимым образом и сама природа стремится к таким пропорциям. Человеческое восприятие объектов, в которых есть такие соотношения ассоциируется с гармонией, что довольно странно на фоне восприятия симметричных объектов, как практически идеальных.

Тем не менее, данный факт известен очень давно и активно применяется.

 

Данное соотношение, полученное из чисел фибоначчи, ложится в основу системы коэффициентов, которые называются уровнями фибоначчи. Они устанавливают пропорции между двумя разнонаправленными движениями, по ним можно определять размеры коррекции и предполагать точки окончания. Но об этом мы поговорим позднее, а сейчас перейдём непосредственно к самим числам фибоначчи, а вернее, последовательности, которая имеет очень важное значение в волновой теории, разработанной

Эллиоттом.

Последовательность чисел фибоначчи в волновой теории

До этого мы говорили о предельном отношении двух соседних членов последовательности чисел фибоначчи. Теперь посмотрим, как волновая теория использует последовательность. Из общего описания нам известно, что все движения делятся на импульсы и коррекции. В глобальном масштабе вся волновая конструкция стремится к циклу роста и снижения, меняется размерность, но эти две фазы последовательно происходят одна за другой. Минимальный набор волн для отличия одной структуры от другой – 5 и 3. У импульсов пять составляющих, у коррекции – три. В этом мы видим первые два числа, которые относятся к последовательности фибоначчи. И даже суперцикл из двух фаз также входит в последовательность – это 1 и 1. Рассмотрим более подробно рост и коррекцию.

1. В составе импульса мы можем выделить 5 элементов – три из них также импульсы, оставшиеся два – коррекции . Соответственно, при таком приближении у нас уже получается 5+3+5+3+5=21 Итого двадцать одна волна составляет импульс.
2. Коррекция, как известно, состоит из трёх движений, в которых два – импульсы и одно – коррекция. При таком раскладе у нас получается 5+3+5=13 волн. Здесь есть исключение, так как иногда первая волна в коррекции может быть представлена тройкой, но зато это компенсируется тем, что вторая волна может быть треугольником, в котором не 3, а уже 5 волн. К тому же треугольники могут встречаться и в четвёртой волне импульса.

 

Что мы видим в итоге: 21 волна в импульсе и 13 волн в коррекции в рамках одного цикла.

Оба числа из последовательности фибоначчи, причём следуют они сразу за 8 и 5 волн из предыдущего примера. И если это покажется совпадением, перейдём ещё на один уровень подробнее. В этом случае получается следующее:

1. Импульс представлен 21 волной, коррекция 13, значит, весь импульс будет состоять из 21+13+21+13+21=89 волн. Это также вытекает из структуры простого 5+3.
2. Коррекция состоит из:  21+13+21=55 волн.

И снова у нас два числа из последовательности фибоначчи. В сумме такой цикл даёт следующее число – 144. Так можно продолжить до бесконечности, и каждый раз будем получать следующие два числа из последовательности фибоначчи. Подобная последовательность свидетельствует о том, что волновая теория имеет глубокую связь с происходящим на рынке, ведь мы имеем не только количество волн, но и самое главное соотношение и его производные, которые также вписываются в гармонию природы и поведения людей. И чем больше объёмы, тем чётче должна прослеживаться зависимость всего происходящего в разных циклах между собой.  Это выражается как в самой структуре, так и в коэффициентах.

 

Читайте далее — Уровни Фибоначчи

Последовательность Фибоначчи — papanya77 — LiveJournal

Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.
Подробнее тут:http://ru.wikipedia.org/wiki/%D4%E8%E1%EE%ED%E0%F7%F7%E8

Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:

Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

Последовательность Фибоначчи и Кролики
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.

У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.

К чему всё это?

Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.

Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Золотое Сечение — Отрезок
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.

Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Золотое сечение и Человеческое тело

Изображение: marcus-frings.de

Последовательность Фибоначчи — Анимация

Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.

Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

Спираль Фибоначчи

Ничего не напоминает?

Фото: ethanhein on Flickr

И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.

Алое многолистный:

Фото: brewbooks on Flickr

Броколи романеско:

Фото: beart.org.uk

Подсолнечник:

Фото: esdrascalderan on Flickr

Сосновая шишка:

Фото: mandj98 on Flickr

А если взглянуть чуть подальше, то можно разглядеть ряд Фибоначчи в недосягаемых галактиках.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.

Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.

Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.

Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.

И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?

Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55…

Источник:http://greenword.ru/2009/06/fibonacci-sequence.html

Подробнее о золотом сечение и ряде Фибоначчи тут:http://www.milogiya2007.ru/fibonachi.htm

И тут: