Математики разрезают фигуры в поисках частей уравнений / Habr
Новая работа над задачей о «равносоставленности» объясняет, когда имеется возможность разрезать одну фигуру и собрать из неё другую
Если у вас есть две плоские фигуры из бумаги и ножницы, можете ли вы разрезать одну фигуру и переставить кусочки так, чтобы получить другую? Если можете, тогда две эти фигуры «ножнично конгруэнтны» [равносоставлены].
Однако математиков интересует, можно ли обнаружить такое взаимоотношение у фигур, не используя ножницы? Иначе говоря, есть ли у этих фигур такие характеристики, которые можно было бы измерить заранее и определить, конгруэнтны ли они?
Для двумерных фигур ответ прост. Нужно просто измерить их площади; если они совпадают, то фигуры ножнично конгруэнтны.
Но для фигур в высших измерениях – к примеру, для трёхмерного мяча или одиннадцатимерного пончика, который невозможно себе представить – вопрос разрезания и пересборки в другом виде становится гораздо сложнее. И несмотря на века попыток, математики не могли определить характеристик, подтверждающих равносоставленность для большинства фигур высшей размерности.
Однако этой осенью два математика совершили наиболее значимый прорыв в решении этой задачи за несколько десятилетий. В работе, представленной в Чикагском университете 6 октября, Джонатан Кэмпбел из университета Дьюка и Инна Захаревич из Корнеллского университета совершили значимый шаг по направлению к доказательству ножничной конгруэнтности для форм любых размерностей.
Но не только. Как и большинство важных задач математики, равносоставленность – это кроличья нора: скромное заявление, затягивающее математиков в глубокую нору сложной математики. В попытках понять ножничную конгруэнтность, Кэмпбелл и Захаревич, возможно, показали новый способ рассуждать о совершенно другой области этой науки: об алгебраических уравнениях.
Первый разрез
Равносоставленность может показаться простой задачей. Более 2000 лет назад Евклид догадался, что две двумерные фигуры одной площади можно переставлять из одной в другую. Разумно предположить, что фигуры высших измерений одинакового объёма можно переделывать аналогично. Но в 1900-м году Давид Гильберт предположил, что эта задача на самом деле не так проста.
В том году, выступая на международном математическом конгрессе в Париже, он определил 23 открытых задачи, которые, по его мнению, будут направлять математическую мысль в ближайшее столетие. Третья из них касалась ножничной конгруэнтности [равносоставленность равновеликих многогранников]. Гильберт предположил, что не все трёхмерные фигуры одного объёма конгруэнтны – и бросил математикам вызов, предложив найти пару фигур, доказывающих это.
Через год после речи ученик Гильберта, Макс Ден, так и сделал. Такой срок показался математикам подозрительным. «Некоторые считают, что Гильберт включил эту задачу в список только потому, что её уже решил его ученик», — сказала Захаревич.
Был ли это заговор или нет, результат Дена перевернул представление математиков о равносоставленности. Он доказал, что тетраэдр единичного объёма не является равносоставленным кубу того же объёма. Неважно, как вы разрежете первый, вы никогда не сможете собрать из кусочков второй.
Кроме демонстрации того, что равенства объёмов недостаточно для определения равносоставленности, Ден предложил новый способ измерения фигур. Он доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём, а также совпадать по новой мере.
Ден сконцентрировался на внутренних углах между двумя гранями трёхмерной фигуры. К примеру, внутри куба все грани встречаются под прямыми углами. Но в более сложных формах углы бывают разными и имеют разную важность. Углы между более длинными рёбрами больше влияют на форму фигуры, чем углы между более короткими рёбрами, поэтому Ден присвоил углам веса на основе длин формирующих их рёбер. Он скомбинировал эту информацию в сложную формулу, выдававшую в итоге единственное число – «инвариант Дена» – для заданной фигуры.
Математики хотят знать, когда фигуру можно разрезать и собрать из неё другую.
Двумерные фигуры равносоставлены, если у них одинаковая площадь.
Куб и тетраэдр не равносоставлены – у них одинаковый объём, но разный инвариант Дена.
Фигуры можно резать на кусочки, а графики уравнений – на подграфики. Математики ищут аналог инварианта Дена, который показывает, что два уравнения состоят из одинаковых кусочков.
Ден доказал, что любые трёхмерные фигуры, равносоставленные друг другу, должны иметь одинаковый объём и инвариант Дена. Но он не смог ответить на более сложный вопрос: если у трёхмерных фигур одинаковый объём и инвариант Дена, значит ли это, что они обязательно равносоставлены? Жан-Пьер Сидлер, наконец, доказал это в 1965. Через три года Бьёрг Джессен показал, что эти же две характеристики определяют равносоставленность в четырёх измерениях.
Результаты Сидлера и Джессена были серьёзными шагами вперёд, но математики – народ жадный: достаточно ли объёма и инварианта Дена для определения равносоставленности фигур во всех измерениях? Достаточно ли этих измерений в других геометрических пространствах, кроме Евклидового – в сферической геометрии (представьте себе широту и долготу на поверхности Земли) или седловидной вселенной гиперболической геометрии?
В конце XX века математик Александр Борисович Гончаров предложил подход, который, по его мнению, мог решить всю задачу раз и навсегда – и при этом связать равносоставленность с совершенно другой областью математики.
Странные связи
Математика полна неожиданных связей. Захаревич говорит, что заниматься математикой – это как наткнуться на нечто странное в природе, и попытаться понять, почему оно такое.
«Если вы встретите в лесу кольцо из грибов, и не будете знать, как грибы растут, вы задумаетесь, откуда им известно, как расти кругом? – сказала она. – Причина же в том, что грибы имеют грибницу, растущую под землёй».
В 1996 году Гончаров сформулировал набор гипотез, говорящих о существовании математической структуры, также скрытой под поверхностью. Если эта структура существует, она сможет объяснить, почему некоторые математические явления – включая равносоставленность – работают именно так.
Одна из гипотез утверждает, что объёма фигуры и её инварианта Дена достаточно для определения равносоставленности фигур любой размерности и в любом пространстве.
«Гончаров сказал, что те же принципы, что применяются в трёх измерениях, применимы во всех», — сказал Чарльз Вейбель из университета Рутгерса.
Но Гончаров, ныне работающий в Йельском университете, также предсказал, что эта скрытая структура объяснит гораздо больше этого. Он сказал, что равносоставленность – это концепция более универсальная, и что она применима не только к разрезанию геометрических фигур, но и к разрезанию форм, порождаемых решениями алгебраических уравнений – к примеру, графика уравнения x2 + y2 + z2 = 1. А информация, необходимая для классификации по равносоставленности, отражает информацию, необходимую для классификации алгебраических уравнений – такую, при которой уравнения одного класса будут составлены из одинаковых кусочков.
Связь была шокирующей, будто бы принцип, подходящий для систематизации животных каким-то образом позволял бы вам систематизировать ещё и химические элементы. Многие математики считают эту идею настолько же странной, насколько она кажется на первый взгляд.
«Это совершенно загадочно. На первый взгляд, эти вещи вообще не должны быть связаны», — сказал Кэмпбелл.
Разрезая уравнения
Чтобы понять, как могут быть аналогичными геометрические фигуры и алгебраические уравнения, сначала полезно будет понять, как можно разбить решения уравнений на части. Для этого давайте вернёмся к нашему предыдущему примеру и нарисуем график уравнения x2 + y2 + z2 = 1.
Это будет сфера. Однако эта поверхность является не только набором решений этого уравнения: это также набор множества более мелких графиков, или подграфиков, решений других уравнений. К примеру, на поверхности сферы можно нарисовать окружность на манер земного экватора. Это один подграфик, представляющий решения алгебраического уравнения x
2 + y2 = 1. Или можно изолировать единственную точку на северном полюсе сферы, соответствующую уравнению z = 1. Изучая различные подграфики, которые можно нарисовать в рамках более крупного графика – нечто вроде его составных частей – вы можете узнать какие-то свойства более крупного графика.Более 50 лет математики разрабатывали теорию подграфиков алгебраических уравнений. Как обычная материя состоит из атомов, так и, по мнению математиков, алгебраические уравнения состоят из фундаментальных частей под названием «мотивы». Термин происходит от французского слова motif, обозначающего базовые элементы мелодии.
Инна Захаревич из Корнеллского университета
«Мотивы – это фундаментальные составные части. Они расскажут обо всём, из чего состоят алгебраические уравнения, как мелодия, состоит из различных составных частей», — сказала Захаревич. Сфера, к примеру, состоит из окружностей, точек и плоскостей. Каждая из них состоит из составных частей (проявляющихся в результате математических действий над ними), и так далее, всё ниже и ниже, пока мы не придём к мотивам, предполагаемому фундаменту алгебраических уравнений.
Математикам нужно классифицировать алгебраические уравнения по их мотивам, чтобы получить полную и систематическую картину уравнений, принадлежащих к важнейшим математическим объектам. Это сложная и незаконченная задача. Но в 1996 году Гончаров предположил, что сортировка фигур по равносоставленности и сортировка алгебраических уравнений по мотивам являются двумя сторонами одной задачи – то есть, классификация одной даст вам принцип, по которому можно классифицировать и другую.
Он предположил, что эта связь имеет в основе аналог инварианта Дена. Только вместо того, чтобы появляться из простейших геометрических подсчётов, этот аналог должен возникнуть из похожего расчёта мотивов алгебраических уравнений («мотивное копроизведение»).
«Идея в том, что задача инварианта Дена параллельна другой задаче, связанной с мотивами», — сказал Вейбель.
Но чтобы обнаружить такую связь, математикам сначала нужно доказать, что инвариант Дена действительно сортирует фигуры по равносоставленным группам. Сам Ден показал, что любые равносоставленные трёхмерные фигуры имеют равные объёмы и инвариант Дена. Однако Ден, и все остальные после него, не опровергли возможность того, что существуют некие фигуры высших измерений одинакового объёма и с одинаковым инвариантом Дена, не являющиеся при этом равносоставленными. В своей новой работе Кэмпбелл и Захаревич попытались навсегда закрыть эту возможность.
Два по цене одного
В июне 2018 года Кэмпбелл и Захаревич три недели работали вместе в Институте передовых исследований в Принстоне, Нью-Джерси. Они давно интересовались равносоставленностью, но Захаревич считала, что гипотезы Гончарова были слишком сложными, чтобы с ними можно было разобраться за такое короткое время. А Кэмпбелл всё равно хотел попытаться, и Захаревич не пришлось долго уговаривать.
В работе они проводят контринтуитивный мысленный эксперимент. Чтобы понять его представьте, что у вас есть гостиница со множеством комнат. Вам нужно расположить все равносоставленные друг с другом фигуры в одной комнате. Нам неизвестно, как определять, что фигуры являются равносоставленными – в этом и есть корень проблемы. Однако для нашего мысленного эксперимента давайте представим, что это возможно. Или, как говорит Захаревич, «Мы притворимся, что существует некая всезнающая личность, которой известно, равносоставлены две фигуры или нет».
Рассортировав фигуры по комнатам, мы проверим, что у всех фигур в одной комнате одинаковый объём и одинаковый инвариант Дена. Также важно проверить, что все фигуры одинакового объёма и с одинаковым инвариантом Дена оказались в нужной комнате – что в баре гостиницы не ошиваются отбившиеся от коллектива фигуры. Цель мысленного эксперимента доказать наличие идеального взаимно однозначного соответствия между группами равносоставленных фигур и группами фигур, имеющих одинаковый объём и одинаковый инвариант Дена. Существование такого соответствия докажет, что для определения равносоставленности фигур вам действительно будет достаточно только объёма и инварианта Дена.
Гончаров предсказал существование такого соответствия, и Кэмпбелл с Захаревич доказали его наличие – при выполнении одного условия. Соответствие существует, если верен ещё один недоказанный результат, связанный с гипотезами Бейлинсона.
Две гипотезы Гончарова – классификация равносоставленных фигур по объёму и инварианту Дена, а также классификация алгебраических уравнений по аналогу инварианта Дена – не доказываются работой Кэмпбелла и Захаревич полностью. Однако их работа всё же обеспечивает математиков более чётким представлением о том, как доказать их все: если у вас получится доказать гипотезы Бейлинсона, тогда, благодаря работе Кэмпбелла и Захаревич, вы бесплатно получите в придачу и равносоставленность.
«Их работа действительно переосмысливает эту задачу, — сказал Вейбель. – Когда вы связываете таким образом две гипотезы, это проливает свет на структуру изучаемого объекта».
Кэмпбелл и Захаревич сейчас работают ещё с одним математиком, Даниилом Руденко из Чикагского университета, пытаясь определить связь между разрезанием фигур и разбором на части уравнений, предложенным Гончаровом. Руденко до этого уже несколько продвинулся в этом направлении. Теперь, совместно с Кэмпбеллом и Захаревич, он надеется продвинуться гораздо дальше.
«Думаю, у нас есть все шансы достичь значительного прогресса. Может быть, таким способом даже получится доказать гипотезы Гончарова», — сказал Руденко.
habr.com
Решение задач по теме «Уравнение окружности». Видеоурок. Геометрия 9 Класс
На прошлом уроке мы вывели уравнение окружности и использовали его для решения простейших задач. На этом уроке мы продолжим изучение уравнения окружности и используем его для решения серии более сложных задач.
Уравнение окружности с центром в точке 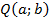 и радиусом
и радиусом  имеет вид:
имеет вид:

 и
и  – это координаты точки
– это координаты точки  , лежащей на этой окружности.
, лежащей на этой окружности.
Выясните, какие из данных уравнений являются уравнениями окружности, найдите центр окружности и ее радиус:
1. 
2. 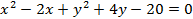
Решение
1. 
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами  ; радиус окружности –
; радиус окружности –  .
.
2. 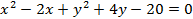
Преобразуем данное уравнение с помощью метода выделения полного квадрата:


Воспользуемся формулой квадрата суммы и разности. В обеих скобках есть квадрат первого выражения и удвоенное произведение, не хватает квадрата второго выражения, прибавим и отнимем его:



Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами  ; радиус окружности –
; радиус окружности –  .
.
Задачи с использованием метода выделения полного квадрата
Выясните, является ли данное уравнение уравнением окружности, найдите центр окружности и ее радиус:
1. 
2. 
Решение
1. 
Преобразуем данное уравнение с помощью метода выделения полного квадрата:


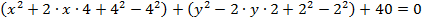


Так как  и
и  (квадрат выражения больше или равен нулю), то выражение в левой части уравнения больше нуля. Следовательно, это уравнение не имеет решения и не является уравнением окружности.
(квадрат выражения больше или равен нулю), то выражение в левой части уравнения больше нуля. Следовательно, это уравнение не имеет решения и не является уравнением окружности.
Доказать отсутствие решений у исходного уравнения можно также с помощью дискриминанта. Для этого рассмотрим это уравнение как квадратное относительно  с параметром
с параметром  .
.


Мы получили квадратный трехчлен с такими коэффициентами:
— коэффициент при  –
–  ;
;
— коэффициент при  –
–  ;
;
— свободный член зависит от параметра  –
– 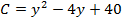 .
.
Найдем корни данного уравнения по известной формуле:
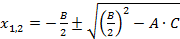
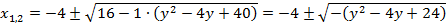
Выделим полный квадрат в подкоренном выражении:

Видно, что подкоренное выражение меньше нуля. А так как подкоренное выражение равно четверти дискриминанта, то и дискриминант будет отрицательным числом.

Следовательно, исходное уравнение не имеет решений.
2. 
Преобразуем данное уравнение с помощью метода выделения полного квадрата:

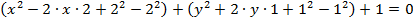
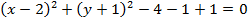
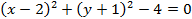

Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами 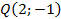 ; радиус окружности –
; радиус окружности –  .
.
Напишите уравнение окружности, проходящей через три заданные точки.
Дано:  ;
;  ;
; 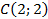 .
.
Найти: уравнение окружности, проходящей через данные точки.
Решение
Уравнение окружности задается тремя параметрами  ,
,  ,
,  , поэтому необходимо найти эти параметры.
, поэтому необходимо найти эти параметры.
Так как данные точки лежат на окружности, то их координаты удовлетворяют уравнению искомой окружности. Подставим координаты точек в уравнение окружности в общем виде:
 :
:
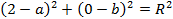

 :
:

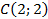 :
:

Мы получили систему из трех уравнений относительно трех неизвестных:

Решим эту систему. Вычтем из третьего уравнения первое:
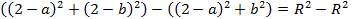
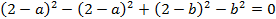
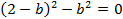
Разложим выражение как разность квадратов:


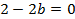

Подставляем найденное значение 
interneturok.ru
Задание пространственных геометрических фигур уравнениями и неравенствами.
Геометрия 10 класс
Задание пространственных геометрических фигур уравнениями и неравенствами.
Цели урока:
Образовательные: формирование знаний о задании пространственных геометрических фигур уравнениями.
Развивающие: Способствовать развитию пространственного воображения учащихся; способствовать выработке решения задач и развития логического мышления учащихся.
Воспитательные: Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Ход урока
1. Организационный момент.
2Актуализация знаний
Как найти середину отрезка в пространстве?
Как вычислить расстояние между точками в пространстве?
3. Изучение нового материала.
Плоскость в трехмерном евклидовом пространстве задается уравнением:
где нормаль к данной плоскости
Сфера в трехмерном евклидовом пространстве задается уравнением:
где R ее радиус
Эллипсоид в трехмерном евклидовом пространстве задается уравнением
Коническая поверхность в трехмерном евклидовом пространстве задается уравнением:
Эллиптический параболоид в трехмерном евклидовом пространстве задается уравнением:
Однополостный гиперболоид в трехмерном евклидовом пространстве задается уравнением:
Двуполостный гиперболоид в трехмерном евклидовом пространстве задается уравнением:
Неравенствами трехмерные поверхности не задаются, неравенства задают лишь область либо внутри поверхности, либо снаружи
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)
2) двумя своими точками M 1 (x 1, y 1, z 1 ) и M 2 (x 2, y 2, z 2 ), тогда прямая, через них проходящая, задается уравнениями:
= ; (3.3)
3) точкой M 1 (x 1, y 1, z 1 ), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
. (3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Закрепление
Пример 1.15. Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение. По условию задачи вектор ОА(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3×3+D = 0 Þ D = -11. Итак, x-y+3z-11=0.
Пример 1.16. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y-z-7=0 угол 60о.
Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не
равно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями
.
Решая квадратное уравнение 3m2 + 8m — 3 = 0, находим его корни
m1 = 1/3, m2 = -3, откуда получаем две плоскости 1/3x+y = 0 и -3x+y = 0.
Домашнее задание
infourok.ru
Тема 5.4. Уравнение фигуры. Приложение метода координат к решению стереометрических задач
Литература: [8], гл.2, §2, стр. 184–195; [11], гл. 4, § 4.1, стр. 335–348; [27], гл.6, § 57-58, стр. 204-211.
Основные определения, теоремы и формулы
Уравнение
(неравенство) или система уравнений
(неравенств), которому удовлетворяют
координаты любой точки фигуры  и не удовлетворяют координаты точки,
не принадлежащей ей, называетсяуравнением(неравенством),определяющим фигуру
и не удовлетворяют координаты точки,
не принадлежащей ей, называетсяуравнением(неравенством),определяющим фигуру в данной системе координат. Уравнение,
определяющее фигуру
в данной системе координат. Уравнение,
определяющее фигуру ,
называют такжеуравнением фигуры
,
называют такжеуравнением фигуры .
.
При выводе уравнения любой фигуры целесообразно действовать в следующей последовательности:
1.
Символически записать рассматриваемую
фигуру, как множество точек в следующем
виде:  ,
где вместо многоточия символически
записывается характеристическое
свойство точек фигуры.
,
где вместо многоточия символически
записывается характеристическое
свойство точек фигуры.
Например,
если  окружность
с центром в точке
окружность
с центром в точке радиуса
радиуса ,
то следовало бы записать так:
,
то следовало бы записать так:
2. Определить, является ли характеристическое свойство аффинным или метрическим.
3. Если свойство является аффинным, то выбирать удобную аффинную систему координат. Если свойство метрическое – прямоугольную систему координат.
4.
Считая координаты точки  произвольными,
записать характеристическое свойство
на языке координат. Это и будет уравнением
фигуры.
произвольными,
записать характеристическое свойство
на языке координат. Это и будет уравнением
фигуры.
Пример. Описать фигуру, для каждой точки которой сумма квадратов расстояний до трех данных взаимно перпендикулярных прямых постоянна.
Решение.
Составим уравнение искомой фигуры и по виду уравнения определим ее вид.
и по виду уравнения определим ее вид.
Пусть 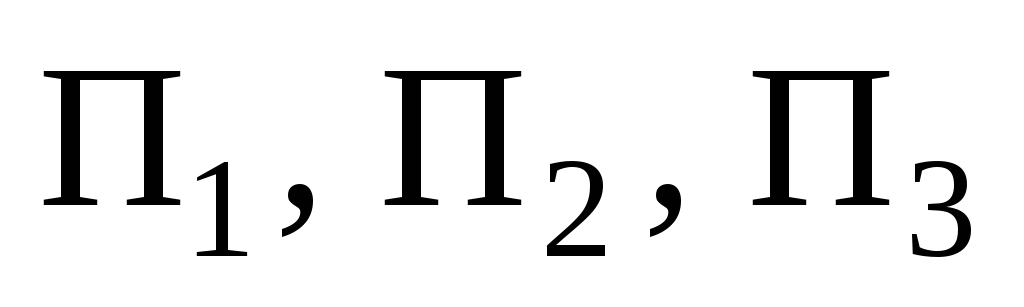 –
данные в условии задачи плоскости. Тогда
–
данные в условии задачи плоскости. Тогда
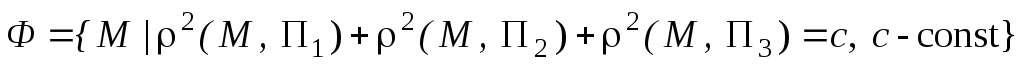 .
.
Характеристическое
свойство точек фигуры является
метрическим, поэтому необходимо выбрать
прямоугольную систему координат. Примем
плоскости  за координатные плоскости
за координатные плоскости Тогда для точки
Тогда для точки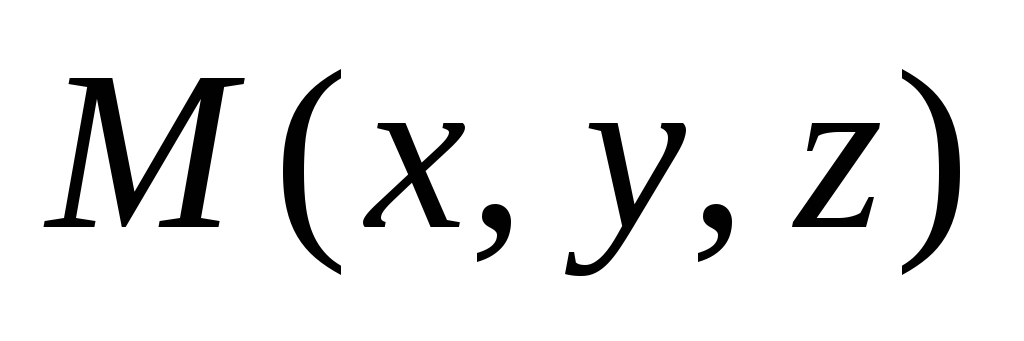 характеристическое свойство примет
вид
характеристическое свойство примет
вид Значит
Значит –
есть сфера с центром в точке пересечения
плоскостей
–
есть сфера с центром в точке пересечения
плоскостей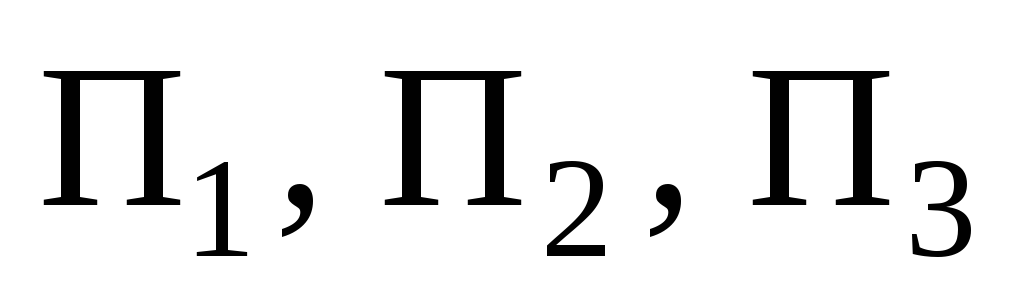 ,
радиус которой равен
,
радиус которой равен
Вопросы для самоконтроля
1. Что называют условием, определяющим фигуру Фв данной системе координат? Что называется уравнением фигурыФ?
2. Какая фигура задаётся в прямоугольной декартовой системе координат уравнением:
а) (х – а)2 + (y — b)2 + (z — c)2 = r2, r > 0,
б) x2 + y2 + z2 + Ax + By + +Cz + D = 0?
3. Фигуры Ф1иФ2имеют в некоторой системе координат уравненияF1(x, y, z) = 0 иF2(x, y, z) = 0. Какая фигура определяется каждым из следующих условий:
а) F1(x, y, z) ¹ 0, б)F1(x, y, z)× F2(x, y, z) = 0,
в) F12(x, y, z) + F22(x, y, z) = 0,
г)
системой уравнений F1(x, y, z)
= 0,F2(x, y, z) = 0, д)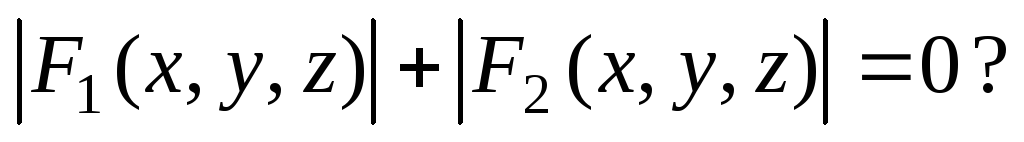
4.
Дана аффинная система координат О .
Написать уравнения её:
.
Написать уравнения её:
а)
координатных плоскостей, б) координатных
осей. Какая фигура определяется уравнением 
5.
Какой вид имеют формулы преобразования
аффинных систем координат? Как получить
уравнение фигуры Фв новых координатах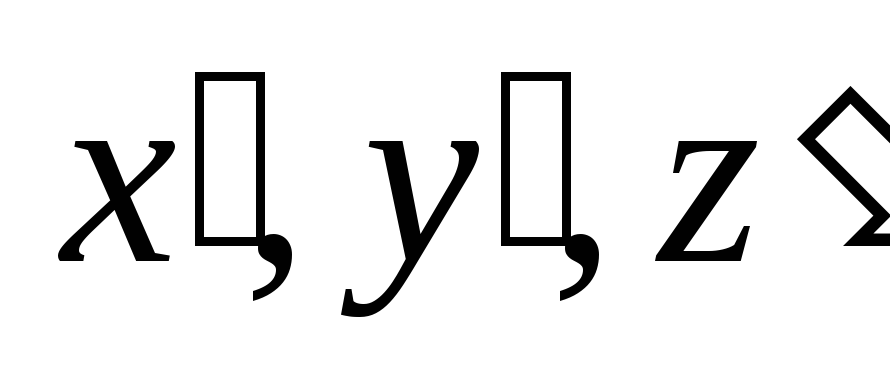 ,
если известно её уравнениеF(x, y, z)=0
в старой системе координат?
,
если известно её уравнениеF(x, y, z)=0
в старой системе координат?
6.
Как получить уравнение сферы радиуса r > 0 с центром в начале координатОв декартовой системе координатО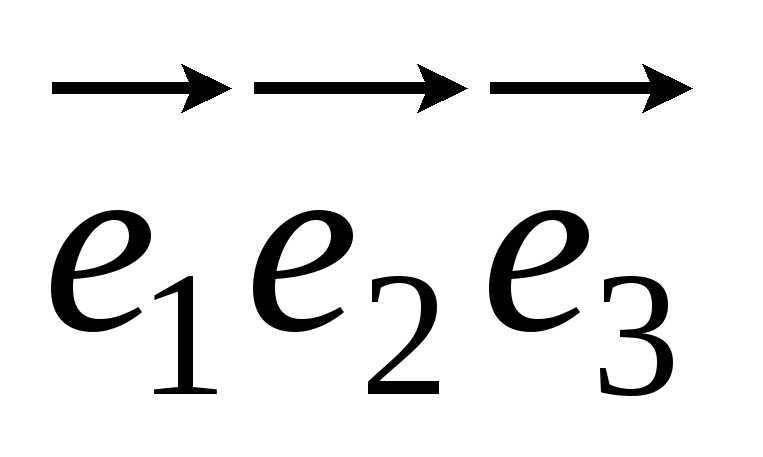 ,
если известно, что
,
если известно, что

Задачи
1. Какая фигура задаётся уравнением:
а) x2 + y2 + z2 = r2, r > 0;
б) x2 + y2 + z2 – r2 + 
в) х = 0,
г) 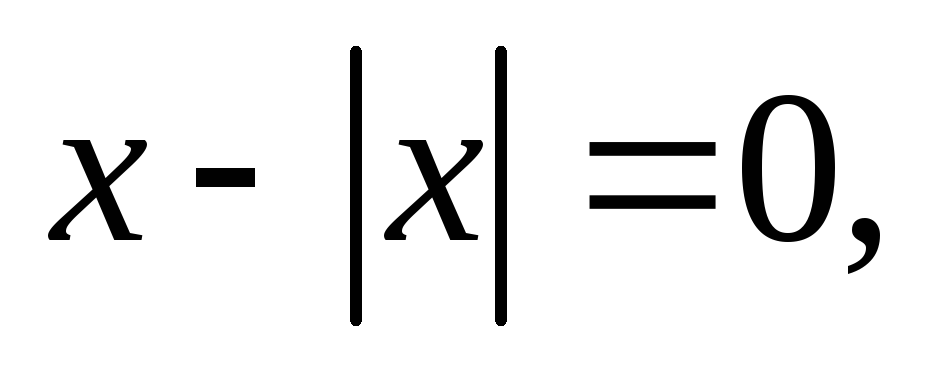 д)
д)

е) x2 + y2 + z2 – 6x + 8y + 2z + 10 = 0?
2. Найти множество всех точек пространства, для каждой из которых:
а) сумма квадратов расстояний до двух данных точек АиВ есть постоянная величинас2,
б) разность квадратов расстояний до точек АиВ есть постоянная величинас2.
3. Найти множество всех точек пространства, для каждой из которых отношение расстояний до данных точек АиВ равно отношению данных отрезковm иn,гдеm ¹ n.
4. Доказать, что плоскости, проходящие через биссектрисы плоских углов трёхгранного угла перпендикулярно к граням этих углов, пересекаются по одной прямой.
Домашнее задание
1. Найти множество всех точек пространства, каждая из которых равноудалена от двух данных точек А иВ.
2. Доказать, что диагональ АС1параллелепипедаАВСDA1B1C1D1делится плоскостямиBDA1иB1D1Cна три равные части.
3. Доказать, что сумма квадратов площадей шести диагональных сечений параллелепипеда в два раза больше суммы квадратов площадей всех его граней.
4. Прямая образует равные углы с ребрами трехгранного угла, все плоские углы которого прямые. Найти косинусы этих углов.
5. Доказать, что противоположные ребра правильного тетраэдра взаимно перпендикулярны.
Задачи повышенной трудности
1. Доказать, что все высоты тетраэдра пересекаются в одной точке тогда и только тогда, когда суммы квадратов его противоположных ребер равны.
2.
Доказать, что точки  лежат на одной прямой, если их радиус-векторы
лежат на одной прямой, если их радиус-векторы удовлетворяют
равенству
удовлетворяют
равенству
3.
Доказать, что грани  и
и тетраэдра
тетраэдра равновелики тогда и только тогда, когда
общий перпендикуляр прямых
равновелики тогда и только тогда, когда
общий перпендикуляр прямых и
и проходит через середину ребра
проходит через середину ребра
4.
Докажите, что плоскость, в которой лежат
проекции  на
плоскости координат, делит отрезок,
соединяющий
на
плоскости координат, делит отрезок,
соединяющий с
началом координат, в отношении, не
зависящем от положения точки
с
началом координат, в отношении, не
зависящем от положения точки .
.
studfile.net
11.7. Упрощение уравнений фигур второго порядка на плоскости
Фигурой второго порядка на плоскости называется множество точек этой плоскости, декартовы координаты которых удовлетворяют уравнению второй степени
(11.12)
ГдеОдновременно в нуль не обращаются. Отметим, что это множест
Во, в частности, может состоять из единственной точки или оказаться пустым.
Первые три члена левой части уравнения (11.12) образуют квадратичную форму двух переменных
(11.13)
С симметрической матрицей
(11.14)
По теореме 11.10 эту квадратичную форму ортогональным преобразованием можно привести к каноническому виду
(11.15)
С матрицей
(11.16)
Где- характеристические числа матрицы, т. е. корни характеристиче
Ского уравнения матрицы:
При этом ортогональном преобразовании уравнение (11.12) примет ввд
(11.17)
(11.18)
Это уравнение можно привести к каноническому виду путем выделения в левой части полных квадратов.
Фигуру второго порядка, определяемую уравнением (11.12), называют центральной, еслиИ нецентральной, когда
Отметим, что при ортогональном преобразовании переменных определитель матрицы квадратичной формы не меняется, т. е.Так как
(см. (11.16)), то
(11.19)
Пусть уравнение (11.18) определяет центральную фигуру, т. е.Здесь
Возможны два случая:(числаОдного знака), фигура называ
Ется фигурой эллиптического типа;(числаИмеют разные
Знаки), фигура называется фигурой гиперболического типа.
ЕслиТо уравнение (11.18), выделив в его левой части полные квадра
Ты, можно привести к виду
Или
(11.20)
Где
(11.21)
Формулы (11.21) выражают зависимость между координатами при параллельном переносе координатных осей в точку
В случаеУравнение (11.20) приводится к одному из канонических видов
(11.22)
(11.23)
(11.24)
В зависимости от знаковИ
Уравнение (11.22) определяет эллипс, уравнению (11.23) не удовлетворяют координаты ни одной точки плоскости, уравнению (11.24) удовлетворяют координаты одной точки
В случаеУравнение (11.20) приводится к одному из канонических видов
(11.25)
(11.26) (11.27)
В зависимости от знаков
Уравнение (11.25) определяет гиперболу с действительной осью, уравнение (11.26) — гиперболу с действительной осьюУравнение (11.27) — пару пересекающихся прямых, так как оно распадается на два уравнения
Или
Обратимся к нецентральным фигурам, т. е. к случаю когдаВ силу
(11.19) из равенстваСледует, чтоПоследнее равенство означа
Ет, что одно из чиселРавно нулю (оба числаВ нуль обратиться не
Могут, так как это означало бы, что квадратичная форма (11.15) является вырожденной, чего быть не может, поскольку). ЕслиТо уравнение (11.18) можно привести к видуИ записать так:
(11.28)
Осуществим параллельный перенос репераНа вектор
Получим новую систему координат, причемОпределяются формулами (11.21). Уравнение (11.28) приведем к виду
(11.29)
Уравнение (11.29) определяет параболу с осью
Если в уравнении (11.18)То, выделив полный квадрат, его
Можно записать так:
(11.30)
Осуществив параллельный перенос репераНа вектор
Т. е. выполнив преобразованиеПолучим новую систему коор
Динат О, АТ, в которой уравнение (11.30) принимает один из видов:
(11.31)
В зависимости от соотношения знаков чиЬелИПер
Вое из уравнений (11.31) определяет пару параллельных прямых второму уравнению не удовлетворяют координаты ни одной точки плоскости, третье уравнение определяет пару совпавших прямых
Операция перехода от уравнения (11.12) к уравнению (11.18) называется отнесением фигуры к главным осям. Новые оси координат параллельны осям симметрии фигуры. Главными направлениями фигуры, заданной уравнением (11.12), называют направления ортогональных собственных векторов матрицы квадратичной формы, соответствующей этому уравнению.
Из теорем п. 11.6 следует, что существует декартова прямоугольная система координат, в которой уравнение (11.12) принимает канонический вид. Чтобы выбрать эту систему координат, необходимо сделать следующее.
1. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму, соответствующую данному уравнению.
2. С помощью этого преобразования определить главные направления фигуры, т. е. векторы- ортонормированные собственные векторы матрицы указанной квадратичной формы.
3. Найти уравнение фигуры в репере
4. Выделить полные квадраты в полученном уравнении.
5. Совершить параллельный перенос системыНа соответствующий векторИ составить каноническое уравнение фигуры в репере
Пример 11.4. Какую линию на плоскости определяет уравнение
С помощью теории квадратичных форм приведем это уравнение к каноническому виду. Левая часть уравнения — квадратичная форма
Которая с точность до обозначений переменных
) (см. п. 11.6, пример 11.3) приведена к каноническому
ВидуПосредством ортогонального преобразования
Это преобразование данное уравнение переводит в уравнение Полученное уравнение определяет эллипс с полуосями
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Площадь фигуры, заданной уравнением
Рассмотрим сегодня несколько задач на определение площади фигуры, состоящей из всех точек, удовлетворяющих некоторому уравнению. С одной стороны, задача алгебраическая, с другой стороны, будет использована формула определения площади треугольника по координатам его вершин, которая редко используется, поэтому задача не чужда и геометрии.
Задача. Чему равна площадь фигуры на координатной плоскости, состоящей из всех точек, удовлетворяющих уравнению
![Rendered by QuickLaTeX.com \[\mid 9q+9p+108\mid+\mid 119q-49p+252\mid +\mid 35q-7p\mid=93q-33p+360\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-60b0de126498c6d2e4b80a09c1d96dee_l3.png)
С чего начать решение этой задачи? Мы уже догадываемся, что под знаками модуля скрываются уравнения прямых. Поэтому необходимо знать, с каким знаком раскрыть этот модуль. В этом нам поможет правая часть уравнения.
Например, составим вот такое «частичное» уравнение.
![Rendered by QuickLaTeX.com \[\mid 9q\mid+\mid 119q\mid +\mid 35q\mid=93q\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c3bbab93a42eba90943214a72217e92c_l3.png)
Важно выяснить, как были раскрыты модули, чтобы в правой части получилось то, что получилось. Несложным перебором получаем:
![Rendered by QuickLaTeX.com \[9q+119q - 35q=93q\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2676cc770e883d5539b66feae9c6eb16_l3.png)
То есть необходимо снять первый и второй модуль со знаками «+», а последний – с минусом. Тогда получим систему прямых:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ 9q+9p+108=0}}\\{ 119q-49p+252=0 }\\{-35q+7p=0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-84dba1124e0cb846c6e0bf174222fddd_l3.png)
Упрощаем:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ q+p+12=0}}\\{ 17q-7p+36=0 }\\{-5q+p=0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-44644aa5f54b04ade8dffe1b5722da6f_l3.png)
Обе переменные совершенно равноправны, поэтому при построении можем воспользоваться как плоскостью  , так и плоскостью
, так и плоскостью  . Выберем вторую. Тогда нам предстоит построить прямые:
. Выберем вторую. Тогда нам предстоит построить прямые:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{p=-q-12}}\\{ p=\frac{17q}{7}+\frac{36}{7} }\\{p=5q}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5584c1499c0e506c91d18f18dac35df1_l3.png)
Прямые будут пересекаться, координаты точек пересечения можно найти попарным приравниванием ординат. Пересечение первой и второй прямых:
![Rendered by QuickLaTeX.com \[-q-12=\frac{17q}{7}+\frac{36}{7}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c343f6ac55c31d81d877b19fc6316118_l3.png)
![Rendered by QuickLaTeX.com \[-7q-84=17q+36\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d24632c4ac045e19da035ac218a4a3df_l3.png)
![Rendered by QuickLaTeX.com \[24q=-120\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7a6cf41fbb04bfab7d9f8c82e8540df8_l3.png)
![Rendered by QuickLaTeX.com \[q_1=-5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a76846cedba0773f90fe14c53e4bf5b8_l3.png)
![Rendered by QuickLaTeX.com \[p_1=-7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-25bc00b1753bbff90309220472bce8d1_l3.png)
Пересечение первой и третьей прямых:
![Rendered by QuickLaTeX.com \[-q-12=5q\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bb51b6afa8b499987dddf533dff0d888_l3.png)
![Rendered by QuickLaTeX.com \[-6q=12\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6ac73d20940388b9f1a882c0a25a6384_l3.png)
![Rendered by QuickLaTeX.com \[q_2=-2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-663f89e5f3037ee63ea357f9755a9026_l3.png)
![Rendered by QuickLaTeX.com \[p_2=-10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1d7e132a6daa04ced836ffb917705f9b_l3.png)
Пересечение второй и третьей прямых:
![Rendered by QuickLaTeX.com \[5q=\frac{17q}{7}+\frac{36}{7}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5fa3aff982028fe3d2a6d271243b14a2_l3.png)
![Rendered by QuickLaTeX.com \[35q=17q+36\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-28570f02efd69ed319ecba69c60bf9d6_l3.png)
![Rendered by QuickLaTeX.com \[18q=36\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-221d38fc85254bd2408e8a8b6d3ad859_l3.png)
![Rendered by QuickLaTeX.com \[q_3=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f054223222db3615790d5cb55df3dd22_l3.png)
![Rendered by QuickLaTeX.com \[p_3=10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d2b8a09d3dc6f37a6563f17fc659ed16_l3.png)
Теперь, зная координаты трех точек пересечения прямых, можем найти площадь фигуры, а именно, треугольника. Запишем формулу и посчитаем:
![Rendered by QuickLaTeX.com \[S=\frac{1}{2}\left(q_1(p_2-p_3)+q_2(p_3-p_1)+q_3(p_1-p_2)\right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9986eb914af8cf583363d99b1e98e27b_l3.png)
![Rendered by QuickLaTeX.com \[S=\frac{1}{2}\left(-5(-10-10)-2(10-(-7))+2(-7-(-10))\right)= \frac{1}{2}\left(100-34)+6)=36\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2820e83ec8fe3a438c61e669b1899914_l3.png)
Ответ: 36
Для тренировки предлагаю вам решить подобные задачи:
Задача. Чему равна площадь фигуры на координатной плоскости, состоящей из всех точек, удовлетворяющих уравнению
![Rendered by QuickLaTeX.com \[\mid 27m-9n-198\mid+\mid 9m-63n+234\mid +\mid -104m-72n-304\mid=86m+18n+736\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2a7d4e192bb8fd35c58c5284260f6cb7_l3.png)
Ответ: Показать

Задача. Чему равна площадь фигуры на координатной плоскости, состоящей из всех точек, удовлетворяющих уравнению
![Rendered by QuickLaTeX.com \[\mid -72x-99y+270\mid+\mid -85x-30y-550\mid +\mid -18x+10y-2\mid=-5x-59y+818\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ca5ed91771bce610adea68178db40306_l3.png)
Ответ: Показать

easy-physic.ru
ГОСЫ / вопрос 2 / Лекция 7
Лекция №7.
Понятие
алгебраической линии. Различные способы
задания прямой. Общее уравнение прямой.
Геометрический смысл коэффициентов в
общем уравнении прямой. Геометрический
смысл знака трехчлена 
При изучении геометрии на плоскости методом координат в качестве фигур чаще всего рассматриваются линии.
Пример: прямая, окружность.
Всякая линия в системе координат определяется своим уравнением.
Определение7
.1 . Алгебраической
линией называется линия, которая в какой-либо
аффинной системе координат имеет
уравнение:  ,где
,где -многочлен,
-многочлен,  —
переменные, а каждый одночлен в многочлене
—
переменные, а каждый одночлен в многочлене  представлен
:
представлен
:  .
.
Определение 7.2. Степенью
одночлена  ,
где
,
где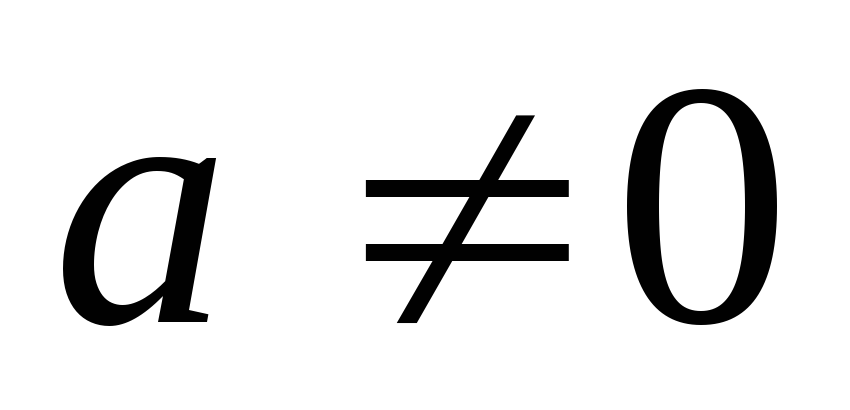 ,
называется число, равное сумме
,
называется число, равное сумме  и
и  .
.
Определение 7.3. Степенью
многочлена 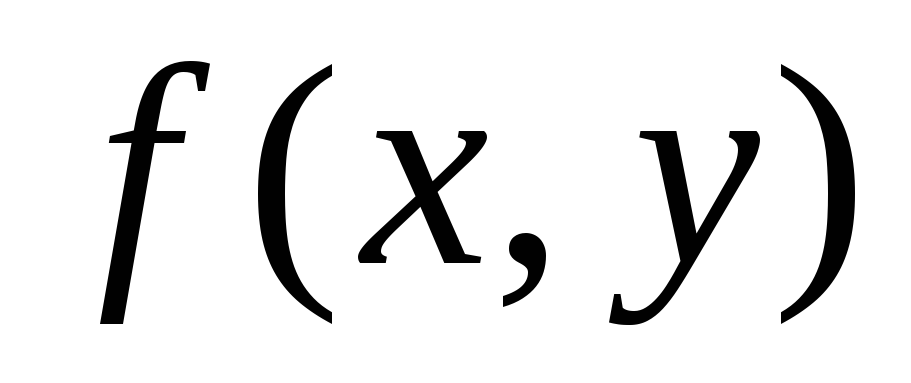 называется
наивысшая степень его членов.
называется
наивысшая степень его членов.
Определение7.4.Степень многочлена называется порядком линии.
 — прямая
первого порядка.
— прямая
первого порядка.
 — окружность второго
порядка.
— окружность второго
порядка.
Теорема 7.5. Понятие алгебраической линии, а также её порядок не зависит от выбора аффинной системы координат.
Доказательство:
1) Пусть
в аффинной системе координат  задана алгебраическая линия уравнением
задана алгебраическая линия уравнением 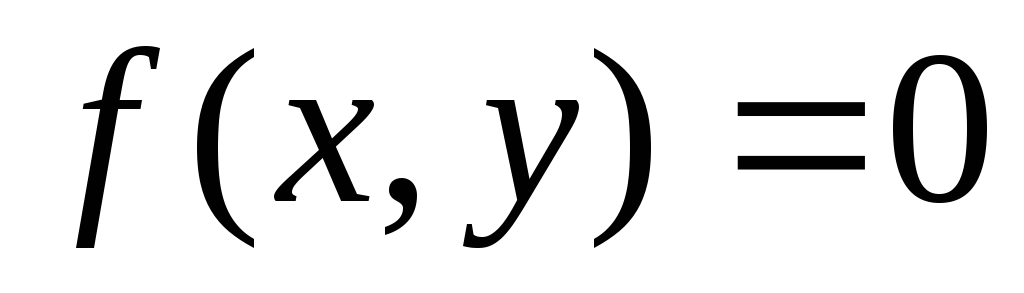 или
или  ;
;
2) Зададим данную
линию в новой системе координат и  ,
используя
формулы
преобразования:
,
используя
формулы
преобразования:
 ,
,  .
.
Подставим
в уравнение алгебраической линии данные
выражения вместо  и
и  :
:
 =
= .
.
Следовательно,  .
.
3) Таким образом,
степень нового многочлена равна степени
старого многочлена, и он представим в
виде: .
.
Различные способы задания прямой
Определение 7.6. Ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой.
Любая прямая имеет бесконечное множество направляющих векторов, причем они коллинеарные.
Положение прямой на плоскости и в пространстве определяется однозначно, если заданы:
1. Направляющий вектор и точка, принадлежащая прямой.
2. Две различные точки этой прямой.
3. Две точки, принадлежащие соответственно осям координат.
Параметрические уравнения прямой.
1) Пусть прямая а содержит точку 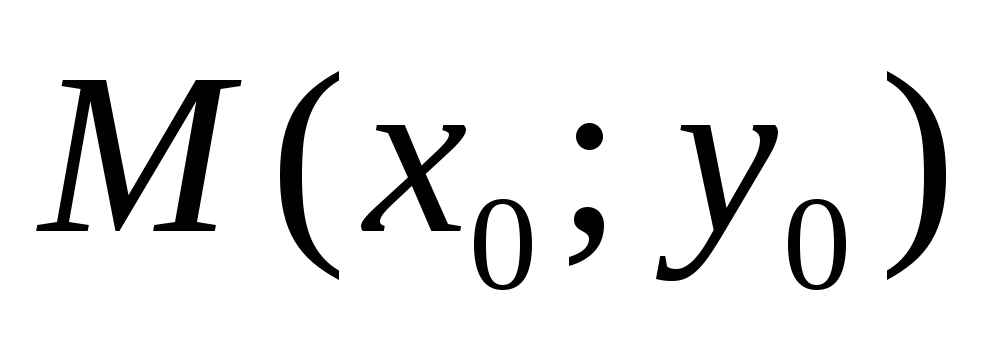 и точку
и точку  ,
тогда вектор
,
тогда вектор 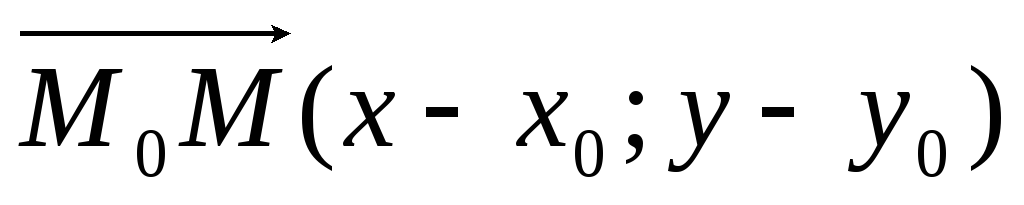 коллинеарен направляющему вектору
коллинеарен направляющему вектору  .
.

Из коллинеарности векторов следует, что:
 или
или 

 — параметрические
уравнения прямой, где
— параметрические
уравнения прямой, где  — параметр.
— параметр.
Смысл этих уравнений
заключается в том, что каково бы не было
действительное число точка
с координатами
точка
с координатами  ,
удовлетворяющая этим уравнениям, всегда
лежит на прямой. И обратно: если точка
с координатами
,
удовлетворяющая этим уравнениям, всегда
лежит на прямой. И обратно: если точка
с координатами  принадлежит прямой, то всегда найдется
такой параметр
принадлежит прямой, то всегда найдется
такой параметр  R
, что
R
, что 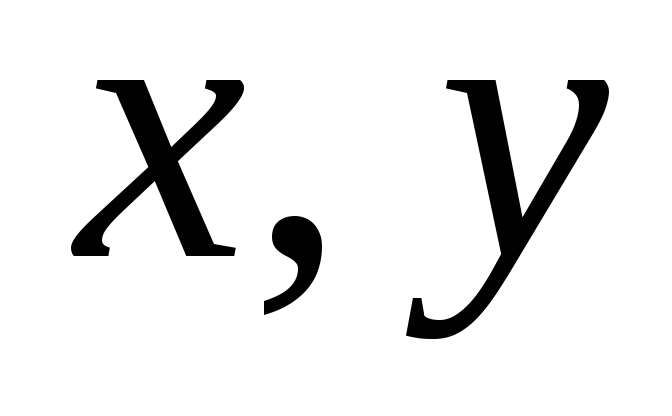 можно выразить через х0,
у0 при помощи параметрических уравнений.
можно выразить через х0,
у0 при помощи параметрических уравнений.
Эти параметрические уравнения можно записать в виде:
 — уравнение
прямой, заданной направляющим вектором
и точкой.
— уравнение
прямой, заданной направляющим вектором
и точкой.
Уравнение прямой с угловым коэффициентом
Этот вид уравнения следует из способа задания прямой направляющим вектором.
Определение
7.7. Угловым
коэффициентом  прямой
называется отношение второй координаты
направляющего вектора прямой к его
первой координате (
прямой
называется отношение второй координаты
направляющего вектора прямой к его
первой координате ( ).
).
У гловой
коэффициент имеет простой геометрический
смысл: если прямая задана в прямоугольной
системе координат
гловой
коэффициент имеет простой геометрический
смысл: если прямая задана в прямоугольной
системе координат  ,
то число
,
то число  позволяет определить направляющий угол
позволяет определить направляющий угол 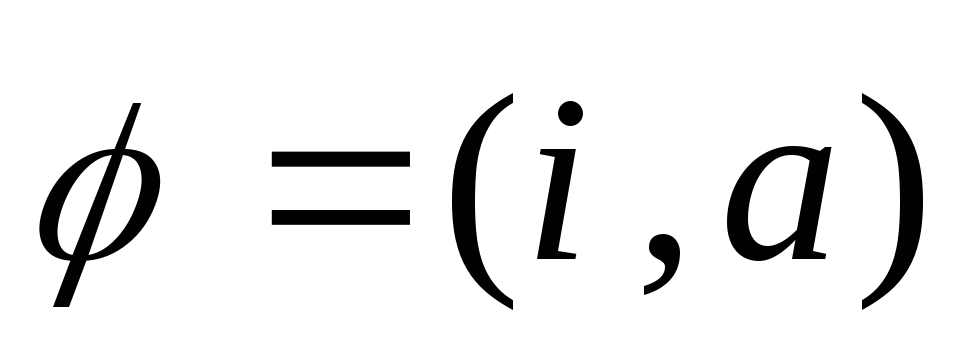 ,
где
,
где  — направляющий вектор прямой.
— направляющий вектор прямой. 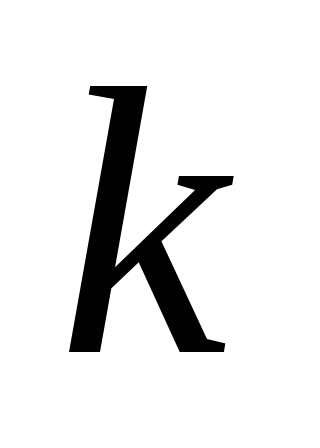 определяет
тангенс угла наклона прямой к оси Ох.
определяет
тангенс угла наклона прямой к оси Ох.
Пусть прямая а содержит точку
 и точку
и точку  .
Тогда имеем, что вектор
.
Тогда имеем, что вектор  –
направляющий вектор прямой а. Координаты вектора
–
направляющий вектор прямой а. Координаты вектора  .
.По определению углового коэффициента имеем, что
 или
или
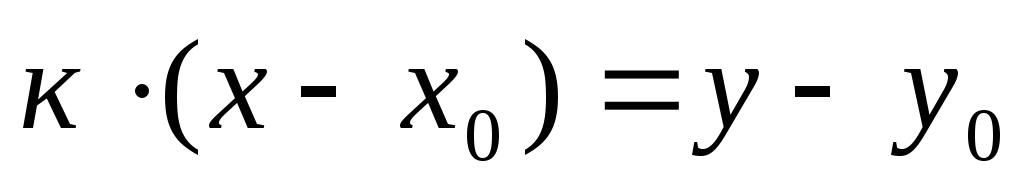 — уравнение
прямой по точке и угловому коэффициенту.
— уравнение
прямой по точке и угловому коэффициенту.
3) Преобразовав,
имеем 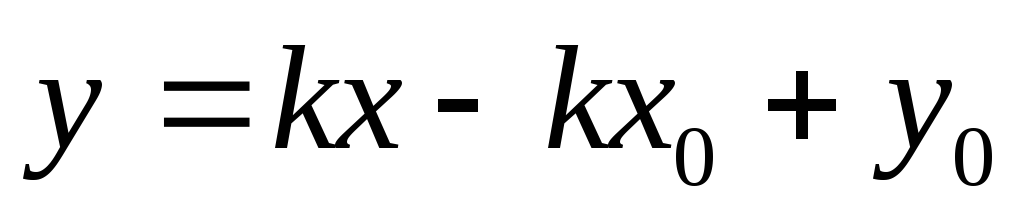 .
Обозначив
.
Обозначив  ,
имеем:
,
имеем:

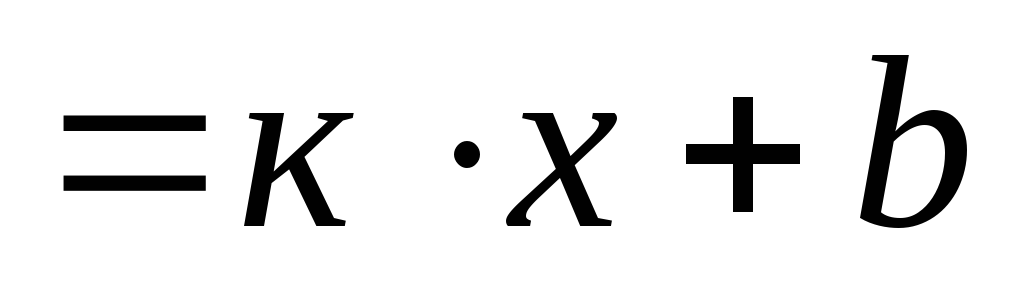 — уравнение
прямой не параллельной оси Oу,
заданной угловым коэффициентом.
— уравнение
прямой не параллельной оси Oу,
заданной угловым коэффициентом.
Эта прямая отсекает
от оси Oy отрезок,
равный 

Уравнение прямой, заданной двумя точками.
П
 усть
на прямой а заданы две точки
усть
на прямой а заданы две точки  и
и  ,
и некоторая точка
,
и некоторая точка  .
. — направляющий
вектор прямой а.
Так как
— направляющий
вектор прямой а.
Так как  ,
то
,
то  .
.Так как
 также является направляющим вектором
прямой а и
также является направляющим вектором
прямой а и  ,
то
,
то  .
.Так как угловой коэффициент прямой определяется однозначно, то
 или
или 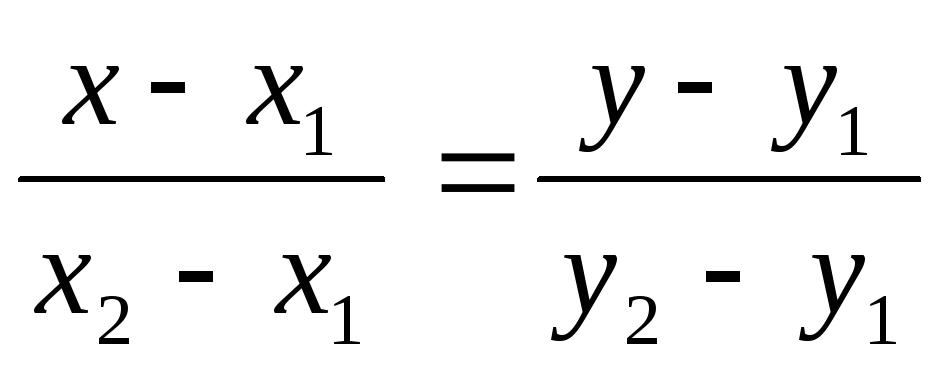 — уравнение
прямой, проходящей через две точки.
— уравнение
прямой, проходящей через две точки.
Уравнение прямой в отрезках.
1) Пусть некоторая прямая a отсекает на осях координат отрезки: на оси Ох —отрезок длиной а, на оси Оу – отрезок длиной b.
2) Определим
координаты точек пересечения прямой а с осями координат:  .
.
3) Напишем уравнение прямой а по двум точкам А и В:
 ;
;
 ;
;
 ;
;

 — уравнение
прямой в отрезках
— уравнение
прямой в отрезках
Общее уравнение прямой.
В аффинной системе
координат прямая задаётся уравнением
первой степени  ,
где
,
где 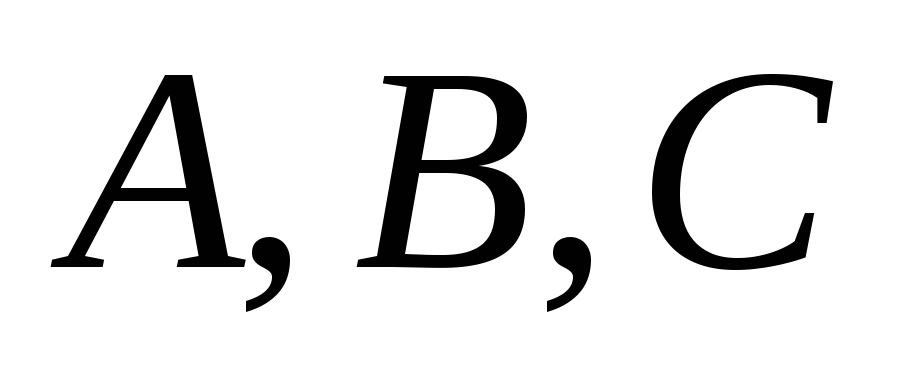 —
действительные числа, причем А и В не равны нулю одновременно,
—
действительные числа, причем А и В не равны нулю одновременно, 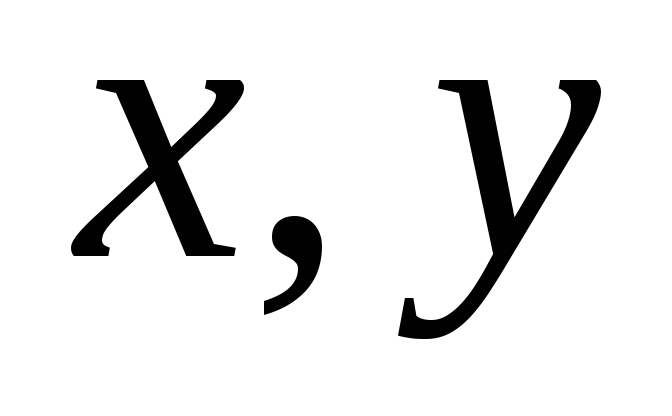 — текущие координаты точки прямой.
— текущие координаты точки прямой.
Теорема 7.8
Линия на плоскости,
заданная в аффинной системе координат
уравнением первой степени: 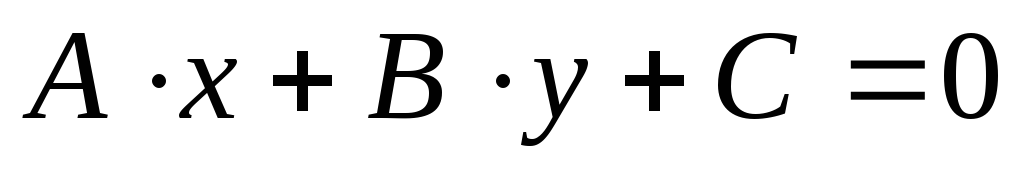 является прямой. Вектор с координатами
является прямой. Вектор с координатами  -правляющий вектор этой прямой.
-правляющий вектор этой прямой.
Доказательство.
1) Пусть некоторая линия φ задана своим уравнением:
φ: (*).
2)
Пусть  принадлежит линии φ,
т.е. её координаты
удовлетворяют
уравнению:
принадлежит линии φ,
т.е. её координаты
удовлетворяют
уравнению:  (**).
(**).
3) Выразим из
уравнения (**) 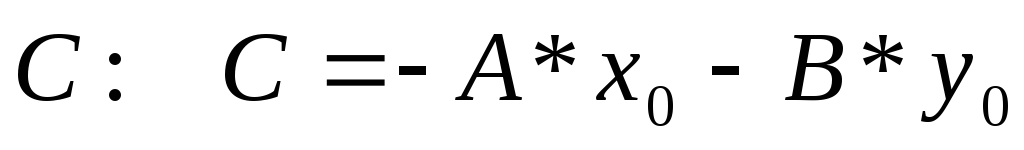 и подставим это значение в равенство
(*), имеем:
и подставим это значение в равенство
(*), имеем:

 (***)- уравнение
прямой, заданной точкой
(***)- уравнение
прямой, заданной точкой  и направляющим вектором с координатами
и направляющим вектором с координатами  .
.
4) Направляющий
вектор действительно имеет координаты  ,
т.к. уравнение (***) можно записать в виде
определителя второго порядка
,
т.к. уравнение (***) можно записать в виде
определителя второго порядка
 — условие
коллинеарности векторов, имеющих
координаты
— условие
коллинеарности векторов, имеющих
координаты  и
и 
4) Значит, линия φ является прямой.
Геометрический смысл коэффициентов в общем уравнении прямой
Геометрический смысл коэффициентов в общем уравнении прямой определяет ее расположение в системе координат.

Прямая, заданная
уравнением  ,
проходит через начало координат. Ее
направляющий вектор имеет координаты
,
проходит через начало координат. Ее
направляющий вектор имеет координаты  .
.

Прямая, заданная
уравнением 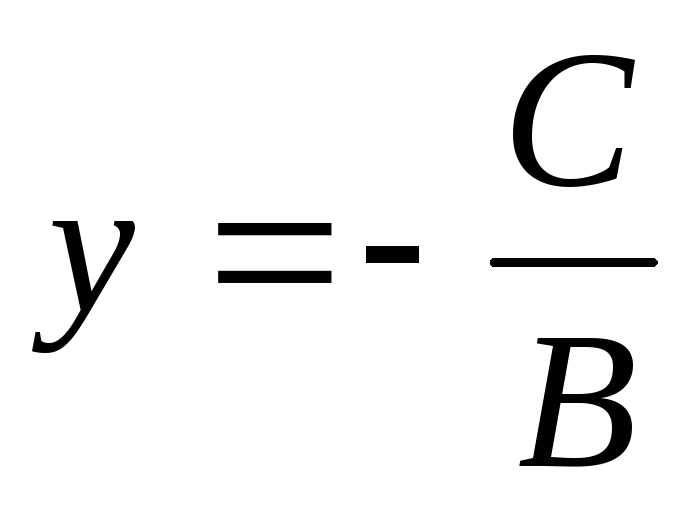 ,
параллельна оси Ох.
Её направляющий вектор имеет координату
,
параллельна оси Ох.
Её направляющий вектор имеет координату .
.

Прямая, заданная
уравнением  ,
параллельна оси Оу.
Её направляющий вектор имеет координату
,
параллельна оси Оу.
Её направляющий вектор имеет координату .
.

Прямая совпадает
с осью Ох. Направляющий
вектор имеет координаты 

Прямая совпадает
с осью Оу. Направляющий вектор имеет координаты 
Геометрический смысл знака трёхчлена.
1) Пусть некоторая
прямая а разбивает
плоскость на две полуплоскости, и задана
она в аффинной системе координат
уравнением 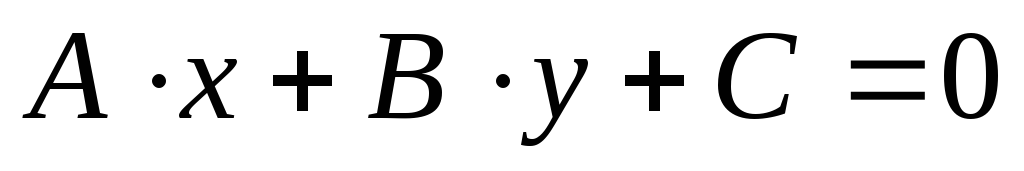
2) Рассмотрим точки:
 ,
т.е.
,
т.е.  .
.
 ,
т.е.
,
т.е. 
3) Рассмотрим 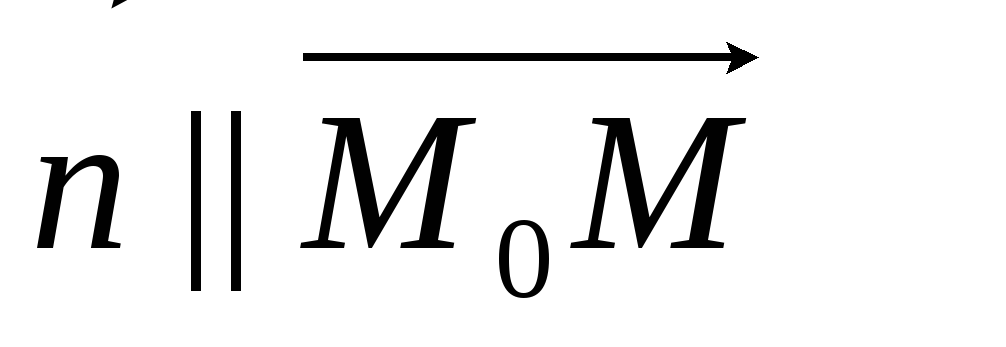 .
Т.к. векторы коллинеарны, то
.
Т.к. векторы коллинеарны, то 
Если
 то
то  и
лежат
в одной полуплоскости относительно
прямой а.
и
лежат
в одной полуплоскости относительно
прямой а.Если
 то
то  и лежат
в разных полуплоскостях относительно
прямой а
и лежат
в разных полуплоскостях относительно
прямой а
4)
Рассмотрим условия, определяющие
расположения векторов 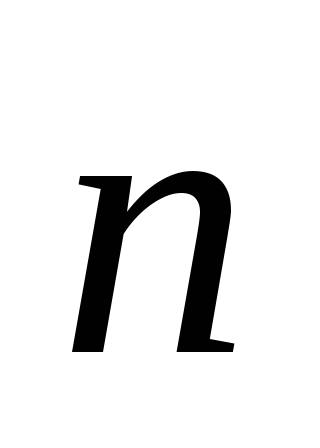 и
и  в одной или различных полуплоскостях:
в одной или различных полуплоскостях:

Эти неравенства позволяют определить, в одной или разных полуплоскостях лежат точки, не принадлежащие прямой.
studfile.net
 или
или 

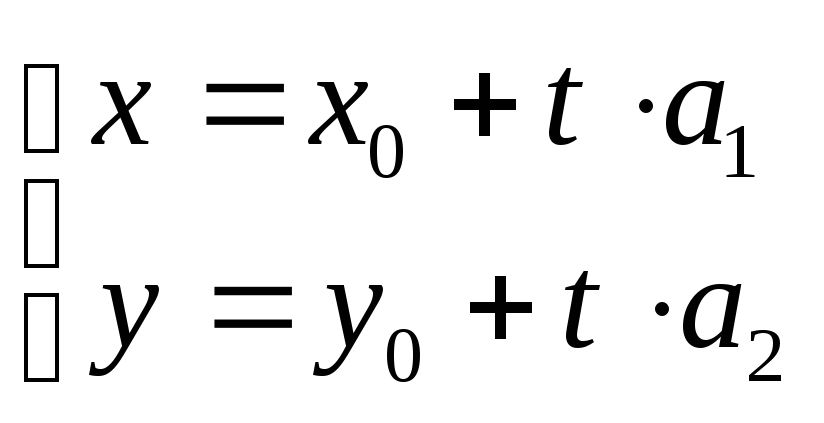 — параметрические
уравнения прямой, где
— параметрические
уравнения прямой, где  — параметр.
— параметр. и точку
и точку  .
Тогда имеем, что вектор
.
Тогда имеем, что вектор 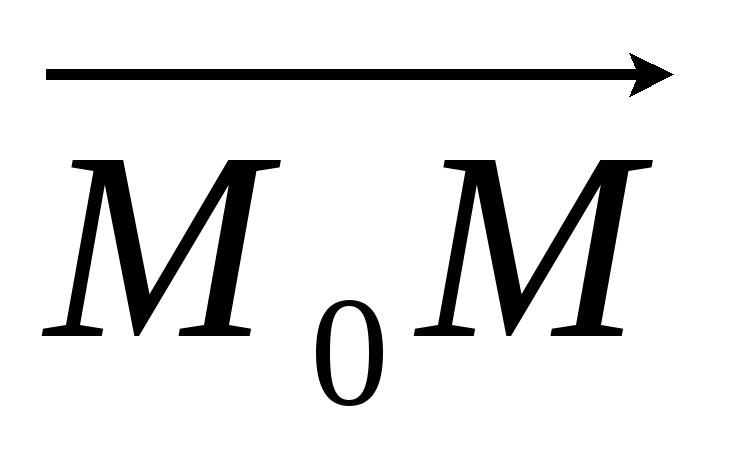 –
направляющий вектор прямой а. Координаты вектора
–
направляющий вектор прямой а. Координаты вектора  .
.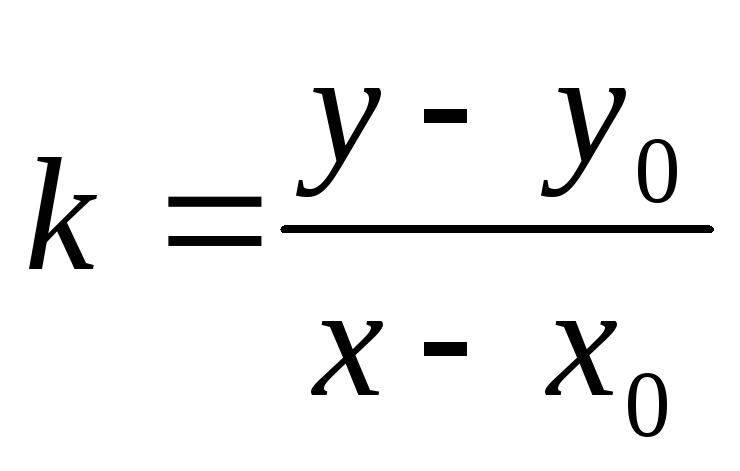 или
или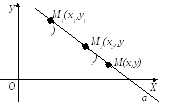 усть
на прямой а заданы две точки
усть
на прямой а заданы две точки  и
и 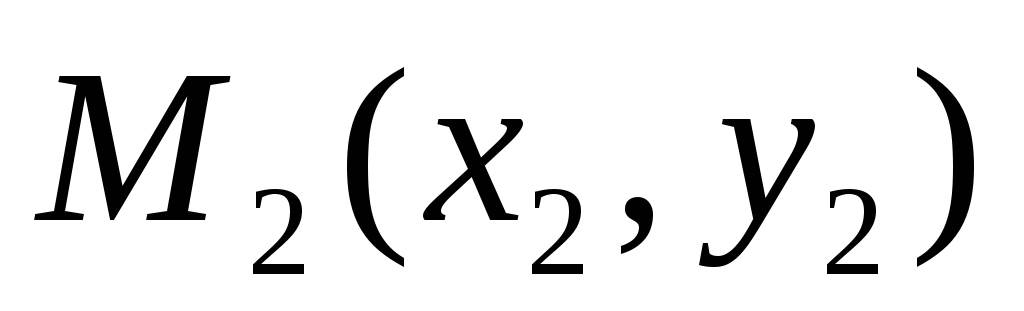 ,
и некоторая точка
,
и некоторая точка  .
. — направляющий
вектор прямой а.
Так как
— направляющий
вектор прямой а.
Так как 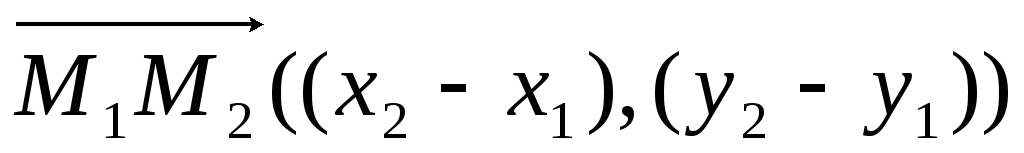 ,
то
,
то  .
. также является направляющим вектором
прямой а и
также является направляющим вектором
прямой а и 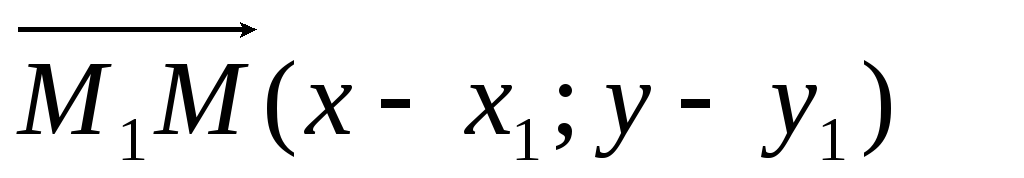 ,
то
,
то  .
.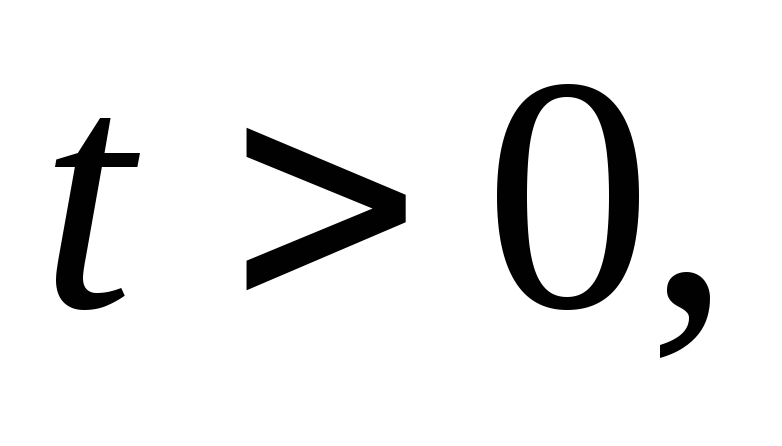 то
то  и
лежат
в одной полуплоскости относительно
прямой а.
и
лежат
в одной полуплоскости относительно
прямой а. то
то  и лежат
в разных полуплоскостях относительно
прямой а
и лежат
в разных полуплоскостях относительно
прямой а